GRA-灰色关联分析(精)
灰色关联度分析

1.灰色关联理论
1982年,华中理工大学邓聚龙教 授首先提出灰色系统的概念,并建立了 灰色系统理论。 灰色系统理论认为,人们对客观 事物的认识具有广泛的灰色性,就是信 息的不完全性和不确定性,因而有客观 事物所形成的是一种灰色系统,即部分 信息已知、部分信息未知的系统。例如: 社会系统、经济系统、生态系统等都可 以看作是灰色系统。
\\
(min) (max) 0i (k ) 0i (k ) (max)
最后分别对各产业与GDP的关联系数求 平均可得: r01= (0.4191+0.3796+0.5808+0.7055+0.3696 +0.2881)/6 =0.4571 同样求出: r02=0.5760, r03=0.7209 r0i称为序列x0和xi(i=1,2,3)的灰 色关联。由于r03˃r02˃ r01,因而第三 产业产值与GDP的关联度最大,其次是 第二产业,第一次去农业。
5.用GRA进行综合评价
灰色关联分析的目的是揭示因素间 关系的强弱,其操作对象是因素的时间 序列,最终的结果表现为通过关联度对 各比较序列做出排列。综合评价的对象 也可以看作是时间序列(每个被评价事 物对应的各项指标值),并且往往需要 对这些时间序列做出排序,因而也可以 借助灰色关联分心来进行。
01 (1) 02 (1) ... 0 n (1) (2) (2) ... (2) 01 02 0n ... ... ... 01 ( N ) 02 ( N ) ... 0 n ( N ) N n 其中 0i (k ) x0 (k ) xi (k ) (05式) i 1,2,...n; k 1,2,..., N 绝对差矩阵中最大数和 最小数就是最大差和最 小差: max 0i (k ) (max)( 式) 06
灰色关联分析法与TOPSIS评价法

3.对指标数据进行无量纲化 无量纲化后的数据序列形成如下矩阵:
x0 1 x0 2 X 0 , X 1 , , X n x m 0 x1 2 x1 1 x n 1 x n 2 x n m
与
maxmax x0 (k ) xi (k )
i 1 k 1
n
m
6.计算关联系数 由(12-5)式,分别计算每个比较序列 与参考序列对应元素的关联系数.
i (k )
min min x 0 (k ) xi (k ) max max x0 ( k ) xi ( k )
03 (t )
0.8687 0.7257 0.5213 0.7338 1.000 0.4758
最后分别对各产业与GDP的关联系数序列求算术 平均可得
1 r01 (0.4191 0.3796 0.5808 0.7055 6 0.3696 0.2881) 0.4571 1 r02 (0.6067 0.5178 0.4903 0.8761 6 0.6141 0.3510) 0.5760 1 r03 (0.8687 0.7257 0.5213 0.7338 6 1.000 0.4758) 0.7209
两序列变化的态势是表现在其对应点的间距上.如果 各对应点间距均较小,则两序列变化态势的一致性强,否 则,一致性弱.分别计算各产业产值与GDP在对应期的间 距(绝对差值),结果见表所示. 年份t
x0 (t ) x1 (t )
0.1044 0.1231 0.0547 0.0319 0.1284 0.1857
一个自然的想法就是分别将三次产业产值的时间序列 与GDP的时间序列进行比较,为了能够比较,先对各序列进 行无量纲化,这里采用均值化法.各序列的均值分别为: 2716,461.5,1228.83,1025.67,上表中每列数据除以其均值可 得均值化序列(如表所示) 年份t GDP x0(t) 一产业 x1(t) 二产业 x2(t) 三产业 x3(t) 2000 0.7320 0.8364 0.6828 0.7440 2001 0.7588 0.8819 0.6885 0.7878 2002 0.8597 0.9144 0.7812 0.9291 2003 1.0125 1.0444 1.0237 0.9847 2004 1.2356 1.1073 1.2833 1.2363 2005 1.4013 1.2156 1.5405 1.3182
灰色关联分析详解+结果解读

灰色关联分析1、作用对于两个系统之间的因素,其随时间或不同对象而变化的关联性大小的量度,称为关联度。
在系统发展过程中,若两个因素变化的趋势具有一致性,即同步变化程度较高,即可谓二者关联程度较高;反之,则较低。
因此,灰色关联分析是指对一个系统发展变化态势的定量描述和比较的方法,其基本思想是通过确定参考数据列和若干个比较数据列的几何形状相似程度来判断其联系是否紧密,它反映了曲线间的关联程度。
2、输入输出描述输入:特征序列为至少两项或以上的定量变量,母序列(关联对象)为 1 项定量变量。
输出:反应考核指标与母序列的关联程度。
3、案例示例案例:分析 09-18 年内,影院数量,观影人数,票价、电影上线数量这些因素对全年电影票房的影响。
其中电影票房是母序列,影院数量,观影人数,票价、电影上线数量是特征序列。
4、案例数据灰色关联分析案例数据5、案例操作Step1:新建分析;Step2:上传数据;Step3:选择对应数据打开后进行预览,确认无误后点击开始分析;step4:选择【灰色关联分析】;step5:查看对应的数据数据格式,【灰色关联分析】要求特征序列为定量变量,且至少有一项;要求母序列为定量变量,且只有一项。
step6:设置量纲处理方式(包括初值化、均值化、无处理)、分辨系数(ρ越小,分辨力越大,一般ρ的取值区间为 ( 0 ,1 ),具体取值可视情况而定。
当ρ≤ 0.5463 时,分辨力最好,通常取ρ = 0.5 )step7:点击【开始分析】,完成全部操作。
6、输出结果分析输出结果 1:灰色关联系数图表说明:关联系数代表着该子序列与母序列对应维度上的关联程度值(数字越大,代表关联性越强)。
输出结果 2:关联系数图分析:输出结果 1 和输出结果 2 是一样的,输出结果 1 用了表格形式来呈现关联系数,输出结果 2 用了图表形式来呈现关联系数。
图表很直观地展现了,大多数年份的银幕数量和电影上线数量对票房影响更大。
灰色关联分析计算实例

80.52 54.22
0.361
3.7 2.0213
50.974 50.4325 40.8828
.
2.矩阵无量纲化(初值化): X=Xij´/ Xi1´(i=1,2,3,4,5,6; j=2,3,4,5)
1
0.9496 0.8005
1 (X)= 1
0.9249 0.7948 1.0113 0.1006
X0,X1,,Xnxx001 2 x0m
x11 x12
x1m
xxnn1 2
xnm
.
常用的无量纲化方法有均值化法(见(12-3)
式)、初值化法(见(12-4)式)和 x x 变
换等。
s
xi
k
xik
1 m
mk1
xi
k
xi
k
xik xi1
i 0,1,, n;k1, 2,, m.
(123) (124)
表2 灾害直接经济损失及各相关影响因素之间的关联度
影响因素 农作物成灾面积 地震灾害损失 海洋灾害损失 森林火灾损失 地质灾害损失
关联度ri
0.9875
0.9131
0.9668
0.7103
0.9786
.
由表2的结果可以看出,灾害经济损失的各相 关影响因素对灾害直接经济损失影响的关联度 大小的顺序为: 农作物成灾面积>地质灾害损失>海洋灾害损失> 地震灾害损失>森林火灾损失 可以说明对灾害直接经济损失影响最大的是 农作物成灾面积、地质灾害损失和海洋灾害损 失,其次为地震灾害损失,森林火灾损失对灾 害直接经济损失影响程度较小。
5.求最值:
nm
minmin i1 k1
x0
灰色关联分析

灰色关联分析灰色关联分析(Grey Relational Analysis, GRA)什么是灰色关联分析灰色关联分析是指对一个系统发展变化态势的定量描述和比较的方法,其基本思想是通过确定参考数据列和若干个比较数据列的几何形状相似程度来判断其联系是否紧密,它反映了曲线间的关联程度[1]。
灰色系统理论是由著名学者邓聚龙教授首创的一种系统科学理论(Grey Theory),其中的灰色关联分析是根据各因素变化曲线几何形状的相似程度,来判断因素之间关联程度的方法。
此方法通过对动态过程发展态势的量化分析,完成对系统内时间序列有关统计数据几何关系的比较,求出参考数列与各比较数列之间的灰色关联度。
与参考数列关联度越大的比较数列,其发展方向和速率与参考数列越接近,与参考数列的关系越紧密。
灰色关联分析方法要求样本容量可以少到4个,对数据无规律同样适用,不会出现量化结果与定性分析结果不符的情况。
其基本思想是将评价指标原始观测数进行无量纲化处理,计算关联系数、关联度以及根据关联度的大小对待评指标进行排序。
灰色关联度的应用涉及社会科学和自然科学的各个领域,尤其在社会经济领域,如国民经济各部门投资收益、区域经济优势分析、产业结构调整等方面,都取得较好的应用效果。
[2]关联度有绝对关联度和相对关联度之分,绝对关联度采用初始点零化法进行初值化处理,当分析的因素差异较大时,由于变量间的量纲不一致,往往影响分析,难以得出合理的结果。
而相对关联度用相对量进行分析,计算结果仅与序列相对于初始点的变化速率有关,与各观测数据大小无关,这在一定程度上弥补了绝对关联度的缺陷。
[2]灰色关联分析的步骤[2]灰色关联分析的具体计算步骤如下:第一步:确定分析数列。
确定反映系统行为特征的参考数列和影响系统行为的比较数列。
反映系统行为特征的数据序列,称为参考数列。
影响系统行为的因素组成的数据序列,称比较数列。
设参考数列(又称母序列)为Y={Y(k) | k = 1,2,Λ,n};比较数列(又称子序列)X i={X i(k)| k = 1,2,Λ,n},i = 1,2,Λ,m。
(整理)灰色关联度分析法
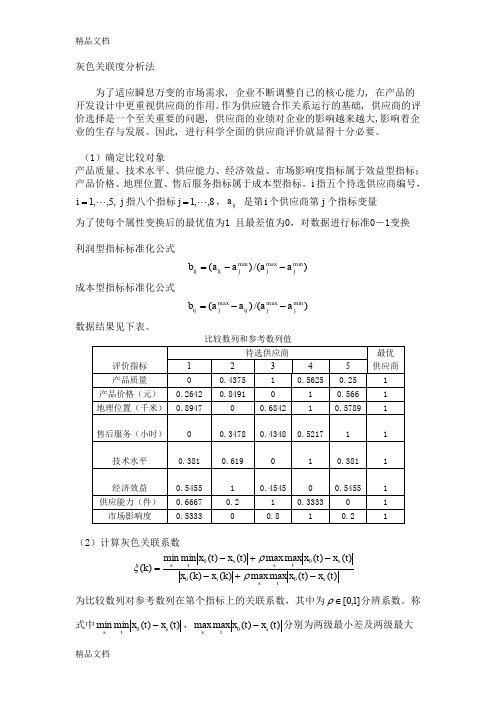
灰色关联度分析法为了适应瞬息万变的市场需求, 企业不断调整自己的核心能力, 在产品的开发设计中更重视供应商的作用。
作为供应链合作关系运行的基础, 供应商的评价选择是一个至关重要的问题, 供应商的业绩对企业的影响越来越大,影响着企业的生存与发展。
因此, 进行科学全面的供应商评价就显得十分必要。
(1)确定比较对象产品质量、技术水平、供应能力、经济效益、市场影响度指标属于效益型指标;产品价格、地理位置、售后服务指标属于成本型指标。
i 指五个待选供应商编号,,5,,1 =i j 指八个指标8,,1j =,ij a 是第i 个供应商第j 个指标变量为了使每个属性变换后的最优值为1 且最差值为0,对数据进行标准0-1变换利润型指标标准化公式)/()(min maxmin j j j ij ij a a a a b --=成本型指标标准化公式)/()(min max max j j ij j ij a a a a b --=数据结果见下表。
(2)计算灰色关联系数)()(max max )()()()(max max )()(min min )(0000t x t x k x k x t x t x t x t x k s tsi s ts s ts -+--+-=ρρξ为比较数列对参考数列在第个指标上的关联系数,其中为]1,0[∈ρ分辨系数。
称式中)()(min min 0t x t x s ts-、)()(max max 0t x t x s ts-分别为两级最小差及两级最大差。
一般来讲,分辨系数ρ越大,分辨率越大;ρ越小,分辨率越小。
在这里ρ取0.5。
(3)计算灰色加权关联度 灰色加权关联度的计算公式为∑==nk i i k w r 1)(ξ这里i r 为第i 个评价对象对理想对象的灰色加权关联度。
关联系数和关联度值(4)评价分析根据灰色加权关联度的大小,对各评价对象进行排序,可建立评价对象的关联序,关联度越大其评价结果越好。
灰色关联分析法与TOPSIS评价法

0 i ( t ) 称为序列xi和序列x0在第t期的灰色关联系 数(或简称为关联系数).
由(6.1)式可以看出, 取 值的大小可以控制 (max)
对数据转化的影响, 取较小的值,可以提高关联系
数间差异的显著性,因而 称为 分辨系数.
利用(6.1)对表6-3中绝对差值 进0 i行( t规) 范化,取
结0.果4,见表6-4,以
计0算1(2为00例0):
( m i n ) 0 .0 0 0 6 , ( m a x ) 0 .1 8 5 7
0 1 (2 0 0 0 ) 0 0 ..0 1 0 0 0 4 6 4 0 0 ..4 4 0 0 ..1 1 8 8 5 5 7 7 0 .4 1 9 1
18987529
27875738
39796647
46888436
58669838
68957648
3.确定参考数据列:
{ x 0 } { 9 , 9 , 9 , 9 , 8 , 9 , 9 }
4.计算 x0(k)xi(k) , 见下表
编号 专业 外语 教学 科研 论文 著作 出勤 量
1
1
0
1
2
参考数据列应该是一个理想的比较标准, 可以以各指标的最优值 (或最劣值)构 成参考数据列,也可根据评价目的选择 其它参照值.记作
X 0 x 0 ( 1 ) , x 0 2 , , x 0 m
3.对指标数据进行无量纲化 无量纲化后的数据序列形成如下矩阵:
X0,X1, ,Xnxx001 2 x0m
年份t GDP x0(t) 一产业 x1(t) 二产业 x2(t) 三产业 x3(t)
灰色关联分析方法

灰色关联分析方法是我国著名学者邓聚龙教授于1982年创立的灰色系统理论中的一种重要方法,它是分析不同数据项之间相互影响、相互依赖的关系.其本质是指在系统动态发展过程中,根据子系统(因素)之间发展趋势的相似或相异程度,作为衡量子系统(因素)间关联程度的一种方法.若两个子系统(因素)变化的趋势具有一致性,即同步变化程度较高,则可以认为两者关联程度较大;反之,认为两者关联程度较小.对于某一个多属性决策问题,设12{,,,}m X x x x = 为方案集,12{,,,C c c =}n c 为属性集,Tn w w w w },,,{21 =为属性的权重向量,且0≥j w ,11=∑=nj j w .方案i x 在属性j c 下的属性值为ij a ,从而得到决策矩阵为:111212122212n n m m mn a a a a a a A a a a ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦. 灰色关联分析方法的步骤可归纳为:第一步:将决策矩阵进行规范化处理.对于多属性决策问题,最常见的属性类型一般分为效益型和成本型两种,其中效益型属性是指属性值越大越好的属性,成本型属性是指属性值越小越好的属性.由于不同的评价属性通常具有不同的物理量纲和量纲单位,且不同量纲和量纲单位会带来不可公度性.为了消除不同物理量纲和量纲单位对决策结果的影响,可按如下规范化公式进行处理,将决策矩阵()ij m nA a ⨯=转化为规范化决策矩阵()ijm nR r ⨯=.对于效益型属性,有:min max min ij ijiij ij ijiia a r a a -=-, (3.1)对于成本型属性,有:max max min ij ijiij ij ijiia a r a a -=-. (3.2)第二步:确定参考数列.确定参考数列的原则是:参考数列中的元素应由各备选方案规范化后的属性值的最优解组成.即:{}001020, ,, .n R r r r = (3.3)这里,0max , 1,2,,.j ij jr x j n ==第三步:计算参考数列与属性值数列对应元素之差的绝对值(即计算参考数列与属性值数列对应元素之间的Hamming 距离)ij ∆,即0(,)i j j i j d r r ∆=,1,2,,; 1,2,,.i m j n == (3.4) 第四步:求最大差max ∆和最小差min ∆.其中:max ,max ij i j∆=∆, (3.5)min ,min ij i j∆=∆. (3.6)第五步:计算各备选方案属性值数列与参考数列之间的关联系数矩阵()ij m n ξ⨯.其中关联系数公式为:min maxmaxij ij ρξρ∆+∆=∆+∆,1,2,,; 1,2,,.i m j n == (3.7)式中,ij ξ是比较数列与参考数列在第j 个评价指标上的相对差值.[0,1]ρ∈称为分辨系数,ρ越小,分辨能力越大.通常情况下取ρ=0.5.第六步:计算各备选方案属性值数列与参考数列之间的灰色关联度i γ.其中:1ni ij j i w γξ==⋅∑,1,2,,.i m = (3.8)第七步:依据灰色关联度i γ(1,2,,)i m = 值的大小对各备选方案进行排序并且择优.关联度值越大,对应的方案就越优.Multiple attribute decision making 多属性决策 Grey relational analysis (GRA) 灰色关联分析 Intuitionistic fuzzy numbers 直觉模糊数Incomplete weight information 不完全权重信息 Degree of grey relation 灰色关联度 positive-ideal solution (PIS) 正理想方案 negative-ideal solution (NIS) 负理想方案 membership degree 隶属度non-membership degree 非隶属度 degree of indeterminacy 不确定度 Hamming distance 海明距离 weighting vector 权重向量grey relational coefficient 灰色关联系数。
灰色关联分析方法

灰色关联分析方法灰色关联分析方法(Grey Relational Analysis,GRA)是一种多指标决策方法,它用于研究因素之间的关联程度。
与传统的关联分析方法相比,灰色关联分析方法具有较强的适用性和灵活性。
它可以用于分析多个指标之间的关联程度,对于复杂决策问题具有较强的应用能力。
灰色关联分析方法的基本思想是将系统的各个指标转化为灰色数列,再利用灰色关联度来评估指标之间的关联程度。
该方法可以对多个指标进行综合评价,找出各个指标之间的关联程度,并根据关联程度来进行排序和决策。
灰色关联分析方法的具体步骤如下:1. 数据预处理:将原始数据进行标准化处理,以确保各指标在同一数量级上进行比较。
2. 构建灰色数列:将标准化后的数据转化为灰色数列,通过建立灰色微分方程来描述数据序列的发展趋势。
3. 确定关联度测度:根据灰色数列的特点,选择适当的关联度测度方法来计算指标之间的关联程度。
4. 计算关联度:根据所选择的关联度测度方法,计算每个指标与其他指标之间的关联度。
5. 排序和决策:根据计算得到的关联度值进行排序,并作出相应的决策。
灰色关联分析方法的优点有以下几个方面:1. 适用性广泛:灰色关联分析方法适用于各种类型的指标数据,包括定量指标和定性指标。
2. 考虑了指标之间的时序关系:灰色关联分析方法考虑了指标数据的时序性,能够更好地反映指标之间的演变趋势。
3. 简单易行:灰色关联分析方法不需要过多的统计方法和复杂的计算过程,容易被理解和操作。
4. 提供了多指标综合评价的能力:灰色关联分析方法可以将多个指标之间的关联程度综合考虑,对于决策问题的综合评价有着较好的效果。
然而,灰色关联分析方法也存在一些限制和局限性:1. 灵敏度不高:由于灰色关联分析方法只考虑了指标之间的线性关联程度,对于非线性关系的刻画较为困难,灵敏度较低。
2. 依赖于初始数据:灰色关联分析方法对初始数据的选取较为敏感,不同的初始数据可能导致不同的关联度结果。
灰色关联度

灰色关联度分析灰色关联分析(Grey Correlation Analysis )是一种分析多因素之间关系的方法,由邓聚龙教授创立,通过不同样本之间关联度分析,对各因素进行排序,对各因素之间关系进行描述的一种统计方法。
我们假设以及知道某一个指标可能是与其他的某几个因素相关的,那么我们想知道这个指标与其他哪个因素相对来说更相关,与哪个因素相对关系弱一点,依次类推,把这些因素排个序,得到一个分析结果,我们就可以知道我们关注的这个指标,与因素中的哪些更相关。
1、确定母数列(参考序列)和子数列(比较序列)设参考数列0X ,比较数列12,,,n X X X ,由于各因素之间的单位等各不相同,可能会造成有的数大有的数很小。
但是这并不是由于它们内禀的性质决定的,而只是由于量纲不同导致的,因此我们需要对它们进行无量纲化。
因此,为了使得不同因素能够进行比较,且保证结果的误差,需要对数据进行无量纲化处理。
GRA 常用的方法是初值化,即把这一个序列的数据统一除以最开始的值,由于同一个因素的序列的量级差别不大,所以通0,1,2,,4.2''0()|()()|(1,2,3,4)j j k X k X k j ∆=-= max 0min 0max max |()()|min min |()()|i i k i i k X k X k X k X k ∆=-∆=- 3、求关联度minmax max ()()j j k k ρζρ∆+∆=∆+∆ 其中,一般调节系数ρ的取值区间为()10,,通常取0.5ρ=。
4、作关联度 4、关联度排序,如果21r r <,则参考数列0x 与比较数列1x 更相似,最终的目的也是为了计算变量之间的关联程度。
GRA 算法本质上来讲就是提供了一种度量两个向量之间距离的方法,对于有时间性的因子,向量可以看成一条时间曲线,而GRA 算法就是度量两条曲线的形态和走势是否相近。
为了避免其他干扰,凸出形态特征的影响,GRA 先做了归一化,将所有向量矫正到同一个尺度和位置,然后计算每个点的距离。
灰色关联法评价果蔬品质及其数据处理程序

灰色关联法评价果蔬品质及其数据处理程序摘要:随着经济的发展,消费者对果蔬品质的要求也越来越高。
然而,传统物理化学检测方法无法准确地反映果蔬品质。
例如,有些品质指标很难采集和准确测定。
为了解决这一问题,灰色关联法(GRA)及其数据处理程序成为果蔬品质评价的一个替代方法。
本文旨在详细介绍GRA及其数据处理程序,以及它们在果蔬品质评价中的应用。
首先,将对灰色关联分析方法进行介绍,以及它与传统物理化学检测方法的比较;其次,将会详细讨论GRA的算法,以及其数据处理程序;最后,将讨论GRA在果蔬品质评价中的应用,以及未来该方法的发展前景。
1、引言随着经济的发展,消费者对果蔬品质的要求也越来越高,以保证果蔬质量是一个非常重要的课题。
传统物理化学检测方法无法准确地反映果蔬品质,有些品质指标很难采集和准确测定,例如口感、气味等。
为了解决这一问题,灰色关联法(GRA)及其数据处理程序成为果蔬品质评价的一个替代方法,它可以从信息有限的数据中提取有效信息和特征,并评价果蔬品质,从而使果蔬品质检测更加准确、可靠。
2、灰色关联分析方法GRA是由中国科学家张维平博士发明的。
它是一种基于灰色理论的非线性数据分析方法,将数据非线性映射到灰度空间,从而对数据进行分析和处理。
GRA结合了统计学、数学和计算机科学等学科,可以从信息有限的数据中提取有效信息和特征。
GRA与传统物理化学检测方法相比,具有计算快速、无需实验样本制备、数据处理简捷等优点,可以有效提高实验效率,产生准确可靠的结果。
想要利用GRA评价果蔬品质,需要准备足够的数据,如营养成分、色泽、气味、口感等指标。
3、灰色关联分析算法GRA的基本原理是将信息有限的数据非线性映射到灰度空间,以解决线性数据实际应用问题。
GRA首先利用灰色系统理论建立数学模型,分析和处理数据,从而得出灰色关联系数,确定果蔬品质等级。
GRA的灰色关联系数计算模型如下:GRA =Σ(Xj - Xj-1) / (Xj + Xj-1)其中,Xj、Xj-1别表示相邻的两组样本的统计描述统计值,ΣΣ表示多组数据求和。
灰色关联分析(GreyRelationAnalysis,GRA)中国经济社会发展指标

灰色关联分析(GreyRelationAnalysis,GRA)中国经济社会发展指标原文链接:/?p=16881灰色关联分析包括两个重要功能。
第一项功能:灰色关联度,与correlation系数相似,如果要评估某些单位,在使用此功能之前转置数据。
第二个功能:灰色聚类,如层次聚类。
灰色关联度灰色关联度有两种用法。
该算法用于测量两个变量的相似性,就像\`cor\`一样。
如果要评估某些单位,可以转置数据集。
*一种是检查两个变量的相关性,数据类型如下:| 参考| v1 | v2 | v3 || ----------- |||| ---- | ---- || 1.2 | 1.8 | 0.9 | 8.4 || 0.11 | 0.3 | 0.5 | 0.2 || 1.3 | 0.7 | 0.12 | 0.98 || 1.9 | 1.09 | 2.8 | 0.99 |reference:参考变量,reference和v1之间的灰色关联度...近似地测量reference和v1的相似度。
*另一个是评估某些单位的好坏。
| 单位| v1 | v2 | v3 || ----------- |||| ---- | ---- || 江苏| 1.8 | 0.9 | 8.4 || 浙江| 0.3 | 0.5 | 0.2 || 安徽 0.7 | 0.12 | 0.98 || 福建| 1.09 | 2.8 | 0.99 |示例##生成数据## 异常控制 #if (any(is.na(df))) stop("'df' have NA" )if (distingCoeff<0 | distingCoeff>1) stop("'distingCoeff' mus t be in range of \[0,1\]" )diff = X #设置差学列矩阵空间for (i inmx = max(diff)#计算关联系数#relations = (mi+distingCoeff\*mx) / (diff + distingCoeff\*mx)#计算关联度## 暂时简单处理, 等权relDegree = rep(NA, nc)for (i in1:nc) {relDegree\[i\] = mean(relations\[,i\]) # 等权}#排序: 按关联度大到小#X_order = X\[order(relDegree,relDes = rep(NA, nc) #分配空间关联关系描述(说明谁和谁的关联度)X\_names = names(X\_onames(relationalDegree) = relDesif (cluster) {greyRelDegree = GRA(economyC# 得到差异率矩阵 #grey_diff = matrix(0grey_diff\[i,j\] = abs(rel#得到距离矩阵#grey_dist = matrix(0, nrowiff\[i,j\]+grey_diff\[j,i\]}}# 得到灰色相关系数矩阵 #grey\_dist\_max = max(grey_dist)grey_correl = matrix(0, nrow = nc, ncol = nc)for (i in1:nc) {for (j in1:nc) {grey\_correl\[i,j\] = 1 - grey\_dist\[i,j\] / grey\_dist\_max}}d = as.dist(1-grey_correl) # 得到无对角线的下三角矩阵(数值意义反向了, 值越小表示越相关 )# 主对角线其实表示了各个对象的相近程度, 画图的时候, 相近的对象放在一起hc = hclust(d, method = clusterMethod) # 系统聚类(分层聚类)函数, single: 单一连接(最短距离法/最近邻)# hc$height, 是上面矩阵的对角元素升序# hc$order, 层次树图上横轴个体序号plot(hc,hang=-1)#hang: 设置标签悬挂位置}#输出#if (cluster) {lst = list(relationalDegree=relationalDegree,return(lst)}## 生成数据rownames(economyCompare) = c("indGV", "indVA", "profit" , "incomeTax")## 灰色关联度greyRelDegree = greya(economyCompare)greyRelDegree灰色关联度。
灰色关联度分析 简介

4、计算 绝对值差
5、确定 极大差值与 极小差值
灰色关联综合评价
6、计算关 联系数
7、确计算 关联序
8、计算综 合评价值
i
()
min i
min x k
x0 (k)
0(k)
xi (k)
max max
i
k
x0 (k)
xi
xi (k)
max max
i
k
x0 (k)
xi (k )
灰色关联分析与回归分析区别
问题:对该地区总收入影响较直接的是养猪业还是养 兔业?
灰色关联综合评价
1、收集 分析数据
2、确定 参考数据列
3、无量纲化 处理
X1, X 2
,
X n
x1 1 x1 2
x1 m
x2 1 x2 2
x2 m
(k)
(12 5)
k 1, , m
r0i
1 m
m
i (k )
k 1
r0i
1 m
m
Wk
k 1
i (k)
(k=1,
式中Wk为各指标权重。
, m)
应用
例1:利用灰色关联分析对6位教师工作 状况进行综合分析
1.分析指标包括:专业素质、外语水平 、教学工作量、科研成果、论文、著作 与出勤.
应用
7.分别计算每个人各指标关联系数的均
值(关联序):
r01
0.778 1.000
0.778
0.636 7
python实现灰色关联分析(GRA)——以红酒质量指标为例
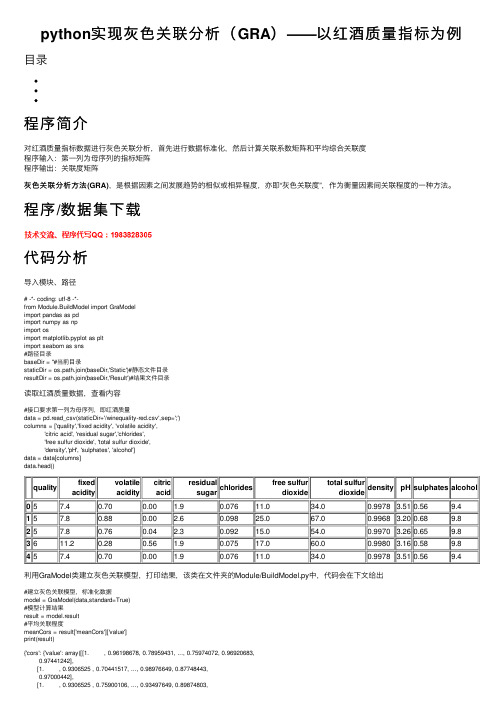
python实现灰⾊关联分析(GRA)——以红酒质量指标为例⽬录程序简介对红酒质量指标数据进⾏灰⾊关联分析,⾸先进⾏数据标准化,然后计算关联系数矩阵和平均综合关联度程序输⼊:第⼀列为母序列的指标矩阵程序输出:关联度矩阵灰⾊关联分析⽅法(GRA),是根据因素之间发展趋势的相似或相异程度,亦即“灰⾊关联度”,作为衡量因素间关联程度的⼀种⽅法。
程序/数据集下载代码分析导⼊模块、路径# -*- coding: utf-8 -*-from Module.BuildModel import GraModelimport pandas as pdimport numpy as npimport osimport matplotlib.pyplot as pltimport seaborn as sns#路径⽬录baseDir = ''#当前⽬录staticDir = os.path.join(baseDir,'Static')#静态⽂件⽬录resultDir = os.path.join(baseDir,'Result')#结果⽂件⽬录读取红酒质量数据,查看内容#接⼝要求第⼀列为母序列,即红酒质量data = pd.read_csv(staticDir+'/winequality-red.csv',sep=';')columns = ['quality','fixed acidity', 'volatile acidity','citric acid', 'residual sugar','chlorides','free sulfur dioxide', 'total sulfur dioxide','density','pH', 'sulphates', 'alcohol']data = data[columns]data.head()quality fixedacidity volatileaciditycitricacidresidualsugarchlorides free sulfurdioxidetotal sulfurdioxidedensity pH sulphates alcohol057.40.700.00 1.90.07611.034.00.9978 3.510.569.4 157.80.880.00 2.60.09825.067.00.9968 3.200.689.8 257.80.760.04 2.30.09215.054.00.9970 3.260.659.8 3611.20.280.56 1.90.07517.060.00.9980 3.160.589.8 457.40.700.00 1.90.07611.034.00.9978 3.510.569.4利⽤GraModel类建⽴灰⾊关联模型,打印结果,该类在⽂件夹的Module/BuildModel.py中,代码会在下⽂给出#建⽴灰⾊关联模型,标准化数据model = GraModel(data,standard=True)#模型计算结果result = model.result#平均关联程度meanCors = result['meanCors']['value']print(result){'cors': {'value': array([[1. , 0.96198678, 0.78959431, ..., 0.75974072, 0.96920683,0.97441242],[1. , 0.9306525 , 0.70441517, ..., 0.98976649, 0.87748443,0.97000442],[1. , 0.9306525 , 0.75900106, ..., 0.93497649, 0.89874803,0.97000442],...,[1. , 0.80296849, 0.92265873, ..., 0.96266425, 0.98630178,0.98636283],[1. , 0.91597473, 0.81988779, ..., 0.72703752, 0.85720372,0.91902831],[1. , 0.78639314, 0.79745798, ..., 0.9909029 , 0.93720807,0.98636283]]), 'desc': '关联系数矩阵'}, 'meanCors': {'value': array([1. , 0.87336194, 0.84594509, 0.87650184, 0.87830158,0.87197282, 0.86374431, 0.85600195, 0.8545979 , 0.86426018,0.89324032, 0.90374 ]), 'desc': '平均综合关联系数'}}这是上⽂使⽤的GraModel类,该代码块可直接运⾏,输⼊矩阵,纵轴为属性名,第⼀列为母序列,输出为关联系数矩阵、平均综合关联系数# -*- coding: utf-8 -*-from sklearn.preprocessing import StandardScalerimport pandas as pdimport numpy as npimport osclass GraModel():'''灰⾊关联度分析模型'''def __init__(self,inputData,p=0.5,standard=True):'''初始化参数inputData:输⼊矩阵,纵轴为属性名,第⼀列为母序列p:分辨系数,范围0~1,⼀般取0.5,越⼩,关联系数间差异越⼤,区分能⼒越强standard:是否需要标准化'''self.inputData = np.array(inputData)self.p = pself.standard = standard#标准化self.standarOpt()#建模self.buildModel()def standarOpt(self):'''标准化输⼊数据'''if not self.standard:return Noneself.scaler = StandardScaler().fit(self.inputData)self.inputData = self.scaler.transform(self.inputData)def buildModel(self):#第⼀列为母列,与其他列求绝对差momCol = self.inputData[:,0].copy()sonCol = self.inputData[:,0:].copy()for col in range(sonCol.shape[1]):sonCol[:,col] = abs(sonCol[:,col]-momCol)#求两级最⼩差和最⼤差minMin = sonCol.min()maxMax = sonCol.max()#计算关联系数矩阵cors = (minMin + self.p*maxMax)/(sonCol+self.p*maxMax)#求平均综合关联度meanCors = cors.mean(axis=0)self.result = {'cors':{'value':cors,'desc':'关联系数矩阵'},'meanCors':{'value':meanCors,'desc':'平均综合关联系数'}}if __name__ == "__main__":#路径⽬录curDir = os.path.dirname(os.path.abspath(__file__))#当前⽬录baseDir = os.path.dirname(curDir)#根⽬录staticDir = os.path.join(baseDir,'Static')#静态⽂件⽬录resultDir = os.path.join(baseDir,'Result')#结果⽂件⽬录#读数data = [[1,1.1,2,2.25,3,4],[1,1.166,1.834,2,2.314,3],[1,1.125,1.075,1.375,1.625,1.75],[1,1,0.7,0.8,0.9,1.2]]data = np.array(data).T#建模model = GraModel(data,standard=True)print(model.result)对平均灰⾊关联系数进⾏热⼒图可视化,系数可理解为所有指标与质量的关联,所以第1个值为1#⽤来正常显⽰中⽂标签plt.rcParams['font.sans-serif']=['SimHei']#⽤来正常显⽰负号plt.rcParams['axes.unicode_minus']=False#可视化矩阵plt.clf()plt.figure(figsize=(8,12))sns.heatmap(meanCors.reshape(1,-1), square=True, annot=True, cbar=False, vmax=1.0,linewidths=0.1,cmap='viridis')plt.yticks([0,],['quality'])plt.xticks(np.arange(0.5,12.5,1),columns,rotation=90)plt.title('指标关联度矩阵')。
灰色关联度评价方法(10)讲解

N
(6.11)
对各比较序列与参考序列的关联度从大到 小排序,关联度越大,说明比较序列与参考序 列变化的态势越一致.
首 页 上 页 下 页 尾 页
从上边也可以看出,关联度的几何含义为比较序 列与参考序列曲线的相似与一致程度.如果两序 列的曲线形状接近,则两者关联度就较大,反之, 两者关联度就较小.
2. 用灰色关联分析进行综合评价
X i ( xi(1), xi(2),
, xi( N ))T , i 0,1, 2,
,n
N为变量序列的长度.
首 页
上 页 下 页
尾 页
2.对变量序列进行无量纲化 一般情况下,原始变量序列具有不同的量纲或数量 级,为了保证分析结果的可靠性,需要对变量序列 进行无量纲化.无量纲化后各因素序列形成如下矩 阵:
式中分辨系数 在(0,1)内取值,一般情况下依据 (6.10)中数据情况多在0.1至0.5取值, 越小越能 提高关联系数间的差异.关联系数 0i (k ) 是不超 过1的正数, 0i (k ) 越小, 0i (k ) 越大,它反映第i 个比较序列Xi与参考序列X0在第k个期关联程度.
首 页 上 页 下 页 尾 页
首 页 上 页 下 页 尾 页
表6-1是某地区2000-2005年国内生产总值的统计 资料.现在提出这样的问题:该地区三次产业中, 哪一产业的变化与该地区国内生产总值(GDP)的 变化态势更一致?也就是哪一产业与GDP的关联 度最大呢? 表6-1 某地区国内生产总值统计资料(百万元)
年份 国内生产总值 第一产业 第二产业 第三产业 2000 1988 386 839 763 2001 2061 408 846 808 2002 2335 422 960 953 2003 2750 482 1258 1010 2004 3356 511 1577 1268 2005 3806 561 1893 1352
灰色关联分析:多因素统计分析新方法

灰色关联分析:多因素统计分析新方法一、本文概述《灰色关联分析:多因素统计分析新方法》一文旨在探讨灰色关联分析在多因素统计分析中的应用及其作为一种新的分析方法的优势。
本文将首先介绍灰色关联分析的基本概念、原理及其在多因素统计分析中的重要性。
随后,将详细阐述灰色关联分析的实施步骤和方法,包括数据的预处理、关联度的计算、关联序的确定等。
文章还将通过实例分析,展示灰色关联分析在实际问题中的应用及其效果评估。
文章将总结灰色关联分析的优势与局限性,并探讨其未来的发展趋势和应用前景。
通过本文的阅读,读者将能够全面了解灰色关联分析在多因素统计分析中的作用和价值,为相关领域的研究和实践提供有益的参考。
二、灰色关联分析的基本原理灰色关联分析(Grey Relational Analysis,GRA)是一种基于灰色系统理论的多因素统计分析方法。
这种方法的核心思想是通过分析系统中各因素之间的关联程度,找出影响系统发展的主要因素和次要因素,进而为决策提供科学依据。
灰色关联度定义:灰色关联度是衡量系统中各因素之间关联程度的一个量化指标。
它表示在一个系统中,某一因素的变化对其他因素变化的影响程度。
灰色关联度越大,说明两个因素之间的关联程度越高,反之则越低。
灰色关联矩阵构建:灰色关联分析首先需要构建灰色关联矩阵。
该矩阵以各因素为行和列,以各因素之间的灰色关联度为元素,从而形成一个全面的、系统的关联关系描述。
灰色关联度计算:灰色关联度的计算主要基于因素间的相似性或差异性。
常用的计算方法有绝对关联度、相对关联度和综合关联度等。
这些方法通过对原始数据进行处理,计算得到各因素之间的关联度值。
关联序分析:根据计算得到的灰色关联度值,可以对各因素进行关联序分析。
关联序反映了各因素对系统发展的重要性排序,有助于决策者识别出关键因素和次要因素。
灰色关联分析通过量化各因素之间的关联程度,为系统分析和决策提供了有效的工具。
这种方法不仅适用于社会经济领域,还可以广泛应用于工程技术、生态环境、医疗卫生等多个领域。
第三章灰色关联分析GRA

实例分析计算过程
灰色关联分析是一种多因素统计分析方法,它是以各因素的样本数据为依 据用灰色联度来描述因素间关系的强弱、大小和次序的.如果样本数据列反映 出两因素变化的态势(方向、大小、速度等)基本一致,则它们之间的关联度较大 ;反之关联度较小。 与其他传统的多因素分析方法相比,灰色关联分析对数据 要求较低且计算量小,便于广泛应用. GRA分析的核心是计算关联度,下面通过一 个例子来说明计算关联度的思路和方法. 表是某地区2000-2005年国内生产总值的统计资料.现在提出这样的问题:该 地区三次产业中,哪一产业的变化与该地区国内生产总值(GDP)的变化态势更一 致?也就是哪一产业与GDP的关联度最大呢?
表 某地区国内生产总值统计资料(百万元) 年份 国内生产总值 第一产业 第二产业 第三产业
2000
2001 2002 2003
1988
2061 2335 2750
386
408 422 482
839
846 960 1258
763
808 953 1010
2004
2005
研究生学院
3356
3806
511
561
• 灰色系统理论(Grey System
Theory)的创立源于20世纪80年
代。邓聚龙教授在1981年上海中美控制系统学术会议上所作的 “含未知数系统的控制问题”的 学术报告中首次使用了“ 灰色系 统”一词。
研究生学院
@copyright by Chunyou完全系统的最小信息正定”、“灰色系统的 控制 问题”等系列论文,奠定了灰色系统理论的基础。他的论文在国际上引起了高度的 重视,美国哈佛大学教授、《系统与控制通信》杂志主编布罗克特(Brockett)给 予灰色系统理论高度评价,因而,众多的中青年学者加入到灰色系统理论的研究行 列,积极探索灰色系统理论及其应用研究。邓聚龙系统理论则主张从事物内部,从 系统内部结构及参数去研究系统,以消除“黑箱”理论从外部研究事物而使已知信 息不能充分发挥作用的弊端,因而,被认为是比“黑箱”理论更为准确的系统研究 方法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
灰色关联分析的步骤[2]
灰色关联分析的具体计算步骤如下:
第一步:确定分析数列。
确定反映系统行为特征的参考数列和影响系统行为的比较数列。
反映系统行为特征的数据序列,称为参考数列。
影响系统行为的因素组成的数据序列,称比较数列。
设参考数列(又称母序列)为Y={Y(k | k = 1,2,Λ,n};比较数列(又称子序列)Xi={Xi(k | k = 1,2,Λ,n},i = 1,2,Λ,m。
第二步,变量的无量纲化
由于系统中各因素列中的数据可能因量纲不同,不便于比较或在比较时难以得到正确的结论。
因此在进行灰色关联度分析时,一般都要进行数据的无量纲化处理。
第三步,计算关联系数
x0(k与xi(k的关联系数
(为一行向量
记,则
,称为分辨系数。
ρ越小,分辨力越大,一般ρ的取值区间为(0,1,具体取值可视情况而定。
当时,分辨力最好,通常取ρ = 0.5。
第四步,计算关联度
因为关联系数是比较数列与参考数列在各个时刻(即曲线中的各点)的关联程度值,所以它的数不止一个,而信息过于分散不便于进行整体性比较。
因此有必要将各个时刻(即曲线中的各点)的关联系数集中为一个值,即求其平均值,作为比较数列与参考数列间关联程度的数量表示,关联度ri公式如下:
第五步,关联度排序
关联度按大小排序,如果r1 < r2,则参考数列y与比较数列x2更相似。
在算出Xi(k序列与Y(k序列的关联系数后,计算各类关联系数的平均值,平均值ri就称为Y(k与Xi(k的关联度。
