环路定理电场强度的线积分

合集下载

9-5-静电场的环路定理解析

•电势是标量，有正有负； •电势的单位：伏特 1V=1J.C-1； •电势具有相对意义，它决定于电势零点的选择。在理论计算中，通常选择无穷远处的电势为零；
•在实际工作中，通常选择地面的电势为零。 •但是对于“无限大”或“无限长”的带电体，只能在有限的范围内选取某点为电势的零点。
3、电势差
在静电场中，任意两点A和点B之间的电势之差，称为电势差，也叫电压。
步骤：
(1)先算场强 (2)选择合适的路径L
(3) 积分(计算)
•2、利用点电荷的电势公式和电势的叠加原理
dq dV
4 0r
dq
V 4 0r
要求电荷的分布区域是已知的；
当电荷分布在有限的区域内，可以选择无穷
远点作为电势的零点的；而当激发电场的电荷分
布延伸到无穷远时，只能根据具体问题的性质，
在场中选择某点为电势的零点。
E
1
4 0
Q r2
er
B
Q
rB
r
rA
dr C r
A
dl
er
E
dW
1
4 0
Qq0 r2
er
dl
1
4 0
Qq0 r2
dr
rB
W
Qq0
dr Qq0 ( 1 1 )
rA 40r 2
40 rA rB
在点电荷的静电场中，电场力对试验电荷所作
的功与其移动时起始位置与终了位置有关，与
其所经历的路径无关。
V
p 3xy
Ey
y
4 0
x2 y2 5/2
-q
+q
电偶极子的延长线上 y 0
2p 1
E x 4 0 x 3

第一章环路定理

电势: 电势: U a = ∫
零点
a
E ⋅ dl
电势差: 静电场中两点电势之差. 电势差: 静电场中两点电势之差
U ab
b 零点零点 Aa − Ab = Ua −Ub = = ∫ E ⋅ dl − ∫ E ⋅ dl = ∫a E ⋅ dl a b q0
意义: 把单位正电荷从a点沿任意路径移到点沿任意路径移到b点时电场力所作的功意义把单位正电荷从点沿任意路径移到点时电场力所作的功
U P = ∫ Edr = ∫ P
Q
R
r
1.6.4 等势面电势梯度一. 等势面
电场中电势相等的点组成的曲面叫等势面电场中电势相等的点组成的曲面叫等势面. 等势面等势面上的任一曲线叫等势线等势面上的任一曲线叫等势线. 等势线
性质：在静电场中沿等势面移动电荷时性质：在静电场中, 沿等势面移动电荷时, 1. 静电场力对电荷不作功证明: 证明 W = q0 等势面 b
将圆环分割成无限多电荷元: 解1: 将圆环分割成无限多电荷元
q
r
R
dU =
dq 4πε 0 r
o
x
环上各点到轴线等距
dU
x
U = ∫ dU =
1 4πε0r
∫0 dq =
∞
q
q 4πε 0 ( x 2 + R 2 )1 / 2
解2: 根据定义式
UP = ∫
零点 P
E ⋅ dl = ∫
xP
qx ⋅ dx 2 2 3/ 2 4πε 0 ( x + R )
U + dU P2 U dn
ˆ n
定义电势梯度矢量: 定义电势梯度矢量 dU 大小: 大小方向: 方向沿等势面的正法线方向 dn

63静电场环路定理电势

E2
q1
4 0 r 2
R1 r R2
E3
q1 +q2
40r 2
r R2
q1 II
I R1
R2 •
III
rE
P•
III区：U3
E dl
P
q2 q1 II III
E3 dr E3dr
r
r
I R1
R2 •
r
q1 q2
4 0 r 2
dr
q1 q2
40r
rr
P• P•
R2
II区： U3
R r
Q
4 0 R3
rdr
Q
R 4 0r 2 dr
Q
8 0 R
Qr 2
8 0 R3
Q
4 0 R
Q (3R 2 r 2 )
8 0 R3
o rp R
rp
路径的线积分为零（电场强度的环流为
零）
3. 电势能比重力做功保守力重力势能
较静电场力做功保守力电势能
静电场力对电荷所做功等于电荷电势能增量的负值
B
WAB A q0E • dl EpB EpA
令 B点为电势能零点，则可得任一点 A
的电势能
0
E p A
q0
E • dl
E dl
P
E dr
E2dr
E3dr
r
r
R2
R2 r
q1
4 0 r 2
dr
R2
q1 q2
4 0 r 2
dr
1
4 0
( q1 r
q2 R2
)
I区：
U3
E dl

10.4静电场环路定理

V V V ( i j k) x y z
V Ez z
E
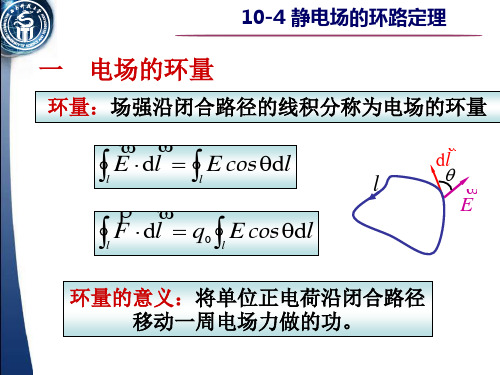
10-4 静电场的环路定理 V V V E ( i j k) x y z V的梯度: gradV 或
E gradV V
E 的方向与V的梯度反向.
10-4 静电场的环路定理
一
电场的环量
E dl E cos dl
l l
环量：场强沿闭合路径的线积分称为电场的环量
dl
l
F dl qLeabharlann E cos dll l
E
环量的意义：将单位正电荷沿闭合路径移动一周电场力做的功。
10-4 静电场的环路定理
RB
q A qB qA 1 1 ( ) 4 0 R B 40 r RB
qA qB 40 r 40 RB
（3）r RA
U
RA r
10-4 静电场的环路定理
RB E dr E dr E dr RA RB 0
V
另一方面，由于场强沿法线方向 dV dV E V n E En n n dn dn 电势梯度是一个矢量，它的大小为电势沿等势面法线方向的变化率（该方向电势的变化率最大），它的方向沿等势面法线方向且指向电势增大的方向。
10-4 静电场的环路定理
静电场力的功 b Aab q E dl qUab q(U a U b )
a
原子物理中能量单位: 电子伏特eV
1 eV 1.6021019 J
10-4 静电场的环路定理
点电荷电场的电势
E q e 2 r 4 πε0 r

第11章电势1

上海大学物理系张金仓第五讲q PC PC ∫∫11012rd E q A p P Cr v ⋅=∫21012对单位正电荷而言，有：称为电场强度E 沿任意路径C 的线积分意义：在电场力作用下移动单位正电荷电场力所作的功！二、静止点电荷电场线积分q ∫∫⋅=⋅2121304p P Cp P C rd r rq r d E r r r v πε１、静止点电荷的电场中，电场强度的线积分（对单位正电荷所作的功！）只与积分路经的起点和终点位置有关，而与积分路径无关；２、推广一：对点电荷系，由于合力的功等于分力功之和，故总电场强度的线积分也具有同样特点；３、推广二：对连续带电体，总电场强度的线积分也具有同样特点；)11(421021r r q r d E p PC −=⋅∫πεr v三、静电场的保守性=⋅∫Cr d E r r 静电场的环路定理ab cd对任何静电场，电场强度的线积分（对单位正电荷所作的功！）只与积分路经的起点和终点位置有关，而与积分路径无关——静电场是一保守力场！！！与路径无关r d E 积分即：21p P C rv ⋅∫表述：静电场中电场强度沿任一闭合路径的线积分等于零。

四、静电场的环路定理qrd E U p P r v ⋅=−=∫212112ϕϕ物理意义：有限大带电体无限远处为电势零点对正电荷，电势高意味着电势能高，对负电荷则相反；二、电势rd E U p P r v ⋅=−=∫212112ϕϕrd E p PP P r v ⋅=−=∫0ϕϕϕ意义：场中某一点Ｐ的电势，在数值上等于把单位正电荷自Ｐ点移动到电势零点Ｐ０处电场力所作的功。

rd E U p P r v ⋅=−=∫212112ϕϕ三、电势与电势差的关系rd E p PP P rv ⋅=−=∫00ϕϕϕ四、电场力的功rd E q q U q A p P r v ⋅=−==∫21021012012)(ϕϕ电势为五、点电荷的电势分布q+1P 1r 2r 2P rv r d r rr +rd r θFrE r 0q C P )11(44210302121r r qrd r rqr d E p P p P P −=⋅=⋅=∫∫πεπεϕr r rv 选择无限远处为电势零点，距静止点电荷为r 处电场中的电势：),(4210∞===r r r rq πεϕ+Vr014q V rπε=q >Vr014q V rπε=q <- q ＞0电势是正的愈远愈小。

静电场的环路定理(北邮)

Wa Aa
W Ua a q0
a

0
q 0 E dl
E

a
E dl
a
4、电势差:
U a U b E dl E dl
a b
E 减少，能量哪里去了？
解: 由高斯定理
0
E
r RA r RB
2
q q
RA

q 4 0 r
RA r RB
RB
U AB U A U B
RB E dl
B A
q q 1 1 dr ( ) 2 40 RA RB RA 40 r
2.如图已知+q 、-q、R ①求单位正电荷沿adc 移至c ，电场力所作的功
例2：求半径为R、电量Q均匀分布的球面在球心O处产生的电势。
dq Q dq 思路(1): dU U 4 0 R 40 R 40 R
好
(2):
U

O
E dl

R
O
E dl E dl
R

E dl R
F-
q
M
能量最低，稳定平衡。
, W pE 能量最大，非稳定平衡。
5、电场力作正功时，电势能减少，能量
哪里去了？
Aa b q0 E dl q0 ( U a U b )
b a
1 q0 ( Ua Ub ) mv 2 2
1eV=1.6×10-19J
求E 。
例：用电势梯度法计算带电圆环轴线上一点的场强。 r
o x p X

6-3静电场的环路定理电势

dV
dE
10
红
已知场强分布 Ex, y, z ，求场中任一点P 的电势时，
可先作不定积分
V E dl C
选择使积分常量 C 0 的点为零电势的参考点，再
电
子工程学院
作积分，可求 P 点的电势 VP
对于有限电荷分布情况，可直接选无限远为零势能
点，作积分可得
VP
E dl
P
x
1 qdl
dVP 4π 0r 2π R
x
院
杨 VP
小
1
4π 0r
qdl q
q
2π R
4π 0r
4π 0
x2
R2 13
红
VP
4π 0
q x2 R2
电讨论
子工程学院
杨
x
0，V0
q
4π 0R
x
R，VP
q
4π 0x
小
红
q
V
4π 0 R
o
x
q
4π 0 (x2 R2 )1 2
14
均匀带电薄圆盘轴线上的电势
点
电
电荷
子的
工程学院
等势面
杨小红
dl2 dl1 E2 E1
dl1 dl2
21
两平行带电平板的电场线和等势面
++++++++++++
电子工程学院
杨
小
22
红
一对等量异号点电荷的电场线和等势面
电
子工
+
程
学

静电场的环路定理

已知q的电场分布 E
根据定义, P点的电势为
4
q
0r
2
er
VP

P

E dl

r
q
40r
2Pdr4q04r2qe0rrP dl
q > 0时, VP为正, r V, r处V= 0 min q < 0时, VP为负, r V, r处V = 0 max
2.电场强度与电势梯度的关系
根据电势差的定义, 把单位正电荷从P1移到P2 电场力所作的功为：
dA E dn V (V dV )
r E
dn
n
P1
P2
V V dV
E dn dV
E

dV dn
grad V
E
ቤተ መጻሕፍቲ ባይዱ

dV dn
n
r E grad V
r 即:电场中某点的场强 E 等于该点电势梯度的负值
无意义
VP

P
E
dr
rP
2 0r
dr

2 0
ln
rP
r
P
P'
令某处 r = r0（有限值） V=0，则
VP

P0
P
E
dl

P
P
E dl

P0
P
E dl
r0 P0

P
P
2
0r
dr

2 0
ln
r0 r
可见：当电荷分布到无穷远时，
22
归纳电场强度与电势的关系
积分关系：

所有分类环路定理电势能电势

所有分类环路定理电势能电势
Wq0a b Ed clo s
dcl o s dr
Wq0ab Edr
点电荷的场
q
Wq0ab 410rq2dr
q0q 1 1
40 ra rb
b
rb
dl r
ra
q0 a
dr F
E
W q0q 1 1
40 ra rb
电场力的功只与始末位置有关，而与路径无关，电场力为保守力，静电场为保守场。
电场力是保守力，可引入势能的概念。
引力是保守力，作功为
W 引[Gm1 rm b2(Gm1 rm a2)]
取无穷远为零势能点，则引力势能为：
电场力作功
Ep
G m1m2 r
W q0q 1
40 ra
r1b (4q0q0rb
q0q )
40ra
1.电势能Ep
定义：单位：焦耳，J
EP
q0q
40r
为点电荷电势能（选无穷远为零势能点）
r
r
r
0R E2dr d l/d /r/E / 高斯面
R410 rq2dr
q
4 0 R
•II区：球壳外电势
II
rR
选无穷远为电势 0 点，
U2 r E2dl
I
qo RE
r
r
r
rE2dr d l/d /r/E / 高斯面
1
r 40
rq2dr
q
4 0 r
II
I
qoR
II
I
qoR
qE
4 0 R 2
qV 4 0 R
oR
r oR
r
例3 如图，两个同心的均匀带电球壳，半径分别

环路定理

∫ B dl = ∑I
L 0 L内
i
∫ B dl = ∑I
L 0
内
几点说明: 几点说明:
1)B是L上dl处的磁感应强度,是由空间所 ) 是上处的磁感应强度处的磁感应强度, 有电流共同产生叠加的结果. 有电流共同产生叠加的结果. 2)I内是被所包围的电流,∑I内则是所包 ) 是被L所包围的电流所包围的电流, 则是L所包围的电流代数和. 围的电流代数和. 3)定理揭示了真空中B的环流只跟被包围的 )定理揭示了真空中的环流只跟被包围的电流代数和有关,没有被L所包围的电流对所包围的电流对B 电流代数和有关,没有被所包围的电流对的环流没有贡献. 的环流没有贡献. 4)∫LB d l ≠ o 说明为非保守场也称涡旋场 . ) 说明为非保守场(也称涡旋场也称涡旋场). 5)学习时注意与电场的高斯定理进行比较. )学习时注意与电场的高斯定理进行比较.
× × × × ×
×
×
×
R1 R2 解:分析磁场分布: 分析磁场分布: 已知:R1,R2匝数N 已知: 匝数电流I 电流
作半径为r的安培环路作半径为的安培环路L 的安培环路
π 当 R R << r 取圆周的平均值代替 2 r 2 1
R +R 2 L =2 π 1 平 2 0NI N B= = 0nI n = L L 平平
R r L
1)作半径为 r (R ≤ r < ∞) ) 的安培环路L 的安培环路L
r
R
也是以中心轴线为对称的分布. 的分布.
∫ B dl = ∑I = I ∫ B dl = ∫ Bcos0 dl = I B∫ dl =B2πr = I I
BC

环路定理_电势

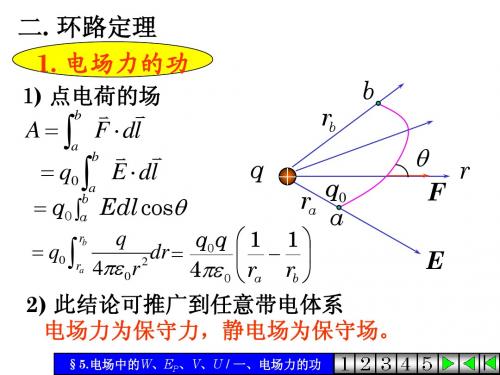
等势面、与的微分关系 §5.等势面、E与U的微分关系 / 二、等势面性质等势面
3) 场强与电势的微分关系
v v U a − U b = −dU = E ⋅ d l v v −dU = E ⋅ dl = Ex dx + E y dy + Ez dz
∂U ∂U ∂U Ey = − Ez = − Ex = − ∂y ∂x ∂z U + dU v ∂U v ∂U v ∂U v E = −( i+ j+ k) U ∂x ∂y ∂z
a
电荷在点电荷场中的电势能（电荷在点电荷场中的电势能（选无穷远为零势能点）为零势能点） q0 q 电势能是标量标量, 电势能是标量 W= 电势能是属于系统的. 4πε 0 r 电势能是属于系统的
电场中的W、 §5.电场中的、EP、V、U / 三、电势能电场中的、
4. 电势差和电势
电势差
电场中的W、 §5.电场中的、EP、V、U / 一、电场力的功电场中的、
2. 环路定理
1) 定理表述静电场中电场强度沿任意闭合路径的线积分等于零。积分等于零。
∫
L
v v E ⋅ dl = 0
高斯定理说明静电场是有源场高斯定理说明静电场是有源场, 环路定理说有源场明静电场是保守力场无旋场。保守力场或明静电场是保守力场或无旋场。
R2 r R2 r
R2
2
∞ R2
q1
− q2
o R1 III II I
=∫
r
∞
q1 − q2 +∫ dr 2 R2 4πε r 0
4πε 0r
q1
2
dr
R2
高斯面
1 q1 1 q2 = − 4πε 0 r 4πε 0 R2

环路定理电势能差电势差

q
dl r
r dr F
E

电场力的功只与始末位置有关，而与路径无关。 2.任意带电体系的场对于由多个静止点电荷组成的系统或静止的连续带电体，可看成是由无数电荷元组成。
由场强叠加原理可得到电场强度的线积分（移动单位电荷的功）为：
3

b
aபைடு நூலகம்
b E dl ( E1 E2 En ) dl a b b b E1 dl E2 dl En dl Aab
a
电场力是保守力
5
二、电势能和电势
电场力是保守力，可引入势能的概念。 1.电势能差
b
q0 a
E
设在静电场中，将检验电荷 q0 从 a 点沿任意路径移动到 b 点，电场力作功为Aab。定义: 电荷 q0 在静电场中a 、b两点间的电势能差定义为， q0从 a 点沿任意路径移动到 b 点的过程中， Wa - Wb等于电场力所作的作功Aab 电势能差（势能增量的负值）等于保守力所作的功。
•对无限带电体不宜选无穷远为电势零点。此时只有电势的相对值（即电势差）有意义。
4.电势能与电势的区别：W 可正可负，取决于 q 和 q0 ； U只取决于场源电荷 q 。
10
另一方面：当已知电势分布时，可由电势差求出点电荷在电场中移动的过程中电场力所做的功：
Aab q0
b
a
E dl q0 (U a U b )
a
式中：Wa、Wb是电荷q0分别在a点和b点时,q0与电场所组成的系统的静电势能。
b
2.电势能
电势能也是一个相对的量，若选择一个零势能点作为参考。若令 W 0, 即选定b点为电势能零点。 b 则，电荷q0在此系统的电场中a点的电势能为：

22-场强环路定理、电势

O
2012年4月26日
∞
∞
q 4πε 0 r
2
dr =
q 4πε 0 r
11 11
r
大连理工大学秦颖
大连理工大学
例 5 ：长为 l 的均匀带电直线，电荷线密度为 λ 。求：图中 p 点的电势。解：如图选取坐标系，
dU = dq 4π ε 0 r
l
dq = λd x
x
o
r
l
dx
dU
a
p
x
=
作功与检验电荷的电量和电场强度的线积分成正比。 ① 单位正电荷放在a点处，系统的电势能。 ② 把单位正电荷从 a 点移到0电势(无限远)处，电场力所做的功。
2. 电势差：在电场中移动单位正电荷时电场作的功。
Ua − Ub =
∫
∞ a
E ⋅ dr −
∫
∞ b
E ⋅ dr =
∫
b a
E ⋅ dr 电压
4πε 0 R 球面内 q U= 4πε 0 r 球面外
a
q
均匀带电 λ ln r 无限长直线 U =
2π ε 0
均匀带电无限长直线
方向垂直于直线
λ E= 2πε 0 r
均匀带电无限大平面
σ ⋅d U = Ed = 2ε 0
σ 均匀带电 E= 无限大平面 2ε 0
方向垂直于平面
秦颖
17 17
2012年4月26日
∫
∞
r
qr ⋅ d r = 3 4π ε 0 r
∫
∞
r
dr
4π ε 0 r 4π ε 0 r r 例2 ：求一对正、负电荷连线中垂线上的电势。
O

安培环路定理在恒定电流的磁场中,磁感强度沿任何闭合路径的线积分

安培环路定理在恒定电流的磁场中，磁感强度沿任何闭合路径的线积分等于此路径所环绕的电流的代数和的μ0倍。

安培载流导线在磁场中所受的作用力。

毕奥-萨伐尔定律实验指出，一个电流元Idl 产生的磁场为场强叠加原理电场中某点的电场强度等于各个电荷单独在该点产生的电场强度的叠加(矢量和)。

磁场叠加原理空间某一点的磁场(以磁感强度示)是各个磁场源(电流或运动电荷)各自在该点产生的磁场的叠加(矢量和)。

磁场能量密度单位磁场体积的能量。

磁场强度是讨论有磁介质时的磁场问题引入的辅助物理量，其定义是磁场强度的环路定理沿磁场中任一闭合路径的磁场强度的环量(线积分)等于此闭合路径所环绕的传导电流的代数和。

磁畴铁磁质中存在的自发磁化的小区域。

一个磁畴中的所有原子的磁矩(铁磁质中起主要作用的是电子的自旋磁矩)可以不靠外磁场而通过一种量子力学效应(交换耦合作用)取得一致方向。

磁化在外磁场作用下磁介质出现磁性或磁性发生变化的现象。

返回页首磁化电流(束缚电流) 磁介质磁化后，在磁介质体内和表面上出现的电流，它们分别称作体磁化电流和面磁化电流。

磁化强度单位体积内分子磁矩的矢量和。

磁链穿过一个线圈的各匝线圈的磁通量之和称作穿过整个线圈的磁链，又称"全磁通"。

磁屏蔽闭合的铁磁质壳体可有效地减弱外界磁场对壳内空间的影响的作用称作磁屏蔽。

磁通连续原理(磁场的高斯定理)在任何磁场中，通过任意封闭曲面的磁通量总为零。

磁通量通过某一面积的磁通量的概念由下式定义磁滞伸缩铁磁质中磁化方向的改变会引起介质晶格间距的改变，从而使得铁磁质的长度和体积发生改变的现象。

磁滞损耗铁磁质在交变磁场作用下反复磁化时的发热损耗。

它是磁畴反复变向时，由磁畴壁的摩擦引起的。

磁滞现象铁磁质工作在反复磁化时，B 的变化落后于H 的变化的现象。

D 的高斯定理通过任意闭合曲面的电位移通量等于该闭合面所包围的自由电荷的代数和。

其表示式是带电体在外电场中的电势能即该带电体和产生外电场的电荷间的相互作用能。

场强环路定理电势

r Qr 4πε 0 r 3
Qq 0 r v A = ∫ F ⋅ dl =
b a
4πε 0
∫
rb
ra
d r Qq 00 ⎛⎛ 11 ⎞ r 1 ⎞ Qq ⎜ = − ⎟ 2 = ⎜⎜−r ⎟ r ⎟ 4 πε 00 ⎝⎝ a ⎠ r b ⎠ r r
b a
——只与起始位置有关，而与路径无关。
• 点电荷系产生的场： b • q• 1 • ri b q2• qi •
静电场中a、b两点间的电势差（电压）等于单位正电荷从a点移动b点处，电场力所做的功。
任意电荷 Q 在电场中从a移动到b，电场力所做的功可以用电势差来表示
Aab = Q(U a − U b )
电势的数值与零参考点选择有关, 电势差与零参考点选择无关。
Aab = Q(U a − U b )
U a> U b
q R
0
r r
P
U =∫
(∞)
( P)
∞ r r E ⋅ d l = ∫rp
q 4 π ε 0r
2
dr
U外
q = 4 π ε 0r
均匀带电球面在外部空间的电势分布与全部电荷集中在球心的点电荷的电势分布一样。
（2）内: r <R
已知 E内= 0
所以U内 = ？
( P) (K)
2
任选一点P U =
∞
求电量分别为Q1 及Q2半径分别为R 1 及R2 的均匀带电同心球面的电势分布。 ⎧ Q1 ⎪ 4 π ε r (r > R1 ) 利用上题结果： ⎪ 0 U1 = ⎨ R1 球面1上电荷的电势： ⎪ Q1 (r ≤ R ) 1 ⎪ 4 π ε 0 R1 R2 ⎩ Q1 球面2的电势： ⎧ Q2 ⎪ 4 π ε r (r > R2 ) Q2 ⎪ 0 两个同心球面的电势： U2 = ⎨ ⎪ Q2 (r ≤ R ) ⎧ Q1 + Q2 2 (r > R1 ) ⎪ 4 π ε 0 R2 ⎪ ⎩ 4 π ε 0r ⎪ ⎪ Q1 Q2 + ( R1 < r ≤ R2 ) U = U1 + U 2 = ⎨ ⎪ 4 π ε 0 r 4 π ε 0 R2 ⎪ Q1 Q2 + (r ≤ R1 ) ⎪ ⎩ 4 π ε 0 R1 4 π ε 0 R2

9-5 静电场的环路定理解析

0
E dl
q0U AB

q0 VA
VB
A
五、点电荷电场的电势

V E dl Edr
r

r
q
4 0r
2
r
dr
V q
4 0r
正电荷的电势为正，离电荷越远，电势越低；
负电荷的电势为负，离电荷越远，电势越高。
六、电势叠加原理
E dl
AB
VB
当电荷分布在有限空间时，无限远处的电势能和电势为零
v v
VA
E dl
A
•电场中某点的电势在数值上等于放在该点的单位正电荷的电势能
•电场中某点的电势在数值上等于把单位正电荷从该点移到势能为零的点时，电场力所作的功。
2、说明：
•电势是标量，有正有负； •电势的单位：伏特 1V=1J.C-1； •电势具有相对意义，它决定于电势零点的选择。在理论计算中，通常选择无穷远处的电势为零；
复习
9-3、4 电场线静电场的高斯定理
• 电场线 • 电场强度通量 • 高斯定律 • 高斯定律应用举例
9-5 静电场的环路定理
一、静电场力所作的功
1、点电荷电场
点电荷Q固定于原点O，试验电荷q0在Q的电场中由A点沿任意路径ACB到达B点，取
微为元ddlW，电场F力 dl对q0q的0 E元 d功l
ADC
ABC
电场力作功
与路径无关

W＝q0 E dl＝0

E
dl＝0
定义：电场强度沿任意闭合路径的线积分叫电场强度的环流。
静电场的环路定理：在静电场中，电场强度的环流为零。
三、电势能

第10章静电学 - 3 - 静电场环路定理

由此可见, 在点电荷q的电场中, 电场力的功只与路径的起点和终点位置有关, 而与路径形状无关。此结论可通过场强叠加原理推广到任意点电荷系(包括带电体)的电场。
2
即：电场力做功只与路径的起点和终点位置有关, 而与所经
过的路径无关——电场力是保守力。
A F dl q0 E dl 0 E dl 0
R2 ln 1 R1
dV R2 E0 ln E0 0 令 dR1 R1
A
R2 e R1
B
R1
Vmax
R2 E0 =33kV e
R2
22
例10-19一半径为R的均匀带电球面，带电量为q；球面外有一均匀带电细线，电荷线密度为 , 长为l, 细线近端离球心距离为ro, 求细线受的力和细线在球面电场中的电势能。
A
A e(U A U B ) eV
B
1 eV m 2 , =1.03107(m/s) 2
21
(4)若击穿场强Eo=200kV/cm, R1可调整, 能承受的最大电压是多少?
E
V R2 r ln R1
显然r=R1处的场强最强，最先击穿，令E=E0
R2 得： V E0 R1 ln R1
§10. 4 1.电场的环量
静电场环路定理 l
dl
----场强沿闭合路径的线积分。即
E dl E cos dl
l l
E
设想将试验电荷q0沿闭合路径移动一周，则电场力作功
A l F dl l q0 E dl q0 l E cos dl
n
n
4 o ri
qi
式中: Ui代表第i个点电荷qi单独存在时在a点产生的电势。

磁场高斯定理安培环路定理

l
Amperian loop
µ0 NI ∴B = 2πr
磁场不均匀
B
µ0 NI B= 2π r
o
R1
R2
r
o
R1
R2
r
若 R1、R2 >> R2 − R1 N n= 2π R1
则:
B = µ0nI
当 2R >> d 时，螺绕环内可视为均匀场。
已知：例题已知：I 、R，电流沿轴向在截面上均匀分，无限长”载流圆柱导体内外磁场的分布。布，求“无限长”载流圆柱导体内外磁场的分布。解：首先分析对称性电流分布——轴对称电流分布轴对称磁场分布——轴对称磁场分布轴对称
r<R r>R
I
R
r<R 0 B = µ0 I r>R 2π r
µ0I B 2πR
r
O
R
无限大平板电流的磁场分布。例题无限大平板电流的磁场分布。设一无限大导体薄平板垂直于纸面放置，薄平板垂直于纸面放置，其上有方向垂直于纸面朝外的电流通过，面电流密度（的电流通过，面电流密度（即指通过与电流方向垂直的单位长度的电流）到处均匀。的单位长度的电流）到处均匀。大小为 j 。解：视为无限多平行长直电流的场。直电流的场。分析求场点p的对称性垂线，做 po 垂线，取对称的长直电流元，长直电流元，其合磁场方向平行于电流平面。方向平行于电流平面。
r r (3)要求环路上各点 B大小相等，B的方向与环路方向要求环路上各点 r大小相等， r 一致，目的是将: B ⋅ dl = µ0 ∑ I 写成 B = µ0 ∑ I 一致，目的是将 ∫L r ∫ dl 的方向与环路方向垂直，或 B 的方向与环路方向垂直， r r r r B ⊥ dl , cosθ = 0 ∫ B ⋅ dl = 0

3-真空中的静电场

v v ΦE = ∫ E ds = ∫SEds
S
= E∫ ds = E 4π r
S
2
r
Q
R
r≥R时:
ΦE = 4π r E外 = Q ε0
2
1 Q 或 ∴E外 = 2 4πε0 r
v 1 Qv E外 = r 3 4πε0 r
r
r
R
r<R时:
1 4 3 2 ΦE = 4πr E内 = ∫ ρdV = ρ π r ε0 3 ε0 3 Q r Q 2 Qρ = π 内 3 ∴4 r E = 3 (4 3)πR R ε0
2
εo
1
3
当 r≤R 时:
Qr E1 = 3 4πεo R
Q
r R
当 r>R 时:
E2 =
Q 4πεor
2
当 r≤R 时:
U1 = ∫ E1dr + ∫ E2dr
r R
R
∞
q R
=∫
R
r
Qr Q dr + ∫ dr 3 2 R4 4πεo R πεor
2
∞
Q Q Q(3R r ) 2 2 = = (R r ) + 3 8πεo R 4πεo R 8πεo R
∫
q3 qi
S
q1
v v v v v v ∴ΦE = ∫ E dS = ∫ (E1 + E2 +L+ En ) dS
S
S
= ΦE1 + ΦE2 +LΦEn =
即:
1
ε0
i
∑q
S内
k
i
M
q2
qn
v v 1 ΦE = ∫ E ds =