语音信号处理-第03章 语音信号的时域分析方法
语音信号处理第3章 语音信号分析方法

如果aN~=0,则IIR滤波器的阶数为N。
IIR滤波器的差分方程表示为:
y ( n)
m 0
bm x(n m) am y(n m)
m 1
M
N
设计经典数字滤波器的步骤:
(1)将设计指标归一化处理,即通带截止频率Wp 和阻带截止频率Ws。
(2)根据归一化频率,确定最小阶数N 和频率参数 Wn。可供选用的阶数选择函数有:buttord, cheb1ord,cheb2ord,ellipord 等。
(3)运用最小阶数N 设计模拟低通滤波器原型,用 到的函数有:butter, chebyl,cheby2, ellip 。
(4)用freqz(b,a,N,fs) 函数验证设计结果。
(5)用filter(b,a,x)函数实现滤波功能。
直接设计数字滤波器的MATLAB函数: [N,wn]=buttord(wp,ws,Rp,Rs) %数字频率采用标 准化频率,取值范围为0~1之间,标准化频率1对 应的数字频率为π,对应的模拟频率为采样频率 的一半。设计带通滤波器时,wp=[wp1,wp2]; ws=[ws1,ws2] [b,a]=butter(N,wn,’ftype’) %N为滤波器的阶数, wn为滤波器的截止频率(0~1),“ftype”为滤 波器的类型:‘high’为高通,‘stop’为带阻, 截止频率为wn=[w1,w2];缺省时为低通和带通滤 波器
[N,Wn]=buttord(wp1,ws1,Rp,Rs);
[b,a] = butter(N,Wn);%确定传递函数的分子、分母系数
[h,f]=freqz(b,a,Nn,Fs);
plot(f,20*log(abs(h)))
%生成频率响应参数
语音信号处理PPT_第三章_语音信号分析

En
xn (m )
2
m 0
T[x]=x2
短时能量及短时平均幅度分析
En是一个度量语音信号幅度值变化的函数,但它有一个缺陷,即 它对高电平非常敏感(因为它计算时用的是信号的平方)。为此, 可采用另一个度量语音信号幅度值变化的函数,即短时平均幅度 N 1 函数Mn,它定义为:
M
n
xn (m )
它与12位线性转换器等效。
预处理
由于语音信号的平均功率谱受声门激励和口鼻辐射影响,高频端 大约在800Hz以上按6dB /倍频程跌落,要在预处理中进行预加重 (Preemphasis)处理。 预加重目的: 提升高频部分,使信号的频谱变得平坦,保持在低频到高频的整 个频带中,能用同样的信噪比求频谱,以便于频谱分析或声道参 数分析。 预加重可在语音信号数字化时在反混叠滤波器之前进行,不仅可 以进行预加重,而且可以压缩吸纳后的动态范围,有效提高信噪 比。 预加重一般在语音信号数字化之后,利用数字滤波器实现: 1 H (z) 1 z 值接近1。
S N R ( d B ) 6 .0 2 B 7 .2
x2 X S N R ( d B ) 1 0 lg 2 6 .0 2 B 4 .7 7 2 0 lg m a x e x
A/D转换器分为线性和非线性转换器两类。 目前的线性A/D转换器绝大部分是12bits的(即每一个采样 脉冲转换为12位二进制数)。非线性A/D转换器则是8位的,
n n
短时相关分析
右图中:N=401,Fs=8kHz a、b是浊音信号,c位清 音信号,由图可以看出浊 音信号的自相关函数具有 一定得周期性,而清音信 号的自相关函数缺乏周期 性。
实验二 语音信号的时域分析

实验二 语音信号的时域分析1 实验目的通过Matlab 编程实现语音信号的时域波形图,并观察清音、浊音信号的时域特点。
掌握语音信号的时域分析技术,如短时平均能量、短时平均幅度、短时平均过零率分析、短时平均自相关、短时平均幅度差。
2 实验原理语音信号的时域分析就是分析和提取语音信号的时域参数。
时域分析通常用于最基本的参数分析及应用,此方法表示语音信号比较直观,物理意义明确,实现起来比较简单,运算量少。
3 实验过程1)观察浊音信号波形图2)观察清音信号波形图3)计算语音信号的短时能量、短时平均幅度并画图120()N n n m E x m -==∑10|()|N n n m M x m -==∑4)计算信号的短时平均过零率并画图 11{|sgn[()]sgn[(1)]|}2N n n m Zn x m x m -==--∑ 5)计算语音信号的短时自相关函数并画图10()()()N k n n n m R k x m x m k --==+∑6)计算语音信号的短时平均幅度差函数并画图10()|()()|N k n n nm F k x m x m k --==-+∑一.短时能量[x,fs,bits]=wavread('c:\WINDOWS\Media\chimes.wav') x=x(:,1);c=x;x=x';N=256;M=N/2;k=1:N;w=0.54-0.46*cos(2*pi/N*k);Fn=fix((L-N)/M)+1;y=[];for i=1:Fnbeg=(i-1)*M+1;ed=beg+N-1;temp=x(beg:ed);temp=temp.*w;y=[y;temp];endEn=[];k=0;for i=1:Fnx=y(i,:);temp=sum(x.*x,2);En=[En,temp];endEn=sum(y.*y,2);subplot(211);plot(c);subplot(212);plot(En);xlabel('time');ylabel('amplitude');title('picture');二.短时自相关函数[x,fs,bits]=wavread('c:\WINDOWS\Media\chimes.wav') x=x(:,1);x=x';N=256;M=N/2;k=1:N;w=0.54-0.46*cos(2*pi/N*k);Fn=fix((L-N)/M)+1;y=[];for i=1:Fnbeg=(i-1)*M+1;ed=beg+N-1;temp=x(beg:ed);temp=temp.*w;y=[y;temp];endZn=sum(abs(sign(y(2:N))-sign(y(1:N-1))),2)*0.5N=256;K=128;for i=1:Fnr=[];x=y(i,:);for k=1:Kr(k)=sum(x(1:N-k).*x(k+1:N),2);endendplot(r);三.短时平均过零率[x,fs,bits]=wavread('c:\WINDOWS\Media\chimes.wav') x=x(:,1);c=x;x=x';N=256;M=N/2;k=1:N;w=0.54-0.46*cos(2*pi/N*k);Fn=fix((L-N)/M)+1;y=[];for i=1:Fnbeg=(i-1)*M+1;ed=beg+N-1;temp=x(beg:ed);temp=temp.*w;y=[y;temp];endfor i=1:Fnx=y(i,:);Zn1=[0];for k=2:NZ=0.5*abs(sign(x(k))-sign(x(k-1)));Zn1=Zn1+Z;endZn=[Zn,Zn1];endsubplot(211);plot(c);subplot(212);plot(Zn);xlabel('time');ylabel('amplitude');title('picture');四.短时平均幅度[x,fs,bits]=wavread('c:\WINDOWS\Media\chimes.wav') x=x(:,1);c=x;x=x';N=256;M=N/2;w=0.54-0.46*cos(2*pi/N*k); Fn=fix((L-N)/M)+1;y=[];for i=1:Fnbeg=(i-1)*M+1;ed=beg+N-1;temp=x(beg:ed);temp=temp.*w;y=[y;temp];endEn=[];k=0;for i=1:Fnx=y(i,:);temp=sum(abs(x),2);En=[En,temp];endEn=sum(y.*y,2);subplot(211);plot(c);subplot(212);plot(En);xlabel('time');ylabel('amplitude');title('picture');五.短时平均幅度差函数[x,fs,bits]=wavread('c:\WINDOWS\Media\chimes.wav') x=x(:,1);x=x';N=256;M=N/2;k=1:N;w=0.54-0.46*cos(2*pi/N*k);Fn=fix((L-N)/M)+1;y=[];for i=1:Fnbeg=(i-1)*M+1;ed=beg+N-1;temp=x(beg:ed);temp=temp.*w;y=[y;temp];endZn=sum(abs(sign(y(2:N))-sign(y(1:N-1))),2)*0.5N=256;K=128;for i=1:Fnr=[];x=y(i,:);for k=1:KF1(k)=abs(x(M)-x(M+k));endendplot(F1);。
语音信号处理第3章-语音信号分析

0.54 0.46cos[2n /( N 1)], 0 n ( N 1) (n) 0, n else
信息科学与工程学院 东南大学
预处理
窗函数的形状和长度对短时参数特征影响 很大 1.窗口形状
时域:要减小时间窗两端的坡度,使窗口边缘 两端不引起急剧变化而平滑过渡到零,这样可 以使截取出的语音波形缓慢降为零,减小语音 帧的截断效应; 频域:要有较窄的3dB带宽以及较大的旁瓣衰 减(较小的边带最大值)。这里只以典型的矩形 窗和汉明窗为例进行比较。
0
20
40
60
80
100
120
140
160
0.1 0.05 0 -0.05 -0.1
0
20
40
60
80 k = -21
100
120
140
160
信息科学与工程学院
东南大学
0.1 0.05 0 -0.05 -0.1
0
20
40
60
80
100
120
140
160
0.1 0.05 0 -0.05 -0.1
0
20
信息科学与工程学院 东南大学
矩形窗与汉明窗的比较
窗类型
矩形窗 汉明窗
旁瓣峰值
-13 -41
主瓣宽度
4π/N 8π/N
最小阻带衰减
-21 -53
汉明窗的主瓣宽度比矩形窗大一倍,即带宽约增 加一倍,同时其带外衰减也比矩形窗大一倍多, 汉明窗比矩形窗更为合适。因此,对语音信号的 短时分析来说,窗口的形状是至关重要的。
信息科学与工程学院 东南大学
数字化和预处理
经过数字化和预处理过程,语音信号就已 经被分割成一帧一帧的加过窗函数的短时 平稳信号 对每一个短时语音帧,利用数字信号处理 技术来提取语音特征参数。
3第三章 语音信号分析---时域分析 语音信号处理 课件

4/25/2021
32/66
存在的问题
短时能量函数一个主要的问题是En对信号电平值 过于敏感。由于需要计算信号样值的平方和,在实 际应用中(如定点设备)很容易溢出。因此,一般 用平均幅度函数Mn来代替En。但这时,清音和浊 音、有声和无声的幅度差不如短时能量明显。
4/25/2021
33/66
二、短时过零率分析
Telephone
Frequency scope
200-3400
Sampling frequency
8 khz
Quantizati on bits
8 bits
Wide band 50-7000
16 khz
16 bits
Broadcasti ng
CD
20-15khz 20-20khz
37.8 khz 44.1 khz
4/25/2021
xa(t) t
xa(nT) n
5/66
• Ideal sampling and real sampling
4/25/2021
6/66
3. A/D转换
对离散时间信号进行量化,在每一时刻对xa(nT) 独立进行量化,把给定的幅度连续的信号变成为有限 多个幅度的集合中某个幅度值的过程。
4/25/2021
37/66
1 0.8 0.6 0.4 0.2
0 -0.2 -0.4 -0.6 -0.8
-1 0
50
100
150
200
250
300
350
400
450
女声汉语拼音a的一帧信号(在采样频 率为22050Hz的情况下,取20ms作为一 帧),短时过零率为46。
4/25/2021
语音信号处理课件__第03章时域分析

x
xmax
)
(3-11)
3.1 语音信号的短时处理方法 脉冲编码调制
若是xmax取为4倍方差(δx)
SNRdB 6.02B 7.27
取样之位数 8 16 24
(3-12)
数字信号的信噪比 41 dB 89 dB 137 dB
3.1 语音信号的短时处理方法 脉冲编码调制
一个数字信号取样之后,变成离散时间信号,接下来就是要用数字 方式来表示这个离散时间信号上的每个取样值。 一个电位波形会有固定的电压范围,一个取样值可以是在此电压范 围内的任何电位。如果只能用固定数目的位来表示这些取样值,那 么这些二进数字就只能代表固定的几个电位值,这个转换就是量化 (quantization),而转换之后只允许存在的几个电位值就是量化阶 数(quantization level)。 执行量化转换的硬件电路,就是量化器(quantizer)。以二进数字 表示的信号就是数字信号(digital signal),而这种将信号波形转 变成二进数字的方法,就叫脉冲编码调制(pulse code modulation, PCM)。
3.1 语音信号的短时处理方法
预处理 平滑滤波器:D/A后面的低通滤波器是平滑滤 波器,对重构的语音波形的高次谐波起平滑 作用,以去除高次谐波失真。 预加重:
现象:由于语音信号的平均功率谱受声门激励和口 鼻辐射的影响,高频端大约在800 Hz以上按6dB/ 倍频程跌落,为此要在预处理中进行预加重。 目的:提升高频部分,使信号的频谱变得平坦,以 便于进行频谱分析或声道参数分析。 位置:预加重可在A/D变换前的反混叠滤波之前进行, 这样不仅能够进行预加重,而且可以压缩信号的动 态范围,有效地提高信噪比。
语音信号处理PPT_第三章_语音信号分析

3.2 数字化和预处理
➢ 语音信号的数字化一般包括放大及增益控制、反混叠滤波、
采样、A/D变换及编码(一般就是PCM码);如下图:
语音信号
带通滤 波器
自动增益控制 (AGC)
模/数转换 (A/D)
脉冲编码 调 制 ( PCM )
存入计算机
➢ 预处理一般包括预加重、加窗和分帧等。 ➢ 分析和处理之前必须把要分析的要分析的语音信号部分从输
② R n (是k )偶函数 ,即 Rn(k)Rn(k)
③ 当k=0时,自相关函数有最大值,即 Rn(0)Rn(k)
并且 等R于n (确0 ) 定性信号序列的能量或随机序列的平均功率。
短时相关分析
右图中:N=401, Fs=8kHz a、b是浊音信号,c位清 音信号,由图可以看出浊 音信号的自相关函数具有 一定得周期性,而清音信 号的自相关函数缺乏周期 性。
但是在一个短时间范围内(一般认为在10-30ms的短时间内), 其特性基本保持不变即相对稳定,因而可以将其看作是一个准稳 态过程,即语音信号具有短时平稳性。
不论是分析怎么样的参数以及采用什么分析方法,在按帧进 行语音分析,提取语音参数之前,有一些经常使用的、共同的短 时分析技术必须预先进行,如语音信号的数字化、语音信号的端 点检测、预加重、加窗和分帧等,这些也是不可忽视的语音信号 析的关键技术。
语音信号分析在语音信号处理中具有举足轻重的地位。
分类:
参数性质
时域分析 频域分析 倒谱域分析
分析方法
模型分析方法 非模型分析方法
简单、计算量小、 物理意义明确
感知特性 较好,更 为重要
依据语音信号 产生的数学模 型来分析和提 取表征这些模 型的特征参数
不进行模型化 分析
3语音信号处理 时频分析

语音产生模型
主要内容 2.1 语音信号的产生模型 2.2 语音的感知 2.3 语音学基础知识
语音产生模型(1)
2.1 语音的产生
鼻 鼻腔 硬腭 齿龈 上唇 牙齿 下唇 下颚骨 舌骨 鼻咽 软腭 口腔 小舌 舌根
发音器官包括:肺、气 管、喉、咽、鼻腔、口 腔、唇。 声道是对发音起重要作 用的器官。 声带每开启和闭合一次 的时间是基音周期 (Pitch Period),其倒 数为基音频率。
1
a z
i 0 i
p
i
P为全极点滤波器的阶,在8-12内取值。一对极点对应一个 共振峰。
语音产生模型(7)
辐射模型 研究表明:辐射效应在高频段较为明显,在低频段影响较小。 可用一个高通滤波器来表示辐射模型。
R( z) (1 rz 1 )
其中r接近1。 在实际信号分析时,常采用这样的预加重技术。即在采样 之后,插入一个一阶高通滤波器。在语音合成时再进行 “去加重”处理,就可以恢复原来的语音。
5
450
570 700 840 1000 1170 1370 1600 1850 2150 2500
110
120 140 150 160 190 210 240 280 320 380
20
21 21 22 22 23 23 24 25 25 26
400
510 630 770 920 1080 1270 1480 1720 2000 2320
2 4 r (n) x(n) a(n) sin ( f (n))
语音产生模型(19)
以 a(n) 和 f (n) 为未知函数,联立求解,可得到 信号的幅值包络和瞬时频率如下:
第3讲语音信号处理第3

其中,
xn (m) (m)x(n m), (0 k K )
(m)
1, 0,
m 0 ~ (N 1) m 其它值
x'n (m) '(m)x(n m), (0 k N 1 K)
'
(m)
1, 0,
m 0 ~ (N 1 K) m 其它值
2.修正的短时自相关函数
图3-7 修正短时自相关函数计算中窗口长度的说明
N 1
M n xn (m) m0
❖ Mn也是一帧语音信号能量大小的表征,它与En的区别在于 计算时小取样值和大取样值不会因取平方而造成较大差异, 在某些应用领域中会带来一些好处。
短时过零率分析
❖ 短时过零率表示一帧语音中语音信号波形穿过横轴(零电平) 的次数。过零分析是语音时域分析中最简单的一种。对于连 续语音信号,过零即意味着时域波形通过时间轴;而对于离 散信号,如果相邻的取样值改变符号则称为过零。过零率就 是样本改变符号的次数。
3.1 概述
❖ 语音信号分析 分析出可表示语音信号特征参数
进行高效的语音通信、语音合成和语音识别的基础 时域特征 频率特征
❖ 短时分析技术:贯穿于语音分析全过程 语音信号从整体来看其特征及表征其本质特征的参数均是
随时间而变化的,所以它是一个非平衡态过程,不能用处理 平衡信号的数字信号处理技术对其进行分析处理。
(m)
1, 0,
m 0 ~ (N 1) m 其它值
❖ 其中,n=0,1T,2T,…,并且N为帧长,T为帧移长度。
❖ 设第n帧语音信号xn(m)的短时能量用En表示,则其计算公 式如下:
N 1
En xn2 (m) m0
短时能量及短时平均幅度分析
❖ En是一个度量语音信号幅度值变化的函数,但它有一个缺陷, 即它对高电平非常敏感(因为它计算时用的是信号的平方)。 为此,可采用另一个度量语音信号幅度值变化的函数,即短 时平均幅度函数Mn,它定义为:
第3章 语音信号分析(全)

x1 (n) x2 (n)
D
L
D
ˆ y ( n)
1
ˆ ˆ x1 (n) x2 (n)
ˆ ˆ y1 (n) y2 (n)
x(n)
ˆ x ( n)
y1 (n) y2 (n)
y(n)
b)同态系统的组成
D1
D 是特征子系统 L
是线性子系统
振 幅
· ·· · · · · ·· · ·· ·· ·
x(n)= x(nT):取样值 时间 采样周期(T)
第3章 语音信号分析
量化: 幅值方向的离散化
量化信噪比
SNR(dB) 6.02 B 7.2
其中,B表示量化字长 B=7bit时,SNR=35dB,可以满足一般通信系统 的要求。
Fn (k )
N k 1 m 0
x ( m) x ( m k )
n n
(0 k K )
第3章 语音信号分析
极小值
图3-9 与图3-5有相同语音段的AMDF函数的例子
第3章 语音信号分析
短时平均幅度差函数的作用 求语音序列的基音周期 用于区分语音中的清音段和浊音段
0 m N 1 K
m 0 ~ ( N 1 K ) m 其他值
第3章 语音信号分析
图3-6 修正短时自相关函数计算中窗口长度的说明
第3章 语音信号分析
3.3.4 短时平均幅度差函数
平均幅度差函数( AMDF) Average Magnitude Difference Function 短时平均幅度差函数的定义
语音信号处理第3章-语音信号分析讲解

信息科学与工程学院
东南大学
预处理:加窗
2.窗口的长度
采样周期Ts=1/fs,窗口长度N和频率分辨率Δf 之间存在下列关系:
采样率一定时,Δf 随窗口宽度N的增加而减小 ,即频率分辨率相应得到提高
• 窗口长,频率分辨率高,时域分辨率降低 • 窗口短,频率分辨率低,时间分辨率提高
1 Vf NTs
其中σx2表示语音方差,2Xmax表示信号的峰值,B 表示量化字长, σe2表示噪声方差。 通常语音信号的幅度符合Laplacian分布,则 SNR(dB) 6.02B 7.2 表明量化器中的每bit字长对SNR的贡献为6dB。
信息科学与工程学院
东南大学
预处理:预加重
语音信号的平均功率谱受声门激励和口鼻 辐射影响,预处理中要进行预加重 (Preemphasis)处理。其目的是提升高频部 分,使信号频谱变得平坦,以便于频谱分 析或声道参数分析。
信息科学与工程学院
东南大学
预处理:加窗
窗口长度的选择,更重要的是要考虑语音 信号的基音周期。通常认为在一个语音帧 内应包含1~7个基音周期。 不同人的基音周期变化很大,从女性和儿 童的2ms到老年男子的14ms(即基音频率的 变化范围为500~70Hz),所以N的选择比较 困难。 通常在10kHz取样频率下,N折中选择为 100~200点为宜(即10~20ms持续时间)。
信息科学与工程学院 东南大学
预处理:加窗
矩形窗与汉明窗的比较
窗类型 旁瓣峰值 主瓣宽度 最小阻带衰减
矩形窗 汉明窗 -13 -41 4π/N 8π/N -21 -53
汉明窗的主瓣宽度比矩形窗大一倍,即带 宽约增加一倍,同时其带外衰减也比矩形 窗大一倍多,汉明窗比矩形窗更为合适。 因此,对语音信号的短时分析来说,窗口 的形状是至关重要的。
《语音信号处理》讲稿第3章

对性的改进。
03 语音信号的特征提取
时域特征提取
过零率
表示语音信号通过零点的 次数,反映了语音信号的 频率特性。
能量和振幅
计算语音信号的短时能量 和振幅,用于区分清音和 浊音。
自相关函数
描述语音信号在不同时间 点的相似程度,常用于语 音信号的周期性分析。
频域特征提取
傅里叶变换
将时域语音信号转换为频域表示, 便于分析语音信号的频谱特性。
滤波器组
将语音信号划分为多个频带,提取 每个频带的能量或振幅作为特征。
功率谱密度
描述语音信号在各个频率上的功率 分布,反映了语音信号的频谱包络。
倒谱特征提取
1 2
倒谱系数
通过对语音信号的频谱进行对数运算和逆变换, 得到倒谱系数,用于描述语音信号的共振峰特性。
梅尔频率倒谱系数(MFCC) 基于人耳听觉特性,将频谱转换为梅尔频率尺度, 再计算倒谱系数,是语音识别中常用的特征参数。
《语音信号处理》讲稿第3章
目录
• 语音信号处理基础 • 语音信号的预处理 • 语音信号的特征提取 • 语音信号的模型分析 • 语音信号的编码技术 • 语音信号的增强与降噪 • 语音信号的识别技术
01 语音信号处理基础
语音信号的特点
非平稳性
语音信号是一个时变的 信号,其特性随时间变
化。
周期性
浊音信号表现出明显的 周期性,清音信号则不
(HMM)、深度神经网络 (DNN)等,通过统计模型对
语音进行建模和识别。
混合方法
结合基于规则和统计模型的 方法,充分利用两者的优点 ,提高识别性能。
语音识别的实际应用及挑战
实际应用
语音识别技术已广泛应用于智能家居、智能客服、语音输入、语音翻译等领域,为人们的日常生活和工作带来便 利。
语音信号处理第三章

第三章语音信号分析1、语音信号分析?语音信号分析的目标是从语音信号中提取出一个或多个能够描述语音信号的参数,以便在语音编码、语音合成和语音识别等应用。
语音信号分析的目的就是在于方便有效地提取并表示语音信号所携带的信息,是语音信号处理的前提和基础,只有分析出可表示语音信号特征的参数,才有可能利用这些参数进行高效的语音通信,语音合成和语音识别等处理。
一般而言,语音处理的目的有两种:对语音信号进行分析,提取特征参数。
如:语音编码中需要判断语音的清浊音特性并提取浊音的基音周期;语音识别中需要提取符合人耳听觉特性的Mel倒谱参数等。
加工语音信号。
如:语音增强中对含噪语音进行背景噪声抑制,以获得相对干净的语音;在语音合成中需要对分段语音进行拼接平滑,获得主观音质较好的合成语音。
根据所分析出的参数性质的不同可以分为:时域分析、频域分析、倒谱域分析、线性预测分析等;根据分析方法的不同:模型分析方法和非模型分析方法。
不论分析怎么样的参数以及采用什么分析方法,在按帧进行语音分析,提取语音参数之前,有一些经常使用的、共同的短时分析技术必须预先进行,如语音信号的数字化,语音信号的端点检测、预加重、加窗和分帧等,这些也是不可忽视的语音信号分析的关键技术。
2、语音信号的数字化和预处理?语音信号的数字化(数字系统具有高速、低成本、低功耗、通用的特点)一般包括放大及增益控制、反混叠滤波、采样、A/D变换及编码(一般就是PCM码):语音信号的数字化过程框图预处理一般包括预加重、加窗和分帧等。
在分析处理之前必须把要分析的语音信号部分从输入信号中找出来,这项工作叫做语音信号的端点检测。
预滤波的目的有两个:抑制输入信号各频域分量中频率超过f的所有分量(s f)为采样频率,以防止混叠干扰s(高频成分产生失真)。
抑制50Hz的电源工频干扰。
(市电电压的频率为50Hz,它会以电磁波的辐射形式,对人们的日常生活造成干扰,这种干扰称为工频干扰)这样,预滤波器必须是一个带通滤波器,设其上、下截止频率分别是Hf 和Lf ,则对绝大多数语音译码器:Hzf H 3400=,Hzf L 100~60=,采样频率kHzf s 8=,要求较高的场合:Hzf H 4500=,Hzf L 60=,采样频率kHzf s 10=。
语音信号时域分析
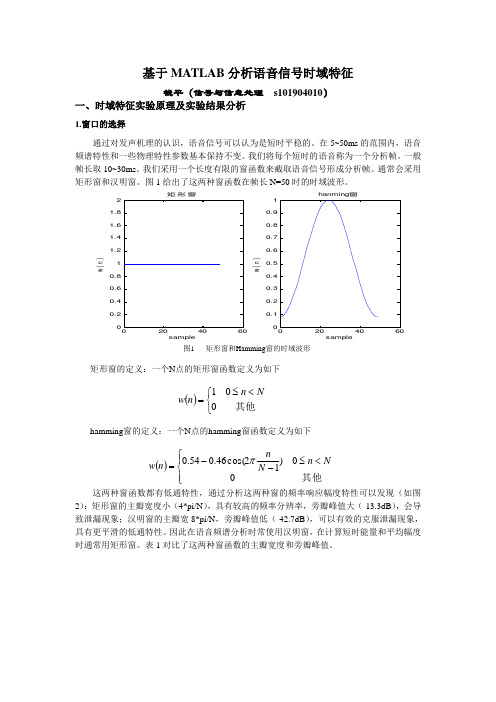
基于MATLAB 分析语音信号时域特征钱平(信号与信息处理 s101904010)一、时域特征实验原理及实验结果分析1.窗口的选择通过对发声机理的认识,语音信号可以认为是短时平稳的。
在5~50ms 的范围内,语音频谱特性和一些物理特性参数基本保持不变。
我们将每个短时的语音称为一个分析帧。
一般帧长取10~30ms 。
我们采用一个长度有限的窗函数来截取语音信号形成分析帧。
通常会采用矩形窗和汉明窗。
图1给出了这两种窗函数在帧长N=50时的时域波形。
0.20.40.60.811.21.41.61.82矩形窗samplew (n )0.10.20.30.40.50.60.70.80.91hanming 窗samplew (n )图1 矩形窗和Hamming 窗的时域波形矩形窗的定义:一个N 点的矩形窗函数定义为如下()⎩⎨⎧<≤=其他001Nn n whamming 窗的定义:一个N 点的hamming 窗函数定义为如下()⎪⎩⎪⎨⎧<≤--=其他00)12cos(46.054.0Nn N n n w π 这两种窗函数都有低通特性,通过分析这两种窗的频率响应幅度特性可以发现(如图2):矩形窗的主瓣宽度小(4*pi/N ),具有较高的频率分辨率,旁瓣峰值大(-13.3dB ),会导致泄漏现象;汉明窗的主瓣宽8*pi/N ,旁瓣峰值低(-42.7dB ),可以有效的克服泄漏现象,具有更平滑的低通特性。
因此在语音频谱分析时常使用汉明窗,在计算短时能量和平均幅度时通常用矩形窗。
表1对比了这两种窗函数的主瓣宽度和旁瓣峰值。
00.10.20.30.40.50.60.70.80.91-80-60-40-200矩形窗频率响应归一化频率(f/fs)幅度/d B00.10.20.30.40.50.60.70.80.91-100-50Hamming 窗频率响应归一化频率(f/fs)幅度/d B图2 矩形窗和Hamming 窗的频率响应表1 矩形窗和hamming 窗的主瓣宽度和旁瓣峰值2.短时能量由于语音信号的能量随时间变化,清音和浊音之间的能量差别相当显著。
语音信号处理第3章分解PPT课件

14
预处理
2.窗口的长度 ❖ 采样周期Ts=1/fs,窗口长度N和频率分辨率Δf
之间存在下列关系: Δf=1/NTs
语音信号
带通滤 波器
自动增益控 制(AGC)
模/数转换 (A/D)
脉冲编码
存入计算机
调制(PCM)
❖ 预处理一般包括预加重、加窗和分帧等。
5
预滤波、采样、A/D变换
预滤波的目的有两个: ❖ 抑制输入信号各频域分量中频率超出fs/2的所有分量(fs)
为采样频率,以防止混叠干扰。 ❖ 抑制50Hz的电源工频干扰。
0n(N1) nelse
(n ) 0 .5 4 0 .4c6 0 ,o 2 n s /N ([ 1 )]0 , n n e (N l1 s ) e
12
预处理
1.窗口的形状 ❖ 好的窗函数的标准是:在时域因为是语音波形乘以
窗函数,所以要减小时间窗两端的坡度,使窗口边 缘两端不引起急剧变化而平滑过渡到零,这样可以 使截取出的语音波形缓慢降为零,减小语音帧的截 断效应;在频域要有较宽的3dB带宽以及较小的边 带最大值。这里只以典型的矩形窗和汉明窗为例进 行比较,其他窗口可参阅FIR数字滤波器或谱分析 的有关书籍。
但是在一个短时间范围内(一般认为在10-30ms的短时间
内),其特性基本保持不变即相对稳定,因而可以将其看作
是一个准稳态过程,即语音信号具有短时平稳性。
3
1 概述
❖ 根据所分析出的参数的性质的不同可以分为: 时域分析、频域分析、倒频域分析,线性预测分析等;
❖ 分析方法的不同: 模型分析方法 和 非模型分析方法
原信号值之间的差值称为量化误差,又称为量化噪声。 ❖ 若量化间隔Δ足够小,可以证明量化噪声符合具有下列特征
第03讲 语音信号变换域(频域+倒谱)分析

由图可见:
由于窗长很短,所选出的语音段甚至不到一个基音周期长度, 因此语音段丢失了关于基音周期的信息,表现在短时谱上 就是反映基音频率和谐波的快速变化特点消失了,短时谱 中只保留着慢速变化的特点,也就是还保持着声道滤波器
的共振峰。由于矩形窗具有更高的频谱分辨率,因此其短
时频谱不如汉明窗平滑。
从以上对窗函数和短时频谱的讨论可以得出以下结论: • 1)矩形窗和汉明窗的主瓣狭窄且旁瓣衰减较大,具有低 通的性质。窗越长,主瓣越窄,加窗后的频谱能更好地逼 近短时语音的频谱。 • 2)窗长越长,频谱分辨率越高,但由于长窗的时间平均 作用导致时间分辨率相应下降,如共振峰在不同的基音周 期是要发生变化,但如果使用较长的窗则会模糊这种变化。 • 3)窗长越短,时间分辨率越高,但频率分辨率相应降低。 如采用短窗可以清楚地观察到共振峰在不同基音周期的变 化情况,但是基频以及谐波的精细结构在短时频谱图上消 失了。 • 4)由于时间分辨率和频谱分辨率的相互矛盾关系,在进 行短时傅里叶变换时,应根据分析的目的来折中选择窗长。
X n (e j ) xn (m)e jm
m 0 N 1
m
x m w n m e jm
m
x m e jm w n m
当w固定不变时, X n (e j ) 可视为信号 x m e jm 与窗函数 w n 的卷积,此时,短时傅立叶变换可看作线性滤波.
• 在语音信号数字处理中,功率谱具有重要意义,在一些语音 应用系统中,往往都是利用语音信号的功率谱。根据功率谱 定义,可以写出短时功率谱与短时傅里叶变换之间的关系:
S n (e ) X n (e ) X (e ) X n (e )
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
白噪声信号
相关分析的依据
修改坐标的自相关函数波形
• 用于确定两个信号在时域内的相似性。常用 的物理量为自相关函数和互相关函数。 • 当两个信号的互相关函数大时,则说明一个 信号可能是另一个信号的时间滞后或提前; • 当互相关函数为0时,则两个信号完全不同。 • 自相关函数用于研究信号本身,如波形的同 步性和周期性。
PG ( x ) = [ 3 8πσ x x ] e
1 2 − 3x 2σ x
PL ( x) =
− 1 e 2σ x 2σ x
2x
二、零均值 三、非平稳时变信号;短时平稳:10~30ms
§3.2语音信号短时分析方法
语音信号的开窗分析技术: (1)均匀窗: (2)非均匀窗:各种国际标准 (3)重叠窗(Overlap) 设:语音信号为S(n),加窗语音记为 Sw(n) = W[S(n)] = S(n) w(n-m),n=0~(N-1) 则语音处理系统可表示为
5
基于能量和过零率的双门限法检测法
首先用短时能量做第一次判断,然后在此基础上 用短时平均过零率做第二次判断。 这种方法端点的确定与以后的判决无关,因此称 为显式法。
三、短时相关分析
短时自相关函数性质 • 1. R w( −l ) = R w(l ) 为偶函数; • 2. 在-N+1~N-1之间有值; • 3. R ( 0 ) = ∑ s ( n ) ≥ R ( k ) 为最大值。 • 4.当时域信号为周期信号时,自相关函 数也是周期性函数,两者周期相同。 浊音:呈现‘准’周期性、逐渐衰减
男声汉语拼音s的一帧信号(在采样频率为22050Hz 的情况下,取20ms作为一帧),清音的短时能量为 3.88。
二.短时过零率分析
• 过零率定义:信号跨越横轴的次数情况。 • 对于连续信号,观察语音时域波形通过 横轴的情况; • 对于离散信号,相邻的采样值具有不同 的代数符号,也就是样点改变符号的次 数。
• 1.在浊音下M0的概率密度高,因此设一高阈 值Mh,当M0>Mh时,可判断出语音信号前后两 点N1和N2,使(N1,N2)区间为有声音区。 • 2.确定精确起终点:再设置一个低阈值ML, 由N1向前找,当M<ML时有N3;由N2向后找,当 M<ML时有N4,则(N3,N4)区间为语音区。 • 3.根据无声时Z均值设置ZT,由N3向前,N4向 后计算过零率Z,Z>3ZT的部分仍为语音区; 至Z<3ZT时,得(N5,N6),搜索结束。
2
1
0 .3
0 .8
0 .2
0 .6
0 .4
0 .1
0 .2
0
0
-0 . 2
-0 . 1
-0 . 4
-0 . 2
-0 . 6
-0 . 8
-0 . 3
-1
0
50
100
150
200
250
300
350
400
450
-0 . 4
0
50
100
150
200
250
300
350
400
450
女声汉语拼音a的一帧信号(在采样频率为 22050Hz的情况下,取20ms作为一帧),浊 音的短时能量为78.61。
清 音 谱
五.Gabor变换和小波变换
平稳信号的分析工具: Fourier变换:将信号分解为正弦波的线性组 合。 非平稳信号的分析工具: Wavelet变换:将信号分解为小波的• 声道的共振峰特性对基音周期的估计造 成干扰,这是因为语音信号包含丰富的 谐波分量。基音频率的范围分布在50~ 450Hz左右。同时,第一共振峰通常在 200~1000Hz的范围内,这样可能导致语 音的谐波分量高于基频分量,对基音周 期的估计造成错误。
-2000
正弦波周期信号的自相关函数波形
-3000
0
1000
2000
3000
4000
5000
6000
6
1
0 .5
相关函数的作用
• 1.区分清/浊音。 浊音的自相关函数具有一定的周期性。 清音的自相关函数不具有周期性,类似噪 声,有点如语音信号本身。 • 2.估计浊音信号的周期,即估计基音周期。
0
-0 . 5
常用语音信号短时分析特征参数
(1)短时能量 E0
E0 = ∑ S w ( n ) = ∑ S w 2 ( n )
2 n=0 n =0 N −1 N −1
(2)短时平均幅度 M0
M 0 = ∑ Sw (n)
n =0 N −1
(3)短时平均过零率 Z0
Q = ∑ W[s(k)]h(n − k)
n k=-∞
t n
过零情况
3
1
短时平均过零的作用
• 1.区分清/浊音: 浊音平均过零率低,集中在低频端; 清音平均过零率高,集中在高频端。 • 2.从背景噪声中找出是否有语音,以及语 音的起点。
0 .8
0 .6
0 .4
0 .2
0
-0 . 2
-0 . 4
-0 . 6
-0 . 8
-1
0
50
100
150
200
250
语音信号处理
Speech Signal Processing
长春工业大学图像工程研究所 史东承教授
dcshi@ 2010.8
第三章 语音信号的分析方法
§3.1 语音信号的统计特性
一、概率密度函数: 语音信号是非平稳超高斯随机信号;近似 Gamma分布,可用 Laplace 分布近似。
用MATLAB的函数randn,产生一帧高斯白噪 声,其自相关函数图。说明清音是噪声激励的 正确性。
8
利用信号的相关性达到消除噪 声的目的
• 主信号s+n0,为有用信号s(来自信号源) 和一个与它不相关的噪声信号混合而成。 • n1为另外拾取的噪声参考信号,与n0相关。 主输入信号x=s+n0 +
-1
0
50
100
150
200
250
300
350
400
450
原始语音信号
100 50 0
-5 0
自相关函数波形
0 50 100 150 200 250 300 350 400 450
-1 0 0
女声汉语拼音a的一帧信号(在采样频率为 22050Hz的情况下,取20ms作为一帧),自相关 波形图。说明浊音的自相关函数具有一定的周 期性。
4
在实际应用中,短时平均过零率容易受到A/D 转换是的直流偏移、50Hz交流电源的干扰以及 噪声的影响。 减少这些干扰可以有两种方法:一种是采用带 通滤波器消除信号中的直流和50Hz低频分量; 另一种是用过门限率来修改过零率,减少随机 噪声的影响。
x(n) Hb(ejw) w Bandpass filte Hb
因
0 50 100 150 200 250
序列 号n
-0.75
序列 号n
4 3 2 1
1.0
s ( exp ( jw) ) = S ( exp ( jw) ) ⊗ W ( exp ( jw) )
w
s ( n ) = s ( n ) ⋅W ( n )
w
,所以
0.8
0.6
• 对于方窗:W(exp(jw))上下冲较大,由 于 Sw(exp(jw))与S(exp(jw))差距较大,此 称为Gibbs效应。
80
原始语音信号和其自相关函数波形
60
Auto-Correlation Peaks
40
20
0
-20
-40
-60
0
50
100
150
200
250
300
350
400
450
500
7
0 .4
0 .2
原始语音信号
原始语音信号
0
-0 . 2
-0 . 4
0
50
100
150
200
250
300
350
400
450
3 2 1 0 -1 -2
∞
Z
0
1 ⎧ N −1 ⎫ = ⎨∑ sgn ⎡ s w ( n ) ⎤ − sgn ⎡ s w ( n − 1) ⎤ ⎬ ⎣ ⎦ ⎣ ⎦ 2 ⎩ n =1 ⎭
1
(4)短时自相关函数 Rw
R (l ) = ∑ s (l + n ) s (n ) = ∑ s (n ) s (n + l )
w n = −∞ w w n =0 w w
N −1 n=0 2 w w w
清音:Rw(0)较大,衰减很快 静默:Rw(0)小,衰减很快
1
3000
0.5
正弦波信号和其自相关函数具有相同周期
2000
0
-0.5
-1
1000
0 1000 2000 3000 4000 5000 6000
正弦波周期信号
3000 2000 1000
0
-1000
0 -1000 -2000 -3000 0 1000 2000 3000 4000 5000 6000
∞
N − l −1
短时能量E0、短时平均幅度M0和短时 平均过零率Z0的分布特性 短时能量 平均幅度M0 过零率Z0
(5)短时傅立叶变换 Fn
E0
S (exp( jw))
w
DTFT ( S W ( n) ) = ∑S W ( n) exp ( − jwn)
n=0
N −1
(6)短时功率谱
| S w ( exp ( jw ) ) |2 =
过门限率反映了穿过正负门限的次数,如果 存在随机噪声,只要信号没有超过[-T,T]的 范围,就没有有过零率产生。
