常见分数、小数及百分数互化-常用平方数、立方数及各种计算方法

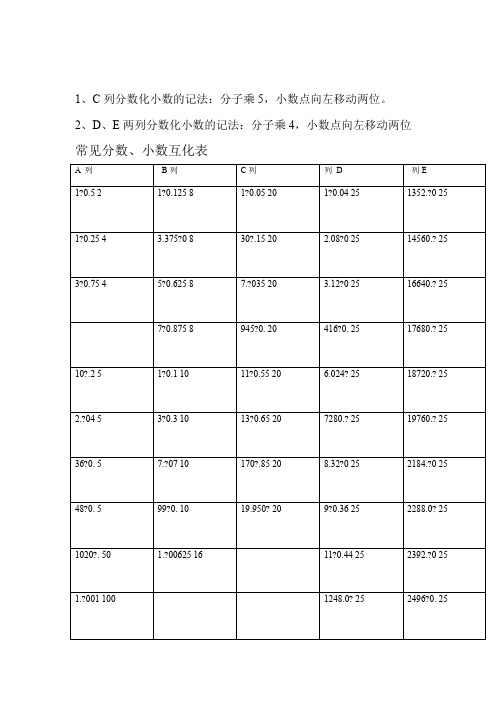
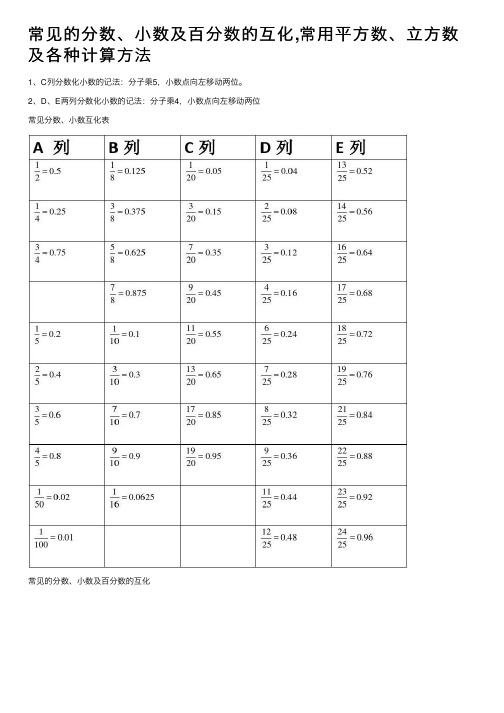
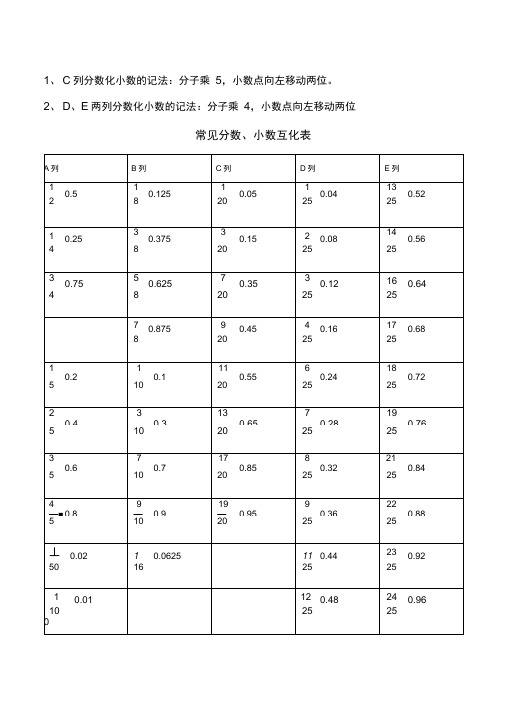
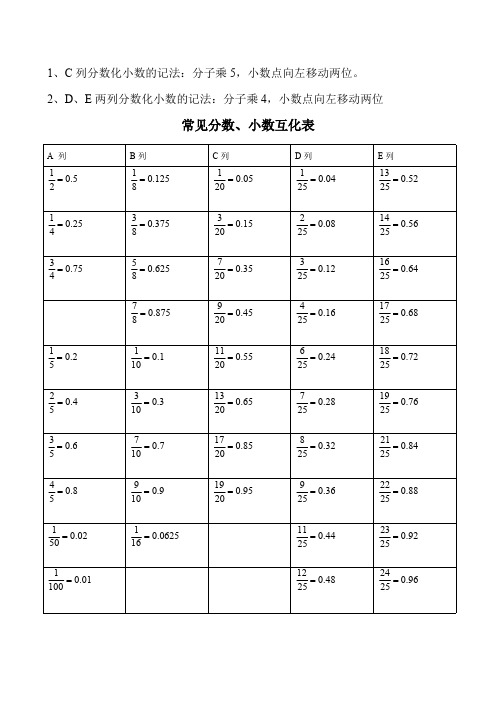
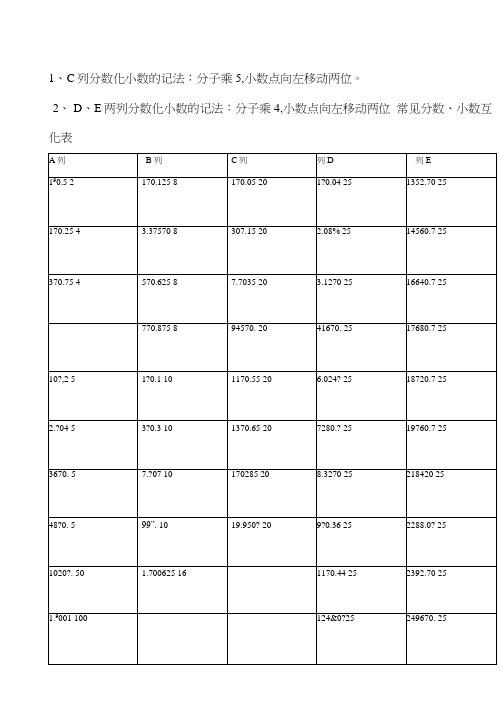
1、C列分数化小数的记法：分子乘5，小数点向左移动两位。

2、D、E两列分数化小数的记法：分子乘4，小数点向左移动两位常见分数、小数互化表常见的分数、小数及百分数的互化常用平方数常见立方数常见特殊数的乘积错位相加/减A×9型速算技巧：A×9= A×10-A；例：743×9=743×10-743=7430-743=6687A×9.9型速算技巧：A×9.9= A×10+A÷10；例：743×9.9=743×10-743÷10=7430-74.3=7355.7A×11型速算技巧：A×11= A×10+A；例：743×11=743×10+743=7430+743=8173A×101型速算技巧：A×101= A×100+A；例：743×101=743×100+743=75043乘/除以5、25、125的速算技巧：A×5型速算技巧：A×5=10A÷2；例：8739.45×5=8739.45×10÷2=87394.5÷2=43697.25A÷5型速算技巧：A÷5=0.1A×2；例：36.843÷5=36.843×0.1×2=3.6843×2=7.3686A×25型速算技巧：A×25=100A÷4；例：7234×25=7234×100÷4=723400÷4=180850A÷25型速算技巧：A÷25=0.01A×4；例：3714÷25=3714×0.01×4=37.14×4=148.56A×125型速算技巧：A×5=1000A÷8；例：8736×125=8736×1000÷8=8736000÷8=1092000A÷125型速算技巧：A÷1255=0.001A×8；例：4115÷125=4115×0.001×8=4.115×8=32.92减半相加：A×1.5型速算技巧：A×1.5=A+A÷2；例：3406×1.5=3406+3406÷2=3406+1703=5109“首数相同尾数互补”型两数乘积速算技巧：积的头=头×（头+1）；积的尾=尾×尾例：23×27=首数均为2，尾数3与7的和是10，互补所以乘积的首数为2×（2+1）=6，尾数为3×7=21，即23×27=621本方法适合11~99 所有平方的计算。

11X11=121 21X21=4141 31X31=961 41X41=168112X12=148 22X22=484 32X32=1024 42X42=1764 52X52=2704从上面的计算我们可以得出公式：个位=个位×个位所得数的个位，如果满几十就向前进几，十位=个位×（十位上的数字×2）+进位所得数的末位，如果满几十就向前进几，百位=两个十位上的数字相乘+进位。

例：26×26=个位=6×6=36，满30 向前进3；十位=6×（2×2）+3=27，满20 向前=进2；百位=2×2+2=6由此可见26×26=67623×23个位=3×3=9十位=3×（2×2）=12，写2 进1百位=2×2+进1=5所以23×23=52946×46 个位=6×6= 36，写6进3十位=6×（4×2）+进3= 5 1，写1 进5百位=4×4+进5= 21，写1 进2所以46×46=2116如果没有满十就不用进位，计算更简便。

例：13×13个位=3×3=9 十位=3×（1×2）=6 百位=1×1 所以13×13=169规律：(1)完全平方数的个位数字只能是0，1，4，5，6，9.(没有2，3，7，8)两个整数的个位数字之和为10，则它们的平方数的个位数字相同。

(2)奇数的平方的个位数字是奇数，十位数字是偶数。

(3)如果完全平方数的十位数字是奇数,则它的个位数字一定是6；反之，如果完全平方数的个位数字是6，则它的十位数字一定是奇数。

(4)偶数的平方是4 的倍数；奇数的平方是4 的倍数加1。

(5)奇数的平方是8n+1 型；偶数的平方为8n 或8n+4 型。

(6)完全平方数的形式必为下列两种之一：3n，3n+1。

(7)不能被5 整除的数的平方为5n±1 型，能被5 整除的数的平方为5n 型。

(8)平方数的形式具有下列形式16n，16n+1，16n+4，16n+9。

(9)完全平方数的各位数字之和的个位数字只能是0，1，3，4，6，7，9.(没有2，5，8)(10)如果质数p 能整除a，但p 的平方不能整除a，则a 不是完全平方数。

(11)在两个相邻的整数的平方数之间的所有整数都不是完全平方数。

(12)一个正整数n 是完全平方数的充分必要条件是n 有奇数个因数(包括1 和n)。

一个数如果是另一个整数的完全立方（即一个整数的三次方,或整数乘以它本身乘以它本身），那么我们就称这个数为完全立方数，也叫做立方数，如0，1，8，27，64，125，216，343，512，729，1000 等。

如果正整数x，y，z 满足不定方程x2+y2=z2 ，就称x，y，z 为一组勾股数。

x，y 必然是一个为奇数另一个为偶数，不可能同时为奇数或同时为偶数。

z 和z²必定都是奇数。

五组常见的勾股数：3²+4²=5²；5²+12²=13²；7²+24²=25²；8²+15²=17²；20²+21²=29²9+16=25；25+144=169；49+576=625；64+225=289；400+441=841记忆技巧：(a+b)²= a²+ b²+ 2ab (a－b)²=a²+ b²－2ab| | | | | |a×a b×b 2×a×b a×a b×b 2×a×b例：13²=(10+3) ²=10²+3²+2×10×3=100+9+60=16988²=(90-2)²=90²+2²－2×90×2=8100+4－360=7744用处：①训练计算能力，使计算更快更准确；②估计某数的平方根所处的范围，在判定某个较大的数n 是不是质数时可以缩小其可能因子的筛选范围,只需检查3 到n 之间的所有质数是不是n 的因子即可，超过n 的都不必检查了例如:判定2431是否为质数，因为49²=2401<2431<2500=50²,所以49<2431 .<50, 2+4+3+1=10不能被3整除, 2341的个位既非0又非5，故只需检查7到47之间的所有质数能否整除2431即可，而53,59,61,67……等更大的质数都不用检查了，实际上2431=11×13×17③增加对数字的熟悉程度，比如16²=256=28，32²=1024=210，64²=4096=212，另外一些特殊结构的数字应该牢记，如88²=7744, 11²=121,22²=484，(121 和484 从左到右与从右到左看是一样的) 12²=144，21²=441，13²=169，31²=961，(a 左右颠倒后a²也左右颠倒)。

小学单位换算一、长度(一) 什么是长度？长度是一维空间的度量。

(二) 长度常用单位* 公里(km) * 米(m) * 分米(dm) * 厘米(cm) * 毫米(mm) * 微米(um)(三) 单位之间的换算1 微米=1000 纳米 1 毫米=1000 微米 1 厘米=10 毫米1 分米=10 厘米 1 米=1000 毫米 1 千米=1000 米1 米=10 分米=100 厘米二、面积(一)什么是面积面积，就是物体所占平面的大小。

对立体物体的表面的多少的测量一般称表面积。

(二)常用的面积单位* 平方毫米* 平方厘米* 平方分米* 平方米* 平方千米(三)面积单位的换算1 平方厘米=100 平方毫米 1 平方分米=100 平方厘米 1 平方米=100 平方分米1 公倾=10000 平方米 1 平方公里=1 平方千米=100 公顷1 公顷=0.01 平方千米≈15 亩 1 平方千米=1000000 平方米1 平方米=100 平方分米=10000 平方厘米三、体积和容积(一)什么是体积、容积体积，就是物体所占空间的大小。

容积，箱子、油桶、仓库等所能容纳物体的体积，通常叫做它们的容积。

(二)常用单位1 体积单位* 立方米* 立方分米* 立方厘米2 容积单位* 升* 毫升(三)单位换算1 平方米=100 平方分米 1 平方分米=100 平方厘米 1 平方厘米=100 平方毫米1 立方米=1000 立方分米 1 立方分米=1000 立方厘米2 容积单位1 升=1 立方米 1 升=1000 毫升 1 毫升=1 立方厘米1 立方米=1000 升 1 立方分米=1 升 1 立方厘米=1 毫升四、质量(一)什么是质量质量，就是表示表示物体有多重。

(二)常用单位* 吨t * 千克kg * 克g(三)常用换算1 吨(t)=1000 千克(kg) 1 千克=1000 克(g)重量单位换算1 吨=1000 千克 1 千克=1000 克 1 千克=1 公斤五、时间(一)什么是时间是指有起点和终点的一段时间世纪、年、月、日、时、分、秒(三)单位换算* 1 世纪=100 年 1 年=12 月 1 年=365 天平年一年=366 天闰年. 一、三、五、七、八、十、十二是大月大月有31 天四、六、九、十一是小月小月有30 天平年2 月有28 天闰年2 月有29 天1 天= 24 小时 1 小时=60 分 1 分=60 秒1秒=1000毫秒（ms）1时=3600秒货币(一)什么是货币货币是充当一切商品的等价物的特殊商品。