2020高考数学立体几何练习题

合集下载

2020年高考数学(理)重难点专练03 空间向量与立体几何(解析版)

2020年高考数学（理）重难点03 空间向量与立体几何【高考考试趋势】立体几何在高考数学是一个必考知识点，一直在高中数学中占有很大的分值，未来的高考中立体几何也会持续成为高考的一个热点，理科高考中立体几何主要考查三视图的相关性质利用，简单几何体的体积，表面积以及外接圆问题.另外选择部分主要考查在点线面位置关系，简单几何体三视图.选择题主要还是以几何体的基本性质为主，解答题部分主要考查平行，垂直关系以及二面角问题.前面的重点专题已经对立体几何进行了一系列详细的说明，本专题继续加强对高考中立体几何出现的习题以及对应的题目类型进行必要的加强.本专题包含了高考中几乎所有题型，学完本专题以后，对以后所有的立体几何你将有一个更加清晰的认识.【知识点分析以及满分技巧】基础知识点考查：一般来说遵循三短一长选最长.要学会抽象问题具体会，将题目中的直线转化成显示中的具体事务，例如立体坐标系可以看做是一个教室的墙角有关外接圆问题：一般图形可以采用补形法，将几何体补成正方体或者是长方体，再利用不在同一个平面的四点确定一个立体平面原理，从而去求.内切圆问题：转化成正方体的内切圆去求.求点到平面的距离问题：采用等体积法.求几何体的表面积体积问题：应注意巧妙选取底面积与高.对于二面角问题应采用建立立体坐标系去求.但是坐标系要注意采用左手系务必要标记准确对应点以及法向量对应的坐标.【常见题型限时检测】（建议用时：35分钟）一、单选题1．（2019·遵义航天高级中学高考模拟（理））一个几何体的三视图如图所示，则该几何体的体积为（）A．83B．163C．203D．8【答案】B 【解析】由图可知该几何体底面积为8，高为2的四棱锥，如图所示：∴该几何体的体积1168233V =⨯⨯= 故选B【点睛】：思考三视图还原空间几何体首先应深刻理解三视图之间的关系，遵循“长对正，高平齐，宽相等”的基本原则，其内涵为正视图的高是几何体的高，长是几何体的长；俯视图的长是几何体的长，宽是几何体的宽；侧视图的高是几何体的高，宽是几何体的宽. 2．（2019·天津高考模拟（理））已知四面体ABCD 的四个面都为直角三角形，且AB ⊥平面BCD ，2AB BD CD ===，若该四面体的四个顶点都在球O 的表面上，则球O 的表面积为（）A ．3πB ．C ．D ．12π【答案】D 【解析】【分析】由已知中的垂直关系可将四面体放入正方体中，求解正方体的外接球表面积即为所求的四面体外接球的表面积；利用正方体外接球半径为其体对角线的一半，求得半径，代入面积公式求得结果. 【详解】2BD CD ==Q 且BCD ∆为直角三角形 BD CD ∴⊥又AB ⊥平面BCD ，CD ⊂平面BCD CD AB ∴⊥CD \^平面ABD由此可将四面体ABCD 放入边长为2的正方体中，如下图所示：∴正方体的外接球即为该四面体的外接球O正方体外接球半径为体对角线的一半，即12R == ∴球O 的表面积：2412S R ππ==本题正确选项：D 【点睛】本题考查多面体的外接球表面积的求解问题，关键是能够通过线面之间的位置关系，将所求四面体放入正方体中，通过求解正方体外接球来求得结果.3．（2019·河南高考模拟（理））如图，点P 在正方体1111ABCD A B C D -的面对角线1BC 上运动，则下列四个结论：①三棱锥1A D PC -的体积不变；1//A P ②平面1ACD ； 1DP BC ⊥③；④平面1PDB ⊥平面1ACD ．其中正确的结论的个数是( )A ．1个B ．2个C ．3个D ．4个【答案】C 【解析】【分析】利用空间中线线、线面、面面间的位置关系求解．【详解】对于①，由题意知11//AD BC ，从而1//BC 平面1AD C ，故BC 1上任意一点到平面1AD C 的距离均相等，所以以P 为顶点，平面1AD C 为底面，则三棱锥1A D PC -的体积不变，故①正确；对于②，连接1A B ，11A C ，111//AC AD 且相等，由于①知：11//AD BC ，所以11//BA C 面1ACD ，从而由线面平行的定义可得，故②正确；对于③，由于DC ⊥平面11BCB C ，所以1DC BC ⊥，若1DP BC ⊥，则1BC ⊥平面DCP ，1BC PC ⊥，则P 为中点，与P 为动点矛盾，故③错误；对于④，连接1DB ，由1DB AC ⊥且11DB AD ⊥，可得1DB ⊥面1ACD ，从而由面面垂直的判定知，故④正确．故选：C ．【点睛】本题考查命题真假的判断，解题时要注意三棱锥体积求法中的等体积法、线面平行、垂直的判定，要注意使用转化的思想．4．（2019·贵州高考模拟（理））设,m n 是两条不同的直线，,αβ是两个不同的平面，有下列四个命题：∴若m α⊂，αβ⊥，则m β⊥； ∴若//a β，m β⊂，则//m α； ∴若m α⊥，//m n ，//αβ，则n β⊥； ∴若//m α，//n β，//m n ，则//αβ其中正确命题的序号是（） A ．∴∴ B ．∴∴C ．∴∴D ．∴∴【答案】C 【解析】∴两个面垂直，推不出面中任意直线和另一个面垂直，错误；故排除A 、B 选项，对于∴，两个平行平面，其中一个平面内的任意直线都和另一个平面平行，故正确，所以选C.5．（2019·福建高考模拟（理））在三棱锥P ABC -中，3PA PB ==，BC =8AC =，AB BC ⊥，平面PAB ⊥平面ABC ，若球O 是三棱锥P ABC -的外接球，则球O 的半径为（）．A B C D ．2【答案】A 【解析】【分析】取AB 中点D ，AC 中点E ，连PD ，ED ，得E 为∴ABC 外接圆的圆心，且OE∴平面PAB ，然后求出∴PAB 的外接圆半径r 和球心O 到平面PAB 的距离等于d ，由勾股定理得R .【详解】解：取AB 中点D ，AC 中点E ，连PD ，ED 因为AB BC ⊥，所以E 为∴ABC 外接圆的圆心因为OE∴PD ，OE 不包含于平面PAB ，所以OE∴平面PAB 因为平面PAB ⊥平面ABC ，3PA PB ==，得PD ⊥AB ，ED ⊥AB 所以PD ⊥平面ABC ，ED ⊥平面PAB且AB ==PD 1=所以球心O 到平面PAB 的距离等于ED d ==在∴PAB 中，3PA PB ==，AB =1sin 3PAB ∠=，所以∴PAB 得外接圆半径2r 9sin PB PAB ∠==，即9r 2=由勾股定理可得球O 的半径R ==故选：A. 【点睛】本题考查了三棱锥的外接球问题，经常用球中勾股定理R =R 是外接球半径，d 是球心到截面距离，r 是截面外接圆半径.二、解答题6．（2019·山东高考模拟（理））如图，在四棱锥P ABCD -中，PC ⊥底面ABCD ，底面ABCD 是直角梯形,//AB AD AB CD ⊥，224AB AD CD ===，4PC =.（1）证明：当点E 在PB 上运动时，始终有平面EAC ⊥平面PBC ；（2）求锐二而角A PB C --的余弦值.【答案】（1）证明见解析；（2）5. 【解析】【分析】（1）由PC ⊥底面ABCD ，证得AC PC ⊥，又由勾股定理，得AC CB ⊥，利用线面垂直的判定定理，得到AC ⊥平面PBC ，再由面面垂直的判定定理，可得平面EAC ⊥平面PBC ，即可得到结论；（2）分别以CD ，CF ，CP 所在直线为x ，y ，z 轴建立空间直角坐标系，求得平面PBC 和平面PAB 的法向量，利用向量的夹角公式，即可求解．【详解】（1）由题意，因为PC ⊥底面ABCD ，AC ⊂平面ABCD ，所以AC PC ⊥，又因为224AB AD CD ===，所以4AB =，2AD CD ==，所以AC BC ==，所以222AC BC AB +=，从而得到AC CB ⊥．又BC ⊂Q 平面PBC ，PC ⊂平面PBC ，BC PC C ⋂=，所以AC ⊥平面PBC ，又AC ⊂Q 平面ACE ，所以平面EAC ⊥平面PBC ，所以当点E 在PB 上运动时，始终有平面EAC ⊥平面PBC. （2）由条件知PC ⊥底面ABCD ，且AB AD ⊥， AB C D ∥所以过点C 作CF CD ⊥交AB 于点F ，分别以CD ，CF ，CP 所在直线为x ，y ，z 轴建立空间直角坐标系（如图所示），所以(0,0,0)C ，(2,2,0)A ，(2,2,0)B -，(0,0,4)P .由（1）知CA u u u r为平面PBC 的一个法向量，因为(2,2,0)CA =u u u r，(2,2,4)PA =-u u u r (2,2,4)PB =--u u u r ，设平面P AB 的一个法向量为(,,)n=x y z r，则(,,)(2,2,4)00(,,)(2,2,4)00x y z n PA x y z n PB ⎧⋅-=⎧⋅=⇒⎨⎨⋅--=⋅=⎩⎩u uu v r u u u v r ，即02x y z=⎧⎨=⎩，令1z =，则2y =，所以(0,2,1)n =r，所以|||cos ,|5||||CA n CA n CA n ⋅〈〉===uu r ruu r r uu r r ，故锐二面角A PB C --的余弦值5．【点睛】本题考查了线面垂直与面面垂直的判定与证明，以及空间角的求解问题，意在考查学生的空间想象能力和逻辑推理能力，解答中熟记线面位置关系的判定定理和性质定理，通过严密推理是线面位置关系判定的关键，同时对于立体几何中角的计算问题，往往可以利用空间向量法，通过求解平面的法向量，利用向量的夹角公式求解.7（2017·广东高考模拟（理））如图，在四棱锥P ABCD -中，90,60ABC ACD BAC CAD ∠=∠=︒∠=∠=︒， PA ⊥平面ABCD ，2,1PA AB ==.(1)设点E 为PD 的中点，求证： //CE 平面PAB ；(2)线段PD 上是否存在一点N ，使得直线CN 与平面PAC 所成的角θ的正弦值为5？若存在，试确定点N 的位置；若不存在，请说明理由. 8．（2019·天津市新华中学高考模拟（理））如图所示的几何体中，PD 垂直于梯形ABCD所在的平面，,2ADC BAD F π∠=∠=为PA 的中点，112PD AB AD CD ====，四边形PDCE 为矩形，线段PC 交DE 于点N .（1）求证：AC P 平面DEF ；（2）求二面角A PB C --的正弦值；（3）在线段EF 上是否存在一点Q ，使得BQ 与平面BCP 所成角的大小为π6？若存在，求出FQ 的长；若不存在，请说明理由.【答案】（1）见解析（23）在线段EF 上存在一点Q 满足题意，且FQ =【解析】【分析】(1)由题意结合线面平行的判定定理即可证得题中的结论；(2)建立空间直角坐标系，利用两个半平面的法向量可得二面角的余弦值，然后利用同角三角函数基本关系可得二面角的正弦值；(3)假设点Q 存在，利用直线的方向向量和平面的法向量计算可得点Q 的存在性和位置. 【详解】（1）因为四边形PDCE 为矩形，所以N 为PC 的中点.连接FN ，在PAC V 中，,F N 分别为,PA PC 的中点，所以FN AC ∥，因为FN ⊂平面DEF ，AC ⊄平面DEF ，所以AC P 平面DEF .（2）易知,,DA DC DP 两两垂直，如图以D 为原点，分别以,,DA DC DP 所在直线为,,x y z 轴，建立空间直角坐标系.则(1,0,0),(1,1,0),(0,2,0)P A B C，所以(1,1,,(1,1,0)PB BC ==-u u u r u u u r.设平面PBC 的法向量为(,,)m x y z =r，则(,,)(1,1,0(,,)(1,1,0)0m PB x y z m BC x y z ⎧⋅=⋅=⎪⎨⋅=⋅-=⎪⎩u u u v r u u u v r即0,0,x y x y ⎧+=⎪⎨-+=⎪⎩解得,,y x z =⎧⎪⎨=⎪⎩令1x =，得1,y z =⎧⎪⎨=⎪⎩所以平面PBC的一个法向量为m =r. 设平面ABP 的法向量为(,,)n x y z =r，(,,)(0,1,0)0(,,)(1,1,0n AB x y z n PB x y z ⎧⋅=⋅=⎪⎨⋅=⋅-=⎪⎩u u uv r u u uv r ，据此可得01x y z ⎧=⎪=⎨⎪=⎩，则平面ABP的一个法向量为)n =r，cos ,3m n <>==u r r，于是sin ,3m n 〈〉=r r. 故二面角A PB C --（3）设存在点Q 满足条件.由1,0,,(0,22F E ⎛⎫ ⎪ ⎪⎝⎭，设(01)FQ FE λλ=u u u r u u u r &剟，整理得1),2,22Q λλλ⎛⎫-+ ⎪ ⎪⎝⎭，则1,22BQ λλ⎛+=-- ⎝⎭u u u r . 因为直线BQ 与平面BCP 所成角的大小为6π，所以1sin |cos ,|||62||||BQ m BQ m BQ m π⋅====⋅u u u r u ru u u r u r u u ur u r 解得21λ=，由知1λ=，即点Q 与E 重合.故在线段EF 上存在一点Q，且FQ EF ==. 【点睛】本题的核心在考查空间向量的应用，需要注意以下问题：(1)求解本题要注意两点：一是两平面的法向量的夹角不一定是所求的二面角，二是利用方程思想进行向量运算，要认真细心，准确计算．(2)设,m n u r r 分别为平面α，β的法向量，则二面角θ与,m n <>u r r互补或相等.求解时一定要注意结合实际图形判断所求角是锐角还是钝角．9．（2019·山东高考模拟（理））如图，在四棱锥P ABCD -中，已知PA ⊥平面ABCD ，ABC ∆为等边三角形，22PA AB ==，AC CD ⊥，PD 与平面PAC 所成角的正切值为5.(∴)证明：//BC 平面PAD ；(∴)若M 是BP 的中点，求二面角P CD M --的余弦值.【答案】（∴）见解析.（∴ 【解析】【分析】(∴)先证明DPC ∠为PD 与平面PAC 所成的角，于是可得CD =60CAD ∠=︒．又由题意得到60BCA ∠=︒，故得//BC AD ，再根据线面平行的性质可得所证结论． (∴) 取BC 的中点N ，连接AN ，可证得AN AD ⊥．建立空间直角坐标系，分别求出平面PCD 和平面CDM 的法向量，根据两个法向量夹角的余弦值得到二面角的余弦值．【详解】(∴)证明：因为PA ⊥平面ABCD ，CD ⊂平面ABCD ，所以PA CD ⊥又AC CD ⊥,CA PA A =I , 所以CD ⊥平面PAC ，所以DPC ∠为PD 与平面PAC 所成的角．在Rt PCD V中，PC ==所以CD =所以在Rt PCD V 中，2AD =,60CAD ∠=︒. 又60BCA ∠=︒，所以在底面ABCD 中，//BC AD , 又AD ⊂平面PAD ，BC ⊄平面PAD ，所以//BC 平面PAD ．(∴)解：取BC 的中点N ，连接AN ，则AN BC ⊥,由(∴)知//BC AD ，所以AN AD ⊥，分别以AN ，AD ，AP 为x ，y ，z 轴建立空间直角坐标系Axyz .则(0,0,2)P，1,02C ⎫⎪⎪⎝⎭，(0,2,0)D，1,14M ⎫-⎪⎪⎝⎭所以3,,022CD ⎛⎫=- ⎪ ⎪⎝⎭uu u r ，(0,2,2)PD =-u u ur，9,,144DM ⎛⎫=- ⎪ ⎪⎝⎭uuu u r设平面PCD 的一个法向量为()1111,,n x y z =u r，由1100n CD n PD ⎧⋅=⎪⎨⋅=⎪⎩u u u vu u u v，即111130220y y z ⎧+=⎪⎨-=⎪⎩，得1111x z y ⎧=⎪⎨=⎪⎩，令11y =，则1,1)n =u r．设平面CDM 的一个法向量为()2222,,n x y z =u ur，由2200n CD n MD ⎧⋅=⎪⎨⋅=⎪⎩u u v u u u v u u v u u u u v，即2222230940y y z ⎧+=⎪-+=，得222232x y z ⎧=⎪⎨=⎪⎩，令21y =，则232n ⎫=⎪⎭u u r ．所以121212331cos ,||||n n n n n n ++⋅<>===⋅u r u u ru r u u r u r u u r 由图形可得二面角P CD M --为锐角，所以二面角P CD M --【点睛】空间向量是求解空间角的有利工具，根据平面的法向量、直线的方向向量的夹角可求得线面角、二面角等，解题时把几何问题转化为向量的运算的问题来求解，体现了转化思想方法的利用，不过解题中要注意向量的夹角和空间角之间的关系，特别是求二面角时，在求得法向量的夹角后，还要通过图形判断出二面角是锐角还是钝角，然后才能得到结论． 10．（2018·吉林高考模拟（理））如图，在棱长为2的正方体1111ABCD A B C D -中，E ，F ， M ， N 分别是棱AB ， AD ， 11A B ， 11A D 的中点，点P ， Q 分别在棱1DD ， 1BB 上移动，且(02)DP BQ λλ==<<.（1）当1λ=时，证明：直线1//BC 平面EFPQ ；（2）是否存在λ，使面EFPQ 与面PQMN 所成的二面角为直二面角？若存在，求出λ的值；若不存在，说明理由.【答案】（1）见解析；（2）12λ=±.【解析】以D 为原点，射线DA ， DC ， 1DD 分别为x ， y ， z 轴的正半轴建立如图所示的空间直角坐标系D xyz -.由已知得()2,2,0B ， ()10,2,2C ，()2,1,0E ，()1,0,0F ， ()0,0,P λ， ()1,0,2N ， ()2,1,2M ，则()12,0,2BC =-u u u u r， ()1,0,FP λ=-u u u r ， ()1,1,0FE =u u u r ， ()1,1,0NM =u u u u r ， ()1,0,2NP λ=--u u u r.（1）当1λ=时， ()1,0,1FP =-u u u r ，因为()12,0,2BC =-u u u u r ，所以12BC FP =u u u u r u u u r，即1//BC FP ，又FP ⊂平面EFPQ ，且1BC ⊄平面EFPQ ，故直线1//BC 平面EFPQ . （2）设平面EFPQ 的一个法向量为(),,n x y z =r，则由0{0FE n FP n ⋅=⋅=u u u r ru u u r r，得0{0.x y x z λ+=-+=，于是可取(),,1n λλ=-r . 设平面MNPQ 的一个法向量为()',','m x y z =r，由0{0NM m NP m ⋅=⋅=u u u u r ru u u r r，得()''0{'2'0x y x z λ+=-+-=，于是可取()2,2,1m λλ=--r. 若存在λ，使面EFPQ 与面PQMN 所成的二面角为直二面角，则()()2,2,1,,10m n λλλλ⋅=--⋅-=r r，即()()2210λλλλ---+=，解得1λ=±，显然满足02λ<<.故存在1λ=±，使面EFPQ 与面PQMN 所成的二面角为直二面角.点睛：立体几何的有关证明题，首先要熟悉各种证明的判定定理，然后在进行证明，要多总结题型，对于二面角问题一般直接建立空间直角坐标系，求出法向量然后根据向量夹角公式求解二面角，要注意每一个坐标的准确性。

2020年高考数学解答题核心：立体几何综合问题(专项训练)(教师版)

专题08 立体几何综合问题（专项训练）1．如图,菱形ABCD 中,∠ABC ＝60°,AC 与BD 相交于点O ,AE ⊥平面ABCD ,CF ∥AE ,AB ＝AE ＝2. (1)求证：BD ⊥平面ACFE ；(2)当直线FO 与平面BED 所成的角为45°时,求异面直线OF 与BE 所成的角的余弦值大小．【答案】见解析【解析】(1)因为四边形ABCD 是菱形,所以BD ⊥AC .因为AE ⊥平面ABCD ,BD ⊂平面ABCD ,所以BD ⊥AE .因为AC ∩AE ＝A ,所以BD ⊥平面ACFE .(2)以O 为原点,OA →,OB →的方向为x ,y 轴正方向,过O 且平行于CF 的直线为z 轴(向上为正方向),建立空间直角坐标系,则B (0,3,0),D (0,－3,0),E (1,0,2),F (－1,0,a )(a >0),OF →＝(－1,0,a )．设平面EBD 的法向量为n ＝(x ,y ,z ),则有⎩⎪⎨⎪⎧n ·OB →＝0，n ·OE →＝0，即⎩⎨⎧3y ＝0，x ＋2z ＝0，令z ＝1,则n ＝(－2,0,1),由题意得sin 45°＝|cos 〈OF →,n 〉|＝|OF →·n ||OF →||n |＝|2＋a |a 2＋1·5＝22.因为a >0,所以解得a ＝3.所以OF →＝(－1,0,3),BE →＝(1,－3,2),所以cos 〈OF →,BE →〉＝OF →·BE →|OF →|·|BE →|＝－1＋610·8＝54.故异面直线OF 与BE 所成的角的余弦值为54.2．(2019·河南郑州模拟)如图,在△ABC 中,∠ABC ＝π4,O 为AB 边上一点,且3OB ＝3OC ＝2AB ,已知PO ⊥平面ABC ,2DA ＝2AO ＝PO ,且DA ∥PO .(1)求证：平面PBAD ⊥平面COD ；(2)求直线PD 与平面BDC 所成角的正弦值．【答案】见解析【解析】(1)证明：因为OB ＝OC ,又因为∠ABC ＝π4,所以∠OCB ＝π4,所以∠BOC ＝π2,即CO ⊥AB .又PO ⊥平面ABC ,OC ⊂平面ABC ,所以PO ⊥OC .又因为PO ,AB ⊂平面PAB ,PO ∩AB ＝O ,所以CO ⊥平面PAB ,即CO ⊥平面PBAD .又CO ⊂平面COD ,所以平面PBAD ⊥平面COD .(2)以OC ,OB ,OP 所在射线分别为x ,y ,z 轴,建立空间直角坐标系,如图所示．设|OA |＝1,则|PO |＝|OB |＝|OC |＝2,|DA |＝1.则C (2,0,0),B (0,2,0),P (0,0,2),D (0,－1,1),所以PD →＝(0,－1,－1),BC →＝(2,－2,0),BD →＝(0,－3,1)．设平面BDC 的法向量为n ＝(x ,y ,z ),所以⎩⎪⎨⎪⎧n ·BC →＝0，n ·BD →＝0，所以⎩⎪⎨⎪⎧2x －2y ＝0，－3y ＋z ＝0，令y ＝1,则x ＝1,z ＝3,所以n ＝(1,1,3)．设PD 与平面BDC 所成的角为θ,则sin θ＝⎪⎪⎪⎪⎪⎪⎪⎪PD →·n |PD →||n |＝⎪⎪⎪⎪⎪⎪1×0＋1×(－1)＋3×(－1)02＋(－1)2＋(－1)2×12＋12＋32＝22211.即直线PD 与平面BDC 所成角的正弦值为22211. 3．(2019·湖北武汉调考)如图, 四棱锥S －ABCD 中,AB ∥CD ,BC ⊥CD ,侧面SAB 为等边三角形,AB ＝BC ＝2,CD ＝SD ＝1.(1)证明：SD ⊥平面SAB ；(2)求AB 与平面SBC 所成角的正弦值．【答案】见解析【解析】方法一 (1)证明：建立如图所示的空间直角坐标系Cxyz ,则D (1,0,0),A (2,2,0),B (0,2,0),设S (x ,y ,z ),则x >0,y >0,z >0,且AS →＝(x －2,y －2,z ,),BS →＝(x ,y －2,z ).DS→＝(x －1,y ,z )．由|AS →|＝|BS →|,得(x －2)2＋(y －2)2＋z 2＝x 2＋(y －2)2＋z 2,得x ＝1,由|DS →|＝1得y 2＋z 2＝1,①由|BS →|＝2得y 2＋z 2－4y ＋1＝0,②由①②解得y ＝12,z ＝32,所以S ⎝ ⎛⎭⎪⎫1，12，32,AS →＝⎝⎛⎭⎪⎫－1，－32，32,BS →＝⎝ ⎛⎭⎪⎫1，－32，32,DS →＝⎝ ⎛⎭⎪⎫0，12，32,所以DS →·AS →＝0,DS →·BS →＝0,所以DS ⊥AS ,DS ⊥BS ,又AS ∩DS ＝S ,所以SD ⊥平面SAB .(2)设平面SBC 的一个法向量为m ＝(a ,b ,c ),BS →＝⎝ ⎛⎭⎪⎫1，－32，32,CB →＝(0,2,0),AB →＝(－2,0,0),由⎩⎪⎨⎪⎧m ·BS →＝0，m ·CB →＝0得⎩⎪⎨⎪⎧a －32b ＋32c ＝0，2b ＝0，所以可取m ＝(－3,0,2),故AB 与平面SBC 所成的角的正弦值为cos 〈m ,AB →〉＝m ·AB →|m |·|AB →|＝－2×(－3)7×2＝217. 方法二 (1)证明：如下图,取AB 的中点E ,连接DE ,SE ,则四边形BCDE 为矩形,所以DE ＝CB ＝2,所以AD ＝DE 2＋AE 2＝ 5.因为侧面SAB 为等边三角形,AB ＝2,所以SA ＝SB ＝AB ＝2,且SE ＝3,又SD ＝1,所以SA 2＋SD 2＝AD 2,SE 2＋SD 2＝ED 2,所以SD ⊥SA ,SD ⊥SB ,又AS ∩DS ＝S ,所以SD ⊥平面SAB .(2)作S 在DE 上的射影G ,因为AB ⊥SE ,AB ⊥DE ,AB ⊥平面SDE ,所以平面SDE ⊥平面ABCD ,两平面的交线为DE ,所以SG ⊥平面ABCD ,在Rt △DSE 中,由SD ·SE ＝DE ·SG 得1×3＝2×SG ,所以SG ＝32,作A 在平面SBC 上的射影H ,则∠ABH 为AB 与平面SBC 所成的角,因为CD ∥AB ,AB ⊥平面SDE ,所以CD ⊥平面SDE ,所以CD ⊥SD ,在Rt △CDS 中,由CD ＝SD ＝1,求得SC ＝ 2.在△SBC 中,SB ＝BC ＝1,SC ＝2,所以S △SBC ＝12×2×22－12＝72,由V A －SBC ＝V S －ABC 得13·S △SBC ·AH ＝13·S △ABC ·SG ,即13×72×AH ＝13×12×2×2×2,得AH ＝2217,所以sin ∠ABH ＝AHAB ＝217,故AB 与平面SBC 所成的角的正弦值为217. 4．(2019·安徽江南名校联考)如图,在四棱锥P －ABCD 中,PD ⊥平面ABCD ,AB ∥DC ,AB ⊥AD ,DC ＝6,AD ＝8,BC＝10,∠PAD ＝45°,E 为PA 的中点． (1)求证：DE ∥平面BPC ；(2)线段AB 上是否存在一点F ,满足CF ⊥DB ？若存在,试求出二面角F －PC －D 的余弦值；若不存在,请说明理由．【答案】见解析【解析】(1)证明：取PB 的中点M ,连接EM 和CM ,过点C 作CN ⊥AB ,垂足为点N .因为CN ⊥AB ,DA ⊥AB ,所以CN ∥DA ,又AB ∥CD ,所以四边形CDAN 为平行四边形,所以CN ＝AD ＝8,DC ＝AN ＝6,在Rt △BNC 中,BN ＝BC 2－CN 2＝102－82＝6,所以AB ＝12,而E ,M 分别为PA ,PB 的中点,所以EM ∥AB 且EM ＝6,又DC ∥AB ,所以EM ∥CD 且EM ＝CD ,四边形CDEM 为平行四边形,所以DE ∥CM .因为CM ⊂平面PBC ,DE ⊄平面PBC ,所以DE ∥平面BPC .(2)由题意可得DA ,DC ,DP 两两互相垂直,如图,以D 为原点,DA ,DC ,DP 分别为x ,y ,z 轴建立空间直角坐标系Dxyz ,则A (8,0,0),B (8,12,0),C (0,6,0),P (0,0,8)．假设AB 上存在一点F 使CF ⊥BD ,设点F 坐标为(8,t,0),则CF →＝(8,t －6,0),DB →＝(8,12,0),由CF →·DB →＝0得t ＝23.又平面DPC 的法向量为m ＝(1,0,0),设平面FPC 的法向量为n ＝(x ,y ,z )．又PC →＝(0,6,－8),FC →＝⎝ ⎛⎭⎪⎫－8，163，0.由⎩⎪⎨⎪⎧n ·PC →＝0，n ·FC →＝0得⎩⎪⎨⎪⎧6y －8z ＝0，－8x ＋163y ＝0，即⎩⎪⎨⎪⎧z ＝34y ，x ＝23y ，不妨令y ＝12,有n ＝(8,12,9)．则cos 〈n ,m 〉＝n ·m |n ||m |＝81×82＋122＋92＝817.又由图可知,该二面角为锐二面角,故二面角F －PC －D 的余弦值为817.5．(2017·山东卷)如图,几何体是圆柱的一部分,它是由矩形ABCD(及其内部)以AB边所在直线为旋转轴旋转120°得到的,G是DF的中点．(1)设P是CE上的一点,且AP⊥BE,求∠CBP的大小；(2)当AB＝3,AD＝2时,求二面角E－AG－C的大小．【答案】见解析【解析】(1)因为AP⊥BE,AB⊥BE,AB,AP⊂平面ABP,AB∩AP＝A,所以BE⊥平面ABP,又BP⊂平面ABP,所以BE⊥BP,又∠EBC＝120°,因此∠CBP＝30°.(2)方法一取EC的中点H,连接EH,GH,CH.因为∠EBC＝120°,所以四边形BEHC为菱形,所以AE＝GE＝AC＝GC＝32＋22＝13.取AG中点M,连接EM,CM,EC,则EM⊥AG,CM⊥AG,所以∠EMC为所求二面角的平面角．又AM＝1,所以EM＝CM＝13－1＝2 3.在△BEC中,由于∠EBC＝120°,由余弦定理得EC2＝22＋22－2×2×2×cos120°＝12,所以EC＝23,因此△EMC为等边三角形,故所求的角为60°.方法二以B 为坐标原点,分别以BE ,BP ,BA 所在的直线为x ,y ,z 轴,建立如图所示的空间直角坐标系．由题意得A (0,0,3),E (2,0,0),G (1,3,3),C (－1,3,0),故AE →＝(2,0,－3),AG →＝(1,3,0),CG →＝(2,0,3),设m ＝(x 1,y 1,z 1)是平面AEG 的一个法向量．由⎩⎪⎨⎪⎧m ·AE →＝0，m ·AG →＝0可得⎩⎨⎧2x 1－3z 1＝0，x 1＋3y 1＝0.取z 1＝2,可得平面AEG 的一个法向量m ＝(3,－3,2)．设n ＝(x 2,y 2,z 2)是平面ACG 的法向量．由⎩⎪⎨⎪⎧n ·AG →＝0，n ·CG →＝0可得⎩⎨⎧x 2＋3y 2＝0，2x 2＋3z 2＝0.取z 2＝－2,可得平面ACG 的一个法向量n ＝(3,－3,－2)．所以cos 〈m ,n 〉＝m ·n |m |·|n |＝12.由图可得此二面角为锐二面角,故所求的角为60°.6．(2017·全国卷Ⅲ)如图,四面体ABCD 中,△ABC 是正三角形,△ACD 是直角三角形,∠ABD ＝∠CBD ,AB ＝BD . (1)证明：平面ACD ⊥平面ABC ；(2)过AC 的平面交BD 于点E ,若平面AEC 把四面体ABCD 分成体积相等的两部分,求二面角D －AE －C 的余弦值．【答案】见解析【解析】(1)证明：由题设可得△ABD ≌△CBD ,从而AD ＝CD . 又△ACD 是直角三角形,所以∠ADC ＝90°. 取AC 的中点O ,连接DO ,BO ,则DO ⊥AC ,DO ＝AO . 又因为△ABC 是正三角形,故BO ⊥AC , 所以∠DOB 为二面角D －AC －B 的平面角．在Rt △AOB 中,BO 2＋AO 2＝AB 2,又AB ＝BD ,所以BO 2＋DO 2＝BO 2＋AO 2＝AB 2＝BD 2, 故∠BOD ＝90°.所以平面ACD ⊥平面ABC .(2)由题设及(1)知,OA ,OB ,OD 两两垂直,以O 为坐标原点,OA →的方向为x 轴正方向,|OA →|为单位长度,建立如图所示的空间直角坐标系Oxyz ,则A (1,0,0),B (0,3,0),C (－1,0,0),D (0,0,1)．由题设知,四面体ABCE 的体积为四面体ABCD 的体积的12,从而E 到平面ABC 的距离为D 到平面ABC 的距离的12,即E 为DB 的中点,得E ⎝ ⎛⎭⎪⎫0，32，12,故AD →＝(－1,0,1),AC →＝(－2,0,0),AE →＝⎝⎛⎭⎪⎫－1，32，12.设n ＝(x ,y ,z )是平面DAE 的法向量,则⎩⎪⎨⎪⎧ n ·AD →＝0，n ·AE →＝0，即⎩⎪⎨⎪⎧－x ＋z ＝0，－x ＋32y ＋12z ＝0，可取n ＝⎝ ⎛⎭⎪⎫1，33，1.设m 是平面AEC 的法向量,则⎩⎪⎨⎪⎧m ·AC →＝0，m ·AE →＝0，同理可取m ＝(0,－1,3),则cos 〈n ,m 〉＝n·m |n||m|＝77.所以二面角D －AE －C 的余弦值为77.。

2020高考数学分类汇编--立体几何

2020年普通高等学校招生全国统一考试理科数学3．埃及胡夫金字塔是古代世界建筑奇迹之一，它的形状可视为一个正四棱锥，以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积，则其侧面三角形底边上的高与底面正方形的边长的比值为A ．14B ．12C ．14D ．1210．已知,,A B C 为球O 的球面上的三个点，⊙1O 为ABC △的外接圆，若⊙1O 的面积为4π，1AB BC AC OO ===，则球O 的表面积为A ．64πB ．48πC ．36πD ．32π16．如图，在三棱锥P –ABC 的平面展开图中，AC =1，AB AD =AB ⊥AC ，AB ⊥AD ，∠CAE =30°，则cos ∠FCB = .18．（12分）如图，D 为圆锥的顶点，O 是圆锥底面的圆心，AE 为底面直径，AE AD =．ABC △是底面的内接正三角形，P 为DO 上一点，PO ．（1）证明：PA ⊥平面PBC ；（2）求二面角B PC E --的余弦值． 3．C 10．A16．14-18．解：（1）设DO a =，由题设可得,,63PO a AO a AB a ===，2PA PB PC ===. 因此222PA PB AB +=，从而PA PB ⊥. 又222PA PC AC +=，从而PA PC ⊥. 所以PA ⊥平面PBC .（2）以O 为坐标原点，OE 的方向为y 轴正方向，||OE 为单位长，建立如图所示的空间直角坐标系O xyz -.由题设可得1(0,1,0),(0,1,0),(,0),(0,0,)22E A C P -.所以31(,,0),(0,2EC EP =--=-.设(,,)x y z =m 是平面PCE 的法向量，则00EP EC ⎧⋅=⎪⎨⋅=⎪⎩m m ，即2023102y z x y⎧-+=⎪⎪⎨⎪--=⎪⎩，可取3(,1,2)=-m . 由（1）知2(0,1,)2AP =是平面PCB 的一个法向量，记AP =n ，则25cos ,|||5⋅==n m n m n m |. 所以二面角B PC E --的余弦值为25.2020年普通高等学校招生全国统一考试理科数学4．北京天坛的圆丘坛为古代祭天的场所，分上、中、下三层，上层中心有一块圆形石板（称为天心石），环绕天心石砌9块扇面形石板构成第一环，向外每环依次增加9块，下一层的第一环比上一层的最后一环多9块，向外每环依次也增加9块，已知每层环数相同，且下层比中层多729块，则三层共有扇面形石板（不含天心石）A ．3699块B ．3474块C ．3402块D ．3339块7．右图是一个多面体的三视图，这个多面体某条棱的一个断点在正视图中对应的点为M ，在俯视图中对应的点为N ，则该端点在侧视图中对应的点为ME F GHA ．EB ．FC ．GD ．H10. 已知ABC △是面积为439的等边三角形，且其顶点都在球O 的表面上，若球O 的表面积为π16，则球O 到平面ABC 的距离为（） A ．3B ．23 C ．1 D ．23 16．设有下列四个命题： 1P ：两两相交且不过同一点的三条直线必在同一平面内． 2P ：过空间中任意三点有且仅有一个平面． 3P ：若空间两条直线不相交，则这两条直线平行． 4P ：若直线⊂l 平面α，直线⊥m 平面α，则l m ⊥．则下述命题中所有真命题的序号是________． ①41p p ∧②21p p ∧③32p p ∨⌝④ 43p p ⌝∨⌝20．（12分）如图，已知三棱柱111C B A ABC -的底面是正三角形，侧面C C BB 11是矩形，M ，N 分别为BC ，11C B 的中点，P 为AM 上一点，过11C B 和P 的平面交AB 于E ，交AC 于F ．（1）证明：MN AA ∥1，且平面F C EB AMN A 111平面⊥；（2）设O 为△111C B A 的中心，若F C EB AO 11平面∥，且AB AO =，求直线E B 1与平面AMN A 1所成角的正弦值．2020年普通高等学校招生全国统一考试理科数学8．下图为某几何体的三视图，则该几何体的表面积是A ．B ．C ．D ．15．已知圆锥的底面半径为1，母线长为3，则该圆锥内半径最大的球的体积为__________．19．（12分）如图，在长方体1111ABCD A B C D -中，点,E F 分别在棱11,DD BB 上，且12DE ED =，12BF FB =．（1）证明：点1C 在平面AEF 内；（2）若2AB =，1AD =，13AA =，求二面角1A EF A --的正弦值．8．C15 19．解：设AB a =，AD b =，1AA c =，如图，以1C 为坐标原点，11C D 的方向为x 轴正方向，建立空间直角坐标系1C xyz -．（1）连结1C F ，则1(0,0,0)C ，(,,)A a b c ，2(,0,)3E a c ，1(0,,)3F b c ，1(0,,)3EA b c =，11(0,,)3C F b c =，得1EA C F =．因此1EA C F ∥，即1,,,A E F C 四点共面，所以点1C 在平面AEF 内．（2）由已知得(2,1,3)A ，(2,0,2)E ，(0,1,1)F ，1(2,1,0)A ，(0,1,1)AE =--，(2,0,2)AF =--，1(0,1,2)A E =-，1(2,0,1)A F =-．设1(,,)x y z =n 为平面AEF 的法向量，则 110,0,AE AF ⎧⋅=⎪⎨⋅=⎪⎩n n 即0,220,y z x z --=⎧⎨--=⎩可取1(1,1,1)=--n ．设2n 为平面1A EF 的法向量，则 22110,0,A E A F ⎧⋅=⎪⎨⋅=⎪⎩n n 同理可取21(,2,1)2=n ．因为121212cos ,||||⋅〈〉==⋅n n n n n n ，所以二面角1A EF A --．2020年普通高等学校招生全国统一考试文科数学3．埃及胡夫金字塔是古代世界建筑奇迹之一，它的形状可视为一个正四棱锥.以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积，则其侧面三角形底边上的高与底面正方形的边长的比值为A ．14B ．12C ．14D ．1211．设12,F F 是双曲线22:13y C x -=的两个焦点，O 为坐标原点，点P 在C 上且||2OP =，则12PF F △的面积为 A ．72B ．3C ．52D ．212．已知,,A B C 为球O 的球面上的三个点，⊙1O 为ABC △的外接圆，若⊙1O 的面积为4π，1AB BC AC OO ===，则球O 的表面积为A ．64πB ．48πC ．36πD ．32π19．（12分）如图，D 为圆锥的顶点，O 是圆锥底面的圆心，ABC △是底面的内接正三角形，P 为DO 上一点，∠APC =90°．（1）证明：平面PAB ⊥平面PAC ；（2）设DO ，求三棱锥P −ABC 的体积. 3．C11．B12．A19．解：（1）由题设可知，PA =PB = PC ．由于△ABC 是正三角形，故可得△PAC ≌△PAB ． △PAC ≌△PBC ．又∠APC =90°，故∠APB =90°，∠BPC =90°．从而PB ⊥PA ，PB ⊥PC ，故PB ⊥平面PAC ，所以平面PAB ⊥平面PAC ．（2）设圆锥的底面半径为r ，母线长为l ．由题设可得rl 222l r ==．解得r =1，l从而AB 1）可得222PA PB AB +=，故PA PB PC ===所以三棱锥P -ABC 的体积为311113232PA PB PC ⨯⨯⨯⨯=⨯⨯=．2020年普通高等学校招生全国统一考试文科数学11．已知△ABC O 的球面上．若球O 的表面积为16π，则O 到平面ABC 的距离为AB ．32C ．1D 16．设有下列四个命题：p 1：两两相交且不过同一点的三条直线必在同一平面内． p 2：过空间中任意三点有且仅有一个平面． p 3：若空间两条直线不相交，则这两条直线平行． p 4：若直线l ⊂平面α，直线m ⊥平面α，则m ⊥l ．则下述命题中所有真命题的序号是__________． ① 14p p ∧②12p p ∧③23p p ⌝∨④34p p ⌝∨⌝20．（12分）如图，已知三棱柱ABC –A 1B 1C 1的底面是正三角形，侧面BB 1C 1C 是矩形，M ，N 分别为BC ，B 1C 1的中点，P 为AM 上一点．过B 1C 1和P 的平面交AB 于E ，交AC 于F ．（1）证明：AA 1//MN ，且平面A 1AMN ⊥平面EB 1C 1F ；（2）设O 为△A 1B 1C 1的中心，若AO =AB =6，AO //平面EB 1C 1F ，且∠MPN =π3，求四棱锥B –EB 1C 1F 的体积． 12．A16．①③④20．解：（1）因为M ，N 分别为BC ，B 1C 1的中点，所以MN ∥CC 1．又由已知得AA 1∥CC 1，故AA 1∥MN ．因为△A 1B 1C 1是正三角形，所以B 1C 1⊥A 1N ．又B 1C 1⊥MN ，故B 1C 1⊥平面A 1AMN ．所以平面A 1AMN ⊥平面EB 1C 1F ．（2）AO ∥平面EB 1C 1F ，AO ⊂平面A 1AMN ，平面A 1AMN ⋂平面EB 1C 1F = PN ，故AO ∥PN ，又AP ∥ON ，故四边形APNO 是平行四边形，所以PN =AO =6，AP = ON =13AM PM =23AM EF =13BC =2．因为BC ∥平面EB 1C 1F ，所以四棱锥B -EB 1C 1F 的顶点B 到底面EB 1C 1F 的距离等于点M 到底面EB 1C 1F 的距离．作MT ⊥PN ，垂足为T ，则由（1）知，MT ⊥平面EB 1C 1F ，故MT =PM sin ∠MPN =3．底面EB 1C 1F 的面积为1111()(62)624.22B C EF PN ⨯+⨯=+⨯=所以四棱锥B -EB 1C 1F 的体积为1243243⨯⨯=．2020年普通高等学校招生全国统一考试文科数学9．如图为某几何体的三视图，则该几何体的表面积是A ．B ．C ．D ．16．已知圆锥的底面半径为1，母线长为3，则该圆锥内半径最大的球的体积为_________． 19．（12分）如图，在长方体1111ABCD A B C D -中，点E ，F 分别在棱1DD ，1BB 上，且12DE ED =，12BF FB =．证明：（1）当AB BC =时，EF AC ⊥；（2）点1C 在平面AEF 内． 9．C16．2π 19．解：（1）如图，连结BD ，11B D ．因为AB BC =，所以四边形ABCD 为正方形，故AC BD ⊥．又因为1BB ⊥平面ABCD ，于是1AC BB ⊥．所以AC ⊥平面11BB D D ．由于EF ⊂平面11BB D D ，所以EF AC ⊥．（2）如图，在棱1AA 上取点G ，使得12AG GA =，连结1GD ，1FC ，FG ，因为1123D E DD =，123AG AA =，11DD AA =∥，所以1ED AG =∥，于是四边形1ED GA 为平行四边形，故1AE GD ∥．因为1113B F BB =，1113AG AA =，11BB AA =∥，所以11FG A B =∥，11FG C D =∥，四边形11FGD C 为平行四边形，故11GD FC ∥．于是1AE FC ∥．所以1,,,A E F C 四点共面，即点1C 在平面AEF 内． 2020年普通高等学校招生全国统一考试（北京卷）（3）某三棱柱的底面为正三角形，其三视图如图所示，该三棱柱的表面积为（A ）63+（B ）623+（C ）123+（D ）1223+（16）（本小题13分）如图，在正方体1111ABCD A B C D -中，E 为1BB 的中点．（Ⅰ）求证：1BC ∥平面1AD E ；（Ⅱ）求直线1AA 与平面1AD E 所成角的正弦值．2020年普通高等学校招生全国统一考试（江苏卷）9．如图，六角螺帽毛坯是由一个正六棱柱挖去一个圆柱所构成的．已知螺帽的底面正六边形边长为2 cm ，高为2 cm ，内孔半轻为0.5 cm ，则此六角螺帽毛坯的体积是 cm.15．（本小题满分14分）在三棱柱ABC －A 1B 1C 1中，AB ⊥AC ，B 1C ⊥平面ABC ，E ，F 分别是AC ，B 1C 的中点．（1）求证：EF ∥平面AB 1C 1；（2）求证：平面AB 1C ⊥平面ABB 1．9．1232π 15．满分14分.证明：因为,E F 分别是1,AC B C 的中点，所以1EF AB ∥. 又/EF ⊂平面11AB C ，1AB ⊂平面11AB C ，所以EF ∥平面11AB C .（2）因为1B C ⊥平面ABC ，AB ⊂平面ABC , 所以1B C AB ⊥.又AB AC ⊥,1B C ⊂平面11AB C ,AC ⊂平面1AB C ,1,B C AC C =所以AB ⊥平面1AB C .又因为AB ⊂平面1ABB ,所以平面1AB C ⊥平面1ABB . 22．（本小题满分10分）在三棱锥A —BCD 中，已知CB =CD 5,BD =2，O 为BD 的中点，AO ⊥平面BCD ，AO =2，E 为AC 的中点．（1）求直线AB 与DE 所成角的余弦值；（2）若点F 在BC 上，满足BF =14BC ，设二面角F —DE —C 的大小为θ，求sin θ的值． 2020年普通高等学校招生全国统一考试（天津卷）5．若棱长为23的正方体的顶点都在同一球面上，则该球的表面积为 A ．12π B ．24πC ．36πD ．144π17．（本小题满分15分）如图，在三棱柱111ABC A B C -中，1CC ⊥平面,,2ABC AC BC AC BC ⊥==，13CC =，点,D E 分别在棱1AA 和棱1CC 上，且2,1,AD CE M ==为棱11A B 的中点．（Ⅰ）求证：11C M B D ⊥；（Ⅱ）求二面角1B B E D --的正弦值；（Ⅲ）求直线AB 与平面1DB E 所成角的正弦值． 5．C17．满分15分．依题意，以C 为原点，分别以1,,CA CB CC 的方向为x 轴，y 轴，z 轴的正方向建立空间直角坐标系（如图），可得1(0,0,0),(2,0,0),(0,2,0),(0,0,3)C A B C ，11(2,0,3),(0,2,3),(2,0,1),(0,0,2)A B D E ，(1,1,3)M ．（Ⅰ）证明：依题意，1(1,1,0)C M =，1(2,2,2)B D =--，从而112200C M B D ⋅=-+=，所以11C M B D ⊥．（Ⅱ）解：依题意，(2,0,0)CA =是平面1BB E 的一个法向量，1(0,2,1)EB =，(2,0,1)ED =-．设(,,)x y z =n 为平面1DB E 的法向量，则10,0,EB ED ⎧⋅=⎪⎨⋅=⎪⎩n n 即20,20.y z x z +=⎧⎨-=⎩不妨设1x =，可得(1,1,2)=-n ．因此有|||6cos ,6|A CA C CA ⋅〈〉==n n n ，于是30sin ,CA 〈〉=n ．所以，二面角1B B E D --的正弦值为306．（Ⅲ）解：依题意，(2,2,0)AB =-．由（Ⅱ）知(1,1,2)=-n 为平面1DB E 的一个法向量，于是3cos ,3||||AB AB AB ⋅==-n n n ．所以，直线AB 与平面1DB E 32020年普通高等学校招生全国统一考试新高考4．日晷是中国古代用来测定时间的仪器，利用与晷面垂直的晷针投射到晷面的影子来测定时间．把地球看成一个球(球心记为O )，地球上一点A 的纬度是指OA 与地球赤道所在平面所成角，点A处的水平面是指过点A且与OA垂直的平面.在点A处放置一个日晷，若晷面与赤道所在平面平行，点A处的纬度为北纬40°，则晷针与点A处的水平面所成角为A．20°B．40°C．50°D．90°D16．已知直四棱柱ABCD–A1B1C1D1的棱长均为2，∠BAD=60°．以1的球面与侧面BCC1B1的交线长为________．20．（12分）如图，四棱锥P-ABCD的底面为正方形，PD⊥底面ABCD．设平面PAD与平面PBC的交线为l．（1）证明：l⊥平面PDC；（2）已知PD=AD=1，Q为l上的点，求PB与平面QCD所成角的正弦值的最大值．4．B 1620．解：（1）因为PD⊥底面ABCD，所以PD AD⊥．⊥，因此AD⊥底面PDC．又底面ABCD为正方形，所以AD DC∥，AD⊄平面PBC，所以AD∥平面PBC．因为AD BC∥．因此l⊥平面PDC．由已知得l AD（2）以D为坐标原点，DA的方向为x轴正方向，建立如图所示的空间直角坐标系D xyz -．则(0,0,0),(0,1,0),(1,1,0),(0,0,1)D C B P ，(0,1,0)DC =，(1,1,1)PB =-．由（1）可设(,0,1)Q a ，则(,0,1)DQ a =．设(,,)x y z =n 是平面QCD 的法向量，则0,0,DQ DC ⎧⋅=⎪⎨⋅=⎪⎩n n 即0,0.ax z y +=⎧⎨=⎩ 可取(1,0,)a =-n ．所以cos ,||||3PB PB PB ⋅〈〉==⋅n nn ．设PB 与平面QCD 所成角为θ，则sin θ==当且仅当1a =时等号成立，所以PB 与平面QCD 所成角的正． 2020年普通高等学校招生全国统一考试（浙江卷）5．某几何体的三视图（单位：cm ）如图所示，则该几何体的体积（单位：cm 3）是A ．73B．143C ．3D ．614．已知圆锥的侧面积（单位：cm 2）为2π，且它的侧面展开图是一个半圆，则这个圆锥的底面半径（单位：cm ）是_______． 19．（本题满分15分）如图，在三棱台ABC —DEF 中，平面ACFD ⊥平面ABC ，∠ACB =∠ACD =45°，DC =2BC ．（Ⅰ）证明：EF ⊥DB ；（Ⅱ）求直线DF 与平面DBC 所成角的正弦值．5．A 14．119．满分15分。

2020高考数学立体几何练习题23题

2020高考数学之立体几何解答題23 題一．解答题（共 23 小题）1．在如图所示的几何体中，四边形 ABCD 是菱形， ADNM 是矩形，平面 ADNM ⊥平面 ABCD ，∠DAB=60 °，AD=2 ， AM=1 ， E 为 AB 的中点．（Ⅰ）求证： AN ∥平面 MEC；（Ⅱ）在线段 AM 上是否存在点 P，使二面角 P﹣ EC﹣D 的大小为？若存在，求出 AP 的长 h；若不存在，请说明理由．2．如图，三棱柱中 ABC ﹣A1B1C1 中，点 A1 在平面 ABC 内的射影 D 为棱 AC 的中点，侧面 A1ACC 1为边长为 2 的菱形， AC⊥CB，BC=1 ．（Ⅰ）证明： AC 1⊥平面 A 1BC；（Ⅱ）求二面角 B﹣ A1C﹣B1的大小．3．如图，已知四棱锥 P﹣ABCD ，PB⊥AD 侧面 PAD 为边长等于 2的正三角形，底面 ABCD 为菱形，侧面PAD 与底面 ABCD 所成的二面角为 120°．（I）求点 P 到平面 ABCD 的距离，（II ）求面 APB 与面 CPB 所成二面角的大小．4．在正三棱锥 P﹣ABC 中，底面正△ ABC 的中心为 O，D 是 PA 的中点， PO=AB=2 ，求 PB 与平面 BDC 所成角的正弦值．5．如图，正三棱锥 O ﹣ABC 的三条侧棱 OA 、OB 、 OC 两两垂直，且长度均为 2．E 、F 分别是 AB 、AC 的中点， H 是 EF 的中点，过 EF 作平面与侧棱 OA 、OB 、OC 或其延长线分别相交于 A 1、B 1、C 1，已知．（ 1）求证： B 1C 1⊥平面 OAH ；（ 2）求二面角 O ﹣A 1B 1﹣C 1 的大小．6．如图，在三棱锥 A ﹣ BCD 中，侧面 ABD 、ACD 是全等的直角三角形， AD 是公共的斜边，且AD= ，BD=CD=1 ，另一个侧面是正三角形．1）求证： AD ⊥BC ．E ，使 ED 与面 BCD 成 30°角？若存在，确定E 的位置；若不存在，说明理由． 2）求二面角 B ﹣AC ﹣D 的大小．7．如图，在四棱锥 P ﹣ ABCD 中， AD ∥ BC ，∠ ADC= ∠ PAB=90 °， BC=CD=PA 与CD 所成的角为 90°．（Ⅰ）在平面 PAB 内找一点 M ，使得直线 CM ∥平面 PBE ，并说明理由；（Ⅱ）若二面角 P ﹣CD ﹣A 的大小为 45°，求直线 PA 与平面 PCE 所成角的正弦值．8．如图，在三棱台 ABC ﹣DEF 中，平面 BCFE ⊥平面 ABC ，∠ ACB=90 °，BE=EF=FC=1， BC=2 ， AC=3 ．（ Ⅰ ）求证： BF ⊥平面 ACFD ；（ Ⅱ ）求直线 BD 与平面 ACFD 所成角的余弦值．9．如图，在以 A ，B ，C ，D ，E ，F 为顶点的五面体中，面 ABEF 为正方形， AF=2FD ，∠AFD=90 °，且二面角 D ﹣AF ﹣E 与二面角 C ﹣BE ﹣ F 都是 60°．（Ⅰ）证明平面 ABEF ⊥平面 EFDC ；（Ⅱ）求二面角 E ﹣ BC ﹣A 的余弦值．AD ．E 为棱 AD 的中点，异面直线10．如图，已知边长为 6的菱形 ABCD ，∠ ABC=120 °，AC 与BD 相交于 O ，将菱形 ABCD 沿对角线 AC 折起，使 BD=3 ．（1）若 M 是 BC 的中点，求证：在三棱锥 D ﹣ABC 中，直线 OM 与平面 ABD 平行；（2）求二面角 A ﹣BD ﹣O 的余弦值；（ 3）在三棱锥 D ﹣ ABC 中，设点 N 是 BD 上的一个动点，试确定 N 点的位置，使得 CN=4 ．11．如图所示的多面体 ABCDE 中，已知 AB ∥DE ，AB ⊥AD ，△ACD 是正三角形， AD=DE=2AB=2 ，BC= ，F 是 CD 的中点．（ 1）求证： AF ∥平面 BCE ；（ 2）求直线 CE 与平面 ABED 所成角的余弦值；（ 3）求多面体 ABCDE 的体积．12．如图，已知矩形 ABCD 所在平面垂直于直角梯形 ABPE 所在平面于直线 AB ，且 AB=BP=2 ，AD=AE=1 ，AE ⊥AB ，且 AE ∥BP ．Ⅰ）设点 M 为棱 PD 中点，求证： EM ∥平面 ABCD ；若不存在，请说明理由．Ⅱ ）线段 PD 上是否存在一点 N ，使得直线 BN 与平面 PCD 所成角的正弦值等于？若存在，试确定点 N 的位置；13．如图，在三棱锥 P ﹣ABC 中，∠ PAB= ∠PAC=∠ ACB=90 °．（ 1）求证：平面 PBC ⊥平面 PAC ；（2）若 PA=1，AB=2 ， BC= ，在直线 AC 上是否存在一点 D ，使得直线 BD 与平面 PBC 所成角为 30°？若存在，求出 CD 的长；若不存在，说明理由．14．如图，在四棱锥 P ﹣ABCD 中，底面 ABCD 是平行四边形， ∠BCD=135 °，侧面 PAB ⊥底面 ABCD ，∠ BAP=90 °， AB=AC=PA=2 ， E ，F 分别为 BC ，AD 的中点，点 M 在线段 PD 上．（ Ⅰ ）求证： EF ⊥平面 PAC ；（ Ⅱ ）如果直线 ME 与平面 PBC 所成的角和直线 ME 与平面 ABCD 所成的角相等，求的值．Ⅰ）求证： CD ⊥AM ；AM 与平面 BDM所成角的正弦值．15．如图，在多面体 ABCDM 平面 BCD ， AB ⊥平面 BCD ．中，△ BCD 是等边三角形，△ CMD 是等腰直角三角形，∠ CMD=90 °，平面 CMD ⊥Ⅱ ）若 AM=BC=2 ，求直16．如图，矩形ABCD 所在的平面和平面ABEF 互相垂直，等腰梯形ABEF 中，AB ∥EF，AB=2 ，AD=AF=1 ，∠ BAF=60°，O，P分别为 AB，CB的中点， M为底面△ OBF的重心．（Ⅰ）求证： PM ∥平面 AFC；（Ⅱ ）求直线 AC 与平面 CEF 所成角的正弦值．17．已知菱形 ABCD ，AB=2 ，∠BAD= ，半圆 O 所在平面垂直于平面 ABCD ，点 P 在半圆弧上．（不同于B ，C）．（1）若 PA与平面 ABCD 所成角的正弦值为，求出点 P 的位置；（2）是否存在点 P，使得 PC⊥ BD ，若存在，求出点 P 的位置，若不存在，说明理由．18．如图，菱形 ABCD 中，∠ ABC=60 °，AC 与BD相交于点 O，AE ⊥平面 ABCD，CF∥AE，AB=AE=2 ．（Ⅰ）求证： BD ⊥平面 ACFE ；（Ⅱ）当直线 FO与平面 BED 所成角的大小为 45°时，求 CF 的长度．19．如图，在四棱锥 P﹣ ABCD 中，等边△ PAD 所在的平面与正方形 ABCD 所在的平面O为 AD 的中点，互相垂直， E 为 DC 的中点，且 AD=2 ．（Ⅰ ）求证： PO⊥平面 ABCD ；（Ⅱ）求二面角 P﹣EB﹣ A 的余弦值；（Ⅲ）在线段 AB 上是否存在点 M，使线段 PM 与△PAD 所在平面成 30°角．若存在，求出 AM 的长，若不存在，请说明理由．20．在斜三棱柱 ABC ﹣ A 1B 1C1中，底面 ABC 是正三角形， E 是 AB 中点， A 1E⊥平面 ABC．（ I）证明： BC1∥平面 A1EC；（II）若 A1A⊥A1B，且 AB=2 ．① 求点 B 到平面 ACC 1A1 的距离；② 求直线 CB1 与平面 ACC 1A 1 所成角的正弦值．1）求证： DF ⊥平面 ABCD ；2）若△ ABD 是边长为 2 的等边三角形，且 BF 与平面 ABCD 所成角的正切值为 1，求点 E 到平面 BDF 的距离．22．如图，在三棱柱 ABC ﹣A 1B 1C 1中，G 为ABC 的重心，（ 1）求证： GE ∥平面 AA 1B 1B ；（2）若侧面 ABB 1A 1⊥底面 ABC ，∠ A 1AB= ∠BAC=60°，AA 1=AB=AC=2 ，求直线 A 1B 与平面 B 1GE 所成角正弦值．21．如图，在多面体 EF ﹣ABCD 中， ABCD ， ABEF 均为直角梯形，∠ 平面 DCEF ⊥平面 ABCD ．ABE= ∠ABC= DCEF 为平行四边形，θ的BC 1．23．如图，在四棱锥 P﹣ABCD 中， PA⊥底面 ABCD，AD∥BC，AD⊥CD，BC=2，AD=CD=1，M是 PB的中点．（Ⅰ ）求证： AM ∥平面 PCD；（Ⅱ ）求证：平面 ACM ⊥平面 PAB；。

高考数学理数立体几何大题训练(含答案)

高考数学理数立体几何大题训练(含答案)1.（2020·新课标Ⅲ·理）在长方体中，点P、Q分别在棱AB、CD上，且AP=CQ.（1）证明：点PQ平分长方体的体对角线；（2）若PQ在平面BCFE内，求二面角的正弦值．2.（2020·新课标Ⅱ·理）如图，已知三棱柱ABC-A1B1C1的底面是正三角形，侧面BB1C1C是矩形，M、N分别为BC、B1C1的中点，P为AM上一点，过B1C1和P的平面交AB于E，交AC于F.（1）证明：AA1∥MN，且平面A1AMN⊥EB1C1F；（2）设O为△A1B1C1的中心，若AO∥平面EB1C1F，且AO=AB，求直线B1E与平面A1AMN 所成角的正弦值.3.（2020·新课标Ⅰ·理）如图，D为圆锥的顶点，O是圆锥底面的圆心，底面是内接正三角形ABC，P为上一点，AP为底面直径，DP⊥底面．（1）证明：DP平分∠ADC；（2）求二面角平面APD与平面ABC的余弦值．4.（2020·新高考Ⅰ）如图，四棱锥P-ABCD的底面为正方形，PD⊥底面ABCD．设平面PAD与平面PBC的交线为l．（1）证明：l⊥平面PDC；（2）已知PD=AD=1，Q为l上的点，求PB与平面QCD所成角的正弦值的最大值．5.（2020·天津）如图，在三棱柱ABC-A1B1C1中，点P、Q分别在棱AB、A1B1上，且AP=A1Q，平面PQC1为棱BC1的中垂面，M为棱AC的中点．（Ⅰ）求证：PM∥B1Q，且PM=B1Q；（Ⅱ）求二面角平面PQC1与直线PM所成角的正弦值；（Ⅲ）求直线B1Q与平面PQC1所成角的正弦值．6.（2020·江苏）在三棱锥ABCD中，已知CB=CD=1，AC=2，BD=2，O为BD的中点，AO⊥平面BCD，AO=2，E为AC上一点，DE⊥平面BCD，DE=1.（1）求直线AB与DE所成角的余弦值；（2）若点F在BC上，满足BF=BC，设二面角F-DE-C的大小为θ，求sinθ的值．7.（2020·北京）如图，正方体ABCD-EFGH中，E为AD的中点，P为BF上一点．（Ⅰ）求证：PE∥CG；（Ⅱ）求直线PE与平面CGH所成角的正弦值．8.（2020·浙江）如图，三棱台DEF-ABC中，面ADFC⊥面ABC，∠ACB=∠ACD=45°，XXX．（Ⅰ）证明：EF⊥DB；（Ⅱ）求DF与面DBC所成角的正弦值．9.（2020·扬州模拟）如图，在等边三角形ABC的三棱锥ABCD中，D为底面的中点，E为线段AD上一动点，记DE=λAD.（1）当λ=1时，求证：DE与平面ABC垂直；（2）当λ=2时，求直线BE与平面ACD所成角的正弦值．求证：直线AD与平面BCD垂直；2）若平面ABD与平面ACD所成二面角为，求二面角ABC与平面BCD所成二面角的正弦值。

高考数学的立体几何多选题及答案

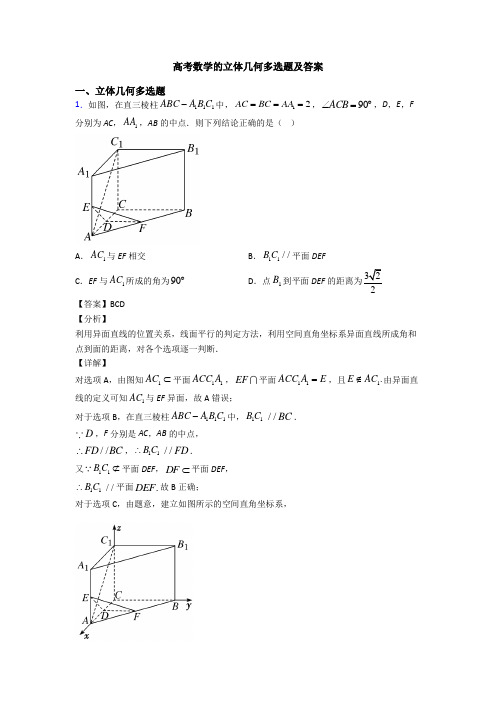
高考数学的立体几何多选题及答案一、立体几何多选题1．如图，在直三棱柱111ABC A B C -中，12AC BC AA ===，90ACB ∠=︒，D ，E ，F分别为AC ，1AA ，AB 的中点．则下列结论正确的是（）A ．1AC 与EF 相交B ．11//BC 平面DEF C ．EF 与1AC 所成的角为90︒D ．点1B 到平面DEF 的距离为322【答案】BCD 【分析】利用异面直线的位置关系，线面平行的判定方法，利用空间直角坐标系异面直线所成角和点到面的距离，对各个选项逐一判断．【详解】对选项A ，由图知1AC ⊂平面11ACC A ，EF 平面11ACC A E =，且1.E AC ∉由异面直线的定义可知1AC 与EF 异面，故A 错误；对于选项B ，在直三棱柱111ABC A B C -中，11B C //BC ．D ，F 分别是AC ，AB 的中点， //∴FD BC ，11B C ∴ //FD ．又11B C ⊄平面DEF ，DF ⊂平面DEF ，11B C ∴ //平面.DEF 故B 正确；对于选项C ，由题意，建立如图所示的空间直角坐标系，则(0C ，0，0)，(2A ，0，0)，(0B ，2，0)，1(2A ，0，2)，1(0B ，2，2)，1(0C ，0，2)，(1D ，0，0)，(2E ，0，1)，(1F ，1，0)．(1EF ∴=-，1，1)-，1(2AC =-，0，2)． 1·2020EF AC =+-=，1EF AC ∴⊥，1EF AC ∴⊥． EF 与1AC 所成的角为90︒，故C 正确；对于选项D ，设向量(n x =，y ，)z 是平面DEF 的一个法向量． (1DE =，0，1)，(0DF =，1，0)， ∴由n DE n DF ⎧⊥⎨⊥⎩，，，即·0·0n DE n DF ⎧=⎨=⎩，，，得00.x z y +=⎧⎨=⎩，取1x =，则1z =-，(1n ∴=，0，1)-，设点1B 到平面DEF 的距离为d ．又1(1DB =-，2，2)，1·102DB n d n-+∴===， ∴点1B 到平面DEF 的距离为2，故D 正确．故选：BCD 【点睛】本题主要考查异面直线的位置关系，线面平行的判定，异面直线所成角以及点到面的距离，还考查思维能力及综合分析能力，属难题．2．如图，正方体1111ABCD A B C D -中的正四面体11A BDC -的棱长为2，则下列说法正确的是（）A ．异面直线1AB 与1AD 所成的角是3πB ．1BD ⊥平面11AC DC ．平面1ACB 截正四面体11A BDC -所得截面面积为3D ．正四面体11A BDC -的高等于正方体1111ABCD A B C D -体对角线长的23【答案】ABD 【分析】选项A ，利用正方体的结构特征找到异面直线所成的角；选项B ，根据正方体和正四面体的结构特征以及线面垂直的判定定理容易得证；选项C ，由图得平面1ACB 截正四面体11A BDC -所得截面面积为1ACB 面积的四分之一；选项D ，分别求出正方体的体对角线长和正四面体11A BDC -的高，然后判断数量关系即可得解. 【详解】A ：正方体1111ABCD ABCD -中，易知11//AD BC ，异面直线1A B 与1AD 所成的角即直线1A B 与1BC 所成的角，即11A BC ∠，11A BC 为等边三角形，113A BC π∠=，正确；B ：连接11B D ，1B B ⊥平面1111DC B A ，11A C ⊂平面1111D C B A ，即111AC B B ⊥，又1111AC B D ⊥，1111B B B D B ⋂=，有11A C ⊥平面11BDD B ，1BD ⊂平面11BDD B ，所以111BD AC ⊥，同理可证：11BD A D ⊥，1111AC A D A ⋂=，所以1BD ⊥平面11AC D ，正确；C ：易知平面1ACB 截正四面体11A BDC -所得截面面积为134ACB S=，错误；D ：易得正方体1111ABCD A B C D -()()()2222226++=2的正四面体11A BDC -22222262213⎛⎫--⨯ ⎪⎝⎭，故正四面体11A BDC -的高等于正方体1111ABCD A B C D -体对角线长的23，正确. 故选：ABD. 【点睛】关键点点睛：利用正方体的性质，找异面直线所成角的平面角求其大小，根据线面垂直的判定证明1BD ⊥平面11AC D ，由正四面体的性质，结合几何图形确定截面的面积，并求高，即可判断C 、D 的正误.3．已知正方体1111ABCD A B C D -的棱长为2，点E ，F 在平面1111D C B A 内，若||5AE =，AC DF ⊥，则（）A ．点E 的轨迹是一个圆B ．点F 的轨迹是一个圆C ．EF 21-D ．AE 与平面1A BD 21530+【答案】ACD 【分析】对于A 、B 、C 、D 四个选项，需要对各个选项一一验证. 选项A ：由2211||5AE AA A E =+=1||1A E =，分析得E 的轨迹为圆；选项B ：由AC DBF ⊥，而点F 在11B D 上，即F 的轨迹为线段11B D ，；选项C ：由E 的轨迹为圆，F 的轨迹为线段11B D ，可分析得min ||EF d r =-；选项D ：建立空间直角坐标系，用向量法求最值. 【详解】对于A:2211||5AE AA A E =+=221|25A E +=1||1A E =，即点E 为在面1111D C B A 内，以1A 为圆心、半径为1 的圆上；故A 正确；对于B: 正方体1111ABCD A B C D -中，AC ⊥BD ，又AC DF ⊥，且BD ∩DF=D ，所以AC DBF ⊥，所以点F 在11B D 上，即F 的轨迹为线段11B D ，故B 错误；对于C:在平面1111D C B A 内，1A 到直线11B D 的距离为2,d =当点E ，F 落在11A C 上时，min ||21EF =-；故C 正确；对于D:建立如图示的坐标系，则()()()()10,0,0,2,0,0,0,0,2,0,2,0A B A D因为点E 为在面1111D C B A 内，以1A 为圆心、半径为1 的圆上，可设()cos ,sin ,2E θθ 所以()()()1cos ,sin ,2,2,0,2,2,2,0,AE A B BD θθ==-=-设平面1A BD 的法向量(),,n x y z =，则有1·220·220n BD x y n A B x z ⎧=-+=⎪⎨=-=⎪⎩不妨令x =1，则()1,1,1n =，设AE 与平面1A BD 所成角为α，则：22|||sin |cos ,|||||5315n AE n AE n AE πθα⎛⎫++ ⎪⎝⎭====⨯⨯当且仅当4πθ=时，sin α有最大值222153015++=，故D 正确故选：CD 【点睛】多项选择题是2020年高考新题型，需要要对选项一一验证．4．在棱长为1的正方体1111ABCD A B C D -中，P 为底面ABCD 内（含边界）一点．（） A ．若13A P =，则满足条件的P 点有且只有一个 B ．若12A P =，则点P 的轨迹是一段圆弧 C ．若1//A P 平面11B D C ，则1A P 长的最小值为2D ．若12A P =且1//A P 平面11B DC ，则平面11A PC 截正方体外接球所得截面的面积为23π【答案】ABD 【分析】选项A ，B 可利用球的截面小圆的半径来判断；由平面1//A BD 平面11B D C ，知满足1//A P 平面11B D C 的点P 在BD 上，1A P 长的最大值为2；结合以上条件点P 与B 或D 重合，利用12sin 60A P r =︒，求出63r =，进而求出面积. 【详解】对A 选项，如下图：由13A P =，知点P 在以1A 为球心，半径为3的球上，又因为P 在底面ABCD 内（含边界），底面截球可得一个小圆，由1A A ⊥底面ABCD ，知点P 的轨迹是在底面上以A 为圆心的小圆圆弧，半径为22112r A P A A =-=，则只有唯一一点C满足，故A 正确；对B 选项，同理可得点P 在以A 为圆心，半径为22111r A P A A =-=的小圆圆弧上，在底面ABCD 内（含边界）中，可得点P 轨迹为四分之一圆弧BD .故B 正确；对C 选项，移动点P 可得两相交的动直线与平面11B D C 平行，则点P 必在过1A 且与平面11B D C 平行的平面内，由平面1//A BD 平面11B D C ，知满足1//A P 平面11B D C 的点P 在BD上，则1A P 长的最大值为12A B =，则C 不正确；对选项D ，由以上推理可知，点P 既在以A 为圆心，半径为1的小圆圆弧上，又在线段BD 上，即与B 或D 重合，不妨取点B ，则平面11A PC 截正方体外接球所得截面为11A BC 的外接圆，利用2126622,,sin 60333A B r r S r ππ==∴=∴==︒.故D 正确.故选：ABD 【点睛】（1）平面截球所得截面为圆面，且满足222=R r d +（其中R 为球半径，r 为小圆半径，d 为球心到小圆距离）；（2）过定点A 的动直线平行一平面α，则这些动直线都在过A 且与α平行的平面内.5．在三棱锥M ABC -中，下列命题正确的是（） A ．若1233AD AB AC =+，则3BC BD = B ．若G 为ABC 的重心，则111333MG MA MB MC =++ C ．若0MA BC ⋅=，0MC AB ⋅=，则0MB AC ⋅=D ．若三棱锥M ABC -的棱长都为2，P ，Q 分别为MA ，BC 中点，则2PQ = 【答案】BC 【分析】作出三棱锥M ABC -直观图，在每个三角形中利用向量的线性运算可得.【详解】对于A ，由已知12322233AD AB AC AD AC AB AD AC AB AD =+⇒=+⇒-=-，即2CD DB =，则32BD BD DC BC =+=，故A 错误；对于B ，由G 为ABC 的重心，得0GA GB GC ++=，又MG MA AG =+，MG MB BG =+，MG MC CG =+，3MA MB MC MG ∴++=，即111333MG MA MB MC =++，故B 正确；对于C ，若0MA BC ⋅=，0MC AB ⋅=，则0MC MA BC AB ⋅+⋅=，即()00MA BC AC CB MA BC AC C MC C M B M C ⋅++=⇒⋅++⋅⋅=⋅()00MA BC A MC MC MC MC C BC MA BC AC ⋅⋅⋅⇒⋅+-=⇒-+=⋅()000MC M CA BC AC AC CB AC CB AC C MC ⇒+=⇒+=⇒+=⋅⋅⋅⋅⋅，即0MB AC ⋅=，故C 正确；对于D ，111()()222PQ MQ MP MB MC MA MB MC MA ∴=-=+-=+- ()21122PQ MB MC MA MB MC MA ∴=+-=+-，又()2222222MB MC MA MB MC MA MB MC MB MA MC MA+-=+++⋅-⋅-⋅2221112222222222228222=+++⨯⨯⨯-⨯⨯⨯-⨯⨯⨯=，1822PQ ∴==，故D 错误. 故选：BC 【点睛】关键点睛：本题考查向量的运算，用已知向量表示某一向量的三个关键点： (1)用已知向量来表示某一向量，一定要结合图形，以图形为指导是解题的关键．(2)要正确理解向量加法、减法与数乘运算的几何意义，如首尾相接的若干向量之和，等于由起始向量的始点指向末尾向量的终点的向量． (3)在立体几何中三角形法则、平行四边形法则仍然成立．6．在长方体1111ABCD A B C D -中，AB =12AD AA ==，P 、Q 、R 分别是AB 、1BB 、1A C 上的动点，下列结论正确的是（）A ．对于任意给定的点P ，存在点Q 使得1D P CQ ⊥B ．对于任意给定的点Q ，存在点R 使得1D R CQ ⊥C ．当1AR A C ⊥时，1ARD R ⊥D ．当113AC A R =时，1//D R 平面1BDC 【答案】ABCD 【分析】本题先建立空间直角坐标系，再运用空间向量在立体几何中的应用逐一判断即可. 【详解】如图所示，建立空间直角坐标系，设(2,,0)P a，0a ⎡∈⎣，(2,)Q b ，[]0,2b ∈，设11A R AC λ=，得到(22,,22)R λλ--，[]0,1λ∈. 1(2,,2)D P a =-，(2,0,)CQ b =，142D P CQ b ⋅=-，当2b =时，1D P CQ ⊥，A 正确；1(22,2)D R λλ=--，12(22)2D R CQ b λλ⋅=--，取22bλ=+时，1D R CQ ⊥，B 正确；1AR A C ⊥，则1(2,22)(2)412440AR AC λλλλλ⋅=--⋅--=+-+=，解得：15λ=，此时12282()()05555AR D R ---⋅=⋅=，1AR D R ⊥，C 正确；113AC A R =，则44()33R，142()33D R =-，设平面1BDC 的法向量为(,,)n x y z =，则100n BD n DC ⎧⋅=⎪⎨⋅=⎪⎩，解得(3,n =-，故10n D R ⋅=，故1//D R 平面1BDC ，D 正确.故选：ABCD.【点睛】本题考查了空间向量在立体几何中的应用，是偏难题.7．已知直三棱柱111ABC A B C -中，AB BC ⊥，1AB BC BB ==，D 是AC 的中点，O 为1A C 的中点.点P 是1BC 上的动点，则下列说法正确的是（）A ．当点P 运动到1BC 中点时，直线1A P 与平面111ABC 5 B ．无论点P 在1BC 上怎么运动，都有11A P OB ⊥C ．当点P 运动到1BC 中点时，才有1A P 与1OB 相交于一点，记为Q ，且113PQ QA = D ．无论点P 在1BC 上怎么运动，直线1A P 与AB 所成角都不可能是30° 【答案】ABD 【分析】构造线面角1PA E ∠，由已知线段的等量关系求1tan EPPA E AE∠=的值即可判断A 的正误；利用线面垂直的性质，可证明11A P OB ⊥即可知B 的正误；由中位线的性质有112PQ QA =可知C 的正误；由直线的平行关系构造线线角为11B A P ∠，结合动点P 分析角度范围即可知D 的正误【详解】直三棱柱111ABC A B C -中，AB BC ⊥，1AB BC BB ==选项A 中，当点P 运动到1BC 中点时，有E 为11B C 的中点，连接1A E 、EP ，如下图示即有EP ⊥面111A B C∴直线1A P 与平面111A B C 所成的角的正切值：1tan EPPA E AE∠= ∵112EP BB =，22111152AE A B B E BB =+= ∴15tan PA E ∠=，故A 正确选项B 中，连接1B C ，与1BC 交于E ，并连接1A B ，如下图示由题意知，11B BCC 为正方形，即有11B C BC ⊥而AB BC ⊥且111ABC A B C -为直三棱柱，有11A B ⊥面11B BCC ，1BC ⊂面11B BCC ∴111A B BC ⊥，又1111A B B C B =∴1BC ⊥面11A B C ，1OB ⊂面11A B C ，故11BC OB ⊥ 同理可证：11A B OB ⊥，又11A B BC B ⋂=∴1OB ⊥面11A BC ，又1A P ⊂面11A BC ，即有11A P OB ⊥，故B 正确选项C 中，点P 运动到1BC 中点时，即在△11A B C 中1A P 、1OB 均为中位线∴Q为中位线的交点∴根据中位线的性质有：112PQQA=，故C错误选项D中，由于11//A B AB，直线1A P与AB所成角即为11A B与1A P所成角：11B A P∠结合下图分析知：点P在1BC上运动时当P在B或1C上时，11B A P∠最大为45°当P在1BC中点上时，11B A P∠最小为23arctan30>=︒∴11B A P∠不可能是30°，故D正确故选：ABD【点睛】本题考查了利用射影定理构造线面角，并计算其正弦值；利用线面垂直证明线线垂直；中位线的性质：中位线交点分中位线为1：2的数量关系；由动点分析线线角的大小8．如图，正方体1111ABCD A B C D-的棱长为1，线段11B D上有两个动点E，F，且2EF=则下列结论正确的是（）A ．三棱锥A BEF -的体积为定值B ．当E 向1D 运动时，二面角A EF B --逐渐变小C ．EF 在平面11ABB A 内的射影长为12D ．当E 与1D 重合时，异面直线AE 与BF 所成的角为π4【答案】AC 【分析】对选项分别作图，研究计算可得. 【详解】选项A:连接BD ,由正方体性质知11BDD B 是矩形，1112212224BEF S EF BB ∆∴=⋅=⨯=连接AO 交BD 于点O由正方体性质知AO ⊥平面11BDD B ,所以，AO 是点A 到平面11BDD B 的距离，即22AO =112213312A BEF BEF V S AO -∆∴=⨯==A BEF V -∴是定值.选项B:连接11A C 与11B D 交于点M ，连接11,AD AB ，由正方体性质知11AD AB =,M 是11B D 中点，AM EF ∴⊥ ,又1BB EF ⊥,11//BB AAA EFB ∴--的大小即为AM 与1AA 所成的角，在直角三角形1AA M 中，12tan 2MAA ∠=为定值. 选项C:如图，作1111,,,FH A B EG A B ET EG ⊥⊥⊥ 在直角三角形EFT 中，221cos 452FT EF =⨯=⨯=12HG FT ∴== 选项D:当E 与1D 重合时，F 与M 重合，连接AC 与BD 交于点R ，连接1D R ,1//D R BM 异面直线AE 与BF 所成的角,即为异面直线1AD 与1D R 所成的角, 在三角形1AD R 中，22111132,2AD D R MB BB M B ===+=2AR =由余弦定理得13cos AD R ∠= 故选：AC 【点睛】本题考查空间几何体性质问题.求解思路：关键是弄清(1)点的变化，点与点的重合及点的位置变化；(2)线的变化，应注意其位置关系的变化；(3)长度、角度等几何度量的变化．求空间几何体体积的思路：若所给定的几何体是柱体、锥体或台体等规则几何体，则可直接利用公式进行求解．其中，求三棱锥的体积常用等体积转换法；若所给定的几何体是不规则几何体，则将不规则的几何体通过分割或补形转化为规则几何体，再利用公式求解.9．如图所示，在长方体1111ABCD A B C D -中，11,2,AB BC AA P ===是1A B 上的一动点，则下列选项正确的是( )A ．DP 35B ．DP 5C ．1AP PC +6D ．1AP PC +170【答案】AD 【分析】DP 的最小值，即求1DA B △底边1A B 上的高即可；旋转11A BC 所在平面到平面11ABB A ，1AP PC +的最小值转化为求AC '即可.【详解】求DP 的最小值，即求1DA B △底边1A B 上的高，易知115,2A B A D BD ===，所以1A B 边上的高为355h =111,AC BC ，得11A BC ，以1A B 所在直线为轴，将11A BC 所在平面旋转到平面11ABB A ，设点1C 的新位置为C '，连接AC '，则AC '即为所求的最小值，易知11122,2,cos AA AC AAC ''==∠=，所以217042222()105AC '=+-⨯⨯⨯-=.故选：AD. 【点睛】本题考查利用旋转求解线段最小值问题.求解翻折、旋转问题的关键是弄清原有的性质变化与否， (1)点的变化，点与点的重合及点的位置变化；(2)线的变化，翻折、旋转前后应注意其位置关系的变化；(3)长度、角度等几何度量的变化．10．半正多面体（semiregularsolid）亦称“阿基米德多面体”，是由边数不全相同的正多边形围成的多面体，体现了数学的对称美．二十四等边体就是一种半正多面体，是由正方体切截而成的，它由八个正三角形和六个正方形构成（如图所示），若它的所有棱长都为2，则（）A．BF⊥平面EABB．该二十四等边体的体积为20 3C．该二十四等边体外接球的表面积为8πD．PN与平面EBFN所成角的正弦值为2 2【答案】BCD【分析】A用反证法判断；B先补齐八个角成正方体，再计算体积判断；C先找到球心与半径，再计算表面积判断；D先找到直线与平面所成角，再求正弦值判断．【详解】解：对于A，假设A对，即BF⊥平面EAB，于是BF AB⊥，90ABF∠=︒，但六边形ABFPQH为正六边形，120ABF∠=︒，矛盾，所以A错；对于B，补齐八个角构成棱长为2的正方体，则该二十四等边体的体积为3112028111323-⋅⋅⋅⋅⋅=，所以B对；对于C，取正方形ACPM对角线交点O，即为该二十四等边体外接球的球心，其半径为2R =，其表面积为248R ππ=，所以C 对；对于D ，因为PN 在平面EBFN 内射影为NS ，所以PN 与平面EBFN 所成角即为PNS ∠，其正弦值为22PS PN ==，所以D 对．故选：BCD ．【点睛】本题考查了正方体的性质，考查了直线与平面所成角问题，考查了球的体积与表面积计算问题．。

高考数学《立体几何》练习题及答案

立体几何1．[四川省宜宾市第四中学高2020届一诊模拟考试理科数学]若某空间几何体的三视图如图所示，则该几何体的体积是A ．2B ．1C ．D ．【答案】B2．[湖南省衡阳县2020届高三12月联考数学（理）试题]【答案】D 【解析】3．[【全国百强校首发】四川省棠湖中学2020届高三一诊模拟考试数学（理）试题] 在正方体1111ABCD A B C D -中，动点E 在棱1BB 上，动点F 在线段11A C 上，O 为底面ABCD 的中心，若1,BE x A F y ==，则四面体O AEF -的体积 A ．与,x y 都有关 B ．与,x y 都无关 C ．与x 有关，与y 无关D ．与y 有关，与x 无关【答案】B4．[黑龙江省哈尔滨师范大学附属中学2020届高三上学期期中考试数学（理）试题]5．[四川省宜宾市第四中学高2020届一诊模拟考试理科数学] 一个圆锥SC的高和底面直径相等，且这个圆锥SC和圆柱OM的底面半径及体积也都相等，则圆锥SC和圆柱OM的侧面积的比值为A．322B．23C．35D．45【答案】C6．[辽宁葫芦岛锦化高中协作校高三上学期第二次考试数学理科试题]【答案】D【解析】7．[广东省三校（广州真光中学、深圳市第二中学、珠海市第二中学）2020届高三上学期第一次联考数学（理）试题] 在如图直二面角ABDC中，△ABD、△CBD均是以BD为斜边的等腰直角三角形，取AD的中点E，将△ABE 沿BE 翻折到△A1BE，在△ABE的翻折过程中，下列不可能成立的是A．BC与平面A1BE内某直线平行B．CD∥平面A1BEC．BC与平面A1BE内某直线垂直D．BC⊥A1B【答案】D8．[湖南省衡阳县2020届高三12月联考数学（理）试题]【答案】D【解析】9．[陕西省汉中市2020届高三教学质量第一次检测考试理科数学试题] 圆锥的侧面展开图是半径为R 的半圆，则该圆锥的体积为________. 【答案】33πR 10．[辽宁省本溪高级中学2020届高三一模考试数学（理）试卷]【答案】4π11．[安徽省合肥一中、安庆一中等六校教育研究会2020届高三上学期第一次素质测试数学（理)试题] 如图，在棱长为 1 的正方体1111ABCD A B C D -中，点M 是AD 的中点，动点P 在底面ABCD 内（不包括边界），若1B P ∥平面1A BM ，则1C P 的最小值是________．【答案】305【解析】【分析】由面面平行找到点P 在底面ABCD 内的轨迹为线段DN ，再找出点P 的位置，使1C P 取得最小值，即1C P 垂直DN 于点O ，最后利用勾股定理求出最小值. 【详解】取BC 中点N ，连接11,,B D B N DN ，作CO DN ⊥，连接1C O ，因为平面1B DN ∥平面1A BM ，所以动点P 在底面ABCD 内的轨迹为线段DN ，当点P 与点O 重合时，1C P 取得最小值，因为11152225DN CO DC NC CO ⋅=⋅⇒==，所以221min 11130()155C P C O CO CC ==+=+=. 故1C P 的最小值是305. 【点睛】本题考查面面平行及最值问题，求解的关键在于确定点P 的位置，再通过解三角形的知识求最值.12．[四川省成都外国语学校2019-2020学年高三（上）期中数学试卷（理科）]已知某几何体的三视图如图所示，则该几何体的外接球的半径为________．21【答案】【解析】【分析】根据三视图还原几何体，设球心为O，根据外接球的性质可知，O与PAB△和正方形ABCD中心的连线分别与两个平面垂直，从而可得到四边形OGEQ 为矩形，求得OQ和PQ后，利用勾股定理可求得外接球半径.【详解】由三视图还原几何体如下图所示：设PAB△的中心为Q，正方形ABCD的中心为G，外接球球心为O，则OQ⊥平面PAB，OG⊥平面ABCD，E为AB中点，∴四边形OGEQ为矩形，112OQ GE BC ∴===，2233PQ PE ==， ∴外接球的半径：22213R GE PQ =+=. 故答案为21. 【点睛】本题考查多面体外接球半径的求解，关键是能够根据球的性质确定球心的位置，从而根据长度关系利用勾股定理求得结果. 13．[湖南省衡阳县2020届高三12月联考数学（理）试题]【答案】【解析】14．[黑龙江省哈尔滨师范大学附属中学2020届高三上学期期中考试数学（理）试题]【答案】1 315．[江苏省南通市2020届高三第一学期期末考试第一次南通名师模拟试卷数学试题]如图，在四棱锥P ABCD-中，底面ABCD是平行四边形，平面ABP⊥平面BCP，90APB=，M为CP的中点．求证：∠=︒，BP BC（1）AP//平面BDM；（2）BM ACP⊥平面．【解析】（1）设AC 与BD 交于点O ，连接OM ，因为ABCD 是平行四边形，所以O 为AC 中点，因为M 为CP 的中点，所以AP ∥OM ，又AP ⊄平面BDM ，OM ⊂平面BDM ，所以AP ∥平面BDM ．（2）平面ABP ⊥平面BCP ，交线为BP ，因为90APB ∠=︒，故AP BP ⊥，因为AP ⊂平面ABP ，所以AP ⊥平面BCP ，因为BM ⊂平面BCP ，所以AP ⊥BM ．因为BP BC =，M 为CP 的中点，所以BM CP ⊥．因为AP CP P =I ，AP CP ⊂，平面ACP ，所以BM ⊥平面ACP .16．[河南省新乡市高三第一次模拟考试（理科数学）] 如图，在四棱锥ABCDV -中，二面角D BC V --为︒60，E 为BC 的中点. （1）证明：VE BC =；（2）已知F 为直线VA 上一点，且F 与A 不重合，若异面直线BF 与VE 所成角为︒60，求.VA VFABCDPMABCDPMO【解析】17．[四川省成都外国语学校2019-2020学年高三（上）期中数学试卷（理科）]如图，在底面是菱形的四棱锥P-ABCD中，PA⊥平面ABCD，∠ABC=60°，PA=AB=2，点E，F分别为BC，PD的中点，设直线PC与平面AEF交于点Q．（1）已知平面PAB∩平面PCD=l，求证：AB∥l．（2）求直线AQ 与平面PCD 所成角的正弦值．【解析】【分析】（1）证明AB ∥平面PCD ，然后利用直线与平面平行的性质定理证明AB ∥l ；（2）以点A 为原点，直线AE 、AD 、AP 分别为轴建立空间直角坐标系，求出平面PCD 的法向量和直线AQ 的方向向量，然后利用空间向量的数量积求解直线AQ 与平面PCD 所成角的正弦值即可．【详解】（1）证明：∵AB ∥CD ，AB ⊄平面PCD ，CD ⊂平面PCD ． ∴AB ∥平面PCD ，∵AB ⊂平面PAB ，平面PAB ∩平面PCD =l ， ∴AB ∥l ；（2）∵底面是菱形，E 为BC 的中点，且AB =2， ∴13BE AE AE BC ==⊥,,， ∴AE ⊥AD ，又PA ⊥平面ABCD ，则以点A 为原点，直线AE 、AD 、AP 分别为x 、y 、z 轴建立如图所示空间直角坐标系，则()()()()020,002,30,300D P C E,,,,,,,,，∴()0,1,1F ，()()()()3000,11310022AE AF DC DP ===-=-u u u r u u u r u u u r u u u r,,,,,,,,,,，设平面PCD 的法向量为(),,x y z =n ，有0PD ⋅=u u u r n ，0CD ⋅=u u u rn ，得()133=，，n ，设()1AQ AC AP λλ=+-u u u r u u u r u u u r，则()()321AQ λλλ=-u u u r ,,，再设(3,,)AQ mAE n m n n AF =+=u u u r u u u r u u u r，则()3321m n nλλλ⎧=⎪=⎨⎪-=⎩，解之得23m n λ===，∴2223333AQ ⎛⎫=⎪⎝⎭u u u r ,,，设直线AQ 与平面PCD 所成角为α，则3105sin cos ,AQ AQ AQα⋅>=<==u u u r u u u r u u u r n n n ，∴直线AQ 与平面PCD 所成角的正弦值为3105．【点睛】本题考查直线与平面平行的判定定理以及性质定理的应用，直线与平面所成角的向量求法，合理构建空间直角坐标系是解决本题的关键，属中档题.18．[安徽省合肥一中、安庆一中等六校教育研究会2020届高三上学期第一次素质测试数学（理)试题] 已知三棱柱111ABC A B C -中，1AB AC AA ==，侧面11ABB A ⊥底面ABC ，D 是BC 的中点，160B BA ∠=︒，1B D AB ⊥.（1）求证：ABC △为直角三角形；（2）求二面角1C AD B --的余弦值．【解析】（1）取AB 中点O ，连接OD ，1B O ，易知1ABB △为等边三角形，从而得到1B O AB ⊥，结合1B D AB ⊥，可根据线面垂直判定定理得到AB ⊥平面1B OD ，由线面垂直的性质知AB OD ⊥，由平行关系可知AB AC ⊥，从而证得结论；（2）以O 为坐标原点可建立空间直角坐标系，根据空间向量法可求得平面1ADC 和平面ADB 的法向量的夹角的余弦值，根据所求二面角为钝二面角可得到最终结果. 【详解】（1）取AB 中点O ，连接OD ，1B O ，在1ABB △中，1AB B B =，160B BA ∠=︒，1ABB ∴△是等边三角形，又O 为AB 中点，1B O AB ∴⊥，又1B D AB ⊥，111B O B D B =I ，11,B O B D ⊂平面1B OD ，AB ∴⊥平面1B OD ，OD ⊂Q 平面1B OD ，AB OD ∴⊥，又OD AC ∥，AB AC ∴⊥， ∴ABC △为直角三角形.（2）以O 为坐标原点，建立如下图所示的空间直角坐标系：令12AB AC AA ===，则()1,2,0C -，()1,0,0A -，()0,1,0D ，()1,0,0B ，()10,0,3B ，()11,0,3BB ∴=-u u u v ，()0,2,0AC =u u u v ，()1,1,0AD =u u u v，()1111,2,3AC AC CC AC BB =+=+=-u u u u v u u u v u u u u v u u u v u u u v，设平面1ADC 的法向量为(),,x y z =m ，10230AD x y AC x y z ⎧⋅=+=⎪∴⎨⋅=++=⎪⎩u u u v u u u u v m m ，令1x =，则1y =-，3z =，()1,1,3∴=-m ，又平面ADB 的一个法向量为()0,0,1=n ，315cos ,5113∴<>==++m n ， Q 二面角1C AD B --为钝二面角，∴二面角1C AD B --的余弦值为15-.【点睛】本题考查立体几何中垂直关系的证明、空间向量法求解二面角的问题，涉及到线面垂直判定定理和性质定理的应用；证明立体几何中线线垂直关系的常用方法是通过证明线面垂直得到线线垂直的关系.19．[江西省宜春市上高二中2020届高三上学期第三次月考数学（理）试题]20．[黑龙江省哈尔滨师范大学附属中学2020届高三上学期期中考试数学（理）试题]21．[辽宁葫芦岛锦化高中协作校高三上学期第二次考试数学理科试题]【解析】22．[【全国百强校首发】四川省棠湖中学2020届高三一诊模拟考试数学（理）试题] 如图，在四棱锥P ABCD-中，底面ABCD为矩形，平面PCD⊥平面ABCD,2AB=,1BC=，2PC PD==，E为PB中点．（1）求证：PD∥平面ACE；（2）求二面角E AC D--的余弦值；（3）在棱PD上是否存在点M，使得AM⊥BD？若存在，求PMPD的值；若不存在，说明理由．【解析】（1）设BD交AC于点F，连接EF. 因为底面ABCD是矩形，所以F为BD中点 . 又因为E为PB中点，所以EF∥PD.因为PD ⊄平面,ACE EF ⊂平面ACE ，所以PD ∥平面ACE.（2）取CD 的中点O ，连接PO ，FO .因为底面ABCD 为矩形，所以BC CD ⊥.因为PC PD =，O CD 为中点，所以,PO CD OF ⊥∥BC ，所以OF CD ⊥. 又因为平面PCD ⊥平面ABCD ，PO ⊂平面,PCD 平面PCD ∩平面ABCD =CD . 所以PO ⊥平面ABCD ，如图，建立空间直角坐标系O xyz -，则111(1,1,0)(0,1,0)(1,1,0),(0,0,1),(,,)222A C B P E -，,，设平面ACE 的法向量为(,,)x y z =m ，131(1,2,0),(,,)222AC AE =-=-u u u r u u u r ，所以20,2,0,131.00222x y x y AC z y x y z AE -+=⎧⎧=⎧⋅=⎪⇒⇒⎨⎨⎨=--++=⋅=⎩⎩⎪⎩u u u v u u u v m m 令1y =，则2,1x z ==-，所以2,11=-（，）m .平面ACD 的法向量为(0,0,1)OP =u u u r ，则6cos ,OP OP OP⋅<>==-⋅u u u r u u u r u u u r m m |m |. 如图可知二面角E AC D --为钝角，所以二面角E AC D --的余弦值为66-. （3）在棱PD 上存在点M ，使AM BD ⊥.设([0,1]),(,,)PM M x y z PD=∈λλ，则,01,0PM PD D =-u u u u r u u u r λ（，）.因为(,,1)(0,1,1)x y z -=--λ，所以(0,,1)M --λλ. (1,1,1),(1,2,0)AM BD =---=--u u u u r u u u r λλ.因为AM BD ⊥，所以0AM BD ⋅=u u u u r u u u r .所以12(1)0λ--=，解得1=[0,1]2∈λ. 所以在棱PD 上存在点M ，使AM BD ⊥，且12PM PD =。

数学立体几何大题

（2020年新高考立体几何）20.如图，四棱锥P-ABCD的底面为正方形，PD垂直底面ABCD。

设平面PAD与平面PBC的交线为L。

（1）证明：l垂直平面PDC；
（2）已知PD=AD=1，Q为L上的点，求PB与平面QCD所成角的正弦值的最大值。

（2020年天津卷立体几何）17.如图，在三棱柱ABC-A1B1C1中，CC1垂直平面ABC，AC垂直BC,AC=BC=2,CC1=3,点D,E分别在棱CC1上，且AD=1,CE=2,M为棱A1B1的中点。

（I）求证：C1M垂直B1D
(II) 求二面角B-B1E-D的正弦值
(III)求直线AB与平面DB1E所成角的正弦值
（2020年浙江卷立体几何）19.如图，在三棱台ABC-DEF中，平面ACFD 垂直平面ABC，角ACB=角ACD=45度，DC=2BC。

（I）证明：EF垂直DB
(II)求直线DF与平面DBC所成角的正弦值。

（2020年北京卷立体几何）16.如图，在正方体ABCD-A1B2C3D4中，E为BB1的中点。

（I）求证：BC1//平面AD1E;
(II)求直线AA1与平面AD1E所成角的正弦值。

三年 (2020-2022 ) 新高考数学真题汇编专题04立体几何

新高考专题04立体几何【2022年新高考1卷】1．南水北调工程缓解了北方一些地区水资源短缺问题，其中一部分水蓄入某水库.已知该水库水位为海拔1485m ．时，相应水面的面积为21400km ．；水位为海拔1575m ．时，相应水面的面积为21800km ．，将该水库在这两个水位间的形状看作一个棱台，则该水库水位从海拔1485m ．上升到1575m ． 2.65）（）A ．931.010m ⨯B ．931.210m ⨯C ．931.410m ⨯D ．931.610m ⨯【答案】C 【解析】【分析】根据题意只要求出棱台的高，即可利用棱台的体积公式求出．【详解】依题意可知棱台的高为157.5148.59MN =-=(m)，所以增加的水量即为棱台的体积V ．棱台上底面积262140.014010S ==⨯km m ，下底面积262180.018010S '==⨯km m ，∴((66119140101801033V h S S =+=⨯⨯⨯+⨯+'(()679933320109618 2.6510 1.43710 1.410(m )=⨯+⨯≈+⨯⨯=⨯≈⨯．故选：C ．【2022年新高考1卷】2．已知正四棱锥的侧棱长为l ，其各顶点都在同一球面上.若该球的体积为36π，且3l ≤≤则该正四棱锥体积的取值范围是（）A ．8118,4⎡⎤⎢⎥⎣⎦B ．2781,44⎡⎤⎢⎥⎣⎦C ．2764,43⎡⎤⎢⎥⎣⎦D ．[18,27]【答案】C 【解析】【分析】设正四棱锥的高为h ，由球的截面性质列方程求出正四棱锥的底面边长与高的关系，由此确定正四棱锥体积的取值范围. 【详解】∴ 球的体积为36π，所以球的半径3R =,设正四棱锥的底面边长为2a ，高为h ，则2222l a h =+，22232(3)a h =+-,所以26h l =，2222a l h =-所以正四棱锥的体积42622411214()=333366936l l l V Sh a h l l ⎛⎫==⨯⨯=⨯-⨯- ⎪⎝⎭，所以5233112449696l l V l l ⎛⎫⎛⎫-'=-= ⎪ ⎪⎝⎭⎝⎭，当3l ≤≤0V '>，当l ≤0V '<，所以当l =时，正四棱锥的体积V 取最大值，最大值为643，又3l =时，274V =，l =814V =,所以正四棱锥的体积V 的最小值为274，所以该正四棱锥体积的取值范围是276443⎡⎤⎢⎥⎣⎦，.故选：C.【2022年新高考2卷】3．已知正三棱台的高为1，上、下底面边长分别为则该球的表面积为（） A ．100π B ．128π C ．144π D ．192π【答案】A 【解析】【分析】根据题意可求出正三棱台上下底面所在圆面的半径12,r r ，再根据球心距，圆面半径，以及球的半径之间的关系，即可解出球的半径，从而得出球的表面积．【详解】设正三棱台上下底面所在圆面的半径12,r r ，所以123432,260sin 60r r ==，即123,4r r ==，设球心到上下底面的距离分别为12,d d ，球的半径为R ，所以1d 2d =故121d d -=或121d d +=，1=1=，解得225R =符合题意，所以球的表面积为24π100πS R ==．故选：A ．【2021年新高考1卷】4）A ．2B ．C ．4D ．【答案】B 【解析】【分析】设圆锥的母线长为l ，根据圆锥底面圆的周长等于扇形的弧长可求得l 的值，即为所求. 【详解】设圆锥的母线长为l ，由于圆锥底面圆的周长等于扇形的弧长，则2l ππ=解得l = 故选：B.【2021年新高考2卷】5．正四棱台的上､下底面的边长分别为2，4，侧棱长为2，则其体积为（）A．20+B ．C ．563D 【答案】D 【解析】【分析】由四棱台的几何特征算出该几何体的高及上下底面面积，再由棱台的体积公式即可得解. 【详解】作出图形，连接该正四棱台上下底面的中心，如图，因为该四棱台上下底面边长分别为2，4，侧棱长为2，所以该棱台的高h下底面面积116S =，上底面面积24S =，所以该棱台的体积((121116433V h S S =+=+ 故选：D.【2020年新高考1卷（山东卷）】6．日晷是中国古代用来测定时间的仪器，利用与晷面垂直的晷针投射到晷面的影子来测定时间．把地球看成一个球(球心记为O )，地球上一点A 的纬度是指OA 与地球赤道所在平面所成角，点A 处的水平面是指过点A 且与OA 垂直的平面.在点A 处放置一个日晷，若晷面与赤道所在平面平行，点A 处的纬度为北纬40°，则晷针与点A 处的水平面所成角为（）A ．20°B ．40°C ．50°D ．90°【答案】B【分析】画出过球心和晷针所确定的平面截地球和晷面的截面图，根据面面平行的性质定理和线面垂直的定义判定有关截线的关系，根据点A 处的纬度，计算出晷针与点A 处的水平面所成角. 【详解】画出截面图如下图所示，其中CD 是赤道所在平面的截线；l 是点A 处的水平面的截线，依题意可知OA l ⊥；AB 是晷针所在直线.m 是晷面的截线，依题意依题意,晷面和赤道平面平行，晷针与晷面垂直，根据平面平行的性质定理可得可知//m CD 、根据线面垂直的定义可得AB m ⊥.. 由于40,//AOC m CD ∠=︒，所以40OAG AOC ∠=∠=︒，由于90OAG GAE BAE GAE ∠+∠=∠+∠=︒，所以40BAE OAG ∠=∠=︒，也即晷针与点A 处的水平面所成角为40BAE ∠=︒. 故选：B【点睛】本小题主要考查中国古代数学文化，考查球体有关计算，涉及平面平行，线面垂直的性质，属于中档题.【2022年新高考1卷】7．已知正方体1111ABCD A B C D -，则（） A ．直线1BC 与1DA 所成的角为90︒ B ．直线1BC 与1CA 所成的角为90︒ C ．直线1BC 与平面11BB D D 所成的角为45︒ D ．直线1BC 与平面ABCD 所成的角为45︒【答案】ABD【分析】数形结合，依次对所给选项进行判断即可. 【详解】如图，连接1B C 、1BC ，因为11//DA B C ，所以直线1BC 与1B C 所成的角即为直线1BC 与1DA 所成的角，因为四边形11BB C C 为正方形，则1B C ⊥1BC ，故直线1BC 与1DA 所成的角为90︒，A 正确；连接1A C ，因为11A B ⊥平面11BB C C ，1BC ⊂平面11BB C C ，则111A B BC ⊥，因为1B C ⊥1BC ，1111A B B C B =，所以1BC ⊥平面11A B C ，又1AC ⊂平面11A B C ，所以11BC CA ⊥，故B 正确；连接11A C ，设1111AC B D O =，连接BO ，因为1BB ⊥平面1111D C B A ，1C O ⊂平面1111D C B A ，则11C O B B ⊥，因为111C O B D ⊥，1111B D B B B ⋂=，所以1C O ⊥平面11BB D D ，所以1C BO ∠为直线1BC 与平面11BB D D 所成的角，设正方体棱长为1，则1C O =1BC 1111sin 2C O C BO BC ∠==，所以，直线1BC 与平面11BB D D 所成的角为30，故C 错误；因为1C C ⊥平面ABCD ，所以1C BC ∠为直线1BC 与平面ABCD 所成的角，易得145C BC ∠=，故D 正确. 故选：ABD【2022年新高考2卷】8．如图，四边形ABCD 为正方形，ED ⊥平面ABCD ，,2FB ED AB ED FB ==∥，记三棱锥E ACD -，F ABC -，F ACE -的体积分别为123,,V V V ，则（）A ．322V V =B ．31V V =C ．312V V V =+D ．3123V V =【答案】CD 【解析】【分析】直接由体积公式计算12,V V ，连接BD 交AC 于点M ，连接,EM FM ，由3A EFM C EFM V V V --=+计算出3V ，依次判断选项即可. 【详解】设22AB ED FB a ===，因为ED ⊥平面ABCD ，FB ED ，则()2311114223323ACDV ED Sa a a =⋅⋅=⋅⋅⋅=， ()232111223323ABCV FB Sa a a =⋅⋅=⋅⋅⋅=，连接BD 交AC 于点M ，连接,EM FM ，易得BD AC ⊥，又ED ⊥平面ABCD ，AC ⊂平面ABCD ，则ED AC ⊥，又ED BD D =，,ED BD ⊂平面BDEF ，则AC ⊥平面BDEF ，又12BM DM BD ==，过F 作FG DE ⊥于G ，易得四边形BDGF 为矩形，则,FG BD EG a ===，则,EM FM ==，3EF a =，222EM FM EF +=，则EM FM ⊥，212EFMS EM FM =⋅=，AC =，则33123A EFM C EFM EFMV V V AC S a --=+=⋅=，则3123V V =，323V V =，312V V V =+，故A 、B 错误；C 、D 正确. 故选：CD.【2021年新高考1卷】9．在正三棱柱111ABC A B C -中，11AB AA ==，点P 满足1BP BC BB λμ=+，其中[]0,1λ∈，[]0,1μ∈，则（）A ．当1λ=时，1AB P △的周长为定值B ．当1μ=时，三棱锥1P A BC -的体积为定值 C ．当12λ=时，有且仅有一个点P ，使得1A P BP ⊥ D ．当12μ=时，有且仅有一个点P ，使得1A B ⊥平面1AB P 【答案】BD 【解析】【分析】对于A ，由于等价向量关系，联系到一个三角形内，进而确定点的坐标；对于B ，将P 点的运动轨迹考虑到一个三角形内，确定路线，进而考虑体积是否为定值；对于C ，考虑借助向量的平移将P 点轨迹确定，进而考虑建立合适的直角坐标系来求解P 点的个数；对于D ，考虑借助向量的平移将P 点轨迹确定，进而考虑建立合适的直角坐标系来求解P 点的个数．【详解】易知，点P 在矩形11BCC B 内部（含边界）．对于A ，当1λ=时，11=BP BC BB BC CC μμ=++，即此时P ∈线段1CC ，1AB P △周长不是定值，故A 错误；对于B ，当1μ=时，1111=BP BC BB BB BC λλ=++，故此时P 点轨迹为线段11B C ，而11//B C BC ，11//B C 平面1A BC ，则有P 到平面1A BC 的距离为定值，所以其体积为定值，故B 正确．对于C ，当12λ=时，112BP BC BB μ=+，取BC ，11B C 中点分别为Q ，H ，则BP BQ QH μ=+，所以P 点轨迹为线段QH ，不妨建系解决，建立空间直角坐标系如图，1A ⎫⎪⎪⎝⎭，()0,0P μ,，10,,02B ⎛⎫⎪⎝⎭，则112A P μ⎛⎫=-- ⎪ ⎪⎝⎭，10,,2BP μ⎛⎫=- ⎪⎝⎭，()110A P BP μμ⋅=-=，所以0μ=或1μ=．故,H Q 均满足，故C 错误；对于D ，当12μ=时，112BP BC BB λ=+，取1BB ，1CC 中点为,M N ．BP BM MN λ=+，所以P 点轨迹为线段MN ．设010,,2P y ⎛⎫ ⎪⎝⎭，因为0,0A ⎫⎪⎪⎝⎭，所以01,2AP y ⎛⎫=- ⎪ ⎪⎝⎭，11,12A B ⎛⎫=-- ⎪ ⎪⎝⎭，所以00311104222y y +-=⇒=-，此时P 与N 重合，故D 正确．故选：BD ．【点睛】本题主要考查向量的等价替换，关键之处在于所求点的坐标放在三角形内．【2021年新高考2卷】10．如图，在正方体中，O 为底面的中心，P 为所在棱的中点，M ，N 为正方体的顶点．则满足MN OP ⊥的是（）A ．B ．C ．D ．【答案】BC 【解析】【分析】根据线面垂直的判定定理可得BC 的正误，平移直线MN 构造所考虑的线线角后可判断AD 的正误. 【详解】设正方体的棱长为2，对于A ，如图（1）所示，连接AC ，则//MN AC ，故POC ∠（或其补角）为异面直线,OP MN 所成的角，在直角三角形OPC ，OC =1CP =，故tanPOC ∠== 故MN OP ⊥不成立，故A 错误.对于B ，如图（2）所示，取NT 的中点为Q ，连接PQ ，OQ ，则OQ NT ⊥，PQ MN ⊥，由正方体SBCM NADT -可得SN ⊥平面ANDT ，而OQ ⊂平面ANDT ，故SN OQ ⊥，而SNMN N =，故OQ ⊥平面SNTM ，又MN ⊂平面SNTM ，OQ MN ⊥，而OQ PQ Q =，所以MN ⊥平面OPQ ，而PO ⊂平面OPQ ，故MN OP ⊥，故B 正确.对于C ，如图（3），连接BD ，则//BD MN ，由B 的判断可得OP BD ⊥，故OP MN ⊥，故C 正确.对于D ，如图（4），取AD 的中点Q ，AB 的中点K ，连接,,,,AC PQ OQ PK OK ，则//AC MN ，因为DP PC =，故//PQ AC ，故//PQ MN ，所以QPO ∠或其补角为异面直线,PO MN 所成的角，因为正方体的棱长为2，故12PQ AC ==OQ ==PO =222QO PQ OP <+，故QPO ∠不是直角，故,PO MN 不垂直，故D 错误. 故选：BC.【2020年新高考1卷（山东卷）】11．已知直四棱柱ABCD –A 1B 1C 1D 1的棱长均为2，∴BAD =60°．以1D 球面与侧面BCC 1B 1的交线长为________．. 【解析】【分析】根据已知条件易得1D E =1D E ⊥侧面11B C CB ，可得侧面11B C CB 与球面的交线上的点到E 可得侧面11B C CB 与球面的交线是扇形EFG 的弧FG ，再根据弧长公式可求得结果. 【详解】如图：取11B C 的中点为E ，1BB 的中点为F ，1CC 的中点为G ，因为BAD ∠=60°，直四棱柱1111ABCD A B C D -的棱长均为2，所以∴111D B C 为等边三角形，所以1D E 111D E B C ⊥，又四棱柱1111ABCD A B C D -为直四棱柱，所以1BB ⊥平面1111D C B A ，所以111BB B C ⊥，因为1111BB B C B =，所以1D E ⊥侧面11B C CB ，设P 为侧面11B C CB 与球面的交线上的点，则1D E EP ⊥，1D E =||EP ==所以侧面11B C CB 与球面的交线上的点到E因为||||EF EG ==11B C CB 与球面的交线是扇形EFG 的弧FG ，因为114B EFC EG π∠=∠=，所以2FEG π∠=，所以根据弧长公式可得2FG π==.. 【点睛】本题考查了直棱柱的结构特征，考查了直线与平面垂直的判定，考查了立体几何中的轨迹问题，考查了扇形中的弧长公式，属于中档题. 【2020年新高考2卷（海南卷）】12．已知正方体ABCD -A 1B 1C 1D 1的棱长为2，M 、N 分别为BB 1、AB 的中点，则三棱锥A -NMD 1的体积为____________ 【答案】13【解析】【分析】利用11A NMD D AMN V V --=计算即可. 【详解】因为正方体ABCD -A 1B 1C 1D 1的棱长为2，M 、N 分别为BB 1、AB 的中点所以11111112323A NMD D AMN V V --==⨯⨯⨯⨯=故答案为：13【点睛】在求解三棱锥的体积时，要注意观察图形的特点，看把哪个当成顶点好计算一些. 【2022年新高考1卷】13．如图，直三棱柱111ABC A B C -的体积为4，1A BC 的面积为(1)求A 到平面1A BC 的距离；(2)设D 为1A C 的中点，1AA AB =，平面1A BC ⊥平面11ABB A ，求二面角A BD C --的正弦值．【答案】【解析】【分析】（1）由等体积法运算即可得解；（2）由面面垂直的性质及判定可得BC ⊥平面11ABB A ，建立空间直角坐标系，利用空间向量法即可得解. （1）在直三棱柱111ABC A B C -中，设点A 到平面1A BC 的距离为h ，则111111112211433333A A BC A A ABC A ABC AB BC C C B V Sh h V S A A V ---=⋅===⋅==，解得h =所以点A 到平面1A BC （2）取1A B 的中点E ,连接AE ,如图，因为1AA AB =，所以1AE A B ⊥, 又平面1A BC ⊥平面11ABB A ，平面1A BC平面111ABB A A B =，且AE ⊂平面11ABB A ，所以AE ⊥平面1A BC ，在直三棱柱111ABC A B C -中，1BB ⊥平面ABC ，由BC ⊂平面1A BC ，BC ⊂平面ABC 可得AE BC ⊥，1BB BC ⊥，又1,AE BB ⊂平面11ABB A 且相交，所以BC ⊥平面11ABB A ，所以1,,BC BA BB 两两垂直，以B 为原点，建立空间直角坐标系，如图，由（1）得AE 12AA AB ==，1A B =2BC =，则()()()()10,2,0,0,2,2,0,0,0,2,0,0A A B C ,所以1A C 的中点()1,1,1D ，则()1,1,1BD =，()()0,2,0,2,0,0BA BC ==,设平面ABD 的一个法向量(),,m x y z =，则020m BD x y z m BA y ⎧⋅=++=⎨⋅==⎩，可取()1,0,1m =-，设平面BDC 的一个法向量(),,n a b c =，则020n BD a b c n BC a ⎧⋅=++=⎨⋅==⎩，可取()0,1,1n =-，则11cos ,22m n m n m n⋅===⨯⋅，所以二面角A BD C --.【2022年新高考2卷】14．如图，PO 是三棱锥P ABC -的高，PA PB =，AB AC ⊥，E 是PB 的中点．(1)证明：//OE 平面PAC ；(2)若30ABO CBO ∠=∠=︒，3PO =，5PA =，求二面角C AE B --的正弦值．【答案】(1)证明见解析 (2)1113【解析】【分析】（1）连接BO 并延长交AC 于点D ，连接OA 、PD ，根据三角形全等得到OA OB =，再根据直角三角形的性质得到AO DO =，即可得到O 为BD 的中点从而得到//OE PD ，即可得证；（2）建立适当的空间直角坐标系，利用空间向量法求出二面角的余弦的绝对值，再根据同角三角函数的基本关系计算可得. （1）证明：连接BO 并延长交AC 于点D ，连接OA 、PD ，因为PO 是三棱锥P ABC -的高，所以PO ⊥平面ABC ，,AO BO ⊂平面ABC ，所以PO AO ⊥、PO BO ⊥，又PA PB =，所以POA POB ≅△△，即OA OB =，所以OAB OBA ∠=∠，又AB AC ⊥，即90BAC ∠=︒，所以90OAB OAD ∠+∠=︒，90OBA ODA ∠+∠=︒，所以ODA OAD ∠=∠所以AO DO =，即AO DO OB ==，所以O 为BD 的中点，又E 为PB 的中点，所以//OE PD ，又OE ⊄平面PAC ，PD ⊂平面PAC ，所以//OE 平面PAC（2）解：过点A 作//Az OP ，如图建立平面直角坐标系，因为3PO =，5AP =，所以4OA ==，又30OBA OBC ∠=∠=︒，所以28BD OA ==，则4=AD，AB = 所以12AC =，所以()O，()B，()P ，()0,12,0C ，所以32E ⎛⎫ ⎪⎝⎭，则332AE ⎛⎫= ⎪⎝⎭，()4AB =，()0,12,0AC =，设平面AEB 的法向量为(),,n x y z =，则33302430n AE y z n AB ⎧⋅=++=⎪⎨⎪⋅==⎩，令2z =，则3y =-，0x =，所以()0,3,2n =-；设平面AEC 的法向量为(),,m a b c =，则33302120m AE ab c m AC b ⎧⋅=++=⎪⎨⎪⋅==⎩，令a =6c =-，0b =，所以()3,0,6m =-；所以cos ,13n m n m n m⋅-===设二面角C AE B --的大小为θ，则43cos cos ,=13n m θ=，所以11sin 13θ==，即二面角C AE B --的正弦值为1113.【2021年新高考1卷】15．如图，在三棱锥A BCD -中，平面ABD ⊥平面BCD ，AB AD =，O 为BD 的中点.（1）证明：OA CD ⊥；（2）若OCD 是边长为1的等边三角形，点E 在棱AD 上，2DE EA =，且二面角E BC D --的大小为45︒，求三棱锥A BCD -的体积.【答案】(1)证明见解析；【解析】【分析】(1)由题意首先证得线面垂直，然后利用线面垂直的定义证明线线垂直即可；(2)方法二：利用几何关系找到二面角的平面角，然后结合相关的几何特征计算三棱锥的体积即可. 【详解】（1）因为AB AD =，O 是BD 中点，所以OA BD ⊥，因为OA ⊂平面ABD ，平面ABD ⊥平面BCD ，且平面ABD ⋂平面BCD BD =，所以OA ⊥平面BCD ．因为CD ⊂平面BCD ，所以OA CD ⊥. （2）[方法一]：通性通法—坐标法如图所示，以O 为坐标原点，OA 为z 轴，OD 为y 轴，垂直OD 且过O 的直线为x 轴，建立空间直角坐标系O xyz -，则1,0),(0,1,0),(0,1,0)2C D B -，设12(0,0,),(0,,)33A m E m ,所以4233(0,,),(,,0)3322EB m BC =--=，设(),,n x y z =为平面EBC 的法向量，则由00EB n EC n ⎧⋅=⎨⋅=⎩可求得平面EBC 的一个法向量为2(3,1,)n m =--．又平面BCD 的一个法向量为()0,0,OA m =，所以cos ,n OA ==1m =．又点C 到平面ABD112132A BCD C ABD V V --==⨯⨯⨯=，所以三棱锥A BCD -[方法二]【最优解】：作出二面角的平面角如图所示，作EG BD ⊥，垂足为点G ．作GF BC ⊥，垂足为点F ，连结EF ，则OA EG ∥．因为OA ⊥平面BCD ，所以EG ⊥平面BCD ，EFG 为二面角E BC D --的平面角．因为45EFG ∠=︒，所以EG FG =．由已知得1OB OD ==，故1OB OC ==．又30OBC OCB ∠=∠=︒，所以BC =因为24222,,,,133333GD GB FG CD EG OA ======，111122(11)13332A BCD BCDBOCV SO S OA A -==⨯⨯=⨯⨯⨯⨯⨯=． [方法三]：三面角公式考虑三面角B EDC -，记EBD ∠为α，EBC ∠为β，30DBC ∠=︒，记二面角E BC D --为θ．据题意，得45θ=︒．对β使用三面角的余弦公式，可得cos cos cos30βα=⋅︒，化简可得cos βα=．∴使用三面角的正弦公式，可得sin sin sin αβθ=，化简可得sin βα．∴ 将∴∴两式平方后相加，可得223cos 2sin 14αα+=，由此得221sin cos 4αα=，从而可得1tan 2α=±．如图可知π(0,)2α∈，即有1tan 2α=，根据三角形相似知，点G 为OD 的三等分点，即可得43BG =，结合α的正切值，可得2,13EG OA ==从而可得三棱锥A BCD -【整体点评】(2)方法一：建立空间直角坐标系是解析几何中常用的方法，是此类题的通性通法，其好处在于将几何问题代数化，适合于复杂图形的处理；方法二：找到二面角的平面角是立体几何的基本功，在找出二面角的同时可以对几何体的几何特征有更加深刻的认识，该法为本题的最优解.方法三：三面角公式是一个优美的公式，在很多题目的解析中灵活使用三面角公式可以使得问题更加简单、直观、迅速. 【2021年新高考2卷】16．在四棱锥Q ABCD -中，底面ABCD 是正方形，若2,3AD QD QA QC ====．（1）证明：平面QAD ⊥平面ABCD ；（2）求二面角B QD A --的平面角的余弦值．【答案】（1）证明见解析；（2）23. 【解析】【分析】（1）取AD 的中点为O ，连接,QO CO ，可证QO ⊥平面ABCD ，从而得到面QAD ⊥面ABCD . （2）在平面ABCD 内，过O 作//OT CD ，交BC 于T ，则OT AD ⊥，建如图所示的空间坐标系，求出平面QAD 、平面BQD 的法向量后可求二面角的余弦值. 【详解】（1）取AD 的中点为O ，连接,QO CO . 因为QA QD =，OA OD =，则QO ⊥AD ，而2,AD QA ==2QO ==.在正方形ABCD 中，因为2AD =，故1DO =，故CO =因为3QC =，故222QC QO OC =+，故QOC 为直角三角形且QO OC ⊥，因为OCAD O =，故QO ⊥平面ABCD ，因为QO ⊂平面QAD ，故平面QAD ⊥平面ABCD .（2）在平面ABCD 内，过O 作//OT CD ，交BC 于T ，则OT AD ⊥，结合（1）中的QO ⊥平面ABCD ，故可建如图所示的空间坐标系.则()()()0,1,0,0,0,2,2,1,0D Q B -，故()()2,1,2,2,2,0BQ BD =-=-.设平面QBD 的法向量(),,n x y z =，则00n BQ n BD ⎧⋅=⎨⋅=⎩即220220x y z x y -++=⎧⎨-+=⎩，取1x =，则11,2y z ==，故11,1,2n ⎛⎫= ⎪⎝⎭.而平面QAD 的法向量为()1,0,0m =，故12cos ,3312m n ==⨯.二面角B QD A --的平面角为锐角，故其余弦值为23. 【2020年新高考1卷（山东卷）】17．如图，四棱锥P -ABCD 的底面为正方形，PD ∴底面ABCD ．设平面P AD 与平面PBC 的交线为l ．（1）证明：l ∴平面PDC ；（2）已知PD =AD =1，Q 为l 上的点，求PB 与平面QCD 所成角的正弦值的最大值．【答案】（1）证明见解析；（2. 【解析】【分析】（1）利用线面垂直的判定定理证得AD ⊥平面PDC ，利用线面平行的判定定理以及性质定理，证得//AD l ，从而得到l ⊥平面PDC ；（2）方法一：根据题意，建立相应的空间直角坐标系，得到相应点的坐标，设出点(,0,1)Q m ，之后求得平面QCD 的法向量以及向量PB 的坐标，求得cos ,n PB <>的最大值，即为直线PB 与平面QCD 所成角的正弦值的最大值. 【详解】（1）证明：在正方形ABCD 中，//AD BC ，因为AD ⊄平面PBC ，BC ⊂平面PBC ，所以//AD 平面PBC，又因为AD ⊂平面PAD ，平面PAD 平面PBC l =，所以//AD l ，因为在四棱锥P ABCD -中，底面ABCD 是正方形，所以,,AD DC l DC ⊥∴⊥且PD ⊥平面ABCD ，所以,,AD PD l PD ⊥∴⊥ 因为CD PD D =，所以l ⊥平面PDC ．（2）［方法一］【最优解】：通性通法因为,,DP DA DC 两两垂直，建立空间直角坐标系D xyz -，如图所示：因为1PD AD ==，设(0,0,0),(0,1,0),(1,0,0),(0,0,1),(1,1,0)D C A P B ，设(,0,1)Q m ，则有(0,1,0),(,0,1),(1,1,1)DC DQ m PB ===-，设平面QCD 的法向量为(,,)n x y z =，则00DC n DQ n ⎧⋅=⎨⋅=⎩，即00y mx z =⎧⎨+=⎩，令1x =，则z m =-，所以平面QCD 的一个法向量为(1,0,)n m =-，则 1cos ,3n PB n PB n PB⋅+<>==根据直线的方向向量与平面法向量所成角的余弦值的绝对值即为直线与平面所成角的正弦值，所以直线PB 与平面QCD 所成角的正弦值等于|cos ,|n PB <>==≤，当且仅当1m =时取等号，所以直线PB 与平面QCD . ［方法二］：定义法如图2，因为l ⊂平面PBC ，Q l ∈，所以Q ∈平面PBC ．在平面PQC 中，设PB QC E =．在平面PAD 中，过P 点作PF QD ⊥，交QD 于F ，连接EF ．因为PD ⊥平面,ABCD DC ⊂平面ABCD ，所以DC PD ⊥．又由,,DC AD ADPD D PD ⊥=⊂平面PAD ，AD ⊂平面PAD ，所以DC ⊥平面PAD ．又PF ⊂平面PAD ，所以DC PF ⊥．又由,,PF QD QDDC D QD ⊥=⊂平面,QOC DC ⊂平面QDC ，所以PF ⊥平面QDC ，从而FEP ∠即为PB 与平面QCD 所成角．设PQ a =，在PQD △中，易求PF =由PQE 与BEC △相似，得1PE PQ a EB BC ==，可得PE =所以sin FEP ∠=≤1a =时等号成立．［方法三］：等体积法如图3，延长CB 至G ，使得BG PQ =，连接GQ ，GD ，则//PB QG ，过G 点作GM ⊥平面QDC ，交平面QDC 于M ，连接QM ，则GQM ∠即为所求．设PQ x =，在三棱锥Q DCG -中，111()(1)326Q DCG V PD CD CB BG x -=⋅⋅+=+．在三棱锥G QDC -中，111323G QDC V GM CD QD GM -=⋅⋅=由Q DCG G QDC V V --=得11(1)63x GM +=解得GM ==，当且仅当1x =时等号成立．在Rt PDB △中，易求PB QG ==，所以直线PB 与平面QCD 所成角的正弦值的最大值为sin MQG ∠== 【整体点评】（2）方法一：根据题意建立空间直角坐标系，直线PB 与平面QCD 所成角的正弦值即为平面QCD 的法向量n 与向量PB 的夹角的余弦值的绝对值，即cos ,n PB <>，再根据基本不等式即可求出，是本题的通性通法，也是最优解；方法二：利用直线与平面所成角的定义，作出直线PB 与平面QCD 所成角，再利用解三角形以及基本不等式即可求出；方法三：巧妙利用//PB QG ，将线转移，再利用等体积法求得点面距，利用直线PB 与平面QCD 所成角的正弦值即为点面距与线段长度的比值的方法，即可求出．【2020年新高考2卷（海南卷）】18．如图，四棱锥P -ABCD 的底面为正方形，PD ⊥底面ABCD ．设平面P AD 与平面PBC 的交线为l ．（1）证明：l ⊥平面PDC ；（2）已知PD =AD =1，Q 为l 上的点，QB ，求PB 与平面QCD 所成角的正弦值．【答案】（1）证明见解析；（2. 【解析】【分析】（1）利用线面平行的判定定理以及性质定理，证得//AD l ，利用线面垂直的判定定理证得AD ⊥平面PDC ，从而得到l ⊥平面PDC ；（2）根据题意，建立相应的空间直角坐标系，得到相应点的坐标，设出点(,0,1)Q m ，之后求得平面QCD 的法向量以及向量PB 的坐标，求得cos ,n PB <>，即可得到直线PB 与平面QCD 所成角的正弦值.【详解】（1）证明：在正方形ABCD 中，//AD BC ，因为AD ⊄平面PBC ，BC ⊂平面PBC ，所以//AD 平面PBC ，又因为AD ⊂平面PAD ，平面PAD 平面PBC l =，所以//AD l ，因为在四棱锥P ABCD -中，底面ABCD 是正方形，所以,,AD DC l DC ⊥∴⊥ 且PD ⊥平面ABCD ，所以,,AD PD l PD ⊥∴⊥ 因为CD PD D = 所以l ⊥平面PDC ；（2）如图建立空间直角坐标系D xyz -，因为1PD AD ==，则有(0,0,0),(0,1,0),(1,0,0),(0,0,1),(1,1,0)D C A P B ，设(,0,1)Q m ，则有(0,1,0),(,0,1),(1,1,1)DC DQ m PB ===-，因为QB 1m = 设平面QCD 的法向量为(,,)n x y z =，则00DC n DQ n ⎧⋅=⎨⋅=⎩，即00y x z =⎧⎨+=⎩，令1x =，则1z =-，所以平面QCD 的一个法向量为(1,0,1)n =-，则2cos ,1n PB n PB n PB⋅<>==== 根据直线的方向向量与平面法向量所成角的余弦值的绝对值即为直线与平面所成角的正弦值，所以直线与平面所成角的正弦值等于6|cos ,|3n PB <>=所以直线PB 与平面QCD 【点睛】该题考查的是有关立体几何的问题，涉及到的知识点有线面平行的判定和性质，线面垂直的判定和性质，利用空间向量求线面角，利用基本不等式求最值，属于中档题目.。

2019-2020年高考数学大题专题练习——立体几何(一)

2019-2020年高考数学大题专题练习——立体几何（一）1.如图所示，四棱锥P ABCD 中，底面ABCD 为正方形，⊥PD 平面ABCD ，2PD AB ，点,,E F G 分别为,,PC PD BC 的中点.(1)求证：EF PA ⊥；(2)求二面角D FG E 的余弦值.2.如图所示，该几何体是由一个直角三棱柱ADE BCF 和一个正四棱锥P ABCD 组合而成，AF AD ⊥，2AEAD .(1)证明：平面⊥PAD 平面ABFE ；(2)求正四棱锥P ABCD 的高h ，使得二面角C AF P 的余弦值是223.3.四棱锥P ABCD-中，侧面PDC是边长为2的正三角形，且与底面垂直，底面ABCD是面积为ADC∠为锐角，M为PB的中点．（Ⅰ）求证：PD∥面ACM．（Ⅱ）求证：PA⊥CD．（Ⅲ）求三棱锥P ABCD-的体积．4.如图，四棱锥S ABCD-满足SA⊥面ABCD，90DAB ABC∠=∠=︒．SA AB BC a===，2AD a=．（Ⅰ）求证：面SAB⊥面SAD．（Ⅱ）求证：CD⊥面SAC．SB A DMC BAPD5.在四棱锥P ABCD -中，底面ABCD 为矩形，测棱PD ⊥底面ABCD ，PD DC =，点E 是BC 的中点，作EF PB ⊥交PB 于F ．（Ⅰ）求证：平面PCD ⊥平面PBC ．（Ⅱ）求证：PB ⊥平面EFD ．6.在直棱柱111ABC A B C -中，已知AB AC ⊥，设1AB 中点为D ，1A C 中点为E ．（Ⅰ）求证：DE ∥平面11BCC B ．（Ⅱ）求证：平面11ABB A ⊥平面11ACC A ．E DABC C 1B 1A 1DAB CEF P7.在四棱锥P ABCD -中，PA ⊥平面ABCD ，//AB CD ，AB AD ⊥，PA PB =，::2:2:1AB AD CD =.（1）证明BD PC ⊥；（2）求二面角A PC D --的余弦值；（3）设点Q 为线段PD 上一点，且直线AQ 平面PAC 所成角的正弦值为23，求PQ PD的值.8.在正方体1111ABCD A B C D -中，O 是AC 的中点，E 是线段D 1O 上一点，且D 1E ＝λEO . （1）若λ=1，求异面直线DE 与CD 1所成角的余弦值；（2）若λ=2，求证：平面CDE ⊥平面CD 1O .9.如图，在四棱锥P ABCD -中，底面ABCD 是平行四边形，135BCD =︒∠，侧面PAB ⊥底面ABCD ，90BAP =︒∠，2AB AC PA ===，E ，F 分别为BC ，AD 的中点，点M 在线段PD 上．（Ⅰ）求证：EF ⊥平面PAC ．（Ⅱ）若M 为PD 的中点，求证：ME ∥平面PAB ．（Ⅲ）如果直线ME 与平面PBC 所成的角和直线ME 与平面ABCD 所在的角相等，求PMPD的值．10.如图，在三棱柱111ABC A B C -，1AA ⊥底面ABC ，AB AC ⊥，1AC AB AA ==，E ，F 分别是棱BC ，1A A 的中点，G 为棱1CC 上的一点，且1C F ∥平面AEG ．（1）求1CGCC 的值．（2）求证：1EG AC ⊥．（3）求二面角1A AG E --的余弦值．A 1B 1C 1G F AB CEM F E CBAPD11.如图，在四棱锥P ABCD -中，PB ⊥底面ABCD ，底面ABCD 为梯形，AD BC ∥，AD AB ⊥，且3PB AB AD ===，1BC =．（Ⅰ）若点F 为PD 上一点且13PF PD =，证明：CF ∥平面PAB ．（Ⅱ）求二面角B PD A --的大小．（Ⅲ）在线段PD 上是否存在一点M ，使得CM PA ⊥？若存在，求出PM 的长；若不存在，说明理由．12.如图，在四棱锥E ABCD -中，平面EAD ⊥平面ABCD ，CD AB ∥，BC CD ⊥，EA ED ⊥，4AB =，2BC CD EA ED ====．Ⅰ证明：BD AE ⊥．Ⅱ求平面ADE 和平面CDE 所成角（锐角）的余弦值．DABCEPF DBCA13.己知四棱锥P ABCD -中，PA ⊥平面ABCD ，底面ABCD 是菱形，且2PA AB ==．60ABC ∠=︒，BC 、PD 的中点分别为E ，F ．（Ⅰ）求证BC PE ⊥．（Ⅱ）求二面角F AC D --的余弦值．（Ⅲ）在线段AB 上是否存在一点G ，使得AF 平行于平面PCG ？若存在，指出G 在AB 上的位置并给予证明，若不存在，请说明理由．14.如图，ABCD 是边长为3的正方形，DE ⊥平面ABCD ，AF DE ∥，3DE AF =，BE 与平面ABCD 所成角为60︒．（Ⅰ）求证：AC ⊥平面BDE ．（Ⅱ）求二面角F BE D --的余弦值．（Ⅲ）设点M 线段BD 上一个动点，试确定点M 的位置，使得AM ∥平面BEF ，并证明你的结论．DDABCEF15.如图，PA ⊥面ABC ，AB BC ⊥，22AB PA BC ===，M 为PB 的中点．（Ⅰ）求证：AM ⊥平面PBC ．（Ⅱ）求二面角A PC B --的余弦值．（Ⅲ）在线段PC 上是否存在点D ，使得BD AC ⊥，若存在，求出PDPC的值，若不存在，说明理由．16.如图所示，在四棱锥P -ABCD 中，AB ⊥平面,//,PAD AB CD E 是PB 的中点,2,5,3,2AHPD PA AB AD HD===== . （1）证明：PH ⊥平面ABCD ；（2）若F 是CD 上的点，且23FC FD ==，求二面角B EF C --的正弦值.MDABCP17.如图，DC ⊥平面ABC ，//EB DC ，22AC BC EB DC ====，120ACB ∠=︒，Q为AB 的中点．（Ⅰ）证明：CQ ⊥平面ABE ；（Ⅱ）求多面体ACED 的体积；（Ⅲ）求二面角A -DE -B 的正切值．18.如图1 ,在△ABC 中，AB =BC =2, ∠B =90°,D 为BC 边上一点，以边AC 为对角线做平行四边形ADCE ，沿AC 将△ACE 折起，使得平面ACE ⊥平面ABC ,如图2.(1)在图 2中，设M 为AC 的中点，求证:BM 丄AE ； (2)在图2中，当DE 最小时，求二面角A -DE -C 的平面角.19.如图所示，在已知三棱柱ABF -DCE 中，90ADE ∠=︒，60ABC ∠=︒，2AB AD AF ==，平面ABCD ⊥平面ADEF ，点M在线段BE 上，点G 是线段AD 的中点．（1）试确定点M 的位置，使得AF ∥平面GMC ；（2）求直线BG 与平面GCE 所成角的正弦值．20.已知在四棱锥P -ABCD 中，底面ABCD 是菱形，AC =AB ，P A ⊥平面ABCD ，E ，F 分别是AB ，PD 的中点.（Ⅰ）求证：AF ∥平面PCE ；（Ⅱ）若22AB AP ==，求平面P AD 与平面PCE 所成锐二面角的余弦值.21.如图，五面体P ABCD 中，CD ⊥平面P AD ，ABCD 为直角梯形，,2BCD PD BC CD π∠===1,2AD AP PD =⊥. （1）若E 为AP 的中点，求证：BE ∥平面PCD ；（2）求二面角P -AB-C 的余弦值.22.如图（1）所示，已知四边形SBCD 是由Rt △SAB 和直角梯形ABCD 拼接而成的，其中90SAB SDC ∠=∠=︒.且点A 为线段SD 的中点，21AD DC ==，2AB =.现将△SAB沿AB 进行翻折，使得二面角S -AB -C 的大小为90°，得到图形如图（2）所示，连接SC ，点E ，F 分别在线段SB ，SC 上. （Ⅰ）证明：BD AF ⊥；（Ⅱ）若三棱锥B -AEC 的体积为四棱锥S -ABCD 体积的25，求点E 到平面ABCD 的距离.23.四棱锥S-ABCD中，AD∥BC，,BC CD⊥060SDA SDC∠=∠=，AD DC=1122BC SD==，E为SD的中点.（1）求证：平面AEC⊥平面ABCD；（2）求BC与平面CDE所成角的余弦值.24.已知三棱锥P-ABC，底面ABC是以B为直角顶点的等腰直角三角形，P A⊥AC，BA=BC=P A=2，二面角P-AC-B的大小为120°.（1）求直线PC与平面ABC所成角的大小；（2）求二面角P-BC-A的正切值.25.如图，在四棱锥P -ABCD 中，平面P AD ⊥平面ABCD ，090=∠=∠BCD ABC ，AB CB DC PD PA 21====，E 是PB 的中点，（Ⅰ）求证：EC ∥平面APD ；（Ⅱ）求BP 与平面ABCD 所成的角的正切值；（Ⅲ）求二面角P -AB -D 的余弦值.26.四棱锥P ﹣ABCD 的底面ABCD 为边长为2的正方形，P A =2，PB =PD =22，E ，F ，G ，H 分别为棱P A ，PB ，AD ，CD 的中点．（1）求CD 与平面CFG 所成角的正弦值；（2）探究棱PD 上是否存在点M ，使得平面CFG ⊥平面MEH ，若存在，求出PDPM的值；若不存在，请说明理由．试卷答案1以点D 为坐标原点，建立如图所示的空间直角坐标系D xyz ，则 0,0,0D ，0,2,0A ，2,0,0C，0,0,2P ，1,0,1E ，0,0,1F ，2,1,0G .(1)∵0,2,2PA ，1,0,0EF，则0PA EF ，∴PA EF .(2)易知0,0,1DF，2,11FG，设平面DFG 的法向量111,,m x y z ，则m DF m FG ，即1111020z x yz ，令11x ，则1,2,0m 是平面DFG 的一个法向量，同理可得0,1,1n 是平面EFG 的一个法向量，∴210cos ,552m n m nm n，由图可知二面角D FG E 为钝角， ∴二面角D FG E 的余弦值为105.2.(1)证明：直三棱柱ADE BCF 中，AB 平面ADE ，所以：AB AD ，又AD AF ，所以：AD平面ABFE ，AD 平面PAD ，所以：平面PAD 平面ABFE .(2)由(1)AD平面ABFE ，以A 为原点，,,AB AE AD 方向为,,x y z 轴建立空间直角坐标系A xyz ，设正四棱锥P ABCD 的高h ，2AE AD ，则0,0,0A ，2,2,0F ，2,0,2C ，1,,1P h . 2,2,0AF，2,0,2AC，1,,1APh .设平面ACF 的一个法向量111,,m x y z ，则：1111220220m AF x y n ACx z ，取11x ，则111y z ，所以：1,1,1m .设平面AFP 的一个法向量222,,n x y z ，则222222200n AF x y n APx hy z ，取21x ，则21y ，21z h ，所以：1,1,1n h ，二面角C AF P 的余弦值是223，所以：211122cos ,3321m n h m n m nh ，解得：1h .3.E ODPABC M（Ⅰ）证明：连结AC 交BD 于O ，则O 是BD 中点， ∵在PBD △中，O 是BD 的中点，M 是PB 的中点， ∴PD MO ∥，又PD ⊄平面ACM ，MO ⊂平面ACM ，∴PD ∥平面ACM ．（Ⅱ）证明：作PE CD ⊥，则E 为CD 中点，连结AE ， ∵底面ABCD 是菱形，边长为2，面积为，∴11sin 222sin 222S AD DC ADC ADC =⨯⨯⨯∠⨯=⨯⨯∠⨯=∴sin ADC ∠，60ADC ∠=︒， ∴ACD △是等边三角形， ∴CD AE ⊥，又∵CD PE ⊥， ∴CD ⊥平面PAE ， ∴CD PA ⊥．（Ⅲ）11233P ABCD ABCD V S PE -=⨯=⨯．4.DABCSE（1）证明：∵SA ⊥平面ABCD ，AB ⊂平面ABCD ， ∴AB SA ⊥，又∵90BAD ∠=︒， ∴AB AD ⊥， ∵SA AD A =， ∴AB ⊥平面SAD ，又AB ⊂平面SAB ， ∴平面SAB ⊥平面SAD ．（Ⅱ）证明：取AD 中点为E ，∵90DAB ABC ∠=∠=︒，2AD a =，BC a =，E 是AD 中点， ∴ABCE ∠是矩形，CE AB a ==，DE a =，∴CD =，在ACD △中，AC，CD =，2AD a =， ∴222AC CD AD +=，即CD AC ⊥，又∵SA ⊥平面ABCD ，CD ⊂平面ABCD ， ∴CD SA ⊥， ∴CD ⊥平面PAC ． 5.P F ECB AD（Ⅰ）证明：∵PD ⊥底面ABCD ，BC ⊂平面ABCD ， ∴PD BC ⊥，又∵底面ABCD 为矩形， ∴BC CD ⊥， ∴BC ⊥平面PCD ， ∵BC ⊂平面PBC ， ∴平面PCD ⊥平面PBC ．（Ⅱ）证明：∵PD DC =，E 是PC 中点， ∴DE PC ⊥，又平面PCD ⊥平面PBC ，平面PCD 平面PBC PC =， ∴DE ⊥平面PBC ， ∴DE PB ⊥，又∵EF PB ⊥，EF DE E =，∴PB ⊥平面EFD ．6.E A 1B 1C 1CBAD（Ⅰ）证明：连结1A B ， ∵D 是1AB 的中点， ∴D 是1A B 的中点，∵在1A BC △中，D 是1A B 的中点，E 是1A C 的中点， ∴DE BC ∥，又DE ⊄平面11BCC B ，BC ⊂平面11BCC B ， ∴DE ∥平面11BCC B ．（Ⅱ）证明：∵111ABC A B C -是直棱柱， ∴1AA ⊥平面ABC ， ∴1AA AB ⊥，又AB AC ⊥， ∴AB ⊥平面11ACC A ， ∵AB ⊂平面11ABB A ， ∴平面11ABB A ⊥平面11ACC A ．7.以A 为坐标原点，建立空间直角坐标系(2,0,0)B，D ，(0,0,2)P，C（1）(BD =-，(1,2)PC =-， ∵0BD PC •=∴BD PC ⊥（2）(1,AC =，(0,0,2)AP =，平面PAC 的法向量为(2,1,0)m =-(0,2)DP =，(1,0,0)AP =，平面DPC 的法向量为(0,2,1)n =--.2cos ,3m n m n m n•==•，二面角B PC D --的余弦值为3.（3）∵AQ AP PQ AP tPD =+=+，[]0,1t ∈ ∴(0,0,2)(0,2,2)(0,2,22)AQ t t t =+-=- 设θ为直线AQ 与平面PAC 所成的角2sin cos ,3AQ m AQ m AQ mθ•===• 2222223684332(22)tt t t t t =⇒=-++-，解得2t =（舍）或23. 所以，23PQ PD =即为所求.8.解:(1)不妨设正方体的棱长为1，以DA ,DC ,1DD 为单位正交基底建立如图所示的空间直角坐标系D xyz -．则A (1，0，0)，()11022O ，，，()010C ，，，D 1(0，0，1)， E ()111442，，，于是，.由cos＝＝.所以异面直线AE 与CD 1所成角的余弦值为36. （2）设平面CD 1O 的向量为m =(x 1，y 1，z 1)，由m ·CO ＝0，m ·1CD ＝0 得取x 1＝1，得y 1＝z 1＝1，即m =(1，1，1) .由D 1E ＝λEO ，则E ，.又设平面CDE 的法向量为n ＝(x 2，y 2，z 2)，由n ·CD ＝0，n ·DE ＝0. 得取x 2=2，得z 2＝－λ，即n ＝(－2，0，λ) .因为平面CDE ⊥平面CD 1F ，所以m ·n ＝0，得λ＝2．9.（Ⅰ）证明：在平行四边形ABCD 中， ∵AB AC =，135BCD =︒∠，45ABC =︒∠， ∴AB AC ⊥，∵E ，F 分别为BC ，AD 的中点， ∴EF AB ∥，∴EF AC ⊥，∵侧面PAB ⊥底面ABCD ，且90BAP =︒∠， ∴PA ⊥底面ABCD ，∴PA EF ⊥，又∵PAAC A =，PA ⊂平面PAC ，AC ⊂平面PAC ，∴EF ⊥平面PAC ．（Ⅱ）证明：∵M 为PD 的中点，F 为AD 的中点， ∴MF PA ∥，又∵MF ⊄平面PAB ，PA ⊂平面PAB ， ∴MF ∥平面PAB ，同理，得EF ∥平面PAB ，又∵MFEF F =，MF ⊂平面M EF ，EF ⊂平面M EF ，∴平面MEF ∥平面PAB ，又∵ME ⊂平面M EF ， ∴ME ∥平面PAB ．（Ⅲ）解：∵PA ⊥底面ABCD ，AB AC ⊥，∴AP ，AB ，AC 两两垂直，故以AB ，AC ，AP 分别为x 轴，y 轴和z 轴建立如图空间直角坐标系，则(0,0,0)A ，(2,0,0)B ，(0,2,0)C ，(0,0,2)P ，(2,2,0)D -，(1,1,0)E ，所以(2,0,2)PB =-，(2,2,2)PD =--，(2,2,0)BC =-，设([0,1])PMPDλλ=∈，则(2,2,2)PM λλλ=--， ∴(2,2,22)M λλλ--，(12,12,22)ME λλλ=+--，易得平面ABCD 的法向量(0,0,1)m =，设平面PBC 的法向量为(,,z)n x y =，则：n BC n PB ⎧⋅=⎪⎨⋅=⎪⎩，即220220x y x z -+=⎧⎨-=⎩，令1x =，得(1,1,1)n =， ∴直线ME 与平面PBC 所成的角和此直线与平面ABCD 所成的角相等， ∴|cos ,||cos ,|ME m ME n <>=<>，即||||||||||||ME m ME n ME m ME n ⋅⋅=⋅⋅，∴|21|λ-=，解得λ=或λ=（舍去），故PM PD ．D10.（1）∵1C F ∥平面AEG ，又1C F ⊂平面11ACC A ，平面11ACC A 平面AEG AG =，∴1C F AG ∥，∵F 为1AA 的点，且侧面11ACC A 为平行四边形， ∴G 为1CC 中点， ∴112CG CC =．（2）证明：∵1AA ⊥底面ABC ，1AA AB ⊥，1AA AC ⊥，又AB AC ⊥，如图，以A 为原点建立空间直角坐标系A xyz -，设2AB =，则由1AB AC AA ==可得(2,0,0)C ，(0,2,0)B ，1(2,0,2)C ，1(0,0,2)A ， ∵E ，G 分别是BC ，1CC 的中点，∴(1,1,0)E ，(2,0,1)G ， ∴1(1,1,1)(2,0,2)0EG CA ⋅=-⋅-=， ∴1EG CA ⊥， ∴1EG AC ⊥．（3）设平面AEG 的法向量为(,,)n x y z =，则：0n AE n AG ⎧⋅=⎪⎨⋅=⎪⎩，即020x y x z +=⎧⎨+=⎩，令1x =，则1y =-，2z =-， ∴(1,1,2)n =--，由已知可得平面1A AG 的法向量(0,1,0)m =， ∴6cos ,6||||n m n m n m ⋅<>==-⋅由题意知二面角1A AG E --为钝角， ∴二面角1A AG E --的余弦值为．111.（Ⅰ）证明：过点F 作FH AD ∥，交PA 于H ，连结BH ，如图所示，∵13PF PD =，∴13HF AD BC ==，又FH AD ∥，AD BC ∥，HF BC ∥， ∴四边形BCFH 为平行四边形， ∴CF BH ∥，又BH ⊄平面PAB ，CF ⊄平面PAB ， ∴CF ∥平面PAB ．z D（Ⅱ）解：∵梯形ABCD 中，AD BC ∥，AD AB ⊥， ∴BC AB ⊥， ∵PB ⊥平面ABCD ， ∴PB AB ⊥，PB BC ⊥，∴如图，以B 为原点，BC ，BA ，BP 所在直线为x ，y ，z 轴建立空间直角坐标系，则(1,0,0)C ，(3,0,0)D ，(0,3,0)A ，(0,0,3)P ，设平面BPD 的一个法向量为(,,)n x y z =，平面APD 的一个法向量为(,,)m a b c =， ∵(3,3,3)PD =-，(0,0,3)BP =，∴00PD n BP n ⎧⋅=⎪⎨⋅=⎪⎩，即333030x y z z +-=⎧⎨=⎩，令1x =得(1,1,0)n =-，同理可得(0,1,1)m =， ∴1cos ,2||||n m n m n m ⋅<>==-⋅，∵二面角B PD A --为锐角， ∴二面角B PD A --为π3．（Ⅲ）假设存在点M 满足题意，设(3,3,3)PM PD λλλλ=-， ∴(13,3,33)CM CP PD λλλλ=+=-+-，∵(0,3,3)PA =-，∴93(33)0PA CM λλ⋅=+-=，解得12λ=，∴PD 上存在点M 使得CM PA ⊥，且12PM PD =．12.Ⅰ∵BC CD ⊥，2BC CD ==，∴BD =，同理EA ED ⊥，2EA ED ==，∴AD =，又∵4AB =，∴由勾股定理可知222BD AD AB +=，BD AD ⊥，又∵平面EAD ⊥平面ABCD ，平面EAD 平面ABCD AD =，BD ⊂平面ABCD ，∴BD ⊥平面AED ，又∵AE ⊂平面AED ， ∴BD AE ⊥．Ⅱ解：取AD 的中点O ，连结OE ，则OE AD ⊥， ∵平面EAD ⊥平面ABCD ，平面EAD 平面ABCD AD =，∴OE ⊥平面ABCD ，取AB 的中点F ，连结DF BD ∥，以O 为原点，建立如图所示的空间直角坐标系O xyz -，则(D ，(C -，E ，(DC =-，(2,0,DE =，设平面CDE 的法向量为(,,)n x y z =，则00DC n DE n ⎧⋅=⎪⎨⋅=⎪⎩即00x z x y +=⎧⎨-+=⎩，令1x =，则1z =-，1y =，∴平面CDE 的法向量(1,1,1)n =-，又平面ADE 的一个法向量为1(0,1,0)n =，设平面ADE 和平面CDE 所成角（锐角）为θ，则1113cos |cos ,|3||||nn n n n n θ⋅=<>==⋅，∴平面ADE 和平面CDE． C13.（1）证明：连结AE ，PE ．∵PA ⊥平面ABCD ，BC ⊂平面ABCD ， ∴PA BC ⊥．又∵底面ABCD 是菱形，AB BC =，60ABC ∠=︒， ∴ABC △是正三角形． ∵E 是BC 的中点， ∴AE BC ⊥．又∵PA AE A =，PA ⊂平面PAE ，PE ⊂平面PAE ，∴BC ⊥平面PAE ， ∴BC PE ⊥．（2）由（1）得AE BC ⊥，由BC AD ∥可得AE AD ⊥．又∵PA ⊥底面ABCD ，∴PA AE ⊥，PA AD ⊥．∴以A 为原点，分别以AE ，AD ，AP 为x 轴，y 轴，z 轴建立空间直角坐标系A xyz -，如图所示，则(0,0,0)A，E ，(0,2,0)D ，(0,0,2)P，1,0)B -，C ，(0,1,1)F ．∵PA ⊥平面ABCD ，∴平面ABCD 的法向量为(0,0,2)AP =．又∵(3,1,0)AC =，(0,1,1)AF =．设平面ACF 的一个法向量(,,)n x y z =，则：AC n AF n ⎧⋅=⎪⎨⋅=⎪⎩，即00y y z +==⎪⎩+，令1x =，则y =z ，∴(1,3,n =-． ∴21cos ,7||||AP n AP n AP n ⋅==． ∵二面角F AC D --是锐角， ∴二面角F AC D -- （3）G 是线段AB 上的一点，设(01)AG t AB t =≤≤． ∵(3,1,0)AB =-，∴,,0)G t -．又∵(3,1,2)PC =-，(3,,2)PG t t =--．设平面PCG 的一个法向量为(,,)n x y z =，则：1100PC n PGn ⎧⋅=⎪⎨⋅=⎪⎩，即1111112020yz ty z-=--=+，∴1()n t t =-+， ∵AF ∥平面PCG ，∴AF n ⊥，0AF n ⋅=1)0t -=，解得12t =．故线段AB 上存在一点G ，使得AF 平行于平面PCG ，G 是AB 中点．14.（1）证明：∵DE ⊥平面ABCD ，AC ⊂平面ABCD ， ∴DE AC ⊥． ∵ABCD 是正方形， ∴AC BD ⊥．又DEBD D =，∴AC ⊥平面BDE ．（2）∵DA ，DC ，DE 两两重叠，∴建立空间直角坐标系D xyz -如图所示．∵BE 与平面ABCD 所成角为60︒，即60DBE ∠=︒，∴EDDB．由3AD =，可知DZ =AF ，则(3,0,0)A，F，E ，(3,3,0)B ，(0,3,0)C ．∴(0,BF =-，(3,0,EF =-，设平面BEF 的法向量为(,,)n x y z =，则00n BF n EF ⎧⋅=⎪⎨⋅=⎪⎩，即3030y x ⎧-=⎪⎨-=⎪⎩，令z (4,2,6)n =． ∵AC ⊥平面BDE ，∴CA 为平面BDE 的一个法向量，(3,3,0)CA =-，∴cos ,||||32n CA n CA n CA ⋅==．∵二面角F BE D --为锐角， ∴二面角F BE D -- （3）点M 线段BD 上一个动点，设(,,0)M t t ，则(3,,0)AM t t =-．∵AM ∥平面BEF ，∴0AM n ⋅=，即4(3)20t t -+=，解得2t =，此时，点M 坐标为(2,2,0)，13BM BD =，符合题意．15.（1）证明：∵PA ⊥平面ABC ，BC ⊂平面ABC ， ∴PA BC ⊥．∵BC AB ⊥，PA AB A =， ∴BC ⊥平面PAB ．又AM ⊂平面PAB ， ∴AM BC ⊥．∵PA AB =，M 为PB 的中点， ∴AM PB ⊥．又∵PBBC B =，∴AM ⊥平面PBC ．（2）如图，在平面ABC 内作AZ BC ∥，则AP ，AB ，AZ 两两垂直，建立空间直角坐标系A xyz -．则(0,0,0)A ，(2,0,0)P ，(0,2,0)B ，(0,2,1)C ，(1,1,0)M ． (2,0,0)AP =，(0,2,1)AC =，(1,1,0)AM =．设平面APC 的法向量为(,,)n x y z =，则：0n AP n AC ⎧⋅=⎪⎨⋅=⎪⎩，即020x y z =⎧⎨+=⎩，令1y =，则2z =-． ∴(0,1,2)n =-．由（1）可知(1,1,0)AM =为平面PBC 的一个法向量，∴cos||||5AM nn AMAM n⋅⋅==∵二面角A PC B--为锐角，∴二面角A PC B--．（3）证明：设(,,)D v wμ是线段PC上一点，且PD PCλ=，(01)λ≤≤，即(2,,)(2,2,1)v wμλ-=-，∴22μλ=-，2vλ=，wλ=．∴(22,22,)BDλλλ=--．由0BD AC⋅=，得4[0,1]5λ=∈，∴线段PC上存在点D，使得BD AC⊥，此时45PDPCλ==．16.解：（1）证明：因为AB⊥平面PAD，所以PH AB⊥，因为3,2AHADHD==，所以2,1AH HD==，设PH x=，由余弦定可得，22221cos22x HD PH xPHDx HD x+--∠==⋅22221cos24x HA PH xPHAx HA x+--∠==⋅因为cos cosPHD PHA∠=-∠，故1PH x==，所以PH AD⊥，因为AD AB A=，故PH⊥平面ABCD.（2）以H为原点，以,,HA HP HP所在的直线分别为,,x y z轴，建立空间直角坐标系，则3139(2,3,0),(0,0,1),(1,,),(1,,0),(1,,0)2222B P E F C--，所以可得，3311(3,,0),(1,,),(2,0,),(0,3,0)2222BF BE EF FC=--=--=-=，设平面BEF的法向量(,,)n x y z=，则有：33002(1,2,4)30022x yBF nnzBE n x y⎧--=⎪⎧⋅=⎪⎪⇒⇒=-⎨⎨⋅=⎪⎪⎩--+=⎪⎩，设平面EFC的法向量(,,)m x y z=，则有：020(1,0,4)2030z EF m x m FC m y ⎧⎧⋅=--=⎪⎪⇒⇒=-⎨⎨⋅=⎪⎪⎩=⎩，故17cos ,21n m n m n m⋅===⋅设二面角B EF C --的平面角为θ ，则sin 21θ=.17.解（Ⅰ）证明：∵DC ⊥平面ABC ，//BE DC ∴BE ⊥平面ABC ∴CQ BE ⊥ ①又∵2AC BC ==，点Q 为AB 边中点 ∴CQ AB ⊥ ②AB BE B =故由①②得CQ ⊥平面ABE（Ⅱ）过点A 作AM BC ⊥交BC 延长线于点M ∵,AM BC AM BE ⊥⊥ ∴AM ⊥平面BEDC ∴13A CED CDE V S AM -∆=sin33AM AC π==11212CDE S ∆=⨯⨯= ∴113A CED V -=⨯= （Ⅲ）延长ED 交BC 延长线于S ，过点M 作MQ ES ⊥于Q ，连结AQ 由（Ⅱ）可得：AQM ∠为A DE B --的平面角∵1//2CD BC ∴2SC CB == ∴SE ==1MC MS ==∵SQM ∆∽SBE ∆∴QM SM BE SE=∴1225QM=即55QM=∴3tan1555AMAQMQM∠===18.（1）证明：∵在中，，∴当为的中点时，∵平面平面，平面，平面平面∴平面∵平面∴（2）如图，分别以射线，的方向为，轴的正方向，建立空间直角坐标系设，则，，，∵，，平面平面∴∴当且仅当时，最小，此时，设，平面，则，即∴令，可得，，则有∴∴观察可得二面角的平面角19.（1）取FE 的中点P ，连接CP 交BE 于点M ，M 点即为所求的点．连接PG ，∵G 是AD 的中点，P 是FE 的中点，∴//PG AF ，又PG ⊂平面MGC ，AF ⊄平面MGC ，所以直线//AF 平面MGC ， ∵//PE AD ，//AD BC ，∴//PE BC ，∴2BM BCME PE==，故点M 为线段BE 上靠近点E 的三等分点．（2）不妨设2AD =，由（1）知PG AD ⊥，又平面ADEF ⊥平面ABCD ，平面ADEF平面ABCD AD =，PG ⊂平面ADEF ，∴PG ⊥平面ABCD ．故PG GD ⊥，PG GC ⊥，以G 为坐标原点，GC ，GD ，GP 分别为x ，y ，z 轴建立空间直角坐标系G xyz -，∵60ABC ∠=︒，2AB AD AF ==，∴ADC ∆为正三角形，3GC =，∴(0,0,0)G ，3,0,0)C ，(0,1,0)D ，(0,1,1)E ，∴(0,1,1)GE =，(3,0,0)GC =，设平面CEG 的一个法向量1(,,)n x y z =，则由10n GE ⋅=，10n GC ⋅=可得0,30,y z x +=⎧⎪⎨=⎪⎩令1y =，则1(0,1,1)n =-，∵(3,1,0)CD =-BA =，且(0,1,0)A -，故3,2,0)B -，故(3,2,0)BG =-，故直线BG 与平面GCE 所成角的正弦值为11||14sin 7||||n BG n BG θ⋅==⋅．20.（Ⅰ）取PC 中点H ，连接、EH FH .∵E 为AB 的中点，ABCD 是菱形，∴//AE CD ，且12AE CD =，又F 为PD 的中点，H 为PC 的中点，∴//FH CD ，且12FH CD =，∴//AE FH ，且AE FH =，则四边形AEHF 是平行四边形，∴//AF EH .又AF ⊄平面PCE ，EH ⊂面PCE ，∴//AF 平面PCE .（Ⅱ）取BC 的中点为O ，∵ABCD 是菱形，AC AB =，∴AO BC ⊥，以A 为原点，,,AO AD AP 所在直线分别为,,z x y 轴，建立空间直角坐标系A xyz -，则)()()3,1,0,3,1,0,0,2,0BCD -，)()313,0,0,0,0,1,,02OP E ⎫-⎪⎪⎝⎭，∴()333,1,1,,,022PC EC ⎛⎫=-= ⎪ ⎪⎝⎭，()3,0,0AO =，设平面的法向量为()1,,n x y z =，则1100n PC n EC ⎧⋅=⎪⎨⋅=⎪⎩，即3033022x y z x y ⎧+-=⎪+=⎪⎩，令1y =-，则3,2x z ==，∴平面PCE 的一个法向量为)13,1,2n =-，又平面PAD 的一个法向量为()21,0,0n =.∴12121236cos ,|n ||n |4314n n n n ⋅<>===⋅++.即平面PAD 与平面PCE 621.解：（1）证明：取PD 的中点F ，连接,EF CF ，因为,E F 分别是,PA PD 的中点，所以//EF AD 且12EF AD =，因为1,//2BC AB BC AD =，所以//EF BC 且EF BC =，所以//BE CF , 又BE ⊄平面,PCD CF ⊂平面PCD ，所以//BE 平面PCD .（2）以P 为坐标原点，,PD PA 所在直线分别为x 轴和y 轴，建立如图所示的空间直角坐标系，不妨设1BC =，则13(0,0,0),3,0),(1,0,0),(1,0,1),(2P A D C B ， 13(0,3,0),(,1),(1,3,0)2PA AB AD ==-=-,设平面PAB 的一个法向量为(,,)n x y z =，则30013002n PA yn AB x z ⎧=⎧⋅=⎪⎪⇒⎨⎨⋅=+=⎪⎪⎩⎩，令2x =，得(2,0,1)n =-，同理可求平面ABD 的一个法向量为6(3,3,0)cos ,55n m m n m n m⋅=⇒===⨯，平面ABD 和平面ABC 为同一个平面，所以二面角P AB C --.22.解：（Ⅰ）证明：因为二面角S AB C --的大小为90°，则SA AD ⊥，又SA AB ⊥，故SA ⊥平面ABCD ，又BD ⊂平面ABCD ，所以SA BD ⊥；在直角梯形ABCD 中，90BAD ADC ∠=∠=︒，21AD CD ==，2AB =，所以1tan tan 2ABD CAD ∠=∠=，又90DAC BAC ∠+∠=︒，所以90ABD BAC ∠+∠=︒，即AC BD ⊥；又ACSA A =，故BD ⊥平面SAC ，因为AF ⊂平面SAC ，故BD AF ⊥.（Ⅱ）设点E 到平面ABCD 的距离为h ，因为B ABC E ABC V V --=，且25E ABC S ABCD V V --=，故511215*********ABCD S ABCD E ABCABC S SAV V S h h --∆⨯⋅⨯===⋅⨯⨯⨯梯形，故12h =，做点E 到平面ABCD 的距离为12.23.（1）E 为SD 的中点，01,602AD DC SD SDA SDC ==∠=∠=.ED EC AD DC ∴===设O 为AC 的中点，连接,EO DO 则EO AC ⊥//,AD BC BC CD ⊥ .AD BC ∴⊥又OD OA OC ==EOC EOD ∴∆≅∆ 从而EO OD ⊥AC ABCD = DO ⊂面ABCD 0AC DO =EO ∴⊥面ABCD EO ⊂面AEC∴面EAC ⊥面ABCD ………………6分（2）设F 为CD 的中点,连接OF EF 、,则OF 平行且等于12AD AD ∥BC EF ∴∥BC不难得出CD ⊥面OEF （EO CD ⊥ FO CD ⊥）∴面ECD ⊥面OEFOF 在面ECD 射影为EF ，EFO ∠的大小为BC 与面ECD 改成角的大小设AD a =，则2aOF =32EF a = 3os OF c EFO EF <== 即BC 与ECD 3（亦可以建系完成） ………………12分24.解（Ⅰ）过点P 作PO ⊥底面ABC ，垂足为O ，连接AO 、CO ，则∠PCO 为所求线面角，,AC PA ⊥,AC PO PA PO P ⊥⋂=且，AC ∴⊥平面PAO .则∠P AO 为二面角P -AC -B 平面角的补角∴∠ 60=PAO ，又23PA =∴，，1sin 2PO PCO CO ∠== 030PCO ∴∠=，直线PC 与面ABC 所成角的大小为30°.（Ⅱ）过O 作OE BC ⊥于点E ,连接PE ，则PEO ∠为二面角P -BC -A 的平面角，AC ⊥平面PAO ,AC OA ⊥045AOE ∠=,设OE 与CA 相交于F 22OE EF FO ∴=+=+在PEO ∆中，3436tan 7222POPEO EO-∠===+则二面角P -BC -A 的正切值为4367-.25.解：（Ⅰ）如图，取PA 中点F ，连接FD EF ,，E 是BP 的中点，AB EF // 且AB EF 21=，又AB DC AB DC 21,//= ∴∴DC EF //四边形EFDC 是平行四边形，故得//EC FD又⊄EC 平面⊂FD PAD ,平面PAD//EC ∴平面ADE（Ⅱ）取AD 中点H ,连接PH ,因为PD PA =，所以AD PH ⊥平面⊥PAD 平面ABCD 于AD ，⊥∴PH 面ABCD ，HB ∴是PB 在平面ABCD 内的射影 PBH ∠∴是PB 与平面ABCD 所成角四边形ABCD 中，090=∠=∠BCD ABC ∴四边形ABCD 是直角梯形AB CB DC 21== 设a AB 2=，则a BD 2=在ABD ∆中，易得a AD DBA 2,450=∴=∠.22212222a a a DH PD PH =-=-=又22224AB a AD BD ==+ABD ∆∴是等腰直角三角形，090=∠ADBa a a DB DH HB 2102212222=+=+=∴ ∴ 在PHB Rt ∆中，5521022tan ===∠a aHB PH PBH（Ⅲ）在平面ABCD 内过点H 作AB 的垂线交AB 于G 点，连接PG ,则HG 是PG 在平面ABCD 上的射影，故AB PG ⊥，所以PGH ∠是二面角D AB P --的平面角，由a HA a AB 22,2==，又a HG HAB 21450=∴=∠ 在PHG Rt ∆中，22122tan ===∠a aHG PH PGH ∴ 二面角D AB P --的余弦值大小为.3326.（1）∵四棱锥P ﹣ABCD 的底面ABCD 为边长为2的正方形，PA=2，PB=PD=2，∴PA 2+AB 2=PB 2，PA 2+AD 2=PD 2， ∴PA ⊥AB ，PA ⊥AD ，∴以A 为原点，AB 为x 轴，AD 为y 轴，AP 为z 轴，建立空间直角坐标系，∵E ，F ，G ，H 分别为棱PA ，PB ，AD ，CD 的中点． ∴C （2，2，0），D （0，2，0），B （2，0，0）， P （0，0，2），F （1，0，1），G （0，1，0）， =（﹣2，0，0），=（﹣1，﹣2，1），=（﹣2，﹣1，0），设平面CFG 的法向量=（x ，y ，z ），则，取x=1，得=（1，﹣2，﹣3），设CD与平面CFG所成角为θ，则sinθ=|cos＜＞|===．∴CD与平面CFG所成角的正弦值为．（2）假设棱PD上是否存在点M（a，b，c），且，（0≤λ≤1），使得平面CFG⊥平面MEH，则（a，b，c﹣2）=（0，2λ，﹣2λ），∴a=0，b=2λ，c=2﹣2λ，即M（0，2λ，2﹣2λ），E（0，0，1），H（1，2，0），=（1，2，﹣1），=（0，2λ，1﹣2λ），设平面MEH的法向量=（x，y，z），则，取y=1，得=（，1，），平面CFG的法向量=（1，﹣2，﹣3），∵平面CFG⊥平面MEH，∴=﹣2﹣=0，解得∈[0，1]．∴棱PD上存在点M，使得平面CFG⊥平面MEH，此时=．。

2020年高考数学立体几何试题分类汇编理

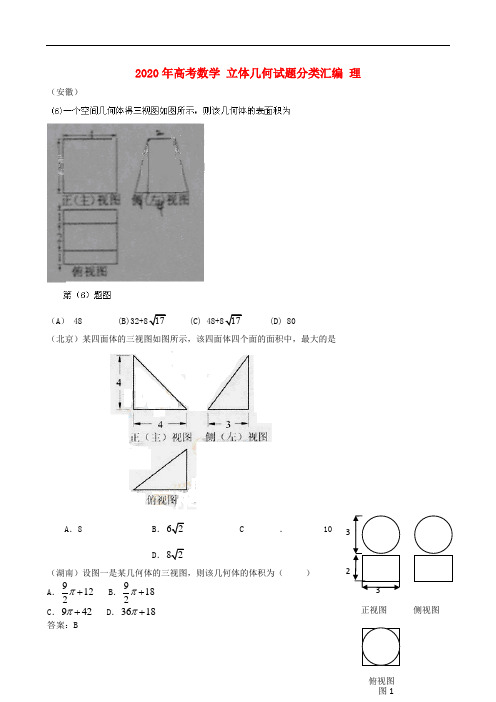
2020年高考数学立体几何试题分类汇编理（安徽）（A ） 48 (B)32+817 (C) 48+817 (D) 80（北京）某四面体的三视图如图所示，该四面体四个面的面积中，最大的是A ．8B ．62C．10D ．82（湖南）设图一是某几何体的三视图，则该几何体的体积为（）A ．9122π+B ．9182π+ C ．942π+ D ．3618π+答案：B3 正视图侧视图解析：有三视图可知该几何体是一个长方体和球构成的组合体，其体积3439+332=18322V ππ=⨯⨯+（）。

（广东）如图l —3．某几何体的正视图(主视图)是平行四边形，侧视图(左视图)和俯视图都是矩形，则该几何体的体积为A.63B.93C.123D.183（江西）已知321,,ααα是三个相互平行的平面,平面21,αα之间的距离为1d ,平面32,αα之间的距离为2d .直线l 与321,,ααα分别交于321,,P P P .那么”“3221P P P P =是”“21d d =的 ( ) A. 充分不必要条件 B. 必要不充分条件C. 充分必要条件D. 既不充分也不必要条件答案：C解析：平面321,,ααα平行，由图可以得知：如果平面距离相等，根据两个三角形全等可知3221P P P P = 如果3221P P P P =，同样是根据两个三角形全等可知21d d =（辽宁）如图，四棱锥S —ABCD 的底面为正方形，SD ⊥底面ABCD ，则下列结论中不正确．．．的是 A ．AC ⊥SB B ．AB ∥平面SCDC ．SA 与平面SBD 所成的角等于SC 与平面SBD 所成的角 D ．AB 与SC 所成的角等于DC 与SA 所成的角（辽宁）已知球的直径SC =4，A ，B 是该球球面上的两点，AB =3，ο30=∠=∠BSC ASC ，则棱锥S —ABC的体积为 A ．33B ．32C ．3D ．1（全国2）已知直二面角l αβ--，点,A AC l α∈⊥,C 为垂足，,,B BD l D β∈⊥为垂足．若AB=2，AC=BD=1，则D 到平面ABC 的距离等于 (A)2 (B)3 (C)6 (D) 1 【思路点拨】本题关键是找出或做出点D 到平面ABC 的距离DE ，根据面面垂直的性质不难证明AC ⊥平面β，进而β⊥平面平面ABC,所以过D 作DE BC ⊥于E ，则DE 就是要求的距离。

2020年高考数学试题分项版—立体几何(解析版)

2020年高考数学试题分项版——立体几何（解析版）一、选择题1.(2020·全国Ⅰ理，3)埃及胡夫金字塔是古代世界建筑奇迹之一，它的形状可视为一个正四棱锥．以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积，则其侧面三角形底边上的高与底面正方形的边长的比值为( )A.5－14 B.5－12 C.5＋14 D.5＋12答案 C解析设正四棱锥的底面正方形的边长为a ，高为h ，侧面三角形底边上的高(斜高)为h ′，则由已知得h 2＝12ah ′.如图，设O 为正四棱锥S －ABCD 底面的中心，E 为BC 的中点，则在Rt △SOE 中，h ′2＝h 2＋⎝⎛⎭⎫a 22， ∴h ′2＝12ah ′＋14a 2，∴⎝⎛⎭⎫h ′a 2－12·h ′a －14＝0，解得h ′a ＝5＋14(负值舍去)．2．(2020·全国Ⅰ理，10)已知A ，B ，C 为球O 的球面上的三个点，⊙O 1为△ABC 的外接圆，若⊙O 1的面积为4π，AB ＝BC ＝AC ＝OO 1，则球O 的表面积为( ) A ．64π B ．48π C ．36π D ．32π 答案 A解析如图，设圆O 1的半径为r ，球的半径为R ，正三角形ABC 的边长为a .由πr 2＝4π，得r ＝2，则33a ＝2，a ＝23，OO 1＝a ＝2 3. 在Rt △OO 1A 中，由勾股定理得R 2＝r 2＋OO 21＝22＋(23)2＝16，所以S 球＝4πR 2＝4π×16＝64π.3．(2020·全国Ⅱ理，7)如图是一个多面体的三视图，这个多面体某条棱的一个端点在正视图中对应的点为M ，在俯视图中对应的点为N ，则该端点在侧视图中对应的点为( )A ．EB ．FC ．GD ．H 答案 A解析由三视图还原几何体，如图所示，由图可知，所求端点在侧视图中对应的点为E .4．(2020·全国Ⅱ理，10)已知△ABC 是面积为934的等边三角形，且其顶点都在球O 的球面上．若球O 的表面积为16π，则O 到平面ABC 的距离为( ) A. 3 B.32 C ．1 D.32答案 C 解析如图所示，过球心O 作OO 1⊥平面ABC ，则O 1为等边三角形ABC 的外心．设△ABC 的边长为a ，则34a 2＝934，解得a ＝3， ∴O 1A ＝23×32×3＝ 3.设球O 的半径为r ，则由4πr 2＝16π，得r ＝2，即OA ＝2. 在Rt △OO 1A 中，OO 1＝OA 2－O 1A 2＝1，即O 到平面ABC 的距离为1.5．(2020·全国Ⅲ理，8)下图为某几何体的三视图，则该几何体的表面积是( )A ．6＋4 2B ．4＋4 2C ．6＋2 3D ．4＋2 3答案 C解析如图，该几何体为三棱锥，且其中有三个面是腰长为2的等腰直角三角形，第四个面是边长为22的等边三角形，所以该几何体的表面积为3×12×2×2＋12×22×22×32＝6＋2 3.6.(2020·新高考全国Ⅰ，4)日晷是中国古代用来测定时间的仪器，利用与晷面垂直的晷针投射到晷面的影子来测定时间．把地球看成一个球(球心记为O )，地球上一点A 的纬度是指OA 与地球赤道所在平面所成角，点A 处的水平面是指过点A 且与OA 垂直的平面．在点A 处放置一个日晷，若晷面与赤道所在平面平行，点A 处的纬度为北纬40°，则晷针与点A 处的水平面所成角为( )A ．20°B ．40°C ．50°D ．90° 答案 B解析如图所示，⊙O 为赤道平面，⊙O 1为A 点处的日晷面所在的平面，由点A处的纬度为北纬40°可知∠OAO1＝40°，又点A处的水平面与OA垂直，晷针AC与⊙O1所在的面垂直，则晷针AC与水平面所成角为40°.7.(2020·新高考全国Ⅱ，4)日晷是中国古代用来测定时间的仪器，利用与晷面垂直的晷针投射到晷面的影子来测定时间．把地球看成一个球(球心记为O)，地球上一点A的纬度是指OA与地球赤道所在平面所成角，点A处的水平面是指过点A且与OA垂直的平面．在点A 处放置一个日晷，若晷面与赤道所在平面平行，点A处的纬度为北纬40°，则晷针与点A处的水平面所成角为()A．20°B．40°C．50°D．90°答案 B解析如图所示，⊙O为赤道平面，⊙O1为A点处的日晷面所在的平面，由点A处的纬度为北纬40°可知∠OAO1＝40°，又点A处的水平面与OA垂直，晷针AC与⊙O1所在的面垂直，则晷针AC与水平面所成角为40°.8．(2020·北京，4)某三棱柱的底面为正三角形，其三视图如图所示，该三棱柱的表面积为()A．6＋ 3 B．6＋2 3 C．12＋ 3 D．12＋2 3答案 D解析由三视图还原几何体，该几何体为底面是边长为2的正三角形，高为2的直三棱柱， S 底＝2×34×22＝2 3. S 侧＝3×2×2＝12，则三棱柱的表面积为23＋12.9．(2020·北京，10)2020年3月14日是全球首个国际圆周率日(π Day)．历史上，求圆周率π的方法有多种，与中国传统数学中的“割圆术”相似．数学家阿尔·卡西的方法是：当正整数n 充分大时，计算单位圆的内接正6n 边形的周长和外切正6n 边形(各边均与圆相切的正6n 边形)的周长，将它们的算术平均数作为2π的近似值．按照阿尔·卡西的方法，π的近似值的表达式是( ) A ．3n ⎝⎛⎭⎫sin 30°n ＋tan 30°n B ．6n ⎝⎛⎭⎫sin 30°n ＋tan 30°n C ．3n ⎝⎛⎭⎫sin 60°n ＋tan 60°n D ．6n ⎝⎛⎭⎫sin 60°n＋tan 60°n 答案 A解析设内接正6n 边形的周长为C 1，外切正6n 边形的周长为C 2，如图(1)所示，sin 360°12n ＝BC 1， ∴BC ＝sin 30°n，∴AB ＝2sin 30°n ，C 1＝12n sin 30°n.如图(2)所示，tan 360°12n ＝B ′C ′1，∴B ′C ′＝tan 30°n，∴A ′B ′＝2tan 30°n ，C 2＝12n tan 30°n .∴2π＝C 1＋C 22＝6n ⎝⎛⎭⎫sin 30°n ＋tan 30°n ， ∴π＝3n ⎝⎛⎭⎫sin 30°n＋tan 30°n . 10．(2020·天津，5)若棱长为23的正方体的顶点都在同一球面上，则该球的表面积为( )A ．12πB ．24πC ．36πD ．144π 答案 C解析由题意知，正方体的体对角线就是球的直径 ∴2R ＝(23)2＋(23)2＋(23)2＝6， ∴R ＝3，∴S 球＝4πR 2＝36π.11．(2020·浙江，5)某几何体的三视图(单位：cm)如图所示，则该几何体的体积(单位：cm 3)是( )A.73B.143 C ．3 D ．6 答案 A解析如图，三棱柱的体积V 1＝12×2×1×2＝2，三棱锥的体积V 2＝13×12×2×1×1＝13，因此，该几何体的体积V ＝V 1＋V 2＝2＋13＝73.12．(2020·浙江，6)已知空间中不过同一点的三条直线l ，m ，n ，“l ，m ，n 共面”是“l ，m ，n 两两相交”的( ) A ．充分不必要条件 B ．必要不充分条件 C ．充要条件D ．既不充分也不必要条件答案 B解析如图，直线l ，m ，n 不过同一点，且l ，m ，n 共面有三种情况：①同一平面内三线平行；②两平行线与另一线相交；③三线两两相交．因此，“l ，m ，n 两两相交”是“l ，m ，n 共面”的一种情况，即“l ，m ，n 共面”是“l ，m ，n 两两相交”的必要不充分条件．13.(2020·全国Ⅰ文，3)埃及胡夫金字塔是古代世界建筑奇迹之一，它的形状可视为一个正四棱锥．以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积，则其侧面三角形底边上的高与底面正方形的边长的比值为( )A.5－14 B.5－12 C.5＋14 D.5＋12答案 C解析设正四棱锥的底面正方形的边长为a ，高为h ，侧面三角形底边上的高(斜高)为h ′，则由已知得h 2＝12ah ′.如图，设O 为正四棱锥S －ABCD 底面的中心，E 为BC 的中点，则在Rt △SOE 中，h ′2＝h 2＋⎝⎛⎭⎫a 22， ∴h ′2＝12ah ′＋14a 2，∴⎝⎛⎭⎫h ′a 2－12·h ′a －14＝0，解得h ′a ＝5＋14(负值舍去)．14．(2020·全国Ⅰ文，12)已知A ，B ，C 为球O 的球面上的三个点，⊙O 1为△ABC 的外接圆．若⊙O 1的面积为4π，AB ＝BC ＝AC ＝OO 1，则球O 的表面积为( ) A ．64π B ．48π C ．36π D ．32π 答案 A解析如图，设圆O 1的半径为r ，球的半径为R ，正三角形ABC 的边长为a . 由πr 2＝4π，得r ＝2，则33a ＝2，a ＝23， OO 1＝a ＝2 3.在Rt △OO 1A 中，由勾股定理得R 2＝r 2＋OO 21＝22＋(23)2＝16，所以S 球＝4πR 2＝4π×16＝64π.15．(2020·全国Ⅱ文，11)已知△ABC 是面积为934的等边三角形，且其顶点都在球O 的球面上．若球O 的表面积为16π，则O 到平面ABC 的距离为( ) A. 3 B.32 C ．1 D.32答案 C解析如图所示，过球心O 作OO 1⊥平面ABC ，则O 1为等边三角形ABC 的外心．设△ABC 的边长为a ，则34a 2＝934，解得a ＝3， ∴O 1A ＝23×32×3＝ 3.设球O 的半径为r ，则由4πr 2＝16π，得r ＝2，即OA ＝2. 在Rt △OO 1A 中，OO 1＝OA 2－O 1A 2＝1，即O 到平面ABC 的距离为1.16．(2020·全国Ⅲ文，9)下图为某几何体的三视图，则该几何体的表面积是( )A ．6＋4 2B ．4＋4 2C ．6＋2 3D ．4＋2 3答案 C解析如图，该几何体为三棱锥，且其中有三个面是腰长为2的等腰直角三角形，第四个面是边长为22的等边三角形，所以该几何体的表面积为3×12×2×2＋12×22×22×32＝6＋2 3.二、填空题1．(2020·全国Ⅱ理，16)设有下列四个命题：p 1：两两相交且不过同一点的三条直线必在同一平面内； p 2：过空间中任意三点有且仅有一个平面； p 3：若空间两条直线不相交，则这两条直线平行； p 4：若直线l ⊂平面α，直线m ⊥平面α，则m ⊥l . 则下述命题中所有真命题的序号是________． ①p 1∧p 4；②p 1∧p 2；③23p p ⌝∨；④34p p ⌝∨⌝. 答案 ①③④解析 p 1是真命题，两两相交且不过同一点的三条直线必定有三个交点，且这三个交点不在同一条直线上，由平面的基本性质“经过不在同一直线上的三个点，有且只有一个平面”，可知p 1为真命题；p 2是假命题，因为当空间中三点在一条直线上时，有无数个平面过这三个点；p 3是假命题，因为空间两条直线不相交时，它们可能平行，也可能异面；p 4是真命题，因为一条直线垂直于一个平面，那么它垂直于平面内的所有直线．由以上结论知綈p 2，綈p 3，綈p 4依次为真命题、真命题、假命题，从而①③④中命题为真命题，②中命题为假命题．2．(2020·全国Ⅲ理，15)已知圆锥的底面半径为1，母线长为3，则该圆锥内半径最大的球的体积为________．答案23π 解析圆锥内半径最大的球即为圆锥的内切球，设其半径为r .作出圆锥的轴截面P AB ，如图所示，则△P AB 的内切圆为圆锥的内切球的大圆．在△P AB 中，P A ＝PB ＝3，D 为AB 的中点，AB ＝2，E 为切点，则PD ＝22，△PEO ∽△PDB ，故PO PB ＝OE DB ，即22－r 3＝r 1，解得r ＝22，故内切球的体积为43π⎝⎛⎭⎫223＝23π.3．(2020·新高考全国Ⅰ，16)已知直四棱柱ABCD －A 1B 1C 1D 1的棱长均为2，∠BAD ＝60°.以D 1为球心，5为半径的球面与侧面BCC 1B 1的交线长为________．答案2π2解析如图，设B 1C 1的中点为E ，球面与棱BB 1，CC 1的交点分别为P ，Q ，连接DB ，D 1B 1，D 1P ，D 1E ，EP ，EQ ，由∠BAD ＝60°，AB ＝AD ，知△ABD 为等边三角形， ∴D 1B 1＝DB ＝2，∴△D 1B 1C 1为等边三角形，则D 1E ＝3且D 1E ⊥平面BCC 1B 1，∴E 为球面截侧面BCC 1B 1所得截面圆的圆心，设截面圆的半径为r ，则r ＝R 2球－D 1E 2＝5－3＝ 2. 又由题意可得EP ＝EQ ＝2，∴球面与侧面BCC 1B 1的交线为以E 为圆心的圆弧PQ . 又D 1P ＝5，∴B 1P ＝D 1P 2－D 1B 21＝1，同理C 1Q ＝1，∴P ，Q 分别为BB 1，CC 1的中点， ∴∠PEQ ＝π2，知PQ 的长为π2×2＝2π2，即交线长为2π2.4．(2020·新高考全国Ⅱ，13)棱长为2的正方体ABCD －A 1B 1C 1D 1中，M ，N 分别为棱BB 1，AB 的中点，则三棱锥A 1－D 1MN 的体积为________．答案 1解析如图，由正方体棱长为2，得S △A 1MN ＝2×2－2×12×2×1－12×1×1＝32，又易知D 1A 1为三棱锥D 1－A 1MN 的高，且D 1A 1＝2， ∴1111A D MN D A MN V V --=＝13·1A MN S △·D 1A 1＝13×32×2＝1. 5.(2020·江苏，9)如图，六角螺帽毛坯是由一个正六棱柱挖去一个圆柱所构成的．已知螺帽的底面正六边形边长为2 cm ，高为2 cm ，内孔半径为0.5 cm ，则此六角螺帽毛坯的体积是________cm 3.答案 ⎝⎛⎭⎫123－π2 解析螺帽的底面正六边形的面积 S ＝6×12×22×sin 60°＝63(cm 2)，正六棱柱的体积V 1＝63×2＝123(cm 3)，圆柱的体积V 2＝π×0.52×2＝π2(cm 3)，所以此六角螺帽毛坯的体积 V ＝V 1－V 2＝⎝⎛⎭⎫123－π2cm 3. 6．(2020·浙江，14)已知圆锥的侧面积(单位：cm 2)为2π，且它的侧面展开图是一个半圆，则这个圆锥的底面半径(单位：cm)是________．答案 1解析如图，设圆锥的母线长为l ，底面半径为r ，则圆锥的侧面积S 侧＝πrl ＝2π， ∴r ＝12l .又圆锥侧面展开图为半圆， ∴12πl 2＝2π， ∴l ＝2，∴r ＝1.7．(2020·全国Ⅱ文，16)设有下列四个命题：p 1：两两相交且不过同一点的三条直线必在同一平面内； p 2：过空间中任意三点有且仅有一个平面； p 3：若空间两条直线不相交，则这两条直线平行； p 4：若直线l ⊂平面α，直线m ⊥平面α，则m ⊥l . 则下述命题中所有真命题的序号是________． ①p 1∧p 4；②p 1∧p 2；③23p p ⌝∨；④34p p ⌝∨⌝. 答案 ①③④解析 p 1是真命题，两两相交且不过同一点的三条直线必定有三个交点，且这三个交点不在同一条直线上，由平面的基本性质“经过不在同一直线上的三个点，有且只有一个平面”，可知p 1为真命题；p 2是假命题，因为当空间中三点在一条直线上时，有无数个平面过这三个点；p 3是假命题，因为空间两条直线不相交时，它们可能平行，也可能异面；p 4是真命题，因为一条直线垂直于一个平面，那么它垂直于平面内的所有直线．由以上结论知綈p 2，綈p 3，綈p 4依次为真命题、真命题、假命题，从而①③④中命题为真命题，②中命题为假命题．8．(2020·全国Ⅲ文，16)已知圆锥的底面半径为1，母线长为3，则该圆锥内半径最大的球的体积为________．答案23π 解析圆锥内半径最大的球即为圆锥的内切球，设其半径为r .作出圆锥的轴截面P AB ，如图所示，则△P AB 的内切圆为圆锥的内切球的大圆．在△P AB 中，P A ＝PB ＝3，D 为AB 的中点，AB ＝2，E 为切点，则PD ＝22，△PEO ∽△PDB ，故PO PB ＝OE DB ，即22－r 3＝r 1，解得r ＝22，故内切球的体积为43π⎝⎛⎭⎫223＝23π.三、解答题1.(2020·全国Ⅰ理，18)如图，D 为圆锥的顶点，O 是圆锥底面的圆心，AE 为底面直径，AE ＝AD .△ABC 是底面的内接正三角形，P 为DO 上一点，PO ＝66DO .(1)证明：P A ⊥平面PBC ； (2)求二面角B －PC －E 的余弦值．(1)证明由题设，知△DAE 为等边三角形，设AE ＝1，则DO ＝32，CO ＝BO ＝12AE ＝12，所以PO ＝66DO ＝24， PC ＝PO 2＋OC 2＝64，PB ＝PO 2＋OB 2＝64，又△ABC 为等边三角形，则BAsin 60°＝2OA ，所以BA ＝32， P A ＝PO 2＋OA 2＝64， P A 2＋PB 2＝34＝AB 2，则∠APB ＝90°，所以P A ⊥PB ，同理P A ⊥PC ，又PC ∩PB ＝P ，所以P A ⊥平面PBC . (2)解过O 作ON ∥BC 交AB 于点N ，因为PO ⊥平面ABC ，以O 为坐标原点，OA 所在直线为x 轴，ON 所在直线为y 轴，OD 所在直线为z 轴，建立如图所示的空间直角坐标系，则E ⎝⎛⎭⎫－12，0，0，P ⎝⎛⎭⎫0，0，24， B ⎝⎛⎭⎫－14，34，0，C ⎝⎛⎭⎫－14，－34，0，PC →＝⎝⎛⎭⎫－14，－34，－24，PB →＝⎝⎛⎭⎫－14，34，－24，PE →＝⎝⎛⎭⎫－12，0，－24，设平面PCB 的一个法向量为n ＝(x 1，y 1，z 1)，由⎩⎪⎨⎪⎧n ·PC →＝0，n ·PB →＝0，得⎩⎨⎧－x 1－3y 1－2z 1＝0，－x 1＋3y 1－2z 1＝0，令x 1＝2，得z 1＝－1，y 1＝0，所以n ＝(2，0，－1)，设平面PCE 的一个法向量为m ＝(x 2，y 2，z 2)，由⎩⎪⎨⎪⎧m ·PC →＝0，m ·PE →＝0，得⎩⎨⎧－x 2－3y 2－2z 2＝0，－2x 2－2z 2＝0，令x 2＝1，得z 2＝－2，y 2＝33，所以m ＝⎝⎛⎭⎫1，33，－2，故cos 〈m ，n 〉＝m ·n|m |·|n |＝223×103＝255，所以二面角B －PC －E 的余弦值为255.2.(2020·全国Ⅱ理，20)如图，已知三棱柱ABC －A 1B 1C 1的底面是正三角形，侧面BB 1C 1C 是矩形，M ，N 分别为BC ，B 1C 1的中点，P 为AM上一点．过B 1C 1和P 的平面交AB 于E ，交AC 于F .(1)证明：AA 1∥MN ，且平面A 1AMN ⊥平面EB 1C 1F ；(2)设O 为△A 1B 1C 1的中心，若AO ∥平面EB 1C 1F ，且AO ＝AB ，求直线B 1E 与平面A 1AMN 所成角的正弦值．(1)证明因为侧面BB 1C 1C 是矩形，且M ，N 分别为BC ，B 1C 1的中点，所以MN ∥CC 1.又由已知得AA 1∥CC 1，故AA 1∥MN . 因为△A 1B 1C 1是正三角形，所以B 1C 1⊥A 1N . 又B 1C 1⊥MN ，故B 1C 1⊥平面A 1AMN . 所以平面A 1AMN ⊥平面EB 1C 1F .(2)解由已知得AM ⊥BC .以M 为坐标原点，MA →的方向为x 轴正方向，|MB →|为单位长度，建立如图所示的空间直角坐标系，则AB ＝2，AM ＝ 3.连接NP ，则四边形AONP 为平行四边形，故PM ＝233，E ⎝⎛⎭⎫233，13，0.由(1)知平面A 1AMN ⊥平面ABC ，作NQ ⊥AM ，垂足为Q ，则NQ ⊥平面ABC . 设Q (a,0,0)，则NQ ＝4－⎝⎛⎭⎫233－a 2，B 1⎝⎛⎭⎪⎫a ，1，4－⎝⎛⎭⎫233－a 2，故B 1E →＝⎝ ⎛⎭⎪⎫233－a ，－23，－4－⎝⎛⎭⎫233－a 2，|B 1E →|＝2103.又n ＝(0，－1,0)是平面A 1AMN 的一个法向量，故sin ⎝⎛⎭⎫π2－〈n ，B 1E →〉＝cos 〈n ，B 1E →〉＝n ·B 1E →|n ||B 1E →|＝1010.所以直线B 1E 与平面A 1AMN 所成角的正弦值为1010. 3.(2020·全国Ⅲ理，19)如图，在长方体ABCD －A 1B 1C 1D 1中，点E ，F 分别在棱DD 1，BB 1上，且2DE ＝ED 1，BF ＝2FB 1.(1)证明：点C 1在平面AEF 内；(2)若AB ＝2，AD ＝1，AA 1＝3，求二面角A －EF －A 1的正弦值．(1)证明设AB ＝a ，AD ＝b ，AA 1＝c ，如图，以C 1为坐标原点，C 1D 1—→，C 1B 1—→，C 1C —→的方向分别为x 轴，y 轴，z 轴正方向，建立空间直角坐标系C 1－xyz .连接C 1F ，则C 1(0,0,0)，A (a ，b ，c )， E ⎝⎛⎭⎫a ，0，23c ，F ⎝⎛⎭⎫0，b ，13c ， EA →＝⎝⎛⎭⎫0，b ，13c ，C 1F →＝⎝⎛⎭⎫0，b ，13c ，所以EA →＝C 1F →，所以EA ∥C 1F ，即A ，E ，F ，C 1四点共面，所以点C 1在平面AEF 内．(2)解由已知得A (2,1,3)，E (2,0,2)，F (0,1,1)，A 1(2,1,0)，则AE →＝(0，－1，－1)，AF →＝(－2,0，－2)， A 1E →＝(0，－1,2)，A 1F →＝(－2,0,1)．设n 1＝(x 1，y 1，z 1)为平面AEF 的法向量，则⎩⎪⎨⎪⎧n 1·AE →＝0，n 1·AF →＝0，即⎩⎪⎨⎪⎧－y 1－z 1＝0，－2x 1－2z 1＝0，可取n 1＝(－1，－1,1)．设n 2＝(x 2，y 2，z 2)为平面A 1EF 的法向量，则⎩⎪⎨⎪⎧n 2·A 1E →＝0，n 2·A 1F →＝0，即⎩⎪⎨⎪⎧－y 2＋2z 2＝0，－2x 2＋z 2＝0，同理可取n 2＝⎝⎛⎭⎫12，2，1. 因为cos 〈n 1，n 2〉＝n 1·n 2|n 1|·|n 2|＝－77，所以二面角A －EF －A 1的正弦值为427. 4.(2020·新高考全国Ⅰ，20)如图，四棱锥P －ABCD 的底面为正方形，PD ⊥底面ABCD .设平面P AD 与平面PBC 的交线为l .(1)证明：l ⊥平面PDC ；(2)已知PD ＝AD ＝1，Q 为l 上的点，求PB 与平面QCD 所成角的正弦值的最大值． (1)证明在正方形ABCD 中，AD ∥BC ，因为AD ⊄平面PBC ，BC ⊂平面PBC ，所以AD ∥平面PBC ，又因为AD ⊂平面P AD ，平面P AD ∩平面PBC ＝l ，所以AD ∥l ，因为在四棱锥P －ABCD 中，底面ABCD 是正方形，所以AD ⊥DC ，所以l ⊥DC ，且PD ⊥平面ABCD ，所以AD ⊥PD ，所以l ⊥PD ，因为DC ∩PD ＝D ，所以l ⊥平面PDC .(2)解以D 为坐标原点，DA →的方向为x 轴正方向，如图建立空间直角坐标系D －xyz ，因为PD ＝AD ＝1，则有D (0,0,0)，C (0,1,0)，A (1,0,0)，P (0,0,1)，B (1，1,0)，设Q (m,0,1)，则有DC →＝(0,1,0)，DQ →＝(m,0,1)，PB →＝(1,1，－1)，设平面QCD 的法向量为n ＝(x ，y ，z )，则⎩⎪⎨⎪⎧DC →·n ＝0，DQ →·n ＝0，即⎩⎪⎨⎪⎧y ＝0，mx ＋z ＝0，令x ＝1，则z ＝－m ，所以平面QCD 的一个法向量为n ＝(1,0，－m )，则cos 〈n ，PB →〉＝n ·PB →|n ||PB →|＝1＋0＋m 3·m 2＋1. 根据直线的方向向量与平面法向量所成角的余弦值的绝对值即为直线与平面所成角的正弦值，所以直线PB 与平面QCD 所成角的正弦值等于 |cos 〈n ，PB →〉|＝|1＋m |3·m 2＋1＝33·1＋2m ＋m 2m 2＋1＝33·1＋2m m 2＋1≤33·1＋2|m |m 2＋1≤33·1＋1＝63，当且仅当m ＝1时取等号，所以直线PB 与平面QCD 所成角的正弦值的最大值为63. 5.(2020·新高考全国Ⅱ，20)如图，四棱锥P －ABCD 的底面为正方形，PD ⊥底面ABCD .设平面P AD 与平面PBC 的交线为l .(1)证明：l ⊥平面PDC ；(2)已知PD ＝AD ＝1，Q 为l 上的点，QB ＝2，求PB 与平面QCD 所成角的正弦值． (1)证明在正方形ABCD 中，AD ∥BC ，因为AD ⊄平面PBC ，BC ⊂平面PBC ，所以AD ∥平面PBC ，又因为AD ⊂平面P AD ，平面P AD ∩平面PBC ＝l ，所以AD ∥l ，因为在四棱锥P －ABCD 中，底面ABCD 是正方形，所以AD ⊥DC ，所以l ⊥DC ，且PD ⊥平面ABCD ，所以AD ⊥PD ，所以l ⊥PD ，因为DC ∩PD ＝D ，所以l ⊥平面PDC .(2)解以D 为坐标原点，DA →的方向为x 轴正方向，建立如图所示的空间直角坐标系D －xyz ，则D (0,0,0)，C (0,1,0)， B (1,1,0)，P (0,0,1)，DC →＝(0,1,0)，PB →＝(1,1，－1)．由(1)设Q (a,0,1)，则BQ →＝(a －1，－1,1)．由题意知(a －1)2＋2＝2， ∴a ＝1，∴DQ →＝(1,0,1)．设n ＝(x ，y ，z )是平面QCD 的一个法向量，则⎩⎪⎨⎪⎧n ·DQ →＝0，n ·DC →＝0，即⎩⎪⎨⎪⎧x ＋z ＝0，y ＝0，可取n ＝(1,0，－1)，∴cos 〈n ，PB →〉＝n ·PB →|n |·|PB →|＝63，故PB 与平面QCD 所成角的正弦值为63. 6.(2020·北京，16)如图，在正方体ABCD －A 1B 1C 1D 1中，E 为BB 1的中点．(1)求证：BC 1∥平面AD 1E ；(2)求直线AA 1与平面AD 1E 所成角的正弦值． (1)证明在正方体ABCD －A 1B 1C 1D 1中， AB ∥A 1B 1且AB ＝A 1B 1，A 1B 1∥C 1D 1且A 1B 1＝C 1D 1， ∴AB ∥C 1D 1且AB ＝C 1D 1，∴四边形ABC 1D 1为平行四边形，则BC 1∥AD 1， ∵BC 1⊄平面AD 1E ，AD 1⊂平面AD 1E ， ∴BC 1∥平面AD 1E .(2)解以点A 为坐标原点，AD ，AB ，AA 1所在直线分别为x ，y ，z 轴建立如图所示的空间直角坐标系A －xyz ，设正方体ABCD －A 1B 1C 1D 1的棱长为2，则A (0,0,0)，A 1(0,0,2)，D 1(2,0,2)，E (0,2,1)， AD 1→＝(2,0,2)，AE →＝(0,2,1)，AA 1→＝(0,0,2)，设平面AD 1E 的法向量为n ＝(x ，y ，z )，由⎩⎪⎨⎪⎧n ·AD 1→＝0，n ·AE →＝0，得⎩⎪⎨⎪⎧2x ＋2z ＝0，2y ＋z ＝0，令z ＝－2，得x ＝2，y ＝1，则n ＝(2,1，－2)． cos 〈n ，AA 1→〉＝n ·AA 1→|n |·|AA 1→|＝－43×2＝－23.因此，直线AA 1与平面AD 1E 所成角的正弦值为23.7.(2020·天津，17)如图，在三棱柱ABC －A 1B 1C 1中，CC 1⊥平面ABC ，AC ⊥BC ，AC ＝BC ＝2，CC 1＝3，点D ，E 分别在棱AA 1和棱CC 1上，且AD ＝1，CE ＝2，M 为棱A 1B 1的中点．(1)求证：C 1M ⊥B 1D ；(2)求二面角B －B 1E －D 的正弦值；(3)求直线AB 与平面DB 1E 所成角的正弦值．(1)证明依题意，以C 为坐标原点，分别以CA →，CB →，CC 1→的方向为x 轴，y 轴，z 轴的正方向建立空间直角坐标系(如图)，可得C (0,0,0)，A (2,0,0)，B (0,2,0)，C 1(0,0,3)，A 1(2,0,3)，B 1(0,2,3)，D (2,0,1)，E (0,0,2)，M (1,1,3)．则C 1M →＝(1,1,0)，B 1D →＝(2，－2，－2)， ∵C 1M →·B 1D →＝2－2＋0＝0，∴C 1M ⊥B 1D .(2)解依题意，CA →＝(2,0,0)是平面BB 1E 的一个法向量，EB 1→＝(0,2,1)，ED →＝(2,0，－1)．设n ＝(x ，y ，z )为平面DB 1E 的法向量，则⎩⎪⎨⎪⎧n ·EB 1→＝0，n ·ED →＝0，即⎩⎪⎨⎪⎧2y ＋z ＝0，2x －z ＝0.不妨设x ＝1，可得n ＝(1，－1,2)．∴cos 〈CA →，n 〉＝CA →·n |CA →||n |＝66，∴sin 〈CA →，n 〉＝1－16＝306. ∴二面角B －B 1E －D 的正弦值为306. (3)解依题意，AB →＝(－2,2,0)，由(2)知，n ＝(1，－1,2)为平面DB 1E 的一个法向量， ∴cos 〈AB →，n 〉＝AB →·n |AB →||n |＝－33，∴直线AB 与平面DB 1E 所成角的正弦值为33. 8.(2020·江苏，15)在三棱柱ABC －A 1B 1C 1中，AB ⊥AC ，B 1C ⊥平面ABC ，E ，F 分别是AC ，B 1C 的中点．(1)求证：EF ∥平面AB 1C 1； (2)求证：平面AB 1C ⊥平面ABB 1.证明 (1)因为E ，F 分别是AC ，B 1C 的中点，所以EF ∥AB 1.又EF ⊄平面AB 1C 1，AB 1⊂平面AB 1C 1，所以EF ∥平面AB 1C 1.(2)因为B 1C ⊥平面ABC ，AB ⊂平面ABC ，所以B 1C ⊥AB .又AB ⊥AC ，B 1C ⊂平面AB 1C ，AC ⊂平面AB 1C ， B 1C ∩AC ＝C ，所以AB ⊥平面AB 1C . 又因为AB ⊂平面ABB 1，所以平面AB 1C ⊥平面ABB 1.9.(2020·江苏，22)在三棱锥A －BCD 中，已知CB ＝CD ＝5，BD ＝2，O 为BD 的中点，AO ⊥平面BCD ，AO ＝2，E 为AC 的中点．(1)求直线AB 与DE 所成角的余弦值；(2)若点F 在BC 上，满足BF ＝14BC ，设二面角F －DE －C 的大小为θ，求sin θ的值．解 (1)如图，连接OC ，因为CB ＝CD ，O 为BD 的中点，所以CO ⊥BD .又AO ⊥平面BCD ，所以AO ⊥OB ，AO ⊥OC .以{OB →，OC →，OA →}为基底，建立空间直角坐标系O －xyz . 因为BD ＝2，CB ＝CD ＝5，AO ＝2，所以B (1,0,0)，D (－1,0,0)，C (0,2,0)，A (0,0,2)．因为E 为AC 的中点，所以E (0,1,1)．所以AB →＝(1,0，－2)，DE →＝(1,1,1)，所以|cos 〈AB →，DE →〉|＝|AB →·DE →||AB →|·|DE →|＝|1＋0－2|5×3＝1515.因此，直线AB 与DE 所成角的余弦值为1515. (2)因为点F 在BC 上，BF ＝14BC ，BC →＝(－1,2,0)．所以BF →＝14BC →＝⎝⎛⎭⎫－14，12，0. 又DB →＝(2,0,0)，故DF →＝DB →＋BF →＝⎝⎛⎭⎫74，12，0.设n 1＝(x 1，y 1，z 1)为平面DEF 的一个法向量，则⎩⎪⎨⎪⎧ DE →·n 1＝0，DF →·n 1＝0，即⎩⎪⎨⎪⎧x 1＋y 1＋z 1＝0，74x 1＋12y 1＝0，令x 1＝2，得y 1＝－7，z 1＝5，所以n 1＝(2，－7,5)．设n 2＝(x 2，y 2，z 2)为平面DEC 的一个法向量，又DC →＝(1,2,0)，则⎩⎪⎨⎪⎧DE →·n 2＝0，DC →·n 2＝0，即⎩⎪⎨⎪⎧x 2＋y 2＋z 2＝0，x 2＋2y 2＝0，令x 2＝2，得y 2＝－1，z 2＝－1，所以n 2＝(2，－1，－1)．故|cos θ|＝|n 1·n 2||n 1|·|n 2|＝|4＋7－5|78×6＝1313. 所以sin θ＝1－cos 2θ＝23913. 10.(2020·浙江，19)如图，在三棱台ABC －DEF 中，平面ACFD ⊥平面ABC ，∠ACB ＝∠ACD ＝45°，DC ＝2BC .(1)证明：EF ⊥DB ；(2)求直线DF 与平面DBC 所成角的正弦值．(1)证明如图(1)，过点D 作DO ⊥AC ，交直线AC 于点O ，连接OB .由∠ACD ＝45°，DO ⊥AC ，得CD ＝2CO . 由平面ACFD ⊥平面ABC ，得DO ⊥平面ABC ，所以DO ⊥BC .由∠ACB ＝45°，BC ＝12CD ＝22CO ，得BO ⊥BC .所以BC ⊥平面BDO ，故BC ⊥DB . 由ABC －DEF 为三棱台，得BC ∥EF ，所以EF ⊥DB .(2)解方法一如图(2)，过点O 作OH ⊥BD ，交直线BD 于点H ，连接CH .由ABC －DEF 为三棱台，得DF ∥CO ，所以直线DF 与平面DBC 所成角等于直线CO 与平面DBC 所成角．由BC ⊥平面BDO ，得OH ⊥BC ，故OH ⊥平面DBC ，所以∠OCH 为直线CO 与平面DBC 所成角．设CD ＝22，则DO ＝OC ＝2，BO ＝BC ＝2，得BD ＝6，OH ＝233，所以sin ∠OCH ＝OH OC ＝33.因此，直线DF 与平面DBC 所成角的正弦值为33. 方法二由ABC －DEF 为三棱台，得DF ∥CO ，所以直线DF 与平面DBC 所成角等于直线CO 与平面DBC 所成角，记为θ.如图(3)，以O 为原点，分别以射线OC ，OD 为y ，z 轴的正半轴，建立空间直角坐标系O－xyz .设CD ＝22，由题意知各点坐标如下：O (0,0,0)，B (1,1,0)，C (0,2,0)，D (0,0,2)．因此OC →＝(0,2,0)，BC →＝(－1,1,0)，CD →＝(0，－2,2)．设平面DBC 的一个法向量为n ＝(x ，y ，z )，由⎩⎪⎨⎪⎧n ·BC →＝0，n ·CD →＝0，即⎩⎪⎨⎪⎧－x ＋y ＝0，－2y ＋2z ＝0，可取n ＝(1,1,1)，所以sin θ＝|cos 〈OC →，n 〉|＝|OC →·n ||OC →|·|n |＝33.因此，直线DF 与平面DBC 所成角的正弦值为33. 11.(2020·全国Ⅰ文，19)如图，D 为圆锥的顶点，O 是圆锥底面的圆心，△ABC 是底面的内接正三角形，P 为DO 上一点，∠APC ＝90°.(1)证明：平面P AB ⊥平面P AC ；(2)设DO ＝2，圆锥的侧面积为3π，求三棱锥P －ABC 的体积． (1)证明 ∵D 为圆锥顶点，O 为底面圆心， ∴OD ⊥平面ABC ，∵P 在DO 上，OA ＝OB ＝OC ， ∴P A ＝PB ＝PC ，∵△ABC 是圆内接正三角形， ∴AC ＝BC ，△P AC ≌△PBC ，∴∠APC ＝∠BPC ＝90°，即PB ⊥PC ，P A ⊥PC ， P A ∩PB ＝P ，∴PC ⊥平面P AB ，PC ⊂平面P AC ，∴平面P AB ⊥平面P AC .(2)解设圆锥的母线为l ，底面半径为r ，圆锥的侧面积为πrl ＝3π，rl ＝3，OD 2＝l 2－r 2＝2，解得r ＝1，l ＝3，AC ＝2r sin 60°＝3，在等腰直角三角形APC 中， AP ＝22AC ＝62，在Rt △P AO 中，PO ＝AP 2－OA 2＝64－1＝22， ∴三棱锥P －ABC 的体积为V P －ABC ＝13PO ·S △ABC ＝13×22×34×3＝68.12.(2020·全国Ⅱ文，20)如图，已知三棱柱ABC －A 1B 1C 1的底面是正三角形，侧面BB 1C 1C 是矩形，M ，N 分别为BC ，B 1C 1的中点，P 为AM 上一点．过B 1C 1和P 的平面交AB 于E ，交AC 于F .(1)证明：AA 1∥MN ，且平面A 1AMN ⊥平面EB 1C 1F ；(2)设O 为△A 1B 1C 1的中心．若AO ＝AB ＝6，AO ∥平面EB 1C 1F ，且∠MPN ＝π3，求四棱锥B－EB 1C 1F 的体积．(1)证明因为侧面BB 1C 1C 是矩形，且M ，N 分别为BC ，B 1C 1的中点，所以MN ∥CC 1.又由已知得AA 1∥CC 1，故AA 1∥MN . 因为△A 1B 1C 1是正三角形，所以B 1C 1⊥A 1N . 又B 1C 1⊥MN ，故B 1C 1⊥平面A 1AMN . 所以平面A 1AMN ⊥平面EB 1C 1F .(2)解因为AO ∥平面EB 1C 1F ，AO ⊂平面A 1AMN ，平面A 1AMN ∩平面EB 1C 1F ＝PN ，所以AO ∥PN ，又AP ∥ON ，故四边形APNO 是平行四边形，所以PN ＝AO ＝6，AP ＝ON ＝13AM ＝3，PM ＝23AM ＝23，EF ＝13BC ＝2.因为BC ∥平面EB 1C 1F ，所以四棱锥B －EB 1C 1F 的顶点B 到底面EB 1C 1F 的距离等于点M 到底面EB 1C 1F 的距离．如图，作MT ⊥PN ，垂足为T ，则由(1)知，MT ⊥平面EB 1C 1F ，故MT ＝PM sin ∠MPN ＝3. 底面EB 1C 1F 的面积为12(B 1C 1＋EF )·PN ＝12×(6＋2)×6＝24. 所以四棱锥B －EB 1C 1F 的体积为13×24×3＝24.13.(2020·全国Ⅲ文，19)如图，在长方体ABCD －A 1B 1C 1D 1中，点E ，F 分别在棱DD 1，BB 1上，且2DE ＝ED 1，BF ＝2FB 1.证明：(1)当AB ＝BC 时，EF ⊥AC ； (2)点C 1在平面AEF 内．证明 (1)如图，连接BD ，B 1D 1. 因为AB ＝BC ，所以四边形ABCD 为正方形，故AC ⊥BD .又因为BB 1⊥平面ABCD ，AC ⊂平面ABCD ，于是AC ⊥BB 1.又BD ∩BB 1＝B ，BD ，BB 1⊂平面BB 1D 1D ，所以AC ⊥平面BB 1D 1D .又因为EF ⊂平面BB 1D 1D ，所以EF ⊥AC .(2)如图，在棱AA 1上取点G ，使得AG ＝2GA 1，连接GD 1，FC 1，FG ，因为ED 1＝23DD 1，AG ＝23AA 1，DD 1∥AA 1且DD 1＝AA 1，所以ED 1∥AG 且ED 1＝AG ，所以四边形ED 1GA 为平行四边形，故AE ∥GD 1.因为B 1F ＝13BB 1，GA 1＝13AA 1，BB 1∥AA 1且BB 1＝AA 1，所以B 1F ∥GA 1，且B 1F ＝GA 1，所以四边形B 1FGA 1是平行四边形，所以FG ∥A 1B 1且FG ＝A 1B 1，所以FG ∥C 1D 1且FG ＝C 1D 1，所以四边形FGD 1C 1为平行四边形，故GD 1∥FC 1. 所以AE ∥FC 1.所以A ，E ，F ，C 1四点共面，即点C 1在平面AEF 内．。

2020高考精品系列之数学(文)专题11 立体几何解答题(原卷版)

专题11立体几何解答题考纲解读三年高考分析1、对于线面关系中的存在性问题，首先假设存在，然后在该假设条件下，利用线面关系的相关定理、性质进行推理论证，寻找假设满足的条件，若满足则肯定假设，若得出矛盾的结论则否定假设．对于探索性问题用向量法比较容易入手．一般先假设存在，设出空间点的坐标，转化为代数方程是否有解的问题，若有解且满足题意则存在，若有解但不满足题意或无解则不存在．2、空间几何体体积问题的常见类型及解题策略(1)若所给定的几何体是可直接用公式求解的柱体、锥体或台体，则可直接利用公式进行求解．(2)若所给定的几何体的体积不能直接利用公式得出，则常用转换法、分割法、补形法等方法进行求解．(3)若以三视图的形式给出几何体，则应先根据三视图得到几何体的直观图，然后根据条件求解．3、空间几何体与球接、切问题的求解方法(1)求解球与棱柱、棱锥的接、切问题时，一般过球心及接、切点作截面，把空间问题转化为平面图形与圆的接、切问题，再利用平面几何知识寻找几何中元素间的关系求解．(2)若球面上四点P，A，B，C构成的三条线段P A，PB，PC两两互相垂直，且P A＝a，PB＝b，PC＝c，一般把有关元素“补形”成为一个球内接长方体，利用4R2＝a2＋b2＋c2求解．垂直关系的证明和平行关系的证明是考查的重点，解题时常用到平行判定定理、垂直判定定理、垂直性质定理、平行性质定理，考查学生的数学逻辑推理能力、数学运算能力、直观想象能力，题型以选择填空题和解答题为主，中等难度.1、直线、平面平行的判定及其性质是高考中的重点考查内容，涉及线线平行、线面平行、面面平行的判定及其应用等内容．题型主要以解答题的形式出现，解题要求有较强的推理论证能力，广泛应用转化与化归的思想.2、直线、平面垂直的判定及其性质是高考中的重点考查内容，涉及线线垂直、线面垂直、面面垂直的判定及其应用等内容．题型主要以解答题的形式出现，解题要求有较强的推理论证能力，广泛应用转化与化归的思想.1．【2019年天津文科17】如图，在四棱锥P﹣ABCD中，底面ABCD为平行四边形，△PCD为等边三角形，平面P AC⊥平面PCD，P A⊥CD，CD＝2，AD＝3．（Ⅰ）设G，H分别为PB，AC的中点，求证：GH∥平面P AD；（Ⅱ）求证：P A⊥平面PCD；（Ⅲ）求直线AD与平面P AC所成角的正弦值．2．【2019年新课标3文科19】图1是由矩形ADEB，Rt△ABC和菱形BFGC组成的一个平面图形，其中AB＝1，BE＝BF＝2，∠FBC＝60°．将其沿AB，BC折起使得BE与BF重合，连接DG，如图2．（1）证明：图2中的A，C，G，D四点共面，且平面ABC⊥平面BCGE；（2）求图2中的四边形ACGD的面积．3．【2019年新课标2文科17】如图，长方体ABCD﹣A1B1C1D1的底面ABCD是正方形，点E在棱AA1上，BE⊥EC1．（1）证明：BE⊥平面EB1C1；（2）若AE＝A1E，AB＝3，求四棱锥E﹣BB1C1C的体积．4．【2019年新课标1文科19】如图，直四棱柱ABCD﹣A1B1C1D1的底面是菱形，AA1＝4，AB＝2，∠BAD＝60°，E，M，N分别是BC，BB1，A1D的中点．（1）证明：MN∥平面C1DE；（2）求点C到平面C1DE的距离．5．【2019年北京文科18】如图，在四棱锥P﹣ABCD中，P A⊥平面ABCD，底面ABCD为菱形，E 为CD的中点．（Ⅰ）求证：BD⊥平面P AC；（Ⅱ）若∠ABC＝60°，求证：平面P AB⊥平面P AE；（Ⅲ）棱PB上是否存在点F，使得CF∥平面P AE？说明理由．6．【2018年新课标2文科19】如图，在三棱锥P﹣ABC中，AB＝BC＝2，P A＝PB＝PC＝AC＝4，O为AC的中点．（1）证明：PO⊥平面ABC；（2）若点M在棱BC上，且MC＝2MB，求点C到平面POM的距离．7．【2018年新课标1文科18】如图，在平行四边形ABCM中，AB＝AC＝3，∠ACM＝90°，以AC 为折痕将△ACM折起，使点M到达点D的位置，且AB⊥DA．（1）证明：平面ACD⊥平面ABC；（2）Q为线段AD上一点，P为线段BC上一点，且BP＝DQ DA，求三棱锥Q﹣ABP的体积．8．【2018年新课标3文科19】如图，矩形ABCD所在平面与半圆弧所在平面垂直，M是上异于C，D的点．（1）证明：平面AMD⊥平面BMC；（2）在线段AM上是否存在点P，使得MC∥平面PBD？说明理由．9．【2018年北京文科18】如图，在四棱锥P﹣ABCD中，底面ABCD为矩形，平面P AD⊥平面ABCD，P A⊥PD，P A＝PD，E，F分别为AD，PB的中点．（Ⅰ）求证：PE⊥BC；（Ⅱ）求证：平面P AB⊥平面PCD；（Ⅲ）求证：EF∥平面PCD．10．【2018年天津文科17】如图，在四面体ABCD中，△ABC是等边三角形，平面ABC⊥平面ABD，点M为棱AB的中点，AB＝2，AD＝2，∠BAD＝90°．（Ⅰ）求证：AD⊥BC；（Ⅱ）求异面直线BC与MD所成角的余弦值；（Ⅲ）求直线CD与平面ABD所成角的正弦值．11．【2017年新课标2文科18】如图，四棱锥P﹣ABCD中，侧面P AD为等边三角形且垂直于底面ABCD，AB＝BC AD，∠BAD＝∠ABC＝90°．（1）证明：直线BC∥平面P AD；（2）若△PCD面积为2，求四棱锥P﹣ABCD的体积．12．【2017年新课标1文科18】如图，在四棱锥P﹣ABCD中，AB∥CD，且∠BAP＝∠CDP＝90°．（1）证明：平面P AB⊥平面P AD；（2）若P A＝PD＝AB＝DC，∠APD＝90°，且四棱锥P﹣ABCD的体积为，求该四棱锥的侧面积．13．【2017年新课标3文科19】如图四面体ABCD中，△ABC是正三角形，AD＝CD．（1）证明：AC⊥BD；（2）已知△ACD是直角三角形，AB＝BD，若E为棱BD上与D不重合的点，且AE⊥EC，求四面体ABCE与四面体ACDE的体积比．14．【2017年北京文科18】如图，在三棱锥P﹣ABC中，P A⊥AB，P A⊥BC，AB⊥BC，P A＝AB＝BC ＝2，D为线段AC的中点，E为线段PC上一点．（1）求证：P A⊥BD；（2）求证：平面BDE⊥平面P AC；（3）当P A∥平面BDE时，求三棱锥E﹣BCD的体积．15．【2017年天津文科17】如图，在四棱锥P﹣ABCD中，AD⊥平面PDC，AD∥BC，PD⊥PB，AD ＝1，BC＝3，CD＝4，PD＝2．（Ⅰ）求异面直线AP与BC所成角的余弦值；（Ⅱ）求证：PD ⊥平面PBC ；（Ⅲ）求直线AB 与平面PBC 所成角的正弦值．1．【2019年湖南省娄底市高三上学期期末】如图1，在直角梯形ABCD 中，//AB CD ，AB BC ⊥，22AB CD BC ==，BD 为梯形对角线，将梯形中的ABD ∆部分沿AB 翻折至ABE 位置，使ABE∆所在平面与原梯形所在平面垂直（如图2）.（1）求证：平面AED ⊥平面BCE ；（2）探究线段EA 上是否存在点P ，使//EC 平面PBD ？若存在，求出EPEA；若不存在说明理由. 2．【四川省威远中学2020届高三上学期第一次月考】如图，AB 是圆O 的直径，点C 是圆O 上异于A ，B 的点，PO 垂直于圆O 所在的平面，且PO ＝OB ＝1.(1)若D 为线段AC 的中点，求证：AC ⊥平面PDO ； (2)求三棱锥P －ABC 体积的最大值； (3)若，点E 在线段PB 上，求CE ＋OE 的最小值．3．【2019年山西重点中学协作体高三暑假联考】如图，在等腰梯形ABCD 中，AB CD ∥，1AD DC CB ===，60ABC =︒，四边形ACFE 为矩形，平面ACFE ⊥平面ABCD ，1CF =.（1）求证：BC ⊥平面ACFE ；（2）求多面体ABCDEF 的体积.4．【2020年四川省雅安市雨城区雅安中学高三上学期开学摸底】如图，已知多面体ABCDEF 中，ABD ∆、ADE ∆均为正三角形，平面ADE ⊥平面ABCD ，AB CD EF P P ，::2:3:4AD EF CD =. （Ⅰ）求证：BD ⊥平面BFC ；（Ⅱ）若2AD =，求该多面体的体积.5．【安徽省合肥一中、安庆一中等六校教育研究会2020届高三上学期第一次素质测试】如图所示，三棱柱111ABC A B C -中，侧面11BB C C 为菱形，160,CBB A ∠=o在侧面11BB C C 上的投影恰为1B C 的中点O ．（1）证明：1B C AB ⊥；（2）若1ACAB ⊥，且三棱柱111ABC A B C -的体积为38，求三棱柱111ABC A B C -的高.6．【湖南省衡阳市第八中学2020届高三上学期月考（二)】如图，在五面体ABCDFE 中，侧面ABCD 是正方形，ABE ∆是等腰直角三角形，点O 是正方形ABCD 对角线的交点EA EB =，26AD EF ==且//EF AD .（1）证明：//OF 平面ABE ；（2）若侧面ABCD 与底面ABE 垂直，求五面体ABCDFE 的体积.7．【江西省南昌市2020届高三上学期开学摸底考试】如图，已知直三棱柱111ABC A B C -中，AB AC ⊥，12AB AC AA ===，E 是BC 的中点，F 是1A E 上一点，且12A F FE =.（Ⅰ）证明：AF⊥平面1A BC ；（Ⅱ）求三棱锥11C A FC -的体积．8．【2020年安徽省江淮十校高三第一次联考】如图，在四棱锥S ABCD -中，底面ABCD 是正方形，SA ⊥底面ABCD ，2SA AB ==，AE SC ⊥，垂足为E ，点A 在面SDC 上的投影为F 。

高考数学复习总结专题05 立体几何(选择题、填空题) (解析版)

立体几何（选择题、填空题）1.【2020年高考全国Ⅰ卷理数】埃及胡夫金字塔是古代世界建筑奇迹之一，它的形状可视为一个正四棱锥，以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积，则其侧面三角形底边上的高与底面正方形的边长的比值为（）515 1 5 1 5 1A. B. C. D.4 2 4 2【答案】C【解析】【分析】1设C D a,PE b，利用P O2 CD PE 得到关于a,b的方程，解方程即可得到答案.22a【详解】如图，设C D a,PE b，则P O PE 2 2 2 ，OE b41 a2 1 b b由题意P O2 ab，即b 2 ab，化简得4() 2 210，2 4 2 a ab1 5解得（负值舍去）.a 4故选：C.【点晴】本题主要考查正四棱锥的概念及其有关计算，考查学生的数学计算能力，是一道容易题.2.【2020年高考全国I I卷理数】如图是一个多面体的三视图，这个多面体某条棱的一个端点在正视图中对应的点为M ，在俯视图中对应的点为N ，则该端点在侧视图中对应的点为（）A. EB. FC.GD.H【答案】A【解析】【分析】根据三视图，画出多面体立体图形，即可求得M 点在侧视图中对应的点.【详解】根据三视图，画出多面体立体图形，D D B C上的点在俯视图中对应的点为N,3 4上的点在正视图中都对应点M,直线1 4∴在正视图中对应M ,在俯视图中对应N 的点是D4,线段D D,上的所有点在侧试图中都对应E ,∴点3 4D4在侧视图中对应的点为E .故选：A【点睛】本题主要考查了根据三视图判断点的位置，解题关键是掌握三视图的基础知识和根据三视图能还原立体图形的方法，考查了分析能力和空间想象，属于基础题.A, B,C 为球O 的球面上的三个点，⊙O为 A B C的外接圆，若⊙O3. 【2020 年高考全国Ⅰ卷理数】已知11的面积为 4π ， AB BC AC OO ，则球O的表面积为（）1A. 64πB. 48πC. 36πD. 32π【答案】A 【解析】【分析】由已知可得等边 AB C 的外接圆半径，进而求出其边长，得出O O的值，根据球的截面性质，求出球的半 1径，即可得出结论. 【详解】设圆O半径为，球的半径为 R ，依题意， r 14,r 2 ， A B C为等边三角形，得r2由正弦定理可得 AB 2rsin 60 2 3 ，O O AB 2 3 ，根据球的截面性质O O 平面 ABC ， 11 O O O A ,R OA O O2 O A 2 OO 1 2 r 4 ， 21 1 1 1 O 球2 的表面积 S 4R 64 .故选：A【点睛】本题考查球的表面积，应用球的截面性质是解题的关键，考查计算求解能力，属于基础题. 4. 【2020 年高考全国Ⅲ理数】下图为某几何体的三视图，则该几何体的的表面积是（）A.6+4 2B.4+4 2C.6+2 3D.4+2 3【答案】C【解析】【分析】根据三视图特征，在正方体中截取出符合题意的立体图形，求出每个面的面积，即可求得其表面积.【详解】根据三视图特征，在正方体中截取出符合题意的立体图形1根据立体图形可得：S△ABC S△AD C S△C DB 22 22根据勾股定理可得：AB A D DB 2 2△A DB是边长为22的等边三角形根据三角形面积公式可得：1 1 3S △A D B AB AD s in60(22) 2 2 32 2 2该几何体的表面积是：3223623.故选：C.【点睛】本题主要考查了根据三视图求立体图形的表面积问题，解题关键是掌握根据三视图画出立体图形，考查了分析能力和空间想象能力，属于基础题. 5. 【2020 年高考全国 I I 卷理数】已知△ABC 是面积为若球 O 的表面积为 16π，则 O 到平面 ABC 的距离为（ 3 9 34的等边三角形，且其顶点都在球 O 的球面上. ）3 A. 3 B.C. 1D.22【答案】C 【解析】【分析】根据球O 的表面积和 ABC 的面积可求得球O 的半径 R 和 AB C 外接圆半径，由球的性质可知所求距r 离 2 2 .d R r 【详解】设球O 的半径为 R ，则 4 R 16 ，解得： R 2 . 2 设 AB C 外接圆半径为，边长为 a，r 9 3ABC是面积为的等边三角形， 41 3 9 32 a 22 9 a 2 ，解得： a 3，r a 2 93 ， 2 24 3 4 3 4球心 O 到平面 ABC 2 2 的距离d R r 43 1.故选：C.【点睛】本题考查球的相关问题的求解，涉及到球的表面积公式和三角形面积公式的应用；解题关键是明确球的性质，即球心和三角形外接圆圆心的连线必垂直于三角形所在平面.6. 【2019 年高考全国Ⅰ卷理数】已知三棱锥 P −AB C 的四个顶点在球 O 的球面上，PA=PB=P C ，△ABC 是边长为 2 的正三角形，E ，F 分别是 PA ，AB 的中点，∠CEF =90°，则球 O 的体积为A ．8 6B ． 4 6 D ． 6C ． 2 6 【答案】D【解析】解法一： PA P B PC, ABC 为边长为 2 的等边三角形，P ABC为正三棱锥，△ PB AC ，又 E ， F 分别为 PA ， AB 的中点，EF ∥PB ，EF AC ，又 EF CE ，C E AC C,EF 平面 PAC ，∴ PB 平面 PAC ，APB PA PB PC 2 ，P ABC 为正方体的一部分， 2R 2 2 2 6 ，即6 4 4 6 68 R, V R 3 π 6，故选 D ． P A, AB 2 3 3解法二：设 PA PB PC 2x ，E, F 分别为的中点， 1EF ∥PB ，且 EF PB x ，△ABC 为边长为 2 的等边三角形，C F 3 ，21 又 CEF 90，CE 3 x 2, AE PA x ， 2 x 243 x 22 x2△AEC 中，由余弦定理可得 cos EAC作 PD AC 于 D ，，A D 1 x 2 4 3 x 4x 21PA PC \ D AC cos EAC ，，为的中点，，PA 2x 2x1 2 2x 2 1 2，x 2，x ，PA PB PC 2 ，2 2又 AB=B C=A C=2 ， PA , PB , PC 两两垂直，6 2R 2 2 2 6 ，R，24 4 6 68 V R 3 6 ，故选 D. 3 3【名师点睛】本题主要考查学生的空间想象能力，补体法解决外接球问题．可通过线面垂直定理，得到三棱两两互相垂直关系，快速得到侧棱长，进而补体成正方体解决．7. 【2019 年高考全国Ⅱ卷理数】设α，β为两个平面，则α∥β的充要条件是 A ．α内有无数条直线与β平行 C ．α，β平行于同一条直线【答案】BB ．α内有两条相交直线与β平行 D ．α，β垂直于同一平面【解析】由面面平行的判定定理知：内两条相交直线都与平行是∥的充分条件，由面面平行性质定理知，若∥，则必要条件，故选 B ．内任意一条直线都与平行，所以平行是∥内两条相交直线都与的【名师点睛】本题考查了空间两个平面的判定与性质及充要条件，渗透直观想象、逻辑推理素养，利用面面平行的判定定理与性质定理即可作出判断．面面平行的判定问题要紧扣面面平行判定定理，最容易犯的错误为定理记不住，凭主观臆断，如：“若 a ,b ,a b ，则 ∥ ∥”此类的错误．8. 【2019 年高考全国Ⅲ卷理数】如图，点 N 为正方形 AB C D 的中心，△EC D 为正三角形，平面 EC D ⊥平面 ABC D ，M 是线段 E D 的中点，则A ．B M =E N ，且直线 B M ，EN 是相交直线 B ．B M ≠EN ，且直线 B M ，E N 是相交直线C ．B M =E N ，且直线 B M ，E N 是异面直线D ．B M ≠EN ，且直线 B M ，EN 是异面直线【答案】B【解析】如图所示，作 EO C D 于O ，连接O N ，B D ，易得直线 B M ，E N 是三角形 EB D 的中线，是相交直线.过 M 作 MF OD 于 F ，连接 BF ，AB C D ，E O C D, E O 平面C DE ，EO平面C D E 平面平面 ABC D ， M F 平面 AB C D ，△MFB 与△EO N 均为直角三角形．设正方形边长为 2 ，易知 E O 3,ON 1,EN 2 ，3 5M F,BF ,BM 7 ，B M EN ，故选 B ．2 2【名师点睛】本题考查空间想象能力和计算能力，解答本题的关键是构造直角三角形.解答本题时，先利用垂直关系，再结合勾股定理进而解决问题．9. 【2018 年高考全国Ⅰ卷理数】某圆柱的高为 2，底面周长为 16，其三视图如图．圆柱表面上的点 M 在正视图上的对应点为 A ，圆柱表面上的点 N 在左视图上的对应点为 B ，则在此圆柱侧面上，从 M 到 N 的路径中，最短路径的长度为A ． 2 17B ． 2 5 D ．2C ．3 【答案】B【解析】根据圆柱的三视图以及其本身的特征，知点 M 在上底面上，点 N 在下底面上，且可以确定点 M 和点 N 分别在以圆柱的高为长方形的宽，圆柱底面圆周长的四分之一为长的长方形的对角线的端点处，所以所求的最短路径的长度为，故选 B ．【名师点睛】该题考查的是有关几何体的表面上两点之间的最短距离的求解问题，在解题的过程中，需要明确两个点在几何体上所处的位置，再利用平面上两点间直线段最短，所以处理方法就是将面切开平铺，利用平面图形的相关特征求得结果.10. 【2018 年高考全国Ⅰ卷理数】已知正方体的棱长为 1，每条棱所在直线与平面所成的角都相等，则截此正方体所得截面面积的最大值为3 342 3 3 A ．C ．B ．D ．3 2 43 2【答案】A【解析】根据相互平行的直线与平面所成的角是相等的，AB C D A B C D 中，1所以在正方体 1 1 1AB D AA , A B , A D 所成的角是相等的，11 11 1平面与线 1 1AB D 所以平面与正方体的每条棱所在的直线所成角都是相等的，11 C BD 1同理，平面也满足与正方体的每条棱所在的直线所成角都是相等的，AB D C BD要求截面面积最大，则截面的位置为夹在两个面与1中间，且过棱的中点的正六边形，且1 12边长为，223 2 3 34所以其面积为S 6，故选A.4 2【名师点睛】该题考查的是有关平面被正方体所截得的截面多边形的面积问题，首要任务是需要先确定截面的位置，之后需要从题的条件中找寻相关的字眼，从而得到其为过六条棱的中点的正六边形，利用六边形的面积的求法，应用相关的公式求得结果.即首先利用正方体的棱是3组每组有互相平行的4条棱，所以与12条棱所成角相等，只需与从同一个顶点出发的三条棱所成角相等即可，从而判断出面的位置，截正方体所得的截面为一个正六边形，且边长是面的对角线的一半，应用面积公式求得结果.11.【2018年高考全国Ⅲ卷理数】中国古建筑借助榫卯将木构件连接起来，构件的凸出部分叫榫头，凹进部分叫卯眼，图中木构件右边的小长方体是榫头．若如图摆放的木构件与某一带卯眼的木构件咬合成长方体，则咬合时带卯眼的木构件的俯视图可以是【答案】A【解析】本题主要考查空间几何体的三视图.由题意知，俯视图中应有一不可见的长方形，且俯视图应为对称图形.故选A．12.【2018年高考全国Ⅲ卷理数】设A ，，，是同一个半径为的球的球面上四点，△A B C 为等边三B C D 4角形且其面积为A．12 3，则三棱锥D ABC 体积的最大值为9 3B．18 3D．54 3C．24 3【答案】B【解析】如图所示，设点 M 为三角形 ABC 的重心，E 为 AC 中点，当点 D 在平面 ABC 上的射影为 M 时，三棱锥 D ABC 的体积最大，此时，O D OB R 4，3 S △AB CAB 9 3 ，AB 6 ,点 M 为三角形 ABC 的重心，2 4 2B M BE 2 3 ，3 Rt △OB M 中，有O M OB 2 2 2，D M O D O M 4 2 6，B M1V DABCm ax9 36 18 3 ，故选 B. 3【名师点睛】本题主要考查三棱锥的外接球，考查了勾股定理，三角形的面积公式和三棱锥的体积公式，判断出当点 D 在平面 ABC 上的射影为三角形 AB C 的重心时，三棱锥 DABC 体积最大很关键，2由 M 为三角形 ABC 的重心，计算得到 B M BE 2 3 ，再由勾股定理得到 O M ，进而得到结果， 3属于较难题型.13. 【2018 年高考全国Ⅱ卷理数】在长方体 AB C D A B C D 中，AB BC 1，AA 3 ，则异面直线 A D 与 1 1 1 1 11 D B 所成角的余弦值为1 1 A ．5 5 B ． D ．6 5 2 C ．52【答案】C【解析】方法一：用一个与原长方体相同的长方体拼到原长方体的前面，B P ∥A D D B DP= 5B P 2，，则11如图，则 1，连接 DP ，易求得 1 DB P A D DB与所成的角，11是异面直线1 D B2 1 B P 2 DP 25 4 5 5 由余弦定理可得cos DB P 1. 12DB PB 4 5 5 1 1故选 C.方法二：以 D 为坐标原点，DA,D C,D D 所在直线分别为 x ,y ,z 轴建立空间直角坐标系， 1D 0, 0, 0, A 1, 0, 0,B 1, 1, 3,D 0, 0, 3A D1, 0, 3 ,DB 1, 1, 3 ,则 ,所以 1 1 1 1cos AD , DB A D DB A D DB 1 3 2 5 5 1 1因为， 1 15 1 15 A D DB 所以异面直线与所成角的余弦值为 1，故选 C. 15【名师点睛】先建立空间直角坐标系，设立各点坐标，利用向量数量积求向量夹角，再根据向量夹角与线线角相等或互补关系求结果.利用法向量求解空间线面角的关键在于“四破”：第一，破“建系关”，构建恰当的空间直角坐标系；第二，破“求坐标关”，准确求解相关点的坐标；第三，破“求法向量关”，求出直线的方向向量或平面的法向量；第四，破“应用公式关”. ABC A B C 中， ABC 120 BC CC 1，AB 2 ，，113. 【2017 年高考全国Ⅱ卷理数】已知直三棱柱1 1 1 AB BC 所成角的余弦值为1则异面直线与 13 15 5 A ．B ．D ．2 103 C ． 53【答案】CAB C D A B C D ，1【解析】如图所示，补成直四棱柱 1 1 1则所求角为 BC D,BC 2, BD 2 21 221cos 60 3,C D AB 5 ，11 1 1 BC12 5105 易得 C D 12 BD 2BC 12 ，因此cos BC D，故选 C ． 1C D1【名师点睛】平移法是求异面直线所成角的常用方法，其基本思路是通过平移直线，把异面问题化归为共面问题来解决，具体步骤如下：①平移：平移异面直线中的一条或两条，作出异面直线所成的角； ②认定：证明作出的角就是所求异面直线所成的角； ③计算：求该角的值，常利用解三角形；④取舍：由异面直线所成的角的取值范围是(0,]，当所作的角为钝角时，应取它的补角作为两条异面2直线所成的角．求异面直线所成的角要特别注意异面直线之间所成角的范围．14.【2017年高考全国Ⅰ卷理数】某多面体的三视图如图所示，其中正视图和左视图都由正方形和等腰直角三角形组成，正方形的边长为2，俯视图为等腰直角三角形.该多面体的各个面中有若干个是梯形，这些梯形的面积之和为A．10 B．12D．16C．14【答案】B【解析】由题意该几何体的直观图是由一个三棱锥和三棱柱构成，如下图，则该几何体各面内只有两个相同的梯形，则这些梯形的面积之和为12(24)212，故选．B2【名师点睛】三视图往往与几何体的体积、表面积以及空间线面关系、角、距离等问题相结合，解决此类问题的关键是由三视图准确确定空间几何体的形状及其结构特征并且熟悉常见几何体的三视图.15.【2017年高考全国Ⅱ卷理数】如图，网格纸上小正方形的边长为1，粗实线画出的是某几何体的三视图，该几何体由一平面将一圆柱截去一部分后所得，则该几何体的体积为A．90 C．42B．63 D．36【答案】B【解析】由题意，该几何体是一个组合体，下半部分是一个底面半径为3，高为4的圆柱，其体积V 32 436，上半部分是一个底面半径为，高为的圆柱的一半，其体积3 611 V (3 26) 27，故该组合体的体积V V V36 27 63．21 2 2故选 B ．【名师点睛】在由三视图还原为空间几何体的实际形状时，要从三个视图综合考虑，根据三视图的规则，空间几何体的可见轮廓线在三视图中为实线，不可见轮廓线在三视图中为虚线．在还原空间几何体实际形状时，一般是以正视图和俯视图为主，结合侧视图进行综合考虑．求解以三视图为载体的空间几何体的体积的关键是由三视图确定直观图的形状以及直观图中线面的位置关系和数量关系，利用相应体积公式求解．16. 【2017 年高考全国Ⅲ卷理数】已知圆柱的高为 1，它的两个底面的圆周在直径为 2 的同一个球的球面上，则该圆柱的体积为3π π A ．C ．B ．D ．4 π π24【答案】B【解析】绘制圆柱的轴截面如图所示：21 1 3 由题意可得： AC 1, AB ，结合勾股定理，底面半径 r 1 2，2 2 223 3由圆柱的体积公式，可得圆柱的体积是V πr 2h π 1 π ，故选 B.2 4【名师点睛】（1）求解空间几何体体积的关键是确定几何体的元素以及线面的位置关系和数量关系，利用相应体积公式求解；（2）若所给几何体的体积不能直接利用公式得出，则常用等积法、分割法、补形法等方法进行求解.17. 【2020 年高考全国 I I 卷理数】设有下列四个命题： p ：两两相交且不过同一点的三条直线必在同一平面内.1p ：过空间中任意三点有且仅有一个平面.2p ：若空间两条直线不相交，则这两条直线平行.3p ：若直线 l 平面α，直线 m ⊥平面α，则 m ⊥l . 4则下述命题中所有真命题的序号是__________.p p p p p ppp③④122334① ② 1 4【答案】①③④【解析】【分析】p p2利用两交线直线确定一个平面可判断命题的真假；利用三点共线可判断命题的真假；利用异面直线可1p p4判断命题的真假，利用线面垂直的定义可判断命题的真假.再利用复合命题的真假可得出结论.3p1l1l2【详解】对于命题，可设与相交，这两条直线确定的平面为；l l若与相交，则交点A 在平面内，3 1l l同理，与的交点B 也在平面内，3 2所以，AB ，即l3，命题为真命题；p1p2对于命题，若三点共线，则过这三个点的平面有无数个，p命题为假命题；2p对于命题，空间中两条直线相交、平行或异面，3p命题为假命题；3p4，若直线m 平面，对于命题m 垂直于平面则内所有直线，直线l 平面，直线m 直线，lp命题为真命题.4综上可知，，为真命题，，为假命题，p p p p为假命题，1 2为真命题，1 4p p p p为真命题.3 4为真命题，2 3故答案为：①③④.【点睛】本题考查复合命题的真假，同时也考查了空间中线面关系有关命题真假的判断，考查推理能力，属于中等题.18. 【2020 年高考全国Ⅲ理数】已知圆锥的底面半径为 1，母线长为 3，则该圆锥内半径最大的球的体积为_________． 2 【答案】 3【解析】【分析】将原问题转化为求解圆锥内切球的问题，然后结合截面确定其半径即可确定体积的值. 【详解】易知半径最大球为圆锥的内切球，球与圆锥内切时的轴截面如图所示，B C 2, AB AC 3 其中，且点 M 为 BC 边上的中点，设内切圆的圆心为O ，1由于A M 3 2 1 22 2 ，故 S △ABC2 2 2 2 2 ， 2r设内切圆半径为，则：1 1 1 S △AB C S △A O B S △BO C S △A O C AB r BC r AC r2 2 21 3 3 2r2 2 ，22 4 2解得： r =，其体积：V r 3 . 2 3 32故答案为：. 3【点睛】与球有关的组合体问题，一种是内切，一种是外接．解题时要认真分析图形，明确切点和接点的位置，确定有关元素间的数量关系，并作出合适的截面图，如球内切于正方体，切点为正方体各个面的中心，正方体的棱长等于球的直径；球外接于正方体，正方体的顶点均在球面上，正方体的体对角线长等于球的直径.19. 【2019 年高考全国Ⅲ卷理数】学生到工厂劳动实践，利用 3D 打印技术制作模型.如图，该模型为长方体AB C D A B C D 挖去四棱锥 O —EF G H 后所得的几何体，其中 O 为长方体的中心，E ，F ，G ，H 分11 1 1AB = BC = 6 cm, AA = 4 cm 别为所在棱的中点，，3D 打印所用原料密度为 0.9 g/cm 3，不考虑打印 1损耗，制作该模型所需原料的质量为___________g .【答案】118.81【解析】由题意得， S 46 4 23 12cm 2 ，四边形EF G H2 1∵四棱锥 O −EF G H 的高为 3cm ， ∴V O EF G H 123 12cm 3 ．3AB C D A B C D V 466 144cm，3又长方体的体积为 1 1 1 1 2 所以该模型体积为 VV V144 12 132cm 3 ，其质量为 0.9132 118.8g ．OEF G H2 【名师点睛】本题考查几何体的体积问题，理解题中信息联系几何体的体积和质量关系，从而利用公式求解．根据题意可知模型的体积为长方体体积与四棱锥体积之差进而求得模型的体积，再求出模型的质量即可.20. 【2019 年高考全国Ⅱ卷理数】中国有悠久的金石文化，印信是金石文化的代表之一．印信的形状多为长方体、正方体或圆柱体，但南北朝时期的官员独孤信的印信形状是“半正多面体”（图 1）.半正多面体是由两种或两种以上的正多边形围成的多面体．半正多面体体现了数学的对称美．图 2 是一个棱数为 48 的半正多面体，它的所有顶点都在同一个正方体的表面上，且此正方体的棱长为 1．则该半正多面体共有________个面，其棱长为_________．（本题第一空 2 分，第二空 3 分．）【答案】26，21【解析】由图可知第一层（包括上底面）与第三层（包括下底面）各有9个面，计18个面，第二层共有8个面，所以该半正多面体共有18826个面．x如图，设该半正多面体的棱长为，则AB BE x，延长CB与FE 的延长线交于点G，延长BC交正方体的棱于H ，由半正多面体对称性可知，△BG E 为等腰直角三角形，2 2BG GE C H x,G H 2x x(21)x1，2 21x21，21即该半正多面体的棱长为21．【名师点睛】本题立意新颖，空间想象能力要求高，物体位置还原是关键，遇到新题别慌乱，题目其实很简单，稳中求胜是关键．立体几何平面化，无论多难都不怕，强大空间想象能力，快速还原图形．721.【2018年高考全国I I卷理数】已知圆锥的顶点为S，母线SA，SB 所成角的余弦值为，SA与圆锥8 底面所成角为45°，若△SAB 的面积为515，则该圆锥的侧面积为__________．【答案】402π7 15 8【解析】因为母线 SA ， SB 所成角的余弦值为，所以母线 SA ， SB 所成角的正弦值为，因为 81 15 8 △SAB 的面积为5 15 ，设母线长为l ,所以l 2 25 15 ,l80 ， 2π 2因为 SA 与圆锥底面所成角为 45°，所以底面半径为 r l cosl , 4 22 因此圆锥的侧面积为 πr lπl 40 2π. 22【名师点睛】本题考查线面角、圆锥的侧面积、三角形面积等知识点，考查学生空间想象与运算能力. 先根据三角形面积公式求出母线长，再根据母线与底面所成角得底面半径，最后根据圆锥侧面积公式求结果.22. 【2017 年高考全国 I 卷理数】如图，圆形纸片的圆心为 O ，半径为 5 c m ，该纸片上的等边三角形 ABC 的中心为 O.D ，E ，F 为圆 O 上的点，△DB C ，△ECA ，△FA B 分别是以 BC ，CA ，AB 为底边的等腰三角形.沿虚线剪开后，分别以 BC ，CA ，AB 为折痕折起△DB C ，△ECA ，△FAB ，使得 D ，E ，F 重合，得到三棱锥.当△ABC 的边长变化时，所得三棱锥体积（单位：cm 3）的最大值为【答案】 4 15.【解析】如下图，连接 DO 交 BC 于点 G ，设 D ，E ，F 重合于 S 点，正三角形的边长为 x(x>0)，则 1 3 3O G x x. 3 2 63FG SG 5x ， 6223 3x3x， SO h SG2GO2 5 x 556 631 1 3 3 15 3 三棱锥的体积V S △ABC h x2 5 5 x 4 x 5 . 5x3 34 3 1233 5 3 设 n x 5x 4x 5 ，x>0，则 n x 20x 3 x 4， 3 3x 4 n x 0 ，即 4x 30，得，易知 n x 在令处取得最大值. x 4 3x 4 3 3 15∴V max 48 5 4 4 15 .12【名师点睛】对于三棱锥最值问题，需要用到函数思想进行解决，本题解决的关键是设好未知量，利用图形特征表示出三棱锥体积.当体积中的变量最高次是2次时可以利用二次函数的性质进行解决，当变量是高次时需要用到求导的方式进行解决.。

2020高考数学冲刺核心考点专题3 第2讲立体几何(大题)(学生试题训练)

第2讲立体几何(大题)热点一平行、垂直关系的证明用向量知识证明立体几何问题，仍然离不开立体几何中的定理.如要证明线面平行，只需要证明平面外的一条直线和平面内的一条直线平行，即化归为证明线线平行，用向量方法证明直线a∥b，只需证明向量a＝λb(λ∈R)即可.若用直线的方向向量与平面的法向量垂直来证明线面平行，仍需强调直线在平面外.例1如图，在直三棱柱ADE－BCF中，平面ABFE和平面ABCD都是正方形且互相垂直，点M为AB的中点，点O为DF的中点.运用向量方法证明：(1)OM∥平面BCF；(2)平面MDF⊥平面EFCD.跟踪演练1如图，在四棱锥P－ABCD中，P A⊥底面ABCD，AD∥BC，AD⊥CD，BC＝2，AD＝CD＝1，M是PB的中点.(1)求证：AM∥平面PCD；(2)求证：平面ACM⊥平面P AB.热点二利用空间向量求空间角设直线l ，m 的方向向量分别为a ＝(a 1，b 1，c 1)，b ＝(a 2，b 2，c 2).平面α，β的法向量分别为μ＝(a 3，b 3，c 3)，v ＝(a 4，b 4，c 4)(以下相同). (1)线线夹角设l ，m 的夹角为θ⎝⎛⎭⎫0≤θ≤π2，则cos θ＝|a ·b ||a ||b |＝|a 1a 2＋b 1b 2＋c 1c 2|a 21＋b 21＋c 21 a 22＋b 22＋c 22. (2)线面夹角设直线l 与平面α的夹角为θ⎝⎛⎭⎫0≤θ≤π2，则sin θ＝|a ·μ||a ||μ|＝|cos 〈a ，μ〉|. (3)二面角设α－a －β的平面角为θ(0≤θ≤π)，则|cos θ|＝|μ·v ||μ||v |＝|cos 〈μ，v 〉|. 例2 (2019·南昌模拟)如图，四棱台ABCD －A 1B 1C 1D 1中，底面ABCD 是菱形，CC 1⊥底面ABCD ，且∠BAD ＝60°，CD ＝CC 1＝2C 1D 1＝4，E 是棱BB 1的中点.跟踪演练2(2019·河南名校联盟联考)如图，在四棱锥P－ABCD中，∠P AB＝90°，AB∥CD，且PB＝BC＝BD＝6，CD＝2AB＝22，∠P AD＝120°.E和F分别是棱CD和PC的中点.(1)求证：CD⊥BF；(2)求直线PB与平面PCD所成的角的正弦值.热点三利用空间向量解决探索性问题与空间向量有关的探究性问题主要有两类：一类是探究线面的位置关系；另一类是探究线面角或二面角满足特定要求时的存在性问题.处理原则是：先建立空间直角坐标系，引入参数(有些是题中已给出)，设出关键点的坐标，然后探究这样的点是否存在，或参数是否满足要求，从而作出判断.例3(2019·临沂模拟)如图，平面ABCD⊥平面ABE，四边形ABCD是边长为2的正方形，AE＝1，F为CE上的点，且BF⊥平面ACE.(1)求证：AE⊥平面BCE；(2)线段AD上是否存在一点M，使平面ABE与平面MCE所成二面角的余弦值为34？若存在，试确定点M的位置；若不存在，请说明理由.跟踪演练3 如图，在直三棱柱ABC －A 1B 1C 1中，AC ⊥BC ，AC ＝BC ＝AA 1＝2，点P 为棱B 1C 1的中点，点Q 为线段A 1B 上一动点.(1)求证：当点Q 为线段A 1B 的中点时，PQ ⊥平面A 1BC ；(2)设BQ →＝λBA 1→，试问：是否存在实数λ，使得平面A 1PQ 与平面B 1PQ 所成锐二面角的余弦值为3010？若存在，求出这个实数λ；若不存在，请说明理由.真题体验(2019·全国Ⅰ，理，18)如图，直四棱柱ABCD－A1B1C1D1的底面是菱形，AA1＝4，AB＝2，∠BAD＝60°，E，M，N分别是BC，BB1，A1D的中点.(1)证明：MN∥平面C1DE；(2)求二面角A－MA1－N的正弦值.押题预测如图1，在梯形ABCD中，AB∥CD，过A，B分别作AE⊥CD，BF⊥CD，垂足分别E，F，AB＝AE＝2，CD＝5，已知DE＝1，将梯形ABCD沿AE，BF同侧折起，得空间几何体ADE －BCF，如图2.(1)若AF⊥BD，证明：DE⊥平面ABFE；(2)若DE∥CF，CD＝3，线段AB上存在一点P，满足CP与平面ACD所成角的正弦值为5 20，求AP的长.A组专题通关1.(2019·全国Ⅱ)如图，长方体ABCD－A1B1C1D1的底面ABCD是正方形，点E在棱AA1上，BE⊥EC1.(1)证明：BE⊥平面EB1C1；(2)若AE＝A1E，求二面角B－EC－C1的正弦值.2.(2019·全国Ⅲ)图1是由矩形ADEB，Rt△ABC和菱形BFGC组成的一个平面图形，其中AB ＝1，BE＝BF＝2，∠FBC＝60°.将其沿AB，BC折起使得BE与BF重合，连接DG，如图2.(1)证明：图2中的A，C，G，D四点共面，且平面ABC⊥平面BCGE；(2)求图2中的二面角B—CG—A的大小.3.(2019·马鞍山模拟)如图，在三棱柱ABC－A1B1C1中，∠ACB＝90°，A1B⊥AC1，AC＝AA1＝4，BC＝2.(1)求证：平面A1ACC1⊥平面ABC；(2)若∠A1AC＝60°，在线段AC上是否存在一点P，使二面角B－A1P－C的平面角的余弦值为34？若存在，确定点P的位置；若不存在，请说明理由.B组能力提高4.如图所示，在四棱锥P－ABCD中，P A＝PD＝AD＝2CD＝2BC＝2，且∠ADC＝∠BCD＝90°.(1)当PB ＝2时，证明：平面P AD ⊥平面ABCD ；(2)当四棱锥P －ABCD 的体积为34，且二面角P －AD －B 为钝角时，求直线P A 与平面PCD所成角的正弦值.5.如图，已知圆锥OO 1和圆柱O 1O 2的组合体(它们的底面重合)，圆锥的底面圆O 1的半径为r ＝5，OA 为圆锥的母线，AB 为圆柱O 1O 2的母线，D ，E 为下底面圆O 2上的两点，且DE ＝6，AB ＝6.4，AO ＝52，AO ⊥AD .(1)求证：平面ABD⊥平面ODE;(2)求二面角B－AD－O的正弦值.数学核心素养练习一、数学抽象、直观想象素养1 数学抽象例1 (2019·全国Ⅱ)设函数f (x )的定义域为R ，满足f (x ＋1)＝2f (x )，且当x ∈(0,1]时，f (x )＝x (x －1).若对任意x ∈(－∞，m ]，都有f (x )≥－89，则m 的取值范围是( )A.⎝⎛⎦⎤－∞，94 B.⎝⎛⎦⎤－∞，73 C.⎝⎛⎦⎤－∞，52 D.⎝⎛⎦⎤－∞，831.如图表示的是一位骑自行车和一位骑摩托车的旅行者在相距80 km的甲、乙两城间从甲城到乙城所行驶的路程与时间之间的函数关系，有人根据函数图象，提出了关于这两个旅行者的如下信息：①骑自行车者比骑摩托车者早出发3 h，晚到1 h；②骑自行车者是变速运动，骑摩托车者是匀速运动；③骑摩托车者在出发1.5 h后追上了骑自行车者；④骑摩托车者在出发1.5 h后与骑自行车者速度一样.其中，正确信息的序号是________.素养2直观想象例2(2019·全国Ⅲ)如图，点N为正方形ABCD的中心，△ECD为正三角形，平面ECD⊥平面ABCD，M是线段ED的中点，则()A.BM＝EN，且直线BM，EN是相交直线B.BM≠EN，且直线BM，EN是相交直线C.BM＝EN，且直线BM，EN是异面直线D.BM≠EN，且直线BM，EN是异面直线2.(2018·北京)某四棱锥的三视图如图所示，在此四棱锥的侧面中，直角三角形的个数为()A.1B.2C.3D.4二、逻辑推理、数学运算素养3逻辑推理例3(2019·全国Ⅱ)在“一带一路”知识测验后，甲、乙、丙三人对成绩进行预测.甲：我的成绩比乙高.乙：丙的成绩比我和甲的都高.丙：我的成绩比乙高.成绩公布后，三人成绩互不相同且只有一个人预测正确，那么三人按成绩由高到低的次序为()A.甲、乙、丙B.乙、甲、丙C.丙、乙、甲D.甲、丙、乙3.(2018·全国Ⅰ)已知双曲线C ：x 23－y 2＝1，O 为坐标原点，F 为C 的右焦点，过F 的直线与C 的两条渐近线的交点分别为M ，N .若△OMN 为直角三角形，则|MN |等于( ) A.32B.3C.2 3D.4 素养4 数学运算例4 (2019·全国Ⅰ)已知非零向量a ，b 满足|a |＝2|b |，且(a －b )⊥b ，则a 与b 的夹角为( ) A.π6 B.π3 C.2π3 D.5π64.(2018·全国Ⅲ)设a＝log0.20.3，b＝log20.3，则()A.a＋b<ab<0B.ab<a＋b<0C.a＋b<0<abD.ab<0<a＋b三、数学建模、数据分析素养5数学建模例5(2019·全国Ⅰ)古希腊时期，人们认为最美人体的头顶至肚脐的长度与肚脐至足底的长度之比是5－12⎝⎛⎭⎪⎫5－12≈0.618，称为黄金分割比例，著名的“断臂维纳斯”便是如此.此外，最美人体的头顶至咽喉的长度与咽喉至肚脐的长度之比也是5－12.若某人满足上述两个黄金分割比例，且腿长为105 cm，头顶至脖子下端的长度为26 cm，则其身高可能是()A.165 cmB.175 cmC.185 cmD.190 cm5.(2019·北京)李明自主创业，在网上经营一家水果店，销售的水果中有草莓、京白梨、西瓜、桃，价格依次为60元/盒、65元/盒、80元/盒、90元/盒.为增加销量，李明对这四种水果进行促销：一次购买水果的总价达到120元，顾客就少付x元，每笔订单顾客网上支付成功后，李明会得到支付款的80%.(1)当x＝10时，顾客一次购买草莓和西瓜各1盒，需要支付________元；(2)在促销活动中，为保证李明每笔订单得到的金额均不低于促销前总价的七折，则x的最大值为________.素养6数据分析例6(2019·全国Ⅲ)为了解甲、乙两种离子在小鼠体内的残留程度，进行如下试验：将200只小鼠随机分成A，B两组，每组100只，其中A组小鼠给服甲离子溶液，B组小鼠给服乙离子溶液.每只小鼠给服的溶液体积相同、摩尔浓度相同.经过一段时间后用某种科学方法测算出残留在小鼠体内离子的百分比.根据试验数据分别得到如下直方图：记C为事件：“乙离子残留在体内的百分比不低于5.5”，根据直方图得到P(C)的估计值为0.70.(1)求乙离子残留百分比直方图中a，b的值；(2)分别估计甲、乙离子残留百分比的平均值(同一组中的数据用该组区间的中点值为代表).6.某市一水电站的年发电量y (单位：亿千瓦时)与该市的年降雨量x (单位：毫米)有如下统计数据：(1)若从统计的5年中任取2年，求这2年的发电量都高于7.5 亿千瓦时的概率；(2)由表中数据求得线性回归方程为y ^＝0.004x ＋a ^，该水电站计划2019年的发电量不低于8.6 亿千瓦时，现由气象部门获悉2019年的降雨量约为1 800 毫米，请你预测2019年能否完成发电任务？。

2020年高考数学(理数)大题专项练习立体几何9题(含答案)

2020年高考数学(理数)大题专项练习立体几何9题1.如系，--减性M3匚中.班ffeAAtr 底面Ain二足总K为二打正二m唯.已知出0 4足H方rX十就.1口东一,麻用坨AC旧的大小；㈠求冲击宜税M 5承’的距离.门)直携4A 上是否。

花点。

.使DC/平面感a C?若存在.清确定点心的性黄土若不存在谙意可用由，2.如图,在矩形期⑶,NH =二】.廿为C。

上的点，以LW为石痕把折起，使点不到达点P 的位置，耳平面乩甘尸i平面ABCD.连接PB,PC、羔N为网的中点.巾CN#平面AMP.(1 )求线段Gf的《事(II )求平向同尸与平曲BCP所成锐二面角的余荥值，3.如图.在四棱如S - AHCD中.侧面30)为惋角三角形艮垂百于底面钻CD,8 =即小V是口的中点，由中Bg上A配= )*.4B=4D{1 )求证■平胤SC”⑵若骏苑与底面TBCD听成的角为60,求平面M3D 与平面SAC所成的锐二面角的余弦值.4.用国.四幢惟F ■用方匚。

中.忸1植FJJ.面目BCD，AB = AC-4M在找蜀HD 上, IL2AM = MD > X 为PE 的中题.AD/JSC. MN"面PCD-U>求9c的长।门口若为1=2,求：面希M—广材一办的余帮富，B5.如图T在二棹抨£8。

一乩80中.上HC8 =/aCB = 90，匕工4(? = 60, 0,芯分金二1 4」.1 卜II 片「：口："」・Il JJ = .4('=81，([)求证：4£"平面SC；D；门口求T面BC0与平而17?「所成错.面角的余强囿6.刎四-在四桎箫P A3+33正面是进枪-2的正川乱尸月=FH= /IT. E为PA中心*"?-自™六门£f |干扣内。

.，”在J乂班M纵L. I H"九N『M J- li. IL 卜H I.( “ 卜叫: 以/■■- f ilir『HLf；i力此点汇1找苣件「i.*若_曲曲砰一”\一只为〜一*求HN m氏度•第2页共14页7.8.如用，长方体阻上口一小瓦a仇的侧面匕他马是正方形. (X)证明:W平面孙i(2)若,蚯=2, A£=4t求二面用用的余弦值9.加图.在风冏体力/。

2020高考—立体几何(选择+填空+答案)

2020年高考——立体几何1.(20全国Ⅰ文3)．埃及胡夫金字塔是古代世界建筑奇迹之一，它的形状可视为一个正四棱锥.以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积，则其侧面三角形底边上的高与底面正方形的边长的比值为A ．514-B ．512-C ．514+D ．512+ 2.(20全国Ⅰ文12)．已知,,A B C 为球O 的球面上的三个点，⊙1O 为ABC △的外接圆，若⊙1O 的面积为4π，1AB BC AC OO ===，则球O 的表面积为A ．64πB ．48πC ．36πD ．32π3.（20全国Ⅱ文11）．已知△ABC 是面积为934的等边三角形，且其顶点都在球O 的球面上．若球O 的表面积为16π，则O 到平面ABC 的距离为A ．3B ．32C ．1D ．324.（20全国Ⅱ理7）．右图是一个多面体的三视图，这个多面体某条棱的一个端点在正视图中对应的点为M ，在俯视图中对应的点为N ，则该端点在侧视图中对应的点为A ．EB ．FC ．GD ．H5.（20全国Ⅱ理10）．已知△ABC是面积为934的等边三角形，且其顶点都在球O的球面上．若球O的表面积为16π，则O到平面ABC的距离为A．3B．32C．1 D．326.（20全国Ⅲ文9）．如图为某几何体的三视图，则该几何体的表面积是A．6+42B．4+42C．6+23D．4+237.（20新高考Ⅰ4）．日晷是中国古代用来测定时间的仪器，利用与晷面垂直的晷针投射到晷面的影子来测定时间．把地球看成一个球(球心记为O)，地球上一点A的纬度是指OA 与地球赤道所在平面所成角，点A处的水平面是指过点A且与OA垂直的平面.在点A处放置一个日晷，若晷面与赤道所在平面平行，点A处的纬度为北纬40°，则晷针与点A 处的水平面所成角为A．20°B．40°C．50°D．90°8.(20天津5)．若棱长为23A．12πB．24πC．36πD．144π9.(20浙江5)．某几何体的三视图（单位：cm ）如图所示，则该几何体的体积（单位：cm 3）是A ．73B ．143C ．3D ．610.(20北京4)．某三棱柱的底面为正三角形，其三视图如图所示，该三棱柱的表面积为（）．A ．63+B ．623+C ．123+D ．123+11.（20新高考Ⅰ16）．已知直四棱柱ABCD –A 1B 1C 1D 1的棱长均为2，∠BAD =60°．以1D 为球5BCC 1B 1的交线长为________．12.(20全国Ⅰ理16)．如图，在三棱锥P –ABC 的平面展开图中，AC =1，3AB AD =AB⊥AC ，AB ⊥AD ，∠CAE =30°，则cos ∠FCB = .13.（20全国Ⅱ文16）．设有下列四个命题：p 1：两两相交且不过同一点的三条直线必在同一平面内．p 2：过空间中任意三点有且仅有一个平面．p 3：若空间两条直线不相交，则这两条直线平行．p 4：若直线l ⊂平面α，直线m ⊥平面α，则m ⊥l ．则下述命题中所有真命题的序号是__________．①14p p ∧ ②12p p ∧ ③23p p ⌝∨ ④34p p ⌝∨⌝ 14.（20全国Ⅲ文16）．已知圆锥的底面半径为1，母线长为3，则该圆锥内半径最大的球的体积为_________．15.(20天津15)．如图，在四边形ABCD 中，60,3B AB ∠=︒=，6BC =，且3,2AD BC AD AB λ=⋅=-，则实数λ的值为_________，若,M N 是线段BC 上的动点，且||1MN =，则DM DN ⋅的最小值为_________．16.(20浙江14)．已知圆锥的侧面积（单位：cm 2）为2π，且它的侧面展开图是一个半圆，则这个圆锥的底面半径（单位：cm ）是_______．17.（20江苏9）．如图，六角螺帽毛坯是由一个正六棱柱挖去一个圆柱所构成的．已知螺帽的底面正六边形边长为2 cm ，高为2 cm ，内孔半轻为0.5 cm ，则此六角螺帽毛坯的体积是 ▲ cm.参考答案：1．C 2．A 3．C 4．A 5．C 6．C 7．B 8．C9．A 10. D 112π12.14-13．①③④215．16；13216．1 17．1232π。

2020届高三数学立体几何专项训练

2020届高三数学立体几何专题(文科)吴丽康2019-111.如图，四棱锥P-ABCD中，底面ABCD为矩形，PA⊥平面ABCD，E为PD的点.（Ⅰ）证明：PB2. 如图，四棱锥PABCD中，AB∥CD，AB＝2CD，E为PB的中点．(1)求证：CE∥平面PAD；(2)在线段AB上是否存在一点F，使得平面PAD∥平面CEF若存在，证明你的结论，若不存在，请说明理由．3如图，在四棱锥P －ABCD 中，平面PAC ⊥平面ABCD ，且PA ⊥AC ，PA ＝AD ＝2，四边形ABCD 满足BC ∥AD ，AB ⊥AD ，AB ＝BC ＝1.点E ，F 分别为侧棱PB ，PC 上的点，且PE PB ＝PF PC＝λ(λ≠0)． (1)求证：EF ∥平面PAD ；(2)当λ＝12时，求点D 到平面AFB 的距离．4.如图，四棱柱ABCD －A 1B 1C 1D 1的底面ABCD 是正方形．(1)证明：平面A 1BD ∥平面CD 1B 1；(2)若平面ABCD ∩平面B 1D 1C ＝直线l ，证明：B 1D 1∥l .5..如图，四边形ABCD是平行四边形，点P是平面ABCD外一点，M是PC的中点，在DM上取一点G，过G和AP作平面交平面BDM于GH.求证：AP∥GH.6.如图，在四棱锥PABCD中，PA⊥底面ABCD，AB⊥AD，AC⊥CD，∠ABC＝60°，PA＝AB＝BC，E是PC的中点．证明：(1)CD⊥AE；(2)PD⊥平面ABE.7.(2018北京通州三模,18)如图,在四棱锥P-ABCD中,平面PA B⊥平面ABCD,四边形ABCD 为正方形,△PAB为等边三角形,E是PB中点,平面AED与棱PC交于点F.(1)求证:AD∥EF; (2)求证:PB⊥平面AEFD;(3)记四棱锥P-AEFD的体积为V1,四棱锥P-ABCD的体积为V2,直接写出的值.8...如图，在四棱锥PABCD中，底面ABCD是∠DAB＝60°且边长为a的菱形，侧面PAD为正三角形，其所在平面垂直于底面ABCD，若G为AD的中点．(1)求证：BG⊥平面PAD；(2)求证：AD⊥PB；(3)若E为BC边的中点，能否在棱PC上找到一点F，使平面DEF⊥平面ABCD并证明你的结论．9.(2016·高考北京卷)如图，在四棱锥PABCD中，PC⊥平面ABCD，AB∥DC，DC⊥AC.(1)求证：DC⊥平面PAC；(2)求证：平面PAB⊥平面PAC；(3)设点E为AB的中点．在棱PB上是否存在点F，使得PA∥平面CEF说明理由．10..如图，在四棱锥P－ABCD中，底面ABCD是矩形，点E在棱PC上(异于点P，C)，平面ABE与棱PD交于点F.(1)求证：AB∥EF；(2)若AF⊥EF，求证：平面PAD⊥平面ABCD.11..如图，在四棱锥P －ABCD 中，PA ⊥平面ABCD ，PA ＝AB ＝BC ＝3，AD ＝CD ＝1，∠ADC ＝120°，点M 是AC 与BD 的交点，点N 在线段PB 上，且PN ＝14PB . (1)证明：MN ∥平面PDC ；(2)求直线MN 与平面PAC 所成角的正弦值．12..(2016·高考四川卷)如图，在四棱锥PABCD 中，PA ⊥CD ，AD ∥BC ，∠ADC ＝∠PAB ＝90°，BC ＝CD ＝12AD ．(1)在平面PAD 内找一点M ，使得直线CM ∥平面PAB ，并说明理由；(2)证明：平面PAB ⊥平面PBD ．13．(2016·高考江苏卷)如图，在直三棱柱ABC A 1B 1C 1中，D ，E 分别为AB ，BC 的中点，点F 在侧棱B 1B 上，且B 1D ⊥A 1F ，A 1C 1⊥A 1B 1.求证：(1)直线DE ∥平面A 1C 1F ；(2)平面B 1DE ⊥平面A 1C 1F .14.【2014,19】如图，三棱柱111C B A ABC -中，侧面C C BB 11为菱形，C B 1的中点为O ，且⊥AO 平面C C BB 11.（1）证明：;1AB C B ⊥（2）若1AB AC ⊥,,1,601==∠BC CBB ο求三棱柱111C B A ABC -的高.15.(2017天津,文17)如图,在四棱锥P-ABCD中,AD⊥平面PDC,AD∥ BC, PD⊥PB,AD=1,BC=3,CD=4,PD=2.(1)求异面直线AP与BC所成角的余弦值;(2)求证:PD⊥平面PBC;(3)求直线AB与平面PBC所成角的正弦值.16.(2016·高考浙江卷)如图，在三棱台ABC DEF中，平面BCFE⊥平面ABC，∠ACB＝90°，BE＝EF＝FC＝1，BC＝2，AC＝3.(1)求证：BF⊥平面ACFD；(2)求直线BD与平面ACFD所成角的余弦值．17..(2018·全国Ⅲ)如图，矩形ABCD所在平面与半圆弧CD所在平面垂直，M是CD上异于C，D的点．(1)证明：平面AMD⊥平面BMC.(2)在线段AM上是否存在点P，使得MC∥平面PBD说明理由．立体几何中的翻折问题18...如图(1)，在直角梯形ABCD 中，AD ∥BC ，∠BAD ＝π2，AB ＝BC ＝12AD ＝a ， E 是AD 的中点，O 是AC 与BE 的交点．将△ABE 沿BE 折起到图(2)中△A 1BE 的位置，得到四棱锥A 1BCDE .(1)证明：CD ⊥平面A 1OC ；(2)当平面A 1BE ⊥平面BCDE 时，四棱锥A 1BCDE 的体积为362，求a 的值．19.．如图1，在直角梯形ABCD 中，∠ADC ＝90°，AB ∥CD ，AD ＝CD ＝12AB ＝2， E 为AC 的中点，将△ACD 沿AC 折起，使折起后的平面ACD 与平面ABC 垂直，如图2.在图2所示的几何体D －ABC 中：(1)求证：BC ⊥平面ACD ；(2)点F 在棱CD 上，且满足AD ∥平面BEF ，求几何体F －BCE 的体积．20．如图，长方体ABCDA1B1C1D1中，AB＝16，BC＝10，AA1＝8.点E，F分别在A1B1，D1C1上，过点E、F的平面α与此长方体的面相交，交线围成一个正方形EFGH.(1)求证：A1E＝D1F；(2)判断A1D与平面α的关系．2020届高三数学立体几何专题(文科) 1解析：（Ⅰ）设AC的中点为O，连接EO. 在三角形PBD中，中位线EOV=（Ⅱ）∵AP=1，AD=-P ABD-11=32P ABD V PA AB AD ∴⋅⋅⋅AB 32AB =，作AH ⊥PB 角PB 于H ，由题意可知BC ⊥平面PAB ，∴BC ⊥AH ，故AH ⊥平面PBC ．又PA AB AH PB ⋅==A 点到平面PBC 2.(1)证明：如图所示，取PA 的中点H ，连接EH ，DH ，因为E 为PB 的中点，所以EH ∥AB ，EH ＝12AB ，又AB ∥CD ，CD ＝12AB ．所以EH ∥CD ，EH ＝CD ，因此四边形DCEH 是平行四边形，所以CE ∥DH ，又DH ⊂平面PAD ，CE ⊄平面PAD ，所以CE ∥平面PAD ． (2)如图所示，取AB 的中点F ，连接CF ，EF ，所以AF ＝12AB ，又CD ＝12AB ，所以AF ＝CD ，又AF ∥CD ，所以四边形AFCD 为平行四边形，所以CF ∥AD ，又CF ⊄平面PAD ，所以CF ∥平面PAD ，由(1)可知CE ∥平面PAD ，又CE ∩CF ＝C ，故平面CEF ∥平面PAD ，故存在AB 的中点F 满足要求．3.(1)证明 ∵PE PB ＝PF PC＝λ(λ≠0)，∴EF ∥BC .∵BC ∥AD ，∴EF ∥AD .又EF ⊄平面PAD ，AD ⊂平面PAD ，∴EF ∥平面PAD . (2)解 ∵λ＝12，∴F 是PC 的中点，在Rt△PAC 中，PA ＝2，AC ＝2，∴PC ＝PA 2＋AC 2＝6，∴PF ＝12PC ＝62.∵平面PAC ⊥平面ABCD ，且平面PAC ∩平面ABCD ＝AC ，PA ⊥AC ，PA ⊂平面PAC ，∴PA ⊥平面ABCD ，∴PA ⊥BC .又AB ⊥AD ，BC ∥AD ，∴BC ⊥AB ，又PA ∩AB ＝A ，PA ，AB ⊂平面PAB ， ∴BC ⊥平面PAB ， ∴BC ⊥PB ，∴在Rt△PBC 中，BF ＝12PC ＝62.连接BD ，DF ，设点D 到平面AFB 的距离为d ，在等腰三角形BAF 中，BF ＝AF ＝62，AB ＝1， ∴S △ABF ＝54，又S △ABD ＝1，点F 到平面ABD 的距离为1， ∴由V F －ABD ＝V D －AFB ，得13×1×1＝13×d ×54，解得d ＝455，即点D 到平面AFB 的距离为455.4.证明 (1)由题设知BB 1∥DD 1且BB 1＝DD 1，所以四边形BB 1D 1D 是平行四边形，所以BD ∥B 1D 1.又BD ⊄平面CD 1B 1，B 1D 1⊂平面CD 1B 1，所以BD ∥平面CD 1B 1.因为A 1D 1∥B 1C 1∥BC 且A 1D 1＝B 1C 1＝BC ，所以四边形A 1BCD 1是平行四边形，所以A 1B ∥D 1C .又A 1B ⊄平面CD 1B 1，D 1C ⊂平面CD 1B 1，所以A 1B ∥平面CD 1B 1.又因为BD ∩A 1B ＝B ，BD ，A 1B ⊂平面A 1BD ，所以平面A 1BD ∥平面CD 1B 1. (2)由(1)知平面A 1BD ∥平面CD 1B 1，又平面ABCD ∩平面B 1D 1C ＝直线l ，平面ABCD ∩平面A 1BD ＝直线BD ，所以直线l ∥直线BD ，在四棱柱ABCD －A 1B 1C 1D 1中，四边形BDD 1B 1为平行四边形，所以B 1D 1∥BD ，所以B 1D 1∥l .5.连接AC 交BD 于点O ，连接MO ，因为PM ＝MC ，AO ＝OC ，所以PA ∥MO ，因为PA⊄平面MBD，MO⊂平面MBD，所以PA∥平面MBD．因为平面PAHG∩平面MBD＝GH，所以AP∥GH.6.[证明] (1)在四棱锥PABCD中，因为PA⊥底面ABCD，CD⊂平面ABCD，所以PA⊥CD，因为AC⊥CD，且PA∩AC＝A，所以CD⊥平面PAC，而AE⊂平面PAC，所以CD⊥AE.(2)由PA＝AB＝BC，∠ABC＝60°，可得AC＝PA.因为E是PC的中点，所以AE⊥PC.由(1)知AE⊥CD，且PC∩CD＝C，所以AE⊥平面PCD．而PD⊂平面PCD，所以AE⊥PD．因为PA⊥底面ABCD，所以PA⊥AB．又因为AB⊥AD且PA∩AD＝A，所以AB⊥平面PAD，而PD⊂平面PAD，所以AB⊥PD．又因为AB∩AE＝A，所以PD⊥平面ABE.7.(1)证明因为ABCD为正方形,所以AD∥BC.因为AD⊄平面PBC,BC⊂平面PBC,所以AD∥平面PBC.因为AD⊂平面AEFD,平面AEFD∩平面PBC=EF, 所以AD∥EF.(2)证明因为四边形ABCD是正方形,所以AD⊥AB.因为平面PAB⊥平面ABCD,平面PAB∩平面ABCD=AB,AD⊂平面ABCD,所以AD⊥平面PAB.因为PB⊂平面PAB,所以AD⊥PB.因为△PA B为等边三角形,E是PB中点,所以PB⊥AE.因为AE⊂平面AEFD,AD⊂平面AEFD,AE∩AD=A,所以PB⊥平面AEFD.(3)解由(1)知,V1=V C-AEFD,V E-ABC=V F-ADC=V C-AEFD=V1,∴V BC-AEFD=V1,则V P-ABCD=V1+V1=V1, ∴.8.[解] (1)证明：在菱形ABCD中，∠DAB＝60°，G为AD的中点，所以BG⊥AD．又平面PAD⊥平面ABCD，平面PAD∩平面ABCD＝AD，所以BG⊥平面PAD．(2)证明：如图，连接PG.因为△PAD为正三角形，G为AD的中点，所以PG⊥AD．由(1)知，BG⊥AD，又PG∩BG＝G，所以AD⊥平面PGB．因为PB⊂平面PGB，所以AD⊥PB．(3)当F为PC的中点时，满足平面DEF⊥平面ABCD．证明如下：取PC的中点F，连接DE、EF、DF.在△PBC中，FE∥PB，在菱形ABCD中，GB∥DE.而FE⊂平面DEF，DE⊂平面DEF，EF∩DE＝E，PB⊂平面PGB，GB⊂平面PGB，PB∩GB＝B，所以平面DEF∥平面PGB．因为BG⊥平面PAD，PG⊂平面PAD，所以BG⊥PG.又因为PG⊥AD，AD∩BG＝G，所以PG⊥平面ABCD．又PG⊂平面PGB，所以平面PGB⊥平面ABCD，所以平面DEF⊥平面ABCD．9.【解】(1)证明：因为PC⊥平面ABCD，所以PC⊥DC.又因为DC⊥AC，且PC∩AC＝C，所以DC⊥平面PAC.(2)证明：因为AB∥DC，DC⊥AC，所以AB⊥AC.因为PC⊥平面ABCD，所以PC⊥AB．又因为PC∩AC＝C，所以AB ⊥平面PAC .又AB ⊂平面PAB ，所以平面PAB ⊥平面PAC . (3)棱PB 上存在点F ，使得PA ∥平面CEF . 理由如下：如图，取PB 中点F ，连接EF ，CE ，CF .又因为E 为AB 的中点，所以EF ∥PA . 又因为PA ⊄平面CEF ，且EF ⊂平面CEF ，所以PA ∥平面CEF .10.证明 (1)因为四边形ABCD 是矩形，所以AB ∥CD . 又AB ⊄平面PDC ，CD ⊂平面PDC ，所以AB ∥平面PDC ，又因为AB ⊂平面ABE ，平面ABE ∩平面PDC ＝EF ，所以AB ∥EF . (2)因为四边形ABCD 是矩形，所以AB ⊥AD . 因为AF ⊥EF ，(1)中已证AB ∥EF ，所以AB ⊥AF .又AB ⊥AD ，由点E 在棱PC 上(异于点C )，所以点F 异于点D ，所以AF ∩AD ＝A ，AF ，AD ⊂平面PAD ，所以AB ⊥平面PAD ，又AB ⊂平面ABCD ，所以平面PAD ⊥平面ABCD . 11.(1)证明因为AB ＝BC ，AD ＝CD ，所以BD 垂直平分线段AC . 又∠ADC ＝120°，所以MD ＝12AD ＝12，AM ＝32. 所以AC ＝3.又AB ＝BC ＝3，所以△ABC 是等边三角形，所以BM ＝32，所以BM MD ＝3，又因为PN ＝14PB ，所以BM MD ＝BNNP ＝3，所以MN ∥PD .又MN ⊄平面PDC ，PD ⊂平面PDC ，所以MN ∥平面PDC .(2)解因为PA ⊥平面ABCD ，BD ⊂平面ABCD ，所以BD ⊥PA ，又BD ⊥AC ，PA ∩AC ＝A ，PA ，AC ⊂平面PAC ，所以BD ⊥平面PAC .由(1)知MN ∥PD ，所以直线MN 与平面PAC 所成的角即直线PD 与平面PAC 所成的角，故∠DPM 即为所求的角．在Rt△PAD 中，PD ＝2，所以sin∠DPM ＝DM DP ＝122＝14，所以直线MN 与平面PAC 所成角的正弦值为14.12.【解】 (1)取棱AD 的中点M (M ∈平面PAD )，点M 即为所求的一个点．理由如下：因为AD ∥BC ，BC ＝12AD ，所以BC ∥AM ，且BC ＝AM ，所以四边形AMCB 是平行四边形，从而CM ∥AB ．又AB ⊂平面PAB ，CM ⊄平面PAB ，所以CM ∥平面PAB ．(说明：取棱PD 的中点N ，则所找的点可以是直线MN 上任意一点)(2)证明：由已知，PA ⊥AB ，PA ⊥CD ，因为AD ∥BC ，BC ＝12AD ，所以直线AB 与CD 相交．所以PA ⊥平面ABCD ，从而PA ⊥BD ．连接BM ，因为AD ∥BC ，BC ＝12AD ，所以BC ∥MD ，且BC ＝MD ．所以四边形BCDM 是平行四边形．所以BM ＝CD ＝12AD ，所以BD ⊥AB ．又AB ∩AP ＝A ，所以BD ⊥平面PAB ．又BD ⊂平面PBD ，所以平面PAB ⊥平面PBD ． 13.[证明] (1)在直三棱柱ABCA 1B 1C 1中，A 1C 1∥AC .在△ABC 中，因为D ，E 分别为AB ，BC 的中点，所以DE ∥AC ，于是DE ∥A 1C 1.又DE ⊄平面A 1C 1F ，A 1C 1⊂平面A 1C 1F ，所以直线DE ∥平面A 1C 1F . (2)在直三棱柱ABCA 1B 1C 1中，A 1A ⊥平面A 1B 1C 1.因为A 1C 1⊂平面A 1B 1C 1，所以A 1A ⊥A 1C 1.又A 1C 1⊥A 1B 1，A 1A ⊂平面ABB 1A 1，A 1B 1⊂平面ABB 1A 1，A 1A ∩A 1B 1＝A 1，所以A 1C 1⊥平面ABB 1A 1.因为B 1D ⊂平面ABB 1A 1，所以A 1C 1⊥B 1D ．又B 1D ⊥A 1F ，A 1C 1⊂平面A 1C 1F ，A 1F ⊂平面A 1C 1F ，A 1C 1∩A 1F ＝A 1，所以B 1D ⊥平面A 1C 1F .因为直线B 1D ⊂平面B 1DE ，所以平面B 1DE ⊥平面A 1C 1F14.证明：(Ⅰ)连接 BC 1，则O 为B 1C 与BC 1的交点，∵AO ⊥平面BB 1C 1C . ∴AO ⊥B 1C ， …2分因为侧面BB 1C 1C 为菱形，∴BC 1⊥B 1C ，…4分 ∴BC 1⊥平面ABC 1，∵AB平面ABC 1，故B 1C ⊥AB . …6分(Ⅱ)作OD ⊥BC ，垂足为D ，连结AD ，∵AO ⊥BC ，∴BC ⊥平面AOD ，又BC 平面ABC ，∴平面ABC ⊥平面AOD ，交线为AD ，作OH ⊥AD ，垂足为H ，∴OH ⊥平面ABC . …9分 ∵∠CBB 1=60°，所以ΔCBB 1为等边三角形，又BC =1，可得OD =34，由于AC ⊥AB 1，∴11122OA B C ==，∴227AD OD OA =+=由 OH·AD=OD·OA ，可得OH=2114，又O 为B 1C 的中点，所以点B 1到平面ABC 的距离为21，所以三棱柱ABC-A 1B 1C 1的高高为217。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

O S B A C08高考数学立体几何练习题1．已知四棱锥P ABCD -的底面为直角梯形，//AB DC ，⊥=∠PA DAB ,90ο底面ABCD ，且1PA AD DC ===，2AB =，M 是PB 的中点．（Ⅰ）证明：面PAD ⊥面PCD ；（Ⅱ）求AC 与PB 所成的角；（Ⅲ）求面AMC 与面BMC 所成二面角的大小．2．如图，在四棱锥P ABCD -中，底面ABCD 为矩形，侧棱PA ⊥底面ABCD ，3AB =，1BC =，2PA =，E 为PD 的中点.（Ⅰ）求直线AC 与PB 所成角的余弦值；（Ⅱ）在侧面PAB 内找一点N ，使NE ⊥面PAC ，并求出点N 到AB 和AP 的距离．3．如图所示的多面体是由底面为ABCD 的长方体被截面1AEC F 所截面而得到的，其中14,2,3,1AB BC CC BE ====．（Ⅰ）求BF 的长；（Ⅱ）求点C 到平面1AEC F 的距离．4．如图，在长方体1111ABCD A B C D -，中，11,2AD AA AB ===，点E 在棱AD 上移动. （Ⅰ）证明：11D E A D ⊥；（Ⅱ）当E 为AB 的中点时，求点E 到面1ACD 的距离；（Ⅲ）AE 等于何值时，二面角1D EC D --的大小为4π.5．（xx 福建•理•18题）如图，正三棱柱ABC －A 1B 1C 1的所有棱长都为2，D 为CC 1中点．（Ⅰ）求证：AB 1⊥面A 1BD ；（Ⅱ）求二面角A －A 1D －B 的大小；（Ⅲ）求点C 到平面A 1BD 的距离． 6．（xx 宁夏•理•19题）如图，在三棱锥S ABC -中，侧面SAB 与侧面SAC 均为等边三角形，90BAC ∠=°，O 为BC 中点．（Ⅰ）证明：SO ⊥平面ABC ；（Ⅱ）求二面角A SC B --的余弦值．7．（xx 陕西•理•19题）如图,在底面为直角梯形的四棱锥P ABCD -中//AD BC ，,90︒=∠ABC 平面⊥PA ABC ，32,2,4===AB AD PA ,BC =6．(Ⅰ)求证：BD PAC ⊥平面； (Ⅱ)求二面角D BD P --的大小．D CBAV立体几何练习题参考答案1．以A 为坐标原点AD 长为单位长度，如图建立空间直角坐标系，则各点坐标为1(0,0,0),(0,2,0),(1,1,0),(1,0,0),(0,0,1),(0,1,)2A B C D P M .（Ⅰ）证明：因.,0),0,1,0(),1,0,0(DC AP DC AP DC AP ⊥=⋅==所以故由题设知AD DC ⊥，且AP 与AD 是平面PAD 内的两条相交直线，由此得DC ⊥面PAD .又DC 在面PCD 上，故面PAD ⊥面PCD . （Ⅱ）解：因),1,2,0(),0,1,1(-==PB AC.510||||,cos ,2,5||,2||=⋅>=<=⋅==PB AC PB AC PB AC PB AC 所以故（Ⅲ）解：在MC 上取一点(,,)N x y z ，则存在,R ∈λ使,MC NC λ=..21,1,1),21,0,1(),,1,1(λλ==-=∴-=---=z y x MC z y x NC要使14,00,.25AN MC AN MC x z λ⊥=-==u u u r u u u u r g 只需即解得),52,1,51(),52,1,51(,.0),52,1,51(,54=⋅-===⋅=MC BN BN AN MC AN N 有此时能使点坐标为时可知当λANB MC BN MC AN MC BN MC AN ∠⊥⊥=⋅=⋅所以得由.,0,0为所求二面角的平面角.30304||,||,.52cos(,).3||||2arccos().3AN BN AN BN AN BN AN BN AN BN ===-∴==-⋅-u u u r u u u r u u u r u u u r Q g u u u r u u u ru u u r u u u r g u u u r u u u r 故所求的二面角为2．解：（Ⅰ）建立如图所示的空间直角坐标系，则,,,,,A B C D P E 的坐标为(0,0,0)A 、(3,0,0)B 、(3,1,0)C 、(0,1,0)D 、(0,0,2)P 、1(0,,1)2E ，从而).2,0,3(),0,1,3(-==PB AC设PB AC 与的夹角为θ，则,1473723||||cos ==⋅=PB AC θ∴AC 与PB 所成角的余弦值为1473.（Ⅱ）由于N 点在侧面PAB 内，故可设N 点坐标为(,0,)x z ，则)1,21,(z x NE --=，由NE ⊥面PAC 可得，⎪⎩⎪⎨⎧=+-=-⎪⎪⎩⎪⎪⎨⎧=⋅--=⋅--⎪⎩⎪⎨⎧=⋅=⋅.0213,01.0)0,1,3()1,21,(,0)2,0,0()1,21,(.0,0x z z x z x AC NE AP NE 化简得即 ∴⎪⎩⎪⎨⎧==163z x 即N 点的坐标为)1,0,63(，从而N 点到AB 和AP 的距离分别为31,. 3．解：（I ）建立如图所示的空间直角坐标系，则(0,0,0)D ，(2,4,0)B1(2,0,0),(0,4,0),(2,4,1),(0,4,3)A C E C 设(0,0,)F z .∵1AEC F 为平行四边形，.62,62||).2,4,2().2,0,0(.2),2,0,2(),0,2(,,11的长为即于是得由为平行四边形由BF BF EF F z z EC AF F AEC =--=∴∴=∴-=-=∴∴（II ）设1n 为平面1AEC F 的法向量，)1,,(,11y x n ADF n =故可设不垂直于平面显然⎩⎨⎧=+⨯+⨯-=+⨯+⨯⎪⎩⎪⎨⎧=⋅=⋅02020140,0,011y x y x n n 得由⎪⎩⎪⎨⎧-==∴⎩⎨⎧=+-=+.41,1,022,014y x x y 即111),3,0,0(n CC CC 与设又=的夹角为α，则.333341161133cos 1111=++⨯==α ∴C 到平面1AEC F 的距离为.11334333343cos ||1=⨯==αCC d 4．解：以D 为坐标原点，直线1,,DA DC DD 分别为,,x y z 轴，建立空间直角坐标系，设AE x =，则11(1,0,1),(0,0,1),(1,,0),(1,0,0),(0,2,0)A D E x A C（1）.,0)1,,1(),1,0,1(,1111D DA x D DA ⊥=-=所以因为（2）因为E 为AB 的中点，则(1,1,0)E ，从而)0,2,1(),1,1,1(1-=-=D ，)1,0,1(1-=AD ，设平面1ACD 的法向量为),,(c b a =，则⎪⎩⎪⎨⎧=⋅=⋅,0,01AD 也即⎩⎨⎧=+-=+-002c a b a ，得⎩⎨⎧==ca ba 2，从而)2,1,2(=n ，所以点E 到平面1ACD 的距离为.3132121=-+==h （3）设平面1D EC 的法向量),,(c b a n =，∴),1,0,0(),1,2,0(),0,2,1(11=-=-=DD C D x CE由⎩⎨⎧=-+=-⇒⎪⎩⎪⎨⎧=⋅=⋅.0)2(02,0,01x b a c b D 令1,2,2b c a x =∴==-， ∴).2,1,2(x -= 依题意.225)2(222||||4cos211=+-⇒=⋅=x DD n π∴321+=x （不合，舍去），322-=x .∴2AE =-1D EC D --的大小为4π. 5．解：（Ⅰ）取BC 中点O ，连结AO ．ABC Q △为正三角形，AO BC ∴⊥． Q 在正三棱柱111ABC A B C -中，平面ABC ⊥平面11BCC B ，AD ∴⊥平面11BCC B ．取11B C 中点1O ，以O 为原点，OB uuu r ，1OO u u u u r ，OA u u ur 的方向为x y z ，，轴的正方向建立空间直角坐标系，则(100)B ，，，(110)D -，，，1(02A，(00A ，1(120)B ，，，1(12AB ∴=u u u r ，，(210)BD =-u u u r ，，，1(12BA =-u u u r．12200AB BD =-++=u u u r u u u r Q g ，111430AB BA =-+-=u u u r u u u rg ， 1AB BD ∴u u u r u u u r ⊥，11AB BA u u u r u u u r⊥．1AB ∴⊥平面1A BD ．（Ⅱ）设平面1A AD 的法向量为(x y =，n (11AD =-u u u r ，，，1(020)AA =u u u r ，，．AD u u u r Q ⊥n ，1AA u u u r⊥n ，100AD AA ⎧=⎪∴⎨=⎪⎩u u u r g u u u r g ，，n n 020x y y ⎧-+-=⎪∴⎨=⎪⎩，，0y x =⎧⎪∴⎨=⎪⎩，．令1z =得(1)=，n 为平面1A AD 的一个法向量．由（Ⅰ）知1AB ⊥平面1A BD ， 1AB ∴u u u r 为平面1A BD 的法向量．cos <n ，1114AB AB AB >===-u u u ru u u r g u u u r g n n ． ∴二面角1A A D B --的大小为arccos4．（Ⅲ）由（Ⅱ），1AB u u u r为平面1A BD 法向量，1(200)(12BC AB =-=u u u r u u u r Q ，，，，．∴点C 到平面1A BD 的距离112BC AB d AB ===u u u r u u u rg u u u r ．6．解：以O 为坐标原点，射线OB OA ，分别为x 轴、y 轴的正半轴，建立如图的空间直角坐标系O xyz -．设(100)B ，，，则(100)(010)(001)C A S -，，，，，，，，．SC 的中点11022M ⎛⎫- ⎪⎝⎭，，， 111101(101)2222MO MA SC ⎛⎫⎛⎫=-=-=-- ⎪ ⎪⎝⎭⎝⎭u u u u r u u u r u u ur ，，，，，，，，．00MOSC MA SC ==u u u u r u u u r u u u r u u u r ，∴··．故,MO SC MA SC MO MA ⊥⊥>u u u u r u u u r，，<等于二面角A SC B --的平面角．cos MO MA MO MA MO MA<>==u u u u r u u u ru u u u r u u u r u u u u r u u u r ，··，所以二面角A SC B --． 7．解：（Ⅰ）如图，建立坐标系，则(000)A ，，，0)B ，，0)C ，，(020)D ，，，(004)P ，，，(004)AP ∴=u u u r ，，，0)AC =u u u r ，，(0)BD =-u u u r，， 0BD AP ∴=u u u r u u u r g ，0BD AC =u u u r u u u rg ．BD AP ∴⊥，BD AC ⊥，又PA AC A =I ，BD ∴⊥平面PAC ．（Ⅱ）设平面PCD 的法向量为(1)x y =，，n ，则0CD =u u u r g n ，0PD =u u u rg n ，又(40)CD =--u u u r ，，(024)PD =-u u u r ，，，40240y y ⎧--=⎪∴⎨-=⎪⎩，，解得32x y ⎧=-⎪⎨⎪=⎩，21⎛⎫∴= ⎪ ⎪⎝⎭，n 平面PAC的法向量取为()20BD ==-u u u r ，m ， cos <m，>==g m n n m n ∴二面角A PC D --的大小为C。