匀变速直线运动平均速度公式
匀变速直线运动的位移差公式

匀变速直线运动是速度均匀变化的直线运动,即加速度不变的直线运动。
其速度时间图像是一条倾斜的直线,表示在任意相等的时间内速度的变化量都相同,即速度的变化量与对应时间的变化量之比保持不变,这样的运动是变速运动中最简单的运动形式,叫做匀变速直线运动。
公式总结:
1.平均速度V平=s/t(定义式)。
2.有用推论Vt2-Vo2=2as。
3.中间时刻速度Vt/2=V平=(Vt+Vo)/2。
4.末速度Vt=Vo+at。
5.中间位置速度Vs/2=[(Vo2+Vt2)/2]1/2。
6.位移s=V平t=Vot+at2/2=Vt/2t。
7.加速度a=(Vt-Vo)/t{以Vo为正方向,a与Vo同向(加速)a>0;反向则a<0}。
8.实验用推论Δs=aT2{Δs为连续相邻相等时间(T)内位移之差}。
9.主要物理量及单位:初速度(Vo):m/s;加速度(a):m/s2;末速度(Vt):m/s;时间(t)秒(s);位移(s):米(m);路程:米;速度单位换算:1m/s=3.6km/h。
匀变速直线运动的公式及推论

匀变速直线运动追及(避免撞车)基本公式:①速度公式:v t=v0+at;②位移公式:s=v0t+at2;③速度位移公式:v t2-v02=2as。
推导公式:①平均速度公式:V=。
②某段时间的中间时刻的瞬时速度等于该段时间内的平均速度:。
③某段位移的中间位置的瞬时速度公式:。
无论匀加速还是匀减速,都有。
④匀变速直线运动中,在任意两个连续相等的时间T内的位移差值是恒量,即ΔS=S n+l–S n=aT2=恒量。
⑤初速为零的匀变速直线运动中的比例关系(设T为相等的时间间隔,s为相等的位移间隔):推论1(持续时间-瞬时速度):T末、2T末、3T末……的瞬时速度之比为:v1:v2:v3:……:v n=1:2:3:……:n;推论2(持续时间-位移):T内、2T内、3T内……的位移之比为:s1:s2:s3:……:s n=1:4:9:……:n2;推论3(相等时间-位移):第一个T内、第二个T内、第三个T内……的位移之比为:sⅠ:sⅡ:sⅢ:……:s N=1:3:5:……:(2N-1);推论4(持续位移-所用时间)前一个s、前两个s、前三个s……所用的时间之比为:t1:t2:t3:……:t n=1:……:;推论5(相等位移-所用时间)第一个s、第二个s、第三个s……所用的时间之比为tⅠ、tⅡ、tⅢ:……:t N=1:……:。
相关运用:追及相遇问题①当两个物体在同一直线上运动时,由于两物体的运动情况不同,所以两物体之间的距离会不断发生变化,两物体间距会越来越大或越来越小,这时就会涉及追及、相遇或避免碰撞等问题。
②追及问题的两类情况:Ⅰ、速度大者减速(如匀减速直线运动)追速度小者(如匀速运动):Ⅱ、速度小者加速(如初速度为零的匀加速直线运动)追速度大者(如匀速运动):③相遇问题的常见情况:Ⅰ、同向运动的两物体追及即相遇;Ⅱ、相向运动的物体,当各自发生的位移大小和等于开始时两物体的距离时即相遇。
例题:A、B两列火车在同一轨道上同向行驶,A在前,速度为v A=10m/s,B车在后,速度v B=30m/s。
匀变速直线运动的公式

匀变速直线运动的公式一、大体公式:一、速度公式:0t a t υυ=+⋅ 二、位移公式:2012s t at υ=+ 二、推论: 一、平均速度公式:02tυυυ+=二、速度——位移公式:2202t as υυ-=推导:0t a t υυ=+⋅,22200122t s t at as υυυ=+⇒-= 3、中时速公式:022t t υυυυ 推导:00002222t t t υυυυttυυa υυt 4、中位速公式:22022t S υυυ。
(22t s υυ)推导:(1)22220000221222222t t t s S s a t t υυυυυυυυυ-+--==⋅⋅⋅⋅=⇒= 22220022222s t S s a as υυυυυ-=-=⇒=或,(2)22222022()04s t t s t υυυυυυ 三、匀变速直线运动的特殊规律一、初速为零的匀加速直线运动的特点:(1)从运动开始,在1T 末、2T 末、3T 末……nT 末的速度之比:υ1::υ2:υ3:…:υn =1:2:3:…:n (提示:t a t υ=⋅)(2)从运动开始,在1T 内、2T 内、3T 内……nT 内的位移之比:S 1:S 2:S 3:……:S n =12: 22: 32:……:n 2 (提示:212s at )(3)从运动开始,在第1个T 内,第二个T 内,第3个T 内……第n 个T 内的位移之比:S Ⅰ:S Ⅱ:S Ⅲ:……:S N =1:3:5:……:(2N -1) (提示:S Ⅰ=S 2-S 1)(4)从运动开始,通过持续相等的位移所历时刻之比:① t Ⅰ:t Ⅱ:t Ⅲ:……:t N =1:1):2):……:1n )② t 总t Ⅰ二、做匀变速直线运动的物体,若是在各个持续相等的时刻T内的位移别离为SⅠ,SⅡ,S III……S N,则△S=SⅡ-SⅠ=S III-SⅡ=……=S N-S N-1=aT2=恒量推论:第n个T时刻内的位移和第m个T时刻内的位移之差:S n-S m=(n-m)aT2。
匀变速直线运动公式、推论推导、及规律总结

一.基本规律:v =ts 1.基本公式a =t v v t 0- a =tvtv =20t v v + v =t v 21at v v t +=0 at v t =021at t v s +=221at s =t v v s t 20+= t vs t 2=2022v v as t -= 22t v as =注意:基本公式中(1)式适用于一切变速运动,其余各式只适用于匀变速直线运动。
二.匀变速直线运动的推论及推理对匀变速直线运动公式作进一步的推论,是掌握基础知识、训练思维、提高能力的一个重要途径,掌握运用的这些推论是解决一些特殊问题的重要手段。
推论1 做匀变速直线运动的物体在中间时刻的即时速度等于这段时间的平均速度,即202t t v v t S v +==推导:设时间为t ,初速0v ,末速为t v ,加速度为a ,根据匀变速直线运动的速度公式at v v +=0得: ⎪⎪⎩⎪⎪⎨⎧⨯+=⨯+=22202t a v v t a v v t t t ⇒ 202t t v v v += 推论2 做匀变速直线运动的物体在一段位移的中点的即时速度22202t s v v v +=推导:设位移为S ,初速0v ,末速为t v ,加速度为a ,根据匀变速直线运动的速度和位移关系公式as v v t 2202+=得:⎪⎪⎩⎪⎪⎨⎧⨯+=⨯+=22222222022S a v v Sa v v s t s ⇒ 22202t s v v v +=推论3 做匀变速直线运动的物体,如果在连续相等的时间间隔t 内的位移分别为1S 、2S 、 3S ……n S ,加速度为a ,则=-=-=∆2312S S S S S……21at S S n n =-=-推导:设开始的速度是0v经过第一个时间t 后的速度为at v v +=01,这一段时间内的位移为20121at t v S +=, 经过第二个时间t 后的速度为at v v +=022,这段时间内的位移为202122321at t v at t v S +=+=经过第三个时间t 后的速度为at v v +=023,这段时间内的位移为202232521at t v at t v S +=+=…………………经过第n 个时间t 后的速度为at nv v n +=0,这段时间内的位移为202121221at n t v at t v S n n -+=+=- 则=-=-=∆2312S S S S S……21at S S n n =-=-点拨:只要是匀加速或匀减速运动,相邻的连续的相同的时间内的位移之差,是一个与加速度a 与时间“有关的恒量”.这也提供了一种加速度的测量的方法:即2tSa ∆=,只要测出相邻的相同时间内的位移之差S ∆和t ,就容易测出加速度a 。
匀变速直线运动公式、推论推导、及规律总结
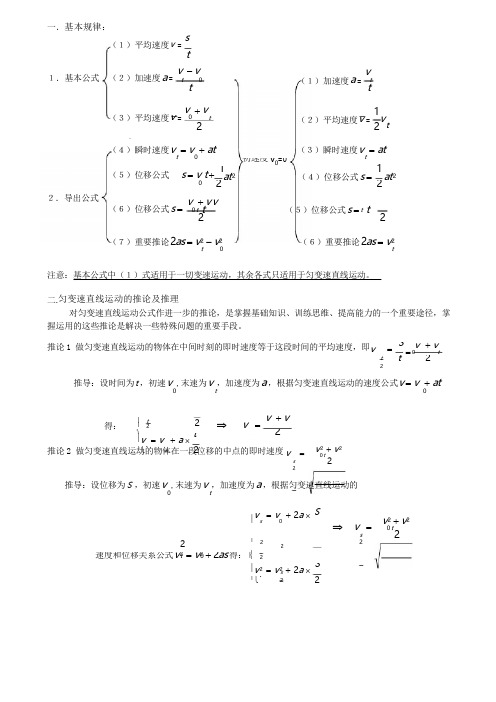
1.基本公式 (2)加速度 a = v - v初速度 v 0=0(5)位移公式 s = v t + 122推论 1 做匀变速直线运动的物体在中间时刻的即时速度等于这段时间的平均速度,即v= St 2⇒ v = v + v ⎪ t 2 ⎪ 2 ⎨ 2 ⎪v = v + a ⨯ t ⎪⎩ t2 ⎧2速度和位移关系公式 v 2 = v 2 + 2as 得: ⎪ 2⎪v 2 = v 2+ 2 a ⨯ S⎪⎩ t 22一.基本规律:(1)平均速度 v =stvt 0(1)加速度 a = ttt(3)平均速度 v = v 0 +v2t1(2)平均速度 v = v2 t(4)瞬时速度 v = v + at(3)瞬时速度 v = attt1at 2(4)位移公式 s = at 22.导出公式(6)位移公式 s = v + v v0 t t (5)位移公式 s = t t2 2(7)重要推论 2as = v 2 - v 2t(6)重要推论 2as = v 2t注意:基本公式中(1)式适用于一切变速运动,其余各式只适用于匀变速直线运动。
二.匀变速直线运动的推论及推理对匀变速直线运动公式作进一步的推论,是掌握基础知识、训练思维、提高能力的一个重要途径,掌握运用的这些推论是解决一些特殊问题的重要手段。
t v + v = 0t2推导:设时间为 t ,初速 v ,末速为 v ,加速度为 a ,根据匀变速直线运动的速度公式 v = v + at0 t得:推论 2 做匀变速直线运动的物体在一段位移的中点的即时速度v=sv 2 + v 20 t22推导:设位移为 S ,初速 v ,末速为 v ,加速度为 a ,根据匀变速直线运动的0 t⎪vs = v 0+ 2 a ⨯2t 0 ⎨ s 2 S⇒ v =s2v 2 + v 20 t2经过第二个时间 t 后的速度为 v =2v +at ,这段时间内的位移为 S = v t + at 2 = v t + at 22 2 经过第三个时间 t 后的速度为 v =3v +at ,这段时间内的位移为 S = v t + at 2 = v t+ at 2 2 2 2 2 3 2 32 2 2 2t推论 3 做匀变速直线运动的物体,如果在连续相等的时间间隔 t 内的位移分别为 S 、 S 、 S …… S123n ,加速度为 a,则 ∆S =S 2- S 1 = S 3 - S 2= …… = S n - S推导:设开始的速度是 vn -1= at2经过第一个时间 t 后的速度为 v = v + a t ,这一段时间内的位移为 S = v t + 1 0 1 0 1 2 at 2,1 32 0 2 1 0 1 52 032…………………经过第 n 个时间 t 后的速度为 v =nv +at ,这段时间内的位移为 S =v t +1 a t 2 =v t + n 0 n n -1 02n -1 2at 2则 ∆S = S 2 - S 1 = S 3 - S 2 = …… = S n - Sn -1= at 2点拨:只要是匀加速或匀减速运动,相邻的连续的相同的时间内的位移之差,是一个与加速度 a 与时间 “有关的恒量”.这也提供了一种加速度的测量的方法: 即 a =∆S,只要测出相邻的相同时间内的位移之差 ∆S 和 t ,就容易测出加速度 a 。
匀变速直线运动的平均速度

匀变速直线运动的平均速度
匀变速直线运动的平均速度可以通过计算物体在整个运动过程中的位移和时间的比值得到。
具体计算公式为:
平均速度 = 总位移 / 总时间
其中,总位移是指物体在整个运动过程中的位移,总时间是指物体在整个运动过程中经过的时间。
在匀变速直线运动中,物体的速度不是恒定的,而是随着时间的变化而变化,但速度的变化是有规律的。
对于匀变速直线运动,可以通过加速度 a 和起始速度 v0 计算出任意时刻 t 的速度 v:
v = v0 + at
其中,v 为时刻 t 的速度,v0 为起始速度,a 为加速度,t 为时间。
根据运动学的知识,对于匀变速直线运动,物体在单位时间内的位移与速度成正比,即位移的变化率等于速度,也就是:
位移的变化率 = 速度
因此,可以将给定的速度公式 v = v0 + at 带入总位移的计算公式,得到:
总位移 = (v0 + v) / 2 * t
将总位移和总时间带入平均速度的计算公式,可以得到匀变速直线运动的平均速度公式:
平均速度 = (v0 + v) / 2
其中,v0 为起始速度,v 为结束速度。
需要注意的是,以上公式适用于匀变速直线运动,即加速度 a 为恒定值的情况。
如果加速度不是恒定值,则需要使用其他的公式计算运动的平均速度。
匀变速运动的基本公式

匀变速运动的基本公式1.三个基本公式速度公式:v t=v0+at;位移公式:s=v0t+12at2;位移速度关系式:v t2-v02=2as.2.三个推论(1)连续相等的相邻时间间隔T内的位移差等于恒量,即s2-s1=s3-s2=…=s n-s(n-1)=aT2.(2)做匀变速直线运动的物体在一段时间内的平均速度等于这段时间初末时刻速度矢量和的一半,还等于中间时刻的瞬时速度.平均速度公式:v=v0+v t2=vt2.(3)匀变速直线运动的某段位移中点的瞬时速度v s2=v02+v t22.3.初速度为零的匀加速直线运动的特殊规律(1)在1T末,2T末,3T末,…nT末的瞬时速度之比为v1∶v2∶v3∶…∶v n=1∶2∶3∶…∶n.(2)在1T内,2T内,3T内,…,nT内的位移之比为s1∶s2∶s3∶…∶s n=12∶22∶32∶…∶n2.(3)在第1个T内,第2个T内,第3个T内,…,第n个T内的位移之比为sⅠ∶sⅡ∶sⅢ∶…∶s n=1∶3∶5∶…∶(2n-1).(4)从静止开始通过连续相等的位移所用时间之比为t1∶t2∶t3∶…∶t n=1∶(2-1)∶(3-2)∶…∶(n-n-1).(5)从静止开始通过连续相等的位移时的速度之比为v1∶v2∶v3∶…∶v n=1∶2∶3∶…∶n.一.匀变速直线运动规律公式的三性(1)条件性:速度公式和位移公式的适应条件必须是物体做匀变速直线运动.(2)矢量性:位移公式和速度公式都是矢量式.(3)可逆性:由于物体运动条件的不同,解题时可进行逆向转换.限时训练1.(2009·江苏单科)图1-2-3如图1-2-3所示,以8 m/s匀速行驶的汽车即将通过路口,绿灯还有2 s就熄灭,此时汽车距离停车线18 m.该车加速时最大加速度大小为2 m/s2,减速时最大加速度大小为5m/s2.此路段允许行驶的最大速度为12.5 m/s.下列说法中正确的有().①如果立即以最大加速度做匀加速运动,在绿灯熄灭前汽车可能通过停车线②如果立即以最大加速度做匀加速运动,在绿灯熄灭前通过停车线汽车一定超速③如果立即以最大加速度做匀减速运动,在绿灯熄灭前汽车一定不能通过停车线④如果距停车线5 m处以最大加速度减速,汽车能停在停车线处A.①②B.③④C.①③D.②④2.(2010·课标全国,24)短跑名将博尔特在北京奥运会上创造了100 m和200 m短跑项目的新世界纪录,他的成绩分别是9.69 s和19.30 s.假定他在100m比赛时从发令到起跑的反应时间是0.15 s,起跑后做匀加速运动,达到最大速率后做匀速运动.200 m比赛时,反应时间及起跑后加速阶段的加速度和加速时间与100 m比赛时相同,但由于弯道和体力等因素的影响,以后的平均速率只有跑100 m时最大速率的96%.求:(1)加速所用时间和达到的最大速率;(2)起跑后做匀加速运动的加速度.(结果保留两位小数)3.(2011·重庆卷,14)某人估测一竖直枯井深度,从井口静止释放一石头并开始计时,经 2 s听到石头落底声.由此可知井深约为(不计声音传播时间,重力加速度g取10 m/s2)().A.10 m B.20 mC.30 m D.40 m4.(2011·安徽卷,16)一物体做匀加速直线运动,通过一段位移Δx所用的时间为t1,紧接着通过下一段位移Δx所用的时间为t2,则物体运动的加速度为().A.2Δx(t1-t2)t1t2(t1+t2)B.Δx(t1-t2)t1t2(t1+t2)C.2Δx(t1+t2)t1t2(t1-t2)D.Δx(t1+t2)t1t2(t1-t2).5.(2011·天津卷)质点做直线运动的位移x与时间t的关系为x=5t+t2(各物理量均采用国际单位制单位),则该质点().A.第1 s内的位移是5 mB.前2 s内的平均速度是6 m/sC.任意相邻的1s内位移差都是1 mD.任意1 s内的速度增量都是2 m/s答案 1 C 2.(1)1.29S 11.24M/S (2)8.71 3.B 4.A 5.D。
匀变速直线运动公式 推论推导 及规律总结

一.基本规律:v =ts 1.基本公式a =t v v t 0- a =tvtv =20t v v + v =t v 21at v v t +=0 at v t =021at t v s +=221at s =t v v s t 20+= t vs t 2=2022v v as t -= 22t v as =注意:基本公式中(1)式适用于一切变速运动,其余各式只适用于匀变速直线运动。
二.匀变速直线运动的推论及推理对匀变速直线运动公式作进一步的推论,是掌握基础知识、训练思维、提高能力的一个重要途径,掌握运用的这些推论是解决一些特殊问题的重要手段。
推论1 做匀变速直线运动的物体在中间时刻的即时速度等于这段时间的平均速度,即202t t v v t S v +==推导:设时间为t ,初速0v ,末速为t v ,加速度为a ,根据匀变速直线运动的速度公式at v v +=0得: ⎪⎪⎩⎪⎪⎨⎧⨯+=⨯+=22202ta v v t a v v t t t ⇒ 202t t v v v +=推论2 做匀变速直线运动的物体在一段位移的中点的即时速度22202t s v v v +=推导:设位移为S ,初速0v ,末速为t v ,加速度为a ,根据匀变速直线运动的速度和位移关系公式as v v t 2202+=得:⎪⎪⎩⎪⎪⎨⎧⨯+=⨯+=22222222022S a v v Sa v v s t s ⇒ 22202t s v v v +=推论3 做匀变速直线运动的物体,如果在连续相等的时间间隔t 内的位移分别为1S 、2S 、 3S ……n S ,加速度为a ,则=-=-=∆2312S S S S S……21at S S n n =-=-推导:设开始的速度是0v经过第一个时间t 后的速度为at v v +=01,这一段时间内的位移为20121at t v S +=, 经过第二个时间t 后的速度为at v v +=022,这段时间内的位移为202122321at t v at t v S +=+=经过第三个时间t 后的速度为at v v +=023,这段时间内的位移为202232521at t v at t v S +=+=…………………经过第n 个时间t 后的速度为at nv v n +=0,这段时间内的位移为202121221at n t v at t v S n n -+=+=- 则=-=-=∆2312S S S S S……21at S S n n =-=-点拨:只要是匀加速或匀减速运动,相邻的连续的相同的时间内的位移之差,是一个与加速度a 与时间“有关的恒量”.这也提供了一种加速度的测量的方法:即2tSa ∆=,只要测出相邻的相同时间内的位移之差S ∆和t ,就容易测出加速度a 。
专题三之匀变速直线运动3个平均速度公式的认识与应用

专题三、匀变速直线运动中3个平均速度公式的认识与应用(高2021级用)质点做匀变速直线运动,它在一段时间内的平均速度有3个计算公式,分别是:t xv =(平均速度=位移÷时间) ()t v v v +=021(平均速度=初末速度的平均)2t v v =(平均速度=中间时刻的瞬时速度)一、认识3个平均速度公式 1、平均速度=位移÷时间,即txv =。
这是平均速度的定义式,不用证明。
由于它是平均速度的定义式,因此它适用于任何运动形式,当然适用于匀变速直线运动形式。
变形式:t v x =2、某段过程的平均速度等于初、末速度的平均值,即()t v v v +=021,此式只适用于匀变速直线运动。
证明:借助v -t 图象可知,它在时间t 内发生的位移=图象下面包围的“面积”,所以t v v x t20+=,又由于t v x =,所以()t v v v +=021变形式: t v v t v x t20+==3、某段过程的平均速度等于该过程中间时刻的瞬时速度,即202tt v v v v +==,此式也只适用于匀变速直线运动。
证明:设匀变速直线运动的初速度为v 0,加速度为a ,那么运动时间t 时的末速度at v v t +=0…① 运动时间t/2时的末速度202tav v t +=…② 由①得0v v at t -=,代入②得 ()00221v v v v t t -+==2200v v v t -+ 化简得:202tt v v v +=,所以202t t v v v v +== 二、相关应用(友情提示:在匀变速直线运动中,用平均速度辅助解题,将会给我们带来很大的方便。
其中最值得运用的是公式2)【例1】某质点做匀变速直线运动,0时刻的速度v 0=+8m/s ,经过6s 时的速度v t =+5m/s ,则质点在3s 时的瞬时速度多大?【解析】已知一段运动的初、末速度,求中间时间的速度,用公式()t v v v +=021。
匀变速直线运动公式规律总结

匀变速直线运动公式、规律总结一.基本规律:v =ts 1. 公式 a =t v v t 0- a =tv tv =20t v v + v =t v 21 at v v t +=0 at v t =021at t v s +=221at s = t v v s t 20+= t v s t 2= 2022v v as t -= 22t v as =注意:基本公式中(1)式适用于一切变速运动,其余各式只适用于匀变速直线运动..................................。
二.匀变速直线运动的两个重要规律:1.匀变速直线运动中某段时间内中间时刻的瞬时速度等于这段时间内的平均速度:即2t v =v ==t s 20t v v + 2.匀变速直线运动中连续相等的时间间隔内的位移差是一个恒量:设时间间隔为T ,加速度为a ,连续相等的时间间隔内的位移分别为S 1,S 2,S 3,……S N ;则∆S=S 2-S 1=S 3-S 2= …… =S N -S N -1= aT 2注意:设在匀变速直线运动中物体在某段位移中初速度为0v ,末速度为t v ,在位移中点的瞬时速度为2s v ,则中间位置的瞬时速度为2s v =2220t v v + 无论匀加速还是匀减速总有2t v =v =20t v v +<2s v =2220t v v +三.自由落体运动和竖直上抛运动:v=2tvgtvt=s=212gt22tvgs=总结:自由落体运动就是初速度v=0,加速度a=g的匀加速直线运动.gtvvt-=2.竖直上抛运动2021gttvs-=222vvgst-=-总结:竖直上抛运动就是加速度ga-=的匀变速直线运动.四.初速度为零的匀加速直线运动规律:设T为时间单位,则有:(1)1s末、2s末、3s末、……ns末的瞬时速度之比为:v1∶v2∶v3∶……:vn=1∶2∶3∶……∶n同理可得:1T末、2T末、3T末、……nT末的瞬时速度之比为:v1∶v2∶v3∶……:vn=1∶2∶3∶……∶n(2)1s内、2s内、3s内……ns内位移之比为:S1∶S2∶S3∶……:S n=12∶22∶32∶……∶n2同理可得:1T内、2T内、3T内……nT内位移之比为:S1∶S2∶S3∶……:S n=12∶22∶32∶……∶n2(3)第一个1s内,第二个2s内,第三个3s内,……第n个1s内的位移之比为:SⅠ∶SⅡ∶SⅢ∶……:S N=1∶3∶5∶……∶(2n-1)同理可得:第一个T内,第二个T内,第三个T内,……第n个T内的位移之比为:SⅠ∶SⅡ∶SⅢ∶……:S N=1∶3∶5∶……∶(2n-1)(4)通过连续相等的位移所用时间之比为:t1∶t2∶t3∶……:t n=1∶(12-)∶(23-)∶………∶(1--nn)课时4:匀速直线运动、变速直线运动基本概念(例题)一.变速直线运动、平均速度、瞬时速度:例1:一汽车在一直线上沿同一方向运动,第一秒内通过5m,第二秒内通过10m,第三秒内通过20m,第四秒内通过5m,则最初两秒的平均速度是_________m/s,则最后两秒的平均速度是_________m/s,全部时间的平均速度是_________m/s.例2:做变速运动的物体,若前一半时间的平均速度为4m/s,后一半时间的平均速度为8m/s,则全程内的平均速度是_________m/s;若物体前一半位移的平均速度为4m/s,后一半位移的平均速度为8m/s,则全程内的平均速度是_________m/s.二.速度、速度变化量、加速度:提示:1、加速度:是表示速度改变快慢的物理量,是矢量。
匀变速直线运动公式
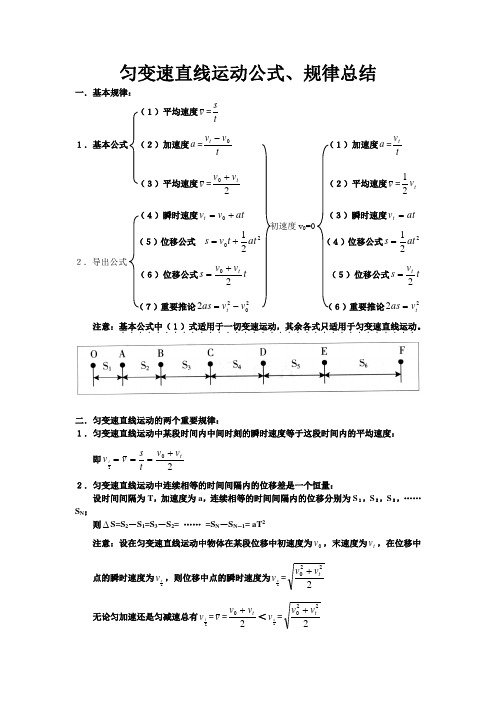
匀变速直线运动公式、规律总结一.基本规律:v =ts 1.基本公式a =t v v t 0- a =tvtv =20t v v + v =t v 21at v v t +=0 at v t =位移公式021at t v s +=位移公式221at s = t v v s t 20+= t vs t 2= 重要推论2022v v as t -= 重要推论22t v as =注意:基本公式中(1)式适用于一切变速运动,其余各式只适用于匀变速直线运动..................................。
二.匀变速直线运动的两个重要规律:1.匀变速直线运动中某段时间内中间时刻的瞬时速度等于这段时间内的平均速度: 即2t v =v ==t s 20t v v + 2.匀变速直线运动中连续相等的时间间隔内的位移差是一个恒量:设时间间隔为T ,加速度为a ,连续相等的时间间隔内的位移分别为S 1,S 2,S 3,……S N ;则∆S=S 2-S 1=S 3-S 2= …… =S N -S N -1= aT 2 注意:设在匀变速直线运动中物体在某段位移中初速度为0v ,末速度为t v ,在位移中点的瞬时速度为2s v ,则位移中点的瞬时速度为2s v =2220t v v +无论匀加速还是匀减速总有2t v =v =20t v v +<2s v =2220t v v +三.自由落体运动和竖直上抛运动:v =2tv gt v t = s =212gt22t v gs =总结:自由落体运动就是初速度0v =0,加速度a =g 的匀加速直线运动. gt v v t -=0 2.竖直上抛运动 2021gt t v s -= 2022v v gs t -=-总结:竖直上抛运动就是加速度g a -=的匀变速直线运动.四.初速度为零的匀加速直线运动规律: 设T 为时间单位,则有:(1)1T 末、2T 末、3T 末、…… nT 末的瞬时速度之比为: v1∶v2∶v3∶…… :vn =1∶2∶3∶…… ∶n (2)1T 内、2T 内、3T 内…… nT 内位移之比为: S 1∶S 2∶S 3∶…… :S n =12∶22∶32∶…… ∶n 2(3)第一个T 内,第二个T 内,第三个T 内,…… 第n 个T 内的位移之比为: S Ⅰ∶S Ⅱ∶S Ⅲ∶…… :S N =1∶3∶5∶…… ∶(2n -1) (4)通过连续相等的位移所用时间之比为:t 1∶t 2∶t 3∶…… :t n =1∶(12-)∶(23-)∶……… ∶(1--n n )。
匀变速直线运动公式归纳与推导

匀变速直线运动公式归纳及推导证明1.匀变速直线运动的两个基本公式:(1)速度公式:v =v 0+at ;(2)位移公式:x =v 0t +12at 2.2.匀变速直线运动的几个常用的导出公式:(1)速度位移公式:v 2-v 20=2ax .(2) ①中间时刻的瞬时速度公式:v t 2=v 0+v2.②中间位置的瞬时速度公式:v x 2=v 20+v22. 大小关系: v t 2< v x 2③平均速度公式:v =v t 2=v 0+v 2,即某段时间内平均速度等于这段时间中间时刻的瞬时速度,等于初、末速度的平均值.(3)在连续相等时间间隔T 内的位移之差为一恒定值,即Δx =aT 2.3.初速度为零的匀变速直线运动的几个比例式:(1).初速度为0的匀加速直线运动,按时间等分(设相等的时间间隔为T)的比例式:①1t 末、2t 末、3t 末、…、nt 末的瞬时速度之比为: v 1∶v 2∶v 3∶…∶v n =1∶2∶3∶…∶n .②前1t 内、前2t 内、前3t 内、…、nt 内的位移之比为: x 1∶x 2∶x 3∶…∶x n =12∶22∶32∶…∶n 2.③第1t 内、第2t 内、第3t 内、…、第n 个t 内的位移之比为: x Ⅰ∶x Ⅱ∶x Ⅲ∶…∶x N =1∶3∶5∶…∶(2n -1). (2).按位移等分(设相等的位移为x )的比例式 ④通过前x 、前2x 、前3x ……时的速度之比: v 1∶v 2∶v 3∶……∶v n =1∶2∶3∶……∶n⑤通过前x 、前2x 、前3x ……的位移所用时间之比: t 1∶t 2∶t 3∶……∶t n =1∶2∶3∶……∶n ⑥通过第1x 、第2x 、第3x ……所用时间之比为:t Ⅰ∶t Ⅱ∶t Ⅲ∶…∶t N =1∶(2-1)∶(3-2)∶…∶(n -n -1). 公式推导1.速度公式 由加速度的定义式a =Δv Δt =v -v 0t -0=v -v 0t,整理得:v=v 0+at .2.位移公式 x =S =12(OC +AB )·OA =12(v 0+v )t =v 0t +12at 23.速度位移公式 x =v t =v 0+v 2·v -v 0a,整理得:v 2-v 20=2ax 4.中间时刻的瞬时速度公式 v t2=v 0+a ·12t ,a =v -v 0t ,整理得:v t 2=v 0+v 2.5.中间位置的瞬时速度公式 前半段位移有v x 22-v 20=2a x2,后半段位移有v 2-v x 22=2a x2两式联立可得v x 2=v 20+v226.匀变速直线运动判别式7. 初速度为零的匀变速直线运动的几个比例式 (1)按时间等分(设相等的时间间隔为t )的比例式图示证明(2).按位移等分(设相等的位移为x )的比例式图示证明T T v 0v 0+aT . x 1=v 0T +12aT 2x 2=(v0+aT )T+12aT 2 得到连续相等时间内的位移之差为:Δx =x 2-x 1=x 3-x 2=…=x n -x n-1=aT 2 v 0=0 v 1=a ·1t v n =a ·nt (第1)t (第2)t (第n )t v 2=a ·2t x 1=12at 2 x 2=12a(2t)2 x n =12a(nt)2x Ⅰ=12at 2 x Ⅱ=x 2-x 1=3×12at 2 x N =x n -x n-1=(2n-1)· 12at 2v t Ⅱ=t 2-t 1=t Ⅰt N =t n -t n-1=v 0+a ·2T .……证②式 …证①式…证③式 …证④式 …证⑥式。
匀变速直线运动三个基本公式

匀变速直线运动的三个基本公式
速度公式:V=V0+at 解析:匀变速直线运动是加速度恒定的直线运动,速度随着时间均匀变化。
此公式为初速度为V0的匀加(减)速直线运动的某个时刻的速度V的计算公式,其中,V0是初速度;a是加速度;t是时间.
位移公式:x=V0t+½at2 解析:匀变速直线运动的初速度为V0,在时间t内的末速度为V t。
匀变速直线运动的所排成的数列可以看作等差数列。
由等差数列算术平均数公式,可知道物体运动的平均速度是(V0+V t)/2,则物体位移等于平均速度和时间的积,即:x=v0t+½at2
位移速度关系式:V2-V02=2ax.解析:通过速度公式和为一共是可以推导得出此公式。
