线性分组码的编码与译码
实验三、线性分组码的编译码

信息论与编码实验报告1、认真阅读课本中关于线性分组码的基本原理及特点等内容,并简要写出其基本原理及特点;解:基本原理:对信源编码器输出的D 进制序列进行分组,设分组长度为k ,相应的码字表示为),,,(12m m m k M ∙∙∙=→,其中每个码元()k i m i≤≤1都是D 进制的显然这样的码字共有kD 个。
特点:一个()k n ,线性分组码中非零码字的最小重量等于该码的最小距离min d 。
2、写出(7,4)线性分组码编解码基本步骤,画出程序流程图;编码流程图 译码流程图 (7,4)汉明码的编码就是将输入的4 位信息码M=[ 3456a a a a ]加上3 位监督码012b b b 从而编成7位汉明码[6a 012345,,,,,a a a a a a ],编码输出B=[6a 5a 4a 3a 2a 1a 0a ].由式A = M ·G=[3456a a a a ]·G 可知,信息码M 与生成矩阵G 的乘积就 是编好以后的(7,4)汉明码3、实现(7,4)线性分组码编解码的Matlab源程序;构造BSC传输信道中采用(7,4)线性分组码的Simulink仿真程序。
(7,4)汉明码的编码程序:library ieee;use ieee.std_logic_1164.all;entity bm isport(a:in std_logic_vector(3 downto 0);but std_logic_vector(6 downto 0));end ;architecture one of bm isbeginb(6)<=a(3);b(5)<=a(2);b(4)<=a(1);b(3)<=a(0);b(2)<=a(3) xor a(2) xor a(1);b(1)<=a(3) xor a(2) xor a(0);b(0)<=a(3) xor a(1) xor a(0);end;(7,4)汉明码的译码程序:library ieee;use ieee.std_logic_1164.all;entity ym isport(a:in std_logic_vector(6 downto 0);sut std_logic_vector(2 downto 0);but std_logic_vector(3 downto 0);cut std_logic_vector(2 downto 0));end ;architecture one of ym isbeginprocess(a)variable ss:std_logic_vector(2 downto 0);variable bb:std_logic_vector(6 downto 0);beginss(2):=a(6) xor a(5) xor a(4) xor a(2);ss(1):=a(6) xor a(5) xor a(3) xor a(1);ss(0):=a(6) xor a(4) xor a(3) xor a(0);bb:=a;if ss> "000" thencase ss iswhen "001" =>bb(0):= not bb(0);c<="000";when "010" =>bb(1):= not bb(1);c<="001";when "100" =>bb(2):=not bb(2);c<="010";when "011" =>bb(3):=not bb(3);c<="011";when "101" =>bb(4):=not bb(4);c<="100";when "110" =>bb(5):=not bb(5);c<="101";when "111" =>bb(6):=not bb(6);c<="110";when others => null;c<="111";end case;else b<= a(6)&a(5)&a(4)&a(3);end if;s<=ss;b<=bb(6)&bb(5)&bb(4)&bb(3);end process;end;4、讨论(7,4)线性分组码的最小码距与码重及纠错能力的关系,讨论采用纠错编码和不采用纠错编码对传输系统的影响。
61线性分组码

C = (Cn-1,Cn-2,…,C1,C0 )
所以码字又称为码矢。
( n, k ) 线性码:信息位长为 k,码长为 n 的线性码。
编码效率/编码速率/码率:R=k /n。它说明了信道的利用效率, R是衡量码性能的一个重要参数。
2013/7/31
2
线性分组码的编码:线性分组码的编码过程分为两步:
面 k 位为信息数字,后面 r=n-k 位为校验字,这种信息数字 在前校验数字在后的线性分组码称为线性系统分组码。
信息数字 校验数字
图6.2.1 系统码的码字结构
当生成矩阵 G 确定之后,(n,k) 线性码也就完全被确定了,只要 找到码的生成矩阵,编码问题也同样被解决了。
[ 参见下面有关(7,4)线性码例子 ]
设码字矢量为C = (C6 C5C4C3C2C1C0) 码的监督矩阵为
2013/7/31
31
6.3.4 线性分组码的编码
根据方程组可直接画出 (7,3) 码的并行编码电路和串行编码 电路,如图。
m2 m1 m0 C6 C5 C4 C3
C m
C2
C1
C0
(a)并行编码电路 (b)串行编码电路
2013/7/31
4
6.3.2 线性分组码的监督方程和监督矩阵
(1) 监督方程
编码就是给已知信息码组按预定规则添加监督码元,以构成码字。 在 k 个信息码元之后附加 r(r=n-k) 个监督码元,使每个监督元是 其中某些信息元的模2和。 举例:k=3, r=4,构成 (7,3) 线性分组码。设码字为
2013/7/31
线性分组码的编码与译码

实践教学大学计算机与通信学院2014年秋季学期计算机通信课稈设计题目:线性分组码(9 , 4)码的编译码仿真设计专业班级:_______________________________姓名:_________________________________________学号:_______________________________________指导教师:______________________________________成绩:______________________________________________摘要该系统是(9, 4)线性分组码的编码和译码的实现,它可以对输入的四位的信息码进行线性分组码编码,对于接收到的九位码字可以进行译码,从而译出四位信息码。
当接收到的九位码字中有一位发生错误时,可以纠正这一位错码;当接收到的码字有两位发生错误时,只能纠正一位错误,但同时能检测出另一位错误不能纠正。
只有特定位有两位错误时,才能纠正两位错误。
这样就译出正确的信息码组,整个过程是用MATLAB语言实现的。
关键词:编码;译码;纠错摘要 目录1. 信道编码概述2.•…1.1信道模型 ............................................................... 2•…1.2抗干扰信道编码定理及逆定理 ............................................ 3…1.3检错与纠错的基本原理 .................................................. 4•…1.4限失真编码定理 ........................................................ 5•…2. 线性分组码的编码 ........................................................... 6 _2.1生成矩阵 ............................................................... 6•…2.2校验矩阵 ............................................................... 9•…2.3伴随式与译码 ......................................................... 1.0....3. 线性分组码编码的 Matlab 仿真 ............................................... 1.2..3.1程序流程图 ............................................................ 1.2....3.2程序执行结果 ......................................................... 12....3.2线性分组码译码的 Matlab 仿真 .......................................... 1.3.3.3结果分析 .............................................................. 1.5.... 参考文献 .................................................................... .1.6..... 总结 ......................................................................... 1.7.... 致谢 ......................................................................... 1.8.... 附录目录19刖言由于计算机、卫星通信及高速数据网的飞速发展,数据的交换、处理和存储技术得到了广泛的应用,数字信号在传输中往往由于各种原因,使得在传送的数据流中产生误码,从而使接收端产生图象跳跃、不连续、出现马赛克等现象,人们对数据传输和存储系统的可靠性提出来了越来越高的要求,经过长时间的努力,通过编译码来控制差错、提高可靠性的方式在信道传输中得到了大量的使用和发展,并形成了一门新的技术叫做纠错编码技术,纠错编码按其码字结构形式和对信息序列处理方式的不同分为两大类:分组码和卷积码。
线性分组码的译码

一、实验目的1、通过实验掌握线性分组码的编码原理2、通过实验掌握线性分组码的译码3、了解编码与检错能力之间的关系二、实验内容1、自行设置线性分组码或汉明码的参数,计算所设计出的线性分组码或汉明码的所有码字集合;2、利用库函数译码或利用通信工具箱设计译码模块译码;3、整理好所有的程序清单或设计模块,并作注释。
三、实验结果1、写出产生(3,1)汉明码的生成矩阵,给出生成码的源程序,并给出运行结果。
(1)、源程序function f=hanmingencod(a) %对信息元a进行编码G=[1 1 1]; %(3,1)的生成矩阵t=input('输入0或1:'); %t=0时产生(3,1),汉明编码所有码字t=1时对输入序列进行编码if t==1;a=input('输入信息元序列:'); %当t=0时,则用户手动输入信息元序列c=mod(a*G,2); %对应码字disp('编码后序列为:');disp(c); %显示编码后的结果elsedisp('(3,1)汉明系统为:');%当t=0时,对for循环得到的信息元序列进行编码for i=0:1%进行for循环,得到信息元序列a=dec2bin(i,1); %生成信息源序列c=mod(a*G,2); %对信息元a进行编码disp(a); %显示信息元disp('对应码字为:');disp(c); %显示编码结果endend(2)运行结果:输入0或者1:0(3,1)汉明系统码为:对应码字为:0 0 01对应码字为: 1 1 1输入0或者1:1输入信息元序列:0编码后序列为: 0 0 0输入0或者1:1输入信息元序列:1编码后序列为: 1 1 1(3)、计算生成矩阵:由(3,1)汉明码可知:n=3,k=1;即信源符号1位一组:{}(),0,1,0,1,2,3;i i u u u i =∈=码符号3位一组:{}210(,,),0,1,0,1,2,3,4,5,6;j c c c c c j =∈=则可得其生成矩阵:[]1,1,1G = 或者校验矩阵H=⎥⎦⎤⎢⎣⎡110110=⎥⎦⎤⎢⎣⎡100111 所以生成矩阵[]1,1,1G =2、用encode函数对随机产生的序列进行汉明编码,给出编码结果。
线性分组码
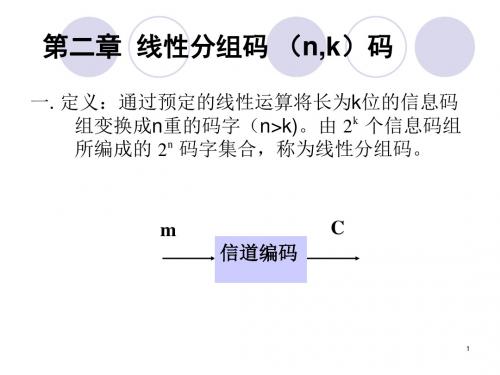
C mG
G是一个k*n阶矩阵,称为(n,k)码的生成矩阵。
7
1 0 G 0
0 0 1 0 0 1
p11 p 21 p k1
p12 p 22 pk 2
p1( n k ) p 2( nk ) I P k pk ( nk )
n 1
u和v之间的距离表示2个码字对应位不同的数目。
如(7,3)码的两个码字:u=0011101
v=0100111
它们之间的距离d=4
4
码的最小距离的dmin :在(n,k)线性码字集合中, 任意两个码字间的距离最小值,是衡量抗干扰能力的 重要参数,dmin越大,抗干扰能力越强。 码字的重量W:码字中非零码元符号的个数;在二元 线性码中,码字的重量是码字中含“1”的个数。 码的最小重量Wmin:线性分组码中,非零码字重量的 最小值,称为码的最小重量,表示为:
限, 性能界限,即码的译码错误概率的上、下 限。 对码距限而言,最重要的限是汉明限,普 洛特金限和吉尔伯特-瓦尔沙莫夫限,汉 明码和普洛特金限告诉我们,在给定码长n 和码的传输速率R=k/n下,最小距离可以达 到的最大值,故它们都是上限,而吉尔伯 特一瓦尔沙莫夫限给出了码的最小距离的 下限。
HC 0
T
T
r=n-k
H
阵是n列,(n-k)行的矩阵;
为了得到确定的码,r个监督方程必须是线性
无关的,即要求H阵的秩为r。
6
2. 生成矩阵G
把方程组写成矩阵的形式为
h11 h 21 h r1
h12 h1k h 22 h 2k h r2 h rk
m 信道编码
C
线性分组码

二、线性分组码的严格数学定义2
2. 定理1 (码的封闭性)
设CH为由监督矩阵H定义的分组码,则c1,c2CH : c1+c2CH 证明: 由c1CH,得Hc1T=0T;
由c2CH,得Hc2T=0T;
所以 H(c1+c2)T=H(c1T+c2T) =Hc1T+Hc2T=0T c1+c2满足HcT=0T,所以c1+c2 CH
+
+
考虑如何用串行方式?
三、G与H的关系4
0 1 2 3 4 5 6 7 8 9 10 11 12 13
D0
D1
+
D2
+
D3
+
D0
D1
+
D2
+
D3
+
m4m5m6
m6
m6
D0
D1
m6+m5 m6
D0
D1
m6
m6
+
D2
+
D3
+
m4m5
m6+m5
m6+m5
+
D2
m6+m5+m6
=m5
+
D3
+
m4
m5+m4
互为对偶码,若CH=CG, 则称为自对偶码(P62)
[Q In-k] [IkP]T= [QIn-k] [IkT PT]T= Q + PT = 0
所以 P= - QT 或 Q = -PT
由此得 G=[Ik P] = [ Ik –QT] H=[Q In-k]= [ -PT In-k]
三、G与H的关系2
8.2 线性分组码 线性分组码编码

8.2 线性分组码
线性分组码的编码
1
引言
• 信道编码,目的是提高数字通信的可靠性
– 差错率是信噪比的函数
• 信道编码,差错控制编码,抗干扰编码
• 信道编码过程:
– 信息码元序列+监督码元→编码码组
• 信道译码过程:
– 编码码组→检错或纠错→信息码元序列
2
1. 线性分组码的概念
1 0 0
G=0 1 0 0 1 1
1 0 1
0 0 1 1 1 0
1 1 0
1 1 1
7
由式
,得码组矩阵为:
0 0 0 0 0 1
0 0 0 0 0 0 0 0 1 1 1 0
0 C=0
1
1 1 0
0 1
0
1 0 0
0 1 0
0 0 1
1 0 1
0 1 1
110=100
1 1 0
0 1 0
0 1 1
6
有缘学习更多+谓ygd3076考证资料或关注桃报:奉献教育(店铺)
例8-1 已知(6,3)码的生成矩阵为G,试求:(1) 编码码组 和各码组的码重;(2) 最小码距 d及min其差错控制能力。
解
(1) 由3位码组成的信息码组矩阵为D:
0 0
0 0
0 1
0 1 0
1 0 0 1 0 1
0 1 1
D=
ck = dk
ck +1 ck+2
= =
h11d1 h12d2 h1k dk h21d1 h22d2 h2k dk
G生成矩阵
cn = hm1d1 hm2d2 hmk dk
5
写成矩阵形式,有 C = D G ,G为生成矩阵(k*n),且:
信息论基础——线性分组码
17
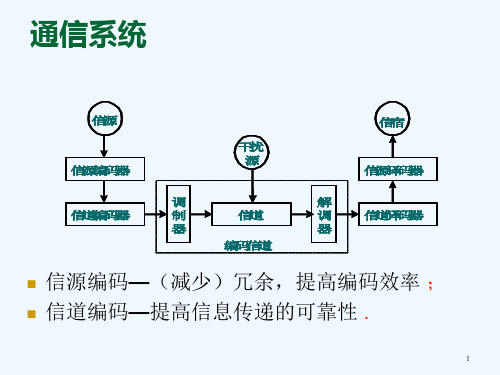
线性分组码的基本概念
信息位 00 01 10 11 x2 x0 x1 00000 x3 x0 x x x 01101 0 1 4 码字 10111 11010
信息位k=2 码字数M=4
可见,码字的三个校验元都由其前两位线 性组合得到,即可由的线性方程组求得;
18
线性分组码的基本概念
f1 : GF (2) 2 GF (2)5
信息位 00 01 10 11 码字 00000 01101 10111 11010
1 ( 0 1 ) 1 ( 1 0 ) 1 1
f( 1 1 ) 1 1 0 1 0
1 ( 0 1 1 0 1 )1 ( 1 0 1 1 1 ) 1 1 0 1 0
30
线性分组码的基本概念
汉明距离: 指(n,k)分组码中两个码字xn 、 yn对应位取 值不同的个数;记为d(xn , yn).
5 5 ( 1 0 1 0 1 ) , y ( 0 1 1 1 1 ) 例: x
d(x ,y ) 3
5 5
31
线性分组码的基本概念
线性分组码的最小距离: 称(n,k)分组码中任两个码字汉明距离的最小 值,为该分组码的最小距离d.
f ( 1 ( 0 1 ) 1 ( 1 0 ) ) 1 ( 0 1 1 0 1 ) 1 ( 1 0 1 1 1 ) 线性编码
19
线性分组码的基本概念
例题1: 下面是某个(n,k)线性二元码的全部码字
x16=000000 x26=100011 x36=010101 x46=001111 x56=110110 x66=101100 x76=011010 x86=111001 求n、k的值;
线性分组码的编译码要点

******************实践教学******************兰州理工大学计算机与通信学院2013年秋季学期计算机通信课程设计题目:线性分组码(7,3)码的编译码仿真设计专业班级:通信工程三班姓名:彭佳峰学号: 10250302 指导教师:彭铎成绩:摘要本课题是应用C语言对(7,3)线性分组码的编译码的软件设计。
主要做了一下几项工作:对三位正确的信息码进行编码;若输入的三位信息码有错,系统输出提醒,可以重新输入;对七位接收到的码字判断是否有错,并在无错和有一位错误时进行译码,在有多位错误时输出提醒,可以选择重新输入。
关键字:线性分组码编码译码 C语言目录前言 (1)1 基本原理 (2)1.1线性分组码的基本概念 (2)1.2差错控制原理 (2)1.3线性分组码的纠检错能力 (3)2线性分组码的编码 (4)2.1监督矩阵 (4)2.2生成矩阵 (5)3线性分组码的译码 (7)4设计与仿真 (9)4.1 C语言平台简介 (9)4.2整体流程图 (9)4.3编码流程图 (10)4.4译码流程图 (10)5 仿真结果及分析 (11)设计总结 (17)参考文献 (18)致谢 (19)附录 (20)前言近年来,随着计算机、卫星通信及高速数据网的飞速发展,数据的交换、处理和存储技术得到了广泛应用,人们对数据传输和存储系统的可靠性提出了越来越高的要求。
因此,如何控制差错、提高数据传输和存储的可靠性,成为现代数字通信系统设计工作者所面临的重要课题。
香农第二定理指出,当信息传输率低于信道容量时,通过某种编译码方法,就能使错误率为任意小。
差错控制编码在此定理指导下迅速发展起来,它使得传输数据本身带有规律性,利用规律性来减少错误。
线性分组码是差错控制编码的重要一种。
它的规律性在于局限在一个码组之内,编码后长为n的一个码组中含有k位信息元和n-k位监督元,监督元是随所传输的信息元而改变的。
接收端正式通过监督元和信息元之间的规律性来发现并纠正错误的。
线性分组码的编码方法

线性分组码的编码方法0 引言随着通信技术的飞速发展,数字信息的存储和交换日益增加,对于数据传输过程中的可靠性要求也越来越高,数字通信要求传输过程中所造成的数码差错足够低。
引起传输差错的根本原因是信道内的噪声及信道特性的不理想。
要进一步提高通信系统的可靠性,就需采用纠错编码技术。
1线性分组码线性分组码是差错控制编码的一种,它的编码规则是在k 个信息位之后附加r=(n-k )个监督码元,每个监督码元都是其中某些信息位的模2和,即(n-k )个附加码元是由信息码元按某种规则设计的线性方程组运算产生,则称为线性分组码(linear block code )。
目前,绝大多数的数字计算机和数字通信系统中广泛采用二进制形式的码元,因此以下对线性分组码的讨论都是在有限域GF (2)上进行的,域中元素为0、1。
以(7,3)线性分组码为例,(7,3)线性分组码的信息组长度k=3,在每个信息组后加上4个监督码元,每个码元取值“0”或“1”。
设该码字为(C 6,C 5,C 4,C 3,C 2,C 1,C 0)。
其中C 6,C 5,C 4是信息位,C 3,C 2,C 1,C 0是监督位,监督位可以按下面的方程计算:463C C C +=4562C C C C ++=(1)561C C C += 450C C C +=以上四式构成了线性方程组,它确定了由信息位得到监督位的规则,称为监督方程或校验方程。
由于所有的码字都按同一规则确定,因此上式又称为一致监督方程或一致校验方程,这种编码方法称为一致监督编码或称一致校验编码。
由式(1)可以得出,每给出一个3位的信息组,就可以编出一个7位的码字,同理可以求出其它7个信息组所对应的码字。
2 生成矩阵和一致校验矩阵(n ,k )线性分组码的编码问题,就是如何从n 维线性空间V n 中,找出满足一定要求的,由2k个矢量组成的k 维线性子空间;或者说在满足一定条件下,如何根据已知的k 个信息元求得n-k 个校验元。
基于MATLAB的线性分组码编译码仿真实现设计说明书

信息工程学院通信工程系设计题目:基于MATLAB的线性分组码编译码仿真设计班级:10通信班学号:姓名:指导老师:2013 年11 月15 日成绩:摘要该系统是(6,3)线性分组码的编码和译码的实现,它可以对输入的三位的信息码进行线性分组码编码,对于接收到的六位码字可以进行译码,从而译出三位信息码。
当接收到的六位码字中有一位发生错误时,可以纠正这一位错码;当接收到的码字有两位发生错误时,只能纠正一位错误,但同时能检测出另一位错误不能纠正。
只有特定位有两位错误时,才能纠正两位错误。
这样就译出正确的信息码组,整个过程是用MATLAB语言实现的。
关键词:编码; 译码; 纠错目录前言 (2)第1章设计目标 (2)第2章 MATLAB简介 (3)第3章基本原理 (3)3.1 线性分组码的编码 (3)3.1.1 生成矩阵 (3)3.1.2 校验矩阵 (5)3.2 伴随式与译码 (6)3.2.1 码的距离及纠检错能力 (6)3.2.2 伴随式与译码 (6)第4章推导过程 (7)4.1 编码过程 (7)4.2 译码过程 (9)第5章仿真程序及结果分析 (11)5.1 仿真程序 (11)5.2 仿真结果图 (13)5.3 结果分析 (15)参考文献 (16)总结 (17)0 1 11 0 1 1 1 0 前言近年来,随着计算机、卫星通信及高速数据网的飞速发展,数据的交换、处理和存储技术得到了广泛的应用,人们对数据传输和存储系统的可靠性提出了越来越高的要求。
因此,如何控制差错、提高数据传输和存储的可靠性,成为现代数字通信系统设计的重要课题。
目前,绝大多数的数字计算机和数字通信系统中广泛采用二进制形式的码。
而线性分组码具有编译码简单,封闭性好等特点,采用差错控制编码技术是提高数字通信可靠性的有效方法,是目前较为流行的差错控制编码技术。
对线性分组码的讨论都在有限域GF(2)上进行,域中元素为{0,1},域中元素计算为模二加法和模二乘法。
线性码与线性分组码

集。汉明限,球包限:k/n 1-H2(d/2n)。随机分组码译码需要2k次长为n的距离计算及比较
Image
第二十页,共20页。
• 说明约束起了作用,但还不够,需要进 一步引入其它约束
第十九页,共20页。
内容(nèiróng)总结
第三讲。现实的做法是对编码方案加以一定的约束,在一个子集中寻找局部最优。群——定义了一种运算 (yùn suàn)的集合。环——定义了两种运算(yùn suàn)的集合。域——一种特殊的环。无限域和有限域。就给定群G
第十六页,共20页。
最大的自由距存在(cúnzài)区间
第十七页,共20页。
线性分组码译码的基本(jīběn)方法
• 码C作为一个(yī ɡè)子群,它的每一个(yī 陪 ɡè) 集在码C的正交空间H中的投影是一个点, 而不同的陪集投影不同。
• 每一个陪集有一个最小码重,作为陪集 首,代表最可能的错误图案。
• 这就引出了伴随式译码:s=rHT,将s与 最可能的e建一张表,即可通过查表法实 现译码。
第十八页,共20页。
小结(xiǎojié):引入线性码的好处
• 简化了分析:距离谱变成了重量谱 • 简化了译码:
– 随机分组码译码需要2k次长为n的距离计算 及比较(bǐjiào)
– 线性分组码译码需要n-k次长为n的矢量内积 和一张大小为2n-k宽度为n的表
码
• 利用线性空间中的子空间作为许用码字的编码称线 性码
• 当线性空间为有限(yǒuxiàn)维空间时即为线性分组码 • GF(q)上的n维线性空间Vn中的一个k维子空间Vn,k称
实验四 线性分组码的信道编码和译码

一致性校验矩阵如下:
一般情况下:G是k*N生成矩阵;H为r*N一致性校验 矩阵,r =N-k为校验数目。
H和G的关系为:G=[Ik*K Ak*r] H=[Ak*r Ir*r] 纠错译码时,若发送码字为 c ,则接收序列为 y ,校
实验四 线性分组码的信道编码和译码
一、实验目的
熟悉 Matlab 工作环境及工具箱; 掌握线性分组码的编码、译码原理以及纠错原
理。
二、实验原理
信源发出的信息序列通常不能直接传送给信道传输, 它们需要经过某种变换使其适合信道传输。
变换——编码和译码 信道编码:
降低平均差错率,提高传送的可靠性——纠错编码。 纠错编码:
简述实验目的; 简述实验原理; 根据不同的线性分组码,观察生成矩阵和校验
矩阵的特性。 根据不同的线性分组码,分析检错和纠错能力。
正s=y*HT=e*HT 。
因此,可以得到译码 c=y e 。 其中,e称为差错图样。 S是传输是否出错的标志,称为伴随式。
三、实验内容
(5,2) 线性分组码的最小汉明距离为dmin=3,能够检出 2位错误或纠正1位错误。
线性分组码的信道编码和译码流程图 信道编码流程图
译码流程图
四、实验报告要求
例如,对于(5,2)分组码,N=5,K=2,其编码函数f
为:信息组是二元符号序列,用矩阵表示为m=[m1,m2] 码字长度为N=5,用矩阵表示为C=[C1,C2,C3,C4,C5]
编码函数fห้องสมุดไป่ตู้
由编码函数可知:c(码字)=m(信息矩阵)G(生成矩阵) 生成矩阵
生成矩阵确定以后,由编码函数的后三个方程可以确 定检验方程。
bch码编码规则

bch码编码规则
BCH码的编码规则如下:
1. 把消息组变换成码字的过程称为编码,其逆过程称为译码。
2. 编码时,给定消息组m=(m1,m2,…,mκ),按照生成矩阵G,m被
编为mG=m1E1+m2E2+…+mκEκ,这就是线性分组码的编码规则。
3. 生成的码字需要满足一定的条件,即秩为n-κ并且满足GH=0,仅当
=(v1,v2,…,vn)∈n满足H=0时,才为κ中的码字。
H为(n,κ)线性分组
码κ的均等校验矩阵,也称为矢量的伴随式。
4. BCH编码实现的关键是通过除法电路得到校验位多项式。
5. 如果发送的码矢量v在接收端获得一个失真的矢量r=v+E,式中E=(e1,e2,…,en)称为错误型,那么rH=(v+e)H=eH线性码的译码原则便以此
为基础。
以上信息仅供参考,如需获取更多信息,建议查阅BCH码相关书籍或咨询
专业人士。
线性分组码

2011/10/31
26
2、某(n,k)系统线性分组码的全部码字如下: 、 )系统线性分组码的全部码字如下: 00000 01011 10110 11101 求: (1)n = ? , k = ? ) 和监督矩阵H。 (2)码的生成矩阵 和监督矩阵 。 )码的生成矩阵G和监督矩阵
2011/10/31
系数矩阵 H 的后四列组成一个 (4×4) 阶单位子阵,用 I4 表示,H 的其余部分用 P 表示
2011/10/31
8
6.3.2 线性分组码的监督方程和监督矩阵
推广到一般情况:对 (n,k) 线性分组码,每个码字中的 r(r=n-k) 个监督元与信息元之间的关系可由下面的线性 方程组确定
2011/10/31
010 011 100 101 110 111
6.3.2 线性分组码的监督方程和监督矩阵
(3) 监督矩阵
为了运算方便,将式 (5.1)监督方程写成 矩阵形式,得 式(5.2)可写成 H CT=0T或 C HT=0 CT、HT、0T分别表 示C、H、0的转置 矩阵。
2011/10/31
7
6.3.2 线性分组码的监督方程和监督矩阵
6. 3 一、名词解释
线性分组码
线性分组码:通过预定的线性运算将长为 k 位的信息码组变换 成 n 长的码字 ( n>k )。由 2k 个信息码组所编成的 2k个码字集 合,称为线性分组码。 码矢:一个 n 长的码字可以用矢量来表示 码矢
C = (Cn-1,Cn-2,…,C1,C0 ) 1 2
所以码字又称为码矢。 ( n, k ) 线性码 线性码:信息位长为 k,码长为 n 的线性码。 编码效率/编码速率/码率:R=k /n。它说明了信道的利用效率, 编码效率 R是衡量码性能的一个重要参数。 是衡量码性能的一个重要参数
基于线性分组码的最优编译码方法

2 编译 码 方 法 分 析
2 1 编 码 过 程 .
表 2 系统 码 字
对 于 ( 志 线 性 分 组 码 , 虑 m 信 息 G 生 , ) 考 成 矩 阵 C 发 码 , 校 验矩 阵 为 : H
M X G— C () 1
2 2 译 码 过 程 .
在 无ቤተ መጻሕፍቲ ባይዱ 错 条件下 ,
收 稿 日期 : 0 1 1 一 7 2 1 - 2O
作者简介 : 刘
1 6 9
可 能 的 E, 据 E 可 以 列 出标 准 矩 阵译 码 表 , 得 根 值 注 意 的 是 在 各 个 S下 的 E 的 解 可 能 不 是 唯 一 的 , 但
则 将 ( ) 入 ( ) 得 H×G—E, 2带 1式 即对 于生 成矩 阵 C的选 择 必须 要 存在 一个 对 应 的校 验矩 阵 H , 使
中 图分 类号 : N9 1 2 T l. 2
文 献标 识 码 : A
文 章 编 号 : 6 4 9 4 ( 0 2 0 — 1 60 1 7 — 9 4 2 1 ) 10 9 — 2
1 引 言
根据 线性 分组 码定 理 , 线 性分 组码 的最小 ( ) , 码 距 必然 小 于 等 于 —k l 即 D ≤ —k 1 使 + , + , 得 等 号取 得 的编码 叫 MD C码 , 二进 制 情 况 下 , 在 除
摘 要 : 出 了信 道 编 码 旨在 增 强 差错 控 制 和 提 高纠 检 错 能 力 。 分 析 了信 息 编 码 在 通 信 系统 中的 作 用 , 指 探
讨 了基 于 线 性 分 组 码 的 最 优 编 译 码 方 法 。 关 键 词 : 道 编 码 ; 性 分 组 码 ; 干扰 ; 错 控 制 信 线 抗 差
线性分组码编码与译码共32页

71、既然我已经踏上这条道路,那么,任何东西都不应妨碍我沿着这条路走下去。——康德 72、家庭成为快乐的种子在外也不致成为障碍物但在旅行之际却是夜间的伴侣。——西塞罗 73、坚持意志伟大的事业需要始终不渝的精神。——伏尔泰 74、路漫漫其修道远,吾将上下而求索。——屈原 7与译码
46、法律有权打破平静。——马·格林 47、在一千磅法律里,没有一盎司仁 爱。— —英国
48、法律一多,公正就少。——托·富 勒 49、犯罪总是以惩罚相补偿;只有处 罚才能 使犯罪 得到偿 还。— —达雷 尔
50、弱者比强者更能得到法律的保护 。—— 威·厄尔
谢谢你的阅读
实验二线性分组码的编译码报告

实验二线性分组码的编译码报告1.实验目的线性分组码是一种常用的编码方式,本实验旨在通过对线性分组码的编码与解码操作,加深对线性分组码的理解,并掌握编码与解码的基本方法。
2.实验原理2.1线性分组码线性分组码是一种纠错码,通过在数据中嵌入冗余信息,使得数据在传输或存储过程中能够进行纠错。
线性分组码中的每个码字都由一系列的信息位和校验位组成,校验位的数量和位置由特定的生成矩阵决定。
2.2编码编码是将信息位转换为码字的过程。
对于线性分组码,编码过程可以通过生成矩阵来实现。
生成矩阵是一个以二进制元素组成的矩阵,其列数等于码字的长度,行数等于信息位的长度。
生成矩阵的乘法运算可以将信息位转换为码字。
2.3解码解码是将接收到的码字转换为信息位的过程。
对于线性分组码,解码过程可以通过校验矩阵来实现。
校验矩阵是生成矩阵的转置矩阵,其列数等于校验位的数量,行数等于码字的长度。
解码过程可以通过校验矩阵的乘法运算来恢复信息位。
3.实验内容3.1编码操作首先,选择一个合适的生成矩阵,根据生成矩阵进行编码操作。
具体步骤如下:1)定义生成矩阵,并将其转换为标准型;2)输入信息位;3)将信息位与生成矩阵相乘,得到码字;4)输出码字。
3.2解码操作在编码操作完成后,进行解码操作,根据生成矩阵得到校验矩阵,并根据校验矩阵进行解码操作。
具体步骤如下:1)根据生成矩阵得到校验矩阵;2)输入码字;3)将码字与校验矩阵相乘,得到校验位;4)判断校验位是否全为0,若是则解码成功,将码字中的信息位输出;若不是,则说明有错误发生,进行纠错操作。
4.实验结果与分析通过编码与解码的操作,得到了编码后的码字,并成功地将码字解码为原始信息位。
在解码过程中,如果校验位全为0,则说明接收到的码字没有发生错误,并且成功恢复出了信息位。
5.实验总结通过本次实验,深入理解了线性分组码的编码与解码原理,并掌握了编码与解码的基本方法。
线性分组码是一种常用的纠错码,其应用广泛,并且在通信与存储领域发挥着重要作用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
···················实践教学···················大学计算机与通信学院2014年秋季学期计算机通信课程设计题目:线性分组码(9,4)码的编译码仿真设计专业班级:姓名:学号:指导教师:成绩:摘要该系统是(9,4)线性分组码的编码和译码的实现,它可以对输入的四位的信息码进行线性分组码编码,对于接收到的九位码字可以进行译码,从而译出四位信息码。
当接收到的九位码字中有一位发生错误时,可以纠正这一位错码;当接收到的码字有两位发生错误时,只能纠正一位错误,但同时能检测出另一位错误不能纠正。
只有特定位有两位错误时,才能纠正两位错误。
这样就译出正确的信息码组,整个过程是用MATLAB语言实现的。
关键词:编码; 译码; 纠错目录摘要 (1)目录 (2)1. 信道编码概述 (2)1.1信道模型 (2)1.2 抗干扰信道编码定理及逆定理 (3)1.3 检错与纠错的基本原理 (4)1.4 限失真编码定理 (5)2.线性分组码的编码 (6)2.1 生成矩阵 (6)2.2 校验矩阵 (9)2.3 伴随式与译码 (10)3. 线性分组码编码的Matlab仿真 (12)3.1 程序流程图 (12)3.2 程序执行结果 (12)3.2 线性分组码译码的Matlab仿真 (13)3.3结果分析 (15)参考文献 (16)总结 (17)致谢 (18)附录 (19)前言由于计算机、卫星通信及高速数据网的飞速发展,数据的交换、处理和存储技术得到了广泛的应用,数字信号在传输中往往由于各种原因,使得在传送的数据流中产生误码,从而使接收端产生图象跳跃、不连续、出现马赛克等现象,人们对数据传输和存储系统的可靠性提出来了越来越高的要求,经过长时间的努力,通过编译码来控制差错、提高可靠性的方式在信道传输中得到了大量的使用和发展,并形成了一门新的技术叫做纠错编码技术,纠错编码按其码字结构形式和对信息序列处理方式的不同分为两大类:分组码和卷积码。
目前,绝大多数的数字计算机和数字通信系统中广泛采用二进制形式的码。
而线性分组码具有编译码简单,封闭性好等特点,采用差错控制编码技术是提高数字通信可靠性的有效方法,是目前较为流行的差错控制编码技术。
对线性分组码的讨论都在有限域GF(2)上进行,域中元素为{0,1},域中元素计算为模二加法和模二乘法。
分组码是一组固定长度的码组,可表示为(n , k),通常它用于前向纠错。
在分组码中,监督位被加到信息位之后,形成新的码。
在编码时,k个信息位被编为n位码组长度,而n-k个监督位的作用就是实现检错与纠错。
对于长度为n的二进制线性分组码,它有种2n可能的码组,从2n种码组中,可以选择M=2k个码组(k<n)组成一种码。
这样,一个k比特信息的线性分组码可以映射到一个长度为n码组上,该码组是从M=2k个码组构成的码集中选出来的,这样剩下的码组就可以对这个分组码进行检错或纠错。
1. 信道编码概述1.1信道模型信息必须首先转换成能在信道中传输或存储的信息后才能通过信道传送给收信者。
在信息传输过程中,噪声或干扰主要是从信道引入的,它使信息通过信道传输后产生错误和失真。
因此信道的输入和输出之间一般不是确定的函数关系,而是统计依赖的关系。
只要知道信道的输入信号、输出信号以及它们之间的统计依赖关系,就可以确定信道的全部特性。
信道的种类很多,这里只研究无反馈、固定参数的单用户离散信道。
1.离散信道的数学模型离散信道的数学模型一般如图6.1所示。
图中输入和输出信号用随机矢量表示,输入信号为X = (X 1, X 2,…, X N ),输出信号为Y = (Y 1, Y 2,…, Y N );每个随机变量X i 和Y i 又分别取值于符号集A ={a 1, a 2, …, a r }和B ={b 1, b 2, …, b s },其中r 不一定等于s ;条件概率P (y |x )描述了输入信号和输出信号之间的统计依赖关系,反映了信道的统计特性。
),...,,(21N X X X X = )|(x y P ),...,,(21N Y Y Y Y =∑=1)|(x y P图1.1 离散信道模型根据信道的统计特性即条件概率P (y |x ) 的不同,离散信道可以分为三种情况:(1)无干扰信道。
信道中没有随机干扰或干扰很小,输出信号Y 与输入信号X 之间有确定的一一对应的关系。
(2)有干扰无记忆信道。
实际信道中常有干扰,即输出符号与输入符号之间没有确定的对应关系。
若信道任一时刻的输出符号只统计依赖于对应时刻的输入符号,而与非对应时刻的输入符号及其他任何时刻的输出符号无关,则这种信道称为无记忆信道。
(3)有干扰有记忆信道。
这是更一般的情况,既有干扰又有记忆,实际信道往往是这种类型。
在这一类信道中某一瞬间的输出符号不但与对应时刻的输入符号有关,而且与此前其他时刻信道的输入符号及输出符号有关,这样的信道称为有记忆信道。
2.单符号离散信道的数学模型单符号离散信道的输入变量为X ,取值于{a 1, a 2, …, a r },输出变量为Y ,取值于{b 1, b 2, …, b s },并有条件概率P (y |x )= P (y=b j |x=a i )= P (b j |a i ) (i =1,2,…,r ;j =1,2,…,s )这一组条件概率称为信道的传递概率或转移概率。
因为信道中有干扰(噪声)存在,信道输入为x =a i 时,输出是哪一个符号y ,事先无法确定。
但信道输出一定是b 1, b 2, …, b s 中的一个,即有∑==s j i j a bP 11)|( (i =1,2,…,r )(1-1) 由于信道的干扰使输入符号x 在传输中发生错误,所以可以用传递概率P (b j |a i );,,2,1(r i =),,2,1s j =来描述干扰影响的大小。
因此,一般简单的单符号离散信道的数学模型可以用概率空间[Y x y P X ),|(,]加以描述。
另外,也可以用图来描述,如图1.2所示。
⎪⎪⎪⎩⎪⎪⎪⎨⎧a a X 21 Yb b b s ⎪⎪⎪⎭⎪⎪⎪⎬⎫21定义1.1 已知发送符号为a i ,通过信道传输接收到的符号为b j 的概率P (b j |a i )称为前向概率。
已知信道输出端接收到的符号为b j ,而发送符号为a i 的概率P (a i |b j ),称为后向概率。
有时,也把P (a i )称为输入符号的先验概率(即在接收到一个输出符号以前输入符号的概率),而对应地把P (a i |b j )称为输入符号的后验概率(在接收到一个输出符号以后输入符号的概率)。
为了讨论方便,下面列出本章讨论中常用的一些关于联合概率和条件概率的关系:(1) 设输入和输出符号的联合概率为P (x = a i , y = b j )=P (a i b j ),则有)|()()|()()(j i j i j i j i b a P b P a b P a P b a P == (2) ∑==r i i j i j a b P a P b P 1)|()()( (s j ,,1 =)。
(3) 根据贝叶斯定律,可得后验概率与先验概率之间的关系)()()|(j j i j i b P b a P b a P = (0)(≠b P j ) =∑=r i ij i i j i a b P a P a b P a P 1)|()()|()( (s j r i ,,2,1;,,2,1 ==)1.2 抗干扰信道编码定理及逆定理 定理1.1 有噪信道编码定理设离散无记忆信道[X ,P (y |x ),Y ], P (y |x )为信道传递概率,其信道容量为C 。
当信息传输率R <C 时,只要码长n 足够长,总可以在输入的符号集中找到2nR 个码字组成的一组码和相应的译码规则,使译码的错误概率任意小(P E 0→)。
在定理6.1中,信道容量C 是平均互信息量的最大值),(max )(Y X I C x p = 其单位是“bit/符号”。
定理1.2 有噪信道编码逆定理(定理6.1的逆定理)设离散无记忆信道[X ,P (y |x ),Y ],其信道容量为C 。
当信息传输率R >C 时,则无论码长n 多长,均找不到一种编码2nR ,使译码错误概率任意小。
定理1.1和定理1.2统称为申农第二定理,它是一个关于有效编码的存在性定理,它具有根本性的重要意义,它说明错误概率趋于零的好码是存在的。
它有助于指导各种通信系统的设计,有助于评价各种通信系统及编码的效率。
申农1948年发表申农第二定理后,科学家就致力于研究信道中的各种易于实现的实际编码方法,赋予码以各种形式的代数结构,出现了各种形式的代数编码、卷积码、循环码等。
1.3 检错与纠错的基本原理在申农第二定理发表后,很长一段时间内人们都在探寻能够简单、有效地编码和译码的好码。
由此形成了一整套纠错码理论。
在此只简单地介绍检错和纠错的一些基本概念及基本原理。
在信息处理过程中,为了保持数据的正确性应对信息进行编码使其具有检错纠错能力,这种编码称为语法信息编码。
它的基本思想是引入剩余度,在传输的信息码元后增加一些多余的码元,以使信息损失或错误后仍能在接收端恢复。
通常将要处理的信息称为原信息,将原信息转化为数字信息后再进行存储、传输等处理过程称为传送。
工程上最容易实现的是二元数字信息(或二元码信息)的传送。
所谓二元数字信息就是由二元数域F 2={0,1}中的数字0与1组成的数组或向量。
定义1.3 设X =(x 1, x 2,…, x n ),Y =(y 1, y 2,…, y n ),x i ∈F 2,y i ∈F 2,i =1,…, n ,称X 和Y 对应分量不相等的分量个数为X 和Y 的汉明(Hamming )距离,记为d (X , Y )。
记则 d (X , Y )= d (x 1, y 1)+ d (x 2, y 2)+…+ d (x n , y n )容易证明以下定理。
定理1.4 设X 和Y 是长为n 的二元码字,则(1)n Y X d ≤≤),(0(非负且有界性)(2)d (X , Y )=0当且仅当X =Y (自反性)(3)d (X , Y )= d (Y , X )(对称性)(4)),(),(),(Z Y d Y X d Z X d +≤(三角不等式)1.4 限失真编码定理申农第一定理和申农第二定理指明:无论是无噪声信道还是有噪声信道,只要信道的信息传输率R 小于信道容量C ,总能找到一种编码,在信道上以任意小的错误概率和任意接近信道容量的信息传输率传输信息。
