统计学复习概念重点-贾俊平
《统计学》(贾俊平第七版)课后题及答案-统计学 贾俊平第七版

第一章导论1.什么是统计学?统计学是搜集、处理、分析、解释数据并从中得出结论的科学。
2.解释描述统计与推断统计。
描述统计研究的是数据搜集、处理、汇总、图表描述、概括与分析等统计方法。
推断统计研究的是如何利用样本数据来推断总体特征的统计方法。
3.统计数据可分为哪几种类型?不同类型的数据各有什么特点?按照计量尺度可分为分类数据、顺序数据和数值型数据;按照数据的搜集方法,可以分为观测数据和试验数据;按照被描述的现象与实践的关系,可以分为截面数据和时间序列数据。
4.解释分类数据、顺序数据和数值型数据的含义。
分类数据是只能归于某一类别的非数字型数据;顺序数据是只能归于某一有序类别的非数字型数据;数值型数据是按照数字尺度测量的观测值,其结果表现为具体的数值。
5.举例说明总体、样本、参数、统计量、变量这几个概念。
总体是包含所研究的全部个体的集合,样本是从总体中抽取的一部分元素的集合,参数是用来描述总体特征的概括性数字度量,统计量是用来描述样本特征的概括性数字度量,变量是用来说明现象某种特征的概念。
6.变量可分为哪几类?变量可分为分类变量、顺序变量和数值型变量。
分类变量是说明书屋类别的一个名称,其取值为分类数据;顺序变量是说明十五有序类别的一个名称,其取值是顺序数据;数值型变量是说明事物数字特征的一个名称,其取值是数值型数据。
7.举例说明离散型变量和连续型变量。
离散型变量是只能去可数值的变量,它只能取有限个值,而且其取值都以整位数断开,如“产品数量”;连续性变量是可以在一个或多个区间中取任何值的变量,它的取值是连续不断的,不能一一列举,如“温度”等。
第二章数据的搜集1.什么是二手资料?使用二手资料需要注意些什么?与研究内容有关、由别人调查和试验而来、已经存在并会被我们所利用的资料为二手资料。
使用时要评估资料的原始搜集人、搜集目的、搜集途径、搜集时间且使用时要注明数据来源。
2.比较概率抽样和非概率抽样的特点。
举例说明什么情况下适合采用概率抽样,什么情况下适合采用非概率抽样。
统计学(第四版)贾俊平复习资料名词解释概念课后思考题答案

统计学(第四版)贾俊平复习资料名词解释概念课后思考题答案l.获得数据的概率抽样方法有哪些?(1)简单随机抽样简单随机抽样又称纯随机抽样,是指在特定总体的所有单位中直接抽取n个组成样本。
它最直观地体现了抽样的基本原理,是最基本的概率抽样。
<2)系统抽样系统抽样也称等距抽样或机械抽样,是按一定的间隔距离抽取样本的方法。
(3)分层抽样分层抽样也叫分类抽样,就是先将总体的所有单位依照一种或几种特征分为若干个子总体,每一个子总体即为一类,然后从每一类中按简单随机抽样或系统随机抽样的办法抽取一个子样本,称为分类样本,它们的集合即为总体样本。
(4)整群抽样整群抽样又称聚类抽样或集体抽样,是将总体按照某种标准划分为一些群体,每一个群体为一个抽样单位,再用随机的方法从这些群体中抽取若干群体,并将所抽出群体中的所有个体集合为总体的样本。
(5)多阶段抽样多阶段抽样又称多级抽样或分段抽样,就是把从总体中抽取样本的过程分成两个或多个阶段进行的抽样方法。
2.茎叶图与直方图相比有什么优点?它们的应用场合是什么?茎叶图与直方图相比,茎叶图既能给出数据的分布状况,又能给出每一个原始数值,即保留了原始数据的信息。
而直方图虽然能很好地显示数据的分布,但不能保留原始的数值。
在应用方面,直方图通常适用于大批量数据,茎叶图通常适用于小批量数据。
3鉴别图标优劣的准则1精心设计,有助于洞察问题的实质。
2使复杂的观点得到简明、确切、高效的阐述。
3能在最短的时间内以最少的笔墨给读者提供最大量的信息。
4是多维的。
5表述数据的真实情况。
4.一组数据的分布特征可以从哪几个方面进行测量?答:数据分布的特征可以从三个方面进行测度和描述:一是分布的集中趋势,反映各数据向其中心值靠拢或聚集的程度;二是分布的离散程度,反映各数据远离其中心值的趋势;三是分布的形状,反映数据分布的偏态和峰态。
这三个方面分别反映了数据分布特征的不同侧面。
5. 标准分数有哪些用途?标准分数给出了一组数据中各数值的相对位置。
统计学(贾俊平版)重点

第一章统计:收集、处理、分析、解释数据并从数据中得出结论得科学。
数据1、分类数据对事物进行分类得结果数据,表现为类别,用文字来表述、例如,人口按性别分为男、女两类2、顺序数据对事物类别顺序得测度,数据表现为类别,用文字来表述例如,产品分为一等品、二等品、三等品、次品等3、数值型数据对事物得精确测度,结果表现为具体得数值、例如:身高为175cm ,168cm,183cm总体–所研究得全部元素得集合,其中得每一个元素称为个体–分为有限总体与无限总体、有限总体得范围能够明确确定,且元素得数目就是有限得、无限总体所包括得元素就是无限得,不可数得样本–从总体中抽取得一部分元素得集合–构成样本得元素数目称为样本容量参数:描述总体特征。
有总体均值( )、标准差(σ)总体比例(π)统计量:描述样本特征。
样本标准差(s),样本比例(p)变量:说明现象某种特征,分类,顺序,数值型:离散型,连续型。
经验,理论变量描述统计研究得就是数据收集,处理,汇总,图表描述,概括与分析等统计方法。
推断统计就是研究如何利用样本数据进行推断总体特征第二章间接数据(查询得)与直接数据:调查(通常就是对社会现象而言得)普查信息全面完整。
再一个就是实验。
概率抽样:也称随机抽样。
按一定得概率以随机原则抽取样本,抽取样本时使每个单位都有一定得机会被抽中–每个单位被抽中得概率就是已知得,或就是可以计算出来得–当用样本对总体目标量进行估计时,要考虑到每个样本单位被抽中得概率简单随机抽样:从总体N个单位中随机地抽取n个单位作为样本,每个单位入抽样本得概率就是相等得分层抽样:优点:保证样本得结构与总体得结构比较相近将抽样单位按某种特征或某种规则划分为不同得层,然后从不同得层中独立、随机地抽取样本,从而提高估计得精度–组织实施调查方便–既可以对总体参数进行估计,也可以对各层得目标量进行估计整群抽样:将总体中若干个单位合并为组(群),抽样时直接抽取群,然后对中选群中得所有单位全部实施调查优点:抽样时只需群得抽样框,可简化工作量–调查得地点相对集中,节省调查费用,方便调查得实施–缺点就是统计得精度较差系统抽样:将总体中得所有单位(抽样单位)按一定顺序排列,在规定得范围内随机地抽取一个单位作为初始单位,然后按事先规定好得规则确定其它样本单位–先从数字1到k之间随机抽取一个数字r作为初始单位,以后依次取r+k,r+2k…等单位操作简便,可提高估计得精度多阶段抽样:先抽取群,但并不就是调查群内得所有单位,而就是再进行一步抽样,从选中得群中抽取出若干个单位进行调查–群就是初级抽样单位,第二阶段抽取得就是最终抽样单位。
统计学原理贾俊平期末考试重点

统计学期末(单选、10个填空、5个判断、三个计算、一道论述)第一章导论1、统计学是收集、处理、分析、解释数据并从数据中得出结论的科学。
分析数据:分为描述统计方法和推断统计方法两种方法。
描述统计:研究的是数据收集、处理、汇总、图表描述、概括与分析等统计方法。
推断统计:是研究如何利用样本数据来推断总体特征的统计方法。
推断统计内容包含参数估计和假设检验2、统计数据的类型:(1)按照采用的计量尺度不同,可以将统计数据分为分类数据、顺序数据与数值型数据。
注意:分类数据和顺序数据都是表现事物的品质特征,通常是用文字来表述的,其结果均表现为类别,因此可以通称为定性数据或品质数据(qualitative data)。
数值型数据说明的是现象的数量特征,通常用数值来表现,因此可以统称为定量数据或数量数据(quantitative data)。
(2)按照统计数据的收集方法,可以将统计数据分为观测数据和实验数据。
(3)按照被描述的现象与时间的关系,可以将统计数据分为截面数据、时间序列数据(和面板数据 panal data)。
3、抽样独立性问题:总体区分为有限总体和无限总体,目的是为了判别在抽样中每次抽取是否独立(类似抽小球是否放回的问题)。
在统计推断中,通常是针对无限总体的,因而通常把总体看做随机变量(random variable)。
统计上的总体通常是一组观测数据,而不是一群人或者一些物品的简单集合。
4、统计指标按其所反映的数量特点和作用不同,分为数量指标、质量指标。
样本(sample)是从总体中抽取的一部分元素的集合,构成样本的元素的数目称为样本量(sample size)。
抽样的目的是根据样本提供的信息推断总体的特征。
5、总体参数(parameter)是用来描述总体特征的概括性数字度量,是研究者想要了解的某种特征值。
样本统计量(statistic)是用来描述样本特征的概括性数字度量,是根据样本数量计算出来的一个量。
统计学贾俊平考研知识点总结

统计学重点笔记第一章导论一、比较描述统计和推断统计:数据分析是通过统计方法研究数据,其所用的方法可分为描述统计和推断统计。
(1)描述性统计:研究一组数据的组织、整理和描述的统计学分支,是社会科学实证研究中最常用的方法,也是统计分析中必不可少的一步。
内容包括取得研究所需要的数据、用图表形式对数据进行加工处理和显示,进而通过综合、概括与分析,得出反映所研究现象的一般性特征。
(2)推断统计学:是研究如何利用样本数据对总体的数量特征进行推断的统计学分支。
研究者所关心的是总体的某些特征,但许多总体太大,无法对每个个体进行测量,有时我们得到的数据往往需要破坏性试验,这就需要抽取部分个体即样本进行测量,然后根据样本数据对所研究的总体特征进行推断,这就是推断统计所要解决的问题。
其内容包括抽样分布理论,参数估计,假设检验,方差分析,回归分析,时间序列分析等等。
(3)两者的关系:描述统计是基础,推断统计是主体二、比较分类数据、顺序数据和数值型数据:根据所采用的计量尺度不同,可以将统计数据分为分类数据、顺序数据和数值型数据。
(1)分类数据是只能归于某一类别的非数字型数据。
它是对事物进行分类的结果,数据表现为类别,是用文字来表达的,它是由分类尺度计量形成的。
(2)顺序数量是只能归于某一有序类别的非数字型数据。
也是对事物进行分类的结果,但这些类别是有顺序的,它是由顺序尺度计量形成的。
(3)数值型数据是按数字尺度测量的观察值。
其结果表现为具体的数值,现实中我们所处理的大多数都是数值型数据。
总之,分类数据和顺序数据说明的是事物的本质特征,通常是用文字来表达的,其结果均表现为类别,因而也统称为定型数据或品质数据;数值型数据说明的是现象的数量特征,通常是用数值来表现的,因此可称为定量数据或数量数据。
三、比较总体、样本、参数、统计量和变量:(1)总体是包含所研究的全部个体的集合。
通常是我们所关心的一些个体组成,如由多个企业所构成的集合,多个居民户所构成的集合。
2024版统计学完整(贾俊平)人大课件ppt课件

统计学完整(贾俊平)人大课件ppt课件•引言•数据收集与整理•描述性统计分析目录•概率论基础•推断性统计分析•方差分析与回归分析•时间序列分析与预测•统计决策与风险管理目录•总结与展望01引言统计学是一门研究如何收集、整理、分析和解释数据的科学。
统计学的定义统计学的历史统计学的分支统计学的发展经历了古典统计学、近代统计学和现代统计学三个阶段。
统计学可以分为描述统计学和推断统计学两大分支。
030201统计学概述社会科学医学与健康工程与技术商业与经济统计学应用领域01020304在社会科学领域,统计学被广泛应用于调查研究、民意测验、市场分析等方面。
在医学和健康领域,统计学被用于临床试验、流行病学研究、健康风险评估等方面。
在工程和技术领域,统计学被用于质量控制、可靠性分析、信号处理等方面。
在商业和经济领域,统计学被用于市场分析、财务分析、经济预测等方面。
通过学习,学生应掌握统计学的基本概念和方法,包括数据收集、整理、描述和分析等方面的内容。
掌握统计学基本概念和方法具备数据处理和分析能力了解统计学的应用领域培养批判性思维学生应具备独立处理和分析数据的能力,能够运用适当的统计方法进行数据分析和解释。
学生应了解统计学的应用领域,能够运用所学知识解决实际问题。
学生应培养批判性思维,能够对统计结果进行合理的解释和评估。
学习目标与要求02数据收集与整理数据来源及类型数据来源包括原始数据和二手数据,原始数据是通过直接调查、实验或观察获得的数据;二手数据则是已经经过他人收集、整理和处理过的数据。
数据类型包括定性数据和定量数据,定性数据是描述性的、非数值的,如文字、图像等;定量数据则是可以用数值表示的,如年龄、收入等。
此外,还可以根据数据的测量尺度将其分为名义型数据、顺序型数据、间隔型数据和比率型数据。
调查法实验法观察法大数据收集数据收集方法通过问卷、访谈、电话调查等方式收集数据,可以获取大量的、详细的信息。
直接观察研究对象的行为、状态等,记录相关数据,适用于无法控制或干预的情况。
统计学贾俊平考研知识点总结

统计学贾俊平考研知识点总结Pleasure Group Office【T985AB-B866SYT-B182C-BS682T-STT18】统计学重点笔记第一章导论一、比较描述统计和推断统计:数据分析是通过统计方法研究数据,其所用的方法可分为描述统计和推断统计。
(1)描述性统计:研究一组数据的组织、整理和描述的统计学分支,是社会科学实证研究中最常用的方法,也是统计分析中必不可少的一步。
内容包括取得研究所需要的数据、用图表形式对数据进行加工处理和显示,进而通过综合、概括与分析,得出反映所研究现象的一般性特征。
(2)推断统计学:是研究如何利用样本数据对总体的数量特征进行推断的统计学分支。
研究者所关心的是总体的某些特征,但许多总体太大,无法对每个个体进行测量,有时我们得到的数据往往需要破坏性试验,这就需要抽取部分个体即样本进行测量,然后根据样本数据对所研究的总体特征进行推断,这就是推断统计所要解决的问题。
其内容包括抽样分布理论,参数估计,假设检验,方差分析,回归分析,时间序列分析等等。
(3)两者的关系:描述统计是基础,推断统计是主体二、比较分类数据、顺序数据和数值型数据:根据所采用的计量尺度不同,可以将统计数据分为分类数据、顺序数据和数值型数据。
(1)分类数据是只能归于某一类别的非数字型数据。
它是对事物进行分类的结果,数据表现为类别,是用文字来表达的,它是由分类尺度计量形成的。
(2)顺序数量是只能归于某一有序类别的非数字型数据。
也是对事物进行分类的结果,但这些类别是有顺序的,它是由顺序尺度计量形成的。
(3)数值型数据是按数字尺度测量的观察值。
其结果表现为具体的数值,现实中我们所处理的大多数都是数值型数据。
总之,分类数据和顺序数据说明的是事物的本质特征,通常是用文字来表达的,其结果均表现为类别,因而也统称为定型数据或品质数据;数值型数据说明的是现象的数量特征,通常是用数值来表现的,因此可称为定量数据或数量数据。
统计学 贾俊平 考研 知识点总结

统计学重点笔记第一章导论一、比较描述统计与推断统计:数据分析就是通过统计方法研究数据,其所用的方法可分为描述统计与推断统计。
(1)描述性统计:研究一组数据的组织、整理与描述的统计学分支,就是社会科学实证研究中最常用的方法,也就是统计分析中必不可少的一步。
内容包括取得研究所需要的数据、用图表形式对数据进行加工处理与显示,进而通过综合、概括与分析,得出反映所研究现象的一般性特征。
(2)推断统计学:就是研究如何利用样本数据对总体的数量特征进行推断的统计学分支。
研究者所关心的就是总体的某些特征,但许多总体太大,无法对每个个体进行测量,有时我们得到的数据往往需要破坏性试验,这就需要抽取部分个体即样本进行测量,然后根据样本数据对所研究的总体特征进行推断,这就就是推断统计所要解决的问题。
其内容包括抽样分布理论,参数估计,假设检验,方差分析,回归分析,时间序列分析等等。
(3)两者的关系:描述统计就是基础,推断统计就是主体二、比较分类数据、顺序数据与数值型数据:根据所采用的计量尺度不同,可以将统计数据分为分类数据、顺序数据与数值型数据。
(1)分类数据就是只能归于某一类别的非数字型数据。
它就是对事物进行分类的结果,数据表现为类别,就是用文字来表达的,它就是由分类尺度计量形成的。
(2)顺序数量就是只能归于某一有序类别的非数字型数据。
也就是对事物进行分类的结果,但这些类别就是有顺序的,它就是由顺序尺度计量形成的。
(3)数值型数据就是按数字尺度测量的观察值。
其结果表现为具体的数值,现实中我们所处理的大多数都就是数值型数据。
总之,分类数据与顺序数据说明的就是事物的本质特征,通常就是用文字来表达的,其结果均表现为类别,因而也统称为定型数据或品质数据;数值型数据说明的就是现象的数量特征,通常就是用数值来表现的,因此可称为定量数据或数量数据。
三、比较总体、样本、参数、统计量与变量:(1)总体就是包含所研究的全部个体的集合。
通常就是我们所关心的一些个体组成,如由多个企业所构成的集合,多个居民户所构成的集合。
统计学 复习重点 贾俊平 2

二手数据的特点:搜集比较容易,采集数据成本低,能很快得到。
局限性不是为特定研究问题产生有欠缺,需要评估。
、二手数据的评估:谁收集,目的,怎么搜集,什么时侯收集?概率抽样与非概率抽样比较:性质不同,非概不依据随机原则选样本,样本统计量分布不确切,无法使用样本的结果对总体相应参数进行推断。
操作简便,时效快,成本低,专业要求不很高。
概率抽样依据随机原则抽选样本,理论分布存在,对总体有关参数可进行估计,计算估计误差,得到总体参数的置信区间。
提出精度要求。
数据收集方法的选择:抽样框中有关信息,目标总体特征,调查问题的内容,有形辅助物的使用,实施调查的资源,管理与控制,质量要求实验中的若干问题:人的意愿,心理问题,道德问题回答误差:理解误差,记忆误差,有意识误差误差的控制:抽样误差是抽样随机性带来的,不可避免可以计算,改大样本量。
选择合适改进的抽样框,设计好的调查问卷,调查过程的质量控制。
抽样误差因素:样本量大小,总体变异性大大抽样方式选组织形式数据审核的目的:检查数据是否有错误,原始数据完整性准确性,二手适用性时效性。
数据筛选的目的:根据需要找出符合特定条件的某类数据。
数据排序是按一定的顺序将数据排列,以便研究者通过浏览数据发现一些明显的特征或趋势,找到解决问题的线索。
数据透视表作用:可以对数据表重要信息按使用者的习惯或分析要求进行汇总和作图,形成一个符合需要的交叉表数据分布表的制作步骤:确定组数,确定组距,根据分组整理成频数分布表,上组限不在内不重不漏直方图与条形图的差别:首先条形图是用条形的长度表示各类别频数的多少,宽度是固定的;直方图用面积表示各组频数的多少,矩形的高度表示每一组的频数或频率,宽度则表示各组的组距,高宽均有意义。
其次由于分组数据具有连续性,直方图的各矩形通常是连续排列,而条形图则是分开排列。
最后条形图主要用于展示分类数据,直方图主要用于展示数值型数据。
茎叶图与直方图的区别:茎叶图既能给出数据的分布情况,又能保留原始数据的信息。
统计学(贾俊平第八版)课后思考题及答案

统计学(贾俊平第八版)课后思考题及答案第一章:统计学基本概念和方法思考题1:什么是统计学?统计学的研究对象是什么?统计学是从观察数据的现象和规律出发,运用数理统计方法进行概括、分析和推断的科学。
统计学研究的对象是数据的概括和整体行为特征,即基本统计量和统计分布。
答案:统计学是一门应用数学的学科,其研究范围包括数据的收集、整理、描述、分析和推断等方面。
统计学通过运用数理统计方法,帮助我们从观察到的数据中发现其中的规律和趋势,从而对现象和问题作出合理的判断和推断。
统计学的研究对象主要包括两个方面。
一方面,统计学关注数据的概括和整体行为特征,例如对数据集的中心趋势(平均数、中位数)和离散程度(标准差、方差)进行描述和分析,这些统计量可以帮助我们对数据进行概括和比较。
另一方面,统计学研究数据的统计分布,即数据的分布形状和特征,例如正态分布、偏态分布等,这些分布有助于我们根据数据的特点进行进一步的推断和推测。
第二章:统计学的数据描述思考题2:试举例说明数据分为哪些类型?数据分为定性数据和定量数据两种类型。
答案:数据可以分为定性数据和定量数据两种类型。
定性数据是指不能用数字表示的数据,其特征主要是描述性的,例如性别、喜好等。
定性数据通常采用文字或符号进行记录和表达。
定量数据是指可以用数字表示的数据,其特征主要是数量性的,例如身高、体重等。
定量数据可以进行数学运算和统计分析。
举例来说,一个学生调查问卷中的“性别”以及“对某个电影的评价(好、中、差)”是属于定性数据;而问卷中的“年龄”和“观看该电影的次数”则是属于定量数据。
第三章:概率与概率分布思考题3:什么是概率?请以一个例子来解释。
概率是指某个事件发生的可能性。
它在统计学中用于描述随机现象的规律性和不确定性。
答案:概率是描述某个事件发生的可能性的数值。
概率可以从0到1之间的任何一个数值,其中0表示不可能发生,1表示肯定会发生。
举个例子来说明,假设有一个标准的骰子,每个面上有1到6的数字。
统计学(贾俊平版)重点

第一章统计:收集、处理、分析、解释数据并从数据中得出结论的科学。
数据1. 分类数据对事物进行分类的结果数据,表现为类别,用文字来表述.例如,人口按性别分为男、女两类2. 顺序数据对事物类别顺序的测度,数据表现为类别,用文字来表述例如,产品分为一等品、二等品、三等品、次品等3. 数值型数据对事物的精确测度,结果表现为具体的数值.例如:身高为175cm ,168cm,183cm总体–所研究的全部元素的集合,其中的每一个元素称为个体–分为有限总体和无限总体.有限总体的范围能够明确确定,且元素的数目是有限的.无限总体所包括的元素是无限的,不可数的样本–从总体中抽取的一部分元素的集合–构成样本的元素数目称为样本容量参数:描述总体特征。
有总体均值()、标准差(σ)总体比例(π)统计量:描述样本特征。
样本标准差(s),样本比例(p)变量:说明现象某种特征,分类,顺序,数值型:离散型,连续型。
经验,理论变量描述统计研究的是数据收集,处理,汇总,图表描述,概括与分析等统计方法。
推断统计是研究如何利用样本数据进行推断总体特征第二章间接数据(查询的)与直接数据:调查(通常是对社会现象而言的)普查信息全面完整。
再一个是实验。
概率抽样:也称随机抽样。
按一定的概率以随机原则抽取样本,抽取样本时使每个单位都有一定的机会被抽中–每个单位被抽中的概率是已知的,或是可以计算出来的–当用样本对总体目标量进行估计时,要考虑到每个样本单位被抽中的概率简单随机抽样:从总体N个单位中随机地抽取n个单位作为样本,每个单位入抽样本的概率是相等的分层抽样:优点:保证样本的结构与总体的结构比较相近将抽样单位按某种特征或某种规则划分为不同的层,然后从不同的层中独立、随机地抽取样本,从而提高估计的精度–组织实施调查方便–既可以对总体参数进行估计,也可以对各层的目标量进行估计整群抽样:将总体中若干个单位合并为组(群),抽样时直接抽取群,然后对中选群中的所有单位全部实施调查优点:抽样时只需群的抽样框,可简化工作量–调查的地点相对集中,节省调查费用,方便调查的实施–缺点是统计的精度较差系统抽样:将总体中的所有单位(抽样单位)按一定顺序排列,在规定的范围内随机地抽取一个单位作为初始单位,然后按事先规定好的规则确定其它样本单位–先从数字1到k之间随机抽取一个数字r作为初始单位,以后依次取r+k,r+2k…等单位操作简便,可提高估计的精度多阶段抽样:先抽取群,但并不是调查群内的所有单位,而是再进行一步抽样,从选中的群中抽取出若干个单位进行调查–群是初级抽样单位,第二阶段抽取的是最终抽样单位。
统计学复习精要(贾俊平版)

《统计学》复习精要(贾俊平 第五版 中国人大出版社)neijiangrui第4章 概率分布1.总体与样本:在统计学中称随机变量(或向量)X 为总体,并把随机变量(或向量)X 的分布称为总体的分布。
称)...,,(21n X X X 为总体X 的一个简单随机样本,若n X X X ...,,21是独立同分布的随机变量,且与总体X 同分布。
n 为样本容量。
2. 四个重要的分布(正态分布、2χ分布、F 分布、t 分布)①正态分布:设随机变量X 有概率密度+∞<<∞-=--x ex f x ,21)(22)(σμπσ其中μ,0>σ为常数。
则称X 服从参数为μ,σ的正态分布,简记为),(~2σμN X 。
特别当μ=0,σ=1时,称X 服从标准正态分布。
简记为X ~N (0,1)。
②2χ分布 设X 1,X 2,…,X n 是相互独立的随机变量,且X i ~N (0,1) (i =1,2,…,n ),则称随机变量22221...n X X X X +++=服从自由度为n 的2χ分布,简记为X ~2χ(n )。
③F 分布 设)(~2m X χ,)(~2n Y χ,且X ,Y 相互独立,则称随机变量nY m X F //=服从F 分布,简记为F ~F (m ,n )。
④t 分布 设)1,0(~N X ,)(~2n Y χ,且X ,Y 相互独立,则称随机变量nY XT /=服从自由度为n 的t 分布,记为)(~n t T 。
3.抽样分布①单总体:设)...,,(21n X X X 是容量为n 的一个样本,X 与2S 分别为此样本的样本均值与样本方差(212)(11X X n S ini --=∑=)则:②双总体:设(1,,1n X X )是取自总体X 的一个样本,(2,,1n Y Y )是取自总体Y 的一个样本,且这两个样本相互独立,即假定1,,1n X X ,2,,1n Y Y 是n 1+n 2个相互独立的随机变量。
应用统计学(贾俊平版)综合复习提纲
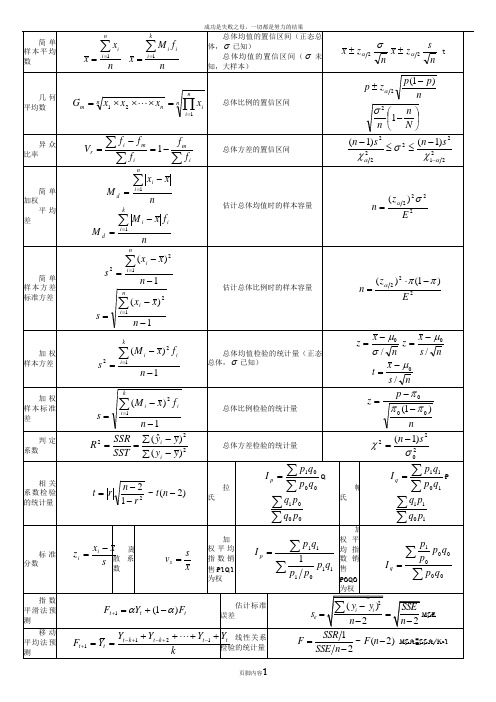
1.统计学:收集处理分析解释数据并从数据中得出结论的科学。
2.描述统计:研究数据收集处理汇总图表描述概括与分析等统计方法。
3.推断统计:研究如何利用样本数据来推断总体特征的统计方法。
4.分类数据:只能归于某一类别的非数字型数据。
5.顺序数据:只能归于某一有序类别的非数字型数据。
6.数值型数据:按数字尺度测量的观察值。
7.观测数据:通过调查或观测而收集到的数据。
8.实验数据:在实验中控制实验对象而收集到的数据。
9.截面数据:在相同或近似相同的时间点上收集的数据。
10.时间序列数据:在不同时间上收集到的数据,这类数据按时间顺序收集到的。
11.抽样调查:从总体中随机抽取一部分单位作为样本进行调查,根据样本调查结果来推断总体特征的数据收集方法。
12.普查:为特定目的而专门组织的全面调查。
13.总体:包含所研究的全部个体(数据)的集合。
14.样本:从总体中抽取的一部分元素的集合。
15.样本容量:也称样本量,是构成样本的元素数目。
16.参数:用来描述总体特征的概括性数字度量。
17.统计量:用来描述样本特征的概括性数字度量。
18.变量:说明现象某种特征的概念。
19.分类变量:说明事物类别的一个名称。
20.顺序变量:说明事物有序类别的一个名称。
21.数值型变量:说明事物数字特征的一个名称。
22.离散型变量:只能取可数值的变量。
25.实验数据:通过实验方法获得的数据26.概率抽样:随机抽样,遵循随机原则进行的抽样,总体中每个单位都有一定的机会被选入样本。
27.非概率抽样:不随机,根据研究目的对数据的要求,采用某种方式从总体中抽出部分单位对其实施调查。
28.简单随机抽样:从包括总体的N个单位的抽样框中随机,一个个抽取n个单位作为样本,每单位等概论。
29.抽样框:用于抽选样本的总体单位信息,是概率抽样中所不可缺30.分层抽样:将抽样单位按某种特征或某种规则划分为不同的层,然后从不同层中独立、随机地抽取样本。
31.整群抽样:总体中若干单位合并为组,群,抽样时直接抽取群,然后对中选群中的所有单位全部实施调查。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
n —1
n
'(X -X)2
i-1
n —1
估计总体比例时的样本容 量
加权样
k
2
(Mi-x) fi
iA
n —1
总体均值检验的统计量
(正态总体,匚已知)
加权样 本标准 差
’(Mi-X)2fi
『广n—1
总体比例检验的统计量
判定系 数
相关系 数检验 的统计 量
标准分
数
指数平 滑法预 测
移动平 均法预 测
R2
SSR「(?i-y)2
SST「、⑶-y)2
总体方差检验的统计量
t
~t(n- 2)
-X
一S
Xi
-
散数
离«系
Ft 1Tt(1-〉)Ft
拉氏
权均数售q1又
加平指销P1q划
Y*丫一2•…匕Yt
Ft1二Yt
k
Ip
P(1-P)
1」
N
2 2(n -1)s岂_2岂(n -1)s
P-乙.2
' pg ' qpo
P0q0q'q°P0
21.离散型变量:只能取可数值的变量。
22.连续型变量:可以在一个或多个区间中取任何值的变量。
23.调查数据:通过调查方法获得的数据
24.实验数据:通过实验方法获得的数据
25.概率抽样:随机抽样,遵循随机原则进行的抽样,总体中每个单位都有一定的机会被选入样本。
26.非概率抽样:不随机,根据研究目的对数据的要求,采用某种方式从总体中抽出部分单位对其实施 调查。
nn
年度化
增长率
Y
r?-1
均方预测 误差
n
2
送(Yi- FJ
MSE =
n
平均百
分比预
测误差
fV— Fzi i>^100
MPE =―乙
n
简单平均
法预测
11t
Fy+Y2+…+丫」=:送Y
tt y
统计学:收集处理分析解释数据并从数据中得出结论的科学。
1.描述统计:研究数据收集处理汇总图表描述概括与分析等统计方法。
27.简单随机抽样:从包括总体的N个单位的抽样框中随机,一个个抽取n个单位作为样本,每单位等 概论。
28.抽样框:用于抽选样本的总体单位信息,是概率抽样中所不可缺
29.分层抽样:将抽样单位按某种特征或某种规则划分为不同的层,然后从不同层中独立、随机地抽取 样本。
30.整群抽样:总体中若干单位合并为组,群,抽样时直接抽取群,然后对中选群中的所有单位全部实 施调查。
35.自愿样本:被调查者自愿参加,成为样本中一分子,向调查人员提供有关信息
36.滚雪球抽样:对稀少群体调查中,首选选择一组调查单位,调查后,请他们提供另外属于研究总体 的调查对象,调查人员根据所提供的线索,进行此后调查。
37.配额抽样:将总体中所有单位按一定的标志分若干类,然后每类采用方便抽样或判断抽样的方案选 取样本单位。
49.累积频率或累积百分比:将有序类别或组百分比逐级累加起来。
50.数据分组:根据统计研究需要,将原始数据按某种标准化分成不同的组别,。
51.组距是一个组的上限与下限的差
38.自填式:没有调查员协助,被调查者自已填写,完成调查问卷。
39.面访式:面对面,调查员提问,被调查者回答。
40.电话式:打电话方式调查。
41.抽样误差:由于抽样的随机性引起的样本结果与总体真值之的误差。
42.非抽样误差:相对抽样误差而言,除抽样误差之外的,由于其它原因引起的样本观察结果与总体真 值之间的差异。
9.时间序列数据:在不同时间上收集到的数据,这类数据按时间顺序收集到的。
10.抽样调查:从总体中随机抽取一部分单位作为样本进行调查,根据样本调查结果来推断总体特征的 数据收集方法。
11.普查:为特定目的而专门组织的全面调查。
12.总体:包含所研究的全部个体(数据)的集合。
13.样本:从总体中抽取的一部分元素的集合。
43.抽样框误差:统计推论的错误是由于抽样框不完善造成的
44.频数:落在某一特定类别或组中的数据个数。
45.频数分布:各个类别及其相应的频数形成的分布。
46.比例:一个样本(或总体)中各个部分的数据占全部数据比值。
47.比率:一个样本(或总体)中各不同类别数据之间的比值。
48.累积频数:将各有序类别或组的频数逐级累加起来得到的频数。
SSE n-2
~F (n -2)MSA=SSA/k-1
MSE=SSE/n-k
环比增
长率
定基
回归系数 检验的统 计的统计 量
?
t丄〜t(n2)相关系数
t=^~t(n_2)
*'1 — r
平均增
长率
Ghnt!」2次…1=nl
\Yc Yi丫心V
平均预测 误差
平均绝对
预测误差
n
—FJ送—Fl
ME = 7MAD =i"
q
P1
z
q1
1
p
P1
2
//_2
估计标准 误差
线性关系 检验的统 计量
2 2
(乙2)二
n=
E2
(Z-.2)2二(1-二)
—E2
X _J
匚/Jn
x
z二
s/\ n
t_X_"0s/\Tn
兀0(1一兀0)
n
Z2
(n-1)s2
2-0
p0
Iq
2pg
瓦P°q1
q1P1q°P1
q为加权平均指数销售Mo权
O
q
o
p
SSR1
31.系统抽样:总体中所有单位按顺序排列,在规定范围内随机抽取一单位作为初始单位,然后按事先 规则确定其它样本单位。
32.多阶段抽样:首先抽取群,再进一步抽样,从选中的群中抽取出若干个单位进行计查,二阶段抽样。
33.方便抽样:依据方便原则,自行确定入抽样本的单位。
34.判段抽样:研究人员根据经验,判断研究对象的了解,有目的选择一些单位作为样本。
简单样 本平均 数
n
' Xi
i丄
X二
n
总体均值的置信区间(正
态总体,◎已知)
总体均值的置信区间(a未知,大样本)
CT_s
—
几何平
均数
总体比例的置信区间
异众比
Vr
fm
fi
fm
fi
总体方差的置信区间
简单加
权
平均差
Md
k
S|Mi -x|fi
i 4
n
估计总体均值时的样本容 量
简单样
本方差
标准方s2
n
' (Xi-x)2
2.推断统计:研究如何利用样本数据来推断总体特征数字型数据。
4.顺序数据:只能归于某一有序类别的非数字型数据。
5.数值型数据:按数字尺度测量的观察值。
6.观测数据:通过调查或观测而收集到的数据。
7.实验数据:在实验中控制实验对象而收集到的数据。
8.截面数据:在相同或近似相同的时间点上收集的数据。
14.样本容量:也称样本量,是构成样本的元素数目。
15.参数:用来描述总体特征的概括性数字度量。
16.统计量:用来描述样本特征的概括性数字度量。
17.变量:说明现象某种特征的概念。
18.分类变量:说明事物类别的一个名称。
19.顺序变量:说明事物有序类别的一个名称。
20.数值型变量:说明事物数字特征的一个名称。
