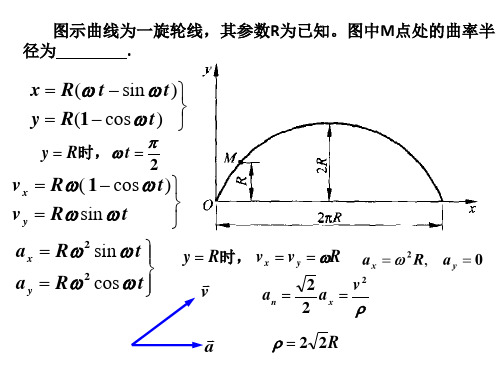
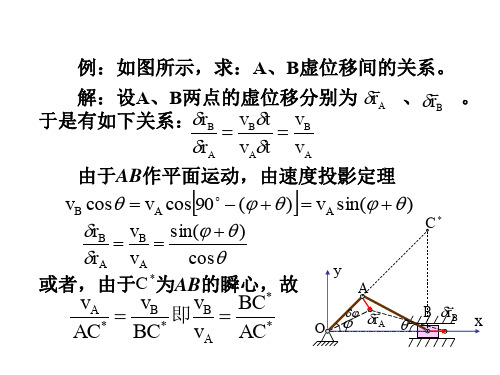
理论力学竞赛辅导2运动学30页PPT
合集下载
理论力学竞赛辅导2运动学

问题3:当平面运动刚体的角速度或角加速度分别为零时, 如何确定加速度瞬心的位置?
2020/6/8
5
BUAA
例题与思考题
习题4:点M做平面曲线运动,已知该点速度的大小 v=at (a>0), 速度的方向与 x 轴的夹角θ=0.5bt2(b>0),求任意时刻(t>0) 动点M的加速度在y轴上的投影以及轨迹的曲率半径。
aOn
vO2 R
r
(r)2
3r
12r
3
aPnO 2r
aPn
aOn
aPnO
42r
3
vP2 aPn
( 2r ) 2 42r
3r
2020/6/8 3
an
P PO
r
O
an O R
14
BUAA
例题与思考题
问题14:圆盘上哪点的加速度的模最大(小)?
为
o
常
量
A
aA O
Ca
B D
aB
CV
纯滚动
OA R, AB 2R
vB vA vBA
2、速度投影法
vB
AB
vA
AB
3、速度瞬心法
vM vMCV , vM MCV
思考题1:上述三种方法的内 在联系和区别是什么?
Ax’y’为平移动系,B为动点
y
y' vBA vB B
A
r0
B
A
vA
x'
o
vA x
M
vM
CV
2020/6/8
4
BUAA
二、刚体的平面运动
4、平面图形上各点的加速度
y
et (t t)
2020年高中物理竞赛(力学篇)02运动、力学定律:力学的相对性原理(共16张PPT)

2-3 动量 动量守恒定律
动量守恒定律
三大 守恒定律
动能转换与守恒定律 物理学大厦 的基石
角动量守恒定律
一、质点的动量定理
由F
ma
可得:F
dp
dt
作用于物体上的合外力的冲量等于物体动量的增量 ——质点的动量定理
t2 t1
Fxdt
mv2 x
m v1 x
分量表示式
t2 t1
Fydt
mv2 y
m v1 y
dp
dx
dx dt
dt
dt
根据动量定理,桌面对柔绳的冲力为:
F =dp
dx
dx
dt =-v 2
dt
dt
柔绳对桌面的冲力F=F'即:
F v2 M v2 而v2 2gx F 2Mgx / L
L
而已落到桌面上的柔绳的重量为mg=Mgx/L
所以F总=F+mg=2Mgx/L+Mgx/L=3mg
30o
45o x n
Fyt
t 0.01s v1 10m/s v2 20m/s
I I xi I y j 0.061i 0.007 j N s
v1
m 2.5g
2
2
Fx 6.1N Fy 0.7N F F x F y 6.14N
tan Fy Fx 0.1148 6.54 为平均冲力与x方向的夹角。
2020全国高中奥林匹克竞赛 物理
力学篇 (基础版)
二、力学的相对性原理 在S系中: 在S´系中:
力学的相对性原理: 力学规律对一切惯性系都是等价的
在任何一个惯性系中牛顿定律都有完全相同的形式
即:伽利略相对性原理 或经典相对性原理
理论力学竞赛指导-PPT课件

2 k 2 0 x ( )x m
当 2
2k m
牵连惯性力大于弹簧的弹性恢复力,
物块不能在x´=0处附近作自由振动,物块在x´=0处 的平衡是不稳定的。 当
2
2k m
牵连惯性力等于弹簧的弹性恢复力
物块在x´=0处为随遇的平衡位置。
4、水流以体积流量qV通过内径为d1管
z
ω
北
解:3. 分析加速度
绝对加速度aa -所要求的 未知量;
z´ ae ar
vr
相对加速度ar - ar=vr2/R 方向指向地心;
牵连加速度ae - ae=Rcos2ae 矢量垂直于 Oz´轴,方向指向Oz´; 科氏加速度aC - aC=2vrsin方向沿过P点纬 线的切向,指向西。
aC
k
P O
k
y´
k x´
解: 1. 非惯性参考系-O x´ y´ 动点-物块P 2. 分析相对速度和各种加速 度: 相对速度vr -沿着x´正向
OP kk
P x´
aIC
牵连加速度aen-由大盘 转动引起
vr
aen
科氏加速度aIC -2m vr
y´ k x´ 解: 3. 分析质点(物块)受力: F -弹簧力F=2k x´ FIC aIC vr aen F FN -槽对物块的约束力 FIC -科氏力 FIen -法向牵连惯性力 FIen=m 2 x´
1
qv
1
2
2
解:分析以喷嘴的左右截面(1-1 和2-2)为边界所包含的质量流根据 体积流量与速度和管道横截面积的 关系,有
2 2 π d π d q v A v A v 1 v 2 V 1 1 2 2 1 2 4 4
当 2
2k m
牵连惯性力大于弹簧的弹性恢复力,
物块不能在x´=0处附近作自由振动,物块在x´=0处 的平衡是不稳定的。 当
2
2k m
牵连惯性力等于弹簧的弹性恢复力
物块在x´=0处为随遇的平衡位置。
4、水流以体积流量qV通过内径为d1管
z
ω
北
解:3. 分析加速度
绝对加速度aa -所要求的 未知量;
z´ ae ar
vr
相对加速度ar - ar=vr2/R 方向指向地心;
牵连加速度ae - ae=Rcos2ae 矢量垂直于 Oz´轴,方向指向Oz´; 科氏加速度aC - aC=2vrsin方向沿过P点纬 线的切向,指向西。
aC
k
P O
k
y´
k x´
解: 1. 非惯性参考系-O x´ y´ 动点-物块P 2. 分析相对速度和各种加速 度: 相对速度vr -沿着x´正向
OP kk
P x´
aIC
牵连加速度aen-由大盘 转动引起
vr
aen
科氏加速度aIC -2m vr
y´ k x´ 解: 3. 分析质点(物块)受力: F -弹簧力F=2k x´ FIC aIC vr aen F FN -槽对物块的约束力 FIC -科氏力 FIen -法向牵连惯性力 FIen=m 2 x´
1
qv
1
2
2
解:分析以喷嘴的左右截面(1-1 和2-2)为边界所包含的质量流根据 体积流量与速度和管道横截面积的 关系,有
2 2 π d π d q v A v A v 1 v 2 V 1 1 2 2 1 2 4 4
力学竞赛资料运动学精品PPT课件
初始时刻的系统位置
P点轨迹是双曲线(的一部分),
(3)设P是AB杆与yz平面的交点,当点P位于AB杆中点且yP>0时,求P点的速度和加速度? 取a=1m,l=4m,β=π/6,ω=1rad/s
(3)求P点的加速度?取a=1m,l=4m,β=π/6,ω=1rad/s
题. 三名舞蹈演员在舞台上(视作平面上三点)组成一正三角形。 音乐一开始,每一演员即朝向右侧的另一演员以常速率 v 缓慢前进。 问演员走过的轨迹是什么曲线?求某点处的曲率半径。
ve vA 10m / s()
vr2
va2
v
2 e
v
2 B
v
2 A
51.0m / s
vrβ
va
ve
例5 OA=x0-vAt,θ=ωt,x0=3000m, vA=10m/s, ω=0. 05rad/s, R=1000m,求: t=0
瞬时:(1) A车上的乘客看到的B车的相对速度;(2)B车上的乘客看到的A车的 相对速度。
解:(1)求t=0瞬时B车上的乘客看到的A车的相对速度
1、选择动点与动系
ve
动点-A车;
动系-固结于B车上;
2、分析三种运动和速度 绝对运动-沿OA的直线运动 相对运动-规律未知
牵连运动—车B绕O的定轴转动
R
vB
vA
A
3、作速度平行四边形,如图。
O
B
4、求解未知量
vB R 50m / s()
运动学反问题:
1、设计一个机构,使其能画出一条直线(可参考上例讨论d) 2、设计一个机构,使其能画出一个椭圆
(哈工大理论力学第7版例5-1)
3、设计一个机构,使其能画四叶玫瑰线(下图):r a sin 2q
P点轨迹是双曲线(的一部分),
(3)设P是AB杆与yz平面的交点,当点P位于AB杆中点且yP>0时,求P点的速度和加速度? 取a=1m,l=4m,β=π/6,ω=1rad/s
(3)求P点的加速度?取a=1m,l=4m,β=π/6,ω=1rad/s
题. 三名舞蹈演员在舞台上(视作平面上三点)组成一正三角形。 音乐一开始,每一演员即朝向右侧的另一演员以常速率 v 缓慢前进。 问演员走过的轨迹是什么曲线?求某点处的曲率半径。
ve vA 10m / s()
vr2
va2
v
2 e
v
2 B
v
2 A
51.0m / s
vrβ
va
ve
例5 OA=x0-vAt,θ=ωt,x0=3000m, vA=10m/s, ω=0. 05rad/s, R=1000m,求: t=0
瞬时:(1) A车上的乘客看到的B车的相对速度;(2)B车上的乘客看到的A车的 相对速度。
解:(1)求t=0瞬时B车上的乘客看到的A车的相对速度
1、选择动点与动系
ve
动点-A车;
动系-固结于B车上;
2、分析三种运动和速度 绝对运动-沿OA的直线运动 相对运动-规律未知
牵连运动—车B绕O的定轴转动
R
vB
vA
A
3、作速度平行四边形,如图。
O
B
4、求解未知量
vB R 50m / s()
运动学反问题:
1、设计一个机构,使其能画出一条直线(可参考上例讨论d) 2、设计一个机构,使其能画出一个椭圆
(哈工大理论力学第7版例5-1)
3、设计一个机构,使其能画四叶玫瑰线(下图):r a sin 2q
2020年高中物理竞赛—力学篇(进阶版)1 绪论(共30张PPT)

其原意是“自然的科学” , 即在古 代欧洲 , 物理学是自然科学的总称.
但随着自然科学的发展 , 各种独立 的学科分别陆续形成 , 如化学 , 生物学, 天文学,地质学及各种工程学科等。
(下一页)
因此后来,物理学成为专门的:
研究物质运动中最普遍、最基本的运动
形式的基本规律的学科。
。
物理学是自然科学的基础
大小
A= A
(矢量的模)
2、矢量相等: 大小相同,方向相同 。
标量不能与矢量相等,即 A A (下一页)
3、矢量的运算法则: (1) 加减法
含平行四边形法则和三角形法则
B
C
C
B
A C A B
A C A B
(下一页)
(2) 数乘
大小
A
C
方向
C A 0 C平行于 A
0 C平行于 A
“×”、“ ·”不能随便乱用。 (6)矢量的非法运算包括
1,
ln B,
C,
A
即:矢量不能作除数、取对数;
eD
不能开方、作指数。
矢量与标量不能相等。 !!!
(下一页)
(7)矢量的导数还是个矢量
若A Ar0 则
dA dt
dA dt
r0
A
dr0 dt
若在直角坐标系,坐标轴方向不变,各
分量互不相干,分别求导。如:
它涉及的范围,最初包括:
力学、 热学和分子物理学、 称为 :
电磁学、
经典物理学
光学.
(下一页)
随着研究的发展,在十九世纪末 , 人们发现了经典物理学的局限性。
在高速运动领域,即速度可与光速比 拟时, 应适用爱因斯坦建立的相对论力学;
但随着自然科学的发展 , 各种独立 的学科分别陆续形成 , 如化学 , 生物学, 天文学,地质学及各种工程学科等。
(下一页)
因此后来,物理学成为专门的:
研究物质运动中最普遍、最基本的运动
形式的基本规律的学科。
。
物理学是自然科学的基础
大小
A= A
(矢量的模)
2、矢量相等: 大小相同,方向相同 。
标量不能与矢量相等,即 A A (下一页)
3、矢量的运算法则: (1) 加减法
含平行四边形法则和三角形法则
B
C
C
B
A C A B
A C A B
(下一页)
(2) 数乘
大小
A
C
方向
C A 0 C平行于 A
0 C平行于 A
“×”、“ ·”不能随便乱用。 (6)矢量的非法运算包括
1,
ln B,
C,
A
即:矢量不能作除数、取对数;
eD
不能开方、作指数。
矢量与标量不能相等。 !!!
(下一页)
(7)矢量的导数还是个矢量
若A Ar0 则
dA dt
dA dt
r0
A
dr0 dt
若在直角坐标系,坐标轴方向不变,各
分量互不相干,分别求导。如:
它涉及的范围,最初包括:
力学、 热学和分子物理学、 称为 :
电磁学、
经典物理学
光学.
(下一页)
随着研究的发展,在十九世纪末 , 人们发现了经典物理学的局限性。
在高速运动领域,即速度可与光速比 拟时, 应适用爱因斯坦建立的相对论力学;
胡勇老师力学01运动学30页PPT

胡勇老师力学01运动学
31、别人笑我太疯癫,我笑他人看不 穿。(名 言网) 32、我不想听失意者的哭泣,抱怨者 的牢骚 ,这是 羊群中 的瘟疫 ,我不 能被它 传染。 我要尽 量避免 绝望, 辛勤耕 耘,忍 受苦楚 。我一 试再试 ,争取 每天的 成功, 避免以 失败收 常在别 人停滞 不前时 ,我继 续拼搏 。
33、如果惧怕前面跌宕的山岩,生命 就永远 只能是 死水一 潭。 34、当你眼泪忍不住要流出来的时候 ,睁大 眼睛, 千万别 眨眼!你会看到 世界由 清晰变 模糊的 全过程 ,心会 在你泪 水落下 的那一 刻变得 清澈明 晰。盐 。注定 要融化 的,也 许是用 眼泪的 方式。
35、不要以为自己成功一次就可以了 ,也不 要以为 过去的 光荣可 以被永 远肯定 。
61、奢侈是舒适的,否则就不是奢侈 。——CocoCha nel 62、少而好学,如日出之阳;壮而好学 ,如日 中之光 ;志而 好学, 如炳烛 之光。 ——刘 向 63、三军可夺帅也,匹夫不可夺志也。 ——孔 丘 64、人生就是学校。在那里,与其说好 的教师 是幸福 ,不如 说好的 教师是 不幸。 ——海 贝尔 65、接受挑战,就可以享受胜利的喜悦 。——杰纳勒 尔·乔治·S·巴顿
谢谢!Biblioteka
31、别人笑我太疯癫,我笑他人看不 穿。(名 言网) 32、我不想听失意者的哭泣,抱怨者 的牢骚 ,这是 羊群中 的瘟疫 ,我不 能被它 传染。 我要尽 量避免 绝望, 辛勤耕 耘,忍 受苦楚 。我一 试再试 ,争取 每天的 成功, 避免以 失败收 常在别 人停滞 不前时 ,我继 续拼搏 。
33、如果惧怕前面跌宕的山岩,生命 就永远 只能是 死水一 潭。 34、当你眼泪忍不住要流出来的时候 ,睁大 眼睛, 千万别 眨眼!你会看到 世界由 清晰变 模糊的 全过程 ,心会 在你泪 水落下 的那一 刻变得 清澈明 晰。盐 。注定 要融化 的,也 许是用 眼泪的 方式。
35、不要以为自己成功一次就可以了 ,也不 要以为 过去的 光荣可 以被永 远肯定 。
61、奢侈是舒适的,否则就不是奢侈 。——CocoCha nel 62、少而好学,如日出之阳;壮而好学 ,如日 中之光 ;志而 好学, 如炳烛 之光。 ——刘 向 63、三军可夺帅也,匹夫不可夺志也。 ——孔 丘 64、人生就是学校。在那里,与其说好 的教师 是幸福 ,不如 说好的 教师是 不幸。 ——海 贝尔 65、接受挑战,就可以享受胜利的喜悦 。——杰纳勒 尔·乔治·S·巴顿
谢谢!Biblioteka
2020年高中物理竞赛(力学篇)02运动、力学定律:质点系的动能定理和功能原理(共14张PPT)

12
fij
• dri
1 2
mi v i22
1 2
mi
v
2 i1
对所有质点求和可得:
n
12
Fi外
i 1
•dr
n
12
i 1
fij
• dri
n
i 1
12mi
i
vi21
注意:
不能先求合力,再求合力的功; 只能先求每个力的功,再对这些功求和。
n
12
Fi外
i 1
•dr
n
12
i 1
fij
• dri
n
i 1
1 2mi
vi22
n
i 1
1 2mi
vi21
质点系的动能定理 A外 A内非 A内保 EK 2 EK1
质点系总动能的增量等于外力的功与质点系内保 守力的功和质点系内非保守力的功三者之和。
A外 A内非 0
A内保 (EP2 EP1) EP
A外 A内非 (EK 2 EK1) (EP2 EP1) A外 A内非 E2 E1
外力对系统和系统非保守内力做功之和等于 系统机械能的增量。
例 一个质量为M、半径为R的定滑
轮(当作均匀圆盘)上面绕有细绳, 绳的一端固定在滑轮边上,另一端挂
一质量为m的物体而下垂。忽略轴处 摩擦,求物体m由静止下落高度h时
的速度和此时滑轮的角速度。
解:据机械能守恒定律:
取滑轮、物体、地球为系统
mgh 1 J 2 1 mv 2
外力对系统和系统非保守内力做功之和等于 系统机械能的增量。
七、机械能守恒定律
若A外 A内非 0
系统的机械能增加
若A外 A内非 0
理论力学说课PPT课件

机械运动实例
总结词
机械运动是理论力学的传统应用领域,涉及 各种实际机械系统的运动规律。
详细描述
机械运动是理论力学中最为常见的应用领域 之一。各种实际机械系统,如汽车、飞机、 机器和机器人等的运动规律,都需要通过理 论力学进行分析和描述。通过研究机械运动, 可以深入理解力矩、动量、动能等力学概念, 以及它们在机械系统中的具体应用。
自我评价
通过本课程的学习,我掌握了理论力 学的基本知识和分析方法,对物理学
的理解更加深入
我认为自己的逻辑思维、抽象思维和 创新能力得到了提高,解决问题的能 力也有所增强
建议
建议增加一些与实际应用相关的案例 和实验,以更好地理解理论力学的应 用价值
对于一些较难理解的概念和公式,希 望能够有更多的解释和练习题
详细描述
力的分析方法包括矢量表示法、直角坐标表示法和极坐标表 示法等。通过力的合成与分解,可以确定物体运动状态的变 化。力矩的计算则涉及到转动惯量、角速度和动量矩等概念 。
运动分析方法
总结词
运动分析方法主要研究物体运动轨迹、速度和加速度等参数。
详细描述
运动分析方法包括对质点和刚体的运动学分析,通过求解运动微 分方程或积分方程,可以确定物体的运动轨迹、速度和加速度等 参数。这些参数对于理解力学系统的运动规律和相互作用至关重 要。
本课程总结
提高了学生解决实际问题的能力 改进方向
针对不同专业需求,调整教学内容和深度,更好地满足学生需求
本课程总结
01
加强实验和实践环节,提高学生 的动手能力和实践经验
02
引入更多现代技术和方法,更新 教材和教学方法,保持课程的前 沿性
力学发展历程与展望
力学发展史
《理论力学》课件

《理论力学》PPT课件
# 理论力学PPT课件 本PPT课件将为你介绍理论力学的基础概念和知识。
物理学基础
经典力学方程
牛顿式方程、拉格朗日方程等经典力学方程
基础知识
力学、热学、光学等基础知识
运动学基础
1 运动学方程
位移、速度、加速度等运动学基本概念
2 轨迹分析
运动学方程、轨迹分析等
动力学基础
1 动力学方程
2 一维运动的应用
力的概念、牛顿三定律等动力学基本概念
动力学方程、一维运动的应用等刚体动力学1Fra bibliotek刚体运动学和动力学
刚体运动学和动力学的基本概念
2 刚体角动量定理
刚体角动量定理、刚体动量定理等
振动与波动
1 单自由度系统 2 多自由度和耦合振动 3 声波和光波
简谐振动分析
多自由度和耦合振动分析
声波和光波等基本概念
相对论力学
1 相对论的基本概念和理论
相对论的基本概念和理论
2 Minkowski时空和洛伦兹变换
Minkowski时空和洛伦兹变换等
结语
基本概念和知识
本PPT课件为您提供了理论力学方面的基本概念和知识,希望对您的学习和工作有所帮助。
# 理论力学PPT课件 本PPT课件将为你介绍理论力学的基础概念和知识。
物理学基础
经典力学方程
牛顿式方程、拉格朗日方程等经典力学方程
基础知识
力学、热学、光学等基础知识
运动学基础
1 运动学方程
位移、速度、加速度等运动学基本概念
2 轨迹分析
运动学方程、轨迹分析等
动力学基础
1 动力学方程
2 一维运动的应用
力的概念、牛顿三定律等动力学基本概念
动力学方程、一维运动的应用等刚体动力学1Fra bibliotek刚体运动学和动力学
刚体运动学和动力学的基本概念
2 刚体角动量定理
刚体角动量定理、刚体动量定理等
振动与波动
1 单自由度系统 2 多自由度和耦合振动 3 声波和光波
简谐振动分析
多自由度和耦合振动分析
声波和光波等基本概念
相对论力学
1 相对论的基本概念和理论
相对论的基本概念和理论
2 Minkowski时空和洛伦兹变换
Minkowski时空和洛伦兹变换等
结语
基本概念和知识
本PPT课件为您提供了理论力学方面的基本概念和知识,希望对您的学习和工作有所帮助。
理论力学的运动学部分.ppt
O1
MO
m2 g
m2 g
m1g
Nx Ny
x
又
xC
m2e 2
m1 m2
cost
故
NyxCmmm212e2emc22ossin t t
Ny m22esint (m1 m2)g
(3)以系统为研究对象,受 y 力如图,由于 X e 0,所以
A rA
rD
rB
C
BrD
D
XD
rD 0且EC cos AE 故 于是支座D的水平反力为 X D
X
1
D
P
AE CC
P
2
0
例1、OA杆绕O轴逆时针转动,均 质圆盘沿OA杆纯滚动。已知圆盘 O 的质量 m 20kg ,半径 R 100mm。 1 在图示位置时,OA杆的倾角为 30
3 11 11 6 8 16
r3
11 16
rB
rE 1 1 r2 1 11 rB 6 rB 2 6 rB 96
11 96
rB
三、求约束反力
于是得
(
1 2
P1
YB
11 8
P2
11 16
P3
11 96
M
)rB
0
rB 0
从而有
YB
理
p2 x
p1x
I
e x
有
p2x p1x Ft
即
W1 g
v
W1 g
v0
Ft
代入已知数据,解得 F 0.5kN
力学竞赛辅导_图文

(a)
vA v
vB (b)
2. 抛体运动
速度:
y
v0
运动方程:
g
O
x
轨道方程:
推论
y
v0
g
O
x
乙
s
甲 h
3. 圆周运动
3.1 圆周运动的加速度
0
v
a P
a
an
s
O R P0 x n0
3.2 圆周运动的角量描述
角位置:=(t)
角速度: 角加速度:
3.3 角量和线量的关系
P
s
椭圆的曲率半径: 轨道方程: 对应运动方程: A点:
y B
b Oa
Ax
同理:
抛物线的曲率半径: 轨道方程: 对应运动方程:
其中:
y
O
x
2. 连体运动问题
解题方法一:运动的分解
情形1:两物体通过刚性细杆或不可伸长的绳子相连, 他们在连线方向的位移、速度和加速度相等。
v1
v2
情形2:两刚性物体接触点的速度沿法向分量相等。
3.刚体平衡的稳定性
满足平衡条件的刚体,若受到扰动,便离开 平衡位置。若它会自动回到平衡位置,则称为稳 定平衡;若它会更远离平衡位置,则称为不稳定 平衡;若平衡位置的周围仍是平衡位置,则称为 随遇平衡。
稳定平衡
不稳定平衡
随遇平衡
4. 质心
y
C
O
x
5.质心运动定理
系统质心加速度的大小与于所受的合外力大小 成正比,与系统的总质量成反比,加速度的方向沿 合外力的方向。
之间的摩擦系数=0.5。今用一恒力F 沿水平方向作
2020年高中物理竞赛—力学篇(进阶版)1-2 质点运动学(2)(共35张PPT)

tan 1( gt )
v0
y
an
a
g
切向加速度
dv at dt
g2t v02 g2t 2
与速度同向
总加速度总是竖直向下的重力加速度 g
法向
an
g2 at2
v0 g 与切向加速度垂直 v02 g2t 2
(下一页)
2.一质点在oxy平面内作曲线运动,其加速度是时间的 函数。已知ax=2, ay=36t2。设质点t=0 r0=0,v0=0。
(下一页)
dx vx dt dx 2tdt
dy v y dt dy 12t 3dt
x
t
0 dx 0 2tdt
x t2
所以质点的运动方程为:
y dy
t 12t 3dt
0
0
y 3t 4
x t2
y
3t 4
r t 2 i 3t 4 j
(2)上式中消去t,得y = 3x2 即为轨道方程。
t 0时x 0c2 0 则x a0 t 2 a0 t3
2 6
(下一页)
例6.一质点沿 x 轴作直线运动,其v-t曲线如图所示, ====如t = 0 时,质点位于坐标原点,求:t= 4.5秒 ====时,质点在 x 轴上的位置,及质点在这段时间
====内通过的路程。 v(m/s)
解: x vdt 2
是加速度的法向分量改变了质点的运动方向。
(下一页)
另v一种v推e导t 法(a课本dPd1vt6):ddvt
et
v
det dt
dddeettt的大 方dd向小 t e为为n e1nden
v
en
et1
et
et2
a
理论力学运动学幻灯片课件

?
v2
6
5、匀速、匀变速公式
(1) aτ=常数,
( 2)v=常数,
v ? v0 ? aτt
?
s
?
s0
?
v0t
?
1 2
aτt 2
?? ? ?
v2 ? v02 ? 2a? (s ? s0 )??
s = so + vt
7
已知运动方程,求导,求得速度、加速度。 已知加速度,运动的初始条件,积分,可求得速度、运动方程。
/ /
点的加速度
a
?
aτ
?
an
?
aτ τ
?
ann
?
dv dt
τ
?
v2
?
n
切向加速度反映速度大小变化
当aτ与v 同号时,点作加速运动,否则作减速运动。
4
法向加速度反映速度方向的变化
aτ ? v?τ ? ?s?τ
v2
an ? ? n
加速度a的大小:
a?
aτ 2+ a n 2 ?
( dv) 2
?
v2 (
ω ? ?k 角加速度矢:
α ? ??k ? ω?? ? k
17
2.用矢积表示点的速度和加速度
用矢径表示转动刚体上任一点M的位置,
aτ 则点M的速度 :
1 an
v ? ω? r
?
点M的加速度为:
×
a ? v?? d (ω ? r) ? ω?? r ? ω ? r? dt
? α ? r ? ω ? v ? a? ? an
解题步骤:
1、运动分析 3、建立运动方程
P11 是非题1-4
P12 题3
2020物理竞赛(提升版)·力学·曲线运动与天体运动课件(共32张PPT)

h tan v0 cos
sin sin
sin
sin
h cos
v0 cos
lim v02 cos
21:50:041h tan
cos
2
sin
2
sin sin
2020物理竞赛(提升版)·力学·曲线运动与天体运动
中学生物理奥林匹克竞赛 专题辅导 (基础版)
力学——曲线运动与天体运动
2020物理竞赛(提升版)·力学·曲线运动与天体运动
一、曲线运动的发生条件
合外力方向与速度方向不在一直线
切向力改变速度大小
法向力改变速度方向
v
Ft
二、曲线运动的特点
速度方向一定变化
v0
v0
vt
vt
A
由加速度定义得: 由几何关系得:
v
A v
则a
a
lim
0
v lim t0 t
v0
sin
1
1 sin
h tan
t
h
cos
vt
lim v02 cos 0 htan
an
lim
t 0
vn t
at
lim vt t0 t
AB
vn vB v
vt
A点曲率圆半径
O
A点曲率圆
vn AB
aAvnA
lvimn
tt0
vA
全国周培源大学生力学竞赛辅导力学竞赛-静力学专题详细版.ppt

Fy 0, FBy FCy P 0 (2)
Fx 0, FBx FCx 0
(3)
2a
aa a a A
2a D
解得: FBy FCy 0.5P
(2)取AB杆为研究对象
Fy 0, FAy FBy P 0
M B (F ) 0, FAx 2a FAy 2a Pa 0
Fx 0, FAx FBx 0
(3)
C D
2m
500N G
FAx
B
FB
E
2m 2m
2m
解上述方程,得
FDy 1000N, FEy 500N (2)取整体为研究对象
M A(F) 0, FB 4 500 2 5006 0
解得: FB1000N
.精品课件.
H
500N
FDy
FEy
C
D
500N
FDx E FEx
15
2m 2m
.精品课件.
4
理论力学(基本部分)
(三)动力学
(1) 掌握建立质点的运动微分方程的方法。了解两类动 力学基本问题的求解方法。
(2) 掌握刚体转动惯量的计算。了解刚体惯性积和惯性主 轴的概念。
(3) 能熟练计算质点系与刚体的动量、动量矩和动能;并 能熟练计算力的冲量(矩),力的功和势能。
(4) 掌握动力学普遍定理(包括动量定理、质心运动定理、 对固定点和质心的动量矩定理、动能定理)及相应的守恒定 理,并会综合应用。
★ 截面法 :截断待求内力的杆件,将桁架截割为两部分,取其 中的一部分为研究对象,应用平面任意力系的平衡方程求出被截 割各杆件的内力。应注意每次截割的内力未知的杆件数目不宜多 于3。
.精品课件.
22
高中物理奥林匹克竞赛——经典力学(共30张PPT)

例1-4 如某质点作直线运动,运动方程为 x 2t. t 2 求①质点在
0 2秒内走的路程。②质点何时到达位置坐标的最大值?
解:(1)由v dx 2 2t
dt
得 S
2
vdt
2
2 2t dt
1
(2 2t)dt
2
(2 2t)dt
0
两边求导
ds r d
dt dt
即线速度与角速度的关系为:v r 两边再求导 dv r d
得切向加速度与角加速度的关系为a r
dt
而法向加速度an
v2 r
dt r 2
质点作匀变速圆周运动时的角速度、角位移与角加速度的关系式 为:
比较知:两者数学形式完全相同,说明用角量描述, 可把平 面圆周运动转化为一维运动形式,从而把问题简化.
C. 瞬时速度
v
lim
t 0
r t
dr dt
dx dt
i
dy dt
j
dz dt
k
vxi vy
j vzk
大小:v v dr dr ds
矢量
dt dt dt
方向沿着该时刻质点所在处运动轨道的切线方向指向前方。
D. 瞬时速率
v lim s ds t0 t dt
sin tj)
dt
速度、加速度也可以用其在x、y方向上的分量来表示
二、自然坐标系下的描述
自然坐标系:以动点为坐标原点,以动点所在轨道处的切线和 法线为坐标轴(切向指向前进方向,法向指向曲率中心),、n 为切、法向的单位矢量。
质点在半径为R的圆周上作匀速圆周运动,
