最短路径与关键路径
第20讲-关键路径与最短路径
数据结构第20次课(续表)`思考题作。
业题试对下图所示的AOE网络,解答下列问题。
(1) 这个工程最早可能在什么时间结束。
.(2) 求每个事件的最早开始时间Ve[i]和最迟开始时间Vl[I]。
(3) 求每个活动的最早开始时间e( )和最迟开始时间l( )。
(4) 确定哪些活动是关键活动。
画出由所有关键活动构成的图,指出哪些活动加速可使整个工程提前完成。
参考资料|《数据结构辅导与提高》,徐孝凯编著,清华大学出版社《数据结构习题解答与考试指导》,梁作娟等编著,清华大学出版社授课内容关键路径~对整个工程和系统,人们关心的是两个方面的问题:一)工程能否顺利进行(对AOV网进行拓扑排序)二)估算整个工程的完成所必须的最短时间(对AOE网求关键路径)1. AOE-网与AOV-网相对应的是AOE-网(Activity On Edge),即边表示活动的网。
AOE-网是一个带权的有向无环图,其中,顶点表示事件(Event),弧表示活动,权表示活动持续的时间。
通常,AOE-网可用来估算工程的完成时间。
"例:下图是一个假想的有11项活动的AOE-网。
其中有9个事件v1,v2,…,v9,每个事件表示在它之前的活动已经完成,在它之后的活动可以开始。
如v1表示整个工程开始,v9表示整个工程结束,v5表示a4和a5已经完成,a7和a8可以开始。
与每个活动相联系的数是执行该活动所需的时间。
比如,活动a1需要6天,a2需要4天等。
和AOV-网不同,对AOE-网有待研究的问题是:(1)完成整项工程至少需要多少时间(2)哪些活动是影响工程进度的关键、2. 关键路径由于在AOE-网中有些活动可以并行地进行,所以完成工程的最短时间备注:回顾是从开始点到完成点的最长路径的长度(这里所说的路径长度是指路径上各活动持续时间之和,不是路径上弧的数目)。
路径长度最长的路径叫做关键路径(Critical Path)。
假设开始点是v1,从v1到v i的最长路径长度叫做事件v i的最早发生时间。
数据结构第19讲_关键路径与最短路径_C

数据结构第19讲_关键路径与最短路径_C 在数据结构的学习过程中,我们经常会遇到需要寻找最短路径的问题。
最短路径问题是指在图中寻找连接两个顶点之间最短路线的问题。
在实际生活中,最短路径问题广泛应用于交通、通信等领域。
在本篇文章中,我们将介绍关键路径和最短路径的概念,以及它们在实际问题中的应用。
首先,让我们来介绍关键路径。
关键路径是指在项目管理中,连接起始点和终止点的最长路径,也是项目完成所需要的最短时间。
关键路径可以通过计算活动的最早开始时间(EST)和最晚开始时间(LST)来确定。
活动的EST是指在没有任何限制条件下,活动可以最早开始的时间;而LST则是指在不影响项目完成时间的前提下,活动可以最晚开始的时间。
关键路径的长度等于项目的最早完成时间和最晚完成时间相等的活动的持续时间之和。
通过确定关键路径,我们可以优化项目进度,提高项目的整体效率。
接下来,让我们来介绍最短路径。
最短路径是指在图中寻找连接两个顶点之间最短路线的问题。
最短路径可以通过使用一些经典的算法来解决,例如迪杰斯特拉算法和弗洛伊德算法。
迪杰斯特拉算法是一种贪心算法,通过计算出从起点到其他顶点的最短路径,然后逐步扩展路径长度来逐步求解最短路径问题。
弗洛伊德算法是一种动态规划算法,通过构建一个关于各个顶点之间最短路径长度的矩阵来求解最短路径问题。
最短路径问题在实际生活中具有广泛应用,例如在地图导航中,我们需要找到从起点到目的地的最短路线;在网络通信中,我们需要找到网络中两个节点之间传输数据的最短路径。
在本篇文章中,我们介绍了关键路径和最短路径的概念,以及它们在实际问题中的应用。
关键路径用于确定项目完成所需的最短时间,而最短路径用于寻找连接两个顶点之间最短路线的问题。
这些概念都是数据结构中的重要内容,对于我们理解和解决实际问题具有重要意义。
为什么关键路径等于最短时间 最短路径计算 案例

为什么关键路径等于最短时间最短路径计算案例这是一篇关于关键路径和最短时间最短路径计算的深度探讨文章,我将从简到繁,由浅入深地解释这个主题,并据此撰写一篇有价值的文章。
文章将采用知识的文章格式,内容会使用序号标注,并多次提及指定的主题文字。
我的个人观点和理解也会在文章中得到充分体现。
我们需要了解什么是关键路径和最短时间最短路径计算。
关键路径是项目管理中的一个重要概念,它指的是项目中的一条或多条路径,如果这些路径上的活动延迟一天,就会导致整个项目的延迟。
而最短时间最短路径计算则是指在一个加权有向图中,从一个顶点到另一个顶点的最短路径问题。
接下来,我们将深入探讨为什么关键路径等于最短时间最短路径计算,并且结合实际案例来说明。
这样的深度和广度的探讨,将帮助我们更全面地理解这个主题。
在这个讨论中,我认为关键路径等于最短时间最短路径计算是因为项目管理中的关键路径实际上就是项目中的最短路径。
通过案例分析,我们可以更加具体地理解这个概念。
比如某个项目中有许多任务需要完成,每个任务都有其完成所需的时间和依赖关系,我们需要找到一条路径,使得这些任务能够在最短的时间内完成。
这个路径就是项目的关键路径,也可以看作是最短时间最短路径。
在文章结尾的总结和回顾性内容中,我将再次强调关键路径和最短时间最短路径计算的重要性,并提出自己对这个主题的个人观点和理解。
总字数会超过3000字,以确保文章的深度和广度。
通过这篇文章,我希望读者能够对关键路径和最短时间最短路径计算有更深入的理解,从而在实际项目管理中能够更加灵活地应用这些概念,提高项目的执行效率和质量。
在实际项目管理中,关键路径和最短时间最短路径计算是非常重要的工具和技术。
它们可以帮助项目经理和团队有效地规划和控制项目进度,确保项目能够按时完成。
在这一部分,我们将进一步讨论关键路径和最短时间最短路径计算的具体应用,并探究如何在实际项目中应用这些概念。
让我们再次强调一下关键路径和最短时间最短路径计算的定义。
离散数学最短路径和关键路径

例1 L1=v0v1v3v5, w(L1)=10, L2=v0v1v4v5, w(L2)=12,
L3=v0v2v4v5, w(L3)=11.
3
标号法(E.W.Dijkstra, 1959)
设带权图G=<V,E,w>, 其中eE, w(e)0. 设V={v1,v2,,vn}, 求v1到其余各顶点的最短路径
的顶点, 称作终点. 通常边的权表示时间, 始点记作v1, 终点记作vn
7
关键路径
关键路径: PETR图中从始点到终点的最长路径 vi的最早完成时间TE(vi): 从始点v1沿最长路径到vi 所需的时间
TE(v1)=0
TE(vi)=max{TE(vj)+wji|vj -(vi)}, i=2,3,,n
vi的最晚完成时间TL(vi): 在保证终点vn的最早完成 时间不增加的条件下, 从始点v1最迟到达vi的时间
TL(vn)=TE(vn)
TL(vi)=min{TL(vj)-wij|vj +(vi)}, i=n-1,n-2,,1
8
关键路径(续)
vi的缓冲时间TS(vi)=TL(vi)-TE(vi), i=1,2,,n vi在关键路径上TS(vi)=0
离散数学最短路径和 关键路径
7.4 最短路径与关键路径
带权图 最短路径与Dijkstra标号法 PERT图与关键路径
2
最短路径
带权图G=<V,E,w>, 其中w:ER.
eE, w(e)称作e的权. e=(vi,vj), 记w(e)=wij . 若vi,vj不 相邻, 记wij =.
设L是G中的一条路径, L的所有边的权之和称作L的 权, 记作w(L). u和v之间的最短路径: u和v之间权最小的通路.
图的最短路径、拓扑排序和关键路径

数据结构课程辅导---图的最短路径、拓扑排序和关键路径一、最短路径由图的概念可知,在一个图中,若从一顶点到另一顶点存在着一条路径(这里只讨论无回路的简单路径),则称该路径长度为该路径上所经过的边的数目,它也等于该路径上的顶点数减1。
由于从一顶点到另一顶点可能存在着多条路径,每条路径上所经过的边数可能不同,即路径长度不同,我们把路径长度最短(即经过的边数最少)的那条路径叫做最短路径,其路径长度叫做最短路径长度或最短距离。
上面所述的图的最短路径问题只是对无权图而言的,若图是带权图,则把从一个顶点i到图中其余任一个顶点j的一条路径上所经过边的权值之和定义为该路径的带权路径长度,从vi到vj可能不止一条路径,我们把带权路径长度最短(即其值最小)的那条路径也称作最短路径,其权值也称作最短路径长度或最短距离。
例如,在图3-1中,从v0到v4共有三条路径:{0,4},{0,1,3,4}和{0,1,2,4},其带权路径长度分别为30,23和38,可知最短路径为{0,1,3,4},最短距离为23。
图3-1 带权图和对应的邻接矩阵实际上,这两类最短路径问题可合并为一类,这只要把无权图上的每条边标上数值为1的权就归属于有权图了,所以在以后的讨论中,若不特别指明,均认为是求带权图的最短路径问题。
求图的最短路径问题用途很广。
例如,若用一个图表示城市之间的运输网,图的顶点代表城市,图上的边表示两端点对应城市之间存在着运输线,边上的权表示该运输线上的运输时间或单位重量的运费,考虑到两城市间的海拔高度不同,流水方向不同等因素,将造成来回运输时间或运费的不同,所以这种图通常是一个有向图。
如何能够使从一城市到另一城市的运输时间最短或者运费最省呢?这就是一个求两城市间的最短路径问题。
求图的最短路径问题包括两个方面:一是求图中一顶点到其余各顶点的最短路径,二是求图中每对顶点之间的最短路径。
下面分别进行讨论。
1. 从一顶点到其余各顶点的最短路径对于一个具有n个顶点和e条边的图G,从某一顶点vi(称此为源点)到其余任一顶点vj(称此为终点)的最短路径,可能是它们之间的边(i,j)或<i,j>,也可能是经过k个(1≤k≤n-2,最多经过除源点和终点之外的所有顶点)中间顶点和k+1条边所形成的路径。
关键路径算法相关概念解读

关键路径算法相关概念解读关键路径VS最短路径关键路径算法⼀般会在最短路径算法的后⾯进⾏讲解。
这就需要我们⾸先区分出关键路径算法和最短路径算法在前提上的不同:最短路径算法是找尽可能短的路来保证路径长度最⼩,你只需要找出⼀条最短的路就⾏。
但是在关键路径⾥,⼀个顶点是有多个前提的,只有前提的路径都⾛完,才能发⽣该顶点的事件,那么只有最长的路径⾛完,保证其余短的路都早已经⾛完,该事件才发⽣。
事件和活动在关键路径算法中,我们将事件定义为AOE图中的“顶点”,将活动定义为AOE图中的“弧”。
事件的发⽣和开始这⾥要⾸先弄明⽩的是两个词,也就是后⾯要学到的概念中的 "发⽣" 和 "开始"。
“发⽣”是针对于事件的,也就是图中的顶点。
什么叫事件发⽣了呢?只有在指向该顶点的所有有向边对应的活动结束,该顶点所代表的事件才发⽣。
举个例⼦,⼀个事件C,它仅被两条边a, b指向,仅当a,b两活动都完成时,事件C发⽣。
“开始”是针对于活动的,也就是图中的弧。
只有在⼀个顶点所代表的事件发⽣后,从该顶点出发的所有边对应的活动才能开始。
什么时候开始?即可以在事件⼀完成就⽴马开始接下来的活动,也可以推迟活动开始的时间。
事件的最早发⽣时间(etv)我们前⾯说过,发⽣是针对于事件的,⼀个事件要发⽣,⾸先要指向它的活动都完成。
⼀个事件C,被两个活动a,b指向,a活动的耗费时间是3, b活动的耗费时间是5。
那么看下图,从开始到C事件的发⽣要多久呢?是最⼤路径长度5,因为C事件发⽣的前提必须是a,b两活动完成(活动可同时进⾏)。
C事件只有等到b完成才发⽣,最早完成时间由耗时最久的路决定,所以这就是为什么要取最长路径长度。
因此:事件的最早发⽣时间推导公式:事件的最晚发⽣时间(ltv)最晚发⽣时间的意义是:在不推迟整个⼯程完成的前提下,该事件最晚的发⽣时间。
因此我们可以想象:在⼀个AOE图中的汇点,其最晚发⽣时间和最早发⽣时间⼀定是相同的,因为汇点事件的发⽣事件⼀定会直接决定整个⼯程的完成时间。
最短路径和关键路径

l
( i
0
)
=0,
P0={v1},
T0=V-{v1},
vj(j=2,3,,n)获t标源自号:l( j
0
)
=wij.
令r1.
2. 设
l(r1) i
vm jTri1{nl(jr1)},
vi获得p标号:
l(r) i
li(r1)
.
令 Pr=Pr-1{vi}, Tr=Tr-1-{vi}.
若Tr=, 则结束.
3. vjTr, 令 l(jr) mi{ln(jr1),li(r)wij}
最短路径与关键路径
带权图 最短路径与Dijkstra标号法 PERT图与关键路径
1
最短路径
带权图G=<V,E,w>, 其中w:ER.
eE, w(e)称作e的权. e=(vi,vj), 记w(e)=wij . 若vi,vj不 相邻, 记wij =.
设L是G中的一条路径, L的所有边的权之和称作L的 权, 记作w(L). u和v之间的最短路径: u和v之间权最小的通路.
例1 L1=v0v1v3v5, w(L1)=10, L2=v0v1v4v5, w(L2)=12,
L3=v0v2v4v5, w(L3)=11.
2
标号法(, 1959)
设带权图G=<V,E,w>, 其中eE, w(e)0. 设V={v1,v2,,vn}, 求v1到其余各顶点的最短路径
p标号(永久性标号)l
vi的最晚完成时间TL(vi): 在保证终点vn的最早完成 时间不增加的条件下, 从始点v1最迟到达vi的时间
TL(vn)=TE(vn)
TL(vi)=min{TL(vj)-wij|vj +(vi)}, i=n-1,n-2,,1
关键路径和最短路径及树

关键路径和最短路径:基本思路:1.关键路径法:关键路径法对于一个项目而言,只有项目网络中最长的或耗时最多的活动完成之后,项目才能结束,这条最长的活动路线就叫关键路径。
2.最短路径法:求一个顶点到其余顶点的最短路径主要运用Dijkstra 算法,把图中的顶点分为两个集合S 和T ,集合S 皴法已确定最短路径的顶点,集合T 存放尚未确定最短路径的顶点。
按最短路径长度递增的次序逐个将T 集合中的顶点加入到S 中,直到从源点出发可以到达的所有顶点都在S 中为止。
演算过程:1.关键路径各项活动的最早时间,t(A)=0t(B)=max{2,15+4}=19t(C)=15t(D)=19+10=29t(E)=max{19+19,15+11}=38t(F)=max{29+6,38+5}=43事项的最早时间为43各事项的最迟时间,t(F)=43t(D)=43-6=37t(E)=43-5=38t(B)=min{37-10,38-19}=19t(C)=min{19-4,38-11}=15t(A)=15-15=0.所以关键路径为:A →C →B →E →FA B C DE F 2 1111 465起终2.最短路径首先将A 点分到S集合中,其余各点分到T集合,S(A)=0,其余各点为T=+∞与A相关的边(A,B),(A,C)T(B)=min{T(B),S(A)+2}=min{+∞,0+2}=2T(C)=min{T(C),S(A)+15}=min{+∞,0+15}=15∴S(C)=15,记录路径(A,C)与C相关的边(C,B),(C,E)T(B)=min{T(B),S(C)+4}=min{2,15+4}=2T(E)=min{T(E),S(C)+11}=min{+∞,15+11}=26∴S(B)=2,记录路径(A,B)与B相关的边(B,D),(B,E)T(D)=min{T(D),S(B)+10}=min{+∞,2+10}=12T(E)=min{T(E),S(B)+19}=min{26,2+19}=21∴S(D)=12,记录路径(B,D)与D相关的边(D,F)T(F)=min{T(F),S(D)+6}=min{+∞,12+6}=18∴S(E)=21,记录路径(B,E)与E相关的边(E,F)T(F)=min{T(F),S(E)+5}=min{18,21+5}=18∴S(F)=18,记录路径(D,F)从A点到到其余各顶点最短路为:所以A到F的最短路为A→B→D→FB+树和B*树:针对上述文件建立4阶的B+树和B*树索引结构,用图形描述在该文件中先后新增ID为50和45的记录,用图形分别描述新增两条记录后索引结构(B+树和B*树)的变化B+树和B*树的区别:B+叶子结点中存储记录,在B+树中,所有的非叶子结点可以看成是索引,而其中的关键字是作为“分界关键字”,用来界定某一关键字的记录所在的子树。
关键路径和最短路径详解过程

1、求下图从事件0出发的关键路径,要求详细过程。
1、事件Vj 可能的最早发生时间ve(j) Ve(0)=0;Ve(1)=ve(0)+weight(<v0,v1>)=0+5=5; Ve(2)=ve(0)+weight(<v0,v2>)=0+9=9; Ve(3)=ve(0)+weight(<v0,v3>)=0+14=14; Ve(4)=ve(1)+weight(<v1,v4>)=5+4=9;Ve(5)=max{ve(2)+weight(<v2,v5>),ve(4)+weight(<v4,v5>)}=max{9+10,9+6}=19; Ve(6)=ve(3)+weight(<v3,v6>)=14+3=17;Ve(7)=max{ve(3)+weight(<v3,v7>),ve(6)+weight(<v6,v7>)}=max{14+7,17+5}=22; Ve(8)=max{ve(6)+weight(<v6,v8>),ve(7)+weight(<v7,v8>)}=max{17+5,22+8}=30; Ve(9)=max{ve(4)+weight(<v4,v9>),ve(5)+weight(<v5,v9>),ve(8)+weight(<v8,v9>)}= Max{9+12,19+10,30+18}=48;56 7855 3141010 9124a 12a 6a 8 a 11 a 5a 2a 13 a 10 a 4a 1 a 9 a 7 a 318a 08 763 142592、事件vi可能的最晚发生时间vl(i)Vl(9)=48;Vl(8)=vl(9)-weight(<v8,v9>)=48-18=30;Vl(7)=vl(8)-weight(<v7,v8>)=30-8=22;Vl(6)=min{ve(7)-weight(<v7,v6>),ve(8)-weight(<v8,v6>)}=min{22-5,30-5}=min{17,25 }=17;Vl(5)=vl(9)-weight(<v5,v9>)=48-10=38;Vl(4)=min{vl(5)-weight(<v4,v5>),vl(9)-weight(<v4,v9>)}=min{38-6,48-12}=min{32,3 6}=32;Vl(3)=min{vl(6)-weight(<v3,v6>),vl(7)-weight(<v3,v7>)}=min{17-3,22-7}=min{14,15 }=14Vl(2)=vl(5)-weight(<v2,v5>)=38-10=28;Vl(1)=vl(4)-weight(<v1,v4>)=32-4=28;Vl(0)=min{vl(1)-weight(<v0,v1>),vl(2)-weight(<v0,v2>),vl(3)-weight(<v0,v3>)}= Min{28-5,28-9,14-14}=min{23,19,0}=0;3、活动a(k)=<vi,vj>的最早开始时间E(k)E(0)=ve(0)=0E(1)=ve(0)=0E(2)=ve(0)=0E(3)=ve(1)=5E(4)=ve(2)=9E(5)=ve(3)=14E(6)=ve(3)=14E(7)=ve(4)=9E(8)=ve(6)=17E(9)=ve(4)=9E(10)=ve(5)=19E(11)=ve(6)=17E(12)=ve(7)=22E(13)=ve(8)=304、活动a(k)的最晚开始时间L(k)L(0)=vl(1)-weight(<v0,v1>)==28-5=23L(1)=vl(2)-weight(<v0,v2>)==28-9=21L(2)=vl(3)-weight(<v0,v3>)==14-14=0L(3)=vl(4)-weight(<v1,v4>)==32-4=28L(4)=vl(5)-weight(<v2,v5>)==38-10=28L(5)=vl(6)-weight(<v3,v6>)==17-3=14L(6)=vl(7)-weight(<v3,v7>)==22-7=15L(7)=vl(5)-weight(<v4,v5>)==38-6=32L(8)=vl(7)-weight(<v6,v7>)==22-5=17L(9)=vl(9)-weight(<v4,v9>)==48-12=36 L(10)=vl9)-weight(<v5,v9>)==48-10=38 L(11)=vl(8)-weight(<v6,v8>)==30-5=34 L(12)=vl(8)-weight(<v7,v8>)==30-8=22 L(13)=vl(9)-weight(<v8,v9>)==48-18=30L(0)-E(0)=23-0=23L(1)-E(1)=21-0=21L(2)-E(2)=0-0=0L(3)-E(3)=28-5=23L(4)-E(4)=28-9=19L(5)-E(5)=14-14=0L(6)-E(6)=15-14=1L(7)-E(7)=32-9=23L(8)-E(8)=17-17=0L(9)-E(9)=36-9=27L(10)-E(10)=38-19=19L(11)-E(11)=34-17=17L(12)-E(12)=22-22=0L(13)-E(13)=30-30=05、题中图的关键路径如下图所示:2、对于下图所示的有向图,试利用Dijkstra算法求源点1到其他各顶点的最367 8 9短路径,可参考教材P207图7.29中的表格形式给出计算过程。
图_拓扑排序关键路径最短路径

6 a 5 d 4
b
1 1 e
8 7
g 4 h
2 k
c 2 4 f
a b c d e f g h k ve vl
0 0 0 0 0 0 15 14 18 6 4 5 5 7 0 11 0 7 0 18 18 18 18 18 18 18 18 18 0 6 6 8 8 10 16 14 7
事件发生时间的计算公式: 事件发生时间的计算公式: ve(源点 = 0; 源点) 源点 ; ve(j) = Max{ve(i) + dut(<i, j>)} <i,j>表示以 为弧头的弧 表示以j为弧头的弧 表示以 vl(汇点 = ve(汇点 ; 汇点) 汇点); 汇点 汇点 vl(i) = Min{vl(j) – dut(<i, k>)} <i,j>表示以 为弧尾的弧 表示以i为弧尾的弧 表示以
(2)弗洛伊德算法的基本思想是:
的所有可能存在的路径中, 从 vi 到 vj 的所有可能存在的路径中,选出一条长 度最短的路径。
可以用如下递推公式描述: 可以用如下递推公式描述: D-1[i][j]=cost[i][j] Dk [i][j]=min{Dk-1[i][j],Dk-1[i][k]+Dk-1[k][j]}(0≤k≤n-1) 其中, 中存放着序号为i的结点到序号为 其中,cost[i][j]中存放着序号为 的结点到序号为 的结点之 中存放着序号为 的结点到序号为j的结点之 表示从结点vi到结点 到结点vj的路径 间的权值 ; Dk[i][j](0≤k≤n-1) 表示从结点 到结点 的路径 上所经过的结点序号不大于k的最短路径长度 的最短路径长度。 上所经过的结点序号不大于 的最短路径长度。
数据结构第19讲关键路径与最短路径

数据结构第19讲关键路径与最短路径关键路径与最短路径是数据结构中非常重要的概念和算法。
它们在许多领域中都有广泛的应用,包括项目管理、网络通信、物流运输等等。
本文将介绍关键路径和最短路径的概念、算法以及它们的应用。
一、关键路径关键路径是指在一个项目中,所有活动中最长的路径,也即完成整个项目所需的最长时间。
关键路径的长度决定了项目的最短完成时间,因此对于项目管理非常重要。
关键路径的计算通常使用网络图来表示项目的各个活动以及它们的前后关系。
在网络图中,每个活动用一个节点表示,活动之间的关系用边来表示。
活动之间的关系可以分为两种:顺序关系和并行关系。
1.顺序关系:活动A必须在活动B之前完成,这种关系用有向边表示。
2.并行关系:活动A和活动B可以同时进行,这种关系用无向边表示。
关键路径算法通过在网络图上进行正向遍历和逆向遍历来计算关键路径。
具体步骤如下:1.正向遍历:从起始节点出发,计算每个节点的最早开始时间。
最早开始时间是指在没有任何延迟的情况下,从起始节点到达该节点所需的最短时间。
2.逆向遍历:从终点节点出发,计算每个节点的最晚开始时间。
最晚开始时间是指在不延误整个项目完成时间的情况下,从终点节点回到该节点所需的最短时间。
3.计算关键路径:根据每个节点的最早开始时间和最晚开始时间,找出那些最早开始时间和最晚开始时间相等的节点,这些节点就是关键路径上的节点。
关键路径的计算可以有效地帮助项目管理者确定项目的最短完成时间,并将各个活动按照优先级进行排序和调度,从而提高项目的管理效率。
二、最短路径最短路径是指在一个加权图中,从起点到终点所经过的边的权值之和最小的路径。
最短路径算法有很多种,下面介绍两种常用的最短路径算法:迪杰斯特拉算法和弗洛伊德算法。
1.迪杰斯特拉算法:迪杰斯特拉算法是一种贪心算法,用于解决单源最短路径问题。
具体步骤如下:-创建两个集合S和V-S,分别用于存放已确定最短路径的节点和待确定最短路径的节点。
图的最短路径、拓扑排序和关键路径

数据结构课程辅导---图的最短路径、拓扑排序和关键路径一、最短路径由图的概念可知,在一个图中,若从一顶点到另一顶点存在着一条路径(这里只讨论无回路的简单路径),则称该路径长度为该路径上所经过的边的数目,它也等于该路径上的顶点数减1。
由于从一顶点到另一顶点可能存在着多条路径,每条路径上所经过的边数可能不同,即路径长度不同,我们把路径长度最短(即经过的边数最少)的那条路径叫做最短路径,其路径长度叫做最短路径长度或最短距离。
上面所述的图的最短路径问题只是对无权图而言的,若图是带权图,则把从一个顶点i到图中其余任一个顶点j的一条路径上所经过边的权值之和定义为该路径的带权路径长度,从vi到vj可能不止一条路径,我们把带权路径长度最短(即其值最小)的那条路径也称作最短路径,其权值也称作最短路径长度或最短距离。
例如,在图3-1中,从v0到v4共有三条路径:{0,4},{0,1,3,4}和{0,1,2,4},其带权路径长度分别为30,23和38,可知最短路径为{0,1,3,4},最短距离为23。
图3-1 带权图和对应的邻接矩阵实际上,这两类最短路径问题可合并为一类,这只要把无权图上的每条边标上数值为1的权就归属于有权图了,所以在以后的讨论中,若不特别指明,均认为是求带权图的最短路径问题。
求图的最短路径问题用途很广。
例如,若用一个图表示城市之间的运输网,图的顶点代表城市,图上的边表示两端点对应城市之间存在着运输线,边上的权表示该运输线上的运输时间或单位重量的运费,考虑到两城市间的海拔高度不同,流水方向不同等因素,将造成来回运输时间或运费的不同,所以这种图通常是一个有向图。
如何能够使从一城市到另一城市的运输时间最短或者运费最省呢?这就是一个求两城市间的最短路径问题。
求图的最短路径问题包括两个方面:一是求图中一顶点到其余各顶点的最短路径,二是求图中每对顶点之间的最短路径。
下面分别进行讨论。
1. 从一顶点到其余各顶点的最短路径对于一个具有n个顶点和e条边的图G,从某一顶点vi(称此为源点)到其余任一顶点vj(称此为终点)的最短路径,可能是它们之间的边(i,j)或<i,j>,也可能是经过k个(1≤k≤n-2,最多经过除源点和终点之外的所有顶点)中间顶点和k+1条边所形成的路径。
数据结构-第七章图(关键路径和最短路径)

时间分析: O( n 2 )
#include<iostream.h>
int search(char e);//查找顶点在顺序表中的下标
#define max 20
class Arcbox{ public: int tailvex,headvex; Arcbox *hlink,*tlink;}; class VexNode{ public: char data; Arcbox *firstin,*firstout;}; class OLgraph{ };
int count=0;
int i=search(e); Arcbox *p=xlist[i].firstout; while(p){ count++; p=p->tlink;} return count;
void main(void){ char ch; OLgraph G;
G.CreateDG();
13 8 g
30
32 7 17
7. Dijkstra 算法的C语言描述 由于C/C++的下标从0开始,所以算法中作相应的改动,用NUM代表 图的顶点数 #define NUM void shortpath_dij(g[][NUM],v0) //v0为源点,值为1到NUM { for(i=0;i<NUM;i++){ set[i]=0; dist[i]=g[v0-1][i];} set[v0-1]=1; for(i=1;i<NUM;i++) { min=MAXINT; for(w=0;w<NUM;w++) if(set[w]= =0 && dist[w]<min) { v=w; min=dist[w]; } set[v]=1; for(w=0;w<NUM;w++) if(set[w]= =0 && dist[v]+g[v][w]<dist[w]) dist[w]=dist[v]+g[v][w]; }//for i } //shortpath_dij
最短路径与关键路径

第四节最短路径与关键路径1.最短路径:对于图G=<V, E>(有向图或无向图)的每一条边e都附加一个实数w(e),w(e)称为e的权,则称G是一个带权图或赋权图,并把它记作G=<V , E, w >,其中w是E上的实函数,叫作权函数。
对于简单图,当 e =(v i ,v j )(或<v i ,v j >),常把w(e) 记作w ij。
设G=<V , E, w >是n阶简单带权图(无向的或有向的),边(v i ,v j)(或<v i ,v j >)的权为w ij,并且约定:w ii = 0;当v i与v j之间无边关联时w ij=∞。
G中一条通路(回路)上各条边的权之和叫作该通路(回路)的权。
G中从v i到v j的权最小的通路叫作v i到v j的最短路径。
根据刚才的约定,若不存在从v i到v j的通路,则认为v i到v j的最短路径的权为∞。
所谓最短路径问题就是求给定图中两点之间的最短路径。
下面介绍求最短路径问题的Dijkstra标号法。
它仅可用于所有的权w ij ≥ 0的情况,可以求从给定顶点(设为v1)到所有顶点的最短路径。
先介绍几个符号和名词。
(1)设l i(r)∗为顶点v1(最短路径的起点)到v i(最短路径的终点)的最短路径的权。
若v i获得li(r)∗,称v i在第r(r ≥ 0)步获得了永久性标号,简称为p标号。
由于v1为起点,且w=0,故当r = 0时,l1(0)∗= 0,首先v1获得永久性标号P。
11(2)设l(jr)为v1到v j的最短路径的权在第r步获得的一个上界,称l(jr)为顶点v j的临时性标号,简称t标号,其中,r ≥ 0,开始的时候,l j = w1j。
(0)(3)设P r = {v v在前r步获p标号},称P r为第r步的通过集,r ≥ 0。
(4)设T r =V −P r,称T r为第r步未通过集。
Dijkstra标号法的计算步骤如下:(1)开始令r ← 0,获p标号:l1(0)∗= 0,P0 ={v1},T0 =V −P0,v j( j ≠1)的t标号为l(0)j= w1j (2)求下一个p标号顶点。
离散数学PPT课件 4最短路径与关键路径(ppt文档)

第二步.若 i=n-1 则停. 否则转第三步
第三步. 对每个u’∈Si’ 计算 d(u0,u’)=muii ∈n{Sdi (u0,u’), d(u0,ui)+c(ui,u’)}
计算 mu’i∈nS{di’ (u0,u’)}
并用ui+1记下达到该最小值的那个结点u’ 置Si+1 =Si∪{ui+1} i=i+1 转第二步.
d(u0,v5)=min{d(u0,v5),d(u0,u0)+c(u0,v5)}=min{∞,0+∞}=∞
d(u0,v6)=min{d(u0,v6),d(u0,u0)+c(u0,v6)}=min{∞,0+∞}=∞
min{3,∞,5, ∞,∞}=3
ui+1 =u1=v2 ,
实际已求出d(u0,v2)=3, 路是u0v2
i=2 S2={v1, v2 ,v4} S2’={v3,v5,v6} u2=v4 d(u0,u2)=4
3 v2 6
v1
1 5
3
v4 1
v3 3
3 6 v6 v5
d(u0,v3)=min{d(u0,v3), d(u0,u2)+c(u2,v3)}=min{9 ,4+3}=7
d(u0,v5)=min{d(u0,v5), d(u0,u2)+c(u2,v5)}=min{∞,4+1}=5
d(u0,v5)=min{d(1,v5)}=min{∞,3+∞}=∞
d(u0,v6)=min{d(u0,v6),d(u0,u1)+c(u1,v6)}=min{∞,3+∞}=∞
min{9,4,∞,∞}=4
ui+1 =u2=v4 ,
详解图的应用(最小生成树、拓扑排序、关键路径、最短路径)
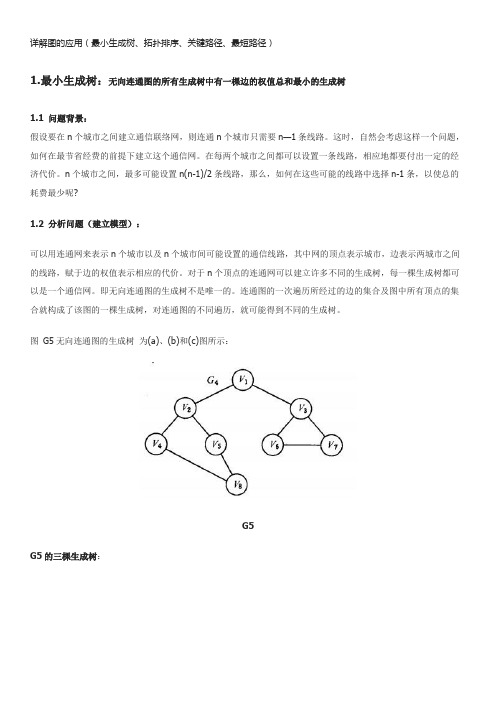
详解图的应用(最小生成树、拓扑排序、关键路径、最短路径)1.最小生成树:无向连通图的所有生成树中有一棵边的权值总和最小的生成树1.1 问题背景:假设要在n个城市之间建立通信联络网,则连通n个城市只需要n—1条线路。
这时,自然会考虑这样一个问题,如何在最节省经费的前提下建立这个通信网。
在每两个城市之间都可以设置一条线路,相应地都要付出一定的经济代价。
n个城市之间,最多可能设置n(n-1)/2条线路,那么,如何在这些可能的线路中选择n-1条,以使总的耗费最少呢?1.2 分析问题(建立模型):可以用连通网来表示n个城市以及n个城市间可能设置的通信线路,其中网的顶点表示城市,边表示两城市之间的线路,赋于边的权值表示相应的代价。
对于n个顶点的连通网可以建立许多不同的生成树,每一棵生成树都可以是一个通信网。
即无向连通图的生成树不是唯一的。
连通图的一次遍历所经过的边的集合及图中所有顶点的集合就构成了该图的一棵生成树,对连通图的不同遍历,就可能得到不同的生成树。
图G5无向连通图的生成树为(a)、(b)和(c)图所示:G5G5的三棵生成树:可以证明,对于有n 个顶点的无向连通图,无论其生成树的形态如何,所有生成树中都有且仅有n-1 条边。
1.3最小生成树的定义:如果无向连通图是一个网,那么,它的所有生成树中必有一棵边的权值总和最小的生成树,我们称这棵生成树为最小生成树,简称为最小生成树。
最小生成树的性质:假设N=(V,{ E}) 是个连通网,U是顶点集合V的一个非空子集,若(u,v)是个一条具有最小权值(代价)的边,其中,则必存在一棵包含边(u,v)的最小生成树。
1.4 解决方案:两种常用的构造最小生成树的算法:普里姆(Prim)和克鲁斯卡尔(Kruskal)。
他们都利用了最小生成树的性质1.普里姆(Prim)算法:有线到点,适合边稠密。
时间复杂度O(N^2)假设G=(V,E)为连通图,其中V 为网图中所有顶点的集合,E 为网图中所有带权边的集合。
最短路径及关键路径

ij
(4)设Tr=V-Pr为第r步未通过集,r≥0.
向边e=<v ,v >时,w(e)也记为w · (3)设Pr={v|v已获得p标号}为第r步通过集,r≥0.
常记带权图为G=<V,E,W>.
ij
ij
这样从v5往前追踪,得v0到v5的最短路径为
修改通过集和未通过集:
最短路径问题
设带权图G=<V,E,W>. wij≥0 .u,v为 G中任意两个顶点,从u到v的所有通 路中带权最小的通路称为u到v的最 短路径.
设G=<V,E,W>是n阶简单带权 图,wij≥0.若顶点vi与vj不相邻,令 wij=∞.求G中顶点v1到其余各顶 点的最短路径.
设点vli(ir处)*,表vm j明Tirnv1{i获l(jr得1)}p标号,将 .修l i改( r ) * 通标过在集相和应未顶 通过集:
Pr=Pr-1∪{vi},Tr=Tr-1-{vi}. ,
查Tr:若Tr=,则算法结束,否则转②.
②修改Tr中各顶点的t标号:
获l( jr得) 标m 号in { 顶lr j点 1 ,的li(r) p* 标 w 号ij} .令,li( rr ←)* 是r+刚1刚, 转①.
例 求图中顶点v0与v5的最短路径.
解 :可以将计算过程用一张表表示 出来(见下页表)
由表可知,v5与v3相邻,v3与v4相 邻,v4与v2相邻,v2与v1相邻,v1与v0 相邻.这样从v5往前追踪,得v0到v5 的最短路径为
Γ=v0v1v2v4v3v5.
W(Γ)=9.
(3)设Pr={v|v已获得p标号}为第r步 通过集,r≥0.
7.4最短路径与关键路径

v0, v1 ,v4,v2 v3 v0, v1 ,v4,v2 v3,v5
V-S
v1,v2,v3,v4,v5 v2,v3,v4,v5
第1 步 第2 步 第3 步 第4 步 第5 步
0
v0v1v2
1+7
[3] v0v1v2
8
4+3
v0v1v2v4,v3
[7] v0v1v2v4,v3
例如: 例如:
该带权图的邻接矩阵是: 该带权图的邻接矩阵是:
v1 1 2 4 v2 7 v3 5 1 v4 3 6 2 v5
v0
0 1 4 ∞ ∞ ∞ 1 0 2 7 5 ∞ 4 2 0 ∞ 1 ∞ AG = ∞ 7 ∞ 0 3 2 ∞ 5 1 3 0 6 ∞ ∞ ∞ 2 6 0
2.事项的最迟(必须 完成时间 TL(vi) .事项的最迟 必须 必须)完成时间
定义:在保证收点 定义:在保证收点vn的最早完成时间不增加 的条件下,该事项 最晚必须完成的时间, 的条件下,该事项vi最晚必须完成的时间,称 为该点v 最晚完成时间,记为TL(vi)。 为该点 i最晚完成时间,记为 。
1.事项的最早完工时间,TE(vi) .事项的最早完工时间,
定义:自发点v 开始沿权和最长路径到达v 定义:自发点v0开始沿权和最长路径到达vi 所需的时间称为该点v 的最早完工时间, 所需的时间称为该点vi的最早完工时间,记作 TE(vi),TE(vi)在前面所有工序均没有耽误的 情况下,该事项最早可能完成时间, 情况下,该事项最早可能完成时间,此时前面 v2 2 v4 的工序均必须完成。 的工序均必须完成。 3 4 2 v1 v5 4 2 3 v7 4 v8 4 v6 v3 4
《数据结构》最短路径关键路径及其应用解析

a3
a8
a1
a7
a4
a9
a2
a5
a6
施工从活动 a1、 a2开始,到达活动 a8和 a9时,整个 施工结束。这类有向图中,顶点表示活动,弧< ai, aj >表示活动 ai优先于活动 aj ,称这类有向图为顶点 表示活动的网(AOV网)。
AOV网可解决如下两个问题: (1)判定工程的可行性。显然,有回路,整个工 程就无法结束
D(-1)
D(0)
D(1)
D(2)
D
0
1
2
0
1
2
0
1
2
0
1
2
0
0
4 11 0
4 11 0
4
6
0
4
6
1
6
0
2
6
0
2
6
0
2
5
0
2
2
3
0
3
7
0
3
7
0
3
7
0
P(-1)
P(0)
P(1)
P(2)
P
0
1
2
0
1
2
0
1
2
0
1
2
0
AB AC
AB AC
AB ABC
AB ABC
1 BA
BC BA
BC BA
BC BCA
BC
2 CA
则图G的邻接矩阵为:
+
甲 乙 丙 丁 戊己
+
甲∞ ∞ 7 4 ∞ ∞
+
+
乙2 ∞ ∞ ∞ ∞ 8
+
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第四节最短路径与关键路径
1.最短路径:对于图G=<V, E>(有向图或无向图)的每一条边e都附加一个实数
w(e),w(e)称为e的权,则称G是一个带权图或赋权图,并把它记作G=<V , E, w>,其中w是E上的实函数,叫作权函数。
对于简单图,当e=(v i,v j)(或<v i,v j>),常把w(e) 记作w ij。
设G=<V , E, w>是n阶简单带权图(无向的或有向的),边(v i,v j)(或<v i,v j>)的权为w ij,并且约定:w ii=0;当v i与v j之间无边关联时w ij=∞。
G中一条通路(回
路)上各条边的权之和叫作该通路(回路)的权。
G中从v i到v j的权最小的通路叫作v i到
v j的最短路径。
根据刚才的约定,若不存在从v i到v j的通路,则认为v i到v j的最短路径
的权为∞。
所谓最短路径问题就是求给定图中两点之间的最短路径。
下面介绍求最短路径问题的Dijkstra标号法。
它仅可用于所有的权w ij≥0的情况,可
以求从给定顶点(设为v1)到所有顶点的最短路径。
先介绍几个符号和名词。
(1)设l i(r)∗为顶点v1(最短路径的起点)到v i(最短路径的终点)的最短路径的权。
若v i获得l
i(r)∗,称v i在第r(r≥0)步获得了永久性标号,简称为p标号。
由于v1为起点,且w=0,故当r=0时,l1(0)∗=0,首先v1获得永久性标号P。
11
(2)设l(jr)为v1到v j的最短路径的权在第r步获得的一个上界,称l(jr)为顶点v j的
临时性标号,简称t标号,其中,r≥0,开始的时候,l j=w1j。
(0)
(3)设P r={v v在前r步获p标号},称P r为第r步的通过集,r≥0。
(4)设T r=V−P r,称T r为第r步未通过集。
Dijkstra标号法的计算步骤如下:
(1)开始
令r←0,获p标号:l1(0)∗=0,P0 ={v1},T0 =V−P0,v j( j≠1)的t标号为l(0)j
=w1j (2)求下一个p标号顶点。
令r ← r +1。
设 min{l (jr −1)}=l i (r −1),则记l i (r )∗ = l i (r −1),将l i (r )∗放在相应顶点v i 处,
v ∈T j r
−1 表明v i 获 p 标号。
修改通过集和未通过集:令
P r = P r −1U {v i },T r =T r −1 −{v i }
检查 T r 。
若T r = ∅,则算法结束,否则执行(3)。
(3)修改T r 中各顶点的 t 标号。
令
l (jr ) = min{l (jr −1),l i (r )∗ + w ij },v j ∈T r 。
转(2)。
例 4.1 求图 4.1中 v 1到其余顶点的最短路径及其权。
解用 Dijkstra 标号法求解计算过程如表 4.1所示。
T 0 ={v 2,v 3,v 4},这里
(1)r =1:
l ,l 3 ,l
}= min{3,1,∞}=1= l 3
3(1)∗
= min{l 2(0) (0) (0) (0) ,l 3(1)∗的下标之所以取作 3,是因为最
4 小值是在第三个顶点处取得。
v 3在第一步获 P 标号(永久性标号),v 1到v 3的最短路 ,因此 v 1到 v 3的最短路径就是边 v 1,v 3 。
这样
T 1 =T 0 −{v 3}={v 2,v 4},这两个顶点的临时性标号(T 标号)为
径的权为
l 3(1)∗=1 l l (1) 2 = min{l 2
(0) ,l 3(1)∗ + w 32}= min{3,1,+3}= 3 (1) 4
= min{l 4 (0)
,l 3(1)∗ + w 34}= min{∞,1,+5}= 6。
(2)r = 2: min{l 2 (1) ,l }= min{3,6}= 3 = l 2
(1) (1) = l 2(2)∗,v 2在第二步获得永久性标号 P, v 1到v 2的
4 最短路径的权就是 3,因此v 1到v 2的最短路径就是边 v 1,v 2。
这样T 2 ={v 4},v 4的临时性
标号为
l (2) 4
= min{l 4 (1),l 2(2)∗ + w 24}= min{6,3+ 2}= 5。
(3)r = 3: 4(3)∗ = min{l 4 l (2)
}= 5,v 4在第三步获永久性标号 P, v 1到v 4的最短路径权就是 5, v 1到 v 4的最短路径就是 v 1,v 2 + v 2,v 4,而T 3 = ∅,算法结束。
表 4.1
j
l (0) j l (1) j l (2) j l (3) j 1
2
3
4 0 3 1 * 3 3 * 1*
∞ 6 5 5
*
上表中的第一列为l 1 ,l ,l 3 ,l = 0;第二列为l 2 = 3,l 3 =1 ,l = 6;
(0) (0) (0) (0)的值,l 1(0)∗ = l 1(0) (1) (1) ∗ (1)
2 4 4 第三列为l 2(2)∗ = 3,l 4(2) = 5;第四列为l 4(3)∗ = 5。
v 2
v 1 v 4
v 3
例 4.2设备更新问题。
某企业使用一台设备,在每年年初,企业领导部门就要决定是购置新 的,还是继续使用旧的。
若购置新设备,就要支付一定的购置费用;若继续使用旧设备,则 需支付一定的维修费用。
现在的问题是如何制定一个几年之内的设备更新计划,使得总的支 付费用最少。
下面以 5年的计划为例,若已知该种设备在各年年初的价格为:
第 1年 第 2年 第 3年 第 4年 第 5年
11 11 12 12 13
还已知使用不同时间(年)的设备所需要的维修费用为:
使用年数 维修费用 0-1 1-2 2-3 3-4 4-5
5 6 8 11 18
可供选择的方案很多,如何制定方案使得总的支付费用最少呢?可以把这个问题转化为最短 路问题。
用点v i 表示“第i 年年初购进一台设备”这种状态。
加点v 6理解为第 5年年底。
从v i 到
( ) v i +1,L ,v 6各画一条弧,弧 v ,v 表示在第i 年初购进的设备一直使用到第 j 年年初。
i j 每条弧的权可按资料计算出来。
例如,(v 1,v 4)是第 1年年初购进一台新设备(购置费
11),一直使用到第 3年年底(维修费 5+6+8=19),故(v 1,v 4)上的权为 30。
这样一来,制定一个最优的设备更新计划的问题就等价于寻求从 v 1到v 6的最短路的问 题。
按求解最短路的计算方法,可以得出{v 1,v 3,v 6}及{v 1,v 4,v 6}均为最短路,即在第 1年 和第 3年各购置一台新设备,或者在第 1年与第 4年各购置一台新设备,5年总的支付费用 均为 53。
请读者自己写出详细的求解过程。
