正方形几何综合专题---40道题目(含答案)

合集下载

初三数学中考复习正方形专题练习题含答案

2019 初三中考数学复习正方形专题练习题1. 已知四边形ABCD中，∠A＝∠B＝∠C＝90°，如果添加一个条件，即可推出该四边形是正方形，那么这个条件可以是( )A．BC＝CD B．AB＝CD C．AD＝BC D．AC＝BD2. 下列说法不正确的是( )A．一组邻边相等的矩形是正方形B．对角线相等的矩形是正方形C．对角线互相垂直的矩形是正方形D．有一个角是直角的菱形是正方形3. 在四边形ABCD中，点O是对角线AC，BD的交点，能判定这个四边形是正方形的条件是( )A．AC＝BD，AB∥CD，AB＝CDB．AO＝BO＝CO＝DO，AC⊥BDC．AD∥BC，∠A＝∠CD．AO＝CO，BO＝DO，AB＝BC4. 如图，在△ABC中，∠ACB＝90°，BC的垂直平分线EF交BC于点D，交AB于点E，且BE ＝BF，添加一个条件，仍不能证明四边形BECF为正方形的是( )A．BC＝AC B．CF⊥BF C．BD＝DF D．AC＝BF5. 如图，四边形ABCD中，AB＝BC，∠ABC＝∠CDA＝90°，BE⊥AD于点E，且四边形ABCD的面积为8，则BE的长为( )A．2 B．3 C．2 2 D．236. 正方形具有而菱形不一定具有的性质是( )A.对角线互相平分B.内角和为360°C.对角线相等D.对角线平分内角7. 能判定一个四边形是平行四边形的条件是( )A.一组对边平行，另一组对边相等B.一组对边平行，一组对角互补C.一组对角相等，一组邻角互补D.一组对角相等，另一组对角互补8. 矩形、菱形、正方形都具有的性质是( )A.对角线相等B.对角线垂直平分C.对角线平分一组对角D.对角线互相平分9. 正方形ABCD在平面直角坐标系中的位置如图所示，已知点A的坐标为(0，4)，点B坐标为(－3，0)，则点C的坐标为( )A．(1，3) B．(1，－3) C．(1，－4) D．(2，－4)10. 如图，正方形ABCD中，对角线AC，BD相交于点O，则图中的等腰三角形有( ) A．4个 B．6个 C．8个 D．10个11. 如图，在正方形ABCD的外侧，作等边△ADE，则∠BED的度数是____________．12. 如图，正方形ABCD的边长为9，将正方形折叠，使顶点D落在BC边上的点E处，折痕为GH.若BE∶EC＝2∶1，则线段CH的长是____．13. 如图，已知正方形ABCD的边长为1，连结AC，BD，CE平分∠ACD交BD于点E，则DE＝_________________.14. 如图，四边形ABCD是正方形，对角线AC与BD相交于O，MN∥AB，且分别与AO，BO交于M，N，求证：(1)BM＝CN；(2)BM⊥CN.15. 如图，正方形ABCD中，G为BC边上一点，BE⊥AG于E，DF⊥AG于F，连结DE.(1)求证：△ABE≌△DAF；(2)若AF ＝1，四边形ABED 的面积为6，求EF 的长．参考答案：1---10 ABBDC CCDBC11. 45°12. 4 13. 2－114. 解：(1)∵MN∥AB，∴∠OMN＝∠OAB，∠ONM ＝∠OBA，∵OA＝OB ，∴∠OAB＝∠OBA，∴∠OMN ＝∠ONM，∴OM＝ON ，∴AM＝OA －OM ＝OB －ON ＝BN ，在△ABM 和△BCN 中，⎩⎨⎧AB ＝BC∠MAB＝∠NBC AM ＝BN，∴△ABM≌△BCN(SAS)，∴BM＝CN(2)由△ABM≌△BCN 得，∠ABM＝∠BCN，又∵∠ABM＋∠CBM＝90°，∴∠BCN＋∠CBM＝90°，∴CN⊥BM15. 解：(1)∵四边形ABCD 是正方形，∴AB＝AD ，∵DF⊥AG，BE⊥A G ，∴∠BAE＋∠DAF＝90°，∠DAF＋∠ADF＝90°，∴∠BAE＝∠ADF，在△ABE 和△DAF 中，⎩⎨⎧∠BAE＝∠ADF，∠AEB＝∠DFA，AB ＝AD ，∴△ABE≌△DAF(AAS)(2)设EF ＝x ，则AE ＝DF ＝x ＋1，由题意2×12×(x＋1)×1＋12×x×(x＋1)＝6，解得x ＝2或－5(舍弃)，∴EF＝2。

挑战中考数学压轴题-几何综合题素质训练之正方形

挑战中考数学压轴题-几何综合题素质训练之正方形1．已知：如图，在正方形ABCD中，E、F分别在AD、DC上，且DE＝DF，BM⊥EF于M．求证：ME＝MF．2．如图，正方形ABCD，E是BC上的一点，延长AB至F使BFBE，延长AE交CF于G．求证：AGCF．3．如图，ABCD、BEFG都是正方形，A、B、Ｅ在一条直线上，连结A、G，且延长交CE的连线为H，求证：AHCE．（1）如图1，正方形ABCD中，作AE交BC于E，DFAE交AB于F，求证：AEDF；（2）如图2，正方形ABCD中，点E，F分别在AD，BC上，点G，H分别在AB，CD上，且EFGH，求EF:GH的值；（3）如图3，矩形ABCD中，ABa，BCb，点E，F分别在AD，BC上，且EFGH，求EF:GH的值．AFDBEC图1AEDHGBFCDH图2AEGBFC图35．已知：如图，正方形ABCD，P是BO上任意一点，DQ⊥AP，垂足是Q，交AC于R，求证：⑴、DP=CR．⑵、若P为OB延长线上一点，其它条件不变，那么上述的结论是否仍然成立，画图并证明.DARQOPBCRQADOBCP6．如图，已知ABCD是正方形，对角线AC与BD相交于O，MN//AB，且分别与AO、BO交于M、N．求证：BMCN．7．如图，已知正方形ABCD中，F为CD延长线上一点，CEAF于E，交AD于M．求：∠MFD的度数．8．已知：如图，正方形ABCD中，M为DC中点，DFAM交AC于E，交BC于F．求证：∠DMA=∠EMC．9．已知：如图，AM为△ABC的中线，四边形ABDE、ACFG均为正方形．求证：AM10．已知：如图，正方形ABCD中，CE垂直于CAD的平分线于E，AE交DC于F．求证：CE1EG．21AF．211．已知：如图，正方形ABCD中，M是CD中点，E是CD上一点，且BAE2DAM．求证：AE＝BC＋CE．12．已知：如图，正方形ABCD中，E、F分别为AB、BC的中点，CE、DF交于M．求证：AM=AD．13、如图正方形ABCD，以CD为边长向正方形内作等边△CDE,连BE交AC于F，连DF，求证：⑴△ADF≌△ABF⑵求∠AFD的大小⑶求证AF+DF=CFDFEACB14．（利用旋转处理正方形问题）△ABC是等腰直角三角形，∠C＝90°，M、N为斜边AB上两点，如果∠MCN＝45求证AM＋BN=MN222BNMCA15、已知M、N分别在正方形ABCD的边BC、CD上，且∠MAN=45°⑴如图1求证：MN=DN+BN⑵如图2，若点M、N分别在CB、DC的延长线上，∠MAN=45°，请探究：MN、BM、DN之间的关系DNCMABDCNBAM如果改∠MAN=45°顶点不在A点，而在正方形的中心O点处，其它的条件不变，请问MC、MB与MN之间的关系DCMONAB16、已知M、N分别在正方形ABCD的边BC、CD上，且MN=DN+BN⑴如图1求∠MAN的度数⑵如图2，若AM、AN分别和BD交于E、F点，请探究：DE、EF、FB之间的关系⑶若点M、N分别在CB、DC的延长线上，∠MAN=45°MN、DN、BN之间的关系；请探究：DE、EF、FB之间的关系画图证明DENCFADCMBNEBMAF17、如图正方形ABCD中，点O为对角线AC的中点，点P为正方形ABCD外的一点，且BP⊥CP⑴如图1，求证BP+CP=2OP⑵如图2，当点P在正方形的内部时，问BP、CP、OP三者又存在什么样的关系？请证明ADOEBPCADPOEB18、正方形ABCD中，点O是对角线AC的中点，P是对角线AC上一动点，过点P作PF⊥CD于点F。

中考数学-几何综合压轴问题(共40题)(学生版)

几何综合压轴问题(40题)1(2023·四川自贡·统考中考真题)如图1，一大一小两个等腰直角三角形叠放在一起，M，N分别是斜边DE，AB的中点，DE=2,AB=4．(1)将△CDE绕顶点C旋转一周，请直接写出点M，N距离的最大值和最小值；(2)将△CDE绕顶点C逆时针旋转120°(如图2)，求MN的长．2(2023·山东烟台·统考中考真题)如图，点C为线段AB上一点，分别以AC,BC为等腰三角形的底边，在AB的同侧作等腰△ACD和等腰△BCE，且∠A=∠CBE．在线段EC上取一点F，使EF=AD，连接BF,DE．(1)如图1，求证：DE=BF；(2)如图2，若AD=2，BF的延长线恰好经过DE的中点G，求BE的长．3(2023·浙江绍兴·统考中考真题)在平行四边形ABCD中(顶点A,B,C,D按逆时针方向排列)，AB= 12,AD=10,∠B为锐角，且sin B=45．(1)如图1，求AB边上的高CH的长．(2)P是边AB上的一动点，点C,D同时绕点P按逆时针方向旋转90°得点C ,D ．①如图2，当点C 落在射线CA上时，求BP的长．②当△AC D 是直角三角形时，求BP的长．4(2023·甘肃武威·统考中考真题)【模型建立】(1)如图1，△ABC和△BDE都是等边三角形，点C关于AD的对称点F在BD边上．①求证：AE=CD；②用等式写出线段AD，BD，DF的数量关系，并说明理由．【模型应用】(2)如图2，△ABC是直角三角形，AB=AC，CD⊥BD，垂足为D，点C关于AD的对称点F在BD边上．用等式写出线段AD，BD，DF的数量关系，并说明理由．【模型迁移】(3)在(2)的条件下，若AD=42，BD=3CD，求cos∠AFB的值．5(2023·江西·统考中考真题)课本再现思考我们知道，菱形的对角线互相垂直．反过来，对角线互相垂直的平行四边形是菱形吗？可以发现并证明菱形的一个判定定理；对角线互相垂直的平行四边形是菱形．(1)定理证明：为了证明该定理，小明同学画出了图形(如图1)，并写出了“已知”和“求证”，请你完成证明过程．己知：在▱ABCD中，对角线BD⊥AC，垂足为O．求证：▱ABCD是菱形．(2)知识应用：如图2，在▱ABCD中，对角线AC和BD相交于点O，AD=5，AC=8，BD=6．①求证：▱ABCD是菱形；②延长BC至点E，连接OE交CD于点F，若∠E=12∠ACD，求OFEF的值．6(2023·湖北随州·统考中考真题)1643年，法国数学家费马曾提出一个著名的几何问题：给定不在同一条直线上的三个点A，B，C，求平面上到这三个点的距离之和最小的点的位置，意大利数学家和物理学家托里拆利给出了分析和证明，该点也被称为“费马点”或“托里拆利点”，该问题也被称为“将军巡营”问题．(1)下面是该问题的一种常见的解决方法，请补充以下推理过程：(其中①处从“直角”和“等边”中选择填空，②处从“两点之间线段最短”和“三角形两边之和大于第三边”中选择填空，③处填写角度数，④处填写该三角形的某个顶点)当△ABC的三个内角均小于120°时，如图1，将△APC绕，点C顺时针旋转60°得到△A P C，连接PP ，由PC=P C，∠PCP =60°，可知△PCP 为三角形，故PP =PC，又P A =PA，故PA+PB+PC =PA +PB+PP ≥A B，由可知，当B，P，P ，A在同一条直线上时，PA+PB+PC取最小值，如图2，最小值为A B，此时的P点为该三角形的“费马点”，且有∠APC=∠BPC=∠APB=；已知当△ABC有一个内角大于或等于120°时，“费马点”为该三角形的某个顶点．如图3，若∠BAC≥120°，则该三角形的“费马点”为点．(2)如图4，在△ABC中，三个内角均小于120°，且AC=3，BC=4，∠ACB=30°，已知点P为△ABC的“费马点”，求PA+PB+PC的值；(3)如图5，设村庄A，B，C的连线构成一个三角形，且已知AC=4km，BC=23km，∠ACB=60°．现欲建一中转站P沿直线向A，B，C三个村庄铺设电缆，已知由中转站P到村庄A，B，C的铺设成本分别为a 元/km，a元/km，2a元/km，选取合适的P的位置，可以使总的铺设成本最低为元．(结果用含a的式子表示)7(2023·山东枣庄·统考中考真题)问题情境：如图1，在△ABC中，AB=AC=17，BC=30，AD是BC边上的中线．如图2，将△ABC的两个顶点B，C分别沿EF,GH折叠后均与点D重合，折痕分别交AB,AC,BC于点E，G，F，H．猜想证明：(1)如图2，试判断四边形AEDG的形状，并说明理由．问题解决；(2)如图3，将图2中左侧折叠的三角形展开后，重新沿MN折叠，使得顶点B与点H重合，折痕分别交AB, BC于点M，N，BM的对应线段交DG于点K，求四边形MKGA的面积．8(2023·湖南·统考中考真题)(1)[问题探究]如图1，在正方形ABCD中，对角线AC、BD相交于点O．在线段AO上任取一点P(端点除外)，连接PD、PB．①求证：PD=PB；②将线段DP绕点P逆时针旋转，使点D落在BA的延长线上的点Q处．当点P在线段AO上的位置发生变化时，∠DPQ的大小是否发生变化？请说明理由；③探究AQ与OP的数量关系，并说明理由．(2)[迁移探究]如图2，将正方形ABCD换成菱形ABCD，且∠ABC=60°，其他条件不变．试探究AQ与CP的数量关系，并说明理由．9(2023·湖南岳阳·统考中考真题)如图1，在△ABC中，AB=AC，点M,N分别为边AB,BC的中点，连接MN．初步尝试：(1)MN与AC的数量关系是，MN与AC的位置关系是．特例研讨：(2)如图2，若∠BAC=90°,BC=42，先将△BMN绕点B顺时针旋转α(α为锐角)，得到△BEF，当点A,E,F在同一直线上时，AE与BC相交于点D，连接CF．(1)求∠BCF的度数；(2)求CD的长．深入探究：(3)若∠BAC<90°，将△BMN绕点B顺时针旋转α，得到△BEF，连接AE，CF．当旋转角α满足0°<α<360°，点C,E,F在同一直线上时，利用所提供的备用图探究∠BAE与∠ABF的数量关系，并说明理由．10(2023·湖北黄冈·统考中考真题)【问题呈现】△CAB和△CDE都是直角三角形，∠ACB=∠DCE=90°,CB=mCA,CE=mCD，连接AD，BE，探究AD，BE的位置关系．(1)如图1，当m=1时，直接写出AD，BE的位置关系：；(2)如图2，当m≠1时，(1)中的结论是否成立？若成立，给出证明；若不成立，说明理由．【拓展应用】(3)当m=3,AB=47,DE=4时，将△CDE绕点C旋转，使A,D,E三点恰好在同一直线上，求BE的长．11(2023·河北·统考中考真题)如图1和图2，平面上，四边形ABCD中，AB=8,BC=211,CD=12, DA=6,∠A=90°，点M在AD边上，且DM=2．将线段MA绕点M顺时针旋转n°(0<n≤180)到MA ,∠A MA的平分线MP所在直线交折线AB-BC于点P，设点P在该折线上运动的路径长为x(x>0)，连接A P．(1)若点P在AB上，求证：A P=AP；(2)如图2．连接BD．①求∠CBD的度数，并直接写出当n=180时，x的值；②若点P到BD的距离为2，求tan∠A MP的值；(3)当0<x≤8时，请直接写出点A 到直线AB的距离．(用含x的式子表示)．12(2023·四川达州·统考中考真题)(1)如图①，在矩形ABCD的AB边上取一点E，将△ADE沿DE翻折，使点A落在BC上A 处，若AB=6,BC=10，求AEEB的值；(2)如图②，在矩形ABCD 的BC 边上取一点E ，将四边形ABED 沿DE 翻折，使点B 落在DC 的延长线上B 处，若BC ⋅CE =24,AB =6，求BE 的值；(3)如图③，在△ABC 中，∠BAC =45°,AD ⊥BC ，垂足为点D ,AD =10,AE =6，过点E 作EF ⊥AD 交AC 于点F ，连接DF ，且满足∠DFE =2∠DAC ，直接写出BD +53EF 的值．13(2023·湖南郴州·统考中考真题)已知△ABC 是等边三角形，点D 是射线AB 上的一个动点，延长BC 至点E ，使CE =AD ，连接DE 交射线AC 于点F ．(1)如图1，当点D 在线段AB 上时，猜测线段CF 与BD 的数量关系并说明理由；(2)如图2，当点D 在线段AB 的延长线上时，①线段CF 与BD 的数量关系是否仍然成立？请说明理由；②如图3，连接AE ．设AB =4，若∠AEB =∠DEB ，求四边形BDFC 的面积．14(2023·湖北宜昌·统考中考真题)如图，在正方形ABCD 中，E ，F 分别是边AD ，AB 上的点，连接CE ，EF ，CF ．(1)若正方形ABCD 的边长为2，E 是AD 的中点．①如图1，当∠FEC =90°时，求证：△AEF ∽△DCE ；②如图2，当tan ∠FCE =23时，求AF 的长；(2)如图3，延长CF ，DA 交于点G ，当GE =DE ,sin ∠FCE =13时，求证：AE =AF ．15(2023·湖北武汉·统考中考真题)问题提出：如图(1)，E 是菱形ABCD 边BC 上一点，△AEF 是等腰三角形，AE =EF ，∠AEF =∠ABC =αa ≥90° ,AF 交CD 于点G ，探究∠GCF 与α的数量关系．问题探究：(1)先将问题特殊化，如图(2)，当α=90°时，直接写出∠GCF 的大小；(2)再探究一般情形，如图(1)，求∠GCF 与α的数量关系．问题拓展：(3)将图(1)特殊化，如图(3)，当α=120°时，若DG CG =12，求BECE的值．16(2023·山西·统考中考真题)问题情境：“综合与实践”课上，老师提出如下问题：将图1中的矩形纸片沿对角线剪开，得到两个全等的三角形纸片，表示为△ABC 和△DFE ，其中∠ACB =∠DEF =90°,∠A =∠D ．将△ABC 和△DFE 按图2所示方式摆放，其中点B 与点F 重合(标记为点B )．当∠ABE =∠A 时，延长DE 交AC 于点G ．试判断四边形BCGE 的形状，并说明理由．(1)数学思考：谈你解答老师提出的问题；(2)深入探究：老师将图2中的△DBE 绕点B 逆时针方向旋转，使点E 落在△ABC 内部，并让同学们提出新的问题．①“善思小组”提出问题：如图3，当∠ABE =∠BAC 时，过点A 作AM ⊥BE 交BE 的延长线于点M ,BM 与AC 交于点N ．试猜想线段AM 和BE 的数量关系，并加以证明．请你解答此问题；②“智慧小组”提出问题：如图4，当∠CBE=∠BAC时，过点A作AH⊥DE于点H，若BC=9,AC=12，求AH的长．请你思考此问题，直接写出结果．17(2023·湖北十堰·统考中考真题)过正方形ABCD的顶点D作直线DP，点C关于直线DP的对称点为点E，连接AE，直线AE交直线DP于点F．(1)如图1，若∠CDP=25°，则∠DAF=°；(2)如图1，请探究线段CD，EF，AF之间的数量关系，并证明你的结论；(3)在DP绕点D转动的过程中，设AF=a，EF=b请直接用含a,b的式子表示DF的长．18(2023·辽宁大连·统考中考真题)综合与实践问题情境：数学活动课上，王老师给同学们每人发了一张等腰三角形纸片探究折叠的性质．已知AB=AC,∠A>90°，点E为AC上一动点，将△ABE以BE为对称轴翻折．同学们经过思考后进行如下探究：独立思考：小明：“当点D落在BC上时，∠EDC=2∠ACB．”小红：“若点E为AC中点，给出AC与DC的长，就可求出BE的长．”实践探究：奋进小组的同学们经过探究后提出问题1，请你回答：问题1：在等腰△ABC中，AB=AC,∠A>90°,△BDE由△ABE翻折得到．(1)如图1，当点D落在BC上时，求证：∠EDC=2∠ACB；(2)如图2，若点E为AC中点，AC=4,CD=3，求BE的长．问题解决：小明经过探究发现：若将问题1中的等腰三角形换成∠A<90°的等腰三角形，可以将问题进一步拓展．问题2：如图3，在等腰△ABC中，∠A<90°,AB=AC=BD=4,2∠D=∠ABD．若CD=1，则求BC的长．19(2023·山东·统考中考真题)(1)如图1，在矩形ABCD中，点E，F分别在边DC，BC上，AE⊥DF，垂足为点G．求证：△ADE∽△DCF．【问题解决】(2)如图2，在正方形ABCD中，点E，F分别在边DC，BC上，AE=DF，延长BC到点H，使CH=DE，连接DH．求证：∠ADF=∠H．【类比迁移】(3)如图3，在菱形ABCD中，点E，F分别在边DC，BC上，AE=DF=11，DE=8，∠AED=60°，求CF 的长．20(2023·福建·统考中考真题)如图1，在△ABC中，∠BAC=90°,AB=AC,D是AB边上不与A,B重合的一个定点．AO⊥BC于点O，交CD于点E．DF是由线段DC绕点D顺时针旋转90°得到的，FD,CA的延长线相交于点M．(1)求证：△ADE∽△FMC；(2)求∠ABF的度数；(3)若N是AF的中点，如图2．求证：ND=NO．21(2023·四川·统考中考真题)如图1，已知线段AB，AC，线段AC绕点A在直线AB上方旋转，连接BC，以BC为边在BC上方作Rt△BDC，且∠DBC=30°．(1)若∠BDC=90°，以AB为边在AB上方作Rt△BAE，且∠AEB=90°，∠EBA=30°，连接DE，用等式表示线段AC与DE的数量关系是；(2)如图2，在(1)的条件下，若DE⊥AB，AB=4，AC=2，求BC的长；(3)如图3，若∠BCD=90°，AB=4，AC=2，当AD的值最大时，求此时tan∠CBA的值．22(2023·广西·统考中考真题)【探究与证明】折纸，操作简单，富有数学趣味，我们可以通过折纸开展数学探究，探索数学奥秘．【动手操作】如图1，将矩形纸片ABCD对折，使AD与BC重合，展平纸片，得到折痕EF；折叠纸片，使点B 落在EF上，并使折痕经过点A，得到折痕AM，点B，E的对应点分别为B ，E ，展平纸片，连接AB ，BB ，BE ．请完成：(1)观察图1中∠1，∠2和∠3，试猜想这三个角的大小关系；(2)证明(1)中的猜想；【类比操作】如图2，N为矩形纸片ABCD的边AD上的一点，连接BN，在AB上取一点P，折叠纸片，使B ，P 两点重合，展平纸片，得到折痕EF ；折叠纸片，使点B ，P 分别落在EF ，BN 上，得到折痕l ，点B ，P 的对应点分别为B ，P ，展平纸片，连接，P B ．请完成：(3)证明BB 是∠NBC 的一条三等分线．23(2023·重庆·统考中考真题)在Rt △ABC 中，∠ACB =90°，∠B =60°，点D 为线段AB 上一动点，连接CD ．(1)如图1，若AC =9，BD =3，求线段AD 的长．(2)如图2，以CD 为边在CD 上方作等边△CDE ，点F 是DE 的中点，连接BF 并延长，交CD 的延长线于点G ．若∠G =∠BCE ，求证：GF =BF +BE ．(3)在CD 取得最小值的条件下，以CD 为边在CD 右侧作等边△CDE ．点M 为CD 所在直线上一点，将△BEM 沿BM 所在直线翻折至△ABC 所在平面内得到△BNM ．连接AN ，点P 为AN 的中点，连接CP ，当CP 取最大值时，连接BP ，将△BCP 沿BC 所在直线翻折至△ABC 所在平面内得到△BCQ ，请直接写出此时NQ CP的值．24(2023·湖南·统考中考真题)如图，在等边三角形ABC 中，D 为AB 上的一点，过点D 作BC 的平行线DE 交AC 于点E ，点P 是线段DE 上的动点(点P 不与D 、E 重合)．将△ABP 绕点A 逆时针方向旋转60°，得到△ACQ ，连接EQ 、PQ ,PQ 交AC 于F ．(1)证明：在点P 的运动过程中，总有∠PEQ =120°．(2)当AP DP为何值时，△AQF 是直角三角形？25(2023·黑龙江·统考中考真题)如图①，△ABC和△ADE是等边三角形，连接DC，点F，G，H分别是DE,DC和BC的中点，连接FG,FH．易证：FH=3FG．若△ABC和△ADE都是等腰直角三角形，且∠BAC=∠DAE=90°，如图②：若△ABC和△ADE都是等腰三角形，且∠BAC=∠DAE=120°，如图③：其他条件不变，判断FH和FG之间的数量关系，写出你的猜想，并利用图②或图③进行证明．26(2023·黑龙江齐齐哈尔·统考中考真题)综合与实践数学模型可以用来解决一类问题，是数学应用的基本途径．通过探究图形的变化规律，再结合其他数学知识的内在联系，最终可以获得宝贵的数学经验，并将其运用到更广阔的数学天地．(1)发现问题：如图1，在△ABC和△AEF中，AB=AC，AE=AF，∠BAC=∠EAF=30°，连接BE，CF，延长BE交CF于点D．则BE与CF的数量关系：，∠BDC=°；(2)类比探究：如图2，在△ABC和△AEF中，AB=AC，AE=AF，∠BAC=∠EAF=120°，连接BE，CF，延长BE，FC交于点D．请猜想BE与CF的数量关系及∠BDC的度数，并说明理由；(3)拓展延伸：如图3，△ABC和△AEF均为等腰直角三角形，∠BAC=∠EAF=90°，连接BE，CF，且点B，E，F在一条直线上，过点A作AM⊥BF，垂足为点M．则BF，CF，AM之间的数量关系：；(4)实践应用：正方形ABCD中，AB=2，若平面内存在点P满足∠BPD=90°，PD=1，则S△ABP=．27(2023·广东深圳·统考中考真题)(1)如图，在矩形ABCD中，E为AD边上一点，连接BE，①若BE=BC，过C作CF⊥BE交BE于点F，求证：△ABE≌△FCB；=20时，则BE⋅CF=．②若S矩形ABCD(2)如图，在菱形ABCD中，cos A=13，过C作CE⊥AB交AB的延长线于点E，过E作EF⊥AD交AD =24时，求EF⋅BC的值．于点F，若S菱形ABCD(3)如图，在平行四边形ABCD中，∠A=60°，AB=6，AD=5，点E在CD上，且CE=2，点F为BC上一点，连接EF，过E作EG⊥EF交平行四边形ABCD的边于点G，若EF⋅EG=73时，请直接写出AG的长．28(2023·内蒙古·统考中考真题)如图，在菱形ABCD中，对角线AC,BD相交于点O，点P,Q分别是边BC，线段OD上的点，连接AP,QP,AP与OB相交于点E．(1)如图1，连接QA．当QA=QP时，试判断点Q是否在线段PC的垂直平分线上，并说明理由；(2)如图2，若∠APB=90°，且∠BAP=∠ADB，①求证：AE=2EP；②当OQ=OE时，设EP=a，求PQ的长(用含a的代数式表示)．29(2023·内蒙古赤峰·统考中考真题)数学兴趣小组探究了以下几何图形．如图①，把一个含有45°角的三角尺放在正方形ABCD中，使45°角的顶点始终与正方形的顶点C重合，绕点C旋转三角尺时，45°角的两边CM ，CN 始终与正方形的边AD ，AB 所在直线分别相交于点M ，N ，连接MN ，可得△CMN ．【探究一】如图②，把△CDM 绕点C 逆时针旋转90°得到△CBH ，同时得到点H 在直线AB 上．求证：∠CNM =∠CNH ；【探究二】在图②中，连接BD ，分别交CM ，CN 于点E ，F ．求证：△CEF ∽△CNM ；【探究三】把三角尺旋转到如图③所示位置，直线BD 与三角尺45°角两边CM ，CN 分别交于点E ，F ．连接AC 交BD 于点O ，求EFNM的值．30(2023·山东东营·统考中考真题)(1)用数学的眼光观察．如图，在四边形ABCD 中，AD =BC ，P 是对角线BD 的中点，M 是AB 的中点，N 是DC 的中点，求证：∠PMN =∠PNM ．(2)用数学的思维思考．如图，延长图中的线段AD 交MN 的延长线于点E ，延长线段BC 交MN 的延长线于点F ，求证：∠AEM =∠F ．(3)用数学的语言表达．如图，在△ABC 中，AC <AB ，点D 在AC 上，AD =BC ，M 是AB 的中点，N 是DC 的中点，连接MN 并延长，与BC 的延长线交于点G ，连接GD ，若∠ANM =60°，试判断△CGD 的形状，并进行证明．31(2023·甘肃兰州·统考中考真题)综合与实践【思考尝试】(1)数学活动课上，老师出示了一个问题：如图1，在矩形ABCD中，E是边AB上一点，DF⊥CE于点F，GD⊥DF，AG⊥DG，AG=CF．试猜想四边形ABCD的形状，并说明理由；【实践探究】(2)小睿受此问题启发，逆向思考并提出新的问题：如图2，在正方形ABCD中，E是边AB上一点，DF⊥CE于点F，AH⊥CE于点H，GD⊥DF交AH于点G，可以用等式表示线段FH，AH，CF的数量关系，请你思考并解答这个问题；【拓展迁移】(3)小博深入研究小睿提出的这个问题，发现并提出新的探究点：如图3，在正方形ABCD中，E是边AB上一点，AH⊥CE于点H，点M在CH上，且AH=HM，连接AM，BH，可以用等式表示线段CM，BH的数量关系，请你思考并解答这个问题．32(2023·贵州·统考中考真题)如图①，小红在学习了三角形相关知识后，对等腰直角三角形进行了探究，在等腰直角三角形ABC中，CA=CB,∠C=90°，过点B作射线BD⊥AB，垂足为B，点P在CB上．(1)【动手操作】如图②，若点P在线段CB上，画出射线PA，并将射线PA绕点P逆时针旋转90°与BD交于点E，根据题意在图中画出图形，图中∠PBE的度数为度；(2)【问题探究】根据(1)所画图形，探究线段PA与PE的数量关系，并说明理由；(3)【拓展延伸】如图③，若点P在射线CB上移动，将射线PA绕点P逆时针旋转90°与BD交于点E，探究线段BA,BP, BE之间的数量关系，并说明理由．33(2023·辽宁·统考中考真题)在RtΔABC中，∠ACB=90°，CA=CB，点O为AB的中点，点D在直线AB上(不与点A,B重合)，连接CD，线段CD绕点C逆时针旋转90°，得到线段CE，过点B作直线l⊥BC，过点E作EF⊥l，垂足为点F，直线EF交直线OC于点G．(1)如图，当点D与点O重合时，请直接写出线段AD与线段EF的数量关系；(2)如图，当点D在线段AB上时，求证：CG+BD=2BC；(3)连接DE，△CDE的面积记为S1，△ABC的面积记为S2，当EF:BC=1:3时，请直接写出S1S2的值．34(2023·四川成都·统考中考真题)探究式学习是新课程倡导的重要学习方式，某兴趣小组拟做以下探究．在Rt△ABC中，∠C=90°,AC=BC，D是AB边上一点，且ADBD=1n(n为正整数)，E是AC边上的动点，过点D作DE的垂线交直线BC于点F．【初步感知】(1)如图1，当n=1时，兴趣小组探究得出结论：AE+BF=22AB，请写出证明过程．【深入探究】(2)①如图2，当n=2，且点F在线段BC上时，试探究线段AE，BF，AB之间的数量关系，请写出结论并证明；②请通过类比、归纳、猜想，探究出线段AE，BF，AB之间数量关系的一般结论(直接写出结论，不必证明)【拓展运用】(3)如图3，连接EF，设EF的中点为M．若AB=22，求点E从点A运动到点C的过程中，点M运动的路径长(用含n的代数式表示)．35(2023·江苏徐州·统考中考真题)【阅读理解】如图1，在矩形ABCD中，若AB=a,BC=b，由勾股定理，得AC2=a2+b2，同理BD2=a2+b2，故AC2+BD2=2a2+b2．【探究发现】如图2，四边形ABCD为平行四边形，若AB=a,BC=b，则上述结论是否依然成立？请加以判断，并说明理由．【拓展提升】如图3，已知BO为△ABC的一条中线，AB=a,BC=b,AC=c．求证：BO2=a2+b22-c24．【尝试应用】如图4，在矩形ABCD中，若AB=8,BC=12，点P在边AD上，则PB2+PC2的最小值为．36(2023·四川南充·统考中考真题)如图，正方形ABCD中，点M在边BC上，点E是AM的中点，连接ED，EC．(1)求证：ED=EC；(2)将BE绕点E逆时针旋转，使点B的对应点B 落在AC上，连接MB′．当点M在边BC上运动时(点M 不与B，C重合)，判断△CMB′的形状，并说明理由．(3)在(2)的条件下，已知AB=1，当∠DEB′=45°时，求BM的长．37(2023·安徽·统考中考真题)在Rt△ABC中，M是斜边AB的中点，将线段MA绕点M旋转至MD 位置，点D在直线AB外，连接AD,BD．(1)如图1，求∠ADB的大小；(2)已知点D和边AC上的点E满足ME⊥AD,DE∥AB．(ⅰ)如图2，连接CD，求证：BD=CD；(ⅱ)如图3，连接BE，若AC=8,BC=6，求tan∠ABE的值．38(2023·浙江宁波·统考中考真题)定义：有两个相邻的内角是直角，并且有两条邻边相等的四边形称为邻等四边形，相等两邻边的夹角称为邻等角．(1)如图1，在四边形ABCD中，AD∥BC,∠A=90°，对角线BD平分∠ADC．求证：四边形ABCD为邻等四边形．(2)如图2，在6×5的方格纸中，A，B，C三点均在格点上，若四边形ABCD是邻等四边形，请画出所有符合条件的格点D．(3)如图3，四边形ABCD是邻等四边形，∠DAB=∠ABC=90°，∠BCD为邻等角，连接AC，过B作BE∥AC交DA的延长线于点E．若AC=8,DE=10，求四边形EBCD的周长．39(2023·江苏扬州·统考中考真题)【问题情境】在综合实践活动课上，李老师让同桌两位同学用相同的两块含30°的三角板开展数学探究活动，两块三角板分别记作△ADB和△A D C,∠ADB=∠A D C=90°,∠B=∠C=30°，设AB=2．【操作探究】如图1，先将△ADB和△A D C的边AD、A D 重合，再将△A D C绕着点A按顺时针方向旋转，旋转角为α0°≤α≤360°，旋转过程中△ADB保持不动，连接BC．(1)当α=60°时，BC=；当BC=22时，α=°；(2)当α=90°时，画出图形，并求两块三角板重叠部分图形的面积；(3)如图2，取BC的中点F，将△A D C绕着点A旋转一周，点F的运动路径长为．40(2023·四川乐山·统考中考真题)在学习完《图形的旋转》后，刘老师带领学生开展了一次数学探究活动【问题情境】刘老师先引导学生回顾了华东师大版教材七年级下册第121页“探索”部分内容：如图，将一个三角形纸板△ABC绕点A逆时针旋转θ到达△AB C 的位置，那么可以得到：AB=AB ，AC =AC ，BC=B C ；∠BAC=∠B AC ，∠ABC=∠AB C ，∠ACB=∠AC B ()刘老师进一步谈到：图形的旋转蕴含于自然界的运动变化规律中，即“变”中蕴含着“不变”，这是我们解决图形旋转的关键；故数学就是一门哲学．【问题解决】(1)上述问题情境中“( )”处应填理由：；(2)如图，小王将一个半径为4cm，圆心角为60°的扇形纸板ABC绕点O逆时针旋转90°到达扇形纸板A BC 的位置．①请在图中作出点O；②如果BB =6cm，则在旋转过程中，点B经过的路径长为；【问题拓展】小李突发奇想，将与(2)中完全相同的两个扇形纸板重叠，一个固定在墙上，使得一边位于水平位置，另一个在弧的中点处固定，然后放开纸板，使其摆动到竖直位置时静止，此时，两个纸板重叠部分的面积是多少呢？如图所示，请你帮助小李解决这个问题．。

初中数学几何综合-含答案

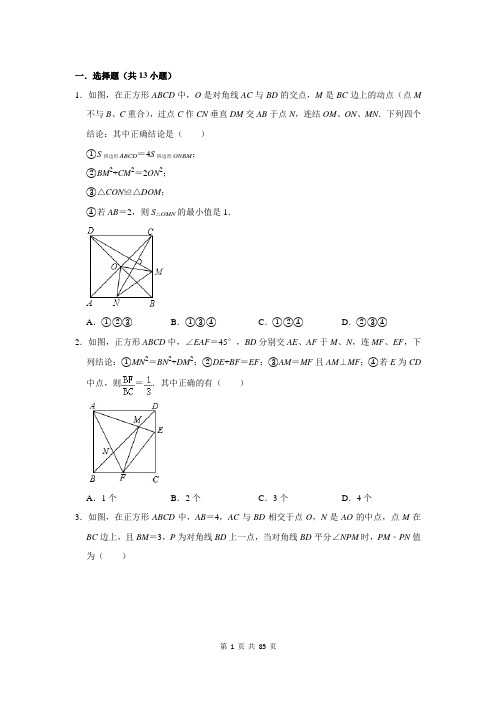
一．选择题（共13小题）1．如图，在正方形ABCD中，O是对角线AC与BD的交点，M是BC边上的动点（点M 不与B、C重合），过点C作CN垂直DM交AB于点N，连结OM、ON、MN．下列四个结论：其中正确结论是（）①S四边形ABCD＝4S四边形ONBM；②BM2+CM2＝2ON2；③△CON≌△DOM；④若AB＝2，则S△OMN的最小值是1．A．①②③B．①③④C．①②④D．②③④2．如图，正方形ABCD中，∠EAF＝45°，BD分别交AE、AF于M、N，连MF、EF，下列结论：①MN2＝BN2+DM2；②DE+BF＝EF；③AM＝MF且AM⊥MF；④若E为CD 中点，则＝．其中正确的有（）A．1个B．2个C．3个D．4个3．如图，在正方形ABCD中，AB＝4，AC与BD相交于点O，N是AO的中点，点M在BC边上，且BM＝3，P为对角线BD上一点，当对角线BD平分∠NPM时，PM﹣PN值为（）A．1B．C．2D．4．如图，在正方形ABCD内一点E连接BE、CE，过C作CF⊥CE与BE延长线交于点F，连接DF、DE．CE＝CF＝1，DE＝，下列结论中：①△CBE≌△CDF；②BF⊥DF；③点D到CF的距离为2；④S四边形DECF＝+1．其中正确结论的个数是（）A．1B．2C．3D．45．如图，已知E，F分别为正方形ABCD的边AB，BC的中点，AF与DE交于点M．则下列结论：①∠AME＝90°，②∠BAF＝∠EDB，③AM＝MF，④ME+MF＝MB．其中正确结论的有（）A．4个B．3个C．2个D．1个6．如图，正方形ABCD和正方形CEFG中，点D在CG上，BC＝1，CE＝3，H是AF的中点，EH与CF交于点O．则HE的长为（）A．2B．C．2D．或27．如图，在正方形ABCD中，E为BC上一点，过点E作EF∥CD，交AD于F，交对角线BD于G，取DG的中点H，连结AH，EH，FH．下列结论：①FH∥AE；②AH＝EH且AH⊥EH；③∠BAH＝∠HEC；④△EHF≌△AHD；⑤若，则．其中哪些结论是正确（）A．①②④⑤B．②③④C．①②③D．②③④⑤8．如图，在正方形ABCD中，AC、BD相交于点O，E、F分别为BC、CD上的两点，BE ＝CF，AE、BF分别交BD、AC于M、N两点，连OE、OF．下列结论：①AE＝BF；②AE⊥BF；③CE+CF＝BD；④S四边形OECF＝S正方形ABCD，其中正确的是（）A．①②B．①④C．①②④D．①②③④9．如图，在正方形ABCD中，M是对角线BD上的一点，点E在AD的延长线上，连接AM、EM、CM，延长EM交AB于点F，若AM＝EM，∠E＝30°，则下列结论：①FM＝ME；②BF＝DE；③CM⊥EF；④BF+MD＝BC，其中正确的结论序号是（）A．①②③B．①②④C．②③④D．①②③④10．如图，在正方形ABCD中，对角线AC，BD交于点O，AG平分∠BAC交BD于G，DE ⊥AG于点H．下列结论：①AD＝2AE：②FD＝AG；③CF＝CD：④四边形FGEA是菱形；⑤OF＝BE，正确的有（）A．2个B．3个C．4个D．5个11．如图，以正方形ABCD的顶点A为圆心，以AD的长为半径画弧，交对角线AC于点E，再分别以D，E为圆心，以大于DE的长为半径画弧，两弧交于图中的点F处，连接AF并延长，与BC的延长线交于点P，则∠P＝（）A．90°B．45°C．30°D．22.5°12．如图，正方形ABCD中，点E在边CD上，连接AE，过点A作AF⊥AE交CB的延长线于点F，连接EF，AG平分∠F AE，AG分别交BC，EF于点G，H，连接EG，DH．则下列结论中：①AF＝AE；②∠EGC＝2∠BAG；③DE+BG＝EG；④AD+DE＝DH；⑤若DE＝CE，则CE：CG：EG＝3：4：5，其中正确的结论有（）A．2个B．3个C．4个D．5个13．如图，矩形ABCD中，O为AC的中点，过点O的直线分别与AB、CD交于点E、F，连接BF交AC于点M，连接DE、BO．若∠COB＝60°，FO＝FC＝2，则下列结论：①FB⊥OC；②△EOB≌△CMB；③四边形EBFD是菱形；④MB＝2．其中正确结论的个数是（）A．1个B．2个C．3个D．4个二．填空题（共3小题）14．如图，点E为正方形ABCD外一点，且ED＝CD，连接AE，交BD于点F．若∠CDE ＝40°，则∠DFC的度数为．15．如图，正方形ABCD中，在AD的延长线上取点E，F，使DE＝AD，DF＝BD，连接BF分别交CD，CE于H，G，下列结论：①EC＝2DG；②∠GDH＝∠GHD；③S△CDG＝S四边形DHGE；④图中只有8个等腰三角形．其中正确的有（填番号）．16．如图，在正方形ABCD中，P为AB的中点，BE⊥PD的延长线于点E，连接AE、BE、F A⊥AE交DP于点F，连接BF，FC．若AE＝2，则FC＝．三．解答题（共24小题）17．如图，在直线l上将正方形ABCD和正方形ECGF的边CD和边CE靠在一起，连接DG，过点A作AH∥DG，交BG于点H．连接HF，AF，其中FH交DG于点M．（1）求证：△AHF为等腰直角三角形．（2）若AB＝3，EC＝4，求DM的长．18．如图，已知正方形ABCD的面积是8，连接AC、BD交于点O，CM平分∠ACD交BD 于点M，MN⊥CM，交AB于点N，（1）求∠BMN的度数；（2）求BN的长．19．如图示，正方形ABCD的对角线交于点O，点E、F分别在AB，BC的延长线上，且∠EOF＝90°，OE与BC交于点M，连接EF，G是EF的中点，连接OG．（1）求证：OE＝OF（2）若∠BOG＝65°，求∠BOE的度数；（3）是否存在点M是BC中点，且使（1）的结论成立，若存在，请给予证明；若不存在，请说明理由．20．如图，正方形ABCD中，AB＝，在边CD的右侧作等腰三角形DCE，使DC＝DE，记∠CDE为α（0°＜α＜90°），连接AE，过点D作DG⊥AE，垂足为G，交EC的延长线于点F，连接AF．（1）求∠DEA的大小（用α的代数式表示）；（2）求证：△AEF为等腰直角三角形；（3）当CF＝时，求点E到CD的距离．21．如图1，在正方形ABCD中，点E在边CD上（不与点C，D重合），AE交对角线BD 于点G，GF⊥AE交BC于点F．（1）求证：AG＝FG．（2）若AB＝10，BF＝4，求BG的长．（3）如图2，连接AF，EF，若AF＝AE，求正方形ABCD与△CEF的面积之比．22．在正方形ABCD中，点E是DC上一点，连结AC，AE．（1）如图1，若AC＝8，AE＝10，求△ACE的面积．（2）如图2，EF⊥AC于点F，连结BF．求证：AE＝BF．23．如图1，正方形ABCD中，点E是边BC延长线上一点，连接DE，过点B作BF⊥DE，垂足为点F，BF与CD相交于点G．（1）求证：△BCG≌△DCE；（2）如图2，连接BD，若，求BG的长．24．如图，在正方形ABCD中，对角线AC、BD相交于点O，E为OC上动点（不与O、C 重合），作AF⊥BE，垂足为G，分别交BC、OB于F、H，连接OG、CG．（1）求证：△AOH≌△BOE；（2）求∠AGO的度数；（3）若∠OGC＝90°，BG＝，求△OGC的面积．25．如图，O为正方形ABCD对角线的交点，E为AB边上一点，F为BC边上一点，△EBF 的周长等于BC的长．（1）若AB＝24，BE＝6，求EF的长；（2）求∠EOF的度数；（3）若OE＝OF，求的值．26．如图，正方形ABCD中，E为BC上一点，过B作BG⊥AE于G，延长BG至点F使∠CFB＝45°（1）求证：∠BAG＝∠CBF；（2）求证：AG＝FG；（3）若GF＝2BG，CF＝，求AB的长．27．如图1，在正方形ABCD中，点P是对角线BD上的一点，点E在AD的延长线上，且P A＝PE，PE交CD于点F，（1）证明：PC＝PE；（2）求∠CPE的度数；（3）如图2，把正方形ABCD改为菱形ABCD，其他条件不变，当∠ABC＝120°，连接CE，试探究线段AP与线段CE的数量关系，并说明理由．28．如图，△ABC中，点O为AC边上的一个动点，过点O作直线MN∥BC，设MN交∠BCA的外角平分线CF于点F，交∠ACB内角平分线CE于E．（1）试说明EO＝FO；（2）当点O运动到何处时，四边形AECF是矩形并证明你的结论；（3）若AC边上存在点O，使四边形AECF是正方形，猜想△ABC的形状并证明你的结论．29．如图，已知平行四边形ABCD中，对角线AC、BD交于点O，E是DB延长线上一点，且△ACE是等边三角形．（1）求证：四边形ABCD是菱形；（2）若∠AEB＝2∠EAB，求证：四边形ABCD是正方形．30．如图1，在正方形ABCD中，G为线段BD上一点，连接AG，过G作AG⊥GE交BC 于E，连接AE．（1）求证：BG＝DG+BE；（2）如图2，AB＝4，E为BC中点，P，Q分别为线段AB，AE上的动点，满足QE＝AP，则在P，Q运动过程中，当以PQ为对角线的正方形PRQS的一边恰好落在△ABE的某一边上时，直接写出正方形PRQS的面积．31．如图，在平行四边形ABCD中，AC⊥AD，延长DA于点E，使得DA＝AE，连接BE．（1）求证：四边形AEBC是矩形；（2）过点E作AB的垂线分别交AB，AC于点F，G，连接CE交AB于点O，连接OG，若AB＝6，∠CAB＝30°，求△OGC的面积．32．如图，在四边形ABCD中，AD∥BC，AB＝BC，对角线AC、BD交于点O，BD平分∠ABC，过点D作DE⊥BC，交BC的延长线于点E，连接OE．（1）求证：四边形ABCD是菱形；（2）若DC＝2，AC＝4，求OE的长．33．如图，在菱形ABCD中，对角线AC、BD交于点O，过点A作AE⊥BC于点E，延长BC至F，使CF＝BE，连接DF．（1）求证：四边形AEFD是矩形；（2）若BF＝8，DF＝4，求CD的长．34．已知：如图，点E为▱ABCD对角线AC上的一点，点F在线段BE的延长线上，且EF ＝BE，线段EF与边CD相交于点G．（1）求证：DF∥AC；（2）如果AB＝BE，DG＝CG，联结DE、CF，求证：四边形DECF是矩形．35．如图，▱ABCD的对角线AC，BD交于点O，过点D作DE⊥BC于E，延长CB到点F，使BF＝CE，连接AF，OF．（1）求证：四边形AFED是矩形．（2）若AD＝7，BE＝2，∠ABF＝45°，试求OF的长．36．如图，平行四边形ABCD中，AC⊥BC，过点D作DE∥AC交BC的延长线于点E，点M为AB的中点，连接CM．（1）求证：四边形ADEC是矩形；（2）若CM＝5，且AC＝8，求四边形ADEC的周长．37．如图，已知△OAB中，OA＝OB，分别延长AO、BO到点C、D．使得OC＝AO，OD ＝BO，连接AD、DC、CB．（1）求证：四边形ABCD是矩形；（2）以OA、OB为一组邻边作▱AOBE，连接CE，若CE⊥BD，求∠AOB的度数．38．如图，在菱形ABCD中，对角线AC，BD交于点O，过点A作AE⊥BC于点E，延长BC到点F，使CF＝BE，连接DF．（1）求证：四边形AEFD是矩形；（2）连接OE，若AD＝10，EC＝4，求OE的长度．39．如图，在平行四边形BPCD中，点O为BD中点，连接CO并延长交PB延长线于点A，连接AD、BC，若AC＝CP，（1）求证：四边形ABCD为矩形；（2）在BA的延长线上取一点E，连接OE交AD于点F，若AB＝9，BC＝12，AE＝3，则AF的长为．40．如图，菱形ABCD中，AC与BD交于点O，DE∥AC，DE＝AC．（1）求证：四边形OCED是矩形；（2）连结AE，交OD于点F，连结CF，若CF＝CE＝1，求AC长．2021年01月06日杨莲莲的初中数学组卷参考答案与试题解析一．选择题（共13小题）1．如图，在正方形ABCD中，O是对角线AC与BD的交点，M是BC边上的动点（点M 不与B、C重合），过点C作CN垂直DM交AB于点N，连结OM、ON、MN．下列四个结论：其中正确结论是（）①S四边形ABCD＝4S四边形ONBM；②BM2+CM2＝2ON2；③△CON≌△DOM；④若AB＝2，则S△OMN的最小值是1．A．①②③B．①③④C．①②④D．②③④【分析】根据正方形的性质，依次判定△CNB≌△DMC，△AON≌△BOM，根据全等三角形的性质以及勾股定理进行计算即可得出结论．【解答】解：∵四边形ABCD是正方形，∴AC⊥BD，AO＝AC，BO＝BD，AC＝BD，∴AO＝BO，∠OAN＝∠OBM＝45°，∠AOB＝90°，∵CN⊥DM，∴∠MCN+∠CMD＝∠CMD+∠CDM＝90°，∴∠CDM＝∠BCN，∵CD＝BC，∠DCM＝∠CBN，∴△CDM≌△BCN（AAS），∴CM＝BN，∴AN＝BM，∴△AON≌△BOM（SAS），∴S△AON＝S△BOM，∴S四边形ONBM＝S△AOB＝S正方形ABCD，∴S四边形ABCD＝4S四边形ONBM；故①正确；∵△AON≌△BOM，∴ON＝OM，∠AON＝∠BOM，∴∠NOM＝∠AOB＝90°，∴△NOM是等腰直角三角形，∴MN2＝2ON2，∵BN2+BM2＝MN2，∴CM2+BM2＝2ON2，故②正确；∵∠MON＝∠COD＝90°，∴∠NOC＝∠MOD，∵OD＝OC，ON＝OM，∴△CON≌△DOM（SAS），故③正确；∵AB＝2，∴S正方形ABCD＝4，∵△AON≌△BOM，∴四边形BMON的面积＝△AOB的面积＝1，即四边形BMON的面积是定值1，∴当△MNB的面积最大时，△MNO的面积最小，设BN＝x＝CM，则BM＝2﹣x，∴△MNB的面积＝x（2﹣x）＝﹣x2+x＝﹣（x﹣1）2+，∴当x＝1时，△MNB的面积有最大值，此时S△OMN的最小值是1﹣＝，故④不正确，故选：A．【点评】本题主要考查了正方形的性质、全等三角形的判定与性质，二次函数的最值以及勾股定理的综合应用，解题时注意二次函数的最值的运用．2．如图，正方形ABCD中，∠EAF＝45°，BD分别交AE、AF于M、N，连MF、EF，下列结论：①MN2＝BN2+DM2；②DE+BF＝EF；③AM＝MF且AM⊥MF；④若E为CD 中点，则＝．其中正确的有（）A．1个B．2个C．3个D．4个【分析】①过B作BD的垂线，截取BH＝MD，连接AH，HN，如图，易证△ADM≌△ABH，△AHN≌△AMN，得MN＝HN，最后根据勾股定理可作判断；②延长CB，截取BI＝DE，连接AI，如图，易证△ADE≌△ABI，△AIF≌△AEF，得IF＝EF，即DE+BF＝EF，成立．③作辅助线，则可证△AFJ为等腰直角三角形，CK＝BF＝KJ，证明∠JCK＝45°，推出四边形BCJK为平行四边形，所以GJ＝BC＝AD，可证△GJM≌△DAM，则M为AJ的中点，又∠AFJ＝90°，故AM＝MF且AM⊥MF，成立．④延长CB，截取BL＝DE，连接AL，可设DE＝a，BF＝x，则EF＝LF＝a+x，CF＝2a﹣x，CE＝a，由勾股定理可知：3x＝2a，则＝＝，成立．【解答】解：①过B作BD的垂线，截取BH＝MD，连接AH，HN，如图，∵四边形ABCD是正方形，∴AD＝AB，∠ADB＝∠ABD＝45°，∠BAD＝90°，∴∠ABH＝45°＝∠ADM，在△ADM和△ABM中，∵，∴△ADM≌△ABH（SAS），∴∠DAM＝∠BAH，AM＝AH，∵∠EAF＝45°，∠BAD＝90°，∴∠DAM+∠BAN＝∠BAH+∠BAN＝45°，∴∠MAN＝∠HAN＝45°，在△AHN和△AMN中，∵，∴△AHN≌△AMN（SAS），∴MN＝HN，Rt△BHN中，HN2＝BH2+BN2，∴MN2＝BN2+DM2，成立．②延长CB，截取BI＝DE，连接AI，如图，在△ADE和△ABI中，∵∴△ADE≌△ABI（SAS），同理得△AIF≌△AEF（SAS），∴IF＝EF，即DE+BF＝EF，成立；③如图，过F作FJ⊥AF交AE的延长线于J，过J作JK⊥BC于K，连接CJ，过J作JG ∥BC交BD于G，∴∠AFJ＝∠AFB+∠JFK＝90°，∵∠AFB+∠BAF＝90°，∴∠BAF＝∠JFK，∵∠EAF＝45°，∠AFJ＝90°，∴△AFJ是等腰直角三角形，在△ABF和△FKJ中，∵，∴△ABF≌△FKJ（SAS），∴AB＝FK＝BC，BF＝KJ，∴CK＝BF＝KJ，∴∠JCK＝45°，∴∠DBC＝∠JCK，∴BG∥CJ，∵JG∥BC，∴四边形BCJK为平行四边形，∴GJ＝BC＝AD，∵AD∥BC∥GJ，∴∠DAM＝∠MJK，在△GJM和△DAM中，∵，∴△GJM≌△DAM（AAS），∴AM＝MJ，则M为AJ的中点，又∠AFJ＝90°，故AM＝MF且AM⊥MF，成立．④延长CB，截取BL＝DE，连接AL，可设DE＝a，BF＝x，则EF＝LF＝a+x，∵E为CD中点，∴CD＝BC＝2a，∴CF＝2a﹣x，CE＝a，在Rt△EFC中，由勾股定理得：EF2＝CE2+CF2∴（a+x）2＝a2+（2a﹣x）2解得：3x＝2a，则＝＝，成立．故选：D．【点评】本题考查了正方形的性质，全等三角形的判定和性质，勾股定理，正确的作出辅助线是解题的关键．3．如图，在正方形ABCD中，AB＝4，AC与BD相交于点O，N是AO的中点，点M在BC边上，且BM＝3，P为对角线BD上一点，当对角线BD平分∠NPM时，PM﹣PN值为（）A．1B．C．2D．【分析】作以BD为对称轴作N的对称点N'，连接MN'，PN'，根据PM﹣PN＝PM﹣PN'≤MN'，当P，M，N'三点共线时，取“＝”，再证得△MCN'∽△BCA，从而推得△MCN'为等腰直角三角形，结合BM＝3．正方形的边长为4，求得CM，即为MN'，问题可解．【解答】解：如图所示，∵对角线BD平分∠NPM，∴作以BD为对称轴N的对称点N'，连接MN'，PN'，根据轴对称性质可知，PN＝PN'，∠NPO＝N′PO，NO＝N′O∵在正方形ABCD中，AB＝4∴AC＝AB＝4，∵O为AC中点∴OA＝OC＝2∵N为OA的中点∴ON＝∴ON'＝CN'＝∴AN'＝3∵BM＝3∴CM＝4﹣3＝1∴＝＝∵∠MCN'＝∠BCA∴△MCN'∽△BCA∴∠CMN'＝∠ABC＝90°∵∠MCN'＝45°∴△MCN'为等腰直角三角形∴MN'＝CM＝1∴PM﹣PN的值为1．故选：A．【点评】本题主要考查了正方形的性质，明确正方形的相关性质及相似三角形的判定、勾股定理等知识点，是解题的关键．4．如图，在正方形ABCD内一点E连接BE、CE，过C作CF⊥CE与BE延长线交于点F，连接DF、DE．CE＝CF＝1，DE＝，下列结论中：①△CBE≌△CDF；②BF⊥DF；③点D到CF的距离为2；④S四边形DECF＝+1．其中正确结论的个数是（）A．1B．2C．3D．4【分析】根据正方形的性质、全等三角形的判定和性质、勾股定理等知识逐项判断即可．【解答】解：∵四边形ABCD是正方形，∴BC＝CD，∠BCD＝90°，∵CF⊥CE，∴∠ECF＝∠BCD＝90°，∴∠BCE＝∠DCF，在△BCE与△DCF中，，∴△BCE≌△DCF（SAS），故①正确；∵△BCE≌△DCF，∴∠CBE＝∠CDF，∴∠DFB＝∠BCD＝90°，∴BF⊥DF，故②正确，过点D作DM⊥CF，交CF的延长线于点M，∵∠ECF＝90°，FC＝EC＝1，∴∠CFE＝45°，∵∠DFM+∠CFB＝90°，∴∠DFM＝∠FDM＝45°，∴FM＝DM，∴由勾股定理可求得：EF＝，∵DE＝，∴由勾股定理可得：DF＝2，∵EF2+BE2＝2BE2＝BF2，∴DM＝FM＝，故③错误，∵△BCE≌△DCF，∴S△BCE＝S△DCF，∴S四边形DECF＝S△DCF+S△DCE＝S△ECF+S△DEF＝+，故④错误，故选：B．【点评】本题考查四边形的综合问题，涉及正方形的性质、全等三角形的性质与判定、勾股定理、三角形面积公式等知识内容，综合程度高，需要学生灵活运用知识解答．5．如图，已知E，F分别为正方形ABCD的边AB，BC的中点，AF与DE交于点M．则下列结论：①∠AME＝90°，②∠BAF＝∠EDB，③AM＝MF，④ME+MF＝MB．其中正确结论的有（）A．4个B．3个C．2个D．1个【分析】根据正方形的性质可得AB＝BC＝AD，∠ABC＝∠BAD＝90°，再根据中点定义求出AE＝BF，然后利用“边角边”证明△ABF和△DAE全等，根据全等三角形对应角相等可得∠BAF＝∠ADE，然后求出∠ADE+∠DAF＝∠BAD＝90°，从而求出∠AMD ＝90°，再根据邻补角的定义可得∠AME＝90°，得出①正确；根据中线的定义判断出∠ADE≠∠EDB，然后求出∠BAF≠∠EDB，判断出②错误；设正方形ABCD的边长为2a，利用勾股定理列式求出AF，再根据似三角形对应边成比例求出AM，然后求出MF，消掉a即可得到AM＝MF，判断出③正确；过点M作MN⊥AB于N，由相似三角形的性质得出＝＝，解得MN＝a，AN＝a，得出NB＝AB﹣AN＝2a﹣a＝a，根据勾股定理得BM＝a，求出ME+MF＝+a＝a，MB＝a，得出ME+MF＝MB，故④正确．于是得到结论．【解答】解：在正方形ABCD中，AB＝BC＝AD，∠ABC＝∠BAD＝90°，∵E、F分别为边AB，BC的中点，∴AE＝BF＝BC，在△ABF和△DAE中，，∴△ABF≌△DAE（SAS），∴∠BAF＝∠ADE，∵∠BAF+∠DAF＝∠BAD＝90°，∴∠ADE+∠DAF＝∠BAD＝90°，∴∠AMD＝180°﹣（∠ADE+∠DAF）＝180°﹣90°＝90°，∴∠AME＝180°﹣∠AMD＝180°﹣90°＝90°，故①正确；∵DE是△ABD的中线，∴∠ADE≠∠EDB，∴∠BAF≠∠EDB，故②错误；设正方形ABCD的边长为2a，则BF＝a，在Rt△ABF中，AF＝＝＝a，∵∠BAF＝∠MAE，∠ABC＝∠AME＝90°，∴△AME∽△ABF，∴＝，即＝，解得：AM＝a，∴MF＝AF﹣AM＝a﹣a＝a，∴AM＝MF，故③正确；如图，过点M作MN⊥AB于N，则MN∥BC，∴△AMN∽△AFB，∴＝＝，即＝＝，解得MN＝a，AN＝a，∴NB＝AB﹣AN＝2a﹣a＝a，根据勾股定理得：BM＝＝＝a，∵ME+MF＝+a＝a，MB＝a，∴ME+MF＝MB，故④正确．综上所述，正确的结论有①③④共3个．故选：B．【点评】本题考查了正方形的性质，全等三角形的判定与性质，相似三角形的判定与性质，勾股定理等知识；仔细分析图形并作出辅助线构造出直角三角形与相似三角形是解题的关键．6．如图，正方形ABCD和正方形CEFG中，点D在CG上，BC＝1，CE＝3，H是AF的中点，EH与CF交于点O．则HE的长为（）A．2B．C．2D．或2【分析】利用直角三角形斜边上的中线等于斜边的一半，分别求得HO和OE的长后即可求得HE的长．【解答】解：∵AC、CF分别是正方形ABCD和正方形CGFE的对角线，∴∠ACD＝∠GCF＝45°，∴∠ACF＝90°，又∵H是AF的中点，∴CH＝HF，∵EC＝EF，∴点H和点E都在线段CF的中垂线上，∴HE是CF的中垂线，∴点H和点O是线段AF和CF的中点，∴OH＝AC，在Rt△ACD和Rt△CEF中，AD＝DC＝1，CE＝EF＝3，∴AC＝，∴CF＝3，又OE是等腰直角△CEF斜边上的高，∴OE＝，∴HE＝HO+OE＝2．故选：C．【点评】本题考查了正方形的性质、直角三角形的性质及勾股定理的知识，综合性较强，难度较大．7．如图，在正方形ABCD中，E为BC上一点，过点E作EF∥CD，交AD于F，交对角线BD于G，取DG的中点H，连结AH，EH，FH．下列结论：①FH∥AE；②AH＝EH且AH⊥EH；③∠BAH＝∠HEC；④△EHF≌△AHD；⑤若，则．其中哪些结论是正确（）A．①②④⑤B．②③④C．①②③D．②③④⑤【分析】①根据正方形对角线互相垂直、过一点有且只有一条直线与已知直线垂直即可得结论；②根据矩形的判定和性质、直角三角形的性质，证明三角形全等即可得结论；③根据全等三角形性质、矩形的性质进行角的计算即可得结论；④根据边边边证明三角形全等即可得结论；⑤根据割补法求四边形的面积，再求等腰直角三角形的面积，即可得结论．【解答】证明：①在正方形ABCD中，∠ADC＝∠C＝90°，∠ADB＝45°，∵EF∥CD∴∠EFD＝90°，得矩形EFDC．在Rt△FDG中，∠FDG＝45°，∴FD＝FG，∵H是DG中点，∴FH⊥BD∵正方形对角线互相垂直，过A点只能有一条垂直于BD的直线，∴AE不垂直于BD，∴FH与AE不平行．所以①不正确．②∵四边形ABEF是矩形，∴AF＝EB，∠BEF＝90°，∵BD平分∠ABC，∴∠EBG＝∠EGB＝45°，∴BE＝GE，∴AF＝EG．在Rt△FGD中，H是DG的中点，∴FH＝GH，FH⊥BD，∴∠AFH＝∠AFE+∠GFH＝90°+45°＝135°，∠EGH＝180°﹣∠EGB＝180°﹣45°＝135°，∴∠AFH＝∠EGH，∴△AFH≌△EGH，∴AH＝EH，∠AHF＝∠EHG，∴∠AHF+AHG＝∠EHG+∠AHG，即∠FHG＝∠AHE＝90°，∴AH⊥EH．所以②正确．③∵△AFH≌△EGH，∴∠F AH＝∠GEH，∵∠BAF＝CEG＝90°，∴∠BAH＝∠HEC．所以③正确．④∵EF＝AD，FH＝DH，EH＝AH，∴△EHF≌△AHD所以④正确．⑤如图，过点H作HM⊥AD于点M，设EC＝FD＝FG＝x，则BE＝AF＝EG＝2x，∴BC＝DC＝AB＝AD＝3x，HM＝x，AM＝x，∴AH2＝（x）2+（x）2＝x2，S四边形DHEC＝S梯形EGDC﹣S△EGH＝（2x+3x）•x﹣×＝2x2S△AHE＝AH•EH＝AH2＝x2∴＝＝．所以⑤不正确．故选：B．【点评】本题考查了正方形的性质、矩形的判定和性质、全等三角形的判定和性质、直角三角形的性质、三角形和梯形的面积等内容，解题关键是综合利用以上知识解决问题．8．如图，在正方形ABCD中，AC、BD相交于点O，E、F分别为BC、CD上的两点，BE ＝CF，AE、BF分别交BD、AC于M、N两点，连OE、OF．下列结论：①AE＝BF；②AE⊥BF；③CE+CF＝BD；④S四边形OECF＝S正方形ABCD，其中正确的是（）A．①②B．①④C．①②④D．①②③④【分析】①易证得△ABE≌△BCF（ASA），则可证得结论①正确；②由△ABE≌△BCF，可得∠FBC＝∠BAE，证得AE⊥BF，选项②正确；③证明△BCD是等腰直角三角形，求得选项③错误；④证明△OBE≌△OCF，根据正方形被对角线将面积四等分，即可得出选项④正确．【解答】解：①∵四边形ABCD是正方形，∴AB＝BC，∠ABE＝∠BCF＝90°，在△ABE和△BCF中，∵，∴△ABE≌△BCF（SAS），∴AE＝BF，故①正确；②由①知：△ABE≌△BCF，∴∠FBC＝∠BAE，∴∠FBC+∠ABF＝∠BAE+∠ABF＝90°，∴AE⊥BF，故②正确；③∵四边形ABCD是正方形，∴BC＝CD，∠BCD＝90°，∴△BCD是等腰直角三角形，∴BD＝BC，∴CE+CF＝CE+BE＝＝BC，故③错误；④∵四边形ABCD是正方形，∴OB＝OC，∠OBE＝∠OCF＝45°，在△OBE和△OCF中，∵，∴△OBE≌△OCF（SAS），∴S△OBE＝S△OCF，∴S四边形OECF＝S△COE+S△OCF＝S△COE+S△OBE＝S△OBC＝S正方形ABCD，故④正确；故选：C．【点评】此题属于四边形的综合题．考查了正方形的性质，全等三角形的判定与性质、勾股定理以及等腰直角三角形的性质．注意掌握全等三角形的判定与性质是解此题的关键．9．如图，在正方形ABCD中，M是对角线BD上的一点，点E在AD的延长线上，连接AM、EM、CM，延长EM交AB于点F，若AM＝EM，∠E＝30°，则下列结论：①FM＝ME；②BF＝DE；③CM⊥EF；④BF+MD＝BC，其中正确的结论序号是（）A．①②③B．①②④C．②③④D．①②③④【分析】①证明△AFM是等边三角形，可判断；②③证明△CBF≌△CDE（ASA），可作判断；④设MN＝x，分别表示BF、MD、BC的长，可作判断．【解答】解：①∵AM＝EM，∠AEM＝30°，∴∠MAE＝∠AEM＝30°，∴∠AMF＝∠MAE+∠AEM＝60°，∵四边形ABCD是正方形，∴∠F AD＝90°，∴∠F AM＝90°﹣30°＝60°，∴△AFM是等边三角形，∴FM＝AM＝EM，故①正确；②连接CE、CF，∵四边形ABCD是正方形，∴∠ADB＝∠CDM，AD＝CD，在△ADM和△CDM中，∵，∴△ADM≌△CDM（SAS），∴AM＝CM，∴FM＝EM＝CM，∴∠MFC＝∠MCF，∠MEC＝∠ECM，∵∠ECF+∠CFE+∠FEC＝180°，∴∠ECF＝90°，∵∠BCD＝90°，∴∠DCE＝∠BCF，在△CBF和△CDE中，∵，∴△CBF≌△CDE（ASA），∴BF＝DE；故②正确；③∵△CBF≌△CDE，∴CF＝CE，∵FM＝EM，∴CM⊥EF，故③正确；④过M作MN⊥AD于N，设MN＝x，则AM＝AF＝2x，AN＝x，DN＝MN＝x，∴AD＝AB＝x+x，∴DE＝BF＝AB﹣AF＝x+x﹣2x＝x﹣x，∴BF+MD＝（x﹣x）+x＝x，∵BC＝AD＝x+x x，故④错误；所以本题正确的有①②③；故选：A．【点评】本题考查了正方形的性质，全等三角形的判定与性质，等腰三角形的性质和判定，熟记正方形的性质确定出△AFM是等边三角形是解题的关键．【点评】此题考查的是正方形的性质，等腰直角三角形的性质和判定以及菱10．如图，在正方形ABCD中，对角线AC，BD交于点O，AG平分∠BAC交BD于G，DE⊥AG于点H．下列结论：①AD＝2AE：②FD＝AG；③CF＝CD：④四边形FGEA是菱形；⑤OF ＝BE，正确的有（）A．2个B．3个C．4个D．5个【分析】①根据正方形的性质和角平分线的定义得：∠BAG＝∠CAG＝22.5°，由垂直的定义计算∠AED＝90°﹣22.5°＝67.5°，∠EAD＝∠EAD＝22.5°，得ED是AG的垂直平分线，则AE＝EG，△BEG是等腰直角三角形，则AD＝AB＞2AE，可作判断；②证明△DAF≌△ABG（ASA），可作判断；③分别计算∠CDF＝∠CFD＝67.5°，可作判断；④根据对角线互相平分且垂直的四边形是菱形可作判断；⑤设BG＝x，则AF＝AE＝x，表示OF和BE的长，可作判断．【解答】解：①∵四边形ABCD是正方形，∴∠BAD＝90°，∠BAC＝45°，∵AG平分∠BAC，∴∠BAG＝∠CAG＝22.5°，∵AG⊥ED，∴∠AHE＝∠EHG＝90°，∴∠AED＝90°﹣22.5°＝67.5°，∴∠ADE＝22.5°，∵∠ADB＝45°，∴∠EDG＝22.5°＝∠ADE，∵∠AHD＝∠GHD＝90°，∴∠DAG＝∠DGA，∴AD＝DG，AH＝GH，∴ED是AG的垂直平分线，∴AE＝EG，∴∠EAG＝∠AGE＝22.5°，∴∠BEG＝45°＝∠ABG，∴∠BGE＝90°，∴AE＝EG＜BE，∴AD＝AB＞2AE，故①不正确；②∵四边形ABCD是正方形，∴AD＝AB，∠DAF＝∠ABG＝45°，∵∠ADF＝∠BAG＝22.5°，∴△DAF≌△ABG（ASA），∴DF＝AG，故②正确；③∵∠CDF＝45°+22.5°＝67.5°，∠CFD＝∠AFE＝90°﹣22.5°＝67.5°，∴∠CDF＝∠CFD，∴CF＝CD，故③正确；④∵∠EAH＝∠F AH，∠AHE＝∠AHF，∴∠AEF＝∠AFE，∴AE＝AF，∴EH＝FH，∵AH＝GH，AG⊥EF，∴四边形FGEA是菱形；故④正确；⑤设BG＝x，则AF＝AE＝x，由①知△BEG是等腰直角三角形，∴BE＝x，∴AB＝AE+BE＝x+x＝（+1）x，∴AO＝＝，∴OF＝AO﹣AF＝﹣x＝，∴＝＝，∴OF＝BE；故⑤正确；本题正确的结论有：②③④⑤；故选：C．形的判定与性质等知识．此题综合性较强，难度较大，注意掌握正方形的性质，注意数形结合思想的应用．11．如图，以正方形ABCD的顶点A为圆心，以AD的长为半径画弧，交对角线AC于点E，再分别以D，E为圆心，以大于DE的长为半径画弧，两弧交于图中的点F处，连接AF并延长，与BC的延长线交于点P，则∠P＝（）A．90°B．45°C．30°D．22.5°【分析】根据正方形的性质得到∠DAC＝∠ACD＝45°，由作图知，∠CAP＝∠DAC ＝22.5°，根据三角形的内角和即可得到结论．【解答】解：∵四边形ABCD是正方形，∴∠DAC＝∠ACD＝45°，由作图知，∠CAP＝∠DAC＝22.5°，∴∠P＝180°﹣∠ACP﹣∠CAP＝22.5°，故选：D．【点评】本题考查了正方形的性质，角平分线定义，正确的理解题意是解题的关键．12．如图，正方形ABCD中，点E在边CD上，连接AE，过点A作AF⊥AE交CB的延长线于点F，连接EF，AG平分∠F AE，AG分别交BC，EF于点G，H，连接EG，DH．则下列结论中：①AF＝AE；②∠EGC＝2∠BAG；③DE+BG＝EG；④AD+DE＝DH；⑤若DE＝CE，则CE：CG：EG＝3：4：5，其中正确的结论有（）A．2个B．3个C．4个D．5个【分析】①正确．证明△ADE≌△ABF（ASA）可得结论．②正确．证明△AGF≌△AGE（SAS），推出∠AGF＝∠AGE＝90°﹣∠BAG，推出∠EGF ＝180°﹣2∠BAG可得结论．③正确．证明△GAF≌△GAE，推出GF＝GE可得结论．④正确．过点H作HM⊥AD于M，HN⊥CD于N，证明△HMA≌△HNE（AAS），推出AM＝EN，HM＝HN，再证明四边形HMDN是正方形可得结论．⑤正确．当DE＝EC时，设DE＝EC＝a，BG＝x，则EG＝a+x，GC＝2a﹣x，利用勾股定理构建方程求出x即可解决问题．【解答】解：∵四边形ABCD是正方形，∴AB＝AD，∠ABC＝∠ABF＝∠ADE＝∠BAD＝90°，∵AE⊥AF，∴∠EAF＝∠BAD＝90°，∴∠BAF＝∠DAE，∴△ADE≌△ABF（ASA），∴AE＝AF，故①正确，∵AG平分∠EAF，∴∠GAF＝∠GAE，∵AF＝AE，AG＝AG，∴△AGF≌△AGE（SAS），∴∠AGF＝∠AGE＝90°﹣∠BAG，∴∠EGF＝180°﹣2∠BAG，∵∠EGF＝180°﹣∠EGC，∴∠EGC＝2∠BAG，故②正确，∵△ADE≌△ABF，∴DE＝BF，∵△GAF≌△GAE，∴GF＝GE，∵FG＝BF+BG＝DE+BG，∴EG＝BG+DE，故③正确，过点H作HM⊥AD于M，HN⊥CD于N，∵AE＝AF，∠EAF＝90°，AH平分∠EAF，∴AH⊥EF，HF＝HE，∴HA＝HE＝HF，∵∠ADE+∠AHE＝180°，∴∠HAD+∠DEH＝180°，∵∠DEH+∠HEN＝180°，∴∠HAM＝∠HEN，∵∠AMH＝∠ENH＝90°，∴△HMA≌△HNE（AAS），∴AM＝EN，HM＝HN，∵∠HMD＝∠HND＝∠MDN＝90°，∴四边形HMDN是矩形，∵HM＝HN，∴四边形HMDN是正方形，∴DM＝DN＝HM＝HN，DH＝DM，∴DA+DE＝DM+AM+DN﹣EN＝2DM＝DH，故④正确，当DE＝EC时，设DE＝EC＝a，BG＝x，则EG＝a+x，GC＝2a﹣x，在Rt△ECG中，∵EG2＝EC2+CG2，∴（x+a）2＝a2+（2a﹣x）2，解得x＝a，∴CG＝a，EG＝a，∴CE：CG：EG＝a：a：＝3：4：5，故⑤正确，故选：D．【点评】本题考查正方形的性质，全等三角形的判定和性质，勾股定理等知识，解题的关键是正确寻找全等三角形解决问题，学会利用参数构建方程解决问题，属于中考选择题中的压轴题．13．如图，矩形ABCD中，O为AC的中点，过点O的直线分别与AB、CD交于点E、F，连接BF交AC于点M，连接DE、BO．若∠COB＝60°，FO＝FC＝2，则下列结论：①FB⊥OC；②△EOB≌△CMB；③四边形EBFD是菱形；④MB＝2．其中正确结论的个数是（）A．1个B．2个C．3个D．4个【分析】连接BD，先证明△BOC是等边三角形，得FO＝FC，BO＝BC，故①正确；因为△EOB≌△FOB≌△FCB，故△EOB不会全等于△CBM，故②错误；再证明四边形EBFD是平行四边形，由OB⊥EF推出四边形EBFD是菱形故③正确，先判断出CM＝，再由∠CBM＝30°，判断出BC＝2，进而判断出④，由此不难得到答案．【解答】解：连接BD，∵四边形ABCD是矩形，∴AC＝BD，AC、BD互相平分，∵O为AC中点，∴BD也过O点，∴OB＝OC，∵∠COB＝60°，OB＝OC，∴△OBC是等边三角形，∴OB＝BC＝OC，∠OBC＝60°，在△OBF与△CBF中，，∴△OBF≌△CBF（SSS），∴△OBF与△CBF关于直线BF对称，∴FB⊥OC，OM＝CM；∴①正确，∵∠OBC＝60°，∴∠ABO＝30°，∵△OBF≌△CBF，∴∠OBM＝∠CBM＝30°，∴∠ABO＝∠OBF，∵AB∥CD，∴∠OCF＝∠OAE，∵OA＝OC，∠AOE＝∠FOC∴△AOE≌△COF（ASA），∴OE＝OF，∴OB⊥EF，∴四边形EBFD是菱形，∴③正确，∵△EOB≌△FOB≌△FCB，∴△EOB≌△CMB错误．∴②错误；∵FO＝FC＝2，FM⊥OC，∠FCM＝30°，∴CM＝，∵∠CBM＝30°，∴BC＝2，∴BM＝3，∴④错误．综上可知其中正确结论的个数是2个，故选：B．【点评】本题属于四边形的综合题，考查矩形的性质、等边三角形的判定和性质．全等三角形的判定和性质、菱形的判定、勾股定理等知识，解题的关键是灵活运用这些知识解决问题，属于中考常考题型．二．填空题（共3小题）14．如图，点E为正方形ABCD外一点，且ED＝CD，连接AE，交BD于点F．若∠CDE ＝40°，则∠DFC的度数为110°．【分析】根据正方形性质和已知得：AD＝DE，利用等腰三角形性质计算∠DAE＝25°，由三角形的内角和定理得：∠AFD＝110°，证明△ADF≌△CDF（SAS），∠DFC＝∠AFD ＝110°．【解答】解：∵四边形ABCD是正方形，∴AD＝DC，∠ADC＝90°，∴∠ADB＝∠BDC＝45°，∵DC＝DE，∴AD＝DE，∴∠DAE＝∠DEA，∵∠ADE＝90°+40°＝130°，∴∠DAE＝＝25°，∴∠AFD＝180°﹣25°﹣45°＝110°，在△ADF和△CDF中，∵，∴△ADF≌△CDF（SAS），∴∠DFC＝∠AFD＝110°，故答案为：110°．【点评】本题考查了正方形的性质、三角形全等的性质和判定、等腰三角形的性质、三角形内角和定理，属于基础题，熟练掌握正方形的性质是关键．15．如图，正方形ABCD中，在AD的延长线上取点E，F，使DE＝AD，DF＝BD，连接BF分别交CD，CE于H，G，下列结论：①EC＝2DG；②∠GDH＝∠GHD；③S△CDG＝S四边形DHGE；④图中只有8个等腰三角形．其中正确的有②③（填番号）．【分析】根据正方形的性质和已知推出四边形DECB是平行四边形，得到BD＝CE，BD ∥CE，无法证出G为CE的中点；得到BD∥CE，推出∠DCG＝∠BDC＝45°，求出∠BGC＝∠GBC，得到BC＝CG＝CD，求出∠CDG＝∠DHG即可；根据三角形的面积公式推出△CDG和四边形DHGE的面积相等；可得有9个等腰三角形．【解答】解：∵正方形ABCD，DE＝AD，∴AD∥BC，DE＝BC，∠EDC＝90°，∴四边形DECB是平行四边形，∴BD＝CE，BD∥CE，∵DE＝BC＝AD，∴∠DCE＝∠DEC＝45°，要使CE＝2DG，只要G为CE的中点即可，但DE＝DC，DF＝BD，∴EF≠BC，即△EFG和△BCG不全等，∴G不是CE中点，∴①错误；∵∠ADB＝45°，DF＝BD，∴∠F＝∠DBH＝∠ADB＝22.5°，∴∠DHG＝180°﹣90°﹣22.5°＝67.5°，∵BD∥CE，∴∠DCG＝∠BDC＝45°，∵∠DHG＝67.5°，∴∠HGC＝22.5°，∠DEC＝45°，∵∠BGC＝180°﹣22.5°﹣135°＝22.5°＝∠GBC，∴BC＝CG＝CD，∴∠CDG＝∠CGD＝（180°﹣45°）＝67.5°＝∠DHG，∴②正确；∵CG＝DE＝CD，∠DCE＝∠DEC＝45，∠HGC＝22.5°，∠GDE＝90﹣∠CDG＝90﹣67.5＝22.5°，∴△DEG≌△CHG，要使△CDG和四边形DHGE的面积相等，只要△DEG和△CHG的面积相等即可，根据已知条件△DEG≌△CHG，∴③S△CDG＝S四边形DHGE；正确，等腰三角形有△ABD，△CDB，△BDF，△CDE，△BCG，△DGH，△EGF，△CDG，△DGF；∴④错误；故答案为：②③．【点评】本题主要考查对三角形的内角和定理，等腰三角形的性质和判定，正方形的性质，平行四边形的性质和判定等知识．综合运用这些性质进行推理是解此题的关键．16．如图，在正方形ABCD中，P为AB的中点，BE⊥PD的延长线于点E，连接AE、BE、F A⊥AE交DP于点F，连接BF，FC．若AE＝2，则FC＝2．【分析】根据正方形的性质可得AB＝AD，再求出∠BAE＝∠DAF，∠ABE＝∠ADF，然后利用“角边角”证明△ABE和△ADF全等，根据全等三角形对应边相等可得AE＝AF，从而判断出△AEF是等腰直角三角形，根据AE的长度求出EF，过点A作AH⊥EF于H，连接BH，根据等腰直角三角形的性质可得AH＝EH＝FH，利用“角边角”证明△APH 和△BPE全等，根据全等三角形对应边相等可得BE＝AH，然后求出△BEH是等腰直角三角形，根据等腰直角三角形的性质可得∠EHB＝45°，然后求出∠AHB＝∠FHB，再利用“边角边”证明△ABH和△FBH全等，根据全等三角形对应边相等可得AB＝BF，再根据全等三角形对应边相等求出BE＝DF，全等三角形对应角相等求出∠BAH＝∠BFE，然后求出∠BFE＝∠ADF，根据等角的余角相等求出∠EBF＝∠FDC，再利用“边角边”证明△BEF和△DFC全等，根据全等三角形对应边相等可得FC＝EF．【解答】解：在正方形ABCD中，AB＝AD，∠BAD＝90°，∵F A⊥AE，∴∠EAF＝90°，∴∠BAE＝∠DAF，∵∠ABE+∠BPE＝∠ADF+∠APD＝90°，∴∠ABE＝∠ADF，在△ABE和△ADF中，，∴△ABE≌△ADF（ASA），∴AE＝AF，BE＝DF，∵F A⊥AE，∴△AEF是等腰直角三角形，∴EF＝AE＝2，过点A作AH⊥EF于H，连接BH，。

九年级数学几何综合专项测试(含答案)

学生做题前请先回答以下问题问题1：举例说明几何综合中常见的结构以及思考角度有哪些？问题2：中点的思考角度有哪些？几何综合专项测试一、单选题(共8道，每道12分)1.如图，在梯形ABCD中，已知AD∥BC，AD=DC=4，BC=8，点N在BC上，CN=2，E是AB 中点．在AC上存在一点M使EM+MN的值最小，则EM+MN的最小值为( )A.6B.8C.4D.答案：A解题思路：试题难度：三颗星知识点：轴对称—最短路线问题2.如图，将边长为12cm的正方形ABCD折叠，使得A点落在边CD上的E点，然后压平得折痕GF，若GF的长为13cm，则线段CE的长为( )cm．A.6B.7C.8D.5答案：B解题思路：试题难度：三颗星知识点：翻折变换（折叠问题）3.如图是两块完全一样的含30°角的直角三角板，分别记作△ABC与．现将两块三角板重叠在一起，设较长直角边的中点为M，绕中点M转动上面的三角板ABC，使其直角顶点C恰好落在三角板的斜边上．若∠A=30°，AC=10，则此时两直角顶点之间的距离是( )A.4B.5C.6D.答案：B解题思路：试题难度：三颗星知识点：旋转的性质4.如图，在平行四边形ABCD中，BC=2AB，CE⊥AB于点E，F为AD的中点，若∠AEF=52°，则∠B=( )A.52°B.54°C.72°D.76°答案：D解题思路：试题难度：三颗星知识点：类倍长中线5.如图，在平面直角坐标系xOy中，正方形ABCD的顶点A的坐标是(0，2)，顶点B在x轴负半轴上，对角线AC，BD相交于点M，，则点D的坐标是( )A.(-2，6)B.(-3，5)C.(-5，2)D.(-6，4)答案：A解题思路：试题难度：三颗星知识点：弦图模型6.如图，已知正方形ABCD的周长为24，△BCE是等边三角形，F是CE的中点，AE，BF交于点G，连接CG，则CG的长为( )A. B. C. D.答案：B解题思路：试题难度：三颗星知识点：三线合一7.如图1，等边△ABD和等边△BCD的边长均为1，将△ABD沿AC方向向右平移到的位置得到图2，则图中阴影部分的周长为( )A.1B.2C.2.5D.3答案：B解题思路：试题难度：三颗星知识点：平移的性质8.如图，在Rt△POQ中，OP=OQ=4，M是PQ的中点，把一块直角三角板的直角顶点放在点M处，并将此三角板绕点M旋转，三角板的两直角边与边OP，OQ分别交于点A，B，连接AB．则在旋转三角板的过程中，△AOB周长的最小值为( )A. B.C.6D.答案：B解题思路：试题难度：三颗星知识点：斜直角的处理思路（斜转直）。

初中正方形的判定专项练习30题

正方形的判定专项练习30题（有答案）1．如图，已知平行四边形ABCD中，对角线AC、BD交于点O，E是DB延长线上一点，且△ACE是等边三角形．（1）求证：四边形ABCD是菱形；（2）若∠AEB=2∠EAB，求证：四边形ABCD是正方形．2．已知：如图，CE、CF分别是△ABC的内外角平分线，过点A作CE、CF的垂线，垂足分别为E、F．（1）求证：四边形AECF是矩形；（2）当△ABC满足什么条件时，四边形AECF是正方形？3．已知：如图，点D、E分别为△ABC的边AB、AC的中点，将△ADE绕点D旋转180°至△BDF．（1）小明发现四边形BCEF的形状是平行四边形，请你帮他把说理过程补齐．理由是：因为△BDF是由△ADE绕点D旋转180°得到的所以△ADE与△BDF全等且点A、D、B在同一条直线上点E、D、F也在同一条直线上．所以BF=AE，∠F=∠_________可得BF∥_________又因为E是AC的中点，所以EC=AE，所以BF= _________因此，四边形BCEF是平行四边形（根据_________ ）（2）小明还发现在原有的△ABC中添加一个条件后，就可以使四边形BFEC成为一种特殊的平行四边形．你也来试试．你认为添加条件_________ 后，四边形BFEC是_________ ．（友情提示：我们将根据你所提出问题的难易程度，给予不同的分值．）理由是：_________ ．4．如图，在矩形ABCD中，AF、BE、CE、DF分别是矩形的四个角的角平分线，E、M、F、N是其交点，求证：四边形EMFN是正方形．5．如图，△ABC中，∠ACB=90°，D为AB中点，四边形BCED为平行四边形，DE、AC相交于点F．求证：（1）点F为AC中点；（2）试确定四边形ADCE的形状，并说明理由；（3）若四边形ADCE为正方形，△ABC应添加什么条件？并证明你的结论．6．求证：对角线相等的菱形是正方形．已知：四边形ABCD是菱形，且AC=BD （又：AC，BD互相平分）求证：四边形ABCD是正方形．7．在△ACD中，∠D=90°，∠D的平分线交AC于点E，EF⊥AD交AD于点F，EG⊥DC交DC于点G，请你说明四边形EFDG是正方形．8．已知：如图，点M是矩形ABCD的边AD的中点，点P是BC边上的一动点，PE⊥CM，PF⊥BM，垂足分别为E、F．（Ⅰ）当四边形PEMF为矩形时，矩形ABCD的长与宽满足什么条件？试说明理由．（Ⅱ）在（Ⅰ）中当点P运动到什么位置时，矩形PEMF变为正方形？为什么？9．如图，D是△ABC的边BC的中点，DE⊥AC，DF⊥AB，垂足分别是E、F，且BF=CE．（2）当∠A=90°时，求证：四边形AFDE是正方形．10．如图，四边形ABCD是矩形，E是BD上的一点，∠BAE=∠BCE，∠AED=∠CED，点G是BC、AE延长线的交点，AG 与CD相交于点F．求证：四边形ABCD是正方形．11．如图，在△ABC中，AB=AC，点D是BC边的中点，DE⊥AB，DF⊥AC，垂足分别是E、F．（1）求证：DE=DF；（2）若再添加一个条件，即可证得四边形AEDF为正方形，这个条件是_________ ．12．在△ABC中，∠C=90°，∠A，∠B的平分线交于点D，DE⊥BC于点E，DF⊥AC于点F，求证：四边形CFDE是正方形．13．已知：如图，在△ABC是，∠ACB=90°，CD平分∠ACB，DE⊥BC，DF⊥AC，垂足分别为EF，求证：四边形CFDE 是正方形．14．如图，在△ABC中，AB=AC，D为BC边的中点，过点D作DE⊥AB，DF⊥AC，垂足分别为E、F．（2）若∠A=90°，判断四边形AEDF的形状，并说明理由．15．如图△ABC中，点O是AC上的一个动点，过点O作直线MN∥BC，设MN交∠BCA的平分线于点E，交∠GCA的平分线于点F．（1）说明 EO=FO．（2）当点O运动到何处，四边形AECF是矩形？说明你的结论．（3）当点O运动到何处，AC与BC具有怎样的关系时，四边形AECF是正方形？为什么？16．如图，在△ABC中，AB=AC，P是边BC的中点，PD⊥AB，PE⊥AC，垂足分别为D、E（1）求证：PD=PE；（2）DE与BC平行吗？请说明理由；（3）请添加一个条件，使四边形ADPE为正方形，并加以证明．17．如图，在直角三角形ABC中，∠C=90°，∠CAB、∠CBA的平分线交于点D，DE⊥BC于E，DF⊥AC于F，（1）求∠ADB的度数；（2）试说明四边形CEDF是什么形状的特殊四边形．18.证明：对角线相等的菱形是正方形．19．已知：如图，△ABC中，D是BC上任意一点，DE∥AC，DF∥AB．①试说明四边形AEDF的形状，并说明理由．②连接AD，当AD满足什么条件时，四边形AEDF为菱形，为什么？③在②的条件下，当△ABC满足什么条件时，四边形AEDF为正方形，不说明理由．20．如图，在△ABC中，∠BAC=90°，AB=AC，点D是BC的中点，DE⊥AB，DF⊥AC垂足分别为E，F．求证：四边形DEAF是正方形．21．如图所示，在Rt△ABC中，CF为直角的平分线，FD⊥CA于D，FE⊥BC于E，则四边形CDFE是怎样的四边形，为什么？22．如图所示，在△ABC中，∠ABC=90°，BD平分∠ABC，DE⊥BC，DF⊥AB．求证：四边形BEDF是正方形．23．如图所示，顺次延长正方形ABCD的各边AB，BC，CD，DA至E，F，G，H，且使BE=CF=DG=AH．求证：四边形EFGH是正方形．24．已知：如图Rt△ABC中，∠ACB=90°，CD为∠ACB的平分线，DE⊥BC于点E，DF⊥AC于点F．求证：四边形CEDF是正方形．25．如图所示，四边形EFGH是由矩形ABCD的外角平分线围成的．求证：四边形EFGH是正方形．26．如图所示，E、F、G、H分别是四边形ABCD的边AB、BC、CD、AD的中点，当四边形ABCD满足什么条件时，四边形EFGH为正方形？并说明理由．27．已知四边形ABCD中，AB=CD，AC=BD，试添加适当的条件使四边形ABCD成为特殊的平行四边形，并说明理由．28．如图，已知在▱ABCD中，对角线AC，BD交于点O，E是BD延长线上的点，且EA=EC．（1）求证：四边形ABCD是菱形；（2）若∠DAC=∠EAD+∠AED，求证：四边形ABCD是正方形．29．如图，在△ABC中，点D、E、F分别在BC、AB、AC边上，且DE∥AC，DF∥AB．（1）如果∠BAC=90°那么四边形AEDF是_________ 形；（2）如果AD是△ABC的角平分线，那么四边形AEDF是_________ 形；（3）如果∠BAC=90°，AD是△ABC的角平分线，那么四边形AEDF是_________ 形，证明你的结论（仅需证明第3）题结论）30．如图，分别以△ABC的三边为边在BC的同侧作三个等边三角形，即△ABD，△BCE，△ACF．请回答下列问题：（1）说明四边形ADEF是什么四边形？（2）当△ABC满足什么条件时，四边形ADEF是矩形？（3）当△ABC满足什么条件时，四边形ADEF是菱形？（4）当△ABC满足什么条件时，四边形ADEF是正方形？（5）当△ABC满足什么条件时，以A，D，E，F为顶点的四边形不存在？（第（2）（3）（4）（5）题不必说明理由）矩形的判定30题参考答案：1.（1）∵四边形ABCD是平行四边形，∴AO=CO．∵△ACE是等边三角形，∴AE=CE．∴BE⊥AC．∴四边形ABCD是菱形．（2）从上易得：△AOE是直角三角形，∴∠AEB+∠EAO=90°∵△ACE是等边三角形，∴∠EAO=60°，∴∠AEB=30°∵∠AEB=2∠EAB，∴∠EAB=15°，∴∠BAO=∠EAO﹣∠EAB=60°﹣15°=45°．又∵四边形ABCD是菱形．∴∠BAD=2∠BAO=90°∴四边形ABCD是正方形．2．（1）证明：∵CE、CF分别是△ABC的内外角平分线，∴∠ACE+∠ACF=×180°=90°，∵AE⊥CE，AF⊥CF，∴∠AEC=∠AFC=90°，∴四边形AECF是矩形．（2）答：当△ABC满足∠ACB=90°时，四边形AECF是正方形，理由是：∵∠ACE=∠ACB=45°，∵∠AEC=90°，∴∠EAC=45°=∠ACE，∴AE=CE，∵四边形AECF是矩形，∴四边形AECF是正方形．3．（1）故答案为∠AED（1分）；BF∥AC（2分）；EC（3分）；一组对边平行且相等的四边形为平行四边形．（2）A层次：（提出问题（1分），说理1分）添加条件∠C=90°后四边形BFEC为矩形．（5分）理由：由（1）得四边形BFEC为平行四边形，又∠C=90°，即有一个角是直角的平行四边形是矩形．（6分）．B层次：（提出问题分，说理1分）添加条件AC=2BC后四边形BFEC为菱形．理由：由（1）得四边形BFEC为平行四边形又知AC=2CE，AC=2BC，所以EC=BC，即一组邻边相等的平行四边形是菱形．C层次：（提出问题（3分），说理3分）添加条件∠C=90°且AC=2BC时四边形BFEC为正方形．（7分）理由：由（1）得四边形BFEC为平行四边形，又∠C=90°，即有一个角是直角的平行四边形是矩形，所以此时四边形BFEC为矩形，又因为AC=2CE，AC=2BC，所以EC=BC，一组邻边相等的矩形是正方形，所以此时四边形BFEC为正方形．4．∵四边形ABCD是矩形，∴四个内角均为90°，∵AF，BE，CE，DF分别是四个内角的平分线，∴∠EBC=∠ECB=45°，∴△EBC为等腰直角三角形，∴∠E=90°，同理∠F=∠EMF=∠ENF=90°，∴四边形MFNE为矩形，∵AD=BC，∠E=∠F=90°，∠DAF=∠EBC=45°，∴△DAF≌△CBE（AAS）∴AF=BE，∵AM=BM，∴AF﹣AM=BE﹣BM，即FM=EM，∴四边形MFNE是正方形．5．（1）∵四边形DBEC是平行四边形，∴DE∥BC，∵D为AB中点，∴DF为△ABC的中位线，即点F为AC的中点；（2）∵平行四边形BDEC，∴CE平行等于BD．∵D为AB中点，∴AD=BD，∴CE平行且等于AD，∴四边形ADCE为平行四边形，又∵AD=CD=BD，∴四边形ADCE为菱形；（3）应添加条件AC=BC．证明：∵AC=BC，D为AB中点，∴CD⊥AB（三线合一的性质），即∠ADC=90°．∵四边形BCED为平行四边形，四边形ADCE为平行四边形，∴DE=BC=AC，∠AFD=∠ACB=90°．∴四边形ADCE为正方形．（对角线互相垂直且相等的四边形是正方形）6．∵四边形ABCD是菱形，∴四边形ABCD也是平行四边形，又∵AC=BD（且AC，BD互相平分），∴四边形ABCD也为矩形，又∵四边形ABCD是菱形，∴四边形ABCD是正方形．7．∵DE平分∠ADE，EF⊥AD，EF⊥AD，∴EF=EG，∵DE=DE，∴△DEF≌△DGE（HL），∴∠DEF=∠EDG，∠DEG=∠EDF，∴FE∥DG，GE∥DF，∴四边形EFDG是平行四边形，∵∠EFD=90°，∴四边形EFDG是矩形，∵EF=EG，∴四边形EFDG是正方形．8．Ⅰ）法1：答：当四边形PEMF为矩形时，矩形ABCD的长是宽的2倍．证明：∵四边形ABCD是矩形，∴∠A=∠D=90°，AB=DC，又∵AM=DM，∴△AMB≌△DMC（SAS）∴∠AMB=∠DMC∵四边形PEMF为矩形，∴∠BMC=90°，∴∠AMB=∠DMC=45°∴AM=DM=DC，即AD=2DC．∴当四边形PEMF为矩形时，矩形ABCD的长是宽的2倍；法2：∵四边形PEMF为矩形，∴∠M为直角，∴B、C、M三点共圆，BC为直径，又∵M为AD的中点，∴BC=2CD，∴当四边形PEMF为矩形时，矩形ABCD的长是宽的2倍．（Ⅱ）答：当点P运动到BC中点时，四边形PEMF变为正方形．∵△AMB≌△DMC，∴MB=MC．∵四边形PEMF为矩形，∴PE∥MB，PF∥MC又∵点P是BC中点，∴PE=PF=MC∴四边形PEMF为正方形．9．（1）证明：∵DE⊥AC，DF⊥AB，∴∠BFD=∠CED=90°，在Rt△BDF和Rt△CDE 中，，∴Rt△BDF≌Rt△CDE（HL）；（2）答：四边形AFDE是正方形．证明：∵∠A=90°，DE⊥AC，DF⊥AB，∴四边形AFDE是矩形，又∵Rt△BDF≌Rt△CDE，∴DF=DE，∴四边形AFDE是正方形10．∵∠CED是△BCE的外角，∠AED是△ABE的外角，∴∠CED=∠CBE+∠BCE，∠AED=∠BAE+∠ABE，∵∠BAE=∠BCE，∠AED=∠CED，∴∠CBE=∠ABE，∵四边形ABCD是矩形，∴∠ABC=∠BCD=∠BAD=90°，AB=CD，∴∠CBE=∠ABE=45°，∴△ABD与△BCD是等腰直角三角形，∴AB=AD=BC=CD，∴四边形ABCD是正方形．11．（1）证明：∵AB=AC，∴∠B=∠C，又∵DE⊥AB，DF⊥AC，∴∠BED=∠CFD=90°，又∵D是BC中点，AB=AC，∴BD=CD，在△BFD与△CED中，∴△BED≌△CFD（AAS），∴DE=DF．（2）解：当△ABC为等腰直角三角形时，则有AE=DE=DF=AF，四边形AEDF为菱形，又∵∠A=90°，∴菱形AEDF为正方形12．过点D作DG⊥AB，垂足为G，∵∠CFD=∠CED=∠C=90°，∴四边形CEDF是矩形．∵AD，BD分别是∠CAB，∠CBA的平分线，∴DF=DG，DG=DE．∴DF=DE．∴四边形CFDE是正方形．13．∵∠ACB=90°，DE⊥BC，DF⊥AC，∴四边形CFDE是矩形．.又∵CD平分∠ACB，DE⊥BC，DF⊥AC，∴DE=DF．∴四边形CFDE是正方形（有一组邻边相等的矩形是正方形）．14．（1）∵在△ABC中，AB=AC，∴∠B=∠C．∵D为BC边的中点，∴BD=CD．在△BED与△CFD中，∵，∴△BED≌△CFD（AAS）；（2）四边形AEDF是正方形．理由如下：∵∠DEB=90°，∠A=90°，∴∠DEB=∠A，∴AF∥ED．同理，AE∥FD，∴四边形AEDF是矩形．又由（1）知，△BED≌△CFD，∴ED=FD，∴矩形AEDF是正方形15．（1）∵MN∥BC，∴∠ECB=∠CEO，∠GCF=∠CFO，∵CE，CF分别为∠BCA，∠GCA的角平分线，∴∠ECB=∠ECO，∠GCF=∠OCF，∴∠CEO=∠ECO，∠CFO=∠OCF，∴OC=OE，OC=OF，∴OE=OF，（2）当O点运动到AC的中点时，四边形AECF为矩形，理由：∵O点为AC的中点，∴OA=OC，∵OE=OF，OC=OE=OF，∴OA=OC=OE=OF，∴AC=EF，∴四边形AECF是矩形，（3）当O点运动到AC的中点时，AC⊥BC时，四边形AECF是正方形，理由：∵O点为AC的中点，∴OA=OC，∵OE=OF，OC=OE=OF，∴OA=OC=OE=OF，∴AC=EF，∵AC⊥BC，MN∥BC，∴AC⊥EF，∴四边形AECF是正方形．16．1）证明：∵AB=AC，∴∠B=∠C，∵PD⊥AB，PE⊥AC，∴∠PDB=∠PEC=90°，∵P是BC的中点，∴BP=PC，即∠BDP=∠PEC=90°，∠B=∠C，PB=PC，∴△PDB≌△PEC，∴PD=PE．（2）答：DE∥BC，理由是：∵△PDB≌△PEC，∴BD=CE，∵AB=AC，∴=，∴DE∥BC．（3）答：当∠A=90°时，使四边形ADPE为正方形，证明：∵∠A=∠ADP=∠AEP=90°，∴四边形ADPE是矩形，∵AB=AC，BD=CE，∴AD=AE，∴矩形ADPE是正方形，即当∠A=90°时，使四边形ADPE为正方形．17．（1）∵△ABC是直角三角形，∠C=90°，∴∠CAB+∠CBA=90°，∴∠DAB+∠DBA=（∠CAB+∠CBA）=×90°=45°，∴∠ADB=180°﹣45°=135°；（2）四边形CEDF是正方形．过D作DG⊥AB于G，∵AD、BD是∠CAB、∠CBA的平分线，∴DF=DG，DE=DG，∴DF=DE，∵△ABC是直角三角形，∠C=90°，DE⊥BC于E，DF⊥AC 于F，∴四边形CEDF是正方形．18．连接AC、BD相交于O∵菱形ABCD∴OA=OC=AC，OB=OD=BD∵AC=BD∴OA=OB∵OA⊥OB（菱形的对角线互相垂直）∴∠OAB=∠OBA=45°同理∠OBC=∠OCB=45°..∴∠OBA+∠OBC=90° ∴∠ABC=90°∴ABCD 是正方形．19．①∵DE ∥AC ，DF ∥AB ， ∴四边形AEDF 为平行四边形； ②∵四边形AEDF 为菱形， ∴AD 平分∠BAC ，则AD 平分∠BAC 时，四边形AEDF 为菱形； ③由四边形AEDF 为正方形，∴∠BAC=90°， ∴△ABC 是以BC 为斜边的直角三角形即可 20．∵DE ⊥AB ，DF ⊥AC ∴∠AED=90°，∠AFD=90° ∵∠BAC=90° ∴∠EDF=90° ∴□AEDF 是矩形在△BDE 和△CDF 中 ∵AB=AC∴∠ABC=∠ACB ∵DE ⊥AB ，DF ⊥AC ∴∠DEB=∠DFC 又∵D 是BC 的中点 ∴BD=DC∴△BDE ≌△CDF ∴DE=DF∴□AEDF 是正方形21．四边形CDFE 是正方形理由如下：∵FD ⊥AC ，FE ⊥BC ，AC ⊥BC ∴四边形CDFE 是矩形 ∵CF 平分∠ACB ∴∠FCD=45° ∴CD=DF∴四边形CDFE 是正方形22．∵∠ABC=90°，DE ⊥BC ，DF ⊥AB ， ∴∠BFD=∠BED=∠ABC=90°． ∴四边形BEDF 为矩形．又∵BD 平分∠ABC ，DE ⊥BC ，DF ⊥AB ， ∴DF=DE ．∴矩形BEDF 为正方形．23．∵四边形ABCD 是正方形，∴AB=BC=CD=DA ，∠EBF=∠HAE=∠GDH=∠FCG ，又∵BE=CF=DG=AH ， ∴CG=DH=AE=BF∴△AEH ≌△CGF ≌△DHG ，∴EF=FG=GH=HE ，∠EFB=∠HEA ， ∴四边形EFGH 为菱形，∵∠EFB+∠FEB=90°，∠EFB=∠HEA ， ∴∠FEB+∠HEA=90°，∴四边形EFGH 是正方形．24．∵CD 平分∠ACB ，DE ⊥BC ，DF ⊥AC ， ∴DE=DF ，∠DFC=90°，∠DEC=90°，又∵∠ACB=90°，∴四边形DECF 是矩形， ∵DE=DF ，∴矩形DECF 是正方形．25．∵矩形的ABCD 的外角都是直角，HE ，EF 都是外角平分线，∴∠BAE=∠ABE=45°． ∴∠E=90°．同理，∠F=∠G=90°． ∴四边形EFGH 为矩形．∵AD=BC ，∠HAD=∠HDA=∠FBC=∠FCB=45°， ∴△ADH ≌△BCF （AAS ）． ∴AH=BF ．又∵∠EAB=∠EBA ， ∴AE=BE ．∴AE+AH=EB+BF ，即EH=EF ． ∴矩形EFGH 是正方形．26．四边形ABCD 满足AC=BD ，AC ⊥BD 时，四边形EFGH 为正方形．理由如下：∵E 、F 、G 、H 分别是四边形ABCD 的边AB 、BC 、CD 、AD 的中点，∴EF ∥AC ，且EF=AC ， EH ∥BD ，且EH=BD ，∵四边形EFGH 是正方形， ∴EF=EH ，EF ⊥EH ， ∴AC=BD ，AC ⊥BD ，∴四边形ABCD 满足对角线互相垂直且相等时，四边形EFGH 是正方形．..即四边形ABCD 满足AC=BD ，AC ⊥BD 时，四边形EFGH 为正方形．27．本题答案不唯一，以下是其中两种解法：（1）添加条件AB ∥DC ，可得出该四边形是矩形；理由：∵AB ∥DC ，AB=DC ， ∴四边形ABCD 是平行四边形． ∵AC=BD ，∴四边形ABCD 是矩形．（2）添加条件AC 垂直平分BD ，那么该四边形是正方形．理由：∵AC 垂直平分BD ， ∴AB=AD ，BC=CD ． ∵AB=DC ，∴AB=AD=BC=DC ．∴四边形ABCD 是菱形． ∵AC 垂直BD ，∴四边形ABCD 是正方形．28．（1）∵四边形ABCD 是平行四边形， ∴AO=CO=AC ，∵EA=EC ， ∴EO ⊥AC ，即BD ⊥AC ，∴平行四边形ABCD 是菱形；（2）∵∠1=∠EAD+∠AED ，∠DAC=∠EAD+∠AED ， ∴∠1=∠DAC ， ∴AO=DO ，∵四边形ABCD 是菱形， ∴AC=2AO ，DB=2DO ， ∴AC=BD ，∴四边形ABCD 是正方形．29．（1）∵DE ∥AC ，DF ∥AB ， ∴四边形AEDF 是平行四边形，又∵∠BAC=90°，∴四边形AEDF 是矩形；（2）∵DE ∥AC ，DF ∥AB ，∴∠ADE=∠DAF ，四边形AEDF 是平行四边形，又∵AD 是△ABC 的角平分线， ∴∠DAE=∠DAF ， ∴∠ADE=∠DAE ， ∴AE=DE ，∴▱AEDF 是菱形；（3）由（1）知四边形AEDF 是矩形，由（2）知四边形AEDF 是菱形，所以四边形AEDF 是正方形． 30．（1）四边形ADEF 是平行四边形． ∵等边三角形BCE 和等边三角形ABD ， ∴BE=BC ，BD=BA ．又∵∠DBE=60°﹣∠ABE ，∠ABC=60°﹣∠ABE ， ∴∠DBE=∠ABC ．在△BDE 和△BCA 中，∴△BDE ≌△BCA ．（2分） ∴DE=AC ．∵在等边三角形ACF 中，AC=AF ， ∴DE=AF ．同理DA=EF ．∴四边形ADEF 是平行四边形．（2）当∠BAC=150°时，四边形ADEF 是矩形．（5分）理由：∵∠DAF=360°﹣∠DAB ﹣∠BAC ﹣∠CAF=90°， ∴▱ADEF 是矩形．（3）当AB=AC ，或∠ABC=∠ACB=15°时，四边形ADEF 是菱形．（6分）理由：∵AB=AC ， ∴AD=AF ，∴▱ADEF 是菱形．（4）当∠BAC=150°且AB=AC ，或∠ABC=∠ACB=15°时，四边形ADEF 是正方形．（7分）（5）当∠BAC=60°时，以A ，D ，E ，F 为顶点的四边形不存在．（8分）。

正方形判定练习题附答案

正方形的判定一．选择题(共８小题)1.已知四边形AＢＣＤ是平行四边形,再从①AB=ＢC,②∠ABC=９0°,③AC＝BD，④AC⊥BD四个条件中，选两个作为补充条件后，使得四边形ABCＤ是正方形,现有下列四种选法，其中错误的是()A．选①②ﻩＢ.选②③ C.选①③ D.选②④2．下列说法中,正确的是（)A.相等的角一定是对顶角B．四个角都相等的四边形一定是正方形C.平行四边形的对角线互相平分D．矩形的对角线一定垂直3.下列命题中是假命题的是（）A.一组对边平行且相等的四边形是平行四边形Ｂ.一组对边相等且有一个角是直角的四边形是矩形C.一组邻边相等的平行四边形是菱形Ｄ．一组邻边相等的矩形是正方形４.已知四边形ABＣＤ是平行四边形，下列结论中不正确的有（）①当AＢ=BＣ时,它是菱形；②当AＣ⊥BD时,它是菱形；③当∠ABC=90°时，它是矩形;④当AC=BD时，它是正方形.A．1组ﻩB．2组C．3组ﻩ D.4组5.四边形ABCD的对角线AC=BD,ＡＣ⊥BＤ,分别过A、B、Ｃ、D作对角线的平行线，所成的四边形EＦＭN是( ）A．正方形ﻩＢ.菱形ﻩＣ．矩形ﻩ D.任意四边形６.如果要证明平行四边形ABＣD为正方形,那么我们需要在四边形ABCD是平行四边形的基础上,进一步证明（）A.AB＝ＡＤ且AC⊥ＢD B．AＢ=AD且AC=BD C.∠A=∠B且AＣ=BDﻩD．AC和ＢD互相垂直平分7.下列命题中，真命题是()A.对角线相等的四边形是矩形Ｂ．对角线互相垂直的四边形是菱形C．对角线互相平分的四边形是平行四边形D．对角线互相垂直平分的四边形是正方形８．如图,在△AＢC中,∠ＡCＢ=９0°，BC的垂直平分线EＦ交BＣ于点Ｄ，交AB于点E，且ＢE=BＦ，添加一个条件,仍不能证明四边形ＢEＣF为正方形的是（）A.BＣ＝ＡＣﻩB．CＦ⊥BFﻩC.ＢD=DF Ｄ．AC=BＦ二.填空题(共6小题）９．能使平行四边形AＢCＤ为正方形的条件是_____＿___ （填上一个符合题目要求的条件即可）．１0.如图,在Ｒｔ△AＢC中,∠C=９0°，ＤE垂直平分ＡC，DＦ⊥BC，当△ＡＢＣ满足条件_＿_____＿_时，四边形DECF是正方形．（要求:①不再添加任何辅助线，②只需填一个符合要求的条件）11．如图，菱形ＡＢCD的对角线相交于点O，请你添加一个条件：＿_____＿＿＿,使得该菱形为正方形．12．如图，在四边形AＢＣD中,AB＝ＢC=CD=DＡ,对角线AC与BD相交于点Ｏ,若不增加任何字母与辅助线，要使四边形ABＣD是正方形，则还需增加一个条件是__＿_＿_＿__.13．已知四边形ABＣD中,∠Ａ=∠Ｂ=∠C=９0°,若添加一个条件即可判定该四边形是正方形,那么这个条件可以是____＿_＿__ ．1４．要使一个菱形成为正方形,需添加一个条件为_＿___＿___．三.解答题(共８小题)15．已知：如图，△AＢC中,∠AＢＣ=9０°，ＢD是∠ＡＢC的平分线,DＥ⊥AB于点E,ＤＦ⊥BC于点F．求证：四边形ＤEBF是正方形．16.如图，在四边形ABＣＤ中，ＡB=BC,对角线BD平分∠ABC，P是ＢD上一点，过点P作PM⊥AD，PN⊥CD，垂足分别为M,N.(1)求证:∠AＤＢ=∠CDB；(2)若∠AＤC=90°,求证:四边形ＭPND是正方形．1７．如图,在Rt△ＡBC中，∠ＡCB＝90°，过点C的直线ＭN∥AB,D为AB边上一点，过点Ｄ作DE⊥BC,交直线MN于E，垂足为F,连接ＣD、BE．(1)求证：CE=AD;(2）当D在AB中点时,四边形BＥCD是什么特殊四边形?说明你的理由；（３)若D为AＢ中点，则当∠A的大小满足什么条件时,四边形BＥＣＤ是正方形？请说明你的理由.18.如图，在△ABC中，点D、E分别是边AB、AC的中点，将△ADE绕点E旋转1８0°得到△CFE．（1）求证:四边形ADCF是平行四边形．（2)当△ＡBＣ满足什么条件时，四边形ADCＦ是正方形？请说明理由．19.如图，分别以线段AB的两个端点为圆心，大于AＢ的长为半径作弧,两弧交于M、N两点,连接MN，交AB于点Ｄ、C是直线MN上任意一点，连接ＣA、CB,过点D作ＤＥ⊥AＣ于点E，ＤＦ⊥ＢＣ于点F.（1）求证:△AED≌△BFＤ；(２）若AB＝2,当CＤ的值为______＿__时,四边形DEＣF是正方形．２0.如图，ＡB是CＤ的垂直平分线,交CD于点Ｍ，过点M作ME⊥A C，MF⊥ＡD,垂足分别为E、F.（１)求证:∠CＡB=∠DAＢ;（2）若∠CＡＤ=90°,求证:四边形ＡEMＦ是正方形.21.如图,△ＡBＣ中,点O是边AC上一个动点，过O作直线MＮ∥BC，设MＮ交∠ＡＣB的平分线于点E，交∠ＡCＢ的外角平分线于点F.（1)探究:线段OE与OF的数量关系并加以证明；（2）当点O运动到何处时,且△ABC满足什么条件时，四边形AＥCＦ是正方形?(3)当点O在边AC上运动时,四边形BCFＥ____＿___＿是菱形吗？（填“可能”或“不可能”)22．已知：如图，△ABＣ中，点O是AＣ上的一动点，过点O作直线MN∥ＡＣ，设ＭN交∠BCA的平分线于点Ｅ，交∠BＣA的外角∠ACG的平分线于点F，连接ＡE、AF．（1）求证:∠ＥCF=90°;（2）当点O运动到何处时,四边形ＡECF是矩形？请说明理由；（3)在(２）的条件下,△ABＣ应该满足条件：_＿_＿_____，就能使矩形AECＦ变为正方形.(直接添加条件，无需证明)正方形的判定参考答案与试题解析一.选择题（共8小题）1．已知四边形AＢCD是平行四边形，再从①ＡB=BC，②∠AＢC=9０°，③AC=BＤ，④AＣ⊥BD四个条件中，选两个作为补充条件后,使得四边形AＢCD是正方形,现有下列四种选法,其中错误的是( ）A. 选①②ﻩB．选②③ﻩＣ．选①③ﻩD. 选②④考点：ﻩ正方形的判定;平行四边形的性质.分析:ﻩ要判定是正方形，则需能判定它既是菱形又是矩形．解答: 解：Ａ、由①得有一组邻边相等的平行四边形是菱形,由②得有一个角是直角的平行四边形是矩形，所以平行四边形ABCD是正方形，正确，故本选项不符合题意;B、由②得有一个角是直角的平行四边形是矩形,由③得对角线相等的平行四边形是矩形,所以不能得出平行四边形ABCD是正方形,错误,故本选项符合题意；C、由①得有一组邻边相等的平行四边形是菱形，由③得对角线相等的平行四边形是矩形，所以平行四边形ABCD 是正方形,正确，故本选项不符合题意；Ｄ、由②得有一个角是直角的平行四边形是矩形,由④得对角线互相垂直的平行四边形是菱形，所以平行四边形ＡBCD是正方形，正确,故本选项不符合题意.故选:B.点评：ﻩ本题考查了正方形的判定方法:①先判定四边形是矩形,再判定这个矩形有一组邻边相等；②先判定四边形是菱形,再判定这个矩形有一个角为直角.③还可以先判定四边形是平行四边形,再用1或2进行判定.2.下列说法中，正确的是（）Ａ．相等的角一定是对顶角B. 四个角都相等的四边形一定是正方形C．ﻩ平行四边形的对角线互相平分D.ﻩ矩形的对角线一定垂直考点：正方形的判定;对顶角、邻补角；平行四边形的性质；矩形的性质．分析：根据对顶角的定义，正方形的判定,平行四边形的性质,矩形的性质对各选项分析判断利用排除法求解.解答：ﻩ解:A、相等的角一定是对顶角错误,例如，角平分线分成的两个角相等，但不是对顶角，故本选项错误；Ｂ、四个角都相等的四边形一定是矩形,不一定是正方形，故本选项错误；C、平行四边形的对角线互相平分正确,故本选项正确；D、矩形的对角线一定相等，但不一定垂直，故本选项错误．故选:C．点评:ﻩ本题考查了正方形的判定，平行四边形的性质，矩形的性质,对顶角的定义,熟记各性质与判定方法是解题的关键．３.下列命题中是假命题的是( )A．ﻩ一组对边平行且相等的四边形是平行四边形B. 一组对边相等且有一个角是直角的四边形是矩形C.ﻩ一组邻边相等的平行四边形是菱形D．一组邻边相等的矩形是正方形考点：正方形的判定；平行四边形的判定;菱形的判定；矩形的判定.专题：证明题．分析: 做题时首先熟悉各种四边形的判定方法，然后作答．解答:ﻩ解:A、一组对边平行且相等的四边形是平行四边形,(平行四边形判定定理）；正确.B、一组对边相等且有一个角是直角的四边形是矩形，不一定是矩形,还可能是不规则四边形，错误.C、一组邻边相等的平行四边形是菱形，正确；D、一组邻边相等的矩形是正方形，正确．故选B．点评：ﻩ本题主要考查各种四边形的判定,基础题要细心．4.已知四边形ABCD是平行四边形，下列结论中不正确的有(）①当ＡＢ=BC时,它是菱形;②当AC⊥BD时，它是菱形；③当∠ＡBC=90°时,它是矩形;④当AC=BＤ时,它是正方形.A．ﻩ1组B．2组C．3组Ｄ.ﻩ4组考点：正方形的判定;平行四边形的性质；菱形的判定;矩形的判定.分析: 根据邻边相等的平行四边形是菱形可判断①正确;根据所给条件可以证出邻边相等，可判断②正确;根据有一个角是直角的平行四边形是矩形可判断③正确；根据对角线相等的平行四边形是矩形可以判断出④错误.解答: 解:①根据邻边相等的平行四边形是菱形可知：四边形ABCD是平行四边形，当ＡB=BC时,它是菱形正确;②∵四边形ＡBCＤ是平行四边形,∴BO=OD,∵AＣ⊥BD，∴ＡＢ2＝BO2+AO２，AＤ2=DO2+AO2,∴AB=ＡＤ，∴四边形ABCＤ是菱形,故②正确;③根据有一个角是直角的平行四边形是矩形可知③正确；④根据对角线相等的平行四边形是矩形可知当AC=BD时,它是矩形，不是正方形，故④错误；故不正确的有1个．故选：A．点评：此题主要考查了菱形的判定、矩形的判定、正方形的判定,关键是熟练掌握三种特殊平行四边形的判定定理．5.四边形ABCＤ的对角线AＣ=BD，ＡＣ⊥ＢD，分别过A、B、C、D作对角线的平行线，所成的四边形EＦMN 是( ）A．ﻩ正方形Ｂ.菱形Ｃ.矩形ﻩD. 任意四边形考点：ﻩ正方形的判定.分析：根据平行线的性质和判定得出∠NAO=∠ＡOD＝∠Ｎ=９0°,EN=NM=ＦM＝ＥF,进而判断即可．解答：ﻩ证明:如图所示:∵分别过A、B、C、D作对角线的平行线，∴AＣ∥MＮ∥EＦ，EＮ∥BD∥MＦ,∵对角线AC=BD，AＣ⊥BD,∴∠NAO＝∠AOD=∠N=90°,EN=NM=FＭ＝EF，∴四边形EＦMN是正方形．故选:A.点评：此题主要考查了正方形的判定以及平行线的性质和判定等知识,熟练掌握正方形的判定定理是解题关键．6.如果要证明平行四边形ABCD为正方形，那么我们需要在四边形ＡBCD是平行四边形的基础上，进一步证明(）A．ﻩAB=AD且AC⊥BD B.ﻩAB=AD且ＡＣ=BＤ C.ﻩ∠A=∠Ｂ且AC=BＤD． AC和ＢＤ互相垂直平分考点: 正方形的判定．分析：ﻩ根据正方形的判定对各个选项进行分析从而得到最后的答案.解答：解：A、根据有一组邻边相等的平行四边形是菱形,或者对角线互相垂直的平行四边形是菱形，所以不能判断平行四边形ABＣD是正方形;B、根据对角线互相垂直的平行四边形是菱形,对角线相等的平行四边形为矩形,所以能判断四边形ABＣＤ是正方形；C、一组邻角相等的平行四边形是矩形,对角线相等的平行四边形也是矩形,即只能证明四边形AＢCD是矩形，不能判断四边形ABCＤ是正方形;D、对角线互相垂直的平行四边形是菱形，对角线互相平分的四边形是平行四边形,所以不能判断四边形ＡBCD是正方形．故选B．点评:ﻩ本题是考查正方形的判别方法，判别一个四边形为正方形主要根据正方形的概念,途经有两种：①先说明它是矩形,再说明有一组邻边相等;②先说明它是菱形，再说明它有一个角为直角．7．下列命题中，真命题是（）A. 对角线相等的四边形是矩形B．ﻩ对角线互相垂直的四边形是菱形C.ﻩ对角线互相平分的四边形是平行四边形D．对角线互相垂直平分的四边形是正方形考点：ﻩ正方形的判定；平行四边形的判定；菱形的判定;矩形的判定；命题与定理．分析：Ａ、根据矩形的定义作出判断；B、根据菱形的性质作出判断;C、根据平行四边形的判定定理作出判断；Ｄ、根据正方形的判定定理作出判断．解答: 解:Ａ、两条对角线相等且相互平分的四边形为矩形;故本选项错误;B、对角线互相垂直的平行四边形是菱形;故本选项错误；C、对角线互相平分的四边形是平行四边形；故本选项正确；D、对角线互相垂直平分且相等的四边形是正方形；故本选项错误;故选Ｃ．点评: 本题综合考查了正方形、矩形、菱形及平行四边形的判定.解答此题时，必须理清矩形、正方形、菱形与平行四边形间的关系.8.如图,在△ＡＢC中，∠ACB=90°，BC的垂直平分线ＥＦ交ＢC于点D,交AＢ于点E，且BE＝ＢF，添加一个条件，仍不能证明四边形BＥCＦ为正方形的是（)A．ＢC＝ACﻩB.ＣF⊥BFﻩC．BD＝DFﻩD.ﻩAC=BF考点: 正方形的判定;线段垂直平分线的性质.分析: 根据中垂线的性质:中垂线上的点到线段两个端点的距离相等，有BＥ=ＥC,ＢF=FＣ进而得出四边形BＥCF是菱形;由菱形的性质知,以及菱形与正方形的关系，进而分别分析得出即可．解答：ﻩ解:∵EF垂直平分BＣ，∴ＢE=EC,ＢF=CF，∵BF=BE，∴BＥ=EC=CＦ=BF,∴四边形ＢECＦ是菱形；当BC=AＣ时，∵∠ACB=90°,则∠A＝45°时,菱形BＥCF是正方形．∵∠A=４5°,∠AＣＢ=90°，∴∠ＥＢC=４5°∴∠ＥBF=2∠ＥBC=2×4５°=9０°∴菱形BEＣＦ是正方形.故选项A正确，但不符合题意;当CF⊥BＦ时，利用正方形的判定得出,菱形BECF是正方形,故选项B正确,但不符合题意；当BＤ=DＦ时,利用正方形的判定得出，菱形BＥCＦ是正方形，故选项C正确，但不符合题意;当AＣ=BF时,无法得出菱形BEＣF是正方形，故选项D错误，符合题意.故选:D．点评：ﻩ本题考查了菱形的判定和性质及中垂线的性质、直角三角形的性质、正方形的判定等知识,熟练掌握正方形的相关的定理是解题关键．二.填空题(共6小题）9.能使平行四边形ABCＤ为正方形的条件是AC＝ＢD且ＡC⊥BＤ(填上一个符合题目要求的条件即可).考点：ﻩ正方形的判定；平行四边形的性质.专题:ﻩ开放型.分析: 对角线互相垂直的平行四边形是菱形,对角线相等的平行四边形是矩形，矩形和菱形的结合体是正方形．解答：ﻩ解：可添加对角线相等且对角线垂直或对角线相等，且一组邻边相等；或对角线垂直,有一个内角是90°．答案不唯一，此处填:AＣ=ＢD且AC⊥BD．点评:ﻩ本题考查正方形的判定,需注意它是菱形和矩形的结合.10．如图,在Ｒt△ＡBC中,∠Ｃ=90°,DE垂直平分AC,DＦ⊥BC，当△ABＣ满足条件ＡC＝BＣ时,四边形DECF 是正方形．（要求：①不再添加任何辅助线，②只需填一个符合要求的条件）考点：正方形的判定．专题: 计算题;开放型．分析: 由已知可得四边形的四个角都为直角，因此再有四边相等即是正方形添加条件．此题可从四边形DE ＣＦ是正方形推出．解答：解:设AC=BC，即△AＢC为等腰直角三角形,∵∠C=90°,DＥ垂直平分ＡC，DF⊥BＣ，∴∠C＝∠ＣED=∠EＤF＝∠DFC=9０°,DＦ＝AＣ=ＣE,DE=BC＝CF,∴DF＝ＣＥ=DＥ＝CＦ,∴四边形DECF是正方形，故答案为:AC＝BＣ．点评: 此题考查的知识点是正方形的判定，解题的关键是可从四边形DECF是正方形推出△ABC满足的条件．11．如图,菱形ABCD的对角线相交于点Ｏ，请你添加一个条件: ＡC＝ＢD或AB⊥BC，使得该菱形为正方形.考点：正方形的判定；菱形的性质．专题：ﻩ压轴题．分析:ﻩ根据正方形判定定理进行分析.解答：解:根据对角线相等的菱形是正方形,可添加:ＡＣ＝BD;根据有一个角是直角的菱形是正方形,可添加的：ＡＢ⊥ＢC；故添加的条件为：ＡC=BD或ＡB⊥BC．点评：本题答案不唯一，根据菱形与正方形的关系求解．１2．如图,在四边形ABCD中，AＢ＝BＣ=CＤ=DA,对角线AC与ＢＤ相交于点O，若不增加任何字母与辅助线，要使四边形ABＣD是正方形，则还需增加一个条件是AC＝BD或AB⊥BC .考点：ﻩ正方形的判定;菱形的判定.专题: 开放型．分析:ﻩ根据菱形的判定定理及正方形的判定定理即可解答．解答：ﻩ解:∵在四边形AＢCD中，AB＝BC=CD=DＡ∴四边形ABCD是菱形∴要使四边形ＡBCD是正方形,则还需增加一个条件是:ＡC=BＤ或ＡB⊥BC．点评：解答此题的关键是熟练掌握正方形的判定定理，即有一个角是直角的菱形是正方形.1３.已知四边形ABCD中，∠A=∠B=∠C=90°，若添加一个条件即可判定该四边形是正方形，那么这个条件可以是AB=AD或ＡC⊥ＢＤ等．考点: 正方形的判定;矩形的判定与性质.专题: 开放型.分析:ﻩ由已知可得四边形AＢCD是矩形,则可根据有一组邻边相等或对角线互相垂直的矩形是正方形添加条件．解答:ﻩ解：由∠A=∠B=∠Ｃ=90°可知四边形AＢCD是矩形，根据根据有一组邻边相等或对角线互相垂直的矩形是正方形,得到应该添加的条件为:AB=AD或AC⊥BD等．故答案为:ＡB=ＡＤ或AC⊥BD等．点评：本题是考查正方形的判别方法,判别一个四边形为正方形主要根据正方形的概念,途经有两种:①先说明它是矩形,再说明有一组邻边相等；②先说明它是菱形,再说明它有一个角为直角.１4.要使一个菱形成为正方形，需添加一个条件为有一个角是直角或对角线相等.考点：正方形的判定；菱形的性质.专题：ﻩ开放型．分析:ﻩ根据菱形的性质及正方形的判定进行分析,从而得到最后答案.解答：解：要使一个菱形成为正方形,需添加一个条件为:有一个角是直角或对角线相等．点评:ﻩ解答此题的关键是熟练掌握正方形的判定定理:（1)有一个角是直角的菱形是正方形;(2）对角线相等的菱形是正方形．三．解答题（共8小题）15.已知:如图，△ABC中,∠ABC=9０°，BD是∠ABC的平分线,DE⊥ＡB于点E，DＦ⊥BＣ于点F．求证:四边形DEBF是正方形．考点：正方形的判定.专题：ﻩ证明题．分析：ﻩ由ＤE⊥AＢ,ＤF⊥BC，∠ABC=9０°,先证明四边形ＤEＢF是矩形，再由BD是∠ABC的平分线,ＤE⊥AB 于点E，DF⊥BC于点F得出DE=DF判定四边形DＥBＦ是正方形.解答: 解：∵DE⊥AB，ＤＦ⊥BＣ，∴∠ＤEＢ=∠DＦB=90°,又∵∠ABC=90°,∴四边形BEDF为矩形,∵BＤ是∠ＡBC的平分线,且ＤＥ⊥ＡB,ＤＦ⊥BC,∴DE＝DＦ，∴矩形ＢEDF为正方形．点评：本题考查正方形的判定、角平分线的性质和矩形的判定．要注意判定一个四边形是正方形,必须先证明这个四边形为矩形或菱形．16．如图,在四边形ABCＤ中，AB=BC，对角线ＢD平分∠ABC，P是ＢＤ上一点，过点P作PＭ⊥AD，ＰN⊥CD,垂足分别为M,N.（１）求证:∠AＤB=∠CＤＢ;（2)若∠ADC＝９０°，求证：四边形MＰＮＤ是正方形.考点：正方形的判定;全等三角形的判定与性质．专题: 证明题．分析: （1)根据角平分线的性质和全等三角形的判定方法证明△ＡBD≌△ＣBD，由全等三角形的性质即可得到：∠ＡDB=∠CDB;(2)若∠ＡDC=９0°,由(１)中的条件可得四边形MPNＤ是矩形，再根据两边相等的四边形是正方形即可证明四边形ＭPNＤ是正方形.解答:ﻩ证明：（1）∵对角线BD平分∠ABC，∴∠ABD=∠CBＤ，在△ＡBD和△CBＤ中，,∴△ＡBD≌△ＣBD（SAS）,∴∠ADB=∠CDB;（2)∵PM⊥AD,ＰN⊥ＣＤ，∴∠PMD=∠ＰND=90°,∵∠ＡDC＝９０°,∴四边形MＰNＤ是矩形,∵∠AＤB=∠CDB，∴∠AＤB=45°∴PM=ＭD，∴四边形ＭPＮD是正方形.点评: 本题考查了全等三角形的判定和性质、角平分线的性质、矩形的判定和性质以及正方形的判定,解题的关键是熟记各种几何图形的性质和判定.17．如图,在Rt△ABC中，∠ＡCB=90°，过点C的直线MN∥ＡＢ，D为AB边上一点,过点D作DE⊥BＣ，交直线MN于Ｅ，垂足为F,连接CＤ、BE.(1)求证:CE=AD；（2)当D在AB中点时，四边形ＢECD是什么特殊四边形？说明你的理由；(3）若Ｄ为AB中点，则当∠A的大小满足什么条件时,四边形BECD是正方形？请说明你的理由.考点：ﻩ正方形的判定；平行四边形的判定与性质；菱形的判定.专题：几何综合题．分析: （１）先求出四边形ADＥＣ是平行四边形，根据平行四边形的性质推出即可;（2)求出四边形BECD是平行四边形，求出ＣD＝BD，根据菱形的判定推出即可;（3)求出∠CDＢ=９0°，再根据正方形的判定推出即可．解答：(1)证明：∵DＥ⊥BC,∴∠ＤFB=90°,∵∠ACB＝90°,∴∠ACB＝∠DFＢ,∴ＡＣ∥ＤE，∵MN∥AＢ,即CE∥AＤ，∴四边形ADＥC是平行四边形，∴CE=AＤ；（２)解:四边形BECD是菱形，理由是：∵D为AＢ中点,∴AD＝BD,∵CE＝ＡＤ，∴BD＝CE,∵BD∥CＥ，∴四边形ＢＥＣＤ是平行四边形,∵∠ＡCB=9０°,Ｄ为AＢ中点，∴CD=ＢD，∴四边形BECD是菱形；(3)当∠A=45°时，四边形BECＤ是正方形，理由是：解:∵∠ACB=90°,∠A＝４5°,∴∠ABＣ=∠A＝4５°，∴AC=BC，∵Ｄ为BA中点，∴CD⊥ＡＢ，∴∠ＣDB=90°,∵四边形BEＣD是菱形,∴四边形ＢECD是正方形,即当∠Ａ=４5°时，四边形BECD是正方形．点评:ﻩ本题考查了正方形的判定、平行四边形的性质和判定，菱形的判定，直角三角形的性质的应用，主要考查学生运用定理进行推理的能力.1８．如图,在△ABＣ中，点Ｄ、E分别是边AB、AC的中点,将△ＡＤE绕点E旋转180°得到△CFE.（1）求证：四边形ADCF是平行四边形.(2)当△ABC满足什么条件时，四边形ADCF是正方形?请说明理由.考点: 正方形的判定；平行四边形的判定.分析：ﻩ(1)利用旋转的性质得出点A、E、C三点共线，点D、E、F三点共线，且AE=CD,DＥ=FE,即可得出答案；（2)首先得出CＤ⊥AB，即∠ADC=９0°，由（1)知,四边形ADCF是平行四边形,故四边形ADＣF是矩形.进而求出CD＝AD即可得出答案.解答: (1）证明:∵△CFE是由△ADＥ绕点E旋转180°得到,∴点A、Ｅ、C三点共线,点D、E、F三点共线，且AＥ=CＥ,DE=ＦＥ，故四边形ＡＤCF是平行四边形.（2）解:当∠ACB=90°,ＡC=BＣ时,四边形ＡＤCＦ是正方形．理由如下：在△ABC中,∵AC=BC，ＡD=BＤ,∴ＣD⊥ＡB,即∠ADC=90°．而由(1)知,四边形ADＣF是平行四边形，∴四边形ＡＤCF是矩形．又∵∠ＡＣB=90°,∴,故四边形ADＣF是正方形.点评: 此题主要考查了平行四边形的判定以及正方形的判定等知识，得出四边形AＤCF是矩形是解题关键.19.如图，分别以线段ＡB的两个端点为圆心,大于AB的长为半径作弧，两弧交于M、N两点，连接MN,交AB于点D、Ｃ是直线ＭN上任意一点,连接CA、CB,过点D作DE⊥ＡC于点Ｅ,DＦ⊥BＣ于点F．（１）求证：△ＡＥD≌△BＦD;（2）若AB=2,当CＤ的值为1时，四边形DECＦ是正方形．考点:ﻩ正方形的判定;全等三角形的判定．分析：（1）先由作图知MN是线段AB的垂直平分线，根据垂直平分线的性质得出ＣA=CB,AD＝BＤ,由等边对等角得到∠Ａ=∠Ｂ,然后利用ＡＡS即可证明△ＡＥD≌△ＢFＤ；（2)若AＢ=２，当CD的值为１时,四边形DEＣF是正方形.先由CD=AD=BＤ=１,MＮ⊥AB，得出△ACD与△BCD 都是等腰直角三角形，则∠ACD=∠BCD=45°,∠ECF＝9０°，根据有三个角是直角的四边形是矩形证明四边形DEＣF是矩形,再由等角对等边得出ＥD=CE，从而得出矩形DECF是正方形．解答：ﻩ(1)证明:由作图知，ＭN是线段AB的垂直平分线，∵C是直线ＭN上任意一点,MN交AB于点D，∴CA=CＢ,ＡD=BD，∴∠A=∠B．在△AED与△BFＤ中，，∴△AEＤ≌△BFD（AAS）;（2)解：若AＢ=2,当CD的值为1时,四边形DEＣF是正方形.理由如下：∵AＢ=2，∴AD=BD=AB=1．∵ＣD=AD＝BD=1，MＮ⊥ＡB，∴△ＡCD与△ＢCD都是等腰直角三角形，∴∠ACD＝∠BＣD=45°，∴∠ＥCF=∠ＡCＤ＋∠BCＤ=90°,∵∠DEC＝∠ＤＦＣ=90°,∴四边形DECF是矩形，∠CDE=90°﹣45°=45°，∴∠EＣD=∠CDＥ＝45°,∴ED=ＣＥ,∴矩形DＥＣＦ是正方形．故答案为1.点评:ﻩ本题考查了线段垂直平分线的性质，全等三角形的判定,正方形的判定，等腰直角三角形的判定与性质,难度适中．20.如图,AB是CD的垂直平分线，交CD于点Ｍ，过点M作ME⊥A C,MF⊥ＡD,垂足分别为E、F．（１）求证：∠CＡB=∠DAB;(２）若∠CAD=9０°,求证:四边形ＡEMF是正方形．考点: 正方形的判定;线段垂直平分线的性质;等腰三角形的判定与性质.专题: 证明题.分析: （1）根据AＢ是CD的垂直平分线，得到AC=AD,然后利用三线合一的性质得到∠CAＢ=∠ＤＡB 即可；(2）首先判定四边形AEMF是矩形,然后证得ME=MF,利用邻边相等的矩形ＡEMＦ是正方形进行判定即可．解答: (1)证明：∵AＢ是ＣＤ的垂直平分线，∴ＡC=AD，又∵AＢ⊥CD∴∠CAB=∠DＡB（等腰三角形的三线合一);(2）证明：∵ME⊥A C,MF⊥AD，∠ＣAＤ=90°，即∠CAD＝∠ＡＥM＝∠AFM=90°,∴四边形ＡEMF是矩形,又∵∠CAB=∠ＤAＢ,MＥ⊥AＣ，ＭＦ⊥AD,∴ＭＥ=ＭF,∴矩形AEMＦ是正方形．点评:ﻩ本题考查正方形的判定，线段的垂直平分线的性质及等腰三角形的判定与性质的知识，综合性较强,难度不大．２１.如图，△ABＣ中,点Ｏ是边AC上一个动点，过O作直线MN∥BＣ，设MN交∠AＣB的平分线于点Ｅ,交∠ACB 的外角平分线于点F．(1）探究：线段OE与OF的数量关系并加以证明;（2）当点O运动到何处时,且△ABC满足什么条件时,四边形AＥＣF是正方形?（3）当点O在边AC上运动时,四边形ＢCFＥ不可能是菱形吗?(填“可能”或“不可能”)考点:ﻩ正方形的判定;菱形的判定．分析：（１）由直线MN∥ＢC，MＮ交∠BＣA的平分线于点E,交∠BCA的外角平分线于点F，易证得△OEC与△OFC是等腰三角形,则可证得ＯE=OF=OＣ；(2)正方形的判定问题,AＥCF若是正方形,则必有对角线OＡ＝OC，所以O为AC的中点，同样在△ABC中,当∠ＡCB=90°时,可满足其为正方形；（3)菱形的判定问题,若使菱形,则必有四条边相等，对角线互相垂直．解答：ﻩ解：（1)OE=ＯF．理由如下:∵CＥ是∠ＡCB的角平分线，∴∠ＡCE=∠BCE，又∵MN∥BC,∴∠NEC=∠ECB,∴∠NEＣ=∠ACE，∴OE=OC，∵OF是∠ＢCＡ的外角平分线，∴∠OCＦ=∠FCD，又∵MN∥BC，∴∠OＦC=∠ECD，∴∠OFＣ=∠CＯF,∴OF=OC，∴OE＝ＯF;（2)当点O运动到AC的中点,且△ABC满足∠AＣB为直角的直角三角形时,四边形ＡECＦ是正方形．理由如下: ∵当点O运动到AＣ的中点时,AＯ＝CO,又∵EO=FO,∴四边形AECＦ是平行四边形,∵ＦO=CO，∴AＯ=ＣO=EO=FO，∴AO+CＯ=ＥＯ+FO，即AC=EF,∴四边形ＡECF是矩形.已知MN∥BＣ,当∠ACB＝90°,则∠AOＦ＝∠COE=∠COF=∠AOE=9０°,∴AC⊥ＥＦ,∴四边形AECＦ是正方形；(３）不可能.理由如下:如图，∵CＥ平分∠ACB，ＣＦ平分∠ＡCD，∴∠ECＦ=∠AＣB＋∠ＡＣD=(∠AＣB+∠ACD）=9０°，若四边形ＢCFE是菱形,则BF⊥EC,但在△ＧFC中,不可能存在两个角为9０°,所以不存在其为菱形．故答案为不可能.点评:ﻩ本题考查了平行线的性质,角平分线的定义，等腰三角形的判定，正方形、菱形的判定，难度适中,注意掌握数形结合思想的应用．22.已知:如图，△ＡBC中,点O是AＣ上的一动点，过点Ｏ作直线MN∥AC，设MＮ交∠BCＡ的平分线于点Ｅ，交∠BCA的外角∠ＡCG的平分线于点F,连接ＡE、AF．(1）求证：∠ＥCＦ=90°；(2）当点O运动到何处时，四边形AECＦ是矩形？请说明理由;（３)在（2）的条件下,△ABＣ应该满足条件: ∠ACＢ为直角的直角三角形，就能使矩形AEＣＦ变为正方形．(直接添加条件,无需证明）考点：正方形的判定;等腰三角形的判定与性质;矩形的判定.分析：（1）由已知ＭN∥ＢC，CE、CF分别平分∠BＣO和∠GCＯ,可推出∠OEＣ=∠OCＥ，∠ＯFC＝∠OC Ｆ,所以得EO=CO=FＯ．（２)由（1)得出的EO＝CＯ=FO，点Ｏ运动到ＡC的中点时，则由ＥＯ=CO＝FO=AO,所以这时四边形AＥCF是矩形.（３)由已知和（２)得到的结论,点O运动到AＣ的中点时,且△ＡBC满足∠ACB为直角的直角三角形时，则推出四边形AＥＣＦ是矩形且对角线垂直,所以四边形AECF是正方形.解答:ﻩ（1)证明：∵CＥ平分∠BCO,CF平分∠DCO,∴∠OCE=∠ＢCE,∠OＣF＝∠DCF，∴∠ECＦ＝×180°=9０°;（2）解:当点O运动到ＡC的中点时，四边形ＡECF是矩形．理由如下:∵MＮ∥BC,∴∠ＯEC=∠BCE，∠OFＣ=∠DCF，又∵CE平分∠ＢCＯ，CＦ平分∠DCO,∴∠ＯＣE=∠BＣＥ，∠OCＦ＝∠DCF，∴∠OＣＥ＝∠ＯEC，∠OCF=∠OFC,∴ＥO=CＯ,FO=ＣO，∴OE＝OF；又∵当点O运动到AC的中点时，AO=CO，∴四边形ＡECＦ是平行四边形，∵∠ECF=９0°，∴四边形AECF是矩形；(3）解：当点O运动到AＣ的中点时，且△ＡBC满足∠ACB为直角的直角三角形时,四边形AECF是正方形．∵由（2）知，当点O运动到AC的中点时，四边形ＡＥＣF是矩形，已知MN∥ＢＣ,当∠ACB=90°,则∠AOF＝∠COＥ=∠COF=∠AＯE＝９0°,∴AC⊥EF，∴四边形AＥＣF是正方形.故答案为：∠ACB为直角的直角三角形.点评:ﻩ此题考查的是正方形和矩形的判定，角平分线的定义,平行线的性质,等腰三角形的判定等知识．解题的关键是由已知得出ＥO＝FO，确定（2）(3)的条件．。

正方形几何综合专题---40道题目(含答案)

01如图，在正方形ABCD中，点G在对角线BD上(不与点B，D 重合)，GE⊥DC于点E，GF⊥BC于点F，连接AG.(1)写出线段AG，GE，GF长度之间的等量关系，并说明理由；(2)若正方形ABCD的边长为1，∠AGF＝105°，求线段BG的长．解：(1)AG2＝GE2＋GF2；理由：如解图，连接CG，∵四边形ABCD是正方形，∴∠ADG＝∠CDG＝45°，AD＝CD，DG＝DG，∴△ADG≌△CDG，∴AG＝CG，又∵GE⊥DC，GF⊥BC，∠BCD＝90°，∴四边形CEGF是矩形，∴CF＝GE，在Rt△GFC中，由勾股定理得，CG2＝GF2＋CF2，∴AG2＝GE2＋GF2；(2)如解图，过点A作AM⊥BD于点M，∵GF⊥BC，∠ABG＝∠GBC＝45°，∴∠BAM＝∠BGF＝45°，∴△ABM，△BGF都是等腰直角三角形，∵AB＝1，∴AM＝BM＝2 2，∵∠AGF＝105°，∴∠AGM＝60°，∴tan60°＝AM GM，∴GM ＝66，∴BG ＝BM ＋GM ＝22＋66＝32＋66.02如图，正方形ABCD 中，AB ＝6，点E在边CD 上，且CD ＝3DE ．将△ADE 沿AE 对折至△AFE ，延长EF 交边BC 于点G ，连结AG 、CF ．下列结论：①△ABG ≌△AFG ；②BG ＝GC ；③AG ∥CF ；④S △FGC ＝3．其中正确结论的个数是( )A ．1B ．2C ．3D ．4A BCD FEG10题图考点：翻折变换（折叠问题）；全等三角形的判定与性质；勾股定理分析：根据翻折变换的性质和正方形的性质可证△ABG ≌△AFG ；在直角△ECG 中，根据勾股定理可证BG =GC ；通过证明∠AGB =∠AGF =∠GFC =∠GCF ，由平行线的判定可得AG ∥CF ；由于S △FGC =S △GCE ﹣S △FEC ，求得面积比较即可．解答：解：①正确．因为AB =AD =AF ，AG =AG ，∠B =∠AFG =90°，∴△ABG ≌△AFG ； ②正确．因为：EF =DE =13CD =2，设BG =FG =x ，则CG =6﹣2+42=（x +2）x ．在直角△ECG 中，根据勾股定理，得（6﹣x ）2，解得x =3．所以BG =3=6﹣3=GC ； ③正确．因为CG =BG =GF ，所以△FGC 是等腰三角形，∠GFC =∠GCF ．又∠AGB =∠AGF ，∠AGB +∠AGF =180°﹣∠FGC =∠GFC +∠GCF ，∴∠AGB =∠AGF =∠GFC =∠GCF ，∴AG ∥CF ； ④错误．过F 作FH ⊥DC ， ∵BC ⊥DH ， ∴FH ∥GC ，∴△EFH ∽△EGC ， ∴FH GC =EFEG， EF =DE =2，GF =3， ∴EG =5， ∴FH GC =EF EG =25， ∴S △FGC =S △GCE ﹣S △FEC =12×3×4﹣12×4×（25×3）=185≠3．故选C ．点评：本题综合性较强，考查了翻折变换的性质和正方形的性质，全等三角形的判定与性质，勾股定理，平行线的判定，三角形的面积计算，有一定的难度．ABCD FE G 10题03如图，在一方形ABCD中．E为对角线AC上一点，连接EB、ED，（1）求证：△BEC≌△DEC：（2）延长BE交AD于点F，若∠DEB=140°．求∠AFE 的度数．考点：正方形的性质；对顶角、邻补角；三角形内角和定理；全等三角形的判定与性质。

22.3正方形的性质习题(含详细的答案解析)

22.3正方形的性质习题解答一、选择题（共13小题）1、如图，△ABC是一个等腰直角三角形，DEFG是其内接正方形，H是正方形的对角线交点；那么，由图中的线段所构成的三角形中相互全等的三角形的对数为（）A、12B、13C、26D、302、（2006•大兴安岭）如图所示，E、F分别是正方形ABCD的边CD，AD上的点，且CE=DF，AE，BF相交于点O，下列结论①AE=BF；②AE⊥BF；③AO=OE；④S△AOB=S四边形DEOF中，错误的有（）A、1个B、2个C、3个D、4个3、如图，在正方形ABCD中，AB=4，E为CD上一动点，AE交BD于F，过F作FH⊥AE于H，过H作GH⊥BD于G，下列有四个结论：①AF=FH，②∠HAE=45°，③BD=2FG，④△CEH的周长为定值，其中正确的结论有（）A、①②③B、①②④C、①③④D、①②③④4、一个围棋盘由18×18个边长为1的正方形小方格组成，一块边长为1.5的正方形卡片放在棋盘上，被这块卡片覆盖了一部分或全部的小方格共有n个，则n的最大值是（）A、4B、6C、10D、125、如图，四边形ABCD是正方形，以CD为边作等边三角形CDE，BE与AC相交于点M，则∠AMD的度数是（）A、75°B、60°C、54°D、67.5°6、在平面直角坐标系中，称横、纵坐标均为整数的点为整点，如下图所示的正方形内（包括边界）整点的个数是（）A、13B、21C、17D、257、在同一平面上，正方形ABCD的四个顶点到直线l的距离只取四个值，其中一个值是另一个值的3倍，这样的直线l可以有（）A、4条B、8条C、12条D、16条8、如图，正方形ABCD的边长为1，E为AD中点，P为CE中点，F为BP中点，则F到BD的距离等于（）A、B、C、D、9、搬进新居后，小杰自己动手用彩塑纸做了一个如图所示的正方形的挂式小饰品ABCD，彩线BD、AN、CM将正方形ABCD分成六部分，其中M是AB的中点，N是BC的中点，AN与CM交于O点．已知正方形ABCD的面积为576cm2，则被分隔开的△CON的面积为（）A、96cm2B、48cm2C、24cm2D、以上都不对10、如图，正方形ABCD的对角线AC与BD相交于O点，在BD上截取BE=BC，连接CE，点P是CE上任意一点，PM⊥BD于M，PN⊥BC于N，若正方形ABCD的边长为1，则PM+PN=（）A、1B、C、D、1+11、顶点为A（6，6），B（﹣4，3），C（﹣1，﹣7），D（9，﹣4）的正方形在第一象限的面积是（）A、25B、36C、49D、3012、ABCD是边长为1的正方形，△BPC是等边三角形，则△BPD的面积为（）A、B、C、D、13、如图，正方形ABCD的面积为16，△ABE是等边三角形，点E在正方形ABCD内，在对角线BD上有一点P，使PC+PE的和最小，则这个最小值为（）A、4B、2C、2D、2二、填空题（共8小题）14、如图，所示，将五个边长都为1cm的正方形按如图所示摆放，其中点A、B、C、D分别是正方形对角线的交点、如果有n个这样大小的正方形这样摆放，则阴影面积的总和是_________cm2．15、如图，若正方体的边长为a，M是AB的中点，则图中阴影部分的面积为_________．16、如图，以矩形OABC的顶点O为原点，OA所在的直线为x轴，OC所在的直线为y轴，建立平面直角坐标系、已知OA=3，OC=2，点E是AB的中点，在OA上取一点D，将△BDA沿BD翻折，使点A落在BC边上的点F处，若在y轴上存在点P，且满足FE=FP，则P点坐标为_________．17、如图，边长为a的正方形ABCD和边长为b的正方形BEFG排放在一起，O1和O2分别是两个正方形的中心，则阴影部分的面积为_________，线段O1O2的长为_________．18、已知正方形纸片ABCD的面积为2007cm2．现将该纸片沿一条线段折叠（如图），使点D落在边BC上的点D′处，点A落在点A′处，A′D′与AB交于点E．则△BD′E的周长等于_________cm．19、已知正方形ABCD在直角坐标系内，点A（0，1），点B（0，0），则点C，D坐标分别为_________和_________．（只写一组）20、如图，在一个正方形被分成三十六个面积均为1的小正方形，点A与点B在两个格点上．在格点上存在点C，使△ABC的面积为2，则这样的点C有_________个．21、已知正方形内接于圆心角为90°，半径为10的扇形（即正方形的各顶点都在扇形上），则这个正方形的边长为_________．三、解答填空题（共6小题）22、如图，在正方形ABCD中，对角线AC与BD相交于点O，AF平分∠BAC，交BD于点F．（1）求证：；（2）点A1、点C1分别同时从A、C两点出发，以相同的速度运动相同的时间后同时停止，如图，A1F1平分∠BA1C1，交BD于点F1，过点F1作F1E⊥A1C1，垂足为E，请猜想EF1，AB与三者之间的数量关系，并证明你的猜想；（3）在（2）的条件下，当A1E1=6，C1E1=4时，则BD的长为_________．23、（2005•扬州）（1）计算：=_________；（2）已知：如图，点E是正方形ABCD的边CD上一点，点F是CB的延长线上一点，且EA⊥AF．求证：DE=BF．24、如图，点E、F分别在正方形ABCD的边DC、BC上，AG⊥EF，垂足为G，且AG=AB，则∠EAF=_________度．25、如图，正方形ABCD中，AB=，点E、F分别在BC、CD上，且∠BAE=30°，∠DAF=15度．（1）求证：DF+BE=EF；（2）则∠EFC的度数为_________度；（3）则△AEF的面积为_________．26、已知正方形ABCD的边长为4cm，E，F分别为边DC，BC上的点，BF=1cm，CE=2cm，BE，DF相交于点G，则四边形CEGF的面积为_________cm2．27、（2007•江苏）如图，正方形ABCD绕点A逆时针旋转n°后得到正方形AEFG，边EF与CD交于点O．（1）以图中已标有字母的点为端点连接两条线段（正方形的对角线除外），要求所连接的两条线段相交且互相垂直，并说明这两条线段互相垂直的理由；（2）若正方形的边长为2cm，重叠部分（四边形AEOD）的面积为，则旋转的角度n=_________度．答案与评分标准一、选择题（共13小题）1、如图，△ABC是一个等腰直角三角形，DEFG是其内接正方形，H是正方形的对角线交点；那么，由图中的线段所构成的三角形中相互全等的三角形的对数为（）A、12B、13C、26D、30考点：全等三角形的判定；等腰直角三角形；正方形的性质。

正方形练习题(含答案)

正方形知识点一：正方形的定义：有一组邻边相等且有一个角是直角的平行四边形叫做正方形。

知识点二：正方形的性质：1.正方形的四个角都是直角，四条边都相等；2.正方形的对角线相等，并且互相垂直平分，每条对角线平分一组对角；3.正方形既是轴对称图形也是中心对称图形。

知识点三：正方形的判定方法：1.正方形的定义：有一组邻边相等且有一个角是直角的平行四边形叫做正方形。

2.有一组邻边相等的矩形是正方形；3.有一个角是直角的菱形是正方形.练习题：1.菱形、矩形、正方形都具有的性质是（ C ）A ．对角线相等且互相平分B ．对角线相等且互相垂直平分C ．对角线互相平分D ．四条边相等，四个角相等2.如图, E 、F 分别是正方形ABCD 的边CD 、AD 上的点，且CE ＝DF ，AE 、BF 相交于点O ，下列结论①AE ＝BF ；②AE ⊥BF ；③AO ＝OE ；④AOB DEOF S S ∆=四边形中，错误的有（ A ） A ．1个 B ．2个 C ．3个 D ．4个3.如图，E 是正方形ABCD 内一点，如果△ABE 为等边三角形，那么∠DCE= 15 度． 4.如图，E 是正方形ABCD 的边BC 延长线上一点，且CE=AC ，AE 交CD 于点F ，则∠E= 22.5 度．5.如图，若P 是边长1的正方形ABCD 内一点且S △ABP =0.4，则S △DCP = 0.1 ．分析：过P 作EF ，使EF ∥BC ，则EF ⊥CD ，EF ⊥AB ，∴S △ABP =错误!未找到引用源。

AB•EP ，S △CDP =错误!未找到引用源。

CD•PF ，根据S △ABP +S △CDP =错误!未找到引用源。

6.如图，在菱形ABCD 中，∠BAD=80°，AB 的垂直平分线交对角线AC 于点F ，E 为垂足，连接DF ，则∠CDF 的度数= 60 度．7.如图，在边长为2的正方形ABCD 中，M 为边AD 的中点，延长MD 至点E ，使ME ＝MC ，以DE 为边作正方形DEFG ，点G 在边CD 上，则DG 的长为 5－18.如图，E F G H ，，，分别为正方形ABCD 的边AB ，BC ，CD ，DA 上的点，且13AE BF CG DH AB ====，则图中阴影部分的面积与正方形ABCD 的面积之比为 2/5 9.如图，菱形ABCD 中，∠B ＝60°，AB ＝2，E 、F 分别是BC 、CD 的中点，连接AE 、EF 、AF ，则△AEF 周长为 3310.如图，已知P 是正方形ABCD 对角线BD 上一点，且BP = BC ，则∠ACP 度数是 22.5度．11.已知正方形ABCD 的边长为1，连接AC ，BD ，CE 平分∠ACD 交BD 于点E ，则DE ＝ 2－ 1 .11.如图，点E 是正方形ABCD 的边AB 上任意一点，过点D 作DF DE ⊥交BC 的延长线于点F ．求证：DE DF =．证明：∵四边形ABCD 是正方形，∴ AD=CD ,∠A=∠DCF=900又∵DF ⊥DE ，∴∠1+∠3=∠2+∠3∴∠1=∠2在Rt △DAE 和Rt △DCE 中，∠1=∠2，AD=CD ，∠A=∠DCF∴Rt △DAE ≅Rt △DCE (ASA) ∴DE=DF ．第2题第3题第4题第5题第6题12.如图，已知平行四边形ABCD 中，对角线AC BD ，交于点O ，E 是BD 延长线上的点，且ACE △是等边三角形．（1）求证：四边形ABCD 是菱形；（2）若2AED EAD ∠=∠，求证：四边形ABCD 是正方形．证明：（1）四边形ABCD 是平行四边形，AO CO ∴=．又ACE Q △是等边三角形，EO AC ∴⊥，即DB AC ⊥． ∴平行四边形ABCD 是菱形；（2）ACE Q △是等边三角形，60AEC ∴∠=o ． EO AC ⊥，1302AEO AEC ∴∠=∠=o ．2AED EAD ∠=∠，15EAD ∴∠=o ．45ADO EAD AED ∴∠=∠+∠=o ．四边形ABCD 是菱形，290ADC ADO ∴∠=∠=o ，∴四边形ABCD 是正方形．13.如图，ABCD 是正方形，AE ∥DB ，BE ＝BD ，BE 交AD 于F ，试说明：ΔDEF 是腰三角形。

专题35 几何综合压轴题(40题)(原卷版)--2024年中考数学真题分类汇编

专题35几何综合压轴题（40题）一、解答题1．（2024·黑龙江大兴安岭地·中考真题）已知ABC 是等腰三角形，AB AC =，12MAN BAC ∠=∠，MAN ∠在BAC ∠的内部，点M 、N 在BC 上，点M 在点N 的左侧，探究线段BM NC MN 、、之间的数量关系．（1）如图①，当90BAC ∠=︒时，探究如下：由90BAC ∠=︒，AB AC =可知，将ACN △绕点A 顺时针旋转90︒，得到ABP ，则CN BP =且90PBM ∠=︒，连接PM ，易证AMP AMN △≌△，可得MP MN =，在Rt PBM △中，222BM BP MP +=，则有222BM NC MN +=．（2）当60BAC ∠=︒时，如图②：当120BAC ∠=︒时，如图③，分别写出线段BM NC MN 、、之间的数量关系，并选择图②或图③进行证明．2．（2024·四川广元·中考真题）小明从科普读物中了解到，光从真空射入介质发生折射时，入射角α的正弦值与折射角β的正弦值的比值sin sin αβ叫做介质的“绝对折射率”，简称“折射率”．它表示光在介质中传播时，介质对光作用的一种特征．(1)若光从真空射入某介质，入射角为α，折射角为β，且7cos 4α=30β=︒，求该介质的折射率；(2)现有一块与（1）中折射率相同的长方体介质，如图①所示，点A ，B ，C ，D 分别是长方体棱的中点，若光线经真空从矩形2121A D D A 对角线交点O 处射入，其折射光线恰好从点C 处射出．如图②，已知60α=︒，10cm CD =，求截面ABCD 的面积．3．（2024·内蒙古呼伦贝尔·中考真题）如图，在平行四边形ABCD 中，点F 在边AD 上，AB AF =，连接BF ，点O 为BF 的中点，AO 的延长线交边BC 于点E ，连接EE(1)求证：四边形ABEF 是菱形：(2)若平行四边形ABCD 的周长为22,1,120CE BAD =∠=︒，求AE 的长．4．（2024·四川甘孜·中考真题）如图，AB 为⊙O 的弦，C 为 AB 的中点，过点C 作CD AB ∥，交OB 的延长线于点D ．连接OA OC ，．(1)求证：CD 是⊙O 的切线；(2)若32OA BD ==，，求OCD 的面积．5．（2024·甘肃临夏·中考真题）如图1，在矩形ABCD 中，点E 为AD 边上不与端点重合的一动点，点F 是对角线BD 上一点，连接BE ，AF 交于点O ，且ABE DAF ∠=∠．【模型建立】（1）求证：AF BE ⊥；【模型应用】（2）若2AB =，3AD =，12DF BF =，求DE 的长；【模型迁移】（3）如图2，若矩形ABCD 是正方形，12DF BF =，求AF AD 的值．6．（2024·黑龙江绥化·中考真题）如图1，O 是正方形ABCD 对角线上一点，以O 为圆心，OC 长为半径的O 与AD 相切于点E ，与AC 相交于点F ．(1)求证：AB 与O 相切．(2)若正方形ABCD 21，求O 的半径．(3)如图2，在（2）的条件下，若点M 是半径OC 上的一个动点，过点M 作MN OC ⊥交 CE于点N ．当:1:4CM FM =时，求CN 的长．7．（2024·内蒙古赤峰·中考真题）数学课上，老师给出以下条件，请同学们经过小组讨论，提出探究问题．如图1，在ABC 中，AB AC =，点D 是AC 上的一个动点，过点D 作DE BC ⊥于点E ，延长ED 交BA 延长线于点F ．请你解决下面各组提出的问题：(1)求证：AD AF =；(2)探究DF DE 与AD DC 的关系；某小组探究发现，当13AD DC =时，23DF DE =；当45AD DC =时，85DF DE =．请你继续探究：①当76AD DC =时，直接写出DF DE 的值；②当AD m DC n =时，猜想DF DE的值（用含m ，n 的式子表示），并证明；(3)拓展应用：在图1中，过点F 作FP AC ⊥，垂足为点P ，连接CF ，得到图2，当点D 运动到使ACF ACB ∠=∠时，若AD m DC n =，直接写出AP AD的值（用含m ，n 的式子表示）．8．（2024·广东·中考真题）【问题背景】如图1，在平面直角坐标系中，点B ，D 是直线()0y ax a =>上第一象限内的两个动点()OD OB >，以线段BD 为对角线作矩形ABCD ，AD x ∥轴．反比例函数k y x=的图象经过点A ．【构建联系】（1）求证：函数k y x=的图象必经过点C ．（2）如图2，把矩形ABCD 沿BD 折叠，点C 的对应点为E ．当点E 落在y 轴上，且点B 的坐标为()1,2时，求k 的值．【深入探究】（3）如图3，把矩形ABCD 沿BD 折叠，点C 的对应点为E ．当点E ，A 重合时，连接AC 交BD 于点P ．以点O 为圆心，AC 长为半径作O ．若OP =O 与ABC 的边有交点时，求k 的取值范围．9．（2024·四川遂宁·中考真题）如图，AB 是O 的直径，AC 是一条弦，点D 是 AC 的中点，DN AB ⊥于点E ，交AC 于点F ，连结DB 交AC 于点G ．(1)求证：AF DF =；(2)延长GD 至点M ，使DM DG =，连接AM ．①求证：AM 是O 的切线；②若6DG =，5DF =，求O 的半径．10．（2024·四川德阳·中考真题）已知O 的半径为5，B C 、是O 上两定点，点A 是O 上一动点，且60,BAC BAC ∠=︒∠的平分线交O 于点D ．(1)证明：点D 为 BC上一定点；(2)过点D 作BC 的平行线交AB 的延长线于点F ．①判断DF 与O 的位置关系，并说明理由；②若ABC 为锐角三角形，求DF 的取值范围．11．（2024·四川泸州·中考真题）如图，ABC 是O 的内接三角形，AB 是O 的直径，过点B 作O 的切线与AC 的延长线交于点D ，点E 在O 上，AC CE =，CE 交AB 于点F ．(1)求证：CAE D ∠=∠；(2)过点C 作CG AB ⊥于点G ，若3OA =，32BD =FG 的长．12．（2024·四川南充·中考真题）如图，正方形ABCD 边长为6cm ，点E 为对角线AC 上一点，2CE AE =，点P 在AB 边上以1cm /s 的速度由点A 向点B 运动，同时点Q 在BC 边上以2cm /s 的速度由点C 向点B 运动，设运动时间为t 秒（03t <≤）．(1)求证：AEP CEQ ∽．(2)当EPQ △是直角三角形时，求t 的值．(3)连接AQ ，当1tan 3AQE ∠=时，求AEQ △的面积．13．（2024·安徽·中考真题）如图1，ABCD Y 的对角线AC 与BD 交于点O ，点M ，N 分别在边AD ，BC 上，且AM CN =．点E ，F 分别是BD 与AN ，CM 的交点．(1)求证：OE OF =；(2)连接BM 交AC 于点H ，连接HE ，HF ．（ⅰ）如图2，若HE AB ∥，求证：HF AD ∥；（ⅱ）如图3，若ABCD Y 为菱形，且2MD AM =，60EHF ∠=︒，求AC BD的值．14．（2024·江苏扬州·中考真题）在综合实践活动中，“特殊到一般”是一种常用方法，我们可以先研究特殊情况，猜想结论，然后再研究一般情况，证明结论．如图，已知ABC ，CA CB =，O 是ABC 的外接圆，点D 在 O 上（AD BD >），连接AD 、BD 、CD ．【特殊化感知】（1）如图1，若60ACB ∠=︒，点D 在AO 延长线上，则AD BD -与CD 的数量关系为________；【一般化探究】（2）如图2，若60ACB ∠=︒，点C 、D 在AB 同侧，判断AD BD -与CD 的数量关系并说明理由；【拓展性延伸】（3）若ACB α∠=，直接写出AD 、BD 、CD 满足的数量关系．（用含α的式子表示）15．（2024·山东·中考真题）一副三角板分别记作ABC 和DEF ，其中90ABC DEF ∠=∠=︒，45BAC ∠=︒，30EDF ∠=︒，AC DE =．作BM AC ⊥于点M ，EN DF ⊥于点N ，如图1．(1)求证：BM EN =；(2)在同一平面内，将图1中的两个三角形按如图2所示的方式放置，点C 与点E 重合记为C ，点A 与点D 重合，将图2中的DCF 绕C 按顺时针方向旋转α后，延长BM 交直线DF 于点P ．①当30α=︒时，如图3，求证：四边形CNPM 为正方形；②当3060α︒<<︒时，写出线段MP ，DP ，CD 的数量关系，并证明；当60120α︒<<︒时，直接写出线段MP ，DP ，CD 的数量关系．16．（2024·江西·中考真题）综合与实践如图，在Rt ABC △中，点D 是斜边AB 上的动点（点D 与点A 不重合），连接CD ，以CD 为直角边在CD 的右侧构造Rt CDE △，90DCE ∠=︒，连接BE ，CE CB m CD CA ==．特例感知（1）如图1，当1m =时，BE 与AD 之间的位置关系是______，数量关系是______；类比迁移（2）如图2，当1m ≠时，猜想BE 与AD 之间的位置关系和数量关系，并证明猜想．拓展应用（3）在（1）的条件下，点F 与点C 关于DE 对称，连接DF ，EF ，BF ，如图3．已知6AC =，设AD x =，四边形CDFE 的面积为y ．①求y 与x 的函数表达式，并求出y 的最小值；②当2BF =时，请直接写出AD 的长度．17．（2024·湖南·中考真题）【问题背景】已知点A 是半径为r 的O 上的定点，连接OA ，将线段OA 绕点O 按逆时针方向旋转9(0)0αα︒<<︒得到OE ，连接AE ，过点A 作O 的切线l ，在直线l 上取点C ，使得CAE ∠为锐角．【初步感知】（1）如图1，当60α=︒时，CAE ∠=︒；【问题探究】（2）以线段AC 为对角线作矩形ABCD ，使得边AD 过点E ，连接CE ，对角线AC ，BD 相交于点F ．①如图2，当2AC r =时，求证：无论α在给定的范围内如何变化，BC CD ED =+总成立：②如图3，当43=AC r ，23CE OE =时，请补全图形，并求tan α及AB BC 的值．18．（2024·河南·中考真题）综合与实践在学习特殊四边形的过程中，我们积累了一定的研究经验，请运用已有经验，对“邻等对补四边形”进行研究定义：至少有一组邻边相等且对角互补的四边形叫做邻等对补四边形．(1)操作判断用分别含有30︒和45︒角的直角三角形纸板拼出如图1所示的4个四边形，其中是邻等对补四边形的有________（填序号）．(2)性质探究根据定义可得出邻等对补四边形的边、角的性质．下面研究与对角线相关的性质．如图2，四边形ABCD 是邻等对补四边形，AB AD =，AC 是它的一条对角线．①写出图中相等的角，并说明理由；②若BC m =，DC n =，2BCD θ∠=，求AC 的长（用含m ，n ，θ的式子表示）．(3)拓展应用如图3，在Rt ABC △中，90B Ð=°，3AB =，4BC =，分别在边BC ，AC 上取点M ，N ，使四边形ABMN 是邻等对补四边形．当该邻等对补四边形仅有一组邻边相等时，请直接写出BN 的长．19．（2024·黑龙江齐齐哈尔·中考真题）综合与实践：如图1，这个图案是3世纪我国汉代的赵爽在注解《周髀算经》时给出的，人们称它为“赵爽弦图”，受这幅图的启发，数学兴趣小组建立了“一线三直角模型”．如图2，在ABC 中，90A ∠=︒，将线段BC 绕点B 顺时针旋转90︒得到线段BD ，作DE AB ⊥交AB 的延长线于点E ．(1)【观察感知】如图2，通过观察，线段AB 与DE 的数量关系是______；(2)【问题解决】如图3，连接CD 并延长交AB 的延长线于点F ，若2AB =，6AC =，求BDF 的面积；(3)【类比迁移】在(2)的条件下，连接CE 交BD 于点N ，则BN BC=______；(4)【拓展延伸】在(2)的条件下，在直线AB 上找点P ，使2tan 3BCP ∠=，请直接写出线段AP 的长度．20．（2024·黑龙江齐齐哈尔·中考真题）综合与探究：如图，在平面直角坐标系中，已知直线122y x =-与x 轴交于点A ，与y 轴交于点C ，过A ，C 两点的抛物线()20y ax bx c a =++≠与x 轴的另一个交点为点(10)B -，，点P 是抛物线位于第四象限图象上的动点，过点P 分别作x 轴和y 轴的平行线，分别交直线AC 于点E ，点F ．(1)求抛物线的解析式；(2)点D 是x 轴上的任意一点，若ACD 是以AC 为腰的等腰三角形，请直接写出点D 的坐标；(3)当EF AC =时，求点P 的坐标；(4)在（3）的条件下，若点N 是y 轴上的一个动点，过点N 作抛物线对称轴的垂线，垂足为M ，连接NA MP ，，则NA MP +的最小值为______．21．（2024·四川广元·中考真题）数学实验，能增加学习数学的乐趣，还能经历知识“再创造”的过程，更是培养动手能力，创新能力的一种手段．小强在学习《相似》一章中对“直角三角形斜边上作高”这一基本图形（如图1）产生了如下问题，请同学们帮他解决．在ABC 中，点D 为边AB 上一点，连接CD ．(1)初步探究如图2，若ACD B ∠=∠，求证：2AC AD AB =⋅；(2)尝试应用如图3，在（1）的条件下，若点D 为AB 中点，4BC =，求CD 的长；(3)创新提升如图4，点E 为CD 中点，连接BE ，若30CDB CBD ∠=∠=︒，ACD EBD ∠=∠，27AC =BE 的长．22．（2024·内蒙古包头·中考真题）如图，在ABCD Y 中，ABC ∠为锐角，点E 在边AD 上，连接,BE CE ，且ABE DCE S S = ．(1)如图1，若F 是边BC 的中点，连接EF ，对角线AC 分别与,BE EF 相交于点,G H ．①求证：H 是AC 的中点；②求::AG GH HC ；(2)如图2，BE 的延长线与CD 的延长线相交于点M ，连接,AM CE 的延长线与AM 相交于点N ．试探究线段AM 与线段AN 之间的数量关系，并证明你的结论．23．（2024·吉林·中考真题）如图，在ABC 中，90C ∠=︒，30B ∠=︒，3cm AC =，AD 是ABC 的角平分线．动点P 从点A /s 的速度沿折线AD DB -向终点B 运动．过点P 作PQ AB ∥，交AC 于点Q ，以PQ 为边作等边三角形PQE ，且点C ，E 在PQ 同侧，设点P 的运动时间为()()s 0t t >，PQE V 与ABC 重合部分图形的面积为()2cm S ．(1)当点P 在线段AD 上运动时，判断APQ △的形状（不必证明），并直接写出AQ 的长（用含t 的代数式表示）．(2)当点E 与点C 重合时，求t 的值．(3)求S 关于t 的函数解析式，并写出自变量t 的取值范围．24．（2024·吉林长春·中考真题）如图，在ABC 中，5AB AC ==，6BC =．点D 是边BC 上的一点（点D 不与点B 、C 重合），作射线AD ，在射线AD 上取点P ，使AP BD =，以AP 为边作正方形APMN ，使点M和点C 在直线AD 同侧．(1)当点D 是边BC 的中点时，求AD 的长；(2)当4BD =时，点D 到直线AC 的距离为________；(3)连结PN ，当PN AC ⊥时，求正方形APMN 的边长；(4)若点N 到直线AC 的距离是点M 到直线AC 距离的3倍，则CD 的长为________．（写出一个即可）25．（2024·湖北·中考真题）如图，矩形ABCD 中，,E F 分别在,AD BC 上，将四边形ABFE 沿EF 翻折，使A 的对称点P 落在CD 上，B 的对称点为G PG ，交BC 于H ．(1)求证：EDP PCH △∽△．(2)若P 为CD 中点，且2,3AB BC ==，求GH 长．(3)连接BG ，若P 为CD 中点，H 为BC 中点，探究BG 与AB 大小关系并说明理由．26．（2024·内蒙古通辽·中考真题）数学活动课上，某小组将一个含45︒的三角尺AEF 利一个正方形纸板ABCD 如图1摆放，若1AE =，2AB =．将三角尺AEF 绕点A 逆时针方向旋转()090αα︒≤≤︒角，观察图形的变化，完成探究活动．【初步探究】如图2，连接BE ，DF 并延长，延长线相交于点,G BG 交AD 于点M ．问题1BE 和DF 的数量关系是________，位置关系是_________．【深入探究】应用问题1的结论解决下面的问题．问题2如图3，连接BD ，点O 是BD 的中点，连接OA ，OG ．求证==OA OD OG ．【尝试应用】问题3如图4，请直接写出当旋转角α从0︒变化到60︒时，点G 经过路线的长度．27．（2024·甘肃·中考真题）【模型建立】（1）如图1，已知ABE 和BCD △，AB BC ⊥，AB BC =，CD BD ⊥，AE BD ⊥．用等式写出线段AE ，DE ，CD 的数量关系，并说明理由．【模型应用】（2）如图2，在正方形ABCD 中，点E ，F 分别在对角线BD 和边CD 上，AE EF ⊥，AE EF =．用等式写出线段BE ，AD ，DF 的数量关系，并说明理由．【模型迁移】（3）如图3，在正方形ABCD 中，点E 在对角线BD 上，点F 在边CD 的延长线上，AE EF ⊥，AE EF =．用等式写出线段BE ，AD ，DF 的数量关系，并说明理由．28．（2024·湖南长沙·中考真题）对于凸四边形，根据它有无外接圆（四个顶点都在同一个圆上）与内切圆（四条边都与同一个圆相切），可分为四种类型，我们不妨约定：既无外接圆，又无内切圆的四边形称为“平凡型无圆”四边形；只有外接圆，而无内切圆的四边形称为“外接型单圆”四边形；只有内接圆，而无外接圆的四边形称为“内切型单圆”四边形；既有外接圆，又有内切圆的四边形称为“完美型双圆”四边形．请你根据该约定，解答下列问题：(1)请你判断下列说法是否正确（在题后相应的括号中，正确的打“√”，错误的打“×”，①平行四边形一定不是“平凡型无圆”四边形；（）②内角不等于90︒的菱形一定是“内切型单圆”四边形；（）③若“完美型双圆”四边形的外接圆圆心与内切圆圆心重合，外接圆半径为R ，内切圆半径为r ，则有2=R r ．（）(2)如图1，已知四边形ABCD 内接于O ，四条边长满足：AB CD BC AD +≠+．①该四边形ABCD 是“______”四边形（从约定的四种类型中选一种填入）；②若BAD ∠的平分线AE 交O 于点E ，BCD ∠的平分线CF 交O 于点F ，连接EF ．求证：EF 是O 的直径．(3)已知四边形ABCD 是“完美型双圆”四边形，它的内切圆O 与AB BC CD AD ，，，分别相切于点E ，F ，G ，H ．①如图2．连接EG FH ，交于点P ．求证：EG FH ⊥．②如图3，连接OA OB OC OD ，，，，若2OA =，6OB =，3OC =，求内切圆O 的半径r 及OD 的长．29．（2024·黑龙江大兴安岭地·中考真题）如图，在平面直角坐标系中，等边三角形OAB 的边OB 在x 轴上，点A 在第一象限，OA 的长度是一元二次方程2560x x --=的根，动点P 从点O 出发以每秒2个单位长度的速度沿折线OA AB -运动，动点Q 从点O 出发以每秒3个单位长度的速度沿折线OB BA -运动，P 、Q 两点同时出发，相遇时停止运动．设运动时间为t 秒（0 3.6t <<），OPQ △的面积为S ．(1)求点A 的坐标；(2)求S 与t 的函数关系式；(3)在（2）的条件下，当63S =M 在y 轴上，坐标平面内是否存在点N ，使得以点O 、P 、M 、N 为顶点的四边形是菱形．若存在，直接写出点N 的坐标；若不存在，说明理由．30．（2024·重庆·中考真题）在Rt ABC △中，90ACB ∠=︒，AC BC =，过点B 作BD AC ∥．(1)如图1，若点D 在点B 的左侧，连接CD ，过点A 作AE CD ⊥交BC 于点E ．若点E 是BC 的中点，求证：2AC BD =；(2)如图2，若点D 在点B 的右侧，连接AD ，点F 是AD 的中点，连接BF 并延长交AC 于点G ，连接CF ．过点F 作FM BG ⊥交AB 于点M ，CN 平分ACB ∠交BG 于点N ，求证：22AM CN =+；(3)若点D 在点B 的右侧，连接AD ，点F 是AD 的中点，且AF AC =．点P 是直线AC 上一动点，连接FP ，将FP 绕点F 逆时针旋转60︒得到FQ ，连接BQ ，点R 是直线AD 上一动点，连接BR ，QR ．在点P 的运动过程中，当BQ 取得最小值时，在平面内将BQR 沿直线QR 翻折得到TQR △，连接FT ．在点R 的运动过程中，直接写出FT CP的最大值．31．（2024·重庆·中考真题）在ABC 中，AB AC =，点D 是BC 边上一点（点D 不与端点重合）．点D 关于直线AB 的对称点为点E ，连接,AD DE ．在直线AD 上取一点F ，使EFD BAC ∠∠=，直线EF 与直线AC 交于点G ．(1)如图1，若60,,BAC BD CD BAD α∠=︒<∠=，求AGE ∠的度数（用含α的代数式表示）；(2)如图1，若60,BAC BD CD ∠=︒<，用等式表示线段CG 与DE 之间的数量关系，并证明；(3)如图2，若90BAC ∠=︒，点D 从点B 移动到点C 的过程中，连接AE ，当AEG △为等腰三角形时，请直接写出此时CG AG的值．32．（2024·江苏连云港·中考真题）【问题情境】（1）如图1，圆与大正方形的各边都相切，小正方形是圆的内接正方形，那么大正方形面积是小正方形面积的几倍？小昕将小正方形绕圆心旋转45°（如图2），这时候就容易发现大正方形面积是小正方形面积的__________倍．由此可见，图形变化是解决问题的有效策略；【操作实践】（2）如图3，图①是一个对角线互相垂直的四边形，四边a 、b 、c 、d 之间存在某种数量关系．小昕按所示步骤进行操作，并将最终图形抽象成图4．请你结合整个变化过程，直接写出图4中以矩形内一点P 为端点的四条线段之间的数量关系；【探究应用】（3）如图5，在图3中“④”的基础上，小昕将PDC △绕点P 逆时针旋转，他发现旋转过程中DAP ∠存在最大值．若8PE =，5PF =，当DAP ∠最大时，求AD 的长；（4）如图6，在Rt ABC △中，90C ∠=︒，点D 、E 分别在边AC 和BC 上，连接DE 、AE 、BD ．若5AC CD +=，8BC CE +=，求AE BD +的最小值．33．（2024·上海·中考真题）在梯形ABCD 中，AD BC ∥，点E 在边AB 上，且13AE AB =．(1)如图1所示，点F 在边CD 上，且13DF CD =，联结EF ，求证：EF BC ∥；(2)已知1AD AE ==；①如图2所示，联结DE ，如果ADE V 外接圆的心恰好落在B ∠的平分线上，求ADE V 的外接圆的半径长；②如图3所示，如果点M 在边BC 上，联结EM 、DM 、EC ，DM 与EC 交于N ，如果4BC =，且2CD DM DN =⋅，DMC CEM ∠=∠，求边CD 的长．34．（2024·四川成都·中考真题）数学活动课上，同学们将两个全等的三角形纸片完全重合放置，固定一个顶点，然后将其中一个纸片绕这个顶点旋转，来探究图形旋转的性质．已知三角形纸片ABC 和ADE 中，3AB AD ==，4BC DE ==，90ABC ADE ∠=∠=︒．【初步感知】（1）如图1，连接BD ，CE ，在纸片ADE 绕点A 旋转过程中，试探究BD CE的值．【深入探究】（2）如图2，在纸片ADE 绕点A 旋转过程中，当点D 恰好落在ABC 的中线BM 的延长线上时，延长ED 交AC 于点F ，求CF 的长．【拓展延伸】（3）在纸片ADE 绕点A 旋转过程中，试探究C ，D ，E 三点能否构成直角三角形．若能，直接写出所有直角三角形CDE 的面积；若不能，请说明理由．35．（2024·河北·中考真题）已知O 的半径为3，弦5MN =ABC 中，90,3,32ABC AB BC ∠=︒==在平面上，先将ABC 和O 按图1位置摆放（点B 与点N 重合，点A 在O 上，点C 在O 内），随后移动ABC ，使点B 在弦MN 上移动，点A 始终在O 上随之移动，设BN x =．(1)当点B 与点N 重合时，求劣弧 AN 的长；(2)当OA MN ∥时，如图2，求点B 到OA 的距离，并求此时x 的值；(3)设点O 到BC 的距离为d ．①当点A 在劣弧 MN上，且过点A 的切线与AC 垂直时，求d 的值；②直接写出d 的最小值．36．（2024·四川乐山·中考真题）在一堂平面几何专题复习课上，刘老师先引导学生解决了以下问题：【问题情境】如图1，在ABC 中，90BAC ∠=︒，AB AC =，点D 、E 在边BC 上，且45DAE =︒∠，3BD =，4CE =，求DE 的长．解：如图2，将ABD △绕点A 逆时针旋转90︒得到ACD '△，连接ED '．由旋转的特征得BAD CAD '∠=∠，B ACD ∠=∠'，AD AD ='，BD CD '=．∵90BAC ∠=︒，45DAE =︒∠，∴45BAD EAC ∠+∠=︒．∵BAD CAD '∠=∠，∴45CAD EAC '∠+∠=︒，即45EAD '∠=︒．∴DAE D AE '∠=∠．在DAE 和D AE ' 中，AD AD ='，DAE D AE '∠=∠，AE AE =，∴___①___．∴DE D E '=．又∵90ECD ECA ACD ECA B ''︒，∴在Rt ECD '△中，___②___．∵3CD BD '==，4CE =，∴DE D E '==___③___．【问题解决】上述问题情境中，“①”处应填：______；“②”处应填：______；“③”处应填：______．刘老师进一步谈到：图形的变化强调从运动变化的观点来研究，只要我们抓住了变化中的不变量，就能以不变应万变．【知识迁移】如图3，在正方形ABCD 中，点E 、F 分别在边BC CD 、上，满足CEF △的周长等于正方形ABCD 的周长的一半，连结AE AF 、，分别与对角线BD 交于M 、N 两点．探究BM MN DN 、、的数量关系并证明．【拓展应用】如图4，在矩形ABCD 中，点E 、F 分别在边BC CD 、上，且45EAF CEF ∠=∠=︒．探究BE EF DF 、、的数量关系：______（直接写出结论，不必证明）．【问题再探】如图5，在ABC 中，90ABC ∠=︒，4AB =，3BC =，点D 、E 在边AC 上，且45DBE ∠=︒．设AD x =，CE y =，求y 与x 的函数关系式．2137．（2024·北京·中考真题）在平面直角坐标系xOy 中，O 的半径为1，对于O 的弦AB 和不在直线AB 上的点C ，给出如下定义：若点C 关于直线AB 的对称点C '在O 上或其内部，且ACB α∠=，则称点C 是弦AB 的“α可及点”．(1)如图，点()0,1A ，()1,0B ．①在点()12,0C ，()21,2C ，31,02C ⎛⎫ ⎪⎝⎭中，点___________是弦AB 的“α可及点”，其中α=____________︒；②若点D 是弦AB 的“90︒可及点”，则点D 的横坐标的最大值为__________；(2)已知P 是直线33y =上一点，且存在O 的弦MN ，使得点P 是弦MN 的“60︒可及点”．记点P 的横坐标为t ，直接写出t 的取值范围．38．（2024·广东·中考真题）【知识技能】（1）如图1，在ABC 中，DE 是ABC 的中位线．连接CD ，将ADC △绕点D 按逆时针方向旋转，得到A DC '' ．当点E 的对应点E '与点A 重合时，求证：AB BC =．【数学理解】（2）如图2，在ABC 中()AB BC <，DE 是ABC 的中位线．连接CD ，将ADC △绕点D 按逆时针方向旋转，得到A DC '' ，连接A B '，C C '，作A BD ' 的中线DF ．求证：2DF CD BD CC ⋅='⋅．【拓展探索】（3）如图3，在ABC 中，4tan 3B =，点D 在AB 上，325AD =．过点D 作DE BC ⊥，垂足为E ，3BE =，323CE =．在四边形ADEC 内是否存在点G ，使得180AGD CGE ∠+∠=︒？若存在，请给出证明；若不存在，请说明理由．2239．（2024·广东广州·中考真题）如图，在菱形ABCD 中，120C ∠=︒．点E 在射线BC 上运动（不与点B ，点C 重合），AEB △关于AE 的轴对称图形为AEF △．(1)当30BAF ∠=︒时，试判断线段AF 和线段AD 的数量和位置关系，并说明理由；(2)若663AB =+O 为AEF △的外接圆，设O 的半径为r ．①求r 的取值范围；②连接FD ，直线FD 能否与O 相切？如果能，求BE 的长度；如果不能，请说明理由．40．（2024·云南·中考真题）如图，AB 是O 的直径，点D 、F 是O 上异于A 、B 的点．点C 在O 外，CA CD =，延长BF 与CA 的延长线交于点M ，点N 在BA 的延长线上，AMN ABM ∠∠=，AM BM AB MN ⋅=⋅．点H 在直径AB 上，90AHD ∠= ，点E 是线段DH的中点．(1)求AFB ∠的度数；(2)求证：直线CM 与O 相切：(3)看一看，想一想，证一证：以下与线段CE 、线段EB 、线段CB 有关的三个结论：CE EB CB +<，CE EB CB +=，CE EB CB +>，你认为哪个正确？请说明理由．。

几何综合（含答案）

24．（8分）已知正方形ABCD ，边长为3，对角线AC ，BD 交点O ,直角MPN 绕顶点P 旋转，角的两边分别与线段AB ,AD 交于点M ，N （不与点B ，A ，D 重合）．设DN =x ，四边形AMPN 的面积为y ．在下面情况下，y 随x 的变化而变化吗？若不变，请求出面积y 的值；若变化，请求出y 与x 的关系式．的关系式．（1）如图1，点P 与点O 重合；重合；（2）如图2，点P 在正方形的对角线AC 上，且AP =2PC ；（3）如图3，点P 在正方形的对角线BD 上，且DP =2PB ．24．（ 8分）解：（1）当x 变化时，y 不变．不变．如图1，94A F O E A M O N y S S ===正方形四边形． ………………………………………………………………………………2分（2）当x 变化时，y 不变．不变．如图2，作OE ⊥AD 于E ，OF ⊥AB 于F ． ……………………………………………………………………………… 3分 ∵AC 是正方形ABCD 的对角线，的对角线， ∴∠BAD =90°，AC 平分∠BAD ．。

∴四边形AFPE 是矩形，PF =PE ．∴四边形AFPE 是正方形．是正方形． ……………………………………………………………………………… 4分 ∵∠ADC =90°，∴PE ∥CD ．∴△APE ∽△ACD ．∴P E A P C D A C=．∵AP =2PC ，CD =3， ∴233P E =．∴PE =2．∵∠FPE =90°，∠MPN =90°，∴∠FPN +∠NPE =90°，∠FPN +∠MPF =90°． ∴∠NPE =∠MPF ．∵∠PEN =∠PFM =90°，PE =PF ，∴△PEN ≌△PFM ． ……………………………………………………………………………… 5分 ∴224AFPEAMPNy SS====正方形四边形． ………………………………………………6分（3）x 变化，y 变化．变化．如图3，3742y x =-+，0＜x ＜3． ………………………………………………8分FE AB C O M DN（P ）图1图2PAB COMD N F E图3PA BCO M DNE F图1（P ）NDMO C B A 图2PABCO M D N图3P A BCOMDN24．（本小题7分）分）如图，在△ABC 中，∠A=90°，AB=8，AC=6，M 是AB 上的动点（不与A 、B 重合），过M 点作MN ∥BC 交AC 于点N ．以MN 为直径作⊙O ，并在⊙O 中作内接矩形AMPN ．令AM=x ．（1）用含x 的代数式表示△MNP 的面积S ；（2）当x 为何值时，⊙O 与直线BC 相切？相切？（3）在点M 的运动过程中，设△MNP 与梯形BCNM 重合的面积为y ，求y 关于x 的函数关系式，并求x 为何值时，y 的值最大，最大值是多少？的值最大，最大值是多少？24．解：（1）∵MN ∥BC ， ∴△AMN ∽△ABC ．∴ AMANAB AC =，即86xA N =．∴AN ＝43x ．∴2133248M N P A M N S S x x x D D ==´×=．…………………………………………………．…………………………………………………2分（2）如图2，作OD ⊥BC 于点D ，当OD =21MN 时，⊙O 与直线BC 相切．相切．在Rt △ABC 中，BC =22AB AC +=10．由（1）知）知 △AMN ∽ △ABC ． ∴ AM M N AB BC=，即108MN x =． ∴MN =x 45．过M 点作ME ⊥BC 于点E ， ∵sinB=M EA CB M BC =，∴6810O Dx =-．∴()385O D x =-． ∴()3158524x x -=´，解得19249x =．∴当19249x =时，⊙O 与直线BC 相切．相切． ……………………………………………………………………………………4分（3）随点M 的运动，当P 点落在直线BC 上时，如图3，连结AP ，则O 点为AP 的中点．的中点． ∵ MN ∥BC ，∴1A M A O M BO P==，即，即AM=MB=4．故分以下两种情况讨论：故分以下两种情况讨论： ① 当0＜x ≤4时，2Δ83x S y PMN ==．∴ 当x =4时，23468y =´=最大．………………．………………5分 ② 当4＜x ＜8时，如图4，设PM 、PN 分别交BC 于E 、F ．∵ 四边形AMPN 是矩形，是矩形，∴ PN ∥AM ，PN=AM=x ． PNMCBAO （第24题图3）（第24题图2）PNMCBA O（第24题）题）又∵又∵ MN ∥BC ， ∴ 四边形MBFN 是平行四边形．是平行四边形． ∴FN=BM=8－x ． ∴PF=PN –FN = x -(8 - x) = 2x -8．又△PEF ∽△ACB ，∴，∴2PEF ABCS PF AB S D D æö=ç÷èø． ∴()2342P E FS x D =-．∴ M N P PEFy S S D D =-＝()22233941224828x x x x --=-+-2916883x æö=--+ç÷èø．∵ 二次项系数089<-，且当163x =时，满足4＜x ＜8，∴ 8y=最大．……………………………………………………………………………．……………………………………………………………………………6分综上所述，当163x =时，y 值最大，最大值是8． ………………………………………………………………………………7分 FE PN M CBAO （第24题图4）25．（本小题8分）分）已知：在△ABC 中，∠ACB=90°，CD ⊥AB 于点D ，点E 在AC 上，BE 交CD 于点G ，EF ⊥BE交AB 于点F ．如图甲，当AC=BC ，且CE=EA 时，则有EF=EG ；（1）如图乙①，当AC=2BC ，且CE=EA 时，则线段EF 与EG 的数量关系是：EFEG ；（2）如图乙②，当AC=2BC ，且CE=2EA 时，请探究线段EF 与EG 的数量关系，并证明你的结论；论；（3）当AC=mBC ，且CE=nEA 时，请探究线段EF 与EG 的数量关系，直接写出你的结论（不必证明）．25.（1）EF=12EG ；…………………………………………………………………………………………；…………………………………………………………………………………………1分（2）解：EF=14EG ； ………………………………………………………………………………2分证明：作EM ⊥AB 于点M ，EN ⊥CD 于点N ，∵EM ∥CD, ∴ΔAEM ∽ΔACD. ∴31==ACAE CDEM ，即CD EM 31=． …………………………3分同理可得，AD EN 32=． ……………………………………………………4分 ∵ ∠ACB=90°，CD ⊥AB ，∴ tanA=21==ACBC ADCD ．∴4121212123231=´=×===ADCD ADCD ADCDENEM． ………………………………………………………………………………5分又∵又∵EM ⊥AB ，EN ⊥CD ， ∴ ∠EMF=∠ENG=90°． ∵ EF ⊥BE ， ∴ ∠FEM=∠GEN ． ∴ ΔEFM ∽ΔEGN ． ∴14E FE M E GE N==，即14E F E G =． ……………………………………………………………………………………………………6分（3） EF=1m nEG ． ………………………………………………………………………………………………………………………………………………………………8分MNG F ECDBA（第25题）题）图乙②G FECDBA图乙① GFECDAB图甲 GFECDAB（第25题）题）23. 如图，如图，BD BD 为⊙为⊙O O 的直径，点A 是弧BC 的中点，的中点，AD AD 交BC 于E 点，点，AE=2AE=2AE=2，，ED=4.（1）求证）求证: :A B E D ～A B D D ； (2) 求tan A D B Ð的值；的值；（3）延长BC 至F ，连接FD FD，使，使B D F D 的面积等于83，求E D FÐ的度数的度数. .23. （１）（１）证明：∵点A 是弧BC 的中点，的中点， ∴∠ＡＢＣ＝∠ＡＤＢ. 又∵∠ＢＡＥ＝∠D ＡB ，∴△ＡＢＥ∽△ＡＤＢ．………………………………………………………………．………………………………………………………………22分（２）解（２）解∵△ＡＢＥ∽△ＡＤＢ， ∴ＡＢ２２＝２×６＝１２＝２×６＝１２. . . ∴ＡＢ＝２3在Ｒｔ△ＡＤＢ中，ｔａｎ∠ＡＤＢ＝33632=……………………………………………………………………44分（３）解：（３）解：连接ＣＤ，∵tan ∠ADB=33，∴∠ADB=30°.又∵A 为的中点，∴∠ABC=∠ADB=30°.∵∠A=90°,∠ABD=60°.∴∠DBC=30°.∴CD=AB=23，BE=DE=4.又∵S △BDF =83，∴BF=8. ∴EF=4.又∵∠FED=∠EBD+∠EDB=60°，∴△EFD 为等边三角形为等边三角形..∴∠EDF=60° (7)7分 F OEADB C海淀23．以坐标原点为圆心，1为半径的圆分别交x ，y 轴的正半轴于点A ，B .（1）如图一，动点P 从点A 处出发，沿x 轴向右匀速运动，与此同时，动点Q 从点B 处出发，沿圆处出发，沿圆周按顺时针方向匀速运动.若点Q 的运动速度比点P 的运动速度慢，经过1秒后点P 运动到点(2,0)，此时PQ 恰好是O 的切线，连接OQ . 求QOP Ð的大小；的大小；解：解：（2）若点Q 按照（1）中的方向和速度继续运动，点P 停留在点(2,0)处不动，求点Q 再经过5秒后直秒后直线PQ 被O 截得的弦长. 解：解：23．（1）解：如图一，连结AQ ．由题意可知：OQ =OA =1.∵OP =2,∴A 为OP 的中点.∵PQ 与O 相切于点Q ,∴OQP △为直角三角形. …………1分 ∴112AQ O P O Q O A ==== .…………2分即ΔOAQ 为等边三角形.∴∠QOP =60°．…………3分（2）解：由（1）可知点Q 运动1秒时经过的弧长所对的圆心角为30°，若Q 按照（1）中的方向和速度）中的方向和速度继续运动，继续运动，那么再过那么再过5秒，则Q 点落在O 与y 轴负半轴的交点的位置轴负半轴的交点的位置（如图二）（如图二）.设直线PQ 与O的交点为D ，过O 作OC ⊥QD 于点C ，则C 为QD 的中点.…………4分 ∵∠QOP =90°，OQ =1，OP =2,∴QP =22125+=. …………5分 ∵1122OQ OP QP OC×=×,∴OC =25.…………6分 ∵OC ⊥QD ，OQ =1，OC =25,∴QC =155.∴QD =255．ABOxy 图二P DQC A BO QP xy 图一A BO xy 图二(备用图)P海淀25．如图一，在△ABC 中，分别以AB ，AC 为直径在△ABC 外作半圆1O 和半圆2O ，其中1O 和2O 分别为两个半圆的圆心. F 是边BC 的中点，点D 和点E 分别为两个半圆圆弧的中点.（1）连结1122,,,,,O F O D DF O F O E EF ，证明：12DO F FO E △≌△；（2）如图二，过点A 分别作半圆1O 和半圆2O 的切线，交BD 的延长线和CE 的延长线于点P 和点Q ，连结PQ ，若∠ACB =90°=90°,,DB =5，CE =3，求线段PQ 的长;（3）如图三，过点A 作半圆2O 的切线，交CE 的延长线于点Q ，过点Q 作直线F A 的垂线，交BD 的延长线于点P ，连结PA . 证明：P A 是半圆1O 的切线.图一ABCF DE1O 2O2O 1O AECF B DP图二QAB CEFDPQ1O 2O 图三25．（1）证明：如图一，∵1O ，2O ，F 分别是AB ，AC ，BC 边的中点，边的中点，∴1O F ∥AC 且1O F =A 2O ，2O F ∥AB 且2O F =A 1O ， ∴∠B 1O F=∠BAC ，∠C 2O F=∠BAC ,∴∠B 1O F=∠C 2O F∵点D 和点E 分别为两个半圆圆弧的中点，分别为两个半圆圆弧的中点， ∴1O F =A 2O =2O E ，2O F =A 1O =1O D ，………………………….2分 ∠B 1O D =90°，∠C 2O E =90°， ∴∠B 1O D=∠C 2O E . ∴∠D 1O F=∠F 2O E .∴12DO F FO E △≌△.………………………….………………………….33分（2）解：如图二，延长CA 至G ，使AG =AQ ,连接BG 、AE .∵点E 是半圆2O 圆弧的中点，圆弧的中点， ∴AE=CE=3 ∵AC 为直径为直径 ∴∠AEC =90°，∴∠ACE =∠EAC =45°，AC =22AE CE +=32， ∵AQ 是半圆2O 的切线，∴CA ⊥AQ ，∴∠CAQ =90°，∴∠ACE =∠AQE =45°，∠GAQ =90° ∴AQ =AC =AG =32同理：∠BAP =90°，AB =AP =52 ∴CG =62,∠GAB =∠QAP ∴AQP AGB △≌△. ……………………..5分∴PQ =BG ∵∠ACB =90°，∴BC =22AB AC -=42 ∴BG =22G C BC +=226 ∴PQ=226.……………………..6分图一AB CF DE1O 2O 2O 1O AECF B DPG图二Q（3）证法一：如图三，设直线F A 与PQ 的垂足为M ，过C 作CS ⊥MF 于S ，过B 作BR ⊥MF 于R ，连接DR 、AD 、DM.∵F 是BC 边的中点，∴ABF ACF S S =△△.∴BR=CS ，由（2）已证∠CAQ =90°=90°,, AC =AQ, ∴∠2+∠3=90°∵FM ⊥PQ , ∴∠2+∠1=90°， ∴∠1=∠3, 同理：∠2=∠4,∴AMQ CSA △≌△，∴AM=CS ，∴AM=BR ，同（2）可证AD=BD ，∠ADB =∠ADP =90°=90°,, ∴∠ADB =∠ARB =90°=90°,, ∠ADP =∠AMP =90° ∴A 、D 、B 、R 四点在以AB 为直径的圆上，A 、D 、P 、M 四点在以AP 为直径的圆上，为直径的圆上，且∠DBR+∠DAR =180°=180°,, ∴∠5=∠8, ∠6=∠7,∵∠DAM +∠DAR =180°=180°,, ∴∠DBR =∠DAM ∴DBR DAM △≌△， ∴∠5=∠9,∴∠RDM =90°， ∴∠5+∠7=90°， ∴∠6+∠8=90°， ∴∠PAB =90°，∴PA ⊥AB ,又AB 是半圆1O 直径， ∴PA 是半圆1O 的切线.……………………..8分证法二：假设P A 不是是半圆1O 的切线，如图四，的切线，如图四，过点A 作半圆1O 的切线交BD 的延长线于点P ¢，则点P ¢异于点P ，连结P Q ¢，设直线F A 与PQ 的垂足为M ，直线FA 与P Q ¢的交点为M ¢.延长AF 至N ，使得AF =FN ，连结BN ，CN ，由于点F 是 BC 中点，所以四边形ABNC 是平行四边形.易知，180B A C A C N Ð+Ð=°， ∵AQ 是半圆2O 的切线,∴∠QAC =90°，同理90P A B ¢Ð=°. ∴180P AQ BAC ¢Ð+Ð=°.A BCEF RDPMQS1O 2O 132684759图三AB CEF DPQ1O 2O P ¢MM ¢N图四∴P AQ ACN¢Ð=Ð.由（2）可知，,AQ AC AB AP¢==,∴P AQ NCA¢△≌△.∴NAC P QA¢Ð=Ð.∵90QACÐ=°,∴90NAC M AQ¢Ð+Ð=°.即 90AQM M AQ¢¢Ð+Ð=°.∴90AM Q¢Ð=°.即 P Q A F¢^.∵ PQ AF^,∴ 过点Q有两条不同的直线P Q¢和PQ同时与AF垂直.这与在平面内过一点有且仅有一条直线与已知直线垂直相矛盾,因此假设错误.所以PA是是半圆O的切线.1西城25. 含30°角的直角三角板ABC 中，∠A =30°.将其绕直角顶点C 顺时针旋转a 角（0120a °<<°且a ≠90°），得到Rt △''A B C ，'A C 边与AB 所在直线交于点D ，过点过点 D 作DE ∥''A B 交'C B 边于点E ，连接BE （1）如图1，当''A B 边经过点B 时，a =°；（2）在三角板旋转的过程中，若∠CBD 的度数是∠CBE 度数的m 倍，猜想m 的值并证明你的结论；（3）设 BC =1，AD =x ，△BDE 的面积为S ，以点E 为圆心，EB 为半径作⊙E ，当S =13ABC S D时，求AD 的长，并判断此时直线'A C 与⊙E 的位置关系的位置关系..25.（1）当''A B 边经过点B 时，a = 60 °； …………………………………………………………………………………… 1分（2）猜想：①如图8，点D 在AB 边上时，m =2；②如图9，点D 在AB 的延长线上时，m =4. （阅卷说明：为与后边证明不重复给分，猜想结论不设给分点）证明：①证明：①当090a °<<°时，点D 在AB 边上（如图8）. （阅卷说明：（阅卷说明：①、②两种情况没写a 的取值范围不扣分） ∵ DE ∥''A B ， ∴CDCE CA CB =¢¢.由旋转性质可知，CA ='C A ，CB ='C B ，∠ACD=∠BCE .∴C DC E C AC B=.∴ △CAD ∽△CBE . ……………2分∴ ∠A =∠CBE=30°. ∵ 点D 在AB 边上，∠CBD=60°，∴ 2C BD C BE Ð=Ð，即 m =2. ………………………………………3分 ② 当90120a °<<°时，点D 在AB 的延长线上（如图9）.与①同理可得与①同理可得∠A =∠CBE=30°. ∵ 点D 在AB 的延长线上，180120C BD C BA Ð=°-Ð=°，∴ 4C BD C BE Ð=Ð，即 m =4.……………………………………4分（阅卷说明：第（2）问用四点共圆方法证明的扣1分.）（3）解：在Rt △ABC 中，∠ACB=90°，∠A =30°，BC =1， ∴ AB = 2 ，3AC =，32ABCS =.图9图8由 △CAD ∽△CBE 得 ADBE ACBC=.∵ AD =x ， ∴13x BE =，33BEx=.①当点D 在AB 边上时，AD =x ，2BD AB AD x =-=-，∠DBE=90°. 此时，2113323(2)2236BD Ex x x SS BD BE x -+==´=-´= .当S =13ABCSD 时，2323366x x-+=.整理，得整理，得 2210x x -+=.解得解得 121x x ==，即AD =1.…………………5分此时D 为AB 中点，∠DCB=60°，∠BCE=30°30°==∠CBE .（如图10） ∴ EC = EB . ∵ ''90A CB Ð=°，点E 在'C B 边上，边上， ∴ 圆心E 到'A C 的距离EC 等于⊙E 的半径EB .∴ 直线'A C 与⊙E 相切相切.. …………………………………………………6分 ②当点D 在AB 的延长线上时，AD =x ，2BD x =-，∠DBE=90°（如图9） 2113323(2)2236B D Ex x x S S B D B E x-==´=-´= .当S =13ABCS D 时，2323366x x-=.整理，得整理，得 2210x x --=.解得解得 112x =+，212x =-（负值，舍去）（负值，舍去）. .即1+2AD =.……………………………………………………………………………………………………………………………… 7分此时∠BCE=a ，而90120a °<<°，∠CBE =30°， ∴ ∠CBE ＜∠BCE . ∴ EC ＜EB ，即圆心E 到'A C 的距离EC 小于⊙E 的半径EB . ∴ 直线'A C 与⊙E 相交相交..……………………………………………………8分图10图1EDCB A图2CBAF图3E DCBA2424．在△．在△ABC 中，∠ACB 为锐角．为锐角．点点D 为射线BC 上一动点，连接AD ，将线段AD 绕点A 逆时针旋转90 º得到AE ，连结EC ．（1）如果AB =AC ，∠BAC =90º．①当点D 在线段BC 上时（与点B 不重合），如图1，请你判断线段CE 、BD 之间的位置和数量关系（直接写出结论）；②当点D 在线段BC 的延长线上时，请你在图2画出图形，判断①中的结论是否仍然成立，并证明你的判断；明你的判断；（2）如图3，当点D 在线段BC 上运动时，DF ⊥AD 交线段CE 于点F ，且∠ACB =45 º ，AC ＝32，试求线段CF 长的最大值．长的最大值．24．解：（1）①）① 线段CE 、BD 之间的位置和数量关系分别是垂直和相等之间的位置和数量关系分别是垂直和相等..…………1分② ①中的结论仍然成立①中的结论仍然成立..证明：画出图形. …………2分.如图1，由题意可知，A B A C =，AD AE =.BAC C AD EAD C AD Ð+Ð=Ð+Ð，即BAD C AE Ð=Ð. ∴ △BAD ≌△CAE .∴ BD =CE ，45B A C E Ð=Ð=°.∴90BC E BC A AC E Ð=Ð+Ð=°.即 CE ⊥BD . …………4分（2）如图2，过点A 作AH ⊥AC ，与CB 的延长线交于点H .由（1）的方法可证）的方法可证CE ⊥BD . 过点A 作AG ⊥BC 于点G .可证△AGD ∽△DCF .∴ A G D G C DC F=.∵ ∠ACB =45 º ，AC ＝32，∴3AG C G ==. 设,CD x CF y ==.∴ 33x x y-=.即 213y x x =-+，0＜x ≤3. ∴43)23(312+--=x y .∴ 线段CF 长的最大值为43.…………7分PABDC23. 如图，在△ABC 中，∠C =60°，BC =4，AC =23，点P 在BC 边上运动，PD ∥AB ，交AC 于D . 设BP 的长为x ，△APD 的面积为y .（1）求AD 的长（用含x 的代数式表示）；（2）求y 与x 之间的函数关系式，并回答当x 取何值时，y 的值最大？最大值是多少？的值最大？最大值是多少？（3）点P 是否存在这样的位置，使得△ADP 的面积是△ABP 面积的23？若存在，请求出BP 的长；若不存在，请说明理由.23．解：（1）∵PD ∥AB ，∴.A D B P A CB C=…………………………1分∵BC =4，AC =23，BP 的长为x ， ∴.423AD x =∴ 3.2AD x =………………………………………………2分（2）过点P 作PE ⊥AC 于E.∵sin ,P E A C B P CÐ=∠C =60°=60°,, ∴()3sin 604.2PE PC x =´=-……………………………………3分∴2113333(4).222282y AD PE x x x x =××=××-=-+…………………4分∴当2x =时，y 的值最大，最大值是3.2……………………………5分（3）点P 存在这样的位置.∵△ADP 与△ABP 等高不等底，∴ΔΔ.AD P ABPS D P S AB=∵△ADP 的面积是△ABP 面积的23，∴ΔΔ2.3AD P ABPS S =∴2.3D P A B=∵PD ∥AB ，∴△CDP ∽△CAB . ∴.D P C P A BC B=∴2.3C P C B= ∴42.43x -=∴4.3x =∴4.3B P =…………………………………………………………………………………………7分 ECD BAPE FDCBA E FDCBAEF DCBA图1 图2图325. △ABC 中，∠BAC =90°，AB=AC ，点D 是BC 的中点，把一个三角板的直角顶点放在点D 处，将三角板绕点D 旋转且使两条直角边分别交AB 、AC 于E 、F .（1）如图1，观察旋转过程，猜想线段AF 与BE 的数量关系并证明你的结论；的数量关系并证明你的结论；（2）如图2，若连接EF ，试探索线段BE 、EF 、FC 之间的数量关系，直接写出你的结论（不需证明）；（3）如图3，若将“AB=AC ，点D 是BC 的中点”改为：“∠B =30°，AD ⊥BC 于点D ”，其余条件不变，探索（1）中结论是否成立？若不成立，请探索关于AF 、BE 的比值.解：解：25 .解：（1）结论：AF=BE . ………………………………………………….………………………………………………….11分证明：连接AD ， ∵ AB=AC ，∠BAC =90°，点D 是BC 的中点的中点 ∴ AD=BD=DC =12BC ，∠ADB =∠ADC =90°=90°,, ∴ ∠B=∠C =∠1=∠2=45°2=45°.. ∴ ∠3+∠5==90°5==90°.. ∵ ∠3+∠4==90°4==90°,, ∴ ∠5=∠4∵ BD=AD , ∴ △BDE ≌△ADF .∴ BE=AF . ………………………………………………………………………3分（2）222EF BE FC =+…………………………………………………………4分（3）（1）中的结论BE=AF 不成立.……………………………………… 5分 ∵ ∠B =30°，AD ⊥BC 于点D ，∠BAC =90°=90°,, ∴ ∠3+∠5==90°， ∠B +∠1==90°1==90°.. ∵ ∠3+∠4==90°，∠1+∠2==90°∴ ∠B =∠2 ， ∠5=∠4. ∴ △BDE ∽△ADF .∴ 3tan 303AF AD BE BD===.…………………………………………………………………………………………………… 6分A BC D FE 5412354EFC DB A 12323．如图①，△ABC 中，90AC B Ð=°，∠ABC =a ，将△ABC 绕点A 顺时针旋转得到△AB ¢C ¢ ，设旋转的角度是b ．（1）如图②，当b = °（用含a 的代数式表示）时，点B ¢恰好落在CA 的延长线上；的延长线上；（2）如图③，连结BB ¢ 、CC ¢， CC ¢ 的延长线交斜边AB 于点E ，交BB ¢于点F ．请写出图中两对相似三角形相似三角形，（不含全等三角形），并选一对证明．，并选一对证明．23．解：（1）90a °+ ……………………………………………………………1分（2）图中两对相似三角形：①△ABB ¢∽△AC C ¢ ，②△ACE ∽△FBE ；……… 3分证明①：∵△ABC 绕点A 顺时针旋转角b 得到△AB ¢C ¢∴∠CA C ¢=∠BAB ¢=b ，AC=A C ¢ ，AB=AB ¢ ………………………………4分 ∴''AB AC ABAC =……………………………………………………5分 ∴△ABB ¢∽△AC C ¢……………………………………………………6分证明②：∵△ABC 绕点A 顺时针旋转角b 得到△AB ¢C ¢ ∴∠CA C ¢=∠BAB ¢=b ，AC=A C ¢ ，AB=AB ¢ ………………………………4分 ∴∠AC C ¢=∠ABB ¢=2180b-………………………………5分又∠A E C =∠FEB∴△ACE ∽△FBE ……………………………………………………6分C 'B 'CBAFEC 'B 'CBA第23题①题① 第23题②题② 第23题③题③C 'B 'CBA。

正方形一题40问+(二中广雅)9张

Q K
M N
结论 36：若 AN⊥EG，求证： BE + BC ＝ BP
分析： ①由（19）、（20）得 BP＝BA＝6
②对称性 BE＝DG＝6 2 －6
③ BE + BC ＝ BP
2
2 ；（结论延伸）
B
E
A 22.5°
22.5°
Q K
B
E
F
C
D
P 67.5° H 67.5° G
MN
F
C
页8
结论 37：若 BF＝FC，求 BD 的值；（结论延伸） DE
由结论 19 和 21，得：GE＝ 2 GC＝ 2 PQ 又 PN＝DG，∴PQ＋PN＝DC＝6
A
D
22.5°
22.5°
Q K
P67.5° H
67.5°
M
G
N
B
E
F
C
A
D
结论 28：若 AN⊥EG，求证：EN2＝AN·MN；（九年级母子相似）
分析：
22.5°
P
H
导角可证：△NAE∽NEM
G M
∴EN2＝AN·MN
②在等腰 Rt△PDH 中，PD＝ 2 b
③∴PB－PD＝ 2 a＝ 2 BE
A
D
P H
G
QM
K
N
B
E
FC
A
D
P bH
G
QM
K
N
B
a
E b Fb C
页1
结论 4：EG＝EB＋DG（半角模型）分析：延长 CB 至点 J，使得 BJ＝DG，连接 AJ ①△ABJ≌△ADG（SAS），得 AJ＝AG ②半角，得∠EAG＝∠EAJ＝45° ③△AEJ≌△AEG（SAS）得 EG＝EJ ∴EG＝EJ＝BE＋BJ＝BE＋DG

小学数学-几何问题专项练习(附答案)

几何问题1.问题：一个正方形的边长为5厘米，它的面积是多少平方厘米？2.问题：一个矩形的长为8厘米，宽为4厘米，它的周长是多少厘米？3.问题：一个三角形的底边长为6厘米，高为4厘米，它的面积是多少平方厘米？4.问题：一个圆的半径为3厘米，它的周长是多少厘米？5.问题：一个正方形的周长为20厘米，它的边长是多少厘米？6.问题：一个梯形的上底长为5厘米，下底长为9厘米，高为6厘米，它的面积是多少平方厘米？7.问题：一个圆的直径为10厘米，它的周长是多少厘米？8.问题：一个正方形的面积为36平方厘米，它的边长是多少厘米？9.问题：一个矩形的周长为16厘米，长为6厘米，它的宽是多少厘米？10.问题：一个三角形的底边长为10厘米，高为8厘米，它的面积是多少平方厘米？11.问题：一个圆的半径为5厘米，它的面积是多少平方厘米？12.问题：一个正方形的周长为24厘米，它的面积是多少平方厘米？13.问题：一个梯形的上底长为8厘米，下底长为12厘米，高为5厘米，它的面积是多少平方厘米？14.问题：一个圆的直径为6厘米，它的面积是多少平方厘米？15.问题：一个正方形的面积为64平方厘米，它的周长是多少厘米？16.问题：一个矩形的周长为20厘米，长为8厘米，它的宽是多少厘米？17.问题：一个三角形的底边长为12厘米，高为10厘米，它的面积是多少平方厘米？18.问题：一个圆的半径为4厘米，它的周长是多少厘米？19.问题：一个正方形的周长为28厘米，它的边长是多少厘米？20.问题：一个梯形的上底长为10厘米，下底长为14厘米，高为7厘米，它的面积是多少平方厘米？21.问题：一个圆的直径为8厘米，它的周长是多少厘米？22.问题：一个正方形的面积为81平方厘米，它的边长是多少厘米？23.问题：一个矩形的周长为24厘米，长为9厘米，它的宽是多少厘米？24.问题：一个三角形的底边长为15厘米，高为12厘米，它的面积是多少平方厘米？25.问题：一个圆的半径为6厘米，它的面积是多少平方厘米？26.问题：一个正方形的周长为32厘米，它的面积是多少平方厘米？27.问题：一个梯形的上底长为12厘米，下底长为16厘米，高为8厘米，它的面积是多少平方厘米？28.问题：一个圆的直径为10厘米，它的周长是多少厘米？29.问题：一个正方形的面积为100平方厘米，它的周长是多少厘米？30.问题：一个矩形的周长为30厘米，长为12厘米，它的宽是多少厘米？答案1.25平方厘米2.24厘米3.12平方厘米4.6π厘米5.5厘米6.35平方厘米7.10π厘米8.6厘米9.2厘米10.40平方厘米11.25π平方厘米12.36平方厘米13.50平方厘米14.9π平方厘米15.16厘米16.2厘米17.60平方厘米18.8π厘米19.7厘米20.48平方厘米21.8π厘米22.9厘米23.3厘米24.90平方厘米25.36π平方厘米26.64平方厘米27.100平方厘米28.10π厘米29.20厘米30.3厘米。

正方形练习题及答案

正方形练习题及答案正方形练习题及答案正方形是数学中一个常见的几何形状，它具有四个相等的边和四个相等的角。

正方形的性质和应用广泛，因此在学习数学的过程中，我们经常会遇到与正方形相关的练习题。

下面，我将为大家提供一些正方形练习题及其答案，希望能够帮助大家更好地理解和掌握正方形的性质。

练习题一：已知正方形ABCD的边长为a，求正方形的周长和面积。

解答：正方形的周长等于四条边的长度之和，即周长=4a。

正方形的面积等于边长的平方，即面积=a^2。

因此，正方形ABCD的周长为4a，面积为a^2。

练习题二：已知正方形ABCD的周长为20cm，求正方形的边长和面积。

解答：设正方形ABCD的边长为a，则周长等于四条边的长度之和，即4a=20。

解方程得到a=5。

因此，正方形ABCD的边长为5cm。

正方形的面积等于边长的平方，即面积=5^2=25cm^2。

练习题三：已知正方形ABCD的面积为36cm^2，求正方形的周长和对角线长度。

解答：设正方形ABCD的边长为a，则面积等于边长的平方，即a^2=36。

解方程得到a=6。

因此，正方形ABCD的边长为6cm。

正方形的周长等于四条边的长度之和，即周长=4a=4×6=24cm。

正方形的对角线长度等于边长乘以√2，即对角线长度=a×√2=6×√2≈8.49cm。

练习题四：已知正方形ABCD的对角线长度为10cm，求正方形的面积。

解答：设正方形ABCD的边长为a，则对角线长度等于边长乘以√2，即10=a×√2。

解方程得到a=10/√2=5√2。

因此，正方形ABCD的边长约为7.07cm。

正方形的面积等于边长的平方，即面积=(5√2)^2=50cm^2。

练习题五：已知正方形ABCD的面积为64cm^2，求正方形的对角线长度。

解答：设正方形ABCD的边长为a，则面积等于边长的平方，即a^2=64。

解方程得到a=8。

因此，正方形ABCD的边长为8cm。

正方形的性质与判定专题练习

正方形专题训练（含答案)一．选择题（共11小题）1．如图，将正方形OABC放在平面直角坐标系中，O是原点，A的坐标为（1，）,则点C的坐标为（）2．）如图，点E在正方形ABCD的对角线AC上，且EC=2AE，直角三角形FEG的两直角边EF、EG分别交BC、DC于点M、N．若正方形ABCD的边长为a，则重叠部分四边形EMCN的面积为(）A．a2B．a2C．a2D．a23．如图，F是正方形ABCD的边CD上的一个动点，BF 的垂直平分线交对角线AC于点E，连接BE，FE，则∠EBF 的度数是（）A．45°B．50°C．60°D．不确定4．平行四边形、矩形、菱形、正方形都具有的是（）A．对角线互相平分B．对角线互相垂直C ．对角线相等D．对角线互相垂直且相等5．正方形的一条对角线长为4,则这个正方形的面积是（)6．（2014•福州）如图，在正方形ABCD的外侧，作等边三角形ADE，AC、BE相交于点F，则∠BFC为（）A．45°B．55°C．60°D．75°7．顺次连接菱形各边的中点所形成的四边形是（）A．等腰梯形B．矩形C．菱形D．正方形8．下列说法中，正确的是（）A．相等的角一定是对顶角B．四个角都相等的四边形一定是正方形C．平行四边形的对角线互相平分D．矩形的对角线一定垂直9．已知四边形ABCD是平行四边形，再从①AB=BC，②∠ABC=90°，③AC=BD，④AC⊥BD四个条件中,选两个作为补充条件后，使得四边形ABCD是正方形,现有下列四种选法，其中错误的是（）A．选①②B．选②③C．选①③D．选②④10．如图，在正方形ABCD中，CE=MN，∠MCE=35°，那么∠ANM等于（）A．45°B．50°C．55°D．60°11．如图,菱形ABCD中,∠B=60°，AB=5，则以AC为边长的正方形ACEF的面积为（）A．9B．16 C．20 D．25二．填空题(共5小题）12．如图，在正方形ABCD的外侧，作等边三角形ADE，则∠AEB=_________度．13．如图，已知P是正方形ABCD对角线BD上一点，且BP=BC，则∠ACP度数是_________度．14．如图，四边形ABCD为正方形，△ADE为等边三角形．AC为正方形ABCD的对角线，则∠EAC=_________度．A．8B．4C．8D．1615．已知：如图，菱形ABCD中，∠B=60°，AB=4，则以AC为边长的正方形ACEF的周长为_________．16．如图所示，正方形ABCD 的周长为16cm，顺次连接正方形ABCD各边的中点,得到四边形EFGH,则四边形EFGH的周长等于_________cm,四边形EFGH的面积等于_________cm．三．解答题（共6小题）17．如图，正方形ABCD中，E、F分别为BC、CD上的点，且AE⊥BF，垂足为点G．求证：AE=BF．18．如图，在正方形ABCD中，P是对角线AC上的一点,连接BP、DP，延长BC到E,使PB=PE．求证：∠PDC=∠PEC．19．如图，四边形ABCD是正方形，BE⊥BF，BE=BF，EF与BC交于点G．（1）求证：AE=CF；（2）若∠ABE=55°，求∠EGC的大小．20．在平面内正方形ABCD与正方形CEFH如图放置，连DE，BH，两线交于M．求证：（1）BH=DE．（2）BH⊥DE．21．已知：如图，▱ABCD中，O是CD的中点，连接AO 并延长,交BC的延长线于点E．(1）求证：△AOD≌△EOC；（2）连接AC，DE,当∠B=∠AEB=_________°时，四边形ACED是正方形？请说明理由．22．（2014•随州）已知：如图,在矩形ABCD中，M、N 分别是边AD、BC的中点,E、F分别是线段BM、CM的中点．（1）求证：△ABM≌△DCM；（2）填空：当AB：AD=_________时，四边形MENF 是正方形．一．选择题（共11小题）1．（2014•南充）如图，将正方形OABC 放在平面直角坐标系中，O 是原点，A 的坐标为（1，)，则点C 的坐标为( ）A ．（﹣，1） B ． (﹣1，） C ． (，1) D ．（﹣，﹣1）考点：全等三角形的判定与性质；坐标与图形性质；正方形的性质．专题：几何图形问题．分析：过点A 作AD ⊥x 轴于D ，过点C 作CE ⊥x 轴于E ，根据同角的余角相等求出∠OAD=∠COE,再利用“角角边”证明△AOD 和△OCE 全等，根据全等三角形对应边相等可得OE=AD ，CE=OD ，然后根据点C 在第二象限写出坐标即可．解答：解：如图，过点A 作AD ⊥x 轴于D ，过点C 作CE ⊥x 轴于E ，∵四边形OABC 是正方形， ∴OA=OC ，∠AOC=90°, ∴∠COE+∠AOD=90°，又∵∠OAD+∠AOD=90°， ∴∠OAD=∠COE, 在△AOD 和△OCE 中，，∴△AOD ≌△OCE （AAS)， ∴OE=AD=，CE=OD=1，∵点C 在第二象限, ∴点C 的坐标为（﹣,1）．故选:A ．点评：本题考查了全等三角形的判定与性质，正方形的性质，坐标与图形性质，作辅助线构造出全等三角形是解题的关键，也是本题的难点．2．（2014•山西)如图，点E 在正方形ABCD 的对角线AC 上，且EC=2AE ，直角三角形FEG 的两直角边EF 、EG 分别交BC 、DC 于点M 、N ．若正方形ABCD 的边长为a,则重叠部分四边形EMCN 的面积为（）A ． a 2B ． a 2C ． a 2D ． a 2考点：全等三角形的判定与性质；正方形的性质．专题：几何图形问题．分析：作EP ⊥BC 于点P ，EQ ⊥CD 于点Q ，△EPM ≌△EQN,利用四边形EMCN 的面积等于正方形MCQE 的面积求解．解答：解：作EP ⊥BC 于点P,EQ ⊥CD 于点Q ，∵四边形ABCD是正方形，∴∠BCD=90°，又∵∠EPM=∠EQN=90°，∴∠PEQ=90°,∴∠PEM+∠MEQ=90°，∵三角形FEG是直角三角形，∴∠NEF=∠NEQ+∠MEQ=90°,∴∠PEM=∠NEQ,∵AC是∠BCD的角平分线，∠EPC=∠EQC=90°，∴EP=EN，四边形MCQE是正方形，在△EPM和△EQN中，，∴△EPM≌△EQN(ASA）∴S△EQN=S△EPM,∴四边形EMCN的面积等于正方形MCQE的面积, ∵正方形ABCD的边长为a，∴AC=a，∵EC=2AE，∴EC=a，∴EP=PC=a，∴正方形MCQE的面积=a ×a=a2，∴四边形EMCN的面积=a2,故选：D．点评:本题主要考查了正方形的性质及全等三角形的判定及性质，解题的关键是作出辅助线,证出△EPM≌△EQN．3．（2014•台州）如图，F是正方形ABCD的边CD上的一个动点，BF的垂直平分线交对角线AC于点E，连接BE，FE，则∠EBF的度数是(）A．45°B．50°C．60°D．不确定考点:全等三角形的判定与性质；正方形的性质．专题：几何图形问题．分析:过E作HI∥BC，分别交AB、CD于点H、I，证明Rt△BHE≌Rt△EIF，可得∠IEF+∠HEB=90°，再根据BE=EF即可解题．解答:解：如图所示，过E作HI∥BC，分别交AB、CD于点H、I，则∠BHE=∠EIF=90°,∵E是BF的垂直平分线EM上的点，∴EF=EB，∵E是∠BCD角平分线上一点，∴E到BC和CD的距离相等，即BH=EI，Rt△BHE和Rt△EIF中，，∴Rt△BHE≌Rt△EIF（HL），∴∠HBE=∠IEF ， ∵∠HBE+∠HEB=90°， ∴∠IEF+∠HEB=90°， ∴∠BEF=90°， ∵BE=EF ，∴∠EBF=∠EFB=45°．故选：A ．点评：本题考查了正方形角平分线和对角线重合的性质,考查了直角三角形全等的判定，全等三角形对应角相等的性质．4．（2014•郴州）平行四边形、矩形、菱形、正方形都具有的是( ) A ．对角线互相平分 B ．对角线互相垂直 C ．对角线相等 D ．对角线互相垂直且相等考点：正方形的性质;平行四边形的性质；菱形的性质；矩形的性质．专题：证明题．分析: 本题主要依据平行四边形、矩形、菱形、正方形都具有对角线相互平分的性质来判断．解答：解：A 、对角线相等是平行四边形、矩形、菱形、正方形都具有的性质;B 、对角线互相垂直是菱形、正方形具有的性质；C 、对角线相等是矩形和正方形具有的性质；D 、对角线互相垂直且相等是正方形具有的性质．故选:A ．点评：本题主要考查平行四边形、矩形、菱形、正方形的性质定理．5．（2014•来宾）正方形的一条对角线长为4，则这个正方形的面积是（）A ． 8B ． 4C ． 8D ． 16考点：正方形的性质．分析：根据正方形的面积等于对角线乘积的一半列式计算即可得解．解答：解:∵正方形的一条对角线长为4, ∴这个正方形的面积=×4×4=8．故选:A ．点评：本题考查了正方形的性质，熟记利用对角线求面积的方法是解题的关键．6．（2014•福州）如图,在正方形ABCD 的外侧,作等边三角形ADE ，AC 、BE 相交于点F ，则∠BFC 为（）A ． 45°B ． 55°C ． 60°D ．75°考点: 正方形的性质；等腰三角形的性质;等边三角形的性质．分析: 根据正方形的性质及全等三角形的性质求出∠ABE=15°，∠BAC=45°,再求∠BFC ．解答：解：∵四边形ABCD 是正方形， ∴AB=AD又∵△ADE 是等边三角形， ∴AE=AD=DE,∠DAE=60° ∴AD=AE∴∠ABE=∠AEB ，∠BAE=90°+60°=150° ∴∠ABE=（180°﹣150°）÷2=15° 又∵∠BAC=45° ∴∠BFC=45°+15°=60°故选:C ．点评：本题主要是考查正方形的性质和等边三角形的性质,本题的关键是求出∠ABE=15°．7．（2014•来宾）顺次连接菱形各边的中点所形成的四边形是（） A ．等腰梯形 B ．矩形 C ．菱形D ．正方形考点:正方形的判定；三角形中位线定理；菱形的性质．分析：根据三角形的中位线定理以及菱形的性质即可证得．解答：解：∵E ，F 是中点， ∴EH ∥BD ，同理，EF ∥AC,GH ∥AC ，FG ∥BD ， ∴EH ∥FG ,EF ∥GH ，则四边形EFGH 是平行四边形．又∵AC ⊥BD ， ∴EF ⊥EH ，∴平行四边形EFGH 是矩形．故选：B ．点评：本题主要考查了矩形的判定定理，正确理解菱形的性质以及三角形的中位线定理是解题的关键．8．（2014•湘西州）下列说法中，正确的是（） A ．相等的角一定是对顶角B ．四个角都相等的四边形一定是正方形C ．平行四边形的对角线互相平分D ．矩形的对角线一定垂直考点：正方形的判定;对顶角、邻补角;平行四边形的性质;矩形的性质．分析：根据对顶角的定义,正方形的判定，平行四边形的性质，矩形的性质对各选项分析判断利用排除法求解．解答：解：A 、相等的角一定是对顶角错误，例如,角平分线分成的两个角相等，但不是对顶角,故本选项错误；B 、四个角都相等的四边形一定是矩形，不一定是正方形,故本选项错误；C 、平行四边形的对角线互相平分正确，故本选项正确；D 、矩形的对角线一定相等，但不一定垂直,故本选项错误．故选：C ．点评：本题考查了正方形的判定，平行四边形的性质，矩形的性质,对顶角的定义，熟记各性质与判定方法是解题的关键．9．（2014•株洲）已知四边形ABCD 是平行四边形，再从①AB=BC ，②∠ABC=90°，③AC=BD,④AC ⊥BD 四个条件中,选两个作为补充条件后，使得四边形ABCD 是正方形，现有下列四种选法，其中错误的是（ ) A ．选①② B ．选②③ C ．选①③ D ．选②④考点：正方形的判定；平行四边形的性质．分析:要判定是正方形，则需能判定它既是菱形又是矩形．解答: 解:A 、由①得有一组邻边相等的平行四边形是菱形，由②得有一个角是直角的平行四边形是矩形，所以平行四边形ABCD 是正方形，正确，故本选项不符合题意；B 、由②得有一个角是直角的平行四边形是矩形，由③得对角线相等的平行四边形是矩形,所以不能得出平行四边形ABCD 是正方形，错误，故本选项符合题意；C 、由①得有一组邻边相等的平行四边形是菱形,由③得对角线相等的平行四边形是矩形，所以平行四边形ABCD 是正方形，正确，故本选项不符合题意； D 、由②得有一个角是直角的平行四边形是矩形，由④得对角线互相垂直的平行四边形是菱形，所以平行四边形ABCD 是正方形，正确，故本选项不符合题意．故选：B ．点评：本题考查了正方形的判定方法：①先判定四边形是矩形，再判定这个矩形有一组邻边相等;②先判定四边形是菱形，再判定这个矩形有一个角为直角．③还可以先判定四边形是平行四边形，再用1或2进行判定．10．（2014•红桥区三模）如图，在正方形ABCD 中,CE=MN ，∠MCE=35°，那么∠ANM 等于（）A ． 45°B ．50° C ．55° D ．60°考点：全等三角形的判定与性质；正方形的性质．分析: 过B 作BF ∥MN 交AD 于F,则∠AFB=∠ANM ，根据正方形的性质得出∠A=∠EBC=90°,AB=BC,AD ∥BC,推出四边形BFNM 是平行四边形，得出BF=MN=CE ，证Rt △ABF ≌Rt △BCE,推出∠AFB=∠ECB 即可．解答：解：过B 作BF ∥MN 交AD 于F ，则∠AFB=∠ANM ， ∵四边形ABCD 是正方形，∴∠A=∠EBC=90°，AB=BC,AD ∥BC ， ∴FN ∥BM,BE ∥MN ，∴四边形BFNM 是平行四边形， ∴BF=MN ， ∵CE=MN ， ∴CE=BF,在Rt △ABF 和Rt △BCE 中∴Rt △ABF ≌Rt △BCE （HL ）, ∴∠AFB=∠ECB=35°， ∴∠ANM=∠AFB=55°，故选C ．点评：本题考查了平行四边形的性质和判定，全等三角形的性质和判定，正方形的性质的应用，主要考查学生的推理能力．11．(2014•四会市一模）如图，菱形ABCD 中,∠B=60°，AB=5,则以AC 为边长的正方形ACEF 的面积为( ）A ． 9B ． 16C ． 20D ． 25考点:菱形的性质；正方形的性质．分析：据已知可求得△ABC 是等边三角形，从而得到AC=AB,从而求出正方形ACEF 的边长,进而可求出其面积．解答：解：∵B=60°,AB=BC ， ∴△ABC 是等边三角形，∴AC=AB=5，∴正方形ACEF 的边长为5， ∴正方形ACEF 的面积为25，故选D ．点评：本题考查菱形与正方形的性质，属于基础题，对于此类题意含有60°角的题目一般要考虑等边三角形的应用．二．填空题(共5小题）12．（2009•江西模拟）如图,在正方形ABCD 的外侧,作等边三角形ADE ，则∠AEB= 15 度．考点:正方形的性质;等边三角形的性质．分析: 由等边三角形的性质可得∠DAE=60°，进而可得∠BAE=150°，又因为AB=AE ，结合等腰三角形的性质，易得∠AEB 的大小．解答: 解：△ADE 是等边三角形;故∠DAE=60°， ∠BAE=90°+60°=150°，又有AB=AE,故∠AEB=30°÷2=15°；故答案为15°．点评: 主要考查了正方形基本性质：①两组对边分别平行;四条边都相等；相邻边互相垂直；②四个角都是90°;③对角线互相垂直；对角线相等且互相平分；每条对角线平分一组对角．13．(2008•佛山）如图,已知P 是正方形ABCD 对角线BD 上一点，且BP=BC,则∠ACP 度数是 22.5 度．考点：正方形的性质．专题:计算题．分析：根据正方形的性质可得到∠DBC=∠BCA=45°又知BP=BC,从而可求得∠BCP 的度数,从而就可求得∠ACP 的度数．解答：解：∵ABCD 是正方形， ∴∠DBC=∠BCA=45°，∵BP=BC ，∴∠BCP=∠BPC=（180°﹣45°）=67。

6.3 正方形(含答案)

6.3 正方形◆基础训练1．若正方形ABCD对角线AC=5，则这个正方形的周长为_____．2．若E是正方形ABCD内一点，△ABE是等边三角形，则∠DEC=_____．3．如图，四边形EFGH是菱形，对角线HF，EG满足条件________________时，四边形EFGH•是正方形．4．如图，四边形ABCD是正方形，M是BC边的中点，将正方形折起，使点A与M重合，设折痕为EF，若正方形的面积为64，则△AEM的面积为_____．5．矩形各内角平分线组成的四边形是（）A．平行四边形 B．矩形 C．菱形 D．正方形6．下面命题中正确的是（）A．对角线相等的四边形一定是矩形B．一组对边相等，另一组对边平行的四边形一定是平行四边形C．两条对角线互相垂直的四边形一定是菱形D．两条对角线互相垂直平分且相等的四边形一定是正方形7．顺次连接正方形各边中点的小正方形的面积是原正方形面积的（）A．12B．13C．14D．158．如图，已知正方形ABCD中，∠ABE=∠CBF，求证：AE=CF．◆综合应用9．如图，已知矩形ABCD中，BE平分∠ABC，交AD于点E，EF⊥BC，垂足为F，求证：四边形ABFE是正方形．10．如图，正方形ABCD中，E是对角线BD上的点，且BE=AB，EF⊥BD，交CD于点F，•DE=2.5cm，求CF的长（结果保留1位小数）．◆拓展提升11．已知△ABC的边3，AC=2，BC边上的高3（1）BC的长；（2）如果有一个正方形的一边在AB上，另外两个顶点分别在AC，BC上，求这个正方形的面积．12．（1）顺次连接正方形ABCD的各边中点，得到一个小正方形EFGH．正方形EFGH与ABCD 的面积比是多少？（2）依次连接矩形（或菱形，或平行四边形）的各边中点，•所得四边形与原四边形的面积比是多少？（3）想一想，对于任意四边形，是否也有类似的结论？答案:1．2．150° 3．HF=EG 4．10 5．D 6．D 7．A8．由△ABE≌△CBF（ASA），•得出AE=CF9．先证四边形ABFE是平行四边形，因为∠ABF=90°，所以四边形ABFE•为矩形，因为BF=FE，所以矩形ABFE是正方形10．CF=2.5cm11．（1）BC=4 （2）•正方形的面积等于（312．（1）1：2 （2）1：2 （3）是.。

正方形练习题及答案

正方形练习题及答案一、选择题1. 正方形的四条边长度相等，其周长是边长的几倍？A. 2倍B. 3倍C. 4倍D. 5倍答案：C2. 如果正方形的边长为10厘米，那么它的面积是多少平方厘米？A. 20B. 50C. 100D. 200答案：C3. 一个正方形的对角线长度是边长的多少倍？A. 1B. √2C. 2D. √3答案：B二、填空题1. 正方形的四个角都是________角。

答案：直角2. 如果正方形的周长为32厘米，那么它的边长是________厘米。

答案：83. 一个正方形的面积为64平方厘米，它的边长是________厘米。

答案：8三、计算题1. 一个正方形的边长为x厘米，如果它的周长为20厘米，求边长x。

解：根据周长公式，4x = 20，解得x = 5厘米。

2. 已知正方形的面积为49平方厘米，求边长。

解：根据面积公式，边长^2 = 49，解得边长为7厘米。

四、应用题1. 一个正方形的花园，边长为15米。

如果花园的周围要围上一圈栅栏，需要多少米的栅栏？解：需要的栅栏长度等于正方形的周长，即4 * 15 = 60米。

2. 一个正方形的地砖，边长为30厘米。

如果要用这种地砖铺满一个面积为900平方厘米的正方形区域，需要多少块地砖？解：每块地砖的面积为30 * 30 = 900平方厘米，所以需要1块地砖。

五、综合题1. 一个正方形的水池，边长为10米。

如果水池的四个角各有一个边长为2米的正方形装饰区，求水池的实际使用面积。

解：水池的总面积为10 * 10 = 100平方米。

四个装饰区的总面积为4 * (2 * 2) = 16平方米。

实际使用面积为100 - 16 = 84平方米。

2. 一个正方形的房间，边长为6米。

如果房间的地面铺满地毯，地毯的面积至少是多少平方米？解：地毯的面积等于房间的面积，即6 * 6 = 36平方米。

结束语通过以上练习题，我们可以看到正方形的基本性质和计算方法。

掌握这些知识点，可以帮助我们解决实际生活中遇到的相关问题。

正方形性质与判定练习(含答案)

C． 2
D． 5 1
18．如图，正方形 ABCD 中，AD 5，点 E 、F 是正方形 ABCD 内的两点，且 AE FC 4 ，
BE DF 3，则以 EF 为直径的圆的面积为 ( )
A． 1 2
B． 3 5
C． 3 4
D．
19．如图，在平面直角坐标系中，正方形 A1B1C1D1 、D1E1E2B2 、A2 B2C2 D2 、D2 E3E4 B3 、A3B3C3D3 ，
D．16
21．如图，在正方形 ABCD 中，对角线 AC ，BD 相交于点 O ，E ，F 分别在 OD ，OC 上，
且 DE CF ，连接 DF ， AE ， AE 的延长线交 DF 于点 M ，则下列四个结论中正确结论的个数是 ( )
① AE DF ；
② AM DF ；
③ DAE CDF ；
．
38．如图，正方形 ABCD 中， AB 12 ，点 E 在边 CD 上，CD 3DE ．将 ADE 沿 AE 对折
至 AFE ，延长 EF 交边 BC 于点 G ，连接 AG ，CF ．则下列结论正确的是
．
① ABG AFG ； ② BG GC ；
为
．
31．如图，RtABC 中，C 90 ，AC 2 ，BC 1 ，以斜边为一边向右上方作正方形 ABDE ，
连接 CD ，则 CD 的长为
．
32．如图，将正方形 OABC 放在平面直角坐标系中， O 是坐标原点，点 A 的坐标是 (2,3) ，
则 C 点坐标是
．
33．如图，在平面直角坐标系中，点 A 的坐标是 (0,3) ，点 B 的坐标是 (4,0) ，以 AB 为边
正方形性质与判定练习
1．如果要证明平行四边形 ABCD 为正方形，那么我们需要在四边形 ABCD 是平行四边形的基础上，进一步证明 ( )

几何综合之面积专题(含答案)

几何综合之面积专题一、单选题（共10 道，每道10 分）1.四边形ABCD与四边形AEFG均为正方形，△ABH 的面积为6，则图中阴影部分的面积为（）A.5B.6C.7D.8答案：B 解题思路：试题难度：三颗星知识点：转化法（等底或等高）求面积2.如图，点E在正方形ABCD的对角线AC 上，且EC=2AE，Rt△FEG的两直角边EF，EG 分别交BC，DC 于点M，N．若正方形ABCD的边长为a，则图中阴影部分（四边形EMCN）的面积为（）A. B. C. D.答案：D 解题思路：试题难度：三颗星知识点：面积处理思路(割补法)3.如图，在7×7的方格纸中，每个小方格都是边长为 1 的正方形，△ ABC 的三个顶点均在小方格的格点上．若P也在小方格的格点上，且不与点B 重合，则使得的点P 共有( )个．A.2B.4C.5D.6答案：C 解题思路：试题难度：三颗星知识点：转化法(等底或等高)求面积4.如图，在△ABC中，已知D，E，F 分别为BC，AD，CE的中点，若，则图中阴影部分的面积为( )A.2B.3C.4D.5答案：A 解题思路：试题难度：三颗星知识点：转化法（等底或等高）求面积5.如图，在Rt△ABC中，∠ACB=90°，∠CAB=30°，BC=2，O，H 分别为边AB，AC的中点．将△ABC绕点B顺时针旋转120°到的位置，则整个旋转过程中线段OH 所扫过部分的面积（即图中阴影部分的面积）为（）答案：C 解题思路：试题难度：三颗星知识点：扇形面积的计算6.如图，在矩形ABCD中，AB=4cm，BC=3cm，P是AB上除A，B 外的任一点，对角线AC，BD 相交于点O，DP，CP分别交AC，BD于点E，F．若△ADE 和△BCF的面积之和为则四边形PEOF的面积为( )C. 答案： A解题思路：试题难度：三颗星知识点：面积处理思路(割补法)7.如图为 △ABC 与△DEC 重叠的情形，其中点 E 在 BC 上，AC 与 DE 相交于点 F ，且 AB ∥DE ．若 △ABC 与△DEC 的面积相等，且 EF=9，AB=12，则 DF 的长为 ()A.3B.7C.12D.15答案： B 解题思路：A. B.D.试题难度：三颗星知识点：面积处理思路（转化法）8.如图，在中，是斜边的中点，过作于，连接交于；过作于，连接交于；过作于，连接交于；⋯；如此继续．若分别记，，，⋯，)A. B.解题思路：试题难度：三颗星知识点：面积处理思路(转化法)9.如图，在矩形ABCD中，E是AD的中点，F是CE的中点，若△BDF的面积为6，则矩形ABCD的面积为( )答案：D第8页共12页A.24B.36C.48D.72答案：C 解题思路：试题难度：三颗星知识点：转化法(等底或等高)求面积10.如图，已知正方形ABCD的面积为120，E 为AB 的中点，F 为BC的中点，EC分别交BD，DF 于点G，H．则四边形BGHF的面积为()A.12B.13C.14D.15答案：C 解题思路：试题难度：三颗星知识点：面积处理思路（割补法）第11页共12。

正方形几何综合专题---40道题目(含答案)

初三数学中考复习 正方形 专题练习题 含答案

挑战中考数学压轴题-几何综合题素质训练之正方形

中考数学-几何综合压轴问题(共40题)(学生版)

初中数学几何综合-含答案

九年级数学几何综合专项测试(含答案)

初中正方形的判定专项练习30题

正方形判定练习题附答案

正方形几何综合专题---40道题目(含答案)

22.3正方形的性质习题(含详细的答案解析)

正方形练习题(含答案)

专题35 几何综合压轴题(40题)(原卷版)--2024年中考数学真题分类汇编

几何综合（含答案）

正方形一题40问+(二中广雅)9张

小学数学-几何问题专项练习(附答案)

正方形练习题及答案

正方形的性质与判定专题练习

6.3 正方形(含答案)

正方形练习题及答案

正方形性质与判定练习(含答案)

几何综合之面积专题(含答案)

初三数学中考复习正方形专题练习题含答案