化工原理沉降ppt课件(最新)
合集下载
化工原理第三章沉降与过滤PPT

真空过滤
利用真空泵降低过滤介质两侧 的压力差进行过滤,适用于易 产生泡沫或悬浮液中含有大量
气体的场合。
过滤设备与操作
板框压滤机
由滤板和滤框组成,适 用于各种颗粒分离,但
操作较繁琐。
转筒真空过滤机
叶滤机
袋式过滤器
结构简单,操作方便, 但只适用于颗粒较大的
分离。
适用于精细颗粒的分离, 但设备成本较高。
过滤原理
利用颗粒大小、形状、密度等物 理性质的差异,使不同颗粒在过 滤介质两侧形成不同的速度或动 量,从而实现分离。
过滤操作的分类
恒压过滤
在恒定压力下进行过滤,适用 于颗粒粒度较小、悬浮液粘度
较大的情况。
变压过滤
在改变压力下进行过滤,适用 于颗粒粒度较大、悬浮液粘度 较小的情况。
热过滤
在加热条件下进行过滤,适用 于悬浮液中含有热敏性物质的 情况。
设备
沉降槽、沉降池、离心机等。
操作
将悬浮液引入沉降设备中,在重力作用下使固体颗粒下沉,上清液从上部排出, 底部沉积的固体经过排出装置排出。操作过程中需控制适当的温度、流量和停留 时间等参数,以保证分离效果。
02
过滤
过滤的定义与原理
过滤定义
通过多孔介质使固体颗粒截留, 从而使液体与固体分离的操作。
实验步骤 1. 准备实验装置,包括过滤器、压力计、流量计等。
2. 将过滤介质放入过滤器中。
过滤实验操作
3. 将待测流体引入过滤器,并施加一定的压力。 5. 收集过滤后的流体样本,测量其中颗粒的浓度。
4. 记录不同时刻的流量和压差数据。
注意事项:确保过滤器密封性好,避免流体泄漏;保持 恒定的流体流量和压力,以获得准确的实验数据。
利用真空泵降低过滤介质两侧 的压力差进行过滤,适用于易 产生泡沫或悬浮液中含有大量
气体的场合。
过滤设备与操作
板框压滤机
由滤板和滤框组成,适 用于各种颗粒分离,但
操作较繁琐。
转筒真空过滤机
叶滤机
袋式过滤器
结构简单,操作方便, 但只适用于颗粒较大的
分离。
适用于精细颗粒的分离, 但设备成本较高。
过滤原理
利用颗粒大小、形状、密度等物 理性质的差异,使不同颗粒在过 滤介质两侧形成不同的速度或动 量,从而实现分离。
过滤操作的分类
恒压过滤
在恒定压力下进行过滤,适用 于颗粒粒度较小、悬浮液粘度
较大的情况。
变压过滤
在改变压力下进行过滤,适用 于颗粒粒度较大、悬浮液粘度 较小的情况。
热过滤
在加热条件下进行过滤,适用 于悬浮液中含有热敏性物质的 情况。
设备
沉降槽、沉降池、离心机等。
操作
将悬浮液引入沉降设备中,在重力作用下使固体颗粒下沉,上清液从上部排出, 底部沉积的固体经过排出装置排出。操作过程中需控制适当的温度、流量和停留 时间等参数,以保证分离效果。
02
过滤
过滤的定义与原理
过滤定义
通过多孔介质使固体颗粒截留, 从而使液体与固体分离的操作。
实验步骤 1. 准备实验装置,包括过滤器、压力计、流量计等。
2. 将过滤介质放入过滤器中。
过滤实验操作
3. 将待测流体引入过滤器,并施加一定的压力。 5. 收集过滤后的流体样本,测量其中颗粒的浓度。
4. 记录不同时刻的流量和压差数据。
注意事项:确保过滤器密封性好,避免流体泄漏;保持 恒定的流体流量和压力,以获得准确的实验数据。
化工原理第三章 沉降

ut
2 d p ( p ) g
1.86 10 Pa s
5
18
(40 106 )2 9.81 ( 2600 1.165) 18 1.86 10 5
0.12m s
校核:
Re dut 0.3 2
(正确)
6.非球形颗粒的沉降速度
同样条件下 因此
1 3
1 则:Re k 18
令
Rep 1
则
k 2.62
层流区:
k 2.6 2 采用斯托克斯公式
过渡区:
湍流区:
2.62 k 60.1
60.1 k 2364
采用阿伦公式
采用牛顿公式
试差法: 假设 流型 选择 公式
验算
计算
ut
计算
Re t
例:求直径40μm球形颗粒在30℃大气中的自由沉降 速度。已知ρ颗粒为2600kg/m3,大气压为0.1MPa。 解: 查30℃、0.1MPa空气: 1.165kg m3 设为层流,则:
ζ是流体相对于颗粒运动时的雷诺数的函数,
(Re) (d pu / )
层流区 过渡区 湍流区
10 4 Re 2
24 Re
2 Re 500
500 Re 2 10
5
10 0.5 Re 0.44
第二节 重力沉降
目的:流体与固体颗粒分离
上部易形成涡流 ——倾斜式、 旁路 尘粒易带走 ——扩散式
螺旋面进口:结构复杂,设计制造不方便。
蜗壳形进口:结构简单,减小阻力。
轴向进口:常用于多管式旋风分离器。
常用型式
标准型、CLT/A型、CLP型、扩散式等。
2 d p ( p ) g
1.86 10 Pa s
5
18
(40 106 )2 9.81 ( 2600 1.165) 18 1.86 10 5
0.12m s
校核:
Re dut 0.3 2
(正确)
6.非球形颗粒的沉降速度
同样条件下 因此
1 3
1 则:Re k 18
令
Rep 1
则
k 2.62
层流区:
k 2.6 2 采用斯托克斯公式
过渡区:
湍流区:
2.62 k 60.1
60.1 k 2364
采用阿伦公式
采用牛顿公式
试差法: 假设 流型 选择 公式
验算
计算
ut
计算
Re t
例:求直径40μm球形颗粒在30℃大气中的自由沉降 速度。已知ρ颗粒为2600kg/m3,大气压为0.1MPa。 解: 查30℃、0.1MPa空气: 1.165kg m3 设为层流,则:
ζ是流体相对于颗粒运动时的雷诺数的函数,
(Re) (d pu / )
层流区 过渡区 湍流区
10 4 Re 2
24 Re
2 Re 500
500 Re 2 10
5
10 0.5 Re 0.44
第二节 重力沉降
目的:流体与固体颗粒分离
上部易形成涡流 ——倾斜式、 旁路 尘粒易带走 ——扩散式
螺旋面进口:结构复杂,设计制造不方便。
蜗壳形进口:结构简单,减小阻力。
轴向进口:常用于多管式旋风分离器。
常用型式
标准型、CLT/A型、CLP型、扩散式等。
化工原理11沉降分离原理及设备

PPT文档演模板
化工原理11沉降分离原理及设备
•第三章、非均相混合物 分离及固体流态化
•3.1 沉降分离原理及设备 •3.1.1 颗粒相对于流体的运动
PPT文档演模板
化工原理11沉降分离原理及设备
•一、颗粒的特性
•1. 球形颗粒:球形颗粒的尺寸由直径d确定。
体 积 表面 积 比表面 积
PPT文档演模板
•二、重力沉降设备
• 位于降尘室最高点的颗粒沉降到室底所需的时间为
•气体通过降尘室的时间为
•降尘室 高
•沉降速 度
•降尘室 长
欲使颗粒被分离出来,则
•气流水平通 过降尘室速
度
PPT文档演模板
或
化工原理11沉降分离原理及设备
•二、重力沉降设备
根据降尘室的生产能力,气体在降尘室内的水平 通过速度为
•降尘室生 产能力
PPT文档演模板
化工原理11沉降分离原理及设备
•概述
机械分离方法,即利用非均相混合物中两 相的物理性质(如密度、颗粒形状、尺寸等) 的差异,使两相之间发生相对运动而使其分离。
机械分离方法
沉降 过滤
PPT文档演模板
化工原理11沉降分离原理及设备
•概述
•非均相混和物分离的应用: •(1)收集分散物质。 •(2)净化分散介质。 •(3)环境保护。
•三、 阻力系数(曳力系数)
•滞流区 •过渡区 •湍流区
•表面摩擦阻力 •形体阻力
PPT文档演模板
化工原理11沉降分离原理及设备
•四、 影响沉降速度的因素
•自由沉降
• 沉降过程中,任一颗粒的沉降不因其它颗 粒的存在而受到干扰 •干扰沉降
• 如果分散相的体积分率较高,颗粒间有明 显的相互作用,容器壁面对颗粒沉降的影响不可 忽略,这时的沉降称为干扰沉降或受阻沉降。
化工原理ppt课件
B
•
•••••
• •
H
u hor izont al
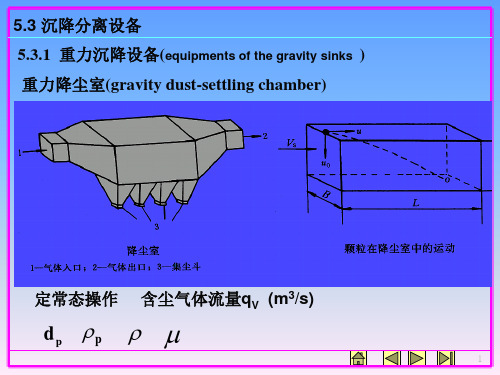
qV BH
设在水平方向上,颗粒与气体流同速。
工程处理方法:寻找颗粒得以分离的条件,从时间上考虑。
((停沉rseemt留降tlain时时ingin间间dgu::rdau颗trioa粒nti)o随n同)t 气流uh在t 降尘h室为中颗的粒时距间离段底平 r面的u距horL离izontal
A
B
D
B D 4
ui
qV A B
ui 的大小影响到器内进口旋涡、锥形底口灰 卷起情况、气流经过设备的总压降均有关。
27
两种常用旋风分离器的各部位尺寸比例
28
根据实验气体旋转圈数N一般去3-5. 例1:已知含尘气体中尘粒速度为2300kg/m3.气体温度为500℃, µ=0.036cp流量为1000m3/h.采用某种形式的旋风分离器,D=400mm, B=D/4,A=D/2,H=2D,d=D/2.试估算临界直dpc(即dmin)
16
2
理 论 上 :i
dp d pc
两边同时取自然对数:
lni
2 ln d p d pc
d p d pc 注意:dmin或者d pc指能够100%被沉降分离的最小颗粒粒径。
17
5.3.2 离心沉降(centrifugal settling) 和 离心沉降设备
在离心力的作用下,使流体中的颗粒产生沉降运动(离心力 方向上的运动),称为离心沉降。
分离器。以旋风分离器为例,分析离心分离设备的工作原理、 生产指标与设备尺寸、操作条件的关系。
处理物料为含尘气体,连续稳定的操作状况。
21
(1)旋风分离器的构造及工作状态
化工原理 沉降PPT课件

。降m尘/室s一般用于分离
的
粗颗粒。
u
u 0.5m / s
dP 50m
• A—降尘室底面积, 。 m 2
A BL
• u t —颗粒的沉降速度,
决定。
d P,min
u 。m /应s根据要t 分离的最小 颗粒直径
第25页/共71页
重力沉降设备
• 讨论:
★1)对一定物系,ut一定,降尘室的处理能力只取决于降尘室的底面积A, 而与高度H无关,故降尘室应设计成扁平形状,或在室内设置多层水平隔 板。
成正比,服从一次方定律。 • ② Allen区(2 < Rep<500) • 开始发生边界层分离,颗粒后部形成旋涡——尾流→尾
流区压强低→形体曳力增大 • ③ Newton区(500 < Rep<2×105) • 形体曳力占主导地位,表面曳力可以忽略。曳力∝u2 ,
曳力系数与Rep无关。 • ④ Rep>2×105 • 曳力系数骤然下降,层流边界层→湍流边界层分离点后
d
P
4dP P
ReP 2
ut
4dP (P )g 3
24 24 ReP d put
ut
dP2(P )g 18
ut
4dP (P )g 3 24
ut
dP2(P )g 18
d put
第14页/共71页
2 ReP 500
500 ReP 2105
• 讨论:
ut
0.781
d
1.6 P
第10页/共71页
(1)沉降的加速阶段
• 问题:将一个表面光滑的球形颗粒置于静止的流体中,
若颗粒在重力的作用下沿重力方向作沉降运动,此时
颗Fg粒受m到g 哪6些d力P3的P g作用呢?
化工原理第三章离心沉降ppt课件

与重力沉降速度的比值。
dP2 (P ) ut2
Kc
ur u
18 r gdP2 (P )
ut2 gr
18
——离心分别因数
【作用】Kc是表示离心力大小的目的。 Kc越大,阐 明离心分别设备性能越好。
【例】当旋转半径r=0.4m,切向速度ut =20m/s时,
求离心分别因数。
Kc
ut2 202 =102 gr 9.810.4
分量 kg
91 152 180 253 338 420
大 型 旋 风 分 别 器
5、旋风分别器的特点 〔1〕构造简单,易于制造、安装和维护管理,设备 投资和操作费用都较低。 〔2〕在普通操作条件下,作用于粒子上的离心力是 重力的5~2500倍〔离心分别要素〕,所以旋风除尘 器的效率显著高于重力沉降室。 〔3〕大多用来去除3μm以上的粒子,并联的多管旋 风除尘器安装对3μm的粒子也具有80~85%的除尘效 率。
气体中所夹带 的尘粒逐渐沉降 到器壁,碰到器 壁后落下,滑向 出灰口。
气体在器内 按螺旋形道路 向器底旋转, 到达底部后折 而向上,成为 内层的上旋的 气流,称为气 芯,然后从顶 部的中央排气 管排出。
旋
风
分
别
器
任
务
气芯
原
理
表
示
图
外旋气流
喷雾枯燥流程图
干料
流化床枯燥器
4、旋风分别器的性能 旋风分别器性能的主要操作参数为: 〔1〕气体处置量; 〔2〕临界粒径; 〔3〕分别效率; 〔4〕气体经过旋风分别器的压强降。
dpc
9b n(P )ui
——临界粒径的计算式
其中气体在器内旋转圈数n经常取5。
〔3〕推导临界粒径计算公式的几点假设 ①进入旋风分别器的气流严厉按照螺旋形道路作等 速运动,且切线速度恒定,等于进口气速ut=ui; ②颗粒沉降过程中所穿过的气流厚度为进气口宽度 b; ③颗粒在层流区内做自在沉降,径向〔沉降〕速度 可用下式表示:
化工原理 沉降
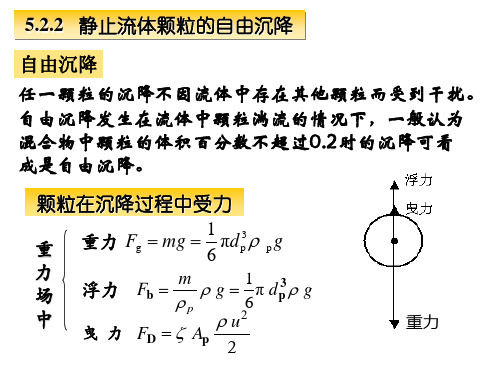
⑶总效率与粒级效率的关系:
0
x
i 1
n
xi ──粒径为dpi颗粒的质量分率 n ──全部颗粒被划分的段数
i i
压降Δ 压降大小是评价其性能好坏的重要指标。
u 2
2
u ──气体在进口管中的流速(进口气速)
──阻力系数,对给定旋风分离器的型号, 为常数
一般其压降约为500~2000Pa。
m ── 颗粒的质量,球形颗粒 ρp ── 颗粒密度
Ap
1 3 m d p p 6
4
2 d p — —垂直沉降方向上的投 影面积
F ma du 重力场: Fg Fb FD m d
据牛顿第二运动定律
或
du P AP 2 g u d 2m P
P P
—— 牛顿公式
沉降速度ut计算方法
计算ut时需先知道所在沉降区域──选择相应式计算。 试差法 设在层流区 计算ut 设在过渡区 no
Re判断
yes
结束
通常微小颗粒的沉降一般属层流区(Stokes区)
沉降速度的影响因素
(1)干扰沉降 发生于颗粒之间距离很小的情况下。多发生于非均 相物系的沉降过程(物系内部有两个以上相)。 当颗粒浓度↑,浮力 ↑ ── ut↓ (2)端效应(器壁效应) 容器壁对颗粒沉降有阻止作用 ,使实际沉降速度 ut<自由沉降速度。当D容器>100dp,可忽略影响。 (3)分子运动 当颗粒直径小到可与流体分子的平均自由程相比拟 时,颗粒可穿过快速运动的流体分子之间,沉降速 度可大于按斯托克斯定律的计算值。
du 0 d
即
du P 3 g u 2 0 d P 4d P P
[高中教育]第3章沉降与过滤ppt
![[高中教育]第3章沉降与过滤ppt](https://img.taocdn.com/s3/m/08dc7dad14791711cd79178c.png)
15.11.2020
16
3.3重力沉降
沉降 在某种力场中利用分散相和连续相之间的密度差异 ,使之发生相对运动而实现分离的操作过程。
重力 作用力
重力 沉降
(分离较大的颗粒)
惯性离心力
离心沉降
3.3.1重力沉降
(分离尺寸小的颗粒)
3.3.1.1球形颗粒的自由沉降
自由沉降:颗粒浓度低,分散好,沉降过程中互不碰 撞、互不影响。
的表面积最小,因此对非球形颗粒,总有S 1 ,颗粒的形 状越接近球形, S 越接近1,对于球形颗粒 S 1。
②颗粒的当量直径
颗粒的当量直径表示非球形颗粒的大小,通常有两种表示
方法: a)等体积当量直径
de
3
6
VP
V P-颗粒体积m3
15.11.2020
7
b)等比表面积当量直径
即与非球形颗粒比表面积相等的球形颗粒的直径为该颗粒的
连续相与分散相 分离
不同的物理性质
机械 分离
分散相和连续相 发生相对运动的方式
15.11.2020
沉降 过滤
3
3.1.2非均相物系分离的目的
(1)收集分散物质
例如从气流干燥器或喷雾干燥器排出的气体中回收固体产品。
(2)净化分散介质
例如:生产硫酸,二氧化硫炉气含杂质,净化。
(3)环境保护
空气中的粉尘、废水、废气治理。
。 (VG/S)/V
一般,乱堆床层ε=0.4~0.7;均匀球体:松排列ε= 0.4,紧密排列ε=0.26。
(2)床层的自由截面积
床层截面上未被颗粒占据的流体可以自由通过的面积, 称为床层的自由截面积。
15.11.2020
10
☆床层的各向同性:小颗粒乱堆床层可以认为是各向同性的 。各向同性床层的重要特性之一是其自由截面积与床层截面 积之比在数值上与床层的空隙率相等。同床层空隙率一样, 由于壁面效应的影响,壁面附近的自由截面积大。
《沉降与过滤》PPT课件

—与真空 管相连
15 不工作区 16-17吹松区、卸料 区 18 不工作区
—h槽 —压缩空气
第4节 膜过滤 一、膜过滤原理与膜组件 〔一〕膜过滤原理
原料液
小分子的 A物质
大分子的 B物质
溢流
膜
A物质
渗透液
?化工原理?课件——第3章 沉降与过滤
第4节 膜过滤
一、膜过滤原理与膜组件
〔二〕膜组件
渗透液
?化工原理?课件——第3章 沉降与过滤
第1节 重力沉降
一、重力沉降速度
球形颗粒: ——Stokes定律
层流区 1 4 0 R e 2区
24
Re
d2()g
ut
s
18
过渡区 2R e50—0—Allen定律区
10
Re0.5
ut d
4g2()2 s 225
?化工原理?课件——第3章 沉降与过滤
40um的颗粒的回收百分率?(4)如欲回收直径为
15um的尘粒,降尘室应各成多少层?
解:(1) VbLu
s
tc
4
utcV s (b)L250.4ms
?化工原理?课件——第3章 沉降与过滤
第1节 重力沉降
二、降尘室
设为层流沉降: utcdc2(1s8)g
dc
18utc (s )g
18 0.0261 030.4 (300 00.7)59.81
(L L e ) W 2 (L L e ) E
〔二〕转筒真空过滤机
转筒及分配头:
?化工原理?课件——第3章 沉降与过滤
第3节 过滤
二、过滤设备
工 作 原
1-7 过滤区 8-10 吸干 区11 不工作区
化工工艺重力沉降技术ppt课件

2.1 沉淀的四种类型
自在沉淀 絮凝沉淀
区域沉淀 (成层沉淀)
紧缩沉淀
2. 沉降的根本实际
2.1 沉淀的四种类型
自在沉淀
絮凝沉淀
区域沉淀 (成层沉淀)
紧缩沉淀
SS(悬浮颗粒浓度)不高; 沉淀过程中悬浮固体之间互不干扰,颗粒各自单独进 展沉淀,颗粒沉淀轨迹呈直线。 沉淀过程中,颗粒的物理性质不变。发生在沉砂池中。
斯公式
单格宽度 b=B/n, 单格池宽>=0.6m
3.3 Camp图解积分 法
给定的沉降时间t内: 对于μ≥μ0的颗粒全部除去 1-p0
对于μ<μ0的颗粒可被部分去除。 p0
给定的沉降时间t内: 对于d≥d0的颗粒全部除去 1-p0
对于d<d0的颗粒可被部分去除。p0
??:对于μ<μ0的颗粒,可去除部分所占比例是多少? 去除率是多少?
H h
3.3 Camp图解积分法〔续〕
(2)颗粒的运动
程度
程度方向:程度流速v等于水流速度;
垂直
垂直方向:沉速即颗粒的自在沉降速度u。
颗粒运动的轨迹为其程度分速v和沉速u的矢量和,是 一组倾斜的直线,其坡度为i=u/v。
设u0为某一指定颗粒d0的最小沉降速度
当颗粒沉速u≥u0时,无论这 种颗粒处于进口端的什么位置, 它都可以沉到池底被去除,即 图a中的迹线xy与x′y′。
uS与d2成正比,因此↑d, uS ↑,提高去除效果。
uS与μ成反比,μ随水温上升而下降;即沉速受水 温影响,水温上升,沉速增大。
3 自在沉降实验和沉降曲线
3.1、实验安装 3.2、常规计算法及沉降曲线 3.3、Camp图解积分法及沉降曲线
φ100 mm
自在沉淀 絮凝沉淀
区域沉淀 (成层沉淀)
紧缩沉淀
2. 沉降的根本实际
2.1 沉淀的四种类型
自在沉淀
絮凝沉淀
区域沉淀 (成层沉淀)
紧缩沉淀
SS(悬浮颗粒浓度)不高; 沉淀过程中悬浮固体之间互不干扰,颗粒各自单独进 展沉淀,颗粒沉淀轨迹呈直线。 沉淀过程中,颗粒的物理性质不变。发生在沉砂池中。
斯公式
单格宽度 b=B/n, 单格池宽>=0.6m
3.3 Camp图解积分 法
给定的沉降时间t内: 对于μ≥μ0的颗粒全部除去 1-p0
对于μ<μ0的颗粒可被部分去除。 p0
给定的沉降时间t内: 对于d≥d0的颗粒全部除去 1-p0
对于d<d0的颗粒可被部分去除。p0
??:对于μ<μ0的颗粒,可去除部分所占比例是多少? 去除率是多少?
H h
3.3 Camp图解积分法〔续〕
(2)颗粒的运动
程度
程度方向:程度流速v等于水流速度;
垂直
垂直方向:沉速即颗粒的自在沉降速度u。
颗粒运动的轨迹为其程度分速v和沉速u的矢量和,是 一组倾斜的直线,其坡度为i=u/v。
设u0为某一指定颗粒d0的最小沉降速度
当颗粒沉速u≥u0时,无论这 种颗粒处于进口端的什么位置, 它都可以沉到池底被去除,即 图a中的迹线xy与x′y′。
uS与d2成正比,因此↑d, uS ↑,提高去除效果。
uS与μ成反比,μ随水温上升而下降;即沉速受水 温影响,水温上升,沉速增大。
3 自在沉降实验和沉降曲线
3.1、实验安装 3.2、常规计算法及沉降曲线 3.3、Camp图解积分法及沉降曲线
φ100 mm
化工原理-沉降

2
例3.2
1)理论最小沉降颗粒直径(临界粒径)
18
(斯托克斯区)
d pc
多级降尘室的dpc更小 多级降尘室的水平隔板数 = N-1
qv NWLut
三、离心沉降
惯性离心力实现的沉降过程
离心沉降速度
切向速 度=rw
4d p ( p ) ui 2 ur 3 r
4d p ( p ) g 3
一、球形颗粒的自由沉降 ----重力沉降
沉降颗粒的受力情况: 重力
Fg
曳力Fd
浮力
曳力
Fb
6
6
d p pg
3
d p 3 g
Fd Ap
曳力 系数
u
2
2
牛顿第二定律
du d p ( p )g d p ( ) ma p d 6 dt 6 4 2 加速段 u 曳力
重力沉降速度的计算
假设沉降 试差法: 属于某一 流型
先假设处于 斯托克斯区 Re<2 Re > 2
计算沉 降速度
核算 Re
dut Re
d 2 s ut g 18
ut 为所求 假设处于 阿伦区
例题: 3-1 再计算 p94 和判断
其它方法简介: 无因次判据法: 计算判据K 的值 由K值确 定沉降所 属区域
标准旋风 分离器: h=D/2, b=D/4, n=5, ξ=8
相关应用:
临界粒径、压强降的计算p100例 3-3
24 Re
10 Re
0.44
已知:
ut
4 gd p ( p ) 3
代入上式:
例3.2
1)理论最小沉降颗粒直径(临界粒径)
18
(斯托克斯区)
d pc
多级降尘室的dpc更小 多级降尘室的水平隔板数 = N-1
qv NWLut
三、离心沉降
惯性离心力实现的沉降过程
离心沉降速度
切向速 度=rw
4d p ( p ) ui 2 ur 3 r
4d p ( p ) g 3
一、球形颗粒的自由沉降 ----重力沉降
沉降颗粒的受力情况: 重力
Fg
曳力Fd
浮力
曳力
Fb
6
6
d p pg
3
d p 3 g
Fd Ap
曳力 系数
u
2
2
牛顿第二定律
du d p ( p )g d p ( ) ma p d 6 dt 6 4 2 加速段 u 曳力
重力沉降速度的计算
假设沉降 试差法: 属于某一 流型
先假设处于 斯托克斯区 Re<2 Re > 2
计算沉 降速度
核算 Re
dut Re
d 2 s ut g 18
ut 为所求 假设处于 阿伦区
例题: 3-1 再计算 p94 和判断
其它方法简介: 无因次判据法: 计算判据K 的值 由K值确 定沉降所 属区域
标准旋风 分离器: h=D/2, b=D/4, n=5, ξ=8
相关应用:
临界粒径、压强降的计算p100例 3-3
24 Re
10 Re
0.44
已知:
ut
4 gd p ( p ) 3
代入上式:
化工原理第三章概述、重力沉降ppt课件

;
(2〕过渡区:2<Re<500,Allen定律区
10
Re (3〕湍流区:500<Re<2×105,Newton定律区
0.44
【阐明】(1〕查ζ-Re关系曲线图,准确但复杂; (2〕经验公式计算简便,但是有误差。
2021/6/5
;
第二节 重力沉降
一、什么是沉降?
2021/6/5
【定义】在某种力场中利用分散相
有关说明
2021/6/5
;
【阻力系数ζ计算的经验公式】 【应用前提】球形颗粒。
根据不同的雷诺数范围〔区域〕内的阻力系数ζ 的变化情况,可用如下经验公式计算阻力系数ζ:
(1〕层流区:10-4<Re<2,Stokes定律区
24
Re
2021/6/5
;
层流区
过渡区
湍流区
2021/6/5
ζ-Re关系曲线图
;
何谓球形度
s
S Sp
S——与物体相同体积的球体的表面积; SP——物体的表面积。
【定义】与物体相同体积的球体的表面积和物体的 表面积之比。
2021/6/5
;
(1〕此处的雷诺数Re是指:
Re d Pu
计算Re时,dP应为足以表征颗粒大小的长度〔特 性尺寸),对球形颗粒而言,就是它的直径。
(2〕此处的区域〔如层流区〕范围与 流动型态的区域范围并不相同。
2021/6/5
;
【准数判别法】如果不能确定流动处在哪个区,亦 可采用以下方法先确定区域。通过实验整理数据可 得到:
其中:
Re
Ar
18 0.6 Ar
Ar
d
3 P
P
2
g
——阿基米德准数
2021/6/5
(2〕过渡区:2<Re<500,Allen定律区
10
Re (3〕湍流区:500<Re<2×105,Newton定律区
0.44
【阐明】(1〕查ζ-Re关系曲线图,准确但复杂; (2〕经验公式计算简便,但是有误差。
2021/6/5
;
第二节 重力沉降
一、什么是沉降?
2021/6/5
【定义】在某种力场中利用分散相
有关说明
2021/6/5
;
【阻力系数ζ计算的经验公式】 【应用前提】球形颗粒。
根据不同的雷诺数范围〔区域〕内的阻力系数ζ 的变化情况,可用如下经验公式计算阻力系数ζ:
(1〕层流区:10-4<Re<2,Stokes定律区
24
Re
2021/6/5
;
层流区
过渡区
湍流区
2021/6/5
ζ-Re关系曲线图
;
何谓球形度
s
S Sp
S——与物体相同体积的球体的表面积; SP——物体的表面积。
【定义】与物体相同体积的球体的表面积和物体的 表面积之比。
2021/6/5
;
(1〕此处的雷诺数Re是指:
Re d Pu
计算Re时,dP应为足以表征颗粒大小的长度〔特 性尺寸),对球形颗粒而言,就是它的直径。
(2〕此处的区域〔如层流区〕范围与 流动型态的区域范围并不相同。
2021/6/5
;
【准数判别法】如果不能确定流动处在哪个区,亦 可采用以下方法先确定区域。通过实验整理数据可 得到:
其中:
Re
Ar
18 0.6 Ar
Ar
d
3 P
P
2
g
——阿基米德准数
2021/6/5
化工原理第三章1沉降

实验装置与步骤
• 实验装置:沉降实验装置主要包括实验管、测量段、流量计、 压力计、搅拌器和数据采集系统等部分。实验管采用透明材料 制成,以便观察颗粒的沉降行为。测量段用于放置光学检测器 或摄像头,以便记录颗粒的沉降过程。流量计用于测量流体的 流量,压力计用于测量流体的压力,搅拌器用于保证流体的均 匀性。数据采集系统用于实时采集实验数据。
沉降的原理
由于颗粒或液滴受到重力 作用,它们会向气体的下 游方向移动,最终在某一 位置沉积下来。
沉降的分类
重力沉降、离心沉降和惯 性沉降。
重力沉降速度的计算
斯托克斯定律
颗粒在静止流体中的沉降速度与颗粒直径的平方成正 比,与流体粘度成反比。
修正的斯托克斯定律
考虑到颗粒形状、密度和流体粘度的影响,对斯托克 斯定律进行修正。
颗粒的密度
颗粒的密度是指颗粒的质量与其体积的比值。密度大的颗粒在流体中更容易下沉 ,而密度小的颗粒则更容易漂浮。
在化工生产中,密度差异是实现固液分离的重要依据之一。
颗粒的粒径和粒径分布
颗粒的粒径是指其直径或宽度,而粒 径分则是指颗粒群中不同粒径颗粒 的分布情况。
粒径和粒径分布对颗粒的沉降速度和 沉降效果有显著影响。在化工生产中, 控制颗粒的粒径和粒径分布对于提高 产品质量和生产效率具有重要意义。
数据分析
对处理后的数据进行统计分析,包括描述性统计、相 关性分析和回归分析等步骤。描述性统计主要是计算 平均值、中位数、标准差等统计量,相关性分析主要 是分析各因素之间的相关性,回归分析主要是建立数 学模型预测沉降速度。通过数据分析可以得出颗粒的 粒径、密度、流体粘度等因素对沉降速度的影响程度 和规律,为实际工业应用提供理论依据。
颗粒的流体阻力特性
(化工原理)第二节 沉降过程

同一种固体物质,球形或近球形颗粒 比同体积的非球形颗粒的沉降要快一些 4、颗粒粒径
布朗运动
沉降速度计算—试差法
四、沉降速度的计算
1、试差法
设Rep选公式 ut核算Rep判断
沉降速度计算—摩擦数群法
2、摩擦数群法
3
沉降速度计算—摩擦数群法
ζ是Ret的已知函数,则 ζRet2 也是Ret的已知函数。
气体在器内的运动情况
离心沉降-7
三、旋风分离器的性能 (分离效果、压强降)
( 一)、临界粒径
旋风分离器中能被完全分离下来的最小颗粒直径。
临界粒径的计算式,可在如下简化条件之下 推导出来。
(1)进入旋风分离器的气流严格按螺旋形路线作等速运动,其 切向速度等于进口气速ui
(2) 颗粒向器壁沉降时,必须穿过厚度等于整个进气口宽度B的 气流层,方能到达壁面 而被分离。
离心沉降-3
颗粒的离心沉降速度 ur与重力沉降速度 ut 具有相似的关系式,只是将重力场强度 g 改为惯性离心力场强度 uT²/R
区别:
离心力沉降速度ur 不是颗粒运动的绝对速度,而是 绝对速度在径向上的分量,且方向不是向下而是沿 半径向外;
离心沉降速度ur 本身就不是一个恒定的数值,而重 力沉降速度ut 则是不变的。
标准型
课本有误
离心沉降-16
xi——粒径在第I小段范围内的颗粒占全部颗粒的质量分率 ηpi——第I小段粒径范围内的颗校的粒级效率, n——全部粒径被划分的段数。
压强降
(三)、 压强降
标准型旋风分离器,其阻力系数ξ=8.0 一般压强降在500-2000Pa
影响旋风分离器性能的因素多而复杂, 物系情况及操作条件是其中的重要方 面。
一、沉 降 速 度 (一)、球形颗粒的自由沉降
布朗运动
沉降速度计算—试差法
四、沉降速度的计算
1、试差法
设Rep选公式 ut核算Rep判断
沉降速度计算—摩擦数群法
2、摩擦数群法
3
沉降速度计算—摩擦数群法
ζ是Ret的已知函数,则 ζRet2 也是Ret的已知函数。
气体在器内的运动情况
离心沉降-7
三、旋风分离器的性能 (分离效果、压强降)
( 一)、临界粒径
旋风分离器中能被完全分离下来的最小颗粒直径。
临界粒径的计算式,可在如下简化条件之下 推导出来。
(1)进入旋风分离器的气流严格按螺旋形路线作等速运动,其 切向速度等于进口气速ui
(2) 颗粒向器壁沉降时,必须穿过厚度等于整个进气口宽度B的 气流层,方能到达壁面 而被分离。
离心沉降-3
颗粒的离心沉降速度 ur与重力沉降速度 ut 具有相似的关系式,只是将重力场强度 g 改为惯性离心力场强度 uT²/R
区别:
离心力沉降速度ur 不是颗粒运动的绝对速度,而是 绝对速度在径向上的分量,且方向不是向下而是沿 半径向外;
离心沉降速度ur 本身就不是一个恒定的数值,而重 力沉降速度ut 则是不变的。
标准型
课本有误
离心沉降-16
xi——粒径在第I小段范围内的颗粒占全部颗粒的质量分率 ηpi——第I小段粒径范围内的颗校的粒级效率, n——全部粒径被划分的段数。
压强降
(三)、 压强降
标准型旋风分离器,其阻力系数ξ=8.0 一般压强降在500-2000Pa
影响旋风分离器性能的因素多而复杂, 物系情况及操作条件是其中的重要方 面。
一、沉 降 速 度 (一)、球形颗粒的自由沉降
化工原理第三章概述重力沉降

•核算流型:
•故原假设层流区正确,求得的沉降速度有效。
••2020/10/11
•(2) 在20℃的空气中的沉降 •用阿基米德准数判断沉降区域: •查得20℃空气:ρ=1.205 kg/m3,μ=1.81×10-5 Pa.s •①计算阿基米德准数:
••2020/10/11
•②计算雷诺准数:
•由于 2<Re<500 , 故知沉降处在过渡区。 •③据阿伦公式: •④由此可知,沉降速度为:
•【例如】粘性流体对球体的低速绕流(也称爬流) 时,可用斯托克斯(Stokes)公式计算,即:
••2020/10/11
• 当流速较高时,Sokes定律不成立。因此,对一般 流动条件下的球形颗粒及其其他形状的颗粒,Fd的 数值尚需通过实验解决。 • 对球形颗粒,经分析并整理后可得:
•——阻力计算的经验公式
••2020/10/11
•五、非均相物系分离的作用
•(1)回收分散物质;(从催化反应器中回收催化 剂颗粒)
•(2)净制连续介质;(二氧化硫气体除尘)
•(3)保护环境。(污水处理、除去烟道气中的粉 尘等)
••2020/10/11
•催化剂再生器
•催裂化反应器
•分馏塔
•旋液分离器
•催化裂化工艺流程图
•旋风分离器
•式中 ζ——形状阻力系数;
•
A——颗粒在运动方向上的投影面积;
•
u——颗粒与流体的相对运动速度。
••2020/10/11
•4、阻力(曳力)系数ζ •【规律】目前尚无法通过理论分析获得阻力系数计 算关系式,但大量的实验证明:阻力(曳力)系数ζ 是雷诺数及球形度的函数,即:
•【获取方法】当球形度一定时,阻力(曳力)系数ζ 获取方法有如下两种: •(1)查取ζ-Re关系曲线图; •(2)使用经验公式。
•故原假设层流区正确,求得的沉降速度有效。
••2020/10/11
•(2) 在20℃的空气中的沉降 •用阿基米德准数判断沉降区域: •查得20℃空气:ρ=1.205 kg/m3,μ=1.81×10-5 Pa.s •①计算阿基米德准数:
••2020/10/11
•②计算雷诺准数:
•由于 2<Re<500 , 故知沉降处在过渡区。 •③据阿伦公式: •④由此可知,沉降速度为:
•【例如】粘性流体对球体的低速绕流(也称爬流) 时,可用斯托克斯(Stokes)公式计算,即:
••2020/10/11
• 当流速较高时,Sokes定律不成立。因此,对一般 流动条件下的球形颗粒及其其他形状的颗粒,Fd的 数值尚需通过实验解决。 • 对球形颗粒,经分析并整理后可得:
•——阻力计算的经验公式
••2020/10/11
•五、非均相物系分离的作用
•(1)回收分散物质;(从催化反应器中回收催化 剂颗粒)
•(2)净制连续介质;(二氧化硫气体除尘)
•(3)保护环境。(污水处理、除去烟道气中的粉 尘等)
••2020/10/11
•催化剂再生器
•催裂化反应器
•分馏塔
•旋液分离器
•催化裂化工艺流程图
•旋风分离器
•式中 ζ——形状阻力系数;
•
A——颗粒在运动方向上的投影面积;
•
u——颗粒与流体的相对运动速度。
••2020/10/11
•4、阻力(曳力)系数ζ •【规律】目前尚无法通过理论分析获得阻力系数计 算关系式,但大量的实验证明:阻力(曳力)系数ζ 是雷诺数及球形度的函数,即:
•【获取方法】当球形度一定时,阻力(曳力)系数ζ 获取方法有如下两种: •(1)查取ζ-Re关系曲线图; •(2)使用经验公式。
