2019小升初奥数几何图形综合训练题(平面图形部分)

合集下载

小升初专项复习《平面图形》(一)练习及答案

小升初专项复习《平面图形》一、填空题1．若等腰三角形的两边长分别为2和6，则它的周长为。

2．一个等腰三角形的两边长分别是米和米，这个三角形的周长是米。

3．长方形的面积是24平方厘米，长和面积的比是1：4，则长方形的宽是厘米。

4．用一根10.28米长的铁丝围成一个半圆，这个半圆的面积是平方米。

5．如图，把圆分成若干等份，剪拼成一个近似的长方形，已知长方形的宽为5cm，则长是cm，长方形的面积是cm2。

6．同一个圆中圆的与的比值叫做圆周率。

7．圆的位置与有关系，圆大小的与有关系。

8．晶晶画了一个平行四边形，它的高是 dm，底是高的。

这个平行四边形的面积是dm2。

9．如图，零件厂要加工一批环形铁片，每个铁片的面积是平方厘米。

10．一个平行四边形的底是8厘米，面积是48.8平方厘米，高是厘米，与它等底等高的三角形的面积是平方厘米。

11．等腰三角形的一个底角是40°，它的顶角是°，这是一个角三角形。

12．一个梯形的上底是5厘米，下底是10厘米，高是5厘米（如图）。

这个梯形的一个钝角是°，这个梯形的面积是平方厘米。

13．一个长方形的长：宽=7：5，长比宽多6厘米，这个长方形的周长是，面积是。

14．在一个长8cm，宽3cm的长方形中剪出一个最大的半圆，这个半圆的周长是cm，面积是cm2。

15．如图，平行四边形的面积是20平方厘米，图中甲乙丙三个三角形的面积比是。

二、单选题16．两个正方形的边长的比是5：3，它们的面积的比是（）A．3：5B．1：3C．5：1D．25：917．在一个长1.25米，宽0.8米的长方形里，最多能剪（）个半径为20厘米的圆。

A．5B．7C．6D．2418．自行车的前轮半径为30厘米，后轮半径为20厘米。

如下图，当前轮向前行驶了5圈回到E点的位置时，后轮F点的位置是下图中的（）。

A．B．C．D．19．如图，把正方形桌子面的四边撑起，就成了一张圆面桌子，经过测量圆面桌子的面积为π平方米，那么这张桌子的正方形桌面的面积为（）平方米。

六年级小升初毕业考试总复习——几何图形专项复习(附答案)

六年级小升初毕业考试——几何图形专项训练⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧⎪⎩⎪⎨⎧→⎪⎪⎪⎩⎪⎪⎪⎨⎧⎩⎨⎧⎩⎨⎧→→圆锥圆柱正方体长方体立体图形扇形圆环圆梯形正方形长方形平行四边形四边形三角形平面图形几何图形一、平面图形知识要点：1. 三角形（1）三角形具有稳定性。

（2）三角形的内角和是180°。

（3）三角形三边关系：在一个三角形中，任意两边之和大于第三边，任意两边之差小于第三边。

（4）三角形的面积=底×高÷22.四边形（1）长方形的周长=(长+宽）×2 长方形的面积=长×宽（2）正方形的周长=边长×4 正方形的面积=边长×边长（3）平行四边形的面积=底×高（4）梯形的面积=（上底+下底）×高÷23.圆（1）圆的周长:c=πd c=2πr 圆的面积：s=πr ²（2）圆环的面积=外圆面积-内圆面积 s=πR ²-πr ²或 s=π（R ²-r ²）（3）扇形的周长=半径×2+弧长 c=2r+2πr ×360n扇形的面积=圆面积×360n s=πr ²×360n28m 近似三角形了，真有意思！1.(西城2019年小学毕业数学测查卷)一个用草绳编织成的茶杯垫的上面是圆形，将它沿半径剪开，下面说法不正确．．．的是( ). A.近似三角形的底相当于圆的周长 B.近似三角形的高相当于圆的半径 C.近似三角形的面积相当于圆的面积 D.近似三角形的面积相当于圆面和的212.(西城2019年小学毕业数学测查卷)一个长方体，有两个相对的面是正方形。

它的长是8cm.宽是5cm.这个长方体的表面积最少是( )cm 2.A.130B. 200C.210D. 2883.(西城2019年小学毕业数学测查卷)如下图小圆贴着大圆的内侧从A 点开始按箭头所指方向滚动(大圆不动．．．．)。

小升初奥数几何图形综合训练题(平面图形部分)

小升初数学几何图形专题训练含参考答案(5篇)

小升初数学几何图形专题知识训练含答案一、单选题1．甲数和乙数的比是4∶7，甲数是乙数的（）A．47B．74C．342．甲数的14和乙数的34相等，那么甲数（）乙数。

A．大于B．小于C．等于D．不能比较3．在一张长8厘米，宽6厘米的长方形纸上，剪下一个最大的正方形，这个正方形的面积是（）。

A．36平方厘米B．48平方厘米C．64平方厘米4．下面图形都是由3个边长1厘米的小正方形组成的，其中周长最长的是（）。

A．B．C．5．旋转能得到（）A．圆柱B．圆锥C．一个空心的球6．如图，图中的物体从（）看到的形状是相同的．A．正面和上面B．正面和右面C．上面和右面7．下面运用“转化”思想方法的是（）。

A．①和②B．①和③C．②和③8．下列叙述正确的是（）A．两个数的最小公倍数是它们最大公因数的倍数。

B．三角形的底和高扩大2倍，它的面积也扩大2倍。

C．相邻两个非0的自然数，其中一定有一个是合数。

9．两个完全相同的长方形（如图），将图①和图②阴影部分的面积相比，（）A．图①大B．图②大C．图①和图②相等10．下列说法中正确的有（）。

①2厘米长的线段向上平移10厘米，线段的长还是2厘米。

②8080008000这个数只读出一个“零”。

③万级包括亿万、千万、百万、十万、万五个数位。

④三位数乘两位数，积不可能是六位数。

A．2个B．3个C．4个二、填空题11．在一个宽为6厘米的长方形里恰好能画两个同样尽量大的圆(如图).圆的直径为厘米，半径为厘米；一个圆的周长为厘米，面积为平方厘米；长方形的面积是平方厘米，阴影部分的面积是平方厘米．12．一个梯形的上底是5.8厘米，下底是6.2厘米，高是2.5厘米，它的面积是平方厘米。

13．是由几个拼成的。

；；。

14．在横线上填上“平移”或“旋转”。

汽车行驶中车轮的运动是现象；推拉门被推开是现象。

15．把一个棱长为6 cm的正方体木块削成一个最大的圆柱，圆柱的体积是，再把这个圆柱削成一个最大的圆锥，这个圆锥的体积是。

小升初(六年级)重点初中招生考试分类试题——平面图形综合

小升初（六年级）重点初中招生考试分类试题平面图形综合求角度1．如下图中，那么：∠1＋∠2＋∠3＋∠4＋∠5= 度。

2．下图中，小于180°的角有个？如果∠2＋∠3=∠1＋∠4，那么当∠AOB 等于度时，图中所有角的和等于360°。

3．在三角形ABC 中，D 、E 是BC 边上的点，BD=AB ，CE=AE ，又,31BAC DAE ∠=∠求BAC ∠的度数？数图形4．如图所示是半个正方形，它被分成一个个小的等腰三角形，图中正方形有个，三角形有个。

5．数一数，图中包含☆的长方形有______个．1 2 345 A OB12 3 4 DEAC6．由三个边长为1的正方形拼成如图所示的左右对称的图形，以图中正方形的10个顶点为顶点可得到许多不同的三角形，那么，在这些三角形中，面积为1的三角形共有个。

（面积为1的三角形的三条边中至少有一条边是水平或垂直的）综合能力提升7．两块直角边分别是6厘米和10厘米的等腰直角三角形板，如下图那样重合。

求重合部分（阴影所示）的面积是平方厘米。

8．求下图中阴影部分的面积（单位：厘米）。

9．如图所示，长方形ABCD 中，AB=24厘米，BC=36厘米，E 是BC 的中点，F ，G 分别是AB ，CD 的4等分点，H 为AD 上任意一点，求阴影部分面积。

10．在图中，长方形长为12厘米，宽为6厘米，把长分成3等份，宽分为2等份，长方形内任一点与分点及顶点连接起来，求阴影部分的面积和是多少平方厘米？11．如图，正六边形ABCDEF 的面积是6平方厘米，M 是AB 中点，N 是CD 中点，P 是EF 中点。

△MNP 的面积是多少平方厘米？AH D12．如图中阴影部分的面积。

13．如图：△ABC 是等腰直角三角形，AB ＝BC ＝10CM ，AB 是半圆的直径，CB 是扇形BCD 的半径，求阴影部分的面积。

14．如图，以10×10的正方形的4条边为直径，在正方形的内部作4个半圆，求阴影部分的面积。

小升初奥数常考题第四讲几何综合

小升初奥数常考题第四讲几何综合内容概述勾股定理，多边形的内角和，两直线平行的判别准则，由平行线形成的相似三角形中对应线段和面积所满足的比例关系．与上述知识相关的几何计算问题．各种具有相当难度的几何综合题．典型问题1．如图30-2，已知四边形ABCD 和CEFG 都是正方形，且正方形ABCD 的边长为10厘米，那么图中阴影三角形BFD 的面积为多少平方厘米?【分析与解】方法一：因为CEFG 的边长题中未给出，显然阴影部分的面积与其有关．设正方形CEFG 的边长为x ，有：=1010=100,ABCD S ⨯正方形2=x ,S 正方形CEFG 21110x-x =DG GF=(10-x)x=,222DGF S ∆⨯ 又1=1010=50,2ABD S ∆⨯⨯2110x+x =(10+x)x=.22BEF S ∆ 阴影部分的面积为:DGF ABD BEF ABCD CEFG S S S S S ∆∆∆++--正方形正方形2221010100505022x x x x x -+=++--=(平方厘米). 方法二：连接FC ，有FC 平行与DB ，则四边形BCFD 为梯形．有△DFB 、△DBC 共底DB ，等高，所以这两个三角形的面积相等，显然,△DBC 的面积11010502⨯⨯=(平方厘米)．阴影部分△DFB 的面积为50平方厘米．2.如图30-4，∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠I等于多少度?【分析与解】为了方便所述，如下图所示，标上数字，有∠I=1800 -(∠1+∠2),而∠1=1800-∠3, ∠2=1800-∠4,有∠I=∠3+∠4-1800同理, ∠H=∠4+∠5-1800, ∠G=∠5+∠6-1800, ∠F=∠6+∠7-1800, ∠E=∠7+∠8-1800,∠D=∠8+∠9-1800, ∠C=∠9+∠10-1800, ∠B=∠10+∠11-1800, ∠A=∠11+∠3-1800则∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠I=2×(∠3+∠4+∠5+∠6+∠7+∠8+∠9+∠10+∠11)-9×1800而∠3+∠4+∠5+∠6+∠7+∠8+∠9+∠10+∠11正是9边形的内角和为(9-2)×1800=12600．所以∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠I=2×12600-9×1800=90003．长边和短边的比例是2：1的长方形称为基本长方形．考虑用短边互不相同的基本长方形拼图，要求任意两个基本长方形之间既没有重叠，也没有空隙.现在要用短边互不相同且最小短边长为1的5个基本长方形拼接成一个更大的长方形．例如，短边长分别是1，2，5，6，12的基本长方形能拼接成大长方形，具体案如图30-6所示．请给出这5个基本长方形所有可能的选择方式.设a1=1<a2<a3<a4<a5分别为5条短边的长度,则我们将这种选择方式记为(a1,a2,a3,a4,a5),这里无需考虑5个基本长方形的拼图方案是否惟一．【分析与解】我们以几个不同的基本长方形作为分类依据，并按边长递增的方式一一列出．第一类情况：以为特征的有7组：第二类情况：以为特征的有6组：第三类情况有如下三组：共有16组解，它们是：(1，2，2.5，5，7.25)，(1，2，2．5，5，14.5)．(1，2，2.25，2.5，3.625)，(1，2，2.25，2.5，7.25)．(1，2，5，5.5，6)，(1，2，5，6，11)，(1，2，2.5，4.5，7)，(1，2，2.5，4.5，14)，(1，2，5，12，14.5)，(1，2，5，12，29)，(1，2，2.25，2.5，4.5)，(1，2，5，6，12).1020251,,2,,,999⎛⎫ ⎪⎝⎭(1,2,2.4,4.8,5), 131025147813101,,,,,1,,,,636333313⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭.4.如图30-8，ABCD 是平行四边形，面积为72平方厘米，E ，F 分别为边AB,BC 的中点．则图形中阴影部分的面积为多少平方厘米?【分析与解】如下图所示，连接EC ，并在某些点处标上字母，因为AE 平行于DC ，所以四边形AECD 为梯形，有AE:DC=1:2，所以:1:4AEG DCG S S ∆∆=,AGD ECG AEG DCG S S S S ∆∆∆∆⨯=⨯,且有AGD ECG S S ∆∆=,所以:1:2AEG ADG S S ∆∆=,而这两个三角形高相同，面积比为底的比，即EG ：GD=1:2，同理FH ：HD=1:2．有AED AEG AGD S S S ∆∆∆=+,而111822AED ABCD S S ∆=⨯⨯=(平方厘米) 有EG:GD=:AEG AGB S S ∆∆, 所以1612AEG AED S S ∆∆=⨯=+(平方厘米) 21212AGD AED S S ∆∆=⨯=+(平方厘米) 同理可得6HFC S ∆=(平方厘米), 12DCH S ∆=(平方厘米) ,44624DCG AEG S S ∆∆==⨯= (平方厘米)又GHD DCG DCH S S S ∆∆∆=-=24-12=12(平方厘米)所以原题平行四边形中空白部分的面积为6+6+12=24(平方厘米)，所以剩下的阴影部分面积为72-24=48(平方厘米)．5．图30-10是一个正方形，其中所标数值的单位是厘米．问：阴影部分的面积是多少平方厘米?【分析与解】如下图所示，为了方便所叙，将某些点标上字母，并连接BG ．设△AEG 的面积为x ，显然△EBG 、△BFG 、△FCG 的面积均为x ，则△ABF 的面积为3x ，120101002ABF S ∆=⨯⨯=即1003x =，那么正方形内空白部分的面积为40043x =. 所以原题中阴影部分面积为400800202033⨯-= (平方厘米)．6．如图30-12，若图中的圆和半圆都两两相切，两个小圆和三个半圆的半径长都是1．求阴影部分的面积．【分析与解】如下图所示，左图中的3个阴影部分面积相等，右图中的3个阴影部分的面积也相等．我们把左下图中的每一部分阴影称为A ，右下图中的每一部分阴影称为B ．大半圆的面积为13332A B ++小圆的面积219322ππ=⨯⨯=.而小圆的面积为π，则9133223A B πππ⎛⎫+=-÷= ⎪⎝⎭，原题图中的阴影部分面积为小半圆面积与阴影A 、B 的面积和，即为5236πππ+=7.如图30-14，将长方形ABCD 绕顶点C 顺时针旋转90度，若AB=4，BC=3，AC=5，求AD 边扫过部分的面积．(π取3.14)【分析与解】如下图所示，如下图所示，端点A 扫过的轨迹为AA A '''，端点D 扫过轨迹为DD D '''，而AD 之间的点，扫过的轨迹在以A 、D 轨迹，AD ，A D ''所形成的封闭图形内，且这个封闭图形的每一点都有线段AD 上某点扫过，所以AD 边扫过的图形为阴影部分．显然有阴影部分面积为A D C ACA ACD S S S S ''''∆∆+--直角扇形直角扇形CD D ,而直角三角形A D C ''、ACD 面积相等．所以=A D C ACA ACD ACA S S S S S S ''''''∆∆+---直角扇形直角扇形CD D 扇形扇形CD D222290909=(54)7.065()36036044AC CD ππππ-=-==平方厘米即AD 边扫过部分的面积为7．065平方厘米．。

人教版六年级下册数学小升初专题训练：平面图形(含答案)

人教版六年级下册数学小升初专题训练：平面图形一、单选题1．用一块长12米、宽8米的长方形铁皮剪成半径是1.5米的小圆（不能剪拼），至多能做（）个。

A．11B．8C．10D．132．如果要搭成一个从正面、左面、上面看到的图形都是如图的几何体，需要（）个小正方体。

A．3B．4C．5D．63．下图是由一个圆分成若干等分后，拼成的一个近似长方形，这个圆的周长与长方形的周长相差约4厘米，这个圆的周长约是（）厘米。

A．6.28B．9.42C．12.56D．无法计算4．从12时到13时，钟的时针与分针可成直角的机会有（）A．1次B．2次C．3次D．4次5．下列时刻中，钟表中时针与分针不成直角的是（）。

A．3：00B．21：00C．9：00D．12：206．一个半径是5cm的半圆，它的周长是（）cm。

A．31.4B．15.7C．25.7D．20.7二、填空题7．已知一个等腰三角形的两条边分别是5厘米、10厘米，那么它的周长是厘米。

8．一个花坛的直径是6m，花坛周围有一条宽1m的环形小路，小路的面积是 m2。

9．一个挂钟的时针长5厘米，一昼夜这根时针的尖端走了厘米，针尖扫的面积是平方厘米。

10．把一个长、宽分别是15厘米和10厘米的长方形，拉成一个一条高为12厘米的平行四边形，它的面积是平方厘米。

11．李大伯用5π米长的篱笆靠墙围了一个半圆形养鸡场，养鸡场的面积是平方米。

12．如图。

∠1＝30°，∠2＝，∠3＝，∠4＝。

13．从9：00到9：15，分针旋转了度，若分针长6厘米，这根分针针尖走过的长度是厘米，扫过的面积是平方厘米。

14．一个三角形内角度数的比是2：3：5，其中最大的内角是度，这是个角三角形。

15．如图中正方形的面积是40cm2，那么涂色部分的面积是 cm2。

16．一辆自行车车轮直径是0.5米，脚踏板齿轮有48个齿，后齿轮有16个齿，脚踏一圈，自行车前进米．17．把两个正方形拼成一个长方形，拼成的长方形周长是30厘米，这个长方形的面积是平方厘米。

小升初奥数课课练-平面几何-通用版

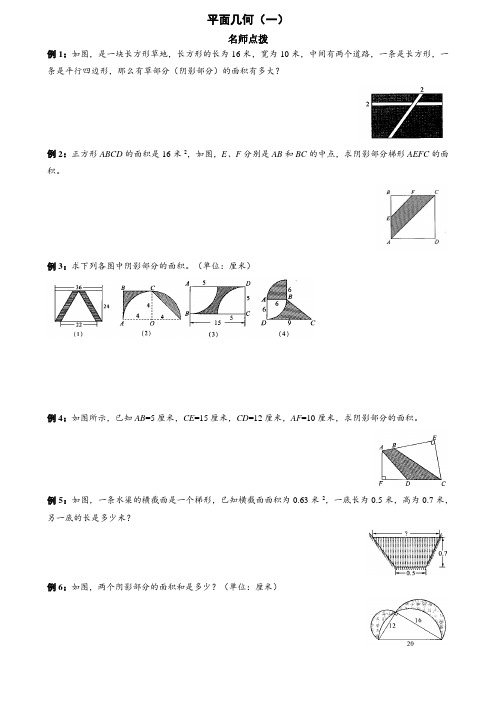
平面几何（一）名师点拨例1：如图，是一块长方形草地，长方形的长为16米，宽为10米，中间有两个道路，一条是长方形，一条是平行四边形，那么有草部分（阴影部分）的面积有多大？例2：正方形ABCD的面积是16米2，如图，E、F分别是AB和BC的中点，求阴影部分梯形AEFC的面积。

例3：求下列各图中阴影部分的面积。

（单位：厘米）例4：如图所示，已知AB=5厘米，CE=15厘米，CD=12厘米，AF=10厘米，求阴影部分的面积。

例5：如图，一条水渠的横截面是一个梯形，已知横截面面积为0.63米2，一底长为0.5米，高为0.7米，另一底的长是多少米？例6：如图，两个阴影部分的面积和是多少？（单位：厘米）名校真题1. 在面积相等的下列平面图形中，周长最小的是（） A. 正方形 B. 等边三角形 C. 长方形 D. 圆形2. 一个三角形的三个角的度数都是质数，这个三角形是（）A. 钝角三角形B. 直角三角形C. 等腰三角形D. 不能确定3. 三角形中最大的一个角一定（）A. 不小于600B. 大于900C. 小于900D. 大于600而小于9004. 一个半圆形零件的周长是17.99厘米，这个半圆的直径是___________厘米。

5. 如图，图形的半径为20厘米，它的周长是___________厘米。

6. 把7个长4厘米、宽3厘米的小长方形，不重叠地拼成一个大长方形，这样拼成的大长方形中最小周长是____________厘米。

名校集训 A 级1. 5127.155123.83.22+⨯+⨯ 2. ⎪⎭⎫ ⎝⎛+⨯⨯913193B 级1. 如图所示，正方形的边长是20厘米，阴影部分的面积是多少平方厘米？2. 如图，四边形ABCD是正方形，ABHE是梯形，ACHE是平行四边形，ECGF是长方形，已知AE=7厘米，BH=12厘米，求阴影部分的面积。

3. 三角形ABC是直角三角形，EG垂直于AC，EG等于3厘米，AB、BC、AC的长度分别是30厘米、40厘米、50厘米，求正方形BDEF的面积。

小升初奥数--点招必备系列课程之三-第3讲-平面几何

4000-636-566
QQ:646615660
7 / 10
如图，在△ABC 中，M 为 AB 边的中点，MD、EC 平行。若△BDE 的面积是 3 平方厘米，则△ ABC 的面积是多少？
如图，△ABC 的面积是 180 平方厘米，D 是 BC 的中点，AD=3AE，EF=3BF。那么△AEF 的面积是多少平方厘米？
1 正方形 ABCD 的边长为 4，E 是 BC 边的中点，F 是 DC 边上的点，且 DF= DC，AE 与 4
BF 相交于 G 点。那么三角形 ABG 的面积是多少？
4000-636-566
QQ:646615660
9 / 10
【答案】例 1：1/7 例 2：22/45 例 3：5/12 例 4:4.8 例 5:59:24 例 6:10 例 7:略例 8:略例 9:24 例 10:8 例 11：5/24 例 12:5 例 13:1:4 思考题：6 练习 1：22.5 练习 2：1/4 练习 3：120 练习 4：6 练习 5：14 练习 6：32/11
◆长方形相关结论(三大面积关系)
S1 S 4 S 2 S3
S 上＋S 下=S 左＋S 右
在梯形中（如上右图），E、F 为 BC、AD 的中点，则有 EF∥DC∥AB，2EF=AB+DC
（1）锯齿定理(左下图)：阴影=空白面积=矩形面积的一半。（2）右下图的三个平等四边形面积相等。
小升初奥数--点招必备系列课程之三第 3 讲—平面几何
知识点概述
1、定理一：如图， ABC 中， D 是 BC 边上一点， E 在 AD 连接（或其延长线上），那么
S ABE BD 。 S ACE CD

小升初数学专项训练——几何图形及其面积(含详细解析)

小升初数学专项训练——几何图形及其面积一、单选题1.求这个图形的面积，可把它分为长方形和（）。

A. 梯形B. 三角形C. 平行四边形D. 正方形2.在下图中你可以找到（）种简单的基本图形。

A. 1B. 2C. 3D. 43.把一个圆分成若干等份，剪开后拼成近似的长方形，那么这两个图形的（）A. 面积、周长都相等B. 面积、周长都不相等C. 面积相等，周长不相等D. 面积不相等，周长相等4.如图中，阴影部分（甲）与空白部分（乙）的周长相比（）A. 甲长B. 乙长C. 一样长5.如图所示，图中三角形的个数为（）A. 9个B. 10个C. 7个D. 4个6.如图中共有（）个三角形．A. 5B. 20C. 157.一个5边形的三个内角是直角，另外两个角相等，那么这两个角的度数是（）。

A. 100°B. 120°C. 135°二、判断题8.105厘米＞1米．9.100厘米比1米长．10. 1米的线段比100厘米的线段长。

11.梯形的内角和是180°。

（）12.任意四边形的内角和都是360°．三、填空题13.如图，CD=15厘米，AE=16厘米．AB﹣BC=1厘米，则三角形ABC的面积是________ 平方厘米．14.把棱长为1分米的正方体表面涂上红色后，再把它分成棱长为1厘米的小正方体．小正方体中只有一面涂色的有________ 个．15.如图，已知三角形ABC中，BD：DC=3：2，E是AD的中点，阴影部分的面积是13.5平方分米，三角形ABC的面积是________ 平方分米16.把这个物体放到地面上，观察并填空。

是由________个小正方体拼成的。

如果把这个图形的表面涂上绿色，不涂色的有________个小正方体；一个面涂绿色的有________个小正方体；有2个面涂绿色的有________个小正方体；有3个面涂绿色的有________个小正方体；有4个面涂绿色的有________个小正方体；有5个面涂红色的有________个小正方体。

小升初数学《平面图形》综合试题及答案

小升初数学《平面图形》综合试题一、填空题1．同一平面内的两条直线的位置关系有两种情况：________和________．2．下面各组直线中，哪两条直线互相垂直？在下面的括号里画“√”。

( ) ( ) ( )3．在两点之间的所有连线中，（____）最短．4．用一个能放大3倍的放大镜看一个15°的角，这个角的度数是（____）。

按度数从小到大，可以把角分为（____）、（____）、（____）、（____）和（____）。

5．一个平行四边形的面积是32m2，与它等底等高的三角形的面积是（____）m2。

6．一个三角形最小的角是60°，那么这个三角形按边分是（_____）三角形。

7．一个等腰梯形的上底是6cm，下底是8cm，一条腰长是7cm，围成这个等腰梯形至少需要（____）cm长的铁丝．8．两个完全一样的三角形可以拼成一个（_____）形。

如果拼成的图形的面积是126cm2，那么一个三角形的面积是（____）cm2。

如果每个三角形的面积是15dm2，那么拼成的图形的面积是（____）dm29．照图操作画出的圆的周长是（____）cm，圆的面积是（____）cm2．10．画圆时，圆规两脚间的距离是2.5cm，则半径是（____）cm，直径是（____）cm。

11．一个边长是20cm的正方形，里面有一个最大的圆，这个圆的半径是（____）cm，面积是（____）cm2。

12．如图，一个平行四边形被分成了甲、乙、丙三部分，已知甲的面积比丙的面积大6cm2，那么丙的面积是（____）cm2。

13．如图，已知大正方形的边长是5cm，小正方形的边长是3cm，那么阴影部分的面积是（____）cm2。

14．一个三角形，其中两个角分别是35°和45°，那么另一个角是（____）°。

按角来分，这是一个（____）三角形。

15．一个直角三角形三条边的长度分别是6cm、8cm、10cm，斜边上的高是（____）cm。

小升初奥数—平面图形计算

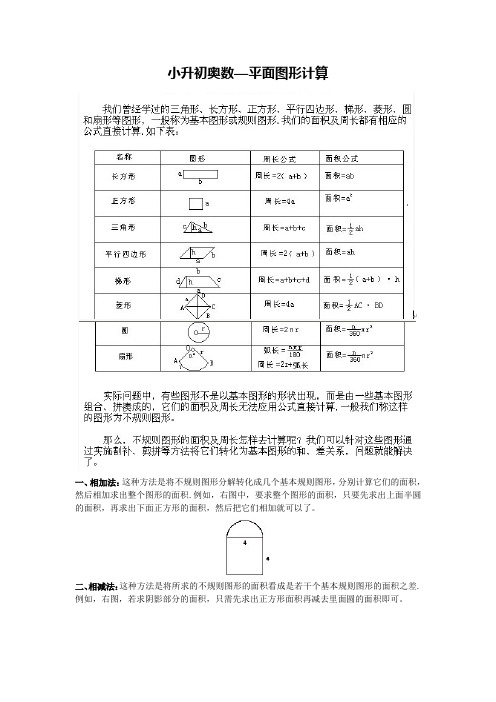
小升初奥数—平面图形计算一、相加法：这种方法是将不规则图形分解转化成几个基本规则图形，分别计算它们的面积，然后相加求出整个图形的面积.例如，右图中，要求整个图形的面积，只要先求出上面半圆的面积，再求出下面正方形的面积，然后把它们相加就可以了。

二、相减法：这种方法是将所求的不规则图形的面积看成是若干个基本规则图形的面积之差.例如，右图，若求阴影部分的面积，只需先求出正方形面积再减去里面圆的面积即可。

三、直接求法：这种方法是根据已知条件，从整体出发直接求出不规则图形面积.如下页右上图，欲求阴影部分的面积，通过分析发现它是一个底2，高4的三角形，就可以直接求面积了。

四、重新组合法：这种方法是将不规则图形拆开，根据具体情况和计算上的需要，重新组合成一个新的图形，设法求出这个新图形面积即可.例如，欲求右图中阴影部分面积，可以把它拆开使阴影部分分布在正方形的4个角处，这时采用相减法就可求出其面积了。

五、辅助线法：这种方法是根据具体情况在图形中添一条或若干条辅助线，使不规则图形转化成若干个基本规则图形，然后再采用相加、相减法解决即可.如右图，求两个正方形中阴影部分的面积.此题虽然可以用相减法解决，但不如添加一条辅助线后用直接法作更简便。

六、割补法：这种方法是把原图形的一部分切割下来补在图形中的另一部分使之成为基本规则图形，从而使问题得到解决.例如，如右图，欲求阴影部分的面积，只需把右边弓形切割下来补在左边，这样整个阴影部分面积恰是正方形面积的一半.七、平移法：这种方法是将图形中某一部分切割下来平行移动到一恰当位置，使之组合成一个新的基本规则图形，便于求出面积.例如，如上页最后一图，欲求阴影部分面积，可先沿中间切开把左边正方形内的阴影部分平行移到右边正方形内，这样整个阴影部分恰是一个正方形。

八、旋转法：这种方法是将图形中某一部分切割下来之后，使之沿某一点或某一轴旋转一定角度贴补在另一图形的一侧，从而组合成一个新的基本规则的图形，便于求出面积.例如，欲求上图（1）中阴影部分的面积，可将左半图形绕B点逆时针方向旋转180°，使A与C 重合，从而构成如右图（2）的样子，此时阴影部分的面积可以看成半圆面积减去中间等腰直角三角形的面积.九、对称添补法：这种方法是作出原图形的对称图形，从而得到一个新的基本规则图形.原来图形面积就是这个新图形面积的一半.例如，欲求右图中阴影部分的面积，沿AB在原图下方作关于AB为对称轴的对称扇形ABD.弓形CBD的面积的一半就是所求阴影部分的面积。

小升初数学平面图形与立体图形综合练习

小升初数学平面图形与立体图形综合练习1、时针和分针一昼夜的路程分别为360°和720°，因为圆的周长为2πr，所以时针和分针一昼夜的路程分别为2π×0.3×360/360°=1.884π厘米和2π×0.4×720/360°=3.768π厘米。

2、根据半圆周长公式C=πr，可得半圆的半径为2.46米，面积为πr²/2=3.783平方米。

3、根据半圆弧长公式L=πr，可得这个半圆的半径为15.7厘米，与之半径相等的圆的面积为πr²=776.7平方厘米。

4、根据半圆周长公式C=πr，可得这个半圆的半径为8.2厘米，与之半径相等的圆的面积为πr²=211.1平方厘米。

5、正方形的面积为31.4²=985.96平方厘米，每个圆的面积为π×5²=78.54平方厘米，所以可以容纳985.96/78.54=12个圆。

6、正方形的面积为12²=144平方厘米，4个圆的总面积为4×π×(12/4)²=36π平方厘米，每个圆的面积为9π平方厘米。

7、前轮每分钟滚动的路程为2×π×7.5×5=235.62厘米，每分钟前进的距离为235.62×2=471.24厘米，每分钟压路面积为2×1×471.24=942.48平方厘米。

8、养鱼池的周长为100.48米，减去圆形小岛的周长2πr=12π米，得到养鱼池的周长为88.48米，根据周长公式C=2πr，可得养鱼池的半径为14.06米，面积为πr²=623.16平方米。

9、大圆的周长是小圆周长的2倍，面积比是4:1.10、围成正方形的绳长为31.4米，所以每条边长为7.85米，正方形的面积为7.85²=61.5225平方米，围成圆形的周长为31.4米，所以半径为5厘米，圆形的面积为π×5²=78.54平方厘米，两者面积相差17.0175平方米。

小升初奥数试题之几何问题附答案)

小升初奥数试题之几何问题（附答案）几何测试题一*境空題〔田蜕玄学业帕分）L 扫图顷示・6： A.l^C中■心门.£> AC r..如*2-7妙，C7F 皿么壬 _ _ i ■LieC £ A2.如工.听于.!L ^fiC t ・ cr ^Cfl r C（） ^CJ. wp-'j rjr..Y ・i\ A^c.rjr';t^jo,則乂酬的面抿答r________ .A ^ S-1.址fWft示，由面积超耕列「X 5 - MCE,」帖上2 r k帀托・已汕Zb - 2 '九注=5 h'迪少\. tUW.Tl -|.. W：'\ABCD f-J I；b_ 12 J'l .<. 7 ,T <■ -ftitt U lull A1«?'K/jhX-D5.如图.四边形ABCD的面积是16平方用米，其中4D = CD・ DE = BE ■ M = 2厘米，那么四边形BCDE的面积是 _______________ 平方厘米•6. ABCD^边长为12的正方形.P是内部任慰一点.BU—. BK=DN = 5・那么阴影部分的面积理•°M二、解答題（每題13分.共52分）7.在三角形中，点E&BC边上的中点，点F是中线AE1.的点，其中AE = 3AF ,己知延长与相交于D,如图所示.若三角形/1BC之而枳为48.说何三角形川的而枳为多少？9. 己知四边形ABCD t CHFG为iE方形” S.v :5^-l：S. a lj止迢冏个止方比的边底”求a:b t3H10. 已知四边形ABCD^正方形，边怏为外殆二13 JF = 1.求阴影削分笛血川“B E小升初奥数试题之几何问题（附答案）（2）2010-05-13 10:16:25来源：智康教育文章作者：匿名进入论坛【分析】山于/D与FG平行，四此Sg严S T也戏有Sg+ 平方厘来.而片"・12x8.2・48半方屋* •旳以Sg^S".S»g・S“” 口48・32 = 16半方座耒.故0(7 = 2$・8寺8 = 2*16于8 = 4圧未.S.【分析】知图斟朴.可幷正方形DF〃恵.正方乜DEFE的占枳是16平方再以边长足4 屋来.四迪怕BCDE 的更积是】6-2x4.2“2 (平方反未).【分斬〕彷卅口条件 Q: ”Z・MC«=】2 —4 = 8. AN=KCZ2-W i£UXP, PC .这许正方彫金阴妙邯分外有6个三血片工几・6个三烏妙的衍釈•九＜-^AOWV -4x5*2 = 10 f过PA分别作ZU甩，APMC , hPAN . APCK的高分躬为人，% W •迖样几* =8x%令2. S屮♦石远Mx仇♦心).2. L&好予于正方妙的边长，侨以仏/几叱=8灯2 + 2 = 48・円胖4$»麻*7*(人+九)令2却7灯2十2 = 42・g 耳(*\VKA 4s^* 毀♦ s un 4 s VMr♦-♦ .y VIK )^12x12 (10 4 10 4 48 4 42)=34.二.解答題(毎題13分.共52分)7.【分析】连按 b.设MEF的®积为凶为E趾BC的中点.AC£F的面枳也是—因a为AE = 3XF t所以EF^lAF .故DBF的面积为囚为血•二仝=2.所以2 CD la42 = !・HAADF的面积为b. ＜4 SCDF的而积为如.囚为ZU〃C时国积为4R.财CD 4a p«162*fl" ,解褂｛8 ＞所以MFD的而积为£・6 4 4A ♦ a « 24 ° 5【分析】如Bh廷长AD・BE .相交于C点，正好可构成一个号麒止角三血形CQE.因此ZC = 45° t i±A^CE的唸线，垂足为则A3 也是一个普腰直角三用邢，A面积正好是正方形面枳的一牛・其对用线C・CD$£M二肋令£M = 8*14・22 (cm )＜所以 $正方專=22* +4x2 = 242 ( cm") •孤据燕足定理：孔呀：耳讥二。

(word完整版)小升初奥数—平面图形计算练习试题

小升初奥数—平面图形计算（一）一、填空题1. 如下图,把三角形ABC 的一条边AB 延长1倍到D ,把它的另一边AC 延长2倍到E ,得到一个较大的三角形ADE ,三角形ADE 的面积是三角形ABC 面积的______倍.2. 如下图,在三角形ABC 中, BC =8厘米, AD =6厘米,E 、F 分别为AB 和AC 的中点.那么三角形EBF 的面积是______平方厘米.3. 如下图,,41,31AC CD BC BE ==那么,三角形AED 的面积是三角形ABC 面积的______.4. 下图中,三角形ABC 的面积是30平方厘米,D 是BC 的中点,AE 的长是ED 的长的2倍,那么三角形CDE 的面积是______平方厘米.5. 现有一个5×5的方格表(如下图)每个小方格的边长都是1,那么图中阴影部分的面积总和等于______.6. 下图正方形ABCD 边长是10厘米,长方形EFGH 的长为8厘米,宽为5厘米.阴影部分甲与阴影部分乙的面积差是______平方厘米.7. 如图所示,一个矩形被分成A 、B 、C 、D 四个矩形.现知A 的面积是2cm 2,B 的面积是4cm 2,C 的面积是6cm 2.那么原矩形的面积是______平方厘米.8.有一个等腰梯形,底角为450,上底为8厘米,下底为12厘米,这个梯形的面积应是______平方厘米.9.已知三角形ABC的面积为56平方厘米、是平行四边形DEFC的2倍,那么阴影部分的面积是______平方厘米.10.下图中,在长方形内画了一些直线,已知边上有三块面积分别是13,35,49.那么图中阴影部分的面积是______.二、解答题11.已知正方形的面积是50平方厘米,三角形ABC两条直角边中,长边是短边的2.5倍,求三角形ABC的面积.12.如图,长方形ABCD中, AB=24cm,BC=26cm,E是BC的中点,F、G分别是AB、CD的四等分点, H为AD上任意一点,求阴影部分面积.13.有两张正方形纸,它们的边长都是整厘米数,大的一张的面积比小的一张多44平方厘米.大、小正方形纸的边长分别是多少?14.用面积为1,2,3,4的四张长方形纸片拼成如图所示的一个长方形.问:图中阴影部分面积是多少?平面图形计算（一）习题答案1. 6.如下图,连接BE ,因为AC CE 2=,所以,ABC BCE S S ∆∆=2,即ABC ABE S S ∆∆=3.又因为BD AB =,所以,BDE ABE S S ∆∆=,这样以来,ABC ADE S S ∆∆=6.2. 6.已知E 、F 分别是AB 和AC 的中点,因此ABF ∆的面积是ABC ∆的面积的21,EBF ∆的面积又是ABF ∆的面积的21.又因为24682121=⨯⨯=⨯=∆AD BC S ABC (平方厘米), 所以6242121=⨯⨯=∆EBF S (平方厘米). 3. 21.由,41,31AC CD BC BE ==可知AC AD BC EC 4,332==.因为ABC ∆与AEC ∆是同一个顶点,底边在同一条线段,所以这两个三角形等高,则三角形面积与底边成正比例关系,因此ABCAEC SS ∆∆=32.同理可知AEC AED S S ∆∆=43.这样以来,AED ∆的面积是ABC ∆的32的43,即是ABC ∆的面积的21. 所以,AED ∆的面积是ABC ∆的21. 4. 5.因为D 是BC 的中点,所以三角形ADC 和三角形ABD 面积相等(等底、等高的三角形等积),从而三角形ADC 的面积等于三角形ABC 面积的一半,即30÷2=15(平方厘米).在CDE ∆与ADC ∆中,DA DE 31=,高相等,所以CDE ∆的面积是ADC ∆面积的31.即CDE ∆的面积是51531=⨯(平方厘米)5. 10三个阴影三角形的高分别为3,2,2,底依次为2,4,3,所以阴影部分面积总和等于10322142212321=⨯⨯+⨯⨯+⨯⨯. 6. 60设正方形ABCD 的面积为a ,长方形EFGH 的面积为b ,重叠部分EFNM 的面积为c ,则阴影部分的面积差是:b a c b c a -=---)()(.即阴影部分的面积差与重叠部分的面积大小无关,应等于正方形ABCD 的面积与长方形EFGH 的面积之差.所求答案:10×10-8×5=60(平方厘米).7. 24图中的四个矩形是大矩形被两条直线分割后得到的,矩形的面积等于一组邻边的乘积.从横的方向看,两个相邻矩形的倍比关系是一致的,B 是A 的2倍,那么D 也应是C 的2倍,所以D 的面积是2×6=122cm ,从而原矩形的面积是2+4+6+12=242cm .8. 20如下图,从上底的两个端点分别作底边的垂线,则BCFE 是矩形, 22)812(=÷-==CD AB (厘米).因为045=∠A ,所以ABE ∆是等腰直角三角形,则2==AB BE (厘米).根据梯形的求积公式得:()2022128=⨯+=梯形S (平方厘米).9. 14由已知条件,平行四边形DEFC 的面积是:56÷2=28(平方厘米)如下图,连接EC ,EC 为平行四行形DEFC 的对角线,由平行四边形的性质如,S S DEC 21=∆DEFC281⨯=14=(平方厘米).在AED ∆与CED ∆中,ED 为公共底边,DE 平行于AC ,从而ED 边上的高相等,所以,CED AEDS S∆∆=14=(平方厘米).10. 97因为长方形的面积等于ABC ∆与ECD ∆的面积和,所以ABC ∆与ECD ∆ 重叠部分的面积等于长方形未被这两个三角形盖住部分的面积和,即97133549=++=影阴S.11. 画两条辅助线如下图,根据条件可知,正方形面积是长方形ABCD 面积的2.5倍.从而 ABCD 的面积是50÷2.5=20(平方厘米).所以ABC ∆的面积是20÷2=10(平方厘米).12. 连结BH ,BEH ∆的面积为)(21624)236(212cm =⨯÷⨯.把BHF ∆和DHG ∆结合起来考虑,这两个三角形的底BF 、DG 相等,且都等于长方形宽的41,它们的高AH 与DH 之和正好是长方形的长,所以这两个三角形的面积之和是:)(212112DH AH BF DH DG AH BF +⨯⨯=⨯⨯+⨯⨯ )(10836244121212cm AD BF =⨯⨯⨯=⨯⨯=.于是,图中阴影部分的面积为216+108=324)(2cm . 13. 把两张正方形纸重叠在一起,且把右边多出的一块拼到上面,成为一个长方形,如图: 这个长方形的面积是44平方厘米,它的长正好是两个正方形的边长的和,它的宽正好是两个正方形的边长的差.因为两个整数的和与它们的差是同奇或同偶,而44又只能分解成下面的三种形式: 44=1×44=2×22=4×11.所以,两个正方形的边长的厘米数的和与差只能是22与2.于是,两个正方形的边长是(22+2)÷2=12(厘米),12-2=10(厘米).14. 如图大长方形面积为1+2+3+4=10.延长RA 交底边于Q ,延长SB 交底边于P .矩形ABPR 面积是上部阴影三角形面积的2倍.矩形ABSQ 是下部阴影三角形面积的2倍.所以矩形RQSP 的面积是阴影部分面积的两倍.知CD CA 31=, CD CB 73=CD CD CD CA CB AB 2123173=-=-=∴因此矩形RQSP 的面积是大矩形面积的212,阴影部分面积是大矩形面积的211.阴影部分面积=211×10=2110.小升初奥数—平面图形计算（二）一、填空题1. 下图是由16个同样大小的正方形组成的,如果这个图形的面积是400平方厘米,那么它的周长是______厘米.2. 第一届保良局亚洲区城市小学数学邀请赛在7月21日开幕,下面的图形中,每一小方格的面积是1.那么7,2,1三个数字所占的面积之和是______.3. 下图中每一小方格的面积都是1平方厘米,那么用粗线围成的图形面积是______平方厘米.4. 下图的两个正方形,边长分别为8厘米和4厘米,那么阴影部分的面积是______平方厘米.5. 在ABC ∆中,DC BD 2=,BE AE =,已知ABC ∆的面积是18平方厘米,则四边形AEDC 的面积等于______平方厘米.6. 下图是边长为4厘米的正方形,AE =5厘米、OB 是______厘米.7. 如图正方形ABCD 的边长是4厘米,CG 是3厘米,长方形DEFG 的长DG 是5厘米,那么它的宽DE 是______厘米.8.如图,一个矩形被分成10个小矩形,其中有6个小矩形的面积如图所示,那么这个大矩形的面积是______.9.如下图,正方形ABCD的边长为12, P是边AB上的任意一点,M、N、I、H分别是边BC、AD 上的三等分点,E、F、G是边CD上的四等分点,图中阴影部分的面积是______.10.下图中的长方形的长和宽分别是6厘米和4厘米,阴影部分的总面积是10平方厘米,四边形ABCD的面积是______平方厘米.二、解答题11.图中正六边形ABCDEF的面积是54.PFAP2=,BQCQ2=,求阴影四边形CEPQ的面积.12.如图,涂阴影部分的小正六角星形面积是16平方厘米.问:大正六角星形面积是多少平方厘米.13.一个周长是56厘米的大长方形,按下图中(1)与(2)所示意那样,划分为四个小长方形.在(1)中小长方形面积的比是: 2:1:=BA,2:1:=CB.而在(2)中相应的比例是3:1:=''BA,3:1:=''CB.又知,长方形D'的宽减去D的宽所得到的差,与D'的长减去在D的长所得到的差之比为1:3.求大长方形的面积.25 20 3036 16 12A CA'C'B DB'D'14. 如图,已知5=CD ,7=DE ,15=EF ,6=FG .直线AB 将图形分成两部分,左边部分面积是38,右边部分面积是65.那么三角形ADG 面积是______.平面图形计算（二）习题答案1. 170.每个小正方形的面积为400÷16=25平方厘米,所以每个小正方形的边长为5cm,因此它的周长是34×5=170厘米.2. 25. 7,2,1所占面积分别为7.5,10和7.5 .3. 6.5.直接计算粗线围成的面积是困难的,我们通过扣除周围的正方形和直角三角形来计算.周围有正方形3个,面积为1的三角形5个,面积为1.5的三角形一个,因此围成面积是4×4-3-5-1.5=6.5(平方厘米).4. 24仿上题,大、小两个正方形面积之和减去两只空白三角形的面积和,所得的差就是阴影部分的面积.]2)84(4288[8422+⨯+⨯-+=16+64-(32+24)=80-56=24(平方厘米)5. 12如下图,连接AD ,因为DC BD 2=,所以ADC ABD S S ∆∆=2;又18==+∆∆∆ABC ADC ABD S S S ,所以12=∆ABD S .因为BE AE =,所以621===∆∆∆ABD ADE BDE S S S ;因此12618=-=-=∆∆BDEABCAEDCSSS(平方厘米).6. 3.2如下图,连接BE ,则8442121=⨯⨯==∆正方形S S ABE (平方厘米).从另一角度看,OB S ABE ⨯⨯=∆521,于是8521=⨯⨯OB .528÷⨯=∴OB =3.2(厘米) 7. 3.2如下图,连接AG ,则AGD ∆的面积是正方形ABCD 面积的21,也是长方形DEFG 的面积的21,于是长方形DEFG 的面积等于正方形ABCD 的面积4×4=16(平方厘米).2.3516=÷=∴DE (厘米).8. 243我们用A ,长是相同的.A25 20 30D36B 16C12因此它们的面积之比,就是宽之比,反之,宽之比,就是面积之比.这样就有:20:16=A :36,45163620=⨯=A ;20:16=25:B ,20202516=⨯=B ;20:16=30:C ,24203016=⨯=C ; 20:16=D :12, 15161220=⨯=D .因此,大矩形的面积是:45+36+25+20+20+16+30+24+15+12=2439. 60 如下图,连接PD ,则阴影部分就是由四个三角形: PDH ∆,PGD ∆,PEF ∆和PMN ∆组成.PGD ∆和PEF ∆的底都有3,高为12,所以1812321=⨯⨯==∆∆PEF PGD S S .PDH ∆和PMN ∆的底都是4,两条高分别为PA 和PB 则:PB PA S S PMN PDH ⨯⨯+⨯⨯=+∆∆421421=2(PA +PB )=2×12=24所以,阴影部分的面积是: ++∆∆PEF PGD S S PMN PDH S S ∆∆+=18+18+24=6010. 4长方形EFGH 的面积是6×4=24(平方厘米)1221==+∴∆∆EFGH AHG AEF S S S (平方厘米)阴影总面积S S S S S AHG AEF ADH EBA -+=+∴∆∆∆∆=12-10=2(平方厘米)又6244141=⨯==∆EFGH ECH S S (平方厘米)所以,四边形ABCD 的面积等于: )(ADHEBA ECH SS S ∆∆∆+-=6-2=4(平方厘米)11. 如图,将正六边形ABCDEF 等分为54个小正三角形.根据平行四边形对角线平分平行四边形面积.采用数小三角形的办法来计算面积.PEF ∆面积=3;CDE ∆面积=9;四边形ABQP 面积=11.上述三块面积之和为3+9+11=23,因此,阴影四边形CEPQ 面积为54-23=31.12. 如图,涂阴影部分小正六角星形可分成12个与三角形OPN 全等(能完全重叠地放在一起)的小三角形.三形OPN 的面积是341216=平方厘米.正三角形OPM 面积是由三个与三角形OPN 全等的三角形组成.所以正三角形OPM 的面积等于4334=⨯(平方厘米). 由于大正方六角星形由12个与正三角形OPM 全等的三角形组成,所以大正六角星形的面积是4×12=48(平方厘米)13. 设大长方形的宽为x ,则长为28-x .因为,x D 32=宽,x D 43='宽, 所以,12x D D =-'宽宽. ()x D -=2854长,()x D -='28109长,()x D D -=-'28101长长.由题设可知, 12x :11028=-x:3 或41028x x =-,于是2071028x=, 8=x .大长方形的长=28-8=20,从而大长方形的面积为8×20=160平方厘米.14. 三角形AEG 面积是三角形AED 面积的(15+6)÷7=3(倍),三角形BEF 面积是三角形BEC 面积的 15÷(5+7)=45(倍).所以65-38×45等于三角形AEG 面积与三角形AED 面积的45之差,因此三角形AED 的面积是(65-38×45)÷(3-45)=10.三角形ADG 面积是10×(3+1)=40.。

小升初奥数思维训练第7讲：几何(一) 平面图形(经典透析)

第7讲几何（一）平面图形【例1】（☆☆☆）如下左图。

将三角形ABC的BA边延长1倍到D，CB边延长2倍到E，AC 边延长3倍到F。

如果三角形ABC的面积等于1，那么三角形DEF的面积是_____。

审题要点：题目中给出的已知条件都是边的倍比关系，其余的条件中只有一个三角形ABC 的面积是已知，要想办法使已知条件能够相互关联，使边的倍比关系可以转化为面积之比，可以选择模型一应用。

详解过程：解：连结AE、BF、CD（如上右图）由EB=2BC，得S△ABE=2。

同理可得S△AED=2S△BEF=2×S△CBF =6。

S△CFD =3×S△ACD =3。

所以 S△DEF= 1+2+3+1+2+6+3=18。

专家点评：这是北京市第一届“迎春杯”刊赛第32题，非常经典。

解题过程中通过连接AE、BF、CD，使题目中所给的边的倍比关系可以构造模型一相互关联，再通过共高三角形面积与相应底边之间的对应比例关系求解。

【例2】（☆☆☆）设13AD AB=，14BE BC=，15FC AC=，如果三角形DEF的面积为19平方厘米，那么三角形ABC的面积是_________平方厘米。

审题要点：和【例1】类似，题目已知条件中边的倍比关系比较多，可以考虑应用模型一。

解：1443515 ADF ABC ABC S S S∆∆∆⎛⎫=⨯=⎪⎝⎭121436BED ABC ABC S S S∆∆∆⎛⎫=⨯=⎪⎝⎭FEDCBAFEDCBAECFA D B3134520FEC ABC ABC S S S ∆∆∆⎛⎫=⨯= ⎪⎝⎭S △ABC =(154+61+203) S △ABC +19 ∴45.6ABC S ∆=专家点评：这是2004年小学数学奥林匹克A 卷的，其实竞赛题不一定都是很难，尤其是平面几何部分，但他们十之八九都是很巧妙的，拿这道题来说，图形长得很普通，而题目当中又给了那么多的倍比关系，那我们是不是可以考虑构造模型一呢？整体看，ABC ADF BDE EFC DEF S S S S S ∆∆∆∆∆=+++，除了19DEF S ∆=，其余三个我们可以直接用“鸟头定理”。

小升初六年级奥数——几何（平面图形）

⼩升初六年级奥数——⼏何（平⾯图形）⼀、分数百分数问题，⽐和⽐例这是六年级的重点内容，在历年各个学校测试中所占⽐例⾮常⾼，重点应该掌握好以下内容：对单位1的正确理解，知道甲⽐⼄多百分之⼏和⼄⽐甲少百分之⼏的区别；求单位1的正确⽅法，⽤具体的量去除以对应的分率，找到对应关系是重点；分数⽐和整数⽐的转化，了解正⽐和反⽐关系；通过对“份数”的理解结合⽐例解决和倍（按⽐例分配）和差倍问题；⼆、⾏程问题应⽤题⾥最重要的内容，因为综合考察了学⽣⽐例，⽅程的运⽤以及分析复杂问题的能⼒，所以常常作为压轴题出现，重点应该掌握以下内容：路程速度时间三个量之间的⽐例关系，即当路程⼀定时，速度与时间成反⽐；速度⼀定时，路程与时间成正⽐；时间⼀定时，速度与路程成正⽐。

特别需要强调的是在很多题⽬中⼀定要先去找到这个“⼀定”的量；当三个量均不相等时，学会通过其中两个量的⽐例关系求第三个量的⽐；学会⽤⽐例的⽅法分析解决⼀般的⾏程问题；有了以上基础，进⼀步加强多次相遇追及问题及⽕车过桥流⽔⾏船等特殊⾏程问题的理解，重点是学会如何去分析⼀个复杂的题⽬，⽽不是⼀味的做题；三、⼏何问题⼏何问题是各个学校考察的重点内容，分为平⾯⼏何和⽴体⼏何两⼤块，具体的平⾯⼏何⾥分为直线形问题和圆与扇形；⽴体⼏何⾥分为表⾯积和体积两⼤部分内容。

学⽣应重点掌握以下内容：等积变换及⾯积中⽐例的应⽤；与圆和扇形的周长⾯积相关的⼏何问题，处理不规则图形问题的相关⽅法；⽴体图形⾯积：染⾊问题、切⾯问题、投影法、切挖问题；⽴体图形体积：简单体积求解、体积变换、浸泡问题；四、数论问题常考内容，⽽且可以应⽤于策略问题，数字谜问题，计算问题等其他专题中，相当重要，应重点掌握以下内容：掌握被特殊整数整除的性质，如数字和能被9整除的整数⼀定是9的倍数等；最好了解其中的道理，因为这个⽅法可以⽤在许多题⽬中，包括⼀些数字谜问题；掌握约数倍数的性质，会⽤分解质因数法，短除法，辗转相除法求两个数的最⼤公因数和最⼩公倍数；学会求约数个数的⽅法，为了提⾼灵活运⽤的能⼒，需了解这个⽅法的原理；了解同余的概念，学会把余数问题转化成整除问题，下⾯的这个性质是⾮常有⽤的：两个数被第三个数去除，如果所得的余数相同，那么这两个数的差就能被这个数整除；能够解决求⼀个多位数除以⼀个较⼩的⾃然数所得的余数问题，例如求1011121314 (9)899除以11的余数，以及求20082008除以13的余数这类问题；五、计算问题计算问题通常在前⼏个题⽬中出现概率较⾼，主要考察两个⽅⾯，⼀个是基本的四则运算能⼒，同时，⼀些速算巧算及裂项换元等技巧也经常成为考察的重点。

小升初奥数专题讲义-第11讲平面图形的面积(学习目标+温故知新+巩固练习)

第11讲平面图形的面积【学习目标】一、燕尾定理S △ABG ：S △AGC ＝S △BGE ：S △GEC ＝BE ：EC ； S △BGA ：S △BGC ＝S △AGF ：S △GFC ＝AF ：FC ； S △AGC ：S △BCG ＝S △ADG ：S △DGB ＝AD ：DB ；二、任意四边形中的比例关系： ① 1243::S S S S 或者1324S S S S②1243::AO OC S S S S梯形中比例关系： ①2213::S S a b②221324::::::S S S S a b ab ab ； ③S 的对应份数为2a bA BCDO ba S 3S 2S 1S 4S 4S 3S 2S 1O DCBA F ED CBA【温故知新】例题1：四边形ABCD的对角线BD被E、F两点三等分，且四边形AECF的面积为15平方厘米。

求四边形ABCD的面积（如图所示）。

【答案】15×3＝45（平方厘米）答：四边形ABCD的面积为45平方厘米。

举一反三1：1、四边形ABCD的对角线BD被E、F、G三点四等分，且四边形AECG的面积为15平方厘米。

求四边形ABCD的面积（如图）。

2、已知四边形ABCD的对角线被E、F、G三点四等分，且阴影部分面积为15平方厘米。