深圳大学712数学分析2021年考研专业课初试大纲
2021年深圳大学考研招生目录
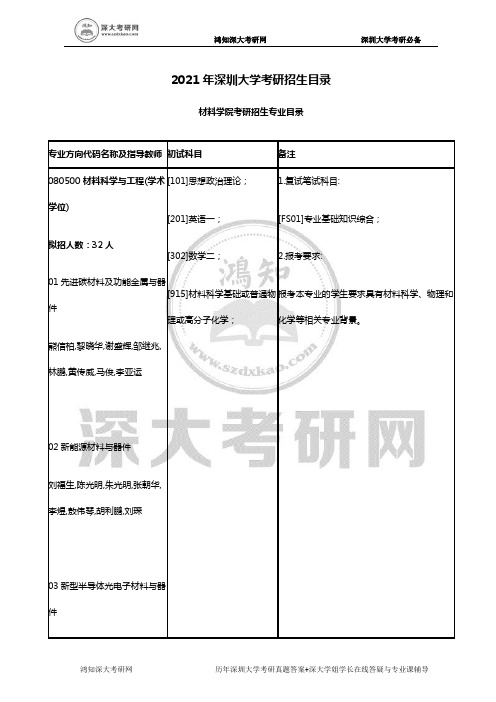
2021年深圳大学考研招生目录材料学院考研招生专业目录专业方向代码名称及指导教师初试科目备注080500材料科学与工程(学术学位)拟招人数:32人01先进碳材料及功能金属与器件熊信柏,黎晓华,谢盛辉,邹继兆,林鹏,黄传威,马俊,李亚运02新能源材料与器件刘福生,陈光明,朱光明,张朝华,李煜,敖伟琴,胡利鹏,刘琛03新型半导体光电子材料与器件[101]思想政治理论;[201]英语一;[302]数学二;[915]材料科学基础或普通物理或高分子化学;1.复试笔试科目:[FS01]专业基础知识综合;2.报考要求:报考本专业的学生要求具有材料科学、物理和化学等相关专业背景。
朱德亮,柳文军,曹培江,刘新科,许望颖,方明04功能高分子光电与能源材料杨楚罗,王雷,陈少军,万学娟,刘斌,刘丹青,潘成军,黄扬,邹洋,刘一,刘贺,王东,李凯,熊玉,韩婷05先进功能与智能高分子材料陈仕国,陈大柱,欧阳星,阎志超,杜冰06电化学能源与电子信息材料LUOJINGLI,饶峰,杨海朋,陈献,姚蕾[FS02]材料工程专[101]思想政治理论;085600材料与化工(专业学位)[201]英语一;拟招人数:100人01先进碳材料及功能金属与器件熊信柏,黎晓华,谢盛辉,钱海霞,邹继兆,林鹏,黄传威,马俊,李亚运02新能源材料与器件刘福生,陈光明,朱光明,张朝华,李煜,敖伟琴,胡利鹏03新型半导体光电子材料与器件朱德亮,柳文军,曹培江,韩舜,刘新科,许望颖,方明[302]数学二;[915]材料科学基础或普通物理或高分子化学;04纳米材料与贵金属和功能薄膜王进,谷坤明,苏轶坤,向雄志,刘琛05功能高分子光电与能源材料杨楚罗,王雷,陈少军,万学娟,刘斌,邓远名,潘成军,刘丹青,黄扬,邹洋,刘一,王东,刘贺,李凯,韩婷,熊玉06先进功能与智能高分子材料陈仕国,陈大柱,欧阳星,左建东,阎志超,杜冰07电化学能源与电子信息材料LUOJINGLI,饶峰,杨海朋,陈献,姚蕾传播学院考研招生专业目录专业方向代码名称及指导教师初试科目备注050300新闻传播学(学术学位)拟招人数:37人01传播学巢乃鹏,周裕琼,杨洸,刘晓燕,于晓峰,曹博林,茅知非,汪翩翩,任玉琛02新闻学尹连根,黄春平,王琛,彭华新,张晗,张田田[101]思想政治理论;[201]英语一;[701]新闻传播学基础;[928]媒体文化;[FS03]新闻传播学综合基础;03广告与传媒经济何建平,黄玉波,胡莹,李莹,张燕,李鹏翔04视觉传播与创意产业常江,郭熙志,刘辉,YE,阎评,杨莉莉,王建磊,战迪,史旻昱,曾温娜,王伟,程遥055200新闻与传播(专业学位)拟招人数:45人01健康传播巢乃鹏,杨洸,周裕琼,曹博林,张燕,任玉琛02数字营销传播[101]思想政治理论;[201]英语一;[334]新闻与传播专业综合能力;[440]新闻与传播专业基础;[FS03]新闻传播学综合基础;何建平,黄玉波,胡莹,史旻昱,陈丽娜,汪翩翩03融合媒体新闻生产黄春平,李明伟,刘劲松,张晗,张田田04视听传播YE,郭熙志,刘辉,彭华新,王建磊,杨莉莉,刘晓燕,曾温娜,于晓峰,王婷,阎评,战迪,王伟,程遥,王小峰电子与信息工程学院考研招生专业目录专业方向代码名称及指导教师初试科目备注081000信息与通信工程(学术学位)[101]思想政治理论;[201]英语一;[FS05]信息与通信工程专业基础知识;拟招人数:67人01数字创意技术丁文华,蒙山,杨晴,邓磊02多媒体信息处理龚元浩,欧阳乐,黄继武,李元满,曹文明,李斌,李岩山,裴继红,骆剑平,QIUGUOPING,贾红,陈昌盛03信息感知与智能处理YATAOYANG,邹文斌,王妙辉,刘宗香,赵博,李良群,黄建军,梁永生,吴晓晓,阳召成,廖斌,张勇,郑能恒,孙维泽,李霞,黄磊,冯大权,康莉,黄海明[301]数学一;[902]电子系统综合;04无线通信系统毕宿志,李晓滨,谢宁,马嫄,张晓,王滔滔,张沛昌,全智,王世伟,冯波涛,林晓辉,郭重涛,钟世达,王晖,陈哲,袁涛,黄冠龙,何业军,钱恭斌,张龙,何春龙05信息编码理论与技术吉建华,陈彬,代明军,张胜利,张鹏,王平080900电子科学与技术(学术学位)拟招人数:13人01微电子学与固体电子学黎冰,贺威,廖武刚,张猛,叶文彬,许威,闫岩,刘俊杰,潘晓芳,赵晓锦[101]思想政治理论;[201]英语一;[301]数学一[901]模拟电路;[FS04]数字电路;02电磁场与微波技术WENLONGHE,葛磊,吴迪,舒国响085400电子信息(专业学位)拟招人数:128人01数字创意技术邓磊,杨晴,丁文华,冯大权02多媒体信息处理及应用张力,张勇,康莉,何志权,李岩山,李霞,黄继武,杜戈果,李元满,贾红,吴昊,曹文明,欧阳乐,周飞,龚元浩,田时舜,张坤华,李斌,王妙辉,QIUGUOPING,王娜,裴继红,骆剑平,郑能恒,徐晨,蔡茂国,梁永生[101]思想政治理论;[201]英语一;[301]数学一;[902]电子系统综合;[FS82]信号与系统;03传感信息检测与处理赵博,黄建军,廖斌,初萍,李良群,刘宗香,孙维泽,阳召成,YATAOYANG,黄磊04光通信系统徐铭,吉建华,王可05无线通信系统何春龙,冯波涛,王滔滔,周小安,谢宁,林晓辉,张晓,李晓滨,舒国响,陈哲,王朔遥,全智,刘静,郭重涛,WENLONGHE,张金凤,何业军,王世伟,代明军,苏恭超,陈佳义,毕宿志,黄冠龙,张龙,袁涛,张沛昌,王兰,钱恭斌,吴迪,葛磊,马嫄,王晖06大数据网络空间安全聂伟,吴晓晓,徐明,张鹏,陈昌盛,张胜利,刘宏伟,王平,秦斌,陈彬,江魁法学院考研招生专业目录专业方向代码名称及指导教师初试科目复试笔试科目030100法学(学术学位)拟招人数:34人01国际法学陈梦,张淑钿,刘阳,王楠,王千华,田晓萍02宪法学与行政法学[101]思想政治理论;[201]英语一;[702]法学基础;[929]法学专业;[FS07]民事诉讼法及刑事诉讼法;孙成,李明超,叶海波,高俊杰,邹平学,黎沛文,底高扬,尤乐,赵桃桃,宋明03刑法学吴学斌,乔远,周娅04经济法学程子薇,叶卫平,侯玲玲,周卫,曾晶,敖希颖,段礼乐05民商法学钟明霞,蔡元庆,吕成龙,丁南,翟玉娟,薛波,齐砺杰,魏启证06法学理论姚秀兰,陈曦,宋旭光,孔庆平07诉讼法学杨剑,左德起,郝晶晶08知识产权法学张轶,段鲁艺,朱谢群035200社会工作(专业学位)拟招人数:30人不区分方向唐咏,马云驰,郑静,唐苏勤,高秋凤,黄国英,黄斌欢,许英,李晓凤[101]思想政治理论;[201]英语一;[331]社会工作原理;[437]社会工作实务;[FS10]社会工作专业综合;035102法律(法学)(专业学位)拟招人数:50人不区分方向张轶,吕成龙,段鲁艺,敖希颖,薛波,乔远,王茂祺,吴学斌,叶海波,[101]思想政治理论;[201]英语一;[397]法硕联考专业基础(法学);[497]法硕联考综合(法学);[FS09]法学综合;张淑钿,周卫,田晓萍,蔡元庆,周娅,丁南,邹平学,郝晶晶,肖又贤,左德起,王楠,朱谢群,钟明霞,王千华,侯玲玲,魏启证,杨剑,翟玉娟,宋明,齐砺杰,段礼乐035101法律(非法学)(专业学位)拟招人数:40人不区分方向尤乐,孙成,陈梦,底高扬,姚秀兰,黎沛文,李明超,叶卫平,刘阳,宋旭光,程子薇,赵桃桃,白云,曾晶,高俊杰,马晶[101]思想政治理论;[201]英语一;[398]法硕联考专业基础(非法学);[498]法硕联考综合(非法学);[FS08]法律综合;高等研究院考研招生专业目录专业方向代码名称及指导教师初试科目复试笔试科目077300材料科学与工程(学术学位)拟招人数:12人不区分方向蔡兴科,赵伟,李秀婷,陈友根,周晔,许杉杉,李昇隆,高永祥,QINGSHANJASONNIU,刘富德,黄思雅仅接推免0713Z1生命健康与环境(学术学位)拟招人数:12人不区分方向李猛,黄裕谦,李正,李文金,江一舟,熊海,郑家荣,潘科,陈峰,胡强,江山[101]思想政治理论;[201]英语一;[703]高级生态学;[930]普通生物学;[FS11]生命健康与环境知识综合;0701Z1复杂系统与数据科学(学术学位)拟招人数:6人仅招收推免生。
深圳大学 实变函数与泛函分析教学大纲

(一)课程性质
1.课程类别:综合选修课 2.适应专业:数学与应用数学专业(数学教育方向) 3.开设学期:第七学期 4.学时安排:周学时 6,总学时 72 5.学分分配:4 学分
(二)开设目的
《实变函数与泛函分析》是数学分析课程的深化和发展。从内容上看,它将微积分中 区域的面积推广到一般集合的测度,将区域上的黎曼积分推广到可测函数的勒贝格积分; 从研究方法上看,它运用点集分析方法揭露函数的许多深刻性质。通过对实变函数与泛函 分析的学习,培养学生综合运用分析数学的几何观点和方法,理解和研究分析数学中的许 多问题,为进一步学习现代数学理论和理解现代科学技术提供必要的基础。
张文俊:《实变函数与泛函分析》课程教学大纲
深圳大学数学与计算科学学院
课程教学大纲
(2006 年 10 月重印版)
课程编号
课程名称 实变函数与泛函分析
课程类别
综合选修
教材名称 实变函数与泛函分析基础
制订人
张文俊
审核人
胡鹏彦
2005 年 4 月修订
- 214 -
张文俊:《实变函数与泛函分析》课程教学大纲
第五章 积分论
教学目的
通过本章的系统学习,使学生理解 Lebesgue 积分的定义,掌握 Lebesgue 积分的基本 性质,Lebesgue 积分的定理(包括这些定理的条件结论),弄懂其证明思路。
主要内容
1. Lebesgue 积分的若干等价定义 2. Lebesgue 积分的初等性质和极限定理(Levi 单调收敛定理,Fatou 引理,
- 218 -
张文俊:《实变函数与泛函分析》课程教学大纲
空间 C、连续函数空间 C[a,b]等都是完备度量空间);知道完备度量空间的压缩 映射原理;知道一个空间是否完备与它被赋予的度量是密切相关的:C[a,b]在 Lp 范数下是不完备的; 3. 掌握可分空间的定义与基本例子(欧氏空间 Rn、连续函数空间 C[a,b]都是可分空 间);熟悉可分空间中任意一点都可以通过它的一个确定的可数稠密子集来逼近 的特点;知道不可分空间是存在的:有界数列空间 l∞是不可分空间;知道一个空 间是否可分与它被赋予的度量是密切相关的; 4. 掌握线性空间、线性空间的维数的定义与基本例子(欧氏空间 Rn、可测函数空间
云南大学823数学分析2020年考研专业课初试大纲

云南大学2020年考研专业课初试大纲
823-《数学分析》考试大纲
一、考试性质
《数学分析》是基础数学专业、计算数学专业、概率论与数理统计专业、应用数学专业、运筹学与控制论专业、系统理论专业硕士学位研究生入学考试的科目之一。
《数学分析》考试要求能反映数学学科的特点,科学、公平、准确地测试考生的基本素质和综合能力,很好地选拔具有科研发展潜力的优秀人才进入硕士阶段学习,为国家培养掌握现代数学方面的基础理论知识,具有较强分析与解决实际问题能力的高层次的应用型的和复合型的数学专业人才。
二、考试要求
考查考生对《数学分析》里的基本概念、基础知识的掌握情况,考察考生的分析能力、计算能力和对知识的综合运用能力。
三、试卷分值、考试时间和答题方式
本科目试卷满分为150分,考试时间为180分钟,答题方式为闭卷、笔试。
四、试题结构
(1)试卷题型结构
填空题:30分
计算题:60分
证明题:60分
(2)内容结构
各部分内容所占分值为
1。
深圳大学数学与计算科学学院

主要内容
1. 内积空间 2. 泛函延拓定理 3. Hilbert 空间的规范正交系 4. 共轭算子
教学要求
(1) 掌握 Banach 空间的定义与基本例子(n 维欧氏空间 Rn、连续函数空间 C(A)、有 界数列空间 l∞ 、 p 次 收敛数列空间 lp、 p 方可积函数空间 Lp 等都是 Banach 空间) ;知道非 Banach 空间是存在的:C[a,b]在 Lp 范数下不是 Banach 空间; (2) 掌握内积与内积空间的定义与基本例子;熟练掌握内积的正定性、首元线性性与 共轭对称性;掌握内积诱导范数的思想;熟练掌握内积诱导范数的基本性质、和 的范数恒等式;掌握内积满足 Schwarz 不等式并且是二元连续函数的事实;掌握 内积空间的特征:范数满足平行四边形法则; (3) 掌握 Hilbert 空间的定义与基本例子;知道在同构的意义下,可分的 Hilbert 空间 只有 Rn 与 l2; (4) 掌握正交向量的定义;知道正交向量满足勾股定理,而且在实内积空间中,勾股 定理是两个向量正交的充分必要条件;了解极小化向量定理与正交分解定理(投 影定理) ; (5) 了解正交系、规范(标准)正交系、完全规范正交系或规范(标准)正交基的概 念与基本例子;掌握 Gram-Schmidt 正交化过程;知道每个非零的可分 Hilbert 空 间 X 必存在规范(标准)正交基; (6) 了解 Fourier 系数、Fourier 级数的定义; 了解最佳逼近定理; 知道 Bessel 不等式、 Parseval 恒等式;知道向量可以展成 Fourier 级数的条件; (7) 掌握 Banach 空间基本定理之 Hahn-Banach 定理;掌握 Hilbert 空间之 Riesz 表示 定理。 注:根据各课程的具体情况编写,但必须写明各章教学目的、教学要求、主要内容。
2021考研数学一考试大纲原文解析及变化解读

五、大数定律和中心极限定理考试内容
切比雪夫(Chebyshev)不等式 切比雪夫大数定律 伯努利(Bernoui)大数定律 辛钦(Khinchin)大数 定律 棣莫弗-拉普拉斯(DeMoivte-Laplace)定理 列维-林德伯格(LevyLindberg)定理 考试要求 1.了解切比雪夫不等式. 2.了解切比雪夫大数定律、伯努利大数定律和辛钦大数定律(独立同分布随机变量序列的大数定律). 3.了解棣莫弗-拉普拉斯定理(二项分布以正态分布为极限分布)和列维-林德伯格定理(独立同分布随机 变量序列的中心极限定理).
考试要求
1.理解矩阵的概念,了解单位矩阵、数量矩阵、对角矩阵、三角矩阵、对称矩阵和反对称矩阵以及它们 的性质.
2.掌握矩阵的线性运算、乘法、转置以及它们的运算规律,了解方阵的幂与方阵乘积的行列式的性质.
3.理解逆矩阵的概念,掌握逆矩阵的性质以及矩阵可逆的充分必要条件,理解伴随矩阵的概念,会用伴 随矩阵求逆矩阵.
随机变量 随机变量分布函数的概念及其性质 离散型随机变量的概率分布连续型随机变量的概率密 度 常见随机变量的分布 随机变量函数的分布
考试要求
1.理解随机变量的概念,理解分布函数F(x)=P(X≤x(-x<x<+xz)的概念及性质,会计算与随 机变量相联系的事件的概率.
2理解离散型随机变量及其概率分布的概念,掌握0-1分布、二项分布B(0p))、几何分布、超 几何分布、泊松(Poisson)分布P(2)及其应用.
2.理解概率、条件概率的概念,掌握概率的基本性质,会计算古典型概率和几何型概率,掌握概率 的加法公式、减法公式、乘法公式、全概率公式以及贝叶斯(Bayes)公式.
深圳大学 数值分析课程教学大纲

第三章函数逼近与计算8学时
第四章数值积分与数值微分6学时
第五章常微分方程数值解法8学时
第六章方程求根6学时
第七章解线性方程组的直接方法8学时
第八章解线性方程组的迭代法6学时
第九章矩阵的特征值与特征向量计算2学时
带*部分可根据实际进度,作选讲内容。
(二)考核要求
1.成绩评价
平时成绩(含考勤、作业与测验)占30%,期末(卷面)成绩占70%。
(九)参考书目
(1)蒋尔雄.《数值逼近》.上海:复旦大学出版社,2004
(2)曹志浩.《数值线性代数》.上海:复旦大学出版社,1996
(3)易大义、沈云宝、李有法.《计算方法》.杭州:浙江大学出版社,2002年第二版
(4)M.T.Heath.《Scientific Computation: an Introductory Survey》.北京:清华大学出版社,2001,Second Edition
并进行初步的理论分析。
主要内容
第一节引言
第二节尤拉方法
第三节龙格-库塔方法
第四节单步法的收敛性和稳定性
第五节线性多步法
第六节方程组和高阶方程的情形
第七节边值问题的数值解法*
教学要求
理解:理解常微分方程初值问题数值求解的基本概念:单步法、多步法、显式、隐式、精度、单步法收敛性、稳定性的概念等。
掌握:掌握尤拉类方法与龙格-库塔方法的推导,精度时数。
二、教学内容
第一章绪论
教学目的
宏观上把握什么是数值问题,数值方法的一般技巧。建立误差的概念,并能够对其
进行基本分析。
主要内容
第一节数值分析的对象与特点
第二节误差来源与误差分析的重要性
华南理工大学623数学分析2021年考研专业课

华南理工大学2021年硕士研究生入学《数学分析(623)》考试大纲
判别法。
连续性、可积性与可微性,Gamma函数。
19.曲线积分
第一型和第二型曲线积分概念与计算,两类曲线积分的联系。
20.重积分
二重积分定义与存在性,二重积分性质,二重积分计算(化为累次积分)。
格林(Green)公式,曲线积分与路径无关条件。
二重积分的换元法(极坐标与一般变换)。
三重积分定义与计算,三重积分的换元法(柱坐标、球坐标与一般变换)。
重积分应用(体积,曲面面积,重心、转动惯量、引力等)。
无界区域上的收敛性概念。
无界函数反常二重积分。
在一般条件下重积分变量变换公式。
21.曲面积分
曲面的侧。
第一型和第二型曲面积分概念与计算,高斯公式。
斯托克斯公式。
场论初步(梯度场、散度场、旋度场)。
备注
选读书目
【1】《数学分析》(上、下册),复旦大学数学系编,高等教育出版社;
【2】《数学分析》(上、下册),华东师范大学数学系编,高等教育出版社;
【3】《数学分析》(上、下册),刘正荣、杨启贵、刘深泉、洪毅编,科学出版社。
哈尔滨工业大学2021年硕士研究生入学考试大纲数学分析

2021 年数学学院硕士研究生入学考试大纲考试科目名称:数学分析考试科目代码:[612]一、考试要求:1)要求考生熟练掌握数学分析的基本概念、基本理论和基本方法。
2)要求考生具有严格的数学论证能力、举反例能力和基本计算能力。
3)要求考生了解数学分析中的基本概念、理论、方法的实际来源和历史背景,清楚它们的几何意义和物理意义,初步具备应用数学分析解决实际问题能力。
二、考试内容:1)极限和连续a.熟练掌握数列极限与函数极限的概念,包括数列的上、下极限和函数的左、右极限。
b.掌握极限的性质及四则运算性质,特别要能够熟练运用两面夹原理和两个特殊极限。
c.熟练掌握实数系的基本定理:区间套定理,确界存在定理,单调有界原理,Bolzano-Weierstrass 定理,Heine-Borel 有限覆盖定理,Cauchy 收敛准则;并理解相互关系。
d.熟练掌握函数连续性的概念及相关的不连续点类型。
能够运用函数连续的四则运算与复合运算性质以及相对应的无穷小量的性质;并理解两者的相互关系。
e.熟练掌握闭区间上连续函数的性质:有界性定理、最值定理、介值定理和Contor 定理。
2)一元函数微分学a.理解导数和微分的概念及其相互关系,理解导数的几何意义和物理意义,理解函数可导性与连续性之间的关系。
b.熟练掌握函数导数与微分的运算法则,包括高阶导数的运算法则,会求分段函数的导数。
c.熟练掌握 Rolle 中值定理,Lagrange 中值定理和 Cauchy 中值定理以及 Taylor 公式。
d.能够用导数研究函数的单调性、极值,最值和凸凹性。
e.掌握用L’Hospital 法则求不定式极限的方法。
3)一元函数积分学a.理解不定积分的概念。
掌握不定积分的基本公式,换元积分法和分部积分法,会求有理函数、三角有理函数和简单元理函数的积分。
b.掌握定积分的概念,包括 Darboux 和,上、下积分及可积条件与可积函数类。
c.掌握定积分的性质,熟练掌握微积分基本定理,定积分的换元积分法和分部积分法。
深圳大学课程教学大纲

深圳大学课程教学大纲李建华:《概率论与数理统计》课程教学大纲深圳大学数学与计算科学学院课程教学大纲(2006年10月重印版)课程编号 22123030C课程名称概率论与数理统计课程类别专业必修教材名称概率论与数理统计教程制订人李建华审核人魏正红2005年4月修订- 31 -李建华:《概率论与数理统计》课程教学大纲一、课程设计的指导思想(一)课程性质 1.课程类别:专业必修课 2.适应专业:数学与应用数学专业(数学教育方向) 3.开设学期:第四学期 4.学时安排:周学时5,总学时90 5.学分分配:5学分(二)开设目的概率论与数理统计是一门讲述随机变量的数学基础课,作为本科各专业的必修课程。
本课程的任务是通过各种教学环节,使学生掌握概率论的基本概念、基本理论、基本计算方法和数理统计的基本思想方法,还要求学生掌握统计推断的两大部分:参数估计、假设检验的基本内容和方法,培养学生能够运用概率统计知识处理实际问题的能力,为以后学习专业课程、从事专业工作和科学研究打下良好的基础。
(三)基本要求通过本课程学习,学生应掌握概率论的基本概念,基本方法,若干重要模型和极限定理;分析整理数据,并从中提炼出有用信息的方法以及掌握利用数据对考察对象进行分析和做出推断的有关理论和方法。
(四)主要内容本课程主要介绍概率论基本理论和基本统计方法及其应用。
首先讲述概率论的基础知识,然后介绍抽样理论和统计推断的内容(包括参数估计、假设检验、一元回归及方差分析)。
(五)先修课程数学分析、高等代数(六)后继课程多元统计公析,以及随机过程等课程(七)考核方式闭卷考试(八)使用教材魏宗舒. 概率论与数理统计教程[M]. 北京: 高等教育出版社, 1988年, 第二版. (九)参考书目 (1) 李贤平, 沈崇圣. 概率论与数理统计[M]. 上海: 复旦大学出版社, 2003年. (2) 盛骤等. 概率论与数理统计[M]. 北京: 高等教育出版社, 1989年. - 32 -李建华:《概率论与数理统计》课程教学大纲二、教学内容第一章事件与概率(15学时)教学目的要求能够理解随机事件、样本空间与随机变量的基本概念,掌握概率的运算公式。
深圳大学数学专业考纲

数学分析一、考试的基本要求《数学分析》考试大纲适用于报考深圳大学基础数学、应用数学专业硕士研究生的入学考试。
本考试是为招收基础数学、应用数学专业硕士生而拟设的具有选拔功能的考试。
其主要目的是测试考生对数学分析最基本内容的理解、掌握和熟练程度。
要求考生熟悉数学分析的基本理论、掌握数学分析的基本方法, 具有较强的抽象思维能力、逻辑推理能力和运算能力。
二、考试内容和考试要求1.极限与连续数列极限、函数极限、函数的连续性和一致连续性、闭区间上连续函数的性质。
(1)掌握数列极限与函数极限的概念,理解无穷大(小)量的概念及基本性质;(2)掌握极限的性质(唯一性、有界性、保号性)及四则运算性质、单调有界收敛定理、Cauchy 收敛准则、迫敛性(两边夹、夹挤)原理、两个重要极限;(3)掌握函数的奇偶性、单调性、周期性、有界性等特殊性质;(4)掌握连续性的概念及间断点的分类,掌握初等函数的连续性;(5)掌握闭区间上连续函数的性质:有界性、最值性、介值性(零点定理)、一致连续性。
2.一元函数微分学导数、微分、求导运算与法则、微分运算、微分中值定理、洛必达法则、泰勒公式、函数单调性、极值与最值、凸性与拐点。
(1)理解可导与可微、可导与连续的概念及其相互关系,理解导数的几何意义;理解函数极值点与极值、凸性、拐点等概念;(2)掌握(高阶)导数、微分的四则运算与复合函数求导运算法则,掌握左、右导数的概念以及分段函数求导方法,掌握导函数的介值定理;(3)会用导数研究函数的单调性与极值性,会用二阶导数研究函数的凸性与拐点;(4)掌握微分中值定理及其在根的判定、不等式、不定式极限(洛必达法则)等方面的应用;(5)掌握泰勒公式及其在极限、极值点判定等方面的应用;(6)掌握极值与最值的求法、凸的等价定义、以及凸性在不等式等方面的应用。
3.实数的完备性区间套、聚点、开覆盖的概念。
(1)理解聚点概念及其刻画,理解区间套、开覆盖等概念;(2)理解关于实数完备性的六大基本定理及其证明思想;(3)会用实数完备性定理证明闭区间上连续函数的有界性、最值性、介值性(零点定理)、一致连续性。
深圳大学 徐希:《数学分析》课程教学大纲

(二)开设目的
本课程是数学与应用数学专业(本科)一门必修的重要基础课。它一方面为后继课程,如微分方程、概率论、经济数学等基础课及专业课和有关的其他选修课提供所需基础,同时还为培养学生的抽象概括问题的能力、逻辑推理能力、空间想象能力、运算能力和综合运用所学知识分析问题、解决问题的能力提供必要的训练。学生学好这门课程的基本内容和方法,对今后的学习研究和应用,对自己本身素质的提高,都会起着关键性的作用。
掌握:函数的傅里叶展开法。
第十六章多元函数的极限与连续
教学目的
理解平面点集、聚点原理,多元函数极限,累次极限,连续函数及知道闭区间上连
续函数的性质。
主要内容
第一节平面点集与多元函数
第二节二元函数的极限
第三节二元函数的连续
基本要求
了解:闭区间上连续函数的性质。
理解:理解平面点集、聚点原理,多元函数极限,累次极限。
主要内容
第一节二重积分概念
第二节直角坐标系下二重积分的计算
第三节格林公式,曲线积分与路线的无关性
第四节二重积分的变量变换
第五节三重积分
第六节重积分的应用
基本要求
了解:了解二重积分可积的充要条件和可积函数类,三重积分的换元法。了解重积分的应用。
理解:理解理解二重积分及三重积分的定义及性质。
掌握:二重、三重积分的计算,包括换元积分法。掌握格林公式及其应用,曲线积分与路线的无关性。
掌握:正项级数敛散性判别法,包括比较判别法、柯西判别法、达朗贝尔判别法、积分判别法。
第十三章函数列与函数项级数
教学目的
理解一致收敛的概念。了解一致收敛的性质,掌握一致收敛的判别法,包括M-判
别法,阿贝尔判别法、狄利克雷判别法。
数学分析考研重点内容及常见题型

数学分析考研重点内容及常见题型数学分析是高等院校数学类各专业主干课程之一,是数学各专业硕士研究生入学考试的必考课程.数学分析内容丰富,知识面广,综合性强,理论体系严谨,解题方法灵活巧妙.主要包括一元函数极限、一元函数的连续性、一元微分学、一元函数积分学、级数、多元函数微分学、多元函数积分学等,分别涉及七章内容[1,2].学生在复习考研数学分析时,主要通过例题体会和掌握相应内容的思想方法和解题技巧,通过习题训练达到巩固基础知识,提高理论水平和应用能力.如何掌握好该课的基本内容并能熟练地运用其中的基本技巧至关重要.本文作者根据多年的教学研究与实践,依据考研大纲[3,4],结合高等院校硕士研究生的入学考试试题,对考研数学分析的重点内容及常见题型进行归纳和总结,使其所涉及的知识点之间相互关系清晰明了,同时也将数学分析课程要求学生掌握的知识体系体现出来,可供学生考研复习数学分析时参考,对教师进行数学分析教学也具有参考价值.1 一元函数极限极限是考研热点问题.本章包含四个部分,即函数;用定义证明极限的存在性;求极限值的若干方法;O.Stolz公式.其中极限的求法是核心.重点内容:(1)极限定义,基本理论.(2)几个常用的不等式.(3)极限存在性的证明.(4)极限的求法.(5)实数基本定理.常见题型:(1)几个常用的不等式的证明.(2)用定义证明极限.(3)利用单调有界原理证明极限存在.(4)求极限(利用等价量、利用已知极限、利用两边夹法则、利用洛必达法则、利用Taylor公式、利用定积分定义、利用级数收敛的必要条件).(5)实数基本定理的应用.2 一元函数的连续性本章包含连续性的证明、连续性的应用、一致连续、半连续、函数方程.重点内容:(1)函数连续性的证明,证明的主要方法有:用定义证明、用左右极限证明(对分段函数)、用归结原则证明.(2)连续性的应用(假定函数连续,证明在某些条件下有什么结果).(3)一致连续性.常见题型:(1)直接证明函数在某区间或某点连续.(2)讨论间断点的类型.(3)连续性的应用(假定函数连续,证明在某些条件下有什么结果).(4)利用一致连续的定义及其否定形式证题.(5)Cantor定理的应用.(6)借助连续模数证明一致连续.3 一元微分学本章是基础性内容,包含导数;微分中值定理;Taylor公式;不等式与凸函数;导数的综合应用.一元函数微分学在微积分学中占有极重要的位置,是微积分学的重要内容之一.重点内容:(1)函数导数与微分的概念.(2)微分中值定理——罗尔中值定理,拉格朗日中值定理,柯西中值定理与泰勒中值定理.(3)Taylor公式.(4)导数的应用.常见题型:(1)利用导数(或左右导数)定义解题.(2)求函数的高阶导数.(3)函数零点问题讨论(利用Rolle定理证明零点的存在性,利用单调性证明零点的唯一性).(4)利用Lagrange定理证明函数与函数的导数同时存在的命题.(5)利用导数法证明恒等式.(6)导数介值性的应用.(7)利用Cauchy中值定理证题.(8)利用Taylor公式证明含有高阶导数的命题.(9)利用Taylor 公式作导数的中值估计、界的估计.(10)利用Taylor公式求极限.(11)不等式的证明(利用单调性、微分中值定理、Taylor公式、函数的极值、单调极限证明).(12)导数在几何中的应用.4 一元函数积分学本章包含积分与极限、定积分的可积性、积分值的估计、积分不等式及定积分的应用、若干著名的不等式、反常积分.一元函数积分学是一元函数微积分学的最重要内容,涉及面较广,影响深远.重点内容:(1)定积分的定义、几何意义、性质.(2)利用定积分定义求极限.(3)积分的极限.(4)积分值的估计.(5)几个著名不等式(Cauchy不等式、Schwarz不等式、平均值不等式).(6)反常积分的概念、计算、敛散性的判断.常见题型:(1)利用定积分的定义求和式的极限.(2)运用定积分的各种特性和运算法则求积分的极限.(3)利用变量替换、分部积分、缩放被积函数或积分区间、微分中值公式或Taylor公式对被积函数进行变形,从而估计积分值.(4)几个著名不等式(Cauchy不等式、Schwarz不等式、平均值不等式)的证明、变形及应用.(5)利用Newton-Leibniz公式、变量替换、分部积分法计算反常积分.(6)判定反常积分的敛散性.(7)讨论无穷限的反常积分的收敛性与无穷远处的极限的关系.5 级数级数是一门工具,又有完善的理论,是《数学分析》课程中三大基本内容之一.历年来均为考研热点.本章包含数项级数、函数项级数、幂级数及Fourier级数四个部分.重点内容:(1)数项级数敛散定义,正项级数敛散判别法(Cauchy准则、判阶法、比较判别法、根式判别法等),变号级数收敛性判别法.(2)函数项级数(及序列)一致收敛的定义及判别法.(3)一致收敛级数的性质(三大解析性质:连续性、可积性、可微性).(4)幂级数的收敛半径与收敛域,幂级数的和函数的性质.(5)傅立叶级数——傅立叶级数的概念,函数展开成傅立叶级数,正弦级数与余弦级数.常见题型:(1)利用Cauchy准则证明级数敛散性.(2)利用判阶法及比较判别法证明正项级数敛散性.(3)利用部分和有界证明正项级数收敛.(4)利用Leibniz定理、Abel判别法、Dirichlet判别法研究变号级数收敛性.(5)利用级数收敛的必要条件求极限或证明极限存在.(6)函数项级数一致收敛的证明(利用定义、Cauchy准则、M判别法、A-D判别法).(7)一致收敛级数逐项取极限定理及其应用.(8)和函数连续性、可微性、可积性的应用.(9)求幂级数收敛半径、收敛域及和函数(将级数通过代数运算、变量置换、逐项求导、逐项积分等手段化成已知和函数的级数,如几何级数,从而求得和函数).(10)求某些数项级数的和(由定义求部分和数列的极限,或将其看作某个幂级数或某个傅立叶级数在某点处的值,先求出该幂级数或傅立叶级数的和函数,再求出该数项级数的和).6 多元函数微分学本章包含多元函数的极限与连续、偏导数和全微分、多元函数的应用三部分.重点内容:(1)多元函数(主要是二元、三元函数)的概念、极限与连续.(2)多元函数的偏导数和全微分.(3)多元函数微分在几何上的应用.(4)多元函数的极值和条件极值.(5)方向导数和梯度.常见题型:(1)多元函数极限的计算.(2)证明二元函数极限不存在.(3)关于全面极限愈特殊路径极限的讨论.(4)求多元函数的一阶、二阶偏导数与全微分.(5)讨论二元函数连续性与可微性.(6)求复合函数的一阶、二阶偏导数.(7)对微分方程作变量替换.(8)求空间曲线的切线与法平面方程.(9)求曲面的切平面和法线方程.(10)求多元函数的极值与最大、最小值.(11)利用极值证明不等式.(12)利用拉格朗日乘数法求多元函数的条件极值.(13)证明隐函数的存在性.(14)求多元函数的方向导数和梯度.7 多元积分学本章包含含参变量积分、重积分、曲线积分与Green公式、曲面积分Gauss 公式及Stokes公式、场论等五大部分.多元函数积分学是多元函数微积分学的重要内容,涉及三大类重要积分,应用面较广.重点内容:(1)含参变量积分的正常积分、含参变量积分反常积分的一致收敛性、含参变量积分反常积分的连续性、可积性、可微性.(2)二重积分的概念、性质与计算.(3)三重积分的概念、性质与计算.(4)曲线积分的概念、性质与计算.(5)格林公式,平面上曲线积分与路径无关的充要条件.(6)曲面积分的概念、性质与计算.(7)高斯公式与斯托克斯公式.(8)梯度、散度与旋度的概念及各种公式.常见题型:(1)含参变量积分正常积分的积分号下求极限、积分号下求导、积分号下求积分.(2)证明含参变量积分反常积分的一致收敛性.(3)含参变量积分反常积分的积分号下求极限、积分号下求导、积分号下求积分.(4)证明含参变量积分反常积分的连续性.(5)利用直角坐标与极坐标计算二重积分.(6)直角坐标、柱面坐标、球面坐标计算三重积分.(7)二重积分、三重积分在几何和物理上的应用,如求面积、体积、质量、重心坐标、引力等.(8)曲线积分的计算(利用对称性、利用格林公式、利用与路径无关性).(9)曲面积分的计算(利用对称性、利用公式、利用高斯公式).(10)斯托克斯公式的应用.。
《数学分析》研究生考试大纲

硕士《数学分析》考试大纲课程名称:数学分析科目代码:661适用专业:数学与应用数学专业参考书目:1、《数学分析》(上下册)第一版,陈纪修,於崇华,金路;高等教育出版社1999.92、《数学分析》(上下册)第二版,陈纪修,於崇华,金路;高等教育出版社2004.103、《数学分析》(上下册),卓里奇;高等教育出版社2006.124、《数学分析》(上下册),华东师范大学,高等教育出版社2010.7一、数列极限1、充分认识实数系的连续性;理解并掌握确界存在定理及相关知识。
2、充分理解数列极限的定义,熟练掌握用数列极限的定义证明有关极限问题,以及数列极限的各种性质及其运算。
3、掌握无穷大量的概念及其相关知识;熟练掌握Stolz定理的内容及其结论及应用。
4、理解单调有界数列收敛定理的内容及其结论,并能熟练解决相关的极限问题。
5、充分理解区间套定理、致密性定理、完备性定理各自的内容和结论;进一步认识实数系的连续性与实数系的完备性的关系;明确有关收敛准则中的各定理之间逻辑关系。
二、函数极限与连续函数1、充分理解函数极限的定义,熟练掌握用函数极限的定义证明有关极限问题;以及函数极限的各种性质及其运算。
2、明确数列极限与函数极限的关系;熟练掌握单侧极限以及各种极限过程的极限。
3、充分理解连续函数的概念,熟练掌握用连续函数的定义和运算解决有关函数连续性问题。
明确不连续点的类型;掌握反函数、复合函数的连续性。
4、熟练掌握无穷小(大)量的概念以及自身的比较,并能熟练应用于极限问题当中。
5、充分掌握闭区间上连续函数的各种性质;充分理解函数的一致连续性及相关定理。
三、微分1、充分理解微分的概念、导数的概念,以及可微、可导、连续三者的关系。
2、熟练掌握导数的运算、反函数、复合函数的求导法则,做到得心应手。
3、理解高阶导数和高阶微分的概念,熟练掌握高阶导数的运算法则。
四、微分中值定理及其应用1、充分理解以Lagrange中值定理为核心的各微分中值定理的内容和结论;掌握应用微分中值定理揭示函数自身的特征和函数之间的关系。
历年深圳大学考研真题试卷与答案汇总深大考研真题哪里找

历年深圳大学考研真题试卷与答案汇总深大考研真题哪里找June 8th, 2022, what a day of hard work.历年深圳大学考研真题试卷与答案汇总-深大考研真题哪里找汇集了深圳大学各专业历年考研真题试卷原版,同时与深圳大学专业课成绩前三名的各专业硕士研究生合作编写了配套的真题答案解析,答案部分包括了解题思路、答案详解两方面内容;首先对每一道真题的解答思路进行引导,分析真题的结构、考察方向、考察目的,向考生传授解答过程中宏观的思维方式;其次对真题的答案进行详细解答,方便考生检查自身的掌握情况及不足之处,并借此巩固记忆加深理解,培养应试技巧与解题能力;具体请点击进入考研资料深圳大学708艺术概论通识考研真题试卷2012-2013年考研资料深圳大学947教育心理学综合考研真题与答案2012-2013年考研资料深圳大学333教育综合考研真题试卷2012-2013年考研资料深圳大学705马克思主义基础理论考研真题试卷2004-2013年考研资料深圳大学925马克思主义中国化基本理论考研真题试卷2007-2013年考研资料深圳大学724建筑专业知识考研真题试卷2009-2013年考研资料深圳大学723城市规划与设计专业知识考研真题试卷2012-2013年考研资料深圳大学503城市规划与城市设计考研真题试卷2012-2013年考研资料深圳大学501建筑设计快题考研真题试卷2011-2013年考研资料深圳大学937工程光学二考研真题试卷2008-2013年考研资料深圳大学902光学考研真题试卷2009-2013年考研资料深圳大学903工程光学一考研真题试卷2008-2013年考研资料深圳大学904电子技术基础考研真题试卷2011-2013年考研资料深圳大学940自动控制原理二考研真题试卷2007-2013年考研资料深圳大学906自动控制原理一考研真题试卷2007-2013年考研资料深圳大学939机械设计基础二考研真题试卷2004-2013年考研资料深圳大学905机械设计基础一考研真题试卷2004-2013年,不含12考研资料深圳大学911材料科学基础考研真题试卷2004-2013年考研资料深圳大学933普通物理考研真题试卷2002-2013年考研资料深圳大学936材料科学基础考研真题试卷2011-2013年考研资料深圳大学908工程经济学考研真题试卷2006-2013年,不含09、10考研资料深圳大学土木工程结构综合知识一考研真题试卷2013年考研资料深圳大学907物流工程考研真题试卷2011-2013年考研资料深圳大学942土木工程结构综合知识二考研真题试卷2013年考研资料深圳大学717有机化学考研真题试卷2011-2013年考研资料深圳大学912物理化学考研真题试卷2004-2013年考研资料深圳大学938无机化学考研真题试卷2011-2013年考研资料深圳大学715生态学考研真题试卷2012-2013年考研资料深圳大学714分子生物学考研真题试卷2002-2013年考研资料深圳大学934细胞生物学考研真题试卷2002-2013年考研资料深圳大学701新闻传播学基础考研真题试卷2004-2016年考研资料深圳大学918媒体文化考研真题试卷2012-2016年考研资料深圳大学723日语语言学、日本文学考研真题试卷2012-2013年考研资料深圳大学722专业英语考研真题试卷2013年考研资料深圳大学950综合日语考研真题试卷2012-2013年考研资料深圳大学949综合英语考研真题试卷2004-2013年考研资料深圳大学919法学专业考研真题试卷2004-2013年,不含10考研资料深圳大学917会计学考研真题试卷2004-2005、2008-2013年考研资料深圳大学919西方经济学考研真题与答案2006-2018年考研资料深圳大学915经济学考研真题与答案2004-2013、2015年考研资料深圳大学434国际商务专业基础考研真题与答案2011-2013年考研资料深圳大学431金融学综合考研真题与答案2002-2018年考研资料深圳大学923行政管理理论考研真题与答案1999-2013年考研资料深圳大学914微观经济学考研真题试卷2011-2013年考研资料深圳大学913运筹学考研真题与答案2005-2013年,不含10考研资料深圳大学924西方政治思想史考研真题试卷2012-2013年考研资料深圳大学704政治学理论考研真题试卷2003-2013年考研资料深圳大学941交通运输工程学考研真题与答案2016-2018年考研资料名校431金融学综合考研真题答案汇编共两册考研资料 398法硕联考专业基础非法学考研真题答案2000-2018年考研资料 498法硕联考综合非法学考研真题答案2000-2018年考研资料 397法硕联考专业基础法学考研真题答案2000-2018年考研资料 497法硕联考综合法学考研真题答案2000-2018年考研资料深圳大学707法学基础考研真题2006-2013年,不含10考研资料各高校346体育综合考研真题汇编考研资料深圳大学501建筑设计考研真题2011-2013年考研资料各高校基础英语历年考研真题答案汇编考研资料各高校日语专业考研真题答案汇编考研资料各高校基础日语历年考研真题答案汇编考研资料各高校语言学历年考研真题答案解析考研资料各高校英美文学考研真题答案汇编考研资料各高校英汉互译考研真题答案汇编考研资料 2019年深圳大学二外法语考研强化冲刺题库考研资料各高校二外法语历年考研真题答案汇编考研资料各高校二外日语历年考研真题答案汇编考研资料深圳大学243英语二外考研真题2012-2013年考研资料深圳大学242法语二外考研真题2007-2013年考研资料深圳大学924二外日语考研真题2005-2012年考研资料 2019年深圳大学二外英语考研强化冲刺题库考研资料 2019年深圳大学二外日语考研强化冲刺题库考研资料各高校中国哲学史历年考研真题汇编考研资料各高校西方哲学史历年考研真题汇编考研资料各高校科学哲学历年考研真题汇编考研资料各高校中国现当代文学考研真题与答案汇编考研资料各高校中国文学史历年考研真题答案汇编考研资料各高校中国古代文学历年考研真题答案汇编考研资料各高校细胞生物学历年考研真题汇编考研资料各高校分子生物学历年考研真题汇编考研资料细胞生物学考试重难点与名校真题详解含期末卷考研资料分子生物学考试重难点与名校真题详解含期末卷考研资料各高校马克思主义基本原理考研真题答案汇编考研资料电路考试重难点与名校真题答案详解邱关源第五版考研资料信号与系统考试重难点与名校真题答案详解郑君里第三版考研资料微型计算机原理与接口技术考试重难点与名校真题答案详解冯博琴第三版考研资料中国美术简史考试重难点与名校真题答案详解中央美院考研资料美术概论考试重难点与名校真题答案详解王宏建考研资料各高校艺术学概论历年考研真题汇编考研资料各高校生理学考研真题试卷汇编考研资料生理学考试重难点与名校真题答案详解朱大年第八版考研资料生物化学考试重难点与名校真题答案详解查锡良第七版考研资料数字电路考试重难点与名校真题详解含期末卷考研资料外国近现代建筑史考试重难点与名校真题答案详解罗小未第二版考研资料外国建筑史考试重难点与名校真题答案详解陈志华第四版考研资料各高校机械设计考研真题汇编考研资料各高校自动控制原理考研真题汇编含部分答案解析考研资料各高校道路工程考研真题汇编考研资料自动控制原理考试重难点与名校真题答案详解胡寿松第六版考研资料机械设计基础考试重难点与名校真题答案详解杨可桢第六版考研资料各高校无机化学历年考研真题汇编考研资料各高校电子技术基础历年考研真题汇编含模拟、数字考研资料各高校材料科学基础考研真题答案汇编考研资料材料科学基础考试重难点与名校真题详解胡赓祥第三版考研资料各高校艺术概论与基础考研真题汇编考研资料戏剧戏曲专业知识考试重难点与名校真题答案详解考研资料影视学专业知识考试重难点与名校真题答案详解考研资料各高校音乐理论与音乐史考研真题汇编考研资料 2019深大333教育综合考研强化冲刺题库考研资料公司理财考研强化冲刺题库罗斯第九版考研资料 2019深大考研917会计学考试重难点与名校真题答案详解考研资料各高校会计学考研真题答案汇编考研资料国际金融新编考研强化冲刺题库姜波克第四版考研资料各高校金融学综合历年考研真题答案汇编考研资料各高校国际关系与国际政治考研真题汇编考研资料各高校工程经济学历年考研真题汇编考研资料各高校经济学考研真题试卷分析与答案汇编共六册考研资料各高校运筹学考研真题与答案解析考研资料政治学原理考试重难点与名校真题详解王惠岩第二版考研资料 199管理类联考综合能力考研真题详解及核心讲义考研资料 199管理类联考综合能力考研真题与典型题详解:写作分册考研资料 199管理类联考综合能力考研真题与典型题详解:数学分册考研资料 199管理类联考综合能力考研真题与典型题详解:逻辑分册考研资料深圳大学711艺术概论考研真题试卷2012-2013年考研资料深圳大学928艺术评论写作考研真题试卷2012-2013年考研资料深圳大学712美术史论考研真题试卷2011-2013年考研资料深圳大学929创作考研真题试卷2011-2013年考研资料深圳大学721专业造型基础考研真题试卷2012-2013年考研资料深圳大学713现代设计史、论考研真题试卷2007-2018年考研资料深圳大学948专业设计二考研真题试卷2012-2013年考研资料深圳大学930专业设计一考研真题试卷2011-2013年考研资料深圳大学910生物医学工程综合考研真题试卷2011-2013年考研资料深圳大学727医学细胞生物学考研真题试卷2011-2013年考研资料深圳大学944数字电子技术基础考研真题试卷2011-2013年考研资料深圳大学943电子系统综合考研真题试卷2011-2013年考研资料深圳大学909数字电路与专业综合考研真题试卷2011-2013年考研资料深圳大学718量子力学考研真题试卷2011-2013年考研资料深圳大学710中国文学史考研真题与答案2009-2013年考研资料深圳大学阅读与评论考研真题试卷2013年考研资料深圳大学709中国哲学史考研真题试卷2007-2013年,不含10考研资料深圳大学926西方哲学史考研真题试卷2007-2013年考研资料深圳大学726体育理论综合考研真题试卷2007-2013年,不含10考研资料深圳大学716数学分析考研真题试卷2004-2013年,不含10考研资料深圳大学932高等代数考研真题试卷2004-2013年,不含10考研资料深圳大学戏剧表演与语言传播艺术通识考研真题试卷2012-2013年。
712-数学分析

数学分析考试大纲《数学分析》(712)考试大纲本考试大纲由数学科学与计算技术学院教授委员会于2013年7月7日通过。
I.考试性质数学分析考试是为中南大学招收数学学科硕士研究生而设置的具有选拔性质的业务水平考试,其目的是科学、公平、有效地测试考生对数学分析基本内容的掌握程度和应用相关知识解决问题的能力。
II.考查目标要求考生理解数学分析的基本概念和基本理论,掌握数学分析的基本思想和方法,具有抽象思维能力、逻辑推理能力、运算能力和综合运用所学的知识分析问题和解决问题的能力。
Ⅲ.考试形式和试卷结构1、试卷满分及考试时间本试卷满分为150 分,考试时间为180 分钟2、答题方式答题方式为闭卷,笔试。
3、试卷内容结构分析基础约20 %一元微积分约30 %多元微积分约30 %级数约20 %Ⅳ.考查内容一、分析基础1. 实数概念、确界2. 函数概念3. 序列极限与函数极限4. 无穷大与无穷小5. 连续概念与基本性质,一致连续性6. 实数完备性定理二、一元微分学1.导数概念与几何意义2.求导公式求导法则3.高阶导数4.微分5.微分中值定理6.L’Hospital法则7.Taylor公式8.应用导数研究函数三、一元积分学1.不定积分法与可积函数类2.定积分的概念、性质与计算3.定积分的应用4.反常积分四、级数1.数项级数的敛散判别与性质2.函数项级数与一致收敛性3.幂级数4.Fourier级数五、多元微分学1、多元函数的极限2、多元连续函数3、偏导数与微分4、隐函数定理5、方向导数与梯度6、Taylor公式7、多元微分学的几何应用8、多元函数的极值六、多元积分学1、重积分的概念与性质2、重积分的计算3、二重、三重积分4、含参变量的正常积分和反常积分5、曲线积分与Green公式6、曲面积分7、Gauss公式、Stokes公式、线积分与路径无关。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
深圳大学2021年硕士研究生入学考试大纲、参考书目
(初试科目只提供考试大纲,复试科目只提供参考书目)
命题学院/部门(盖章):数学与统计学院
考试科目代码及名称:[712]数学分析
一、考试的基本要求
《数学分析》考试大纲适用于报考深圳大学基础数学、应用数学专业硕士研究生的入学考试。
本考试是为招收基础数学、应用数学专业硕士生而拟设的具有选拔功能的考试。
其主要目的是测试考生对数学分析最基本内容的理解、掌握和熟练程度。
要求考生熟悉数学分析的基本理论、掌握数学分析的基本方法, 具有较强的抽象思维能力、逻辑推理能力和运算能力。
二、考试内容和考试要求
1.极限与连续
数列极限、函数极限、函数的连续性和一致连续性、闭区间上连续函数的性质。
(1)掌握数列极限与函数极限的概念,理解无穷大(小)量的概念及基本性质;
(2)掌握极限的性质(唯一性、有界性、保号性)及四则运算性质、单调有界收敛定理、Cauchy收敛准则、迫敛性(两边夹、夹挤)原理、两个重要极限;
(3)掌握函数的奇偶性、单调性、周期性、有界性等特殊性质;。
