matlab绘图
Matlab实验报告(三)-MATLAB绘图

实验目的1.掌握MATLAB的基本绘图命令。
2.掌握运用MATLAB绘制一维、二维、三维图形的方法.3.给图形加以修饰。
一、预备知识1.基本绘图命令plotplot绘图命令一共有三种形式:⑴plot(y)是plot命令中最为简单的形式,当y为向量时,以y的元素为纵坐标,元素相应的序列号为横坐标,绘制出连线;若y为实矩阵,则按照列绘出每列元素和其序列号的对应关系,曲线数等于矩阵的列数;当y为复矩阵时,则按列以每列元素的实部为横坐标,以虚部为纵坐标,绘出曲线,曲线数等于列数。
⑵ plot(x,y,[linspec])其中linspec是可选的,用它来说明线型。
当x和y为同维向量时,以x为横坐标,y为纵坐标绘制曲线;当x是向量,y是每行元素数目和x维数相同的矩阵时,将绘出以x为横坐标,以y中每行元素为纵坐标的多条曲线,曲线数等于矩阵行数;当x为矩阵,y为相应向量时,使用该命令也能绘出相应图形。
⑶ plot(x1,y1,x2,y2,x3,y3……)能够绘制多条曲线,每条曲线分别以x和y为横纵坐标,各条曲线互不影响。
线型和颜色MATLAB可以对线型和颜色进行设定,线型和颜色种类如下:线:—实线:点线 -.虚点线——折线点:.圆点 +加号 *星号 x x型 o 空心小圆颜色:y 黄 r 红 g 绿 b 蓝 w 白 k 黑 m 紫 c 青特殊的二维图形函数表5 特殊2维绘图函数[1] 直方图在实际中,常会遇到离散数据,当需要比较数据、分析数据在总量中的比例时,直方图就是一种理想的选择,但要注意该方法适用于数据较少的情况。
直方图的绘图函数有以下两种基本形式。
·bar(x,y) 绘制m*n 矩阵的直方图.其中y 为m *n 矩阵或向量,x 必须单向递增。
·bar(y) 绘制y 向量的直方图,x 向量默认为x=1:m close all; %关闭所有的图形视窗。
x=1:10;y=rand (size(x )); bar(x,y ); %绘制直方图.123456789100.51Bar()函数还有barh ()和errorbar ()两种形式,barh()用来绘制水平方向的直方图,其参数与bar()相同,当知道资料的误差值时,可用errorbar ()绘制出误差范围,其一般语法形式为:errorbar (x,y,l,u)其中x,y 是其绘制曲线的坐标,l ,u 是曲线误差的最小值和最大值,制图时,l 向量在曲线下方,u 向量在曲线上方。
matlab实验 绘图

实验三 Matlab 绘图实验目的熟悉MTALAB 中几种常用的绘图命令,掌握几种常用图形的画法。
实验内容1.二维:用 matlab 二维绘图命令 plot 作出函数图形。
形式: plot(x,y) 2.空间三维作图:三维曲线:plot3(x,y,z,s);三维曲面:mesh(X,Y,Z) 网格生成函数:meshgridsurf(X,Y,Z):绘制由矩阵 X,Y,Z 所确定的曲面图,参数含义同 mesh sphere(n): 专用于绘制单位球面实验方法与步骤1.利用 plot 函数在一个坐标系下绘制以下函数的图形,要求采用不同的颜色、线型、点标记。
方程组: sin(),cos(),sin(2),02x t y t z t t π===<< 步骤:t=[0:0.05:2*pi] x=sin(t);y=cos(t);z=sin(2*t)plot(t,x,'r+:',t,y,'bd-.',t,z,'k*-') 2.plot3 绘制类似田螺线的一条三维螺线方程组:步骤:t=[0:0.1:10*pi]x=2.*(cos(t)+t.*sin(t)) y=2.*(cos(t)-t.*sin(t)) z=1.5*tplot3(x,y,z)3.墨西哥帽子方程:z=步骤:[x,y]=meshgrid(-8:.5:8); z=sqrt(x.^2+y.^2)+eps;Z=sin(z)./z;mesh(X,Y,Z)axis square4. 利用 surf 函数绘制马鞍面方程:2294x y z=-步骤:x=[-25:0.5:25];y=[-25:0.5:25] [X,Y]=meshgrid(x,y)Z=(X.^2/9)-(Y.^2/4)surf(X,Y,Z)5.双曲抛物面方程:22222 x yz a b-=步骤:x=[-25:0.5:25];y=[-25:0.5:25] ezsurfc('X.^2./16-Y.^2./12')实验结果1.2.100-100-1010104.-4040-4-224XX 2/16-Y 2/12Y总结与思考matlab 的常见错误分析Inner matrix dimensions must agree因为在matlab 的输入变量是矩阵,参与运算的矩阵维数必须对应,矩阵响应元素的运算必须全部加dot (点)。
Matlab 绘图大全

要设置曲线样式可以在plot函数中加绘图选项,其调用格式为:
plot(x1,y1,选项1,x2,y2,选项2,…,xn,yn,选项n)
例1-6 在同一坐标内,分别用不同线型和颜色绘制曲线y1=0.2e-0.5xcos(4πx) 和y2=2e-0.5xcos(πx),标记两曲线交叉点。
title('bar(x,y,''g'')');axis([0,7,-2,2]);
subplot(2,2,2);stairs(x,y,'b');
title('stairs(x,y,''b'')');axis([0,7,-2,2]);
subplot(2,2,3);stem(x,y,'k');
例1-7 在0≤x≤2p区间内,绘制曲线y1=2e-0.5x和y2=cos(4πx),并给图形添加图形标注。
程序如下:
x=0:pi/100:2*pi;
y1=2*exp(-0.5*x);
y2=cos(4*pi*x);
plot(x,y1,x,y2)
title('x from 0 to 2{\pi}'); %加图形标题
1.6 对函数自适应采样的绘图函数
fplot函数的调用格式为:
fplot(fname,lims,tol,选项)
其中fname为函数名,以字符串形式出现,lims为x,y的取值范围,tol为相对允许误差,其系统 默认值为2e-3。选项定义与plot函数相同。
axis off:取消坐标轴。
axis on:显示 坐标轴。
给坐标加网格线用grid命令来控制。grid on/off命令控制是画还是不画网格线,不带参数的grid命令在两种状态之间进行切换。
matlab绘图指令大全22页word文档
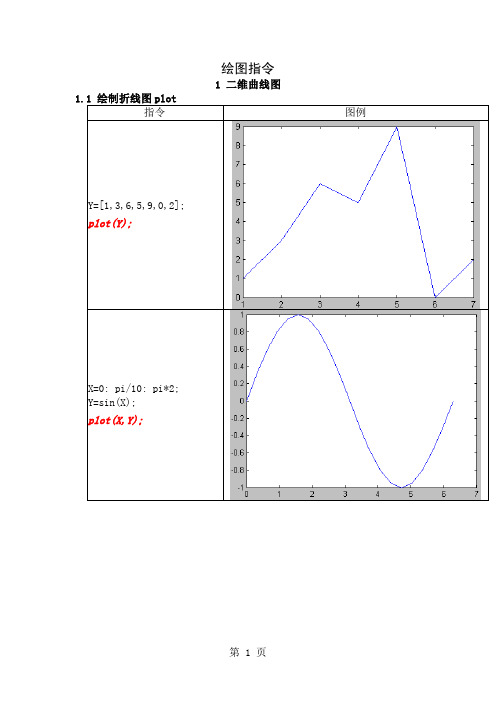
绘图指令1 二维曲线图指令图例Y=[1,3,6,5,9,0,2];plot(Y);X=0: pi/10: pi*2;Y=sin(X);plot(X,Y);X=0: pi/10: pi*2;Y1=sin(X);Y2=cos(X);Plot(X,Y1,X,Y2);调整坐标范围:axisaxis([0,300,0,2])DrawCircle.mfunction DrawCircle(Point,Radius)Hold ont=0: pi/10: 2*pi;x=Point(1)+ Radius*cos(t);y=Point(2)+ Radius*sin(t);plot(x,y);DrawCircle([10 10],1)DrawCircle([20 10],2)DrawCircle([10 20],3)显函数ezplot('sin(x)',[0,2*pi])隐函数ezplot('x^2+y^2-10',[-5,5],[-6,6])参数方程ezplot('cos(t)^3','sin(t)^3',[0,2*pi])function y=myf1(x)y=sqrt(100-x^2);fplot('myf1',[-15 15])fplot('[sin(x) cos(x) myf1(x)]',[-15 15])1.5 图形修饰设置颜色 y m c r g b w k设置线型 - : -. --指令图例Y=[1,3,6,5,9,0,2];plot(Y, 'r-+');X=0: pi/10: pi*2;Y1=sin(X); Y2=cos(X);plot(X,Y1,'r+-',X,Y2,'b-*');text(3.5, 0.6, '曲线比较');x=[1.6*pi, 1.6*pi]; y=[-0.3, 0.8];s=['曲线cos'; '曲线sin'];text(x,y,s);指令图例bar直方图X=0:pi/10:2*pi;Y=sin(X);bar(X,Y);polar极坐标图T=0: pi/10: 4*pi;R=T;polar(T, R);误差棒棒图X=0:pi/10:2*pi;Y=sin(X);e=0.2*rand(size(X)); errorbar(X,Y,e);火柴杆图X=0:pi/10:2*pi; Y=sin(X); stem(X,Y);stairs楼梯图X=0:pi/10:2*pi; Y=sin(X); stairs(X,Y);多边形填色图X=[1,2,3,4,5];Y=[3,5,2,1,6];fill(X,Y,'r');hold on; % 保持图形plot(X,Y,'o')1.7 数值函数的二维图fplot('0.5*cos(x)',[-pi,pi]) % 绘图[X,Y] = fplot('0.5*cos(x)',[-pi,pi]); % 返回点坐标fplot('cos(x)',[-pi,pi],'r-+'); % 观察点的位置控制采样点的密度fplot('cos(x)',[-pi,pi],'r-+',0.05);fplot('cos(x)',[-pi,pi],'r-+',0.1);可绘制系统函数,也可绘制自定义函数的图形。
Matlab绘图

第二章绘图要画一个函数的图像,先是选取一堆x,求出相对应的y值,然后按照数值描点,接着用光滑的曲线把点连接起来。
和数学课讲的一样,在matlab中,我们画图也分为三步1. 建立一个x的点集;2. 根据函数关系式算出每个x对应y的点集;3. 将这些点用平滑的曲线连接起来。
例如要画y=sinx在[0,10]区间内的图像,首先我们要确定出x的区间>>x = [0:0.1:10];命令的意思是,产生一个数集,它从0开始,每次加0.1,一直加到10为止注意,命令后面的分号记得加上,否则matlab会把x的元素都打印出来,下面就是不加分号的后果:有了x的数集后,我们再根据函数关系式y=sinx得出y的点集>>y = sin(x);同样的,别忘了把分号加上抑制程序输出y的具体值,以及sin(x)的括号别忘了加到这里,我们已经把x和y确定下来,接下来只需用plot(x,y)命令即可绘制出图像>>plot(x,y)当然,如果你不定义y,而直接用一下嵌套命令也是可以的>>plot(x,sin(x))我们将x的增量变大一点,改为0到10,每次增幅为1,即>>x = [0:1:10];然后我们输入>>plot(x,y)我们会得到错误信息:原因是之前我们定义的y是由之前的x决定的,当x改变后,y依然没有改变,为了解决这个问题,我们要把y重新定义一遍,即命令要完整再输入一遍>>x = [0:1:10];>>y = sin(x);>>plot(x,y)然后程序会绘制出和我们预期相同的图像没错,我们将看到不光滑的曲线,这告诉我们,当使用plot(x,y)画图的时候x的增加幅度尽可能小一些,画出的图像才精确(跟数学里点越多图像越精确原理一样的)为了美化图像(有时是为了更清楚的辨析图像),我们经常要为图像加上网格,为坐标轴命名,改变曲线的颜色、形状这些命令2.1 加上网格我们使用grid on 命令我们这样书写:>>x=[0:0.1:10];y=sin(x);>>plot(x,y),grid on这样就画出了带网格的图像当然,也可以先画出没有网格的图像,再把窗口切回matlab命令输入窗口,输入grid on,这样图像就会加上网格,即>>x=[0:0.1:10];y=sin(x);>>plot(x,y)>>grid on2.2 为坐标轴命名为x坐标轴命名的命令是xlabel(),显然,y的就应该是ylabel()比如这里,我想让x命名为x,y命名为sinx,则如下输入:>>x=[0:0.1:10];y=sin(x);>>plot(x,y),xlabel(‘x’),ylabel(‘sinx’)注意,坐标轴的名字要用引号括起来,表示字符串当然也可以画图后再标坐标轴,即:>>x=[0:0.1:10];y=sin(x);>>plot(x,y)>>xlabel(‘x’)>>ylabel(‘sinx’)然后我们就可以看到坐标轴带命名的图像:2.3 绘制多条曲线绘制多条曲线有两种情况,一种是在同一个坐标面内画多条曲线,另一种是在一个面内画多个独立的曲线我们先讲第一种,假设我们要在一个坐标面内画sinx,cosx,tanx的图像先定义x,y>>x=[0:0.1:10]>>y1=sin(x);>>y2=cos(x);>>y3=tan(x);接着画图>>plot(x,y1)这时候函数绘制出了sinx的图像接着我们继续画>>plot(x,y2)我们会发现程序会把之前的sinx图像抹掉,然后绘制cosx的图像为了让他们同时存在,我们使用hold on命令,即画完一个图后,hold on,继续画当我们再加上tanx后会得到这个图像这是因为函数显示区间设置的原因,后面讲2.4 更改图像显示区间从楼上我们已经在一个图中画出了sinx、cosx、tanx的图像,但是我们知道tanx的值域是负无穷到正无穷,而sin,cos的值域是-1到1,这导致了我们基本上看不到sin,cos的图像,为了解决这个问题,我们只需用axis命令即可,命令格式为axis([xmin xmax ymin ymax])即括号内跟一个区间,四个数字分别是x的起点,x的终点,y的起点,y的终点。
matlab画图大全

@绘图%二维画图x=linspace(0,2*pi,30);y=sin(x);z=cos(x);plot(x,y,'r',x,z,'g')%ezplot符号函数(显函数、隐函数和参数方程)画图subplot(1,3,1)ezplot('cos(x)',[0,pi])subplot(1,3,2)ezplot('cos(t)^3','sin(t)^3',[0,2*pi])subplot(1,3,3)ezplot('exp(x)+sin(x*y)',[-2,0.5,0,2])%在[-2,0.5],[0,2](坐标轴的范围)上画隐函数的图.1%fplot(‘fun’,lims) 表示绘制字符串fun指定的函数在lims=[xmin,xmax]的图形.%[1] fun必须是M文件的函数名或是独立变量为x的字符串.%[2] fplot函数不能画参数方程和隐函数图形,但在一个图上可以画多个图形.fplot('tanh',[-2,2],':')hold onfplot('[tanh(x),sin(x),cos(x)]',2*pi*[-1 1 -1 1])%对数坐标图 loglog(Y):表示 x、y坐标都是对数坐标系 semilogx(Y):表示 x坐标轴是对数坐标系%semilogy(…):表示y坐标轴是对数坐标系 plotyy:有两个y坐标轴,一个在左边,一个在右边x=0:.1:10;semilogy(x,10.^x)2x=logspace(-1,2);loglog(x,exp(x),'-s')%-s是方形标注符grid onx=[1:1:100];subplot(2,3,1);plot(x,x.^3);grid on;title 'plot-y=x^3';subplot(2,3,2);3loglog(x,x.^3);grid on;title 'loglog-logy=3logx';subplot(2,3,3);plotyy(x,x.^3,x,x);grid on;title 'plotyy-y=x^3,logy=3logx';subplot(2,3,4);semilogx(x,x.^3);grid on;title 'semilogx-y=3logx';subplot(2,3,5);semilogy(x,x.^3);grid on;title 'semilogy-logy=x^3';%三维绘图%空间曲线 plot3(x,y,z,s) x,y,z为n维向量,分别表示曲线上点集的横坐标、纵坐标、函数值 s为指定颜色、线形等t=0:pi/50:10*pi;plot3(sin(t),cos(t),t)%在区间[0,10π]画出参数曲线 x=sint,y=cost,z=t.rotate3d %旋转图形 在图形窗口上面的选项栏里有4x=-3:0.1:3;y=1:0.1:5;[X,Y]=meshgrid(x,y);Z=(X+Y).^2;plot3(X,Y,Z)%其中x,y,z是都是m×n矩阵,其对应的每一列表示一条曲线.%%空间曲面 surf(x,y,z) x,y,z为数据矩阵.分别表示数据点的横坐标、纵坐标、函数值,画出数据点(x,y,z)表示的曲面x=-3:0.1:3;y=1:0.1:5;[X,Y]=meshgrid(x,y);%生成x,y的数据网格使曲面更光滑Z=(X+Y).^2;surf(X,Y,Z)shading flat%使图形变得光滑rotate3dshading interp%除去网格 只在surf函数下起作用 mesh不能5doc shading%shading flat; shading faceted(缺省); shading interp; shading (axes_handle,...)@%%mesh(x,y,z)x,y,z为数据矩阵.分别表示数据点的横坐标、纵坐标、函数值,画网格曲面(中间没有曲面)x=-3:0.1:3; y=1:0.1:5;[X,Y]=meshgrid(x,y);%在特定区域内生成网格Z=(X+Y).^2;mesh(X,Y,Z)6[X,Y]=meshgrid(-3:.125:3);Z=peaks(X,Y);subplot(1,2,1)meshz(X,Y,Z)subplot(1,2,2)surf(X,Y,Z)shading flat7%%图形处理%加栅格、图例和标注%grid off/onx=linspace(0,2*pi,30);y=sin(x);plot(x,y)xlabel('自变量X')ylabel('函数Y')title('示意图')grid on8% 命令gtext(‘string’)用鼠标放置标注在现有的图上. x=linspace(0,2*pi,30);y=sin(x);z=cos(x);plot(x,y,x,z)gtext('sin(x)');gtext('cos(x)');9% 命令gtext(‘string’)用鼠标放置标注在现有的图上. x=linspace(0,2*pi,30);y=sin(x);z=cos(x);plot(x,y,x,z)gtext('sin(x)');gtext('cos(x)');10%图形保持 hold on/offx=linspace(0,2*pi,30);z=cos(x);y=sin(x);plot(x,z,:)%“:”表示虚线hold onplot(x,y)zoom on%放大命令11%figure(h)新建h窗口,激活图形使其可见,并把它置于其它图形之上%割窗口 subplotx=linspace(0,2*pi,100);y=sin(x); z=cos(x);a=sin(x).*cos(x);b=sin(x)./(cos(x)+eps)subplot(2,2,1);plot(x,y),title('sin(x)')subplot(2,2,2);plot(x,z),title('cos(x)')subplot(2,2,3);plot(x,a),title('sin(x)cos(x)')subplot(2,2,4);plot(x,b),title('sin(x)/cos(x)')12%缩放模式:zoom on/off%改变视角:view(a,b)a为方位角,b为仰角;view([x,y,z])x,y,z为笛卡尔坐标x=-3:0.1:3; y=1:0.1:5;[X,Y]=meshgrid(x,y);Z=(X+Y).^2;subplot(2,2,1); mesh(X,Y,Z)subplot(2,2,2);mesh(X,Y,Z);view(50,-34)subplot(2,2,3);mesh(X,Y,Z);view(-60,70)subplot(2,2,4);mesh(X,Y,Z);view([0,1,1])13%%制作动画 Moviein(),getframe,movie():函数Moviein()产生一个帧矩阵来存放动画中的帧;函数getframe对当前的图像进行快照;函数movie()按顺序回放各帧.[x,y,z]=peaks(30);surf(x,y,z)axis([-3 3 -3 3 -10 10])axis offshading interpcolormap(hot)m=moviein(360);for i=1:360view(-37.5+1*(i-1),30)m(:,i)=getframe;endmovie(m)14%特殊图形%1. 极坐标图:polar (theta,rho,s)theta=linspace(0,2*pi),rho=sin(2*theta).*cos(2*theta);polar(theta,rho,'g')title('Polar plot of sin(2*theta).*cos(2*theta)');%2. 散点图: scatter(X,Y,S,C)在向量X和Y的指定位置显示彩色圈.X和Y必须维数相同.load seamountscatter(x,y,5,z)15%3. 平面等值线图: contour(x,y,z,n) 绘制n个等值线的二维等值线图[X,Y]=meshgrid(-2:.2:2,-2:.2:3);Z=X.*exp(-X.^2-Y.^2);[C,h]=contour(X,Y,Z);clabel(C,h)colormap cool16%空间等值线图:contour3(x,y,z,n)[x,y,z]=peaks;subplot(1,2,1)contour3(x,y,z,16,'s')grid, xlabel('x-axis'), ylabel('y-axis') zlabel('z-axis')title('contour3 of peaks');subplot(1,2,2)contour(x,y,z,16,'s');grid, xlabel('x-axis'), ylabel('y-axis') title('contour of peaks');17%三维散点图2. 三维散点图 scatter3(X,Y,Z,S,C) s为size c为color 在向量X,Y和Z指定的位置上显示彩色圆圈.向量X,Y和Z的维数必须相同. [x,y,z]=sphere(16);X=[x(:)*.5 x(:)*.75 x(:)];Y=[y(:)*.5 y(:)*.75 y(:)];Z=[z(:)*.5 z(:)*.75 z(:)];S=repmat([1 .75 .5]*10,numel(x),1);C=repmat([1 2 3],numel(x),1);scatter3(X(:),Y(:),Z(:),S(:),C(:),'filled'),view(-60,60)18%要在某山区方圆大约27km2范围内修建一条公路,从山脚出发经过一个居民区,再到达一个矿区.横向纵向分别每隔400m测量一次,得到一些地点的高程:(平面区域0≤x≤ 5600,0≤y≤4800),需作出该山区的地貌图和等高线图. x=0:400:5600;y=0:400:4800;z=[370 470 550 600 670 690 670 620 580 450 400 300 100 150 250;...510 620 730 800 850 870 850 780 720 650 500 200 300 350 320;...650 760 880 970 1020 1050 1020 830 900 700 300 500 550 480 350;...740 880 1080 1130 1250 1280 1230 1040 900 500 700 780 750 650 550;...830 980 1180 1320 1450 1420 1400 1300 700 900 850 840 380 780 750;...880 1060 1230 1390 1500 1500 1400 900 1100 1060 950 870 900 930 950;...910 1090 1270 1500 1200 1100 1350 1450 1200 1150 1010 880 1000 1050 1100;...950 1190 1370 1500 1200 1100 1550 1600 1550 1380 1070 900 1050 1150 1200;...1430 1430 1460 1500 1550 1600 1550 1600 1600 1600 1550 1500 1500 1550 1550;...1420 1430 1450 1480 1500 1550 1510 1430 1300 1200 980 850 750 550 500;...1380 1410 1430 1450 1470 1320 1280 1200 1080 940 780 620 460 370 350;...1370 1390 1410 1430 1440 1140 1110 1050 950 820 690 540 380 300 210;...1350 1370 1390 1400 1410 960 940 880 800 690 570 430 290 210 150];meshz(x,y,z)xlabel('X'),ylabel('Y'),zlabel('Z')%插值使曲面光滑[x1,y1]=meshgrid(0:10:5600,0:10:4800);z1=griddata(x,y,z,x1,y1,'cubic');figure(2),surf(x1,y1,z1)shading flatfigure(3)contour(x,y,z)19figure(4)contour3(x,y,z)202122。
MATLAB画图——基础篇
MATLAB画图——基础篇MATLAB画图——基础篇在MATLAB使⽤的过程中,学会画图是⼀项必要的技能。
在这⾥,我总结了部分简单的画图函数,同时附上代码(本⽂中的程序为了⽅便给出的数据都很简单,⼤家可以⾃⼰去尝试其他数据)。
这对刚刚开始接触MATLAB的⼩⽩来说,我认为还是很有帮助的。
⽂章⽬录⼀、plot()函数1.⼆维图形(1)绘图选项线型颜⾊标记符号-实线b蓝⾊.点s⽅块:虚线g绿⾊o圆圈d菱形.-点划线r红⾊x叉v朝下三⾓符号-双划线c青⾊+加号^朝上三⾓符号m品红*星号<朝左三⾓符号y黄⾊>朝右三⾓符号p五⾓星k⿊⾊h六⾓星w⽩⾊(2)图形的辅助标注和窗⼝的分割title(图形说明)xlabel(x轴说明)ylabel(y轴说明)text(x,y图形说明)——在x,y轴处添加⽂字说明legend(图例⼀,图例⼆,…)subplot(m,n,p)——将绘图区域分割成m*n个⼦区域,并按照⾏从左⾄ 右,从上⾄下依次编号。
p表⽰第p个绘图⼦区域。
注意:如果是要两个图画到同⼀个坐标⾥⾯,则在两个plot函数之间添加⼀⾏hold on(3)格式plot(x)——缺省⾃变量绘图格式plot(x,y)——基本格式。
以y(x)的函数关系作图。
如果y是n*m的矩 阵,则x为⾃变量,作出m条曲线。
plot(x1,y1,x2,y2,…,xn,yn)——多条曲线绘图格式plot(x1,y1,选项1,x2,y2,选项2,…,xn,yn,选项n)——含选项的绘图格式x1=[1 2 3 4 5 6 7 8 9];x2=[2 4 6 8 10 12 14 16 18];y1=[1 4 9 16 25 36 49 64 81];y2=[18 16 14 12 10 8 6 4 2];subplot(4,1,1);plot(x1);title('例⼀');xlabel('⾃变量');ylabel('因变量');subplot(4,1,2);plot(x1,y1);title('例⼆');xlabel('⾃变量');ylabel('因变量');subplot(4,1,3);plot(x1,y1,x2,y2);title('例三');xlabel('⾃变量');ylabel('因变量');subplot(4,1,4);plot(x1,y1,'m+',x2,y2,'c*');title('例四');xlabel('⾃变量');ylabel('因变量');2.三维图形(1)格式plot3(x1,y1,z1,‘选项⼀’,x2,y2,z1,‘选项⼆’,…)x,y,z是长度相同的向量:⼀条曲线x,y,z是维度相同的矩阵:多条曲线(2)⽹格矩阵⽣成函数:meshgrid[X,Y]=meshgrid(x,y)x,y是给定的向量,X,Y是⽹格划分后得到的⽹格矩阵注意,这个函数⽤来⽣成⽹格矩阵,不是直接⽤来画图的,配合mesh使⽤。
MATLAB第三节 绘图

2,0.5],[0,2]上画隐函数 的图. 【例】 在[-2,0.5],[0,2]上画隐函数 e x + sin( xy ) = 0 的图 ezplot('exp(x)+sin(x*y)',[ezplot('exp(x)+sin(x*y)',[-2,0.5,0,2])
ezplot(‘x(t) , y(t) ezplot( x(t)’,’y(t) ,[tmin,tmax]) x(t) y(t)’,[tmin,tmax])
上画y=cos x 的图形 的图形. 【例】 在[0,π ]上画 上画
ezplot('sin(x)',[0,pi])
ezplot(‘f(x,y) ,[xmin,xmax,ymin,ymax]) ezplot( f(x,y)’,[xmin,xmax,ymin,ymax]) f(x,y)
note:表示在区间xmin<x<xmax和 ymin<y<ymax绘制隐 函数f(x,y)=0的函数图.
4.2特殊坐标图形 特殊坐标图形
semilogx(x,y)—单对数X semilogx(x,y) 单对数X轴绘图命令 semilogy(x,y)—单对数Y轴绘图命令 semilogy(x,y) 单对数Y
【例】以X轴为对数重新绘制上述曲线; 轴为对数重新绘制上述曲线; x=[0:0.01:2*pi] y=abs(1000*sin(4*x))+1 单对数X semilogx(x,y) %单对数X轴绘图 【例】以Y轴为对数重新绘制上述曲线; 轴为对数重新绘制上述曲线; x=[0:0.01:2*pi] y=abs(1000*sin(4*x))+1 单对数Y semilogy(x,y) %单对数Y轴绘图
Matlab绘图命令

Matlab绘图命令:1.p lot(x,y):该命令用于描点法作图,给出x的范围,然后利用函数式计算出每一个x对应的y,注意,x间距取得越小,图像会画的越圆滑,这是因为plot描点法作图的原因.如:plot(x,y,’--’)2.f plot(y,[xstart xend]):该命令同样用于绘制图像,但是只需要给出x范围与y关于x的函数式即可,相比于plot 函数更加方便。
3.g rid on可以给图像加上网格4.h old on:用于连续绘图,如果想要在一个坐标系中画出多个图形的话,则需要在每次画完图形之前加入这个命令。
5.l egend(‘y’):在图上标出y曲线线型6.设置图线颜色:plot(x,y,’颜色’)7.a xis ( [xmin xmax ymin ymax] ):设置图像横纵坐标范围例:fplot('cos(x)',[-5 5],'r--'),axis ( [-5 5 -1 1] ),8.s ubplot(m, n, p):用于在一个窗口中绘制多个图像。
例:subplot(1, 2, 1);fplot('sin(x)',[-5 5],'b--');subplot(1, 2, 2);fplot('cos(x)',[-5 5],'r--');9.p lot(thea,r): 绘制极坐标图形,thea 是角变量,r是极轴长度例:a = 2;theta = [0:pi/90:2*pi];r = a*theta;polar(theta,r), title('阿基米德螺线')10.bar(x,y):画直方图11.stem(t,f):绘制针头图,这种图经常用来表示波动情况,或者各值和平均值的偏差,可以一目了然。
例:subplot(1, 2, 1);plot(t,f),xlabel('时间(秒)'),ylabel('弹簧响应');subplot(1, 2, 2);stem(t,f),xlabel('时间(秒)'),ylabel('弹簧响应');12.counter3(x,y,z,n):绘制三维等高图例:[x,y] = meshgrid(-2:0.1:2);z = y.*exp(-x.^2 - y.^2);contour3(x, y, z, 30);surface(x,y,z,'EdgeColor',[.8 .8 .8],'FaceColor','none');grid off;view(-15,20);13.mesh(x,y,z):绘制普通三维图14.surf(x,y,z):绘制颜色渐变三维图15.。
matlab画图大全[资料]
![matlab画图大全[资料]](https://img.taocdn.com/s3/m/0e578e91bdeb19e8b8f67c1cfad6195f312be8c8.png)
matlab绘图大全Matlab绘图系列之高级绘图一、目录1.彗星图二维彗星图三维彗星图2.帧动画3.程序动画4.色图变换5.Voronoi图和三角剖分Voronoi图三角剖分6.四面体7.彩带图彩带图三维流彩带图8.伪彩图9.切片图切片图切片轮廓线图10.轮廓图显示轮廓线显示围裙瀑布效果带光照模式的阴影图11.函数绘图轮廓线、网格图、曲面图、轮廓网格图轮廓曲面图、二维曲线、极坐标曲线图、自定义函数12.三维图形控制视点灯光效果色彩控制二、图形示例1.彗星图二维彗星图t=0:.01:2*pi;x=cos(2*t).*(cos(t).^2);y=sin(2*t).*(sin(t).^2);comet(x,y);title('二维彗星轨迹图')hold onplot(x,y)三维彗星图a=12;b=9;T0=2*pi;%T0是轨道的周期T=5*T0;dt=pi/100;t=[0:dt:T]';f=sqrt(a^2-b^2);%地球与另一焦点的距离th=12.5*pi/180;%未经轨道与x-y平面的倾角E=exp(-t/20);%轨道收缩率x=E.*(a*cos(t)-f);y=E.*(b*cos(th)*sin(t));z=E.*(b*sin(th)*sin(t));plot3(x,y,z,'g')%画全程轨线hold on,sphere(20);%画地球axis offtitle('卫星返回地球示例')x1=-18*T0;x2=6*T0;y1=-12*T0;y2=12*T0;z1=-6*T0;z2=6*T0;axis([x1 x2 y1 y2 z1 z2])% axis([-15 10 -15 10 -10 10])axis equalcomet3(x,y,z,0.02);%画运动轨线hold off2.帧动画Z=peaks;surf(Z)%绘制网格表面图axis tightset(gca,'nextplot','replacechildren');%设定axis覆盖重画模式title('帧动画播放示例')for j=1:20surf(sin(2*pi*j/20)*Z,Z)%重新绘制网格表面图,这里后面一个Z当成了颜色矩阵F(j)=getframe;%创建帧endmovie(F,20)%播放动画20次3.程序动画t=0:pi/50:10*pii=1;h=plot3(sin(t(i)),cos(t(i)),t(i),'*','erasemode','none');%设定擦除模式grid onaxis([-2 2 -2 2 -1 10*pi])title('程序动画示例')for i=2:length(t)set(h,'xdata',sin(t(i)),'ydata',cos(t(i)),'zdata',t(i));drawnowpause(0.01)end4.色图变换load spineimage(X)colormap coolspinmap(10)5.Voronoi图和三角剖分Voronoi图rand('state',5)x=rand(1,10);y=rand(1,10);subplot(131)voronoi(x,y);%绘制voronoi图形axis equalaxis([-0.2 1.6 -0.5 2.5])subplot(132)[vx,vy]=voronoi(x,y);plot(x,y,'r+',vx,vy,'b-');%应用返回值绘制axis equalaxis([-0.2 1.6 -0.5 2.5])subplot(133)rand('state',5);x=rand(10,2);[v,c]=voronoin(x);%返回值v参数维voronoi顶点矩阵,返回值c 参数为voronoi元胞数组for i=1:length(c)if all(c{i}~=1)patch(v(c{i},1),v(c{i},2),i);%应用色图iendendaxis equalaxis([-0.2 1.6 -0.5 2.5])box on三角剖分[x,y]=meshgrid(1:15,1:15);tri=delaunay(x,y);z=peaks(15);trimesh(tri,x,y,z)6.四面体d=[-1 1];[x,y,z]=meshgrid(d,d,d);%定义一个立方体x=[x(:);0];y=[y(:);0];z=[z(:);0];%[x,y,z]分别为加上中心的立方体顶点X=[x(:) y(:) z(:)];Tes=delaunayn(X);%返回m×n的数组值tetramesh(Tes,X);%绘制四面体图camorbit(20,0);%旋转摄像目标位置7.彩带图彩带图[x,y]=meshgrid(-3:.5:3,-3:.1:3);z=peaks(x,y);ribbon(y,z)三维流彩带图load wind%打开保存的数据lims=[100.64 116.67 17.25 28.75 -0.02 6.86];%定义坐标轴范围[x,y,z,u,v,w]=subvolume(x,y,z,u,v,w,lims);%lims来定义数据子集[sx sy sz]=meshgrid(110,20:5:30,1:5);%定义网格点verts=stream3(x,y,z,u,v,w,sx,sy,sz,.5);%计算彩带顶点cav=curl(x,y,z,u,v,w);%计算卷曲角速度wind_speed=sqrt(u.^2+v.^2+w.^2);%计算流速h=streamribbon(verts,x,y,z,cav,wind_speed,2);%绘制流彩带图view(3)8.伪彩图n=6%定义轮数r=(0:n)'/n;%定义轮的半径theta=pi*(-n:n)/n;%定义轮的扇区角X=r*cos(theta);Y=r*sin(theta);%定义网格顶点C=r*cos(2*theta);%定义色图pcolor(X,Y,C)%绘制伪彩图axis equal tight9.切片图切片图[x,y,z] = meshgrid(-2:.2:2,-2:.25:2,-2:.16:2);v = x.*exp(-x.^2-y.^2-z.^2);xslice = [-1.2,.8,2]; yslice = 2; zslice = [-2,0];slice(x,y,z,v,xslice,yslice,zslice)colormap hsv切片轮廓线图[x y z v]=flow;%打开水流数据h=contourslice(x,y,z,v,[1:9],[],[0],linspace(-8,2,10));%切片轮廓线view([-12 30])10.轮廓图显示轮廓线[x,y,z]=peaks;subplot(1,2,1)meshc(x,y,z);%同时画出网格图与轮廓线title('meshc 网格图与轮廓线')axis([-inf inf -inf inf -inf inf]);subplot(1,2,2)surfc(x,y,z);%同时画出曲面图与轮廓线title('surfc 曲面图与轮廓线')axis([-inf inf -inf inf -inf inf]);显示围裙[x y z]=peaks;meshz(x,y,z);瀑布效果[X,Y,Z]=peaks(30);waterfall(X,Y,Z)带光照模式的阴影图[x,y]=meshgrid(-3:1/8:3);z=peaks(x,y);surfl(x,y,z);shading interp%着色处理colormap(gray);%灰度处理axis([-3 3 -3 3 -8 8])11.函数绘图轮廓线、网格图、曲面图、轮廓网格图%图1绘制轮廓线、网格图、曲面图、轮廓网格图subplot(221)f=['3*(1-x)^2*exp(-(x^2)-(y+1)^2)-10*(x/5-x^3-y^5)*exp(-x^2-y^2)-1/3*exp(-(x+1)^2-y^2)'];%定义双变量x、y的函数式ezcontour(f,[-3,3],49)%x、y为[-3 3],网格为49×49subplot(222)ezmesh('sqrt(x^2+y^2)');subplot(223)ezsurf('real(atan(x+i*y))')%经过滤波,如果相同数据surf绘图没有滤波subplot(224)ezmeshc('y/(1+x^2+y^2)',[-5,5,-2*pi,2*pi])%x、y的数值范围分别为[-5 5]、[-2*pi 2*pi]轮廓曲面图、二维曲线、极坐标曲线图、自定义函数%图2绘制轮廓曲面图、二维曲线、极坐标曲线图、自定义函数figure(2)subplot(221)ezsurfc('sin(u)*sin(v)')subplot(222)ezplot('x^2-y^4');subplot(223)ezpolar('1+cos(t)')subplot(224)fplot('myfun',[-20 20])function Y=myfun(x)Y(:,1)=200*sin(x(:))./x(:);Y(:,2)=x(:).^2;三维曲线图%绘制三维曲线图figure(3)ezplot3('sin(t)','cos(t)','t',[0,6*pi])12.三维图形控制视点View图形旋转subplot(121)surf(peaks);title('旋转前图形');subplot(122)h=surf(peaks);rotate(h,[1 0 1],180)title('旋转后图形');灯光效果%灯光效果(1)camlight(2)light(3)lightangle(4)lighting(5)materialsphere;camlight色彩控制%色彩控制(1)缺省设置colordef、whitebg(2)色图colormap(3)浓淡处理shadingload flujetimage(X)colormap(jet)subplot(131)sphere(16)axis squareshading flattitle('Flat Shading')subplot(132)sphere(16)axis squareshading facetedtitle('Faceted Shading') subplot(133)sphere(16)axis squareshading interptitle('Interpolated Shading')。
MATLAB中的绘图函数介绍

MATLAB中的绘图函数介绍概述:MATLAB是一种非常强大的数值计算和科学绘图软件,在各个领域中都得到广泛的应用。
在MATLAB中,绘图函数是其中一个非常重要的功能,它可以帮助我们将数据可视化,并进行分析和解释。
在本文中,我们将详细介绍一些常用的MATLAB绘图函数及其功能。
一、plot函数:plot函数是MATLAB中最基本的绘图函数之一,它可以绘制线性图。
通过将一系列的点连接起来,我们可以绘制出数据的变化趋势。
下面是plot函数的一个简单示例:```matlabx = 0:0.1:10;y = sin(x);plot(x, y);```在这个例子中,我们首先定义了x的取值范围为0到10,间隔为0.1。
然后通过使用sin函数计算出对应的y值。
最后,调用plot函数将x和y的数值传入,即可得到一条关于sin函数的图形。
除了基本的线性图,plot函数还可以绘制不同颜色和线型的曲线,并添加标题、标签等。
它是进行简单数据可视化的利器。
二、scatter函数:相比于plot函数,scatter函数可以绘制散点图,用于展示多个不同数据点之间的分布关系。
通过scatter函数,我们可以方便地比较不同变量之间的相关性。
以下是scatter函数的一个示例:```matlabx = randn(100,1);y = 0.5*x + randn(100,1);scatter(x, y);```在这个例子中,我们首先生成了两组随机数x和y。
然后使用scatter函数将它们绘制成散点图。
通过观察散点图的分布,我们可以判断出x和y之间是否存在线性相关性。
scatter函数还支持设置散点的颜色、大小和透明度等参数,以满足不同的需求。
它是进行多变量分析的重要工具之一。
三、bar函数:bar函数可以用于绘制柱状图,常用于展示各个类别的数据之间的差异。
通过柱状图,我们可以清晰地比较不同类别之间的数值大小。
以下是bar函数的一个示例:```matlabx = categorical({'A', 'B', 'C', 'D'});y = [10, 15, 8, 12];bar(x, y);```在这个例子中,我们首先定义了四个类别,分别是'A'、'B'、'C'和'D'。
怎样用Matlab绘图

help plothelp axisa1=plot();hlod ona2=plot();legend([a1 a2],'图1 名',‘图2 名')hold offx1=-pi:pi/12:pi;x2=-pi:pi/12:pi;y1=sin(x1);y2=cos(x2);plot(x1,y1,x2,y2);axis([-2*pi 2*pi -2 2]);xlabel('x');ylabel('y');title('sin(x) & cos(x)');MATLAB受到控制界广泛接受的一个重要原因是因为它提供了方便的绘图功能.这里主要介绍2 维图形对象的生成函数及图形控制函数的使用方法,还将简单地介绍一些图形的修饰与标注函数及操作和控制MATLAB 各种图形对象的方法.第一节图形窗口与坐标系一.图形窗口1.MATLAB 在图形窗口中绘制或输出图形,因此图形窗口就像一张绘图纸.2.在MATLAB 下,每一个图形窗口有唯一的一个序号h,称为该图形窗口的句柄.MATLAB 通过管理图形窗口的句柄来管理图形窗口;3.当前窗口句柄可以由MATLAB 函数gcf 获得;4. 在任何时刻, 只有唯一的一个窗口是当前的图形窗口( 活跃窗口);figure(h)----将句柄为h 的窗口设置为当前窗口;5.打开图形窗口的方法有三种:1)调用绘图函数时自动打开;2)用File---New---Figure 新建;3)figure 命令打开,close 命令关闭.在运行绘图程序前若已打开图形窗口,则绘图函数不再打开,而直接利用已打开的图形窗口;若运行程序前已存在多个图形窗口,并且没有指定哪个窗口为当前窗口时,则以最后使用过的窗口为当前窗口输出图形.6.窗口中的图形打印:用图形窗口的File 菜单中的Print 项.7.可以在图形窗口中设置图形对象的参数.具体方法是在图形窗口的Edit 菜单中选择Properties 项,打开图形对象的参数设置窗口,可以设置对象的属性.二.坐标系1.一个图形必须有其定位系统,即坐标系;2.在一个图形窗口中可以有多个坐标系,但只有一个当前的坐标系;3.每个坐标系都有唯一的标识符,即句柄值;4.当前坐标系句柄可以由MATLAB 函数gca 获得;5.使某个句柄标识的坐标系成为当前坐标系,可用如下函数:axes(h) h 为指定坐标系句柄值.6.一些有关坐标轴的函数:1)定义坐标范围:一般MATLAB 自动定义坐标范围,如用户认为设定的不合适,可用:axis([Xmin, Xmax, Ymin, Ymax])重新设定;2)坐标轴控制:MATLAB 的缺省方式是在绘图时,将所在的坐标系也画出来,为隐去坐标系,可用axis off;axis on 则显示坐标轴(缺省值).3)通常MATLAB 的坐标系是长方形,长宽比例大约是4:3,为了得到一个正方形的坐标系可用:axis square4)坐标系横纵轴的比例是自动设置的,比例可能不一样,要得到相同比例的坐标系,可用:axis equal第二节二维图形的绘制一. plot 函数plot 函数是最基本的绘图函数,其基本的调用格式为:1.plot(y)------绘制向量y 对应于其元素序数的二维曲线图,如果y 为复数向量,则绘制虚部对于实部的二维曲线图.例:绘制单矢量曲线图.y=[0 0.6 2.3 5 8.3 11.7 15 17.7 19.4 20];plot(y)由于y 矢量有10 个元素,x 坐标自动定义为[1 2 3 4 5 6 7 8 9 10].2.plot(x,y)------绘制由x,y 所确定的曲线.1)x,y 是两组向量,且它们的长度相等,则plot(x,y)可以直观地绘出以x 为横坐标,y 为纵坐标的图形.如:画正弦曲线:t=0:0.1:2*pi;y=sin(t);plot(t,y)2)当plot(x,y)中,x 是向量,y 是矩阵时,则绘制y 矩阵中各行或列对应于向量x的曲线.如果y 阵中行的长度与x 向量的长度相同,则以y 的行数据作为一组绘图数据;如果y 阵中列的长度与x 向量的长度相同,则以y 的列数据作为一组绘图数据;如果y 阵中行,列均与x 向量的长度相同,则以y 的每列数据作为一组绘图数据.例:下面的程序可同时绘出三条曲线.MATLAB 在绘制多条曲线时,会按照一定的规律自动变化每条曲线的的颜色.x=0:pi/50:2*pi;y(1,:)=sin(x);y(2,:)=0.6*sin(x);y(2,:)=0.3*sin(x);plot(x,y)或者还可以这样用:x=0:pi/50:2*pi;y=[ sin(x); 0.6*sin(x); 0.3*sin(x)];plot(x,y)3) 如果x,y 是同样大小的矩阵,则plot(x,y)绘出y 中各列相应于x 中各列的图形.例:x(1,:)=0:pi/50:2*pi;x(2,:)=pi/4:pi/50:2*pi+pi/4;x(3,:)=pi/2:pi/50:2*pi+pi/2;y(1,:)=sin(x(1,:));y(2,:)=0.6*sin(x(2,:));y(3,:)=0.3*sin(x(3,:));plot(x,y)x=x';y=y';figureplot(x,y)在这个例子中,x------3x101,y------3x101,所以第一个plot 按列画出101 条曲线,每条3 个点;而x'------101x3,y'------101x3,所以第二个plot 按列画出3 条曲线,每条101 个点.3.多组变量绘图:plot(x1, y1, 选项1, x2, y2, 选项2, ……)上面的plot 格式中,选项是指为了区分多条画出曲线的颜色,线型及标记点而设定的曲线的属性.MATLAB 在多组变量绘图时,可将曲线以不同的颜色,不同的线型及标记点表示出来.这些选项如下表所示:各种颜色属性选项'r' 红色'm' 粉红'g' 绿色'c' 青色'b' 兰色'w' 白色'y' 黄色'k' 黑色各种线型属性选项'-' 实线'--' 虚线':' 点线'-.' 点划线各种标记点属性选项'.' 用点号绘制各数据点'^' 用上三角绘制各数据点'+' 用'+'号绘制各数据点'v' 用下三角绘制各数据点'*' 用'*'号绘制各数据点'>' 用右三角绘制各数据点' .' 用'.'号绘制各数据点'<' 用左三角绘制各数据点's'或squar 用正方形绘制各数据点'p' 用五角星绘制各数据点'd'或diamond 用菱形绘制各数据点'h' 用六角星绘制各数据点这些选项可以连在一起用,如:'-.g'表示绘制绿色的点划线,'g+'表示用绿色的'+'号绘制曲线.注意:1)表示属性的符号必须放在同一个字符串中;2)可同时指定2~3 个属性;3)与先后顺序无关;4)指定的属性中,同一种属性不能有两个以上.例:t=0:0.1:2*pi;y1=sin(t);y2=cos(t);y3=sin(t).*cos(t);plot(t,y1, '-r',t,y2, ':g',t,y3, '*b')该程序还可以按下面的方式写:t=0:0.1:2*pi;y1=sin(t);y2=cos(t);y3=sin(t).*cos(t);plot(t,y1, '-r')hold onplot(t,y2, ':g')plot(t,y3, '*b')hold off注:在MATLAB 中,如画图前已有打开的图形窗口,则再画图系统将自动擦掉坐标系中已有的图形对象,但设置了hold on 后,可以保持坐标系中已绘出的图形.还可以进一步设置包括线的宽度(LineWidth), 标记点的边缘颜色(MarkerEdgeColor),填充颜色(MarkerFaceColor)及标记点的大小(MarkerSize)等其它绘图属性.例:设置绘图线的线型,颜色,宽度,标记点的颜色及大小.t=0:pi/20:pi;y=sin(4*t).*sin(t)/2;plot(t,y,'-bs','LineWidth',2,... %设置线的宽度为2'MarkerEdgeColor','k',... %设置标记点边缘颜色为黑色'MarkerFaceColor','y',... %设置标记点填充颜色为黄色'MarkerSize',10) %设置标记点的尺寸为104.双Y 轴绘图:plotyy()函数.其调用格式为: plotyy(x1,y1,x2,y2)------绘制由x1,y1 和x2,y2 确定的两组曲线,其中x1,y1 的坐标轴在图形窗口的左侧,x2,y2 的坐标轴在图形窗口的右侧.Plotyy(x1,y1,x2,y2, 'function1','function2')------功能同上,function 是指那些绘图函数如:plot,semilogx,loglog 等.例如:在一个图形窗口中绘制双Y 轴曲线.x=0:0.3:12;y=exp(-0.3*x).*sin(x)+0.5;plotyy(x,y,x,y,'plot','stem')stem:绘制stem 形式的曲线(上端带圈的竖线).绘图结果:两条图线自动用不同的颜色区分,两个坐标的颜色与图线的颜色相对应,左边的Y 轴坐标对应的是plot 形式的曲线,右边的Y 坐标对应的是stem 形式的曲线.二.对数坐标图绘制函数:在对数坐标图的绘制中,有三种绘图函数:semilogx,semilogy 和loglog 函数.1)semilogx( )------绘制以X 轴为对数坐标轴的对数坐标图. 其调用格式为:semilogx(x,y,'属性选项')其中属性选项同plot 函数.该函数只对横坐标进行对数变换,纵坐标仍为线性坐标.2)semilogy( )------绘制以Y 轴为对数坐标轴的对数坐标图. 其调用格式为:semilogy(x,y,'属性选项')该函数只对纵坐标进行对数变换,横坐标仍为线性坐标.3)loglog( )------ 绘制X,Y 轴均为对数坐标轴的图形.其调用格式为:loglog(x,y,'属性选项')该函数分别对横,纵坐标都进行对数变换.例:x=0:0.1:6*pi;y=cos(x/3)+1/9;subplot(221), semilogx(x,y);subplot(222), semilogy(x,y);subplot(223), loglog(x,y);4)MATLAB 还提供了一个实用的函数:logspace( )函数,可按对数等间距地分布来产生一个向量,其调用格式为:x=logspace(x1,x2,n)这里,x1 表示向量的起点;x2 表示向量的终点;n 表示需要产生向量点的个数(一般可以不给出,采用默认值50).在控制系统分析中一般采用这种方法来构成频率向量w.关于它的应用后面还要讲到.三.极坐标图的绘制函数:绘极坐标图可用polar( )函数.其调用格式如下:polar(theta, rho,'属性选项')------theta:角度向量,rho:幅值向量,属性内容与plot 函数基本一致.例如:极坐标模型为:3145/)/)cos((+ =θρ, ],[πθ80∈则绘出极坐标图的程序为:theta=0:0.1:8*pi;p=cos((5*theta)/4)+1/3;polar(theta,p)四.绘制多个子图:subplot( )函数MATLAB 允许在一个图形窗口上绘制多个子图(如对于多变量系统的输出),允许将窗口分成nxm 个部分.分割图形窗口用subplot 函数来实现,其调用格式为:subplot(n,m,k)或subplot(nmk)------n,m 分别表示将窗口分割的行数和列数,k 表示要画图部分的代号,表示第几个图形,nmk 三个数可以连写,中间不用符号分开.例如:将窗口划分成2x2=4 个部分,可以这样写:subplot(2,2,1),plot(……)subplot(2,2,2),……subplot(2,2,3),……subplot(2,2,4),……注:subplot 函数没有画图功能,只是将窗口分割.第三节图形的修饰与标注MATLAB 提供了一些特殊的函数修饰画出的图形,这些函数如下: 1)坐标轴的标题:title 函数其调用格式为:title('字符串')------字符串可以写中文如:title('My own plot')2)坐标轴的说明:xlabel 和ylabel 函数格式:xlabel('字符串')ylabel('字符串')如:xlabel('This is my X axis') ylabel('My Y axis')3)图形说明文字:text 和gtext 函数A.text 函数:按指定位置在坐标系中写出说明文字.格式为:text(x1, y1, '字符串', '选项') x1,y1 为指定点的坐标;'字符串'为要标注的文字;'选项'决定x1,y1 的坐标单位,如没有选项,则x1,y1 的坐标单位和图中一致;如选项为'sc', 则x1,y1 表示规范化窗口的相对坐标,其范围为0到1.如:text(1,2, '正弦曲线')B.gtext 函数:按照鼠标点按位置写出说明文字.格式为:gtext('字符串')当调用这个函数时,在图形窗口中出现一个随鼠标移动的大十字交叉线,移动鼠标将十字线的交叉点移动到适当的位置,点击鼠标左键,gtext 参数中的字符串就标注在该位置上.4)给图形加网格:grid 函数在调用时直接写grid 即可.上面的函数的应用实例:例:在图形中加注坐标轴标识和标题及在图形中的任意位置加入文本.t=0:pi/100:2*pi;y=sin(t);plot(t,y),grid,axis([0 2*pi -1 1])xlabel('0 leq itt rm leq pi','FontSize',16)ylabel('sin(t)','FontSize',20)title('正弦函数图形','FontName','隶书' ,'FontSize',20) text(pi,sin(pi),'leftarrowsin(t)=0','FontSize',16)text(3*pi/4,sin(3*pi/4),'leftarrowsin(t)=0.707','FontSize',16)text(5*pi/4,sin(5*pi/4),' sin(t)=-0.707rightarrow',... 'FontSize',16,'HorizontalAlignment','right')5)在图形中添加图例框:legend 函数其调用格式为:A.legend('字符串1', '字符串2', ……)------以字符串1,字符串2……作为图形标注的图例.B.legend('字符串1', '字符串2', ……, pos)------pos 指定图例框显示的位置.图例框被预定了6 个显示位置:0------取最佳位置;1------右上角(缺省值);2------左上角;3------左下角;4------右下角;-1------图的右侧.例:在图形中添加图例.x=0:pi/10:2*pi;y1=sin(x);y2=0.6*sin(x);y3=0.3*sin(x);plot(x,y1,x,y2,'-o',x,y3,'-*')legend('曲线1','曲线2','曲线3')6)用鼠标点选屏幕上的点:ginput 函数格式为:[x, y, button]=ginput(n)其中:n 为所选择点的个数;x,y 均为向量,x 为所选n 个点的横坐标;y 为所选n个点的纵坐标.button 为n 维向量,是所选n 个点所对应的鼠标键的标号:1------左键;2------中键;3------右键.可用不同的鼠标键来选点,以区别所选的点.此语句可以放在绘图语句之后,它可在绘出的图形上操作,选择你所感兴趣的点,如峰值点,达到稳态值的点等,给出点的坐标,可求出系统的性能指标.第四节MATLAB 下图形对象的修改MATLAB 图形对象是指图形系统中最基本,最底层的单元,这些对象包括:屏幕(Root), 图形窗口(Figures), 坐标轴(Axes), 控件(Uicontrol), 菜单(Uimenu),线(Lines),块(Patches),面(Surface),图像(Images),文本(Text)等等.根据各对象的相互关系,可以构成如下所示的树状层次:RootFiguresAxes Uicontrol Uimenu Uicontextmenu (对象菜单)Images Line Patch Surface Text对各种图形对象进行修改和控制,要使用MATLAB 的图形对象句柄(Handle).在MATLAB 中,每个图形对象创立时,就被赋予了唯一的标识,这个标识就是该对象的句柄.句柄的值可以是一个数,也可以是一个矢量.如每个计算机的根对象只有一个,它的句柄总是0,图形窗口的句柄总是正整数,它标识了图形窗口的序号等.利用句柄可以操纵一个已经存在的图形对象的属性,特别是对指定图形对象句柄的操作不会影响同时存在的其它图形对象,这一点是非常重要的.一.对图形对象的修改可以用下面函数:1)set 函数:用于设置句柄所指的图形对象的属性.Set 函数的格式为:set(句柄, 属性名1, 属性值1, 属性名2, 属性值2, ……) 例:h=plot(x,y)set(h, 'Color', [1,0,0])------将句柄所指曲线的颜色设为红色.2)get 函数:获取指定句柄的图形对象指定属性的当前值.格式为:get(句柄, '属性名')如: get(gca, 'Xcolor')------获得X 轴的当前颜色属性值. 执行后可返回X 轴的当前颜色属性值[0,0,0](黑色).3)如果没有设置句柄,则可以使用下列函数获得:gcf:获得当前图形窗口的句柄;gca:获得当前坐标轴对象的句柄;gco:获得当前对象的句柄.如:A.要对图形窗口的底色进行修改,可用:set(gcf, 'Color', [1,1,1])------将图形窗口底色设为白色B.要把当前X 轴的颜色改为绿色,可用:set(gca, 'Xcolor', [0,1,0])C.还可对坐标轴的显示刻度进行定义:t=-pi:pi/20:pi;y=sin(t);plot(t,y)set(gca,'xtick',[-pi:pi/2:pi],'xticklabel',['-pi','-pi/ 2','0','pi/2','pi'])本例中用'xtick'属性设置x 轴刻度的位置(从-pi~pi,间隔pi/2,共设置5 个点),用'xticklabel'来指定刻度的值,由于通常习惯于用角度度量三角函数,因此重新设置['-pi','-pi/2','0','pi/2','pi']5 个刻度值.二.一些常用的属性如下:1)Box 属性:决定图形坐标轴是否为方框形式,选项为'on'(有方框), 'off'(无方框);2)'ColorOrder'属性:设置多条曲线的颜色顺序,默认值为:[1 1 0;1 0 1;0 1 1;1 0 0;0 1 0;0 0 1]黄色粉色天蓝红色绿色兰色颜色向量还有:[1 1 1]------白色;[0 0 0]------黑色.3)坐标轴方向属性:'Xdir','Ydir','Zdir',其选项为:'normal'------正常'reverse'------反向4)坐标轴颜色和线型属性:'Xcolor','Ycolor','Zcolor'------ 轴颜色, 值为颜色向量如何在画好曲线后再在图上标刻度就是想在一些特定的点边上标上一串30.60.90~7200递增的数据,共有96个点要标!!im = imread(url);imshow(im)然后输入:text(100,100,'\o ','Color','red');matlab,用imread 读入一个图片,我想在图上的一些坐标点上做标记。
MATLAB绘图的指令

绘图的指令1、plot函数MATLAB中最常用的绘图函数是plot( )。
其基本调用格式为:plot(x, y ),其中x, y均为向量,该函数表示以x向量作为X轴,以y向量作为Y轴。
示例3:绘制从0 ~ 4范围的正弦函数曲线。
t = 0 : pi/20 : 4*pi;y = sin(t);plot(t, y);2、stem函数对于离散序列,MATLAB用stem( )命令实现其绘制。
示例4:绘制从0 ~ 4范围的正弦函数序列。
t = 0 : pi/10 : 4*pi;y = sin(t);stem(t, y);3、subplot函数如果要在一个绘图窗口中显示多个图形,可用subplot函数实现。
其基本调用格式为:subplot(m, n, k) 或subplot(m n k),其中m, n, k取值为1 ~ 9。
该函数表示将绘图窗口划分为m×n个子窗口(子图),并在第k个子窗口中绘图。
示例5:在一个绘图窗口中绘制下列函数的图形。
t = 0 : 0.1 : 2;y1 = 2*exp(-3*t); % (a) 指数函数figure;subplot(221);plot(t,y1);xlabel('(a)');y2 = 2*t.*exp(-3*t); % (b) t乘指数函数subplot(222);plot(t,y2);xlabel('(b)');t1 = -4 : 0.1 : 4;y3 = 1/(2^0.5)*exp(-0.5*t1.^2); % (c) 正态分布函数subplot(223);plot(t1,y3);xlabel('(c)');t2 = -5 : 0.1 : 5;y4 = sinc(t2); % (d) 取样函数subplot(224);plot(t2,y4);xlabel('(d)');ylabel('sinc(t)');axis([-5 5 -0.25 1.1])grid on二维图形的修饰1、坐标轴名称标识函数xlabel、ylabel、title绘制 的nyquist 图和bode 图102.110)(2++=s s s G解MATLAB编程如下:»num=[10];»den=[1,1.2,10];»w=logspace(-2,2,1000); » nyquist(num,den,w)»grid»bode(num,den,w)»grid极小化»fx='10*exp(-x)*cos(x)';»fplot(fx,[2,5])»xmin=fmin(fx,2,5)xmin =2.35619746669214求零点»xzero=fzero(fx,5)xzero =4.71238898038469»xzero=fzero(fx,2)xzero =1.57079632679490曲线拟合»x=0:0.1:1;»y=[-.447 1.978 3.28 6.16 7.08 7.34 7.66 9.56 9.48 9.30 11.2];»p=polyfit(x,y,2);»xi=0:0.01:1;»yi=polyval(p,xi);»plot(x,y,xi,yi) 三维图形»x=-4:0.1:4;»y=x;»[x,y]=meshgrid(x,y);»z = 3*(1-x).^2.*exp(-(x.^2) - (y+1).^2) ...- 10*(x/5 - x.^3 - y.^5).*exp(-x.^2-y.^2) ...- 1/3*exp(-(x+1).^2 - y.^2);»mesh(x,y,z)二维图形»x=0:0.01:pi*3;»y=sin(x);»plot(x,y)»title('First Figure Example')»xlabel('Time(s)')»ylabel('Value(v)')»grid on»gtext(‘sinx’)»legend(‘sinx’)管理命令和函数help 在线帮助文件doc 装入超文本说明what M、MA T、MEX文件的目录列表 type 列出M文件lookfor 通过help条目搜索关键字which 定位函数和文件Demo 运行演示程序Path 控制MATLAB的搜索路径管理变量和工作空间Who 列出当前变量Whos 列出当前变量(长表) Load 从磁盘文件中恢复变量 Save 保存工作空间变量Clear 从内存中清除变量和函数Pack 整理工作空间内存Size 矩阵的尺寸Length 向量的长度disp 显示矩阵或与文件和*作系统有关的命令cd 改变当前工作目录Dir 目录列表Delete 删除文件Getenv 获取环境变量值! 执行DOS*作系统命令Unix 执行UNIX*作系统命令并返回结果Diary 保存MA TLAB任务控制命令窗口Cedit 设置命令行编辑 Clc 清命令窗口Home 光标置左上角Format 设置输出格式Echo 底稿文件内使用的回显命令more 在命令窗口中控制分页输出启动和退出MA TLABQuit 退出MATLABStartup 引用MA TLAB时所执行的M文件Matlabrc 主启动M文件*作符和特殊字符+ 加—减* 矩阵乘法.* 数组乘法^ 矩阵幂.^ 数组幂\ 左除或反斜杠/ 右除或斜杠./ 数组除Kron Kronecker张量积: 冒号( ) 圆括号[ ] 方括号. 小数点.. 父目录…继续, 逗号; 分号% 注释! 感叹号‘转置或引用= 赋值= = 相等< > 关系*作符& 逻辑与| 逻辑或~ 逻辑非xor 逻辑异或逻辑函数Exist 检查变量或函数是否存在Any 向量的任一元为真,则其值为真All 向量的所有元为真,则其值为真Find 找出非零元素的索引号三角函数Sin 正弦Sinh 双曲正弦Asin 反正弦Asinh 反双曲正弦Cos 余弦Cosh 双曲余弦Acos 反余弦Acosh 反双曲余弦Tan 正切Tanh 双曲正切Atan 反正切Atan2 四象限反正切Atanh 反双曲正切Sec 正割Sech 双曲正割Asech 反双曲正割Csc 余割Csch 双曲余割Acsc 反余割Acsch 反双曲余割Cot 余切Coth 双曲余切Acot 反余切Acoth 反双曲余切指数函数Exp 指数Log 自然对数Log10 常用对数Sqrt 平方根复数函数Abs 绝对值Argle 相角Conj 复共轭Image 复数虚部Real 复数实部特殊变量和常数Ans 当前的答案Eps 相对浮点精度Realmax 最大浮点数Realmin 最小浮点数Pi 圆周率I,j 虚数单位Inf 无穷大Nan 非数值Flops 浮点运算次数Nargin 函数输入变量数Nargout 函数输出变量数基本X—Y图形Plot 线性图形Loglog 对数坐标图形Semilogx半对数坐标图形(X轴为对数坐标) Semilogy 半对数坐标图形(Y轴为对数坐标) Fill 绘制二维多边形填充图特殊X—Y图形Polar 极坐标图Bar 条形图Stem 离散序列图或杆图Stairs 阶梯图Errorbar 误差条图Hist 直方图Rose 角度直方图Compass 区域图Feather 箭头图Fplot 绘图函数Comet 星点图图形注释Title 图形标题Xlabel X轴标记Ylabel Y轴标记Text 文本注释Gtext 用鼠标放置文本Grid 网格线MATLAB不但擅长於矩阵相关的数值运算,也适合用在各种科学目视表示(Scientific visualization)。
MATLAB中绘图命令介绍

MATLAB中绘图命令介绍本节将介绍MATLAB基本xy平面及xyz空间的各项绘图命令,包含一维曲线及二维曲面的绘制。
plot是绘制一维曲线的基本函数,但在使用此函数之前,我们需先定义曲线上每一点的x 及y座标。
下例可画出一条正弦曲线:close all;x=linspace(0, 2*pi, 100); % 100个点的x坐标y=sin(x); % 对应的y坐标plot(x,y);小整理:MATLAB基本绘图函数plot: x轴与y轴均为线性刻度(Linear scale)loglog: x轴与y轴均为对数刻度(Logarithmic scale)semilogx: x轴为对数刻度,y轴为线性刻度semilogy: x轴为线性刻度,y轴为对数刻度若要画出多条曲线,只需将座标对依次放入plot函数即可:hold on 保持当前图形,以便继续画图到当前坐标窗口hold off 释放当前图形窗口title(’图形名称’)(都放在单引号内)xlabel(’x轴说明’)ylabel(’y轴说明’)text(x,y,’图形说明’)legend(’图例1’,’图例2’,…)plot(x, sin(x), x, cos(x));若要改变颜色,在座标对後面加上相关字串即可:plot(x, sin(x), 'c', x, cos(x), 'g');若要同时改变颜色及图线型态,也是在座标对後面加上相关字串即可:plot(x, sin(x), 'co', x, cos(x), 'g*');小整理:plot绘图函数的叁数字元、颜色元、图线型态,y 黄色 .点k 黑色o 圆w 白色x xb 蓝色++g 绿色* *r 红色- 实线c 亮青色: 点线m锰紫色-. 点虚线-- 虚线plot3 三维曲线作图图形完成后,我们可用axis([xmin,xmax,ymin,ymax])函数来调整图轴的范围: axis([0, 6, -1.2, 1.2]);axis函数的功能丰富,其常用的用法有:axis equal :纵横坐标轴采用等长刻度axis square:产生正方形坐标系(默认为矩形)axis auto:使用默认设置axis off:取消坐标轴axis on :显示坐标轴此外,MATLAB也可对图形加上各种注解与处理:xlabel('Input Value'); % x轴注解ylabel('Function Value'); % y轴注解title('Two Trigonometric Functions'); % 图形标题legend('y = sin(x)','y = cos(x)'); % 图形注解grid on; % 显示格线我们可用subplot来同时画出数个小图形於同一个视窗之中:subplot(2,2,1); plot(x, sin(x));subplot(2,2,2); plot(x, cos(x));subplot(2,2,3); plot(x, sinh(x));subplot(2,2,4); plot(x, cosh(x));MATLAB还有其他各种二维绘图函数,以适合不同的应用,详见下表。
第4章 MATLAB 绘图

4.图例标注
菜单Insert---legend 命令legend('string1','string2',...)
4.1.6 一个图形窗口多个子图的绘制
subplot(m,n,i)把图形窗口分为m*n个子图,并在第i个子图 中画图 例 4-11 在同一坐标系中画出两个函数,y=cos2x,y=sinxsin6x 的图形,自变量的范围为0≤ x ≤π,函数y=cos2x用红色星号,函数 y=sinxsin6x用蓝色实线,并加图名、坐标轴、图形、图例标注 解 MATLAB命令为: x=0:pi/50:pi; y1=cos(2*x);y2=sin(x).*sin(6*x); plot(x,y1,'r*',x,y2,'b-'),grid on title(‘曲线y1=cos(2x)曲线y2=sin(x)sin(6x)') xlabel('x轴'),ylabel('y轴') gtext('y1=cos(2x)'),gtext('y2=sin(x)sin(6x)') legend('y1=cos(2x)','y2=sin(x)sin(6x)')
group 8 6 4 2 0 10 30 20
stack
1
2
3
4 stack
5
6
0
1
2
3
4 stack
5
6
8 6 5 4 3 2 1 0 10 20 30 6 4 2 0
其它特殊绘图略(见教科书 )
1
2
3
4
5
6
4.3 三维曲线绘图
matlab绘图知识点总结

matlab绘图知识点总结一、Matlab基本绘图函数1. plot函数plot函数是Matlab中最基本的绘图函数之一,用于绘制二维图表。
其基本语法为:plot(x, y)。
其中x是横轴坐标数据,y是纵轴坐标数据。
通过plot函数可以绘制折线图、散点图等。
2. bar函数bar函数用于绘制条形图,其基本语法为:bar(x, y)。
其中x是条形的横轴坐标位置,y是条形的高度。
3. pie函数pie函数用于绘制饼图,其基本语法为:pie(x, labels)。
其中x是用来指定各个扇形区域的大小的矩阵,labels则是用来指定每个扇形区域的标签。
4. hist函数hist函数用于绘制直方图,其基本语法为:hist(x, bins)。
其中x是待绘制的数据,bins则是用来指定直方图的条形数目。
5. scatter函数scatter函数用于绘制散点图,其基本语法为:scatter(x, y)。
其中x和y分别是散点的横轴和纵轴坐标数据。
6. contour函数contour函数用于绘制等高线图,其基本语法为:contour(x, y, z)。
其中x和y分别是网格的横轴和纵轴坐标,z则是用来指定等高线的数值。
二、自定义图形1. 设置标题、标签和图例在Matlab中,可以使用title、xlabel、ylabel和legend等函数分别设置图表的标题、横轴和纵轴标签以及图例。
2. 设置图表样式可以使用line属性、marker属性以及color属性等来设置折线图、散点图等的样式。
3. 修改图表坐标轴可以使用xlim、ylim函数来设置图表的横轴和纵轴范围,并使用xticks和yticks函数来设置坐标刻度。
4. 绘制多个数据集可以使用hold on函数来绘制多个数据集,并使用hold off函数来结束绘制多个图表。
5. 设置图表背景可以使用grid、box、axis equal等函数来设置图表的背景。
三、子图表绘制1. subplot函数subplot函数用于在一个图形窗口中绘制多个子图表,其基本语法为:subplot(m,n,p)。
