材料力学课堂例题(湖南大学)-静力学.

合集下载

工程力学(静力学与材料力学)习题及答案 - 内力分析

习题6-1图习题6-2图习题6-3图工程力学（静力学与材料力学）习题第6章杆件的内力分析6－1 平衡微分方程中的正负号由哪些因素所确定？简支梁受力及Ox 坐标取向如图所示。

试分析下列平衡微分方程中哪一个是正确的。

（A ）)(d d Q x q x F =；Q d d F x M=；（B ）)(d d Q x q x F -=，Q d d F x M-=；（C ）)(d d Q x q x F -=，Q d d F x M=；（D ）)(d d Q x q x F =，Q d d F xM-=。

正确答案是。

6－2 对于图示承受均布载荷q 的简支梁，其弯矩图凸凹性与哪些因素相关？试判断下列四种答案中哪几种是正确的。

正确答案是。

6－3 已知梁的剪力图以及a 、e 截面上的弯矩M a 和M e ，如图所示。

为确定b 、d 二截面上的弯矩M b 、M d ，现有下列四种答案，试分析哪一种是正确的。

（A ）)(Q F b a a b A M M -+=，)(Q F d e e d A M M -+=；（B ）)(Q F b a a b A M M --=，)(Q F d e e d A M M --=；（C ）)(Q F b a a b A M M -+=，)(Q F d e e d A M M --=；（D ）)(Q F b a a b A M M --=，)(Q F d e e d A M M -+=。

上述各式中)(Q F b a A -为截面a 、b 之间剪力图的面积，以此类推。

正确答案是。

6－4 应用平衡微分方程，试画出图示梁的剪力图和弯矩图，并确定 max Q ||F 。

习题6-4图6－5 应用平衡微分方程，试画出图示梁的剪力图和弯矩图，并确定 max Q ||F 。

习题6-5图6－6 应用平衡微分方程，试画出图示梁的剪力图和弯矩图，并确定 max Q ||F 。

习题6-6图6－7 应用平衡微分方程，试画出图示梁的剪力图和弯矩图，并确定 max Q ||F 。

湖南大学812材料力学试题回忆版

湖南大学812材料力学试题回忆版
1。

和02年的刚板类似，中间的是刚板，两个F相等，求下面两根杆的内力。

2.就是画剪力，弯矩图，小心即可，具体图忘了。

3.求最大拉应力和最大切应力：左边均布载荷为5kn/m,右边为10kn/m，两段距离都是1.5m貌似。

数据不一定，但图应该是对的。

4.图各段匀为L，中间为杆，告知EA，EI,求A点垂直位移。

5.已知G=80,r=5X10^-4，且告知两个垂直方向的应该之和为27.5Mpa，求主应力。

6.和12年的类似，普通的三维机构的校核，要求用的第四强度理论，不复杂，但图忘了。

7.告知1.2杆相同及形状尺寸等，1.2角均为30，求许用的F
8.如图各杆匀我L，x为何值时A的竖直位移为0.
/。

《材料力学》第6章-简单超静定问题-习题解

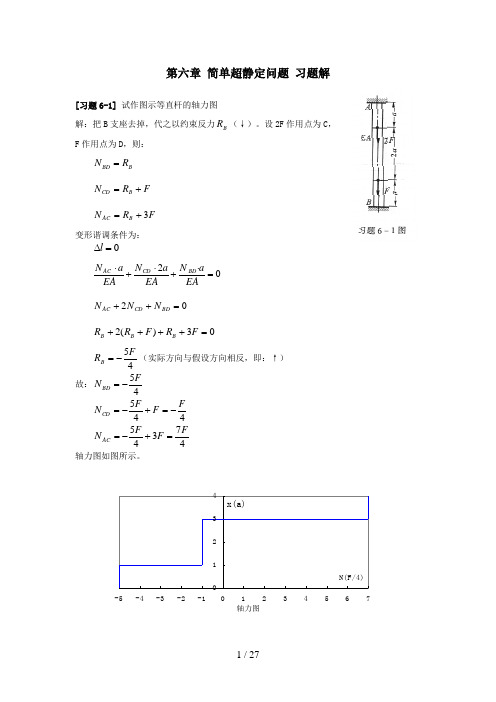
轴力图1234-5-4-3-2-11234567N(F/4)x(a)第六章简单超静定问题习题解[习题6-1] 试作图示等直杆的轴力图解：把B 支座去掉，代之以约束反力B R （↓）。

设2F 作用点为C ， F 作用点为D ，则：B BD R N = F R N B CD += F R N B AC 3+=变形谐调条件为：0=∆l02=⋅+⋅+⋅EA aN EA a N EA a N BD CD AC 02=++BD CD AC N N N03)(2=++++F R F R R B B B45FR B -=（实际方向与假设方向相反，即：↑）故：45FN BD-= 445F F F N CD -=+-=47345FF F N AC=+-= 轴力图如图所示。

[习题6-2] 图示支架承受荷载kN F 10=，1，2，3各杆由同一种材料制成，其横截面面积分别为21100mm A =，22150mm A =，23200mm A =。

试求各杆的轴力。

解：以节点A 为研究对象，其受力图如图所示。

∑=0X030cos 30cos 01032=-+-N N N0332132=-+-N N N 0332132=+-N N N (1)∑=0Y030sin 30sin 0103=-+F N N2013=+N N (2)变形谐调条件：设A 节点的水平位移为x δ，竖向位移为y δ，则由变形协调图（b ）可知：00130cos 30sin x y l δδ+=∆x l δ=∆200330cos 30sin x y l δδ-=∆03130cos 2x l l δ=∆-∆2313l l l ∆=∆-∆设l l l ==31，则l l 232=223311233EA l N EA lN EA l N ⋅⋅=- 22331123A N A N A N =- 15023200100231⨯=-N N N23122N N N =-21322N N N -= (3)(1)、(2)、(3)联立解得：kN N 45.81=；kN N 68.22=；kN N 54.111=（方向如图所示，为压力，故应写作：kN N 54.111-=）。

工程力学(静力学与材料力学)课后习题问题详解

1-1试画出以下各题中圆柱或圆盘的受力图。

与其它物体接触处的摩擦力均略去。

解：1-2 试画出以下各题中AB 杆的受力图。

(a) B(b)(c)(d)A(e)A(a)(b) A(c)A(d)A(e)(c)(a)(b)解：1-3 试画出以下各题中AB 梁的受力图。

(d)(e)BB(a)B(b)(c)F B(a)(c)(b)(d)(e)解：1-4 试画出以下各题中指定物体的受力图。

(a) 拱ABCD ；(b) 半拱AB 部分；(c) 踏板AB ；(d) 杠杆AB ；(e) 方板ABCD ；(f) 节点B 。

解：(a)(b)(c)(d)D (e)F Bx(a)(b)(c)(d)(e)W (f)(a)D(b)B(c)BF D1-5 试画出以下各题中指定物体的受力图。

(a) 结点A ，结点B ；(b) 圆柱A 和B 及整体；(c) 半拱AB ，半拱BC 及整体；(d) 杠杆AB ，切刀CEF 及整体；(e) 秤杆AB ，秤盘架BCD 及整体。

解：(a)(d)F(e)WB(f)F FBC(c)(d)AT F BAF (b)(e)(b)(c)(d)(e)CC’ DDB2-2 杆AC 、BC 在C 处铰接，另一端均与墙面铰接，如图所示，F 1和F 2作用在销钉C 上，F 1=445 N ，F 2=535 N ，不计杆重，试求两杆所受的力。

解：(1) 取节点C 为研究对象，画受力图，注意AC 、BC 都为二力杆，(2) 列平衡方程：12140 sin 600530 cos6005207 164 o y AC o x BC AC AC BC F F F F F F F F F N F N=⨯+-==⨯--=∴==∑∑ AC 与BC 两杆均受拉。

2-3 水平力F 作用在刚架的B 点，如图所示。

如不计刚架重量，试求支座A 和D 处的约束力。

解：(1) 取整体ABCD 为研究对象，受力分析如图，画封闭的力三角形：(2) 由力三角形得F 1FFDF F AF D211 1.1222D A D D A F F FF F BC AB AC F F F F F =====∴===2-4 在简支梁AB 的中点C 作用一个倾斜45o 的力F ，力的大小等于20KN ，如图所示。

材料力学(湖南大学)智慧树知到答案章节测试2023年

绪论单元测试1.结构承受载荷时，为保证能正常工作，构件和零件必须符合哪些要求？A:振动要求B:强度要求C:刚度要求D:稳定性要求答案:BCD2.包装袋的锯齿状封口设计蕴含了材料力学的什么原理？A:疲劳破坏B:应力集中C:压杆失稳D:冲击破坏答案:B3.建立力学模型进行理论研究时，应尽可能还原结构的细节，以确保计算结果的准确性。

上述说法是否正确？A:错B:对答案:A4.材料力学作为一门独立的学科是从何处发展起来的？A:欧洲B:日本C:中国D:美国答案:A5.下述哪项不属于材料力学的基本假设？A:连续性B:均匀性C:各向同性D:大变形答案:D第一章测试1.所有脆性材料，它与塑性材料相比，其拉伸力学性能的最大特点是（）。

A: 断裂前几乎没有塑性变形。

B: 相同拉力作用下变形小。

C: 应力-应变关系严格遵循胡克定律。

D: 强度低，对应力集中不敏感。

答案:A2.现有三种材料的拉伸曲线如图所示。

分别由此三种材料制成同一构件，其中：1）强度最高的是（）；2）刚度最大的是（）；3）塑性最好的是（）；4）韧性最高，抗冲击能力最强的是（）。

A: BACCB: BACAC: ABCAD: ABCC答案:D3.正应变的定义为：A:错B:对答案:A4.任何温度改变都会在结构中引起应变与应力。

A:对B:错答案:B5.对于拉伸曲线上没有屈服平台的合金塑性材料，工程上规定作为名义屈服极限，此时相对应的应变量为。

A:对B:错答案:B第二章测试1.在连接件上，剪切面和挤压面分别为：A:分别平行、垂直于外力方向。

B:分别垂直、平行于外力方向。

C:分别垂直于外力方向。

D:分别平行于外力方向。

答案:A2.在连接件剪切强度的实用计算中，切应力许用应力是由：A:精确计算得到的。

B:剪切试验得到的。

C:扭转试验得到的。

D:拉伸试验得到的。

答案:B3.连接件切应力的实用计算是以：A:剪切面积大于挤压面积。

B:切应力不超过材料的剪切比例极限为基础的。

材料力学例题 workbench静力学

材料力学例题 workbench静力学下载温馨提示：该文档是我店铺精心编制而成，希望大家下载以后，能够帮助大家解决实际的问题。

文档下载后可定制随意修改，请根据实际需要进行相应的调整和使用，谢谢!并且，本店铺为大家提供各种各样类型的实用资料，如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等，如想了解不同资料格式和写法，敬请关注!Download tips: This document is carefully compiled by the editor. I hope that after you download them, they can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you!In addition, our shop provides you with various types of practical materials, suchas educational essays, diary appreciation, sentence excerpts, ancient poems, classic articles, topic composition, work summary, word parsing, copy excerpts, other materials and so on, want to know different data formats and writing methods, please pay attention!材料力学是研究材料在外力作用下的力学性能和变形规律的学科。

静力学练习题及参考答案

静力学练习题及参考答案1. 问题描述：一根长度为L的均质杆以一端固定在墙上，另一端悬挂一重物。

重物造成的杆的弯曲应力最大为σ。

杆的质量可以忽略不计。

计算重物的质量m。

解答：根据静力学原理，杆的弯曲应力可以用公式计算：σ = M / S，其中M是杆的弯矩，S是杆的截面横截面积。

因为杆是均质杆，所以它的截面横截面积在整个杆上都是相等的。

设杆的截面横截面积为A。

杆的弯矩M可以通过杆的长度L和重物的力矩T计算得到：M = T * (L/2)。

代入上面的公式，我们可以得到：σ = (T * (L/2)) / A。

根据题目的描述，我们可以得到如下等式：σ = (m * g * (L/2)) / A，其中g是重力加速度。

我们可以将这个等式转换成求解未知质量m的方程。

将等式两边的A乘以m，并将等式两边的m乘以g，我们可以得到如下方程：m^2 = (2 * σ * A) / (g * L)解这个方程，我们可以求得未知质量m。

2. 问题描述：一根均质杆的长度为L，质量为M。

杆的一端固定在墙上，另一端悬挂一重物。

杆与地面的夹角为θ。

重物造成的杆的弯曲应力最大为σ。

求重物的质量m。

解答：在这个问题中，除了重物的力矩，还需要考虑到重力对杆的力矩。

由于杆是均质杆，其质量可以均匀分布在整个杆上。

假设杆上的每个微小质量元都受到与其距离一致的力矩。

重物造成的力矩可以用公式计算：M1 = m * g * (L/2) * sinθ，其中g 是重力加速度。

由于杆是均质杆，它的质心位于杆的中点。

因此重力对杆的力矩可以用公式计算：M2 = M * g * (L/2) * cosθ。

根据静力学的原理，杆的弯曲应力可以用公式计算：σ = M / S，其中M是杆的弯矩，S是杆的截面横截面积。

在这个问题中，我们可以将弯曲应力的计算公式推广到杆的中点（也就是质心）：σ = (M1 + M2) / S代入上面的公式，我们可以得到：σ = ((m * g * (L/2) * sinθ) + (M *g * (L/2) * cosθ)) / S根据题目的描述，我们可以得到如下等式：σ = ((m * g * (L/2) * sinθ) + (M * g * (L/2) * cosθ)) / (A / 2)，其中A是杆的横截面积。

材料力学力法典型例题解

l
q
RB
B
l q
X1
B Δ1F
B δ11
1
Example 2 .画图示钢架旳弯矩图，EI=const .
P
a
B
A
CP B
A
a
CP
a
B
C
B
C
X1
M
1
M
A
A
Pa
a
解 : 1）选图示相当系统（：一次超静定）
2）力法方程：
X 0
11 1
1P
3）利用图乘法求系数:
a
P
a
B
A
a
C
P
a
B
C
B
C
M
1
M
A
A
PPal
X1
2）力法方程
F
X 0
11 1
1P
3）图乘法求系数
11
2 EI
(1 2
aa
2 3
a)
2a3 3EI
1P
2 EI
(1 2
a
Fa
2 3
a)
a a
2Fa3
M
3EI
4）解得:
1
C
X1
1P
11
F
1
C
Fa
X1=1 Fa
F
1
M
F
F1 C
F
Example 1 . 求RB (EI=const.).
解: 1）选图示相当系统（一次超静定）
B
CP
P
P
a
a
X1
a a
X1 1
A
Pa
解：1）选图示静定基及相当系统

工程力学(静力学与材料力学)习题及答案 )-正应力分析

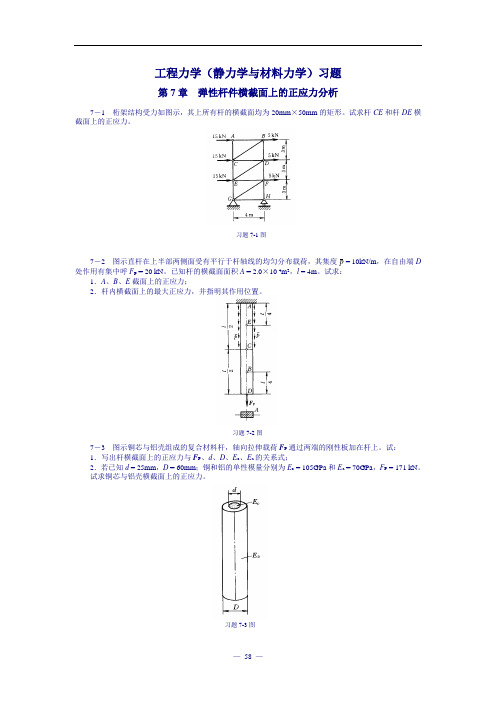
习题7-1图习题7-2图习题7-3图工程力学（静力学与材料力学）习题第7章弹性杆件横截面上的正应力分析7－1 桁架结构受力如图示，其上所有杆的横截面均为20mm ×50mm 的矩形。

试求杆CE 和杆DE 横截面上的正应力。

7－2 图示直杆在上半部两侧面受有平行于杆轴线的均匀分布载荷，其集度p = 10kN/m ，在自由端D 处作用有集中呼F P = 20 kN 。

已知杆的横截面面积A = 2.0×10-4m 2，l = 4m 。

试求：1．A 、B 、E 截面上的正应力；2．杆内横截面上的最大正应力，并指明其作用位置。

7－3 图示铜芯与铝壳组成的复合材料杆，轴向拉伸载荷F P 通过两端的刚性板加在杆上。

试：1．写出杆横截面上的正应力与F P 、d 、D 、E c 、E a 的关系式；2．若已知d = 25mm ，D = 60mm ；铜和铝的单性模量分别为E c = 105GPa 和E a = 70GPa ，F P = 171 kN 。

试求铜芯与铝壳横截面上的正应力。

习题7-4图习题7-5图习题7-6图习题7-7图 7－4 图示由铝板钢板组成的复合材料柱，纵向截荷F P 通过刚性平板沿着柱的中心线施加在其上。

试：1．导出复合材料柱横截面上正应力与F P 、b 0、b 1、h 和E a 、E s 之间的关系式；2．已知F P = 385kN ；E a = 70GPa ，E s = 200GPa ；b 0 = 30mm ，b 1 = 20mm ，h = 50mm 。

求铝板与钢板横截面上的最大正应力。

7－5 从圆木中锯成的矩形截面梁，受力及尺寸如图所示。

试求下列两种情形下h 与b 的比值：1．横截面上的最大正应力尽可能小；2．曲率半径尽可能大。

7－6 梁的截面形状为正方形去掉上、下角，如图所示。

梁在两端力偶M z 作用下发生弯曲。

设正方形截面时，梁内最大正应力为0σ；去掉上、下角后，最大正应力变为0max σσk =，试求：1．k 值与h 值之间的关系；2．max σ为尽可能小的h 值，以及这种情形下的k 值。

工程力学(静力学与材料力学)习题及答案 -章位移分析

习题10-1图习题10-2图习题10-3图工程力学（静力学与材料力学）习题第10章杆件横截面的位移分析10－1 直径d = 36mm 的钢杆ABC 与铜杆CD 在C 处连接，杆受力如图所示。

若不考虑杆的自重，试：1．求C 、D 二截面的铅垂位移；2．令F P1 = 0，设AC 段长度为l 1，杆全长为l ，杆的总伸长EAl F l 2P =∆，写出E 的表达式。

10－2 承受自重和集中载荷作用的柱如图所示，其横截面积沿高度方向按P 0e)(0F x A A x A ρ=变化，其中ρ为材料的比重。

试作下列量的变化曲线：1．轴力N ()F x ；2．应力)(x x σ；3．位移)(x u 。

10－3 图示连接件由两片宽20mm 、厚6mm 的铜片与一片同样宽厚的钢片在B 处连接而成。

已知钢与铜的弹性模量分别为E s = 200GPa ，E c = 105GPa ，钢片与铜片之间的摩擦忽略不计。

试求E 和B 处的位移。

(b)max f (b)max ω 10－4 长为1.2m 、横截面面积为31010.1-⨯m 2的铝制筒放置在固定刚块上，直径为15.0mm 的钢杆BC 悬挂在铝筒顶端的刚性板上，若二者轴线重合、载荷作用线与轴线一致，且已知钢和铝的弹性模量分别为E s = 200Gpa ，E a = 70GPa ，F P = 60kN 。

试求钢杆上C 处位移。

10－5 变截面圆锥杆下端B 处固定，上端A 处承受外力偶矩T 作用，如图所示，试证明A 端扭转角表达式为4π127Gr Tl A =ϕ10－6 试比较图示二梁的受力、内力（弯矩）、变形和位移，总结从中所得到的结论。

两者弯矩相同，挠曲线曲率相同，但（b ）梁的最大挠度比（a ）梁要大，即不相等。

10－7 对于图a 、b 、c 、d 所示的坐标系，小挠度微分方程可写成EI M x w /d /d 22-=形式有以下四种。

试判断哪一种是正确的。

（A ）图b 和c ；（B ）图b 和a ；（C ）图b 和d ；（D ）图c 和d 。

工程力学(静力学与材料力学)习题及答案 -力系的平衡

工程力学（静力学与材料力学）习题第3章力系的平衡3－1 试求图示两外伸梁的约束反力F R A、F R B，其中（a）M = 60kN·m，F P = 20 kN；（b）F P = 10 kN，F P1 = 20 kN，q = 20kN/m，d = 0.8m。

（a）（b）习题3－1图3－2 直角折杆所受载荷，约束及尺寸均如图示。

试求A处全部约束力。

习题3－2图3－3 图示拖车重W = 20kN，汽车对它的牵引力F S = 10 kN。

试求拖车匀速直线行驶时，车轮A、B 对地面的正压力。

习题3－3图3－4 图示起重机ABC具有铅垂转动轴AB，起重机重W = 3.5kN，重心在D。

在C处吊有重W1 = 10kN 的物体。

试求滑动轴承A和止推轴承B的约束力。

习题3－4图习题3－5图习题3－6图习题3－8图习题3－7图 3－5 图示钥匙的截面为直角三角形，其直角边AB = d 1，BC = d 2。

设在钥匙上作用一个力偶矩为M 的力偶。

试求其顶点A 、B 、C 对锁孔边上的压力。

不计摩擦，且钥匙与锁孔之间的隙缝很小。

3－6 图示一便桥自由放置在支座C 和D 上，支座间的距离CD = 2d = 6m 。

桥面重321kN/m 。

试求当汽车从桥上面驶过而不致使桥面翻转时桥的悬臂部分的最大长度l 。

设汽车的前后轮的负重分别为20kN 和40kN ，两轮间的距离为3m 。

3－7 直解三角形平板OBC 的载荷，约束及尺寸（OB = d 1，OC = d 2）如图所示。

试求A 、O 处约束力。

3－8 起重机装有轮子，可沿轨道A 、B 移动。

起重机桁架下弦DE 的中点C 上挂有滑轮（图未画出），用来提起挂在索链CG 上的重物。

从材料架上提起的物料重W = 50 kN ，当此重物离开材料架时，索链与铅垂线成 = 20°角。

为了避免重物摆动，又用水平绳索GH 拉住重物。

设索链张力的水平分力仅由右轨道B 承受，试求当重物离开材料架时轨道A 、B 的受力。

静力学30个例题

iy
iz
解得例 7
FDA FCA 869 N
FBA 1950 N
力 F 作用于支架上的点 C,如图所示，设 F 100 N ，试求力 F 分别对点
A,B 之矩。
A
B
3mC60 NhomakorabeaF 解：因为求力 F 对 A、B 两点的力臂比较麻烦，故利用合力矩定理求解。
M A ( F ) M A ( Fx ) M A ( Fy ) 2 F sin 60 3F cos 60 23 N m M B ( F ) M B ( Fx ) M B ( Fy ) 0 3F cos 60 150 N m
在梁上离 A 端 x 处取微元 dx ，由于载荷线性分布，在 x 处的集度 q1 q 0 x ， l 于是在 dx 上作用力的大小为： dF q1dx q 0 x dx l
合力的大小为 F dF
0
l
l
0
q0 x ql dx 0 l 2
利用合力矩定理计算合力作用线的位置。设合力 F 的作用线离 A 端的距离为 xc ，
先计算沿轴 OC 的单位矢量 ec ： ec OC OC (3i 5k )
有 M OC ( F ) M 0 ( F ) OC M O ( F ) ec 145.5 N m
34

例9
已知：简支梁 AB 上作用有两个平行力，F ，F 和一个力偶。 l 5m a 1m ，
y
B D
P
A
B FB
B FB
D
P
x
A
a
a

工程力学(静力学与材料力学)习题及答案 - 应力状态分析

习题9-1图习题9-2图习题9-2图工程力学（静力学与材料力学）习题第9章应力状态分析9－1 木制构件中的微元受力如图所示，其中所示的角度为木纹方向与铅垂方向的夹角。

试求：1．面内平行于木纹方向的切应力；2．垂直于木纹方向的正应力。

9－2 层合板构件中微元受力如图所示，各层板之间用胶粘接，接缝方向如图中所示。

若已知胶层切应力不得超过1MPa 。

试分析是否满足这一要求。

9－3 结构中某点处的应力状态为两种应力状态的叠加结果。

试求叠加后所得应力状态的主应力、面内最大切应力和该点处的最大切应力。

9－4 已知平面应力状态的最大正应力发生在与外力作用的自由表面AB 相垂直的面上，其值为0σ。

试求应力分量x σ、y σ和xy τ。

习题9-6图习题9-4图习题9-5图习题9-7图习题9-8图9－5 从构件中取出的微元受力如图所示，其中AC 为自由表面（无外力作用）。

试求x σ和xy τ。

9－6 构件微元表面AC 上作用有数值为14MPa 的压应力，其余受力如图所示。

试求x σ和xy τ。

9－7 受力物体中某一点处的应力状态如图所示（图中p 为单位面积上的力）。

试求该点处的主应力。

9－8 从构件中取出的微元，受力如图所示。

试：1．求主应力和最大切应力；2．确定主平面和最大切应力作用面位置。

(b)习题9-9图(a) 习题9-11图习题9-12图 9－9 一点处的应力状态在两种坐标中的表示方法分别如图a 和b 所示。

试：1．确定未知的应力分量xy τ、y x ''τ、y 'σ的大小；2．用主应力表示这一点处的应力状态。

9－10 试确定图示应力状态中的最大正应力和最大切应力。

图中应力的单位为MPa 。

习题9-10图9－11 对于图示的应力状态，若要求其中的最大切应力max τ＜160MPa ，试求xy τ取何值。

9－12 对于图示的应力状态，若要求垂直于xy 平面的面内最大切应力≤'τ150MPa ，试求y σ的取值范围。

第I篇静力学习题课ppt课件

D
F DB F D B
B
FF P
F AB
解：对象：D点；受力：如左图；方程：
Fx 0, F Ec Do sF D B0对象：B点；受力：如右图；方程：
Fy 0, F ED sinF P0 Fx 0, F CsBinF D B 0
FDBtaFn10FP
Fy 0, F Cc B o sFAB 0
F AB tF a D n BF DB 10.F 1 0 P8k 0N#
附录1：第3章习题解答
补充习题2
补充习题2 图示结构。试求：铅直杆AO上的铰链A、C和O所受的约束力。
a
a
F
F
F'Cy
F FR
F'Cx
C
E
D
FOy
a
a
FOx
FBy O
FBx
解：对象：整体
受力：如图
方程：
M B(F)0, 2aFOy0,
对象：杆CD
受力：如图
FOy 0
＃（1）
方程：
M E ( F ) 0 , a F C y a F 0F,CyFFCy＃（2）
附录1：第3章习题解答
3－6
解：对象：图（a）中梁受力：如图所示方程：
（b）
FC
FD
O
FB
MO(F)0
6 F C 4 F 1 M 2 F 2 c3 o 0 s 0
FC3.45kN ＃
MB(F)0
8 F C 6 F 1 M 4 F D s4 i n 2 5 F 2 s3 i n 0 0
M O ( F ) 0 , a F C F x2 a 0FC ,x2FFCx＃（3）
附录1：第3章习题解答

工程力学课后习题答案（静力学和材料力学）

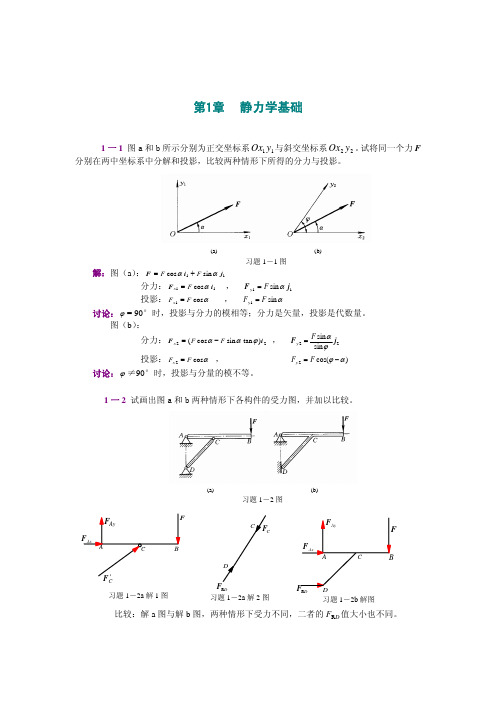
1 一 3 试画出图示各构件的受力图。
F
D
习题 1－3 图
C
F
D
C
A
B
FA
FB
习题 1－3a 解 1 图
F Ax
A
B
FAy
FB
习题 1－3a 解 2 图
C
BF
B
D
FB
FD
C
A
FA 习题 1－3b 解 2 图
W
FAx
FAy
习题 1－3c 解图
F
A
A
F
α
B C
FA
D
FAFD 习题 1－3d 解 2 图
E F
D C
FH
H
习题 1－6 解 2 图
A
D
F
FH ′ H
C
H
FH 习题 1－6 解 3 图
1—7 试画出图示连续梁中的 AC 和 CD 梁的受力图。
习题 1－7 图
FAx A FAy
C
F FC' x Cx
B
FB
FC' y
F1
C
FCy
习题 1－7 解图
F2
D
FDx
FDy
1—8 图示为一液压冷铆机，活塞同铆枪为一整体。工作时油缸内油压力推动活塞下降，铆枪冲压铆钉将钢板铆接。活塞与油缸间为光滑接触。试分别画出：
(1) 油缸的受力图； (2) 活塞铆枪的受力图； (3) 铆钳的受力图。
习题 1－8 图
p
q FQ
p q'
FQ'
(b)
(c)
习题 1－8 解图
1—9 安置塔器的竖起过程如图所示，下端搁在基础上，C 处系以钢绳，并用绞盘拉住；上端在 B 处系以钢缆，通过定滑轮 D 连接到卷扬机 E 上。设塔器的重量为 FW，试画出塔器的受力图。

材料力学习题课(超静定问题)-版演示课件-精选.ppt

11

l 1 EI

l EI
X1
F
A
C
l
1
A
X1 B
1 B
1 M1
精品
F
A
C
B
l
1P

1 l Fl 24
EI
1

Fl 2 8EI
MP
Fl 4
1 M1精品
11

l EI
Fl 2 1P 8EI
11 X1 1P 0
X1

Fl 8
M MP X1M1
MP
Fl 4
2 FNP1 FNP3 2 F
显然有 FNP2 0
精品
FNP1
FNP 3 A
F
同理计算 FN
aa
B
C
D
1
a
A
1
FN 1
FN 3
A
2 FN 1 FN 3 2
FN 2 1
计算系数
11
FN2i li ( 2 1)a
EA
EA
精品
2 FNP1 FNP3 2 F
x X1 q
M max

qx2 X1 x 2

X
2 1
2q

ql 2 2

X1
X1 ( 2 1)ql 0.414ql
X1

3EI l3

3ql 8
X1l 3 ql 4 0.013ql 4 3EI 8EI EI
精品
思考：塑性材料梁，弯曲刚度为EI，力F作用于跨中，为使从强度方面考虑最合理，支座B应上移的距离应为多少？

工程力学(静力学与材料力学)习题及答案 - 剪应力分析

工程力学（静力学与材料力学）习题第8章剪应力分析8－1 扭转切应力公式p /)(I M x ρρτ=的应用范围有以下几种，试判断哪一种是正确的。

（A ）等截面圆轴，弹性范围内加载；（B ）等截面圆轴；（C ）等截面圆轴与椭圆轴；（D ）等截面圆轴与椭圆轴，弹性范围内加载。

正确答案是。

8－2 两根长度相等、直径不等的圆轴受扭后，轴表面上母线转过相同的角度。

设直径大的轴和直径小的轴的横截面上的最大切应力分别为max 1τ和max 2τ，切变模量分别为G 1和G 2。

试判断下列结论的正确性。

（A ）max 1τ＞max 2τ；（B ）max 1τ＜max 2τ；（C ）若G 1＞G 2，则有max 1τ＞max 2τ；（D ）若G 1＞G 2，则有max 1τ＜max 2τ。

正确答案是。

8－3 承受相同扭矩且长度相等的直径为d 1的实心圆轴与内、外径分别为d 2、)/(222D d D =α的空心圆轴，二者横截面上的最大切应力相等。

关于二者重之比（W 1/W 2）有如下结论，试判断哪一种是正确的。

（A ）234)1(α-；（B ）)1()1(2234αα--；（C ）)1)(1(24αα--；（D ）)1/()1(2324αα--。

正确答案是。

8－4 由两种不同材料组成的圆轴，里层和外层材料的切变模量分别为G 1和G 2，且G 1 = 2G 2。

圆轴尺寸如图所示。

圆轴受扭时，里、外层之间无相对滑动。

关于横截面上的切应力分布，有图中所示的四种结论，试判断哪一种是正确的。

正确答案是。

8－5 等截面圆轴材料的切应力－切应变关系如图中所示。

圆轴受扭后，已知横截面上点)4/(d a a =ρ的切应变s γγ=a ，若扭转时截面依然保持平面，则根据图示的γτ-关系，可以推知横截面上的切应力分布。

试判断图中所示的四种切应力分布哪一种是正确的。

正确答案是。

8－6图示实心圆轴承受外扭转力偶，其力偶矩T = 3kN ·m 。

工程力学(静力学与材料力学)-3-静力学平衡问题1

平面一般力系的平衡条件与平衡方程－例题 1
FTB＝
FW x＋FQ lsin
l 2 ＝ 2 FW x F Q l
解： 3．讨论由结果可以看出，当x＝l，即电动机移动到吊车大梁右端B点处时，钢索所受拉力最大。钢索拉力最大值为：
FTB＝
2 FW l＋FQl 2lsin
＝
2 FW＋FQ 2sin30
B A A、B 连线不垂直于x 轴
FR
这是因为，当上述3个方程中的第二式和第三式同时满足时，力系不可能简化为一力偶，只可能简化为通过AB两点的一合力或者是平衡力系。但是，当第一式同时成立时，而且AB与x轴不垂直，力系便不可能简化为一合力FR，否则，力系中所有的力在x轴上投影的代数和不可能等于零。因此原力系必然为平衡力系。
FAy FAx A
FBy FBx
B
D

平面力系的平衡条件与平衡方程

平面力系的平衡条件与平衡方程
返回

平面力系的平衡条件与平衡方程

平面一般力系的平衡条件与平衡方程平面一般力系平衡方程的其他形式

平面力系的平衡条件与平衡方程

平面一般力系的平衡条件与平衡方程

平面力系的平衡条件与平衡方程
平面一般力系的平衡条件与平衡方程
当力系的主矢和对于任意一点的主矩同时等于零时，力系既不能使物体发生移动，也不能使物体发生转动，即物体处于平衡状态。是平面力系平衡的充分条件。另一方面，如果力系为平衡力系，则力学的主矢和对于任意一点的主矩必同时等于零。这是平面力系平衡的必要条件。力系平衡的充分必要条件是力系的主矢和对任意一点的主矩同时等于零。这一条件简称为平衡条件。满足平衡条件的力系称为平衡力系。

材料力学课堂例题(湖南大学)-静力学.

工程力学(静力学与材料力学)习题及答案 - 内力分析

湖南大学812材料力学试题回忆版

《材料力学》第6章-简单超静定问题-习题解

工程力学(静力学与材料力学)课后习题问题详解

材料力学(湖南大学)智慧树知到答案章节测试2023年

材料力学例题 workbench静力学

静力学练习题及参考答案

材料力学力法典型例题解

工程力学(静力学与材料力学)习题及答案 )-正应力分析

工程力学(静力学与材料力学)习题及答案 -章 位移分析

工程力学(静力学与材料力学)习题及答案 -力系的平衡

静力学30个例题

工程力学(静力学与材料力学)习题及答案 - 应力状态分析

第I篇 静力学习题课ppt课件

工程力学课后习题答案（静力学和材料力学）

材料力学习题课(超静定问题)-版演示课件-精选.ppt

工程力学(静力学与材料力学)习题及答案 - 剪应力分析

工程力学(静力学与材料力学)-3-静力学平衡问题1

工程力学(静力学与材料力学)习题及答案 -章位移分析

第I篇静力学习题课ppt课件