熟练使用SPSS进行假设检验
利用SPSS对期望进行区间估计和假设检验

利用SPSS对期望进行区间估计和单样本假设检验
一、启动SPSS
二、在数据窗中建立数据文件
定义变量x,输入样本观测值。
三、单击Analyze菜单,选择Compare Means中的One-Sample T Test
打开单样本T检验主对话框:
(1)将变量x放入Test栏。
(2)在下方的Test栏中,输入要检验的期望值。
如只对期望进行区间估计,则不必输入待检验期望值μ0。
(3)击活Option框确定检验的显著性水平α的值,系统默认值为0.05,单击continue返回单样本T检验主对话框。
其
他选项默认即可。
(4)单击Ok可得结果清单。
四、(1)当进行区间估计时,可在结果清单中找到置信区间;
(2)当进行假设检验时,可在结果清单中找到Sig的值。
若Sig 大于检验的显著性水平α,则接受假设μ=μ0;若Sig小于或等于检验的显著性水平α,则拒绝假设μ=μ0。
参数估计与假设检验SPSS

3
区别
参数估计更侧重于总体参数的估计和推断,而假 设检验更侧重于对总体参数的假设进行验证和决 策。
02
SPSS软件介绍
SPSS软件的特点与优势
强大的统计分析功能
SPSS提供了广泛的统计分析方法,包括描述性统计、推论性统计、 多元统计分析等,能够满足各种数据分析和科学研究的需求。
易用性
SPSS的用户界面友好,操作简单,使得用户可以快速上手,减少了 学习成本。
参数估计与假设检验的应用场景与注 意事项
参数估计与假设检验的应用场景
社会科学研究 在社会科学研究中,参数估计与 假设检验是常用的统计方法,用 于检验理论模型和假设,评估变 量之间的关系。
心理学研究 在心理学研究中,参数估计与假 设检验用于研究人类行为、认知 和情感等方面的规律和特点。
医学研究 在医学研究中,参数估计与假设 检验常用于临床试验和流行病学 研究中,以评估治疗效果、疾病 发病率和风险因素等。
04
05
根据输出结果判断假设是否 成立。
假设检验的实例分析
以一个实际研究问题为例,如比较两组人群的平均身高是否存在显著差异。
在SPSS中实现该实例分析,包括数据导入、选择统计方法、设置参数、运 行统计方法和结果解读等步骤。
根据SPSS的输出结果,判断提出的假设是否成立,并解释结果的实际意义。
05
数据处理技术,提高分析效率和准确性。
多变量分析方法
03
多变量分析方法的发展将促进参数估计与假设检验的进一步应
用,能够更全面地揭示变量之间的关系。
THANKS
感谢观看
使用SPSS进行参数估计,例如使用逻辑回归分 析来估计吸烟与肺癌之间的关系。
04
假设检验在SPSS中的实现
spss假设检验

SPSS假设检验1. 简介SPSS(Statistical Package for the Social Sciences)是一种非常常用的统计软件,被广泛应用于社会科学研究中。
其中,假设检验是SPSS中常用的统计方法之一,用于验证研究者对总体或样本的某种假设。
2. 假设检验的概念假设检验是统计学中的一种重要方法,用于判断一个统计推断是否与样本数据一致。
在假设检验中,通常会提出一个原假设(H0)和一个备择假设(H1),然后根据样本数据对两个假设进行检验,以确定是否拒绝原假设,从而对总体进行推断。
3. SPSS中的假设检验SPSS中提供了丰富的假设检验方法,涵盖了多种统计推断的情况。
下面将介绍几种常见的假设检验方法。
3.1 单样本 t 检验单样本 t 检验用于判断一个样本的均值是否与一个已知的常数有显著性差异。
在SPSS中,进行单样本 t 检验的步骤如下:1.导入数据:在SPSS中打开或导入数据文件。
2.选择变量:选择要进行 t 检验的变量。
3.进行检验:选择菜单栏上的“分析”-“比较均值”-“单样本 t 检验”。
4.设置参数:选择相关的变量和检验参数,点击“确定”进行分析。
5.查看结果:SPSS将显示 t 检验的结果,包括均值、标准差、t 值、自由度和显著性等。
3.2 独立样本 t 检验独立样本 t 检验用于判断两个独立样本的均值是否存在显著性差异。
在SPSS中,进行独立样本 t 检验的步骤如下:1.导入数据:在SPSS中打开或导入数据文件。
2.选择变量:选择需要进行对比的两个变量。
3.进行检验:选择菜单栏上的“分析”-“比较均值”-“独立样本 t 检验”。
4.设置参数:选择相关的变量和检验参数,点击“确定”进行分析。
5.查看结果:SPSS将显示独立样本 t 检验的结果,包括均值、标准差、t 值、自由度和显著性等。
3.3 配对样本 t 检验配对样本 t 检验用于判断同一组个体在两个不同时间点或条件下的均值是否存在显著性差异。
SPSS假设检验

SPSS假设检验实验⽬的::实验⽬的1、学会使⽤SPSS的简单操作。
2、掌握假设检验。
:实验内容:实验内容1.⼀个总体均值的检验(⼩样本);2.两个总体均值之差的检验;3.绘制正态概率图;4.S—W检验。
实验步骤: 1.⼀个总体均值的检验(⼩样本):单总体的Z检验和t检验。
设是取⾃正态总体的⼀个样本,要检验。
其中为已知的常数。
为了说明如何构造检验统计量和拒绝域,先看⼀个简单的情形。
设总体⽅差是已知的,记为,设为样本均值,则。
设为真,即,对作标准化,得到上述的Z就是要构造的检验统计量。
设定显著性⽔平为0.05,因为,的概率为0.05,所以检验的拒绝域是。
如果由样本计算得到,与⼩概率原理⽭盾,从⽽拒绝原假设。
在实际应⽤中,总体的⽅差是未知的。
因⽽需要样本⽅差代替总体⽅差,相应地,检验统计量编程了t统计量。
设与分别为样本的均值和样本⽅差,当为真时,可知统计量对于给定的显著性⽔平,检验的拒绝域是。
其中临界值满⾜条件。
它就是⾃由度为(N-1)的t分布的双侧分为点。
如果由样本观测值代⼊,计算得到的t值满⾜,则拒绝原假设。
SPSS检验结果不给出临界值,⽽是在给出t值的同时给出它的显著性概率(也成为p值或相伴概率,记为p或Sig)。
计算⼀个双侧检验问题,SPSS操作如下:“分析”→“⽐较均值”→“单样本T检验”,在打开的对话框中填好“检验变量”列表框和“检验值”⽂本框。
单击“确定”。
输出结果中的Sig.(双侧)就是p值。
⽐较p值与检验⽔准。
1 T-TEST2 /TESTVAL=803 /MISSING=ANALYSIS4 /VARIABLES=score5 /CRITERIA=CI(.95).⼀个总体的均值检验 差齐性检验:Sig=0.397>0.05,⽅差不显著,可以认为两个独⽴样本的⽅差⼀致。
均值之差t检验:在⽅差相等的条件下,Sig=0.004<0.05,均值之差显著,可以认为两个独⽴样本均值有显著差异。
实验3 假设检验

实验报告课程名称试验设计与数据分析姓名邵建智学号3110100122专业生物系统工程实验名称假设检验浙江大学生物系统工程与食品科学学院二O一三年八月制实验三:假设检验实验类型:上机操作实验地点:农生环D-414指导老师:傅霞萍实验日期:2013 年10 月8 日一、实验目的和要求(1)熟练使用SPSS进行假设检验(工具/Analyze/Compare means)二、实验内容和原理2.1实验原理假设检验是一种由样本的差异去推断样本所在总体是否存在差异的统计方法。
常用于解决两种工艺方法的比较、一种新添加剂与对照两处理的比较、两种食品内含物测定方法的比较、检验某产品是否达到某项质量标准、检验某项有害物指标是否超标等问题。
根据涉及的统计量不同,选择进行u检验、t检验、F检验等显著性检验。
2.2 实验内容(显著性水平α=5%)(1)单样本t检验问题1:某公司经理宣称他的雇员英语水平很高,如果按照英语六级考试,一般平均得分为75分,现从雇员中随机选出11人参加考试,得分如下:80,81,72,60,78,65,56,79,77,87,76问:该经理的宣称是否可信?(2)两独立样本t检验问题2:分别在10个食品厂各自测定了大米饴糖和玉米饴糖的还原糖含量,结果见下表,试比较两种饴糖的还原糖含量有无显著差异?(3)成对样本(两配对样本)t检验目的:利用来自两个总体的配对样本数据,推断两个总体的均值是否存在显著差异。
问题3:以下是对促销人员进行培训前后的促销数据,试问该培训是否产生了显著效果。
三、主要仪器设备/实验环境(使用的软件等)IBM SPSS 19.0等四、操作方法与实验步骤(必填,上机操作过程,可以插图)a)提出原假设H0b)选择检验统计量c)计算检验统计量观测值和概率P值d)给定显著性水平α并作出决策(1)单样本t检验选择“分析”-“比较均值”-“单样本T检验”检验变量选择“成绩”,检验值设为75,单击“确定”(2)两独立样本t检验选择“分析”-“比较均值”-“独立样本T检验”使用指定值,组1为:1,组2为:2,单击“继续”检验变量选择“含糖量”,分组变量选择“品种”,单击“确定”(3)成对样本(两配对样本)t检验选择“分析”-“比较均值”-“配对样本T检验”成对变量选择“培训前”和“培训后”为一对,单击“确定”五、实验数据记录和处理(必填,图表数据、计算结果、对图表的处理)(1)单样本t检验(3)成对样本(两配对样本)t检验六、实验结果与分析(必填)(1)单样本t检验1)11个样本的均值,标准差,均值的标准误分别为73.73,9,51,2,880。
SPSS中的相关分析及假设检验

SPSS中的相关分析及假设检验相关分析和假设检验是统计学中常用的方法。
在SPSS中,相关分析可以用来探究两个或多个变量之间的关系。
而假设检验可以用来验证研究者对一个或多个总体参数的假设。
相关分析是用来确定两个或多个变量之间的关系的统计方法。
SPSS 中可以通过选择菜单中的“相关”选项来进行相关分析。
在弹出的对话框中,用户可以选择要进行相关分析的变量,以及选择所需的统计指标。
最常用的统计指标是皮尔逊相关系数(Pearson correlation coefficient),可以用来度量两个连续变量之间的线性关系。
除了皮尔逊相关系数外,还可以选择斯皮尔曼等级相关系数(Spearman's rank correlation coefficient),用于度量两个有序变量之间的关联。
在进行相关分析时,我们还需要对相关系数进行显著性检验,以确定相关系数是否显著不为零。
SPSS会自动计算相关系数的显著性水平(p-value)。
p-value小于我们预先设定的显著性水平(通常为0.05),则可以拒绝原假设,认为相关系数显著不为零。
接下来,我们将介绍SPSS中常用假设检验的方法。
假设检验用于验证研究者对一个或多个总体参数的假设。
常用的假设检验方法包括单样本t检验、独立样本t检验、配对样本t检验和方差分析等。
单样本t检验用于检验一个总体均值是否等于一个给定的值。
SPSS 中可以通过选择菜单中的“分析”、“比较均值”、“单样本t检验”进行单样本t检验。
在弹出的对话框中,用户需要输入要进行检验的变量和给定的均值。
SPSS会给出t值、自由度和p值等统计结果。
如果p值小于我们设定的显著性水平,则可以拒绝原假设,认为总体均值与给定值存在显著差异。
独立样本t检验用于检验两个独立样本的均值是否相等。
SPSS中可以通过选择菜单中的“分析”、“比较均值”、“独立样本t检验”进行独立样本t检验。
在弹出的对话框中,用户需要输入两个独立样本的变量。
如何在spss上进行假设检验
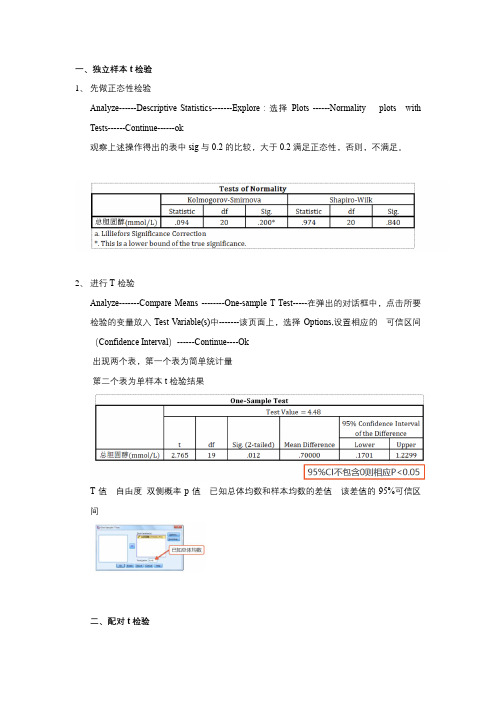
三、两独立样本均数的t检验
1、文件拆分:Data---Split File----选择Organize output by groups,将分组变量选入右侧对话框----Ok
2、正态性及方差齐性检验:Analyze----Descriptive Statistics-----Explore:选择Plots ------Normality plots with Tests,Untransformed------Continue------ok
4、多重比较
Analyze----General Linear Model---- Univariate----Post Hoc----block(区组)----group(处理)------ Bonferroni---- Continue------OK
析因设计
非参数检验——秩和检验
一、配对样本秩和检验
3、秩和检验旧方法
Analyze-----Nonparametric Tests----Legacy Dialogs----2 Related Samples-----在弹出的对话框中,点击所要检验的两个变量放入Paired Variables框内-----Continue----Ok
4、智能分析模块
看结果中正态性sig〉0.2方差齐性sig〉0.1
2、单因素方差分析
Analyze-----compare means----one-way anova------选择dependent list、factor list-----ok
3、多重比较
Analyze----Compare means----One-wayANOVA----PostHoc----Bonferroni(最常用)、SNK、Dunnett(control category一个对照组和多个组比,分组最大、最小、first、last)-----Options----Descriptive(统计描述), Homogeneity of variance test(方差齐性检验), Means plot(均数图), Exclude cases analysis by analysis(缺失值选项)---- Continue------OK
spss管理统计课程设计参数估计与假设检验

S P S S管理统计课程设计参数估计与假设检验-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN实验名称:实验二实验要求:1、撰写实验报告。
每个操作要写出实验步骤,及操作结果2、要求电子版实验报告,用文件名“学号+实验二”保存,学期结束打印上交。
三、实验步骤及结果:一、利用数据“CH4CH8茎叶箱方差工资性别岗位300余”进行参数估计。
1.分别对“一线工人”当前工资的均值进行点估计、区间估计。
1.1实验步骤1)启动SPSS,调入样本值2)依次点击analyze—descriptive statistics—explorer,弹出小窗口,将“当前工资”送入右框中的“dependent list”中,将“工作类型”放入“factor list”中,如图1.113)点击statistics按钮出现如图1.12,此框中可输入1-α的值,如95%,为其置信度,点击continue返回。
4)点击OK。
图1.11 explore 对话框图1.12统计量设置窗口1.2实验结果:如图1.13和图1.14,由图1.13得知其点估计为mean:31888.6,“一线工人”当前工资的均值的区间估计为(30470.2, 33306.9),其中lower bound表示置信区间的下限,upper bound表示置信区间的上限。
图1.13图1.14统计量描述2.“一线工人”、“科以上干部”、“一般机关员工”分别占总职工的比例。
2.1实验步骤1)启动SPSS,调入样本值2)依次点击analyze—descriptive statistics—frequencies,点击左边框中的变量“工作类型”并用中间的箭头放入右边的框中,如图2.11所示,3)再点击OK图:1.21 频次分析模块主窗口2.2实验结果:如图2.22所示,可知“一线工人”、“科以上干部”、“一般机关员工”分别占总职工比例中的77.9% ,7.1% ,15.0%。
实验三 假设检验的SPSS实现

实验三假设检验的SPSS实现一、实验目的与要求1.掌握单样本t检验的基本原理和spss实现方法。
2.掌握两样本t检验的基本原理和spss实现方法。
3.熟悉配对样本t检验的基本原理和spss实现方法。
二、实验内容提要1.从一批木头里抽取5根,测得直径如下(单位:cm):12.3 12.8 12.4 12.1 12.7(1) 求总体直径95%的置信区间。
(2)是否能认为这批木头的平均直径是12.3cm ?2.比较两批电子器材的电阻,随机抽取的样本测量电阻如题表2所示,试比较两批电子器材的电阻是否相同?A批0.140 0.138 0.143 0.142 0.144 0.148 0.137 B批0.135 0.140 0.142 0.136 0.138 0.140 0.1413. 配对t检验的实质就是对差值进行单样本t检验,要求按此思路对上题进行重新分析,比较其结果和配对t检验的结果有什么异同。
三、实验步骤为完成实验提要1.可进行如下步骤1.在变量视图中新建一个数据,在数据视图中录入数据,在分析中选择比较均值,单样本t检验,将直径添加到检验变量,点击确定。
單一樣本統計資料N 平均數標準偏差標準錯誤平均值直径 5 12.4600 .28810 .12884單一樣本檢定檢定值= 12.3T df 顯著性(雙尾)平均差異95% 差異數的信賴區間下限上限直径 1.242 4 .282 .16000 -.1977 .5177为完成实验提要2.可进行如下步骤2.1 新建一个数据,在变量视图中输入电阻和批次,然后再数据视图中录入数据,分析——比较均值——独立样本T检验(分组选批次,输入1,2)确定群組統計資料批次 N平均數 標準偏差 標準錯誤平均值电阻1 7 .14171 .003773 .001426 27.13886.002610.000986会根据方差齐性检验结果选择T 检验中结果中有用的信息。
为完成内容提要3.需进行如下步骤:3.1. 方法一:在变量视图中添加差值,选择转换的计算变量,在目标变量智能光添加差值,数字表达式为A 组 – B 组,点击确定。
第4章假设检验SPSS

-3.67 1.541 .002 -228.75 62.396 -361.43 -96.07
2012-6-26
统计学实验》第4章假设检验
【程序方式】
T-TEST GROUPS=Group(1 2) /MISSING=ANALYSIS /VARIABLES=XY /CRITERIA=CI(.9500).
F
s12 cs22
(4.6)
2012-6-26
统计学实验》第4章假设检验
【菜单方式】
打开数据文件li4.2.sav, 选择Analyze→Compare Means→ Independent-
Samples T Test, 然后将灯泡寿命XY选入Test Variable, 在
Grouping Variable中选入Group,点击Define Groups输入1对应Group 1和2对应Group 2, 点击Options选置信度(本例取默认值95%), 最后点击Continue→点击OK。
2012-6-26
统计学实验》第4章假设检验
Grouping Variable中选入Group,点击Define Groups输入1对应Group 1和2对应Group 2, 点击Options选置信度(本例取默认值95%), 最后点击Continue→点击OK。
2012-6-26
统计学实验》第4章假设检验
表4.3 两种牌号灯泡平均使用寿命的检验表
N 10 10
Std. Deviation
Std. Error Mean
4.81779
1.52352
4.94862
1.56489
Pair 1
表4.5 配对样本相关系数表
Paired Samples Correlations
SPSS中的相关分析及假设检验

相关分析及假设检验 spss1.概念变量之间相关;但是又不能由一个或几个变量值去完全和唯一确定另一个变量值的这种关系称为相关关系..相关关系是普遍存在的;函数关系仅仅是相关关系的特例..事物之间有相关关系;不一定是因果关系;也可能仅是伴随关系;但是事物之间有因果关系;则两者必然相关..相关分析用于分析两个随机变量的关系;可以检验两个变量之间的相关度或多个变量两两之间的相关程度;也可以检验两组变量之间的相关程度偏相关分析是指在控制了其他变量的效应以后;对两个变量相关程度的分析..、2.皮尔逊积差相关系数pearson product-moment correlation coefficient变量之间的相关程度由相关系数来度量;pearson相关系数是应用最广的一种..它用于检验连续型变量之间的线性相关程度2.1前提假设1正态分布皮尔逊积差相关只适用于双元正态分布的变量;即两个变量都是正态分布; 注意只有pearson要求正态分布如果正态分布的前提不满足;两变量间的关系可能属于非线性相关2样本独立样本必须来自总体的随机样本;而且样本必须相互独立3替换极值变量中的极端值如极值、离群值对相关系数的影响较大;最好加以删除或代之以均值或中数2.2相关分析的前提假设检验一般情况下是对是否满足正态分布进行检验;对于正态分布的检验有好几种方法;总的可分为非参数检验和图形检验法1非参数检验法spss中的1-sample K-S检验;检验样本数据是否服从某种特定的分布;方法有三种a. Asymptotic only 是一种基于渐进分布的显著性水平的检验指标;通常显著性水平小于0.05则认为显著;适用于大样本..如果样本过小或分布不好;该指标的适用性会降低b.Monte Carlo 精确显著性水平的无偏估计;适用于样本过大无法使用渐进方法估计显著性水平的情况;可以不必依赖渐近方法的假设前提c.Exact 精确计算观测结果的概率值;通常小于0.05即被认为显著;表明横变量和列变量之间存在相关;同时允许用户键入每次检验的最长时间显著;可以键入1到9999999999之间的数字;但只要一次检验超过指定时间的30分钟;就应该用monte carlo假设是服从某种分布所以如果计算出的值比如Asymp. Sig 小于0.05;那么拒绝原假设;说明样本为非正态分布;否则值越大越服从某种分布单样本K-S首先计算每一阶段实际值与观察值的差异值;再计算每一阶段差异值的绝对值Z;即K-S的Z值;Z值越大;样本服从理论分布的可能性越小还有一个是2 -sample Kolmogorov—Smirnov用于检验2个样本的分布是相同的假设2图形法spss中grapha.Q-Q正态检验图图中横坐标为实际观测值;纵坐标为正态分布下的期望值;如果实际观测值取自正态分布的整体;那么图中所示的落点应该分布在趋势线的附近;并且应该表现出一定的集中趋势;即平均数附近应该聚集较多的落点;越靠近两个极端落点越少..此外还输出一种无趋势正态检验图;横坐标为观测值;纵坐标为观测值于期望值的差值..在符合正态分布的情况下;图中的落点应该分布在中央横线的附近;甚至完全落到这条横线上;而且也应表现出集中在平均数周围的趋势..如果需要正态分布;应该考虑对数据进行必要的变换b.P-P图判断方式和qq图相同c.直方图根据直方图的形状来判断是否为正态分布d.箱式图boxplot箱式图可用于表现观测数据的中位数、四分位数和两头极端值方框中的粗黑横线为中位数;方框之外的上下两条细横线成为须线;是除了离群值和极值之外的最大值和最小值..符合正态分布的情况下;箱式图应该是以中位线为轴上下对称的;并且上下须线之间的距离应该是盒距方框上下边缘的三倍左右;Binomial test 二项分布检验该过程用于检验的假设是一个来自二项分布的总体的变量具有指定事件发生的概率;该变量只能有两个值例如检验组装生产线上一种工件的废品率为1/10 即P=0.1可以抽取300 个工件;查看并记录每个工件是否是废品;使用本过程检验这个概率3.spss中相关分析过程analyze-correlate-bivariate相关分析的检验:检验的假设是总体中两个变量之间的相关系数为0.一般情况下我们给出假设成立概率p的阈值为0.05;当概率p小于0.05时;认为原假设不成立;否则接受原假设;认为两个变量之间的相关系数为0spss中进行相关分析有三种方法a.pearson 积差相关计算相关系数并作显著性检验;适用于两列变量都为正态分布的连续变量或等间距测度的变量b.kendall tau-b等级相关计算相关系数并作显著性检验;对数据分布没有严格要求;适用于检验等级变量之间的关联程度秩相关c.spearman 等级相关计算相关系数并做显著性检验;对数据分布没有严格要求;适用于等级变量或者等级变量不满足正态分布的情况..对于非等间距测度的连续变量;因为分布不明可以使用等级相关分析;也可以使用Pearson 相关分析;对于完全等级的离散变量;必须使用等级相关分析相关性当资料不服从双变量正态分布或总体分布型未知;或原始数据是用等级表示时;宜用Spearman 或Kendall相关一般情况下我们都某人数据服从正态分布;采用pearson相关系数等级相关系数等级相关系数;又称顺序相关系数;它也是描述两要素之间相关程度的一种统计指标..等级相关系数是将两要素的样本值按照数值的大小顺序排列为此;以各要素样本值的位次代替实际数据而求得的一种统计量..例如x y有n对样本值;记R1代表x的位次序号;R2代表y的序号位次代表x y同一组样本的位次差的平方和;他们的等级相关系数为显著性检验类型two-tailed 双尾检验选项当事先不知道相关方向正相关还是负相关时选择此项One tailed 单尾检验选项如果事先知道相关方向可以选择此项Flag significant Correlations 复选项如果选中此项输出结果中在相关系数数值右上方使用* 表示显著水平为0.05 用** 表示其显著水平为0.01计算相关系数是;为了方便起见;通常采用如下公式:在spss中进行相关分析时;自动会输出一个显著性sig的值;值越大越显著a0.05 0.01n—2125 0.174 0.228150 0.159 0.208200 0.138 0.181300 0.113 0.148400 0.098 0.1281000 0.062 0.081表中f表示自由度为n-2;a代表不同的置信水平公式p={|r|>ra}=a 的意思是当所计算的相关系数r 的绝对值大于在a 水平下的临界值ra 时;两要素不相关即ρ=0的可能性只有a此外还有一个t双侧检验的相关系数阈值也可以用t 统计量检验t值大于查表的t时;说明相关系数显著附录3 t分布临界值tg表P{|t|≥ta}=a自由度A=0.05 A=0.05 A=0.10 自由度A=0.01 A=0.05 A=0.101 2 3 4 5 6 7 8 91011121314151617 63·6579·9255·8414·6044·0323·7073·4993·3553·2503·1693·1063·0553·0122·9772·9472·9212·89812·7064·3033·1822·7762·5012·4472·3652·3062·2622·2282·2012·1792·1002·1452·1312·1202·1106·3142·9202·3532·1322·0151·9431·8951·8601·8331·8121·7961·7821·7711·7611·7531·7461·740181920212223242526272829304060120002·8782·8612·8452·8315·8192·0872·7972·782·7792·7712·7632·7562·7502·7042·6602·6172·5762·1012·0932·0862·0802·0742·0692·0642·0602·0562·0522·0482·0452·0422·0212·0001·9801·9601·7341·7291·7251·7211·7171·7141·7111·7081·7061·7081·7011·6991·6971·6841·6711·6581·645进行t检验时用上面两个表都可以;第一个表直接比较r和表中的阈值即可;而第二个表需要进行计算t值;然后比较t和表中的t如果计算的值大于表中的值;则说明相关系数是显著的在以上几个表中;相关系数检验的自由度都是n-2等级相关的系数检验的临界值r越大越好spss中会自动对等级相关的显著性进行检验sig。
熟练使用SPSS进行假设检验

熟练使用SPSS进行假设检验试验内容:[试验][例]某克山病区测得11例克山病患者与13名健康人的血磷值mmol/L如下,问该地急性克山病患者与健康人的血磷值是否不同。
表1 克山病区调查数据结果患者0。
84 1.05 1。
20 1.20 1.39 1。
53 1.67 1.80 1。
87 2.07 2。
11健康0.54 0.64 0.64 0。
75 0.76 0。
81 1。
16 1.20 1。
34 1.35 1。
48 1。
56 1.87人1。
录入数据。
将组别设为g,可将患者组设为1 ,健康人设为2,血磷值设为x ,如患者组中第一个测量到的血磷值为0。
84,则g为1,x为0.84,其他数据均仿此录入,如下图所示。
图1 数据输入界面2.统计分析。
依次选择“Analyze"、“Compare means"、“Independent Samples T Test”。
图2 选择分析工具3。
弹出对话框如下图所示,将x选入Test Variables、g选入Grouping Variable,并单击下方的Define Groups按钮,弹出定义组对话框,默认选项为Use Specified Value,在Group1和Group2框中分别填入1和2,即要对组别变量值为1和2的两个组做t检验,另外Options对话框中可选择置信度和处理缺失值的方法.图3 选择变量进入右侧的分析列表SPSS输出的结果和结果说明:图4 输出结果表2 统计量描述列表G N Mean Std.DeviationStd. Error MeanVAR00001 1 11 1.5209 。
4218 .12722 13 1.0846 .4221 .1171表3 假设检验结果表F Sig.t df Sig。
MeanDifference Std. ErrorDifference95% Confidence Interval of theDifferenceLower UpperEqual variances assumed .032。
直线相关假设检验SPSS步骤

直线相关假设检验SPSS步骤直线相关假设检验是统计学中常用的一种假设检验方法,用于确定两个变量之间是否存在线性相关关系。
SPSS是一种常用的统计分析软件,可以方便地进行直线相关假设检验。
本文将介绍直线相关假设检验的步骤,并以实例说明如何在SPSS中进行相关性分析。
进行直线相关假设检验前,我们需要明确两个变量之间的关系是线性的。
线性关系是指两个变量之间的关系可以用一条直线来描述。
为了验证这个假设,我们可以绘制散点图来观察变量之间的关系。
如果散点图呈现出明显的直线趋势,那么我们可以认为变量之间存在线性关系。
接下来,我们需要进行直线相关系数的计算。
直线相关系数是衡量两个变量之间线性关系强度的指标,常用的直线相关系数有皮尔逊相关系数和斯皮尔曼相关系数。
皮尔逊相关系数适用于连续变量之间的线性关系检验,而斯皮尔曼相关系数适用于有序变量之间的线性关系检验。
在SPSS中进行直线相关假设检验,我们需要进行以下步骤:第一步,导入数据。
打开SPSS软件,选择“文件”菜单下的“导入”选项,选择需要进行直线相关假设检验的数据文件进行导入。
第二步,选择变量。
在导入数据后,我们需要选择需要进行直线相关假设检验的两个变量。
在SPSS的数据视图中,可以通过选中变量名称来选择变量。
第三步,进行相关性分析。
选择“分析”菜单下的“相关”选项,然后在弹出的对话框中选择需要进行直线相关假设检验的两个变量,并点击“确定”按钮。
SPSS会自动计算出皮尔逊相关系数和斯皮尔曼相关系数,并给出显著性水平。
第四步,解读结果。
在进行直线相关假设检验后,SPSS会给出相关系数的大小和显著性水平。
相关系数的取值范围在-1到1之间,绝对值越接近1表示相关性越强。
显著性水平则用来判断相关系数是否具有统计学意义,通常取0.05作为显著性水平的标准。
如果相关系数的显著性水平小于0.05,则可以认为变量之间存在线性相关关系。
以一个具体的例子来说明。
假设我们有一组数据,包括两个变量X 和Y,我们想要检验X和Y之间是否存在线性相关关系。
管理统计学 假设检验的SPSS实现 实验报告

管理统计学假设检验的SPSS实现实验报告一、实验目的学会利用SPSS软件实现假设检验,进一步掌握基本的统计分析方法,分析数据,并能从分析结果中得出结论。
二、实验内容A组亲子关系满意度得分和B组亲子关系满意度得分,利用SPSS软件进行独立样本t 检验。
三、实验步骤1. 导入数据打开SPSS软件,选择“打开”命令,导入数据文件。
本实验中,我们选择脚本文件将数据文件输入SPSS软件中。
2. 数据描述性统计选择“描述性统计”命令进行数据描述统计。
在这里,我们可以查看平均值、中位数、标准差等数据。
我们注意到A组的平均得分是3.91,标准差为0.951;B组的平均得分是3.60,标准差为1.029。
3. 独立样本方差齐性检验选择“独立样本T检验”命令进行方差齐性检验。
在弹出窗口中选择两个样本变量,此时可看到独立样本T检验窗口出现。
我们选择“T检验”下方的“选项”命令,进入“选项”界面设置参数类型。
在参数类型界面中,我们选择“不等方差”选项,因为本实验中两组样本数据的方差不相等。
此时,选择“1”作为样本A,选择“2”作为样本B,然后点击“OK”按钮。
SPSS将输出方差齐性的Levene's Test结果,P=0.426>0.05,说明两个样本数据方差齐性假设成立。
在已经设置好参数类型的独立样本T检验对话框里,点击“OK”按钮,SPSS将输出独立样本平均值、标准误、t值、自由度、P值等结果。
这里我们注意到,P值为0.034<0.05,故可以拒绝原假设,认为A组和B组的亲子关系满意度得分有显著差异。
5. 结果分析通过数据描述统计和独立样本T检验,我们可以得出以下结论:A组的平均得分是3.91,标准差为0.951;B组的平均得分是3.60,标准差为1.029。
两组样本数据方差齐,A组和B组的亲子关系满意度得分有显著差异,P值为0.034<0.05。
四、实验结论本实验通过SPSS软件实现了假设检验,分析研究对象的两个样本数据在亲子关系满意度方面的显著性差异,并得出结论:A组和B组的亲子关系满意度得分有显著差异,P值为0.034<0.05。
spss学习第4章-假设检验

(1)假设检验含义
利用统计方法检验一个事先所作出的假设的真伪, 这一假设称为统计假设,对这一假设所作出的检验就 是假设检验
(2)假设检验基本思路
ⅰ. 对总体参数作出某种假设,并假定它是成立的。 ⅱ.根据样本得到的信息(统计量),考虑接受这个 假设后是否会导致不合理的结果,如果合理就接受这个 假设,不合理就拒绝这个假设。 所谓合理性,就是看是否在一次的观察中出现了小 概率事件。
[Ⅰ.提出原假设] [Ⅱ.选择检验统计量]
[Ⅲ.计算检验统计量的观测值和概率P-值]
[Ⅳ.给定显著性水平α,并作出决策]
举例2
利用住房状况问卷调查数据,推断家庭人均住房面积的平均 值是否为20平方米。 [Ⅰ.提出原假设]
[Ⅱ.选择检验统计量]
[Ⅲ.计算检验统计量的观测值和概率P-值]
SPSS软件计算结果
课堂体验 调查内容1:学生视力
抽取22名学生调查他们的视力,假设全校学生的视
力服从于正态分布,是否可以认为学生的视力均值 为0.8?(取显著性水平α=0.05)
调查内容2:每月消费支出(分男、女)
抽取22名学生调查他们的每月消费支出,假设全校学生的消费 支出服从正态分布,比较不同性别同学的消费支出平均值和方 差?是否可以认为该校学生的消费支出均值为 500元 (取显著性水平α=0.05) 男、女同学的月消费支出是否存在显著差异?
[Ⅲ.计算检验统计量的观测值和概率P-值] [Ⅳ.给定显著性水平α,并作出决策]
第二问
[Ⅰ.提出原假设] [Ⅱ.选择检验统计量]
[Ⅲ.计算检验统计量的观测值和概率P-值]
[Ⅳ.给定显著性水平α,并作出决策]
课堂习题
知识点:一个总体参数比例检验 检验量:Z检验
SPSS-数值变量的假设检验

二、SPSS13.0软件操作 (t 检验)
(一)样本均数与已知总体均数的比较(单样本t检验)
例:通过大量调查,已知某地正常男婴出生体重为 3.26kg。某医生随机抽取20名难产男婴,测得体重(见 数据文件p192.sav)。问该地难产男婴出生体重均数是 否与正常男婴不同? 变量说明:weight:出生体重。
三、SPSS13.0软件操作 (t 检验)
(二)完全随机设计的两样本均数比较(两独立样本t检验)
独立样本t检验
(二)完全随机设计的两样本均数比较(两独立样本t检验)
需要检验的变量
组别
(二)完全随机设计的两样本均数比较(两独立样本t检验)
方差齐性检验
F值
P值
当P>0.05,选择t检验;当 P0.05 ,选择校正t检验。
(一)完全随机设计(两独立样本)的秩和检验
非参数检验
两独立 样本的 检验
(一)完全随机设计(两独立样本)的秩和检验
需要检验的变量
分组变量
(一)完全随机设计(两独立样本)的秩和检验
Z值,近似的P值
(二)配对设计的秩和检验
例:对10名健康人分别用新旧两种方法测定其尿汞值, 数据见文件p199.sav。问两法所得结果有无差别?
变量说明:X1:旧法测定的尿汞值。X2:新法测定的 尿汞值。
(二)配对设计的秩和检验
两相关样本
(配对设计)
(二)配对设计的秩和检验
配对的变量
(二)配对设计的秩和检验
Z值,近似的P值
(二)假设检验方法的选择
t检验和z检验的应用条件和计算公式
*资料中已知时,可以用代替公式中相应的s。
配对设计的假设检验 优点:与完全随机设计的两样本均数比较的假设检验相比, 可以提高两组间的可比性,统计学检验的效率提高。 t检验与置信区间之间具有等价性。
用SPSS作假设检验PPT

常行驶条件下大于40000km,对一个由120个轮胎组成的随机样本作了试验, 测得平均值和标准差分别为41000km和5000km。已知轮胎寿命的公里数近 似服从正态分布。能否根据这些数据作出该制造商的产品同他所说的标准相
符的结论(α=0.05)。
H 0: 40000km H 1: 40000km
H 0: 5cm
H 1: 5cm
___
t x 0 5.3 5 3.16
s n 0.3 10
拒绝域
接受域
拒绝域
2 0.005
1 0.90
2 0.005
3.2498
0 3.16 t0.005 9 3.2498
一个汽车轮胎制造商声称,某一等级轮胎的平均寿命在一定的汽车重量和正
方差已知的均值检验 方差未知的均值检验
某厂加工一种零件,根据经验知道,该厂加工的零件的椭圆度渐近服从正态 分布,其总体均值为0.081mm,总体标准差为0.025mm。今另换一种新机 床进行加工,取200个零件进行检验,得到椭圆度均值为0.076mm。问新 机床加工零件的椭圆度总体均值与以前有无显著差别。
中随机抽取了100个灯泡,得其均值为960小时,批发商是否应该购进这批灯
泡。
解二: H 0: 1000小时
H 1: 1000小时
___
Z x 0 960 1000 2 n 20 100
接受域
拒绝域
1 0.95 0.05
2
0
1.645
电视机显像管批量生产的质量标准为平均使用寿命1200小时,标准差为300 小时。某电视机厂宣称其生产的显像管质量大大超过规定标准。为了进行验 证,随机抽取100件为样本,测得平均使用寿命为1245小时。能否说该厂的 显像管质量显著地高于规定标准。
如何在SPSS数据分析报告中进行假设检验?

如何在SPSS数据分析报告中进行假设检验?关键信息项:1、假设检验的类型独立样本 t 检验配对样本 t 检验单因素方差分析多因素方差分析卡方检验2、数据准备要求数据的完整性数据的准确性数据的正态性异常值处理3、假设的设定原假设和备择假设的明确表述假设的合理性和基于的理论或经验基础4、检验步骤选择合适的检验方法在 SPSS 中输入数据和执行检验操作解读检验结果5、结果报告内容检验统计量的值自由度p 值效应量(如适用)6、结果的解释和结论根据 p 值做出决策对效应大小的解释结果在研究背景下的意义11 假设检验的类型在 SPSS 数据分析报告中,常见的假设检验类型包括但不限于以下几种:111 独立样本 t 检验用于比较两个独立样本的均值是否存在显著差异。
例如,比较两组不同治疗方法下患者的康复时间。
112 配对样本 t 检验适用于配对数据,即同一组对象在不同条件下或不同时间点的测量值。
比如,比较同一批患者治疗前后的体重变化。
113 单因素方差分析用于检验一个因素的不同水平对因变量的均值是否有显著影响。
例如,研究不同教育程度对收入的影响。
114 多因素方差分析当存在多个因素同时影响因变量时,使用多因素方差分析。
比如,研究教育程度和工作经验对收入的共同影响。
115 卡方检验主要用于检验两个分类变量之间是否存在关联。
例如,分析性别与某种疾病的患病率是否有关。
12 数据准备要求在进行假设检验之前,确保数据满足以下要求:121 数据的完整性数据应包含所需的所有变量和观测值,不允许有缺失值。
若存在缺失值,需要采取适当的方法进行处理,如删除含缺失值的观测、均值插补或多重插补等。
122 数据的准确性对数据进行仔细检查,确保其没有录入错误或异常值。
异常值可能会对假设检验的结果产生较大影响,需要谨慎处理。
123 数据的正态性对于一些基于正态分布假设的检验方法(如 t 检验和方差分析),需要检查数据是否近似服从正态分布。
可以通过绘制直方图、正态概率图或进行正态性检验(如 ShapiroWilk 检验)来判断。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.录入数据。
将组别设为g,可将患者组设为1 ,健康人设为2,血磷值设为x ,如患者组中第一个测量到的血磷值为0.84,则g为1,x为0.84,其他数据均仿此录入,如下图所示。
2.统计分析。
依次选择“Analyze”、“Compare means”、“Independent Samples T Test”。
图2 选择分析工具
3.弹出对话框如下图所示,将x选入Test Variables、g选入Grouping Variable,并单击下方的Define Groups按钮,弹出定义组对话框,默认选项为Use Specified Value,在Group1和Group2框中分别填入1和2,即要对组别变量值为1和2的两个组做t检验,另外Options对话框中可选择置信度和处理缺失值的方法。
图3 选择变量进入右侧的分析列表
SPSS输出的结果和结果说明:
(1)方差齐次检验(Levene 检验)。
F=0.032、P(Sig)=0.860 。
(2)t 检验。
因方差齐次与不齐方法不同,(Equal variances assumed 方差齐次和Equal variances not assumed 方差不齐),结果分两行给出。
由使用者根据方差齐次检验结果来判断。
本例尚不能认为方差不齐,故取方差齐次的结果t= 2.524,df 自由度22, 双侧t 检验概率=0.019 即可认为两组间血磷值有差别。
结果中还给出了两组间差值的均值标准误差和95%置信区间。
