玻尔的氢原子模型
氢原子光谱与玻尔的原子模型PPT课件

2、氢气发光时的光谱
思考与讨论
氢原子光谱有什么特点?
2、氢气发光时的光谱
光谱特点:
1.不连续,只是些亮线组成 2.不同色,每种颜色对应着一种波长 3.不等距,相邻两种光的波长间距不相同
明线光谱:只含有一些不连续的亮线的光谱叫做明线 光谱。明线光谱中的亮线叫谱线,各条谱线对应不同 波长的光。稀薄气体或金属的蒸气的发射光谱是明线 光谱。明线光谱是由游离状态的原子发射的,所以也 叫原子的光谱。实践证明,原子不同,发射的明线光 谱也不同,每种原子只能发出具有本身特征的某些波 长的光,因此明线光谱的谱线也叫原子的特征谱线。
人们早在了解原子内部结构之前就已经观 察到了气体光谱,不过那时候无法解释为什么气 体光谱只有几条互不相连的特定谱线
玻尔的原子模型
五、玻尔的原子结构假说
1913年玻尔提出了自己的原子结构假说
1、围绕原子核运动的电子轨道半 径只能是某些分立的数值,这些 现象叫做轨道量子化;
2、不同的轨道对应着不同的状态, 在这些状态中,尽管电子在做变 速运动,却不辐射能量,因此这 些状态是稳定的;
连续光谱:
连续光谱:连续分布的包含有从红光到紫 光各种色光的光谱叫做连续光谱。炽热 的固体、液体和高压气体的发射光谱是 连续光谱。例如白炽灯丝发出的光、烛 焰、炽热的钢水发出的光都形成连续光 谱。
是否所有物质发的光都是这样的光谱?
观察氢原子的光谱实验:
1.装置:
氢气光谱管
分光镜
高2压~发3k生v器
n 1 n2 n3
n4
电子轨道
E
E
4 3
激 发
E 2 态
E 1 基态
能级
光子的发射和吸收
原子在始、末 两个能级Em和En ( Em>En )间跃 迁时发射光子的 频率可以由下式 决定:
玻尔模型

玻尔模型(Bohr model)玻尔模型是丹麦物理学家尼尔斯·玻尔于1913年提出的关于氢原子结构的模型。
玻尔模型引入量子化的概念,使用经典力学研究原子内电子的运动,很好地解释了氢原子光谱和元素周期表,取得了巨大的成功。
玻尔模型是20世纪初期物理学取得的重要成就,对原子物理学产生了深远的影响。
玻尔模型的提出丹麦物理学家尼尔斯·玻尔(1885—1962)20世纪初期,德国物理学家普朗克为解释黑体辐射现象,提出了量子论,揭开了量子物理学的序幕。
19世纪末,瑞士数学教师巴耳末将氢原子的谱线表示成巴耳末公式,瑞典物理学家里德伯总结出更为普遍的光谱线公式里德伯公式:其中λ为氢原子光谱波长,R为里德伯常数。
然而巴耳末公式和式里德伯公式都是经验公式,人们并不了解它们的物理含义。
1911年,英国物理学家卢瑟福根据1910年进行的α粒子散射实验,提出了原子结构的行星模型。
在这个模型里,电子像太阳系的行星围绕太阳转一样围绕着原子核旋转。
但是根据经典电磁理论,这样的电子会发射出电磁辐射,损失能量,以至瞬间坍缩到原子核里。
这与实际情况不符,卢瑟福无法解释这个矛盾。
1912年,正在英国曼彻斯特大学工作的玻尔将一份被后人称作《卢瑟福备忘录》的论文提纲提交给他的导师卢瑟福。
在这份提纲中,玻尔在行星模型的基础上引入了普朗克的量子概念,认为原子中的电子处在一系列分立的稳态上。
回到丹麦后玻尔急于将这些思想整理成论文,可是进展不大。
1913年2月4日前后的某一天,玻尔的同事汉森拜访他,提到了1885年瑞士数学教师巴耳末的工作以及巴耳末公式,玻尔顿时受到启发。
后来他回忆到“就在我看到巴耳末公式的那一瞬间,突然一切都清楚了,”“就像是七巧板游戏中的最后一块。
”这件事被称为玻尔的“二月转变”。
1913年7月、9月、11月,经由卢瑟福推荐,《哲学杂志》接连刊载了玻尔的三篇论文,标志着玻尔模型正式提出。
这三篇论文成为物理学史上的经典,被称为玻尔模型的“三部曲”。
玻尔氢原子轨道半径公式

玻尔氢原子轨道半径公式
当人们谈到物理学时,常常会提到“玻尔模型”。
玻尔模型是描
述氢原子的轨道结构的一种经典模型。
在这种模型中,氢原子的电子
绕着原子核做匀速圆周运动,形成一系列轨道。
在玻尔模型中,我们
可以利用公式得出氢原子不同轨道的半径。
氢原子轨道半径公式为:
r = n²h²/4π²me²Z
其中,r表示氢原子的轨道半径,n表示主量子数,h表示普朗克
常数,me表示电子的质量,e表示元电荷,Z表示氢原子核的原子序数。
这个公式的意义是,氢原子的轨道半径与主量子数的平方成正比,与普朗克常数的平方、电子质量、原子序数成反比。
换句话说,当主
量子数增加时,氢原子轨道的半径也会增加,但是当普朗克常数、电
子质量或原子序数增加时,氢原子轨道的半径则会减小。
氢原子轨道半径公式有很重要的意义。
它帮助我们理解氢原子的
结构和性质,例如氢原子吸收和辐射特定波长的光线的能力取决于电
子跃迁前后轨道半径的差异。
此外,这个公式也可以用来解释其他元
素的原子结构和化学性质,因为这些元素的原子结构都可以用主量子
数和其他参数来描述。
总之,氢原子轨道半径公式是物理学和化学学科中的重要公式之一。
了解这个公式的意义和应用可以帮助我们更好地理解原子的结构和性质,把它应用到更广泛的领域中。
氢原子光谱和玻尔的原子模型课件-高二物理人教版(2019)选择性必修第三册

3. n=1定态(基态),原子能 量最小,电子轨道半径最小;
4.能级为n 的原子,电子
轨道半径为 rn n2r1
能级越高,电子轨道半径越大
1 2
3
5.原子从高能级向低能级跃迁时_辐__射_光子,
轨道半径_减__小_,库仑力_做__正__功__,电势能_减__小_, 电子动能_增__加___,原子能量_减__小_。
氢原子光谱的其他线系
紫
外 线
莱曼线系
区
1
R
1
12
1 n2
n 2,3,4,
红
外 线
帕邢系
区
1
R
1
32
1 n2
n 4,5,6,
三、经典理论的困难
核外电子绕核运动
辐射电磁波
电子轨道半径连续变小
原子不稳定
原子是稳定的
辐射电磁波频率连续变化
原子光谱是线状谱 —— 分立
经 电子绕核运动将不断 典 向外辐射电磁波,电 理 子损失了能量,其轨 论 道半径不断缩小,最 认 终落在原子核上,而使 为 原子变得不稳定。
实物粒子:电子、质子、中子等 原子能吸收实物粒子的部分动能。
例1 对于基态氢原子,下列说法中正确的是 A.它能吸收10.2 eV的光子 B.它能吸收11 eV的光子 C.它能吸收14 eV的光子 D.它能吸收具有11 eV动能的电子的部分动能
答案:ACD
2.如图所示为氢原子的能级图,若用能量为10.5 eV 的光子去照射一群处于基态的氢原子,则氢原子
答案:D
六、玻尔模型的局限性
玻尔理论成功的解释并预言了氢原子辐射 的电磁波的问题,但是也有它的局限性.
在解决核外电子的运动时 成功引入了量子化的观念
玻尔模型相关公式

玻尔模型相关公式
玻尔模型是描述氢原子及其类似物的一种简化模型。
它基于经典力学和量子力学的原理,给出了氢原子能量量子化的表达式。
其中,最为重要的公式包括:
1. 玻尔半径公式
$r_n=frac{n^2h^2epsilon_0}{pi me^2}$
其中,$r_n$表示第n级能级电子的轨道半径,$h$为普朗克常量,$epsilon_0$为真空介电常量,$m$为电子质量,$e$为元电荷。
2. 能级公式
$E_n=-frac{me^4}{8epsilon_0^2h^2}frac{1}{n^2}$ 其中,$E_n$为第n级能级的能量。
3. 轨道角动量公式
$L=nhbar$
其中,$L$为电子的轨道角动量,$hbar$为约化普朗克常量,$n$为量子数。
4. 能量差公式
$Delta
E=-frac{me^4}{8epsilon_0^2h^2}left(frac{1}{n_f^2}-frac{1}{n _i^2}right)$
其中,$Delta E$表示能级变化所带来的能量差,$n_f$和$n_i$分别表示电子从终态能级$n_f$跃迁到初态能级$n_i$。
以上公式是玻尔模型中比较基础和重要的一些公式,它们被广泛
应用于氢原子及其类似物的研究中。
氢原子光谱和玻尔的原子结构模型

Hale Waihona Puke 内容:无法同时精确测量粒子的位置和动量 提出者:海森堡 意义:否定了经典物理学的确定性和因果关系 对玻尔原子结构模型的影响:解释了原子光谱的离散性
光的波粒二象性:光既具有波动特性又具有粒子特性 德布罗意波长公式:λ=h/p其中λ是波长h是普朗克常数p是动量 光的粒子性:光子是光的基本单位具有能量和动量 光的波动性:光在空间中传播形成电磁波具有频率和波长
受普朗克、爱因斯坦等物理学家的量子理论启发玻尔提出了自己的原子结构模型。
PRT FIVE
对应原理是玻尔原子结构模型的理论基础它认为电子只能在特定的轨道上运动每个轨道对应 一定的能量。 玻尔引入了量子化的概念认为电子只能存在于具有确定能量的稳定状态中这些状态称为定态。
对应原理还指出当电子从一个定态跃迁到另一个定态时会释放或吸收一定频率的光子。
,
汇报人:
CONTENTS
PRT ONE
PRT TWO
发现者:罗伯特·米立根 时间:19世纪末 实验装置:真空管和棱镜 意义:揭示了氢原子光谱的存在和特征
稳定性:氢原子光谱具有高度的稳定性是研究原子结构的重要手段。 连续性:氢原子光谱线覆盖了从长波到短波的连续范围为研究原子能级提供了重要信息。
PRT SIX
1913年玻尔提出了原子结 构模型
模型基于经典力学和量子 化假设
模型成功解释了氢原子光 谱线
模型为后续原子结构研究 奠定了基础
提出假设:玻尔在1913年提出了氢原子光谱的假设奠定了玻尔原子结构模型的基础。
解释实验现象:玻尔的原子结构模型能够解释氢原子光谱的实验现象如巴尔末公式和里德伯公式等。
玻尔的氢原子理论

玻尔的氢原子理论
为此,J.汤姆孙在1904年提出了原子结构的枣糕式模型.该模型认 为,原子可以看作一个球体,原子的正电荷和质量均匀分布在球内, 电子则一颗一颗地镶嵌其中.1909年,J.汤姆孙的学生卢瑟福为了验证 原子结构的枣糕式模型,完成了著名的α粒子散射实验.实验发现α粒 子在轰击金箔时,绝大多数α粒子都穿透金箔,方向也几乎不变,但 是大约有1/8 000的α粒子会发生大角度偏转,即被反弹回来.这样的 实验结果是枣糕式模型根本无法解释的,因为如果说金箔中的金原子 都是枣糕式的结构,那么整个金箔上各点的性质应该近乎均匀,α粒 子轰击上去,要么全部透射过去,要么全部反弹回来,而不可能是一 些穿透过去,一些反弹回来.
玻尔的氢原子理论
二、 原子结构模型
1897年,J.汤姆孙发现了电子.在此之前,原 子被认为是物质结构的最小单元,是不可分的,可 是电子的发现却表明原子中包含带负电的电子.那 么,原子中必然还有带正电的部分,这就说明原子 是可分的,是有内部结构的.执着的科学家就会继 续追问:原子的内部结构是什么样的?简洁的里德 伯光谱公式是不是氢原子内部结构的外在表现?
玻尔的氢原子理论
三、 玻尔的三点基本假设
为了解决原子结构有核模型的稳定性和氢原子光谱的分 立性问题,玻尔提出以下三个假设:
(1)定态假设.原子中的电子绕着原子核做圆周运动, 但是只能沿着一系列特定的轨道运动,而不能够任意转动, 当电子在这些轨道运动时,不向外辐射电磁波,原子系统处 于稳定状态,具有一定的能量.不同的轨道,具有不同的能 量,按照从小到大的顺序记为E1、E2、E3等.
玻尔的氢原子理论
可是这个模型却遭到很多物理学家的质疑.因为按照当时的物 理理论(包括经典力学、经典电磁理论及热力学统计物理),这 样一个模型是根本不可能的,原因有以下两个:
氢原子标准模型

氢原子标准模型
氢原子标准模型是一种描述氢原子结构和行为的理论模型。
这个模型基于量子力学和电磁学原理,能够解释氢原子光谱的线系、能级跃迁以及其他相关现象。
在氢原子标准模型中,氢原子由一个质子和一个电子组成,它们之间通过库仑力相互吸引。
电子在氢原子中绕核运动,其轨道是量子化的,即只能取特定的、离散的轨道半径。
这些轨道半径满足玻尔半径公式,即r_n = n^2 * a_0,其中n 是主量子数,a_0 是玻尔半径,约为0.529 ×10^-10 米。
电子在不同的轨道上运动时,具有不同的能量,这些能量值也是量子化的。
氢原子的能级可以由巴耳末公式来描述,即E_n = -R_H / n^2,其中R_H 是里德伯常量,n 是主量子数。
电子只能在特定的能级之间跃迁,吸收或发射特定波长的光子,这使得氢原子光谱呈现出特定的线系。
除了电子的轨道和能级是量子化的之外,氢原子还具有一些其他的量子化性质,如自旋、磁矩等。
这些性质使得氢原子在磁场中表现出特定的行为,例如塞曼效应等。
总的来说,氢原子标准模型是一种基于量子力学和电磁学原理的理论模型,能够准确描述氢原子的结构和行为,为我们理解原子结构和量子力学提供了重要的基础。
玻尔原子模型解析

玻尔原子模型解析玻尔原子模型是物理学家尼尔斯·玻尔于1913年提出的一个关于原子结构的理论模型。
该模型通过对氢原子的独立研究,揭示了原子的结构和能级分布,为量子力学的发展奠定了基础。
在本文中,我们将对玻尔原子模型进行解析,探讨其基本原理和对原子结构的贡献。
玻尔原子模型的基本原理是以核心为中心的原子结构。
根据该模型,原子由一个中央的带电核心(通常是一个或多个质子)和围绕核心旋转的电子组成。
电子在不同的轨道上运动,每个轨道对应着特定的能级。
这些能级是量子化的,只有特定的能量值才能被电子占据。
当电子不受外界干扰时,它们会在最低能级上稳定地旋转。
如果电子受到光或热等能量的激发,它们将跃迁到更高的能级。
当电子回到低能级时,会释放出光子,从而产生光谱线。
玻尔原子模型的重要性在于它成功地解释了氢原子光谱现象。
原子的光谱是指当原子受到能量激发时,会发射出一系列离散的光线。
玻尔通过研究氢原子的光谱现象,发现了一些规律。
他观察到,氢原子的光谱线只出现在特定的波长位置,并且呈现出一定的序列和间距关系。
根据这些观察结果,玻尔提出了几个重要结论。
首先,玻尔认为电子在轨道上只能存在于特定的能级。
这些能级之间有固定的能量差,电子只能在这些能级间进行跃迁,不会停留在中间位置。
这一观点被称为量子化条件。
玻尔用了一个很著名的公式,即能级差的大小等于普朗克常数和电子频率乘积。
这个公式成功地解释了氢原子的光谱线的波长、频率和能级之间的关系。
其次,玻尔提出了一个量子数概念,即主量子数、角量子数和磁量子数。
主量子数用来描述电子所处的能级,角量子数用来描述电子在轨道上的角动量,磁量子数用来描述电子在轨道上的磁矩。
这些量子数限制了电子的运动状态,使得它们的运动具有一定的规律性。
最后,玻尔原子模型还对玻尔半径进行了描述。
玻尔半径是电子在轨道上运动时与核心之间的平均距离。
根据玻尔半径的计算公式,玻尔提出了一个关于电子运动稳定性的条件,即电子在轨道上运动时所受到的离心力与库伦引力之间达到平衡。
高中物理玻尔氢原子模型

高中物理玻尔氢原子模型玻尔氢原子模型是由丹麦物理学家尼尔斯·玻尔在1913年提出的一种原子模型,它是描述氢原子中电子的位置和能量的理论。
这是一种经典的模型,不考虑量子力学的影响,但它对于许多实验观测提供了相当准确的预测,是量子力学的发展过程中的基础。
氢原子由一个质子和一个电子组成,质子带正电荷,电子带负电荷。
玻尔氢原子模型假设电子在原子的轨道上旋转,并且仅在一些特定的轨道上旋转,这些轨道的能量是确定的。
电子可以从一条轨道跳到另一条轨道上,跳跃的过程中吸收或释放能量。
玻尔氢原子模型通过量子条件和量子化概念将原子轨道和轨道能量的分立现象引入了物理学中。
在玻尔氢原子模型中,每个轨道都有一定的能量,电子在轨道间跳跃时,它所接受或放出的能量是一个确定的值,这个值正好等于两个轨道的能量差。
量子条件是指只有某些特定的轨道能够存在于氢原子中,其他的轨道是不可能存在的。
这些特定的能量被称为能级,它们对应着不同的轨道。
玻尔氢原子模型中能级是通过以下公式计算得出的:E=-\frac{13.6\textrm{ eV}}{n^2}其中E是能级,n是一个整数,称为主量子数。
随着n的增加,能量越来越小。
因此,当电子从一个能级向低能级跳跃时,会放出能量,当它从低能级向高能级跳跃时,会吸收能量。
在一个稳定的氢原子中,电子会停留在最低能级(n=1)上。
当外界施加能量时,电子就可以从这个能级跃迁到更高的能级,这个过程被称为激发(excitation)。
当电子回到最低能级时,它会释放出能量,这个过程被称为放射(emission),通常以光的形式显示出来。
总之,玻尔氢原子模型提供了一种经典的理论框架来解释氢原子的行为。
虽然它并不是完全准确的,但它为量子力学的研究奠定了基础,并帮助科学家更好地理解了原子的结构和性质。
玻尔氢原子模型

二、玻尔氢原子理论
1. 定态假设 原子系统只能存在于一系列不连续的能量状态中 ),在这些状态中 (E1、E2、E3···),在这些状态中,电子绕核作加速运 ),在这些状态中, 动而不辐射能量, 动而不辐射能量,这种状态称这为原子系统的稳定状态 (定态) 定态) 定态条件:轨道角动量量子化 定态条件 轨道角动量量子化 轨道角动量
四、玻尔理论的成功与局限 成功:解释 了H光谱,尔后有人推广到类H原子 成功: 光谱,尔后有人推广到类 原子 光谱 + +2 +3 也获得成功( 电量换成Ze (He .L .B )也获得成功(只要将 电量换成 i e 为原序数)。解释了电子绕核运动的稳定性, (Z为原序数)。解释了电子绕核运动的稳定性,理 为原序数)。解释了电子绕核运动的稳定性 论导出里德堡常数, 论导出里德堡常数,计算得到氢原子的大小和电离能 他的定态跃迁的思想至今仍是正确的。 他的定态跃迁的思想至今仍是正确的。并且它是导致 新理论的跳板。 新理论的跳板。1922年获诺贝尔奖 年获诺贝尔奖 局限:只能解释 及类 原子, 及类H原子 局限:只能解释H及类 原子,也解释不了原子 的精 细结构。 细结构。 原因:它是半经典半量子理论的产物。 原因:它是半经典半量子理论的产物。还应用了经典物理 的轨道和坐标的概念
1
实验取, 实验取,里德堡常数 RH =1.0967758×107 m-1 × 当 m = 2,取 n = 3,4,5,6,…,巴尔末系,在可见光区 , , , , , ,巴尔末系, 1914,紫外区, 赖曼系, m =1, n =2,3,4,… ,紫外区, 赖曼系, , , , , 1908,近红外区,帕邢系, m =3, n =4,5,6,… ,近红外区,帕邢系, , , , , 1922,红外区, 布喇开系,m =4, n =5,6,7,… ,红外区, 布喇开系, , , , , 1924,远红外区,普丰特系, m =5,n =6,7,8,… ,远红外区,普丰特系, , , , ,
17.2 玻尔的氢原子模型
5
大学物 理学
17.2玻尔的氢原子模型
v
行星模型
1 原子能量及频率
e2 v2 Fn F 2 m 4 0 r r 1 e2 Ek 4 0 2r 1
F
e
e2 1 e2 E p EP 4 0 r 4 0 r 1 e2 E Ek EP 4 0 2r v e 1 2r 2 4 0 m r2 1
第17章 量子物理基础
2
大学物 理学
1 1 n 3,4,5 R 2 2 (1)巴尔末线系(可见光): 2 n 1 1 (2)赖曼线系(紫外区): R 2 2 n 2,3,4, 1 n 1 1 (3)帕邢线系(红外区): R 2 2 3 n
(1)极限波长
n , min B 3645 .98A0
(2)频率
1 1 Rc 2 2 2 n c
R 1.09710107 m1
H H
H H
min
---里德伯常量
1 1 R 2 2 (3)波数: 2 n 波数:单位长度上所含完整波的数目 1
hc
2.86ev 1ev 1.6010
量子物理基础
19
J
第17章
20
大学物 理学
17.2玻尔的氢原子模型
(2)En→Ek,n=?,k=?
巴尔末线系 k 2
E1 13.6 Ek 2 3.4eV 2 k 2 E1 En 2 Ek h n
n E1 5 E k h
8
大学物 理学
17.2玻尔的氢原子模型
玻尔模型解析

玻尔模型解析玻尔模型是物理学家尼尔斯·玻尔在1913年提出的,该模型用于解释原子中电子的行为和电子能级的排布。
它被认为是理解和描述原子结构的一种简化模型。
本文将对玻尔模型的原理和应用进行详细解析。
一、玻尔模型的原理玻尔模型基于下面几个假设:1. 氢原子中的电子绕着原子核作圆周运动,类似于一个行星绕着太阳运行。
这种运动被称为量子化运动,即只能存在特定的能量级别。
2. 电子在特定轨道上运动时,不会辐射出能量。
只有当电子从一个轨道跃迁到另一个轨道时,才会吸收或辐射能量。
3. 电子只能处于特定的能级,不会停留在能级之间的状态。
根据这些假设,玻尔模型可以推导出以下几个关键结论:1. 电子的能级与距离原子核的距离相关。
能级越高,距离核心的距离越远。
2. 跃迁时,电子会吸收或放出特定能量的光子。
吸收的光子能量与跃迁前后的能级差相关。
3. 能级越高,电子的能量越大,光子的频率越高。
二、玻尔模型的应用玻尔模型的提出对原子物理学的发展起到了重要作用。
它的应用主要包括以下几个方面:1. 解释氢光谱根据玻尔模型,氢原子的电子处于特定的能级,当电子从一个能级跃迁到另一个能级时,会放出特定频率的光子。
这就解释了氢光谱中的发射线为何是不连续的,每条发射线对应着一个特定的能级差。
2. 描述原子结构玻尔模型将原子中的电子比作行星绕太阳运行,这种图像有助于人们形象地理解原子结构。
通过描述电子的分布和能级,可以更好地解释化学反应和分子的形成。
3. 基础教学工具玻尔模型作为原子结构的简化模型被广泛应用于物理和化学的教学中。
它为学生提供了一个更容易理解的框架,并为他们进一步学习原子结构的复杂理论打下基础。
综上所述,玻尔模型是理解原子结构和描述电子行为的一种简化模型。
它通过将原子中的电子比作绕核的行星,解释了实验中观察到的现象,并为进一步研究原子物理学提供了基础。
尽管玻尔模型在解释较为简单的系统中有效,但随着科学技术的进展,我们已经发现了更为复杂的原子结构和电子行为,这使得玻尔模型在现代物理学中的应用受到了一定的限制。
4.4氢原子光谱和玻尔的原子模型2023-2024学年高二下学期物理人教版(2019)选择性必修三

1.定义:用棱镜或光栅把物质发出的光按波长(频率)
展开,获得波长(频率)和强度分布的记录.
2.分类
目标一 光谱
(1) 连续谱 (2) 线状谱
3.特征谱线:不同原子的发光频率不一样,光谱中的
亮线称为原子的特征谱线.
4.应用:光谱分析
氢原子光谱和
玻尔的原子模
型
目标二 氢原子
光谱的实验规律
目标三 玻尔原子
线状谱: 稀薄气体或金属蒸气发光形成的光谱,一些不连续的明线组成,
(原子光谱)不同元素的线状谱不同
(明线光谱)
谱
定义:连续光谱中某些波长的光被物质吸收后产生的光谱
吸
收
光
谱
产生条件:炽热的白光通过温度较白光低的气体后,再色散形成的
光谱形式:连续光谱背景上出现一些暗线(与特征谱线相对应)
太阳光谱是吸收光谱,有暗线
大量处于n=4能级的氢原子
最多能辐射出几种光? 6种
大量处于n=5能级的氢原子
最多能辐射出几种光? 10种
氢原子能级图
一个氢原子跃迁和一群氢原子跃迁的区别
一个处于n能级的氢原子:n-1种
大量氢原子跃迁:
①确定氢原子所处能级n
nn-1
②辐射多少种不同频率的光子:C2n= 2
③hν=Em-En(m>n),计算各种光子的频率.
吸收能量, 若给它10.1eV的能量,电子能否发生跃迁? 10.4eV呢?
不能
不能
若给它大于13.6eV的能量呢?
原子能吸收,但吸收后原子
发生电离
从高能级向低能级跃迁(自发跃迁)
从低能级向高能级跃迁(受激跃迁)
复合光被原子吸收了特定波长的光子后,连续光谱中这些波长的位置
2[1].3波尔的氢原子理论
![2[1].3波尔的氢原子理论](https://img.taocdn.com/s3/m/fd78334e5acfa1c7aa00cc6d.png)
hcT (n)
13.6
1 n2
(ev),其中hcR
13.6ev
n , En ,而T(n) 氢原子能级图(P 33):
注意:(P 34第2段)因为 E Em En
h
h
在同一谱线系,跃迁间隔 ,谱线 ;随跃迁间隔 ,
E的增加量 , ,到线系限处, 0
二、玻尔假设
玻尔深信量子化这一新概念,特别是当它看到巴 耳末氢光谱公式后,原子内部结构全然呈现在他 的想象中。
玻尔的氢原子理论,可分三部分
1、定态假设
原子内部存在一系列离散的具有确定能量的稳定状态——定态。 电子在这些定态上运动,其量子化的能量守恒,电子不会辐射 能量,这称为玻尔的定态假设
量子化能级的出现是原子稳定性的基石,因为能级之间是禁 区。
(1).原子稳定性问题:卢瑟福将行星模型用于原子世界, 电子绕核运动,电子带-e电荷,轨道加速运动会向外辐射
电磁能,从而: E , r 这样电子将会在10-9s时间内落入
核内,正负电荷中和,原子宣告崩溃(塌缩)。但现实世界 原子是稳定的。
(2). 原子线状光谱问题:按经典电动力学,原子发光的频率= 电子轨道运动的频率,r连续减小,f连续增大,原子发出连续光 谱。但事实是:原子光谱是分立线状光谱
2e2 1 称精细结构常数 4 0hc 137
对氢Z 1,其可能半径r a1,4a1,9a1,...。
2.氢原子系统的定态能量为
1 Ze2
将
En rn 带入
2
4 rn
rn
4 0h2 4 2mee2
n2 Z
a1
n2 Z
波尔氢原子模型的三个基本假设

玻尔氢原子理论的三条假说N.玻尔首创的第一个将量子概念应用于原子现象的理论。
1911年E.卢瑟福提出原子核式模型,这一模型与经典物理理论之间存在着尖锐矛盾,原子将不断辐射能量而不可能稳定存在;原子发射连续谱,而不是实际上的离散谱线。
玻尔着眼于原子的稳定性,吸取了M.普朗克、A.爱因斯坦的量子概念,于1913年考虑氢原子中电子圆形轨道运动,提出原子结构的玻尔理论[1]。
理论的三条基本假设是:①定态假设:原子只能处于一系列不连续的能量的状态中,在这些状态中原子是稳定的,这些状态叫定态。
原子的不同能量状态跟电子沿不同的圆形轨道绕核运动相对应,原子的定态是不连续的,因此电子的可能轨道的分布也是不连续的,电子在这些可能的轨道上的运动是一种驻波形式的振动。
②跃迁假设:原子系统从一个定态过渡到另一个定态,伴随着光辐射量子的发射和吸收。
辐射或吸收的光子的能量由这两种定态的能量差来决定,即hν=|E初-E末|③轨道量子化:电子绕核运动,其轨道半径不是任意的,只有电子在轨道上的角动量满足下列条件的轨道才是可能的:mvr=nh/(2π)(n=1,2,3…)式中的n是正整数,称为量子数。
玻尔理论在氢原子中的应用⑴氢原子核外电子轨道的半径— 1 —设电子处于第n条轨道,轨道半径为(rn),根据玻尔理论的轨道量子化得m(vn)(rn)=mvr=nh/(2π)(n=1,2,3…)①电子绕核作圆周运动时,由电子和原子核之间的库仑力来提供向心力,所以有m(vn)^2/(rn)=1/(4πε0)*[e^2/(rn)^2]②由①②式可得(rn)=ε0h^2*n^2/(πme^2)(n=1,2,3…)当n=1时,第一条轨道半径为r1=ε0h^2/(πme^2)=5.3*10^-11(m),其他可能的轨道半径为(rn)=r1,4r1,9r1,25r1…⑵氢原子的能级当电子在第n条轨道上运动时,原子系统的总能量E叫做第n 条轨道的能级,其数值等于电子绕核转动时的动能和电子与原子的电势能的代数和En=1/2*m*(vn)^2-e^2/(4πε0(rn))③由②式得1/2*m*(vn)^2=e^2/(8πε0(rn))④将④式代入③式得En=-me^4/(8(ε0)^2h^2n^2)⑤这就是氢原子的能级公式当n=1时,第一条轨道的能级为E1==-me^4/(8(ε0)^2h^2)=-13.6eV.其他可能轨道的能级为En=E1/n^2=-13.6/n^2(eV)(n=2,3,4…)由轨道半径的表达式可以看出,量子数n越大,轨道的半径越大,— 2 —能级越高.n=1时能级最低,这时原子所处的状态称为基态,n=2,3,4,5…时原子所处的状态称为激发态.⑶玻尔理论对氢光谱的解释由玻尔理论可知,氢原子中的电子从较高能级(设其量子数为n)向较低能级(设其量子数为m)跃迁时,它向外辐射的光子能量为hν=En-Em=-me^4/(8(ε0)^2h^2)(1/n^2-1/m^2)由于c=λν,上式可化为1/λ=me^4/(8(ε0)^2h^2)(1/m^2-1/n^2)将上式和里德伯公式作比较得R=me^4/(8(ε0)^2h^3c)=1.097373*10^7m^(-1)这个数据和实验所得的数据1.0967758*10^7m^(-1)基本一致,因此用玻尔理论能较好的解释氢原子的光谱规律,包括氢原子的各种谱线系.例如:赖曼系、巴尔末系、帕邢系、布喇开系等的规律。
玻尔原子模型

玻尔原子模型玻尔原子模型是由丹麦物理学家尼尔斯·玻尔在1913年提出的一种描述原子结构的模型。
该模型通过量子力学的观点解释了氢原子的光谱现象,为后续的量子力学理论奠定了基础。
本文将介绍玻尔原子模型的发展背景、基本原理以及其对于原子结构的重要影响。
一、发展背景在20世纪初,对原子结构的认识相对模糊。
传统的理论无法解释氢原子光谱发射线的不连续性。
为了解决这个问题,玻尔提出了他独特的原子模型。
二、玻尔原子模型的基本原理玻尔原子模型在经典物理学的基础上引入了量子化概念,通过以下几点理论来解释氢原子光谱现象:1. 原子中的电子绕着原子核旋转,但只能存在于特定的能级上。
2. 电子在不同能级之间跃迁时会吸收或者发射特定频率的光子。
3. 电子旋转半径与能级高低有关,能级越高,电子离原子核越远。
三、玻尔原子模型对原子结构的影响玻尔原子模型的提出对后续物理学的发展产生了深远的影响:1. 玻尔原子模型的量子化概念为后来的量子力学理论提供了基础。
量子力学为解释原子结构和性质提供了更为精确的数学模型。
2. 玻尔原子模型通过电子跃迁释放或吸收特定频率的光子解释了原子光谱,为光谱分析提供了理论基础。
3. 玻尔原子模型的影响延伸至其他粒子和物理体系。
类似的量子化概念被应用于核物理和粒子物理领域。
四、玻尔原子模型的局限性尽管玻尔原子模型是对当时来说非常重大的突破,但它也存在一些局限性:1. 该模型仅适用于氢原子,无法准确描述其他原子的光谱现象。
2. 玻尔原子模型无法解释电子为什么会围绕核旋转,并且为何只能在特定轨道上存在。
3. 该模型无法解释复杂原子的结构和性质,对于更高能级的电子行为无法给出详细描述。
五、总结玻尔原子模型是描述氢原子结构的突破性模型,通过量子化概念和电子跃迁现象解释了氢原子光谱的不连续性。
该模型对后续的量子力学理论和光谱分析学产生了重要影响,为解释原子结构和探索微观世界奠定了基础。
尽管存在局限性,玻尔原子模型对于现代物理学的发展仍然具有不可低估的价值。
《氢原子光谱和玻尔的原子模型》 知识清单

《氢原子光谱和玻尔的原子模型》知识清单一、氢原子光谱氢原子光谱是研究原子结构的重要途径之一。
它指的是氢原子在不同能级之间跃迁时所发射或吸收的光的频率和波长所形成的光谱。
氢原子光谱的特点十分显著。
首先,它是线状光谱,不是连续的。
这意味着氢原子只能发出特定频率的光,而不是在所有频率上都有发射。
氢原子光谱中的谱线可以分为几个系列,其中较为重要的有莱曼系、巴尔末系、帕邢系等。
莱曼系位于紫外光区域,巴尔末系在可见光区域,而帕邢系则在红外光区域。
这些谱线的位置和频率不是随机的,而是遵循一定的规律。
通过对氢原子光谱的研究,科学家们发现了这些规律,并试图寻找背后的理论解释。
二、玻尔的原子模型在解释氢原子光谱的众多理论中,玻尔的原子模型具有重要的地位。
玻尔提出,原子中的电子并不是在任意轨道上运动,而是只能在一些特定的、分立的轨道上运动。
这些轨道被称为定态轨道。
在定态轨道上,电子不会辐射能量。
当电子从一个能量较高的定态轨道跃迁到一个能量较低的定态轨道时,就会以光子的形式放出能量,其能量等于两个轨道的能量差。
反之,当电子吸收一定能量的光子时,会从能量较低的定态轨道跃迁到能量较高的定态轨道。
玻尔还引入了三个重要的假设。
第一,电子绕核运动的轨道半径是量子化的,即只能取某些特定的值。
第二,电子在不同轨道上运动时具有不同的能量,这些能量也是量子化的。
第三,电子在定态轨道上运动时,其角动量是量子化的。
玻尔原子模型成功地解释了氢原子光谱的规律。
例如,它能够解释为什么氢原子光谱是线状的,以及不同谱线系列出现的位置和频率。
然而,玻尔的原子模型也存在一定的局限性。
它虽然能够很好地解释氢原子的光谱现象,但对于多电子原子的光谱以及其他一些更复杂的原子现象,其解释能力就显得不足。
三、氢原子光谱与玻尔原子模型的关系氢原子光谱的实验观测结果为玻尔原子模型的建立提供了重要的依据。
正是由于氢原子光谱呈现出的规律性和特殊性,促使玻尔思考并提出了他的原子模型。
氢原子光谱和波尔的原子模型ppt课件
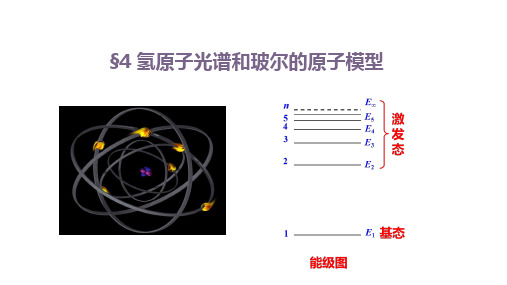
Na原子的发射光谱(明线)
H原子的吸收光谱(暗线)
H原子的发射光谱(明线)
吸收光谱和线状谱(发射光谱)的关系:
各种原子的吸收光谱中的每一条暗线都跟该种原子的发射光谱(线状光谱)中的
一条明线相对应。
3.光谱分析
既然每种原子都有自己的特征谱线,我们就可以利用它来鉴别物质和确定物质的组
成成分。这种方法称为光谱分析。
4.由于不同的原子具有不同的结构,能级各不
相同,因此辐射(或吸收)的光子频率也不相
同。这就是不同元素的原子具有不同的特征谱
线的原因。
六、玻尔理论的局限性
1.玻尔理论的不足之处在于保留了
经典粒子的观念,仍然把电子的运
动看作经典力学描述下的轨道运动。
2.玻尔理论成功地解释了氢原子光
谱的实验规律。但对于稍微复杂一
1
E1
激
发
态
h E n E m
基态
原子从低能级向高能级跃迁(电子从低轨道向高轨道跃迁): 吸收光子,原子能量增大
电子从低轨道向高轨道跃迁,电子克服库仑引力做
功,电势能增大,原子的能量增加,要吸收能量。
吸收光子能量:
h E n E m
原子从高能级向低能级跃迁(电子从高轨道向低轨道跃迁): 辐射光子,原子能量减小
优点:灵敏度高
样本中一种元素的含量达到10-13kg时就可
以被检测到。
利用白炽灯的光谱,能否检测出灯丝的成分?
不能,白炽灯的光谱是连续谱,不是原子
的特征谱线,因而无法检测出灯丝的成分
原子的特征光谱
二、氢原子光谱(发射光谱)的实验规律
氢原子是最简单的原子,其光谱也最简单。
n=6
n=5
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实际: 线状谱
8
玻 尔 (Bohr . Niels 1885—1962)
丹麦理论物理学家,现代 物理学的创始人之一. 在卢瑟福原子有核模型基础上 提出了关于原子稳定性和量子 跃迁理论的三条假设,从而完 满地解释了氢原子光谱的规律.
经典力学:
e2
4π 0rn2
m vn2 rn
+ rn
量子化条件:
mvn rn
n
h 2π
rn
0h2
π me 2
n2
r1n2 (n
1,2,3,
)
13
rn
0h2
π me 2
n2
r1n2
(n 1,2,3, )
n 1 , 玻尔半径
r1
0h2
π me 2
5.29 10 11
m
即轨道半径是量子化的
(2) 能量
E 1 e2
4 0 2r
e 2
1
4 0mr2
(1)稳定与不稳定的矛盾
v e
F
理论: 由于辐射,原子总能量减小
, E 电子r 将 逐渐的接近原子 核而后相遇,原子不稳定.
e
e
实际: 1014 r 1010
7
稳定
(2)连续与不连续的矛盾
e 2
z
4 0mr2
按经典理论该频率就是氢原子辐射的光的频率
1 n2
h Ei E f
1
c
me4 1
802h3c ( n2f
1 ni2 ) ,
ni n f
R me4
8
2 0
h3c
1.097107 m1
(里德伯常量)
R( 1 1 )
n
2 f
ni2
16
与实验规律一致
氢原子能级跃迁与光谱图
n= n=5 n=4
n=3
帕
布 拉
0 -0.54 eV
巴 耳 末
n 第 轨道电子总能量:
En
1 2
mvn2
e2
4π 0rn
14
En
me4
8 02 h 2
1 n2
E1 n2
基态能量
(n 1)
E1
me4
8
2 0
h
2
13.6 eV (基态电离能)
激发态能量
(n 1) En E1 n2
即能量是量子化的
15
3 玻尔理论对氢原子光谱的解释
En
me4
8 02 h 2
6562.8A0 4861.3A0 4340.5A0 4101.7A0 3645.98A0
(1)极限波长
n , min B 3645 .98 A0
(2)频率
c
Rc
1 22
1 n2
H
H H H
m in
R 1.09710107 m1 ---里德伯常量
(3)波数:
1
R
1 22
1 n2
i
n f 1,2,3,4, , ni nf 1,nf 2,nf 3,
一个确定的nf对应一个线系
一个确定的ni对应一个线系的一条谱线
3 ni : 对应线系限,波长最短,频率最高(电离)
6562.8A0 4861.3A0 4340.5A0 4101.7A0 3645.98A0
(2)线状谱(非连续谱)
与定态相应的能量分别为 E1, E2… , E1 < E2< E3
11
E1 + E3
(2) 频率条件
h Ei E f
(3)量子化条件
吸 Ei
发
收
射
Ef
电子作圆周运动的角动量
满足子化如下条件:
L mvr n h 2π
E1 + E3
n 1,2,3,
主量子数
12
2 氢原子轨道半径和能量的计算 (1)轨道半径
1922年玻尔获诺贝尔物理学奖.
9
二 玻尔的氢原子理论 1913年玻尔在卢瑟福的原子结构模型的基础上,将量子化概念应用于原子
系统,提出三条假设:
(1)定态假设 (2)频率条件 (3)量子化条件
10
1 玻尔的氢原子理论
(1)定态假设
电子在原子中可以在一些特定的、分离的圆轨道上运动而不辐射电磁波, 这时,原子处于稳定状态,简称定态.
邢 系
开 系
-0.85 eV
-1.51 eV
系
n=2
莱 曼 系
-3.40 eV
n=1
-13.6 eV
17
三 氢原子玻尔理论的意义和困难 1 意义
(1)正确地指出原子能级的存在(原子能量量子化).
(2)正确地指出定态和角动量量子化的概念. (3)正确地解释了氢原子及类氢离子光谱规律.
18
2 缺陷 (1)无法解释比氢原子更复杂的原子. (2)微观粒子的运动视为有确定的轨道. (3)对谱线的强度、宽度、偏振等一系列问题无法处理.
(4)原因:半经典半量子理论,既把微观粒子看成是遵守经典力学的质点,同 时,又赋予它们量子化的特征.
L
mvn rn
n
h 2π
19
例1. 氢原子光谱巴尔末线系中,有一条谱线波长为4340
A0,求:
(1)与这条谱线相对应的光子能量为多少电子伏特?
(2)En→Ek,n=?,k=? (3)最高能级为E5的大量氢原子,最多可发射几个线系,共几条谱线
波数:单位长度上所含完整波的数目
2
2. 氢原子光谱实验规律
(1)巴尔末线系(可见光):
R
1 22
1 n2
n 3,4,5
(2)赖曼线系(紫外区):
R
1 12
1 n2
n 2,3,4,
(3)帕邢线系(红外区):
R
1 32
1 n2
n 4,5,6
总结:
(1)
波数
1
R( 1 n2
f
1) n2
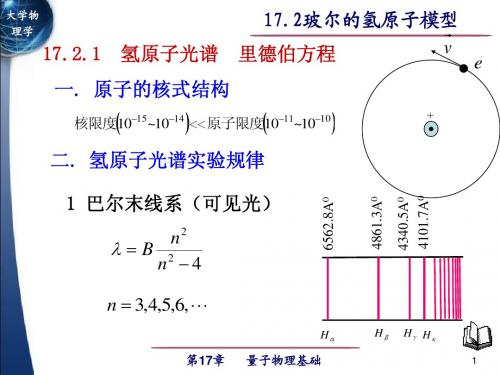
17.2.1 氢原子光谱 里德伯方程 一. 原子的核式结构
核限度1015~1014 原子限度1011~1010
二. 氢原子光谱实验规律
1 巴尔末线系(可见光) B n2
n2 4
n 3,4,5,6,
H
1
6562.8A0 4861.3A0 4340.5A0 4101.7A0
v e
H H H
(白)
1 R( 1 1 )
n n 2
2
f
i
原因:n f , ni只能取整数
(3)其他原子一样
H
H H H
m in
碱金属原子光谱:
R
nf
1
2
ni
1
2
式中n f , ni仍只能取整数, 、为两个常数
说明了原子内部存在固有的规律性
4
17.2.3 玻尔的氢原子理论 一 经典有核模型的困难 根据经典电磁理论,电子绕核作匀速圆周运动,作加速运动的电子 将不断向外辐射电磁波。所以用经典理论可以解释氢原子为什么能辐射电 磁波。
但是能否解释氢原子光谱的实验规律呢?比如氢原子光谱的谱线波长 所满足的规律?
5
1 原子能量及频率
Fn
F
1
4 0
e2 r2
m v2 r
行星模型
v e
F
Ek
1
4 0
e2 2r
1 e2
1 e2
Ep EP 4 0
r
4 0
r
E
Ek
EP
1
4 0
e2 2r
v e 2r 2
1
4 0mr2
6
2 经典理论困难
解: 1h hc 2.86ev 1ev 1.60 1019 J
20
(2)En→Ek,n=?,k=?
