湖南长沙四大名校初升高数学测试卷
长沙市高中四大名校自主招生考试试卷附答案(中考理科数学竞赛必备)

长郡中学20XX年高一实验班选拔考试试卷注意:(1) 试卷共有三大题16小题,满分120分,考试时间80分钟.(2) 请把解答写在答题卷的对应题次上, 做在试题卷上无效.一、选择题(本题有6小题,每小题5分,共30分)下面每小题给出的四个选项中,只有一个是正确的,请把正确选项前的字母填在答题卷中相应的格子)(A) 直线y = –x上(B) 抛物线y =x2上(C) 直线y = x上(D) 双曲线xy = 1上2.以等速度行驶的城际列车,若将速度提高25%,则相同距离的行车时间可节省k%,那么k的值是( )(A) 35 (B) 30 (C) 25 (D) 203.若-1<a<0,则a,a,a,(A)(C) 1a1a31a一定是( ) 最小,a3最大(B) 最小,a最大(D) a最小,a 最大 1a最小,a最大4.如图,将△ADE绕正方形ABCD的顶点A顺时针旋转90°,得△ABF,连结EF交AB于H,则下列结论错误的是()(A) AE⊥AF (B)EF:AF =2:1(C) AF= FH²FE (D)FB :FC = HB :EC5.在△ABC中,点D,E分别在AB,AC上,且CD与BE相交于点F,已知△BDF的面积为10,△BCF的面积为20,△CEF的面积为16,则四边形区域ADFE的面积等于()(A) 22 (B) 24 (D) 36 (D)446.某医院)(A)30 (B)35 (C)56 (D)448二、填空题(本题有6个小题,每小题5分,共30分)7.若4sinA – 4sinAcosA + cosA = 0, 则tanA. 222 第4题146424296.doc 第1页8.在某海防观测站的正东方向12海浬处有A、B两艘船相会之后,A船以每小时12海浬的速度往南航行,B船则以每小时3海浬的速度向北漂流. 则经过小时后,观测站及A、B两船恰成一个直角三角形.9.如右图,在坐标平面上,沿着两条坐标轴摆着三个相同的长方形,其长、宽分别为4、2,则通过A,B,C三点的拋物线对应的函数关系式是.10.桌面上有大小两颗球,相互靠在一起。
长沙四大名校招生数学试卷

精心整理数学试卷 1一.填空题:(每题 4 分,此题满分 32 分)1.若 ab>0,则ab ab的值等于 ____________.abab2.已知实数 a ,b 知足 a 2+4b 2-a+4b+ 5=0, 那么 -ab 的平方根是43.等腰三角形一腰上的中线把这个三角形的周长分红12cm 和 21cm 两部分 ,则这个等腰三角形的底边长是 _______________.4.计算: 15 (1 1 )235.已知实数 x 、y 知足 x 2+ 2 y = 3 ,y 2+ 2 x = 3 ,且 x ≠ y ,则: x + y的值是yx6.小华有若干个苹果向若干只篮子里散发,若每只篮子分 4 个苹果,还剩 20 个未分完;若每只 篮子里分放 8 个苹果,则还有一只篮子没有放够,那么小华本来共有苹果个 7.若 y =— 2x - 3+ 4x 13 ,则 y 的最大值是8.已知对于 的方程:(22 3) 3( 2)4有独一解,则 m 的取值范围x mm x xm为话二.选择题:(每题 4分,此题满分 32分)电 别9.已知 a =355,b = 444,c =533, 则有 ()姓名 A .a <b <cB .c < b < aC .c <a <bD . a < c < b姓 10. 假如方程 x 2校 px 1 0 p0 的两根之差是 1,那么 p 的值为()学(A) 2(B) 4(C) 3(D) 511. 假如不等式组9 x a 0的整数解仅为 1, 2, 3,那么合适这个不等式组的整数8x b 0数对( a 、b )共有()(A) 17 个(B) 64 个(C) 72 个(D) 81 个12. 若正整数 x,y 知足 x 2 y 2 64 , 则这样的正整数对 (x,y) A1B2C3D4SAPB2 13. 如图 ,P 是 □ABCD 内的一点 ( 不在线段 BD 上),, 则SABCD51 13 3(A) (B)(C)10(D)510514. 每面标有 1 至 6 点的三颗骰子堆成一串,如右图所示, 此中可见精心整理a 、b 的有序的个数是 ()SCPD()SABCD七个面,而精心整理十一个面是看不到的 ( 反面、底面之间的面 ) ,试问看不见的面其点数总和是 () (A)37(B)38(C)39 (D)4115. 方程 7x 2(k13) xk 2 k20 (k是实数 ) 有两个实根 、,且0<< , <1 1<2,那么 k 的取值范围是 ()(A )3<k <4;(B )- 2<k <- 1; (C )3<k <4 或- 2<k <- 1 ( D )无解。
湖南长沙四大高校初升高数学测试卷

湖南长沙四大高校初升高数学测试卷一、选择题(共10题,每题2分,共20分)1. 若函数 f(x) = x^2 - 3x + 2,则 f(1) 的值为()。
- A. -2- B. 0- C. 2- D. 42. 已知等差数列 {an} 的通项公式为 an = 2n - 1,求该数列的第10 项的值为()。
- A. 10- B. 12- C. 18- D. 193. 在等差数列 {bn} 中,已知 b1 = 2,d = 3,若 b5 = 14,则该数列的公差 d 为()。
- A. 2- B. 3- C. 4- D. 54. 若函数 g(x) = 3x^2 - 4x + 1,则 g(2) 的值为()。
- A. 8- B. 9- C. 10- D. 115. 若函数 h(x) = |x| + 2,则 h(-3) 的值为()。
- A. 1- B. 2- C. 3- D. 46. 在等比数列 {cn} 中,已知 c1 = 2,q = 3,若 c4 = 162,则该数列的公比 q 为()。
- A. 2- B. 3- C. 4- D. 57. 若函数 f(x) = 2x^2 + 3x + 1,则 f(-1) 的值为()。
- A. -8- B. -3- C. 0- D. 28. 已知函数 g(x) = -x^2 + 4x - 3,则 g(2) 的值为()。
- A. -5- B. -3- C. 1- D. 59. 若函数 h(x) = x^3 + 2x^2 - x + 1,则 h(0) 的值为()。
- A. -1- B. 0- C. 1- D. 210. 若函数 f(x) = x^2 + 4x + 4,则 f(-2) 的值为()。
- A. 0- B. 2- C. 4- D. 8二、填空题(共5题,每题4分,共20分)1. 若 (3x^2 - 5x + 2) ÷ (x - 2) = 3x - 1,则 x = __。
长沙四大名校初中招生真题试卷—数学(10)

长沙四大名校初中招生真题试卷—数学(10)时量:90分钟满分:100分 一. 计算(每小题3分,共24分) 1. =⨯2525243______________________ 2. =⨯-+60)6712743(3. =⨯+⨯⨯399973125888.04. =÷-⨯+⨯4.0155.009.075.3851875.3 5.=-⨯⨯+333456123122456123 6.=+÷⨯)15019123.0()5625.01.0( 7.=+++30119201171211561138.=÷⨯÷001.001.01.01二、填空题(每小题3分,共45分)9.有1、2、3、4、5、6数字卡片各一张,每次取两张组成一个两位数,可以组成__________个偶数。
10.+⨯+1232123…+123123⨯的和除以7的余数是11. 分数中125,1912,2310,74,2215中,最小的分数与最大的分数的最简整数比是_______________12.为迎接五城运动会,某校设计一个正方形与一个圆形的花坛种花,它们的周长相等,则这个正方形花坛的面积是圆形的花坛的面积是圆形的花坛面积的百分之几?(14.3=π)答13.价格为40元的某种商品的税额一般在%5.6和%6之间,这两种税额差是 元(税额指:缴纳的税款)14.观察等式:22333223323636)321(321,39)21(21,111==++=++==+=+==;请计算 =+++++333333654321 。
共卖出______________双拖鞋。
16.有一串数,前面两个数分别是1,2003,从第3个数开始,每个数都是前2个数的差(以大数减小数),则这串数的第205个数是________________________.17.“八一建军节”那天,某中队少先队员以每小时4千米的速度从学校往相距17千米的舟桥部队去慰问,出发0.5小时后,战士们闻讯前往迎接,每小时比少先队员快2千米,再过几小时他们在途中相遇?答__ _____________小时。
长沙四大名校高一入学考试数学卷

长郡中学高新入学试卷(十二)一、选择题(每题5分,共30分)1、若x< -2,则y=11x-+等于()A 2+XB -2—XC XD –X2、在同一直角坐标系中,函数kyx=(k≠0)与y=kx+k(k≠0)的图像大致是()3、一列“动车组”高速列车和一列普通列车的车身长分别是80米与100米,它们相向行驶在平行的轨道上,若坐在高速列车上的旅客看见普通列车驶过窗口的时间是5秒,则坐在普通列车上的旅客看见高速列车驶过窗口的时间是()A 7.5B 6C 5D 44、从分别写有数字1,2,3,4,5的5张卡片中任意取出两张,把第一张卡片上的数字作为十位数字,第二张卡片上的数字作为个位数字,组成一个两位数,则所组成的数是3的倍数的概率是()A 15B310C25D125、如图所示,在直角梯形ABCD中,AB CD, ∠B=90°,动点p从B出发,沿梯形的边B—C---D—A运动,设点p运动的路程为x,ABP的面积为y,把y看做x的函数,函数图像如图2所示,则ABC的面积为()A 10B 16C 18D 326、设抛物线y=x2+kx+4与x轴有两个不同的交点(x1,0),(x2,0),则下列结论中,一定成立的是()A X12+X22=17B X12+X22=8C X12+X22 <17D X12+X22>8二、填空题(每题6分,共36分)7、在直径为4cm的O中,长度为2 的弦BC所对的圆周角的度数为_________8、若a,b为实数,满足1111a ba b+-=-+,则(1+a+b)(1—a--b)的值是__________9、将一张分别为a,b(a>b)的矩形纸片ABCD折叠,使点C与点A重合,则折痕的长为________10、已知ABC中,AB=AC=4 ,高AD=4,则ABC的外接圆半径是__________11、已知实数X,Y满足x2—3x+4y=7,则3x+4y的最大值为__________12、观察图形,用S i表示第i个三角形的面积,有;;,…,若S1+S2+S3+…+S n>10,则n的最小值为( ).三、解答题(13、14题各11分,15题12分)13、已知一次函数y=ax+b的图像经过点A)B (-1求a2+b2+c2﹣ab﹣ac﹣bc的值14、某农机租凭公司共有50台收割机,其中甲型20台、乙型30台,现将这50台联合收割机派往A,B两地区收割水稻,其中30台派往A地区,20台派往B地区,两地区与该农机公司商定的每天租凭价格如下表:15、如图,已知抛物线y= --12x2+x+4交x轴的正半轴于点A,交y轴于点B。
长沙市高级中学四大名校自主招生考试试卷附规范标准答案(中考,理科数学竞赛必备)

长郡中学2008年高一实验班选拔考试试卷注意:(1) 试卷共有三大题16小题,满分120分,考试时间80分钟. (2) 请把解答写在答题卷的对应题次上, 做在试题卷上无效.一、 选择题(本题有6小题,每小题5分,共30分)下面每小题给出的四个选项中,只有一个是正确的,请把正确选项前的字母填在答题卷中相应的格子内.1.在直角坐标系中,若一点的横坐标与纵坐标互为相反数,则该点一定不在( ) (A) 直线y = –x 上 (B) 抛物线 y =2x 上 (C) 直线y = x 上 (D) 双曲线xy = 1上2.以等速度行驶的城际列车,若将速度提高25%,则相同距离的行车时间可节省k%,那么k 的值是 ( )(A) 35 (B) 30 (C) 25 (D) 20 3.若-1<a <0,则aa a a 1,,,33一定是 ( ) (A) a1最小,3a 最大 (B) 3a 最小,a 最大(C)a 1最小,a 最大 (D) a1最小, 3a 最大4.如图,将△ADE 绕正方形ABCD 的顶点A 顺时针旋转90°,得△ABF ,连结EF 交AB 于H ,则下列结论错误的是( )(A) AE ⊥AF (B )EF :AF =2:1 (C) AF 2 = FH ·FE(D )FB :FC = HB :EC5.在△ABC 中,点D ,E 分别在AB ,AC 上,且CD 与BE 相交于点F ,已知△BDF 的面积为10,△BCF 的面积为20,△CEF 的面积为16,则四边形区域ADFE 的面积等于( ) (A) 22 (B) 24 (D) 36 (D)446.某医院内科病房有护士15人,每2人一班,轮流值班,每8小时换班一次,某两人同值一班后,到下次两人再同班,最长需要的天数是( ) (A )30 (B )35 (C )56 (D ) 448 二、填空题(本题有6个小题,每小题5分,共30分)7.若4sin 2A – 4sinAcosA + cos 2A = 0, 则tanA = ___ ___ .第4题8.在某海防观测站的正东方向12海浬处有A 、B 两艘船相会之后,A 船以每小时12海浬的速度往南航行,B 船则以每小时3海浬的速度向北漂流. 则经过 小时后,观测站及A 、B 两船恰成一个直角三角形.9.如右图,在坐标平面上,沿着两条坐标轴摆着三个相同的长方形,其长、宽分别为4、2,则通过A,B,C 三点的拋物线对应的函数关系式是 .10.桌面上有大小两颗球,相互靠在一起。
长沙四大名校招生数学试卷-精选.pdf

( 2)抛物线的对称轴与 x 轴交于点 C,在( 1)的条件下试判断是否存在 m 的值,使经过 点 C 及抛物线与 x 轴一个交点的⊙ M与 y 轴正半轴相切于点 D,且⊙ M被 x 轴截得的劣弧
若每只篮子里分放 8 个苹果,则还有一只篮子没有放够,那么小华原来共有苹果
别
姓
个
7.若 y=— 2x- 3+ 4 x 13 ,则 y 的最大值是
8.已知关于 x的方程:( m2 2m 3) x 3( x 2) m 4 有唯一解, 则 m的取值范围
名
姓
为
二.选择题: (每小题 4分,本题满分 32分)
BC = 5, AB = 1 ,把线段 CD 绕点 D 逆时针旋转 90 °到 DE 位 A
校 学
置,连结 AE ,则 AE=________________..
二、选择题 (本大题共 8 题,每题 4 分,共 32 分)
B
E D
C
9、设 x 为正整数,若 x 1 是完全平方数,则它前面的一个完全平方数是(
的整数解仅为 1,2,3,那么适合这个不等式组的整数
8x b 0
的有序数对( a、b)共有(
)
(A) 17 个 (B) 64 个 (C) 72 个
(D) 81 个
12. 若正整数 x,y 满足 x2 y 2 64 , 则这样的正整数对 (x,y)
的个数是 ( )
A1 B2
C3
D4
13. 如图 ,P 是 □ABCD内的一点 ( 不在线段 BD上 ),
长沙四大名校初中招生真题试卷—数学(7)

博源教育长沙四大名校初中招生真题试卷—数学(7)一、选择题(每题 3 分,共 30 分)1、一个三角形,假如它的两个内角的度数之和,等于第三个内角的度数,那么这个三角形是()A 、锐角三角形B 、直角三角形C、钝角三角形D、没法确立2、 79× 99+79=79 ×( 99+1 ) =79× 100=7900 这是依据乘法()进行简易运算的。
A 、分派律B 、互换律C、联合D、分派律和联合律3、钟面上 5 时,时针和分针成()度数。
A、50B、100C、150D、 1204、盒内有包装同样的巧克力糖 5 颗,水果糖 3 颗,奶糖 2 颗,摸出奶糖的可能是()2 3 1 2A 、B 、C、D、5 5 2 35、一个平行四边形与一个三角形等底等高,平行四边形与三角形的面积之和为36 cm2,那么三角形的面积是 ( )A 、 18 cm2B 、 24cm2 C、6 cm2 D、 12 cm26、一个正方形的边长为奇数,它的周长定是(),面积必定是()A 、奇数B 、偶数C、质数D、奇数且为质数7、要使x 6是分母为15 的最简真分数,那么 x 可取的整数共有 ( )个。
15A 、 2B 、 3 C、4 D、 58、某种细菌在培育过程中,细菌每半小时分裂一次(由一个分裂成二个),经过两小时,这种细菌由 1 个分裂成()A、16 个B、8 个C、4 个D、32 个9、某品牌的电脑降价30% 后,每台售价为 a 元,则该品牌电脑每台原价应为()A 、 0.7aB 、 0.3a C、a/0.3 D、 a/0.710、一游客携带了 30 千克行李乘飞机,按民航规定,游客最多可免费携带20 千克行李,超重部分每千克按飞机票价的 1.5% 购置行李票;现该游客购置了120 元行李票,则它的飞机票价应是()二、填空题(每题 3 分,共 30 分)11、将 2 5 ,14, 2 1 , 8和 2 这五个数按从小到大的次序摆列为。
长沙四大名校初升高招生考试数学真题卷

数学测试题A 一、 填空题(共10题,每小题5分,共计50分)11223-的结果是_______。
2、方程 324x x +-=的解为_______。
3、已知正整数a,b ,c 满足a<b <,ab+ac+bc=abc,则abc=_______。
4、若 24213,1x x x x x +==++则_______。
5、若 222121,23y z x x y z +--==++则的最小值为_______。
6已知x 1,x 2,……x 40都是正整数,且22212401240...58,.....,,+x x x x x x A B A B +++=+++=若最大值为最小值为则_______7、20,,x x px q p q pq ++==若关于的一元二次方程的两根为则_______=8、如图在ABC 中,EF BC,AEF 和BCE 的面积相等,若ABC 的面积为1,则CEF 的面积()9、若函数1(0)y k x k yx =>=与函数的图像交于A,C 两点,AB 垂直x 抽于点B,则ABC 的面积为_______。
10、某乐队指挥需要给乐队成员排成方队,若排成一个正方形方队,将剩下5个人,若排成一个行数比列数多7的矩形方阵,恰好排完, 则乐队成员数的最大值为_______。
二、 解答题(共6题,共计100分)。
11.某队伍长)1 千米,在长途行军中,通讯员从排尾追赶排头,到派头后立即赶回,当他回到排尾时,整个队伍已经行进)1 千米,若通讯员和队伍在整个过程的速度不变,问通讯员所走的路程是多少千米?(15分)12.已知关于x 的方程()221, 2.221222121,2,22330(1),6.11x m x m m m x x x x m m x x x x +-+-+=≥-+=+--有两个不相等的实根(1)若求m 的值。
(1)求的最大值。
13.为了参加市科技节展览,同学们制造了一个截面为抛物线的隧道模型,用了三种正方形的钢筋支架,在画设计图时,如果在直角坐标系中,抛物线的函数解析式为2y x c =-+,正方形ABCD 的边长和正方形EFGH 的边长之比为5:1,求(1)抛物线解析式中的常数c 的值。
长沙四大名校初中招生真题试卷—数学(4)

长沙四大名校初中招生真题试卷—数学(4)考生注意:本卷共五个大题,考试时量为90 分钟,满分 120 分。
请仔细检查试卷是否缺页、漏题!一、填空题( 20× 3 分 = 60 分)1 =1、 13212、一个圆周角的1= __________度513、 1.75 中含有 _______ 个84、甲数是乙数的3,则甲数与乙数的比 ___________45、 20 克糖完整溶解在 80 克水中,则该糖水的含糖率为________% 。
6、在 2、 67% 、 0.667, 0.66 这四个数中,最大的数是 _______,37、 4 3吨 =__________ 千克58、 42 和 70 的最大条约数为 _______,9、一个多位数读作 :三百零七万零五百二十 ,那么这个数 写作 __________________10、在一幅地图上用 15 厘米表示实质距离 900 千米,这幅地图的比率尺是 __________。
11、等底等高的圆柱和圆锥的体积的和是64 cm 3,则圆柱的体积是 __________ cm 3 12、把一个边长为一个 6 cm 的正方形剪成一个最大的圆 ,则圆的周长为 ____________ cm (π 取 3.14 ) 13、一个两位小数保存一位小数后,获得的数是7.4 则这个两位小数最小为 ________。
5 14、 30 的6与 12 的差除以 20 与 6 的和的商为 _______15、如下图:直角三角形的三边长 分别为 6 cm 、 8 cm 、 10 cm ,则边长为 10cm 的边上的高为 _____________ cm16 、小明有 4.2 元钱 ,给小虎 0.5 元后 ,还比小虎多 3 元 ,则小虎原有 ________元。
17 、某同学在三次考试中的得分的均匀值为 93 分,此中一次得满分 100 分,另两次的分差为5 分,则该同学的三次成绩中最低的是 ___________分 ,18 、一个分数的分子与分母的和是171,约分后是7 ,则本来这个分数为 _______7123 , 19 、某校六年级女生人数占总人数的,以后又转进 15 名女生 ,这时女生人数占总人数的125则某校六年级女生人数原有______人 .A20、如图,三角形 ABC 中, EF 平行于 BC , AB=4AE ,E 三角形甲、乙、丙的面积之比是________________ 。
湖南长沙四大名城初升高数学测试卷

湖南长沙四大名城初升高数学测试卷第一部分:选择题 (共 20 题,每题 2 分,共 40 分)请在括号中选择正确答案,并将其字母编号填写在题后的括号内。
1. 在下列数字中,最大的是:- A. 236 B. 743 C. -251 D. -631 E. 427 ( )2. 设数列 {an} 的通项公式为 an = 3 * n,若 a1 = 6,则 a4 的值是:- A. 2 B. 4 C. 6 D. 8 E. 9 ( )3. 解方程 2x - 5 = 7,得到的解是:- A. -1 B. 1 C. 2 D. 3 E. 4 ( )4. 以下是一些几何图形,请选择其中是平行四边形的图形:- A. 三角形 B. 正方形 C. 梯形 D. 长方形 E. 椭圆 ( )5. 若 a + b = 7,且 a - b = 3,则 a 的值是:- A. 2 B. 3 C. 5 D. 7 E. 10 ( )... (继续填写题目)第二部分:解答题 (共 3 题,每题 20 分,共 60 分)请解答下列数学问题:1. 在一个庆祝晚会上,小明用 12 张贺卡写下了 1 ~ 12 这些自然数。
他将这些贺卡随机放入一个盒子中,然后从盒子里抽出了 5 张贺卡。
请问,抽出的贺卡中最小的数字是多少?2. 在一个三角形 ABC 中,∠ABC = 90°,AB = 6 cm,BC = 8 cm。
请问,三角形 ABC 的面积是多少?3. 已知直线 y = 2x - 3,求出 x = 5 时,直线上的点的坐标。
第三部分:应用题 (共 2 题,每题 30 分,共 60 分)1. 小华去超市买了若干笔和同样多的本子,每支笔售价 5 元,每本书售价 6 元,小华花了 114 元。
请问,小华一共买了多少支笔和本子?2. 甲乙两个城市相距 160 公里,甲城到乙城开车需要 4 小时,而乙城到甲城开车只需要 3 小时。
请问,两个城市离还有多远?总分:200 分祝你考试顺利!。
长沙四大名校高一入学考试数学卷
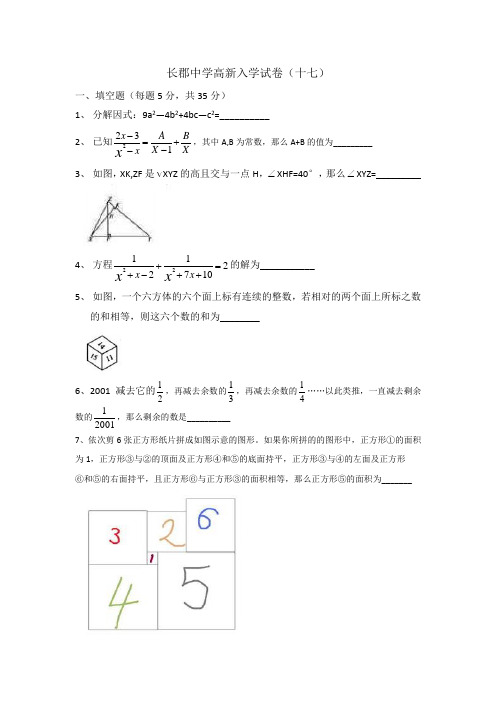
长郡中学高新入学试卷(十七)一、填空题(每题5分,共35分)1、 分解因式:9a 2—4b 2+4bc —c 2=__________2、 已知2231x A B X Xx x -=+--,其中A,B 为常数,那么A+B 的值为_________ 3、 如图,XK,ZF 是XYZ 的高且交与一点H ,∠XHF=40°,那么∠XYZ=_________4、 方程221122710x x x x +=+-++的解为___________5、 如图,一个六方体的六个面上标有连续的整数,若相对的两个面上所标之数的和相等,则这六个数的和为________6、2001减去它的12,再减去余数的13,再减去余数的14……以此类推,一直减去剩余数的12001,那么剩余的数是__________ 7、依次剪6张正方形纸片拼成如图示意的图形。
如果你所拼的的图形中,正方形①的面积为1,正方形③与②的顶面及正方形④和⑤的底面持平,正方形③与④的左面及正方形 ⑥和⑤的右面持平,且正方形⑥与正方形③的面积相等,那么正方形⑤的面积为_______二、选择题(每题4分,共28分)8、如图,仪表板上有四个开关,如果相邻的两个开关不能同时是关的,那么所有不同的状态有()A 4B 6C 8D 129、自然数n满足(n2—2n--2)n2+47=(n2—2n--2)16n-16,这样的n的个数是()A 2B 1C 3D 410、把10个相同的小正方形按如图所示的位置堆放,它的外表含有若干个小正方形。
如果将图1中标有字母A的一个小正方形撤去,这时外表含有的小正方形个数与搬动前相比()A 不增不减B 减少1个C 减少2个D 减少3个11、已知b=)A 6B 5C 4D 312、如图,四边形ABCD中,∠BAD=90°,AB=BC=2 AC=6,AD=3则CD的长是()A 4B 4C 3D 313、如图所示,一个大长方形被两条线段AB,CD分成四个小正方形。
湖南长沙四大名校初升高数学测试卷

测试卷1一、选择题每小题4分,共32分1、已知3344555,4,3===c b a ,则有 A. a<b<c B. c<b<a C. c<a<b D a<c<b2、如果方程()0012>=++p px x 的两根之差为1,那么P 的值为 A 2 B 4 C 3 D 53、如果不等式组{0908≥-<-a x b x 的整数解仅为1,2,3;那么适合这个不等式组的整数a 、b 的有序实数对a,b 共有 个 A 17 B 64 C 72 D 814、若正整数x 、y 满足6422=-y x 则这样的正整数对x,y 的个数是A 1B 2C 3D 45、如图,P 是平行四边形ABCD 内一点不在线段BD 上,52=ABCD APB S S 则=ABCD CPD S S 51⋅A 101⋅B 103⋅C 53⋅D6、每面标有16的三颗骰子堆成一串,如图,其中7面可见,而11面是看不到的背面、底面之间的面,试问看不见的面其点数总和是A 37B 38C 39D 417、方程()0213722=---+-k k x k x k 是实数有两个实根21,x x 且101<<x , 212<<x 那么k 的取值范围是43.<<k A 12-<<-k B 43.<<k C 或 12-<<-k D.无解8、已知一个梯形的四条边长分别是1、2、3、4;则此梯形的面积是A .4B 6C 328D 3210 二、填空题每小题4分,共32分9.若0>ab 则c c b ba a++的值等于是_______ 10.已知实数a,b 满足0454422=++-+b a b a 那么-ab 的平方根是________- 11.等腰三角形一腰上的中线把这个三角形的周长分成12cm 和21cm 两部分,则这个等腰三角形的底边长是_______________12.计算:____________)3121(15=+÷13.已知实数x 、y 满足322=+y x , 322=+x y , 且x ≠y, 则x y y x +=_________ 14.小华有若干个苹果向若干只篮子里分发,若每只篮子分4个苹果,还剩20个没分完;若每只篮子分8个苹果,则还有一只篮子没有放够,那么小华原来共有苹果________个15.若13432-+--=x x y , 则y 的最大值是________________16.已知关于的方程 ()4)2(3322-++=++m x x m m 有唯一解,则m 的取值范围是____________________三、解答题每小题12分,共36分17.某校初三班余班费元,打算为每位同学买1本相册;某批发兼零售文具店规定:购相册50本起可按批发价出售,少于50本则按零售价出售,批发价比零售价每本便宜2元;班长若按零售价为每位同学买1本相册,刚好用完m 元;若多买12本相册送给任课老师,可按批发从价结算,也恰好只有m 元;问该班有多少名同学每本相册的零售价为多少元18.如图所示,在等腰梯形ABCD 中,AB=DC=5, AD=4, BC=10 ,点E 在下底边BC 上,点F 在腰AB 上.1若EF 平分等腰梯形ABCD 的周长,设BE 的长为x,试用含x 的代数式表示△BEF 的面积 2是否存在线段EF 将等腰梯形ABCD 的周长和面积同时平分 若存在,求出此时BE 的长;若不存在,请说明理由.3是否存在线段EF 将等腰梯形ABCD 的周长和面积同时分成1:2的两部分 若存在,求出此时BE 的长;若不存在,请说明理由.19.已知抛物线64)12(2-+--=m x m x y1设抛物线与x 轴的两个交点Ax 1,0和B 0,2x 分别在原点的两侧其中21x x <,且A 、B 两点的距离小于6,求m 的取值范围.2抛物线的对称轴与x 轴交于点C,在1条件上试判断是否存在m 的值,使经过点C 及抛物线与x 轴的另一个交点的⊙M 与y 轴正半轴相切于点D,且⊙M 被x 轴截得的劣弧与弧CD 是等弧 若存在,求出满足条件的m 的值;若不存在,请说明理由.。
2023年湖南省长沙市中考数学真题(解析版)全文

2023年湖南省长沙市中考数学试卷一、选择题(在下列各题的四个选项中,只有一项是符合题意的.请在答题卡中填涂符合题意的选项,本大题共10个小题,每小题3分,共30分)1.【答案】B【解析】解:A 选项,17是分数,属于有理数,故本选项不符合题意;B 选项,π是无限不循环小数是无理数,故本选项符合题意;C 选项,﹣1是整数,属于有理数,故本选项不符合题意;D 选项,0是整数,属于有理数,故本选项不符合题意.故选:B .2.【答案】D【解析】解:根据轴对称图形的定义可知:A 、B 、C 都不是轴对称图形,只有D 是轴对称图形.故选:D .3.【答案】A【解析】解:A 选项,235x x x ×=,本选项符合题意;B 选项,()339x x =,本选项不符合题意;C 选项,()21x x x x +=+,本选项不符合题意;D 选项,()2221441a a a -=-+,本选项不符合题意;故选:A .4.【答案】C【解析】解:134+= ,∴1,3,4不能组成三角形,故A 选项不符合题意;227+< ,∴2,2,7不能组成三角形,故B 不符合题意;457+> ,754-<∴4,5,7能组成三角形,故C 符合题意;336+= ,∴3,3,6不能组成三角形,故D 不符合题意,故选:C .5.【答案】A【解析】解:∵科学记数法的表现形式为10n a ⨯的形式,其中110a ≤<,∴121400000000000 1.410⨯=,故选:A .6.【答案】C【解析】解:如图所示,∵直线m ∥直线n ,∴2180CAD ∠+∠=︒,∴12180BAC ∠+∠+∠=︒∵AC AB ⊥,∴90BAC ∠=︒,∵140∠=︒,∴40902180∠︒+︒+=︒,∴250∠=︒,故选:C .7.【答案】B【解析】解:A 选项,由纵坐标看出,这一天中最高气温是32℃,说法正确,故A 不符合题意;B 选项,这组数据的中位数是27,原说法错误,故B 符合题意;C 选项,这组数据的众数是24,说法正确,故C 不符合题意;D 选项,周四与周五的最高气温相差8℃,由图,周四、周五最高温度分别为32℃,24℃,故温差为32248-=(℃),说法正确,故D 不符合题意;故选:B .8.【答案】A【解析】解:由240x +>得2x >-,由10x -≤得1x ≤,解集在数轴上表示为:,则不等式组的解集为21x -<≤.故选:A .9.【答案】D【解析】解:由一次函数、正比例函数增减性知,x 系数小于0时,y 随x 的增大而减小,1y x =-+,10-<故只有D 符合题意,故选:D .二、填空题(本大题共6个小题,每小题3分,共18分)10.【答案】(n -10)(n +10)【解析】解:n 2-100=n 2-102=(n -10)(n +10).故答案为:(n -10)(n +10).11.【答案】9【解析】解:()109108859++++÷=(小时).即该学生这5天的平均睡眠时间是9小时.故答案为:9.12.【答案】65【解析】解:根据题意可得:BD BE =,∴BDE BED ∠=∠,∵18050ABC BDE BED ABC ∠+∠+∠=︒∠=︒,,∴65BDE BED ∠=∠=︒.故答案为:65.13.【答案】196##136【解析】解:AOB 的面积为||192212k k ==,所以k =196.故答案为:196.14.【答案】1【解析】解:如图,连接OB ,∵60ACB ∠=︒,∴2120AOB ACB ∠=∠=︒,∵OD AB ⊥,∴ AD BD=,90OEA ∠=︒,∴1602AOD BOD AOB ∠=∠=∠=︒,∴906030OAE ∠=︒-︒=︒,∴112122OE OA ==⨯=,故答案为:1.15.【答案】4【解析】解:设地球的半径为r 万里,则2π8r =,解得4πr =,∴火星的半径为2π万里,∴经过火星球心的截面的圆的周长大约为2π⨯2π4(=万里).故答案为:4.三、解答题(本大题共9个小题,第17、18、19题每小题6分,第20、21题每小题6分,第22、23题每小题6分,第24、25题每小题6分,共72分,解答应写出必要的文字说明、证明过程或演算步骤)16.【答案】1-【解析】解:原式1222=+-⨯-12=+--1=-.17.【答案】46a -,6【解析】解:()()()222233a a a a a -+-++,2224263a a a a =---+,46a =-;当13a =-时,原式1464263⎛⎫=-⨯-=+= ⎪⎝⎭.18.【答案】(1)4km (2)飞船从A 处到B 处的平均速度约为0.3km /s【解析】(1)解:在Rt AOC 中,90AOC ∠=︒ ,30ACO ∠=︒,8km AC =,AO ∴=12AC =1842⨯=()km ,(2)在Rt AOC 中,90AOC ∠=︒ ,30ACO ∠=︒,8km AC =,OC ∴=24AC =()km ,在Rt BOC 中,90BOC ∠=︒ ,45BCO ∠=︒,45BCO OBC ∠∠∴==︒,4OB OC ∴==km ,(4AB OB OA ∴=-=4)km ,∴飞船从A 处到B 处的平均速度=410()0.3km /s ≈.19.【答案】(1)150,36;(2)见解析(3)144(4)估计该校参加竞赛的3000名学生中达到“优秀”等级的学生人数有480人【解析】(1)6040%150n =¸=,∵54%100%36%150m =⨯=,∴36m =;故答案为:150,36;(2)D 等级学生有:150********---=(人),补全的频数分布直方图,如图所示:(3)扇形统计图中B 等级所在扇形的圆心角度数为36040%144⨯︒=︒;故答案为:144;(4)300016%480´=(人),答:估计该校参加竞赛的3000名学生中达到“优秀”等级的学生人数有480人.20.【答案】(1)见解析(2)4BD =【解析】(1)证明:CD AB ⊥ ,BE AC ⊥,90AEB ADC ∴∠=∠=︒,在ABE 和ACD 中,AEB ADC BAE CAD AB AC ∠=∠⎧⎪∠=∠⎨⎪=⎩,()AAS ABE ACD ∴ ≌;(2)解:ABE ACD ≌,6AD AE ∴==,在Rt ACD中,AC ==,10AB AC == ,1064BD AB AD ∴=-=-=.21.【答案】(1)该班级胜负场数分别是13场和2场;(2)该班级这场比赛中至少投中了4个3分球.【解析】(1)解:设胜了x 场,负了y 场,根据题意得:15341x y x y +=⎧⎨+=⎩,解得132x y =⎧⎨=⎩,答:该班级胜负场数分别是13场和2场;(2)设班级这场比赛中投中了m 个3分球,则投中了()26m -个2分球,根据题意得:()322656m m +-≥,解得4m ≥,答:该班级这场比赛中至少投中了4个3分球.22.【答案】(1)见解析(2)3BF =;ADF △的面积为【解析】(1)证明:在ABCD Y 中,∴AB CD ∥,∴CDE F ∠=∠,∵DF 平分ADC ∠,∴ADE CDE ∠=∠,∴F ADF ∠=∠,∴AD AF =.(2)解:∵63AD AF AB ===,,∴3BF AF AB =-=;过D 作DH AF ⊥交FA 的延长线于H ,∵120BAD ∠=︒,∴60DAH ∠=︒,∴30ADH ∠=︒,∴132AH AD ==,∴2233D H A D A H =-=∴ADF △的面积1163922AF DH =⋅=⨯⨯=.23.【答案】(1)BD 是O 的切线,证明见解析(2)152+(3)()01y x x =<≤【解析】(1)解:BD 是O 的切线.证明:如图,在ABC 中,222AB BC AC =+,∴90ACB ∠=︒.又点A ,B ,C 在O 上,∴AB 是O 的直径.∵90ACB ∠=︒,∴90CAB ABC ∠+∠=︒.又DBC CAB ∠=∠,∴90DBC ABC ∠+∠=︒.∴90ABD Ð=°.∴BD 是O 的切线.(2)由题意得,12112122S BC CD S BC AC S AD BC ⋅⋅===⋅,,.∵()212S S S ⋅=,∴2112122BC CD AD BC BC AC =⎛⎫⋅⋅⋅⋅ ⎪⎝⎭.∴2•CD AD AC =.∴()2CD CD AC AC +=.又∵9090D DBC ABC A DBC A ∠+∠=︒∠+∠=︒∠=∠,,,∴D ABC ∠=∠.∴tan tan BC AC D ABC CD BC∠==∠=.∴2BC CD AC=.又()2CD CD AC AC +=,∴4222BC BC AC AC+=.∴4224BC AC BC AC +⋅=.∴241AC AC BC BC ⎛⎫⎛⎫+= ⎪ ⎪⎝⎭⎝⎭.由题意,设()2tan D m =,∴2AC m BC ⎛⎫= ⎪⎝⎭.∴21m m +=.∴12m =.∵0m >,∴12m =.∴()22t an 1D =.(3)设A α∠=,∵90A ABC ABC DBC ABC N ∠+∠=∠+∠=∠+∠=︒,∴A DBC N α∠=∠=∠=.如图,连接OM .∴在Rt OFM △中,OF ==∴1BF BO OF =+=1AF OA OF =-=∴在Rt AFE 中,(tan 1tan EF AF αα=⋅=-⋅,1cos cos AF AE αα==.在Rt ABC △中,sin 2sin BC AB αα=⋅=.(∵1r =,∴2AB =)cos 2cos AC AB αα=⋅=.在Rt BFN △中,11sin sin BF BN αα+==,11tan tan BF FN αα+==.∴y FE FN =⋅2x =2x =2x =21x x =⋅x =.即y x =.∵FM AB ⊥,∴FM 最大值为F 与O 重合时,即为1.∴01x <≤.综上,()01y x x =<≤.24.【答案】(1)k 的值为1-,m 的值为3,n 的值为2;(2)①函数y 2的图像的对称轴为13x =-;②函数2y 的图像过两个定点()01,,2,13⎛⎫- ⎪⎝⎭,理由见解析;(3)能构成正方形,此时2S >.【解析】(1)解:由题意可知:2212120a c a c b b ===-≠,,,∴321m n k ===-,,.答:k 的值为1-,m 的值为3,n 的值为2.(2)解:①∵点()P r t ,与点()()Q s t r s ≠,始终在关于x 的函数212y x rx s =++的图像上运动,∴对称轴为222r s r x +==-,∴3s r =-,∴2221y sx xx =-+,∴对称轴为2123r r x s s -=-==-.答:函数2y 的图像的对称轴为13x =-.②()222321321y rx rx x x r =--+=-++,令2320x x +=,解得1220,3x x ==-,∴过定点()01,,2,13⎛⎫- ⎪⎝⎭.答:函数y 2的图像过定点()01,,2,13⎛⎫-⎪⎝⎭.(3)解:由题意可知21y ax bx c =++,22y cx bx a =-+,∴224,,2,4244b ac b b ac b A B aa c c ⎛⎫⎛⎫--- ⎪ ⎪⎝⎭⎝⎭,∴CD a =,11EF =-,∵CD EF =且240b ac ->,∴a c =;①若a c =-,则2212,y ax bx a y ax bx a =+-=--+,要使以A ,B ,C ,D 为顶点的四边形能构成正方形,则CAD CBD ,为等腰直角三角形,∴2A CD y =,∴2242||||4a b a a--=⋅,∴224b a =+,∴2244b a +=,∴2222222114142222b ac b a S CD a a a-+==⋅=⋅=正,∵22440b a =->,∴201a <<,∴2S >正;②若a c =,则A 、B 关于y 轴对称,以A ,B ,C ,D 为顶点的四边形不能构成正方形,综上,以A ,B ,C ,D 为顶点的四边形能构成正方形,此时2S >.。
长沙四大名校初中招生真题试卷—数学(2)

博源教育(肖)长沙四大名校初中招生真题试卷—数学(2)时间: 90 分钟总分: 100 分得分: ___________一、我能填对。
(每空 1 分,共 22 分)1.1米的1是()米1 小时 36 分=()小时422.9.2 立方分米=()立方厘米6吨 78 千克=( )吨3.4÷( )== 0.8 =( ) %=( ):( )204. 12的分数单位是(),再增添()个这样的分数单位就与最小的合数相等。
95. 已知A※B=(A +B) +A÷B,则( 2※ 3)※ 4=( )6.从A到B地,甲车用了5 小时,乙车用了 4 小时,甲车速度与乙车速度的比是( )7.,3.14,22, 3.14 四个数中,最大的是()78.计算:1 1 11()1 2 2 3 34 2011 20129. 在 24 克含盐 15%的盐水中加水使盐水含盐9 %,需要加水( )千克。
10.一个分数约分后是5,原分数的分子和分母之和是72, 则原分数是()711.徒弟加工部件 45 个,比师傅加工部件个数的1 多 5 个。
师傅加工()个。
212. 2012 年有()天,第一季度有()天。
13. 大圆和小圆的半径之比是 5:1, 则周长之比是(),面积之比是()。
二、我会判断。
(对的打√,错的打×,每题1 分,共 5 分)。
1. 棱长是 6 厘米的正方体,它的体积与表面积相等。
( )2. 分数的分子和分母同时加上一个数(0除外) ,分数的大小不变。
( )3. 一种商品的价钱,先涨价10 %,后又降价10 %,因此又回到了原价。
()4.甲数的3和乙数的3相等,甲数比乙数大。
()545.0.5 米是50 %米( )三、精心选一选。
(把正确答案的字母填在括号里) (10分)1. 小明植树 100 棵,小红植树比小明多 80 棵,小红植树棵数比小明多()A .20% B .80%C .25%D.125%2.已知一个三角形的两个角是锐角,这个三角形是()A . 锐角三角形 B . 直角三角形C . 钝角三角形 D. 不可以确立3.要使x 6是分母为 15 的最简真分数,那么 x 可取的整数共有()个。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
测试卷1
一、选择题(每小题4分,共32分)
1、已知33
44555,4,3===c b a ,则有( )A. a<b<c B. c<b<a C. c<a<b D a<c<b
2、如果方程()0012>=++p px x 的两根之差为1,那么P 的值为( ) A 2 B 4 C 3 D 5
3、如果不等式组{0
908≥-<-a x b x 的整数解仅为1,2,3。
那么适合这个不等式组的整数a 、b 的有序实数对(a,b )共有( )个 A 17 B 64 C 72 D 81
4、若正整数x 、y 满足6422=-y x 则这样的正整数对(x,y )的个数是( )
A 1
B 2
C 3
D 4
5、如图,P 是平行四边形ABCD 内一点(不在线段BD 上),5
2=ABCD APB S S 则=ABCD CPD S S ( ) 51⋅A 101⋅B 103⋅C 5
3⋅D
6、每面标有16的三颗骰子堆成一串,如图,其中7面可见,
而11面是看不到的(背面、底面之间的面,试问看不见的面
其点数总和是( )
A 37
B 38
C 39
D 41
7、方程()021372
2=---+-k k x k x (k 是实数)有两个实根21,x x 且101<<x , 212<<x 那么k 的取值范围是( )
43.<<k A 12-<<-k B 43.<<k C 或 12-<<-k D.无解
8、已知一个梯形的四条边长分别是1、2、3、4。
则此梯形的面积是( )
A .4
B 6
C 328
D 3
210 二、填空题(每小题4分,共32分)
9.若0>ab 则c c b b
a a
+
+的值等于是_______ 10.已知实数a,b 满足04
54422=++-+b a b a 那么-ab 的平方根是________- 11.等腰三角形一腰上的中线把这个三角形的周长分成12cm 和21cm 两部分,则这个等腰三角形的底边长是_______________
12.计算:____________)31
21
(15=+÷
13.已知实数x 、y 满足322=+y x , 322=+x y , 且x ≠y, 则
x y y x +=_________ 14.小华有若干个苹果向若干只篮子里分发,若每只篮子分4个苹果,还剩20个没分完;若每只篮子分8个苹果,则还有一只篮子没有放够,那么小华原来共有苹果________个
15.若13432-+--=x x y , 则y 的最大值是________________
16.已知关于的方程 ()
4)2(3322-++=++m x x m m 有唯一解,则m 的取值范围是____________________
三、解答题(每小题12分,共36分)
17.某校初三班余班费元,打算为每位同学买1本相册。
某批发兼零售文具店规定:购相册50本起可按批发价出售,少于50本则按零售价出售,批发价比零售价每本便宜2元。
班长若按零售价为每位同学买1本相册,刚好用完m 元;若多买12本相册送给任课老师,可按批发从价结算,也恰好只有m 元。
问该班有多少名同学?每本相册的零售价为多少元?
18.如图所示,在等腰梯形ABCD 中,AB=DC=5, AD=4, BC=10 ,点E 在下底边BC 上,点F 在腰AB 上.
(1)若EF 平分等腰梯形ABCD 的周长,设BE 的长为x,试用含x 的代数式表示△BEF 的面积 (2)是否存在线段EF 将等腰梯形ABCD 的周长和面
积同时平分?若存在,求出此时BE 的长;若不存在,请说
明理由. (3)是否存在线段EF 将等腰梯形ABCD 的周长和面
积同时分成1:2的两部分?若存在,求出此时BE 的长;若不存在,请说明理由.
19.已知抛物线64)12(2-+--=m x m x y
(1)设抛物线与x 轴的两个交点A(x 1,0)和B (0,2x )分别在原点的两侧其中21x x <,且A 、B 两点的距离小于6,求m 的取值范围.
(2)抛物线的对称轴与x 轴交于点C,在(1)条件上试判断是否存在m 的值,使经过点C 及抛物线与x 轴的另一个交点的⊙M 与y 轴正半轴相切于点D,且⊙M 被x 轴截得的劣弧与弧CD 是等弧?若存在,求出满足条件的m 的值;若不存在,请说明理由.
(注:文档可能无法思考全面,请浏览后下载,供参考。
可复制、编制,期待你的好评与关注)。
