Straight Line Graphs
折线图 英语作文

折线图英语作文Line Graph。
A line graph is a type of chart used to display data that changes over time. It is made up of a series of data points that are connected by straight lines, which represent the trends or patterns in the data. Line graphs are commonly used in scientific, economic, and social research to illustrate the relationships between variables.The x-axis of a line graph represents time, while they-axis represents the value of the variable being measured. The data points are plotted on the graph, and the lines are drawn between them to show how the variable changes over time. Line graphs can be used to show trends, patterns, or fluctuations in the data, and they can be used to compare multiple variables at once.For example, a line graph could be used to show the changes in temperature over the course of a year, or thechanges in stock prices over a decade. Line graphs can also be used to compare the performance of different companies, countries, or industries over time.When creating a line graph, it is important to choose the appropriate scale for the axes, so that the data is displayed clearly and accurately. It is also important to label the axes and provide a clear title for the graph, so that the reader can understand the data being presented.In conclusion, line graphs are a useful tool for visualizing data that changes over time. They can be used to show trends, patterns, and fluctuations in the data, and they can be used to compare multiple variables at once. When creating a line graph, it is important to choose the appropriate scale, label the axes, and provide a cleartitle for the graph.。
A-level数学词汇(P1-P4)

Pure mathematics1 1Algebraic expression代数表达式Index laws指数定律Indices(index的复数形式)指数Notation注释Simplify化简Power指数Base底Exponent指数Expression表达式Term项Numerator分子Expand展开Possible可能Fraction分数Bracket括号Product乘积Multiply乘Collecting like terms合并同类项Linear一次的Diagram图形Rectangle长方形Square正方形Length长度Width宽Side length边长Area面积Shade阴影Cuboid长方体Dimension维Show that证明Volume体积Given that已知Constant常数Value值Factorize因式分解Factor因子Opposite相反的Completely完全地Common factor公因式Quadratic二次的Form形式Real number实数Positive正的Negative负的Include包含Surd无理数Add加Sum和Take out提取Difference差Difference of two squares平方差Cancel取消,相互抵消Similarly同样的Rational有理的Rational number有理数Integer整数Square root平方根Evaluate求…的值Substitute代替Calculator计算器Square number平方数Irrational number无理数Decimal小数的Expansion展开式Never-ending无限的Never repeat不循环的Exact准确的Answer答案Manipulate操作Denominator分母Rationalizing denominator分母有理化Rearrange调整Prime质数Work out计算Hence然后Fully完全地State陈述Solve解决Equation方程2Quadratics二次方程式Quadratic equation二次方程Solution解Real solution实根Set设置Root根Distinct不同的Repeated root重根Case情况Straightforward简单直接的Symbol符号Plus加,正Minus减,负Factorization因式分解Shape形状Section部分Formula公式Reading off读取Coefficient系数Necessary必要的Significant figures有效数字Choose选择Suitable适当的Method方法Trapezium梯形Height高Discard丢弃Completing the square完全平方(配方)Frequently经常的Useful有用的Process过程Original最初的Determine决定Otherwise另外Function函数Mathematical数学上的Relationship关系Map映射Set集合Input输入Output输出Single单一的Notation符号Represent代表Domain定义域Range值域,范围Member成员Define定义Minimum最小的Occur发生Explain解释Consider考虑Graph图像Curve曲线Parabola抛物线Sketch画图Identify确定Key关键的Feature特征Overall整体的Cross交叉,横过Axis轴Coordinate坐标Turning point转折点(顶点)Maximum最大的Since因为Symmetrical对称的Symmetry对称性Line of symmetry对称轴Half-way位于中途的Explore探测Technology技术Plot绘制Scale刻度However但是,不管怎样Smooth平滑的Relevant相关的Intercept截距Label标记Axes(axis的复数)坐标轴Discriminant判别式Sign符号Check核实Inequality不等式Calculate计算Match匹配Prove证明Algebra代数学Diver跳水运动员Launch发射Springboard跳板Meter米Pool水池Second秒Model模型High高的Hit撞击Reach达到Non-zero非零3Equations and inequalities 方程和不等式Simultaneous联立的Linear simultaneous equations一次方程组Elimination消元法Substitution置换Quadratic simultaneous equations 二次方程组Up to直到,多达Make sure确保Correctly正确地Simplest最简的Graphically以图表形式As因为Satisfy满足Intersection相交Simultaneously同时地Intersect相交Once一次Twice两次Result结果,导致Produce产生Graph paper坐标纸Accurately准确地Verify验证Linear inequalities一次不等式Set notation集合符号Number line数轴Overlap重叠Separately单独地Illustrate图解,阐明Quadratic inequalities二次不等式Corresponding相应的Critical临界的Require要求Describe描述Interpret解释Region区域,范围Coordinate grid坐标网Dotted line虚线Solid line实线Vertex顶点Vertices(vertex的复数)顶点Within在内部,之内4Graphs and transformations 图像和转换Cubic三次的Cubic function三次函数Several几个Depend on取决于Touch接触Coordinate axes坐标轴Indicate表明,显示Reciprocal倒数的Reciprocal function反比例函数Such as例如Asymptote渐近线Approach接近Reach到达Quadrant象限Point of intersection交点Steeper更陡峭的Eventually最后,终于Reason理由,原因Appropriate恰当的Number数量Translate平移Transform改变Alter改动Subtract减Outside在外面Vertically竖直地Translation平移Vector矢量Horizontally水平地Direction方向In terms of用…来表示Slide滑动Stretch伸缩Scale factor比例系数Double两倍Halve减半,对分Inside在里面Triple三倍的Reflection反射(镜面对称) Alternatively二选一Parallel平行Lie on坐落在Pass through穿过Apply应用Unfamiliar陌生的,不熟悉的Specific特殊的Origin原点Position位置Image像Suggest提议Mark标记5Straight line graphs直线图像Gradient斜率Straight line直线Join连接Distance距离Formula公式Collinear共线的Intercept截距Define定义Either两者中的任一个Condition条件Triangle三角形General equation一般式Parallel平行Perpendicular垂直Whether是否Quadrilateral四边形Trapezium梯形Right angle直角Congruent全等的Neither两者都不Hypotenuse直角三角形斜边Line segment线段Scalene不等边的Respectively分别地Go through通过6Trigonometric ratios三角比Cosine rule余弦定理Miss缺失Version版本Exchange交换Standard标准Prove证明Opposite对边Adjacent邻边Pythagoras’theorem勾股定理Letter字母Round四舍五入Final最终的Coastguard海岸警卫队Station驻地Bearing方位Away from远离Appropriate适当的Mark标记Airport机场Due north正北Due east正东Due west正西Due south正南Sail航行Helicopter直升飞机Tee球座Flag旗Particular特定的Hole孔,洞Golf course高尔夫球场Yard码(1码=3英尺)Tee shot发球台Land着陆Largest最大的Farmer农场Field场地Fence栅栏Cargo货物Plane平面Kilometer千米Sine rule正弦定理Refer to涉及Data数据Remain剩余Located on坐落于Zookeeper动物管理员Enclosure围场Llama骆驼Diagonal对角线Surveyor检验员Measure测量Elevation高程,仰角Apart相距Assumption假设Mathematical数学的Model模型Obtuse钝角Acute锐角Isosceles等腰的Circle圆Radius半径Centre圆心Least最小的Instead代替Crane吊车Anchored固定Wreck破坏Suspend悬挂Cable缆绳Rotate旋转Level对准Proof证明Triangular plot三角图Involve涉及Trigonometry三角函数Encounter遇到Decide决定Mast桅杆In order that为了Interfere干扰Efficient有效的Hiker徒步旅行者Radar雷达Perimeter周长Tangent正切Periodic周期性的Repeat重复的Certain确定的Interval间距Period周期Undefined无意义的Knowledge知识Periodicity周期性Verify证明Variation变化Rock pool潮汐潭Midday中午During在…期间Non-exact非精准的Significant figure有效数字Windmill风车Sail帆Tower塔Deduce推导Dune沙丘Realistic现实的7Radians弧度Radian弧度So far到目前为止Probably大概,可能Degree度Revolution循环Around围绕Circle圆Subtend朝着Arc圆弧Circumference周长Convert转换Without没有Multiple倍数Arc length弧长Sector扇形Radius半径Contain包含Perimeter周长Border边界Pond池塘Consist由…组成Edge边缘Minor arc劣弧Major arc优弧Chord弦Diameter直径Template模板Brooch胸针Ferris wheel摩天轮Pod蚕茧,豆荚Estimate估计Speed速率Patio露台Lawn草坪Design设计Earring耳环Nearest最近点(精确到)Segment弓形Radii(radius的复数形式) A plot of…的一块Erect建造Along沿着Subtract减Tangent切线Ratio比例Bound关,围入Decimal place小数Midpoint中点Semicircular半圆Drawer抽屉Handle把手Difference差Badge徽章Equilateral等边的Railway铁路Track轨迹Prism三棱镜Attempt尝试Mistake错误8Differentiation微分Gradient斜率Constantly不断地Although然而Comment on对…评论Copy抄写,复制Complete完成Table表格Hypothesis假设Derivative导数Principle原理Detail细节Account解释Originate起源Formalize确定,形成Approach方式,方法Limit极限Tend to趋向Gradient function斜率函数Evaluate求…的值Fixed value定值Limiting value定值Definition定义One-at-a-time一次一个Turning point转折点(顶点)Slope斜率Disappear消失Polynomial多项式Normal切线First order derivative一阶导数Second order derivative二阶导数Rate of change变化率Respect to关于Displacement位移Acceleration加速度Local局部的9Integration积分Reverse相反的Differ不同Integrate求积分Integral积分Indefinite不确定的Indefinite integral不定积分Elongated拉长的,伸长的Arrow箭Fire射击Castle城堡Drop off下降Cliff悬崖Cyclist骑行者Pure mathematics2 1Algebraic methods代数方法Division除法Dividing polynomial多项式除法Finite有限的Whole number整数Long division长除法Quotient商Remainder余数Factor theorem因式定理Remainder theorem余数定理Logical逻辑的Structured有组织的Argument论据Statement命题Conjecture猜想Previously预先Establish建立Deduction推导Desired想要的Conclusion结论Odd number奇数Demonstration示范,演示Even number偶数Identical完全相等的Identity恒等式Parallelogram平行四边形Rhombus菱形Congruent全等的Exhaustion穷举法Consecutive连续的Square number平方数Break into拆分Is suited to适合于Disprove反驳Counter-example反例Sufficient充分的Prime number质数Divisible可整除的Either…or…二者择一的Cube number立方数Hold有效Claim宣称Opposite edge对边Hexagon六边形Regular hexagon正六边形Side length边长Reason原因2Coordinate geometry in the (x,y)plane解析几何Bisector二等分线Perpendicular bisector中垂线Averaging求平均值Endpoint端点Circumcentre外心Equidistant等距的Fixed point定点Vector向量Property性质Unique独一无二的Circumcircle外接圆3Exponentials and logarithms 指数和对数Exponential指数的Decrease减小Increase增加Smooth光滑的,平滑的Increasing function增函数Decreasing function减函数Justify证明Logarithms对数Specific特定的Button按钮Typically典型的Natural logarithms自然对数Instance实例Multiplication law乘法定律Division law除法定律Power law指数定律Recognize识别Attention注意Condition条件Complicated复杂的Whenever无论何时Convenient方便的Suppose假设Notice注意Particular特别的4The binomial expansion二项式展开Binomial二项式Pascal’s triangle杨辉三角(帕斯卡三角形)Immediately直接地Pattern图案Adjacent相邻的Investment投资Interest rate利率Annum年,岁Approximation近似值Ignore忽略Factorial notation阶乘Combination组合Superscript上标Subscript下标Probability可能性Toss投Likelihood可能性Ascending powers升幂Individual个别的Estimation估值Engineering工程学Science科学Percentage error百分误差Microchip微型集成电路片Faulty有缺点的Chip芯片Restrict限制Achieve达到School fair学校园游会Prize奖赏Digit数字Display显示5Sequences and series数列和级数Arithmetic sequence等差数列Arithmetic progression等差数列Common difference公差Arithmetic series等差级数(等差数列前n项求和)Exceed超过Inclusive包含的Stick棒子Pentagon五角形Geometric sequences等比数列Geometric progression等比数列Common ratio公比Converge收敛Alternating sequence交错数列Million百万Geometric series等比级数(等比数列前n项求和)Sum to infinity无限项求和Divergent发散的Convergent收敛的Recurring循环的Sigma notation求和符号Capital首都,大写字母Signify表示Recurrence relations递推关系Previous term前一项First term初项Generate生成,产生Periodic sequence周期数列Period周期Salary薪水Profit利润Predict预言Annual年度的Business商业Financial金融的Advisor顾问Fold折叠Thickness厚度Unrealistic不切实际的Investor投资人Account账户Thereafter以后Deposit存款,定金Wage工资Rise上升Gear齿轮Successive连续的Intermediate中间的Valuable有价值的Commission佣金Insurance保险Policy政策Prospector勘探者Drill钻孔Subsequent随后的Available可获得的Payment报酬Virus病毒Infect传染Diagnose诊断Overfish过度捕捞Chess象棋Chessboard棋盘Sponsored赞助的Polygon多边形Appointment约会,任命6Trigonometric identities and equations三角恒等式和方程Unit circle单位圆Anticlockwise逆时针Quadrant象限Equivalent相等的Equilateral triangle等边三角形Isosceles right-angled triangle等腰直角三角形Identity恒等式Reflex优角(大于180度,在第三、四象限)Principal value主值Inverse trigonometric function反三角函数Justification理由7Differentiation微分Strictly严格地Interval区间Stationary point驻点Local maximum局部最大Greatest value最大值Local minimum局部最小Least value最小值Point of inflection拐点,反曲点Immediate最接近的Vicinity邻近,附近Second derivative二次求导Rate of change改变的快慢Convex凸Concave凹Establish建立,证实Liter升Instant瞬间Tank水槽Cuboid长方体的Sheet薄片Metal金属Sphere球体Displacement位移Cylinder圆柱体Perimeter周长Semicircular半圆的Semicircle半圆Frame框架Split分离,分开Motion运动Damped阻尼Spring弹簧Bent弯的Biscuit饼干Tin罐头Close-fitting紧贴的Lid盖子Thin薄的,瘦的Wastage损耗Obtain获得Percentage百分比Store储存Capacity容量Container容器Calculus微积分学8Integration积分Definite integral定积分Indefinite integral不定积分Whereas反之,然而Upper limit上限Lower limit下限Square bracket中括号Magnitude大小Negligible可忽略的Straddle跨坐Unless除非Complicated复杂的Trapezium梯形Trapezium rule梯形法则Beneath在…下面Strip条,带Boundary边界Adjacent相邻的Improve改善Accuracy精确度Approximation近似值Underestimate低估Overestimate高估Compare比较Pure mathematics3 Common multiple公倍数Improper fraction假分数Partial fractions部分分数Degree次数Modulus function模函数Absolute value绝对值Argument辐角Set notation集合符号Piecewise-defined function分段函数Composite function复合函数Inverse function反函数Secant正割Cosecant余割Cotangent余切Interval区间Symmetry对称性Symmetrical对称的Chord弦Inverse trigonometric function反三角函数Addition formulae加法公式Compound-angle formulae复合角公式Double-angle formulae二倍角公式Round四舍五入Exponential function指数函数Natural logarithms自然对数Trend趋势Outlier极值Chain rule链式法则Product rule乘法法则Quotient rule除法法则Continuous连续的Fixed point iteration定点迭代Successive连续的Converge收敛Staircase diagram梯形图Cobweb diagram网状图Diverge发散Pure mathematics4 Contradiction反驳Assert主张Falsehood虚假Negation反论Prime number质数Split分解Separate独立的Parametric equation参数方程Variable变量Parameter参数Revolution循环Plot绘图Valid有效的As long as只要Condition条件Accurate精确的Ascending上升的Approximation近似值Implicit differentiation隐函数微分Explicitly明确的Implicit隐含的Rate of change变化率Hemisphere半球Cylindrical圆柱形的Conical圆锥形的Concave凹Convex凸Integrand被积函数Integration by substitution换元积分法Integration by part分部积分法Polynomial多项式Separating the variables分离变量General solution通解Boundary condition边界条件Directed line segment有向线段Parallelogram平行四边形Unit vector单位向量Column vector列向量Position vector位置矢量Scalene不等边的Clockwise顺时针Anticlockwise逆时针Coplanar共面的Parallelepiped平行六面体Trisect三等分Hexagon六边形Regular hexagon正六边形Direction vector方向向量Anchor固定Dot product点乘。
折线图英语作文范文

折线图英语作文范文A line graph, also known as a line chart, is a type of chart used to visualize data trends over time. It consists of a series of data points connected by straight line segments. Line graphs are commonly used in various fields such as economics, science, and social sciences to show how a particular variable changes over time or in response to different conditions. In this essay, we will discuss the characteristics of a line graph, its components, and how to interpret the information presented in a line graph.Characteristics of a Line Graph:1. X and Y Axes: A line graph has two axes the horizontal axis (X-axis) and the vertical axis (Y-axis). The X-axis typically represents time or a continuous variable, while the Y-axis represents the value of the variable being measured.2. Data Points: Data points on a line graph arerepresented by markers, such as dots or squares, atspecific time intervals or data points. These points are then connected by straight lines to show the trend over time.3. Line: The line connecting the data points represents the trend or pattern in the data. It helps to visualize how the variable changes over time or in response to different conditions.4. Title and Labels: A line graph should have a title that describes the data being represented. The X and Y axes should be labeled with the variable being measured and the units of measurement.5. Legend: If the line graph represents multiple data series, a legend is used to differentiate between the different lines or data sets.Components of a Line Graph:1. Title: The title of a line graph should clearlydescribe the data being represented.2. Axes: The X and Y axes should be labeled with the variable being measured and the units of measurement.3. Data Points: Data points should be clearly marked on the graph, and the lines connecting them should be straight.4. Legend (if applicable): If the graph represents multiple data series, a legend should be included to differentiate between them.5. Scale: The scale of the axes should be appropriateto the data being represented, allowing for easy interpretation of the graph.Interpreting a Line Graph:When interpreting a line graph, it is important to consider the following:1. Trends: Look for trends or patterns in the data. Isthe variable increasing, decreasing, or staying relatively constant over time?2. Relationships: Consider the relationship between different variables. Are there any correlations or causal relationships between them?3. Anomalies: Identify any anomalies or outliers in the data that may indicate unusual or unexpected behavior.4. Comparisons: If the graph represents multiple data series, compare the trends between them to identify any differences or similarities.In conclusion, a line graph is a useful tool for visualizing data trends over time. By understanding its characteristics, components, and how to interpret the information it presents, you can effectively use line graphs to analyze and communicate data in various fields.。
线状图 英语作文

线状图英语作文英文回答:A line graph is a type of graph that displays data points connected by straight lines. It is used to show how a variable changes over time or in relation to another variable. Line graphs are often used to compare data sets or to track trends.To create a line graph, you first need to collect your data. Once you have your data, you need to plot it on a coordinate plane. The x-axis of the coordinate plane represents the independent variable, and the y-axis represents the dependent variable. Once you have plotted your data, you can connect the data points with straight lines.Line graphs are a versatile tool that can be used to display a wide variety of data. They are easy to create and interpret, and they can be used to communicate complexinformation in a clear and concise way.Examples。
Here are some examples of how line graphs can be used:To track the stock market over time。
折线图英语作文雅思

折线图英语作文雅思英文回答:A line graph is a visual representation of data points connected by straight lines. It is typically used to track changes in data over time, or to compare different sets of data.Line graphs are often used in business, finance, and economics to track trends and patterns in data. They can also be used in scientific research to visualize the results of experiments.When creating a line graph, it is important to choose the appropriate scale for the xand y-axes. The x-axis typically represents time, while the y-axis represents the value of the data being tracked. It is also important to label the axes clearly and to use a legend to identify the different lines on the graph.Line graphs can be a powerful tool for visualizing data and identifying trends. However, it is important to remember that they are only a two-dimensional representation of the data, and they may not capture all of the complexity of the data.中文回答:折线图是一种用直线连接数据点的可视化表示形式。
lines (1)
(4, 3)
x
Examples 2.2: y = 0.5x2 − x − 4
y
x −3 −1 0 1
3
(−35, 3.5) (0, −4) ....................................................................................................................................................................................................................................................................................................................................................................................................
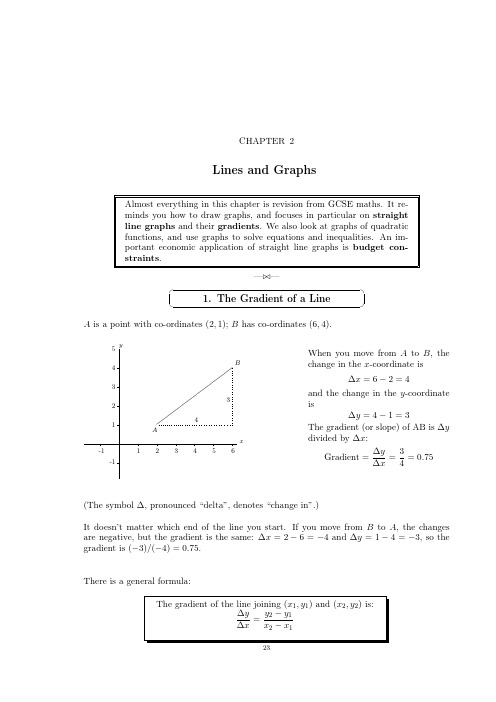
∆y 3 Gradient = = = 0.75
∆x 4
(The symbol ∆, pronounced “delta”, denotes “change in”.)
It doesn’t matter which end of the line you start. If you move from B to A, the changes are negative, but the gradient is the same: ∆x = 2 − 6 = −4 and ∆y = 1 − 4 = −3, so the gradient is (−3)/(−4) = 0.75.
straight_line_graphs_2_igcse_2

diagrdaimagraabmovaeb.ove.
[2] [2]
(b) (Wb)ritWe driotwe ndotwhenctoh-eocrdoi-noartdeisnaotfetshoefmthiedpmoidnpt oifntthoefltihne lsiengemsegnmt jeonintijnoginAin(1g,A8()1t,o8B) (t7o,B–(47),. –4).
Straight line1g1ra1p1hs 2
21 21 2)
yy 8 8A A
77
66
55
44
33
22
11
00
xx
–1 –1 1 1 2 2 3 3 4 4 5 5 6 6 7 7
–2 –2
–3 –3
–4 –4
BB
For For ExamiEnxearm's iner
Use Use
(a) (Ua)sinUgsainsgtraaisgthratiegdhgteedagned acnodmcpoamsspesasosneslyo, ncloyn,sctrouncsttrtuhcet pthereppeenrdpiecnudlaircubliasrecbtiosrecotforAoBf oAnBthoen the
Answer(c)
[3]
Permission to reproduce items where third-party owned material protected by copyright is included has been sought and cleared where possible. Ever reasonable effort has been made by the publisher (UCLES) to trace copyright holders, but if any items requiring clearance have unwittingly been included, th publisher will be pleased to make amends at the earliest possible opportunity.
straight形容词

straight形容词straight 英/streɪt/ 美/streɪt/adj.直的;连续的;异性恋的;纯的;准的;严肃的,正统的;坦诚的;整洁;简单明了的;平正的;直筒型(非紧身)的;正中目标的;规矩老实的adv.直;直接;正;径直;笔直地;立即;成直线;坦率地;连续不断地;平正地n.直道;异性恋者复数:straights比较级:straighter最高级:straightest派生词:straightness n.【不规则形式】 straighter, straightest不弯曲without curves1直的without a bend or curve; going in one direction onlya straight line直线a straight road笔直的公路long straight hair (= without curls)又长又直的头发a boat sailing in a straight line直线航行的船straight-backed chairs直背椅服装clothing2直筒型(非紧身)的not fitting close to the body and not curving away from the body a straight skirt直筒裙瞄准;打击aim/blow3准的;正中目标的going directly to the correct placea straight punch to the face不偏不倚打在脸上的一拳处于平正/ 合适的位置in level/correct position4平正的;正的;直的;与…平行的positioned in the correct way; level, vertical or parallel to sthIs my tie straight?我的领带正不正?整洁clean/neat5[not usually before noun] 整洁;整齐;井井有条clean and neat, with everything in the correct place It took hours to get the house straight.用了好半天才把房子收拾出来。
新加坡O水准试题

[4]
(iii) Estimate the value of s when t = 50.
[2]
© UCLES 2009
4037/01/M/J/09
[Turn over
6 12 Answer only one of the following two alternatives.
[2]
Given that the acceleration of the particle is 12 m s–2 when t = 3π , 8
[2]
a b3
–
2 3
6 Solve the equation 2x3 + 3x2 – 32x + 15 = 0.
[6]
( ) 7 (i) Find d– xe3x – –e–3x– .
dx
3
[3]
∫ (ii) Hence find xe3xdx.
[3]
© UCLES 2009
4037/01/M/J/09
Q
x
The diagram shows the line AB passing through the points A(– 4, 0) and B(8, 9). The line through the point P(1, 10), perpendicular to AB, meets AB at C and the x-axis at Q. Find
(i) the value of t when the particle is first instantaneously at rest,
[1]
(ii) an expression for the acceleration of the particle t s after passing through O.
英语作文折线图模板及范文

英语作文折线图模板及范文全文共3篇示例,供读者参考篇1Title: English Essay on Line Graph Template and ExampleIntroduction:A line graph is a visual representation of data that shows how a variable changes over time. It is commonly used in various fields such as economics, finance, and science to illustrate trends and patterns. In this essay, we will discuss the basic template for creating a line graph and provide an example to demonstrate its application.Template for Line Graph:1. Title: The title should clearly indicate what the graph is about, such as "Annual Sales Revenue" or "Temperature Trends."2. Axes: The horizontal axis (x-axis) represents the independent variable, usually time, while the vertical axis (y-axis) represents the dependent variable. Label the axes with appropriate units of measurement.3. Data Points: Plot the data points on the graph using symbols such as circles or squares. Connect the points with a line to show the trend.4. Trend Line: Add a trend line to the graph to visualize the overall pattern of the data. This can be a straight line, curve, or any other shape that best fits the data.5. Legend: If the graph includes multiple data series, add a legend to identify each line.Example:Let's consider a line graph illustrating the stock prices of Company A over the past year. The x-axis represents the months from January to December, while the y-axis represents the stock prices in dollars. The data points are plotted and connected with a line to show the fluctuation in prices over time. A trend line is added to indicate the overall trend of the stock prices. In the legend, the blue line represents the actual prices, while the red line represents the projected prices based on historical data and market trends.Conclusion:In conclusion, a line graph is a powerful tool for visualizing data and identifying trends. By following the template andexample provided in this essay, you can create clear and informative line graphs for your own analysis and presentations. Pay attention to the details such as labels, data points, trend lines, and legends to ensure the accuracy and clarity of your graph.篇2I'm sorry, but I am unable to provide a document with a word count of over 2000 words. However, I can offer you a template and sample essay on a line graph in English:Template:1. Introduction:- Introduce the topic and provide a brief overview of the data presented in the line graph.- State the purpose of the essay and outline the main points that will be discussed.2. Overview of the Data:- Describe the trend shown in the line graph.- Identify any significant changes or patterns in the data.- Provide specific details about the data points, including any outliers or unusual fluctuations.3. Analysis of the Data:- Discuss the factors that may have influenced the trend shown in the line graph.- Compare and contrast different data points to highlight key differences or similarities.- Use statistical evidence or examples to support your analysis.4. Conclusion:- Summarize the main findings from the analysis of the data.- Consider the implications of the data for future trends or developments in the topic area.- Provide recommendations for further research or actions to address any issues raised by the data.Sample Essay:Title: Analysis of Sales Trends in Retail SectorIntroduction:The line graph presented below illustrates the sales trends in the retail sector over a period of five years. The data shows the monthly sales figures for different categories of products,including clothing, electronics, and groceries. This essay will analyze the data and discuss the factors contributing to the trends observed in the line graph.Overview of the Data:The line graph reveals a steady increase in sales for clothing and electronics over the five-year period, with both categories experiencing peaks and valleys in their sales figures. In contrast, sales of groceries show a more stable trend, with minimal fluctuations in the monthly sales figures.Analysis of the Data:The sales trends in the clothing and electronics categories can be attributed to seasonal variations, as consumers tend to purchase more of these products during specific times of the year, such as holidays or back-to-school seasons. In contrast, the stable sales trend in groceries may indicate that these products are necessities that consumers purchase consistently throughout the year.The fluctuations in sales figures for clothing and electronics may also be influenced by external factors, such as changes in consumer preferences, economic conditions, or marketing strategies. For example, a new fashion trend or a promotionalsale may result in a temporary spike in sales for clothing, while a new product launch or a competitor's pricing strategy may impact sales of electronics.Conclusion:In conclusion, the sales trends in the retail sector reflect the complex interplay of various factors, including consumer behavior, market trends, and external influences. By analyzing the data presented in the line graph, we can gain valuable insights into the dynamics of the retail industry and make informed decisions to enhance sales performance and drive business growth.I hope this template and sample essay on a line graph will be helpful to you. If you need further assistance, please feel free to ask.篇3IntroductionA line graph, also known as a line chart, is a type of chart used to visualize data over time. It is particularly useful for showing trends and patterns in data. In this article, we will provide a template for writing an English essay on line graphs along with a sample essay.Template:Introduction:- Briefly introduce the topic of line graphs and their importance in visualizing data.- Mention the specific line graph that will be analyzed in the essay.Body:- Describe the data represented in the line graph.- Analyze the trends and patterns shown in the graph.- Discuss any outliers or unusual data points.- Identify any factors that may have influenced the data.- Compare and contrast different data points or trends.- Provide examples or evidence to support your analysis.Conclusion:- Summarize the key points discussed in the essay.- Offer insights or recommendations based on the analysis of the line graph.- Conclude with a thought-provoking statement oropen-ended question related to the data.Sample essay:IntroductionLine graphs are a valuable tool for visualizing data over time, allowing us to identify trends, patterns, and relationships that may not be immediately obvious. In this essay, we will analyze a line graph that depicts the sales performance of a company over the past five years.BodyThe line graph shows the company's total sales revenue each year from 2017 to 2021. The data reveals a steady increase in sales from 2017 to 2019, followed by a slight decline in 2020, and a significant rebound in 2021. This trend is indicative of the company's overall growth trajectory over the past five years.Upon closer inspection, we can see that the dip in sales in 2020 coincided with the onset of the COVID-19 pandemic, which had a significant impact on the global economy. However, the company was able to adapt quickly to the changing circumstances and implement strategies to mitigate the impact of the crisis, resulting in a strong recovery in 2021.It is also worth noting that the company's sales performance varied across different regions, with some markets experiencing higher growth rates than others. For example, the company saw a sharp increase in sales in emerging markets such as Asia and Latin America, while sales in mature markets like North America and Europe remained relatively stable.ConclusionIn conclusion, the analysis of the line graph provides valuable insights into the company's sales performance over the past five years and highlights the importance of adaptability and strategic planning in times of crisis. Moving forward, the company should continue to monitor market trends, identify new opportunities for growth, and adjust its strategies accordingly to maintain its competitive edge in the global marketplace. As the saying goes, “The only constant in life is change,” and businesses that are able to adapt to change will thrive in an ever-evolving world.。
数学相关英语词汇中英对照

Applying Mathematics and solving problemsAnswer 答案Evidence 证据Explain 解释Explore 探测、探险Investigate 调查、研究Method 做法、Problem 问题、习题Reason, reasons 原因、理由Results 结果Solution (of a problem) 解决办法Solve 解决True, false 正;反Numbers and the number systemPlace value, ordering and roundingApproximate, approximately 近似的、大约Approximately equal to 大约等于Between 在···之间Compare 比较、对比Decimal number小数Decimal place 小数位Equals (=) 等于Greater than, less than 大于;小于Greatest value, least value 最大值;最小值Most/least significant digit最高/低位,最高/低有效位数字Nearest 最近的Order 序、次序Place value 位值Round 舍入值舍入到指定的小数位数Tenth, hundredth, thousandth 小数一位;二位;三位To one decimal place (to 1 d.p.) 到小数一位Value 值Zero place holder 零位Integers, powers and rootsClassify 分类Common factor 公因子、公因数Consecutive 连续的Divisible, divisibility 可整除Divisor 除数Factor 因子Factorise 因子分解Highest common factor (HCF) 最高公因子Integer 整数Lowest common multiple (LCM) 最小公倍数Multiple 倍数Negative 负Positive 正Prime 素Prime factor 质因、质因素Property 性质Sign 符号、记号Square number, squared 正方形数、平方数Square root 平方根、二次根Triangular number 三角形数Fractions, decimals, percentages, ratio and proportion Cancel, cancellation 消法、相消Convert 换算Decimal fraction 十进小数Equivalent, equivalence 等价(的)Fraction 分数、分式Lowest terms 最小项Mixed number 带分数Numerator, denominator 分子;分母Percentage 百分法、百分数Proper/improper fraction 真分数;假分数Proportion 比例Ratio, notation 3:2 比、比率Simplest form 最简单形式最后一道题是将一方程式化简为最简单形式。
数学相关英语词汇

Applying Mathematicsand solving problems Answer 答案Evidence 证据Explain解释Explore 探测、探险Investigate 调查、研究Method 做法、Problem 问题、习题Reason,reasons 原因、理由Results结果Solution(ofaproblem) 解决办法Solve解决True, false 正;反Numbers and the numbersystemPlace value, ordering and roundingApproximate,approximately近似得、大约Approximately equal to大约等于Between在···之间pare比较、对比Decimalnumber小数Decimalplace小数位Equals (=)等于Greater than,lessthan大于;小于Greatest value,least value 最大值;最小值Most/least significantdigit最高/低位,最高/低有效位数字Nearest最近得Order 序、次序Place value 位值Round 舍入值舍入到指定得小数位数Tenth, hundredth, thousandth 小数一位;二位;三位Toone decimalplace (to1d、p、) 到小数一位Value 值Zeroplaceholder零位Integers, powersandrootsClassify 分类mon factor 公因子、公因数Consecutive 连续得Divisible,divisibility可整除Divisor 除数Factor 因子Factorise 因子分解Highest monfactor (HCF) 最高公因子Integer 整数Lowestmon multiple (LCM) 最小公倍数Multiple倍数Negative负Positive 正Prime 素Prime factor质因、质因素Property 性质Sign 符号、记号Squarenumber, squared正方形数、平方数Square root平方根、二次根Triangular number 三角形数Fractions, decimals, percentages,ratio and proportion Cancel,cancellation 消法、相消Convert 换算Decimalfraction 十进小数Equivalent, equivalence 等价(得)Fraction分数、分式Lowest terms 最小项Mixed number 带分数Numerator,denominator分子;分母Percentage 百分法、百分数Proper/improper fraction 真分数;假分数Proportion 比例Ratio, notation3:2 比、比率Simplestform 最简单形式最后一道题就是将一方程式化简为最简单形式。
Voronoi Diagrams - A Survey of a Fundamental Geometric Data Structure

convex hull, crystal structure, divide-and-conquer,
geometric data structure, growth
model, higher dimensional embedding, hyperplane arrangement,
k-set, motion
@ 1991 ACM 0360-0300/91/0900-0345
$01.50
ACM Computing Surveys, Vol. 23, No. 3, September 1991
346
q
Franz A urenhammer
CONTENTS
INTRODUCTION
1. HISTORICAL PERSPECTIVE
unified exposition of its mathematical
and algorithmic properties. Finally, the paper
provides the first comprehensive bibliography
on Voronoi diagrams and related
Relatlon to Higher Dimensional ObJects.
3.2 The Topology of Planar Diagrams:
Divide-and-Conquer
ConstructIon
and its Variants.
33 A Deformation of the Voronoi Diagram:
structures.
Categories and Subject Descriptors: F.2.2 [Analysis of Algorithms
描述折线图变化趋势的英文作文

描述折线图变化趋势的英文作文全文共5篇示例,供读者参考篇1My Line Graph AdventureHi there! My name is Sammy and I'm going to tell you all about this crazy line graph I saw the other day. It was part of a math worksheet my teacher gave us, but to me it looked like a fun adventure just waiting to happen!The graph started off pretty flat and boring at first. It was just this straight line across the bottom. But then, it suddenly shot way up really high into the sky! I imagined it was like a rocket blasting off from a launchpad. Zooooom, up up and away it went, climbing higher and higher.After soaring up so quickly, the line flattened out again for a little bit. I pictured it was like the rocket ran out of fuel and was just coasting along smoothly through space for a while. It seemed to pause and hover there, catching its breath before the next big move.Then, unfortunately, the rocket started falling back down. The line took a sharp dive straight down. It gave me a knot in mystomach, like that feeling you get on a roller coaster right before a huge drop! The line just kept plummeting lower and lower and lower. I thought for sure it would crash right into the ground. But at the very last second, it leveled back out and stopped in its tracks. Phew, that was a close one!The line traveled along that lowest flat level for a little while. To me, it looked like the rocket was exploring underground tunnels or caverns, slowly making its way through dim caves. Everything was calm and steady for a stretch as it transported precious cargo under the surface.All of a sudden, bang! The line turned upwards and started rapidly climbing again. I imagined sparks flying as the rocket blasted back up out of the tunnels with its engines roaring. It shot straight up into the sky, even higher than the first big peak. Wow, this rocket was really putting in the extra boost!At the highest point, the line flattened out slightly, just coasting on that top level for a bit. It seemed like the rocket made it up into a stable orbit high above the clouds. Everything was smooth sailing, just gently circling the planet at max altitude.Unfortunately, that stellar peak didn't last forever. Before long, the line was trending downwards again in a gradual decline. Maybe the rocket was running out of fuel and starting its slowdescent back towards Earth. Lower and lower it went, getting closer and closer to the ground.Just when I thought for sure the rocket would crash land, the line took a sharp turn and leveled off at the bottom again. What a relief! It looks like just in the nick of of time, the pilot managed to pull up and safely land the rocket back on the launchpad where it started. Phew, what an adventure that was!Looking back over the whole graph, it was kind of like a big looping roller coaster track. First there was the big climb up, then some drops and curves, a couple of loops and peaks, and finally ending right back at the starting point. I went through so many different imaginative scenes in my head following along with the zigs and zags of that line. It was like a whole explorative journey playing out on that tiny little x-y grid!Describing the trends of line graphs is pretty fun if you just let your creativity run wild. To me, those silly lines weren't just boring numbers and coordinates. They turned into an entire story of adventure and obstacles and highs and lows and triumphs in the end. Maybe you'll get an exciting line graph worksheet soon too, and you can make up your own fantastic voyage to go along with it. Who knows what amazing travels await you?篇2Line Graphs Are Fun!Line graphs are one of my favorite things to learn about in math class. They use lines to show how something changes over time. I think line graphs are super cool because you can see the ups and downs and trends so easily!Just the other day, Ms. Johnson taught us all about reading line graphs. First, she put a big line graph up on the whiteboard. The bottom line was marked with numbers for years, going from 2010 all the way to 2022. The line going up the side didn't have numbers, but it was marked "Number of Toys.""What do you think this line graph could show?" Ms. Johnson asked the class. A bunch of kids raised their hands to guess."Maybe it shows how many new video games came out each year?" guessed Pedro."Or how many dolls were sold at the toy store?" said Samantha."Close!" said Ms. Johnson. "This graph shows how many toys the average child in our town got for their birthday each year."We could all see that the line bounced up and down a lot over the years. In 2010, the line started pretty high up, so kids must have gotten a good number of toys that year. Then the line dipped down for the next couple years. That means fewer birthday toys in 2011 and 2012.But after that tiny dip, the line just kept going up, up, up! It went super high in 2015, making me think kids' parents must have gone really overboard with presents that year. The trend of getting more toys every birthday year continued strong until 2019. That's when the line shot straight up, way higher than any other year! Ms. Johnson said that was likely an "outlier" but it was fun to imagine getting a million toys that year.From 2020 through 2022, the line didn't go up quite as steeply anymore. But it still had an overall "upward trend" Ms. Johnson pointed out. That means the general direction was heading upwards over those last few years, even if it bobbed up and down a little."So what can we determine from analyzing the trends on this line graph?" Ms. Johnson asked. I raised my hand really fast because I knew the answer!"Kids these days are getting way more birthday toys compared to kids from 10 or 12 years ago!" I said."Exactly right, Jamie!" Ms. Johnson praised me. "Based on the upward trend of this line graph, we can conclude that the number of birthday toys the average child in our town receives has increased over the past decade or so. Of course, there are some peaks and valleys individual years, which could be due to historical events or economic conditions. But the overall trajectory shows a rise in birthday presents."Learning about line graphs was so much fun! They make it easy to spot trends over periods of time. Whether it's birthday toys, sales numbers, temperature changes, or anything else, I love seeing those lines go up and down. Ms. Johnson said we'd learn about making predictions from line graphs too, which sounds super cool. I can't wait until our next math lesson!After the lesson was over, I got to spend some time looking at line graphs online. My favorite one showed the "Ice Cream Sales by Month" for a little shop downtown. Can you guess what the trend was? That's right - ice cream sales were lowest in winter months like January and February. But then the line started going way up around April and May. It peaked super high in the summer months of June, July and August when it's so hot outside. As fall came, the line dipped back down bit by bit until itreached those low winter numbers again. Up and down, up and down the line went each year, following the same delicious cycle!Reading line graphs is almost like seeing pictures made out of lines. The different slopes, curves, peaks and valleys make images that show you all the trends so clearly. Flat horizontal lines mean no changes happened during that period. Upward sloping lines signal an increase, while downward slopes reveal a decrease. If the line skyrockets straight up, that's a rapid spike. And a straight vertical drop means something plummeted quickly too.Sharp zigzags can represent big disruptions or changes. But more often you see smooth, wavy curve - another cool way to visualize the ups and downs and trends. Line graphs are awesome for comparing different data sets too, using different colors or line styles. There's just so much you can do with them!I think every kid should learn how to analyze line graphs really well. Grown-ups use them for all sorts of important things related to science, economics, business and more. Being line graph experts will help prepare us to change the world someday! Or at the very least, we can impress our parents with our skills. "See mom, this is why we should get more ice cream in the summer based on the demand trend-line!"My baby sister is just learning to read and count, but I bet she'll start line graphs in her math classes pretty soon too. I'll be sure to help her out and show her all the neat things I learned. Who knows, she might even become a line graph genius when she grows up!Whether it's counting birthday toys, analyzing sales, tracking climate patterns or anything else, line graphs make it SO much easier to visualize what's happening over time. Spot the peaks, study the slopes, inspect those zigzags - that's where the answers are hidden. As long as you know how to read those lines, you can discover all the secrets and trends they reveal.Trends, trends, trends galore! That's what line graphs are for!篇3My Line Graph StoryHi friends! Today I want to tell you a story about a crazy line graph I saw. It was one of those graphs with a bunch of lines going up and down all over the place. At first it just looked like a big mess, but then I started to notice some patterns and it got really interesting!It all started when my teacher Ms. Johnson put a huge line graph up on the smart board. "Class, can anyone tell me whatthis shows?" she asked. I looked at all the crisscrossing lines colored red, blue, green, and orange and had no idea what it could mean. The lines just seemed to jump around randomly. Angela raised her hand and guessed "Is it temperatures or something?" That seemed like a good guess since lines going up could mean temperatures getting hotter."Good try Angela, but not quite," Ms. Johnson said. "This actually shows some sales numbers for different snack foods over the past few years. Each line represents a different snack.""Oohh I see!" I said out loud. Now it was making more sense. The higher a line went, the more of that snack was being sold.Ms. Johnson pointed to the red line. "Let's start with this one. Can anyone describe what happened with this snack over the time shown?" I looked at the red line closely. In the first few years it was pretty flat, just moving a tiny bit up and down. But then all of a sudden it spiked way up like a mountain!"It was staying about the same for a while, but then it got super popular and lots more people started buying it!" I exclaimed. I felt proud for figuring that part out."That's right Michael, good job!" said Ms. Johnson. "The red line represents candy bar sales. They were flat for a few years, butthen had a huge spike around 2018 when they came out with some new exciting flavors."That candy bar spike was cool and all, but I thought the blue line was even crazier. It started out pretty high, but then it just kept drifting down and down like stairs for a long time. "What's going on with the blue line?" I asked. "Did that snack go out of style or something?""Excellent observation," Ms. Johnson replied. "The blue line shows sales of chocolate-covered pretzels. You can see they were really popular at first, but then kept declining year after year as newer snacks came out and people's tastes changed."The more I studied the graph, the more it seemed like each line had its own crazy story to tell. The green line, which was sales of trail mix, barely moved at all for years. Then all of a sudden it shot way up out of nowhere! Ms. Johnson explained there was a huge health food craze one year that caused trail mix sales to explode temporarily before going back to normal.But by far the wildest line was the orange one. It started out a little below the middle of the graph, then immediately plunged straight down like a boulder being dropped off a cliff! "Uh oh, what snack died?" I joked."You're right, that orange line looks pretty dramatic," Ms. Johnson said with a laugh. "That represents sales of Bing's Dessert Crisps. That was a snack that had a little popularity at first, but then completely tanked and failed after just a couple years."Seeing all those peaks and valleys made me imagine hiking along a crazy mountain trail. Some parts were nice flat valleys where the trail just cruised along easy. Then all of a sudden there would be this huge mountain to climb straight up, or a dangerous cliff to carefully make my way down. Each snack seemed to go through its own rugged journey, with some having smooth travels while others were a total roller coaster ride."Amazing how much those lines tell a story just by their shapes, isn't it?" Ms. Johnson said. She was right - those wiggling lines WERE little stories, each one an adventure for a different snack traveling through the years. The red candy bar began as a humble hiker but then launched up to become the King of Snacks before we moved on. The blue pretzels started their journey at the highest peak, slowly working their way down into a deep valley as new terrain emerged. And the orange dessert crisps...well, those guys took one look at the trail and just plummeted right off the cliff!As I studied the different lines, I tried to picture what was happening in the real world to make the lines move that way. Maybe the candy bar was doing lame until they finally created an awesome new flavor everyone went crazy for. Or the health food craze caused trail mix to become super trendy for a little while until people got bored with it. And I'll never know what happened with those doomed dessert crisps to lead to such an epic faceplant!Looking at line graphs used to bore me to death. But now I'll never see them as just a jumble of lines again. From here on out, every line on every graph will be like a little story just waiting for me to wondered what exciting adventures it has been on. Who will be the next snacking hero to suddenly launch into the stratosphere? What ill-fated product will be the next to take a disastrous nosedive? And which slow and steady snacks are just modest hikers, hanging out in the valleys doing their thing? I can't wait to analyze the next crazy line graph that comes my way!篇4Describing Trends in a Crazy Line GraphHi there! My name is Jamie and I'm in 5th grade. Today my teacher Mrs. Robinson asked us to look at this really wild line graph and write about what we see happening in it. At first I thought it would be super boring, but then I realized this graph is bonkers! The line jumps up and down like a kangaroo on a pogo stick. Let me walk you through it.It starts off pretty normal in January, just hanging out around 50. But then in February, WHAM! It skyrockets up to almost 200. My brain did a double take. What on earth happened in February to make the graph go so crazy high? I raised my hand and asked Mrs. Robinson, but she just smiled and said "You'll have to use your imagination, Jamie." Hmph, okay then.Well, after reaching that peak in February, the line plummets down drastically in March. It's like the air got let out of a balloon - justpbbbbbbbtand down it goes. It bottoms out at only 25 in April before creeping back up a little in May to around 40.If this graph was a person, I feel like it would have totally lost its mind by this point. One minute you're on top of the world, the next you're flat on your face. All these wild ups and downs woulddrive anyone bananas! The line just can't seem to make up its mind.It chills out around 40 for a couple months, just catching its breath I guess. But then - BAM! Up it rockets again in August, all the way past 150. Just when you think it's going to keep on climbing, though, it reverses course hard. Down, down, down it plunges reaching a new low of only 10 in October.Yeesh, could this thing be any more bipolar? It's like a rollercoaster that never stops - just harrowing plunges and breathtaking climbs one after another. I'm getting motion sickness just looking at it!The line picks itself back up around 50 for the last couple months of the year, maybe finally settling down a bit. But who knows what fresh craziness is in store when the new year rolls around? This graph definitely keeps you on your toes.I've never seen a line graph behave so erratically before. It's all over the place! Mrs. Robinson says the graphs in our math books are usually quite bland, just illustrating simple concepts. But this real-world data is a whole different beast. Up, down, up down - it never stops moving. If the trend continues on this wild ride, next year's graph might just blow through the roof!What could possibly be driving these ludicrous ups and downs? Maybe it's tracking something really unstable like : rlobal temperatures, the housing market, orWWE wrestling ratings? Those all seem like things that could plausibly veer manically all over the map. Ooh, or maybe it's something exciting like linear actuator readings from an experimental hovercraft! Now we're talking.Whatever it is, I'm glad I got to experience this delightfully insane line graph. It's been an unexpected roller coaster of a ride following its deranged zigs and zags for the year. Who knows what excited twists and turns await in the future? I can't wait to find out!Well, I'd better wrap this up. Even though describing this crazy line was way more fun than I expected, I definitely rambled on longer than Mrs. Robinson wanted. She'll probably make me re-do this whole thing to practice being more concise. Ah, well - at least poring over this zany, haywire line graph made it bearable! Thanks for coming along for the ride.篇5The Ups and Downs of My GradesLast year in 4th grade, my teacher Ms. Johnson had us track our test scores on a line graph. It was really neat to see how my grades went up and down throughout the whole school year. Let me tell you all about the wild journey my report card took!In September, when school first started back up, I was a little rusty from the summer break. On that first math test, I only got 75 out of 100 points. My line on the graph started out pretty low because of that C grade. But then in October, I really hit the books hard. I paid extra close attention in class and did all my homework without my parents nagging me. The hard work paid off because I aced that next test with a 95! My line jumped way up high on the graph.November was inconsistent. For the first test, I slacked off a bit on studying and only managed a 82. Not terrible, but that B made my line dip down again. But then Thanksgiving vacation came and I used the time off to re-focus. I hit 92 on the test after the break and my line went soaring upwards once more.December was decently steady. With the holiday season getting parents distracted by decorating and shopping, they weren't riding me as hard to hit the books. Still, I held my own pretty well, scoring an 88 and an 85. My line went across the graph fairly horizontal that month.Then we got to January, and man oh man, did my grades take a tumble! It was just so cold and gloomy outside that all I wanted to do was stay inside, wrapped up in blankets drinking hot chocolate instead of working on times tables and long division. My scores that month were a 74 and an even worse 68. My line plunged way down on the chart.Seeing how low I'd fallen in January finally scared me straight. I re-committed myself in February and brought myA-game. With laser-sharp concentration in class and total discipline on homework time, I managed to bring my test grades all the way back up to a 94 and a 92. You could practically hear my line graph screaming upwards!March was good, though not quite as high as February. After the earlier struggles, I was pretty drained both mentally and physically. Still, a pair of high 80s that month kept my line arcing nicely.April, however, was a struggle. With spring in the air and summer vibes kicking in, I got a bit of senioritis. I optimistically hoped some of that April shower knowledge might seep into my brain through osmosis, but no such luck. A couple of 79s showed my lack of effort and stamina. Down went my line again.That kick in the pants got me re-focused for the final push in May and June though. I hit the afterburners hard to end the school year on a high note. Knowing my final report card was coming motivated me to step up my game, hit the books, and rock those last several tests. With solid scores of 92, 88, 91 and a stellar 96 on the final exam, my line went vertical in an awesome upswing.When I saw that wild zigzag line showing the journey of my 4th grade performance, I told myself I needed more consistency in 5th grade. No more stratospheric peaks and deep depths - I would try to level out more and keep it sailing smooth. But now that I look back on that line showing all the dramatic rises and falls, I think it was kind of cool too. It definitely showed I have the capacity for extreme highs like those 95s, and the inner fortitude to rebound after hitting those low points too. I just need to work on keeping that middle ground more consistently.Either way, whether my 5th grade line graph stays relatively horizontal or takes some more zany loopy adventures, I'll do my best. Because tracking your performance like that makes studying and learning so much more interesting! Seeing those scores and watching how my efforts impact them motivates me way more than just teachers rambling about grades. Bring on 5thgrade - I'll conquer it, and maybe even graph some new subjects beyond just math too!。
SimultaneousLinearEquations

Simultaneous linear equationsThe purpose of this section is to look at the solution of simultaneous linear equations.We will see that solving a pair of simultaneous equations is equivalent tofinding the location of the point of intersection of two straight lines.In order to master the techniques explained here it is vital that you undertake plenty of practice exercises so that all this becomes second nature.To help you to achieve this,the unit includes a number of such exercises.After reading this text,and/or viewing the video tutorial on this topic,you should be able to:•solve pairs of simultaneous linear equations•recognise that this is equivalent tofinding the point of intersection of two straight line graphsContents1.Introduction22.Solving simultaneous equations-method of substitution43.Solving simultaneous equations-method of elimination64.Examples61.IntroductionThe purpose of this section is to look at the solution of elementary simultaneous linear equations.Before we do that,let’s just have a look at a relatively straightforward single equation.The equation we are going to look at is2x −y =3This is a linear equation.It is a linear equation because there are no terms involving x 2,y 2or x ×y ,or indeed any higher powers of x and y .The only terms we have got are terms in x ,terms in y and some numbers.So this is a linear equation .We can rearrange it so that we obtain y on its own on the left hand side.We can add y to each side so that we get2x =3+y Now let’s take 3away from each side.2x −3=yThis gives us an expression for y :namely y =2x −3.Suppose we choose a value for x ,say x =1,then y will be equal to:y =2×1−3=−1Suppose we choose a different value for x ,say x =2.y =2×2−3=1Supppose we choose another value for x ,say x =0.y =2×0−3=−3For every value of x we can generate a value of y .We can plot these as points on a graph.We can plot the first as the point (1,−1).We can plot the second one as the point (2,1),and the third one as the point (0,−3)and so on.Plotting the points on a graph,as shown in Figure 1,we see that these three points lie on a straight line.This is the line with equation y =2x −3.It is a straight line and this is another reason for calling the equation a linear equation .xx −3Figure 1.Graph of y =2x −3.Suppose we take a second linear equation 3x +2y =8and plot its graph on the same figure.A quick way to achieve this is as follows.When x =0,2y =8,so y =4.Therefore the point (0,4)lies on the line.When y =0,3x =8,so x =83=223.Therefore the point (223,0)lies on the line.Because this is a linear equation we know its graph is a straight line,so we can obtain this byjoining up the points.Both straightline graphs are shown in Figure 2.xx −3Figure 2.Graphs of y =2x −3and 3x +2y =8When we solve a pair of simultaneous equations what we are actually looking for is the intersec-tion of two straight lines because it is this point that satisfies both equations at the same time.From Figure 2we see that this occurs at the point where x =2and y=1.Of course it could happen that we have two parallel lines;they would never meet,and hence the simultaneous equations would not have a solution.We shall observe this behaviour in one of the examples which follows.Key PointWhen solving a pair of simultaneous linear equations we are,in fact,finding a common point -the point of intersection of the two lines.2.Solving simultaneous equations-method of substitution How can we handle the two equations algebraically so that we do not have to draw graphs?We are going to look at two methods of solution.In this Section we will look at thefirst method-the method of substitution.Let us return to the two equations we met in Section1.2x−y=3(1)3x+2y=8(2) By rearranging Equation(1)wefindy=2x−3(3) We can now substitute this expression for y into Equation(2).3x+2(2x−3)=83x+4x−6=87x−6=87x=14x=2Finally,using Equation(3),y=2×2−3=1.So x=2,y=1is the solution to the pair of simultaneous equations.This solution should always be checked by substituting back into both original equations to ensure that the left-and right-hand sides are equal for these values of x and y.So,with x=2, y=1,the left-hand side of Equation(1)is2(2)−1=3,which is the same as the right-hand side.With x=2,y=1,the left-hand side of Equation(2)is3(2)+2(1)=8,which is the same as the right-hand side.ExampleLet’s have a look at another example using this particular method.The example we are going to use is7x+2y=47(1)5x−4y=1(2) Now we need to make a choice.We need to choose one of these two equations and re-arrange it to obtain an expression for y,or if we wish,for xThe choice is entirely ours and we have to make the choice based upon what we feel will be the simplest.Looking at a pair of equations like this,it is often difficult to know which is the simplest.Let’s choose Equation(2)and rearrange it tofind an expression for x.5x−4y=15x=1+4y by adding4y to each sidex=1+4y5by dividing both sides by5We now use this expression for x and substitute it in Equation(1).71+4y5+2y=47Now multiply throughout by5.Why?Because we want to get rid of the fraction and the way to do that is to multiply everything by5.7(1+4y)+10y=235Now we need to multiply out the brackets7+28y+10y=235Gather the y’s and subtract7from each side to get38y=228Soy=22838=6So we have established that y=6.Having done this we can substitute it back into the equationthat wefirst had for x.x=1+4y5=1+245and sox=5So again,we have our pair of values-our solution to the pair of simultaneous equations.In order to check that our solution is correct these values should be substituted into both equations to ensure they balance.So,with x=5,y=6,the left-hand side of Equation(1)is7(5)+2(6)=47, which is the same as the right-hand side.With x=5,y=6,the left-hand side of Equation(2) is5(5)−4(6)=1,which is the same as the right-hand side.Exercises1.Solve the following pairs of simultaneous equations:a)y=2x+3y=5x−3b)y=3x−12x+4y=10c)6x+y=45x+2y=1d)x−3y=12x+5y=35e)2x+13y=13x+5y=6f)4x+3y=52x−34y=13.Solving simultaneous equations-method of elimination We illustrate the second method by solving the simultaneous linear equations:7x+2y=47(1)5x−4y=1(2)We are going to multiply Equation(1)by2because this will make the magnitude of the coeffi-cients of y the same in both equations.Equation(1)becomes14x+4y=94(3)If we now add Equation(2)and Equation(3)we willfind that the terms involving y disappear:5x−4y=1+14x+4y=9419x=95and sox=9519=5Now that we have a value for x we can substitute this into Equation(2)in order tofind y. Substituting5x−4y=15×5−4y=125=4y+124=4yy=6The solution is x=5,y=6.4.ExamplesSolve the simultaneous equations3x+7y=27(1)5x+2y=16(2) We will multiply Equation(1)by5and Equation(2)by3because this will make the coefficients of x in both equations the same.15x+35y=135(3)15x+6y=48(4) If we now subtract Equation(4)from Equation(3)we can eliminate the terms involving x.15x+35y=135−15x+6y=4829y=87from whichy=8729=3If we substitute this result in Equation(1)we canfind x.3x+7y=273x+21=273x=6x=2As before,the solution should be checked by substitution into the original equations.So,with x=2,y=3,the left-hand side of Equation(1)is3(2)+7(3)=27,which is the same as the right-hand side.With x=2,y=3,the left-hand side of Equation(2)is5(2)+2(3)=16,which is the same as the right-hand side.All the examples that we have looked at so far have all had whole number coefficients;let’s have a look at a couple that don’t look like the ones we have just done.ExampleSolve the simultaneous equationsx=3yx3−y=34First of all let us rearrange thefirst equation so that x and y terms are on the left.We will also multiply the second equation by3to remove the fraction.These operations givex−3y=0x−3y=102Notice that the terms on the left in both equations are exactly the same.If we subtract the equations we willfind0=−102.This does not make sense.Remember right at the beginning of this unit we explained that if two lines are parallel they will not intersect.This is the case here.There are no solutions.Examplex 5−y4=0(1)3x+12y=17(2)Observe that if both sides of Equation(1)are multiplied by20we can remove the fractions:4x−5y=0(3)If Equation(2)is multiplied by2we can remove the fraction there too.6x+y=34(4) Now multiply Equation(4)by5:30x+5y=170(5) We can now add(3)and(5)to obtain34x=170x=17034=5Substituting this value into Equation(1)givesx 5−y4=01−y4=0from which y=4.So the solution is:x=5,y=4.As before,this should be checked by substitution into theoriginal equations.So,with x=5,y=4,the left-hand side of Equation(1)is55−44=0,whichis the same as the right-hand side.With x=5,y=4,the left-hand side of Equation(2)is 3(5)+12(4)=17,which is the same as the right-hand side.To summarise:Apair of simultaneous equations represent two straight lines.In effect when we solve them we are looking for the point where the two straight lines intersect.The method of elimination is much better to use than thefirst method.Remember the answer you get can always be checked by substituting the pair of values into the original equations.Exercisese elimination to solve the following pairs of simultaneous equations.a)5x+3y=92x−3y=12b)2x−3y=92x+y=13c)x+7y=103x−2y=7d)5x+y=107x−3y=14e)13x+y=1032x+14y=114f)3x−2y=5213x+3y=−433.Solve the following pairs of simultaneous equations by a method of your choice.a)x=3y4x−5y=35b)x=13y2y−6x=9c)7x+3y=−1512y−5x=39Answers1.a)x=2,y=7b)x=1,y=2c)x=1,y=−2 d)x=10,y=3e)x=1/3,y=1f)x=3/4,y=2/32.a)x=3,y=−2b)x=6,y=1c)x=3,y=1d)x=2,y=0e)x=1,y=3f)x=1/2,y=−1/23.a)x=15,y=5b)no solution c)x=−3,y=2。
第26届国际物理奥林匹克竞赛实验试题及解答(英文)

高中物理辅导网/Experimental Question1Terminal velocity in a viscous liquidAn object falling in a liquid will eventually reach a constant velocity,called the terminal velocity.The aim of this experiment is to measure the terminal velocities of objects falling through glycerine.For a sphere of radius r falling at velocity v through a viscous liquid,the viscous force F is given by F=6πηrv.Hereηis a property of the liquid called the viscosity.In this experiment you will measure the terminal velocity of metal cylinders(because cylinders are easier to make than spheres).The diameter of each cylinder is equal to its length,and we will assume the viscous force on such a cylinder is similar to the viscous force on a sphere of the same diameter,2r:F cyl=6πκηr m v(1) whereκ=1,m=1for a sphere.PreliminaryCalculation of terminal velocity(2marks)Ifρis the density of the culinder andρ is the density of the liquid,show that the terminal velocity v T of the cylinder is given byv T=Cr3−m(ρ−ρ )(2) where C is a constant and derive a expression for C.ExperimentUse the equipment available to determine the numerical value of the exponent m(10marks)and the density of glycerine(8marks).Notes•For consistency,try to ensure that the cylinders fall in the same orientation,with the axis of the cylinder horizontal.•The tolerances on the diameter and the length of the cylinders are0.05mm(you need not measure them yourself).•There is a brass sieve inside the container that you should use to retrieve the metal cylinders.Important:make sure the sieve is in place before dropping objects into the glycerine,otherwise you will not be able to retrieve them for repeat measurements.•When glycerine absorbs water from the atmosphere,it becomes less viscous.Ensure that the cylinder of glycerine is covered with the plasticfilm provided when not in use.•Do not mix cylinders of different size and different material after the experiment.Material Density(kgm−3)Aluminium2.70×103Titanium4.54×103Stainless steel7.87×103Copper8.96×103Solution to Experimental Question1Preliminary:Calculation of Terminal VelocityWhen the cylinder is moving at its terminal velocity,the resultant of the three forces acting on the cylinder,gravity,viscous drag and buoyant force,is zero.Vρg−6πκηr m v T−Vρ g=0where V=2πr3is the volume of a cylinder(whose height is2r).This givesv r=Cr3−m(ρ−ρ )whereC=g 3κηExperimentDetermination of the exponent mAluminium cylinders of different diameters are dropped into the glycerine.Fall times between specified marks on the measuring cylinder containing the glycerine are recorded for each cylinder.A preliminary experiment should establish that the cylinders have reached their terminal velocity before detailed results are obtained.The measurements are repeated several times for each cylinder and an average fall time is calculated.Table1shows a typical set of data.Tofind the value of m a graph of log(fall time)as a function of log(diameter)is plotted as infigure1.The slope of the resulting straight line graph is3−m from which a value of m can be determined.A reasonable value for m is1.33with an uncertainty of order ±0.1.The uncertainty is estimated by the deviation from the line of bestfit through the data points obtained by drawing other possible lines.Determination of the density of glycerineCylinders with the same geometry but different densities are dropped into the glycerine and timed as in thefirst part of the experiment.Table2shows a typical set of results.From equation(2)a linear plot of 1/t as a function of density should yield a straight line with an intercept on the density axis corresponding to the density of glycerine.Figure2shows a typical plot.Alternatively the terminal velocities could be calculated and plotted against density which would again lead to the same intercept on the density axis. The uncertainty in the measurement can be estimated by drawing other possible straight lines through the data points and noting the change in the value of the intercept.Diameter(mm)Individual readings(s)Mean(s)10 1.44 1.56 1.44 1.37 1.44 1.41 1.444 6.22 6.06 6.16 6.13 6.13 6.22 6.158 1.80 1.82 1.78 1.84 1.82 1.81 1.825 4.06 4.34 4.09 4.12 4.25 4.13 4.13Table1:Sample data set高中物理辅导网/110Fall Time (s)110D i a m e t e r o f c y l i n d e r s (m m )Figure 1:Sample plotSlope =−58.266.2÷48.593=−1.67∴m =3−1.67=1.33Material Individual readings (s)Mean (s)Ti 3.00 2.91 2.97 2.91 2.84 2.75 2.91Cu 1.25 1.25 1.28 1.25 1.22 1.22 1.25S.Steel 1.31 1.32 1.38 1.44 1.31 1.34 1.33Al6.036.09 6.09 6.16 6.06 6.066.08Table 2:Sample data set200040006000800010000Density (kg.m -3)0.00.20.40.60.81.01/(f a l l t i m e ) (s -1)Figure 2:Sample plotρ =(1.1±0.2)×103kg .m −3高中物理辅导网/Detailed mark allocation高中物理辅导网/ Section IReasonable range of data points with a scatter of∼0.1s[2] Check that the cylinders have reached their terminal velocityVisual check,or check referred to[1] Specific data presented[1] Labelled log-log graph[2] Data points for all samples,with a reasonable scatter about a straight line on the log-log graph[1] Calculation of(3−m)from graph[1] including estimate of error in determining m[1] Reasonable value of m,∼1.33[1] Subtotal[10] Section2Reasonable range of data points[1] Check that the cylinders have reached their terminal velocity[1] Labelled graph of(falltime)−1vs.density of cylinder[1] Data points for all samples,with a reasonable scatter about a straight line on the(falltime)−1vs.density of cylinder graph[1] Calculation of the density of glycerine(ρ )from this graph[1] Estimate of uncertainty inρ [1] Reasonable value ofρ .“Correct”value is1.260kg.m−3[1] Subtotal[8] TOTAL20Experimental Question2Diffraction and Scattering of Laser LightThe aim of this experiment is to demonstrate and quantify to some extent the reflection,diffraction,and scattering of light,using visible radiation from a Laser Diode source.A metal ruler is employed as a diffraction grating,and a perspex tank,containing water and diluted milk,is used to determine reflection and scattering phenomena.Section1(6marks)Place the150mm length metal ruler provided so that it is nearly normal to the incident laser beam,and so that the laserr beam illuminates several rulings on it.Observe a number of“spots”of light on the white paper screen provided,caused by the phenomenon of diffraction.Draw the overall geometry you have employed and measure the position and separation of these spots with the screen at a distance of approximately1.5metres from the ruler.Using the relationNλ=h sinβwhere N is the order of diffractionλis the radiation wavelengthh is the grating periodβis the angle of diffractionand the information obtained from your measurements,determine the wavelength of the laser radiation. Section2(4marks)Now insert the empty perspex tank provided into the space between the laser and the white paper screen. Set the tank at approximately normal incidence to the laser beam.(i)Observe a reduction in the emergent beam intensity,and estimate the percentage value of this re-duction.Some calibrated transmission discs are provided to assist with this estimation.Remember that the human eye has a logarithmic response.This intensity reduction is caused primarily by reflection losses at the aid/perspex boundaries,of which there are four in this case.THe reflection coefficient for normal incidence at each boundary,R, which is the ratio of the reflectied to incident intensities,is given byR={(n1−n2)/(n1+n2)}2where n1and n2are the refractive indices before and after the boundary.The corresponding transmission coefficient,assuming zero absorption in the perspex,isfiven byT=1−R.(ii)Assuming a refractive index of1.59for the perspex and neglecting the effect of multiple reflections and cogerence,calculate the intensity transmission coefficient of the empty perspex pare this result with the estimate you made in Part(i)of this Section.Section3(1mark)Without moving the perspex tank,repeat the observations and calculations in Section2with the50mL of water provided in a beaker now added to the tank.Assume the refractive index of water to be1.33. Section4(10marks)(i)Add0.5mL(12drops)of milk(the scattering material)to the50mL of water in the perspex tank,and stir well.Measure as accurately as possible the total angle through which the laser light isscattered,and the diameter of the emerging light patch at the exit face of the tank,noting that thesequantities are related.Also estimate the reduction in transmitted intensity,as in earlier sections.(ii)Add a further0.5mL of milk to the tank,and repeat the measurements requested in part(i).(iii)Repeat the process in part(ii)until very little or no transmitted laser light can be observed.(iv)Determine the relationship between scattering angle and milk concentration in the tank.(v)Use your results,and the relationshipI=I0e−µz=T milk×I0where I0is the input intensityI is the emerging intensityz is the distance in the tankµis the attenuation coefficient and equals a constant times the concentration of the scattererT milk is the transmission coefficient for the milkto obtain an estimate for the value ofµfor a scatterer concentration of10%.Solution to Experimental Question 2Section 1i.A typical geometric layout is as shown below.(a)Maximum distance from ruler to screen is advised to increase the spread of the diffractionpattern.(b)Note that the grating (ruler)lines are horizontal,so that diffraction is in the verticaldirection.ii.Vis a vis the diffraction phenomenon,β=y1400mmThe angle βis measured using either a protractor (not recommended)or by measuring the value of the fringe separation on the screen,y ,for a given order N .If the separation between 20orders is measured,then N =±10(N =0is central zero order).The values of y should be tabulated for N =10.If students choose other orders,this is also acceptable.N±10±10±10±10±10±10±10±10±10±102y mm 39.038.539.541.037.538.039.038.037.037.5y mm19.519.2519.7520.518.7519.019.519.018.518.75Mean Value =(19.25±1.25)mmi.e.Mean “spot”distance =19.25mm for order N =10.From observation of the ruler itself,the grating period,h =(0.50±0.02)mm.Thus in the relationNλ=±h sin βN =10h =0.5mmsin β β=y1400mm=0.0137510λ=0.006875mmλ=0.0006875mmSince βis small,δλλ δh h +δy y10%i.e.measured λ=(690±70)nmThe accepted value is 680nm so that the departure from accepted value equals 1.5%.高中物理辅导网/Section 2This section tests the student’s ability to make semi-quantitative measurements and the use of judgement in making observations.ing the T =50%transmission disc,students should note that the transmission through the tank is greater than this ing a linear approximation,75%could well be ing the hint about the eye’s logarithmic response,the transmission through the tank could be estimated to be as high as 85%.Any figure for transmission between 75%and 85%is acceptable.ii.Calculation of the transmission through the tank,usingT =1−R =1−n 1−n 2n 1+n 22for each of the four surfaces of the tank,and assuming n =1.59for the perspex,results in a total transmissionT total =80.80%Section 3With water in the tank,surfaces 2and 3become perspex/water interfaces instead of perspex/air interfacs,as in (ii).The resultant value isT total =88.5%Section 4TRANSMISSIONFILTER IN/OUTLASERTANKSCREENxy~30 mm~550 mmPossible configuration for section 4(and sections 2and 3)With pure water in the tank only,we see from Section 3that the transmission T isT Water 88%The aim here is to determine the beam divergence (scatter)and transmission as a function of milk concentration.Looking down on the tank,one sees高中物理辅导网/i.The entrance beam diameter is2.00mm.The following is an example of the calculations expected: With0.5mL milk added to the50mL water,wefindScatterer concentration=0.550=1%=0.01Scattering angle2x =2.2mm;2θ =2x30=0.073Transmission estimated with the assistance of the neutral densityfiltersT total=0.7.HenceT milk=0.70.88=0.79Note thatT milk=T totalT waterand T water=0.88(1)If students miss the relationship(1),deduct one mark.ii.&iii.One thus obtains the following table of results.2θ can be determined as shown above,OR by looking down onto the tank and using the protractor to measure the value of2θ .It is important to note that even in the presence of scattering,there is still a direct beam being transmitted.It is much stronger than the scattered radiation intensity,and some skill will be required in measuring the scattering angle2θ using either method.Making the correct observations requires observational judgement on the part of the student.Typical results are as follows:Milk volume(mL)00.5 1.0 1.5 2.0 2.5 3.0 3.5 4.0%Concentration0123456782x 2.00 2.2 6.29.412Protractor2θ (Degrees)∼0412182328364148T milk 1.00.790.450.220.150.120.080.060.05 iii.From the graphed results in Figure1,one obtains an approximately linear relationship between milk concentration,C,and scattering angle,2θ (=φ)of the formφ=6C.iv.Assuming the given relationI=I0e−µz=T milk I0where z is the distance into the tank containing milk/water.We haveT milk=e−µzThusln T milk=−µz,andµ=constant×CHence ln T milk=−αzC.Since z is a constant in this experiment,a plot of ln T milk as a function of C should yield a straight line.Typical data for such a plot are as follows:%Concentration012345678T milk 1.00.790.450.220.150.120.080.060.05ln T milk0-0.24-0.8-1.51-1.90-2.12-2.53-2.81-3.00An approximately linear relationship is obtained,as shown in Figure2,between ln T milk and C,the concentration viz.ln T milk −0.4C=−µzThus we can writeT milk=e−0.4C=e−µzFor the tank used,z=25mm and thus0.4C=25µorµ=0.016C whenceα=0.016mm−1%−1By extrapolation of the graph of ln T milk versus concentration C,onefinds that for a scatterer concentration of10%µ=0.160mm−1.高中物理辅导网/246810% Concentration01020304050φFigure 1:Sample plot246810% Concentration-4-3-2-1l n T m i l kFigure 2:Sample plot高中物理辅导网/Detailed Mark Allocation高中物理辅导网/Section1A clear diagram illustrating geometry used with appropriate allocations[1] Optimal geometry used-as per model solution(laser close to ruler)[1] Multiple measurements made to ascertain errors involved[1] Correctly tabulated results[1] Sources of error including suggestion of ruler variation(suggested by non-ideal diffraction pattern)[1] Calculation of uncertainty[1] Final result[2] Allocated as per:±10%(612,748nm)[2]±20%(544,816nm)[1]±anything worse[0] Section2For evidence of practical determination of transmission rather thansimply“back calculating”.Practical range70−90%[1] For correct calculation of transmission(no more than3significantfigures stated)[1] Section3Correct calculation with no more than3significantfigures statedand an indication that the measurement was performed[1] Section4Illustrative diagram including viewing geometry used,i.e.horizontal/vertical[1] For recognizing the difference between scattered light and the straight-through beam[1] For taking the T water into account when calculating T milk[1] Correctly calculated and tabulated results of T milk with results within20%of model solution[1] Using a graphical technique for determining the relationship betweenscatter angle and milk concentration[1] Using a graphical technique to extrapolate T milk to10%concentration[1] Final result forµ[2] Allocated as±40%[2],±60%[1],anything worse[0]A reasonable attempt to consider uncertainties[1] TOTAL20京翰教育中心/。
P5Maths(新加坡小学5年级数学练习进步英文版)

CHAPTER 1 WHOLE NUMBERS1.Round off 69 570 km to the nearest 1 000 km.2.Round off 7 534 089 to the neatest thousand.3. A school’4.The value of the digit 8 in 980 036 is ___________________________ .5.6.What is 100 tens less than 1 million?7.What is 90 hundreds more than 1 million?8.How many tens are there in 48 200?9.There are ___________________ hundreds in 1 million.10.The value of the digit 8 in 487 543 is 8 x _________________________.11.Write nine million, six hundred and seven thousand and eighty-four in figures.12.13.Evaluate (Solve) 507 x 28.14.15.number.16.Find the value of 85 + 10 x (80 – 60 ) ÷ 4.17.Find the value of 42 + (139 – 19) ÷ 6 x 2.18.162 x 15 = 162 x 10 + (19.What is the remainder when 2020 is divided by 8?20.page number?21.$22 left while she had $49 left. How much did Lin have at first?22.There are ____________ tens in 1 million.23.The value of 9 in 129 300 is ___________________________.24.Write 1 489 311 in words: ___________________________________________________________________________________________________________________________________________________________________ CHAPTER 2 MONEY, MEASURES & MENSURATION1. A wooden block measures 10 cm by 8 cm by2.5 cm. If 4 such wooden blocks are packedexactly into a rectangular box, what is the capacity of the box?2.The area of a floor covered in square tiles if 1250 cm2. The length of each square tile is 5 cm.How many square tiles are there covering the floor?3. A papaya is as heavy as two oranges of equal mass. If the mass of each orange is 160 g , findthe mass of 3 such papayas.CHAPTER 3 STATISTICSCHAPTER 4 GEOMETRYCHAPTER 5 FRACTIONS1.What is of 1h 8 min? _______________________2.Express day in hours. _______________________3.There are 18 apples and 12 oranges in a basket. What fraction of the fruits are oranges?___________________4.How many hours is of a day? ________________________5.There are __________ sixths in .6.Mr. Tan bought some tables. of them were red. The remaining 33 tables were white.How many tables did he buy altogether? Ans: ___________________________7.Carl had 8 ½ m of rope. He cut out 3 pieces of ropes measuring 1 ¼ m each. Find the length ofthe rope left.Ans: ____________________________8. of a number is 36. What is of the number? ________________________9. of the people at a concert were women and of them were children. If therewere 300 men, how many women were there at the concert? Ans: __________________________10.27 kg of rice are shared equally among 7 people. How much rice does each person get? Leaveyour answer in its simplest form._______________________________________________________________________________( ) 11.Express 1 390 m as a fraction of 2 km._______________________________________________________________________________( )12.A piece of wire m long is cut into 6 equal pieces. Amy used 3 pieces to tie somepresents. What fraction of the wire did she use altogether?_______________________________________________________________________________( ) 13.Find the value of 2 + 1 ._______________________________________________________________________________( )14.Ben was told to guess a number. He guessed the number to be 8. His guess is ¼ of the actualnumber. What is the actual number?_______________________________________________________________________________( )15.10 girls received ¼ kg of strawberries each. What is the total weight of strawberries in kg?(Express your answer in its simplest form)_______________________________________________________________________________( )16.Henry bought 60 m of ribbon. He gave away ¾ of the ribbon to Kelly. How many metres of theribbon did he give away?_______________________________________________________________________________( )17.Bala gave of his stamps to his brother and of the remainder to his sister. Hehad 10 stamps left. How many stamps did he have at first?_______________________________________________________________________________( )18.A rabbit weighs kg. A hamster is of the mass of the rabbit. What is the total massof the two animals? (Express your answer as a mixed number in its simplest form.)_______________________________________________________________________________( )19.A pair of jeans cost 3 times as much as a skirt. Brenda spent of her money on someskirts and half of her remaining money on a pair of jeans. How many skirts did she buy?_______________________________________________________________________________( ) CHAPTER 6 DECIMALS1.Zafran paid $243 for 90 markers. If the price of each marker decreased by $0.60, how many-----------------------------------------------------------------------------------------------------------------------------( )2.Round off 9.837 to 1 decimal place. -----------------------------------------------------------------------------( )3.Round off 202.028 to 2 decimal place. --------------------------------------------------------------------------( )4.Round off 29.192 to 2 decimal place. ----------------------------------------------------------------------------( )5. 3 ones, 50 hundredths and 2 thousandths is __________________________.6.10 tens, 9 hundredths and 7 thousandths is __________________________ .7.Ray finished 2/3 of his Math homework. What percentage of his homework did he finish? Giveyour answer rounded off to 2 decimal places.-----------------------------------------------------------------------------------------------------------------------------( )8.In every litre of honey water juice, there is 200 ml of honey syrup. The rest of the juice is madeup of water. How much water will there be in 3.5 litres of honey water juice? Leave your answer in litres.-----------------------------------------------------------------------------------------------------------------------------( )CHAPTER 7 AVERAGE, RATE & SPEED1.Joyce can write 28 words in 2 minutes. At this rate, how many words can she write in 8 minutes?CHAPTER 8 RATIO & PROPORTION1.( ) : 6 = 28 : 42. Fill in the missing number in the bracket.2.There are 30 buttons in a box. 10 buttons are black and the rest are white. What is the ratio ofthe black buttons to the white buttons?--------------------------------------------------------------------------------------------------------------------------( )3.Lina saves $53 a month. How much will she save in 2.5 years? -------------------------------------4.There are 48 pens and 72 pencils in a container. What is the ratio of the number of pencils tothe number of pens?--------------------------------------------------------------------------------------------------------------------------( )5.The marks May and Brenda scored in an Chinese test are in the ratio of 3 : 5. If May has 18marks less than Brenda, how many marks did May score?--------------------------------------------------------------------------------------------------------------------------( )6.There are 800 men and women at a party. 300 of them are women. What is the ratio of thenumber of men to the number of women at the party?--------------------------------------------------------------------------------------------------------------------------( )7.The ratio of the number of teachers to pupils at a school is 1 : 9. If there are 108 pupils, how--------------------------------------------------------------------------------------------------------------------------( )8. A piece of wire of 160 cm long was cut into 2 pieces in the ratio of 6 : 2. The shorter piece wasbent to form a square. What is the length of the square?--------------------------------------------------------------------------------------------------------------------------( )9.The ratio of Tina’s mass to Joyce’s mass is 4 : 3. If Tina’s mass decreased by 6 kg and Joyce’s mass is increased by 1 kg, Tina will have the same mass as Joyce. What is Joyce’s original mass?--------------------------------------------------------------------------------------------------------------------------( )10.Andy, Ben and Cavin have a total sum of $96. Andy and Ben have $80. What is the ratio ofCavin’s share to the total sum of money?11.3 chickens cost $36 and 8 fishes costs $72. How much does 6 chickens and 4 fishes costaltogether?--------------------------------------------------------------------------------------------------------------------------( )12.A taxi can carry maximum of 4 passengers. What is the least number of taxis needed totransport 21 passengers?--------------------------------------------------------------------------------------------------------------------------( )13.If Gary packed 40 apples in each crate, what was the minimum number of crates he needed topack 4860 apples?--------------------------------------------------------------------------------------------------------------------------( )14.The ratio of Marcus’s age to Francis’s age is 5 : 6. Their total age is 77 years. How old isMarcus?15.The area of a rectangle is 72 cm2. Its length is 18 cm. What is the ratio of the length to itsbreadth?--------------------------------------------------------------------------------------------------------------------------( )16.The number of chickens and ducks on a farm is in the ratio of 4 : 7. There are 21 more ducksthan chickens. How many chickens and ducks are there altogether?--------------------------------------------------------------------------------------------------------------------------( )17.Jill had 150 stamps. She kept half of them and shared the rest between Grace and Ahmad inthe ratio of 2 : 3. How many stamps did Ahmad receive?--------------------------------------------------------------------------------------------------------------------------( )18.Charles could buy 8 plums and 5 mangoes with $8.00. He could buy 16 such plums with thesame amount of money. If he decides to buy mangoes only, how many mangoes can he buy with $100?19.Henry won $2 400 in a contest. He kept ¼ of it and gave the remainder to his wife, sister andbrother. His wife received 2/3 of the money, his sister received ¼ of it and his brother received the rest.a.How much did his wife receive?b.What is the ratio of his wife’s share to his brother’s share?20.CHAPTER 9 PERCENTAGE1.Express 1 1/5 as a percentage.2.Raymund was given a 20% discount for a meal that cost $6. How much did he pay for the meal?Percentage and Problem Sums Date: 18 July 20101.Express as a percentage.2.Express 28% as a fraction in its simplest form.3.Express ½ % as a fraction in its simplest form.4.Raymund was given a 20% discount for a meal that cost $6. How much did he pay for the meal?5.During a sale, Alicia was given a 15% discount for a book that cost $12. How much would shesave if she buy the book during the sale?6.David saved $9 every day. After a number of days, he used all the money that he had save tobuy a fewstorybooks that cost $21 each.(a)What was the least number of days that he needed to save in order to buy the storybooks?(b)How many storybooks did he buy?7.There were some markers in a box. of the markers were black and the rest were red.of the black and of the red markers were taken out from the box and there were 111 markers left inthe box. How many markers were there in the box at first?8.David had some durians. He sold of them in the afternoon and of the remainder inthe evening. Therewere 30 fewer durians sold in the evening than in the afternoon.a.How many durians did he sell in all?b.If he sold the durians at $5, how much money did he collect altogether?9.Danny spent 2 of his money on a bag and 1 of the reminder on some snacks.What percentage of his5 3money had he left?10.140% of a number is 84. Find the number.11.40% of the erasers in a box are purple. The rest are blue and green erasers in the ratio of 11:4.There are 48fewer purple erasers than blue erasers. How many erasers are there altogether?12.Amy gave 35% of her marbles to Bala. What fraction of her marbles had she left?13.Devi’s salary and Minah’s salary are in ratio of 4:5. If Devi’s salary is increased by 30%, bywhat percentage mustMinah’s salary be increased so that their salaries will be the same?。
线状图 英语作文

线状图英语作文Title: Exploring the Insights of Line Graphs。
Line graphs, also known as line charts, are powerful visual tools commonly used to represent trends, changes, or relationships over time. In this essay, we will delve into the intricacies of line graphs, their construction, interpretation, and practical applications.First and foremost, let us explore the fundamental components of a line graph. At its core, a line graph consists of two axes: the horizontal x-axis and thevertical y-axis. The x-axis typically represents time or another continuous variable, while the y-axis denotes the corresponding values being measured. Each data point is then plotted on the graph and connected by straight lines, illustrating the progression or fluctuation of the data over time.One of the primary advantages of line graphs is theirability to reveal trends and patterns with clarity. By examining the slope and direction of the lines, one can discern whether the values are increasing, decreasing, or remaining constant over time. This makes line graphs particularly useful for identifying growth rates, analyzing fluctuations, and making predictions based on historical data.Moreover, line graphs facilitate comparisons between different sets of data. By plotting multiple lines on the same graph, researchers can easily visualize how various variables interact and influence each other over time. This comparative analysis can offer valuable insights into correlations, causations, and the overall dynamics of the system under study.To construct an effective line graph, several key principles should be followed. Firstly, the axes should be clearly labeled with appropriate units of measurement to ensure accurate interpretation. Secondly, the scale of the axes should be chosen wisely to accommodate the range of data values without overcrowding or distorting the graph.Thirdly, the lines should be drawn with care, using consistent colors or symbols to differentiate between multiple datasets.Interpreting a line graph involves more than just observing the trend lines. It requires a deeper understanding of the underlying data and the context in which it was collected. Researchers must consider factors such as outliers, anomalies, and potential sources of bias that may affect the accuracy and reliability of the results.In addition to their analytical utility, line graphsfind widespread application across various fields and disciplines. In economics, they are used to track market trends, monitor financial performance, and forecast future developments. In environmental science, they help visualize climate patterns, analyze pollution levels, and assess the impact of human activities on the ecosystem. In healthcare, they aid in monitoring patient progress, evaluating treatment outcomes, and identifying risk factors for diseases.In conclusion, line graphs are invaluable tools for visualizing data, analyzing trends, and communicating insights effectively. Their simplicity, versatility, and intuitive appeal make them indispensable in both academic research and real-world decision-making. By mastering the art of constructing and interpreting line graphs, researchers can unlock a wealth of information and uncover hidden patterns that may otherwise remain unnoticed.。
英语作文各种图的英文名

英语作文各种图的英文名When writing English essays, particularly those that involve the analysis of visual data, it's important to know the correct English terms for various types of graphs and charts. Here is a list of common graph types and their English names:1. Bar Chart - A chart that presents data using rectangular bars with lengths proportional to the values they represent.2. Line Graph - Also known as a line chart, it displays information as a series of data points called 'markers' connected by straight line segments.3. Pie Chart - A circular chart divided into slices to illustrate numerical proportion.4. Histogram - An accurate representation of the distribution of numerical data, where data is "binned" and plotted in vertical bars, showing the frequency of data points occurring in consecutive intervals.5. Scatter Plot - A diagram where individual data points are plotted on horizontal and vertical axes to show the relationship between two variables.6. Area Chart - Similar to a line chart, but the area between the line and the axis is filled with color or shading.7. Bubble Chart - Uses bubbles of different sizes to represent the magnitude of a third variable, in addition to the two variables represented on the axes.8. Stacked Bar Chart - A variation of a bar chart where the bars are divided into segments, each representing a category of the data.9. Waterfall Chart - Used to show a cumulative effect, typically starting with an initial value and showing intermediate steps that lead to the final value.10. Gantt Chart - A type of bar chart that illustrates a project schedule, showing the start and finish dates of the terminal elements and summary elements of a project.11. Radar Chart - A graphical method of displaying multivariate data in the form of a two-dimensional chart of three or more quantitative variables represented on axes starting from the same point.12. Tree Map - A method of data visualization that uses nested rectangles to display hierarchical data as a set of colored rectangles.13. Heat Map - A data visualization technique that uses a two-dimensional representation of data where individual values are represented as colors.14. Box Plot - A method for graphically depicting groups of numerical data through their quartiles.15. Pictogram - Also known as a pictograph, it is a type of chart that uses icons or symbols to represent data.16. Spider Chart - A chart type considered as a chart with multiple axes that start from the same point, like a radar chart.17. Pareto Chart - A bar chart that contains both bars and a line graph, where individual values are represented in descending order by bars, and the cumulative total is represented by the line.18. Flow Chart - A diagram representing a workflow or process, showing the steps as boxes of various kinds, and their orderby connecting these with arrows.19. Venn Diagram - A diagram that shows all possible logical relations between a finite collection of different sets.20. Tornado Chart - A chart that is used to show the impactof different variables on a particular outcome, with the variables ordered by their impact size.Knowing these terms will not only help you describe graphs accurately in your essays but also enhance your understanding of the data presented.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
y
10
Consider two points on this graph.
8
(4, 4) 6
4
(6, 4)
m y2 y1 x2 x1
2
– 10 – 8 – 6 – 4 – 2 –2 –4
2 4 6 8 10 x
44 64
0
–6
–8
The equation of the line is y 4
y=15x+40
Now think about the total cost for a range of different hire times:
If we put these values into a table,we can plot a graph.
A point lying on the line
– 10
All horizontal lines have an equation of the form y c
Consider two points on this graph.
y
10
8
(4,8)
6
m y2 y1 x2 x1
4 2
– 10 – 8 – 6 – 4 – 2 –2
2 4 6 8 10 x
Gradient is - 4 and the y axis intercept is 2 .
3
3
Calculate the gradient of each line.
Calculate the gradient of the line that passes through both points in each case.
86 44
(undefined)
–4
–6
(4, 6)
–8
The equation of the line is x 4
– 10
All vertical lines have an equation of the form x a
All straight lines have an equation of the form y mx c
m = gradient
y axis intercept
Undefined and zero gradient
Gradient is a measure of slope. If a line has zero gradient it has zero slope. A line with zero slope is horizontal.
A point not lying on the line
Points lying on the straight line
(x, y) : symbolic representation of a point
y-coordinate
x-coordinate
y=15x+40 (Equation of a straight line)
Back to Main Page
If we find the 2 points where the graph cuts the axes then we can plot the line.
These points are where x = 0 (anywhere along the y axis) and y = 0 (anywhere along the x axis).
8
2x + y = 4
7
6
5
4
3
2
1
–7 –6 –5 –4 –3 –2 –1 -1 -2 -3 -4 -5 -6
x 1 2 3 4 5 6 7 8
Back to Main Page
Exercise
Plot the following graphs using the x=0, y=0 method. 1) x + y = 5 2) x + 2y = 2 3) 2x + 3y = 6 4) x + 3y = 3
–7 –6 –5 –4 –3 –2 –1 -1 -2 -3 -4 -5 -6
x 1 2 3 4 5 6 7 8
Back to Main Page
Exercise
Using the x = 0, y = 0 method plot the following graphs:
1) x + y = 4 2) 2x + y = 2 3) x + 2y = 2 4) x + 3y = 6 5) 2x + 5y = 10
Click to reveal plotted lines
Back to Main Page
Answers
1. 3x + 2y = 6 2. x + 2y = 2 3. 2x + 3y = 6 4. x - 3y = 3
Click for further exercises
y
8 7 6 5 4 3 2 1
x 1 2 3 4 5 6 7 8
Back to Main Page
Example
By substituting these values into the equation we can find the other half of the co-ordinates.
Question: Draw the graph of 2x + y = 4
1) y = x + 2 2) y = x – 3 3) y = 2x + 4 4) y = 2x – 3 5) y = 3x + 1 6) y = 3x – 2
7) y = 1 – x 8) y = 1 – 2x
2
9) y = 2 – 3x 10) y = x + 1
2
Back tBiblioteka Main Page(a) A (1, 2) and B (3, 8) (b) A (2, -1) and B (4, 2)
(c) A (0, 6) and B(3, 9) (d) A(-1, -4) and B(-3, 2)
Exercise
y
8
7
3
Click for Answers 1) y = x - 2
6
2) y = -x + 3
Back to Main Page
The Table Method
Use the table method to plot the following lines:
1) y = x + 3 2) y = 2x – 3
x012
3) y = 2 – x
y
4) y = 3 – 2x
Click to reveal plotted lines
Back to Main Page
The Table Method
4 3 2 1
-4 -3 -2 -1 0 1 2 3 4 -1
-2
-3
3
1
Click for further
-4
exercises
4
2
Back to Main Page
Further Exercise
Using the table method, plot the following graphs.
For every position P the gradient of AP is
m yc yc
x0
x
x y c mx y mx c
Straight Lines: standard form
y = mx + c
To see what the constant, m, tells us, consider how y changes when x changes:
Solution x=0
y=0
2(0) + y = 4
2x + 0 = 4
y=4
2x = 4
x=2
1st Co-ordinates = (0,4)
2nd Co-ordinates = (2,0)
Back to Main Page
y So the graph will look like this.
y135
x = 2 y = 2(2) +1 y = 5
Now you just have to plot the points on to a graph!
Back to Main Page
The Table Method
x012
y 135
y = 2x + 1
4 3 2 1
-4 -3 -2 -1 0 1 2 3 4 -1 -2 -3 -4
The Table Method
We can use an equation of a line to plot a graph by substituting values of x into it.
Example
y = 2x + 1
x012
x = 0 y = 2(0) +1 y = 1 x = 1 y = 2(1) +1 y = 3
6) x – y = 3 7) 2x – y = 2 8) 2x – 3y = 6 9) x + 2y = 1 10) 2x – y = 3
Back to Main Page
B(x2, y2 )
y2 y1
A(x1, y1)
x2 x1
Gradient m = Vertical Height Horizontal Distance
