2002滑铁卢竞赛试题

合集下载

2005滑铁卢竞赛试题答案

1.(a)Answer:a=5Since(a,a)lies on the line3x−y=10,then3a−a=10or2a=10or a=5.(b)Answer:(6,2)Solution1To get from A to B,we move2units to the right and1unit up.xSince C lies on the same straight line as A and B,then to get from B to C we move2 units to the right and1unit up twice,or4units to the right and2units up.Thus,the coordinates of C are(6,2).Solution2Label the origin as O and drop a perpendicular from C to P on the x-axis.xThen AOB is similar to CP B since both are right-angled and they have equal angles at B.Since BC=2AB,then CP=2AO=2(1)=2and BP=2BO=2(2)=4.Therefore,the coordinates of C are(2+4,0+2)=(6,2).(c)By the Pythagorean Theorem,AO2=AB2−OB2=502−402=900,so AO=30.Therefore,the coordinates of A are(0,30).By the Pythagorean Theorem,CD2=CB2−BD2=502−482=196,so CD=14.x Therefore,the coordinates of C are(40+48,14)=(88,14). Since M is the midpoint of AC,then the coordinates of M are1 2(0+88),12(30+14)=(44,22)2.(a)Answer:x=−2Solution1Since y=2x+3,then4y=4(2x+3)=8x+12.Since4y=8x+12and4y=5x+6,then8x+12=5x+6or3x=−6or x=−2.Solution2Since4y=5x+6,then y=54x+64=54x+32.Since y=2x+3and y=54x+32,then2x+3=54x+32or34x=−32or x=−2.Solution3Since the second equation contains a“5x”,we multiply theﬁrst equation by52to obtaina5x term,and obtain52y=5x+152.Subtracting this from4y=5x+6,we obtain32y=−32or y=−1.Since y=−1,then−1=2x+3or2x=−4or x=−2.(b)Answer:a=6Solution1Adding the three equations together,we obtain a−3b+b+2b+7c−2c−5c=−10+3+13 or a=6.Solution2Multiplying the second equation by3,we obtain3b−6c=9.Adding this new equation to theﬁrst equation,we obtain c=−1.Substituting this back into the original second equation,we obtain b=3+2c=1.Substituting into the third equation,a=−2b+5c+13=−2−5+13=6.(c)Solution1Let J be John’s score and M be Mary’s score.Since two times John’s score was60more than Mary’s score,then2J=M+60.Since two times Mary’s score was90more than John’s score,then2M=J+90.Adding these two equations,we obtain2J+2M=M+J+150or J+M=150orJ+M2=75.Therefore,the average of their two scores was75.(Note that we didn’t have to solve for their individual scores.)Solution2Let J be John’s score and M be Mary’s score.Since two times John’s score was60more than Mary’s score,then2J=M+60,so M=2J−60.Since two times Mary’s score was90more than John’s score,then2M=J+90.Substituting theﬁrst equation into the second,we obtain2(2J−60)=J+904J−120=J+903J=210J=70Substituting into M=2J−60gives M=80.Therefore,the average of their scores(ie.the average of70and80)is75.3.(a)Answer:x=50Simplifying using exponent rules,2(1612)+2(816)=2((24)12)+2((23)16)=2(248)+2(248)=4(248)=22(248)=250Therefore,since2x=2(1612)+2(816)=250,then x=50.(b)Solution1We factor the given equation(f(x))2−3f(x)+2=0as(f(x)−1)(f(x)−2)=0.Therefore,f(x)=1or f(x)=2.If f(x)=1,then2x−1=1or2x=2or x=1.If f(x)=2,then2x−1=2or2x=3or x=3..Therefore,the values of x are x=1or x=32Solution2Since f(x)=2x−1and(f(x))2−3f(x)+2=0,then(2x−1)2−3(2x−1)+2=04x2−4x+1−6x+3+2=04x2−10x+6=02x2−5x+3=0(x−1)(2x−3)=0Therfore,x=1or x=3.24.(a)Answer:1415Solution1The possible pairs of numbers on the tickets are(listed as ordered pairs):(1,2),(1,3), (1,4),(1,5),(1,6),(2,3),(2,4),(2,5),(2,6),(3,4),(3,5),(3,6),(4,5),(4,6),and(5,6).There areﬁfteen such pairs.(We treat the pair of tickets numbered2and4as being the same as the pair numbered4and2.)The pairs for which the smaller of the two numbers is less than or equal to4are(1,2), (1,3),(1,4),(1,5),(1,6),(2,3),(2,4),(2,5),(2,6),(3,4),(3,5),(3,6),(4,5),and(4,6).There are fourteen such pairs.Therefore,the probability of selecting such a pair of tickets is14.15Solution 2We ﬁnd the probability that the smaller number on the two tickets is NOT less than or equal to 4.Therefore,the smaller number on the two tickets is at least 5.Thus,the pair of numbers must be 5and 6,since two distinct numbers less than or equal to 6are being chosen.As in Solution 1,we can determine that there are ﬁfteen possible pairs that we can se-lected.Therefore,the probability that the smaller number on the two tickets is NOT less than orequal to 4is 115,so the probability that the smaller number on the two tickets IS less than or equal to 4is 1−115=1415.(b)Solution 1Since ∠HLP =60◦and ∠BLP =30◦,then ∠HLB =∠HLP −∠BLP =30◦.Also,since ∠HLP =60◦and ∠HP L =90◦,then ∠LHP =180◦−90◦−60◦=30◦.Therefore, HBL is isosceles and BL =HB =400m.In BLP ,BL =400m and ∠BLP =30◦,so LP =BL cos(30◦)=400 √32 =200√3m.Therefore,the distance between L and P is 200√3m.Solution 2Since ∠HLP =60◦and ∠BLP =30◦,then ∠HLB =∠HLP −∠BLP =30◦.Also,since ∠HLP =60◦and ∠HP L =90◦,then ∠LHP =180◦−90◦−60◦=30◦.Also,∠LBP =60◦.Let LP =x .HSince BLP is 30◦-60◦-90◦,then BP :LP =1:√3,so BP =1√3LP =1√3x .Since HLP is 30◦-60◦-90◦,then HP :LP =√3:1,so HP =√3LP =√3x .But HP =HB +BP so√3x =400+1√3x3x =400√3+x2x =400√3x =200√3Therefore,the distance from L to P is 200√3m.5.(a)Answer:(6,5)After 2moves,the goat has travelled 1+2=3units.After 3moves,the goat has travelled 1+2+3=6units.Similarly,after n moves,the goat has travelled a total of 1+2+3+···+n units.For what value of n is 1+2+3+···+n equal to 55?The fastest way to determine the value of n is by adding the ﬁrst few integers until we obtain a sum of 55.This will be n =10.(We could also do this by remembering that 1+2+3+···+n =12n (n +1)and solving for n this way.)So we must determine the coordinates of the goat after 10moves.We consider ﬁrst the x -coordinate.Since starting at (0,0)the goat has moved 2units in the positive x direction,4units in the negative x direction,6units in the positive x direction,8units in the negative x direction and 10units in the positive x direction,so its x coordinate should be 2−4+6−8+10=6.Similarly,its y -coordinate should be 1−3+5−7+9=5.Therefore,after having travelled a distance of 55units,the goat is at the point (6,5).(b)Solution 1Since the sequence 4,4r ,4r 2is also arithmetic,then the diﬀerence between 4r 2and 4r equals the diﬀerence between 4r and 4,or4r 2−4r =4r −44r 2−8r +4=0r 2−2r +1=0(r −1)2=Therefore,the only value of r is r =1.Solution 2Since the sequence 4,4r ,4r 2is also arithmetic,then we can write 4r =4+d and 4r 2=4+2d for some real number d .(Here,d is the common diﬀerence in this arithmetic sequence.)Then d =4r −4and 2d =4r 2−4or d =2r 2−2.Therefore,equating the two expressions for d ,we obtain 2r 2−2=4r −4or 2r 2−4r +2=0or r 2−2r +1=0or (r −1)2=0.Therefore,the only value of r is r =1.6.(a)Answer:4πFirst,we notice that whenever an equilateral triangle of side length 3is placed inside acircle of radius3with two of its vertices on the circle,then the third vertex will be at the centre of the circle.This is because if we place XY Z with Y and Z on the circle and connect Y and Z to the centre O,then OY=OZ=3,so OY Z is equilateral(since all three sides have length3).Thus XY Z and OY Z must be the same,so X is at the same point as O. Thus,in the starting position,A is at the centre of the circle.As the triangle is rotated about C,the point B traces out an arc of a circle of radius3. What fraction of the circle is traced out?When point A reaches point A1on the circle,we have AC=3and CA1=3.Since A is at the centre of the circle,then AA1=3as well,so AA1C is equilateral,and∠A1CA=60◦, so the triangle has rotated through60◦.1Therefore,B has traced out60◦360◦=16of a circle of radius3.Notice that A has also traced out an arc of the same length.When A reaches the circle, we have A and C on the circle,so B must be at the centre of the circle.Thus,on the next rotation,B again rotates through16of a circle of radius3as it movesto the circle.On the third rotation,the triangle rotates about B,so B does not move.After three rotations,the triangle will have A at the centre and B and C on the circle,with the net result that the triangle has rotated180◦about the centre of the circle.Thus,to return to its original position,the triangle must undergo three more of these rotations,and B will behave in the same way as it did for theﬁrst three rotations.Thus,in total,B moves four times along an arc equal to16of a circle of radius3.Therefore,the distance travelled by B is4(16)(2π(3))=4π.(b)In order to determine CD,we must determine one of the angles(or at least some infor-mation about one of the angles)in BCD.To do this,we look at∠A use the fact that∠A+∠C=180◦.ADCB 5674Using the cosine law in ABD ,we obtain72=52+62−2(5)(6)cos(∠A )49=61−60cos(∠A )cos(∠A )=15Since cos(∠A )=15and ∠A +∠C =180◦,then cos(∠C )=−cos(180◦−∠A )=−15.(We could have calculated the actual size of ∠A using cos(∠A )=15and then used this to calculate the size of ∠C ,but we would introduce the possibility of rounding error by doing this.)Then,using the cosine law in BCD ,we obtain72=42+CD 2−2(4)(CD )cos(∠C )49=16+CD 2−8(CD ) −150=5CD 2+8CD −1650=(5CD +33)(CD −5)So CD =−335or CD =5.(We could have also determined these roots using the quadratic formula.)Since CD is a length,it must be positive,so CD =5.(We could have also proceeded by using the sine law in BCD to determine ∠BDC and then found the size of ∠DBC ,which would have allowed us to calculate CD using the sine law.However,this would again introduce the potential of rounding error.)7.(a)Answer:Maximum =5,Minimum =1We rewrite by completing the square as f (x )=sin 2x −2sin x +2=(sin x −1)2+1.Therefore,since (sin x −1)2≥0,then f (x )≥1,and in fact f (x )=1when sin x =1(which occurs for instance when x =90◦).Thus,the minimum value of f (x )is 1.To maximize f (x ),we must maximize (sin x −1)2.Since −1≤sin x ≤1,then (sin x −1)2is maximized when sin x =−1(for instance,when x =270◦).In this case,(sin x −1)2=4,so f (x )=5.Thus,the maximum value of f (x )is 5.(b)From the diagram,the x -intercepts of the parabola are x =−k and x =3k .xy Since we are given that y =−14(x −r )(x −s ),then the x -intercepts are r and s ,so r and s equal −k and 3k in some order.Therefore,we can rewrite the parabola as y =−14(x −(−k ))(x −3k ).Since the point (0,3k )lies on the parabola,then 3k =−14(0+k )(0−3k )or 12k =3k 2or k 2−4k =0or k (k −4)=0.Thus,k =0or k =4.Since the two roots are distinct,then we cannot have k =0(otherwise both x -intercepts would be 0).Thus,k =4.This tells us that the equation of the parabola is y =−14(x +4)(x −12)or y =−14x 2+2x +12.We still have to determine the coordinates of the vertex,V .Since the x -intercepts of the parabola are −4and 12,then the x -coordinate of the vertex is the average of these intercepts,or 4.(We could have also used the fact that the x -coordinate is −b2a =−22(−14).)Therefore,the y -coordinate of the vertex is y =−14(42)+2(4)+12=16.Thus,the coordinates of the vertex are (4,16).8.(a)We look at the three pieces separately.If x <−4,f (x )=4so g (x )= 25−[f (x )]2=√25−42=√9=3.So g (x )is the horizontal line y =3when x <−4.If x >5,f (x )=−5so g (x )= 25−[f (x )]2= 25−(−5)2=√0=0.So g (x )is the horizontal line y =0when x >5.So far,our graph looks like this:If−4≤x≤5,f(x)=−x so g(x)=25−[f(x)]2=25−(−x)2=√25−x2.What is this shape?If y=g(x),then we have y=√25−x2or y2=25−x2or x2+y2=25.Therefore,this shape is a section of the upper half(since y is a positive square-root)of the circle x2+y2=25,ie.the circle with centre(0,0)and radius5.We must check the endpoints. When x=−4,we have g(−4)=25−(−4))2=3.When x=5,we have g(5)=√25−52=0.Therefore,the section of the circle connects up with the other two sections of our graph already in place.Thus,ourﬁnal graph is:(b)Solution 1Let the centres of the two circles be O 1and O 2.Join A and B to O 1and B and C to O 2.Designate two points W and X on either side of A on one tangent line,and two points Y and Z oneither side of C on the other tangent line.ZLet ∠XAB =θ.Since W X is tangent to the circle with centre O 1at A ,then O 1A is perpendicular to W X ,so ∠O 1AB =90◦−θ.Since O 1A =O 1B because both are radii,then AO 1B is isosceles,so ∠O 1BA =∠O 1AB =90◦−θ.Since the two circles are tangent at B ,then the line segment joining O 1and O 2passes through B ,ie.O 1BO 2is a straight line segment.Thus,∠O 2BC =∠O 1BA =90◦−θ,by opposite angles.Since O 2B =O 2C ,then similarly to above,∠O 2CB =∠O 2BC =90◦−θ.Since Y Z is tangent to the circle with centre O 2at C ,then O 2C is perpendicular to Y Z .Thus,∠Y CB =90◦−∠O 2CB =θ.Since ∠XAB =∠Y CB ,then W X is parallel to Y Z ,by alternate angles,as required.Solution2Let the centres of the two circles be O1and O2.Join A and B to O1and B and C to O2.Since AO1and BO1are radii of the same circle,AO1=BO1so AO1B is isosceles,so ∠O1AB=∠O1BA.Since BO2and CO2are radii of the same circle,BO2=CO2so BO2C is isosceles,so ∠O2BC=∠O2CB.Since the two circles are tangent at B,then O1BO2is a line segment(ie.the line segment joining O1and O2passes through the point of tangency of the two circles).Since O1BO2is straight,then∠O1BA=∠O2BC,by opposite angles.Thus,∠O1AB=∠O1BA=∠O2BC=∠O2CB.This tells us that AO1B is similar to BO2C,so∠AO1B=∠BO2C or∠AO1O2=∠CO2O1.Therefore,AO1is parallel to CO2,by alternate angles.But A and C are points of tangency,AO1is perpendicular to the tangent line at A and CO2is perpendicular to the tangent line at C.Since AO1and CO2are parallel,then the two tangent lines must be parallel.9.(a)Solution1We have(x−p)2+y2=r2and x2+(y−p)2=r2,so at the points of intersection,(x−p)2+y2=x2+(y−p)2x2−2px+p2+y2=x2+y2−2py+p2−2px=−2pyand so x=y(since we may assume that p=0otherwise the two circles would coincide).Therefore,a and b are the two solutions of the equation(x−p)2+x2=r2or2x2−2px+(p2−r2)=0or x2−px+12(p2−r2)=0.Using the relationship between the sum and product of roots of a quadratic equation andits coeﬃcients,we obtain that a+b=p and ab=12(p2−r2).(We could have solved for a and b using the quadratic formula and calculated these di-rectly.)So we know that a+b=p.Lastly,a2+b2=(a+b)2−2ab=p2−2 12(p2−r2)=r2,as required.Solution2Since the circles are reﬂections of one another in the line y=x,then the two points of intersection must both lie on the line y=x,ie.A has coordinates(a,a)and B has coordinates(b,b).Therefore,(a−p)2+a2=r2and(b−p)2+b2=r2,since these points lie on both circles.Subtracting the two equations,we get(b −p )2−(a −p )2+b 2−a 2=0((b −p )−(a −p ))((b −p )+(a −p ))+(b −a )(b +a )=0(b −a )(a +b −2p )+(b −a )(b +a )=0(b −a )(a +b −2p +b +a )=02(b −a )(a +b −p )=0Since a =b ,then we must have a +b =p ,as required.Since a +b =p ,then a −p =−b ,so substituting back into (a −p )2+a 2=r 2gives (−b )2+a 2=r 2,or a 2+b 2=r 2,as required.(b)We ﬁrst draw a diagram.yxWe know that C has coordinates (p,0)and D has coordinates (0,p ).Thus,the slope of line segment CD is −1.Since the points A and B both lie on the line y =x ,then the slope of line segment AB is 1.Therefore,AB is perpendicular to CD ,so CADB is a kite,and so its area is equal to 12(AB )(CD ).(We could derive this by breaking quadrilateral CADB into CAB and DAB .)Since C has coordinates (p,0)and D has coordinates (0,p ),then CD = p 2+(−p )2= 2p 2.(We do not know if p is positive,so this is not necessarily equal to √2p .)We know that A has coordinates (a,a )and B has coordinates (b,b ),soAB = (a −b )2+(a −b )2=√2a 2−4ab +2b 2= 2(a 2+b 2)−4ab = 2r 2−4 12(p 2−r 2) = 4r 2−2p 2Therefore,the area of quadrilateral CADB is 12(AB )(CD )=124r 2−2p 2 2p 2= 2r 2p 2−p 4To maximize this area,we must maximize 2r 2p 2−p 4=2r 2(p 2)−(p 2)2.Since r is ﬁxed,we can consider this as a quadratic polynomial in p 2.Since the coeﬃcient of (p 2)2is negative,then this is a parabola opening downwards,so we ﬁnd its maximum value by ﬁnding its vertex.The vertex of 2r 2(p 2)−(p 2)2is at p 2=−2r 22(−1)=r 2.So the maximum area of the quadrilateral occurs when p is chosen so that p 2=r 2.Since p 2=r 2,then (a +b )2=p 2=r 2so a 2+2ab +b 2=r 2.Since a 2+b 2=r 2,then 2ab =0so either a =0or b =0,and so either A has coordinates (0,0)or B has coordinates (0,0),ie.either A is the origin or B is the origin.(c)In (b),we calculated that AB = 4r 2−2p 2=√2 2r 2−p 2.Since r and p are integers (and we assume that neither r nor p is 0),then 2r 2−p 2=0,so the minimum possible non-negative value for 2r 2−p 2is 1,since 2r 2−p 2must be an integer.Therefore,the minimum possible distance between A and B should be √2√1=√2.Can we ﬁnd positive integers p and r that give us this value?Yes –if r =5and p =7,then 2r 2−p 2=1,so AB =√2.(There are in fact an inﬁnite number of positive integer solutions to the equation 2r 2−p 2=1or equivalently p 2−2r 2=−1.This type of equation is called Pell’s Equation.)10.(a)We proceed directly.On the ﬁrst pass from left to right,Josephine closes all of the even numbered lockers,leaving the odd ones open.The second pass proceeds from right to left.Before the pass,the lockers which are open are 1,3,...,47,49.On the second pass,she shuts lockers 47,43,39, (3)The third pass proceeds from left to right.Before the pass,the lockers which are open are 1,5,...,45,49.On the third pass,she shuts lockers 5,13, (45)This leaves lockers 1,9,17,25,33,41,49open.On the fourth pass,from right to left,lockers 41,25and 9are shut,leaving 1,17,33,49.On the ﬁfth pass,from left to right,lockers 17and 49are shut,leaving 1and 33open.On the sixth pass,from right to left,locker 1is shut,leaving 33open.Thus,f (50)=33.(b)&(c)Solution 1First,we note that if n =2k is even,then f (n )=f (2k )=f (2k −1)=f (n −1).See Solution 2for this justiﬁcation.Therefore,we only need to look for odd values of n in parts (b)and (c).Suppose that there was an n so that f (n )=2005,ie.2005is the last locker left open.On the ﬁrst pass,Josephine closes every other locker starting at the beginning,so she closes all lockers numbered m with m ≡0(mod 2).This leaves only odd-numbered lockers open,ie.only lockers m with m ≡1or 3(mod 4).On her second pass,she closes every other open locker,starting from the right-hand end.Thus,she will close every fourth locker from the original row.Since we want 2005to be left open and 2005≡1(mod 4),then she must close all lockers numbered m with m ≡3(mod 4).This leaves open only the lockers m with m ≡1(mod 4),or equivalently lockers with m ≡1or 5(mod 8).On her third pass,she closes every other open locker,starting from the left-hand end.Thus,she will close every eighth locker from the original row.Since locker1is still open,then she starts by closing locker5,and so closes all lockers mwith m≡5(mod8).But since2005≡5(mod8),then she closes locker2005on this pass,a contradiction.Therefore,there can be no integer n with f(n)=2005.Next,we show that there are inﬁnitely many positive integers n such that f(n)=f(2005).To do this,weﬁrst make a table of what happens when there are2005lockers in the row.We record the pass#,the direction of the pass,the leftmost locker that is open,therightmost locker that is open,all open lockers before the pass,which lockers will be closedon the pass,and which lockers will be left open after the pass:Pass#Dir.L Open R Open Open To close Leaves Open 1L to R12005All≡0(mod2)≡1(mod2) 2R to L12005≡1,3(mod4)≡3(mod4)≡1(mod4) 3L to R12005≡1,5(mod8)≡5(mod8)≡1(mod8) 4R to L12001≡1,9(mod16)≡9(mod16)≡1(mod16) 5L to R12001≡1,17(mod32)≡17(mod32)≡1(mod32) 6R to L11985≡1,33(mod64)≡33(mod64)≡1(mod64) 7L to R11985≡1,65(mod128)≡65(mod128)≡1(mod128) 8R to L11921≡1,129(mod256)≡1(mod256)≡129(mod256) 9L to R1291921≡129,385(mod512)≡385(mod512)≡129(mod512) 10R to L1291665≡129,641(mod1024)≡129(mod1024)≡641(mod1024) 11L to R6411665≡641,1665(mod2048)≡1665(mod2048)≡641(mod2048) Since there is only one integer between1and2005congruent to641(mod2048),thenthere is only one locker left open:locker641.Notice also that on any pass s,the“class”of lockers which are closed depends on what thenumber of the leftmost(on an odd-numbered pass)or rightmost(on an even-numberedpass)open locker number is congruent to mod2s.Consider n=2005+22a,where22a>2005,ie.a≥6.We show that f(n)=f(2005)=641.(See Solution2for a justiﬁcation of why we mighttry these values of n.)Suppose we were to try to make a table as above to calculate f(n).Then theﬁrst11passes in the table would be identical to the table above,except for therightmost open number;this number in the new table would be the number above plus22a.What will happen after pass11?After pass11,the lockers which are open are lockers with numbers≡641(mod2048).Thus,the leftmost open locker is641and the rightmost is22a+641.As the12th pass starts,the lockers which are still open are those with numbers≡641or2689(mod212).Since the rightmost open locker number(22a+641)is congruent to641(mod212),then alllockers with numbers≡2689(mod212)are closed,leaving open only those lockers withnumbers≡641(mod212).So after this12th pass,the lockers which are open are641,641+212,641+2(212),641+3(212),...,641+22a−12(212)=641+22a.The number of open lockers is22a−12+1.If we can now show that whenever we start with a number of lockers of the form22c+1,thelast locker remaining open is the leftmost locker,then we will be done,since of the lockersleft open above(22a−12+1of them,ie.2to an even power plus1),then the last locker re-maining open will be the leftmost one,that is locker641,so f(22a+2005)=641=f(2005).So consider a row of22c+1lockers.Notice that on any pass,if the number of lockers is odd,then the number of lockers whichwill be closed is one-half of one less than the total number of lockers,and theﬁrst andlast lockers will be left open.So on theﬁrst pass,there are22c−1lockers closed,leaving22c+1−22c−1=22c−1+1lockersopen,ie.an odd number of lockers open.On the next pass,there are22c−2lockers closed(since there are an odd number of lockersopen to begin),leaving22c−2+1lockers open.This continues,until there are21+1=3lockers open just before an even-numbered(ie.right to left)pass.Thus,the middle of these three lockers will be closed,leaving only theoriginal leftmost and rightmost lockers open.On the last pass(an odd-numbered pass from left to right),the rightmost locker will beclosed,leaving only the leftmost locker open.Therefore,starting with a row of22c+1open lockers,the leftmost locker will be the lastremaining open.Translating this to the above,we see that the leftmost locker of the22a−12+1still openis the last left open,ie.f(22a+2005)=641=f(2005)if a≥6.Therefore,there are inﬁnitely many positive integers n for which f(n)=f (2005).Solution2First,we calculate f(n)for n from1to32,to get a feeling for what happens.We obtain 1,1,3,3,1,1,3,3,9,9,11,11,9,9,11,11,1,1,3,3,1,1,3,3,9,9,11,11,9,9,11,11. This will help us to establish some patterns.Next,we establish two recursive formulas for f(n).First,from our pattern,it looks like f(2m)=f(2m−1).Why is this true in general?Consider a row of2m lockers.On theﬁrst pass through,Josephine shuts all of the even numbered lockers,leaving open lockers1,3,...,2m−1.These are exactly the same open lockers as if she had started with2m−1lockers in total. Thus,as she starts her second pass from right to left,the process will be the same now whether she started with2m lockers or2m−1lockers.Therefore,f(2m)=f(2m−1).This tells us that we need only focus on the values of f(n)where n is odd.Secondly,we show that f(2m−1)=2m+1−2f(m).(It is helpful to connect n=2m−1to a smaller case.)Why is this formula true?Starting with2m−1lockers,the lockers left open after theﬁrst pass are1,3,...,2m−1, ie.m lockers in total.Suppose f(m)=p.As Josephine begins her second pass,which is from right to left,we can think of this as being like theﬁrst pass through a row of m lockers.Thus,the last open locker will be the p th locker,counting from the right hand end,from the list1,3,...,2m−1.Theﬁrst locker from the right is2m−1=2m+1−2(1),the second is2m−3=2m+1−2(2), and so on,so the p th locker is2m+1−2p.Therefore,theﬁnal open locker is2m+1−2p,ie.f(2m−1)=2m+1−2p=2m+1−2f(m). Using these two formulae repeatedly,f(4k+1)=f(2(2k+1)−1)=2(2k+1)+1−2f(2k+1)=4k+3−2f(2(k+1)−1)=4k+3−2(2(k+1)+1−2f(k+1))=4k+3−2(2k+3−2f(k+1))=4f(k+1)−3andf(4k+3)=f(2(2k+2)−1)=2(2k+2)+1−2f(2k+2)=4k+5−2f(2k+1)=4k+5−2f(2(k+1)−1)=4k+5−2(2(k+1)+1−2f(k+1))=4k+5−2(2k+3−2f(k+1))=4f(k+1)−1From our initial list of values of f(n),it appears as if f(n)cannot leave a remainder of5 or7when divided by8.So we use these recursive relations once more to try to establish this:f(8l+1)=4f(2l+1)−3(since8l+1=4(2l)+1)=4(2l+3−2f(l+1))−3=8l+9−8f(l+1)=8(l−f(l+1))+9f(8l+3)=4f(2l+1)−1(since8l+3=4(2l)+3)=4(2l+3−2f(l+1))−1=8l+11−8f(l+1)=8(l−f(l+1))+11Similarly,f(8l+5)=8l+9−8f(l+1)and f(8l+7)=8l+11−8f(l+1). Therefore,since any odd positive integer n can be written as8l+1,8l+3,8l+5or8l+7, then for any odd positive integer n,f(n)is either9more or11more than a multiple of8. Therefore,for any odd positive integer n,f(n)cannot be2005,since2005is not9more or11more than a multiple of8.Thus,for every positive integer n,f(n)=2005,since we only need to consider odd values of n.Next,we show that there are inﬁnitely many positive integers n such that f(n)=f(2005). We do this by looking at the pattern we initially created and conjecturing thatf(2005)=f(2005+22a)if22a>2005.(We might guess this by looking at the connection between f(1)and f(3) with f(5)and f(7)and then f(1)through f(15)with f(17)through f(31).In fact,it appears to be true that f(m+22a)=f(m)if22a>m.)Using our formulae from above,f(2005+22a)=4f(502+22a−2)−3(2005+22a=4(501+22a−2)+1) =4f(501+22a−2)−3=4(4f(126+22a−4)−3)−3(501+22a−2=4(125+22a−4)+1)=16f(126+22a−4)−15=16f(125+22a−4)−15=16(4f(32+22a−6)−3)−15(125+22a−4=4(31+22a−6)+1)=64f(32+22a−6)−63=64f(31+22a−6)−63=64(4f(8+22a−8)−1)−63(31+22a−6=4(7+22a−8)+3)=256f(8+22a−8)−127=256f(7+22a−8)−127=256(4f(2+22a−10)−1)−127(7+22a−8=4(1+22a−10)+3)=1024f(2+22a−10)−383=1024f(1+22a−10)−383(Notice that we could have removed the powers of2from inside the functions and used this same approach to show that f(2005)=1024f(1)−383=641.)But,f(22b+1)=1for every positive integer b.Why is this true?We can prove this quickly by induction.For b=1,we know f(5)=1.Assume that the result is true for b=B−1,for some positive integer B≥2.Then f(22B+1)=f(4(22B−2)+1)=4f(22B−2+1)−3=4(1)−3=1by our induction hypothesis.Therefore,if a≥6,then f(1+22a−10)=f(1+22(a−5))=1sof(2005+22a)=1024(1)−383=641=f(2005)so there are inﬁnitely many integers n for which f(n)=f(2005).。

滑铁卢竞赛数学题

滑铁卢竞赛数学题概述
滑铁卢竞赛数学题通常比较难，涉及的知识点广泛，包括代数、几何、数论、组合数学等多个领域。

以下是一些滑铁卢竞赛数学题的示例：
1. 有100个球，其中有一个与其他99个重量不同，但外观相同。

用一个天平，最少需要称多少次才能确定这个重量不同的球？
2. 一个正方形的面积为1，将其四边中点连接起来，形成另一个正方形。

如此重复，得到第五、第六个正方形，求第五个正方形的面积。

3. 一个圆被分成n个相等的扇形，其中一个是空心的，其他n-1个是实心的。

求空心扇形的圆心角是多少度？
4. 有100个人站成一排，从第1个人开始报数，每次报到奇数的人离开队伍。

经过若干轮后，只剩下一个人。

求这个人最初站在第几位？
5. 有5个不同质因数的最小正整数是多少？
以上仅是滑铁卢竞赛数学题的一些示例，实际上还有更多难题和技巧题。

如果想要深入了解滑铁卢竞赛数学题的解题技巧和策略，建议参考相关的竞赛书籍和资料，或者参加专业的数学竞赛培训课程。

欧几里得滑铁卢数学竞赛_2003EuclidContest

parts are indicated like this: .Enter the answer in the appropriate box in the answer booklet.be given for a correct answer which is placed in the box. Part marks will be awarded parts are indicated like this: .Finished solutions must be written in the appropriate location in the answer booklet.Sybasei Anywhere SolutionsCanadian Instituteof ActuariesChartered Accountants Great West Lifeand London LifeNOTE: 1.Please read the instructions on the front cover of this booklet.2.Place all answers in the answer booklet provided. 3.For questions marked “”, full marks will be given for a correct answer placed in theappropriate box in the answer booklet. Marks may be given for work shown . Students are strongly encouraged to show their work.4.It is expected that all calculations and answers will be expressed as exact numbers such as4π, 27+, etc., except where otherwise indicated.1.(a)In the diagram, the parabola cuts the y -axis at the point 08,(), cuts the x -axis at the points 20,() and 40,(),and passes through the point a ,8(). What is the value of a ?(b)The quadratic equation x x k 260++= has two equal roots. What is the value of k ?(c)The line y x =+22 intersects the parabola y x x c =+23– at two points. One of these points is 14,(). Determine the coordinates of the second point of intersection.2.(a)If 090o o <<x and 3150sin cos x ()−()=o , what is the value of x to the nearest tenth of a degree?(b)In the diagram, ∆ABC is right-angled at B and AC =20. If sin C =35, what is the length ofside BC ?(c) A helicopter is flying due west over level ground at a constant altitude of 222 m and at aconstant speed. A lazy, stationary goat, which is due west of the helicopter, takes two measurements of the angle between the ground and the helicopter. The first measurement the goat makes is 6° and the second measurement, which he makes 1 minute later, is 75°. If the helicopter has not yet passed over the goat, as shown, how fast is the helicopter travelling to the nearest kilometre per hour?A B C3.(a)The function f x () has the property that f x f x 2323+()=()+ for all x .If f 06()=, what is the value of f 9()?(b)Suppose that the functions f x () and g x () satisfy the system of equations f x g x x x f x g x x ()+()=++()+()=+36242422for all x . Determine the values of x for which f x g x ()=().4.(a)In a short-track speed skating event, there are five finalists including two Canadians. Thefirst three skaters to finish the race win a medal. If all finalists have the same chance of finishing in any position, what is the probability that neither Canadian wins a medal?(b)Determine the number of positive integers less than or equal to 300 that are multiples of 3or 5, but are not multiples of 10 or 15.5.(a)In the series of odd numbers 1357911131517192123+++++––––––... the signs alternate every three terms, as shown. What is the sum of the first 300 terms of the series?(b)A two-digit number has the property that the square of its tens digit plus ten times its units digit equals the square of its units digit plus ten times its tens digit. Determine all two-digit numbers which have this property, and are prime numbers.6.(a)A lead box contains samples of two radioactive isotopes of iron. Isotope A decays so that after every 6 minutes, the number of atoms remaining is halved. Initially, there are twice as many atoms of isotope A as of isotope B, and after 24 minutes there are the same number of atoms of each isotope. How long does it take the number of atoms of isotopeB to halve?(b)Solve the system of equations:log log log log 103102102103113x y x y ()+()=()−()=7.(a) A regular hexagon is a six-sided figure which has all of its angles equal and all of its side lengths equal. Inthe diagram, ABCDEF is a regular hexagon with anarea of 36. The region common to the equilateral triangles ACE and BDF is a hexagon, which isshaded as shown. What is the area of the shadedhexagon?(b)At the Big Top Circus, H erc theHuman Cannonball is fired out of the cannon at ground level. (For the safetyof the spectators, the cannon ispartially buried in the sand floor.)Herc ’s trajectory is a parabola until he catches the vertical safety net, on his way down, at point B . Point B is 64 mdirectly above point C on the floor ofthe tent. If Herc reaches a maximumheight of 100 m, directly above a point30 m from the cannon, determine thehorizontal distance from the cannon tothe net.8.(a) A circle with its centre on the y-axis intersects the graph of y x = at the origin, O , and exactly two otherdistinct points, A and B , as shown. Prove that the ratioof the area of triangle ABO to the area of the circle isalways 1 : π.(b)In the diagram, triangle ABC has a right angle at Band M is the midpoint of BC . A circle is drawn usingBC as its diameter. P is the point of intersection of thecircle with AC . The tangent to the circle at Pcuts ABat Q . Prove that QM is parallel to AC .9.Cyclic quadrilateral ABCD has AB AD ==1, CD ABC =∠cos , and cos –∠=BAD 13. Provethat BC is a diameter of the circumscribed circle.10. A positive integer n is called “savage” if the integers 12,,...,n{} can be partitioned into three sets A, B and C such thati)the sum of the elements in each of A, B, and C is the same,ii)A contains only odd numbers,iii)B contains only even numbers, andiv)C contains every multiple of 3 (and possibly other numbers).(a)Show that 8 is a savage integer.(b)Prove that if n is an even savage integer, then n+412is an integer.(c)Determine all even savage integers less than 100.PUBLICATIONS2003 Euclid Contest(English)。

欧几里得滑铁卢数学竞赛_2002EuclidSolution

Solution 2
Since TM AB, and CM = MB, then CT = TA = AB.
A
Join T to B.
T
Since ∠ABC = 90o, then AC is the diameter of a circle
passing through A, C and B, with T as its centre.
Solution 3
2x2 +1 x2 − 3
=
2x2 − 6 + x2 − 3
7
( ) 2 x2 − 3 + 7
= x2 − 3
=
2
+
7 x2 −
3
Therefore, A = 7.
Answer: A = 7
(c) Solution 1
The original parabola can be written as
2002 Euclid Solutions
3
2x + 3 = 8x + 15
−12 = 6x
x = −2
Substituting x = −2 into the first equation, we obtain y = 2(−2) + 3 = −1, so the point of intersection is (−2, −1), which must lie on the third line.
common angle and each have a right angle.
B
M
C
But CM = 1 so CT = CM = 1 , and thus CT = AT = AB , ie. AB = 1 or sin(∠ACB) = 1 .

20012002年国内外数学竞赛题选解二

甘ｊ于Ｘ，至少与３个点之间有连线段。设不同于ｘ，的两个点为ｙ和ｚ．由于Ｐ是最长的，所以ｙ、ｚ ∈｛墨，丘．…．膏，｛．设ｒ＝置，ｚ＝置．ｉ（ｊ．则ｃ＝
万方数据
竺竺！竺！塑——————————！！一
数，则每个人得到—ａ，ｒ＋ａｊ个问ｇ；如果它足奇数．则
‘
吖：ｍ““／ｖ一∽
Ｊ≤』≤Ｙ
ｆｍ２．
当Ⅳ＝２ｍ，
１≤４１＜如＜…＜Ａ＂《６０，
Ｊ４≤』？＋Ｊ３＜Ａ２
纛蠢薹田田
。。：’竺至罢三墨笔篓璺＿－
列）．那么，这两行４－１３＜…＜４”＋】３≤７３．
７４个整数在１至７３中，一定存在ｊ、｝，使得ａ．
＝Ａ‘＋１３．即Ａ｛一Ａ＾＝１３．
７．设平面上ｎ（ｎ≥４）个点Ａ。，Ａ：，…，Ａ。，且任意三点不共线．每点至少与３个点之间有连线段．证明：在这ｎ个点中存在不同的２女个点置．卫，…，
于ｔｌ≤，，则口…＋…＋Ⅱ…《０；否则，ｎ。＋以＋ｌ＋ …＋Ⅱ…Ｉ＜ｑ＋口川＋…＋吼…与和是最小的．
矛盾．于是，从ａ…＋，开始，得到一个好的排列，即若某个和以…ｌ十¨・＋ｄ…＋★≤０，则ｎ．＋吼＋Ｉ＋…＋ Ⅱ…＋‘≤ｎ，＋“，，Ｉ＋…＋Ⅱ…，－３和的最小及，的最大性矛盾周此，对于ｎ！个排列，ｊＥｎ边形的顶点【每一种放法．按顺时针对应着ｎ个排列，这ｎ个排列中至少有一个是好的．所以至少有（ｎ一１）！个好的排
（２）１１＝１０．Ⅳ＝ｆ００
（第５３届门俄罗斯数学奥林肌电（决赛Ｄ类））解：将原命题改写为如Ｆ命题：有ｎ个非负整数之和为～．每一步选择任意两个具有相同奇偶性的数ｎ－Ｎ６．均用！生芸』替换原来 ‘ 的。和６问若干步后是否有可能使所有的数均相
同？
（１）证明Ｒ＝８，＿｜ｖ＝踟时答案是肯定的．假定数目的总和是０（因为我们町以将每个均

滑铁卢数学竞赛

滑铁卢数学竞赛1、21.|x|>3表示的区间是（）[单选题] *A.（-∞，3）B.(-3,3)C. [-3,3]D. （-∞，-3）∪（3，+ ∞）(正确答案)2、15.下列数中，是无理数的为（）[单选题] *A.-3.14B.6/11C.√3(正确答案)D.03、9.一棵树在离地5米处断裂，树顶落在离树根12米处，问树断之前有多高（）[单选题] *A. 17(正确答案)B. 17.5C. 18D. 204、若tan（π-α）>0且cosα>0，则角α的终边在（）[单选题] *A.第一象限B.第二象限C.第三象限D.第四象限(正确答案)5、下列说法正确的是[单选题] *A.带“+”号和带“-”号的数互为相反数B.数轴上原点两侧的两个点表示的数是相反数C.和一个点距离相等的两个点所表示的数一定互为相反数D.一个数前面添上“-”号即为原数的相反数(正确答案)6、16、在中,则( ). [单选题] *A. AB<2AC (正确答案)B. AB=2ACC. AB>2ACD. AB与2AC关系不确定7、260°是第（）象限角？[单选题] *第一象限第二象限第三象限(正确答案)第四象限8、4.已知两圆的半径分别为3㎝和4㎝，两个圆的圆心距为10㎝,则两圆的位置关系是（）[单选题] *Ａ.内切Ｂ.相交Ｃ.外切Ｄ.外离(正确答案)9、下列各角中，是界限角的是（）[单选题] *A. 1200°B. -1140°C. -1350°(正确答案)D. 1850°10、下列各对象可以组成集合的是（）[单选题] *A、与1非常接近的全体实数B、与2非常接近的全体实数(正确答案)C、高一年级视力比较好的同学D、与无理数相差很小的全体实数11、若2?＝a2＝4 ?，则a?等于( ) [单选题] *A. 43B. 82C. 83(正确答案)D. 4?12、47、若△ABC≌△DEF，AB＝2，AC＝4，且△DEF的周长为奇数，则EF的值为（）[单选题] *A．3B．4C．1或3D．3或5(正确答案)13、8. 下列事件中，不可能发生的事件是(? ? )．[单选题] *A．明天气温为30℃B．学校新调进一位女教师C．大伟身长丈八(正确答案)D．打开电视机，就看到广告14、3．中国是最早采用正负数表示相反意义的量，并进行负数运算的国家．若零上10℃记作+10℃，则零下10℃可记作（）[单选题] *A．10℃B．0℃C.-10 ℃(正确答案)D．-20℃15、19．对于实数a、b、c,“a>b”是“ac2(c平方)>bc2(c平方) ; ”的（）[单选题] * A．充分不必要条件B．必要不充分条件(正确答案)C．充要条件D．既不充分也不必要条件16、22．如图棋盘上有黑、白两色棋子若干，找出所有使三颗颜色相同的棋在同一直线上的直线，满足这种条件的直线共有（）[单选题] *A．5条(正确答案)B．4条C．3条D．2条17、f（x）=-2x+5在x=1处的函数值为（）[单选题] *A、-3B、-4C、5D、3(正确答案)18、10. 如图所示，小明周末到外婆家，走到十字路口处，记不清哪条路通往外婆家，那么他一次选对路的概率是(? ? ?)．[单选题] *A．1/2B．1/3(正确答案)C．1/4D．119、15．如图所示，下列数轴的画法正确的是（）[单选题] *A．B．C．(正确答案)D．20、-950°是（）[单选题] *A. 第一象限角B. 第二象限角(正确答案)C. 第三象限角D. 第四象限角21、1．如图，∠AOB＝120°，∠AOC＝∠BOC，OM平分∠BOC，则∠AOM的度数为（）[单选题] *A．45°B．65°C．75°(正确答案)D．80°22、27．下列计算正确的是（）[单选题] *A．（﹣a3）2＝a6(正确答案)B．3a+2b＝5abC．a6÷a3＝a2D．（a+b）2＝a2+b223、16．“x2（x平方）－4x－5=0”是“x=5”的( ) [单选题] *A．充分不必要条件B．必要不充分条件(正确答案)C．充要条件D．既不充分也不必要条件24、19．下列两个数互为相反数的是（）[单选题] *A．（﹣）和﹣（﹣）B．﹣5和(正确答案)C．π和﹣14D．+20和﹣（﹣20）25、13．在数轴上，下列四个数中离原点最近的数是（）[单选题] *A．﹣4(正确答案)B．3C．﹣2D．626、14．命题“?x∈R，?n∈N*，使得n≥x2（x平方）”的否定形式是（）[单选题] * A．?x∈R，?n∈N*，使得n<x2B．?x∈R，?x∈N*，使得n<x2C．?x∈R，?n∈N*，使得n<x2D．?x∈R，?n∈N*，使得n<x2(正确答案)27、8．(2020·课标Ⅱ)已知集合U={－2，－1,0,1,2,3}，A={－1,0,1}，B={1,2}，则?U(A∪B)=( ) [单选题] *A．{－2,3}(正确答案)B．{－2,2,3}C．{－2，－1,0,3}D．{－2，－1,0,2,3}28、7人小组选出2名同学作正副组长，共有选法（）种。

Fermat滑铁卢数学竞赛(Grade 11)-数学Mathematics-2002-试题 exam

Canadian Instituteof Actuaries Chartered AccountantsSybasei Anywhere SolutionsScoring:There is no penalty for an incorrect answer.Each unanswered question is worth 2, to a maximum of 10 unanswered questions.Part A: Each correct answer is worth 5.1.If x =3, the numerical value of 522–x is(A ) –1(B ) 27(C ) –13(D )–31(E ) 32.332232++ is equal to(A ) 3(B ) 6(C ) 2(D )32(E ) 53.If it is now 9:04 a.m., in 56 hours the time will be(A ) 9:04 a.m.(B ) 5:04 p.m.(C ) 5:04 a.m.(D ) 1:04 p.m.(E ) 1:04 a.m.4.Which one of the following statements is not true?(A ) 25 is a perfect square.(B ) 31 is a prime number.(C ) 3 is the smallest prime number.(D ) 8 is a perfect cube.(E ) 15 is the product of two prime numbers.5. A rectangular picture of Pierre de Fermat, measuring 20 cmby 40 cm, is positioned as shown on a rectangular postermeasuring 50 cm by 100 cm. What percentage of the areaof the poster is covered by the picture?(A ) 24%(B ) 16%(C ) 20%(D ) 25%(E ) 40%6.Gisa is taller than Henry but shorter than Justina. Ivan is taller than Katie but shorter than Gisa. Thetallest of these five people is(A ) Gisa (B ) Henry (C ) Ivan (D ) Justina (E ) Katie7. A rectangle is divided into four smaller rectangles. Theareas of three of these rectangles are 6, 15 and 25, as shown.The area of the shaded rectangle is(A ) 7(B ) 15(C ) 12(D ) 16(E) 108.In the diagram, ABCD and DEFG are squares with equal side lengths, and ∠=°DCE 70. The value of y is (A ) 120(B ) 160(C ) 130(D ) 110(E ) 1409.The numbers 1 through 20 are written on twenty golf balls, with one number on each ball. The golfballs are placed in a box, and one ball is drawn at random. If each ball is equally likely to be drawn,what is the probability that the number on the golf ball drawn is a multiple of 3?(A )320(B )620(C )1020(D )520(E )12010.ABCD is a square with AB x =+16 and BC x =3, as shown.The perimeter of ABCD is(A ) 16(B ) 32(C ) 96(D ) 48(E ) 24Part B: Each correct answer is worth 6.11. A line passing through the points 02,−() and 10,() also passes through the point 7,b (). The numericalvalue of b is(A ) 12(B )92(C ) 10(D ) 5(E ) 1412.How many three-digit positive integers are perfect squares?(A ) 23(B ) 22(C ) 21(D ) 20(E ) 1913. A “double-single” number is a three-digit number made up of two identical digits followed by adifferent digit. For example, 553 is a double-single number. How many double-single numbers are there between 100 and 1000?(A ) 81(B ) 18(C ) 72(D ) 64(E ) 9014.The natural numbers from 1 to 2100 are entered sequentially in 7 columns, with the first 3 rows asshown. The number 2002 occurs in column m and row n . The value of m n + isColumn 1Column 2Column 3Column 4Column 5Column 6Column 7Row 1 1 2 3 4 5 6 7Row 2 8 91011121314Row 315161718192021M M M M M M M M(A ) 290(B ) 291(C ) 292(D ) 293(E ) 294x + 163xA BD C15.In a sequence of positive numbers, each term after the first two terms is the sum of all of the previousterms . If the first term is a ,the second term is 2, and the sixth term is 56, then the value of a is(A ) 1(B ) 2(C ) 3(D ) 4(E ) 516.If ac ad bc bd +++=68 and c d +=4, what is the value of a b c d +++?(A ) 17(B ) 85(C ) 4(D ) 21(E ) 6417.The average age of a group of 140 people is 24. If the average age of the males in the group is 21 andthe average age of the females is 28, how many females are in the group?(A ) 90(B ) 80(C ) 70(D ) 60(E ) 5018. A rectangular piece of paper AECD has dimensions 8 cm by 11 cm. Corner E is folded onto point F , which lies on DC ,as shown. The perimeter of trapezoid ABCD is closest to (A ) 33.3 cm (B ) 30.3 cm (C ) 30.0 cm(D ) 41.3 cm (E ) 35.6 cm 19.If 238610a b =(), where a and b are integers, then b a − equals(A ) 0(B ) 23(C )−13(D )−7(E )−320.In the diagram, YQZC is a rectangle with YC =8 and CZ = 15. Equilateral triangles ABC and PQR , each withside length 9, are positioned as shown with R and B on sidesYQ and CZ , respectively. The length of AP is (A ) 10(B )117(C ) 9(D ) 8(E )72Part C: Each correct answer is worth 8.21.If 31537521219⋅⋅⋅⋅+−=L n n , then the value of n is(A ) 38(B ) 1(C ) 40(D ) 4(E ) 3922.The function f x () has the property that f x y f x f y xy +()=()+()+2, for all positive integers x and y .If f 14()=, then the numerical value of f 8() is(A ) 72(B ) 84(C ) 88(D ) 64(E ) 80continued ...Figure 1Figure 223.The integers from 1 to 9 are listed on a blackboard. If an additional m eights and k nines are added tothe list, the average of all of the numbers in the list is 7.3. The value of k m + is(A ) 24(B ) 21(C ) 11(D ) 31(E ) 8924. A student has two open-topped cylindrical containers. (Thewalls of the two containers are thin enough so that theirwidth can be ignored.) The larger container has a height of20 cm, a radius of 6 cm and contains water to a depth of 17cm. The smaller container has a height of 18 cm, a radius of5 cm and is empty. The student slowly lowers the smallercontainer into the larger container, as shown in the cross-section of the cylinders in Figure 1. As the smaller container is lowered, the water first overflows out of the larger container (Figure 2) and then eventually pours into thesmaller container. When the smaller container is resting onthe bottom of the larger container, the depth of the water in the smaller container will be closest to(A ) 2.82 cm (B ) 2.84 cm (C ) 2.86 cm(D ) 2.88 cm (E ) 2.90 cm25.The lengths of all six edges of a tetrahedron are integers. The lengths of five of the edges are 14, 20,40, 52, and 70. The number of possible lengths for the sixth edge is(A ) 9(B ) 3(C ) 4(D ) 5(E ) 6。

欧几里得滑铁卢数学竞赛_2006EuclidSolution

y = x2−2(21)x+212−212+440 = (x−21)2−212+440 = (x−21)2−441+440 = (x−21)2−1
From this form, we immediately see that the coordinates of the vertex are (21, −1).
(c) Solution 1 To determine B, the point of intersection of the lines y = x and x + 2y = 12, we set y = x in the second equation to obtain x + 2x = 12 or 3x = 12 or x = 4.
3. (a) Answer: (21, −1)
Solution 1
The x-intercepts of the given parabola are x = 20 and x = 22.
The x-coordinate of the vertex of the parabola is the average of the x-intercepts, or
10A + B
resulting number is
.
10
So we want to determine A and B so that
10A + B
A+B
=
10
2
10A + B = 5(A + B)
5A = 4B
Since A and B are digits such that 5A = 4B, then A = 4 and B = 5 is the only possibility. Therefore, n = 45. (We can quickly check that the average of the digits of n is 4.5, the number obtained by putting a decimal point between the digits of n.)

2014-2012加拿大滑铁卢大学11年级数学竞赛试题

1.For real numbers a and b with a≥0and b≥0,the operation is deﬁned bya b=√a+4b.For example,5 1=5+4(1)=√9=3.(a)What is the value of8 7?(b)If16 n=10,what is the value of n?(c)Determine the value of(9 18) 10.(d)With justiﬁcation,determine all possible values of k such that k k=k.2.Each week,the MathTunes Music Store releases a list of the Top200songs.A newsong“Recursive Case”is released in time to make it onto the Week1list.The song’s position,P,on the list in a certain week,w,is given by the equation P=3w2−36w+110.The week number w is always a positive integer.(a)What position does the song have on week1?(b)Artists want their song to reach the best position possible.The closer that theposition of a song is to position#1,the better the position.(i)What is the best position that the song“Recursive Case”reaches?(ii)On what week does this song reach its best position?(c)What is the last week that“Recursive Case”appears on the Top200list?3.A pyramid ABCDE has a square base ABCD of side length 20.Vertex E lies on theline perpendicular to the base that passes through F ,the centre of the base ABCD .It is given that EA =EB =EC =ED =18.(a)Determine the surface area of the pyramidABCDEincluding its base.(b)Determine the height EF of the pyramid.A B C D EF 2018(c)G and H are the midpoints of ED and EA ,respectively.Determine the area of thequadrilateral BCGH .4.The triple ofpositive integers (x,y,z )is called an Almost Pythagorean Triple (or APT)if x >1and y >1and x 2+y 2=z 2+1.For example,(5,5,7)is an APT.(a)Determine the values of y and z so that (4,y,z )is an APT.(b)Prove that for any triangle whose side lengths form an APT,the area of thetriangle is not an integer.(c)Determine two 5-tuples (b,c,p,q,r )of positive integers with p ≥100for which(5t +p,bt +q,ct +r )is an APT for all positive integers t .1.At the JK Mall grand opening,some lucky shoppers are able to participate in a moneygiveaway.A large box has beenﬁlled with many$5,$10,$20,and$50bills.The lucky shopper reaches into the box and is allowed to pull out one handful of bills.(a)Rad pulls out at least two bills of each type and his total sum of money is$175.What is the total number of bills that Rad pulled out?(b)Sandy pulls out exactlyﬁve bills and notices that she has at least one bill of eachtype.What are the possible sums of money that Sandy could have?(c)Lino pulls out six or fewer bills and his total sum of money is$160.There areexactly four possibilities for the number of each type of bill that Lino could have.Determine these four possibilities.2.A parabola has equation y=(x−3)2+1.(a)What are the coordinates of the vertex of the parabola?(b)A new parabola is created by translating the original parabola3units to the leftand3units up.What is the equation of the translated parabola?(c)Determine the coordinates of the point of intersection of these two parabolas.(d)The parabola with equation y=ax2+4,a<0,touches the parabola withequation y=(x−3)2+1at exactly one point.Determine the value of a.3.A sequence of m P’s and n Q’s with m>n is called non-predictive if there is some pointin the sequence where the number of Q’s counted from the left is greater than or equal to the number of P’s counted from the left.For example,if m=5and n=2the sequence PPQQPPP is non-predictive because in counting theﬁrst four letters from the left,the number of Q’s is equal to the number of P’s.Also,the sequence QPPPQPP is non-predictive because in counting theﬁrst letterfrom the left,the number of Q’s is greater than the number ofP’s.(a)If m=7and n=2,determine the number of non-predictive sequences that beginwith P.(b)Suppose that n=2.Show that for every m>2,the number of non-predictivesequences that begin with P is equal to the number of non-predictive sequences that begin with Q.(c)Determine the number of non-predictive sequences with m=10and n=3.4.(a)Twenty cubes,each with edge length1cm,are placed together in4rows of5.What isthe surface area of this rectangularprism?(b)A number of cubes,each with edge length1cm,are arranged to form a rectangularprism having height1cm and a surface area of180cm2.Determine the number of cubes in the rectangular prism.(c)A number of cubes,each with edge length1cm,are arranged to form a rectangularprism having length l cm,width w cm,and thickness1cm.A frame is formed byremoving a rectangular prism with thickness 1cm located k cm from each of the sides of the original rectangular prism,as shown. Each of l,w and k is a positive integer.If the frame has surface area532cm2,determine all possible values for l and w such that l≥w.l cmw cmk cmk cmk cmk cm1 cm1.Quadrilateral P QRS is constructed with QR =51,as shown.The diagonals of P QRS intersect at 90◦at point T ,such that P T =32and QT =24.322451P QRST (a)Calculate the length of P Q.(b)Calculate the area of P QR .(c)If QS :P R =12:11,determine the perimeter of quadrilateral P QRS .2.(a)Determine the value of (a +b )2,given that a 2+b 2=24and ab =6.(b)If (x +y )2=13and x 2+y 2=7,determine the value of xy .(c)If j +k =6and j 2+k 2=52,determine the value of jk .(d)If m 2+n 2=12and m 4+n 4=136,determine all possible values of mn .3.(a)Points M (12,14)and N (n,n 2)lie on theparabola with equation y =x 2,as shown.Determine the value of n such that∠MON =90◦.yx(b)Points A (2,4)and B (b,b 2)are the endpointsofa chord of the parabola with equationy =x 2,as shown.Determine the value of bso that ∠ABO =90◦.y x(c)Right-angled triangle P QR is inscribed inthe parabola with equation y =x 2,asshown.Points P,Q and R have coordinates(p,p 2),(q,q 2)and (r,r 2),respectively.If p ,qand r are integers,show that 2q +p +r =0.y x4.The positive divisors of 21are 1,3,7and 21.Let S (n )be the sum of the positive divisors of the positive integer n .For example,S (21)=1+3+7+21=32.(a)If p is an odd prime integer,ﬁnd the value of p such that S (2p 2)=2613.(b)The consecutive integers 14and 15have the property that S (14)=S (15).Determine all pairs of consecutive integers m and n such that m =2p and n =9q for prime integers p,q >3,and S (m )=S (n ).(c)Determine the number of pairs of distinct prime integers p and q ,each less than 30,with the property that S (p 3q )is not divisible by 24.。

加拿大数学竞赛历年试题(滑铁卢大学)

Each question is worth 10 marks
Calculating devices are allowed, provided that they do not have any of the following features: (i) internet access, (ii) the ability to communicate with other devices, (iii) information previously stored by students (such as formulas, programs, notes, etc.), (iv) a computer algebra system, (v) dynamic geometry software.
Parts of each question can be of two types: 1. SHORT ANSWER parts indicated by
• worth 3 marks each • full marks given for a correct answer which is placed in the box • part marks awarded only if relevant work is shown in the space provided
WRITE ALL ANSWERS IN THE ANSWER BOOKLET PROVIDED. • Extra paper for your ﬁnished solutions must be supplied by your supervising teacher and inserted into your answer booklet. Write your name, school name, and question number on any inserted pages. • Express answers as simpli√ﬁed exact numbers except where otherwise indicated. For example, π + 1 and 1 − 2 are simpliﬁed exact numbers.

美国2002高中物理竞赛题及答案整理

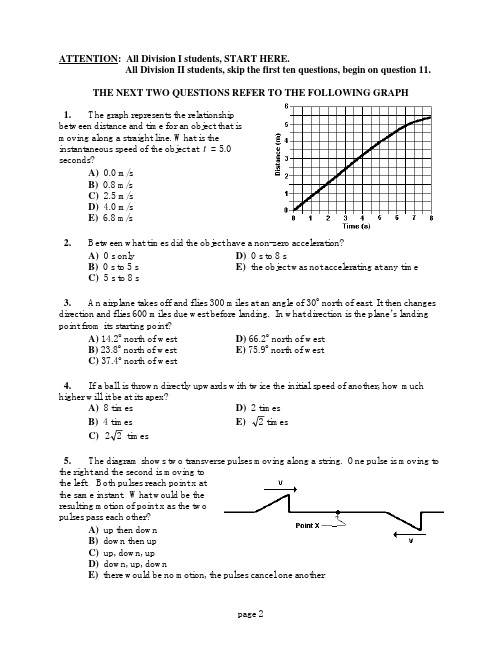
ATTENTION: All Division I students, START HERE.All Division II students, skip the first ten questions, begin on question 11.THE NEXT TWO QUESTIONS REFER TO THE FOLLOWING GRAPH1. The graph represents the relationshipbetween distance and time for an object that ismoving along a straight line. What is theinstantaneous speed of the object at t = 5.0seconds?A) 0.0 m/sB) 0.8 m/sC) 2.5 m/sD) 4.0 m/sE) 6.8 m/s2. Between what times did the object have a non-zero acceleration?A) 0 s only D) 0 s to 8 sB) 0 s to 5 s E) the object was not accelerating at any timeC) 5 s to 8 s3. An airplane takes off and flies 300 miles at an angle of 30o north of east. It then changes direction and flies 600 miles due west before landing. In what direction is the plane’s landing point from its starting point?A) 14.2o north of west D) 66.2o north of westB) 23.8o north of west E) 75.9o north of westC) 37.4o north of west4. If a ball is thrown directly upwards with twice the initial speed of another, how much higher will it be at its apex?A) 8 times D) 2 timesB) 4 times E)2timesC)22 times5. The diagram shows two transverse pulses moving along a string. One pulse is moving to the right and the second is moving tothe left. Both pulses reach point x atthe same instant. What would be theresulting motion of point x as the twopulses pass each other?A) up then downB) down then upC) up, down, upD) down, up, downE) there would be no motion, the pulses cancel one another6. Three resistors of different values can be connected together in different configurations. If all three resistors are used in a circuit, how many different values of total resistance can be produced?A) 2 B) 3 C) 5 D) 6 E) 87. The diagram shows two water pulseswhich were originally produced at point A andare beginning to be reflected from a wide barrieras shown. Which of the points in the diagramwould represent a virtual source for thereflected waves?A) Point AB) Point BC) Point CD) Point DE) There would be no virtual source forthe reflected pulses.8. A gas is enclosed in a cylindrical piston. When the gas is heated from 0o C to 100o C, the piston is allowed to move to maintain a constant pressure. According to the Kinetic-Molecular Theory of MatterA) the mass of the gas will increaseB) the number of molecules of gas must increaseC) the size of the individual molecules has increasedD) the average speed of the molecules has increasedE) the molecules continue to strike the sides of the container with the same energy9. When a positive electrically charged glass rod is brought near a neutral hollow metal sphere suspended by an insulating string, the sphere will be attracted to the rod because:A) the rod is much larger than the sphereB) the rod removes electron from the sphereC) the electric charge produces a magnetic field to attract the sphereD) the charge on the rod causes a separation of charge in the sphereE) some of the protons from the rod have been given to the sphere10. In Rutherford's famous gold foil scattering experiment, he found that most alpha particles would pass through the foil undeflected. Which of the following nuclear properties can be inferred from this observation?A) The nucleus must have a positive chargeB) Most of the mass of an atom is in the nucleusC) The nucleus contains both protons and neutronsD) The diameter of the nucleus is small compared to the diameter of the atomE) None of the aboveATTENTION: All Division I students, continue to question 40.All Division II students, START HERE. Numbers 1-10 on you answer sheet should remain blank. Your first answer should be number 11.THE NEXT THREE QUESTIONS REFER TO THE FOLLOWING SCENARIO The diagram below represents a toy car starting from rest and uniformly accelerating across the floor. The time and distance traveled from the start are shown in the diagram.11. What was the average speed of the cart between 0.1 seconds and 0.3 seconds?A) 0.6 m/s D) 4.8 m/sB) 1.9 m/s E) 60 m/sC) 2.4 m/s12. What was the acceleration of the cart during the first 0.4 seconds?A) 6.0 m/s/s D) 25 m/s/sB) 9.8 m/s/s E) 50 m/s/sC) 12 m/s/s13. What was the instantaneous velocity of the cart at 96 centimeters from the start?A) 0.6 m/s D) 4.8 m/sB) 1.9 m/s E) 60 m/sC) 2.4 m/s14. An intrinsic property of matter is one that does not depend on the quantity of matter present. Which of the following properties is NOT an intrinsic property?A) Density B) Temperature C) Specific Heat D) Half-life E) Inertia15. A positively charged particle moves to the right. Itenters a region of space in which there is an electric fielddirected up the plane of the paper (see figure). In whichdirection does a magnetic field have to point in this region sothat the particle maintains a constant velocity?A) Into the plane of the pageB) Out of the plane of the pageC) To the rightD) To the leftE) Up the plane of the page16. During a particular kind of radioactive decay, a particle is emitted from the nucleus of an atom and the atom's atomic number increases by one. This decay necessarily involves the emission of ______________ from the nucleus?A) an alpha particle D) a protonB) a beta particle E) a neutronC) a gamma rayTHE NEXT TWO QUESTIONS REFER TO THE FOLLOWING SCENARIO The motion of a circus clown on a unicycle moving in a straight lineis shown in the graph at the right.17. What would be the acceleration of the clown at 5 s?A) 1.6 m/s2D) 8.0 m/s2B) 2.0 m/s2E) none of the aboveC) 3.4 m/s218. After 12 seconds, how far is the clown from her originalstarting point?A) 0 m B) 10 m C) 34 m D) 47 m E) 74 m19. As a rocket blasts away from the earth with a cargo for the international space station, which of the following graphs would best represent the gravitational force on the cargo versus distance from the surface of the Earth?20. The graph shows the relationship between themass of a number of rubber stoppers and their resultingweight on some far-off planet. The slope of the graph is arepresentation of the:A) mass of a stopperB) density of a stopperC) volume of a stopperD) acceleration due to gravityE) number of stoppers for each unit of weightAn ideal battery, an ideal ammeter,a switch and three resistors are connectedas shown. With the switch open as shownin the diagram the ammeter reads 2.0amperes.21. With the switch open, what would be the potential difference across the 15 ohm resistor?A) 30 V B) 40 V C) 60 V D) 70 V E) 110V22. With the switch open, what must be the voltage supplied by the battery?A) 30 V B) 40 V C) 60 V D) 70 V E) 110 V23. When the switch is closed, what would be the current in the circuit?A) 1.1 A B) 1.7 A C) 2.0 A D) 2.3 A E) 3.0 A24. Two small hollow metal spheres hung on insulating threads attract oneanother as shown. It is known that a positively charged rod will attract ball A.I. Ball A has a positive chargeII. Ball B has a negative chargeIII. Ball A and Ball B have opposite chargesWhich of the above can be correctly concluded about the charge on the balls?A) I only B) II only C) III only D) all of these E) none of these25. If M represents units of mass, L represents units of length, and T represents units of time, the dimensions of power would be:A)MLT2B)MLT22C)MLT23D)MLTE)MLT226. Consider two laboratory carts of different masses but identical kinetic energies and the three following statements.I. The one with the greatest mass has the greatest momentumII. The same impulse was required to accelerate each cart from restIII. Both can do the same amount of work as they come to a stopWhich of the above statements would be correct?A) I only D) I and II onlyB) II only E) I and III onlyC) III onlyThe diagram below shows three roller coaster tracks of equal length. Assume that on all tracks the roller coaster carts start from rest at the same elevation and moves frictionlessly over the tracks to the finish.27. If all roller coaster carts start at the positions shown, on which track would the roller coaster cart be traveling the fastest at the finish?A) Cart A D) All would reach the finish with the same speedB) Cart B E) More information would be requiredC) Cart C28. If all roller coaster carts start at the positions shown, on which track would the roller coaster cart reach the finish first?A) Cart A D) All would reach the finish at the same timeB) Cart B E) More information would be requiredC) Cart C29. Assume the roller coaster cart rollsfrictionlessly along the curved track from point A topoint C under the influence of gravity. What would bethe direction of the cart's acceleration at point B?A) upwardB) downwardC) forwardD) backwardE) no acceleration30. A box falls to the ground from a delivery truck traveling at 30 m/s. After hitting the road, it slides 45 meters to rest. How long does it take the box to come to rest?A) 0.67 s B) 1.5 s C) 2.0 s D) 3.0 s E) 6.0 s31. A compass is placed near a coil of wire. A conventionalelectrical current is then run through the coil from left to right asshown. This will cause the North pole of the compass to:A) point toward the leftB) point toward the rightC) point toward the bottom of the paperD) not move since the magnetic field of the coil is into thepaperE) not move since the magnetic field of the coil is out of the paper32. An automobile engine delivers 24,000 watts (about 32 hp) of power to a car's driving wheels. If the car maintains a constant speed of 30 m/s (about 65 mph), what is the magnitude of the retarding force acting on the car?A) 800 N D) 720,000 NB) 960 N E) 1,560,000 NC) 1950 N33. A short burst of white light strikes a rectangular glass block with an angle of incidence of 0o. Which color of transmitted light would be the first to emerge from the opposite side?A) red D) violetB) yellow E) all colors would emerge at the same instantC) green34. Two containers are filled with gases at the sametemperature. In the container on the left is a gas of molar mass2M, volume 2V, and number of moles 2n. In the container onthe right is a gas of molar mass M, volume V, and moles n.Which is most nearly the ratio of the pressure of the gas on theleft to the pressure of the gas on the right?A) 1:1 D) 8:1B) 2:1 E) 16:1C) 4:135. A 300 eV electron is aimed midway between twoparallel metal plates with a potential difference of 400 V. Theelectron is deflected upwards and strikes the upper plate asshown. What would be the kinetic energy of the electron justbefore striking the metal plate?A) 360 eV B) 400 eV C) 500 eV D) 700 eV E) 740 eV36. Two masses, m 1 and m 2, are connected by a cord and arrangedas shown in the diagram with m 1 sliding along on a frictionless surfaceand m 2 hanging from a light frictionless pulley. What would be themass of the falling mass, m 2, if both the sliding mass, m 1, and thetension, T , in the cord were known?A) 11()g − D) m g T g1− B) 12Tg E) ()()T gm g T m −−11) C) Tm gm T 11()−37. A diffraction grating of 1000 lines/cm has red light of wavelength 700nm pass through it. The distance between the first and third principal bright spots on a screen 2.0m away isA) 14 cm B) 28 cm C) 42 cm D) 140 cm E) 280 cm38. A 5 x 10-6 coulomb electric charge is placed midway between two parallel metal plates connected to a 9-volt battery. If the electric charge experiences a force of 1.5 x 10-4 newtons, what is the separation of the metal plates?A) 6.75 x 10-9m B) 2.7 x 10-4m C) 3.7 x 10-3m D) 0.30 m E) 3.3 m39. A parallel-plate capacitor is connected to a resistanceless circuit with a battery having emf î until the capacitor is fully charged. The battery is then disconnected from the circuit and the plates of the capacitor are moved to half of their original separation using insulated gloves. Let V new be the potential difference across the capacitor plates when the plates are moved together. Let V old be the potential difference across the capacitor plates when connected to the battery. V V new old= A) 41 B) 21 C) 1 D) 2 E) 440. A box with a mass of 50 kg is dragged across thefloor by a rope which makes an angle of 30o with thehorizontal. Which of the following would be closest to thecoefficient of kinetic friction between the box and the floor ifa 250 newton force on the rope is required to move the crateat a constant speed of 20 m/s as shown in the diagram?A) 0.26 B) 0.33 C) 0.44 D) 0.59 E) 0.77ATTENTION: All Division I students, STOP. All Division II students, turn page and continue to question 50.41. A person throws a small object from the top of a building at an angle of 300 above the horizontal. At the instant that the object returns to the same height from which it was thrown, at what rate is the speed of the object changing? Ignore air resistance and let g be the acceleration due to gravity.A) 0 B) g tan 30o C) g sin 30o D) g cos 30o E) g42. A small box of mass m is placed on top of a larger box of mass2m as shown in the diagram at right. When a force F is applied to thelarge box, both boxes accelerate to the right with the same acceleration.If the coefficient of friction between all surfaces is ì, what would be theforce accelerating the smaller mass?A) µmg F −3 B) µmg F 3− C) µmg F − D) 3µmg F − E) 3F43. A light ray is incident normal to a thin layer ofglass. Given the figure, what is the minimum thicknessof the glass that gives the reflected light an orangish color( ëair = 600 nm) ?A) 50 nm D) 200 nmB) 100 nm E) 500 nmC) 150 nm44. A thermally insulating container has a membrane separating the container into two equal parts. In one part is a vacuum. In the other part is an ideal gas of temperature T and internal energy U. The membrane is punctured and the gas rushes into the region which was vacuum. After the system has returned to equilibrium, which of the following is NOT true for the gas?A) The temperature of the gas is unchanged.B) No work is done by the gas on the surroundings.C) There is no heat exchanged by the gas with the surroundings.D) There is no entropy change of the system.E) The internal energy of the gas is unchanged.45. A light inextensible string is connected to a mass, M , that provides the tension in the string. A length L of the string has a fundamental frequency of vibration of f M . If a second identical mass is now connected to the original mass, the newfundamental frequency of the string (f 2M ) of string length L incomparison to the fundamental frequency with only one massconnected f M isA) f f M M 22= D) f f M M 212= B) f f M M 22= E) f f M M 212= C) f f M M 2=46. A hotplate is designed such that it has a resistance of 12 Ù when operating at 120 volts. What is the minimum amount of time that it would take to warm 0.45 kg of water from 15o C to 85o C?A) 20 s B) 26 s C) 110 s D) 180 s E) 220 s47. A car heads toward a brick wall in a crash test at 30 m/s. The horn is emitting a sound with frequency 250 Hz as it approaches the wall. If the air is still and the speed of sound in air is 340 m/s, what beat frequency from the horn would the driver of the car detect?A) 0 Hz B) 22 Hz C) 24 Hz D) 41 Hz E) 48 Hz48. An object of mass M is dropped from a height H above the ground. The object crashes into some soft earth and comes to rest by compressing the earth a distance of H /2. Assuming that air resistance is negligible, what is the magnitude of the average constant force exerted by the ground on the object while coming to rest?A) 0 B) 32 Mg C) Mg D) 2Mg E) 3Mg49. A solid, uncharged conducting sphere of radius 3a contains a hollowed spherical region of radius a . A point charge +Q is placed at the common center of the spheres. Taking V = 0 as r →∞, the potential at position r =2a from the center of the spheres is:A) 0 D) 23kQ aB) kQ a 3 E) kQ aC) kQ a24050. Two thin lenses each with afocal length of +10 cm are located30 cm apart with their optical axesaligned as shown. An object isplaced 35 cm from the first lens.After the light has passed throughboth lenses, at what distance fromthe second lens will the final image be formed?A) 65 cm B) 35 cm C) 27 cm D) 17 cm E) -14 cmATTENTION: All Division II students STOP. All Division II answers should appear inNumbers 11-50 on your answer sheet. Numbers 1-10 on you answer sheet should remain blank.2002 PhysicsBowl Answer SheetQuestion Answer Question Answer1 B 26 E2 C 27 B3 B 28 A4 B 29 A5 C 30 D6 E 31 A7 C 32 A8 D 33 A9 D 34 A10 D 35 C11 C 36 C12 C 37 B13 D 38 D14 E 39 B15 B 40 D16 B 41 C17 B 42 A18 E 43 B19 E 44 D20 D 45 B21 A 46 C22 D 47 E23 D 48 E24 E 49 B25 C 50 Cpage 12。

欧几里得滑铁卢数学竞赛_2011EuclidSolution

=
6,
then
∠BDA
=
∠BAD
=
1 2
(180◦
− ∠DBA)
=
1 2
(180◦
−
30◦)
=
75◦.
We calculate the length of AD.
Method 1
AD
BA
By the Sine Law in DBA, we have
=
.
sin(∠DBA) sin(∠BDA)
6 sin(30◦)
4. (a) We consider choosing the three numbers all at once. We list the possible sets of three numbers that can be chosen:
{1, 2, 3} {1, 2, 4} {1, 2, 5} {1, 3, 4} {1, 3, 5} {1, 4, 5} {2, 3, 4} {2, 3, 5} {2, 4, 5} {3, 4, 5}
∠B C D)
=
1 2
(180◦
−
60◦)
=
60◦.
Therefore, BCD is equilateral, and so BD = BC = CD = 6.
Consider DBA.
Note that ∠DBA = 90◦ − ∠CBD = 90◦ − 60◦ = 30◦.
Since
BD
=
BA
∠ADC = 360◦ − ∠ADB − ∠CDB = 360◦ − 130◦ − 150◦ = 80◦ .
(c) By the Pythag√orean Theorem in EAD, we have EA2 +AD2 = ED2 or 122 +AD2 = 132, and so AD = 169 − 144 = 5, since AD > 0. By the Pythag√orean Theorem in ACD, we have AC2 + CD2 = AD2 or AC2 + 42 = 52, and so AC = 25 − 16 = 3, since AC > 0. (We could also have determined the lengths of AD and AC by recognizing 3-4-5 and 5-12-13 right-angled triangles.) By the Pythag√orean The√orem in ABC, we have AB2 + BC2 = AC2 or AB2 + 22 = 32, and so AB = 9 − 4 = 5, since AB > 0.

2002年IMO中国国家集训队选拔考试

( 1 + an - 2 ) 2 an - 1 1 ≤ ・ δ( ) = , n + 1 x n + δ( n) + 1 4 xn + [ ( 1 - a n - 2) ( x n + δ( n - 1) + 1) + 2 ( n - 1) ] 且当 xn - 1 = 1 + an - 2 an - 1 时 , 取最大值 . x n + δ( n) + 1 xn - n an - 1 + x n + δ( n) + 1 ( x n + δ( n) + 1) 2 an 1 ( 1 + an - 1 ) ≤ ・ = , n ○ 4 δ( n + 1) + 1 δ( n + 1) + 1 ( 1 - an - 1 ) (δ( n) + 1) + 2 n 且当 x n = 时 , 取最大值 1 + an - 1 an
下证当 n ≥5 时 , 不存在 a1 , …, an 适合题设条件. 证法一 :令 0 ≤a1 < a2 < … < an , bi = ai + 1 - ai ,
i = 1 , 2 , …, n - 1 . 则当 i < j 时 ,
有 1 个红点 , 则该行最后 7 个方格中的红点数为 2 或
引理 3 对任意 n ≥ 1, 且可以取等号 . 证明 :由引理 1 , 有
k =1
∑A
k
1 ≤ δ( n + 1) + 1 an ,
x1 - 1 1 1 ≤ ・ 4 x2 + …+ x n + 2 ( x1 + …+ x n + 1) 2

滑铁卢数学竞赛高中试题

滑铁卢数学竞赛高中试题一、选择题1. 已知函数$ f(x) = ax^2 + bx + c $，其中$ a, b, c $为实数，且$ f(1) = 2 $，$ f(-1) = 0 $，$ f(2) = 6 $。

求$ a $的值。

2. 一个圆的半径为5，圆心位于原点，求圆上点$ P(3,4) $到圆心的距离。

3. 若$ \sin(\alpha + \beta) = \frac{1}{2} $，$ \cos(\alpha + \beta) = \frac{\sqrt{3}}{2} $，且$ \alpha $在第二象限，$ \beta $在第一象限，求$ \sin(\alpha) $的值。

二、填空题1. 计算$ \int_{0}^{1} x^2 dx $。

2. 若$ \log_{2}8 = n $，则$ n $的值为______。

3. 一个等差数列的前三项分别为2，5，8，求该数列的第10项。

三、解答题1. 证明：对于任意正整数$ n $，$ 1^3 + 2^3 + ... + n^3 =\frac{n^2(n+1)^2}{4} $。

2. 一个矩形的长是宽的两倍，若矩形的周长为24，求矩形的面积。

3. 已知一个等比数列的前三项分别为3，9，27，求该数列的第5项。

四、应用题1. 一个工厂每天生产相同数量的零件，如果每天生产100个零件，工厂可以在30天内完成订单。

如果每天生产150个零件，工厂可以在20天内完成订单。

求工厂每天实际生产的零件数量。

2. 一个圆环的外圆半径是内圆半径的两倍，且圆环的面积为π。

求外圆的半径。

五、证明题1. 证明：对于任意实数$ x $，$ \cos(x) + \cos(2x) + \cos(3x) $可以表示为一个单一的余弦函数。

六、开放性问题1. 考虑一个无限大的棋盘，每个格子可以放置一个硬币。

欧几里得滑铁卢数学竞赛_2001EuclidSolution

Solution
If f (k) = k , then k2 – 3k – 5 = k
k2 – 4k – 5 = 0
(k – 5)(k + 1) = 0
so
k = 5 or k = –1.
(c) Determine all (x, y) such that x2 + y2 = 25 and x – y = 1.
25
Therefore BC = 59 m to the nearest metre.
Solution 2
Since QR AC, ∠QRP = ∠ BAC (alternating angles).
B
This means ∆ ABC ~ ∆ RPQ (two equal angles).
By Pythagoras, PR2 = QP2 + QR2
2. (a) The vertex of the parabola y = (x – b)2 + b + h has coordinates (2, 5). What is the value of h?
Solution Since the x-coordinate of the vertex is 2, then b = 2. Since the y-coordinate of the vertex is 5, then b + h = 5. Since b = 2, then h = 3.
Solution
Let n be the smallest integer in one of these sequences.
So we want to solve the equation n2 + (n + 1)2 + (n + 2)2 = (n + 3)2 + (n + 4)2 (translating the

2002年第33届国际奥林匹克物理竞赛试题

2002年第33届国际奥林匹克物理竞赛试题题1、穿地雷达穿地雷达（GPR ）通过向地下发射电磁波并接受地下物体反射回来的电磁波来检测和定位近地表面处的物体。

天线和探测器直接放在地面上，并放在同一位置。

角频率为ω，沿Z 方向传播的线偏振平面电磁波的电场由下式表示：)cos(0z t e E E az βω-=- ①其中0E 为常数，α为衰减常数，β为波数，分别由下式表示 2121222112⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-⎪⎪⎭⎫ ⎝⎛+=ωεσμεωα ② 2121222112⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎪⎪⎭⎫ ⎝⎛+=ωεσμεωβ 其中μ、ε和σ分别为磁导率、介电常数和电导率。

当到达物体时的雷达信号振幅下降为初始值的%)37(1≈e时，将无法被探测到。

常用频率在（10MHz~1000MHz ）之间的电磁波进行探测，以便调节探测范围和分辨率。

GPR 的性能取决于它的分辨率。

分辨率由两个相邻的被测反射体的最小间距决定，最小间距对应于两个反射波在探测处的最小相位差为180°。

问题：（已知：m F m h /1085.8,/10412070--⨯=⨯=επμ）1．假定大地为非磁性物质)(0μμ=，并满足条件12≤⎪⎭⎫⎝⎛ωεσ，利用方程①和②导出传播速度v 的表达式（用μ和ε表示）。

（1.0分）2．确定地下被探测物体的最大深度，设大地的电导率为 1.0mSm ，介电常数为90ε，并满足条件12≤⎪⎭⎫ ⎝⎛ωεσ。

（1s=1,1-Ω0μμ=）（2.0分）3．考虑两根水平方向平行埋在地下的导电杆，两杆深4m ，已知大地的电导率为1.0mSm ，介电常数为90ε，假设GPR 近似就在其中一根导电杆的所在位置上方进行测量，并假设探测器为点状，试确定使横向分辨率达50㎝所需的最低频率。

（3.5分）4．为确定埋在与上问2中同样条件的地层中的导体杆的深度d ，考虑沿垂直于导体杆方向进行的测量。

Fryer滑铁卢数学竞赛(Grade 9)-数学Mathematics-2012-试题 exam

1.(a)In Carrotford,candidate A ran for mayor and received 1008votes out of a totalof 5600votes.What percentage of all votes did candidate A receive?(b)In Beetland,exactly three candidates,B,C and D,ran for mayor.Candidate Bwon the election by receiving 35of all votes,while candidates C and D tied withthe same number of votes.What percentage of all votes did candidate C receive?(c)In Cabbagetown,exactly two candidates,E and F,ran for mayor and 6000votes were cast.At 10:00p.m.,only 90%of these votes had been counted.Candidate E received 53%of those votes.How many more votes had been countedfor candidate E than for candidate F at 10:00p.m.?(d)In Peaville,exactly three candidates,G,H and J,ran for mayor.When all of thevotes were counted,G had received 2000votes,H had received 40%of the votes,and J had received 35%of the votes.How many votes did candidate H receive?2.The prime factorization of 144is 2×2×2×2×3×3or 24×32.Therefore,144is a perfect square because it can be written in the form (22×3)×(22×3).The prime factorization of 45is 32×5.Therefore,45is not a perfect square,but 45×5is a perfect square,because 45×5=32×52=(3×5)×(3×5).(a)Determine the prime factorization of 112.(b)The product 112×u is a perfect square.If u is a positive integer,what is thesmallest possible value of u ?(c)The product 5632×v is a perfect square.If v is a positive integer,what is thesmallest possible value of v ?(d)A perfect cube is an integer that can be written in the form n 3,where n is aninteger.For example,8is a perfect cube since 8=23.The product 112×w is aperfect cube.If w is a positive integer,what is the smallest possible value of w ?3.The positive integers are arranged in rows and columns,as shown,and described below.A B C D E F GRow1123456Row2121110987Row3131415161718Row4242322212019...The odd numbered rows list six positive integers in order from left to right beginning in column B.The even numbered rows list six positive integers in order from right toleft beginning in columnF.(a)Determine the largest integer in row30.(b)Determine the sum of the six integers in row2012.(c)Determine the row and column in which the integer5000appears.(d)For how many rows is the sum of the six integers in the row greater than10000and less than20000?4.The volume of a cylinder with radius r and height h equalsπr2h.The volume of a sphere with radius r equals43πr3.(a)The diagram shows a sphere thatﬁts exactlyinside a cylinder.That is,the top and bottomfaces of the cylinder touch the sphere,and thecylinder and the sphere have the same radius,r.State an equation relating the height of thecylinder,h,to the radius of the sphere,r.(b)Forthe cylinder and sphere given in part(a),determine the volume of the cylinder if the volume of the sphere is288π.(c)A solid cube with edges of length1km isﬁxed in outer space.Darla,the babyspace ant,travels on this cube and in the space around(but not inside)this cube.If Darla is allowed to travel no farther than1km from the nearest point on the cube,then determine the total volume of space that Darla can occupy.Fryer Contest(English) 2012。

2004滑铁卢竞赛试题答案

www.linstituteatics Competition
An activity of The Centre for Educati on in Ma the matics and Computing , University of W aterloo, Wa terloo, Ontario
[
]
square units.

Solution 2 Since ABCD is a square of side length 6 and each of AE : EB, BF : FC, CG : GD, and DH : HA is equal to 1 : 2, then AE = BF = CG = DH = 2 and EB = FC = GD = HA = 4 . Thus, each of the triangles HAE, EBF, FCG, and GDH is right-angled, with one leg of length 2 and the other of length 4. By the Pythagorean Theorem,
EF = FG = GH = HE = 2 2 + 4 2 = 20 . Since the two triangles HAE and EBF are congruent (we know the lengths of all three o sides of each), then ∠AHE = ∠BEF . But ∠AHE + ∠AEH = 90 , so o o ∠BEF + ∠AEH = 90 , so ∠HEF = 90 . In a similar way, we can show that each of the four angles of EFGH is a right-angle, and so EFGH is a square of side length 20 .