回归分析报告实验课实验8
《应用回归分析》自相关性的诊断及处理实验报告

《应用回归分析》自相关性的诊断及处理实验报告
二、实验步骤:(只需关键步骤)
1、分析→回归→线性→保存→残差
2、转换→计算变量;分析→回归→线性。
3、转换→计算变量;分析→回归→线性
三、实验结果分析:(提供关键结果截图和分析)
1.用普通最小二乘法建立y与x1和x2的回归方程,用残差图和DW检验诊断序列的自相关性;
由图可知y与x1和x2的回归方程为:
Y=574062+191.098x1+2.045x2
从输出结果中可以看到DW=0.283,查DW表,n=23,k=2,显著性水平由DW<1.26,也说明残差序列存在正的自相关。
自相关系数,也说明误差存在高度的自相关。
分析:从输出结果中可以看到DW=0.745,查DW表,n=52,k=3,显著性水平 =0.05,dL=1.47,dU=1.64.由DW<1.47,也说明残差序列存在正的自相关。
α
625.0745.02
1121-1ˆ=⨯-=≈DW ρ 也说明误差项存在较高度的自相关。
2.用迭代法处理序列相关,并建立回归方程;
回归方程为:y=-178.775+211.110x1+1.436x2
从结果中看到新回归残差的DW=1.716,
查DW 表,n=52,k=3,显著性水平0.5 由此可知DW 落入无自相关性区
域,说明残差序列无自相关
3.用一阶差分法处理序列相关,并建立回归方程;
从结果中看到回归残差的DW=2.042,根据P 104表4-4的DW 的取值范围来诊断 ,误差项。
统计学回归分析实训报告

一、实训背景随着社会的不断发展,统计学在各个领域都得到了广泛的应用。
回归分析作为一种重要的统计方法,广泛应用于预测、关联性分析、控制变量以及优化等多个领域。
为了提高学生对回归分析的实际应用能力,我们组织了本次统计学回归分析实训。
二、实训目的1. 使学生掌握回归分析的基本概念和原理;2. 培养学生运用回归分析方法解决实际问题的能力;3. 提高学生对统计学理论知识的实际应用水平。
三、实训内容1. 回归分析的基本概念和原理2. 线性回归分析3. 非线性回归分析4. 回归模型的诊断与检验5. 回归分析的实际应用四、实训过程1. 回归分析的基本概念和原理首先,我们向学生介绍了回归分析的基本概念和原理。
回归分析是一种研究变量之间关系的方法,通过建立回归模型来预测或解释因变量的变化。
回归模型包括线性回归模型和非线性回归模型。
线性回归模型假设因变量与自变量之间存在线性关系,而非线性回归模型则假设因变量与自变量之间存在非线性关系。
2. 线性回归分析接下来,我们讲解了线性回归分析的基本步骤。
首先,收集数据;其次,进行数据可视化,观察变量之间的关系;然后,建立线性回归模型,使用最小二乘法估计模型参数;最后,对模型进行诊断与检验,包括拟合优度检验、显著性检验等。
3. 非线性回归分析非线性回归分析是线性回归分析的扩展,可以处理变量之间存在非线性关系的情况。
我们介绍了常用的非线性回归模型,如指数回归、对数回归等,并讲解了如何进行非线性回归分析。
4. 回归模型的诊断与检验回归模型的诊断与检验是保证模型有效性的关键。
我们讲解了如何进行拟合优度检验、显著性检验、残差分析等,帮助学生掌握诊断与检验方法。
5. 回归分析的实际应用最后,我们通过实际案例展示了回归分析在各个领域的应用。
例如,在市场营销领域,可以运用回归分析预测销售量;在医学领域,可以运用回归分析研究疾病与风险因素之间的关系。
五、实训成果通过本次实训,学生们对回归分析的基本概念、原理和应用有了更深入的了解。
回归分析实验报告
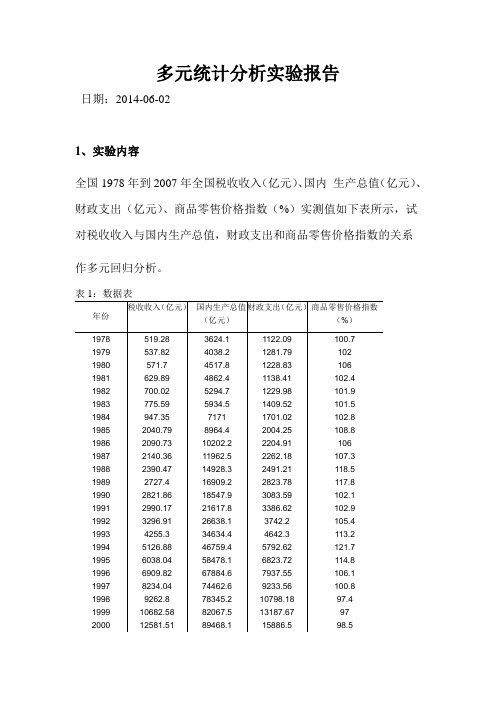
多元统计分析实验报告日期:2014-06-021、实验内容全国1978年到2007年全国税收收入(亿元)、国内生产总值(亿元)、财政支出(亿元)、商品零售价格指数(%)实测值如下表所示,试对税收收入与国内生产总值,财政支出和商品零售价格指数的关系作多元回归分析。
2、实验目的多元线性回归分析在SAS系统中也是用PROC REG过程进行分析的,只是在一元线性回归分析基础上多了一些选择项而已。
此时回归模型的选择具有很大的灵活性。
对于全部的自变量,可以将他们全部放在模型中,也可以只选择其中的一部分进行回归分析。
而选择变量的途径也有很多种,一般常用的有前进法、后退法以及逐步回归法。
因此,本实验运用SAS实现,为了了解和认识多元回归分和SAS的用法。
3、实验方案分析本实验是一个以全国1978年到2007年全国税收收入(亿元)、国内生产总值(亿元)、财政支出(亿元)、商品零售价格指数(%)实测值实,对税收收入与国内生产总值,财政支出和商品零售价格指数的关系,运用逐步回归法进行实验的。
4、操作过程SAS程序:data a;input y x1-x3 @@;cards;519.28 3624.1 1122.09 100.7537.82 4038.2 1281.79 102571.7 4517.8 1228.83 106629.89 4862.4 1138.41 102.4700.02 5294.7 1229.98 101.9775.59 5934.5 1409.52 101.5947.35 7171 1701.02 102.82040.79 8964.4 2004.25 108.8 2090.73 10202.2 2204.91 106 2140.36 11962.5 2262.18 107.3 2390.47 14928.3 2491.21 118.5 2727.4 16909.2 2823.78 117.8 2821.86 18547.9 3083.59 102.1 2990.17 21617.8 3386.62 102.9 3296.91 26638.1 3742.2 105.4 4255.3 34634.4 4642.3 113.25126.88 46759.4 5792.62 121.7 6038.04 58478.1 6823.72 114.8 6909.82 67884.6 7937.55 106.1 8234.04 74462.6 9233.56 100.8 9262.8 78345.2 10798.18 97.4 10682.58 82067.5 13187.67 97 12581.51 89468.1 15886.5 98.5 15301.38 97314.8 18902.58 99.2 17636.45 104790.6 22053.15 98.7 20017.31 135822.8 24649.95 99.9 24165.68 159878.3 28486.89 102.8 28778.54 183217.4 33930.28 100.8 34804.35 211923.5 40422.73 101 45621.97 249529.9 49781.35 103.8 ;proc reg;model y=x1 x2 x3;print cli;run;5、实验结果图1图2图1给出了由REG过程得到的方差分析与参数估计,方差分析给出了直线拟和这组数据的效果的信息。
SPSS回归分析实验报告

中国计量学院现代科技学院实验报告实验课程:应用统计学实验名称:回归分析班级:学号:姓名:实验日期: 2012.05.23 实验成绩:指导教师签名:一.实验目的一元线性回归简单地说是涉及一个自变量的回归分析,主要功能是处理两个变量之间的线性关系,建立线性数学模型并进行评价预测。
本实验要求掌握一元线性回归的求解和多元线性回归理论与方法。
二.实验环境中国计量学院现代科技学院机房310三.实验步骤与内容1打开应用统计学实验指导书,新建excel表地区供水管道长度(公里)全年供水总量(万平方米)北京15896 128823 天津6822 64537 河北10771.2 160132 山西5669.3 77525 内蒙古5635.5 59276 辽宁21999 280510 吉林6384.9 159570 黑龙江9065.9 153387 上海22098.8 308309 江苏36632.4 380395 浙江24126.9 235535 安徽7389.4 204128 福建6270.4 118512 江西5094.7 143240 山东26073.9 259782 河南11405.6 185092 湖北15668.6 257787 湖南9341.8 262691 广东35728.8 568949 广西6923.1 134412 海南1726.7 20241 重庆6082.7 71077 四川12251.3 165632 贵州3275.3 45198 云南5208.5 52742 西藏364.9 5363陕西4270 73580甘肃5010 62127青海893 14390宁夏1538.2 22921新疆3670.2 766852.打开SPSS,将数据导入3.打开分析,选择回归分析再选择线性因变量选全年供水总量,自变量选供水管道长度统计里回归系数选估计,再选择模型拟合按继续再按确定会出来分析的结果对以上结果进行分析:(1)回归方程为:y=28484.712+11.610X(X是自变量供水管道长度,Y是因变量全年供水总量)(2)检验1)拟合效果检验根据表2可知,R2=0.819,即拟合效果好,线性成立。
回归分析实验报告

师范学院
实验报告
课程名称:应用回归分析
班级:
学号:
姓名:
指导教师:
实验时间:2019年00月00日
一、实验题目:线性回归模型
二、实验目的及要求
在熟悉SPSS的操作基础上,实现数据创建、数据录入、数据读取与保存、数据使用与编辑、数据的类型与编辑、绘制散点图残差图等拟合回归方程,对回归系数做区间估计,对回归方程进行方差分析,显著性检验等内容。
利用模型做相应的经济分析与预测并给出相应置信度的置信区间。
三、实验环境
二教五楼网络实验室
四、实验内容与实验过程
五、实验分析及总结
提升了SPSS软件的实践能力,更好的实现课本与实际操作的结合,让我更好的学习并理解了应用回归分析这门课。
六、附加内容
(本次实验的建议以及注意事项等)。
多元线性回归模型实验报告

多元线性回归模型实验报告实验报告:多元线性回归模型1.实验目的多元线性回归模型是统计学中一种常用的分析方法,通过建立多个自变量和一个因变量之间的模型,来预测和解释因变量的变化。
本实验的目的是利用多元线性回归模型,分析多个自变量对于因变量的影响,并评估模型的准确性和可靠性。
2.实验原理多元线性回归模型的基本假设是自变量与因变量之间存在线性关系,误差项为服从正态分布的随机变量。
多元线性回归模型的表达形式为:Y=b0+b1X1+b2X2+...+bnXn+ε,其中Y表示因变量,X1、X2、..、Xn表示自变量,b0、b1、b2、..、bn表示回归系数,ε表示误差项。
3.实验步骤(1)数据收集:选择一组与研究对象相关的自变量和一个因变量,并收集相应的数据。
(2)数据预处理:对数据进行清洗和转换,排除异常值、缺失值和重复值等。
(3)模型建立:根据收集到的数据,建立多元线性回归模型,选择适当的自变量和回归系数。
(4)模型评估:通过计算回归方程的拟合优度、残差分析和回归系数的显著性等指标,评估模型的准确性和可靠性。
4.实验结果通过实验,我们建立了一个包含多个自变量的多元线性回归模型,并对该模型进行了评估。
通过计算回归方程的拟合优度,我们得到了一个较高的R方值,说明模型能够很好地拟合观测数据。
同时,通过残差分析,我们检查了模型的合理性,验证了模型中误差项的正态分布假设。
此外,我们还对回归系数进行了显著性检验,确保它们是对因变量有显著影响的。
5.实验结论多元线性回归模型可以通过引入多个自变量,来更全面地解释因变量的变化。
在实验中,我们建立了一个多元线性回归模型,并评估了模型的准确性和可靠性。
通过实验结果,我们得出结论:多元线性回归模型能够很好地解释因变量的变化,并且模型的拟合优度较高,可以用于预测和解释因变量的变异情况。
同时,我们还需注意到,多元线性回归模型的准确性和可靠性受到多个因素的影响,如样本大小、自变量的选择等,需要在实际应用中进行进一步的验证和调整。
应用回归分析实验报告

重庆交通大学学生实验报告实验课程名称应用回归分析开课实验室数学实验室学院理学院年级专业班学生姓名学号开课时间2013 至2014 学年第2 学期评分细则评分报告表述的清晰程度和完整性(20分)程序设计的正确性(40分)实验结果的分析(30分)实验方法的创新性(10分)总成绩教师签名邹昌文2.15 一家保险公司十分关心其总公司营业部加班的程度,决定认真调查一下现状。
经过10周时间,收集了每周加班工作时间的数据和签发新保单数目,x 为每周签发的新保单数目,y 为每周加班工作时间(小时)。
表2.7 y 3.5 1 4 2 1 3 4.5 1.5 3 5 x825215107055048092013503256701215(1)画散点图;(2)x 与y 之间是否大致呈线性关系? (3)用最小二乘估计求出回归方程;(4)求回归标准误差ˆσ; (5)给出0ˆβ、1ˆβ的置信度为95%的区间估计; (6)计算x 与y 的决定系数;(7)对回归方程做方差分析;(8)做回归系数1ˆβ显著性检验; (9)做相关系数的显著性检验;(10)对回归方程做残差图并作相应的分析;(11)该公司预计下一周签发新保单01000x =张,需要的加班时间是多少? (12)给出0y 的置信水平为95%的精确预测区间和近视预测区间。
(13)给出0()E y 置信水平为95%的区间估计。
(1)将数据输入到SPSS 中,画出散点图如下:(2)由下表可知x与y的相关系数高达0.949,大于0.8,所以x与y之间线性相关性显著。
相关性y xPearson 相关性y 1.000 .949x .949 1.000Sig. (单侧)y . .000x .000 .N y 10 10x 10 10(3)用SPSS 进行最小二乘估计得到了如下系数表:系数a模型非标准化系数 标准系数tSig. B 的 95.0% 置信区间相关性共线性统计量B标准 误差 试用版下限 上限 零阶偏部分 容差VIF1(常量) .118.355.333 .748 -.701 .937x.004 .000 .949 8.509 .000 .003 .005 .949 .949 .949 1.000 1.000a. 因变量: y由上表可知0β、1β的参数估计值0ˆβ、1ˆβ分别为0.118和0.004,所以y 对x 的线性回归方程为0.1180.004x y ∧=+(4)由SPSS 得到如下模型汇总表:模型汇总模型RR 方调整 R 方标准 估计的误差1.949a.900.888.4800a. 预测变量: (常量), x 。
回归分析实验报告

实验报告实验名称:数据整理与分析相关分析实验报告实验课程:统计学数据的整理与分析一、实验目的:学会运用 Excel 中次数分布表、透视表、统计图以及描述性统计功能来分析一组有调查意义的数据;从而通过分析得出有意义的结论以及推测预计。
二、实验原理:次数分布表的制作过程,第一步找出最大、最小值,确定全距R;第二步利用斯透奇斯规则确定组数m,再根据组数与组距的关系确定组距;第三步分组,根据分组标志和分组上限确定在组内数据的频数以及频率。
数据透视表,选中当前数据库表中人一个单元格,单击菜单中的“数据”—“数据透视表与数据透视图”。
直方图是在平面坐标上一横轴根据各组组距的宽度标明各组组距,一纵轴根据次数的高度表示各组次数绘制成的统计图。
折线图是在直方图的基础上,用折线连接各个直方形顶边中点并在直方图形两侧各延伸一组,使者限于横线相连。
三、实验环境:实验地点:实训楼计算机实验中心五楼实验室 3试验时间:第五周周二实验软件: Microsoft Excel 2003四、实验内容1、(1)在数据源中选取所需数据,对数据进行分析。
利用Excel 对数据进行描述性统计分析。
实验内容包括:数据分组、直方图、描述性分析、透视表、实验结果分析。
(2)数据资料:数据来源“9-33各地区农村居民家庭平均每人主要食品消费量(2008 年 )”如下图所示。
2、实验步骤第一步:在数据库中把所要研究的数据对象复制黏贴到新建的Excel 工作表sheet1 中。
我要研究的是“各地区农村居民家庭平均每人主要食品消费量 (2008 年 ) ”挑选了其中的蔬菜。
第二步:对 sheet2 中的数据进行分组。
(1)找出这31个数据中的最大、最小值,得到全距R(2)其次利用斯透奇斯规则确定组数m,再根据组数与组距的关系确定组距 i ;(3)然后分组,根据分组标志和分组上限确定在组内数据的频数以及频率(4)最后得到全国各地区蔬菜消费量的次数分布表。
SPSS回归分析实验报告

中国计量学院现代科技学院实验报告实验课程:应用统计学实验名称: 回归分析_____________ 班级:___________________________ 学号:______________________________ 姓名:__________________________ 实验日期:2012.05.23 ____________实验成绩:________________ 指导教师签名: __________________实验目的一元线性回归简单地说是涉及一个自变量的回归分析个变量之间的线性关系,建立线性数学模型并进行评价预测一元线性回归的求解和多元线性回归理论与方法。
二. 实验环境中国计量学院现代科技学院机房310三. 实验步骤与内容1打开应用统计学实验指导书,新建excel表,主要功能是处理两本实验要求掌握新疆 3670.2 766852 •打开SPSS,将数据导入3 •打开分析,选择回归分析再选择线性因变量选全年供水总量,自变量选供水管道长度 统计里回归系数选估计,再选择模型拟合空旧I 圖囤 丨_ |韵虫| 叮鬥 口圭|冃 钥10 11 12 13 14 15W 17 1R19 2021232425 26 272831地区|供水管道|全年供水 天肄 1J 西对蒙古黒龙江:工芯 晰江 安徵 江西闕北云甫宁裏var var var var var var1ESS E6S22 W771 5669 5&36 21999 E385906G' 22099j 3663'f 24127627011406 15669 3572969231727 6063 12251 3275 5209 365 42705010393 T&39 367C120323165632 45198527425363 735S06212714390^921 76685-SP5S Data Editor訳肋(囲恚 E ■ T -S i.U64537 160132 110512 143240568949 134412 202417107777525 5^276 2田7氐185C92257787彳胎狞■!235535 20412B 230610 159570 153367 308309^ 360395"按继续再按确定会出来分析的结果7EB■* b |\M> Ww & Vslife Vtowfi2iZ736^91却朋134412 2W*i 71(177FE£EZ2第I*口川 鼻州出常-* MKlt "Ell“ f j. |4iJI+ Regressionbth De pe n den tVa rt attie'(万平方米)a. Predictors: (ConstamtJ.ft^Xa. Predittnrs: (Ccnstant ),ftzKr®Iff Io. Dcpen dent Vari at>le :(万平右米)3DependentVariabie'对以上结果进行分析:(1)回归方程为:y=28484.712+11.610X (X 是自变量供水管道长度,丫是因 变量全年供水总量)(2)检验1) 拟合效果检验根据表2可知,R2=0.819 ,即拟合效果好,线性成立。
回归分析 实验报告

回归分析实验报告回归分析实验报告引言:回归分析是一种常用的统计方法,用于探究变量之间的关系。
本实验旨在通过回归分析来研究某一自变量对因变量的影响,并进一步预测未来的趋势。
通过实验数据的收集和分析,我们可以得出一些有关变量之间关系的结论,并为决策提供依据。
数据收集:在本次实验中,我们收集了一组数据,包括自变量X和因变量Y的取值。
为了保证数据的可靠性和准确性,我们采用了随机抽样的方法,并对数据进行了严格的统计处理。
数据分析:首先,我们进行了数据的可视化分析,绘制了散点图以观察变量之间的分布情况。
通过观察散点图,我们可以初步判断变量之间是否存在线性关系。
接下来,我们使用回归分析方法对数据进行了拟合,并得到了回归方程。
回归方程:通过回归分析,我们得到了如下的回归方程:Y = a + bX其中,a表示截距,b表示斜率。
回归方程可以用来预测因变量Y在给定自变量X的取值时的期望值。
回归系数的解释:在回归方程中,截距a表示当自变量X为0时,因变量Y的取值。
斜率b表示自变量X每变动一个单位时,因变量Y的平均变动量。
通过对回归系数的解释,我们可以更好地理解变量之间的关系。
回归方程的显著性检验:为了验证回归方程的有效性,我们进行了显著性检验。
通过计算回归方程的F值和P值,我们可以判断回归方程是否具有统计学意义。
如果P值小于显著性水平(通常为0.05),则我们可以拒绝零假设,即回归方程是显著的。
回归方程的拟合优度:为了评估回归方程的拟合程度,我们计算了拟合优度(R²)。
拟合优度表示因变量的变异程度可以被自变量解释的比例。
拟合优度的取值范围为0~1,值越接近1表示回归方程对数据的拟合程度越好。
回归方程的预测:通过回归方程,我们可以进行因变量Y的预测。
当给定自变量X的取值时,我们可以利用回归方程计算出因变量Y的期望值。
预测结果可以为决策提供参考,并帮助我们了解自变量对因变量的影响程度。
结论:通过本次实验,我们成功地应用了回归分析方法,研究了自变量X对因变量Y的影响,并得到了回归方程。
统计学实训回归分析报告

一、引言回归分析是统计学中一种重要的分析方法,主要用于研究变量之间的线性关系。
本次实训报告将结合实际数据,运用回归分析方法,探讨变量之间的关系,并分析影响因变量的关键因素。
二、实训目的1. 理解回归分析的基本原理和方法。
2. 掌握使用统计软件进行回归分析的操作步骤。
3. 分析变量之间的关系,并找出影响因变量的关键因素。
三、实训数据本次实训数据来源于某地区2019年居民消费情况调查,包含以下变量:1. 家庭月收入(万元)作为因变量。
2. 家庭人口数、教育程度、住房面积、汽车拥有量、子女数量作为自变量。
四、实训步骤1. 数据整理:将数据录入统计软件,进行数据清洗和整理。
2. 描述性统计:计算各变量的均值、标准差、最大值、最小值等指标。
3. 相关性分析:计算各变量之间的相关系数,分析变量之间的线性关系。
4. 回归分析:建立多元线性回归模型,分析各自变量对因变量的影响程度。
5. 模型检验:进行残差分析、方差分析等,检验模型的可靠性。
五、实训结果与分析1. 描述性统计结果家庭月收入均值为8.5万元,标准差为2.1万元;家庭人口数均值为3.2人,标准差为1.5人;教育程度均值为2.5年,标准差为0.6年;住房面积均值为100平方米,标准差为20平方米;汽车拥有量均值为1.2辆,标准差为0.7辆;子女数量均值为1.5个,标准差为0.8个。
2. 相关性分析结果家庭月收入与家庭人口数、教育程度、住房面积、汽车拥有量、子女数量之间存在显著正相关关系。
3. 回归分析结果建立多元线性回归模型如下:家庭月收入 = 5.6 + 0.3 家庭人口数 + 0.2 教育程度 + 0.1 住房面积 + 0.05 汽车拥有量 + 0.02 子女数量模型检验结果如下:- F统计量:76.23- P值:0.000- R方:0.642模型检验结果表明,该模型具有较好的拟合效果,可以用于分析家庭月收入与其他变量之间的关系。
4. 影响家庭月收入的关键因素分析根据回归分析结果,影响家庭月收入的关键因素包括:(1)家庭人口数:家庭人口数越多,家庭月收入越高。
回归分析实验报告模板及范例

填写说明1、填写实验报告须字迹工整,使用黑色钢笔或签字笔填写。
2、课程编号和课程名称必须和教务系统中保持一致,实验项目名称填写须完整规范,不能省略或使用简称。
3、每个实验项目应填写一份实验报告。
如同一个实验项目分多次进行,可在实验报告中写明。
实验目录及成绩登记说明:实验项目顺序和名称由学生填写,必须前后保持一致;实验成绩以百分制计,由实验指导教师填写并签名;实验报告部分最终成绩为所有实验项目成绩的平均值。
实验报告实验日期: 2020 年 4 月 15日星期三4.点击“分析”——“相关”——“双变量”,弹出双变量相关性对话框,如下图2所示,选中IQ、语文成绩和数学成绩作为我们研究的变量;因为变量都是等距变量,选中系统默认的”皮尔逊(N)”这一相关系数,选中系统默认的“双侧检验(T)”;勾选”标记显著性相关(F)”以便于在导出的结果中将具有统计学意义的数据标记出来。
表25.在双变量相关性对话框中,点击“选项”,弹出对话框,如下图3所示,选中“平均值和标准差(M)、叉积偏差和协方差(C)”就可以在输出的数据中,显示上述三个变量的这两种的统计情况;在缺失值中,勾选系统默认的“成对排除个案(P)”,这样在我们分析过程中,遇到缺失值,就会成对排除在数据之外。
表36.点击“确定”,自动导出数据CORRELATIONS/VARIABLES=IQ 语文成绩数学成绩/PRINT=TWOTAIL NOSIG/STATISTICS DESCRIPTIVES XPROD/MISSING=PAIRWISE.相关性(1)描述性统计量表,如下表a;(2)相关性表,如下表b。
(二)第六章第四题——简单线性回归分析1、课程了解学习回归分析则是研究分析某一变量受别的变量影响的分析方法,它以被影响变量为因变量,以影响变量为自变量,研究因变量与自变量之间的因果关系,SPSS的简单线性回归分析也称一元线性回归分析,是最简单也是最基本。
简单线性回归分析的特色是只涉及一个自变量,它主要用来处理一个因变量与一个自变量之间的线性关系,建立变量之间的线性模型并根据模型做评价和预测。
统计回归模型实验报告(3篇)

第1篇一、实验背景与目的随着社会科学和自然科学研究的深入,统计分析方法在各个领域得到了广泛应用。
回归分析作为统计学中一种重要的预测和描述方法,在经济学、医学、心理学等领域发挥着重要作用。
本次实验旨在通过EViews软件,对统计回归模型进行实践操作,掌握回归分析的原理和方法,并验证模型在实际问题中的应用效果。
二、实验内容与步骤1. 数据准备(1)收集实验所需数据:选取某地区近五年居民消费支出与居民收入作为实验数据。
(2)数据整理:将数据录入EViews软件,并进行必要的预处理,如剔除异常值、缺失值等。
2. 模型设定(1)根据实验目的,设定回归模型为:消费支出= β0 + β1 居民收入+ ε,其中β0为截距项,β1为居民收入对消费支出的影响系数,ε为误差项。
(2)选择合适的回归模型:根据实验数据特点,选择线性回归模型进行建模。
3. 模型估计(1)在EViews软件中,输入数据并选择线性回归模型。
(2)进行参数估计:利用最小二乘法(OLS)估计模型参数,得到β0和β1的估计值。
4. 模型检验(1)检验模型的整体拟合优度:计算R²、F统计量等指标,判断模型是否显著。
(2)检验参数估计的显著性:进行t检验,判断β0和β1是否显著异于零。
(3)检验误差项的正态性:进行正态性检验,判断误差项是否符合正态分布。
5. 模型应用(1)预测居民消费支出:利用估计出的模型,预测居民收入在一定范围内的消费支出。
(2)分析居民收入对消费支出的影响:根据β1的估计值,分析居民收入对消费支出的影响程度。
三、实验结果与分析1. 模型整体拟合优度根据实验数据,计算R²为0.9,F统计量为35.12,表明模型整体拟合优度较好,可以用于预测和描述居民消费支出与居民收入之间的关系。
2. 参数估计的显著性t检验结果显示,β0和β1的t值分别为2.12和3.45,均大于临界值,表明β0和β1在统计上显著异于零,居民收入对消费支出有显著影响。
线性回归分析实验报告

实验一:线性回归分析实验目的:通过本次试验掌握回归分析的基本思想和基本方法,理解最小二乘法的计算步骤,理解模型的设定T检验,并能够根据检验结果对模型的合理性进行判断,进而改进模型。
理解残差分析的意义和重要性,会对模型的回归残差进行正态型和独立性检验,从而能够判断模型是否符合回归分析的基本假设。
实验内容:用线性回归分析建立以高血压作为被解释变量,其他变量作为解释变量的线性回归模型。
分析高血压与其他变量之间的关系。
实验步骤:1、选择File | Open | Data 命令,打开gaoxueya.sav图1-1 数据集gaoxueya 的部分数据2、选择Analyze | Regression | Linear…命令,弹出Linear Regression (线性回归) 对话框,如图1-2所示。
将左侧的血压(y)选入右侧上方的Dependent(因变量) 框中,作为被解释变量。
再分别把年龄(x1)、体重(x2)、吸烟指数(x3)选入Independent (自变量)框中,作为解释变量。
在Method(方法)下拉菜单中,指定自变量进入分析的方法。
图1-2 线性回归分析对话框3、单击Statistics按钮,弹出Linear Regression : Statistics(线性回归分析:统计量)对话框,如图1-3所示。
1-3线性回归分析统计量对话框4、单击 Continue 回到线性回归分析对话框。
单击Plots ,打开Linear Regression:Plots (线性回归分析:图形)对话框,如图1-4所示。
完成如下操作。
图1-4 线性回归分析:图形对话框5、单击Continue ,回到线性回归分析对话框,单击Save按钮,打开Linear Regression;Save 对话框,如图1-5所示。
完成如图操作。
图1-5 线性回归分析:保存对话框6、单击Continue ,回到线性回归分析对话框,单击Options 按钮,打开Linear Regression ;Options 对话框,如图1-6所示。
《应用回归分析 》---多元线性回归分析实验报告

《应用回归分析》---多元线性回归分析实验报告
二、实验步骤:
1、计算出增广的样本相关矩阵
2、给出回归方程
Y=-65.074+2.689*腰围+(-0.078*体重)3、对所得回归方程做拟合优度检验
4、对回归方程做显著性检验
5、对回归系数做显著性检验
三、实验结果分析:
1、计算出增广的样本相关矩阵相关矩阵
2、给出回归方程
回归方程:Y=-65.074+2.689*腰围+(-0.078*体重)
3、对所得回归方程做拟合优度检验
由表可知x与y的决定性系数为r2=0.800,说明模型的你和效果一般,x与y 线性相关系数为R=0.894,说明x与y有较显著的线性关系,当F=33.931,显著性Sig.p=0.000,说明回归方程显著
4、对回归方程做显著性检验
5、对回归系数做显著性检验
Beta的t检验统计量t=-6.254,对应p的值接近0,说明体重和体内脂肪比重对腰围数据有显著影响
6、结合回归方程对该问题做一些基本分析
从上面的分析过程中可以看出腰围和脂肪比重以及腰围和体重的相关性都是很大的,通过检验可以看出回归方程、回归系数也很显著。
其次可以观察到腰围、脂肪比重、体重的数据都是服从正态分布的。
《统计学》实验报告(一元线性回归分析)
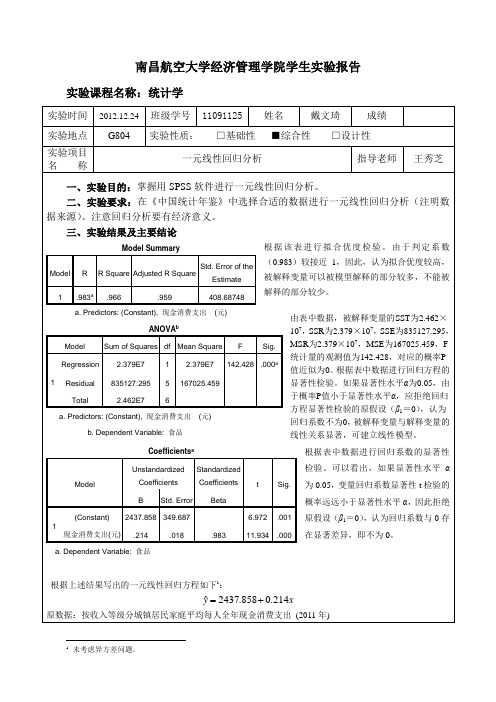
南昌航空大学经济管理学院学生实验报告实验课程名称:统计学实验时间 2012.12.24 班级学号 11091125 姓名戴文琦成绩实验地点 G804实验性质: □基础性 ■综合性 □设计性实验项目名 称一元线性回归分析指导老师王秀芝一、实验目的:掌握用SPSS 软件进行一元线性回归分析。
二、实验要求:在《中国统计年鉴》中选择合适的数据进行一元线性回归分析(注明数据来源)。
注意回归分析要有经济意义。
三、实验结果及主要结论根据该表进行拟合优度检验。
由于判定系数(0.983)较接近1,因此,认为拟合优度较高,被解释变量可以被模型解释的部分较多,不能被解释的部分较少。
由表中数据,被解释变量的SST 为2.462×107,SSR 为2.379×107,SSE 为835127.295,MSR 为2.379×107,MSE 为167025.459,F 统计量的观测值为142.428,对应的概率P 值近似为0。
根据表中数据进行回归方程的显著性检验。
如果显著性水平α为0.05,由于概率P 值小于显著性水平α,应拒绝回归方程显著性检验的原假设(β1=0),认为回归系数不为0,被解释变量与解释变量的线性关系显著,可建立线性模型。
根据表中数据进行回归系数的显著性检验。
可以看出,如果显著性水平α为0.05,变量回归系数显著性t 检验的概率远远小于显著性水平α,因此拒绝原假设(β1=0),认为回归系数与0存在显著差异,即不为0。
根据上述结果写出的一元线性回归方程如下1:x y214.0858.2437ˆ+= 原数据:按收入等级分城镇居民家庭平均每人全年现金消费支出 (2011年)Model SummaryModel R R Square Adjusted R Square Std. Error of theEstimate 1.983a.966.959408.68748a. Predictors: (Constant), 现金消费支出 (元)ANOVA bModel Sum of Squares df Mean Square F Sig.1 Regression 2.379E7 1 2.379E7 142.428 .000aResidual 835127.295 5 167025.459 Total 2.462E7 6a. Predictors: (Constant), 现金消费支出 (元)b. Dependent Variable: 食品 Coefficients aModelUnstandardizedCoefficients Standardized CoefficientstSig.BStd. ErrorBeta1(Constant) 2437.858 349.6876.972.001现金消费支出(元).214.018.98311.934 .000a. Dependent Variable: 食品1未考虑异方差问题。
回归分析实验课 实验8

实验报告八实验课程:回归分析实验课专业:统计学年级:姓名:学号:指导教师:完成时间:得分:教师评语:学生收获与思考:实验八含定性变量的回归模型(4学时)一、实验目的1.掌握含定性变量的回归模型的建模步骤3.运用SAS计算含定性变量的各种回归模型的各参数估计及相关检验统计量二、实验理论与方法在实际问题的研究中,经常会遇到一些非数量型的变量。
如品质变量;性别;战争与和平。
我们把这些品质变量也称为定性变量,在建立回归模型的时候我们需要考虑到这些定性变量。
定性变量的回归模型分为自变量含定性变量的回归模型和因变量是定性变量的回归模型。
自变量含有定性变量的时候,我们一般引进虚拟变量,将这些定性变量数量化。
例如研究粮食产量问题,y为粮食产量,x为施肥量,另外考虑气候问题,分为正常年份和干旱年份两种情况,这个问题数量化方法就是引入一个0-1型变量D,令D i=1 表示正常年份,D i=0表示干旱年份,粮食产量的回归模型为:yi =β+β1xi+β2Di+εi。
因变量是定性变量时,一般用logistic回归模型(分组数据的logistic回归模型,未分组数据的logistic回归模型,多类别的logistic回归模型),probit回归模型等。
三. 实验内容1.用DATA步建立一个永久SAS数据集,数据集名为xt103,数据见表21;对数据集xt103,建立y对公司规模和公司类型的回归,并对所得到的模型进行解释。
2.研制一种新型玻璃,对其做耐冲实验。
用一个小球从不同的高度h对玻璃做自由落体撞击,玻璃破碎记为y=1,玻璃未破碎记y=0.数据见表22.是对表中数据建立玻璃耐冲性对高度h的logistic回归,并解释回归方程的含义。
3.某学校对本科毕业生的去向做了一个调查,分析影响毕业去向的相关因素,结果见表23.其中毕业去向“1”=工作,“2”=读研,“3”=出国留学。
性别“1”=男生,“0”=女生。
用多类别的Logisitic回归分析影响毕业去向的因素。
回归分析实验报告
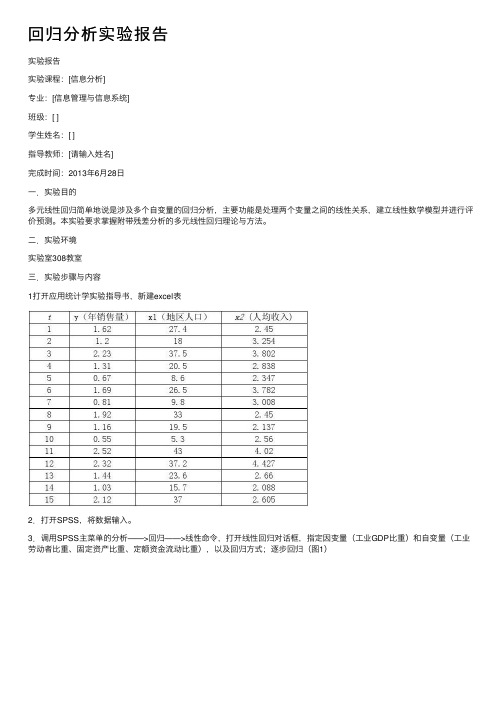
回归分析实验报告实验报告实验课程:[信息分析]专业:[信息管理与信息系统]班级:[ ]学⽣姓名:[ ]指导教师:[请输⼊姓名]完成时间:2013年6⽉28⽇⼀.实验⽬的多元线性回归简单地说是涉及多个⾃变量的回归分析,主要功能是处理两个变量之间的线性关系,建⽴线性数学模型并进⾏评价预测。
本实验要求掌握附带残差分析的多元线性回归理论与⽅法。
⼆.实验环境实验室308教室三.实验步骤与内容1打开应⽤统计学实验指导书,新建excel表2.打开SPSS,将数据输⼊。
3.调⽤SPSS主菜单的分析——>回归——>线性命令,打开线性回归对话框,指定因变量(⼯业GDP⽐重)和⾃变量(⼯业劳动者⽐重、固定资产⽐重、定额资⾦流动⽐重),以及回归⽅式;逐步回归(图1)图1 线性对话框4.在统计栏中,选择估计以输出回归系数B的估计值、t统计量等,选择Duribin-watson以进⾏DW检验;选择模型拟合度输出拟合优度统计量值,如R^2、F统计量值等(图2)。
图2 统计量栏5.在线性回归栏中选择直⽅图和正态概率图以绘制标准化残差的直⽅图和残差分析与正态概率⽐较图,以标准化预测值为纵坐标,标准化残差值为横坐标,绘制残差与Y的预测值的散点图,检验误差变量的⽅差是否为常数(图3)。
图3 绘制栏6.提交分析,并在输出窗⼝中查看结果,以及对结果进⾏分析。
系统在进⾏逐步分析的过程中产⽣了两个回归模型,模型1先将与因变量(销售收⼊)线性关系的⾃变量地区⼈⼝引⼊模型,建⽴他们之间的⼀元线性关系。
⽽后逐步引⼊其他变量,表1中模型2表明将⾃变量⼈均收⼊引⼊,建⽴⼆元线性回归模型,可见地区⼈⼝和⼈均收⼊对销售收⼊的影响同等重要。
从表2中给出了两个模型各⾃的R^2和调整后的R^2,第⼀个模型中的销售收⼊中有99%的变动可以⽤地区⼈⼝的变动解释,第⼆个模型中地区⼈⼝和⼈均收⼊的变动可以解释销售收⼊中99.9%的变动,显然第⼆个模型的拟合数据效果⽐较好⼀点。
回归分析实验报告

回归分析实验报告财政收入研究摘要本文是对财政收入与农业增加值、工业增加值、建筑业增加值、人口数、社会消费总额、受灾面积进行多元线性回归。
首先,根据所给数据,对数据进行标准化,然后进行相关性分析,初步确定各因素与财政收入的相关程度。
再运用逐步回归分析,确定了变量子集为工业增加值、人口数和社会消费总额。
之后,为了消除复共线性,用主成分估计对回归系数进行有偏估计,获得了模型的回归系数估计值。
最后,对所得结果作了分析,并给出了适当建议。
一、数据处理为了消除变量间的量纲关系,从而使数据具有可比性,运用spss对所给数据进行标准化。
二、相关性分析要对某地财政收入影响因素进行多元回归分析,首先要分析财政收入与各自变量的相关性,只有与财政收入有一定相关性的自变量才能对财政收入变动进行解释。
运用spss得到变量间的相关系数表如下:表一:由上表可知,财政收入与农业增加值、工业增加值、建筑业增加值、人口数、社会消费总额呈高度正相关,但与受灾面积相关程度不高。
由此表明所选取的大部分变量是可以用来解释财政收入变动的。
为进一步确定最优子集,下面用逐步回归法。
三、回归分析回归分析就是对具有相关关系的变量之间数量变化的一般关系进行测定,确定一个相关的数学表达式,以便于进行估计或预测的统计方法。
在此利用逐步回归法选定回归方程。
逐步回归思想:综合运用前进法和后退法,将变量一个一个引入,引入变量的条件是其偏回归平方和经检验是显著的。
同时,每引入一个新变量,对已入选方程的老变量逐个进行检验,将经检验认为不显著的变量剔除,以保证所得自变量子集中的每个变量都是显著的。
此过程经若干步直到不能再引入新变量为止。
运用spss得到逐步回归的输出结果:表二:回归系数表模型 非标准化系数标准化系数 t Sig. CollinearityStatistics B 标准误差BetaToleranceVIF1(Constant) -1.292E-16.029 .0001.000x5:社会消费总额.991 .029 .991 33.990.000 1.000 1.0002(Constant) -1.210E-16.024 .000 1.000x5:社会消费总额 2.649 .555 2.6494.776.000 .002 499.022 x2: 工业增加值-1.660 .555 -1.660 -2.992.007 .002 499.0223(Constant) -2.451E-17.017 .000 1.000x5:社会消费总额 4.021 .485 4.021 8.292.000 .001 783.048 x2: 工业增加值 -2.829 .460 -2.829 -6.147 .000 .001 705.453 x4: 人口数-.225.048-.225 -4.697.000.1317.663a. Dependent Variable: y: 财政收入由表二可知,模型三是最终模型,最终选入方程的自变量为:x2:工业增加值;x4:人口数;x5:社会消费总额。
回归分析实验

第 1 章回归分析实验目次1.1线性回归模型1.2非线性回归模型1.3线性回归分析实验示范1.3.1背景资料1.3.2实验步骤分解1.4非线性回归分析实验示范1.4.1背景资料1.4.2回归报告1.4.3结果解释1.5回归分析实验练习注记 1参考文献附表 11.1线性回归模型考虑线性计量经济模型Y i=a0+b1X1i+ +b m X mi+u i( 1-1)其中: a0为截距, b1, , b m为回归系数, X 1i ,, X mi为解释变量,它们是非随机变量, u i为随机扰动项。
当m1时,模型1-1 称为一元线性回归模型或单变量线性模型;当时,模型 1-1称为多元线性回归模型。
m 1模型 1-1 的应用效果取决于模型的系数是否被有效确定,即与其估计系数的 t 检验和模型的F检验是否显著有关,而这些检验则必须满足一定的前提条件才行。
在应用普通最小二乘法(OLS )做回归分析时,如果模型1-1 满足以下假设:假设 1-1解释变量和随机扰动项线性无关:cov( u i, X ji )0, j1,2, , m 假设 1-2随机扰动项的期望为0: E (u i )0假设 1-3随机扰动项服从同方差分布:var( u i )21,2, , i假设 1-4随机扰动项没有自相关关系:cov( u i , u j )0, i j假设 1-5随机扰动项服从正态分布:u i2 ~ N(0, )假设 1-6解释变量之间没有共线性关系,即任一个解释变量均不能被其余解释变量线性表示得到。
那么,模型 1-1 的 OLS 估计量就是最优线性无偏估计量,估计系数的t 检验和模型的 F 检验就是有效的。
只要其中的任意一个假设没有得到满足,模型系数的 OLS 估计量就变成无效或不是最优线性无偏估计的了。
OLS 是线性回归模型系数估计的常用方法之一,其实,最大似然估计法(ML )也是常用方法之一。
在满足六个假设前提下,除了ML 方法估计残差项可能会导致渐进有偏估计以及低估值外,OLS 和 ML 在系数的估计上是一致的,即均是无偏估计。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验报告八实验课程:回归分析实验课专业:统计学年级::学号:指导教师:完成时间:得分:教师评语:学生收获与思考:实验八含定性变量的回归模型(4学时)一、实验目的1.掌握含定性变量的回归模型的建模步骤3.运用SAS计算含定性变量的各种回归模型的各参数估计及相关检验统计量二、实验理论与方法在实际问题的研究中,经常会遇到一些非数量型的变量。
如品质变量;性别;战争与和平。
我们把这些品质变量也称为定性变量,在建立回归模型的时候我们需要考虑到这些定性变量。
定性变量的回归模型分为自变量含定性变量的回归模型和因变量是定性变量的回归模型。
自变量含有定性变量的时候,我们一般引进虚拟变量,将这些定性变量数量化。
例如研究粮食产量问题,y为粮食产量,x为施肥量,另外考虑气候问题,分为正常年份和干旱年份两种情况,这个问题数量化方法就是引入一个0-1型变量D,令D i=1 表示正常年份,D i=0表示干旱年份,粮食产量的回归模型为:yi =β+β1xi+β2Di+εi。
因变量是定性变量时,一般用logistic回归模型(分组数据的logistic回归模型,未分组数据的logistic回归模型,多类别的logistic回归模型),probit回归模型等。
三. 实验容1.用DATA步建立一个永久SAS数据集,数据集名为xt103,数据见表21;对数据集xt103,建立y对公司规模和公司类型的回归,并对所得到的模型进行解释。
2.研制一种新型玻璃,对其做耐冲实验。
用一个小球从不同的高度h对玻璃做自由落体撞击,玻璃破碎记为y=1,玻璃未破碎记y=0.数据见表22.是对表中数据建立玻璃耐冲性对高度h的logistic回归,并解释回归方程的含义。
3.某学校对本科毕业生的去向做了一个调查,分析影响毕业去向的相关因素,结果见表23.其中毕业去向“1”=工作,“2”=读研,“3”=出国留学。
性别“1”=男生,“0”=女生。
用多类别的Logisitic回归分析影响毕业去向的因素。
四.实验仪器计算机和SAS软件五.实验步骤和结果分析1.用DATA步建立一个永久SAS数据集,数据集名为xt103,数据见表21;对数据集xt103,建立y对公司规模和公司类型的回归,并对所得到的模型进行解释。
R 检验中R 方为0.8951,可以认为回归拟合效果较好。
回归方程通过F 检验,说明模型是显著成立的。
由参数估计表,可以看出,全部变量都是显著的,回归方程为:21^06.8102.087.33x x y +-=其中,x2是虚拟变量,当公司类型为“互助”时,x2为0,为“股份”时,x2为1。
由方程可知,x2为1,即股份制公司的保险革新措施速度y 会更大。
股份制公司采取保险革新措施的积极性比互助型公司高,股份制公司建立在共同承担风险上,更愿意革新。
公司规模越大,采取保险革新措施的倾向越大:大规模公司保险制度的更新对公司的影响程度比小规模公司大。
SAS 程序:data xt103;input y x1 x2 ;/*引入虚拟变量,将公司类型的互助设为0,股份设为1*/ cards ; 17 151 026 92 021 175 030 31 022 104 00 277 012 210 019 120 04 290 016 238 028 164 115 272 111 295 138 68 131 85 121 224 120 166 113 305 130 124 114 246 1;run;proc reg data=xt103;model y=x1 x2;run;2.研制一种新型玻璃,对其做耐冲实验。
用一个小球从不同的高度h对玻璃做自由落体撞击,玻璃破碎记为y=1,玻璃未破碎记y=0.数据见表22.是对表中数据建立玻璃耐冲性对高度h的logistic回归,并解释回归方程的含义。
模型信息:模型解出的是y=0的概率。
由三个检验中,统计量的P值都小于0.05,可以认为模型是显著的。
由Wald检验的显著性概率及其P值,可以看出,h变量对方程的影响是显著的。
由极大似然估计,各个参数系数也通过检验。
因此模型有效。
二元logit 模型为)98.759.14ex p(1)98.759.14ex p()0(h h y p -+-==模型意义为,小球掉落高度为h ,则玻璃未破碎的概率为p,而y=0表示玻璃未破碎。
也就是说,该种新型的玻璃,用小球对其撞击,当小球的掉落高度为h 时,玻璃未破碎的概率就是)98.759.14ex p(1)98.759.14ex p()0(h h y p -+-==,那么,玻璃会破碎的概率就为1-p(y=0),这也可以看成是一种比例,就是大量实验中,同个高度h ,玻璃会被击破的比例。
SAS 程序:data wjz;input h y ;/*引入虚拟变量,将公司类型的互助设为0,股份设为1*/ cards ; 1.50 0 1.52 0 1.54 0 1.56 0 1.58 1 1.60 0 1.62 0 1.64 0 1.66 0 1.68 1 1.70 0 1.72 0 1.74 0 1.76 1 1.78 0 1.80 1 1.82 0 1.84 0 1.86 1 1.88 1 1.90 0 1.92 1 1.94 0 1.96 1 1.98 1 2.00 1; run ;proc logistic data=wjz;model y=h;run;proc logistic data=wjz;class h;model y=h/link=glogit aggregate scale=none;run;3.某学校对本科毕业生的去向做了一个调查,分析影响毕业去向的相关因素,结果见表23.其中毕业去向“1”=工作,“2”=读研,“3”=出国留学。
性别“1”=男生,“0”=女生。
用多类别的Logisitic 回归分析影响毕业去向的因素。
专业课x1英语x2性别x3月生活费x4毕业去向y两个统计量的P值均大于0.05,说明模型拟合的较好。
检验全局零假设: BETA=0 无效假设检验结果(似然比,评分)的结果P值均小于0.01,具有显著统计学意义。
三个变量中,有两个是不显著的变量,x3,x2,剔除x3:两个统计量的P值均大于0.05,说明模型拟合的较好。
检验全局零假设: BETA=0 无效假设检验结果(似然比,评分,wald )的结果P 值均小于0.01,具有显著统计学意义。
三个变量都是显著的。
以x4=“1”,即参加工作,为参照。
由模型可以看出:)0101.0122.0012.08.011-ex p()004.0038.017.0116.19-ex p(1)004.0038.017.0116.19-ex p()2(421421421x x x x x x x x x y p ++-++++++++==)0101.0122.0012.08.011-ex p()004.0038.017.0116.19-ex p(1)0101.0122.0012.08.011-ex p()3(421421421x x x x x x x x x y p ++-+++++++-==从参数估计表中,与参加工作的同学相比,读研的(y=2)的同学相比,读研的同学其专业课成绩更好(x1的P值=0.003),而外语成绩(x2的p值=0.356)和经济状况(x4的P值=0.184)没有显著差异;出国留学的(y=3)学生其专业课成绩和参加工作的没有显著差异,外语成绩和经济状况则更好。
Sas程序:data a;input x1 x2 x3 x4 y;cards;95 65.0 1 600 263 62.0 0 850 182 53.0 0 700 260 88.0 0 850 372 65.0 1 750 185 85.0 0 1000 395 95.0 0 1200 292 92.0 1 950 263 63.0 0 850 178 75.0 1 900 190 78.0 0 500 182 83.0 1 750 280 65.0 1 850 383 75.0 0 600 260 90.0 0 650 375 90.0 1 800 263 83.0 1 700 185 75.0 0 750 273 86.0 0 950 286 66.0 1 1500 393 63.0 0 1300 273 72.0 0 850 186 60.0 1 950 276 63.0 0 1100 196 86.0 0 750 271 75.0 1 1000 163 72.0 1 850 260 88.0 0 650 167 95.0 1 500 186 93.0 0 550 163 76.0 0 650 186 86.0 0 750 276 85.0 1 650 182 92.0 1 950 373 60.0 0 800 182 85.0 1 750 275 75.0 0 750 172 63.0 1 650 181 88.0 0 850 392 96.0 1 950 2;run;proc print;run;proc logistic;class x3;model y(ref='3')=x1 x2 x3 x4/link=glogit aggregate scale=none ;run;proc logistic;class x3;model y(ref='3')=x1 x2 x4/link=glogit aggregate scale=none ;run;proc logistic;class x3;model y(ref='1')=x1 x2 x4/link=glogit aggregate scale=none ;run;六.收获与思考七. 思考题当自变量是定性变量的时候,我们需要引进虚拟变量进行数量化,当定性变量有n个水平的时候,我们该引进多少的虚拟变量,否则会怎样?不妨试试在sas中试试会出现什么问题。
答:当定性变量有n个水平时应该引进n-1个虚拟变量。
否则最后一个虚拟变量无法用最小二乘估计计算出来。
例:X1-X3为虚拟变量。
Data a;input x1 x2 x3 x y;cards;1 0 0 1.26 75 1 0 0 1.35 77 1 0 0 1.40 78 1 0 0 1.58 820 1 0 1.71 65 0 1 0 1.76 66 0 1 0 1.80 68 0 1 0 1.85 700 0 1 1.22 68 0 0 1 1.35 69 0 0 1 1.46 70 0 0 1 1.44 72;proc reg data=a;model y=x1-x3 x;run;X3没有参数估计结果。
