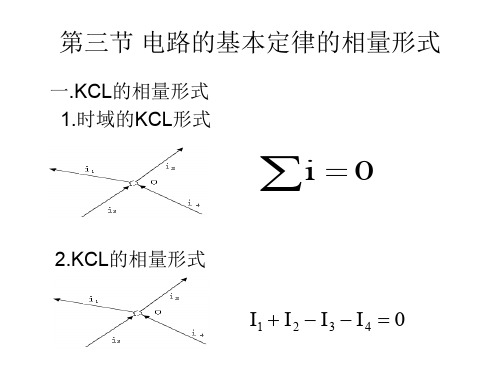
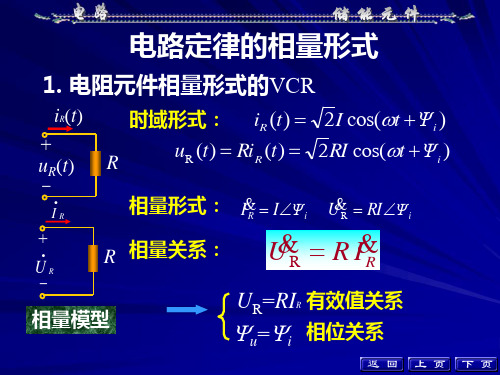
电路定律的相量形式
合集下载
最新电工学电力学课程第八章《电路定律的相量形式》
由相量形式KVL有 : V V 1 V 2 600 8090 (V)
（2）相量图解法
60 j80 10053.1 (V) 故 : |V | 100(V)
相量法的三个基本公式
UR RIR
U L jL IL
1
UC
j
C
IC
以上公式是在电压、电流关联参考方向的条件
错误的写法
1 u
C i
1
C
U I
(2) 容抗的绝对值和频率成反比。
0, XC , 直流开路( 隔直作用) ;
XC
, XC 0, 高频短路（旁路作用）;
(3) 由于容抗的存在使电流领先电压。
4、受控源 如果受控源（线性）的控制电压或电流是正弦量， 则受控源的电压或电流将是同一频率的正弦量。
i 超前u 90° I
0
所示，反映电压电流瞬时 值关系的波形图如图(b)所示。由此图可以看出电容电流超 前于电容电压90°，当电容电压由负值增加经过零点时，其 电流达到正最大值。
容抗
I= CU
U 1
I C
容抗的物理意义：
X
C
定义
1
C
(1) 表示限制电流的能力；
相量关系
+
U R R I
U R
-
有效值关系：UR = RI 相位关系：u , i 同相
I
R
U
相量图
相量模型
2. 电感
时域
频域
i(t)
i(t) 2I cost
+ u (t)
u(t) L di(t)
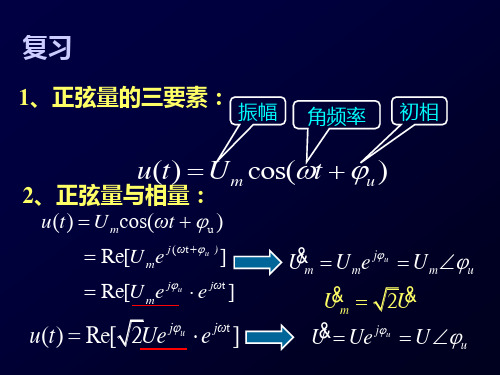
电工基础5.3 电路基本定律的相量形式
结论：①电容元件电压电流大小关系为：
U 1 I
C
②电容元件电压电流相量关系为：
i
u
2
或i
u
2
即电流I超前电压U π/2.
3、容抗与容纳
（1）容抗Xc：表示电容对正弦电流得
1 单位为欧【姆】()
2f C
① ω＝0，Xc→∞ 电容元件相当于开路 ② ω →∞ ，Xc＝0 电容元件相当于短路
3、KVL在相量图上体现为——封闭多 边形。 三、电阻元件电压电流关系的相量形式： 1、电阻元件 （1）电阻元件时域 形式的电压与电流 关系：
u = Ri
图4-18电阻元件电压电流瞬时值关系
（2）电阻元件的相量形式：
U RI
结论：①电阻元件的电压与电流关系
U=RI 或 I=GU(G=1/R)
①
电感相当于短路
② 0, X L 0 电感相当于开路
（2)感纳： 表示电, X感L 对正弦电流的导通能力。
单位西【门子】（S）
BL
1 XL
故又得：
U jX L I
I jBL U
例4－6：已知0.5H的电感两端电压为
uL 220 2 sin(314t 30)V ，求：XL、BL和IL， 并画出相量图。
2、电容元件的相量形式
I jCU
U
1
jC
或U
1
I j
1
I
jC
C
证：2I
sin(t
i )
d dt
[
电路基本定律相量形式
当 C一定时,电容的容抗与频率f 成反比。频率越高， 感抗越小，在直流电路中容抗为无限大，可视为开路。
2. 电压电流的相位关系
uUms iω nt
iImsiω nt (90 )
U mUm00 ImIm900
i uC
i 超前u
2
3. 电压电流的相量关系
ui u
i
UImm
p
（1）瞬时功率
p u U i( 1 c I2 o t)s
（2）平均功率
（有功功率）
0
PT 10 TpdtU IU R 2I2R
t
P=U I
t
四、电感元件的电压电流关系的相量式
设在电感元件的交流电路中
，电压、电流参考方向如图示。
+
1.电压电流的数值关系
ui L
瞬时值 设： iImsi nt
2. 电压电流的相位关系
iImsi nt ImIm00U mUm900 u+
u L I m co t U m s sit n 9 )( 0
u 超前i
eu 2 e滞后i
ui
u
i
–
e
i
e
L
2
3. 电压电流的相量关系
0
t
U Im mUIm m 09000U Im m900jXL
Um00 Im900
jXC
I
0
2
•
UjIXC
U
CHale Waihona Puke ItU• 相量图
3、功率
设：uU m sin t
iu
iIm si n t(90 ) 0
t
其波形图如右：
电路(第五版).-邱关源原著-电路教案--第8章相量法
电路(第五版).-邱关源原著-电路教案--第8章相量法第8章 相量法● 本章重点1、正弦量的两种表示形式；2、相量的概念；3、KVL 、KCL 及元件VCR 的相量形式。
● 本章难点1、 正确理解正弦量的两种表示形式的对应关系；2、 三种元件伏安关系的相量形式的正确理解。
● 教学方法本章是相量法的基础，对复数和正弦量两部分内容主要以自学为主，本章主要讲授相量法的概念、电路定律的相量形式以及元件V AR 的相量形式。
讲述中对重点内容不仅要讲把基本概念讲解透彻，而且要讲明正弦量的相量与正弦时间函数之间的对应关系；元件V AR 的相量形式与时域形式之间的对应关系，使学生加深对内容的理解并牢固掌握。
本章对元件的功率和能量这部分内容作了简单讲解，以便为下一章的学习打下基础。
本章共用4课时。
● 授课内容8.1复数1. 复数的三种表示bj a A += 直角坐标=θ∠r 极坐标 =θj re 指数形式θθθsin cos 22r b r a ab arctgb a r ==⇒=+=⇒直极极直θθsin cos jr r A += 三角表示形式欧拉公式：θθθsin cos j e j +=2. 复数的运算已知：11111θ∠=+=r jb a A ，22222θ∠=+=r jb a A求：212121,,A AA A A A ⋅±i()()212121b b j a a A A ±+±=±212121212121θθθθ+∠=+∠=⋅r r A A r r A A 8.2正弦量一、正弦量：随时间t 按照正弦规律变化的物理量，都称为正弦量，它们在某时刻的值称为该时刻的瞬时值，则正弦电压和电流分别用小写字母i 、u 表示。
周期量：时变电压和电流的波形周期性的重复出现。
周期T ：每一个瞬时值重复出现的最小时间间隔，单位：秒（S ）； 频率f ： 是每秒中周期量变化的周期数，单位：赫兹（Hz ）。
电路分析课件第八章相量法
KVL：任意时刻，任一回路，U=0
三、受控源的相量形式
i1
I1
R
正弦电流
i 1 电路时：
R
1I1
本章小结：
所谓相量法，就是电压、电流用相量表示， RLC元件用阻抗、感抗、容抗表示，画出电路的相 量模型，利用KCL、KVL和欧姆定律的相量形式写 出未知电压、电流相量的代数方程加以求解，因此， 应用相量法应熟练掌握:
∴ i =46.2 2cos(314t–27º)A j I1
+1 I
相量图
I2
注意：
在分析正弦交流电路时字母的写法：
i — 瞬时值 I — 有效值 Im — 最大值 I — 有效值相量 Im— 最大值相量
三、不同频率的正弦量不能用相量法运算。
相量只含有正弦量的有效值(最大值)和初相 位的信息，不包含频率的信息，即：在运用相量 法分析正弦量时，默认为同频率。
将 I (或 U)定义为电流i (或电压u) 的相量，它含有 正弦量的振幅和相位的信息。
注意：
有一个正弦量便可以得到一个相量； 有一个相量也可以写出对应的正弦
量。两者是一一对应的关系，决不
是相等的关系。
u=220 2 cos(314t+45º)V
U=220 45ºV u U
I=50 –30ºA 一一对应 i =50 2 cos(ωt–30º)A i I
U 相量形式电路图
相量关系既反映了u、i 的有效 值关系又反映了相位的关系。
I U 相量图
2、电感
iL
u
若：i = 2 Icos(ωt+ψi )
则：u=L
di dt
=–
2 IωLsin(ωt+ψi )
电路分析相量法
量的相量乘以 jω ，即表示di/dt 的相量为
j I I( i 90o )
该相量的模为ωI ，辐角则超前原相量π/2 。
对 i 的高阶导数 dni/dtn ，其相量为 ( j )。n I
3)正弦量的积分
设 i 2I cos( t i )，则
idt Re[ 2Ie j t ] dt Re[ (
F1F2 | F1 | 1 | F2 | 2 | F1 || F2 | (1 2 )
可见复数的乘法运算使用指数形式或极坐标形式较为简便。
3)除法运算
a)代数形式
F1 F2
a1 a2
jb1 jb2
(a1 (a2
jb1 )(a2 jb2 )(a2
jb2 ) jb2 )
(a1a2
b1b2 ) j(a2b1 a22 b22
设 F1 a1 jb1 ， F2 a2 jb2 ，则
F1 F2 (a1 jb1 ) (a2 jb2 ) (a1 a2 ) j(b1 b2 )
平行四边形法则：
+j F1 +F2 F1
F2 o
+1
+j F1
F2 o
F1－F2 +1
2)乘法运算 a)代数形式
F1F2 (a1 jb1 )(a2 jb2 ) (a1a2 b1b2 ) j(a1b2 a2b1 )
di d Re[ 2Ie j t ] Re[ d ( 2Ie j t )] Re[ 2( j I)e j t ]
dt dt
dt
Re[ 2 Ie ] j( ti 90o ) 2 I cos( t i 90o )
上式表明：
复指数函数实部的导数等于复指数函数导数的实部；
84 电路定律的相量形式
§8.4 电路定律的相量形式
一. 基尔霍夫定律的相量形式 正弦电流电路中的各支路电流和支路电压都
是同频正弦量，所以可以用相量法将KCL和KVL转 换为相量形式。
•
i(t) 0 I 0
•
u(t) 0 U 0
注：但一般 I 0 ， U 0
二、电阻、电感和电容元件的VCR相量形式
1. 电阻
相量模型
IL IC IR
jLIL
1
jC
IC
U S
RIR
1
jC
IC
相量形式代数方程
相量模型：电压、电流用相量；元件用复数阻抗或导纳。
例8-6：正弦电流源的电流，其有效值IS=5A，角频率 ω=103rad/s， R=3Ω，L=1H，C=1μF。求电压uad和ubd。
ai
b
c
iS
+ uR - + uL - +
i(t)
+ uR(t) -
已知 i(t) 2I cos(t ) 则 uR (t) Ri(t) 2RI cos(t )
R
相量形式：
I I
U R RI I
相量关系
U R R I
+
U R
-
有效值关系：UR = RI
相位关系：u , i 同相
I
R
U
相量图
相量模型
2. 电感
时域
频域
i(t)
i(t) 2I cost
= 15 /0 °V
•
•
U L jL I = 5000 / 90°V
•
UC j
1
•
I
= 5000 / - 90 °V
C
•
一. 基尔霍夫定律的相量形式 正弦电流电路中的各支路电流和支路电压都
是同频正弦量，所以可以用相量法将KCL和KVL转 换为相量形式。
•
i(t) 0 I 0
•
u(t) 0 U 0
注：但一般 I 0 ， U 0
二、电阻、电感和电容元件的VCR相量形式
1. 电阻
相量模型
IL IC IR
jLIL
1
jC
IC
U S
RIR
1
jC
IC
相量形式代数方程
相量模型：电压、电流用相量；元件用复数阻抗或导纳。
例8-6：正弦电流源的电流，其有效值IS=5A，角频率 ω=103rad/s， R=3Ω，L=1H，C=1μF。求电压uad和ubd。
ai
b
c
iS
+ uR - + uL - +
i(t)
+ uR(t) -
已知 i(t) 2I cos(t ) 则 uR (t) Ri(t) 2RI cos(t )
R
相量形式：
I I
U R RI I
相量关系
U R R I
+
U R
-
有效值关系：UR = RI
相位关系：u , i 同相
I
R
U
相量图
相量模型
2. 电感
时域
频域
i(t)
i(t) 2I cost
= 15 /0 °V
•
•
U L jL I = 5000 / 90°V
•
UC j
1
•
I
= 5000 / - 90 °V
C
•
电路原理课件 第8章 相量法
三. 相位差 ：
两个同频率正弦量相位角之差。
i(t) 0
Im um
设 u(t)=Umcos(w t+ u)
2
i(t)=Imcos(w t+ i)
0
wt
则 相位差j : j = (w t+ u)- (w t+ i)
u- i
同频率正弦量的相位差等于它们的初相之差。 不同频率的两个正弦量之间的相位差不再是一个常数，而是 随时间变动。
j u与i正交; j u与i反相;
2
§8 - 3相量法的基础
1. 正弦量的相量表示
复函数 F F ej(wt)
没有物理意义
F cos(wt ) j F sin(wt Ψ )
若对F取实部：
Re[F] F cos(ωt Ψ ) 是一个正弦量，有物理意义。
对于任意一个正弦时间函数都可以找到唯一的与其对应的 复指数函数：
F e j
4、极坐标形式：
F F ej
=|F|
二 复数运算
(1)加减运算——代数形式
+j F2
若 F1=a1+jb1
F2=a2+jb2 O
则 F1±F2= (a1±a2) +j (b1±b2)
F= F1 +F1
F1 +1
+j
O - F2
F2 F1
F= F1 - F2 +1
(2) 乘除运算——指数形式或极坐标形式
⑶∫i2dt。
解： ⑴设 i i1 i2 2I cos(wt i ), 其相量为 I=I/Ψi
I I1 I2 10/600A+22/-1500A=（5+j8.66）A+（-19.05-j11）A
4-3电路定律的向量形式
I
u i
U
3）电阻的uR (t )的相位 iR (t ) 的相位同相；
4 ) 振幅关系 U Rm RI Rm
u (t )
i (t )
R
时域模型
例2：在正弦稳态电路中，
i ( t ) 2cos(100t 30 )A 流过10Ω电阻的电流
求： u (t )
10 2 cos(100t 30 )V
k 1 k
n
对于线性时不变的正弦稳态电路（单一频率激 励）各支路电压、电流为同频率的正弦量。 设：
n
jωt ik (t ) I km cos(ωt ik ) Re[ I km e ]
n
n jωt jωt ik (t ) Re[I km e ] Re I kme k 1 k 1 k 1
0 I
元件 电阻 电感 相量模型
I
0 U
伏安关系 相量图
R
U
I
jL
U
I
1 jC
电容
U
例 4：
u (t )
4H电感端电压 u (t ) 8 2cos(t 50 )V 100rad/s 求 i (t )
i(t )
解：1）画出电路的相量模型
i3
i1 i2
求：
i3 (t )
解：方法1）由KCL的时域形式： 1060
0
6.236.2
10 60 5 90 I3 I1 I 2
5 90
相量图
10 cos 60 10 j sin 60 j5
5 j3.66 6.236.2 A
第20讲 电路定律的相量形式、阻抗与导纳
频域
&L = I L∠φi I
& UL
有效值关系 UL=ω L IL
UL = ωLIL π φu = φi + 2
& IL
& U
+ L
π φ + = ωL I L∠ i 2
相位关系 uL 超前 iL 90° °
& U
jω L
L
相量模型
相量图
& IL
感抗 U=ω L I XL= U/I =ω L= 2π f L， 单位 欧 π ， 单位: 感抗的物理意义： 感抗的物理意义： (1) 表示限制电流的能力； 表示限制电流的能力； (2) 感抗和频率成正比。 感抗和频率成正比。 XL
& U
φ = U∠ u
π φ + & I = ω C U∠ u 2
有效值关系 I=ω C U
+
I&
U&
1 jω C
& I
& U
相位关系 i 超前 90° 超前u °
-
相量模型
相量图
容抗 I=ω CU
U 1 = I ωC 容抗的物理意义： 容抗的物理意义：
1 XC = ωC
def
错误的写法 1 u = ωC i
θ = φu - φi
θ
R 阻抗三角形
X
具体分析一下 R-L-C 串联电路 Z=R+j(ω L-1/ω C)=|Z|∠
ω L > 1/ω C ，X>0， >0，u领先 ，电路呈感性； 领先i， ， ， 领先 电路呈感性； ω L<1/ω C ，X<0， <0，u落后 ，电路呈容性； 落后i， ， ， 落后 电路呈容性； ω L=1/ω C ，X=0， =0，u与i同相，电路呈电阻性。 同相， ， ， 与 同相 电路呈电阻性。
电路基本定律的相量形式
U
i
L
u
U IX L di jX L 则 uL X L L dt jL u 2 IL sin(t 90 )
jX C
i 2 I sin t
UI
I
u领先 i 90°
U I jX L
0
I2XL
设
i
C
u
iC
du dt
1 j C 1 j C
？
？
单一参数正弦交流电路的分析计算小结
电路 电路图 基本 参数 （正方向） 关系
i 复数 阻抗 设 电压、电流关系 瞬时值 有效值 相量图 相量式 功率 有功功率 无功功率
u 2U sin t
I
U IR
U
R
u
u iR
R
则
U IR
UI
0
i 2 I sin t
设
u、 i 同相
图 KVL的相量形式
回路的电压方程： 其KVL相量表达式为：
u1 u 2 u 3 u 4 0
U1 U 2 U 3 U 4 0
小 结
电路参数
R L
基本关系 复阻抗
u iR
R
I
U
U
电路参数
基本关系
复阻抗
电路参数
jX L j L
di uL dt
项目十九 电路基本定律的相量形式
电压、电流瞬时值的关系符合欧姆定律、基尔霍 夫定律 。
i
R
u
L
uR uL
u uR uL di iR L dt
电流、电压相量符合相量形式的欧姆定律、 基尔霍夫定律。
I
i
L
u
U IX L di jX L 则 uL X L L dt jL u 2 IL sin(t 90 )
jX C
i 2 I sin t
UI
I
u领先 i 90°
U I jX L
0
I2XL
设
i
C
u
iC
du dt
1 j C 1 j C
？
？
单一参数正弦交流电路的分析计算小结
电路 电路图 基本 参数 （正方向） 关系
i 复数 阻抗 设 电压、电流关系 瞬时值 有效值 相量图 相量式 功率 有功功率 无功功率
u 2U sin t
I
U IR
U
R
u
u iR
R
则
U IR
UI
0
i 2 I sin t
设
u、 i 同相
图 KVL的相量形式
回路的电压方程： 其KVL相量表达式为：
u1 u 2 u 3 u 4 0
U1 U 2 U 3 U 4 0
小 结
电路参数
R L
基本关系 复阻抗
u iR
R
I
U
U
电路参数
基本关系
复阻抗
电路参数
jX L j L
di uL dt
项目十九 电路基本定律的相量形式
电压、电流瞬时值的关系符合欧姆定律、基尔霍 夫定律 。
i
R
u
L
uR uL
u uR uL di iR L dt
电流、电压相量符合相量形式的欧姆定律、 基尔霍夫定律。
I
第8章 相量法
o
j ＝ 0， 同相
u i o o
u i wt
wt
u
j= /2：u 领先 i /2
i o
wt
同样可比较两个电压或两个电流的相位差。
例
解
计算下列两正弦量的相位差。
(1) i1 (t ) 10 cos( π t 3π 4) 100 i2 (t ) 10 cos( π t π 2) 100
j π 2
F
0
Re
jF
π j π π π 2 , e cos( ) jsin( ) j 2 2 2
F
π , e
j π
cos( π) jsin( π) 1
注意 +j, –j, -1 都可以看成旋转因子。
8.2
1. 正弦量
瞬时值表达式
180.2 j126.2 2.238 j6.329
182.5 j132.5 225.536
③旋转因子 复数
ej =cos +jsin =1∠
Im F• ej
F• ej
旋转因子 0
F Re
特殊旋转因子
jF
Im
π , 2 π π e cos jsin j 2 2
若交流电压有效值为 U=220V ，
注意
U=380V 其最大值为 Um311V Um537V
① 工程上说的正弦电压、电流一般指有效值，如 设备铭牌额定值、电网的电压等级等。但绝缘水平、 耐压值指的是最大值。因此，在考虑电器设备的耐 压水平时应按最大值考虑。
②测量中，交流测量仪表指示的电压、电流读 数一般为有效值。
o
j ＝ 0， 同相
u i o o
u i wt
wt
u
j= /2：u 领先 i /2
i o
wt
同样可比较两个电压或两个电流的相位差。
例
解
计算下列两正弦量的相位差。
(1) i1 (t ) 10 cos( π t 3π 4) 100 i2 (t ) 10 cos( π t π 2) 100
j π 2
F
0
Re
jF
π j π π π 2 , e cos( ) jsin( ) j 2 2 2
F
π , e
j π
cos( π) jsin( π) 1
注意 +j, –j, -1 都可以看成旋转因子。
8.2
1. 正弦量
瞬时值表达式
180.2 j126.2 2.238 j6.329
182.5 j132.5 225.536
③旋转因子 复数
ej =cos +jsin =1∠
Im F• ej
F• ej
旋转因子 0
F Re
特殊旋转因子
jF
Im
π , 2 π π e cos jsin j 2 2
若交流电压有效值为 U=220V ，
注意
U=380V 其最大值为 Um311V Um537V
① 工程上说的正弦电压、电流一般指有效值，如 设备铭牌额定值、电网的电压等级等。但绝缘水平、 耐压值指的是最大值。因此，在考虑电器设备的耐 压水平时应按最大值考虑。
②测量中，交流测量仪表指示的电压、电流读 数一般为有效值。
o
第8章 相量法
12.47 j 0.569 12.48 2.61
(17 j 9) (4 j 6) 220 35 ? 20 2 ： j5 例
19.24 27.9 7.21156.3 原式 180.2 j126.2 20.6214.04
180.2 j126.2 6.72870.16
我国国家标准规定的电力网额定电压有 10KV、35 kV、110 kV、220 kV、330 kV、500 kV，目前大力研究750KV,1000KV，已经有线路 试运行。 市区一般输电电压为 10 kV 左右（江苏在 试点 20KV）电压等级，通常需要设臵降压变电 所， 经配电变压器将电压降为 380/ 220 V， 再引出若干条供电线到各用电点的配电箱上， 配电箱将电能分配给各用电设备。
第8章
相量法
本章重点
8.1 8.2 8.3 8.4 复数 正弦量 相量法的基础
电路定律的相量形式
目的：交流电路的分析基础!
日常生活，交流电应用广泛!
回顾：直流电路中学习了哪些定理与方法？
i1
20
5
i2
u 1
140V
6
u 2
i3
u3
90V
三个基本工具：欧姆定理，(a) KCL,
几种不同值时的旋转因子：
Im
jI
0
I cos j sin j 2 2
Re
jI
j 2 , e cos( ) j sin( )j 2 2 2
I
, e j cos( ) j sin( ) 1
交流情况下电容如何处理？
i +
(17 j 9) (4 j 6) 220 35 ? 20 2 ： j5 例
19.24 27.9 7.21156.3 原式 180.2 j126.2 20.6214.04
180.2 j126.2 6.72870.16
我国国家标准规定的电力网额定电压有 10KV、35 kV、110 kV、220 kV、330 kV、500 kV，目前大力研究750KV,1000KV，已经有线路 试运行。 市区一般输电电压为 10 kV 左右（江苏在 试点 20KV）电压等级，通常需要设臵降压变电 所， 经配电变压器将电压降为 380/ 220 V， 再引出若干条供电线到各用电点的配电箱上， 配电箱将电能分配给各用电设备。
第8章
相量法
本章重点
8.1 8.2 8.3 8.4 复数 正弦量 相量法的基础
电路定律的相量形式
目的：交流电路的分析基础!
日常生活，交流电应用广泛!
回顾：直流电路中学习了哪些定理与方法？
i1
20
5
i2
u 1
140V
6
u 2
i3
u3
90V
三个基本工具：欧姆定理，(a) KCL,
几种不同值时的旋转因子：
Im
jI
0
I cos j sin j 2 2
Re
jI
j 2 , e cos( ) j sin( )j 2 2 2
I
, e j cos( ) j sin( ) 1
交流情况下电容如何处理？
i +
7向量法-电路定律的相量形式
7电路定律的相量形式1. 电阻元件 VCR 的相量形式设图8.13（a）中流过电阻的电流为则电阻电压为：其相量形式：图8.13（a）以上式子说明：（1）电阻的电压相量和电流相量满足复数形式的欧姆定律：，图8.13（b）为电阻的相量模型图。
图 8.13（ b ）（2）电阻电压和电流的有效值也满足欧姆定律：U R = RI（3）电阻的电压和电流同相位，即：ψu = ψi电阻电压和电流的波形图及相量图如图8.14（a）和（b）所示。
图 8.14（a）（b）电阻的瞬时功率为：即瞬时功率以2ω交变，且始终大于零，如图8.14（a）所示，表明电阻始终吸收功率。
2. 电感元件 VCR 的相量形式设图 8.15（a）中流过电感的电流为则对应的相量形式分别为：图 8.15 （ a ）（ b ）以上式子说明：（1）电感的电压相量和电流相量满足关系：，其中X L=ωL=2πfL ，称为感抗，单位为Ω(欧姆)，图8.16（b）为电感的相量模型图。
（2）电感电压和电流的有效值满足关系：，表示电感的电压有效值等于电流有效值与感抗的乘积。
（3）电感电压超前电流相位，即：电感电压和电流的波形图及相量图如图8.16（a）和（b）所示。
注意:（1）感抗表示限制电流的能力；（2）感抗和频率成正比如图8.16（c）所示，当；电感电压和电流的波形图及相量图如图8.16（a）和（b）所示。
图 8.16 （a）（b）（c）电感的瞬时功率为：即电感的瞬时功率以 2ω交变，有正有负，如图8.16（a）所示。
电感在一个周期内吸收的平均功率为零。
3. 电容元件 VCR 的相量形式图 8.17 （ a ）（ b ）设图8.17（a）中电容的电压为：则对应的相量形式分别为：以上式子说明：（1）电容的电压相量和电流相量满足关系：其中X C =1/ωC ，称为容抗，单位为Ω(欧姆)，图8.17（b）为电容的相量模型图。
（2）电容电压和电流的有效值满足关系：，表示电容的电压有效值等于电流有效值与容抗的乘积。
电路基本定律的相量形式
uC －
RI 100 0.5 245 50 245 U R
jX I U C C j100 0.5 245 50 2 45
i sin( 100t 45) A u R 100 sin( 100t 45) V u C 100 sin( 100t 45) V
i
2
解：
1000V U s 1 1 XC 100 6 C 100 100 10
+
us －
+
R C uR －
+
U U U s R C
RI U R U U RI jX I U s R C C ( R jX C ) I jX I U C C U 1000 1000 s I 0.5 245A R jX C 100 j100 100 2 45
2、电感元件
di 电感元件伏安关系： u L dt 根据相量运算的规则1、规则3和规则4 ，有：
jLI jX I U L
U 、 I I 代入，得： 将U u i U u j LI i LI ( i 90)
U LI X L I
u i 90
i
L
+ u － (a) 电感元件
U
θ u θ i
I
感抗：XL=ωL，与频率成正比。
(b) 相量图
du 电感元件伏安关系： i C dt 根据相量运算的规则1、规则3和规则4 ，有：
3、电容元件
jCU I
U 、 I I 代入上式，得： 将U u i I i j CU u CU ( u 90)
电工与电子技术电路定理的相量形式
i(t) =10 2 cos(5t + 36.90 )A
ɺ U _ ɺ I
+
ɺ I
1
-j10Ω 15Ω j20Ω
ɺ I2
返 回
ɺ I3
上 页 下 页
jω L 相量关系： 相量关系：
ɺ ɺ ɺ UL = jωL IL = jXL IL
Ψu=Ψi +90°
返 回 上 页 下 页
相量模型
有效值关系： UL=ω L IL 相位关系： 相位关系：
感抗和感纳
XL=ωL=2πfL，称为感抗，单位为 (欧姆) 称为感抗，单位为Ω 欧姆) BL=1/ω L =1/2πfL， 称为感纳，单位为 S 称为感纳 感纳，
ɺ IC
Ψu
ɺ UC
ωt
pC = uCiC = 2UC IC cos(ω t +Ψu ) sin( ω t +Ψu ) = UC IC sin 2(ω t +Ψu )
瞬时功率以2ω交变，有正有负， 瞬时功率以 交变，有正有负，一周期 交变 内刚好互相抵消，表明电容只储能不耗能。 内刚好互相抵消，表明电容只储能不耗能。 有功功率P 有功功率 P=0
1 ωC
ɺ IC
+ ɺ UC -
−j
相量模型
ɺ ɺ 相量关系： 相量关系： ɺC = 1 IC = −j 1 IC U jωC ωC 1 IC 有效值关系： UC = 有效值关系： ωC 相位关系： 相位关系： Ψu=Ψi -90°
返 回 上 页 下 页
容抗与容纳
XC=1/ω C， 称为容抗，单位为 Ω(欧姆) 称为容抗， (欧姆) Β C = ω C， 称为容纳，单位为 S 称为容纳，
返 回 上 页 下 页
电路相量法
正弦电流表达式： 正弦电流表达式：
i=Imcos(ω t+φi)
周期T 和频率f 周期 和频率
φi
O
1 f = T
周期T 重复变化一次所需的时间。 单位： ， 周期 ：重复变化一次所需的时间。 单位：s，秒 频率f 每秒重复变化的次数。 频率 ：每秒重复变化的次数。 单位： ， 单位：Hz，赫兹
2. 正弦量的三要素
周期电流、 3. 周期电流、电压的有效值 周期电流、电压的瞬时值随时间而变， 周期电流、电压的瞬时值随时间而变，为了衡 量其大小工程上采用有效值来表示。 量其大小工程上采用有效值来表示。 工程中将周期电流或电压在一个周期内产生的 平均效应换算为在效应上与其相等的直流量， 平均效应换算为在效应上与其相等的直流量，以衡 量和比较周期电流或电压的效应， 量和比较周期电流或电压的效应，该直流量就称为 周期量的有效值。 周期量的有效值。
1. 正弦量的相量表示
两个正弦量的相加
i1 = 2 I1 cos(ω t + φ1 )
i2 = 2 I2 cos(ω t + φ2 )
角频率： 角频率： 有效值： 有效值： 初相位： 初相位：
ω φ1
u, i i1 I1
i1 0
ω
i2
i2 I2
i1+i2 →i3 i3 ω I3 ωt
φ2
φ3
无论是波形图逐点相加，或用三角函数做都很繁琐。 无论是波形图逐点相加，或用三角函数做都很繁琐。 因同频率的正弦量相加仍得到同频率的正弦量，所以， 因同频率的正弦量相加仍得到同频率的正弦量，所以， 只要确定初相位和有效值(或最大值)就行了。 只要确定初相位和有效值(或最大值)就行了。
i = 2 I cos(ω t + φ i ) ⇔ I = I∠φ i
电路元件和基本定律的相量形式
iC dt
1 C
Re[
ImCe jt
]dt
Re[
1 C
ImCe jtdt]
Re[
1
jC
ImCe jt ]
K
(0)
因为这里讨论的是正弦稳态电路，电容电压中不含恒定分量，因此K = 0。再将式(0)与式(5.18)相
比较，得到
VmC
1
jC
ImC
jX C ImC
或
VC
1
jC
IC
jX C IC
32 90(V)
V VR VL VC 160 4890 3290
其相量图如图5.10(c1)所6 示j4。8 j32 16 j16 16 245(V) 将电压相量变换为时域形式为
v(t) =16cos(5t + 45°) = 32cos(5t + 45°) (V)
I 0
和 V 0
(3)
上式称为基尔霍夫定律的相量形式。
从上面两个式子可以看出，基尔霍夫定律的相量形式和时域形式在形式上是相同 的，差别仅在于一个用相量为变量，另一个用时域函数为变量。
2006-1-1
！
9
电路元件和基本定律 的相量形式(9)
• 例5.3 如图5.10(a)所示电路，已知i(t) =4cos(5t) A，求电压 v。
电路元件和基本定律 的相量形式 (1)
1.1 R、L、C的相量模型 这里介绍几种基本电路元件的特性方程的相量形式。 电阻元件
iR(t) R
v(t)
+j
VR
+ vR(t) −
i(t)
(a)
İR
R
+
VR
−
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
滞后于电源电压/3，问R、C应如何选择。
解1 Us RI jXC I
I Us ,
U s U C
R jXC
jCR 1
UC
jX C
R
Us jXC
CR tan 60
解2 画相量图计算。
tan 60 3 UR RI CR UC I /C
I+
U _
R+
jXC
U C -
3 U R
I
U C
60
I
jBLU
j 1U
L
1 U
jL
返回 上页 下页
波形图及相量图
uL pL
U L
i
O
2 t
电压超前 电流90°
I
i
功率 pL uLi ULmIm cos(t i )sin(t i ) ULI sin 2(t i )
瞬时功率以2交变，有正有负，一周期内刚
好互相抵消，表明电感只储能不耗能。
返回 上页 下页
i(t)
+ u-L(t)
I
+
•
U-L
时域形式 i(t) 2I cos( t i )
L
uL (t) L
相量形式
di(t)
dt
2
2L
LIc
I sin( t os( t
i
i
) π 2
)
I I i UL LI i π 2
jL
相量关系
UL jL I jX LI
相量模型
有效值关系 UL= L I 相位关系 u=i +90°
3. 电容元件VCR的相量形式
iC(t) + u(t) -
IC
时域形式 u(t) 2U cos(t u )
C
iC (t) C
相量形式
du(t) dt
2CU
2CU sin( t cos( t u
u
π) 2
)
1
U U u IC CU u π 2
+
U
-
jωC 相量关系
U
j 1
C
I
表明 流入某一结点的所有正弦电流用相量表示
时仍满足KCL；而任一回路所有支路正弦电压用
相量表示时仍满足KVL。
返回 上页 下页
例4-1试判断下列表达式的正、误。
1. Uu LiI
2. i 5cos t 50
5.
U C IC
1
j C Ω
jC
3. Im j CUmm
4.
XL
U L I L
Um Im
jXC I
相量模型
有效值关系 IC= CU 相位关系 i=u+90°
返回 上页 下页
容抗与容纳
XC=-1/ C， 称为容抗，单位为(欧[姆]) B C = C， 称为容纳，单位为S(西[门子])
容抗和频率成反比。
|XC|
0， |XC| 直流开路(隔直)。
，|XC|0 高频短路。
O
相量表达式
U s
返回 上页
返回 上页 下页
感抗和感纳
XL=L=2fL，称为感抗，单位为 (欧[姆]) BL=-1/ L =-1/2fL，称为感纳，单位为S(西[门子])
感抗的性质
①表示限制电流的能力。
XL
O
相量表达式
②感抗和频率成正比。
0(直流), X L 0, 短路 , X L , 开路
U jX LI jLI ,
u=i 相位关系
返回 上页 下页
波形图及相量图 URI
O
U R
同
pR
I
相 位
uR
u=i
i
t
瞬时功率 pR uRi 2UR 2I cos2 (ωt i ) URI[1 cos 2(ωt i )]
瞬时功率以2交变，始终大于零，表明
电阻始终吸收功率。
返回 上页 下页
2. 电感元件VCR的相量形式
6. UL j LIL
7. u CL di dt
返回 上页 下页
例4-2 已知电流表读数： A1 ＝8A， A2 ＝6A。
若 1. Z1 R, Z2 jXC , A0 ＝?
A0
2. Z1 R, Z2为何参数使
A0 ＝I0max=?
U
Z1
A1
3.
Z1
jX L,
Z
为何参数使
2
A0 ＝I0min=?
30 j40
A
I
B
jXL
U BC j40I
U AC
U AB
C
解 UAB (30I )2 (40I )2 50I
30I
I 1A, UR 30V, UL 40V
UAC 78 (30)2 (40 UBC )2
U BC
(78)2 (30)2 40 V 32V
返回 上页 下页
例4-6图示电路I1=I2=5A，U＝50V，总电压与总电流
U jX C
120
1 15
1 j20
1 j10
A
(8 j6 j12)A (8 j6)A 10 36.9 A
i(t) 10 2 cos(5t 36.9 )A
I
-j10
_+U 15 j20
I1 I2
I3
返回 上页 下页
例4-4 已知i(t) 5 2 cos(106t 15)A, 求uS(t)
同相位，求I、R、XC、XL。
解法1 设 UC UC 0
I1 5 0 A, I2 j5A
I (5 j5)A 5 2 45 A
+ I jXL
U
_
R
I1
jXC +
I2
UC -
U
50
45
(5
j5)
jX L
5R
50 2
(1
j)V
令等式两边实部等于实部，虚部等于虚部
5X L 50 2 X L 5 2
i
I
+ 5
uS _
0.2F
相量模型
+ 5
U _
-j5
解 I 5 15 A
1
jX C
j 106
0.2 106
Ω
j5Ω
Us U R UC 5 15 5 j5 V
5 15 5 2 45 V 25 2 30 V
I,U R U C U s
返回 上页 下页
例4-5 已知 UAB 50V, UAC 78V, 问：UBC ?
8-4 电路定律的相量形式
1. 电阻元件VCR的相量形式
i(t) 时域形式 i(t) 2I cos(t i )
+ u-R(t)
•
I
R uR (t) Ri(t) 2RI cos(t i )
相量形式
I I i
UR
UR RI i
u
+
•
UR
R 相量关系 U R R I
-
相量模型
UR=RI 有效值关系
5R 50 5 5 2
2 50
2 R XC 10
2Ω
返回 上页 下页
解法2 画相量图计算。
I2
U
I 5 2
450 I1
U L
UR UC
+ I jXL
U
_
R
I1
jXC +
I2
UC -
U UL 50V
XL
50 52
5
2
XC
R 50 5
2 Ω 10
2Ω
返回 上页 下页
例4-7 图示电路为阻容移项装置，如要求电容电压
刚好互相抵消，表明电容只储能不耗能。
返回 上页 下页
4. 基尔霍夫定律的相量形式
同频率的正弦量加减可以用对应的相量形式 来进行计算。因此，在正弦电流电路中，KCL和 KVL可用相应的相量形式表示为
i(t) 0
i(t) Re 2 I1 I2 ej t 0
I 0
u(t) 0
U 0
返回 上页 下页
例t)
i
+
0.02F 15
_u
4H
相量模型
I
-j10
_+U 15 j20
I1 I2
I3
解 U 120 0
jX L j4 5Ω j20Ω
1
jX C
j 5 0.02
Ω
j10Ω
返回 上页 下页
I
IR
IL
IC
U R
U jX L
Z2 A2
4. Z1 jXL, Z2为何参数使 A0 ＝ A1 ？ A2 ＝?
解 1. I0 82 62 A 10A
2. Z2 R，I0max (8 6)A 14A
I2
I0
3. Z2 jXC, I0min (8 6)A 2A
U , I1
4. Z2 jXC, I0 I1 8A, I2 16A
UU
jXjXC IC
I
j1j 1I
CC
I
I jBCU jCU
返回 上页 下页
波形图及相量图
iC
pC u
IC
O
2 t
电流超前 电压90°
U
u
功率 pC uiC 2UIC cos(ω t u )sin(ω t u ) UIC sin 2(ω t u )
瞬时功率以2交变，有正有负，一周期内