伯努利方程的应用实际液体流动 (1)
伯努利方程原理以及在实际生活中的运用

xx方程原理以及在实际生活中的运用67陈高威在我们传输原理学习当中有很多我们实际生活中运用到的原理,其中伯努利方程是一个比较重要的方程。
在我们实际生活中有着非常重要广泛的作用,下面就伯努利方程的原理以及其运用进行讨论下。
xx方程p+ρρv ²=c式中p、ρ、v分别为流体的压强,密度和速度;h为铅垂高度;g 为重力加速度;c为常量。
它实际上流体运动中的功能关系式,即单位体积流体的机械能的增量等于压力差说做的功。
伯努利方程的常量,对于不同的流管,其值不一定相同。
相关应用(1)等高流管中的流速与压强的关系根据xx方程在水平流管中有ρv ²=常量故流速v大的地方压强p就小,反之流速小的地方压强大。
在粗细不均匀的水平流管中,根据连续性方程,管细处流速大,所以管细处压强小,管粗处压强大,从动力学角度分析,当流体沿水平管道运动时,其从管粗处流向管细处将加速,使质元加速的作用力来源于压力差。
下面就是一些实例伯努利方程揭示流体在重力场中流动时的能量守恒。
由伯努利方程可以看出,流速高处压力低,流速低处压力高。
三、伯努利方程的应用:1.飞机为什么能够飞上天?因为机翼受到向上的升力。
飞机飞行时机翼周围空气的流线分布是指机翼横截面的形状上下不对称,机翼上方的流线密,流速大,下方的流线疏,流速小。
由伯努利方程可知,机翼上方的压强小,下方的压强大。
这样就产生了作用在机翼上的方向的升力。
2.喷雾器是利用流速大、压强小的原理制成的。
让空气从小孔迅速流出,小孔附近的压强小,容器里液面上的空气压强大,液体就沿小孔下边的细管升上来,从细管的上口流出后,空气流的冲击,被喷成雾状。
3.汽油发动机的汽化器,与喷雾器的原理相同。
汽化器是向汽缸里供给燃料与空气的混合物的装置,构造原理是指当汽缸里的活塞做吸气冲程时,空气被吸入管内,在流经管的狭窄部分时流速大,压强小,汽油就从安装在狭窄部分的喷嘴流出,被喷成雾状,形成油气混合物进入汽缸。
浅谈伯努利方程在流体力学中的应用

浅谈伯努利方程在流体力学中的应用作者:张丽来源:《教育教学论坛》2016年第28期摘要:伯努利方程是流体力学的重要理论基础,它为我们计算工程数据及解释日常生活中的一些现象,如管道总水头的计算、香蕉球的形成原理等,提供了重要的理论依据。
关键词:伯努利方程;流体力学;研究中图分类号:G642 文献标志码:A 文章编号:1674-9324(2016)28-0207-02作为力学的一个重要分支,流体力学以流体为主要研究对象,是研究流体平衡和运动规律的科学。
流体力学在许多工业科技中有着广泛的应用。
水利工程的建设、造船工业的迅速发展都离不开水静力学和水动力学的建立和研究,航空事业则离不开气体动力学的深入发展。
一、伯努利方程的推导伯努利方程只能应用于一条流线上的不同点,且必须是不可压缩理想流体在重力场中做定常流动。
二、伯努利方程的应用(一)当流体为液体时,伯努利方程的应用(二)当流体为气体时,伯努利方程的应用能量方程④的适用条件是:流动绝热但并不要求等熵,流动可以有摩擦。
即使通过强间断面,能量方程仍然使用。
伯努利方程⑤的适用条件是:无黏性,因而无机械能损失,流动过程有无热量的输入都不影响它的应用。
只有在等熵的流动中④和⑤才能相等[3]。
三、结语在生活中的很多方面都有伯努利方程的应用,工程中有很多这样的例子,如矿山通风机工况点确定[4]、都江堰修建等,都需要很多关于流体的计算来保证工程的安全,伯努利方程就在其中起了很大的作用。
参考文献:[1]孔珑.工程流体力学[M].第三版.中国电力出版社,2007.[2]刘仁隆.故事物理学[M].科学出版社,1980:52-58.[3]刘大有.伯努利方程应用中的若干问题[J].力学与实践,1991,(4).[4]赵昌友.伯努利方程及应用[J].池州学院学报,2014,28(6):。
流体力学 伯努力方程
测流速原理该点在水面下的深度为d故该处的压强pgdb点在管口之前流速v根据伯努利方程所以在实际应用时上式须修正为其中c为比多管的修正系数由实验来确定
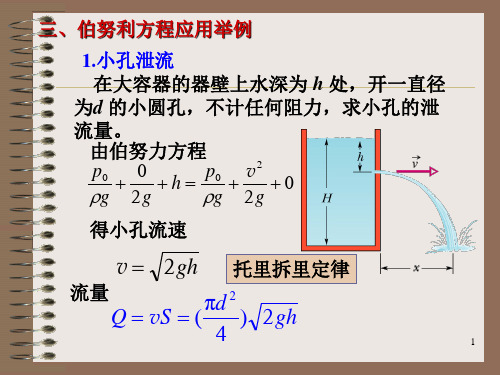
三、伯努利方程应用举例 1.小孔泄流 在大容器的器壁上水深为 h 处,开一直径 为d 的小圆孔,不计任何阻力,求小孔的泄 流量。 由伯努力方程 p0 p0 v 2 0 h 0 g 2 g g 2 g
h1
B
C A
pC p0 gh1
h2
其中p0为大气压
11
(2)当虹吸管下端开启时, h1 下端和A处的压强仍为:
p下 端 p0 , pA p0
B
C A
h2
而vB vc v下端 , v A 0 . 所以 pB p0 g( h2 h1 ) , pC p0 gh2
(2)取1-2-4的一个流线,由伯努利方程
P1 1 2 1 1 v1 P2 v 2 P4 v2 2 4 2 2 2 P4 P0
1 2 2 P1 P0 v 4 v1 P0 100, P1 -P0 100Pa 2 1 2 2 P2 P0 v 4 v 2 P0 , 2 P3 =P0 P2 P0 0 P3 P0 0
Qv v1S1 v2 S2
2( 汞 )g hS1 S 2
2 2
( S1 S 2 )
2 2
6
H
1 1 2 2 p1 v1 p2 v2 2 2
v1S1 v2 S2
v1 主管 细管 v2
p p1 p2 gh
•
Q v1S1 S1S2
例题2 在如图所示的虹吸管装置中,已 知 h1 和 h2 ,试问:(1)当截面均匀的虹吸管 下端被塞住时,A、B和C处的压强各为多大? (2)当虹吸管下端开启时,A、B和C处的压 强又各为多大? 这时水流出虹吸管的速率为 多大?
§1-2伯努利方程及其应用

§1-2伯努利方程及其应用
例1.3 如图1—5所示,液槽内离开液面h处开一小孔。液体密度为ρ, 液面上方是空气,它被液槽盖封闭住,其绝对压强为p,在液槽侧面小 孔处的压强为大气压强p0。当p>>p0时,试证明小孔处的液流速度 为: v2 = 2( p − p0 ) / ρ
解:将整个流体当作一个流管,用 v1和v分别表示水面处和 2 孔口处的流速。由连续性方程知 v 2 且因为S1>>S2,故 v 2 >> v1 可以近似地取 v1 = 0
第一章 流体的运动
§1-2伯努利方程及其应用
大 学 物 理
主讲教师:杨宏伟
第一章 流体的运动
§1-2伯努利方程及其应用
一 、 伯努利方程 伯努利方程是由瑞士物理学家伯努利 (D.Bernoulli)提出来的,是理想流体 作稳定流动时的基本方程,对于确定流 体内部各处的压力和流速都有很大的实 际意义,在水利、造船、航空航天等部门 有着广泛的应用。
第一章 流体的运动
§1-2伯努利方程及其应用
例1.2水管里的水在压强P=4×105Pa的作用下流入房 间,水管内直径为2.0cm,管内水的流速为4m/s。引入 到5m高处二层楼浴室的水管,内直径为1.0cm,试求浴 室内水的流速和压强(已知水的密度ρ=1000kg/m3)。 解:由连续性原理知
2
S1v1 = S 2 v2
A
B
将整个管子作流管,由连续性方 程 S1v1 = S 2 v2 以及伯努利方程 (1-5) 2
C
D E
p + 0.5 ρv = 恒量
图1—6 空吸作用 图1—6 空吸作用
第一章 流体的运动 由于 S1 >> S 2
伯努利方程的应用实际液体的流动 (1)

8.3 8.8 13
影响液体和气体流动性的因素是不同的。
在国际单位制中黏度的单位是Pas (帕秒)。黏度也 常用P (泊)作单位
1 P = 0.1 Pa s
17
二、 黏性流体的运动规律
p1
1 2
2 v1
gh1 p2
1 2
2 v2
gh2 w
黏性流体作稳定流动时所遵从的规律。 如果黏性流体沿着粗细均匀的管道作定常流动
vr Re
21
由层流过渡到湍流的雷诺数,称为临界雷诺数 Rec 。圆形管道的临界雷诺数Rec在1000 ~ 1500的 范围内。 当流速的值使雷诺数Re处于临界值Rec时,此时 的流速就是临界流速,大小为
Rec vc r
如果流速从低于vc增大到高于vc,那么流动将 会从层流转变为湍流。
黏性流体在水平放置的圆形截面的管道中作层流时, 算得流量 为
p1 p2 4 QV ( )r 8 l
l 和 r 分别是管道的长度和半径。上式称为泊肃叶定律。
流阻 如果令 R f 8l ,那么上式可写成: 4
R
P P 1P 2 Q Rf Rf
20
*四、湍流和雷诺数 (Turbulent flow ) 湍流 流体中沿垂直于管轴方向的速度分量的 不规则流动。 实验表明,发生湍流的临界流速与雷诺数 Re 相对应。 雷诺数
若流体密度为,小球密度为,半径为r,速率为 v,则小球所受的三个力平衡,即 23
4 3 4 3 r g 6 r v r g 3 3
由此可得小球下落的速率
2r v ( ) g 9
假如测出速率v,可求出液体的黏度 ; 若流体的 黏度已知, v已测出,可求得小球(或液滴)的半径。
伯努利方程在液压系统中的应用

伯努利方程在液压系统中的应用
伯努利方程是描述流体在流动过程中能量守恒的基本方程之一,它在液压系统中有着广泛的应用。
液压系统中的液体流动可以被看作是一种能量转换的过程,而伯努利方程可以用来描述这种能量转换的过程。
在液压系统中,我们经常需要计算液体的流速、压力、流量等参数。
这些参数的计算需要用到伯努利方程。
伯努利方程可以描述液体在流动过程中,压力、速度和高度之间的关系。
具体地说,伯努利方程可以表示为:
P1 + ρgh1 + 1/2ρv1^2 = P2 + ρgh2 + 1/2ρv2^2 其中,P1、P2分别为管道两端的压力,ρ为液体的密度,g为重力加速度,h1、h2分别为两端的高度,v1、v2分别为两端的速度。
这个方程表明,当液体从一段管道流向另一段管道时,压力、速度和高度之间的变化是相互关联的。
伯努利方程在液压系统中的应用十分广泛。
例如,在液压缸的设计中,我们需要计算液体的流速和压力,以保证液压缸的运动正常。
在液体泵的设计中,我们需要计算液体的流量和压力,以保证泵的输出满足要求。
在水力发电厂的设计中,我们需要计算水流的速度和压力,以求得最大的发电效率。
总之,伯努利方程在液压系统中的应用非常广泛,它可以用来计算液体的各种参数,从而帮助我们设计出更加高效、可靠的液压系统。
- 1 -。
实际流体总流的伯努利方程式

实际流体总流的伯努利方程式在流体力学的世界里,伯努利方程可谓是个“大咖”。
想象一下,咱们在河边,看着水流淌,水流的快慢、流向,都是由这位“伯努利”爷爷来掌控的。
没错,流体的流动其实很有意思,像一场精心编排的舞蹈,每一个动作都有它的道理。
想要理解这些道理,咱们不妨轻松聊聊这方程的实际应用。
你知道的,科学可不一定是枯燥的,相反,它常常让生活充满惊喜。
你可千万别小看这方程,它告诉我们流体在不同地方的压强、速度和高度之间的关系。
比如说,你在河里放了一根小木棒,水流一冲,木棒就开始随水漂流。
这个时候,水的速度快慢就会直接影响木棒的漂浮状态。
就像人生,有时候水流缓慢,让你悠哉游哉;有时候水流汹涌,让你不得不拼命抓住木棒。
伯努利方程就像一位智者,告诉我们在不同情况下该怎么应对。
有趣的是,咱们喝的饮料也与伯努利方程有千丝万缕的联系。
想想当你用吸管喝饮料,吸管里的液体就像是个小小的流体,它的流动是因为你在吸的时候创造了一个低压区。
这一低压区就把饮料“吸”了上来,这背后也有伯努利的影子在默默地起作用。
这真是个神奇的现象!感觉就像是魔法一样,只不过这魔法有科学依据而已。
咱们在开车的时候,风阻也是伯努利方程的一个应用。
车速越快,车身周围的空气流动就越快,压强就会降低。
这就是为什么运动型车的设计常常像流线型一样,减少空气阻力,帮你飞速前行。
想象一下,你坐在车里,耳边呼啸而过的风声,那感觉简直爽翻了。
开车不仅是为了到达目的地,还是一场与空气的对决,谁都想在这场对决中占据上风。
再说说飞行,飞机的翅膀可真是聪明得很。
飞机在飞行时,翅膀上方的空气流动速度更快,压力更低,下面的压力较高,这就让飞机飞得又高又稳。
简直是个完美的例子,展示了伯努利方程的魅力。
飞机一旦起飞,真像一只鸟儿,翱翔在蔚蓝的天空中,心情自然美滋滋。
水管里的水流也是伯努利方程的典型案例。
水管不同的直径会影响水流的速度和压力。
当水流过一个变窄的地方,速度自然会加快,压力就会降低。
流体力学-总流伯努利方程的应用

四、一般的水力计算
一、一般的水力计算
A
0
泵
C B
0.2m 3.0m
0
Eg 1. 如图所示消防水龙,泵出口压力为2个大气压(表压), dA为50mm,dC为20mm,水龙带水头损失为0.5m,喷嘴水头 损失为0.1m,求Vc,Q,Pb?,
A
0
泵
C B
0.2m 3.0m
0
令α 为孔板流量系数,实际流量为:
d 2 Q
2g p1 p2
4
注: α在出厂前需要对其依赖的参数进行试验测 定, 并对用户给出图表。
(3)喷嘴流量计
0
Q
D
2 2
2g p1 p2
4
注: μ 为喷嘴流量计的流量系数。
二、毕托管测速
1 滞止现象
滞止现象:绕流流过物体表面时,会在流体正前方和固体 壁面的接触位置形成一个速度等于零的点。该点称为滞止 点,该点的压强称为滞止压强。
道截面面积A1与喷嘴出口截面面积A2之间应满足什么条件才能使 抽水装置开始工作?
1
1
2
2
3 3
思考题:
1.拿两张薄纸,平行提在手中,当用嘴顺纸间缝隙 吹气时,问薄纸是不动、靠拢、还是张开?为什么?
2.水流在等径斜管中流动,高处为A点,低处为B点, 讨论压强出现以下二种情况时的流动方向。 pA>pB; pA=pB A
3 毕托管测速
静压测量
△h 1A
驻压测量 单孔测速
流线上任一点速度为:
u1
2g pA p1
注:1、过程中忽略了阻力; 2、测速时安装的准确性;
实际流体速度:
实际液体的伯努利方程

实际液体的伯努利方程
实际液体在管道内流动时,因液体黏性会使液体与固体壁面间
及液体与液体间产生摩擦力而损耗能量,管道形状和尺寸的变化会对液流产生扰动而消耗能量,所以实际液体流动时存在能量损失。
根据能量守恒定律, 在考虑能量损失, 并引进动能修正因数后, 实际液体的伯努利方程为z1+p1 ρg +α1v2 1 2g =z2+ρpg2+α22vg2 2+hw 其中, hw为单位质量液体在管路两截面之间流动的能量损失; α为动能修正系数, α的数值与管路中液体的流态有关, 液体在圆管中层流时α=2, 紊流时α≈1.05, 实际计算时常取α=1。
流体力学-04-2 伯努利方程的应用.

伯努利方程的应用伯努利方程对于流动体系除了掌握体系的对于流动体系,除了掌握体系的物料衡算关系以外,还必须找出体系各种形式能量之间的转换关系系各种形式能量之间的转换关系。
伯努利(Bernoulli)方程:描述了流体流动过程中各种形式能量之间的转换关系,是流体在定常流动情。
是热力学第一Daniel Bernoulli ,1700-1782况下的能量衡算式是热力学第定律对流体流动过程的具体描述。
流动系统的能量流动系统的能量:流动系统的能量流动系统的能量:(3) 动能:流体以一定的速度运动时便具有一定的动能,大时所需要的功小等于流体从静止加速到流速v时所需要的功。
(4) 静压能:流体进入划定体积时需要对抗压力所做的功。
流体进入划定体积时需要对抗压力所做的功若质量为m的流体体积为,某截面处的静压强为p,截面面积为A,则将质量为m的流体压入划定体积的功为:则将质量为的流体压入划定体积的功为质量为能量还可以通过其他外界条件与流动系统进行交换,包括::流体通过换热器吸热或放热Q e吸热时为正,放热时为负。
:泵等流体输送机械向系统做功W em 的流体交换热量=m Q e流体接受外功为正流体对外作功为负作功为负的流体所接受的功= mW e以截面两边同除以m单位质量流体稳定流动过程的总能量衡算式,流动系统的力学第一定律表达式系统内能变化系统内能变化:是单位质量流体从截面1-1到截面是单位质量流体从截面1-1到截面2-2流体通过环境直接获得的热量,Q e(1)流体通过环境直接获得的热量流体流动时需克服阻力做功,因而消耗机械能转化为热量,若流体等温流动,这部分热量则散失到系统外部。
设单位流体因克服阻力而损失的,则则不可压缩流体ρ=const=0无外加功W e=0理想流体,Σhf伯努力方程努力方程的有关伯努力方程的讨论(1)伯努力方程的适用条件:不可压缩的理想流体做定常流动而无外功输入的情况,选取截面符合缓变流条件。
单位质量流体在任一截面上所具有的势能、动能和静压能之和是一常数。
大学物理伯努利方程及其应用

即流体从小孔流出的速度与流体质量元由液面处自由下落到小孔处的流
速大小相等。
虹吸管
左图是利用虹吸管从水库引水的示意图。
B A
hA
hB
虹吸管粗细均匀,选取 A、C 作为参考点。
水库表面远大于虹吸管截面,由连续性原理可
C
知
hc
v A,所0 以此例实质为小孔流速问题
v 2g(hA hC )
如果hA-hB<0 ,管内流速没有意义。如果管口比水库面高,在没有外界帮
选d 点所在平面为参考平面,对a 、d 两
h1 ab
h2
点应用伯努力方程,有
d
g (h2
h1 )
1 2
vd2
解得
vd 2gh2 h1
因b、c、d 各点处于截面积相同的同一流管中,所以
由连续性原理,有:
对于a、b 两点,有 对于a、c 两点,有
得:
vb vc vd 2gh2 h1
pb p0
S2
A2 F2v2t P2S2v2t P2V Δt
P1
h2
由功能原理 : A Ek E p 即
S1
h1
( P1
PP12)12Vv1212(vg22h1
v12 )V
P2
1 2
g(h2 h1)V
v22 gh2
或 P 1 v 2 gh C
2
上式即为伯努利方程的数学表达式。
二、伯努利方程的意义
求 (1)管2、3、4的流量; (2)管2、3、4的流速; (3)管1、4中的压强差.
2
v2
1
v1
4
v4
3
v3
解 (1)由连续性原理知 Q4= Q1 = 900cm3•s-1
流体稳定流动伯努利方程

p2 v2
•
p1 v1 2
•
1
h2
h1
第8页/共15页
伯努利方程的推导
如图所示,在作定常流动的理想 流体中任取一根流管,用截面隔 出一段流体。在时间间隔Δt内, 左端的S1从位置a1移到b1,右端的 S2从位置a2移到b2。
令
分别是在同一时间间隔内 流入和流出的流体体积
对于不可压缩流 体的定常流动
A1 F1l1 p1S1l1 p1V
右端的压强为p2,作用在S2上的力F2=p2S2, 外力作功为
A2 -F2l2 p2S2l2 p2V 故 A外=A1+A2=(p1- p2) △V
第10页/共15页
由功能原理
(p1- p2) △V
因1、2是同一流管内的任意两点,所以上式也可表达为沿同一流线
p 1 v2 gh 常量 (伯努利方程)
2
对于伯努利方程,应注意以下几点: 1、方程在惯性系中成立; 2、只有对同一条细流管(或同一条流 线)上的各点才有方程所表明的关系; 3、对于不同的细流管或流线,方程的常量具有不同的值。 4.把伯努利方程运用于水平流管,或在气体中高度差效
应不显著的情况,则有 p 1 v2 常量, 即高速则低压。
一般在我们研究的问题中,压缩性和粘滞性是影响流体运动 的次要因素,只有流动性才是决定运动的主要因素。为了突出 流体的这一主要特征,我们引入理想流体这一模型:
完全不可压缩又无粘性的流体叫做理想流体。
又称“干水”
本章基本上只讨论理想流体,第1将页/共其15看页成流体微团的连续分布。
根据平衡条件有:
y
水平方向: pxyl pnsl cos 0
第4页/共15页
二、定常流动
伯努利方程的几种形式的应用

伯努利方程的几种形式的应用
1.流体在管道中的应用:伯努利方程可以用于研究管道流动中的压力
变化。
在理想情况下,管道中的液体或气体流动时,其速度增加,而压力
降低。
通过伯努利方程,可以计算出不同位置的压力以及液体或气体通过
管道的流量。
2.飞机飞行的应用:伯努利方程适用于研究飞机的气动原理。
当飞机
飞行时,空气在飞机的机翼上面流动速度增加,而在下面流动速度减低,
根据伯努利方程,飞机上下表面的压强就会产生差异,从而产生升力和重
力之间的平衡。
3.喷射器和涡轮机的应用:伯努利方程可以用于分析流体在喷射器和
涡轮机中的运动。
喷射器中的高速流体喷出,通过伯努利方程可以计算出
流体的速度和压力。
涡轮机则是利用流体的速度对转子产生动力,通过伯
努利方程可以计算出转子的输出功率。
4.水平管道的应用:伯努利方程可以用于研究水平管道中的流动情况。
在水平管道中,流体的速度减慢,而压力增加。
根据伯努利方程,可以计
算出不同位置的压力和流体的速度。
5.车辆行驶的应用:伯努利方程适用于研究车辆行驶时的空气动力学
原理。
当车辆高速行驶时,车辆前部的气流速度增加,而车辆后部的气流
速度减低,根据伯努利方程,车辆前后部的压强就会产生差异,从而产生
阻力和驱动力之间的平衡。
以上仅是伯努利方程几种形式的应用的一些例子,实际上伯努利方程
在流体力学和流体工程学的应用非常广泛。
它是研究流体力学问题的基础
方程之一,通过对伯努利方程的研究和应用,可以更好地理解和解决与流体力学相关的问题。
化工原理伯努利方程的应用

化工原理伯努利方程的应用1. 介绍伯努利方程是流体力学中常用的一个基本方程,描述了流体在不同位置的能量变化。
在化工工程中,伯努利方程被广泛应用于气体和液体的流动分析和设计。
2. 伯努利方程的表达式伯努利方程可以表示为:P + 1/2 * ρ * V^2 + ρ * g * h = 常数其中,P为流体的压力,ρ为流体的密度,V为流体的速度,g为重力加速度,h为流体的高度。
3. 化工原理中的应用伯努利方程在化工原理中有许多实际应用,以下列举了一些常见的应用场景。
3.1 流体管道的设计在化工工程中,流体管道是常见的输送介质的设备之一。
通过伯努利方程,可以分析流体在管道中的压力变化以及流速变化,从而进行管道的设计与优化。
•首先,可以根据伯努利方程计算出流体在管道中的流速,通过调整管道的直径、长度等参数,以达到需要的流速。
•其次,可以通过伯努利方程计算出在不同位置的压力变化,从而确定管道中是否需要设置减压阀、安全阀等装置。
3.2 气体喷射在化工过程中,喷射装置常常被用于混合、吹扫、喷洒等操作。
伯努利方程可以帮助我们理解喷射装置的工作原理。
•伯努利方程可以用来计算气体在喷嘴中速度的变化,从而确定喷射装置的喷射性能。
•通过分析伯努利方程,可以确定喷射装置中压力和流速的关系,从而调整喷射装置的工作参数,以达到需要的效果。
3.3 阀门的选择和调节在化工过程中,阀门是常见的流体控制设备。
通过伯努利方程,可以对阀门进行选择和调节。
•通过伯努利方程,可以计算出阀门两侧的压力变化,从而选择合适的阀门类型和规格。
•伯努利方程可以帮助分析阀门调节时的流体流速变化,从而确定阀门的调节参数。
4. 结论伯努利方程的应用在化工原理中具有重要的意义。
通过伯努利方程,可以对流体的压力、速度和高度进行分析和计算,从而实现流体管道的设计、喷射装置的优化以及阀门的选择和调节。
伯努利方程的应用可以帮助化工工程师更好地理解和解决实际问题,提高工艺流程的效率和安全性。
伯努利及伯努利方程的应用

伯努利及伯努利方程的应用
伯努利(Bernoulli)方程式是描述液体压强与流速之间关系的一种力学方程式。
它对液体流速、压力和液体密度有影响,但是它是最常用于描述水流动的,在一维流动中最为广泛。
它式由荷兰科学家Daniel Bernoulli(1700年-1782年)在17$年发明的。
伯努利方程的可用形式如下:$\frac{1}{2}\rho v^{2}+\rho gh+\rho \frac{P}{\gamma}=c$
其中,ρ表示液体的密度,v表示流速,g表示重力加速度,$h$表示液体表面相对于管底部的高度,P表示液体内的压力,C是常数。
伯努利方程应用比较多,尤其是水力学领域,如:水力机械工程与水资源开发;计算控制渗流情况;研究室内水位差以及流量;识别河流洪涝形势;快速液力学的研究等。
伯努利方程在流体力学中的最重要的应用是管道或缸室内水流的流速分析,管道或缸室内水压在管道或缸室不同位置的变化,也可以使用伯努利方程来计算,因此它的应用非常普遍。
此外,它也可以用于描述流体流动的其他性质,包括温度、其他物质的浓度、气勤之类。
伯努利方程表明,流体在场内以一种连续黑塞流动,同时记录了液体的能量平衡,表明机械能量和势能之间的转换,在水力学及流体力学交叉研究等领域发挥着至关重要作用。
伯努利方程原理以及在实际生活中的运用

伯努利方程原理以及在实际生活中的运用2011444367 陈高威在我们传输原理学习当中有很多我们实际生活中运用到的原理,其中伯努利方程是一个比较重要的方程。
在我们实际生活中有着非常重要广泛的作用,下面就伯努利方程的原理以及其运用进行讨论下。
伯努利方程p+ρgh+(1/2)*ρv ²=c 式中p、ρ、v分别为流体的压强,密度和速度;h为铅垂高度;g为重力加速度;c为常量。
它实际上流体运动中的功能关系式,即单位体积流体的机械能的增量等于压力差说做的功。
伯努利方程的常量,对于不同的流管,其值不一定相同。
相关应用(1)等高流管中的流速与压强的关系根据伯努利方程在水平流管中有p+(1/2)*ρv ²=常量故流速v大的地方压强p就小,反之流速小的地方压强大。
在粗细不均匀的水平流管中,根据连续性方程,管细处流速大,所以管细处压强小,管粗处压强大,从动力学角度分析,当流体沿水平管道运动时,其从管粗处流向管细处将加速,使质元加速的作用力来源于压力差。
下面就是一些实例伯努利方程揭示流体在重力场中流动时的能量守恒。
由伯努利方程可以看出,流速高处压力低,流速低处压力高。
三、伯努利方程的应用:1.飞机为什么能够飞上天?因为机翼受到向上的升力。
飞机飞行时机翼周围空气的流线分布是指机翼横截面的形状上下不对称,机翼上方的流线密,流速大,下方的流线疏,流速小。
由伯努利方程可知,机翼上方的压强小,下方的压强大。
这样就产生了作用在机翼上的方向的升力。
2.喷雾器是利用流速大、压强小的原理制成的。
让空气从小孔迅速流出,小孔附近的压强小,容器里液面上的空气压强大,液体就沿小孔下边的细管升上来,从细管的上口流出后,空气流的冲击,被喷成雾状。
3.汽油发动机的汽化器,与喷雾器的原理相同。
汽化器是向汽缸里供给燃料与空气的混合物的装置,构造原理是指当汽缸里的活塞做吸气冲程时,空气被吸入管内,在流经管的狭窄部分时流速大,压强小,汽油就从安装在狭窄部分的喷嘴流出,被喷成雾状,形成油气混合物进入汽缸。
伯努利方程原理及其应用

伯努利方程原理及其应用伯努利方程原理是流体力学中的一个重要定理,描述了流体在不同位置的压力、速度和高度之间的关系。
它是基于质量守恒和动量守恒定律得出的。
伯努利方程的应用非常广泛,涉及许多领域,如水力工程、航空航天工程、血液循环等。
P + 1/2ρv² + ρgh = 可以称之为 Bernoulli's Principle 分成三个代表量就是 (pressure), (velocity) and (height)其中,P代表流体的压力,ρ代表流体的密度,v代表流体的流速,g代表重力加速度,h代表流体的高度。
这个方程的意义是,当流体在稳定非粘性的情况下沿着流线流动时,流体在不同位置上的压力、速度和高度之间是相互关联的。
1.水力工程:伯努利方程可以用来研究液体在管道流动中的压力和速度变化。
在水力工程中,通过伯努利方程可以计算水管中的液体流速、压力等参数,从而确定水力机械设备的设计和运行参数。
2.航空航天工程:伯努利方程可以用来研究气体在飞行器周围的流动。
当气体流动速度增加时,伯努利方程能够说明气体的压力减小。
这一原理被应用在飞机的翼型设计中,通过加速飞行器周围的气流,可以产生升力,从而使飞机升起。
3.血液循环:伯努利方程可以用来研究血液在血管中的流动。
血液在动脉和静脉中的流速和压力变化可以通过伯努利方程来描述。
在生理学中,伯努利方程被用来分析血管疾病的发生机制,如动脉瘤、血栓形成等。
4.分离气体传输:伯努利方程在管道气体输送过程中也有重要应用。
通过伯努利方程可以计算气体在管道中的流速和压力变化,从而确定管道的设计和运行参数。
此外,伯努利方程还可以应用于喷射器、超声波仪器、气象学中的风场分析等领域。
总的来说,伯努利方程通过描述流体在不同位置的压力、速度和高度之间的关系,为流体力学的研究和应用提供了基础。
通过对伯努利方程进行分析和应用,可以更好地理解和预测流体力学现象的发生和发展。
通过实际应用浅谈流体力学中的伯努利方程

通过实际应用浅谈流体力学中的伯努利方
程
一、伯努利方程生活中最常见的一个应用是飞机的起飞。
飞机的整体设计中,发动机是为了给飞机提供向前行驶的动力,但是飞机向上的上升力还是需要对机翼的特殊设计来实现。
飞机的飞行过程中会遇到空气的阻力,飞机双翼的特殊设计让机翼两侧存在压强差,给飞机提供了向上的力量,这才使飞机真正飞起来。
虽然飞机飞行时的空气阻力起到了很大作用,但是实际上当飞机速度达到一定程度时,就可以忽略空气阻力而飞行。
二、足球中的“香蕉球”。
足球赛场上经常能见到这情况,前场球员被罚球。
足球迅速飞出去的同时,自身也因为受力不均而高速旋转,足球的转动带动周围的空气形成气流,分布在球的四周。
因为旋转的球一侧空气流动快而另一侧流动慢,所以两侧的力相互抵消形成了一个力的作用,让足球方向发生变化,最终射进球门。
这个力垂直于足球的运动方向,被称为马格努斯力。
如果足球向某一侧旋转,球的摩擦力就会出现上下的差异,这个差异最终会使得足球下方的摩擦速度增大,减缓足球下落。
并且最终让足球的运动表现为一个弧形,绕过并排站立的人。
这就是“香蕉球”的由来和原理。
三、随处可见的喷雾器。
背负式的喷雾器在液体从药箱
中喷出的时候,会首先通过一处狭窄,使液体的压强增大,当液体继续通过一段上升的竖直管时,因为液体上下压强的差异,液体会上升。
并最终在上方的喷射口高速(出液口狭窄,流速较大)喷射出去,空气中存在一些气流与喷射出的液体相互垂直,会在液体喷射出的同时把液体吹剪成一个一个的小雾滴,直径甚至只有100 μm左右。
其他喷雾器原理也大多是这样,都是伯努利方程的运用。
伯努利方程的应用概述

伯努利方程的应用概述伯努利方程是流体力学中十分重要的方程之一,它描述了在不可压缩和不黏滞的流体中,沿着流线,流速增加时压力减小的现象。
这个方程被广泛应用于各种领域,包括流体力学、空气动力学、水力学、航空航天工程等。
本文将对伯努利方程的应用进行概述。
一、流体力学中的应用:1.流体力学实验:伯努利方程可以用来解释在流体力学实验中观察到的现象。
例如,在喷气装置中,当液体从小孔中喷射出来时,其速度增加,压力减小,这可以通过伯努利方程解释。
2.水力学:伯努利方程在研究液体流动、水流以及水力工程中具有广泛的应用。
例如,在水力发电站中,伯努利方程可以用来计算水流速度、水压力以及能量转换等。
3.管道流动:在管道中的流体流动中,伯努利方程可以用来分析不同位置的压力变化。
例如,在一个升压站或者消防设备中,伯努利方程可以用来计算流体的流速、压力以及流量等。
4.飞行器的气动性能:伯努利方程在航空航天工程中的应用是非常重要的。
例如,它可以用来计算飞机机翼产生的升力以及飞机的飞行性能。
二、空气动力学中的应用:1.喷气发动机:伯努利方程在喷气发动机中的应用是十分重要的。
当高速气流通过喷射嘴时,嘴内速度增加,压力降低,通过伯努利方程可以计算出发动机喷气的动力和效率。
2.空气动力学实验:伯努利方程也可以用来解释空气动力学实验中的现象。
例如,在风洞实验中,通过空气通过不同形状的模型,可以通过伯努利方程计算流体的流速、压力以及飞机的气动性能。
三、航空航天工程中的应用:1.飞行器气动性能分析:伯努利方程可以用来分析飞行器在不同飞行状态下的气动性能,例如飞机的升力、阻力等。
通过伯努利方程,可以对飞行器的设计和改进提供重要的参数和数据支持。
2.火箭发动机推力计算:伯努利方程在火箭发动机的设计和性能分析中也具有重要的应用。
通过伯努利方程,可以计算火箭喷射气流的速度、压力以及推力等。
综上所述,伯努利方程在流体力学、空气动力学以及航空航天工程中的应用是广泛而重要的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
v B 2 gh
可见, 小孔处水的流速,与物体从h处自由 下落到小孔处的速率是相同的。
10
3.粘滞流体在半径为R的水平流管中流动,流量为 Q,如在半径为R/4的水平流管中流动,其流 量为_____________。 4. 如图所示,在大水桶侧面开一小孔,要使流出液体 的射程L最大,其孔的高度h应开在______处。
6
解:在A 处气流速率为零, 在流线OA上运用伯努 利方程, 得到
p A gh A pO ghO
对于流线QB
1
2
vO
2
p B ghB
1 2
v B pQ ghQ
2
1 2
vQ
2
点O和点Q非常接近, 可认为各量相等。又因皮托 管一般都很细, 点A与点B的高度相差很小, hA = hB 。 考虑到这些条件, 得
y
一般情况下, 速率梯度的大小不是常量, z0 处速 率梯度的大小为 dv ( ) z0 dz 实验表明, 流体内部相邻两流体层间黏力的大小 正比于接触面积, 正比于该处速率梯度的大小,即
f 的方向如图中的箭头。 比例系数称为流体的黏 z0 度, 是流体黏性的量度, o 与温度有密切关系。
dv f ( ) z0 S dz
22
*五、斯托克斯黏性公式 (Stokes’ viscosity resistance formula )
当固体物在黏性流体中作相对运动时,将受到流 体的阻力作用。
斯托克斯黏性公式 固体小球以不大的速率在流 体中运动时,所受黏性阻力大小为
F = 6rv
流体黏度,r小球半径,v小球相对流体运动速率。
若流体密度为,小球密度为,半径为r,速率为 v,则小球所受的三个力平衡,即 23
4 3 4 3 r g 6 r v r g 3 3
由此可得小球下落的速率
2r v ( ) g 9
假如测出速率v,可求出液体的黏度 ; 若流体的 黏度已知, v已测出,可求得小球(或液滴)的半径。
1
3. 流线 为了形象地描述流体的 运动 , 在流体中画一系列 曲线 , 每一点的切线方向 与流经该点流体质点的速 度方向相同,称为流线。 定常流动中的流线 · 不随时间变化; · 质点的运动轨迹; · 任何两条流线不相交。 4. 流管 流线围成的管状区域。
· · · ·
· · · ·
2
理想流体的连续性方程 (the equation of continuity )
/ (10-3
Pas)
1.792 1.0050 0.6560 0.4688 0.3565 0.2838
16
表 3
气 体
几种气体的黏度随温度的变化
空 气 0 20 671 18 18.1 42 二氧化碳 0 20 302 14 14.8 27 氢 气
温 度 /℃
-1
20 251
/ (10-6 Pas)
8.3 8.8 13
影响液体和气体流动性的因素是不同的。
在国际单位制中黏度的单位是Pas (帕秒)。黏度也 常用P (泊)作单位
1 P = 0.1 Pa s
17
二、 黏性流体的运动规律
p1
1 2
2 v1
gh1 p2
1 2
2 v2
gh2 w
黏性流体作稳定流动时所遵从的规律。 如果黏性流体沿着粗细均匀的管道作定常流动
关于理想流体的几个概念 (perfect fluid ) 1. 理想流体
理想流体 绝对不可压缩和完全没有黏性的流体。
2. 定常流动 一般情况下,同一时刻流体各处的流速不同,但有 些场合 , 流体质点流经空间任一给定点的速度是确 定的,且不随时间变化,称为定常流动。例如, 沿 着管道或渠道缓慢流动的水流, 在一段不长的时间 内可以认为是定常流动。
A
B
C
pA
1 2
v A gh A p B v B ghB
2
9
2
1
2
其中水面上点A和孔口处点B都与大气接触, 所以 那里的压强都等于大气压p0 。
取小孔处的高度为零,则 hA = h。容器的横截面 比小孔的截面大得多, 根据连续性方程, vA << vB ,故 认为vA = 0。将以上条件代入上式, 即可求得小孔处 的流速为
vr Re
21
由层流过渡到湍流的雷诺数,称为临界雷诺数 Rec 。圆形管道的临界雷诺数Rec在1000 ~ 1500的 范围内。 当流速的值使雷诺数Re处于临界值Rec时,此时 的流速就是临界流速,大小为
Rec vc r
如果流速从低于vc增大到高于vc,那么流动将 会从层流转变为湍流。
黏性流体在水平放置的圆形截面的管道中作层流时, 算得流量 为
p1 p2 4 QV ( )r 8 l
l 和 r 分别是管道的长度和半径。上式称为泊肃叶定律。
流阻 如果令 R f 8l ,那么上式可写成: 4
R
P P 1P 2 Q Rf Rf
20
*四、湍流和雷诺数 (Turbulent flow ) 湍流 流体中沿垂直于管轴方向的速度分量的 不规则流动。 实验表明,发生湍流的临界流速与雷诺数 Re 相对应。 雷诺数
对于不可压缩流体
v2
S2
S1 v1= S2 v2 或
S v = 恒量
v1
S1
上式称为理想流体的连续性方程。 在方程两边同乘以流体密度, 即
S v = 恒量
上式是一般流体的连续性方程。
3
伯努利(Bernoulli)方程
1 2 1 2 p1 v1 gh1 p2 v 2 gh2 2 2
p A pB
vB 是待测气流的流速。
1
2
vB
2
7
如果压强计中液体的密度为 , 则
p A p B gh
比较上面两式得
1 2
所以
v B gh
2 gh
2
vB
这样,就可以由压强计两液面的高度差h, 计算 出待测气流速率。
8
例2:求水从容器壁小孔中流出时的速率。 解:水从小孔中流出时的流速可 以根据伯努利方程求解。设水面距 离小孔的高度为h,ABC为一条流 线(见图)。A和B分别是这条流线在 水面和小孔处的两点, 在这条流线 上运用伯努利方程, 得
24
2
25
p1 gh1 p2 gh2 w
或
( p1 p2 ) g (h1 h2 ) w
18
可见,由于黏力的存在, 要流体在管道中作定常 流动,须保证管道两端的压强差 (p1p2) 或保证管道 两端的高度差 (h1h2) 或者两者兼而有之。
19
*三、泊肃叶定律 (Poiseuille’s law )z f源自 fy15
表 1 流 体
酒精 甘油 水银 氧 氮 氦 表2 温 度/℃
几种流体的黏度 黏 度 / (10-3 Pas)
16 830 1.55 0.0196 0.0177 0.0196
温 度/℃
20 20 20 15 23 23
水的黏度随温度的变化 0 100 20 40 60 80
p A v A gh A 2 1
2
pB
1 2
v B ghB
5
2
练 习
题
B 例1:皮托管是测定流体流 Q A 速的仪器, 常用来测定气体的 流速。 它由两个同轴细管组 o 成, 内管的开口在正前方。外 h 管的开口在管壁上, 如图中B 所示。两管分别与U型管的两 臂相连, 在U型管中盛有液体(如水银), 构成了一个压 强计, 由U型管两臂的液面高度差h确定气体的流速。
S2
v2
S′ 2
1 p v 2 gh 恒量 2
S1
v1 ′ S1 h1 h2
上面两式都称为伯努利方程, 它们描述了理想流 体作定常流动时的基本规律。
4
例1、有流量为0.12m3/s的水流过如图所示的管子。A点 的压强为2×105N/m2,A点的截面积为100cm2,B点截面积 为60cm2。假设水的内摩擦可以忽略不计,求A、B点的 流速和B点的压强。 解:由连续性方程,得 SA vA= SB vB=Q 得vA= ? vB=? 由伯努利(Bernoulli)方程 得PB=?
H h
L
11
5.伯努力方程的适用条件是( ) 6. 注射器活塞面积为1.2cm2,注射用针头截面积为 1mm2,当注射器水平放置时用4.9N的力推动活塞, 使活塞移动了4cm,问水从注射器中流出所需的 时间为多少? 7.课本第38页,全部掌握.
12
13
黏性流体的运动
一、流体的黏性 (viscosity of fluid ) 黏性 作相对运动的两层流体之间的接触面上, 存在一对阻碍两流体层相对运动的大小相等而方 向相反的摩擦力 ,这种摩擦力称为流体的黏力, 或内摩擦力。 由于黏性的存在 , 管道中流动的流体出现了分层 流动, 各层只作相对滑动而彼此不相混合, 这种现象 z 称为层流。 v 图示为充满两个平行板之 间的流体的流动。两板之间 各流体层的速率梯度的大小 14 为 dv / dz ,在此处是常量。o
