逻辑运算符号
四种基本逻辑运算

四种基本逻辑运算一、与运算与运算是逻辑运算中的一种基本运算,也称为“与”操作。
与运算的结果只有在所有输入变量都为真(即为1)时才为真,否则为假(即为0)。
与运算的运算符通常用符号“∧”或“&”表示。
例如,对于两个输入变量A和B,A∧B表示A和B的与运算结果。
与运算在实际生活中的应用非常广泛。
例如,在某些情况下,我们需要判断多个条件是否同时满足,只有当所有条件都满足时,我们才能得出最终的结论。
这时,我们可以使用与运算来判断这些条件是否同时成立。
二、或运算或运算是逻辑运算中的另一种基本运算,也称为“或”操作。
或运算的结果只要有一个输入变量为真(即为1),就为真,否则为假(即为0)。
或运算的运算符通常用符号“∨”或“|”表示。
例如,对于两个输入变量A和B,A∨B表示A和B的或运算结果。
或运算在实际生活中也有广泛的应用。
例如,当我们需要判断多个条件中是否有一个满足时,只要有一个条件满足,我们就可以得出最终的结论。
这时,我们可以使用或运算来判断这些条件是否有满足的情况。
三、非运算非运算是逻辑运算中的另一种基本运算,也称为“非”操作。
非运算的结果是输入变量的反面,即如果输入变量为真(即为1),则非运算结果为假(即为0);如果输入变量为假(即为0),则非运算结果为真(即为1)。
非运算的运算符通常用符号“¬”或“!”表示。
例如,对于一个输入变量A,¬A表示A的非运算结果。
非运算在实际生活中也有一些应用。
例如,当我们需要判断一个条件是否不成立时,我们可以使用非运算来得出相反的结论。
四、异或运算异或运算是逻辑运算中的另一种基本运算,也称为“异或”操作。
异或运算的结果只有在输入变量不同时为真时才为真,否则为假。
异或运算的运算符通常用符号“⊕”或“xor”表示。
例如,对于两个输入变量A和B,A⊕B表示A和B的异或运算结果。
异或运算在实际生活中也有一些应用。
例如,在某些情况下,我们需要判断两个条件是否恰好有一个满足,即只有一个条件为真,而另一个条件为假。
离散数学逻辑运算符

离散数学逻辑运算符
1.否定运算符(NOT):表示取反,也称为补数运算符。
符号为~或¬。
例如,~P表示P不成立。
2.合取运算符(AND):表示“与”操作,也称为逻辑乘法。
符号为
∧或者&&。
例如,P∧Q表示P和Q都成立。
3.析取运算符(OR):表示“或”操作,也称为逻辑加法。
符号为∨
或者||。
例如,P∨Q表示P或Q中至少有一个成立。
4.异或运算符(XOR):表示“异或”操作,两边的结果不同则为真,否则为假。
符号为⊕。
例如,P⊕Q表示P和Q结果不同。
5.条件运算符(IF-THEN):表示如果P成立,则Q成立,也称为蕴
含运算符。
符号为→或者⇒。
例如,P→Q表示如果P成立,那么Q也必
须成立。
6.反条件运算符(IF-NOT-THEN):表示如果P不成立,则Q成立。
符号为←或者⇐。
例如,P←Q表示如果Q成立,那么P也必须成立。
7.双条件运算符(IF-AND-ONLY-IF):表示P和Q两者其中一个成立,或者都成立,则整个表达式为真;否则为假,也称为等价运算符。
符号为
↔或者≡。
例如,P↔Q表示P和Q互相成立或互相不成立。
逻辑运算的逻辑符号

逻辑运算的逻辑符号
逻辑运算的逻辑符号包括以下几种:
1. 与运算符(&&):也被称为短路与,用于检查两个操作数是否都为真,只有当两个操作数都为真时,表达式的最终结果才会为真。
2. 或运算符(||):也被称为短路或,用于检查两个操作数中是否至少有一个为真,只要有一个操作数为真,整个表达式的最终结果就会为真。
3. 非运算符(!):也被称为逻辑非,用于反转操作数的真假值,即当一个操作数为真时,非运算符将其转为假;当一个操作数为假时,非运算符将其转为真。
4. 异或运算符(^):也被称为逻辑异或,用于检查两个操作数的真假值是否不同,当两个操作数的真假值不同时,整个表达式的最终结果为真,否则为假。
以上是关于逻辑运算的逻辑符号的详细描述,不同的编程语言可能有所差异,但这些逻辑运算符是编程中常用的基本运算符之一,用于判断条件和进行逻辑处理。
基本逻辑符号

基本逻辑符号基本逻辑符号是用来表达命题逻辑中的逻辑关系和运算符的符号。
它们用于构建逻辑论证、推理和证明的过程。
在下面的文档中,我将介绍一些常见的基本逻辑符号及其含义。
1.命题符号命题符号用于表示命题。
命题是一个陈述句,可以判断为真或假。
常用的命题符号包括字母p、q、r等来表示不同的命题。
2.逻辑关系符号逻辑关系符号用于表示命题之间的关系。
•否定符号(¬):表示对命题的否定。
•合取符号(∧):表示命题的合取(与)关系,当且仅当两个命题都为真时,合取命题为真。
•析取符号(∨):表示命题的析取(或)关系,当且仅当两个命题中至少有一个为真时,析取命题为真。
•条件符号(→):表示命题的条件关系,当且仅当前件为真时,后件为真,否则为假。
•双条件符号(↔):表示命题的双条件关系,当且仅当两个命题同时为真或同时为假时,双条件命题为真。
3.量词符号量词符号用于表示命题的范围。
•全称量词符号(∀):表示“对于所有”的意思,用来表达命题在所有情况下都成立。
•存在量词符号(∃):表示“存在至少一个”的意思,用来表达命题至少存在一个情况使其成立。
4.推理符号推理符号用于表示命题之间的推理关系。
•等价符号(≡):表示两个命题是等价的,它们具有相同的真值。
•合取推出符号(∴):表示前提命题合取为真时,结论命题为真。
•假言推出符号(⇒):表示前提命题为真时,结论命题为真。
除了上述常见的基本逻辑符号,还有其他一些扩展的逻辑符号用于表示更复杂的逻辑关系和运算,如存在唯一量词符号(∃!)用于表示“存在唯一一个”的意思。
基本逻辑符号在数理逻辑和计算机科学等领域中扮演着重要的角色。
它们帮助我们描述和分析命题之间的关系,以及进行推理和证明。
通过正确运用基本逻辑符号,我们可以建立严谨而有效的逻辑论证和推理结构。
总结起来,基本逻辑符号是用来表示命题逻辑中的逻辑关系和运算符的符号。
它们用于构建逻辑论证、推理和证明的过程。
熟练掌握和运用基本逻辑符号对于深入理解和应用命题逻辑具有重要意义。
c语言逻辑运算符号及其含义

c语言逻辑运算符号及其含义
在C语言中,逻辑运算符号用于连接两个条件表达式,以便对其进行比较和处理。
以下是C语言中常见的逻辑运算符号及其含义:
1. && (逻辑与):如果两个条件都为真,则表达式的值为真。
2. || (逻辑或):如果两个条件之一为真,则表达式的值为真。
3. ! (逻辑非):如果条件为假,则表达式的值为真。
反之,如果条件为真,则表达式的值为假。
这些逻辑运算符号在编写程序时非常有用,可以帮助程序员在代码中判断和处理各种情况。
例如,可以使用逻辑运算符号来检查一个变量是否满足一组特定的条件,或者在一个程序中处理多个不同的输入。
总之,在C语言中,逻辑运算符号是非常重要的工具,可以帮助程序员有效地处理各种输入和输出。
学习逻辑运算符号的基本知识是编写高质量程序的重要一步。
- 1 -。
linux 逻辑运算符号

在Linux中,逻辑运算符用于执行逻辑运算。
以下是Linux中使用的逻辑运算符:
1.逻辑非(!):逻辑非运算符用于对一个条件进行否定。
如果条件为真,则
逻辑非运算符将其转换为假;如果条件为假,则将其转换为真。
2.逻辑与(&&):逻辑与运算符用于检查两个条件是否都为真。
只有当两个
条件都为真时,整个表达式才为真。
3.逻辑或(||):逻辑或运算符用于检查至少一个条件是否为真。
只要有一
个条件为真,整个表达式就为真。
4.逻辑异或(<||>):逻辑异或运算符用于比较两个值是否相等。
如果两个
值相等,则结果为假;如果两个值不相等,则结果为真。
这些逻辑运算符在脚本和命令行中非常有用,可以用来组合多个条件并进行复杂的逻辑判断。
八种逻辑门电路符号
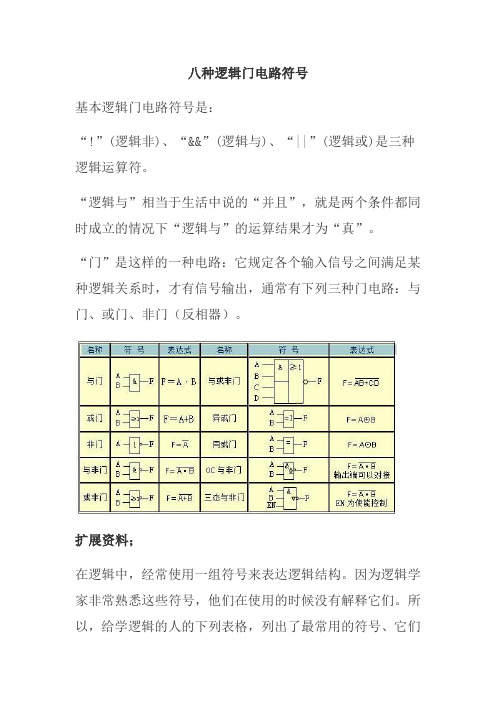
八种逻辑门电路符号
基本逻辑门电路符号是:
“!”(逻辑非)、“&&”(逻辑与)、“||”(逻辑或)是三种逻辑运算符。
“逻辑与”相当于生活中说的“并且”,就是两个条件都同时成立的情况下“逻辑与”的运算结果才为“真”。
“门”是这样的一种电路:它规定各个输入信号之间满足某种逻辑关系时,才有信号输出,通常有下列三种门电路:与门、或门、非门(反相器)。
扩展资料;
在逻辑中,经常使用一组符号来表达逻辑结构。
因为逻辑学家非常熟悉这些符号,他们在使用的时候没有解释它们。
所以,给学逻辑的人的下列表格,列出了最常用的符号、它们
的名字、读法和有关的数学领域。
此外,第三列包含非正式定义,第四列给出简短的例子。
要注意,在一些情况下,不同的符号有相同的意义,而同一个符号,依赖于上下文,有不同的意义。
逻辑表达式的符号

逻辑表达式的符号一、引言在数学和计算机科学中,逻辑表达式的符号被广泛使用,用于描述和表示逻辑问题和推理。
逻辑表达式的符号包括逻辑运算符、关系运算符和量词符号等,它们协助我们对命题进行逻辑分析和推断。
在本文中,我将详细介绍逻辑表达式的符号以及它们的应用。
二、逻辑运算符逻辑运算符用于操作逻辑表达式,常用的逻辑运算符包括与运算、或运算、非运算和异或运算。
下面分别介绍这些逻辑运算符的符号以及它们在逻辑表达式中的应用。
2.1 与运算与运算用符号“∧”表示,其作用是当且仅当两个操作数都为真时结果为真,否则结果为假。
与运算可以用于判断多个条件成立的情况,例如:1.如果一个人既是男性且年龄大于18岁,则可以购买烟酒。
2.如果一个学生既完成了作业且及时交了作业,则可以获得奖励。
2.2 或运算或运算用符号“∨”表示,其作用是当且仅当两个操作数中至少有一个为真时结果为真,否则结果为假。
或运算可以用于判断多个条件中至少有一个成立的情况,例如:1.如果一个人是男性或者年龄大于18岁,则可以购买烟酒。
2.如果一个学生完成了作业或者及时交了作业,则可以获得奖励。
2.3 非运算非运算用符号“¬”表示,其作用是对操作数的逻辑值取反。
非运算可以用于否定一个条件,例如:1.如果一个人不是男性,则不能购买烟酒。
2.如果一个学生没有完成作业,则不能获得奖励。
异或运算用符号“⊕”表示,其作用是当且仅当两个操作数中有且仅有一个为真时结果为真,否则结果为假。
异或运算可以用于判断两个条件中只有一个成立的情况,例如:1.如果一个学生只完成了作业或者只及时交了作业,则可以获得奖励。
三、关系运算符关系运算符用于比较两个值之间的关系,常用的关系运算符包括等于、不等于、大于、小于、大于等于和小于等于。
下面分别介绍这些关系运算符的符号以及它们在逻辑表达式中的应用。
3.1 等于运算符等于运算符用符号“=”表示,其作用是判断两个值是否相等。
等于运算符可以用于判断两个条件是否成立,例如:1.如果一个人的性别等于男性,则可以购买烟酒。
tcl语言中的逻辑运算符号

tcl语言中的逻辑运算符号一、引言Tcl(Tool Command Language)是一种简单而强大的脚本语言,广泛应用于各种软件的开发和自动化任务。
在Tcl中,逻辑运算符号是用于执行逻辑运算的重要工具。
逻辑运算包括“与”(and)、“或”(or)和“非”(not)等。
这些运算符号在Tcl中具有特定的语法和用途,有助于简化复杂的逻辑运算。
二、逻辑运算符号1. “与”运算(and):只有当所有操作数都为真时,结果才为真。
语法为 `expr var1 && var2`,其中 `var1` 和 `var2` 是变量,`&&` 是逻辑与运算符。
2. “或”运算(or):只要任一操作数为真,结果就为真。
语法为 `expr var1 || var2`,其中 `var1` 和 `var2` 是变量,`||` 是逻辑或运算符。
3. “非”运算(not):用于将一个操作数的逻辑状态反转。
语法为 `expr not var`,其中 `var` 是变量。
4. 逻辑与和逻辑或的组合:Tcl还提供了与和或的组合运算,如`expr var1 && var2 || var3`,这将首先执行逻辑与运算,如果结果为真,则执行逻辑或运算。
三、示例代码以下是一个简单的示例,展示了如何在Tcl中使用逻辑运算符号:```tcl#!/usr/bin/env tclshset a 10set b 5set c 0set d "hello"if {$a > 5} {puts "a大于5"} elseif {$b > $c} {puts "b大于c"} else {# 如果以上条件都不满足,使用逻辑或运算puts "a、b都不大于c"}```四、总结在Tcl语言中,逻辑运算符号对于实现复杂的逻辑控制非常重要。
总结逻辑门的符号

总结逻辑门的符号逻辑门是计算机领域中重要的基础组件,用于处理不同的逻辑运算。
逻辑门可以根据不同的输入产生特定的输出,从而实现不同的逻辑功能。
在逻辑门中,符号扮演着重要的角色,它们用于表示逻辑运算的输入、输出和运算规则。
本文将总结逻辑门中常见的符号,并探讨它们的用途和含义。
一、基本符号1. “0”和“1”“0”和“1”是逻辑门中最基本的符号,它们分别代表逻辑运算中的“假”和“真”。
在逻辑门的输入和输出中,数字“0”表示逻辑低电平,而数字“1”表示逻辑高电平。
这两个符号用于表示逻辑门的输入状态和输出状态,是逻辑运算的基础。
2. “+”和“·”“+”和“·”是逻辑门中常用的符号,它们分别表示逻辑运算中的“或”和“与”。
•“+”表示逻辑运算中的“或”,表示只要有一个输入位为真(1),输出位就为真(1)。
•“·”表示逻辑运算中的“与”,表示所有输入位都为真(1),输出位才为真(1)。
这两个符号常用于表示逻辑门之间的连接和逻辑运算的规则,是逻辑运算中最基本的运算符号。
二、逻辑门的符号1. 与门(AND Gate)与门是逻辑电路中最常见的门之一,它根据所有输入位的状态来确定输出位的状态。
与门的符号为“·”,可以表示为以下形式:A ·B = Q其中,A和B为输入位,Q为输出位。
当A和B同时为真(1)时,输出位Q 为真(1)。
否则,输出位Q为假(0)。
2. 或门(OR Gate)或门是逻辑电路中常用的门之一,它根据输入位的任何一个位的状态来确定输出位的状态。
或门的符号为“+”,可以表示为以下形式:A +B = Q其中,A和B为输入位,Q为输出位。
当A和B中有任何一个为真(1)时,输出位Q为真(1)。
只有当A和B同时为假(0)时,输出位Q才为假(0)。
3. 非门(NOT Gate)非门是逻辑电路中最简单的门之一,它只有一个输入位和一个输出位。
非门的符号通常为一个小圆圈,表示逻辑反转的操作。
数字逻辑 表达式

数字逻辑表达式
数字逻辑表达式是由逻辑运算符和逻辑变量组成的表达式,用于描述数字电路的逻辑功能。
常见的逻辑运算符包括:
- 与运算(AND):符号为“∧”或“*”,表示两个输入同时为1
时输出为1,否则输出为0。
- 或运算(OR):符号为“∨”或“+”,表示两个输入至少有一
个为1时输出为1,否则输出为0。
- 非运算(NOT):符号为“¬”或“!”,表示输入为1时输出为0,输入为0时输出为1。
- 异或运算(XOR):符号为“⊕”,表示两个输入不相同时输
出为1,否则输出为0。
逻辑变量可以是逻辑常量(0或1)或逻辑变量(例如,A、B、C等)。
数字逻辑表达式可以用来描述数字电路的逻辑功能,如加法器、多路选择器等。
例如,一个4位全加器的数字逻辑表达式可以表示为:
S = A ⊕ B ⊕ C
C_out = (A ∧ B) ∨ (C ∧ (A ⊕ B))
其中,S表示输出和,C_out表示进位输出,A、B和C分别
表示加法器的三个输入。
与或非逻辑符号运算规则

与或非逻辑符号运算规则与、或、非是逻辑符号中常见的三种运算规则。
它们在逻辑学和计算机科学中扮演着重要的角色,用于描述和推理真值逻辑。
下面我将详细介绍这三种逻辑符号的运算规则。
"与"逻辑符号,通常用符号“∧”表示。
它的运算规则是当且仅当两个命题同时为真时,结果为真;否则结果为假。
例如,如果命题P表示"今天是星期一",命题Q表示"天气晴朗",那么P∧Q表示"今天是星期一且天气晴朗",只有当这两个命题同时为真时,才能得到真值。
"或"逻辑符号,通常用符号“∨”表示。
它的运算规则是当且仅当两个命题中至少有一个为真时,结果为真;只有当这两个命题都为假时,结果才为假。
例如,如果命题P表示"我喜欢音乐",命题Q表示"我喜欢运动",那么P∨Q表示"我喜欢音乐或者我喜欢运动",只要有一个命题为真,整个命题就为真。
"非"逻辑符号,通常用符号“¬”表示。
它的运算规则是将命题的真值取反。
当命题为真时,结果为假;当命题为假时,结果为真。
例如,如果命题P表示"今天是下雨天",那么¬P表示"今天不是下雨天",即取反原命题。
这三种逻辑符号的运算规则可以通过真值表来展示。
真值表是一个二进制表格,列出了所有可能的命题组合和对应的结果。
根据真值表,可以准确确定逻辑运算的结果。
总结起来,与、或、非逻辑符号运算规则可以通过真值表来描述。
通过理解和应用这些规则,我们可以进行精确的逻辑推理和计算。
这对于解决问题、设计算法和构建复杂系统是非常重要的。
异或和同或的逻辑符号

异或和同或的逻辑符号一、引言逻辑符号是数学和计算机科学中重要的基础概念之一。
其中,异或和同或是两个常见的逻辑符号。
本文将详细介绍异或和同或的定义、性质、应用等方面的内容。
二、异或的定义异或(XOR)是一种二元逻辑运算符,用于比较两个位。
当两个位相同时,结果为0;当两个位不同时,结果为1。
其符号为“ ⊕ ”。
三、异或的性质1. 交换律:a ⊕ b = b ⊕ a2. 结合律:(a ⊕ b) ⊕ c = a ⊕ (b ⊕ c)3. 自反性:a ⊕ a = 04. 恒等式:a ⊕ 0 = a四、异或的应用1. 加密解密:在现代密码学中,常使用异或运算进行加密解密操作。
2. 校验码:通过将数据与一个特定值进行异或运算得到一个校验码,可以检测数据是否被篡改。
3. 数据传输:在数据传输过程中,可以使用异或运算对数据进行处理,在接收端再次进行异或运算还原原始数据。
五、同或的定义同或(XNOR)是一种二元逻辑运算符,与异或相反。
当两个位相同时,结果为1;当两个位不同时,结果为0。
其符号为“ ⊙ ”。
六、同或的性质1. 交换律:a ⊙ b = b ⊙ a2. 结合律:(a ⊙ b) ⊙ c = a ⊙ (b ⊙ c)3. 自反性:a ⊙ a = 14. 恒等式:a ⊙ 1 = a七、同或的应用1. 逻辑运算:在逻辑电路中,常使用同或运算进行比较操作。
2. 数据传输:在数据传输过程中,可以使用同或运算对数据进行处理,在接收端再次进行同或运算还原原始数据。
八、异或和同或的区别异或和同或是两种不同的逻辑运算符。
异或是当两个位不同时结果为1,相同时结果为0;而同或则恰好相反,当两个位相同时结果为1,不同时结果为0。
在应用方面也有所区别,异或常用于加密解密、校验码、数据传输等方面;而同或则更多地应用于逻辑电路中的比较操作。
九、总结本文详细介绍了异或和同或的定义、性质、应用等方面的内容,并对它们进行了比较和总结。
了解和掌握这些基础概念是学习数学和计算机科学的重要基础。
不属于逻辑运算符号

不属于逻辑运算符号
在逻辑运算中,常见的逻辑运算符号有与(AND)、或(OR)、非(NOT)、异或(XOR)等。
以下是一些不属于逻辑运算符号的示例:
1. 加法(+)和减法(-):这两个符号用于数学中的数值计算,不属于逻辑运算。
2. 乘法(×)和除法(÷):同样用于数值计算,不是逻辑运算符号。
3. 等于(=)、大于(>)、小于(<)等关系运算符:这些符号用于比较数值大小或顺序,也不属于逻辑运算。
不同的编程语言和逻辑系统可能会使用不同的符号来表示逻辑运算,但常见的逻辑运算符号如与、或、非、异或等在大多数情况下是通用的。
与或非逻辑符号运算规则

与或非逻辑符号运算规则
与逻辑符号运算规则:
1. 与运算(AND):如果两个命题都为真,则结果为真;如
果其中至少一个命题为假,则结果为假。
例子: A AND B 的真值表如下:
A |
B | A AND B
------------------
真 | 真 | 真
真 | 假 | 假
假 | 真 | 假
假 | 假 | 假
或逻辑符号运算规则:
1. 或运算(OR):如果两个命题至少一个为真,则结果为真;如果两个命题都为假,则结果为假。
例子: A OR B 的真值表如下:
A |
B | A OR B
-----------------
真 | 真 | 真
真 | 假 | 真
假 | 真 | 真
假 | 假 | 假
非逻辑符号运算规则:
1. 非运算(NOT):取反操作,如果命题为真,则结果为假;如果命题为假,则结果为真。
例子: NOT A 的真值表如下:
A | NOT A ------------- 真 | 假
假 | 真。
逻辑运算符号定义

逻辑运算符号定义逻辑运算是理性思维的基本元素,也是程序设计的基本原理。
用来描述和表达计算机算法的基本运算项是由逻辑运算符号定义的。
逻辑运算符号是由数学逻辑学家占特在二十世纪早期定义的,他将逻辑运算的基本符号定义为“析取”(逻辑乘),“合取”(逻辑加),“非”(逻辑减),“异或”(逻辑乘减),“同或”(逻辑加减),“反蕴含”(逻辑反蕴含)。
首先,关于“析取”(逻辑乘),它是一种“逻辑乘法”,又称为交叉运算或积分。
它是指将两个变量相“与”或“析取”,是当两个变量同时同时为真时计算结果才为真,其表示形式为:A∧B,它类似于数学中的乘法,A、B为相应的变量。
其次,关于“合取”(逻辑加),它是一种“逻辑加法”,又称为汇总运算或和取。
它是指将两个变量相“且”或“合取”,是当两个变量至少有一个为真时计算结果为真,其表示形式为:A∨B,它类似于数学中的加法,A、B为相应的变量。
然后,关于“非”(逻辑减),它是一种“逻辑减法”,又称为取反运算或反转运算。
它是指将一个变量相“非”,是指当变量为真时计算结果为假,反之亦然,其表示形式为:A,它类似于数学中的减法,A为相应的变量。
再次,关于“异或”(逻辑乘减),它是一种“逻辑乘减法”,又称为异或运算。
它是指将两个变量相“异或”,是当两个变量有一个为真而另一个为假时计算结果为真,其表示形式为:AB,它类似于数学中的乘减法,A、B为相应的变量。
最后,关于“同或”(逻辑加减),它是一种“逻辑加减法”,又称为同或运算或反向运算。
它是指将两个变量相“同或”,是当两个变量至多有一个为真时计算结果为真,其表示形式为:AB,它类似于数学中的加减法,A、B为相应的变量。
此外,还有关于“反蕴含”(逻辑反蕴含),它是一种“逻辑反蕴含法”,又称为反蕴含运算或反向蕴含运算。
它是指当A为真而B为假时计算结果为真,其表示形式为:AB,它类似于数学中的反蕴含法,A、B为相应的变量。
总的来说,逻辑运算符号是一种独特的符号,它们可以帮助我们理解和表达计算机算法,并且也可以代替文字进行计算运算。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
逻辑OR
优先级为:NOT AND OR
同级运算从左到右
在形式逻辑中,逻辑运算符或逻辑联结词把语句连接成更复杂的复杂语句。例如,假设有两个逻辑命题,分别是“正在下雨”和“我在屋里”,我们可以将它们组成复杂命题“正在下雨,并且我在屋里”或“没有正在下雨”或“如果正在下雨,那么我在屋里”。一个将两个语句组成的新的语句或命题叫做复合语句或复合命题。
为了减少需要的括号的数量,有以下的优先规则:¬高于∧,∧高于∨,∨高于→。例如,P ∨ Q ∧ ¬ R → S是 (P ∨ (Q ∧ (¬ R)) → S的简便写法。
表格 15-7. 逻辑运算符
例子
名称
结果
$a and $b
And(逻辑与)
TRUE,如果 $a 与 $b 都为 TRUE。
$a or $b
Or(逻辑或)
TRUE,如果 $a 或 $b 任一为 TRUE。
$a xor $b
Xor(逻辑异或)
TRUE,如果 $a 或 $b 同位相异。
! $a
Not(逻辑非)
TRUE,如果 $a 不为 TRUE。
$a && $b
And(逻辑与)
TRUE,如果 $a 与 $b 都为 TRUE。
$a || $b
Or(逻辑或)
TRUE,如果 $a 或 $b 任一为 TRUE。
“与”和“或”有两种不同形式运算符的原因是它们运算的优先级不同(见运算符优先级)。
基本的操作符有:“非”(¬)、“与”(∧)、“或”(∨)、“条件”(→)以及“双条件”(?)。“非”是一个一元操作符,它只操作一项(¬ P)。剩下的是二元操作符,操作两项来组成复杂语句(P ∧ Q, P ∨ Q, P → Q, P ? Q)。[1]
注意,符号“与”(∧)和交集(∩),“或”(∨)和并集(∪)的相似性。这不是巧合:交集的定义使用“与”,并集的定义是用“或”。[1]
在形式逻辑中,逻辑运算符或逻辑联结词把语句连接成更复杂的复杂语句。例如,假设有两个逻辑命题,分别是“正在下雨”和“我在屋里”,我们可以将它们组成复杂命题“正在下雨,并且我在屋里”或“没有正在下雨”或“如果正在下雨,那么我在屋里”。一个将两个语句组成的新的语句或命题叫做复合语句或复合命题。[1]
逻辑NOT
