matlab非线性拟合函数lsqcurvefit
matlab回归拟合

在MATLAB中进行回归拟合的方法有很多种,包括线性回归、多项式回归和非线性回归。
1. 线性回归拟合:使用“polyfit”函数进行线性回归拟合。
例如,如果你有一组x和y数据,可以使用以下代码进行线性回归拟合:```matlabx = [1, 2, 3, 4, 5];y = [2, 4, 5, 4, 5];p = polyfit(x, y, 1);```这将返回一个多项式系数数组p,其中p(1)是斜率,p(0)是截距。
2. 多项式回归拟合:使用“polyfit”函数进行多项式回归拟合。
你需要指定多项式的阶数。
例如,如果你想进行二次多项式回归,可以使用以下代码:```matlabx = [1, 2, 3, 4, 5];y = [2, 4, 5, 4, 5];p = polyfit(x, y, 2);```这将返回一个二次多项式系数数组p。
3. 非线性回归拟合:非线性回归可以通过非线性函数来拟合数据,可以更好地适应复杂的数据模式。
在MATLAB中,可以使用“lsqcurvefit”函数来进行非线性回归拟合,需要指定拟合函数和初始参数。
例如,如果你有一个非线性函数形式,可以定义一个函数句柄,然后使用“lsqcurvefit”进行拟合:```matlab定义非线性函数句柄f = @(b,x) b(1)*exp(b(2)*x(:,1)) + b(3)*sin(b(4)*x(:,2));定义初始参数b0 = [1,1,1,1];进行非线性回归拟合xdata = [1:10];ydata = [2*exp(1)+sin(1:10)]; 生成一些模拟数据b = lsqcurvefit(f, b0, xdata', ydata');```这将返回拟合参数b,你可以使用这些参数来预测新的数据点。
基于MATLAB的非线性曲线拟合

基于MATLAB的非线性曲线拟合一、本文概述随着科技的不断进步,数据分析和处理在各个领域中都发挥着越来越重要的作用。
非线性曲线拟合作为一种重要的数据处理方法,被广泛应用于科学研究、工程实践以及日常生活等多个领域。
MATLAB作为一款强大的数学计算和数据分析软件,为非线性曲线拟合提供了便捷的工具和丰富的函数库。
本文旨在介绍基于MATLAB的非线性曲线拟合方法,包括非线性模型的建立、参数估计、模型验证等步骤,并通过具体实例展示MATLAB在非线性曲线拟合中的应用。
本文首先简要介绍了非线性曲线拟合的基本概念和研究背景,阐述了非线性曲线拟合在实际应用中的重要性。
接着,详细介绍了MATLAB 中非线性曲线拟合的实现过程,包括非线性模型的构建、数据预处理、参数估计方法的选择、模型拟合和评估等方面。
在此基础上,通过实例分析,展示了MATLAB在非线性曲线拟合中的实际应用,并对拟合结果进行了分析和讨论。
对全文进行了总结,指出了非线性曲线拟合在实际应用中的潜在价值和未来研究方向。
通过本文的学习,读者可以了解非线性曲线拟合的基本原理和方法,掌握MATLAB在非线性曲线拟合中的应用技巧,提高数据处理和分析能力,为相关领域的研究和实践提供有力支持。
二、非线性曲线拟合基础在数据分析和科学研究中,我们经常遇到需要通过一组离散的数据点来寻找其潜在的非线性关系。
非线性曲线拟合就是这样一个过程,它旨在找到最能描述数据点之间关系的非线性函数。
与线性拟合不同,非线性拟合的模型函数通常包含非线性参数,这些参数需要通过一定的优化算法来求解。
MATLAB作为一款强大的数学软件,提供了多种非线性曲线拟合的工具和函数。
在MATLAB中,非线性曲线拟合通常通过lsqcurvefit、lsqnonlin或fit等函数实现。
这些函数允许用户定义自己的非线性模型函数,并通过迭代优化算法来寻找最佳拟合参数。
在进行非线性曲线拟合时,选择合适的模型函数至关重要。
matlab曲线曲面拟合讲解及实例

例如:
x1=[1.0500 1.0520 1.0530 1.0900 1.0990 1.1020 1.1240 1.1420...
1.1490 1.0500 1.0520 1.0530 1.0900 1.0990 1.1020 1.1240 1.1420 1.1490];
x2=[3.8500 1.6500 2.7500 5.5000 7.7000 3.3000 4.9500 8.2500 11.5500...
52.5000 62.0000];
data=[x1;x2]; ห้องสมุดไป่ตู้ %类似于将x1 x2整合成一个2维数组。
a0= [-0.0014,0.07];
option=optimset('MaxFunEvals',5000);
format long;
同理用Symbolic Math Toolbox可以直接执行
>> ezmesh('X.^2 - Y.^2', [-2 2], [-2 2])
surf函数
在函数不能表示成z = f(x, y)时,需要用surf函数。比如x2+y2+z2=1.
先需要用柱面坐标或者球坐标来表示。这里用柱面坐标表示为 r2+z2=1
x = sqrt(1-z2)cosθ, x = sqrt(1-z2)sinθ;
执行matlab指令:
>> [theta, Z] = meshgrid((0:0.1:2)*pi, (-1:0.1:1));
>> X =sqrt(1 - Z.^2).*cos(theta);
>> Y =sqrt(1 - Z.^2).*sin(theta);
非线性拟合

[x,renorm]=lsqcurvefit(@myfun,x0,xdata,ydata); %确定待定系数
disp(x);
disp(renorm);
function F=myfun(x,xdata)
F=x(1)*(xdata.^2)+x(2)*sin(xdata)+x(3)*(xdata.^3); %预定义函数关系式
matlab中nlinfit和lsqcurvefit的功能和用法有什么区别?
悬赏分:5 - 解决时间:2009-5-31 10:36
如题!
提问者: 珊珊小魔女 - 助理 三级 最佳答案
如果你懂英语,就用matlab最强大的函数help(一般人我不告诉他)
help nlinfit
help lsqcurvefit
f = A + B exp(C*x)+D*exp(E*x)
对数据集x与y进行拟合,其中y是在给定x的情况下的期望输出(可以是方程给出数组,也可以是单独数据组成的数组)。
为了解决这个问题,先建立下面的名为 fit_simp.m的函数,它利用数据x与y,将他们作为优化输入参数传递给LSQNONLIN。
关于采用matlab进行指定非线性方程拟合的问题
一。优化工具箱函数
LSQNONLIN 解决非线性最小二乘法问题,包括非线性数据拟合问题
LSQCURVEFIT 解决非线性数据拟合问题
下面给出利用这两个函数的例子:
LSQNONLIN:利用这个函数最小化连续函数只能够找到句柄解。下面的例子说明利用LSQNONLIN函数用下面的函数进行拟合:
也就是说,给定输入数据xdata,以及观测的输出数据ydata,找到系数x,使得函数F(x,xdata)能够最好的拟合向量值
lsqcurvefit拟合函数代码

lsqcurvefit是MATLAB中用于最小二乘曲线拟合的函数,它可以帮助我们找到一条曲线,使得该曲线与数据点之间的误差平方和最小。
下面我们来详细介绍一下lsqcurvefit函数的使用方法和参数设置。
1. 函数介绍lsqcurvefit函数是MATLAB Optimization Toolbox中的一个函数,用于非线性最小二乘曲线拟合。
该函数可以拟合一般形式的非线性模型,求解最优参数,使得模型与实际数据之间的拟合效果最好。
2. 使用方法lsqcurvefit函数的基本调用格式为:```[x,resnorm,residual,exitflag,output,lambda,jacobian] = lsqcurvefit(fun,x0,xdata,ydata,lb,ub,options)```其中各参数含义如下:- fun:拟合模型函数,即要拟合的曲线模型,其输入参数为x和xdata,输出为模型的预测值- x0:模型参数的初始值- xdata:自变量数据,即要拟合的数据点的横坐标- ydata:因变量数据,即要拟合的数据点的纵坐标- lb和ub:模型参数的上下界限制,可选参数- options:优化设置选项,可选参数3. 参数设置在使用lsqcurvefit函数时,我们需要注意以下几点参数设置:- 拟合模型函数fun:这是lsqcurvefit函数最重要的参数,需要根据实际问题选择合适的曲线模型来进行拟合。
常见的拟合模型包括多项式模型、指数模型、对数模型等,根据实际问题选择合适的模型来进行拟合。
- 模型参数初始值x0:这是拟合过程中的初始参数值,一般需要根据实际情况进行合理的设定,初始值的选择对拟合效果有较大影响。
- 参数限制lb和ub:在一些情况下,模型参数可能需要满足一定的限制条件,比如参数不能为负值等,这时候可以通过设置lb和ub来进行限制。
- 优化设置选项options:lsqcurvefit函数还提供了很多优化设置选项,比如最大迭代次数、容许误差等,可以根据实际情况进行设置。
lsqcurvefit函数

lsqcurvefit函数lsqcurvefit函数是MATLAB中的一个非线性最小二乘拟合函数,它可以用于拟合非线性模型,使得拟合结果与实际数据之间的误差最小化。
在实际应用中,非线性模型的拟合是非常常见的,因此lsqcurvefit函数也是MATLAB中非常重要的一个函数。
lsqcurvefit函数的基本语法如下:[x,resnorm,residual,exitflag,output,lambda,jacobian] = lsqcurvefit(fun,x0,xdata,ydata,lb,ub,options)其中,fun是一个函数句柄,用于定义非线性模型;x0是模型参数的初始值;xdata和ydata是实际数据;lb和ub是参数的上下限;options是一个结构体,用于设置拟合的参数。
lsqcurvefit函数的工作原理是通过最小化残差平方和来拟合非线性模型。
具体来说,它会将实际数据代入非线性模型中,得到模型预测值,然后计算预测值与实际值之间的误差,最终通过最小化误差的平方和来确定模型参数的最优值。
在使用lsqcurvefit函数时,需要注意以下几点:1. 非线性模型的定义:fun函数必须返回一个列向量,表示模型预测值与实际数据之间的误差。
2. 初始值的选择:初始值的选择对拟合结果有很大的影响,一般需要通过试验或经验来确定。
3. 参数的上下限:如果参数的上下限不合理,可能会导致拟合失败或得到不合理的结果。
4. 拟合结果的评估:需要通过残差平方和、拟合曲线与实际数据的对比等指标来评估拟合结果的好坏。
lsqcurvefit函数是MATLAB中非常重要的一个函数,它可以用于拟合非线性模型,使得拟合结果与实际数据之间的误差最小化。
在实际应用中,需要注意非线性模型的定义、初始值的选择、参数的上下限以及拟合结果的评估等问题。
matlab 非线性拟合函数lsqcurvefit

matlab 非线性拟合函数lsqcurvefit---logistic人口模型参数估计x= lsqcurvefit(fun,x0,xdata,ydata)x = lsqcurvefit(fun,x0,xdata,ydata,lb,ub)x = lsqcurvefit(fun,x0,xdata,ydata,lb,ub,options)x = lsqcurvefit(problem)[x,resnorm] = lsqcurvefit(...)[x,resnorm,residual] = lsqcurvefit(...)[x,resnorm,residual,exitflag] = lsqcurvefit(...)[x,resnorm,residual,exitflag,output] = lsqcurvefit(...)[x,resnorm,residual,exitflag,output,lambda] = lsqcurvefit(...)[x,resnorm,residual,exitflag,output,lambda,jacobian] = lsqcurvefit(.. .)x0为初始解向量;xdata,ydata为满足关系ydata=F(x, xdata)的数据;lb、ub为解向量的下界和上界,若没有指定界,则lb=[ ],ub=[ ];options为指定的优化参数;fun为拟合函数,其定义方式为:x = lsqcurvefit(@myfun,x0,xdata,ydata),其中myfun已定义为 function F = myfun(x,xdata)F = … % 计算x处拟合函数值fun的用法与前面相同;resnorm=sum ((fun(x,xdata)-ydata).^2),即在x处残差的平方和;residual=fun(x,xdata)-ydata,即在x处的残差;exitflag为终止迭代的条件;output为输出的优化信息;lambda为解x处的Lagrange乘子;jacobian为解x处拟合函数fun的jacobian矩阵。
matlab拟合方法

matlab拟合方法Matlab拟合方法摘要:拟合是一种常见的数据分析方法,用于通过数学模型来描述和预测数据的趋势。
Matlab是一种功能强大的数学软件,提供了多种拟合方法来处理不同类型的数据。
本文将介绍几种常用的Matlab 拟合方法,并给出实际案例来说明其应用。
1. 多项式拟合多项式拟合是一种基于多项式函数的拟合方法,通过拟合数据点来获得一个多项式函数,从而近似描述数据的趋势。
Matlab中的polyfit函数可以实现多项式拟合,用户可以指定多项式的阶数,从而控制拟合的复杂程度。
通过最小二乘法,polyfit函数可以找到最佳拟合曲线。
2. 曲线拟合除了多项式拟合,Matlab还提供了其他的曲线拟合方法,包括指数、对数、幂函数等。
这些方法可以根据数据的特点选择适当的曲线形式来进行拟合。
例如,使用fittype函数可以指定拟合的曲线类型,然后使用fit函数进行拟合。
用户还可以根据拟合结果进行参数估计和预测。
3. 非线性拟合当数据无法用简单的线性模型拟合时,可以使用非线性拟合方法。
Matlab提供了lsqcurvefit函数来实现非线性拟合,用户需要提供一个自定义的非线性函数,并指定初始参数值。
lsqcurvefit函数会通过最小二乘法来求解最佳参数值,从而得到最佳拟合曲线。
4. 插值插值是一种通过已知数据点来估计未知点的方法。
Matlab中的interp1函数可以实现插值拟合,用户需要提供已知数据点的坐标和对应的函数值,然后可以使用interp1函数来估计未知点的函数值。
interp1函数支持不同的插值方法,包括线性插值、样条插值等。
5. 统计拟合除了数学模型拟合,Matlab还提供了统计拟合方法,用于分析数据的概率分布。
Matlab中的normfit函数可以根据数据点的均值和标准差来拟合正态分布曲线。
用户还可以使用histfit函数来绘制数据的直方图和拟合曲线,从而比较数据的分布和理论模型的拟合程度。
关于采用matlab进行指定非线性方程拟合的问题

关于采用matlab进行指定非线性方程拟合的问题(1)※1。
优化工具箱的利用函数描述LSQLIN 有约束线性最小二乘优化LSQNONNEG 非负约束线性最小二乘优化问题当有约束问题存在的时候,应该采用上面的方法代替Polyfit与反斜线(\)。
具体例子请参阅优化工具箱文档中的相应利用这两个函数的例子。
d. 非线性曲线拟合利用MATLAB的内建函数函数名描述FMINBND 只解决单变量固定区域的最小值问题FMINSEARCH 多变量无约束非线性最小化问题(Nelder-Mead 方法)。
下面给出一个小例子展示一下如何利用FMINSEARCH1.首先生成数据>> t=0:.1:10;>> t=t(:);>> Data=40*exp(-.5*t)+rand(size(t)); % 将数据加上随机噪声2.写一个m文件,以曲线参数作为输入,以拟合误差作为输出function sse=myfit(params,Input,Actural_Output)A=params(1);lamda=params(2);Fitted_Curve=A.*exp(-lamda*Input);Error_Vector=Fitted_Curve-Actural_Output;%当曲线拟合的时候,一个典型的质量评价标准就是误差平方和sse=sum(Error_Vector.^2);%当然,也可以将sse写作:sse=Error_Vector(:)*Error_Vector(:);3.调用FMINSEARCH>> Strarting=rand(1,2);>> options=optimset('Display','iter');>> Estimates=fiminsearch(@myfit,Strarting,options,t,Data);>> plot(t,Data,'*');>> hold on>> plot(t,Estimates(1)*exp(-Estimates(2)*t),'r');Estimates将是一个包含了对原数据集进行估计的参数值的向量。
matlab 阻抗 最小二乘法

matlab 阻抗最小二乘法“最小二乘法”(Least Squares)是一种数学优化方法,用于解决线性方程组或者非线性方程组的问题。
在MATLAB中,最小二乘法可通过使用内置函数lsqcurvefit 或者nlinfit 来实现。
这两个函数用于非线性最小二乘法的拟合问题。
lsqcurvefit 用于对非线性方程进行曲线拟合,使用的是Gauss-Newton 算法。
% 定义模型函数function y = model(params, x)a = params(1);b = params(2);y = a * x + b;end% 定义初始参数值params0 = [0, 0];% 定义数据xData = [1, 2, 3, 4, 5];yData = [2, 3, 4, 5, 6];% 最小二乘拟合params = lsqcurvefit(@model, params0, xData, yData); disp(params);nlinfit 用于非线性模型的参数估计。
matlabCopy code% 定义模型函数function y = model(params, x)a = params(1);b = params(2);y = a * x + b;end% 定义初始参数值params0 = [0, 0];% 定义数据xData = [1, 2, 3, 4, 5];yData = [2, 3, 4, 5, 6];% 最小二乘拟合params = nlinfit(xData, yData, @model, params0);disp(params);在上面的例子中,我们定义了一个简单的一次线性模型 y = a * x + b,然后通过最小二乘法来拟合数据集 (xData, yData),从而估计参数 a 和 b 的值。
matlab数据拟合函数

matlab数据拟合函数数据拟合是一种通过寻找最佳拟合曲线来近似描述给定数据的统计技术。
在Matlab中,有多种方法可以用于数据拟合,包括线性拟合、多项式拟合、曲线拟合等。
下面将介绍其中几种常用的数据拟合函数。
1. polyfit函数:多项式拟合polyfit函数可以用于进行多项式拟合。
它接受两个参数:x为自变量数据,y为因变量数据。
拟合结果是一个多项式的系数向量,可以通过polyval函数将其用于预测。
例如:```matlabx=[1,2,3,4,5];y=[2,3,5,7,9];degree = 2; % 设置多项式的次数为2p = polyfit(x, y, degree);fitted_y = polyval(p, x);```2. fit函数:通用拟合fit函数是一个通用的拟合函数,可以用于拟合各种类型的曲线模型,包括线性、非线性、统计分布等。
它接受四个参数:x和y为数据,model为拟合模型,method为求解方法。
示例:```matlabx=[1,2,3,4,5];y=[2,3,5,7,9];model = 'a*x^b'; % 使用指数模型进行拟合f = fit(x', y', model);fitted_y = f(x);```3. lsqcurvefit函数:曲线拟合lsqcurvefit函数用于曲线拟合,可以拟合各种非线性函数。
它接受五个参数:fun为拟合函数,x0为初始参数值,xdata和ydata为数据,lb和ub为参数范围(可选)。
示例:```matlabx=[1,2,3,4,5];y=[2,3,5,7,9];x0=[1,1];%初始参数值[fitted_params, resnorm] = lsqcurvefit(fun, x0, x, y);fitted_y = fun(fitted_params, x);```4. cftool工具箱:交互式拟合cftool是一个交互式的拟合工具箱,可以通过图形界面直观地进行数据拟合。
利用lsqcurvefit拟合多个微分方程matlab代码

利用lsqcurvefit拟合多个微分方程的Matlab代码1. 简介在数学建模和科学计算中,拟合是一个常见的任务。
拟合可以帮助我们找到数据中的模式和趋势,从而更好地理解和预测现象。
在本文中,我们将介绍如何使用Matlab中的lsqcurvefit函数来拟合多个微分方程。
2. 拟合多个微分方程的目的和背景拟合多个微分方程的目的是根据实验数据找到一组参数,使得模型的输出与实验数据尽可能接近。
这可以帮助我们验证模型的有效性,并通过参数的估计来预测未来的行为。
3. lsqcurvefit函数的基本用法lsqcurvefit函数是Matlab中用来进行最小二乘拟合的函数。
它的基本用法如下:% 设置参数初始值x0 = [a, b, c];% 最小二乘拟合x = lsqcurvefit(fun, x0, xdata, ydata, lb, ub);其中,fun是一个函数句柄,用来定义待拟合的模型。
x0是参数的初始值,xdata和ydata是实验数据。
lb和ub是参数的范围,用来限制参数的取值范围。
4. 拟合多个微分方程的具体步骤4.1 收集实验数据首先,我们需要收集实验数据。
实验数据应该包括自变量和因变量的取值,以及可能的误差范围。
这些数据将用于拟合微分方程模型。
在建立模型之前,我们需要根据实验数据设置初始参数的值。
初始参数值的选择可能是一个关键问题,可以通过试验和经验来确定。
4.3 建立模型方程基于实际情况,我们可以建立一组微分方程来描述系统的动态行为。
这个方程应该包括未知参数,这些参数将通过拟合来求解。
4.4 定义待拟合的函数根据建立的模型方程,我们可以定义一个函数,该函数接受自变量和参数作为输入,并返回因变量的预测值。
4.5 进行最小二乘拟合使用lsqcurvefit函数进行最小二乘拟合。
将定义的函数句柄fun作为参数传递给lsqcurvefit函数。
4.6 分析拟合结果根据拟合结果,我们可以计算各个参数的估计值,并评估拟合的质量。
matlab:最小二乘法线性和非线性拟合
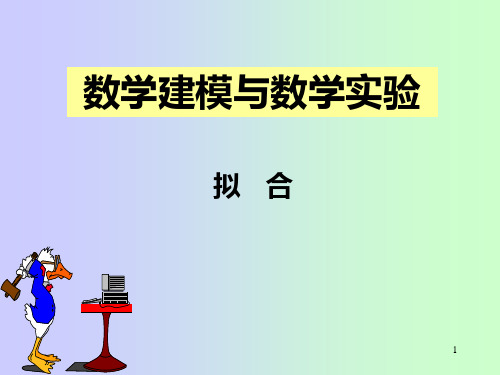
x f 1 1.5 2 3.9 4 6.6 7 11.7 9 15.6 12 13 18.8 19.6 15 20.6 17 21.1
MATLAB(cn)
7
最临近插值、线性插值、样条插值与曲线拟合结果:
25
0 0 2 4 6 8 10 12 14 16 18
MATLAB(zxec2)
%作出数据点和拟合曲线的图形 20.1293 -0.0317
2)计算结果: A = -9.8108
f ( x) 9.8108x 2 20.1293x 0.0317
17
用MATLAB作非线性最小二乘拟合
Matlab的提供了两个求非线性最小二乘拟合的函数: lsqcurvefit和lsqnonlin。两个命令都要先建立M-文件fun.m, 在其中定义函数f(x),但两者定义f(x)的方式是不同的,可参 考例题. 1. lsqcurvefit 已知数据点: xdata=(xdata1,xdata2,…,xdatan), ydata=(ydata1,ydata2,…,ydatan) lsqcurvefit用以求含参量x(向量)的向量值函数
最小。 其中 fi(x)=f(x,xdatai,ydatai) =F(x,xdatai)-ydatai
20
输入格式为: 1) x=lsqnonlin(‘fun’,x0); 2) x= lsqnonlin (‘fun’,x0,options); 3) x= lsqnonlin (‘fun’,x0,options,‘grad’); 4) [x,options]= lsqnonlin (‘fun’,x0,…); 5) [x,options,funval]= lsqnonlin 说明: x= lsqnonlin (‘ fun’ x0 ,…); (‘fun’,x0,options); fun是一个事先建立的 定义函数f(x)的M-文件, 自变量为x 选项见无 迭代初值 约束优化
matlab中lsqcurvefit的用法

MATLAB中lsqcurvefit的用法概述在M AT LA B中,`ls qc u rv ef it`是一个用于非线性最小二乘拟合的函数。
该函数可以求解一组非线性方程或拟合一组数据,以最小化残差平方和。
函数语法```m at la b[x,r es no rm,r es idu a l,ex it fl ag,o utp u t,la mb da,j ac obi a n]=l s q c ur ve fi t(fu n,x0,x da ta,y da ta,l b,u b,o pt io ns)```参数说明-`fu n`:自定义函数句柄,用于计算模型预测值和实际观测值之间的残差。
该函数应接受参数x和xd at a作为输入,返回模型预测值。
-`x0`:拟合参数的初始猜测值。
-`xd at a`:实际观测值的自变量数据。
-`yd at a`:实际观测值的因变量数据。
-`lb`:拟合参数的下界限制。
-`ub`:拟合参数的上界限制。
-`op ti on s`:可选参数,用于指定拟合过程中的详细设置,如最大迭代次数、收敛容限等。
示例假设我们有一组数据,需拟合出一个指数函数模型。
首先定义自定义函数`e xp Fu nc`,用于计算指数函数的预测值和实际观测值之间的残差。
```m at la bf u nc ti on y=ex pF unc(x,xd at a)y=x(1)*e xp(x(2)*x d at a);e n d```然后,我们准备好数据和初始猜测值,并调用`l sq cu rv ef it`进行拟合。
```m at la bx d at a=[01234];y d at a=[12.66.714.529.6];x0=[11];[x,r es no rm,r es idu a l,ex it fl ag,o utp u t,la mb da,j ac obi a n]=l s q c ur ve fi t(@e xp Fun c,x0,xd at a,yd ata);```输出结果-`x`:拟合出的参数值。
MATLAB教学视频:详解数据拟合的MATLAB实现(非线性拟合)

◼ 不合理的初值 → 可能导致求解失败
◼ 超出国界的出发地点 → 无法跨越的障碍
5 # 初值
O
珠 穆 朗 印玛
1 # 初值
2 # 初值
初
3 # 初值
4 # 初值
值
的
度峰
四
新川
X
疆
四
X
川
吐
盆
鲁
地
X
上
海
钓
海
平
鱼
面
岛
选 取 要 合 理
番
拟合效果的评价
◼ 不同的参数初值 → 可能会得到不同的局部最优解 ◼ 引发两个基本问题
◼ 待定参数初值的确定 param0 = [0.15, 400]
✓ 当人口总数较少时,近似成指数增长,令 x = 5
y = erx y1975 = 20.3 e5r r 0.15
y0
y1970 9.7
✓ 人口数量的极限为 ym → ym > 2015 年人口数量 (330.7)
y=
ym
✓ 人口指数增长模型 —— Malthus 模型 ✓ 人口阻滞增长模型 —— Logistics 模型
◼ MATLAB 实现非线性拟合 —— lsqcurvefit ◼ 寻优算法 —— 局部最优解 ◼ 拟合效果的评价 ◼ 土壤含水率问题的分析 ◼ 结束语 —— 拟合问题总结
拟合残差及残差平方和
◼ 残差:已知的测量点到拟合曲线 y = f(x) 的距离,即拟合值 (估计值) 与测量值 (观察值) 之差 ◼ 残差平方和:即残差的平方和 → 拟合值 (估计值) 与测量值 (观察值) 之差的平方和 ◼ 回顾线性拟合教学视频:拟合的定义 → 求解 y = f(x) 里的待定参数,使得残差平方和最小
使用Matlab进行曲线拟合

使用Matlab进行曲线拟合引言在科学研究和工程应用中,曲线拟合是一个非常常见和重要的问题。
通过拟合实验数据或者观测数据,我们可以找到一条曲线,以最佳地描述数据的趋势。
Matlab是一个功能强大的数值计算软件,提供了丰富的工具和函数,可以帮助我们对数据进行曲线拟合。
本文将介绍如何使用Matlab进行曲线拟合,并给出一些实际案例。
一、简单线性回归简单线性回归是曲线拟合中最基础的一种方法。
它假设数据可以用一条直线来表示。
在Matlab中,使用"polyfit"函数可以很方便地进行简单线性回归。
该函数可以从数据中拟合出一个多项式,我们可以选择线性多项式来进行简单线性回归。
下面是一个例子:```matlabx = [1, 2, 3, 4, 5];y = [2, 3, 4, 5, 6];p = polyfit(x, y, 1);f = polyval(p, x);plot(x, y, 'o'); % 绘制原始数据点hold on;plot(x, f, 'r-'); % 绘制拟合曲线```在这个例子中,我们有一个包含5个数据点的数据集,分别存储在向量"x"和"y"中。
通过polyfit函数,我们可以拟合出一个线性多项式的系数"p",然后使用polyval函数来计算拟合曲线上各个x点对应的y值。
最后,使用plot函数将原始数据点和拟合曲线绘制在同一张图上。
这样我们就可以直观地看到拟合效果。
二、非线性曲线拟合除了简单线性回归,Matlab还提供了许多其他方法来进行非线性曲线拟合。
这些方法通常需要指定一个函数形式,然后通过调整函数的参数来拟合数据。
其中最常用的方法之一是最小二乘法。
在Matlab中,可以使用lsqcurvefit函数来进行非线性曲线拟合。
下面是一个例子:```matlabx = [1, 2, 3, 4, 5];y = [5.1, 6.2, 7.1, 8.5, 9.9];f = @(c,x) c(1) * exp(-c(2)*x) + c(3); % 定义拟合函数c0 = [1, 1, 1]; % 初始参数猜测c = lsqcurvefit(f, c0, x, y); % 进行曲线拟合plot(x, y, 'o'); % 绘制原始数据点hold on;plot(x, f(c, x), 'r-'); % 绘制拟合曲线```在这个例子中,我们有一个包含5个数据点的数据集,存储在向量"x"和"y"中。
用MATLAB作线性和非线性最小二乘法拟合

新乡学院数学与信息科学系实验报告
实验名称插值与拟合Ⅱ
所属课程数学软件与实验
实验类型综合型实验
专业信息与计算科学
班级 2011级1班
学号
姓名李欢丽
指导教师朱耀生老师
4.结论及分析
经多次试验可知分析无误
问题二增加生产、发展经济所依靠的主要因素有增加投资、增加劳动力以及技术革新等,在研究国民经济产值与这些因素的数量关系时,由于技术水平不像资金、劳动力那样容易定量化,作为初步的模型,可认为技术水平不变,只讨论产值和资金、劳动力之间的关系。
在科学技术发展不快时,如资本主义经济发展的前期,这种模型是有意义的。
用Q,K,L分别表示产值、资金、劳动力,要寻求的数量关系。
经过简化假设与分析,在经济学中,推导出一个著名的Cobb-Douglas生产函数:(*)
式中
要由经济统计数据确定。
现有美国马萨诸塞州1900—1926年上述三个经济指数的统计数据,如下表,试用数据拟合的方法,求出式(*)中的参数。
表2
t Q K L t Q K L
1900 1.05 1.04 1.05 1901 1.18 1.06 1.08 1902 1.29 1.16 1.18 1903 1.30 1.22 1.22 1914 2.01 3.24 1.65 1915 2.00 3.24 1.62 1916 2.09 3.61 1.86 1917 1.96 4.10 1.93。
用Matlab进行数据拟合

x0 x1 x*
xn
节点可视为由 y = g(x) 产生,
g 表达式复杂, 甚至无表达式
实用插 值方法
1.分段线性插值
••• •
• •
2. 三次样条插值
x0
xj-1 xj xj+1 xn
细木条: 样条
机翼下轮廓 线
用Matlab作插值计算
1. 分段线性插值: 已有程序 y=interp1(x0,y0,x) y=interp1(x0,y0,x,’linear’)
t=[0:1:16] y=[30.0 29.1 28.4 28.1 28.0 27.7 27.5 27.2 27.0 26.8 26.5 26.3 26.1 25.7 25.3 24.8 24.0] plot(t,y,'*')
a=polyfit(t,y,1)
a= -0.3012 29.3804
hold on
化为 k1, k2 的线性函数.
于是,
ln= σ ε
ln k1 − k2ε
σ
令
z
= ln ,
ε
a0
= −k2 , a1
= ln k1
即 =z a0ε + a1
在命令窗口输入:
x=[500*1.0e-6 1000*1.0e-6 1500*1.0e-6 2000*1.0e-6 2375*1.0e-6] y=[3.103*1.0e+3 2.465*1.0e+3 1.953*1.0e+3 1.517*1.0e+3 1.219*1.0e+3] z=log(y) a=polyfit(x,z,1) k1=exp(8.3009) w=[1.55 2.47 2.93 3.03 2.89] plot(x,w,'*')
matlab非线性拟合函数lsqcurvefit

matlab非线性拟合函数lsqc urvef it---logist ic人口模型参数估计x= lsqcur vefit(fun,x0,xdata,ydata)x = lsqcur vefit(fun,x0,xdata,ydata,lb,ub)x = lsqcur vefit(fun,x0,xdata,ydata,lb,ub,option s)x = lsqcur vefit(proble m)[x,resnor m] = lsqcur vefit(...)[x,resnor m,residu al] = lsqcur vefit(...)[x,resnor m,residu al,exitfl ag] = lsqcur vefit(...)[x,resnor m,residu al,exitfl ag,output] = lsqcur vefit(...)[x,resnor m,residu al,exitfl ag,output,lambda] = lsqcur vefit(...)[x,resnor m,residu al,exitfl ag,output,lambda,jacobi an] = lsqcur vefit(.. .)x0为初始解向量;xdata,ydata为满足关系y data=F(x, xdata)的数据;lb、ub为解向量的下界和上界,若没有指定界,则lb=[ ],ub=[ ];option s为指定的优化参数;fun为拟合函数,其定义方式为:x = lsqcur vefit(@myfun,x0,xdata,ydata),其中myfu n已定义为 functi on F = myfun(x,xdata)F = … % 计算x处拟合函数值fu n的用法与前面相同;resnor m=sum ((fun(x,xdata)-ydata).^2),即在x处残差的平方和;residu al=fun(x,xdata)-ydata,即在x处的残差;exitfl ag为终止迭代的条件;output为输出的优化信息;lambda为解x处的Lagra nge乘子;jacobi an为解x处拟合函数fun的j acobi an矩阵。
