第12章习题解答
运营管理第6版习题与参考答案_第12章

习题与参考答案_第12章一、名词解释1、作业计划答案:把企业的作业任务分解为短期的具体任务,规定每个环节(如车间、工段、生产线和工作站)、每个单位时间(周、日、班或小时)的具体任务,并组织计划的实施。
答案解析:略。
难易程度:易。
知识点:作业计划。
2、排序答案:确定各个作业在加工中心的处理顺序。
答案解析:略。
难易程度:易。
知识点:排序。
3、先到先服务准则(FCFS)答案:优先选择最早进入可排序列的作业,也就是按照作业到达的先后顺序进行加工。
答案解析:略。
难易程度:中。
知识点:先到先服务准则(FCFS)。
4、最短作业时间准则(SPT)答案:优先选择作业时间最短的作业。
答案解析:略。
难易程度:中。
知识点:最短作业时间准则(SPT)。
5、最早交货期准则(EDD)答案:优先选择完工期限最紧的作业。
答案解析:略。
难易程度:中。
知识点:最早交货期准则(EDD)。
6、最短松驰时间准则(SST)答案:优先选择松弛时间最短的作业。
答案解析:略。
难易程度:中。
知识点:最短松驰时间准则(SST)。
7、最长剩余作业时间准则(MWKR)答案:优先选择余下作业时间最长的作业。
答案解析:略。
难易程度:中。
知识点:最长剩余作业时间准则(MWKR)。
8、最短剩余作业时间准则(LWKR)答案:优先选择余下作业时间最短的作业。
答案解析:略。
难易程度:中。
知识点:最短剩余作业时间准则(LWKR)。
9、最多剩余作业数准则(MOPNR)答案:优先选择余下作业数最多的工件。
答案解析:略。
难易程度:中。
知识点:最多剩余作业数准则(MOPNR)。
10、最小临界比准则(SCR)答案:优先选择临界比最小的作业。
答案解析:略。
难易程度:中。
知识点:最小临界比准则(SCR)。
11、随机准则(Random)答案:随机地挑选出一项作业。
答案解析:略。
难易程度:中。
知识点:随机准则(Random)。
12、生产调度答案:生产调度部门,行使调度权力,协助各级行政领导指挥生产,协调各部门工作,处理生产中出现的问题。
组织胚胎学习题 第12章

第12章免疫系统一、A型题1.关于胸腺,哪项错误( )A.是培育T细胞的中枢淋巴器官B.在抗原刺激下,胸腺细胞增殖分化成T细胞C.培育中的胸腺细胞,只有5%能分化成初始T细胞D.胸腺小体仅分布于髓质2.胸腺上皮细胞的主要功能是( )A.向胸腺细胞呈递抗原信息B.形成网状纤维,构成胸腺支架C.分泌胸腺激素,培育T淋巴细胞D.分泌细胞因子,保护胸腺细胞3.血-胸腺屏障的血管周隙内常有( )A.白细胞B.胸腺细胞C.巨噬细胞D.成纤维细胞4.胸腺小体位于( )A.皮质和髓质B.皮质与髓质交界处C.髓质D.皮质5.关于胸腺,哪项错误( )A.属于中枢淋巴器官B.胸腺实质分为皮质和髓质C.髓质内有胸腺小体D.皮质内有许多淋巴小结6.淋巴结内毛细血管后微静脉主要分布于( )A.浅层皮质B.皮质与髓质交界处C.髓索D.副皮质区二、C型题A. T淋巴细胞C.两者皆是B.B淋巴细胞D.两者皆非7.在骨髓内早期分化( )8.在胸腺内早期分化( )9.表面有特异性抗原受体( )10.效应细胞分泌抗体( )11.类型多,分工细()三、X型题12.下列哪些细胞属于抗原提呈细胞( )A.巨噬细胞B.郎格汉斯细胞C.交错突细胞D.网状细胞13.属于单核吞噬细胞系统的有( )A.肺巨噬细胞B.小胶质细胞C.破骨细胞D.网状细胞14.血液内淋巴细胞进入淋巴组织的通道是( )A.脾血窦B.淋巴结的毛细血管后微静脉C.脾的边缘窦D.胸腺小体四、名词解释1.B细胞(B-lymphocyte)2.胸腺依赖区(thymus dependent area)五、论述题、1.试述单核吞噬细胞系统的组成、分布和功能特点。
2.简述淋巴细胞再循环的途径和意义。
【参考答案】一、A型题:1.B2.C3. C4. C5. D6.D二、C型题:7. B 8. A 9.C 10.B 11. A三、X型题:12. ABC 13. ABC 14. ABC四、名词解释1. B细胞(B-lymphocyte)即骨髓依赖淋巴细胞。
机械课后习题答案第12章习题及解答

(2) 由表 14.8 查得 fT=0.95,载荷负荷平稳,由表 14.9 查得 fF=1.0,对球轴承取=3, 对
滚子轴承=10/3。将以上有关数据代入下式
Lh
106 60n
fT C fPF
对球轴承
Lh
106 0.95 22800 3 60 1000 5880
833.1
h,
不满足要求,
再选 6408 (Cr=50200, C0r=37800),得
T 9.55106 P 9.55106 2.6 64661.4 N·mm
n
384
Ft 2T1 129322.8 2917.5 N d1 44.326
Fr 1107.5 N
Fa 864.2 N
(2) 计算轴向力
R2V=457.98 R1V=649.5 R1H= R2H =1458.75
由机械零件设计手册得 30307 圆锥滚子轴承的 Cr=71200 N, C0r=50200 N , Y = 1.9, e=0.31 表 14.12 可知圆锥滚子轴承轴承的内部轴向力 SA、SB 为
S1= R1/2Y=584/(2×1.9)=153.6 N S2= R2/2Y=1776/(2×1.9)=467.4 N
h
所选轴承型号为 N410 合适。
12.15一齿轮轴由一对 30206 轴承支承,支点间的跨距为 200 mm,齿轮位于两支点的中央。
已知齿轮模数 mn=2.5 mm,齿数 z1=17,螺旋角=16.5,传递功率 P=2.6 kW,齿轮轴
的转速 n=384r/min。试求轴承的额定寿命。
解: (1) 计算齿轮的作用力
每个轴承的径向载荷 R=5880 N,载荷平稳,工作温度 t=125C,预期寿命 Lh=5000 h,
《大学物理学》习题解答(第12章 静电场中的导体和电介质)(1)

(2)两输电线的电势差为 U
xR
E dl
R
Ed x
d R ln 0 R
(3)输电线单位长度的电容 C
U
0 / ln
d R d 0 / ln 4.86 1012 F R R
【12.9】半径为 R1 的导体球被围在内半径为 R2 、外半径为 R3 、相对电容率为 r 的介质球壳内,它们是同 球心的。若导体带电为 Q ,则导体内球表面上的电势为多少? 【12.9 解】先求各区域电场 (1)
Q 4 0 R3
( R3 r )
B 球壳为等势体,其电势为
V
R3
E dr
Q 4 0
R3
r
dr
2
【12.2】一导体球半径为 R1,外罩一半径为 R2 的同心薄导体球壳,外球壳所带总电荷为 Q,而内球的电势为 V0.求此系统的电势和电场分布。 【12.2 解】已知内球电势为 V0 ,外球壳带电 Q 。 (1)先求各区域的电场强度:设内球带电荷 q 。由高斯定理,有
E
U
z
2R
( 1 )一根带电 的输电线在两线之间、距其轴心 x 处 p 点的场强为
x
dx
p
E i 2 0 x
另一根带电 的输电线在 p 点产生的电场强度为
x
E
2 0 ( d x )
i
p 点的总电场强度为
E E E
d R
1 1 ( )i 2 0 x d x
E1 0
(r R1 ) ( R1 r R2 ) 4 r 2 D Q , D 0 r E3
第12章 习题(带答案)

9、垄断厂商利润最大化时( A C P=MR=MC; P>MR=MC;
10、完全垄断厂商的平均收益曲线为直线时,边际收益曲线也是直线。边际收益曲线的 斜率为平均收益曲线斜率的( A )。 A 2 倍; B 1/2 倍; C 1 倍; D 4 倍。
11、若一个管理机构对一个垄断厂商的限价正好使经济利润消失,则价格要等于( C )。 A C 边际收益; 平均成本; B D D B D 边际成本; 平均可变成本。 )。 取得最大利润; 上述情况都可能发生。 D )。
dTC 2Q 40 . dQ
该厂商实行三级价格歧视时利润最大化的原则可以写为 MR1=MR2=MC. 于是: 关于第一个市场: 根据 MR1=MC,有: 120-20Q1=2Q+40 关于第二个市场: 根据 MR2=MC,有: 7Q2=10 即 22Q1+2Q2=80
1 1 ),得 116=138( 1 )解得 ed ≈6 ed ed
所以,厂商长期均衡时主观需求曲线 d 上的需求的价格点弹性 ed ≈6. (3)令该厂商的线性的主观需求 d 曲线上的需求的函数形式 P=A-BQ,其中,A 表示该线 性需求 d 曲线的纵截距,-B 表示斜率.下面,分别求 A 值和 B 值. 根据线性需求曲线的点弹性的几何意义,可以有 ed
A.如果在某一行业中存在许多厂商,则这一市场是完全竞争的 B.如果厂商所面临的需求曲线是向下倾斜的,则这一市场是不完全竞争的 C.如果行业中所有厂商生产相同的产品,且厂商的数目大于 1,则这个市场是不完全竞争的 D.如果某一行业中有不止一家厂商,他们都生产相同的产品,都有相同的价格,则这个市场 是完全竞争的 2、垄断厂商面临的需求曲线是( A 向下倾斜的; A )。 B 向上倾斜的;
电工与电子技术第十二章习题详解(陶桓齐)华中科技大学出版社
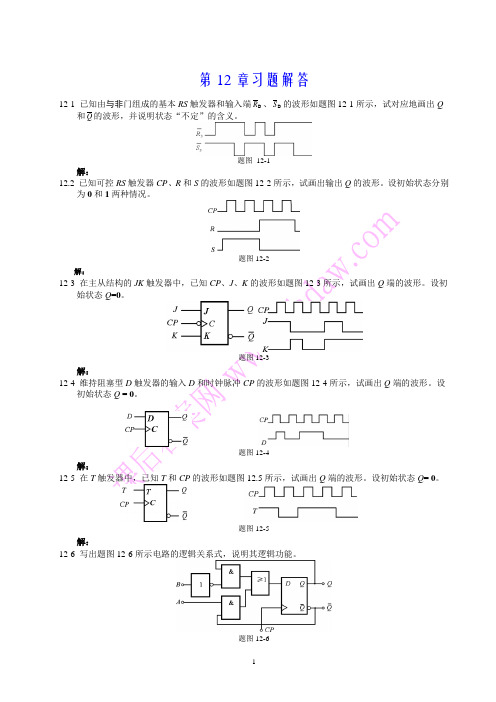
第12章习题解答12-1 已知由与非门组成的基本RS触发器和输入端D R、D S的波形如题图12-1所示,试对应地画出Q 和Q的波形,并说明状态“不定”的含义。
题图12-1解:12.2 已知可控RS触发器CP、R和S的波形如题图12-2所示,试画出输出Q的波形。
设初始状态分别为0和1两种情况。
题图12-2解:12-3 在主从结构的JK触发器中,已知CP、J、K的波形如题图12-3所示,试画出Q端的波形。
设初始状态Q=0。
题图12-3解:12-4 维持阻塞型D触发器的输入D和时钟脉冲CP的波形如题图12-4所示,试画出Q端的波形。
设初始状态Q = 0。
题图12-4解:12-5 在T触发器中,已知T和CP的波形如题图12.5所示,试画出Q端的波形。
设初始状态Q= 0。
题图12-5解:12-6 写出题图12-6所示电路的逻辑关系式,说明其逻辑功能。
题图12-6解:逻辑关系为:Q D AQ BQ==+所以其功能为JK触发器。
12-7 如题图12-7所示的电路和波形,试画出D端和Q端的波形。
设初始状态Q= 0。
题图12-7解:12-8 将主从型JK触发器转换为T'触发器有几种方案?画出外部连线图。
解:12-9 电路如题图12-9所示。
画出Q0端和Q1端在六个时钟脉冲CP作用下的波形。
设初态Q1=Q0= 0。
题图12-9解:12-10 用题图12.10(a)所给器件构成电路,并在示波器上观察到如图12.10(b)所示波形。
试问电路是如何连接的?请画出逻辑电路图。
(a) (b)题图12-10解:12-11 已知如题图12.11(a)所示电路的各输入端信号如题图12-11(b)所示。
试画出触发器输出端Q0和Q1的波形。
设触发器的初态均为0。
(a) (b)题图12-11解:12-12 已知电路和时钟脉冲CP及输入端A的波形如题图12-12所示,试画出输出端Q、1Q的波形。
假定各触发器初态为1。
(a ) (b )题图12-12解:12-13 已知题图12-13(a )所示电路中输入A 及CP 的波形如题图12-13(b )所示。
无机化学(上册):第12章 氧化还原与电化学 习题与答案

第12章氧化还原与电化学习题与详细答案1.计算下列化合物中右上角带“*”元素的氧化态:KCl*O3,NaCl*O,H2O*2,O*3,S*8,C*60,KO*2,Na2S*2O3,Cr*2O72-,S*4O62-,N*H4+,N*2H4,Fe*3O4,Ni*(CO)4,Na[Co*(CO)4],H[Mn*(CO)5],[Fe*(CN)6]4-,[Fe(N*CS)6]3-.解:+5 +1 -1 0 0 0 -½ +2 +6 +2.5 -3KCl*O3,NaCl*O,H2O*2,O*3,S*8,C*60,KO*2,Na2S*2O3,Cr*2O72-,S*4O62-,N*H4+,-2 +8/3 0 -1 -1 +2 -3N*2H4,Fe*3O4,Ni*(CO)4,Na[Co*(CO)4],H[Mn*(CO)5],[Fe*(CN)6]4-,[Fe(N*CS)6]3-.2.用“氧化数法”配平以下列各氧化还原反应的方程式;(8)-(15)同时用“离子-电子法”配平:(1)AgNO3(s) → Ag(s) + NO2(g) + O2(g)(2)(NH4)2Cr2O7(s) → N2(g) + Cr2O3(s)(3)H2O2(aq) → H2O(l) + O2(g)(4)Cu(s) + HNO3(稀)→ Cu(NO3)2 + NO(g)(5)CuS(s) + HNO3(浓)→ CuSO4 + NO2(g)(6)H2S(g) + H2SO4(浓)→ S(s) + SO2(g)(7)C(s) + H2SO4(浓)→ CO2(g) + SO2(g) + H2O(8)SO2(g) + MnO4-→ Mn2+ + SO42-(9)Cr2O72- + H2O2→ Cr3+ + O2(g)(10)CrO42- + CN-→ Cr(OH)3(s) + OCN-(11)Cl2(g) + CN- + OH-→ Cl- + OCN-(12)I2(s) + OH-→ I- + IO3-(13)I- + IO3-→ I2(s) + H2O(14)I2(s) + S2O32-→ I- + S4O62-(15)NaBiO3(s) + Mn2+ + H+→ Bi3+ + MnO4-解:(1)氧化数+1 +5 -2 0 +4 -2 02 AgNO3(s) = 2 Ag(s) + 2 NO2(g) + O2(g)(2)(NH4)2Cr2O7(s) = N2(g) + Cr2O3(s) + 4 H2O(3)2 H2O2(aq) = 2 H2O(l) + O2(g)(4)3 Cu(s) + 8 HNO3(稀)= 3 Cu(NO3)2 + 2 NO(g) + 4 H2O(5)CuS(s) + 8 HNO3(浓)= CuSO4 + 8 NO2(g) + 4 H2O(6)H2S(g) + H2SO4(浓)= S(s) + SO2(g) + 2 H2O(7)C(s) + 2 H2SO4(浓)→ CO2(g) + 2 SO2(g) + 2 H2O(8)“氧化数法”:5 SO2(g) + 2 MnO4- + 2 H2O = 2 Mn2+ + 5 SO42- + 4 H+“离子-电子法”:5 SO2(g) + 10 H2O = 5 SO42- + 20 H+ + 10 e2 MnO4- + 10 e + 16 H+ = 2 Mn2+ + 5 SO42-两式相加,得:5 SO2(g) + 2 MnO4- + 2 H2O = 2 Mn2+ + 5 SO42- + 4 H+(9)“氧化数法”:Cr2O72- + 3 H2O2 + 8 H+ = 2 Cr3+ + 3 O2(g) + 7 H2O“离子-电子法”:3 H2O2 = 3 O2(g) + 6 H+ + 6 eCr2O72- + 14 H+ + 6 e = 2 Cr3+ + 7 H2O两式相加,得:Cr2O72- + 3 H2O2 + 8 H+ = 2 Cr3+ + 3 O2(g) + 7 H2O (10)“氧化数法”:2 CrO42- + 3 CN- + 5 H2O = 2 Cr(OH)3(s) + 3 OCN- + 4 OH-“离子-电子法”:3 CN- + 6 OH- = 3 OCN- + 3 H2O + 6 e2 CrO42- + 8 H2O + 6 e = 2 Cr(OH)3(s) +10 OH-两式相加,得:2 CrO42- + 3 CN- + 5 H2O = 2 Cr(OH)3(s) + 3 OCN- + 4 OH- (11)“氧化数法”:Cl2(g) + CN- + 2 OH- = 2 Cl- + OCN- + H2O“离子-电子法”:CN- + 2 OH- = OCN- + H2O + 2 eCl2(g) + 2 e = 2 Cl- + H2O两式相加,得:Cl2(g) + CN- + 2 OH- = 2 Cl- + OCN- + H2O(12)“氧化数法”:3 I2(s) + 6 OH- = 5 I- + IO3- + 3 H2O“离子-电子法”:I2(s) + 12 OH- = 2 IO3- + 6 H2O + 10 e5 I2(s) + 10 e = 10 I-两式相加,约简系数,得:3 I2(s) + 6 OH- = 5 I- + IO3- + 3 H2O(13)“氧化数法”:5 I- + IO3- + 6 H+ = 3 I2(s) + 3 H2O“离子-电子法”:10 I- = 5 I2(s) + 10 e2 IO3- + 12 H+ + 10 e = I2(s) + 6 H2O两式相加,约简系数,得:5 I- + IO3- + 6 H+ = 3 I2(s) + 3 H2O(14)“氧化数法”:I2(s) + 2 S2O32- = 2 I- + S4O62-“离子-电子法”:2 S2O32- = S4O62- + 2 eI2(s) + 2 e = 2 I-两式相加,得:I2(s) + 2 S2O32- = 2 I- + S4O62-(15)“氧化数法”:5 NaBiO3(s) + 2 Mn2+ + 14 H+ = 5 Bi3+ + 5 Na+ + 2 MnO4- + 7 H2O “离子-电子法”:2 Mn2+ + 8 H2O= 2 MnO4- + 16 H+ + 10 e5 NaBiO3(s) + 30 H+ + 10 e = 5 Bi3+ + 5 Na+ + 15 H2O两式相加,得:5 NaBiO3(s) + 2 Mn2+ + 14 H+ = 5 Bi3+ + 5 Na+ + 2 MnO4- + 7 H2O 3.含氰(CN-)工业废水可以用漂白粉[有效成份Ca(ClO)2]或氯气或H2O2在碱性介质中进行氧化处理后排放,写出各反应方程式。
大学物理课后习题答案(上下册全)武汉大学出版社 第12章 习题解答

第12章 习题与答案12-1 在真空中波长为λ的单色光,在折射率为n 的透明介质中从A 沿某路径传播到B ,若A 、B 两点相位差为3π,则此路径AB 的光程为[ ]A. 1.5λ.B. 1.5λ/n .C. 1.5n .D. 3λ. [答案:A ]12-2 平行单色光垂直照射到薄膜上,经上下两表面反射的两束光发生干涉,若薄膜的厚度为e ,并且n 1<n 2>n 3,λ1为入射光在折射率为n 1的媒质中的波长,则两束反射光在相遇点的相位差为[ ]A. 2πn 2e / ( n 1λ1).B. 4πn 1e / ( n 2λ1)] +π.C. 4πn 2e / ( n 1λ1) ]+π.D. 4πn 2e / ( n 1λ1).[答案: C ]12-3 两块平玻璃构成空气劈形膜,左边为棱边,用单色平行光垂直入射.若上面的平玻璃以棱边为轴,沿逆时针方向作微小转动,则干涉条纹的[ ]A. 间隔变小,并向棱边方向平移.B. 间隔变大,并向远离棱边方向平移.C. 间隔不变,向棱边方向平移.D.间隔变小,并向远离棱边方向平移. [答案: A ]12-4 用劈尖干涉法可检测工件表面缺陷,当波长为λ的单色平行光垂直入射时,若观察到的干涉条纹如题12-4图所示,每一条纹弯曲部分的顶点恰好与其左边条纹的直线部分的连线相切,则工件表面与条纹弯曲处对应的部分[ ]A. 凸起,且高度为4λ.B. 凸起,且高度为2λ.C. 凹陷,且深度为2λ.D. 凹陷,且深度为4λ.[答案: C ]12-5 若把牛顿环装置(都是用折射率为1.52的玻璃制成的)由空气搬入折射率为1.33的水中,则干涉条纹[ ]A .中心暗斑变成亮斑. B. 间距变大. C. 间距变小. D. 间距不变. [答案: C ]题12-4图12-6 在光栅光谱中,假如所有偶数级次的主极大都恰好在单缝衍射的暗纹方向上,因而实际上不出现,那么此光栅每个透光缝宽度a 和相邻两缝间不透光部分宽度b 的关系为[ ] A. =3a b . B. =2a b . C. =a b . D. =0.5a b [答案: C ]12-7 对某一定波长的垂直入射光 衍射光栅的屏幕上只能出现零级和一级主极大,欲使屏幕上出现更高级次的主极大,应该[ ]A. 换一个光栅常数较小的光栅.B. 换一个光栅常数较大的光栅.C. 将光栅向靠近屏幕的方向移动.D. 将光栅向远离屏幕的方向移动.[答案: B ]12-8如果两个偏振片堆叠在一起,且偏振化方向之间夹角为60°,光强为I 0的自然光垂直入射在偏振片上,则出射光强为[ ]A. I 0 / 8.B. I 0 / 4.C. 3 I 0 / 8.D. 3 I 0 / 4.[答案: A ]12-9一束自然光自空气射向一块平板玻璃(如题12-9图),设入射角等于布儒斯特角i 0,则在上表面的出射光2是[ ]A. 自然光.B. 线偏振光且光矢量的振动方向平行于入射面.C. 线偏振光且光矢量的振动方向垂直于入射面.D. 部分偏振光.[答案: C ]12-10相干光的必要条件为________________________,________________________,________________________。
人教版数学八年级上册 第12章 12.1---12.2练习题含答案

12.1全等三角形一.选择题1.如图,△ABD≌△CDB,下面四个结论中,不正确的是()A.∠ABD=∠CBD B.△ABD和△CDB的周长相等C.AD=BC D.△ABD和△CDB的面积相等2.如图所示,△ABC≌△DEC,∠ACB=60°,∠BCD=100°,点A恰好落在线段ED上,则∠B的度数为()A.50°B.60°C.55°D.65°3.已知:△ABC≌△DCB,若BC=10cm,AB=5cm,AC=7cm,则CD为()A.10cm B.7cm C.5cm D.5cm或7cm4.如图,Rt△ABC≌Rt△CED,点B、C、E在同一直线上,则结论:①AC=CD,②AC ⊥CD,③BE=AB+DE,④AB∥ED,其中成立的有()A.仅①B.仅①③C.仅①③④D.①②③④5.已知图中的两个三角形全等,则∠α的度数为()A.105°B.75°C.60°D.45°6.下列说法不正确的是()A.全等三角形对应角平分线相等,对应边上的高、中线也分别相等B.全等三角形的周长和面积都相等C.全等三角形的对应角相等,对应边相等D.全等三角形是指周长和面积都相等的三角形7.如图,△ABC≌△DEF,BE=2,AE=1,则BD的长是()A.5 B.4 C.3 D.28.已知:如图,△ABC≌△ADE,AB与AD是对应边,AC与AE是对应边,若∠B=31°,∠C=95°,∠EAB=20°,则∠BAD等于()A.77°B.74°C.47°D.44°9.已知△ABC与△DEF全等,BC=EF=4cm,△ABC的面积是12cm2,则EF边上的高是()A.3cm B.4cm C.6cm D.无法确定10.如图,已知△ABC≌△EDF,点F,A,D在同一条直线上,AD是∠BAC的平分线,∠EDA=20°,∠F=60°,则∠DAC的度数是()A.50°B.60°C.100°D.120°二.填空题11.如图,△ABC≌△DEF,∠A=35°,∠B=50°,则∠DFE=.12.已知:如图,△ABC≌△DEF,∠A=85°,∠B=60°,AB=8,EH=2.则∠F的度数;DH的长.13.已知△ABC≌△DEF,AB=DE=8cm,△DEF的面积为20cm2,则△ABC的边AB上的高为cm.14.如图,已知△ABC≌△DEF,AD=1cm,则BE的长为cm.15.如图,已知△ABC≌△DBE,如果∠CBD=96°,∠CBE=28°,那么∠ABC=.三.解答题16.如图,A,D,E三点在同一直线上,且△BAD≌△ACE.(1)求证:BD=DE+CE;(2)请你猜想△ABD满足什么条件时,BD∥CE.17.如图,已知△ABF≌△CDE.(1)若∠B=30°,∠DCF=40°,求∠EFC的度数;(2)求证:AE=CF.18.如图,△ACF≌△DBE,其中点A、B、C、D在同一条直线上.(1)若BE⊥AD,∠F=63°,求∠A的大小.(2)若AD=11cm,BC=5cm,求AB的长.19.已知:如图,△ABC≌△DEF,AM、DN分别是△ABC、△DEF的对应边上的高.求证:AM=DN.参考答案与试题解析一.选择题1.【解答】解:A、∵△ABD≌△CDB,∴∠ABD=∠CBD,选项说法错误;B、∵△ABD≌△CDB,∴△ABD和△CDB的周长相等,选项说法正确;C、∵△ABD≌△CDB,∴AD=BC,选项说法正确;D、∵△ABD≌△CDB,∴△ABD和△CDB的面积相等,选项说法正确;故选:A.2.【解答】解:∵△ABC≌△DEC,∴∠DCE=∠ACB=60°,AC=CD,∠D=∠BAC,∴∠D=∠DAC,∵∠BCD=100°,∠ACB=60°,∴∠ACD=∠BCD﹣∠ACB=100°﹣60°=40°,∴∠BAC=∠D=×(180°﹣40°)=70°,∴∠B=180°﹣∠ACB﹣∠BAC=180°﹣70°﹣60°=50°,故选:A.3.【解答】解:∵△ABC≌△DCB,∴CD=AB=5cm,故选:C.4.【解答】解:∵Rt△ABC≌Rt△CED,∴AC=CD,①成立;∵Rt△ABC≌Rt△CED,∴∠1=∠D,又∠2+∠D=90°,∴∠2+∠1=90°,即∠ACD=90°,∴AC⊥DC,②成立;∵Rt△ABC≌Rt△CED,∴AB=CE,BC=ED,又BE=BC+EC,∴BE=ED+AB,③成立;∵∠B+∠E=180°,∴AB∥DE,④成立,故选:D.5.【解答】解:∵△ABC≌△DEF,∴∠D=∠A=60°,∴∠α=180°﹣60°﹣45°=75°,故选:B.6.【解答】解:A、全等三角形对应角平分线相等,对应边上的高、中线也分别相等,正确;B、全等三角形的周长和面积都相等,正确;C、全等三角形的对应角相等,对应边相等,正确;D、全等三角形是指形状和大小都相等的三角形,故D说法错误;故选:D.7.【解答】解:∵△ABC≌△DEF,∴AB=DE,∴BA﹣AE=DE﹣AE,∴AD=BE=2,∴BD=BE+AE+AD=2+1+2=5,故选:A.8.【解答】解:∵∠B=31°,∠C=95°,∴∠CAB=180°﹣∠B﹣∠C═54°,∵△ABC≌△ADE,∴∠EAD=∠CAB=54°,∵∠EAB=20°,∴∠BAD=∠EAB+∠EAD=74°,故选:B.9.【解答】解:∵△ABC与△DEF全等,△ABC的面积是12cm2,∴△DEF的面积为12cm2,∵BC=EF=4cm,∴EF边上的高为2×12÷4=6(cm).故选:C.10.【解答】解:∵△ABC≌△EDF,∠EDA=20°,∠F=60°,∴∠B=∠EDF=20°,∠F=∠C=60°,∴∠BAC=180°﹣∠B﹣∠C=100°,∵AD是∠BAC的平分线,∴∠DAC=∠BAC=50°,故选:A.二.填空题(共5小题)11.【解答】解:∵∠A=35°,∠B=50°,∴∠ACB=180°﹣35°﹣50°=95°,∵△ABC≌△DEF,∴∠EFD=∠ACB=95°.故答案为:95°.12.【解答】解:∵∠A=85°,∠B=60°,∴∠C=35°,∵△ABC≌△DEF,∴∠F=∠C=35°,∵△ABC≌△DEF,∴DE=AB=8,∴DH=DE﹣EH=6,故答案为:35°;6.13.【解答】解:如图所示:过C作CH⊥AB,∵△ABC≌△DEF,∴S△ACB =S△DEF=20cm2,∵AB=8cm,∴ABCH=20,解得:CH=5cm.故答案为:5.14.【解答】解:∵△ABC≌△DEF,∴DE=AB,∴DE﹣AE=AB﹣AE,∴AD=EB=1cm,故答案为:1.15.【解答】解:∵△ABC≌△DBE,∴∠ABC=∠DBE,即∠ABE+∠CBE=∠ABE+∠ABD,∴∠ADB=∠CBE=28°,∴∠ABC=∠CBD﹣∠ABD=96°﹣28°=68°.故答案为68°.三.解答题(共4小题)16.【解答】(1)证明:∵△BAD≌△ACE,∴AD=CE,BD=AE,∵A,D,E三点在同一直线上,∴AE=AD+DE,∴BD=CE+DE;(2)解:假如BD∥CE,则∠BDE=∠E,∵△BAD≌△ACE,∴∠ADB=∠E,∴∠ADB=∠BDE,又∵∠ADB+∠BDE=180°,∴∠ADB=∠BDE=90°,∴当∠ADB=∠E=90°时,BD∥CE.17.【解答】(1)解:∵△ABF≌△CDE,∴∠D=∠B=30°,∴∠EFC=∠D+∠DCF=70°;(2)证明:∵△ABF≌△CDE,∴∠AFB=∠CED,AF=CE,在△AFE和△CEF中,,∴△AFE≌△CEF(SAS),∴AE=CF.18.【解答】解:(1)∵BE⊥AD,∴∠EBD=90°,∵△ACF≌△DBE,∴∠FCA=∠EBD=90°,∴∠A=90°﹣∠F=27°;(2)∵△ACF≌△DBE,∴CA=BD,∴CA ﹣CB =BD ﹣BC ,即AB =CD , ∵AD =11cm ,BC =5cm , ∴AB +CD =11﹣5=6cm , ∴AB =3cm . 19.【解答】方法一: 证明:∵△ABC ≌△DEF , ∴AB =DE ,∠B =∠E ,∵AM ,DN 分别是△ABC ,△DEF 的对应边上的高, 即AM ⊥BC ,DN ⊥EF , ∴∠AMB =∠DNE =90°, 在△ABM 和△DEN 中,∴△ABM ≌△DEN (AAS ), ∴AM =DN . 方法二: ∵△ABC ≌△DEF12.2《全等三角形的判定》1、下列说法正确的是( )A 、全等三角形是指形状相同的两个三角形B 、全等三角形的周长和面积分别相等C 、全等三角形是指面积相等的两个三角形D 、所有的等边三角形都是全等三角形2、如图,若△ABE ≌△ACF ,且AB=5,AE=2,则EC 的长为( )A 、2B 、3C 、5D 、2.5 3、如图,若△ABC ≌△EAC ,则∠EAC 等于( )A 、∠ACB B 、∠BAFC 、∠CAFD 、∠BAC4、如图,AB=AD ,AE 平分∠BAD ,则图中有( )对全等三角形。
基础化学第8版-自测题及课后习题解答-第12章

0.05000mol ⋅ L−1 × 22.14 ×10−3 L × 252 g ⋅ mol−1
2. ω(C6H8O6 ) =
2 0.1988g
= 0.7045
章后习题解答
习题
1. 下列数据,各包括几位有效数字?
(1) 2.0321 (4) 0.01﹪
(2) 0.0215 (5) 1.0×10-5
(3) pKHIn = 6.30
学生自测答案
一、判断题 1.√ 2.× 3. √ 4.× 5.×
4
二、选择题
1.B 2.A 3.B 4.B 5.A
三、填空题
1. (1)酸碱浓度 2. (2)浓 HCl 易挥发 3. (3)10mL (4)40mL 四、问答题
1.答(1)H 2 C 2 O 4 ·H 2 O风化后会失去结晶水,使H 2 C 2 O 4 ·H 2 O变为H 2 C 2 O 4 ,由于H 2 C 2 O 4 的相对分 子质量小于H2C2O4·H2O,会使标定的NaOH溶液浓度偏低。(2)用于含有少量杂质,使所称的邻苯二 甲酸氢钾的物质的量减少,会使测定结果偏高。
3. 两人分析同一试样中的含铜量,其结果质量分数(ω)如下:
甲 0.3610
0.3612
0.3603
乙 0.364l
0.3642
0.3643
巳知此试样中含铜量的真实值为 0.3606。试问何人所得结果的准确度高?何人的结果精密度高?
为什么?
解 甲的 X = (0.3610 + 0.3612 + 0.3603)/3 = 0.3608
2.某一弱酸型指示剂HIn的pKHIn=4.1,那么它的理论变色范围是( )
A. 3.1∼5.1 B. 2.1∼3.1 C. 3.2∼6.2
第12章机械的效率__思考题及练习题解答

思考题及练习题解答5-1机械正反行程的效率是否相同?其自锁条件是否相同?原因何在?答:机械通常可以有正行程和反行程,它们的机械效率一般并不想等。
其自锁条件不相同,一般来说,正行程不自锁,而反行程可以自锁也可以不自锁。
因为一个具有自锁性的机械,只是在满足自锁条件的驱动力的作用下,在一定运动方向上产生自锁,而在其它运动方向上则不一定自锁。
而正反行程力的方向不同。
5-2 当作用在转动副中轴颈上的外力为一单力,并分别作用在其摩擦圆之内、之外或相切时,轴颈将作何种运动?当作用在转动副中轴颈上的外力为一力偶矩时,也会发生自锁吗? 答:(1)当外力作用在摩擦圆之内时,因外力对轴颈中心的力矩始终小于它本身所引起的最大摩擦力矩,因此出现自锁现象;当外力外力作用在摩擦圆之外时,因外力对轴颈中心的力矩大于它本身所引起的摩擦力矩,故轴颈将加速运动;当外力与其摩擦圆相切时,因外力对轴颈中心的力矩等于它本身所引起的摩擦力矩,故轴颈处于临界状态,将作等速运动(当轴颈原来是转动的)或静止不动(当轴颈原来是静止的)。
(2) 当作用在转动副中轴颈上的外力为一力偶矩时,若该力偶矩小于它本身所引起的摩擦力矩,也会发生自锁。
5-3眼镜用小螺钉(M1×0.25)与其他尺寸螺钉(例如M1×1.25)相比,为什么更容易发生自动松脱现象(螺纹中经=螺纹大径-0.65×螺距)? 答:M1×0.25螺钉的螺纹中径 mm mm d 8375.0)25.065.01(2=⨯-= 螺纹升角43.58375.025.0arctanarctan2===d p αM1×1.25螺钉的螺纹中径 mm mm d 1875.7)25.165.08(2=⨯-=' 螺纹升角αα<==='17.31875.725.1arctanarctan2d p综合螺旋副的自锁条件可知,眼镜用小螺钉较其它尺寸螺钉更容易发生自动松脱现象。
机械设计基础习题解答第12章

思考题及练习题12.1用轴肩或轴环可以对轴上零件作轴向固定吗?答:轴肩或轴环可以对轴上零件作单向轴向固定12.2圆螺母也可以对轴上零件作周向固定吗?答:圆螺母不能对轴上零件作周向固定,可以轴向固定。
12.3轴肩或轴环的过渡圆角半径是否应小于轴上零件轮毂的倒角高度? 答:轴肩或轴环的过渡圆角半径应小于轴上零件轮毂的倒角高度,以保证装拆方便可靠。
12.4汽车下部变速器与后桥间的轴是否传动轴?答:是传动轴。
12.5轴上零件的轴向固定方法有:1)轴肩和轴环;2)圆螺母与止动垫圈;3)套筒; 4)轴端挡圈和圆锥面;5)弹性挡圈、紧定螺钉或销钉等。
当受轴向力较大时,可采用几种方法?答:轴向力较大时,可采用:1)轴肩和轴环;2)圆螺母与止动垫圈;3)套筒; 4)轴端挡圈和圆锥面。
12.6若轴上的零件利用轴肩来轴向固定,轴肩的圆角半径R 与零件轮毅孔的圆角半径1R 或倒角1C 的关系如何?答:轴肩的圆角半径R 要小于零件轮毅孔的圆角半径1R 或倒角1C 。
12.7为了便于拆卸滚动轴承,轴肩处的直径d (或轴环直径)与滚动轴承内圈外径1D 应保持何种关系?答:1d D <,大约2 mm 。
12.8平键连接的工作原理是什么?主要失效形式是什么?平键的剖面尺寸b ×h 和键的长度L 是如何确定的?举例说明平键连接的标注方法。
答:工作原理:平键的上表面与轮毂键槽顶面留有间隙,依靠键与键槽间的两侧面挤压力 ,传递转矩 。
所以两侧面为工作面。
主要失效形式:键连接的主要失效形式是挤压破坏。
键的剖面尺寸b ×h 和键的长度L 的确定:按照轴的公称直径d ,从国家标准中选择平键的尺寸h b ×。
键的长度L 应略小于轮毂的长度,键长L 应符合标准长度系列。
12.9 圆头(A 型)、方头(B 型)及单圆头(C 型)普通平键各有何优缺点?它们分别用在什么场合?轴上的键槽是如何加工出来的?轮毂上的键槽是如何加工出来的?答:圆头(A 型)对中性好,安装方便,使用广泛;方头(B 型)应力集中小,对轴影响小。
第12章 羧酸衍生物习题解答
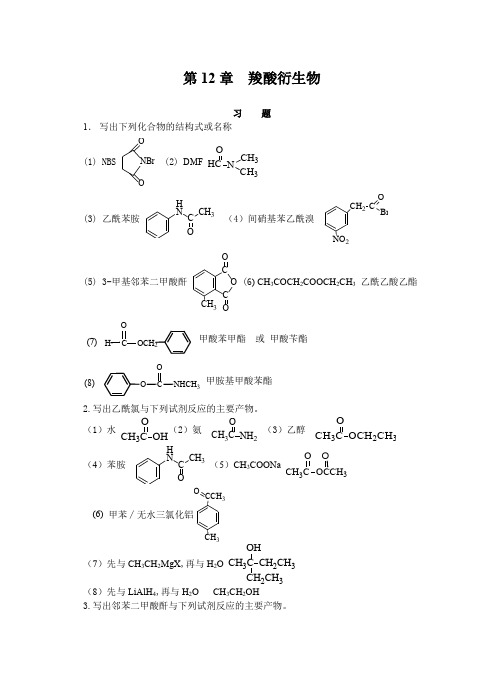
第12章 羧酸衍生物习 题1. 写出下列化合物的结构式或名称(1) NBSOONBr (2) DMF HC N O3CH 3(3) 乙酰苯胺H NC CH 3(4)间硝基苯乙酰溴CH 2NO 2CO Br(5) 3-甲基邻苯二甲酸酐CCH 3C O O (6) CH 3COCH 2COOCH 2CH 3 乙酰乙酸乙酯OCH 2CHO(7) 甲酸苯甲酯 或 甲酸苄酯O CONHCH 3(8)甲胺基甲酸苯酯2.写出乙酰氯与下列试剂反应的主要产物。
(1)水 CH 3C OHO (2)氨 CH 3C NH 2O(3)乙醇 CH 3C OCH 2CH 3O(4)苯胺HN C CH 3(5)CH 3COONa CH 3C 3O O (6) 甲苯∕无水三氯化铝CH 3CCH 3O(7)先与CH 3CH 2MgX ,再与H 2O CH 3C CH 2CH 3CH 2CH 3OH(8)先与LiAlH 4,再与H 2O CH 3CH 2OH3.写出邻苯二甲酸酐与下列试剂反应的主要产物。
(1)水∕△C C O OHOH (2)氨∕△ C C OONH 2ONH 4(3)乙醇∕△ C C O2CH 3OH (6)甲苯∕无水三氯化铝CC O OH CH 3(7)先与CH 3CH 2MgX ,再与H 2OC C OH CH 3OH CH 3 (8)先与LiAlH 4,再与H 2OCH 2OHCH 2OH4.写出乙酸苯酯与下列试剂反应的主要产物。
(1)水∕△CH 3C OCH 2CH 3OOH(2)氨∕△CH 3C NH 2OOH(3)甲酸乙酯∕乙醇钠 HCCH 2CO O(4)钠+乙醇 CH 3CH 2OH + OH(5)先与CH 3CH 2MgX ,再与H 2O CH 3C CH 2CH 3CH 2CH 3OHOH(6)先与LiAlH 4,再与H 2O CH 3CH 2OH +OH5.写出丁酰胺与下列试剂反应的主要产物。
第12章习题答案

第12章习题答案习题解答第12章⼀、填空题1.汽车、拖拉机装配中⼴泛采⽤完全互换法。
2. “⼊体原则”的含义为:当组成环为轴、键宽等时,上偏差取零,下偏差为负;对于孔、键槽宽等下偏差为零。
3.竖式计算的⼝诀为增环,上下偏差照抄;减环,上下偏差对调变号之后竖式相加。
⼆、判断题1. ⼀个尺⼨链须由增环、减环和封闭环组成。
(×)2. 零件是机械产品装配过程中最⼩的装配单元。
(√)3.零件尺⼨链中⼀般选择最重要的尺⼨作为封闭环。
(×)4. 封闭环的公差值⼀定⼤于任⼀组成环的公差值。
(√)三、简答题1.什么叫尺⼨链? 它有何特点?答:在机器装配或零件加⼯过程中,由相互连接的尺⼨形成封闭的尺⼨组,称为尺⼨链。
尺⼨链的主要特点:1)封闭性尺⼨链应该是⼀组关联尺⼨顺序⾸尾相接⽽形成的封闭轮廓,其中应包含⼀个间接保证的尺⼨和若⼲个与之有关的直接获得的尺⼨。
2)关联性尺⼨链内间接保证的尺⼨的⼤⼩和变化范围(即精度) 是受该链内直接获得的尺⼨⼤⼩和变化范围所制约的彼此间具有特定的函数关系2.如何确定⼀个尺⼨链的封闭环?如何区分组成环中的增环与减环?答:根据封闭环的特征,应查明加⼯或装配完成以后所⾃然形成的尺⼨为封闭环,它是由其它尺⼨派⽣出来的,通过其它尺⼨⽽间接保证的尺⼨。
⼀个尺⼨链中只能有⼀个封闭环。
从⼀系列组成环中分辨出增环和减环,有以下⼏种⽅法:a)按定义判断根据增环、减环的定义,逐个分析组成环尺⼨的增减对封闭环尺⼨的影响,以判断其为增环或减环。
此法⽐较⿇烦,在环数较多、链的结构较复杂时,容易产⽣差错,但这是基本⽅法。
b)按联结封闭环的形式判断凡与封闭环串联的组成环属于减环,与封闭环并联的则属于增环,当尺⼨链的结构形式较复杂时,这种判断⽅法更加简便。
c)按箭头⽅向(回路法)判断在封闭环符号下⽅按任意指向画箭头,从其⼀端起始,顺着⼀个⽅向,在各组成环的符号下⽅也加上箭头符号,使所画各箭头依次彼此头尾相连,凡箭头⽅向与封闭环相同者为减环,相反者为增环。
第12章 羧酸衍生物习题解答

第12章 羧酸衍生物习 题1. 写出下列化合物的结构式或名称(1) NBSOONBr (2) DMF HC N O3CH 3(3) 乙酰苯胺H NC CH 3(4)间硝基苯乙酰溴CH 22CO Br(5) 3-甲基邻苯二甲酸酐CCH 3C O O (6) CH 3COCH 2COOCH 2CH 3 乙酰乙酸乙酯OCH 2CHO(7) 甲酸苯甲酯 或 甲酸苄酯O ONHCH 3(8)甲胺基甲酸苯酯2.写出乙酰氯与下列试剂反应的主要产物。
(1)水 CH 3C OHO (2)氨 CH 3C NH 2O(3)乙醇 CH 3C OCH 2CH 3O(4)苯胺HN C CH 3(5)CH 3COONa CH 3C 3O O (6) 甲苯∕无水三氯化铝CH 3CCH 3O(7)先与CH 3CH 2MgX ,再与H 2O CH 3C CH 2CH 3CH 2CH 3OH(8)先与LiAlH 4,再与H 2O CH 3CH 2OH3.写出邻苯二甲酸酐与下列试剂反应的主要产物。
(1)水∕△C C O OHOH (2)氨∕△ C C OO2ONH 4(3)乙醇∕△ C C OOCH 2CH 3OH (6)甲苯∕无水三氯化铝CC O OH CH 3(7)先与CH 3CH 2MgX ,再与H 2OC C OH CH 3OH CH 3 (8)先与LiAlH 4,再与H 2OCH 2OHCH 2OH4.写出乙酸苯酯与下列试剂反应的主要产物。
(1)水∕△CH 3C OCH 2CH 3OOH(2)氨∕△CH 3C NH 2OOH(3)甲酸乙酯∕乙醇钠 HCCH 2CO O(4)钠+乙醇 CH 3CH 2OH + OH(5)先与CH 3CH 2MgX ,再与H 2O CH 3C CH 2CH 3CH 2CH 3OHOH(6)先与LiAlH 4,再与H 2O CH 3CH 2OH +OH5.写出丁酰胺与下列试剂反应的主要产物。
(1)水∕OH ˉ,△ CH 3CH 2CH 2COOH (2)氨∕△ 无反应 (3)Br 2∕NaOH CH 3CH 2CH 2NH 2(4)先与CH 3CH 2MgX ,再与H 2O CH 3CH 2CH 2C CH 2CH 3CH 2CH 3OH(5)先与LiAlH 4,再与H 2O CH 3CH 2CH 2CH 2NH 2 6.完成下列反应方程式。
无机化学 第12章 配位化学基础习题及全解答-

第12章配位化学基础1 M为中心原子,a, b, d 为单齿配体。
下列各配合物中有顺反异构体的是(A)(A) Ma2bd(平面四方)(B) Ma3b (C) Ma2bd(四面体)(D) Ma2b(平面三角形)2 在下列配合物中,其中分裂能最大的是(A)(A) Rh(NH3)36+(B)Ni(NH3)36+(C) Co(NH3)36+(D) Fe(NH3)36+3 在八面体强场中,晶体场稳定化能最大的中心离子d 电子数为(B)(A) 9 ,(B) 6 , (C)5 , (D)34 化合物[Co(NH3)4Cl2]Br 的名称是溴化二氯•四氨合钴(III);化合物[Cr(NH3)(CN)(en)2]SO4的名称是硫酸氰•氨•二乙二胺合铬(III)。
5 四硫氰·二氨合铬(Ⅲ)酸铵的化学式是 NH4[Cr(SCN)4(NH3)2] ;二氯·草酸根·乙二胺合铁(Ⅲ)离子的化学式是[Fe Cl2(C2O4)en]-4。
6. 下列物质的有什么几何异构体,画出几何图形(1)[Co(NH3)4Cl2]+(2)[Co(NO2)3(NH3)3]答:(1)顺、反异构(图略),(2)经式、面式异构(图略)。
7.根据磁矩,判断下列配合物中心离子的杂化方式,几何构型,并指出它们属于何类配合物(内/外轨型。
(1)[Cd (NH3)4]2+ μm=0 ;(2)[Ni(CN)4]2-μm=0 ;(3)[Co(NH3)6]3+μm=0 ;(4)[FeF6]3-μm=5.9μB;答:8判断下列配离子属何类配离子9 配合物K3[Fe(CN)5(CO)]中配离子的电荷应为 -3 —,配离子的空间构型为 八面体 ,配位原子为 C (碳) ,中心离子的配位数为 6 ,d 电子在t 2g 和e g 轨道上的排布方式为 t 2g 6e g 0—,中心离子所采取的杂化轨道方式为 d 2sp 3,该配合物属 反 磁性分子。
第12章 机械的运转及其速度波动的调节习题解答

11.1 在图示的搬运机构中,已知滑块5质量m 5=20kg ,l AB =l ED =100mm ,L BC =L CD =L EF =200mm , 903231===ϕϕϕ。
作用在滑块5上的工作阻力F 5=1000N ;其他构件的质量和转动惯量均忽略不计,如选构件1为等效构件,试求机构在图示位置的等效阻力矩M r 和等效转动惯量J e 。
图11.1【分析】对于本题,由于除滑块5外,其余构件的质量和转动惯量均忽略不计。
所以只要求得15/ωv 的值,就可求得所需的等效阻力矩和等效转动惯量。
解: (1)求15/ωv由于 903231===ϕϕϕ,所以在矢量方程CB B C +=中,C 和B v 大小相等,方向相同;同理,在矢量方程F EE F v v v +=中,F v 和E v 也是大小相等,方向相同。
对于构件3,由于L CD =2L ED ,所以2/C E v v =。
这样:A B B C E F l v v v v v 15212121ω=====从而m l v A B 05.021.0215===ω (2) 求M rm N v F M r ⋅=⨯==5005.01000)(155ω(3) 求J e根据公式∑=⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=n i i Si Si i eJ v m J 122ωωω得: ()22215505.005.020m kg v m J e ⋅=⨯=⎪⎪⎭⎫ ⎝⎛=ω 【评注】本例比较简单,关键在于进行运动分析,由于机构处于特殊位置,给速度的分析带来一定的困难,但只要弄清楚速度的关系,特殊位置的机构速度分析又非常简单。
11.2 在图11.2(a)所示的机构中,曲柄l 的长度为l 1,其对轴A 的转动惯量为J l 。
连杆2的长度为l 2,质心在S ,且l BS =l 2/2,质量为m 2,绕质心S 的转动惯量为J 2,滑块3为一齿条,质量为m 3。
齿轮4的转动惯量为J 4,其分度圆半径为r 4。
组织行为学习题解答第12章

第十二章组织结构设计思考题1. 什么是组织结构?组织结构在组织运作中的作用是什么?答:组织结构指的是为了完成组织目标而设计的组织内各要素的排列顺序、空间位置、聚散状态、联系方式以及各要素之间相互关系的一种特定安排,是组织内部分工协作的基本形式或框架。
组织结构的作用是阐述组织内部的分工协作之间的关系。
组织结构以企业战略为目标,转化成相应的体系和制度,融入企业的日常管理活动中,确保企业战略的实现,比如日事清的计划管理模块,就可以根据需要设立不同的组织部门,保证组织在有限的资源下,减少损耗,实现资源的最大化利用。
组织结构直接影响着内部组织行为的效果和效率,从而影响组织目标的实现。
2. 组织结构设计的基本内容有什么?答:管理者在进行组织结构设计时,必须考虑六大关键因素:工作专门化、工作部门化、指挥链、管理幅度、集权与分权、正规化。
(1)工作专门化:是指把组织中的工作任务进一步划分成单独工作单元的程度。
工作划分得越细,则工作的专门化越强。
(2)工作部门化:是指在工作专门化基础上,严格按照工作领域的划分,区分不同的部门,把各个有关的或者类似的工作进行归类合并,使性质相同或者相似的工作可以进行有效协调,从而形成专门化的部门。
(3)指挥链:是一种从组织最高层贯穿到最基层的不间断的职权线路,它表明组织中的人是如何相互联系的,清晰界定谁向谁报告。
(4)管理幅度:指的是一位管理者能够直接有效地指挥下属成员的数目。
(5)集权:是指决策权在组织系统中较高层次的一定程度的集中;分权:是指决策权在组织系统中较低层次的一定程度的分散。
(6)正规化:指在组织内部工作实行标准化的程度。
3. 影响组织结构设计的因素有哪些?答:影响组织结构设计的因素有很多,其中主要的影响因素有组织战略、组织规模、技术条件和组织环境。
(1)组织战略是指组织依据自身资源、能力和使命,在考虑各类利益相关者的情况下对自身进行定位的方式。
组织的战略是一个组织区别于其他组织的目的和竞争性要素,他们决定组织的经营范围、战略业务单位、资源分配、行动计划以及员工、客户和竞争者之间的关系等。
第12章习题解答哈工大习题册

第12章非线性电阻电路习题解答电路如图题所示,已知非线性电阻的特性方程为2111.2I U =(单位:V ,A ),10U >求支路电流1I 和2I 。
24Ω图题 图(a)解:将非线性电阻以外电路用戴维南电路进行等效化简,如图(a)所示。
列KVL 方程 1125V I U Ω⨯+= (1) 将非线性电阻特性2111.2I U =代入方程(1),得2112.450U U +-=解得 1 1.25V U '=,1 1.667V U ''=-(舍去)22111.2() 1.2 1.25 1.875A I U '=⨯=⨯= 21/4 1.25/40.3125A I U '==="图题所示电路,已知非线性电阻的特性方程为221U I =+(单位:V ,A ),求电压U 。
图题 图(a)解:将非线性电阻以外电路用戴维南电路进行等效化简,如图(a)所示。
列KVL 方程 811V I U Ω⨯+= (1) 将非线性电阻特性221U I =+代入方程(1),得2450I I +-=解得 1A I '=,5A I ''=-22()13V U I ''=+= 22()151VU I ''''=+=图示电路,已知1I =单位:A,V) ( U 1≥0) ,2I =(单位:A,V) (U 2≥0)。
求I 1和U 1。
'52图题解:由非线性电阻的电压电流关系特性1I =2I =得211100U I = ,222400U I = (1)对回路列KVL 方程125V U U += (2)将式(1)代入式(2) 22121004005I I += 由非线性电阻串联可知 12I I =.即 215005I = 解得 10.1A I '= ,10.1A I ''=-(舍去) 即 10.1A I =2111001V U I ==设图示电路中非线性电阻均为压控的,I 1=f 1(U 1),I 2=f 2(U 2)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第12章习题解答12.1 求解下列本征值问题的本征值和本征函数1(1)()()0;(0)0,()0(2)()()0;(0)0,()0(3)()()0;()0,()0X x X x x x l X x X x x x l X x X x x a x b λλλ'''+===''''+===''+===【答案 2222121(1)(π),0,1,2,;()sin π22(2)(π),0,1,2,;()cos ππ(3)(π),1,2,;()sin ()n n n n n n n n n X x xl l n nn X x x l l n n n X x x a b a b aλλλ++=========---】12.2 长为l 的杆,一端固定;另一端受力0F 而伸长,求解放手杆的振动.【 答案 022011()π()π8122(1)cos sin π(21)n n n at n x F l YS n l l ∞=++-+∑】12.3 长为l 的的弦,两端固定,弦中张力为T . 在距一端为0x 的一点以力0F 把弦拉开,然后突然撤除此力,求弦的振动. 【答案初始位移=00()/(), (0)F l x x lT x x -<<,00000221()/()()2π1π(,)sin sin cosπn F x l x lT x x l F l n x n x n at u x t T n l l lπ∞==-<<=∑】12.4 一个长宽各为a 的方形膜,边界固定,膜的振动方程为 222222()0; (0,0)u u ux a y a t x y∂∂∂-+=<<<<∂∂∂2v 试求方形膜振动的本征频率.【答案,1,2,3,nm n m ν==】 12.5 求解细杆导热问题,杆长l ,两端保持为零度,初始温度分布为20|()/t u bx l x l ==-.【答案 2(21)π[]33081(21)πsin π(21)k a tl k b k x e k l+∞-=++∑】12.6 一根均匀弦两端固定在0,x x l ==处.假设初始时刻速度为零,而在初始时刻弦的形状是一条顶点为(/2,)l h 的抛物线。
试求弦振动的位移.【答案 33032(21)π(21)π(,)cos sin (21)πn h n at n xu x t n l l ∞=++=+∑】 12.7 解定解解问题22222, (0,),0 (1)(0,)(,)0 0 (2)(,0)(), x u ua x l t t x u t u l t t u x x ϕ∂∂=∈>∂∂==>= (3)(,0)(), (0,) (4)t u x x x l ψ⎧⎪⎪⎪⎨⎪⎪⎪⎩=∈解: 用分离变量法解,令(,)()() (5)u x t T t X x = 并将(5)代入(1),(2),得固有值问题 ''()()0 (6)(0)'()0 (7)X x X x X X l λ+=⎧⎨==⎩及 2()() (8)T t a T t λ+ 解(6)—(7)得 221()(), 0,1,2,2n n x n lλπ+== 21()sin , 0,1,2,2n n X x x n lπ+==将n λ代入(8)解得2121cossin , (0,1,2,)22n n n n n T C at D at n l lππ++=+=∴ (,)()() (0,1,2,)n n n u x t T t X x n ==叠加得212121(,)cossin sin (9)222n n n n n n u x t C at D at x l l l πππ∞=+++⎛⎫=+⎪⎝⎭∑ 令(9)满足(3),(4)得21(,0)()sin(10)2n n n u x x C x lϕπ∞=+==∑ 02121(,0)()sin (11)22t nn n n u x x Da x l lψππ∞=++==∑ 由Fourier 展式的唯一性知,n C 与212nn D a lπ+分别为()x ϕ与()x ψ关于021sin 2n n x l π∞=+⎧⎫⎨⎬⎩⎭的展开式系数. ∴ l0221 ()sin d (12) 2n n C x x x l lϕπ+=⎰002221()sin d (21)2421()sin d (0,1,2,) (13)(21)2ln ll n D x x xn a l l n x x x n n a lψππψππ+=⋅++==+⎰⎰所以,带有系数(12)~(13)的(9)即为定解问题(1)~(4)的形式解。
12.8 解定解问题22222110, 0, 02 (1)() 0<2 (2) r Ru u ur R r r r r u f θπθθθπ=⎧∂∂∂++=<<≤<⎪∂∂∂⎨⎪=≤⎩解: 这是圆域上的Laplace 方程第一边值问题.设(1)具有变量分离形式解(,)()() (3)u r F r θθ=Φ将(3)代入(1)得221''()()''()1()()r F r F r r F r rθλθ+Φ==-Φ- 令则有 ''()()0 (4)()(2)0 (5)θλθθθπΦ+Φ=⎧⎨Φ=Φ+=⎩及2''()'()()0 (6)(0) (7)r F r rF r F r F λ⎧+-=⎪⎨<+∞⎪⎩这里条件(5)是由区域的形状及(,)u r θ的单值性决定的。
即(,2)(,)u r u r θπθ+=成立。
((0,]r R ∈)。
而条件(7)是由问题的物理意义决定的,即(,)u r θ在圆心处有界。
问题(4)~(5)称为定解问题(1)~(2)的固有值问题。
解(4)~(5)得:2,0,1,2,n n n λ==0()1,()cos sin (1,2,)n n n a n b n n θθθθΦ=Φ=+=(,n n a b 为任意常数)将n λ代入(6)~(7)解得000()' (A'0F r A =≠为任意常数) n ()' (A'0 1,2nn n F r A r n =≠=为任意常数)∴ 0000(,)()()',2n A u r F r A θθ=Φ==(,)()()'(cos sin )n n n n n n n u r F r A r a n b n θθθθ=Φ=+cos sin (1,2,)nnn n A r n B r n n θθ=+=叠加得01(,)cos sin (8)2n n n n n n A u r A r n B r n θθθ∞==++∑令(8)满足(2)的得01(,()cos sin 2n n n n n A u R f A R n B R n θθθθ∞===++∑右端即为()f θ的Fourier 完全展示。
由于()f θ定义在[]02π,上,故应有(2)(),f f θπθ+=于是有2001() (9)A f d πθθπ=⎰201()cos (10)n n A f nd R πθθπ=⎰201()sin (11)n nB f nd R πθθπ=⎰(1,2,)n =带有系数(9)~(11)的(8)即为定解问题(1)~(2)的解。
()()()y x u y x u y x u ,,,21+=.12.9 解定解问题222220110 0, 0 (1)0 0<r<R (2)() r R u u ur R r r r r u u u f θθαθαθθ===∂∂∂++=<<<<∂∂∂=== 0<< (3)θα⎧⎪⎪⎪⎨⎪⎪⎪⎩解: 注意到方程就关于未知函数为线性齐次的,且在0θθα==与边界上具有线性齐次边界条件,故可用分离变量法求解。
为此,设(1)有非零解(,)()() (4)u r F r θθ=Φ 代入(1)并分离变量得2''()'()''()()()r F r rF r F r θλθ+Φ==--Φ 令即兴 2''()'()()0 (5)r F r rF r F r λ+-=令(4)满足(2)得(0)()0 (7) αΦ=Φ= (6)与(7)联立得''()()0 (6)(0)()0 (7) θλθαΦ+Φ=⎧⎨Φ=Φ=⎩注意问题的物理意义知,在0r =处,应满足条件 (0,,(0) (5)'u F θ<+∞有界故(5)与(5)'联立2''()'()()0 (5)(0) (5)'r F r rF r F r F λ⎧+-=⎪⎨<+∞⎪⎩(5)是一个二群众监督齐次欧拉方程,所带条件(5)'不具可叠加性。
故应由(6)~(7)确定λ值,即(6)(7)为定解问题(1)~(3)的固有值问题。
解解(6)~(7)得固有值 2()(), 1,2,n n x n πλα==固有函数系()sin , 1,2, n n n πθθαΦ==将2()()n n x πλα=代入(5),解(5)~(5)':令tr e =。
在(5)中变换自变量为t ,得22222d 0 (1,2,)d n n F n F n t πα-==其通解为2222(1,2,)n n ttn n n F C eD en ππαα-=+=即() (1,2,)n n n n n F r C r D rn ππαα-=+=由条件(5)'得0.n D =∴ () (1,2,)n n n F r C r n πα==于是 (,)sin (1,2,)n n n n u r C r n παπθθα==叠加这得1(,)sin(8)n n n n u r C r παπθθα∞==∑令(8)满足(3)得 1(,)sin () (9)n nn n u R C R f παπθθθα∞===∑(9)表明n n C R πα即为()f θ在[]0,α上Fourier 正弦展式的系数,即2()sin d (1,2,)n n n f C R n απαπθθθαα==⎰∴ 02()sind (1,2,)n n n C f n R απαπθθθαα==⎰代入(8)即得定解问题(1)~(3)的解。
12.10 解定解问题12221222212110 ,02 (1)()0 (2)() r r u u ur r r r r u f u f ρρρρθπθθθ==∂∂∂++=<<≤<∂∂∂=== 0<2 (3)θπ⎧⎪⎪⎪⎨⎪≤⎪⎪⎩解:这是圆环域12r ρρ<<上Laplacd 方程第一边值问题。
