算法基础限时训练
算法竞赛入门经典 题单

算法竞赛入门经典题单以下是算法竞赛入门经典的一些题目:1. 两数之和2. 三数之和3. 最长回文子串4. 数组中去除重复项5. 盛最多水的容器6. 最长递增子序列7. 买卖股票的最佳时机8. 翻转二叉树9. 合并两个有序链表10. 合并K个升序链表11. 二分查找12. 寻找旋转排序数组中的最小值13. 矩阵中的路径14. 三数之积最大值15. 盛最多水的容器 II16. 最长回文子串 II17. 最长回文子串 III18. 最长公共子序列19. 二分查找的变种20. 二分搜索树中的第K小元素21. 二叉树的最大深度22. 二叉树的层序遍历23. 二叉树的镜像24. 二叉树中每个节点的值都不重复的子树个数25. 二叉树的叶子节点之和26. 二叉树中所有的路径长度之和27. 斐波那契数列28. 快慢指针解决链表问题29. 单链表中的插入节点问题30. 单链表中的删除节点问题31. 判断链表中是否有环32. 在链表中查找第k个节点33. 反转链表34. 对链表进行排序35. 约瑟夫环问题36. 括号匹配问题37. 二进制中1的个数问题38. 寻找数组中两个数,使得它们的和等于一个给定的值39. 寻找数组中最大的k个数40. 求一个数组中所有元素的和41. 求一个数组中的第k大元素42. 寻找数组中只出现一次的数字(经典的异或解法)43. 二分查找的变种(数组中连续子数组的长度)44. 在二叉搜索树中插入节点问题(先序、中序、后序遍历)45. 在二叉搜索树中查找最大值和最小值节点问题46. 二叉搜索树中查找是否存在某个节点的问题47. 二叉搜索树转换为排序的双向链表问题(中序遍历)。
算法练习题及答案

算法练习题及答案算法练习题及答案随着计算机科学的发展,算法成为了计算机科学的核心内容之一。
算法是一种解决问题的方法和步骤,它可以将复杂的问题简化为一系列简单的操作。
为了提高算法设计和分析的能力,许多学生和程序员经常进行算法练习。
在这篇文章中,我将给出一些常见的算法练习题及其答案,希望能对读者有所帮助。
1. 反转字符串题目:给定一个字符串,将其反转并返回。
解答:可以使用两个指针,一个指向字符串的开头,一个指向字符串的末尾。
然后交换两个指针指向的字符,然后分别向中间靠拢,直到两个指针相遇。
2. 判断回文数题目:给定一个整数,判断它是否是回文数。
回文数是指正序和倒序读都一样的整数。
解答:可以将整数转换为字符串,然后使用反转字符串的方法判断是否相等。
另一种方法是将整数反转后与原来的整数进行比较。
3. 寻找两个有序数组的中位数题目:给定两个有序数组,找出这两个数组合并后的中位数。
要求时间复杂度为O(log(m+n))。
解答:可以使用二分查找的思想。
首先将两个数组合并成一个有序数组,然后找到中位数的位置。
如果数组长度为奇数,中位数就是中间的元素;如果数组长度为偶数,中位数就是中间两个元素的平均值。
4. 搜索旋转排序数组题目:给定一个按照升序排列的整数数组,经过旋转后的数组,搜索一个给定的目标值。
如果目标值存在于数组中,则返回它的索引,否则返回-1。
解答:可以使用二分查找的思想。
首先找到数组的中间元素,然后判断中间元素与目标值的关系。
如果中间元素等于目标值,直接返回索引;如果中间元素小于目标值,说明目标值在右半部分,继续在右半部分进行二分查找;如果中间元素大于目标值,说明目标值在左半部分,继续在左半部分进行二分查找。
5. 最长公共前缀题目:给定一个字符串数组,找到这些字符串的最长公共前缀。
解答:可以将第一个字符串作为初始的最长公共前缀,然后逐个比较后面的字符串与最长公共前缀的相同部分。
如果相同部分为空,则返回空;如果相同部分不为空,则更新最长公共前缀。
算法训练入门知识点总结

算法训练入门知识点总结1. 算法的概念算法是一个有限步骤的集合,描述了如何完成特定任务。
通常情况下,算法由输入、输出和一系列具体步骤组成。
算法的设计需要考虑执行效率、运行时间等因素。
2. 算法的特性(1)有穷性:算法必须在有限步骤内结束。
(2)确定性:算法的每一步骤必须明确且无二义性。
(3)可行性:算法的每一步骤必须是可行的。
(4)输入:算法必须接受输入。
(5)输出:算法必须产生输出。
3. 算法的表示算法可以用自然语言描述,也可以用伪代码或流程图表示。
伪代码是一种结构化的描述算法的语言,它可以更直观地表达算法的具体步骤。
流程图是一种用图形符号表示算法的方法,它可以更直观地描述算法的执行流程。
4. 算法的分析算法的分析是评价一个算法性能的过程,通常包括时间复杂度和空间复杂度的分析。
时间复杂度描述了算法的执行时间与输入规模的关系,空间复杂度描述了算法需要的存储空间与输入规模的关系。
5. 算法的分类算法可以按照不同的标准进行分类,包括应用领域、数据结构、解决问题的方法等。
常见的算法分类包括:搜索算法、排序算法、图算法、动态规划算法等。
6. 算法的应用算法在计算机科学领域有着广泛的应用,如搜索引擎的排序算法、社交网络的推荐算法、物流配送的路径规划算法等。
此外,算法也应用于人工智能、机器学习、数据挖掘等领域。
7. 算法的设计算法的设计是解决问题的关键,通常包括以下几种方法:(1)贪心算法:每一步都选择当前最优解,最终得到的结果是全局最优解。
(2)分治算法:将问题分解成若干个小问题,分别解决小问题,再将小问题的解合并成大问题的解。
(3)动态规划算法:将问题分解成若干个子问题,通过保存子问题的解来避免重复计算,从而降低时间复杂度。
(4)回溯算法:通过不断地试探和回溯来搜索解空间,找到问题的解。
8. 算法的训练学习算法需要进行大量的练习,掌握不同类型的算法和解决问题的方法。
在训练算法过程中,需要注意以下几点:(1)了解常用的数据结构,如数组、链表、栈、队列、树、图等。
2013最新高考复习专题限时练习:数学第18讲 算法与复数

专题限时集训(十八)A[第18讲算法与复数](时间:10分钟+25分钟)1.i是虚数单位,1+i3等于()A.i B.-i C.1+i D.1-i2.设复数z满足i z=1,其中i为虚数单位,则z=()A.-i B.i C.-1 D.13.阅读图18-1所示的程序框图,运行相应的程序,输出的结果是()A.3 B.11 C.38 D.1234.若a-ii=b+2i,其中a,b∈R,i是虚数单位,则a-b的值为()A.-1 B.-3 C.3 D.11.若a,b∈R,i为虚数单位,且(() A.a=1,b=1 B.a=-1,b=1C.a=1,b=-1 D.a=-1,b=-12.i为虚数单位,1i+1i3+1i5+1i7=()A.0 B.2i C.-2i D.4i3.某程序框图如图18-2()图18-2A .f (x )=x 2B .f (x )=1xC .f (x )=e xD .f (x )=sin x4.运行如下所示的程序,输出的结果是________. a=1b =2a =a +b PRINT a END5.执行下面的程序框图,则输出的结果是________.6.若执行如图18-4所示的框图,输入x 1=1,x 2=2,x 3=4,x 4=8,则输出的数等于________.图18-47.图18-5________.专题限时集训(十八)B[第18讲 算法与复数](时间:10分钟+25分钟)1.复数11+i +i2的值是( )A .-12 B.12 C.1+i 2 D.1-i 22.设i 为虚数单位,复数z 1=1+i ,z 2=2i -1,则复数z 1·z 2在复平面上对应的点在( )A .第一象限B .第二象限C .第三象限D .第四象限3.如图18-6所示的程序框图输出的结果是( )A .6B .-6C .5D .-54.设i 为虚数单位,则复数2i1-i的虚部为( )A .1B .iC .-1D .-i1.复数z =2-i2+i(i 为虚数单位)在复平面内对应的点所在象限为( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限2.已知x ∈R ,i 为虚数单位,若(1-2i)(x +i)为纯虚数,则x 的值等于( )A .-12B .-2C .2 D.123.已知复数a -ii-i 在复平面内对应的点在第二、四象限的角平分线上,则实数a 的值为( )A .-2B .-1C .0D .24.阅读下列程序,输出结果为2的是( )A .n =0 DOn =n +1LOOP UNTIL n>=2 PRINT nEND B .n =0 DOn =n +1LOOP UNTIL n<=2 PRINT n END C.n =0WHILE n<=2 n =n +1WEND PRINT n ENDD.n =0WHILE n>=2 n=n +1WEND PRINT n END5.阅读如图18-7所示的程序框图,输出的结果s 的值为( )A .0 B.32C. 3 D .-326.下列程序执行后输出的结果是________.i =1S =0WHILE i<=50 S =S +i i =i +1 WEND PRINT S END7.已知复数z 满足z 2+z ·z +z =3+i ,则复数z =__________________.图18-88.某城市缺水问题比较突出,为了制定节水管理办法,对全市居民某年的月均用水量进行了抽样调查,其中4位居民的月均用水量分别为x1,x2,x3,x4(单位:吨).根据图18-8所示的程序框图,若x1,x2,x3,x4分别为1,1.5,1.5,2,则输出的结果s为________.专题限时集训(十八)A【基础演练】1.D【解析】由1+i3=1+i2·i=1-i,故选D.2.A【解析】由i z=1得z=1i=ii2=-i,所以选A.3.B【解析】该程序框图是当型的循环结构,由程序框图可知,第一次循环,a=12+2=3;第二次循环,a=32+2=11;当a=11时,a<10不成立,输出a=11,故选B.4.A【解析】a-iib+2i,得a-i=-2+b i,所以a=-2,b=-1,a-b=-1,故选A.【提升训练】1.C【解析】由(a+i)i=b+i得-1+a i=b+i,根据复数的相等,a=1,b=-1,故选C.2.A 【解析】 1i +1i 3+1i 5+1i7=-i +i -i +i =0,故选A.3.D 【解析】 由程序框图可知输出的函数为奇函数且有零点,只有f (x )=sin x 满足. 4.3 【解析】 由已知,输入a =1,b =2,把a +b 的值赋给a ,输出a =3. 5.10 【解析】 s =1+(1+2)+(1+2+3)=10. 6.154【解析】 由累加的赋值符号x =x +x i 得到x =x 1+x 2+x 3+x 4=1+2+4+8=15,而最后输出的结果为x =14x =14×15=1547.27 【解析】 第一次:s =(0+1)×1=1,n =1+1=2,第二次:s =(1+2)×2=6,n =3,第三次:s =(6+3)×3=27,n =4,而n =4>3,退出循环,输出s =27.8.[0,4] 【解析】 由已知,复数z 对应的点Z 在复平面上的轨迹是以原点O 为圆心、2为半径的圆.设ω=1+3i +z =z -(-1-3i),则|ω|表示动点Z 到点C (-1,-3)的距离,因为|OC →|=2,根据圆的几何性质知,动点Z 到点C (-1,-3)的距离最大值为2+r =2+2=4,最小值为2-r =0,所以|1+3i +z |的取值范围是[0,4].专题限时集训(十八)B【基础演练】1.B 【解析】11+i +i 2=1-i 2+i 2=12. 2.A 【解析】 根据复数的运算法则,把复数z 1·z 2具体求出来,根据复数的几何意义作出判断.z 1·z 2=(1-i)(2i -1)=1+3i.3.C 【解析】 第一次S =-1,i =2;第二次S =1,i =3;第三次S =-2,i =4;第四次S =2,i =5,第五次S =-3,i =6;第六次S =3,i =7;第七次S =-4,i =8;第八次S =4,i =9;第九次S =-5,i =10;第十次S =5,i =11.故输出结果是5.4.A 【解析】 2i1-i1+i ,虚部是1. 【提升训练】1.D 【解析】 z =2-i 2+i =(2-i )2(2+i )(2-i )3-4i 4+1=35-45i ,又点⎝⎛⎭⎫35,-45在第四象限,所以该复数在复平面内对应的点也在第四象限.2.B 【解析】 (1-2i)(x +i)=(x +2)+(1-2x )i 为纯虚数,所以x =-2.3.A 【解析】 化复数为代数形式后,其代表的点在直线y =-x 上.化简复数a -ii -i =-1-(a +1)i ,由题意知a +1=-1,解得a =-2.4.A 【解析】 根据算法程序的意义,逐个计算可知.5.B 【解析】 算法的功能是计算s = 2011n =1sin n π3的值.函数y =sin n π36,当n 取正整数时,在一个周期内函数值之和为0,故s = 2011n =1sin n π3=sin π3=32. 6.1275 【解析】 S =1+2+…+50=1275.7.1+i 或-32-14i 【解析】 设z =a +b i(a ,b ∈R ),则(a +b i)2+(a +b i)(a -b i)+(a -b i)=3+i ,即2a 2+a +(2ab -b )i =3+i ,由复数相等的充要条件得方程组⎩⎪⎨⎪⎧2a 2+a =3,2ab -b =1,解得⎩⎪⎨⎪⎧a =1,b =1或⎩⎨⎧a =-32,b =-14.故所求的复数z =1+i 或z =-32-14i.8.32【解析】 程序运行过程中,各变量值变化情况如下: 第一(i =1)步:s 1=s 1+x 1=0+1=1, 第二(i =2)步:s 1=s 1+x 2=1+1.5=2.5, 第三(i =3)步:s 1=s 1+x 3=2.5+1.5=4,第四(i =4)步:s 1=s 1+x 4=4+2=6,s =14×6=32,第五(i =5)步:i =5>4,输出s =32,故答案为32.。
算法练习题——精选推荐

算法练习题1. 斐波那契数列:1 1 2 3 5 8 13 21 …… 求第20个数;2. 今有雉兔同笼,上有三⼗五头,下有九⼗四⾜,问雉兔各⼏何?3. 求1000以内的⽔仙花数4. 求⼀个数的阶乘5. 求多个连续数的阶乘之和6. 如果今天是星期⼆,那么1000天后是星期⼏?⽤户输⼊⼀个天数,计算这个天数后是星期⼏?7. 苹果3元⼀个,鸭梨2元⼀个,桃⼦1元⼀个。
现在想⽤200元买100个⽔果,在控制台中列出所有可能性8. 求任意⼀个⼩于100000的正整数的位数,并逆序打印每⼀位数字⽐如:567,位数是3位,以此打印7 ,6 ,59. 有⼀分数序列:2/1,3/2,5/3,8/5,13/8,21/13...求出这个数列的前20项之和。
程序分析:请抓住分⼦与分母的变化规律。
10. 有⼀些苹果,每⼈分5个多1个,每⼈分6个多2个,每⼈分7个多3个,⼀共有多少个苹果11. 判断⼀个数字是不是素数12. 利⽤条件运算符的嵌套来完成此题:学习成绩>=90分的同学⽤A表⽰,60-89分之间的⽤B表⽰,60分以下的⽤C表⽰。
1.程序分析:(a>b)?a:b这是条件运算符的基本例⼦。
13. 求s=a+aa+aaa+aaaa+aa...a的值,其中a是⼀个数字。
例如2+22+222+2222+22222(此时共有5个数相加),⼏个数相加由⽤户输⼊(prompt)14. ⼀球从100⽶⾼度⾃由落下,每次落地后反跳回原⾼度的⼀半;再落下,求它在第10次落地时,共经过多少⽶?第10次反弹多⾼?15. 求10000以内的完美数如果⼀个数恰好等于它的约数之和,则称该数位“完美数”。
16. 寻找丑数题⽬:我们把只包含因⼦2、3 和5 的数称作丑数(Ugly Number)。
例如6、8 都是丑数,但14 不是,因为它包含因⼦7。
习惯上我们把1 当做是第⼀个丑数。
求按从⼩到⼤的顺序的第1500 个丑数。
17. 猴⼦吃桃问题:猴⼦第⼀天摘下若⼲个桃⼦,当即吃了⼀半,还不瘾,⼜多吃了⼀个第⼆天早上⼜将剩下的桃⼦吃掉⼀半,⼜多吃了⼀个。
北森技术算法题库

北森技术算法题库
北森技术算法题库包括了一些基本的编程和算法问题,以帮助候选人展示他们的技术能力和思维方式。
以下是一些可能的题目示例:
1. 二分查找:给定一个已排序的数组和一个目标值,请编写一个函数来查找目标值在数组中的索引。
如果目标值不在数组中,则返回-1。
2. 链表操作:给定一个链表的头节点,请编写一个函数来反转链表。
反转后,原链表的头节点将成为反转后链表的尾节点。
3. 动态规划:给定一个矩阵,其中包含正整数和零,请编写一个函数来计算从矩阵的左上角到右下角的最长路径长度,要求路径上只允许水平或垂直移动。
4. 深度优先搜索:给定一个二叉树,请编写一个函数来遍历树并输出每个节点的值。
可以使用递归或迭代的方式实现。
5. 并查集:给定一个整数集合,请编写一个函数来将集合划分为若干个不相交的子集(并查集)。
每个子集中的元素都是相邻的,并且任意两个子集之间没有公共元素。
这只是北森技术算法题库的一部分,具体的题目和难度可能因不同的招聘岗位和技术领域而有所不同。
如果您正在寻找相关题目以进行练习,可以在编程网站上搜索类似的题目或使用在线算法题库进行练习。
C语言算法训练题

C训练题一题1:未名湖边的烦恼每年冬天,北大未名湖上都是滑冰的好地方。
北大体育组准备了许多冰鞋,可是人太多了,每天下午收工后,常常一双冰鞋都不剩。
每天早上,租鞋窗口都会排起长龙,假设有还鞋的m个,有需要租鞋的n个。
现在的问题是,这些人有多少种排法,可以避免出现体育组没有冰鞋可租的尴尬场面。
(两个同样需求的人(比如都是租鞋或都是还鞋)交换位置是同一种排法)输入格式两个整数,表示m和n输出格式一个整数,表示队伍的排法的方案数。
样例输入3 2样例输出5数据规模和约定m,n∈[0,18]问题分析题2:最大的算式题目很简单,给出N个数字,不改变它们的相对位置,在中间加入K个乘号和N-K-1个加号,(括号随便加)使最终结果尽量大。
因为乘号和加号一共就是N-1个了,所以恰好每两个相邻数字之间都有一个符号。
例如:N=5,K=2,5个数字分别为1、2、3、4、5,可以加成:1*2*(3+4+5)=241*(2+3)*(4+5)=45(1*2+3)*(4+5)=45……输入格式输入文件共有二行,第一行为两个有空格隔开的整数,表示N和K,其中(2<=N<=15, 0<=K<=N-1)。
第二行为 N个用空格隔开的数字(每个数字在0到9之间)。
输出格式输出文件仅一行包含一个整数,表示要求的最大的结果样例输入5 21 2 3 4 5样例输出120样例说明(1+2+3)*4*5=120题3:图形显示编写一个程序,首先输入一个整数,例如5,然后在屏幕上显示如下的图形(5表示行数):* * * * ** * * ** * ** **题4:排序编写一个程序,输入3个整数,然后程序将对这三个整数按照从大到小进行排列。
输入格式:输入只有一行,即三个整数,中间用空格隔开。
输出格式:输出只有一行,即排序后的结果。
输入输出样例样例输入9 2 30样例输出30 9 2题5:2的次幂表示任何一个正整数都可以用2进制表示,例如:137的2进制表示为10001001。
小数的混合运算和简便算法

小数的混合运算和简便算法。
(第 7、8题,练习九第5—7题。
)复习要求:1.使学生进一步掌握小数混合运算的运算顺序,并能准确地实行计算。
2.使学生进一步掌握小数乘、除法中的一些简便算法,并能准确地实行小数乘、除法的简便计算。
复习重点:小数的混合运算和简便计算的准确率及熟练水准。
复习过程:一、基本训练练习九第5题:4.5+1.5 0.75+0.25 0.25+3.1+1.752.5×4 1-0.63 10-1.8-2.20.46÷2 8×0.125 4.8×0.2×0.50.7×1.4 2.4÷30 0.3÷0.15÷2根据学生情况限时做在课本上,集体订正。
二、复习指导1.第7题。
5.51×9.5×0.12 4.07×8.6+9.12524.84÷2.7-7.35 32.34÷2.1÷0.14(1)看题说一说各题的运算顺序。
(2)学生独立计算。
(指4名学生板演。
)(3)集体订正。
2.P.34页的第7题:先想想下面各题怎样计算简便,再计算。
(1)学生看题说一说每题应该怎样算简便?根据是什么?(2)学生独立简算。
(指4名学生板演。
)(3)集体订正。
三、课堂练习1.练习九第6题。
学生独立实行简算,教师实行个别辅导。
集体订正时要求学生说出每一题是根据什么简算的。
(1)首先让学生讨论怎样才能填出篮球的个数、总价和排球的单价?并选代表发言。
(2)学生填写,教师巡视。
(3)集体订正。
四、攻破难题1.练习九第9题:小华在计算3.6除以一个数时,因为小数点向右点错了一位,结果得24。
这道题的除数是多少?分析与解:此题先考虑正确商是多少,题中告诉“由于小数点向右点错了一位,结果得24”,那么正确商应为2.4。
再根据除法中各部分之间的关系,用被除数3.6除以商2.4,得到除数是1.5。
算法测试题及答案

算法测试题及答案一、选择题1. 以下哪个选项不是排序算法?A. 冒泡排序B. 选择排序C. 快速排序D. 深度优先搜索答案:D2. 在二叉树中,深度为5的节点最多有多少个?A. 16B. 32C. 64D. 31答案:D二、填空题1. 递归算法的基本思想是 _ ,即把问题分解成相同但规模更小的问题。
答案:分而治之2. 动态规划与分治法的不同之处在于动态规划会 _ ,而分治法则不会。
答案:存储子问题的解三、简答题1. 请简述什么是贪心算法,并给出一个例子。
答案:贪心算法是一种在每一步选择中都采取在当前状态下最好或最优的选择,从而希望导致结果是全局最好或最优的算法策略。
例如,活动选择问题,给定一系列活动,每个活动都有一个开始时间和结束时间,贪心算法会按照结束时间的早晚来选择活动,从而最大化参与活动的数量。
2. 描述快速排序算法的基本思想。
答案:快速排序算法是一种分治策略,基本思想是选择一个元素作为“基准”(pivot),然后将数组分为两个子数组,一个包含所有小于基准的元素,另一个包含所有大于基准的元素。
这个过程称为分区(partitioning)。
之后,递归地将分区过程应用到两个子数组上,直到每个子数组只有一个元素或为空。
四、计算题1. 给定一个数组 [3, 1, 4, 1, 5, 9, 2, 6, 5, 3, 5],请使用快速排序算法对其进行排序,并给出排序后的数组。
答案:使用快速排序算法对给定数组进行排序后,得到的数组为 [1, 1, 2, 3, 3, 4, 5, 5, 5, 6, 9]。
2. 假设有一个二叉搜索树,其根节点的值为10,现在要删除值为5的节点,请描述删除过程。
答案:删除二叉搜索树中的节点分为三种情况:- 情况1:要删除的节点没有子节点,直接删除该节点。
- 情况2:要删除的节点只有一个子节点,用其子节点替换该节点。
- 情况3:要删除的节点有两个子节点,找到该节点的直接前驱或直接后继,用其值替换要删除的节点,然后删除直接前驱或直接后继。
算法初步
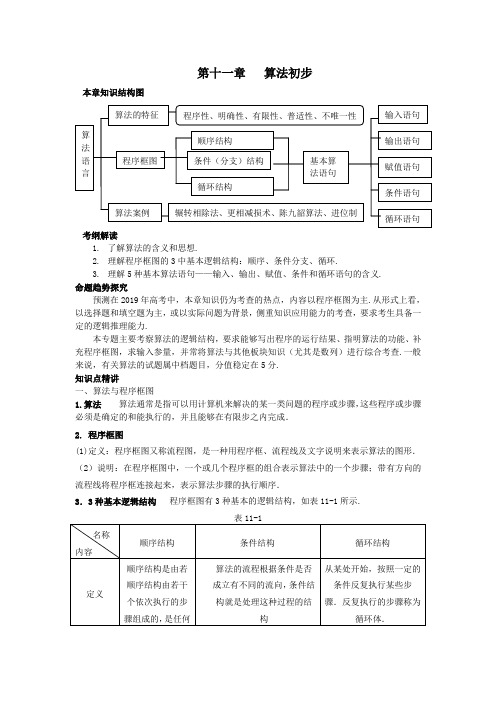
第十一章算法初步本章知识结构图考纲解读1.了解算法的含义和思想.2.理解程序框图的3中基本逻辑结构:顺序、条件分支、循环.3.理解5种基本算法语句——输入、输出、赋值、条件和循环语句的含义.命题趋势探究预测在2019年高考中,本章知识仍为考查的热点,内容以程序框图为主.从形式上看,以选择题和填空题为主,或以实际问题为背景,侧重知识应用能力的考查,要求考生具备一定的逻辑推理能力.本专题主要考察算法的逻辑结构,要求能够写出程序的运行结果、指明算法的功能、补充程序框图,求输入参量,并常将算法与其他板块知识(尤其是数列)进行综合考查.一般来说,有关算法的试题属中档题目,分值稳定在5分.知识点精讲一、算法与程序框图1.算法算法通常是指可以用计算机来解决的某一类问题的程序或步骤,这些程序或步骤必须是确定的和能执行的,并且能够在有限步之内完成.2. 程序框图(1)定义:程序框图又称流程图,是一种用程序框、流程线及文字说明来表示算法的图形.(2)说明:在程序框图中,一个或几个程序框的组合表示算法中的一个步骤;带有方向的流程线将程序框连接起来,表示算法步骤的执行顺序.3.3种基本逻辑结构程序框图有3种基本的逻辑结构,如表11-1所示.二、基本算法语句1.3中基本算法语句的一般格式和功能3中基本算法语句的一般格式和功能如表11-2所示.2.条件语句(1)算法中的条件结构由条件语句来表达. (2)条件语句的格式及框图如图11-1和11-2所示. ①IF—THEN 格式IF 条件 THEN 语句体 END②IF—THEN —ELSE 格式 IF 条件 THEN 语句体1 ELSE 语句体2END图11-23.循环语句(1)算法中的循环结构是由循环语句来实现. (2)循环语句的格式及框图如图11-3和11-4所示. ①UNTIL 语句DO循环体LOOP UNTIL 条件②WHILE 语句 WHILE 条件循环体END(3)WHILE 语句与UNTIL 语句之间的区别与联系如表11-3所示.三、算法案例 1.辗转相除法辗转相除法又叫欧几里德算法,是一种求最大公约数的古老而有效的算法,其步骤如下: (1)用两数中较大的数除以较小的数,求得商和余数; (2)以除数和余数中较大的数除以较小的数; (3)重复上述两步,直到余数为0; (4)较小的数是两数的最大公约数. 2.更相减损术更相减损术是我国古代数学专著《九章算术》中介绍的一种求两数最大公约数的算法,其基本过程为:对于任意给定的两个正整数,以大数减小数,接着把所得的差与较小的数比较,并以大数减小数,继续该操作,直到所得的数相等为止,这个数(等数)就是所求的最大图11-3图11-4公约数.3.秦九韶算法秦九韶算法是我国南宋数学家秦九韶在他的代表作《数书九章》中提出的一种用于计算一元n次多项式的值的方法。
算法练习题

算法练习题一、基础算法1. 编写一个程序,实现一个冒泡排序算法。
2. 实现一个选择排序算法。
3. 实现一个插入排序算法。
4. 编写一个函数,计算一个整数数组中的最大值和最小值。
5. 编写一个函数,实现二分查找算法。
6. 编写一个函数,实现快速排序算法。
7. 编写一个函数,判断一个整数是否为素数。
8. 编写一个函数,实现反转一个整数数组。
9. 编写一个函数,计算两个整数数组的交集。
10. 编写一个函数,判断一个字符串是否为回文。
二、数据结构11. 实现一个单链表的基本操作,包括插入、删除、查找。
12. 实现一个双向链表的基本操作,包括插入、删除、查找。
13. 实现一个栈的基本操作,包括压栈、出栈、查看栈顶元素。
14. 实现一个队列的基本操作,包括入队、出队、查看队首元素。
15. 实现一个二叉树的基本操作,包括插入、删除、查找。
16. 实现一个二叉搜索树的基本操作,包括插入、删除、查找。
17. 实现一个哈希表的基本操作,包括插入、删除、查找。
三、搜索与图论18. 编写一个程序,实现深度优先搜索(DFS)算法。
19. 编写一个程序,实现广度优先搜索(BFS)算法。
20. 编写一个程序,求解迷宫问题。
21. 编写一个程序,计算一个有向图的拓扑排序。
22. 编写一个程序,计算一个无向图的欧拉回路。
23. 编写一个程序,计算一个加权无向图的最小树(Prim算法)。
24. 编写一个程序,计算一个加权有向图的最短路径(Dijkstra算法)。
25. 编写一个程序,计算一个加权有向图的所有顶点对的最短路径(Floyd算法)。
四、动态规划26. 编写一个程序,实现背包问题。
27. 编写一个程序,计算最长公共子序列(LCS)。
28. 编写一个程序,计算最长递增子序列(LIS)。
29. 编写一个程序,实现编辑距离(Levenshtein距离)。
30. 编写一个程序,实现硬币找零问题。
31. 编写一个程序,实现矩阵链乘问题。
算法基础试题及答案

算法基础试题及答案一、单项选择题(每题2分,共10分)1. 以下哪个选项是算法的基本特征之一?A. 有穷性B. 可行性C. 确定性D. 以上都是答案:D2. 在算法设计中,以下哪个步骤是不必要的?A. 问题定义B. 算法描述C. 算法实现D. 算法测试答案:D3. 算法的时间复杂度通常用来描述什么?A. 算法的运行时间B. 算法的空间需求C. 算法的执行步骤数量D. 算法的输入数据大小答案:A4. 以下哪个不是算法设计的基本方法?A. 递归B. 排序C. 搜索D. 迭代答案:B5. 在算法分析中,大O符号表示什么?A. 算法执行的时间B. 算法执行的空间C. 算法执行的最坏情况D. 算法执行的平均情况答案:C二、填空题(每题2分,共10分)1. 算法的输入输出定义了算法的______,算法的步骤定义了算法的______。
答案:功能;实现2. 算法的时间复杂度和空间复杂度是衡量算法______的两个重要指标。
答案:效率3. 在算法设计中,______是一种通过重复执行代码块来实现的算法结构。
答案:循环4. 递归算法通常包括两个基本部分:______和______。
答案:基本情况;递归情况5. 在算法分析中,______复杂度描述了算法执行过程中所需的存储空间。
答案:空间三、简答题(每题5分,共20分)1. 请简述算法的五个基本特征。
答案:算法的五个基本特征包括有穷性、确定性、可行性、输入和输出。
有穷性指算法必须在执行有限步骤后结束;确定性指算法的每一步都必须有明确的定义;可行性指算法的每一步都必须足够基本,以至于可以精确地执行;输入指算法有0个或多个输入,以描述运算的对象和初始条件;输出指算法至少有一个输出,输出表示算法运行的结果。
2. 算法的时间复杂度和空间复杂度有什么区别?答案:时间复杂度主要关注算法执行所需的时间,它通常与算法中操作的数量有关,而空间复杂度则关注算法执行过程中所需的存储空间。
算法训练测试题及答案

算法训练测试题及答案
一、选择题
1. 以下哪种算法属于贪心算法?
A. 动态规划
B. 回溯算法
C. 贪心算法
D. 分支限界法
答案:C
2. 在二叉树的遍历算法中,前序遍历的顺序是什么?
A. 根-左-右
B. 左-根-右
C. 右-根-左
D. 根-右-左
答案:A
3. 快速排序算法的时间复杂度在最好情况下是?
A. O(n^2)
B. O(nlogn)
C. O(n)
D. O(1)
答案:B
二、填空题
1. 在图论中,一个图中所有顶点的度数之和等于图中边数的_____倍。
答案:2
2. 动态规划算法解决的问题通常具有_____性质。
答案:最优子结构
3. 哈希表的平均查找时间复杂度是_____。
答案:O(1)
三、简答题
1. 请简述分治算法的基本思想。
答案:分治算法的基本思想是将一个复杂的问题分解成若干个相同或相似的子问题,递归地解决这些子问题,然后将子问题的解合并以解决原问题。
2. 什么是深度优先搜索(DFS)?
答案:深度优先搜索是一种用于遍历或搜索树结构或图的算法。
它从根节点开始,尽可能深地搜索树的分支,回溯到上一个节点后,再继续搜索下一个分支。
四、编程题
1. 给定一个整数数组,请编写一个函数,使用快速排序算法对数组进行排序,并返回排序后的数组。
答案:[此处应提供快速排序算法的具体代码实现]
结束语:通过以上题目的练习,可以帮助你更好地理解和掌握算法的基本概念和应用。
希望这些测试题能够对你的学习有所帮助。
scratch算法练习题

scratch算法练习题Scratch算法练习题在计算机科学领域中,算法是解决问题的一种方法或步骤。
而Scratch是一种编程语言,通过使用图形化编程块,可以帮助初学者更容易地理解和学习编程。
本文将介绍一些Scratch算法练习题,帮助读者提高算法思维和编程能力。
1. 反转字符串题目描述:给定一个字符串,将其反转并输出。
解题思路:首先,创建一个变量用于存储反转后的字符串。
然后,使用一个循环,从字符串的最后一个字符开始,依次将每个字符添加到新的字符串变量中。
最后,输出新的字符串变量。
Scratch代码示例:```当 flag 点击时设置变量反转后的字符串为空重复直到 length of (字符串) = 0把 (字符串) 的第 (length of (字符串)) 个字符添加到 (反转后的字符串)删除 (字符串) 的第 (length of (字符串)) 个字符结束重复显示 (反转后的字符串)```2. 查找最大值题目描述:给定一个整数列表,找到其中的最大值并输出。
解题思路:首先,创建一个变量用于存储最大值,初始值设为列表中的第一个数。
然后,使用一个循环,依次比较列表中的每个数与最大值的大小,如果大于最大值,则更新最大值。
最后,输出最大值。
Scratch代码示例:```当 flag 点击时设置变量最大值为 (列表的第一个数)重复 (length of (列表) - 1) 次如果 (列表的第 (重复次数) 个数) > (最大值) 则设置变量最大值为 (列表的第 (重复次数) 个数)结束如果结束重复显示 (最大值)```3. 斐波那契数列题目描述:输出斐波那契数列的前n项。
解题思路:斐波那契数列是一个数列,每个数都是前两个数的和。
首先,创建一个列表用于存储斐波那契数列。
然后,使用一个循环从第三项开始,依次计算每一项的值并添加到列表中。
最后,输出列表。
Scratch代码示例:```当 flag 点击时设置变量斐波那契数列为 [0, 1]重复 (n - 2) 次把 (斐波那契数列的第 (length of (斐波那契数列) - 1) 项 + 斐波那契数列的第 (length of (斐波那契数列) - 2) 项) 添加到 (斐波那契数列)结束重复显示 (斐波那契数列)```通过以上练习题,我们可以锻炼算法思维和编程能力。
算法经典必刷题

算法经典必刷题
以下是一些经典的算法必刷题目,供您参考:
1. 两数之和(LeetCode 1):给定一个整数数组 nums 和一个目标值target,请你在该数组中找出和为目标值的那两个整数,并返回他们的数组下标。
2. 三数之和(LeetCode 498):给定一个包含 n 个整数的数组 nums,判断 nums 中是否存在三个元素 a,b,c ,使得 a + b + c = 0 ?找出所有
满足条件且不重复的三元组。
3. 最长回文子串(LeetCode 5):给定一个字符串 s,找到 s 中最长的回
文子串。
你可以假设 s 的最大长度为 1000。
4. 二分查找(LeetCode 7):给定一个排序数组和一个目标值,在数组中
查找目标值,并返回其索引。
如果目标值不存在于数组中,则返回 -1。
5. 盛最多水的容器(LeetCode 11):给定 n 个非负整数 a1,a2,...,an,每个数代表一个坐标点 (i, ai)。
在坐标内画 n 条垂直线,使得 i 垂直线的两
个端点分别为 (i, ai) 和 (i, 0)。
找出其中的一条线,使得该条线落在这 n 条
垂直线构成的区域内时,它到 x 轴的垂线段区域内的水最多。
6. 合并两个有序链表(LeetCode 20):将两个升序链表合并为一个新的升序链表并返回。
新链表是通过拼接给定的两个链表的所有节点组成的。
这些题目都是经典的算法问题,对于提高算法和数据结构方面的能力非常有帮助。
当然,还有很多其他的经典算法必刷题目,您可以根据自己的实际情况选择题目进行练习。
算法考试题及答案

算法考试题及答案一、选择题(每题5分,共20分)1. 以下哪个算法的时间复杂度是O(n^2)?A. 冒泡排序B. 快速排序C. 二分查找D. 归并排序答案:A2. 在图的遍历中,深度优先搜索(DFS)使用的是哪种数据结构?A. 栈B. 队列C. 链表D. 哈希表答案:A3. 哈希表解决冲突的方法不包括以下哪种?A. 分离链接法B. 开放寻址法C. 链地址法D. 排序法答案:D4. 以下哪个算法不是动态规划算法?A. 斐波那契数列B. 0/1背包问题C. 最长公共子序列D. 二分查找答案:D二、填空题(每题5分,共20分)1. 在算法分析中,____复杂度表示算法执行时间与输入数据量的关系。
答案:时间2. 动态规划算法的核心是____问题,通过将问题分解为更小的子问题来解决。
答案:最优子结构3. 在排序算法中,____排序是一种不稳定的排序算法,它通过不断地交换相邻元素来达到排序的目的。
答案:冒泡4. 在图论中,____树是一种特殊的树,其中每个节点都只有一个父节点。
答案:二叉三、简答题(每题10分,共30分)1. 请简述贪心算法的基本思想。
答案:贪心算法的基本思想是在每一步选择中都采取在当前状态下最好或最优的选择,从而希望导致结果是全局最好或最优的算法。
贪心算法不保证能得到最优解,但在某些情况下它能产生近似最优解。
2. 什么是分治算法?请举例说明。
答案:分治算法是一种递归算法,它将一个难以直接解决的大问题分解成若干个规模较小的相同问题,递归解决这些子问题,然后再合并这些子问题的解以解决原始问题。
例如,归并排序就是分治算法的一个典型例子,它将一个数组分成两半,分别排序,然后再合并。
3. 请解释什么是时间复杂度,并给出一个例子。
答案:时间复杂度是衡量算法运行时间的量度,它描述了算法执行时间随输入数据规模增长的变化趋势。
例如,对于一个简单的线性搜索算法,其时间复杂度是O(n),意味着搜索的时间随着数据规模的增加而线性增长。
算法考卷参考答案

一、选择题(每题1分,共5分)A. Dijkstra算法B. Kruskal算法C. Huffman编码D. 动态规划算法2. 下列排序算法中,哪个算法的时间复杂度最稳定?A. 冒泡排序B. 快速排序C. 堆排序D. 插入排序A. 二分查找B. 深度优先搜索C. 广度优先搜索D. 动态规划A. 初始化状态B. 确定状态转移方程C. 计算最优值D. ABC都是A. Floyd算法B. Warshall算法C. Prim算法D. BellmanFord算法二、判断题(每题1分,共5分)1. 算法的空间复杂度与时间复杂度成正比。
(×)2. 贪心算法总能得到最优解。
(×)3. 快速排序的平均时间复杂度为O(nlogn)。
(√)4. 二分查找算法适用于顺序存储的有序表。
(√)5. 深度优先搜索和广度优先搜索在遍历图时,时间复杂度相同。
(×)三、填空题(每题1分,共5分)1. 算法的五个基本特性分别是:可行性、确定性、______、有穷性和输入输出。
2. 在排序算法中,堆排序的时间复杂度为______。
3. 求解背包问题通常采用______算法。
4. 图的遍历方法有深度优先搜索和______。
5. 在动态规划算法中,状态转移方程描述了______之间的关系。
四、简答题(每题2分,共10分)1. 简述冒泡排序的基本思想。
2. 什么是贪心算法?请举例说明。
3. 简述二分查找算法的基本步骤。
4. 什么是动态规划算法?它适用于哪些问题?5. 请列举三种常见的图遍历算法。
五、应用题(每题2分,共10分)1. 设有数组arr = [3, 5, 1, 4, 2],请用冒泡排序算法对数组进行排序。
2. 给定一个整数数组nums,请找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
3. 编写一个递归函数,实现求斐波那契数列的第n项。
A B| |C DA B (3)| |C D (4)六、分析题(每题5分,共10分)def func(n):sum = 0for i in range(n):for j in range(i):sum += 1return sum2. 给定一个字符串str,请设计一个算法,找出最长不重复子串的长度。
2020版高考数学一轮复习课后限时集训52算法与算法框图文含解析北师大版2

课后限时集训(五十二)(建议用时:60分钟) A 组 基础达标一、选择题1.阅读如图所示的程序框图,运行相应的程序,若输入x 的值为1,则输出y 的值为 ( )A .2B .7C .8D .128 C [由程序框图知,y =⎩⎪⎨⎪⎧2x,x ≥2,9-x ,x <2.∵输入x 的值为1,比2小,∴执行的程序要实现的功能为9-1=8,故输出y 的值为8.]2.(2019·佛山调研)执行如图所示的程序框图,输出的结果是( )A .-5B .-1C .3D .11A [开始S =1,n =1,第一次循环:S =1+(-2)1=-1,n =2; 第二次循环:S =-1+(-2)2=3,n =3; 第三次循环:S =3+(-2)3=-5,n =4,此时4<4不成立,退出循环, 故输出S =-5.]3.执行如图所示的程序框图,则输出n 的值为( )A .9B .11C .13D .15C [由程序框图可知,S 是对1n 进行累乘,直到S <12 018时停止运算,即当S =1×13×15×17×19×111<12 018时循环终止,此时输出的n =13.] 4.某算法的程序框图如图所示,其中输入的变量x 在1,2,3,…,24这24个整数中等可能随机产生,则按程序框图正确编程运行时输出y 的值为3的概率为 ( )A .12B .13C .16D .18C [由程序框图知,输出y 的值为3时,x 为3的倍数,且为偶数,即x =6,12,18,24,所以其概率为424=16,故选C .]5.执行如图所示的程序框图,假如输入的S ,k 的值分别为1,2,那么输出的S =( )A .1+15B .15C .4D .17C [初始值:S =1,k =2;第1步循环结果:S =1+12+1,k =3;第2步循环结果:S =1+12+1+13+2,k =4;…;第15步循环结果:S =1+12+1+13+2+…+116+15,k =17>16,退出循环.此时输出的结果为S =1+12+1+13+2+…+116+15=1+(2-1)+(3-2)+…+(16-15)=4,故选C .]6.我国古代数学著作《周髀算经》有如下问题:“今有器中米,不知其数.前人取半,中人三分取一,后人四分取一,余米一斗五升.问,米几何?”如图是解决该问题的程序框图,执行该程序框图,若输出的S =1.5(单位:升),则输入k 的值为( )A .4.5B .6C .7.5D .9B [由题中程序框图知S =k -k 2-k 2×3-k3×4=1.5,解得k =6,故选B.]7.(2018·湘中名校联考)执行如图所示的程序框图,如果运行结果为5 040,那么判断框中应填入( )A.k<6 B.k<7C.k>6 D.k>7D[执行程序框图,第一次循环,得S=2,k=3;第二次循环,得S=6,k=4;第三次循环,得S=24,k=5;第四次循环,得S=120,k=6;第五次循环,得S=720,k=7;第六次循环,得S=5 040,k=8.此时满足题意,退出循环,输出的S=5 040,故判断框中应填入“k>7”.]二、填空题8.(2019·吉林长春质检)更相减损术是出自《九章算术》的一种算法.如图所示的程序框图是根据更相减损术写出的,若输入a=91,b=39,则输出的值为________.13[输入a=91,b=39,执行程序框图,第一次:a=52,b=39;第二次:a=13,b =39;第三次:a=13,b=26;第四次:a=13,b=13;a=b,满足输出条件,输出的值为13.]9.(2019·广东七校联考)公元263年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形面积可无限逼近圆的面积,并创立了“割圆术”,利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值3.14,这就是著名的“徽率”.如图是利用刘徽的“割圆术”思想设计的一个程序框图,则输出的n的值为________.(参考数据:sin 15°≈0.258 8,sin 7.5°≈0.130 5)24 [执行程序框图,n =6,S =332≈2.598<3.10;n =12,S =3<3.10;n =24,S ≈3.1056>3.10,满足条件,退出循环.故输出的n 的值为24.]10.(2019·长沙模拟)已知函数f (x )=ax 3+12x 2在x =-1处取得极大值,记g (x )=1f ′x .程序框图如图所示, 若输出的结果S >2 0182 019,则判断框中可以填入的关于n 的判断条件是________.(填序号)①n ≤2 018;②n ≤2 019;③n >2 018;④n >2 019. ② [由题意得f ′(x )=3ax 2+x , 由f ′(-1)=0,得a =13,∴f ′(x )=x 2+x ,即g (x )=1x 2+x =1xx +1=1x -1x +1. 由程序框图可知S =0+g (1)+g (2)+…+g (n ) =0+1-12+12-13+…+1n -1n +1=1-1n +1=n n +1,由nn +1>2 0182 019,得n >2 018. 故进行循环的条件应为n ≤2 019. 故可填入②.]B 组 能力提升1.(2019·郑州模拟)某品牌洗衣机专柜在国庆期间举行促销活动,如图1所示的茎叶图中记录了每天的销售量(单位:台),把这些数据经过如图2所示的程序框图处理后,输出的S =( )A .28B .29C .196D .203B [由程序框图可知,该程序框图输出的是销售量的平均值,结合茎叶图可知,输出的S =20+22+26+33+33+34+357=29,故选B.]2.(2017·全国卷Ⅲ)执行如图所示的程序框图,为使输出S 的值小于91,则输入的正整数N 的最小值为( )A .5B .4C .3D .2D [假设N =2,程序执行过程如下:t =1,M =100,S =0,1≤2,S =0+100=100,M =-10010=-10,t =2,2≤2,S =100-10=90,M =--1010=1,t =3,3>2,输出S =90<91.符合题意. ∴N =2成立.显然2是N 的最小值. 故选D.]3.(2018·惠州三调)执行如图所示的程序框图,则输出的结果为________.9 [法一:i =1,S =lg 13=-lg 3>-1;i =3,S =lg 13+lg 35=lg 15=-lg 5>-1; i =5,S =lg 15+lg 57=lg 17=-lg 7>-1; i =7,S =lg 17+lg 79=lg 19=-lg 9>-1; i =9,S =lg 19+lg 911=lg 111=-lg 11<-1;故输出的i =9.法二:因为S =lg 13+lg 35+…+lg ii +2=lg 1-lg 3+lg 3-lg 5+…+lg i -lg(i +2)=-lg(i +2),当i =9时,S =-lg(9+2)<-lg 10=-1,所以输出的i =9.]4.执行如图所示的程序框图,若输入m =209,n =121,则输出的m 的值为________.11[当m=209,n=121时,m除以n的余数r=88,此时m=121,n=88,m除以n的余数r=33,此时m=88,n=33,m除以n的余数r=22,此时m=33,n=22,m除以n的余数r=11,此时m=22,n=11,m除以n的余数r=0,此时m=11,n=0,退出循环,输出m的值为11.]。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
12.将数值型变量x的值输出至list1:
em str(x)
13.在txt1中输入的值赋值给字符串型变量s:
S=
14.在txt2中显示s字符串长度:
=str(len(s))
15.在txt2中显示s字符串从第3个起至结束的字符串:
=mid(s,3,len(s)-3+1)
16.将s字符串中的小写字母都改为大写字母:
21.若f=true,则x= ,否则x=0,用块if语句写:
If f=true then
x=sqr(b)/(2*a)
else
x=0
end if
22.For i=-5.5 to 6.5 step 0.8循环次数是多少,列式及答案:
(6.5-(-5.5))/0.8+1=16
23.用do while语句写一段程序:求1到100内所有3的倍数的和,即sum=3+6+9+…+99
C=x mod 10
9.设x不知是几位数,试用循环语句将x倒置:(即x=456变为x=654)
S=0
X=val()
Do while x<>0
a=xmod 10
X=x\10
S=s*10+a
Loop
=trim(str(s))
10.将数值型变量x的值输出至txt2:
=str(x)
11.将数值型变量x的值输出至label2:
If mid(s,i,1)<>mid(s,len(s)-i+1,1) then
F=false
End if
Next i
If f=true then print“是回文”else print“不是回文”
18.给s字符串加密,若是字母,则输出其ascii码加3后的字母,其余不变
S=
For i=1 to len(s)
For i=1 to len(s):
A=mid(s,i,1)
If asc(a)>=97 and asc(a)<=122 then
A=chr(asc(a)-32)
End if
S1=s1+a
Next i
17.判断s字符串是否为回文(回文如:“abcba”,即从左到右与从右到Fra bibliotek相同)S=
F=true
For i=1 to len(s)
X=int(x)
5.判断x是一个偶数:
Xmod 2=0
6.判断x是一个负数:
X<0或x=-abs(x)
7.X是一个能被5整除,但不能被3整除的数:
Xmod 5=0 and x mod 3<>0
8.设x是一个三位数,将x分离成百位上的数a,十位上的数b,个位上的数c:
A=x\100
B=x\10 mod 10
i=3
Do while i<=99
Sum=sum+i
i=i+3
Loop
Print sum
A=mid (s,i,1)
If a>=”A”and a<=“Z”or a>=”a”and a<=”z”then
A=chr(asc(a)+3)
End if
S1=s1+a
Next i
=s1
19.将s字符串输出在label2中
on=s
20.若f=true,则x= ,否则x=0,用行if语句写:
If f=true then x=sqr(b)/(2*a) else x=0
算法基础限时训练:
行政班:教学班:姓名:教学班学号:
1.试描述变量名命名规则:
字母开头,后面跟字母、数字、下划线,vb中有特殊用途的单词不能作为变量名
2.在txt1中输入的值赋值给数值型变量x:
X=val()
3.判断x是一个平方数:(写一个表达式,下同)
Sqr(x)=int(sqr(x))
4.判断x是一个整数:
