数字信号处理(吴镇扬)课后习题答案(比较详细的解答过程)chap5-6PPT课件
数字信号处理教程课后习题及答案

分析:已知边界条件,如果没有限定序列类型(例如因果序列、反因果序列等), 则递推求解必须向两个方向进行(n ≥ 0 及 n < 0)。
解 : (1) y1 (0) = 0 时, (a) 设 x1 (n) = δ (n) ,
按 y1 (n) = ay1 (n − 1) + x1 (n) i) 向 n > 0 处递推,
10
T [ax1(n)+ bx2 (n)] =
n
∑
[ax1
(n
)
+
bx2
(n
)]
m = −∞
T[ax1(n) + bx2(n)] = ay1(n) + by2(n)
∴ 系统是线性系统
解:(2) y(n) =
[x(n )] 2
y1(n)
= T [x1(n)] = [x1(n)] 2
y2 (n) = T [x2 (n)] = [x2 (n)] 2
β α
n +1
β α β =
n +1− N −n0
N−
N
α −β
y(n) = Nα n−n0 ,
(α = β )
, (α ≠ β )
如此题所示,因而要分段求解。
2 .已知线性移不变系统的输入为 x( n ) ,系统的单位抽样响应
为 h( n ) ,试求系统的输出 y( n ) ,并画图。
(1)x(n) = δ (n)
当n ≤ −1时 当n > −1时
∑ y(n) = n a −m = a −n
m=−∞
1− a
∑ y(n) =
−1
a−m =
数字信号处理(吴镇扬)课后习题答案(比较详细的解答过程)chap6

至今, 至今,我们讨论的信号处理的各种理论与算法 视为恒定值, 都是把抽样频率 f s 视为恒定值,即在一个数字系 统中只有一个采样率。 统中只有一个采样率。 在实际数字信号处理系统中, 在实际数字信号处理系统中,经常会遇到采样 率转换问题。 率转换问题 。 或者要求一个数字系统能工作在 多采样率”状态, “多采样率”状态,或者要求其将采样信号转换 为新的采样率下工作。 为新的采样率下工作。
6.2 信号的插值
如果将 x(n) 的抽样频率 f s 增加 L 倍, w(n), w(n) 即 得 的插值,用符号↑ 表示。插值的方法很多, 是对 x(n) 的插值,用符号↑L 表示。插值的方法很多, 一个简单的方法就是信号抽取的逆处理过程。 一个简单的方法就是信号抽取的逆处理过程。 回想信号抽取前后的傅立叶变换关系
而 X 1 (e ) =
jω n = −∞
∞
∑ x ( n ) p ( n)e
− jωn
1 M −1 j 2πnk / M − jωn = ∑ [ x ( n) ]e ∑e n = −∞ M k =0 1 M −1 = X (e j (ω − 2πk / M ) ) (6.3b (6.3b) ∑ M k =0
信号抽取示意图,M=3, 图6.1.1 信号抽取示意图,M=3,横坐标为抽样点数 原信号; 中间信号; (a)原信号;(b)中间信号;(c)抽取后的信号
显然
X ′(e ) = ∑ x′(n)e
jω n = −∞ ∞ n = −∞ ∞
∞
− j ωn
= ∑ x( Mn)e
n = −∞
∞
− j ωn
= ∑ x1 ( Mn)e − jωn = X 1 (e jω / M ) (6.3a) (6.3a
数字信号处理(吴镇扬)第一章习题解答
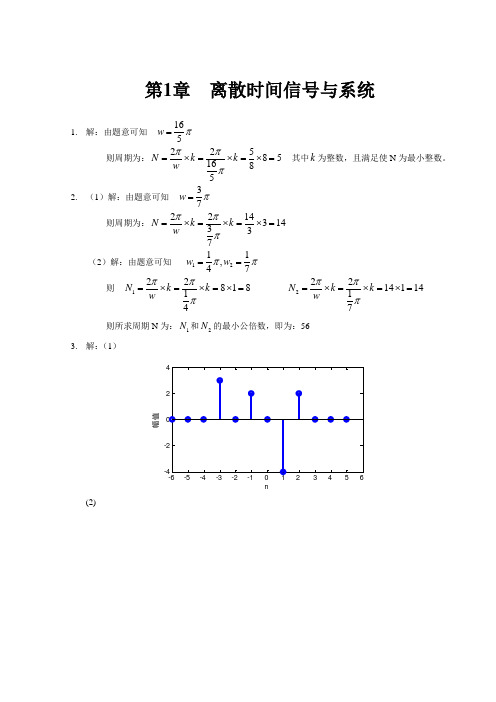
(3)解:
1.18y(n)=1,n=0
y(n)=3*2-n,n≥1
解:
1.19
(1)解:
无论 还是 ,右边序列的围线C内包含 两个极点。
当 时
当 时
因此
思考:1、为何讨论当 时的情况;2、为何不用讨论 的情况
解答过程如下:
(2)解:
右边序列的围线C内包含 一个极点。故
当 时
因此,
思考:1、为何只讨论当 时的情况
(2)解:
该系统不是线性系统;
该系统是时不变系统。
(3)解:
令 ,则
而
该系统是线性系统时不变系统。
注:
令 ,则
而
该系统是线性时不变系统。
(4)解:
该系统是线性系统时不变系统。
(5)解:
该系统是线性系统时变系统。
1.14解:
(1)
(2)
(3)
1.16
(1)解:因果、稳定。
(2)当n0<0时,系统非因果,不稳定。
(2)解:
所求序列为双边序列,采用留数法求解。
当n>=1时,围线C内只有一个极点 ,
则:
当n<1时,围线外只有一个极点 ,利用辅助留数定理,则:
因此
(4)解:
1.12
(1)解:定理:
(3)解:直接法
帕氏定理:
1.13
(1)解:
该系统不是线性系统;
该系统是时不变系统。
第1章
1.解:由题意可知
则周期为: 其中 为整数,且满足使N为最小整数。
2.(1)解:由题意可知
则周期为:
(2)解:由题意可知
则
则所求周期N为: 和 的最小公倍数,即为:56
《数字信号处理》第三版课后习题答案

数字信号处理课后答案1.2 教材第一章习题解答1. 用单位脉冲序列()n δ及其加权和表示题1图所示的序列。
解:()(4)2(2)(1)2()(1)2(2)4(3) 0.5(4)2(6)x n n n n n n n n n n δδδδδδδδδ=+++-+++-+-+-+-+-2. 给定信号:25,41()6,040,n n x n n +-≤≤-⎧⎪=≤≤⎨⎪⎩其它(1)画出()x n 序列的波形,标上各序列的值;(2)试用延迟单位脉冲序列及其加权和表示()x n 序列; (3)令1()2(2)x n x n =-,试画出1()x n 波形; (4)令2()2(2)x n x n =+,试画出2()x n 波形; (5)令3()2(2)x n x n =-,试画出3()x n 波形。
解:(1)x(n)的波形如题2解图(一)所示。
(2)()3(4)(3)(2)3(1)6() 6(1)6(2)6(3)6(4)x n n n n n n n n n n δδδδδδδδδ=-+-+++++++-+-+-+-(3)1()x n 的波形是x(n)的波形右移2位,在乘以2,画出图形如题2解图(二)所示。
(4)2()x n 的波形是x(n)的波形左移2位,在乘以2,画出图形如题2解图(三)所示。
(5)画3()x n 时,先画x(-n)的波形,然后再右移2位,3()x n 波形如题2解图(四)所示。
3. 判断下面的序列是否是周期的,若是周期的,确定其周期。
(1)3()cos()78x n A n ππ=-,A 是常数;(2)1()8()j n x n e π-=。
解:(1)3214,73w w ππ==,这是有理数,因此是周期序列,周期是T=14; (2)12,168w wππ==,这是无理数,因此是非周期序列。
5. 设系统分别用下面的差分方程描述,()x n 与()y n 分别表示系统输入和输出,判断系统是否是线性非时变的。
吴镇扬数字信号处理课后习题答案

jw0 n
u (n)] e jw0n z n
n 0
1 1 (e jw0 z 1 )
(1) 解:令 y (n) RN (n)
由题意可知,所求序列等效为 x (n 1) y (n) y (n) 。
Z [ y (n)] z n
n 0
N 1
1 zN z N 1 , 1 z 1 z N 1 ( z 1)
1
A B 1 2 1 1 1 1 z 1 2z 1 z 1 2 z 1 B 1 | 1 2 1 z 1 z 1 2
1 | 1 1 1 2 z 1 z 1
x(n) u (n) 2 2 n u ( n 1) u (n) 2 n 1u ( n 1)
n0
若n0 0时,收敛域为:0 z ;
(2) 解: Z [0.5 u (n)]
n
若n0 0 时,收敛域为: z 0 z 0.5
0.5
n 0
n
z n
1
1 , 1 0.5 z 1
n
(3) 解: Z [ 0.5 u ( n 1)]
n
n
j j 1 1 (3) X (e 2 ) X ( e 2 ) 2 2 j
(2) e
j n0
X (e j ) (移位特性)
2
数字信号处理习题指导
G ( z ) ZT [ x (2n)] G( z)
n
g ( n )e
jwn
令n' 2n, 则
n ' 取偶数
( z 5) z n |z 0.5 (1 0.5 z)
数字信号处理课后答案课件

傅里叶变换的性质
线性性质
若离散信号x(n)和y(n)的 傅里叶变换分别为 X(e^jωn)和Y(e^jωn), 则对于任意实数a和b,有 aX(e^jωn) + bY(e^jωn) 的傅里叶变换等于 aX(e^jωn)和bY(e^jωn) 的傅里叶变换之和。
从而实现信号的分离、抑制或提 取。
滤波器分类
根据不同的特性,滤波器可分为 低通、高通、带通和带阻滤波器,
每种滤波器都有各自的应用场景 和特点。
滤波器原理
滤波器的原理是基于频率响应, 即不同频率的信号经过滤波器后, 其幅度和相位会发生不同的变化。
IIR滤波器设计
IIR滤波器概述
IIR滤波器设计方法
IIR滤波器稳定性
在设计IIR滤波器时,需要考虑其稳定 性。如果系统函数的极点位于单位圆 外,则系统不稳定,可能会导致无穷 大的输出。因此,在设计过程中需要 进行稳定性分析。
FIR滤波器设计
FIR滤波器概述
FIR(Finite Impulse Response)滤 波器是一种具有有限冲击响应的数字 滤波器,其系统函数可以表示为有限 项之和。
插值法
对于非周期性的连续时间信号,可以通过插值法得到离散时间信号。常用的插值方法包括 线性插值、多项式插值、样条插值等。
傅里叶变换法
对于任何连续时间信号,可以通过傅里叶变换将其转换为频域表示形式,然后对频域表示 形式进行采样,得到离散时间信号。再通过逆傅里叶变换将其转换回时域表示形式。
05 第五章 信号的分 析与合成
抽样定理的充分性
对于任何连续时间信号,如果其最高频率分量小于等于fmax,则可 以通过其抽样信号无失真地重建出原信号。
数字信号处理_吴镇扬_第二版_第五章习题答案

5.7 (1)由于h2(n)是h1(n)圆周移位的序列,根据DFT的 2π 性质有: −j 4k − jπ k
H 2 (k ) = e
8
H 1 (k ) = e
H 1 (k )
~ ~ H1 ( k ) = H 2 ( k ) 成立 所以
(2)由于h1 (n ) 和h2 (n ) 均为偶对称序列,以其构成的低通滤波器
(3)若采用海明窗设计,则
⎡ ⎛ 2πn ⎞⎤ wHam ( n) = ⎢0.54 − 0.46 cos ⎜ ⎟ ⎥ RN ( n ) ⎝ N − 1 ⎠⎦ ⎣ 2 h( n) = sin[(n − α )ωc ]cos[(n − α )ω0 ]wHam (n) N 为奇数时, (n − α )π
h( n N 为偶数时, ) =
0 −ωc
e − jωα e jω nd ω
可见h(n)关于(N-1)/2偶对称,即 h( n) = h( N − 1 − n)
(1)当 N 为奇数时,为第一类滤波器。 (2)当N为偶数时,为第二类滤波器
⎧hd ( n) h( n) = hd ( n) ⋅ R(n ) = ⎨ ⎩0 0 ≤ n ≤ N −1
解:由经验公式可知若 不小于 At 40dB , 则
β = 0.5842 At - 21)0.4 + 0.07886(At - 21) ≈ 3.3953 ( At − 8 40 − 8 N= = ≈ 22.28 2.286∆ω 2.286× 0.2π ωc + ωr ωc′ = = 0.2π 2 ′ ⎧ωc ′ ⎪ π Sa[ωc (n − α )] n ≠ α ′ 1 ωc − jωα jωn ⎪ hd (n) = ∫ ′ e e dω = ⎨ ′ 2π −ωc ωc ⎪ n =α ⎪ ⎩ π
数字信号处理(吴镇扬)课后习题答案(比较详细的解答过程)第二章测试训练题解

数字信号处理(吴镇扬)课后习题答案(比较详细的解答过程)第二章测试训练题解1.DFT和DTFT之间的关系是2.DFT和DFS之间的关系是3.对于一个128点的DFT,最先4个DFT相应于数字频率4.某滤波器的频响为H(ω) = 0.3cos2ω- 0.2cosω+ 0.05,相应于6点的DFT的H[k]为5.采样频率为22.05kHz的1024点DFT所对应的频率分辨率为6.采样率为8kHz的信号的256点DFT的第一个周期覆盖的频率范围是从0Hz至7.信号[ 1 0 2 ]的DFT每隔3个样点值重复,为8.以1600Hz对一220Hz的信号采样,进行64点DFT,最接近的DFT频率为9.以12kHz的信号对一4.25kHz的信号抽样,其256点DFT幅谱图的基带最大峰值点所对应的下标为10.采样频率为6kHz,1kHz信号的频率分辨率要达到50Hz,需11.采样频率为16kHz,1024点DFT的窗口长度为12.关于谱泄漏与窗口长度的关系是13.频谱图是展现信号的什么14.周期性方波的频谱图15.在FFT中的乘数因子是16.与512点的DFT相比,512点的FFT只需约几分之一的计算量17、一个长度为N的有限长序列可否用N个频域的采样值唯一地确定?18、计算两个N点序列的线性卷积,至少要做多少点的DFT?19、x(2n)与x(n)的关系20、对于高斯序列x(n)=exp[-(n-p)2/q],取16点作FFT,其幅度谱中低频分量最多的是21、一般地说按时间抽取基二FFT的_______序列是按位反转重新排列的。
22、信号x(n)=sin(nπ/4) - cos(nπ/7)的数字周期为23、N=2L点基二FFT,共有______列蝶形,每列有____个蝶形。
24、信号s(t)=sin(4000πt)+sin(600πt),则采样频率至少应为25、用按时间抽取法计算256点的FFT时,n=233的二进制位反转值是26、FFT之所以能减少DFT的运算量,是因为:,FFT减少DFT 运算量的基本处理思想是。
数字信号处理课后答案第6章

A2 s1
比较分子各项系数可知, A1、 A2应满足方程:
A1A1s2A2
1 A2 s1
a
解之得, A1=1/2, A2=1/2, 所以
Ha
(s)
s
1/ 2 (a
jb)
s
1/ 2 (a
jb)
套用教材(6.3.4)式, 得到
H (z)
2
Ak
k 1 1 es k T z 1
1/ 2 1 e(a jb)T z 1
2. 设计一个切比雪夫低通滤波器, 要求通带截止频率 fp=3 kHz,通带最大衰减αp=0.2 dB,阻带截止频率fs=12 kHz, 阻带最小衰减αs=50 dB。 求出滤波器归一化系统函数G(p)和实 际的Ha(s)。
解: (1) 确定滤波器技术指标。 αp=0.2 dB, Ωp=2πfp=6π×103 rad/s αs=50 dB, Ωs=2πfs=24π×103 rad/s
fp=20 kHz, 阻带截止频率fs=10 kHz, fp处最大衰减为3 dB,
阻带最小衰减as=15 dB。 求出该高通滤波器的系统函数Ha(s)。
解: (1) 确定高通滤波器技术指标要求:
p=20 kHz, ap=3 dB fs=10 kHz, as=15 dB
(2) 求相应的归一化低通滤波器技术指标要求: 套用图 5.1.5中高通到低通频率转换公式②, λp=1, λs=Ωp/Ωs, 得到
sp
s p
2π 12103 2π 6103
2
将ksp和λsp值代入N的计算公式, 得
N lg17.794 4.15 lg 2
所以取N=5(实际应用中, 根据具体要求, 也可能取N=4, 指标稍微差一点, 但阶数低一阶, 使系统实现电路得到 简化)。
数字信号处理课后习题答案(全)1-7章PPT课件

第 1 章 时域离散信号和时域离散系统
(2) 令输入为
输出为
x(n-n0)
y′(n)=2x(n-n0)+3 y(n-n0)=2x(n-n0)+3=y′(n) 故该系统是非时变的。 由于
T[ax1(n)+bx2(n)]=2ax1(n)+2bx2(n)+3 T[ax1(n)]=2ax1(n)+3 T[bx2(n)]=2bx2(n)+3 T[ax1(n)+bx2(n)]≠aT[x1(n)]+bT[x2(n)] 故该系统是非线性系统。
T[ax1(n)+bx2(n)]=ax1(n) sin(ωn)+bx2(n) sin(ωn) =aT[x1(n)]+bT[x2(n)]
故系统是线性系统。
第 1 章 时域离散信号和时域离散系统
6. 给定下述系统的差分方程, 试判定系统是否是因果稳定系统, 并说明 理由。
(1) y(n)=
1 x(Nn-1 k)
第 1 章 时域离散信号和时域离散系统
(3) 这是一个延时器, 延时器是线性非时变系统, 下面证明。 令输入为
输出为
x(n-n1)
y′(n)=x(n-n1-n0) y(n-n1)=x(n-n1-n0)=y′(n) 故延时器是非时变系统。 由于
T[ax1(n)+bx2(n)]=ax1(n-n0)+bx2(n-n0) =aT[x1(n)]+bT[x2(n)]
因此系统是非线性系统。
第 1 章 时域离散信号和时域离散系统
(6) y(n)=x(n2)
数字信号处理课后习题答案(吴镇扬)(精编文档).doc

【最新整理,下载后即可编辑】习题一 (离散信号与系统)1.1周期序列,最小周期长度为5。
1.2 (1) 周期序列,最小周期长度为14。
(2) 周期序列,最小周期长度为56。
1.5()()()()()()()11s a s s s a n s s a s n X j x t p t X j ΩP j Ω2n τn τj sin j Ωjn e X 2n π2n n τj Sa X j jn e 2T 2πττ∞=-∞∞=-∞Ω==*⎡⎤⎣⎦ΩΩ⎛⎫-=-Ω ⎪⎝⎭ΩΩ⎛⎫-=Ω-Ω ⎪⎝⎭∑∑ 1.6 (1) )(ωj e kX (2) )(0ωωj n j e X e (3) )(21)(2122ωωj j e X e X -+ (4) )(2ωj e X1.7 (1) 0n z -(2) 5.0||,5.0111>--z z (3) 5.0||,5.0111<--z z (4)0||,5.01)5.0(11101>----z z z1.8 (1) 0,)11()(211>--=---z zz z z X N(2) a z az az z X >-=--,)1()(211 (3) a z az z a az z X >-+=---,)1()(311211.91.10 (1))1(2)(1----+n u n u n (2))1(24)()5.0(6--⋅--n u n u n n (3))()sin sin cos 1(cos 000n u n n ωωωω++(4) )()()(1n u a a a n a n ---+-δ 1.11(1))(1z c X - (2) )(2z X (3))()1(21z X z -+ (4)-+<<x x R z R z X /1/1),/1(1.12 (1) 1,11<-ab ab(2) 1 (3)00n a n1.13 (1) 该系统不是线性系统;该系统是时不变系统。
数字信号处理 吴镇扬 第二版 第三章习题答案
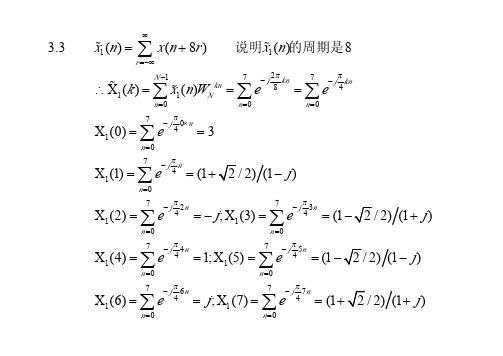
3.15(2)()1()()()()()X k x n n Y k N y n N n δδ=∴==∴=3.18()[()]019()[()]019;()()()019,()[()]019;()()()20()*()27()*()207()719()*()X k DFT x n k Y k DFT y n k R k X k Y k k r n IDFT R k k r n x n y n x n y n x n y n r n x n y n =≤≤=≤≤=≤≤=≤≤=⊗解:根据循环卷积定理可知(点循环卷积);但不为零长度为,所以若以为周期进行延拓必然会产生点的重叠;因此,中至点与相同。
773.19(1)()(){6,3,6,10,14,12,9};(2)(){6,3,6,10,14,12,9};3(){1,3,6,10,14,12,9,5,0,0,0,0}f n R n f n f n ===%周期卷积的主值序列为:循环卷积()线性卷积为440246014(16=2)1;2;4,,;8,N N N N N N N N N W W W W W W W W W 3.21按时间抽取算法:输出顺序,输入倒序(0,8,4,12,2,10,6,14,1,9,5,13,3,11,7,15);共有节第一节:数据点间距、蝶形类型均是,所乘因子:第二节:数据点间距、蝶形类型均是,所乘因子:,第三节:数据点间距、蝶形类型均是,所乘因子:,第四节:数据点间距、蝶形类型均是,所乘因子:,234567,,,,,;N N N N N N N W W W W W W3.27()50100 128 50-110028492849128-49-2851 49~99h n N M ===解:的长度为,每段数据的长度为,循环卷积的长度为;所以根据重叠保留法可知相邻两段数据必有()点重叠,在点之后须加个零值点,所以卷积之后必须去掉前点和后点;所以,,,取数的序号为。
数字信号处理(吴镇扬)课后习题答案(比较详细的解答过程)chap5_6

在数字信号处理的滤波器、FFT、卷积及各种矢量 运算中,由于要执行Σb(n)*x(n - k)一类的运算,这类运 算的乘法和加法总是同时出现,因此DSP中就希望将乘法
器和加法器相结合,在一个时钟周期完成一次乘、加运算,
并且累加乘法运算的结果。这样的运算单元称为乘法累加 器(MAC)。
对于乘法累加器,除了要求能在一个时钟周期完成一
5.6-1。
输入设备
运算器
输出设备
控制器
存储器
数据线 控制线
图5.6-1 冯.诺曼结构
冯.诺曼结构处理器具有以下几个特点:
(1) 必须有一个存储器;
(2) 必须有一个控制器;
(3) 必须有一个运算器,用于完成算术
运算和逻辑 运算;
(4) 必须有输入和输出设备,用于进行
人机通信。
冯.诺曼的主要贡献就是提出并实现了“ 存储程序”的概念。由于指令和数据都是二
若干位 。右移使得符号位扩展,也就是在左边填
入符号位,这样可以保留原有的正号或负号。左 移操作用0填入最低位,如果数的最高位不是符号 位,则左移的结果就造成了溢出,这时溢出标志 被置1。逻辑移位用来做某些逻辑操作,如用于位
屏蔽等。逻辑移位把无符号数左移或右移,腾空
位填0。
通用微处理器的移位操作是一位一位移的
生。
5.6.2 DSP硬件构成 典型的DSP处理器中的运算/处理功能单元 主要包括以下几个部分: ● 乘法器/乘加器(MAC) ● 算术逻辑运算单元(ALU) ● 移位器 ● 数据地址发生器(DAG) ● 程序定序器,又称指令定序器 ● 存储器
5.6.2.1 DSP的乘法器/乘加器(MAC) DSP乘法器应具有以下基本功能: 1. 要求在一个时钟周期里对两个字长为 b位的输入由硬件作快速并行乘法; 2. 应能通过格式控制来执行无符号或带 符号或混合的乘法操作、小数或整数乘法操 作以及扩展精度或双精度运算,并有合适的 舍位方法; 3.应有输入和输出寄存器,这样可以锁 存数据,配合流水线操作。也可不用寄存器 ,使乘法器在透明方式下工作,这样可以有 最小的等待时间。
数字信号处理 Chapter05答案

2011/4/10
3
Notice: Skipped Sections
5.7 5.8 (all) 5.9 (all) 5.10 5.11
2011/4/10
4
5.1
Introduction
2011/4/10
5
5.1 Introduction
Digital processing of a real-world continuous-time signal involves the following basic steps:
The multiplication operation yields an impulse train
Note: Analog Filters are very important for digital systems. Since both the anti-aliasing filter and the reconstruction filter are analog lowpass filters, we review first the theory behind the design of such filters Also, the most widely used IIR digital filter design method is based on the conversion of an analog lowpass prototype
g[n ] = ga (nT ), -¥ <n < ¥
(5.1)
With T being the sampling period. The reciprocal of T is called the sampling frequency , i.e., 1⁄ . It is known that the frequency-domain of the analog signal is given by its FT:
数字信号处理_吴镇扬_习题解答

(k
)
+
F*
(
N
−
k
)⎤⎦
=
1− aN 1 − aWNk
Y
(k)
=
DFT
⎡⎣Im{
f
( n )}⎤⎦
=
DFT
⎡1 ⎢⎣ 2 j
{
f
(n)
−
f
* (n)}⎤⎥ ⎦
=
1 2j
⎡⎣ F
(k)
−
F*(N
−
k )⎤⎦
=
1− bN 1 − bWNk
对 X (k ) 、Y (k ) 作 IDFT 得到:
⎧⎪x (n) = anRN (n)
(3) 通过 z 平面上作图,可以发现,极点 a 在单位圆内的实轴上,零点 1/a 在单位圆外的实轴上, 它们各自到单位圆上任一点的矢量长度可由余弦定理求取,分别为
极点矢量长度= a 2 + 1 − 2acos(ω)
零点矢量长度= a -2 + 1 − 2a -1cos(ω) = 1 a 2 + 1 − 2acos(ω) a
⎨ ⎪⎩
y
(
n
)
=
b
n
RN
(
n
)
注意:
根据 DFT 的线性性质可以得到,当 f (n) = x(n) + jy (n) 时, F (k ) = X (k ) + jY (k ) ,其中
X (k ) 、 Y (k ) 均为复序列。但并不是对于形如 F (k ) = X (k ) + jY (k ) 进行 IDFT 就一定形成
= e 2N
-j2π k n
=e N 2
kn
南邮数字信号处理吴镇扬-课后习题详细答案-DSP期末复习PPT课件

• 解:
DTxF n T n0 xnn0ejwn
n
令 n ' n n 0 xn ' e jw n ' n 0xn ' e jw ' jn w 0
n '
n '
e jw 0 nxn 'e jw ' n e jw 0 D n T xn ' F e jT w 0X n e jw
•pp 34: 1.5 (3)
1
X Z x n Z n 0 . 5 n u n 1 Z n 0 . 5 n Z n
n
n
n
变 量 n ' n 替 换 0 .5 n 'Z n ' 0 .5 1 Z n '
n ' 1
n ' 1
0
Re[z]
• pp 34: 1.5 (2n Z n0 .5 n u n Z n0 .5 n Z n
n
n
n 0
n 00 .5 Z 1 n 1 0 1 .5 Z 1 ,0 .5 Z 1 1 1 0 1 .5 Z 1 ,0 .5 Z
n ' 1
n ' 1
•变量替换易出问题
1 0 . 0 5 . 5 1 Z 1 Z 1 0 1 . 5 Z 1 ,0 . 5 1 Z 1 1 0 1 . 5 Z 1 ,Z 0 . 5
零点:z
2z 1 2z
0
z
z
1 2
j Im[z]
极点: z 1
收敛域:
2 z
1
2
1/2
DSP考试题型
• 填空题20分(每空1分) • 判断题10分(每题2分) • 简答题10分 • 画图题15分 • 计算题45分
数字信号处理答案ppt

01
CPLD(Complex Programmable Logic Device)是一种复杂的可编程逻辑器件,可以实现各种复杂的数字电路。
利用CPLD实现数字信号处理
02
利用CPLD实现数字信号处理,可以针对特定的数字信号处理算法进行优化,实现高速、高效的处理。
03
CPLD还具有低功耗、低成本等优点,适用于对功耗和成本要求较高的应用场景。
医学成像
超声波、核磁共振、CT等医学成像技术的数字化处理。
图像处理
图像的数字化处理、压缩和传输。
声音处理
音乐、语言等声音信号的数字化处理和压缩。
02
数字信号处理的基本原理
离散信号的时域表示
离散信号可以表示为在时间轴上离散点的函数值。
离散信号的频域表示
通过傅里叶变换,可以将离散信号从时域转换到频域,便于分析信号的频率特性。
在图像处理中的应用
01
图像压缩
通过去除图像数据中的冗余信息,实现图像的压缩,降低存储和传输成本。
02
图像增强
改善图像的质量,例如去除噪声、提高清晰度、增强颜色等。
将原始信号转换为适合在信道中传输的形式,实现数据的传输。
调制解调
补偿信道对信号造成的失真,提高信号的传输质量。
信道均衡
对信号进行加密处理,防止未经授权的访问和窃听。
03
拉普拉斯变换的主要应用:控制系统设计、信号处理、图像处理等。
拉普拉斯变换
01
拉普拉斯变换的定义:将时域函数转换到复频域,用于分析线性时不变系统。
02
拉普拉斯变换的公式和计算过程。
Z变换
小波变换
小波变换的定义:将信号分解成小波函数,用于多尺度分析信号。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
-
6
5.6.1.2 哈佛结构
数字信号处理一般需要较大的数据流量和较 高的运算速度,为了提高数据吞吐量,在数字 信号处理器中大多采用哈佛结构,如图5.6-2。
程序总线
数据总线
程序 存储器
CPU
操作数 存储器
图5.6-2 哈佛结构
-
7
与冯.诺曼结构处理器比较,哈佛结构处理 器有两个明显的特点:
(1)使用两个独立的存储器模块,分别存储 指令和数据,每个存储模块都不允许指令和数 据并存;
,而是数据的组织和地址的产生。以FFT运算为
例,要求并行存取N/2个数据点,由于一般的存
储器在每个周期里只能在总线上传输一个数据,
因此,并行处理要有专门的缓冲区以要求的吞吐
率来高速度地供应数据,数据地址也必须高速产
生。
-
19
5.6.2 DSP硬件构成
典型的DSP处理器中的运算/处理功能单元 主要包括以下几个部分:
•采用哈佛结构(多总线结构,即程序存储器 和数据存储器分开,各有各的总线,或地址总 线和数据总线分开),甚至采用多地址总线 和多数据总线。还采用流水线及并行结构。
-
2
5.6.1 数字信号处理器结构特点
5.6.1.1 冯.诺曼结构 1945年,冯.诺曼首先提出了“存储程序”
的概念和二进制原理,后来,人们把利用这种 概念和原理设计的电子计算机系统统称为“冯. 诺曼型结构”计算机。冯.诺曼结构的处理器使 用同一个存储器,经由同一个总线传输,如图 5.6-1。
期的循环操作足够长时,或是对一系列数据反
复执行同一指令时,采用流水线处理方式才是
合理的。
-
17
5.6.1.4 并行处理
加快运算速度的另一种方法是采用并行处 理,这种方法克服了流水线方法要把一个处理 分解为若干子处理的困难。
并行处理指: 1)DSP充分利用哈佛结构多重总线的优点, 在一个周期里使内部的各个处理单元同时工作 ,实现高度的并行处理。
(2)使用两条独立的总线,分别作为CPU与 每个存储器之间的专用通信路径,而这两条总 线之间毫无关联。
-
8
改进的哈佛结构: 为了提高传输效率,节省总线,又提出了
改进的哈佛结构,如图5.6-3。
地址总线
程序 存储器
CPU
操作数 存储器
数据总线
图5.6-3 改进型哈佛结构
-
9
改进型哈佛结构特点:
(1)使用两个独立的存储器模块,分别
-
10
指令流的定时关系:
可反映冯.诺曼结构与哈佛结构处理方式的
差别。
典型情况下,完成一条指令需要3个步读写操作的指令,如图5.6-4,
指令1至指令3均为存、取数指令。
对冯.诺曼结构处理器,由于指令和数据要
从同一个存储空间存取,经由同一总线传输,
-
14
流水线概念取自工厂自动化生产线,它是 一种可以使两个或更多的操作在执行时发生重 叠的技术,在流水线操作中,一个任务被分解 为若干子任务,这样它们就可在执行时相互重 叠。一个子任务被称为一个流水段。
在上面讨论哈佛结构的例子中,一个指令 可以分为3步完成,每一步可作为一个流水段, 当流水段填满时,处理器就可同时执行3个指令 ,所以平均每个指令只用1个时钟周期就可完成 。
因而它们无法重叠执行,只能顺序执行。
-
11
图6-5 哈佛结构处理器- 指令流的定时关系示意12图
如果采用哈佛结构处理以上同样的3条存 取数指令,如图5.6-5,由于取指令和存取数据 分别经由不同的存储空间和不同的总线,使得 各条指令可以重叠执行,这样,也就克服了数 据流传输的瓶颈,提高了运算速度。
存储指令和数据,每个存储模块都不允许指令
和数据并存,以便实现并行处理;
(2)具有一条独立的地址总线和一条独
立的数据总线,利用公用地址总线访问两个存
储模块(程序存储模块和数据存储模块),公
用数据总线则被用来完成程序存储模块或数据
存储模块与CPU之间的数据传输;
(3)两条总线由程序存储器和数据存储
器分时共用。
如在一个周期里可以同时完成取指令、计 算下一个指令的地址、执行一个或两个数据传 输、更新一个或两个地址指针并且进行计算等 等。
-
18
2)使用若干同样的处理单元对若干处理内容
相同(具有互换性)的操作同时作平等的处理。
并行处理的硬件开销很大,而且需要对各个
处理单元的输入和输出作复杂的管理。事实上,
在高度并行的结构里,主要的困难不是运算本身
5.6 数字信号处理硬件基础
数字信号处理中的主要运算是乘(除)加 (减)运算,在一般的计算机与微处理器中,乘 (除)法运算是用若干次加(减)法运算及移位 操作方式实现的;在处理器的结构方面,通用计 算机及微处理器采用冯.诺曼结构。
数字信号处理处理器在以上两方面有所不同。
-
1
数字信号处理器特点:
•乘法运算直接用硬件乘法器完成,以提高 运算速度。
-
15
图5.6-6 流水线的概念
-
16
关于使用流水线方式的两个问题:
(a) 一项处理一般很难分解成若干个处理
规模一致、因而时间上有最佳配合(无须等待
)的流水段,为此需要用若干个寄存器来协调
流水线的节奏。
(b) 在流水线的启动和停止阶段,流水线
要逐步地被填满或出空。因此,对于一次性的
非重复计算,流水线方式并不适用,只有当预
哈佛结构强调了总的系统速度以及通讯和 处理器配置方面的灵活性。
-
13
5.6.1.3 流水线处理
加快程序执行的一个途径是提高处理器 的时钟速度。但时钟速度的提高受工艺等的限 制,并不是可以无限提高的。而改进处理方法 则是提高程序流执行速度的另一个有效途径。
先进的处理方法有流水线处理和并行处 理,它们使得各项运算或处理都能在同一个时 钟周期里完成。
-
3
输入设备
运算器
输出设备
控制器
存储器
图5.6-1 冯.诺曼结构
-
数据线 控制线
4
冯.诺曼结构处理器具有以下几个特点: (1) 必须有一个存储器; (2) 必须有一个控制器; (3) 必须有一个运算器,用于完成算术
运算和逻辑 运算; (4) 必须有输入和输出设备,用于进行
人机通信。
-
5
冯.诺曼的主要贡献就是提出并实现了“ 存储程序”的概念。由于指令和数据都是二 进制码,指令和操作数的地址又密切相关, 因此,当初选择这种结构是自然的。但是, 这种指令和数据共享同一总线的结构,使得 信息流的传输成为限制计算机性能的瓶颈, 影响了数据处理速度的提高。
