游戏二进制
1-3 游戏二进制解析

位权与基数是进制数中的两个要素。
计算机采用二进制数的原因
1、电路简单,在技术上容易实现。 2、可靠性高。 3、运算规则简单。 4、可与逻辑运算对应。
1.3.2 不同进制之间的数的转换
为什么要进行进制数之间的转换? (1)八进制数码符号有0、1、2、3、4、5、6、7 基数为8, 运算规则是“逢八进一”。 (2)十六进制数码符号有 0、1、2、3、4、5、6、7 、8、 9、A、B、C、D、E、F,用英文字母A~F分别表示数 字10~15。基数是16,运算规则是“逢十六进一”。 (3)二进制数码符号只有0和1两个数字,基数为2,运算规 则是“逢二进一”。
1-3 游戏二进制
1.能进行不通进制数之间的转换 2.会通过ASCII码表查阅ASCII字符所对应的二进制数 3.了解常用的汉字编码标准
十二生肖编码
1.3.1 进位计数制
定义:进位数制,简称“进制”是按进位的原则进行计算的数制。 进位计数制的表示方法:
1、(101111)2 是二进制数,(188)16 是十六进制数。
(3)采用位权表示方法。
处在不同位置上的相同数字所代表的值不同,一个数字在某个位置上所表示的实 际数值等于该数值与这个位置的因子的乘积,而该位置的因子由所在位置相对于小数 点的距离来确定,简称为位权(Weight)。例如:十进制数的位权是10的整数次幂, 其个位的位权是100,十位的位权是101…… 。
十进制转二进制
方法为:十进制数除2取余法,即十进制数除2,余数为权位 上的数,得到的商值继续除2,依此步骤继续向下运算直到 商为0为止。
二进制转十进制
方法为:把二进制数按权展开、相加即得十进制数。
二进制转八进制
方法为:3位二进制数按权展开相加得到1位八进制数。(注 意事项,3位二进制转成八进制是从右到左开始转换,不足 时补0)。
信息编码游戏二进制教学案例

信息编码"游戏二进制"教学案例作者:刘丽丽来源:《读写算》2012年第50期一、教材分析本节课选自江苏教育出版社出版的《计算机应用基础》中的项目1-3,主要任务是使学生掌握二进制系统,学会二进制的信息编码,熟悉十进制与二进制之间的相互转化。
在教学中引入游戏,帮助学生理解,从而使学生对信息的数字化有所认识。
二、教学目标知识目标1、熟悉数制、基数、权的概念2、理解二进制数、八进制、十六进制的特点3、能进行十进制数、二进制数之间的相互转化技能目标1、通过玩生肖游戏,解开游戏的奥秘,能自行编制游戏卡片情感目标1、通过猜生肖的游戏,揭秘游戏的奥秘游戏的奥秘,宣传科学,破除迷信三、学情分析本节课的教学对象为高一新生,学生基本上在初中都学习过信息技术课程,熟悉计算机的基本操作,学生操作兴趣浓厚,对信息技术的理论学习兴趣不高,针对这样一种现象,教师必须将理论学习的课时安排得更加丰富多彩。
二进制是计算机系统极其重要的一个概念,但一些高一学生认为这个知识的学习与否根本不会影响自己的计算机操作能力,因此教师要更加努力地寻求解决问题的办法,让学生在积极主动的探索环境中学习二进制,掌握十进制与二进制间的相互转换。
同时,教材中的这部分内容表述的相对简单且抽象,仅凭高一学生的认知结构还很难理解这个概念。
在设计教学时,教师要特别注重学生对数制转化问题的理解。
针对上述情况,我在教学过程,引入了学生感兴趣的猜生肖游戏,让学生在玩游戏的过程中认识二进制,掌握进制之间的转化,四、教学重点、难点重点:理解各进制数的基本特征。
难点:能进行十进制数、二进制数之间的相互转化。
五、教学过程1、游戏导入(1)请同学们思考你所了解的生肖方面的一些知识。
(2)请同学打开教师提前准备好的猜生肖游戏,让学生通过游戏,来猜生肖游戏规则:这是一个对手游戏,由一方给出四组图片,每组图片有若干张。
另一方则根据具体的生肖,回答"有"或"没有",除此之外什么都不许说,然后由出图的一方猜出结果。
二进制猜数字原理

二进制猜数字原理宝子们!今天咱们来唠唠二进制猜数字这个超酷的事儿。
咱先从简单的说起哈。
想象一下,你心里想了一个数字,我要把它猜出来。
要是这个数字在1到8之间呢,我用二进制的方法可就能很快搞定哦。
这就像是一场神秘的数字捉迷藏。
你看啊,我可以把这1到8的数字分成两组。
第一组是1、3、5、7,第二组是2、4、6、8。
我先问你,你想的数字在第一组吗?如果是,那我就把范围缩小到1、3、5、7这几个奇数里啦;如果不是,那这个数字肯定就在2、4、6、8这几个偶数里喽。
这就像是把一大群小动物,按照一个小特点分成了两小群。
比如说你说在第一组,那我再把1、3、5、7分成两组,1、5一组,3、7一组。
我又问你,在1、5这组吗?要是在的话,那范围又进一步缩小啦。
要是不在,那就在3、7这组。
这时候你可能会问啦,为啥这样就能猜出来呢?这就是二进制的神奇之处啦。
在二进制里,数字可以用0和1表示。
就像我们分的这两组,就有点像二进制里的0和1的概念。
每次我们分一次组,就像是确定了这个数字在二进制里的某一位是0还是1。
再比如说这个数字在1到16之间。
那我就可以先把它们分成两组,1到8一组,9到16一组。
然后按照前面的方法不断地分下去。
就像在走迷宫一样,每次的分组都是一个岔路口,但是每走一次岔路口,我们就离正确的答案更近一步。
而且呀,这个二进制猜数字还有一种像是玩推理游戏的感觉。
你就像是那个出题的神秘人,我呢,就像个小侦探,通过不断地提问和推理,一点点揭开这个数字的神秘面纱。
有时候你可能觉得这数字好难猜呀,但只要按照这个二进制的思路,就像是有条小绳子牵着我们,一直朝着正确的方向走。
每一次的回答都是一个小线索,我就像个寻宝者,根据这些线索,在数字的宝藏堆里找到你心里想的那个宝贝数字。
这二进制猜数字可不仅仅是个简单的游戏呢。
它背后的原理其实也反映了一种很高效的信息处理方式。
就像我们在生活里,有时候要在很多选择里找到正确的那个,也可以像这样分组、排除,一步一步来。
数学游戏 猜数字(二进制)

115 成
116 戴 124 屈
117 谈 125 项
118 宋 126 祝
119 茅 127 董
120 庞
121 熊
122 纪
123 舒
表(七) 64 唐 72 汤 80 常 88 康 96 黄 65 费 73 滕 81 乐 89 伍 97 和 66 廉 74 殷 82 于 90 余 98 穆 67 岑 75 罗 83 时 91 元 99 萧 68 薛 76 毕 84 傅 92 卜 100 尹 69 雷 77 郝 85 皮 93 顾 101 姚 70 贺 78 邬 86 卞 94 孟 102 邵 71 倪 79 安 87 齐 95 平 103 湛
55
58
59
62
63
66
67
70
71
74
75
78
79
82
83
86
87
90
91Biblioteka 94959899
102
103
106
107
101
111
114
115 成
118 宋
119 茅
122 纪
123 舒
126 祝
127 董
表(三) 4 李 20 许 36 5 周 21 何 37 6 吴 22 吕 38 7 郑 23 施 39 44 45 46 47 12 卫 28 13 蒋 29 14 沈 30 15 韩 31
40
41
42
43
44
45
46
47
56
57
58
59
60
61
62
63
72
73
74
75
欢迎进入思科二进制游戏!

在键盘上输入数字10.
在键盘键盘上输入数字10.
最后,点击回车键.
您成功地得到了这个答案!
使用控制面板中的按键: 暂停游戏 音乐静音 更改音乐 结束游戏
拓展网络知识. 参加更多游戏 ,拓展网络知识.
/go/arcade
最后,使0出现在所有剩余数字的上方.
因为32 + 2 = 34 ,所以您已经得到了答案.
有时方框是空白的. 为了解决这个问题,请点击空白方框.
有时方框是空白的. 为了解决这个问题,请点击空白方框.
方框上方会出现一个数字小键盘.
接下来,将1下面出现的各个数字相加. 在本例中,您将得到8 + 2 = 10 .
欢迎进入思科二进制游戏! 迎进入思科二进制游戏! 科二进制游戏
这个二进制游戏通过寓教于乐的方式, 帮助您学习二进制.
您的速度越快,得分就越高. 用不了多久您就会变成二进制算术的天才! 只需点击"开始"按钮即可开始游戏.
游戏只需点击1和0
游戏只需点击1和0
游戏只需点击1和0
游戏只需点击1和0
/go/learningnetwork
�
游戏只需点击1和0
游戏只需点击1和0
举例说明: 下面的方框中出现数字34.
现在,使1分别出现在数字32和数字2的上方.
现在,使1分别出现在数字32和数字2的上方.
现在,使1分别出现在数字32和数字2的上方.
现在,使1分别出现在数字32和数字2的上方.
最后,使0出现在所有剩余数字的上方.
(完整word版)游戏二进制教案

《游戏二进制》教学设计课题名称:游戏二进制所属课程:《计算机应用基础》所属专业:计算机应用专业任教班级:计算机高职1601班授课课时:1课时任课教师:《游戏二进制》教学设计【教学目标】知识目标:1.理解数制的含义,知道计算机常用数制。
2.掌握二进制、八进制、十进制、十六进制数的表示方法。
3.能进行十进制与二进制之间的转换。
能力目标:1.培养学生逻辑运算能力。
2.通过“猜生肖”游戏,逐步揭开游戏的奥秘,培养学生分析问题、解决问题以及独立思考问题的能力。
3.培养学生自主使用各种学习资源以及网络软件的能力。
情感目标:1. 通过练习数制转换,让学生体验成功,提高学生自信心。
2.利用小组竞赛、导学案、列表检测,反思与探究等方法进行合作和探究式的学习,培养协作意识,养成良好的学习习惯,寻找合适有效的学习方法。
【教材分析】教材选用江苏教育出版社的《计算机应用基础》第2版,马成荣主编。
教材着重培养学生的能力,以提高学生计算机应用能力和信息素养为宗旨。
本节内容为《学习领域一:令人惊奇的小机器——计算机基础知识简介》中的第三个项目。
【学情分析】学生只学习了“计算机基础”中的“拆装计算机”和“操作系统”,对计算机硬件和操作系统有了一个基础的认识,计算机数制的概念还没有形成。
学生对动手操作有很大的兴趣,但是对于数制转换这种逻辑运算存在一定的畏难心理。
【设计理念】本次课的设计理念是“混合学习模式”,让学生在“猜生肖”的游戏项目中学会数制的表示方法以及数制的转换方法。
玩中学,玩中思,着重将枯燥的的逻辑运算变得生动有趣,做到“以玩促学”。
在教学过程中采用多种学习模式,即“混合学习模式”来适应不同的教学环节。
课前利用“蓝墨云班课”平台发放“猜生肖”游戏软件,让学生试玩该游戏并思考游戏的奥秘。
课堂教学上教师和学生进行游戏,两者做比较,激发学生思考两种游戏方式的区别;知识点讲授时采用教学课件、自制微课等手段进行辅助,给学生的自主学习留足时间;借鉴“翻转课堂”的教学理念,利用线上教学平台将课堂教学延伸至课后,强化学生练习。
简易的二进位和十进位的互换:猜出你的生日来
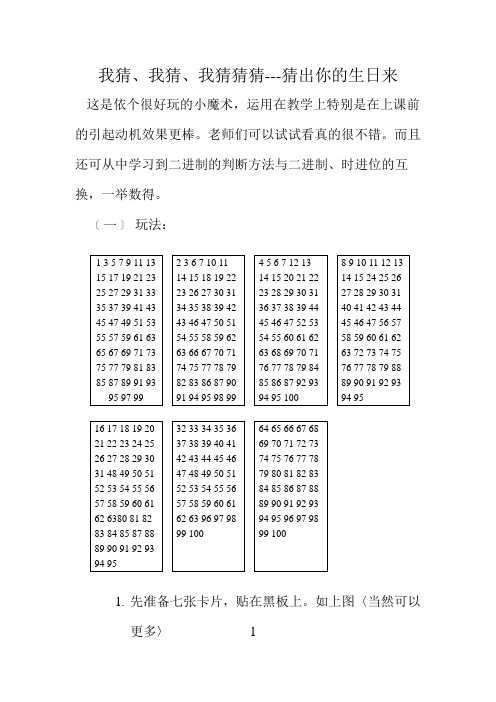
我猜、我猜、我猜猜猜---猜出你的生日来这是依个很好玩的小魔术,运用在教学上特别是在上课前的引起动机效果更棒。
老师们可以试试看真的很不错。
而且还可从中学习到二进制的判断方法与二进制、时进位的互换,一举数得。
﹝一﹞玩法:1.先准备七张卡片,贴在黑板上。
如上图〈当然可以更多〉 12.请一位小朋友上台,用纸板写下他的出生年、月日,并让全班同学都知道。
当然不能让老师知道!然后将纸板返盖在黑板上。
3.请该位小朋友回答在黑板上的卡片中,有那几张出现他所写的生日数字。
4.当小朋友回答完之后,老师已经把生日写在黑板上。
相信小朋友都会瞠目结舌把你当成偶像。
﹝二﹞方法:1.只要将有出现数字的卡片,把左上角第一个数字相加即可。
很简单的,试试看吧!2.老师们在问学生时最好从数字大的卡片先问,心算时较方便。
﹝三﹞解析:1.这个游戏的原理很简单:所有的整数都可以用1和二的倍数来组成,即1 2 4 8 16 3264 …………2.例如:14=8+4+2所以14只会在左上角是2、4、8三张卡片中出现又如:23=16+4+2+1所以23只会在左上角是1、2、4、16四张卡片中出现3.所以要自行制作卡片的方法很简单:【1】先准备七张白色板报纸〈大小事中即可〉【2】先在各张左上角分别写上1、2、4、8、16、32、64〈当然您也可以继续写上128、256让数字更多〉如下图。
在依2所述方法及可填满卡片。
1=1 7=4+2+12=2 【以此类推】.3=2+14=45=4+16=4+2 3﹝四﹞延伸:1.如果把上面的卡片反过来由大排到小,如下图2.取1到100中的任一数字,把数字分解成二的倍数例:19=16+2+13.再将0和1分别填进卡片中,其中16、2、1三张填进1。
8、4二张未被分解到,所以填04.您会发现结果是1 0 0 1 1,也就是说19在二进制的写法是1 0 0 1 1,如下图再看个例子吧例:65=64+1所以只把1填进64和1二张卡片中即可,其他卡片填0 所以64=1 0 0 0 0 0 1。
幼小数学题练习认识二进制的游戏

幼小数学题练习认识二进制的游戏在数学学习中,幼小的孩子们常常需要通过趣味性的游戏来加深对各种数学概念的理解。
其中,认识二进制数系统是培养孩子们逻辑思维和解决问题能力的重要一环。
本文将介绍一个基于游戏的幼小数学题,旨在帮助孩子们在轻松愉快的环境下认识二进制。
1. 游戏目标通过玩这个游戏,孩子们将能够了解二进制数系统的基本概念,包括只有0和1两个数字、位权的概念以及二进制数的计数方法。
2. 游戏准备为了进行这个游戏,我们需要以下准备:- 一个十进制数卡片组,上面印有0至9的数字,每个数字一个卡片;- 一个二进制位权卡片组,上面印有2的幂,从右到左依次为1、2、4、8、16...依次类推;- 一块沙盘或写字板,用来记录输入和输出的结果。
将十进制数卡片和二进制位权卡片集中放在一起,孩子们就可以开始游戏了。
3. 游戏规则(1) 孩子们首先随机选择一张十进制数卡片,展示给其他孩子看;(2) 其他孩子可以根据卡片上的数字,通过选择二进制位权卡片来表示这个数字;(3) 游戏进行者将选择的二进制位权卡片放在沙盘上,并对应选择合适的位权相加;(4) 孩子们对这个二进制数进行阅读并猜测对应的十进制数;(5) 游戏进行者逐位比对,将猜测的二进制数与实际的二进制数进行比对,教会孩子们在不同位权上的错误或正确;(6) 如果猜测错误,孩子们可以反复尝试直到猜对为止;(7) 孩子们可以轮流担任游戏进行者的角色,加深对二进制数系统的理解。
4. 游戏优势通过这个基于游戏的数学题练习,孩子们不仅能够学习认识二进制数系统,还能够培养他们的解决问题的能力。
此外,这个游戏还有以下几个优势:- 趣味性:通过游戏的方式,使孩子们能够在轻松愉快的氛围中学习数学知识;- 参与性:每个孩子都能够积极参与并亲自体验,增强学习的效果;- 合作性:孩子们可以在小组中互相协作,共同解决问题,培养团队合作意识;- 实践性:通过实际操作卡片和位权的组合,孩子们能够更好地理解二进制数系统的概念。
游戏二进制教案

《游戏二进制》教学设计课题名称:游戏二进制所属课程:《计算机应用基础》所属专业:计算机应用专业任教班级:计算机高职1601班授课课时:1课时任课教师:《游戏二进制》教学设计【教学目标】知识目标:1.理解数制的含义,知道计算机常用数制。
2.掌握二进制、八进制、十进制、十六进制数的表示方法。
3.能进行十进制与二进制之间的转换。
能力目标:1.培养学生逻辑运算能力。
2.通过“猜生肖”游戏,逐步揭开游戏的奥秘,培养学生分析问题、解决问题以及独立思考问题的能力。
3.培养学生自主使用各种学习资源以及网络软件的能力。
情感目标:1. 通过练习数制转换,让学生体验成功,提高学生自信心。
2.利用小组竞赛、导学案、列表检测,反思与探究等方法进行合作和探究式的学习,培养协作意识,养成良好的学习习惯,寻找合适有效的学习方法。
【教材分析】教材选用江苏教育出版社的《计算机应用基础》第2版,马成荣主编。
教材着重培养学生的能力,以提高学生计算机应用能力和信息素养为宗旨。
本节内容为《学习领域一:令人惊奇的小机器——计算机基础知识简介》中的第三个项目。
【学情分析】学生只学习了“计算机基础”中的“拆装计算机”和“操作系统”,对计算机硬件和操作系统有了一个基础的认识,计算机数制的概念还没有形成。
学生对动手操作有很大的兴趣,但是对于数制转换这种逻辑运算存在一定的畏难心理。
【设计理念】本次课的设计理念是“混合学习模式”,让学生在“猜生肖”的游戏项目中学会数制的表示方法以及数制的转换方法。
玩中学,玩中思,着重将枯燥的的逻辑运算变得生动有趣,做到“以玩促学”。
在教学过程中采用多种学习模式,即“混合学习模式”来适应不同的教学环节。
课前利用“蓝墨云班课”平台发放“猜生肖”游戏软件,让学生试玩该游戏并思考游戏的奥秘。
课堂教学上教师和学生进行游戏,两者做比较,激发学生思考两种游戏方式的区别;知识点讲授时采用教学课件、自制微课等手段进行辅助,给学生的自主学习留足时间;借鉴“翻转课堂”的教学理念,利用线上教学平台将课堂教学延伸至课后,强化学生练习。
数学活动二进制游戏.doc

数学活动二进制及其转换【教学目标】l 、了解二进制的含义;2、会进行二进制与十进制之间的相互转换;【教学重点】掌握二进制的含义【教学难点】会进行二进制与十进制之间的相互转换【教学方法】这节课主要采用探究教学和讲授法结合的教学方法,运用二进制的含义,会进行二进制与十进制之间的相互转换,使学生容易理解,同时结合习题让学生加深对逻辑运算的理解。
【教学过程】环节教学内容设计意图教师提出问题,学生回顾旧知识,做回1、了解散点图的概念,能说出变量相关关系的含义;出解答,教师讲解。
顾2、能根据给出的回归直线方程系数公式建立回归直线方程;通过回顾旧知,唤起旧3、会用科学计算器求回归系数。
学生对旧知识的回知顾,为学习新知识做好铺垫。
1、十进制的基数是?进位规则是?教师提出问2、二进制的基数是?每个数位上的数码个数是?数码分别是?题.学生回顾逻辑运进位规则是?算的规则和真值表的导入我们目前所接触的数都是十进制,它是用0、1、2、3、4、5、知识,概括、认识逻辑运算律,符合职校6、7、8、9 这十个数码符号来表示的,今天我们来学习另一种学生的认知能力.常见的表示数的方法——二进制相关概念:新1. 十进制:用0、1、2、3、4、5、6、7、8、9 这十个数码符号介绍法课放到相应的位置来表示数的一种方法。
如563652. 数位:数码符号在数中的位置3. 基数:每个数位上可以使用的数码符号的个数。
十进制的每一个数位都可以用十个数码符号。
4. 位权数:每个数位所代表的数。
十进制的进位规则为“逢10进位1”,位权数如下:整数部分小数点位置第三位第二位第一位起点位权数100 10 1二进制的概念及十进制、二进制的意义:十进制的意义:各个十位的数码与其位权数的乘积和。
例如:讲述法举例说明56365 5 4 6 103 3 102 6 101 5 10010二进制:用0、1 这两个数码符号表示数的一种方法。
例如110101整数部分小数点位置第三位第二位第一位起点位权数 4 2 1新二进制的意义:各个十位的数码与其位权数的乘积和。
二进制游戏22

十进制 0 1 2 3 4 5 6
字符 nul soh stx etx eot enq ack
十进制 16 17 18 19 20 21 22
字符 dle dc1 dc2 dc3 dc4 nak syn
十进制 32 33 34 35 36 37 38
字符 sp ! " # $ % &
十进制 48 49 50 51 52 53 54
字符 ' a b c d e f
十进制 112 113 114 115 116 117 118
字符 p q r s t u v
7
8 9 10
bel
bs ht nl
23
24 25 26
etb
can em sub
39
40 41 42
`
( ) *
55
56 57 58 :
7
8 9
71
72 73 74
G
H I J
休息片刻
你来试试设计一个游戏
0
李01王02张03刘04陈05杨06黄07赵08吴09周10 徐11孙12马13朱14胡15郭16何17高18林19罗20 郑21梁22谢23宋24唐25许26韩27冯28邓29曹30 彭31曾32肖33田34董35袁36潘37于38蒋39蔡40 余41杜42叶43程44苏45魏46吕47丁48任49沈50 姚51卢52姜53崔54钟55谭56陆57汪58范59金60 石61廖62贾63夏64韦65付66方67白68邹69孟70 熊71秦72邱73江74尹75薛76闫77段78雷79侯80 龙81史82陶83黎84贺85顾86毛87郝88龚89邵90 万91钱92严93覃94武95戴96莫97孔98向99汤100
解密 卡片猜数字游戏 二进制码的应用

记集合 ={只在k张表里出现的数},
A 记 中元k素个数为
,
A A (k k=1,2,3,4,k 5,6)
易知,只出现在k张表里的数的个数
= 从六张表中取k张的不同取法的个数
C A 所以, k =
k 6
6
C C C C C C A k1
= 1
k
6
2
6
3 6
4 6
5 6 2 ^ 6 1 63
③只在三张表格上出现的:
(一二三)→22,(一二四)→23,(一二五)→24, (一二六)→25,(一三四)→26,(一三五)→27, (一三六)→28,(一四五)→29,(一四六)→30, (一五六)→31,(二三四)→32,(二三五)→33, (二三六)→34,(二四五)→35,(二四六)→36, (二五六)→37,(三四五)→38,(三四六)→39, (三五六)→40,(四五六)→41,
a a a a a a a 6 5 4 3 2 1 ,其中 i只取0或1
ai=0表示在第i张上不出现, ai=1表示在第i张上出现;(1≤i≤6)
例1:某数只在第四张和第五张表上出现,则有
(四,五) ←→(011000) 2
(011000) = (24) ,那么该数就是24。
2
10
例2:某数只在第三、四、五、六张上出现
张表中出现的数} ,
(j=1,2,3,4,5,6;k=1,2,3,4,5,6)
B 记 k j
的个数为
Bk j
,则
对任何
j
,
Bk j
=从其他5张中取k-1张的不同取法个数=C5k1
故每张表中这6类数的总个数是:
6
二进制与编码

从小比特到大数字
•
31
从小比特到大数字
•
32
从小比特到大数字
• 读心术
33
从小比特到大数字
• 读心术
– 将包含某个数字的卡片标上1,其他为0
17 = 0 1
0
001
63 = 1 1
1
111
23 = 0 1
0
111
34
从小比特到大数字
• 负数在计算机中如何表示呢?
– 在8位机中+8表示为00001000,那么-8呢? – 将一个二进制位规定为符号位,它等于0时就
表示正数,等于1时就表示负数 – 直观上,-8就是10001000 – 但是计算机内部采用2的补码表示负数
– 5张卡片能表示的最大数字是多少? – 它们能表示的最小数字又是多少? – 在0至31之间,有你无法表示的数字吗? – 令数字递增1最简单的方法是什么?
15
二进制数与“比特”
• 二进制卡片游戏
– 利用了二进制数的原理 – 计算机仅用两个数字0和1表示信息,称之为二
进制 – 每位只有两种数值可供选择,二进制有时候也
?
在实际应用中,计算机系统处理连续存储的8位数据时非 常便利的,一般将上述连续存储的8比特称为一个字节 (byte)
24
从小比特到大数字
• 如何转换十进制到二进制
– 假设我们使用8比特表示数值 – 试试用二进制数怎样得到77 – 写下下面的数字
25
从小比特到大数字
• 如何转换77到二进制
– 从128开始 – 这个数太大了,无论如何都无法表示出77来 – 因此划掉
二进制数与“比特”
• 认识二进制
– 二进制中仅有0和1,如何只用这两个数来数数 ?
二进制游戏密室逃脱规则

二进制游戏密室逃脱规则
二进制游戏密室逃脱是一种逻辑推理和解谜的游戏。
以下是一般的规则:
1. 游戏玩家通常会被锁在一个密室中,需要解开各种谜题和难题,最终找到钥匙或密码离开密室。
2. 密室内可能会有各种线索、密码、谜题以及隐藏的物品,玩家需要通过观察、推理和解谜来逐步了解密室的秘密。
3. 密室内的线索和谜题可能是文字、图案、音频、视频或物品等各种形式的。
玩家需要仔细观察和分析,尝试解码或连接这些线索,以获得更多的信息。
4. 玩家在求助其他人时,不要泄露太多的关键信息,可以适当地给出暗示来帮助其他人解谜。
5. 游戏通常会设置限时,即玩家需要在规定的时间内完成任务。
如果时间到了,而玩家还没有成功逃出密室,游戏可能会失败。
6. 在游戏过程中,玩家需要遵守游戏规则和注意自身安全。
不要使用暴力手段或造成财产损失,保持合理的行为。
请注意,以上规则为一般情况下的描述,具体的游戏规则可能会因游戏设计而有所不同。
在参与具体的二进制游戏密室逃脱时,请仔细阅读游戏说明和规则,并按照规定的方式进行游戏。
1-3游戏二进制(2)

课时编号授课时间授课地点机房课题名称项目1-3 游戏二进制(2) 课时数2课时教学目标知识与技能目标能进行十进制、二进制、八进制、十六进制数之间的转换会通过ASCII码表查阅ASCII字符所对应的二进制数了解常用的汉字编码标准过程与方法目标1.通过任务驱动、自主探究、小组互助等方法,培养学生主动参与、乐于探索、勤于动手的学习习惯。
2.通过小组竞赛,提高学生获取信息能力、思维能力、分析能力、表达及评价能力。
情感态度与价值观目标1.通过对实际问题的解决,培养学生的信息素养,能将所学知识和技能当作工具解决生活和后续学习中遇到的问题。
2.引导学生树立奋发向上、勇于争先、积极进取的意识。
教学重点十进制数与二进制数的相互转换二进制数与八进制数、十六进制数之间的快速转换教学难点认识并查阅ASCII编码表十进制数与二进制数的相互转换教材处理增加二进制知识讲解教学方法教法设计任务驱动法••演示讲解学法设计游戏学习法•小组讨论•展示汇报教学资源准备教学资料课本、多媒体课件信息资源互联网仪器设备多媒体教室耗材作业布置常用数制的转换、查阅ASCII码表教学反思教学环节教学内容与活动教学方法与手段新课导入提出任务分析任务实施任务[导语]我们学习了二进制和二进制编码,掌握了几种进制之间的转换方法。
今天我们继续学习字符编码---ASCII码编码表,汉字的编码,了解汉字的编码原则。
[新课]【学习任务】1、学习字符编码----ASCII码表2、了解汉字编码类型和编码规律【且行且思】一、资源准备教师学生准备:ASCII码表二、任务实施探讨ASCII码和汉字编码的编码规律1)字符编码:目前采用的字符编码主要是ASCII码,它是American Standard Code for Information Interchange的缩写(美国标准信息交换代码),已被国际标准化组织ISO采纳,教学环节教学内容与活动教学方法与手段作为国际通用的信息交换标准代码。
二进制搜索算法在游戏开发中的应用实例

二进制搜索算法在游戏开发中的应用实例在当今的游戏开发领域,二进制搜索算法已经成为了一种非常重要的工具。
它不仅可以帮助开发者快速地查找和定位问题,还可以提高游戏的性能和用户体验。
本文将通过一些实际的应用实例来介绍二进制搜索算法在游戏开发中的应用。
首先,我们来看一个经典的应用场景:游戏中的地图寻路。
在许多游戏中,玩家需要通过地图来寻找目标位置,而二进制搜索算法可以帮助我们在地图中快速找到最短路径。
例如,假设我们有一个迷宫地图,其中包含了许多障碍物。
我们可以使用二进制搜索算法来找到从起点到终点的最短路径。
通过将地图划分为一个个小方格,并使用二进制搜索算法来判断每个方格是否可以通过,我们可以快速地找到最短路径,并将其显示给玩家。
除了地图寻路,二进制搜索算法还可以应用于游戏中的物品搜索。
在许多角色扮演游戏中,玩家需要在游戏世界中搜索各种物品,如武器、装备、药品等。
而这些物品通常会根据一定的规则和属性进行分类和排序。
通过使用二进制搜索算法,我们可以快速地找到符合玩家需求的物品。
例如,当玩家需要一把攻击力高于某个数值的剑时,我们可以使用二进制搜索算法来快速地在物品列表中找到满足条件的剑,并将其展示给玩家。
此外,二进制搜索算法还可以应用于游戏中的AI决策。
在许多游戏中,AI角色需要根据一定的策略和规则来做出决策,如攻击敌人、躲避障碍物等。
而这些决策通常需要考虑到各种因素,如距离、生命值、攻击力等。
通过使用二进制搜索算法,我们可以快速地找到最优的决策,并将其应用于AI角色。
例如,当AI角色需要找到一个离自己最近的敌人时,我们可以使用二进制搜索算法来快速地在敌人列表中找到最近的敌人,并让AI角色进行攻击。
综上所述,二进制搜索算法在游戏开发中有着广泛的应用。
它可以帮助我们快速地解决各种问题,提高游戏的性能和用户体验。
无论是地图寻路、物品搜索还是AI决策,二进制搜索算法都能够发挥重要的作用。
因此,作为游戏开发者,我们应该熟练掌握并灵活运用二进制搜索算法,以提升游戏的质量和竞争力。
解密卡片猜数字游戏二进制码的应用

16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63
(五)
2 3 6 7 10 11 14 15 18 19 22 23 26 27 30 31 34 35 38 39 42 43 46 47 50 51 54 55 58 59 62 63
“1 + 1 = 10”
—浅谈二进制的妙用
例如你选的是20,那么你只要说出 它在第三张和第五张表里,玩游戏的 人就能立刻猜到它是 20。
为什么呢? 我们可以看到,只同时出现在第三 张和第五张表里的数只有20,所以只 要记住20在哪几张表中出现,就可以 猜出答案了。
下面我们用数学方法更一般地分析其中 的道理。 问:
⑤只在五张表格中出现的:
(一二三四五)→57,(一二三四六)→58, (一二三五六)→59,(一二四五六)→60, (一三四五六)→61,(二三四五六)→62,
⑥六张都出现的: (一二三四五六)→63,
但这样的方法不容易记忆。
为了便于记忆和提高速度,我们要借 助于二进制数的方法。
任何一个数X(1≤X≤63)在6张ai 表上出现 的状况都一一对应于一个二进制的6位 数:
③只在三张表格上出现的:
(一二三)→22,(一二四)→23,(一二五)→24, (一二六)→25,(一三四)→26,(一三五)→27, (一三六)→28,(一四五)→29,(一四六)→30, (一五六)→31,(二三四)→32,(二三五)→33, (二三六)→34,(二四五)→35,(二四六)→36, (二五六)→37,(三四五)→38,(三四六)→39, (三五六)→40,(四五六)→41,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.能进行不通进制数之间的转换 2.会通过ASCII码表查阅ASCII字符所对应的二进制数 3.了解常用的汉字编码标准
十二生肖编码
1.3.1 进位计数制
定义:进位数制,简称“进制”是按进位的原则进行计算的数制。 进位计数制的表示方法:
1、(101111)2 是二进制数,(188)16 是十六进制数。
八进制与十六进制之间的转换
第一种:他们之间的转换可以先转成二进制 然后再相互转换。 第二种:他们之间的转换可以先转成十进制 然后再相互转换。
拓展知识
拓展知识
综合例题:
例1:将十进制数314.16按权展开:
314.16=3 × 102+1 × 101+4 × 100+1 × 10-1 +6 × 10-2 例2:把(1101.01)B写出展开式,并指出它表示的十进制数。
十进制转二进制
方法为:十进制数除2取余法,即十进制数除2,余数为权位 上的数,得到的商值继续除2,依此步骤继续向下运算直到 商为0为止。
二进制转十进制
方法为:把二进制数按权展开、相加即得十进制数。
二进制转八进制
方法为:3位二进制数按权展开相加得到1位八进制数。(注 意事项,3位二进制转成八进制是从右到左开始转换,不足 时补0)。
2、在数字后面加上一个英文字母表示。其中,十进制用D(Decimal)表 示,二进制用B(binary)表示,八进制用O(Octal)表示,十六进制 的用H(Hexadecimal)表示。 例如:1011B为二进制数,188H是十六进制数。
进制的特点:
进制数的特点
(1)数制的基数确定了所采用的进位计数制。
1、进位制数的表示
一个任意的十进制数都可以表示成:
Kn Kn 1 K1 K0 .K 1 K 2 K m+1 K m K n 10n K n 1 10n 1 K1 101 K2 102 K m1 10 m1 K m 10 m K1 101 K0 100
例如:十进制数1234.56的展开式为: 1234.56=1×103+2×102+3×101+4×100+5×10-1+6×10-2
2、进制数之间的转换
1、二、八、十六进制转换成十进制数。 转换方法:将二、八、十六制数按位权进行多项式展开,然后在十进制 中按照“逢十进一”的运算规则进行运算。 进制 原始数 按位权展开 9×102+2×101+3×100+4×101+5×10-2 1×23+1×22+0×21+1×20+1×2-1 对应十进 制数 923.45 13.5
十进制转八进制与十六进制
十进制转八进制或者十六进制有两种方法
第一:间接法—把十进制转成二进制,然后再由二进制转成八进制或者 十六进制。 第二:直接法—把十进制转八进制或者十六进制按照除8或者16取余, 直到商为0为止。
八进制或者十六进制转成十进制
方法为:把八进制、十六进制数按权展开、相加即得十进制 数。
表示一个数时所用的数字符号的个数称为 基数(Radix)。如十进制数制的基数 为10;二进制的基数为2。对于N进位数制,有N个数字符号。如十进制中有10个数字 符号:0~9;二进制有2个符号:0和1;八进制有8个符号:0~7;十六进制共有16个符 号:0~9、A~F。
(2)逢N进一。
如十进制中逢10进1;八进制中逢8进1;二进制中逢2进1;十六进制中逢16进1。
十进制 923.45 二进制 1101.1
八进制 572.4
十六进 3B4.4 制
5×82+7×81+2×80+4×8-1 3×162+B×161+4×160+4×16-1
378.5 948.25
进制转换
ห้องสมุดไป่ตู้
十进制数转换成二、八、十六进制数
转换方法是整数部分和小数部分分别转换。整数部 分采用“求商逆取余”,小数部分采用“求积顺取 整”。 例1-4 将(87)10转换成二进制数。 转换如下: 余数 87 2 ………… 1 2 43 二进制整数低位 ………… 1 2 21 10 ………… 1 2 ………… 0 5 2 ………… 1 2 2 ………… 0 2 1 ………… 1 二进制整数高位 0
1 ×23+1 ×22+0 ×21+1 ×20+0 ×2-1+1 ×2-2=(13.25)10
例3: (317)O相当于十进制数的多少? 3 × 82+1 × 81+7 × 80=(207)10 练习:(3C4)H代表的十进制数是什么?
进制之间数的对应关系
十进制 (D) 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 二进制 (B) 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111 八进制 (O) 0 1 2 3 4 5 6 7 10 11 12 13 14 15 16 17 十六进制 (H) 0 1 2 3 4 5 6 7 8 9 a b c d e f
八进制转成二进制
方法为:八进制数通过除2取余法,得到二进制数,对每个 八进制为3个二进制,不足时在最左边补零。
二进制转十六进制
方法为:与二进制转八进制方法近似,八进制是取三合一, 十六进制是取四合一。(注意事项,4位二进制转成十六进 制是从右到左开始转换,不足时补0)。
十六进制转二进制
方法为:十六进制数通过除2取余法,得到二进制数,对每 个十六进制为4个二进制,不足时在最左边补零。
(3)采用位权表示方法。
处在不同位置上的相同数字所代表的值不同,一个数字在某个位置上所表示的实 际数值等于该数值与这个位置的因子的乘积,而该位置的因子由所在位置相对于小数 点的距离来确定,简称为位权(Weight)。例如:十进制数的位权是10的整数次幂, 其个位的位权是100,十位的位权是101…… 。
位权与基数是进制数中的两个要素。
计算机采用二进制数的原因
1、电路简单,在技术上容易实现。 2、可靠性高。 3、运算规则简单。 4、可与逻辑运算对应。
1.3.2 不同进制之间的数的转换
为什么要进行进制数之间的转换? (1)八进制数码符号有0、1、2、3、4、5、6、7 基数为8, 运算规则是“逢八进一”。 (2)十六进制数码符号有 0、1、2、3、4、5、6、7 、8、 9、A、B、C、D、E、F,用英文字母A~F分别表示数 字10~15。基数是16,运算规则是“逢十六进一”。 (3)二进制数码符号只有0和1两个数字,基数为2,运算规 则是“逢二进一”。
