2013中考全分类汇编特殊的平行四边形
中考数学 特殊的平行四边形(含中考真题解析)

特殊的平行四边形☞解读考点☞2年中考1.下列命题是假命题的是()A.对角线互相垂直且相等的平行四边形是正方形.B.对角线互相垂直的矩形是正方形.C.对角线相等的菱形是正方形.D.对角线互相垂直平分的四边形是正方形.【答案】D.考点:1.正方形的判定;2.平行四边形的判定;3.菱形的判定;4.矩形的判定.2.(连云港)已知四边形ABCD,下列说法正确的是()A.当AD=BC,AB∥DC时,四边形ABCD是平行四边形B.当AD=BC,AB=DC时,四边形ABCD是平行四边形C.当AC=BD,AC平分BD时,四边形ABCD是矩形D.当AC=BD,AC⊥BD时,四边形ABCD是正方形【答案】B.【解析】试题分析:∵一组对边平行且相等的四边形是平行四边形,∴A不正确;∵两组对边分别相等的四边形是平行四边形,∴B正确;∵对角线互相平分且相等的四边形是矩形,∴C不正确;∵对角线互相垂直平分且相等的四边形是正方形,∴D不正确;故选B.考点:1.平行四边形的判定;2.矩形的判定;3.正方形的判定.3.(徐州)如图,菱形中,对角线AC、BD交于点O,E为AD边中点,菱形ABCD的周长为28,则OE的长等于()A.3.5 B.4 C.7 D.14【答案】A.【解析】试题分析:∵菱形ABCD的周长为28,∴AB=28÷4=7,OB=OD,∵E为AD边中点,∴OE是△ABD的中位线,∴OE=12AB=12×7=3.5.故选A.考点:菱形的性质.4.(柳州)如图,G,E分别是正方形ABCD的边AB,BC的点,且AG=CE,AE⊥EF,AE=EF,现有如下结论:①BE=12GE;②△AGE≌△ECF;③∠FCD=45°;④△GBE∽△ECH其中,正确的结论有()A.1个B.2个C.3个D.4个【答案】B.考点:1.全等三角形的判定与性质;2.正方形的性质;3.相似三角形的判定与性质;4.综合题.5.(内江)如图所示,正方形ABCD的面积为12,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为()A B.C.D【答案】B.考点:1.轴对称-最短路线问题;2.最值问题;3.正方形的性质.6.(南充)如图,菱形ABCD的周长为8cm,高AE长为3cm,则对角线AC长和BD长之比为()A.1:2 B.1:3 C.1:2D.1:3【答案】D.【解析】试题分析:如图,设AC,BD相较于点O,∵菱形ABCD的周长为8cm,∴AB=BC=2cm,∵高AE长为3cm,∴=1(cm),∴CE=BE=1cm,∴AC=AB=2cm,∵OA=1cm,AC⊥BD,∴=3(cm),∴BD=2OB=cm,∴AC:BD=1:3.故选D.考点:菱形的性质.7.(安徽省)如图,矩形ABCD中,AB=8,BC=4.点E在边AB上,点F在边CD上,点G、H在对角线AC上.若四边形EGFH是菱形,则AE的长是()A.B.C.5 D.6【答案】C.考点:1.菱形的性质;2.矩形的性质.8.(十堰)如图,正方形ABCD 的边长为6,点E 、F 分别在AB ,AD 上,若CE=53,且∠ECF=45°,则CF 的长为( )A .102B .53 CD【答案】A .考点:1.全等三角形的判定与性质;2.勾股定理;3.正方形的性质;4.综合题;5.压轴题.9.(鄂州)在平面直角坐标系中,正方形A1B1C1D1、D1E1E2B2、A2B2C2D2、D2E3E4B3、A3B3C3D3…按如图所示的方式放置,其中点B1在y轴上,点C1、E1、E2、C2、E3、E4、C3…在x轴上,已知正方形A1B1C1D1的边长为1,∠B1C1O=60°,B1C1∥B2C2∥B3C3…则正方形A2015B2015C2015D2015的边长是()A.2014 21)(B.2015 21)(C.2015 33)(D.2014 33)(【答案】D.考点:1.正方形的性质;2.规律型;3.综合题.10.(广安)如图,已知E、F、G、H分别为菱形ABCD四边的中点,AB=6cm,∠ABC=60°,则四边形EFGH的面积为cm2.【答案】【解析】试题分析:连接AC,BD,相交于点O,如图所示,∵E、F、G、H分别是菱形四边上的中点,∴EH=12BD=FG,EH∥BD∥FG,EF=12AC=HG,∴四边形EHGF是平行四边形,∵菱形ABCD中,AC⊥BD,∴EF⊥EH,∴四边形EFGH是矩形,∵四边形ABCD是菱形,∠ABC=60°,∴∠ABO=30°,∵AC⊥BD,∴∠AOB=90°,∴AO=12AB=3,∴AC=6,在Rt△AOB中,由勾股定理得:OB==,∴BD=,∵EH=12BD,EF=12AC,∴EH=EF=3,∴矩形EFGH的面积=EF•FG=cm2.故答案为:.考点:1.中点四边形;2.菱形的性质.11.(凉山州)菱形ABCD在平面直角坐标系中的位置如图所示,顶点B(2,0),∠DOB=60°,点P是对角线OC上一个动点,E(0,﹣1),当EP+BP最短时,点P的坐标为.【答案】(3,2-).的交点,∴点P的坐标为方程组(11y xy x⎧=⎪⎨⎪=-⎩的解,解方程组得:32xy⎧=⎪⎨=⎪⎩,所以点P的坐标为(3,2-),故答案为:(3-,2).考点:1.菱形的性质;2.坐标与图形性质;3.轴对称-最短路线问题;4.动点型;5.压轴题;6.综合题.12.(潜江)菱形ABCD在直角坐标系中的位置如图所示,其中点A的坐标为(1,0),点B的坐标为(0),动点P从点A出发,沿A→B→C→D→A→B→…的路径,在菱形的边上以每秒0.5个单位长度的速度移动,移动到第2015秒时,点P的坐标为.【答案】(0.5,.考点:1.菱形的性质;2.坐标与图形性质;3.规律型;4.综合题.13.(北海)如图,已知正方形ABCD的边长为4,对角线AC与BD相交于点O,点E在DC边的延长线上.若∠CAE=15°,则AE= .【答案】8.【解析】试题分析:∵正方形ABCD的边长为4,对角线AC与BD相交于点O,∴∠BAC=45°,AB ∥DC,∠ADC=90°,∵∠CAE=15°,∴∠E=∠BAE=∠BAC﹣∠CAE=45°﹣15°=30°.∵在Rt△ADE中,∠ADE=90°,∠E=30°,∴AE=2AD=8.故答案为:8.考点:1.含30度角的直角三角形;2.正方形的性质.14.(南宁)如图,在正方形ABCD的外侧,作等边△ADE,则∠BED的度数是.【答案】45°.考点:1.正方形的性质;2.等边三角形的性质.15.(玉林防城港)如图,已知正方形ABCD边长为3,点E在AB边上且BE=1,点P,Q 分别是边BC,CD的动点(均不与顶点重合),当四边形AEPQ的周长取最小值时,四边形AEPQ的面积是.【答案】92.【解析】试题分析:如图1所示,作E 关于BC 的对称点E′,点A 关于DC 的对称点A′,连接A′E′,四边形AEPQ 的周长最小,∵AD=A′D=3,BE=BE′=1,∴AA′=6,AE′=4.∵DQ ∥AE′,D是AA′的中点,∴DQ 是△AA′E′的中位线,∴DQ=12AE′=2;CQ=DC ﹣CQ=3﹣2=1,∵BP ∥AA′,∴△BE′P ∽△AE′A′,∴'''BP BE AA AE =,即164BP =,BP=32,CP=BC ﹣BP=332-=32,S 四边形AEPQ=S 正方形ABCD ﹣S △ADQ ﹣S △PCQ ﹣SBEP=9﹣12AD•DQ ﹣12CQ•CP ﹣12BE•BP=9﹣12×3×2﹣12×1×32﹣12×1×32=92,故答案为:92.考点:1.轴对称-最短路线问题;2.正方形的性质.16.(达州)在直角坐标系中,直线1y x =+与y 轴交于点A ,按如图方式作正方形A1B1C1O 、A2B2C2C1、A3B3C1C2…,A1、A2、A3…在直线1y x =+上,点C1、C2、C3…在x 轴上,图中阴影部分三角形的面积从左到游依次记为1S 、2S 、3S 、…n S ,则n S 的值为(用含n的代数式表示,n为正整数).【答案】232n-.故答案为:232n-.考点:1.一次函数图象上点的坐标特征;2.正方形的性质;3.规律型;4.综合题.17.(齐齐哈尔)如图,正方形ABCB1中,AB=1.AB与直线l的夹角为30°,延长CB1交直线l于点A1,作正方形A1B1C1B2,延长C1B2交直线l于点A2,作正方形A2B2C2B3,延长C2B3交直线l于点A3,作正方形A3B3C3D4,…,依此规律,则A2014A2015= .【答案】2014.考点:1.相似三角形的判定与性质;2.正方形的性质;3.规律型;4.综合题.18.(梧州)如图,在正方形ABCD中,点P在AD上,且不与A、D重合,BP的垂直平分线分别交CD、AB于E、F两点,垂足为Q,过E作EH⊥AB于H.(1)求证:HF=AP;(2)若正方形ABCD的边长为12,AP=4,求线段EQ的长.【答案】(1)证明见试题解析;(2.【解析】考点:1.正方形的性质;2.全等三角形的判定与性质;3.勾股定理;4.综合题.19.(恩施州)如图,四边形ABCD、BEFG均为正方形,连接AG、CE.(1)求证:AG=CE;(2)求证:AG⊥CE.【答案】(1)证明见试题解析;(2)证明见试题解析.【解析】试题分析:(1)由ABCD、BEFG均为正方形,得出AB=CB,∠ABC=∠GBE=90°,BG=BE,得出∠ABG=∠CBE,从而得到△ABG≌△CBE,即可得到结论;(2)由△ABG≌△CBE,得出∠BAG=∠BCE,由∠BAG+∠AMB=90°,对顶角∠AMB=∠CMN,得出∠BCE+∠CMN=90°,证出∠CNM=90°即可.试题解析:(1)∵四边形ABCD、BEFG均为正方形,∴AB=CB,∠ABC=∠GBE=90°,BG=BE,∴∠ABG=∠CBE,在△ABG和△CBE中,∵AB=CB,∠ABG=∠CBE,BG=BE,∴△ABG ≌△CBE(SAS),∴AG=CE;(2)如图所示:∵△ABG≌△CBE,∴∠BAG=∠BCE,∵∠ABC=90°,∴∠BAG+∠AMB=90°,∵∠AMB=∠CMN,∴∠BCE+∠CMN=90°,∴∠CNM=90°,∴AG⊥CE.考点:1.全等三角形的判定与性质;2.正方形的性质.20.(武汉)已知锐角△ABC中,边BC长为12,高AD长为8.(1)如图,矩形EFGH的边GH在BC边上,其余两个顶点E、F分别在AB、AC边上,EF交AD于点K.①求EFAK的值;②设EH=x,矩形EFGH的面积为S,求S与x的函数关系式,并求S的最大值;(2)若AB=AC,正方形PQMN的两个顶点在△ABC一边上,另两个顶点分别在△ABC 的另两边上,直接写出正方形PQMN的边长.【答案】(1)①32;②3(8)2S x x=-,S的最大值是24;(2)245或24049.试题解析:(1)①∵EF∥BC,∴AK EFAD BC=,∴EF BCAK AD==128=32,即EFAK的值是32;考点:1.相似三角形的判定与性质;2.二次函数的最值;3.矩形的性质;4.正方形的性质;5.分类讨论;6.综合题;7.压轴题.21.(荆州)如图1,在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且PA=PE,PE交CD于F.(1)PC=PE;(2)求∠CPE的度数;(3)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120°时,连接CE,试探究线段AP与线段CE的数量关系,并说明理由.【答案】(1)证明见试题解析;(2)90°;(3)AP=CE.【解析】试题分析:(1)先证出△ABP≌△CBP,得到PA=PC,由PA=PE,得到PC=PE;(2)由△ABP≌△CBP,得到∠BAP=∠BCP,进而得到∠DAP=∠DCP,由PA=PC,得到∠DAP=∠E,∠DCP=∠E,最后∠CPF=∠EDF=90°得到结论;(3)借助(1)和(2)的证明方法容易证明结论.考点:1.正方形的性质;2.全等三角形的判定与性质;3.菱形的性质;4.探究型;5.综合题;6.压轴题.1.(宜宾)如图,将n个边长都为2的正方形按如图所示摆放,点A1,A2,…An分别是正方形的中心,则这n个正方形重叠部分的面积之和是()A.n B.n﹣1 C.(14)n﹣1 D.14n【答案】B.【解析】试题分析:由题意可得一个阴影部分面积等于正方形面积的14,即是14×4=1,5个这样的正方形重叠部分(阴影部分)的面积和为:1×4,n个这样的正方形重叠部分(阴影部分)的面积和为:1×(n﹣1)=n﹣1.故选B.考点:1.正方形的性质2.全等三角形的判定与性质.2.(山东省淄博市)如图,矩形纸片ABCD中,点E是AD的中点,且AE=1,BE的垂直平分线MN恰好过点C.则矩形的一边AB的长度为()A. 1 BCD. 2【答案】C.考点:1.勾股定理;2.线段垂直平分线的性质;3.矩形的性质.3.(山东省聊城市)如图,在矩形ABCD中,边AB的长为3,点E,F分别在AD,BC上,连接BE,DF,EF,BD.若四边形BEDF是菱形,且EF=AE+FC,则边BC的长为()A .B .3C .D【答案】B . 【解析】试题分析:∵四边形ABCD 是矩形,∴∠A=90°,即BA ⊥BF ,∵四边形BEDF 是菱形,∴EF ⊥BD ,∠EBO=∠DBF ,∴AB=BO=3,∠ABE=∠EBO ,∴∠ABE=∠EBD=∠DBC=30°,∴BE=cos30BO=︒,∴BF=BE=,∵EF=AE+FC ,AE=CF ,EO=FO∴,故选B .考点:1.矩形的性质;2.菱形的性质. 4.(广西来宾市)顺次连接菱形各边的中点所形成的四边形是( ) A . 等腰梯形 B . 矩形 C . 菱形 D . 正方形 【答案】B .考点:1.正方形的判定;2.三角形中位线定理;3.菱形的性质. 5.(贵州铜仁市)如图所示,在矩形ABCD 中,F 是DC 上一点,AE 平分∠BAF 交BC 于点E ,且DE ⊥AF ,垂足为点M ,BE=3,,则MF 的长是( )ABC.1 D.【答案】D.考点:1.相似三角形的判定与性质;2.角平分线的性质;3.勾股定理;4.矩形的性质.6.(襄阳)如图,在矩形ABCD中,点E,F分别在边AB,BC上,且AE=13AB,将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q,对于下列结论:①EF=2BE;②PF=2PE;③FQ=4EQ;④△PBF是等边三角形.其中正确的是()A.①②B.②③C.①③D.①④【答案】D.【解析】试题分析:∵AE=13AB,∴BE=2AE.由翻折的性质得,PE=BE,∴∠APE=30°.∴∠AEP=90°﹣30°=60°,∴∠BEF=12(180°﹣∠AEP)=12(180°﹣60°)=60°.∴∠EFB=90°﹣60°=30°.∴EF=2BE.故①正确.∵BE=PE,∴EF=2PE.∵EF>PF,∴PF>2PE.故②错误.由翻折可知EF⊥PB,∴∠EBQ=∠EFB=30°.∴BE=2EQ,EF=2BE.∴FQ=3EQ.故③错误.由翻折的性质,∠EFB=∠BFP=30°,∴∠BFP=30°+30°=60°.∵∠PBF=90°﹣∠EBQ=90°﹣30°=60°,∴∠PBF=∠PFB=60°.∴△PBF是等边三角形.故④正确;综上所述,结论正确的是①④.故选D.考点:1.矩形的性质;2.含30度角直角三角形的判定和性质;3.等边三角形的判定.7.(宁夏)菱形ABCD中,若对角线长AC=8cm,BD=6cm,则边长AB= cm.【答案】5.考点:1.菱形的性质;2.勾股定理.8.(山东省聊城市)如图,四边形ABCD是平行四边形,作AF∥CE,BE∥DF,AF交BE 与G点,交DF与F点,CE交DF于H点、交BE于E点.求证:△EBC≌△FDA.【答案】证明见解析.考点:1.平行四边形的性质;2.全等三角形的判定.9.(梅州)如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.(1)求证:CE=CF;(2)若点G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?【答案】(1)证明见解析;(2)GE=BE+GD成立,理由见解析.【解析】试题分析:(1)由DF=BE,四边形ABCD为正方形可证△CEB≌△CFD,从而证出CE=CF.(2)由(1)得,CE=CF,∠BCE+∠ECD=∠DCF+∠ECD即∠ECF=∠BCD=90°又∠GCE=45°所以可得∠GCE=∠GCF,故可证得△ECG≌△FCG,即EG=FG=GD+DF.又因为DF=BE,所以可证出GE=BE+GD成立.试题解析:(1)在正方形ABCD中,∵BC=CD,∠B=∠CDF,BE=DF,∴△CBE≌△CDF (SAS).∴CE=CF.(2)GE=BE+GD成立.理由是:考点:1.正方形的性质;2.全等三角形的判定和性质;3.等腰直角三角形的性质.☞考点归纳归纳1:矩形基础知识归纳:1、矩形的概念有一个角是直角的平行四边形叫做矩形.2、矩形的性质(1)具有平行四边形的一切性质(2)矩形的四个角都是直角(3)矩形的对角线相等(4)矩形是轴对称图形3、矩形的判定(1)定义:有一个角是直角的平行四边形是矩形(2)定理1:有三个角是直角的四边形是矩形(3)定理2:对角线相等的平行四边形是矩形基本方法归纳:关于矩形,应从平行四边形的内角的变化上认识其特殊性:一个内角是直角的平行四边形,进一步研究其特有的性质:是轴对称图形、内角都是直角、对角线相等.同时平行四边形的性质矩形也都具有.注意问题归纳:证明一个四边形是矩形,若题设条件与这个四边形的对角线有关,通常证这个四边形的对角线相等.【例1】如图,在矩形ABCD中,对角线AC、BD相交于点O,∠ACB=30°,则∠AOB 的大小为()A、30°B、60°C、90°D、120°【答案】B.考点:矩形的性质.归纳2:菱形基础知识归纳:1、菱形的概念有一组邻边相等的平行四边形叫做菱形2、菱形的性质(1)具有平行四边形的一切性质(2)菱形的四条边相等(3)菱形的对角线互相垂直,并且每一条对角线平分一组对角(4)菱形是轴对称图形3、菱形的判定(1)定义:有一组邻边相等的平行四边形是菱形(2)定理1:四边都相等的四边形是菱形(3)定理2:对角线互相垂直的平行四边形是菱形4、菱形的面积S菱形=底边长×高=两条对角线乘积的一半注意问题归纳:菱形是在平行四边形的前提下定义的,首先它是平行四边形,但它是特殊的平行四边形,特殊之处就是“有一组邻边相等”,因而就增加了一些特殊的性质和不同于平行四边形的判定方法.【例2】如图,已知AC、BD是菱形ABCD的对角线,那么下列结论一定正确的是().(A)△ABD与△ABC的周长相等;(B)△ABD与△ABC的面积相等;(C)菱形的周长等于两条对角线之和的两倍;(D)菱形的面积等于两条对角线之积的两倍.【答案】B.考点:菱形的性质.归纳3:正方形基础知识归纳:1、正方形的概念有一组邻边相等并且有一个角是直角的平行四边形叫做正方形.2、正方形的性质(1)具有平行四边形、矩形、菱形的一切性质(2)正方形的四个角都是直角,四条边都相等(3)正方形的两条对角线相等,并且互相垂直平分,每一条对角线平分一组对角(4)正方形是轴对称图形,有4条对称轴(5)正方形的一条对角线把正方形分成两个全等的等腰直角三角形,两条对角线把正方形分成四个全等的小等腰直角三角形(6)正方形的一条对角线上的一点到另一条对角线的两端点的距离相等.注意问题归纳:正方形的判定没有固定的方法,只要判定既是矩形又是菱形就可以判定.【例3】如图,ABCD是正方形场地,点E在DC的延长线上,AE与BC相交于点F.有甲、乙、丙三名同学同时从点A出发,甲沿着A﹣B﹣F﹣C的路径行走至C,乙沿着A﹣F﹣E ﹣C﹣D的路径行走至D,丙沿着A﹣F﹣C﹣D的路径行走至D.若三名同学行走的速度都相同,则他们到达各自的目的地的先后顺序(由先至后)是()A.甲乙丙B.甲丙乙C.乙丙甲D.丙甲乙【答案】B.考点:正方形的性质.☞1年模拟1.(山东省潍坊市昌乐县中考一模)下列说法中,错误的是()A.平行四边形的对角线互相平分B.对角线互相平分的四边形是平行四边形C.菱形的对角线互相垂直D.对角线互相垂直的四边形是菱形【答案】D.【解析】试题分析:根据平行四边形的菱形的性质得到A、B、C选项均正确,而D不正确,因为对角线互相垂直的四边形也可能是梯形.故选D.考点:1.菱形的判定与性质;2.平行四边形的判定与性质.2.(广东省广州市中考模拟)如图,在矩形ABCD中,对角线AC,BD相交于点O,∠ACB=30°,则∠AOB的大小为()A.30°B.60°C.90°D.120°【答案】B.考点:矩形的性质.3.(山东省日照市中考模拟)如图,在边长为2的菱形ABCD中,∠B=45°,AE为BC边上的高,将△ABE沿AE所在直线翻折得△AB1E,则△AB1E与四边形AECD重叠部分的面积为()A .0.7B .0.9C .−2 D【答案】C . 【解析】试题分析:如图,∵∠B=45°,AE ⊥BC ,∴∠BAE=∠B=45°,∴AE=BE ,由勾股定理得:BE2+AE2=22,解得:,由题意得:△ABE ≌△AB1E ,∴∠BAB1=2∠BAE=90°,,∴,-2,∵四边形ABCD 为菱形,∴∠FCB1=∠B=45°,∠CFB1=∠BAB1=90°,∴∠CB1F=45°,CF=B1F ,∵CF ∥AB ,∴△CFB1∽△BAB1,∴11B C CF AB BB =,解得:,∴△AEB1、△CFB1的面积分别为:112=,21(232⨯=-,∴△AB1E 与四边形AECD 重叠部分的面积=1(32--=.故选C .考点:1.菱形的性质;2.翻折变换(折叠问题). 4.(山东省济南市平阴县中考二模)如图,菱形OABC 的顶点O 在坐标系原点,顶点A 在x 轴上,∠B=120°,OA=2,将菱形OABC 绕原点O 顺时针旋转105°至OA′B′C′的位置,则点B′的坐标为( )A.(B.,)C.(2,-2)D.,【答案】B.考点:1.菱形的性质;2.坐标与图形变化-旋转.5.(山东省青岛市李沧区中考一模)如图,在矩形ABCD中,点E,F分别在边AB,BC上,且AE=13AB,将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q,对于下列结论:①EF=2BE;②PF=2PE;③FQ=4EQ;④△PBF是等边三角形.其中正确的是()A.①②B.②③C.①③D.①④【答案】D.综上所述,结论正确的是①④.故选D.考点:1.翻折变换(折叠问题);2.矩形的性质.6.(山东省日照市中考一模)小明在学习了正方形之后,给同桌小文出了道题,从下列四个条件:①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD中选两个作为补充条件,使▱ABCD 为正方形(如图),现有下列四种选法,你认为其中错误的是()A.①②B.②③C.①③D.②④【答案】B.考点:正方形的判定.7.(山东省青岛市李沧区中考一模)如图,在矩形ABCD 中,,AD=1,把该矩形绕点A 顺时针旋转α度得矩形AB′C′D′,点C′落在AB 的延长线上,则图中阴影部分的面积是 .4π-.考点:1.旋转的性质;2.矩形的性质;3.扇形面积的计算.8.(河北省中考模拟二)如图,在矩形ABCD中,AB=3,⊙O与边BC,CD相切,现有一条过点B的直线与⊙O相切于点E,连接BE,△ABE恰为等边三角形,则⊙O的半径为.【答案】【解析】试题分析:过O点作GH⊥BC于G,交BE于H,连接OB、OE,∴G是BC的切点,OE ⊥BH,∴BG=BE,∵△ABE为等边三角形,∴BE=AB=3,∴BG=BE=3,∵∠HBG=30°,∴,BH=2,设OG=OE=x,则-3,-x,在RT△OEH中,EH2+OE2=OH2,即(-3)2+x2=-x)2,解得,∴⊙O的半径为.故答案为:考点:1.切线的性质;2.矩形的性质.9.(山东省日照市中考一模)边长为1的一个正方形和一个等边三角形如图摆放,则△ABC 的面积为.【答案】1 4.考点:1.正方形的性质;2.等边三角形的性质;3.含30度角的直角三角形.10.(山东省青岛市李沧区中考一模)如图,正方形ABCD和正方形CEFG中,点D在CG 上,BC=1,CE=3,H是AF的中点,那么CH的长是.考点:1.正方形的性质;2.直角三角形斜边上的中线;3.勾股定理.11.(山西省晋中市平遥县九年级下学期4月中考模拟)如图,已知Rt△ABC中,∠ABC=90°,先把△ABC绕点B顺时针旋转90°至△DBE后,再把△ABC沿射线平移至△FEG,DE、FG相交于点H.(1)判断线段DE、FG的位置关系,并说明理由;(2)连结CG,求证:四边形CBEG是正方形.【答案】(1)FG⊥ED.理由见解析;(2)证明见解析.【解析】考点:1.旋转的性质;2.正方形的判定;3.平移的性质;4.探究型.12.(北京市平谷区中考二模)如图,已知点E,F分别是□ABCD的边BC,AD上的中点,且∠BAC=90°.(1)求证:四边形AECF是菱形;(2)若∠B=30°,BC=10,求菱形AECF面积.【答案】(1)见解析(2【解析】试题分析:(1)利用平行四边形的性质和菱形的性质即可判定四边形AECF是菱形;(2)连接EF交于点O,运用解直角三角形的知识点,可以求得AC与EF的长,再利用菱形的面积公式即可求得菱形AECF的面积.试题解析:(1)证明:∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC.在Rt△ABC中,∠BAC=90°,点E是BC边的中点,∴AE=CE=12BC.同理,AF=CF=12AD.∴AF=CE.∴四边形AECF是平行四边形.∴平行四边形AECF是菱形.考点:1.菱形的性质;2.平行四边形的性质;3.解直角三角形.13.(山东省日照市中考模拟)如图,▱ABCD在平面直角坐标系中,AD=6,若OA、OB的长是关于x的一元二次方程x2-7x+12=0的两个根,且OA>OB.(1)求sin∠ABC的值;(2)若E为x轴上的点,且S△AOE=163,求经过D、E两点的直线的解析式,并判断△AOE与△DAO是否相似?(3)若点M在平面直角坐标系内,则在直线AB上是否存在点F,使以A、C、F、M为顶点的四边形为菱形?若存在,请直接写出F点的坐标;若不存在,请说明理由.【答案】(1)45.(2)△AOE∽△DAO.(3)F1(3,8);F2(-3,0);F3(4751-,722-),F4(-4225,4425).【解析】 试题分析:(1)求得一元二次方程的两个根后,判断出OA 、OB 长度,根据勾股定理求得AB 长,那么就能求得sin ∠ABC 的值; (2)易得到点D 的坐标为(6,4),还需求得点E 的坐标,OA 之间的距离是一定的,那么点E 的坐标可能在点O 的左边,也有可能在点O 的右边.根据所给的面积可求得点E 的坐标,把A 、E 代入一次函数解析式即可.然后看所求的两个三角形的对应边是否成比例,成比例就是相似三角形;(3)根据菱形的性质,分AC 与AF 是邻边并且点F 在射线AB 上与射线BA 上两种情况,以及AC 与AF 分别是对角线的情况分别进行求解计算. 试题解析:(1)解x2-7x+12=0,得x1=4,x2=3.∵OA >OB ,∴OA=4,OB=3.在Rt △AOB 中,由勾股定理有5=,∴sin ∠ABC=54OA AB =;(3)根据计算的数据,OB=OC=3,∴AO 平分∠BAC ,①AC 、AF 是邻边,点F 在射线AB 上时,AF=AC=5,所以点F 与B 重合,即F (-3,0);②AC 、AF 是邻边,点F 在射线BA 上时,M 应在直线AD 上,且FC 垂直平分AM ,点F (3,8);③AC 是对角线时,做AC 垂直平分线L ,AC 解析式为y=-43x+4,直线L 过(32,2),且k 值为34(平面内互相垂直的两条直线k 值乘积为-1),L 解析式为y=34x+78,联立直线L与直线AB 求交点,∴F (4751-,722-);④AF 是对角线时,过C 做AB 垂线,垂足为N ,根据等积法求出CN=245,勾股定理得出,AN=75,做A 关于N 的对称点即为F ,AF=145,过F 做y 轴垂线,垂足为G ,FG=145×35=4225,∴F (-4225,4425).综上所述,满足条件的点有四个:F1(3,8);F2(-3,0);F3(4751-,722-),F4(-4225,4425).考点:1.相似三角形的判定;2.解一元二次方程-因式分解法;3.待定系数法求一次函数解析式;4.平行四边形的性质;5.菱形的判定;6.分类讨论;7.存在型;8.探究型. 14.(河北省中考模拟二)如图,已知正方形ABCD ,E 是AB 延长线上一点,F 是DC 延长线上一点,连接BF 、EF ,恰有BF=EF ,将线段EF 绕点F 顺时针旋转90°得FG ,过点B 作EF 的垂线,交EF 于点M ,交DA 的延长线于点N ,连接NG .(1)求证:BE=2CF ;(2)试猜想四边形BFGN 是什么特殊的四边形,并对你的猜想加以证明. 【答案】(1)证明见解析.(2)四边形BFGN 为菱形,证明见解析.(2)解:四边形BFGN为菱形,证明如下:考点:1.正方形的性质;2.全等三角形的判定与性质;3.菱形的判定;4.旋转的性质;5.和差倍分.15.(广东省广州市中考模拟)如图,在菱形ABCD中,AB=1,∠DAB=60°,把菱形ABCD绕点A顺时针旋转30°得到菱形AB′C′D′,其中点C的运动路径为CC ,则图中阴影部分的面积为.【答案】342π+.【解析】试题分析:连接CD′和BC′,∵∠DAB=60°,∴∠DAC=∠CAB=30°,∵∠C′AB′=30°,∴A 、D′、C 及A 、B 、C′分别共线∴,∴扇形ACC′4π=.∵AC=AC′,AD′=AB ,∴在△OCD′和△OC'B 中,CD BC ACO AC D COD C OB ''=⎧⎪''∠=∠⎨⎪''∠=∠⎩,∴△OCD′≌△OC′B(AAS ),∴OB=OD′,CO=C′O .∵∠CBC′=60°,∠BC′O=30°,∴∠COD′=90°.∵CD′=AC --1,OB+C′O=1,∴在Rt △BOC′中,BO2+(1-BO )2=-1)2,解得BO=12-,32C O '=-,∴考点:1.菱形的性质;2.全等三角形的判定与性质;3.扇形面积的计算;4.旋转的性质.。
中考数学专题知识点精讲1:特殊的平行四边形

特殊的平行四边形一、知识要点概述、边(或两底和)的一半.4、平行线等分线段定理:如果一组平行线在一条直线上截得的线段相等,那么在其他直线上截得的线段也相等.推论1:过三角形一边中点且平行于另一边的直线必平分第三边.推论2:过梯形一腰中点且平行于两底的直线必平分另一腰.二、典型例题剖析例1、已知四边形ABCD和对角线AC、BD,顺次连结各边中点得四边形MNPQ,给出以下六个命题:①若所得四边形MNPQ为矩形,则原四边形ABCD是菱形;②若所得四边形MNPQ为菱形,则原四边形ABCD是矩形;③若所得四边形MNPQ为矩形,则AC⊥BD;④若所得四边形MNPQ为菱形,则AC=BD;⑤若所得四边形MNPQ为矩形,则∠BAD=90°;⑥若所得四边形MNPQ为菱形,则AB=AD.以上命题中,正确的是()A.①②B.③④C.③④⑤⑥D.①②③④答案:选B.例2、下列命题:①一组对边平行且相等的四边形是梯形;②一组对边平行且不相等的四边形是梯形;③一组对边平行,另一组对边相等的四边形是梯形;④一条直线与矩形的一组对边相交,必分矩形为两个直角梯形.其中真命题的序号是__________.分析:可采用反例法,即举的例子符合题设但不符合结论,从而说明原命题是假命题.①可举反例:平行四边形;②可证得另一组对边不平行,故符合定义;③可举反例:矩形;④直线与矩形垂直相交,则得到两个矩形.答案:②例3、已知:如图AB∥CD,AE⊥DC,AE=12,BD=15,AC=20,则梯形的面积是()A.130B.140C.150D.160分析:要求梯形的面积,由于,而AE=12,所以关键是求(AB+DC)的长,注意已知BD和AC,这样我们可过B作对角线AC的平行线交DC的延长线于F,则可证AB=CF,于是转化求(DC+CF)的长,又过B作BH⊥DC于H,则BH=AE=12,现在只要求DH和HF即可.在Rt△BDH中,利用勾股定理得在Rt△BHF中,故DF=DH+HF=DC+AB=9+16=25.这样梯形的面积为.答案:选C.例4、如图,梯形ABCD中,AD∥BC,中位线EF分别与BD、AC交于点G,H,若AD=6,BC=10,则GH=__________.分析:本题主要考查三角形、梯形的中位线定理.因为EF是中位线,,EG、HF分别是△ABD、△ACD的中位线,,故GH=EF-EG-HF=8-3-3=2.答案:2.例5、如图,将矩形ABCD沿着直线BD折叠,使点C落在C′处,BC′交AD于E,AD=8,AB=4,求△BED的面积.解:由△BCD沿直线BD折叠与△BC′D重合,∠1=∠2,又∵AD∥BC,∴∠2=∠3.∠1=∠3,故△BED是等腰三角形.∴BE=ED.设ED=x,则AE=AD-ED=8-x.在Rt△ABE中,AB2+AE2=BE2,∴42+(8-x)2=x2.解之得x=5.故例6、如图,M、N分别是□ABCD的对边AD、BC的中点,且AD=2AB.求证:PMQN为矩形.证明:∵ABCD是平行四边形,∴AD BC.又M、N分别是AD、BC的中点,∴MD BN,BNDM为平行四边形.∴BM∥ND,同理AN∥MC,∴PMQN为平行四边形.连结MN,∵AM BN,∴ABNM为平行四边形.又AD=2AB,M为AD中点,∴AM=AB.∴ABNM为菱形,∴AN⊥BM.∴PMQN为矩形.说明:本例是一道平行四边形、菱形、矩形性质定理和判定定理反复运用的较好的综合题,同学们认真体会其证题思路和证明方法.例7、如图,过正方形ABCD的顶点B作BE∥AC且使AE=AC,又CF∥AE,求证:.分析:按常规思路将∠AEB取半或将∠BCF加倍,但由于图形的“不规则”性,难于达到目的,易见AEFC为菱形,∠ACB=45°,若结论成立,则∠ACF=∠AEF=30°,不妨利用正方形和菱形的特性求出∠E=30°.证明:连结BD交AC于O,作AH⊥BE于H.∵ABCD为正方形,∴AC与BD互相垂直平分于点O,且AO=BO.已知BE∥AC,已知AH⊥BE易证四边形AOBH为正方形,.∴∠AEH=30°又BE∥AC,AE∥CF,AE=AC.∴ACFE为菱形,∴∠AEF=∠ACF=30°,又∠ACB=45°,∴∠BCF=15°..例8、在梯形ABCD中,AD∥BC且AB=AD+BC,M为DC的中点,求证:AM⊥BM.分析:由题设AB=AD+BC,应将两底集中.证明:延长AM交BC延长线于N,∵M是DC的中点,AD∥BC,则△ADM≌△NCM.∴AD=CN,AM=MN.故AB=AD+BC=CN+BC=BN.由等腰三角形“三线合一”知BM⊥AM.说明:根据证题的需要,集中梯形的两底是常用辅助线之一,本例也可以先延长BC到N使BN=AB,再证A、M、N共线而得.例9、如图,在等腰梯形ABCD中AD∥BC,AB=DC,点P为BC边上的一点,PE⊥AB,PF⊥CD,BG⊥CD,垂足分别为E、F、G,求证:PE+PF=BG.证明:过P点作PH⊥BG于点H,∵BG⊥CD,PF⊥CD,PH⊥BG,∴四边形PHGF为矩形.∴PF=HG,PH∥CD,∴∠BPH=∠C.又在等腰梯形ABCD中AB=DC,∵∠PBE=∠C,∴∠PBE=∠BPH.故Rt△BPH≌Rt△PBE,∴BH=PE.∴PE+PF=BH+HG=BG.说明:在梯形的有关问题中常是化归为特殊的平行四边形及三角形来处理.例10、如图,ABCD为等腰梯形,AB∥CD,对角线AC、BD交于O,且∠AOB=60°,又E、F、G分别为DO、AO、BC的中点,求证:△EFG为等边三角形.分析:这里中点较多,显然,又AD=BC,要能证EG,FG为BC的一半才行,但无法用中位线定理,只有另辟蹊径,注意∠AOB=60°.证明:连结EC,∵ABCD为等腰梯形,∴AD=BC且AC=BD,又DC=DC,∴△ADC≌△BCD,∠ACD=∠BDC.∴△ODC为等腰三角形.∵∠DOC=∠AOB=60°,∴△ODC为等边三角形.又E为OD中点,∴∠OEC=90°.在Rt△BEC中,G为斜边的中点,,在△OAD中,∵E、F分别是OD、OA的中点,,∴△EFG为等边三角形.说明:本例中除揭示等腰梯形的诸性质外,还提醒同学们注意遇到中点应联想中位线,但不要只想到中位线,须将所学过的知识综合运用,这里运用了“直角三角形斜边上的中线等于斜边的一半”.。
2013中考试题-平行四边形精选真题

2013中考试题-平行四边形一:选择题1、(德阳市2013年)如图.在ABCD中,AB=6、AD=9,∠BAD的平分线交BC于点E,DC的延长线于点F, BG⊥AE,垂足为G,若BG=CEF的面积是A、B C、D、2、(2013•内江)如图,在▱ABCD中,E为CD上一点,连接AE、BD,且AE、BD交于点F,S△DEF:S△ABF=4:25,则DE:EC=()的平分线交BC于E,交DC的延长线于F,BG⊥AE于G,BG=,则△EFC的周长为()、BD相交于点O,给出下列四个条件:①AD∥BC;②AD=BC;③OA=OC;④OB=ODBD相交于点O,E为OD的中点,连接AE并延长交DC于点F,1、(2013菏泽)如图,▱ABCD中,对角线AC与BD相交于点E,∠AEB=45°,BD=2,将△ABC沿AC所在直线翻折180°到其原来所在的同一平面内,若点B的落点记为B′,则DB′的长为.2、(2013•铁岭)如图,在平面直角坐标中,直线l经过原点,且与y轴正半轴所夹的锐角为60°,过点A(0,1)作y轴的垂线l于点B,过点B1作作直线l的垂线交y轴于点A1,以A1B.BA为邻边作▱ABA1C1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2,以A2B1.B1A1为邻边作▱A1B1A2C2;…;按此作法继续下去,则C n的坐标是.三:解答证明题1、(2013•宁夏压轴题)在▱ABCD中,P是AB边上的任意一点,过P点作PE⊥AB,交AD 于E,连结CE,CP.已知∠A=60°;(1)若BC=8,AB=6,当AP的长为多少时,△CPE的面积最大,并求出面积的最大值.(2)试探究当△CPE≌△CPB时,▱ABCD的两边AB与BC应满足什么关系?2、(2013•莱芜)如图,在Rt△ABC中,∠C=90°,以AC为一边向外作等边三角形ACD,点E为AB的中点,连结DE.(1)证明DE∥CB;(2)探索AC与AB满足怎样的数量关系时,四边形DCBE是平行四边形.3、(2013•新疆)如图,▱ABCD中,点O是AC与BD的交点,过点O的直线与BA、DC 的延长线分别交于点E、F.(1)求证:△AOE≌△COF;(2)请连接EC、AF,则EF与AC满足什么条件时,四边形AECF是矩形,并说明理由.。
特殊的平行四边形讲义矩形部分(2013中考题版)

CLARK-EDU小康老师8年级讲义—特殊平行四边形(一)考点综述:特殊平行四边形即矩形、菱形、正方形,它们是初二的必考内容之一,主要出现的题型多样,注重考查学生的基础证明和计算能力,以及灵活运用数学思想方法解决问题的能力。
内容主要包括:矩形、菱形、正方形的性质与判定,以及相关计算,了解平行四边形与矩形、菱形、正方形之间的联系,掌握平行四边形是矩形、菱形、正方形的条件。
三角形中位线以及直角三角形斜边中线的性质也是近几年考试的重点!知识点归纳:例1:(2013江苏扬州)矩形的两邻边长的差为2,对角线长为4,则矩形的面积为 . 例2:(2013江苏南京) 如图,将矩形ABCD 绕点A 顺时针旋转到矩形A ’B ’C ’D ’的位置,旋转角为α (0︒<α<90︒)。
若∠1=110︒,则∠α= 。
例3:(2013湖北宜昌)如图,在矩形ABCD 中,AB <BC ,AC ,BD 相交于点O ,则图例4:13.(2013·济宁)如图,矩形ABCD 的面积为20cm 2,对角线交于点O ;以AB 、AO 为邻边做平行四边形AOC 1B ,对角线交于点O 1;以AB、AO 1为邻边做平行四边形AO 1C 2B ;…;依此类推,则平行四边形AO 4C 5B 的面积为( ) A .5/4 cm 2 B .5/8 cm 2 C.5/16 cm 2 D.5/32 cm 2例5:(2013河南省15)如图,矩形ABCD 中,3,4A B B C ==,点E 是BC 边上一点,连接AE ,把B ∠沿AE 折叠,使点B落在点'B 处,当△'CEB 为直角三角形时,BE 的长为例6:(2013重庆市:)如图,在矩形ABCD 中,E 、F 分别是边AB 、CD 上的点,AE =CF ,连接EF 、BF ,EF 与对角线AC 交于点O ,且BE =BF ,∠BEF =2∠BAC .(1)求证:OE =OF ;(2)若BC =AB 的长.A BCD B ’ 1 C ’D ’例7:如图,矩形ABCD 中,AB =4cm ,BC =8cm ,动点M 从点D 出发,按折线DCBAD 方向以2cm/s 的速度运动,动点N 从点D 出发,按折线DABCD 方向以1cm/s 的速度运动.(1)若动点M 、N 同时出发,经过几秒钟两点相遇?(2)若点E 在线段BC 上,且BE =3cm ,若动点M 、N 同时出发,相遇时停止运动,经过几秒钟,点A 、E 、M 、N 组成平行四边形?例8:如图,将矩形纸片ABCD 沿对角线AC 折叠,使点B 落到点B ′的位置,AB ′与CD 交于点E .(1)试找出一个与△AED 全等的三角形,并加以证明.(2)若AB =8,DE =3,P 为线段AC 上的任意一点,PG ⊥AE 于G ,PH ⊥EC 于H ,试求PG +PH 的值,并说明理由.例9:过矩形ABCD 对对角线AC 的中点O 作EF ⊥AC 分别交AB 、DC 于E 、F ,点G 为AE 的中点,若∠AOG =30o 求证:3OG=DCACABEDFA例10:如图所示,以△ABC 的三边为边,分别作三个等边三角形. (1)求证四边形ADEF 是平行四边形.(2)△ABC 满足什么条件时,四边形ADEF 是菱形?是矩形? (3)四边形ADEF 一直存在吗?例11:如图所示;过矩形ABCD 的顶点A 作一直线,交BC 的延长线于点E ,F 是AE 的中点,连接FC 、FD 。
中考复习课件特殊平行四边形38页PPT

56、死去何所道,托体同山阿。 57、春秋多佳日,登高赋新诗。 58、种豆南山下,草盛豆苗稀。晨兴 理荒秽 ,带月 荷锄归 。道狭 草木长 ,夕露 沾我衣 。衣沾 不足惜 ,但使 愿无违 。 59、相见无杂言,但道桑麻长。 60、迢迢新秋夕,亭亭月将圆。
31、只有永远躺在泥坑里的人,才不会再掉进坑里。——黑格尔 32、希望的灯一旦熄灭,生活刹那间变成了一片黑暗。——普列姆昌德 33、希望是人生的乳母。——科策布 34、形成天才的决定因素应该是勤奋。——郭沫若 35、学到很多东西的诀窍,就是一下子不要学很多。——洛克
中考数学知识点梳理第20讲 特殊平行四边形

(1)四个角都是直角
(2)对角线相等且互相平分.即
AO=CO=BO=DO.
(3)面积=长×宽
=2S△ABD=4S△AOB.
(1)四边相等
(2)对角线互相垂直、平分,一条对角线平分一组对角
(3)面积=底×高
=对角线_乘积的一半
4.中点四边形
(1)任意四边形多得到的中点四边形一定是平行四边形.
(2)对角线相等的四边形所得到的中点四边形是矩形.
(3)对角线互相垂直的四边形所得到的中点四边形是菱形.
(4)对角线互相垂直且相等的四边形所得到的中点四边形是正方形.
如图,四边形ABCD为菱形,则其中点四边形EFGD的形状是矩形.
5.特殊四边形中的解题模型
第20讲特殊的平行四边形
一、知识清单梳理
知识点一:特殊平行四边形的性质与判定
关键点拨及对应举例
1.性质
(具有平行四边形的一切性质,对边平行且相等)
矩形
菱形
正方形
(1)矩形中,Rt△ABD≌Rt△DCA≌Rt△CDB≌Rt△BAC;_两对全等的等腰三角形.所以经常结合勾股定理、等腰三角形的性质解题.
(2)菱形中,有两对全等的等腰三角形;Rt△ABO≌Rt△ADO≌Rt△CBO≌Rt△CDO;若∠ABC=60°,则△ABC和△ADC为等边三角形,且四个直角三角形中都有一个30°的锐角.
(1)定义法:有一个角是直角,且有一组邻边相等的平行四边形
(2)一组邻边相等的矩形
(3)一个角是直角的菱形
(4)对角线相等且互相垂直、平分
例:判断正误.
邻边相等的四边形为菱形.()
2013年全国各地中考数学试卷分类汇编:多边形与平行四边形

多边形与平行四边形一、选择题 1.(2013江苏扬州,6,3分)一个多边形的每个内角均为108°,则这个多边形是( ). A .七边形 B . 六边形 C .五边形 D .四边形 【答案】C . 【解析】根据多边形的内角和公式可知,这个n 边形满足:(n -2)×180=108n .解得n =5.所以应选C .【方法指导】多边形的内角和公式:(n -2)×180°.每个内角相等的多边形是正多边形. 【易错警示】记不住多边形的内角和公式而出错. 2.(2013重庆市(A ),9,4分)如图,在平行四边形ABCD 中,点E 在AD 上,连接CE 并延长与BA 的延长线交于点F ,若AE =2ED ,CD =3cm ,则AF 的长为( )A .5cmB .6cmC .7 cmD . 8cm 【答案】B .【解析】由平行四边形ABCD ,得AF ∥CD ,所以∠F =∠ECD ,∠F AE =∠D ,则有△AFE ∽△DEC ,从而得到错误!未找到引用源。
=错误!未找到引用源。
=2,即3AF=2,解得AF =6.故答案选B .【方法指导】本题考查平行四边形的性质,相似三角形.本题图形中蕴涵两个相似三角形基本图:1.“X ”型,即△AFE ∽△DEC .2.“A ”型,即△F AE ∽△FBC .2. (2013湖南益阳,6,4分)如图2,在平行四边形ABCD 中,下列结论中错误..的是( ) A .∠1=∠2B .∠BAD =∠BCDC .AB =CD D . AC ⊥BD【答案】:D【解析】根据平行四边形的性质可知D 是错误的。
【方法指导】根据平行四边形性质可知:平行四边形的对边相等,平行四边形的对角相等,平行四边形的对角线互相平分。
3.(2013广东湛江,5,4分)已知一个多边形的内角和是540°,则这个多边形是( )A .四边形B .五边形C .六边形D .七边形 【答案】B.【解析】根据题意有错误!未找到引用源。
【初中数学】初中数学知识点总结:特殊的平行四边形

【初中数学】初中数学知识点总结:特殊的平行四边形(1)平行四边形的所有性质矩形、菱形、正方形都具有,但矩形、菱形、正方形具有的性质平行四边形不一定具有,这点易出现混淆;(2)矩形、菱形具有的性质正方形都具有,而正方形具有的性质,矩形不一定具有,菱形也不一定具有,这点也易出现混淆;(3)不能正确的理解和运用判定定理进行证明,(如在证明菱形时,把四条边相等的四边形是菱形误解成两组邻边相等的四边形是菱形);(3)再利用对角线长度求菱形的面积时,忘记乘;(3)判定一个四边形是特殊的平行四边形的条件不充分。
【典型例题】(2021天门、潜江、仙桃)正方形ABCD中,点O是对角线DB的中点,点P是DB所在直线上的一个动点,PE⊥BC于E,PF⊥DC于F.(1)当点P与点O重合时(如图①),猜测AP与EF的数量及位置关系,并证明你的结论;(2)当点P在线段DB上 (不与点D、O、B重合)时(如图②),探究(1)中的结论是否成立?若成立,写出证明过程;若不成立,请说明理由初三;(3)当点P在DB的长延长线上时,请将图③补充完整,并判断(1)中的结论是否成立?若成立,直接写出结论;若不成立,请写出相应的结论.【解析】(1)AP=EF,AP⊥EF,理由如下:连接AC,则AC必过点O,延长FO交AB于M;∵OF⊥CD,OE⊥BC,且四边形ABCD是正方形,∴四边形OECF是正方形,∴OM=O F=OE=AM,∵∠MAO=∠OFE=45°,∠AMO=∠EOF=90°,∴△AMO≌△FOE,∴AO=EF,且∠AOM=∠OFE=∠FOC=45°,即OC⊥EF,故AP=EF,且AP⊥EF.(2)题(1)的结论仍然成立,理由如下:延长AP交BC于N,延长FP交AB于M;∵PM⊥AB,PE⊥BC,∠MBE=90°,且∠MBP=∠EBP=45°,∴四边形MBEP是正方形,∴MP=PE,∠AMP=∠FPE=90°;又∵AB-BM=AM,BC-BE=EC=PF,且AB=BC,BM=BE,∴AM=PF,∴△AMP≌△FPE,∴AP=EF,∠APM=∠FPN=∠PEF∵∠PEF+∠PFE=90°,∠FPN=∠PEF,∴∠FPN+∠PFE=90°,即AP⊥EF,故AP=EF,且AP⊥EF.(3)题(1)(2)的结论仍然成立;如右图,延长AB交PF于H,证法与(2)完全相同感谢您的阅读,祝您生活愉快。
2013-2022北京中考真题数学汇编:平行四边形
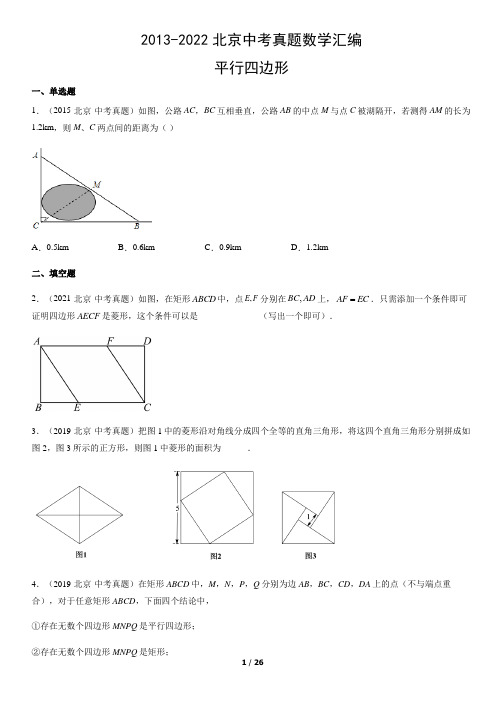
2013-2022北京中考真题数学汇编平行四边形一、单选题1.(2015·北京·中考真题)如图,公路AC ,BC 互相垂直,公路AB 的中点M 与点C 被湖隔开,若测得AM 的长为1.2km ,则M 、C 两点间的距离为( )A .0.5kmB .0.6kmC .0.9kmD .1.2km二、填空题 2.(2021·北京·中考真题)如图,在矩形ABCD 中,点,E F 分别在,BC AD 上,AF EC .只需添加一个条件即可证明四边形AECF 是菱形,这个条件可以是______________(写出一个即可).3.(2019·北京·中考真题)把图1中的菱形沿对角线分成四个全等的直角三角形,将这四个直角三角形分别拼成如图2,图3所示的正方形,则图1中菱形的面积为______.4.(2019·北京·中考真题)在矩形ABCD 中,M ,N ,P ,Q 分别为边AB ,BC ,CD ,DA 上的点(不与端点重合),对于任意矩形ABCD ,下面四个结论中,①存在无数个四边形MNPQ 是平行四边形;②存在无数个四边形MNPQ 是矩形;③存在无数个四边形MNPQ 是菱形;④至少存在一个四边形MNPQ 是正方形.所有正确结论的序号是______.5.(2013·北京·中考真题)如图,O 是矩形ABCD 的对角线AC 的中点,M 是AD 的中点.若5AB =,12AD =,则四边形ABOM 的周长为_______.三、解答题6.(2022·北京·中考真题)如图,在ABCD 中,AC BD ,交于点O ,点E F ,在AC 上,AE CF =.(1)求证:四边形EBFD 是平行四边形;(2)若,BAC DAC ∠=∠求证:四边形EBFD 是菱形.7.(2022·北京·中考真题)在ABC 中,90ACB ∠=,D 为ABC 内一点,连接BD ,DC ,延长DC 到点E ,使得.CE DC =(1)如图1,延长BC 到点F ,使得CF BC =,连接AF ,EF ,若AF EF ⊥,求证:BD AF ⊥;(2)连接AE ,交BD 的延长线于点H ,连接CH ,依题意补全图2,若222AB AE BD =+,用等式表示线段CD 与CH 的数量关系,并证明.8.(2020·北京·中考真题)在ABC 中,∠C=90°,AC >BC ,D 是AB 的中点.E 为直线上一动点,连接DE ,过点D 作DF ⊥DE ,交直线BC 于点F ,连接EF .(1)如图1,当E 是线段AC 的中点时,设,AE a BF b ==,求EF 的长(用含,a b 的式子表示);(2)当点E 在线段CA 的延长线上时,依题意补全图2,用等式表示线段AE ,EF ,BF 之间的数量关系,并证明.9.(2020·北京·中考真题)如图,菱形ABCD 的对角线AC ,BD 相交于点O ,E 是AD 的中点,点F ,G 在AB 上,EF ⊥AB ,OG ∥EF .(1)求证:四边形OEFG 是矩形;(2)若AD =10,EF =4,求OE 和BG 的长.10.(2018·北京·中考真题)如图,在正方形ABCD 中,E 是边AB 上的一动点(不与点A 、B 重合),连接DE ,点A 关于直线DE 的对称点为F ,连接EF 并延长交BC 于点G ,连接DG ,过点E 作EH ⊥DE 交DG 的延长线于点H ,连接BH .(1)求证:GF=GC ;(2)用等式表示线段BH 与AE 的数量关系,并证明.11.(2018·北京·中考真题)如图,在四边形ABCD中,AB//DC,AB AD=,对角线AC,BD交于点O,AC平分⊥交AB的延长线于点E,连接OE.BAD∠,过点C作CE AB(1)求证:四边形ABCD是菱形;(2)若AB=2BD=,求OE的长.12.(2018·北京·中考真题)下面是小东设计的“过直线外一点作这条直线的平行线”的尺规作图过程.已知:直线及直线外一点P.求作:PQ,使得PQ l.作法:如图,①在直线上取一点A,作射线PA,以点A为圆心,AP长为半径画弧,交PA的延长线于点B;②在直线上取一点C(不与点A重合),作射线BC,以点C为圆心,CB长为半径画弧,交BC的延长线于点Q;③作直线PQ.所以直线PQ就是所求作的直线.根据小东设计的尺规作图过程,(1)使用直尺和圆规,补全图形;(保留作图痕迹)(2)完成下面的证明.证明:∵AB =_______,CB =_______,∴PQ l (____________)(填推理的依据).13.(2017·北京·中考真题)数学家吴文俊院士非常重视古代数学家贾宪提出的“从长方形对角线上任一点作两条分别平行于两邻边的直线,则所容两长方形面积相等(如图所示)”这一推论,他从这一推论出发,利用“出入相补”原理复原了《海岛算经》九题古证.,(以上材料来源于《古证复原的原理》、《吴文俊与中国数学》和《古代世界数学泰斗刘徽》)请根据上图完成这个推论的证明过程.证明:S 矩形NFGD =S △ADC -(S △ANF +S △FGC ),S 矩形EBMF =S △ABC -(____________+____________).易知,S △ADC =S △ABC ,_____________=______________,______________=_____________.可得S 矩形NFGD = S 矩形EBMF .14.(2017·北京·中考真题)如图,在四边形ABCD 中,BD 为一条对角线,AD BC ∥,2AD BC =,90ABD ∠=︒,E 为AD 的中点,连接BE .(1)求证:四边形BCDE 为菱形;(2)连接AC ,若AC 平分BAD ∠,1BC =,求AC 的长.15.(2016·北京·中考真题)如图,四边形ABCD 是平行四边形,AE 平分∠BAD ,交DC 的延长线于点E .求证:DA=DE .16.(2016·北京·中考真题)如图,在四边形ABCD 中,∠ABC=90°,AC=AD ,M ,N 分别为AC ,CD 的中点,连接BM ,MN ,BN .(1)求证:BM=MN ;(2)∠BAD=60°,AC 平分∠BAD ,AC=2,求BN 的长.17.(2015·北京·中考真题)在ABCD ,过点D 作DE ⊥AB 于点E ,点F 在边CD 上,DF =BE ,连接AF ,BF .(1)求证:四边形BFDE 是矩形;(2)若CF =3,BF =4,DF =5,求证:AF 平分∠DAB .18.(2014·北京·中考真题)在正方形ABCD 外侧作直线AP ,点B 关于直线AP 的对称点为E ,连接BE ,DE ,其中DE 交直线AP 于点F .(1)依题意补全图1.(2)若20PAB ∠=︒,求ADF ∠的度数.(3)如图2,若4590PAB ︒<∠<∠︒,用等式表示线段AB ,FE ,FD 之间的数量关系,并证明.19.(2013·北京·中考真题)如图,在ABCD中,F是AD的中点,延长BC到点E,使CE=1BC,连结DE,2CF.(1)求证:四边形CEDF是平行四边形;(2)若AB=4,AD=6,∠B=60°,求DE的长.参考答案1.D【分析】根据直角三角形斜边上的中线等于斜边的一半即可求得.【详解】解:根据题意可得,AM =1.2,∵M 为中点,∴AB =2AM =2.4,∴CM =1 1.22AB = 故选:D .【点睛】题目主要考查直角三角形斜边上的中线的性质,理解题意,熟练掌握运用这个性质是解题关键. 2.AF AE =(答案不唯一)【分析】由题意易得四边形AECF 是平行四边形,然后根据菱形的判定定理可进行求解.【详解】解:∵四边形ABCD 是矩形,∴//AD BC ,∵AF EC =,∴四边形AECF 是平行四边形,若要添加一个条件使其为菱形,则可添加AF AE =或AE =CE 或CE =CF 或AF =CF ,理由:一组邻边相等的平行四边形是菱形;故答案为AF AE =(答案不唯一).【点睛】本题主要考查菱形的判定定理、矩形的性质及平行四边形的判定,熟练掌握菱形的判定定理、矩形的性质及平行四边形的判定是解题的关键.3.12【分析】由菱形的性质得出OA =OC ,OB =OD ,AC ⊥BD ,设OA =x ,OB =y ,由题意得:51x y x y +=⎧⎨-=⎩,解得:32x y =⎧⎨=⎩,得出AC =2OA =6,BD =2OB =4,即可得出菱形的面积. 【详解】解:如图1所示:∵四边形ABCD是菱形,∴OA=OC,OB=OD,AC⊥BD,设OA=x,OB=y,由题意得:51x yx y+=⎧⎨-=⎩,解得:32xy=⎧⎨=⎩,∴AC=2OA=6,BD=2OB=4,∴菱形ABCD的面积=116412 22⨯=⨯⨯=AC BD;故答案为12.【点睛】本题考查了菱形的性质、正方形的性质、二元一次方程组的应用;熟练掌握正方形和菱形的性质,由题意列出方程组是解题的关键.4.①②③【分析】根据矩形的判定和性质,菱形的判定,正方形的判定,平行四边形的判定定理即可得到结论.【详解】解:①如图,∵四边形ABCD是矩形,连接AC,BD交于O,∴OA=OB=OC=OD,AB∥CD,AD∥BC,∴∠OBM=∠ODP,∠OAQ=∠OCN,过点O的直线MP和QN,分别交AB,BC,CD,AD于M,N,P,Q,∴∠BOM=∠DOP,∠AOQ=∠CON,所以△BOM≌△DOP(ASA),△AOQ≌△CON(ASA),所以OM=OP,OQ=ON,则四边形MNPQ是平行四边形,故存在无数个四边形MNPQ是平行四边形;故正确;②如图,当PM =QN 时,四边形MNPQ 是矩形,故存在无数个四边形MNPQ 是矩形;故正确;③如图,当PM ⊥QN 时,存在无数个四边形MNPQ 是菱形;故正确;④当四边形MNPQ 是正方形时,MQ =PQ ,则△AMQ ≌△DQP ,∴AM =QD ,AQ =PD ,∵PD =BM ,∴AB =AD ,∴四边形ABCD 是正方形,当四边形ABCD 为正方形时,四边形MNPQ 是正方形,故错误;故正确结论的序号是①②③.故答案为:①②③.【点睛】本题考查了矩形的判定和性质,菱形的判定,正方形的判定,平行四边形的判定定理,熟记各定理是解题的关键.5.20【分析】先由5AB =,12AD =得到13AC =,然后结合矩形的性质得到 6.5OB =,再结合点O 和点M 分别是AC 和AD 的中点得到OM 和AM 的长,最后得到四边形ABOM 的周长.【详解】解:5AB =,5CD ∴=,12AD =∵,90D ∠=︒,13AC ∴=,点O 和点M 分别是AC 和AD 的中点,6.5OB ∴=,162AM AD ==,OM 是ACD ∆的中位线, 1 2.52OM CD ∴==, 5 6.5 2.5620ABOM C AB BO OM MA ∴=+++=+++=四边形.故答案为:20.【点睛】本题考查了矩形的性质、三角形的中位线定理,解题的关键是熟知矩形的性质.6.(1)见解析(2)见解析【分析】(1)先根据四边形ABCD 为平行四边形,得出AO CO =,BO DO =,再根据AE CF =,得出EO FO =,即可证明结论;(2)先证明DCA DAC ∠=∠,得出DA DC =,证明四边形ABCD 为菱形,得出AC BD ⊥,即可证明结论. (1)证明:∵四边形ABCD 为平行四边形,∴AO CO =,BO DO =,∵AE CF =,∴AO AE CO CF -=-,即EO FO =,∴四边形EBFD 是平行四边形.(2)∵四边形ABCD 为平行四边形,∴AB CD ∥,∴DCA BAC ∠=∠,∵,BAC DAC ∠=∠∴DCA DAC ∠=∠,∴DA DC =,∴四边形ABCD 为菱形,∴AC BD ⊥,即EF BD ⊥,∵四边形EBFD 是平行四边形,∴四边形EBFD 是菱形.【点睛】本题主要考查了平行四边形的性质和性质,菱形的判定和性质,平行线的性质,熟练掌握菱形和平行四边形的判定方法,是解题的关键.7.(1)见解析(2)CD CH =;证明见解析【分析】(1)先利用已知条件证明()SAS FCE BCD ≅,得出CFE CBD ,推出EF BD ∥,再由AF EF ⊥即可证明BD AF ⊥;(2)延长BC 到点M ,使CM =CB ,连接EM ,AM ,先证()SAS MEC BDC ≅,推出ME BD =,通过等量代换得到222AM AE ME =+,利用平行线的性质得出90BHE AEM ,利用直角三角形斜边中线等于斜边一半即可得到CD CH =.(1)证明:在FCE △和BCD △中, CE CD FCE BCD CF CB =⎧⎪∠=∠⎨⎪=⎩,∴ ()SAS FCE BCD ≅,∴ CFE CBD ,∴ EF BD ∥,∵AF EF ⊥,∴BD AF ⊥.(2)解:补全后的图形如图所示,CD CH =,证明如下:延长BC 到点M ,使CM =CB ,连接EM ,AM ,∵90ACB ∠=,CM =CB ,∴ AC 垂直平分BM ,∴AB AM =,在MEC 和BDC 中,CM CB MCE BCD CE CD =⎧⎪∠=∠⎨⎪=⎩,∴ ()SAS MEC BDC ≅,∴ ME BD =,CME CBD ,∵222AB AE BD =+,∴ 222AM AE ME =+,∴ 90AEM ∠=︒,∵CME CBD , ∴BH EM ∥,∴ 90BHE AEM ,即90DHE ∠=︒, ∵12CE CD DE , ∴ 12CH DE , ∴ CD CH =.【点睛】本题考查全等三角形的判定与性质,垂直平分线的性质,平行线的判定与性质,勾股定理的逆用,直角三角形斜边中线的性质等,第二问有一定难度,正确作辅助线,证明90DHE ∠=︒是解题的关键.8.(12)图见解析,222EF AE BF =+,证明见解析.【分析】(1)先根据中位线定理和线段中点定义可得//DE BC ,12DE BC =,CE AE a ==,再根据平行四边形的性质、矩形的判定与性质可得DE CF =,从而可得CF BF b ==,然后利用勾股定理即可得;(2)如图(见解析),先根据平行线的性质可得EAD GBD ∠=∠,DEA DGB ∠=∠,再根据三角形全等的判定定理与性质可得ED GD =,AE BG =,然后根据垂直平分线的判定与性质可得EF FG =,最后在Rt BGF 中,利用勾股定理、等量代换即可得证.【详解】(1)∵D 是AB 的中点,E 是线段AC 的中点∴DE 为ABC 的中位线,且CE AE a ==∴//DE BC ,12DE BC =∵90C ∠=︒∴18090DEC C ∠=︒-∠=︒∵DF DE ⊥∴90EDF ∠=︒∴四边形DECF 为矩形∴DE CF =11()22CF BC BF CF ∴==+ ∴CF BF b ==则在Rt CEF 中,EF(2)过点B 作AC 的平行线交ED 的延长线于点G ,连接FG∵//BG AC∴EAD GBD ∠=∠,DEA DGB ∠=∠∵D 是AB 的中点∴AD BD =在EAD 和GBD △中,EAD GBD DEA DGB AD BD ∠=∠⎧⎪∠=∠⎨⎪=⎩∴()EAD GBD AAS ≅∴ED GD =,AE BG =又∵DF DE ⊥∴DF 是线段EG 的垂直平分线∴EF FG =∵90C ∠=︒,//BG AC∴90GBF C ∠=∠=︒在Rt BGF 中,由勾股定理得:222FG BG BF =+∴222EF AE BF =+.【点睛】本题考查了中位线定理、矩形的判定与性质、三角形全等的判定定理与性质、垂直平分线的判定与性质、勾股定理等知识点,较难的是题(2),通过作辅助线,构造全等三角形和直角三角形是解题关键.9.(1)见解析;(2)OE =5,BG =2.【分析】(1)先证明EO 是△DAB 的中位线,再结合已知条件OG ∥EF ,得到四边形OEFG 是平行四边形,再由条件EF ⊥AB ,得到四边形OEFG 是矩形;(2)先求出AE =5,由勾股定理进而得到AF =3,再由中位线定理得到OE =12AB =12AD =5,得到FG =5,最后BG =AB -AF -FG =2.【详解】解:(1)证明:∵四边形ABCD 为菱形,∴点O 为BD 的中点,∵点E 为AD 中点,∴OE 为△ABD 的中位线,∴OE ∥FG ,∵OG ∥EF ,∴四边形OEFG 为平行四边形∵EF ⊥AB ,∴平行四边形OEFG 为矩形.(2)∵点E 为AD 的中点,AD =10,∴AE =152AD = ∵∠EFA =90°,EF =4,∴在R t △AEF 中,3AF .∵四边形ABCD 为菱形,∴AB =AD =10,∴OE =12AB =5,∵四边形OEFG 为矩形,∴FG =OE =5,∴BG =AB -AF -FG =10-3-5=2.故答案为:OE =5,BG =2.【点睛】本题考查了矩形的性质和判定,菱形的性质、勾股定理等知识点,解题的关键是掌握特殊四边形的性质和判定属于中考常考题型,需要重点掌握.10.(1)证明见解析;(2),理由见解析【分析】(1)连接DF .根据对称的性质可得AD FD =.AE FE =.证明ADE FDE △≌△,根据全等三角形的性质得到DAE DFE ∠=∠.进而证明Rt DCG △≌Rt DFG △,即可证明;(2)在AD 上取点M 使得AM AE =,连接ME .证明DME ≌EBH △,根据等腰直角三角形的性质即可得到线段BH 与AE 的数量关系.【详解】(1)证明:连接DF .∵A ,F 关于DE 对称.∴AD FD =.AE FE =.在ADE 和FDE 中AD FDAE FE DE DE=⎧⎪=⎨⎪=⎩,∴ADE FDE △≌△,∴DAE DFE ∠=∠.∵四边形ABCD 是正方形,∴90A C ∠=∠=︒.AD CD =,∴90DFE A ∠=∠=︒,∴18090DFG DFE ∠=︒-∠=︒,∴DFG C ∠=∠ ,∵AD DF =,AD CD =,∴DF CD =.在Rt DCG △和Rt DFG △中DC DFDG DG =⎧⎨=⎩.∴Rt DCG △≌Rt DFG △,∴CG FG =.(2)BH .证明:在AD 上取点M 使得AM AE =,连接ME .∵四这形ABCD 是正方形.∴AD AB =,90A ADC ∠=∠=︒.∵DAE △≌DFE △,∴ADE FDE ∠=∠.同理:CDG FDG ∠=∠, ∴11145222EDG EDF GDF ADF CDF ADC ∠=∠+∠=∠+∠=∠=︒ ∵DE EH ⊥,∴90DEH ∠=︒,∴18045EHD DEH EDH ∠=︒-∠-∠=︒,∴EHD EDH ∠=∠.∴DE EH =.∵90A ∠=︒,∴90ADE AED ∠+∠=︒.∵90DEH ∠=︒,∴90AED BEH ∠+∠=︒,∴ADE BEH ∠=∠.∵AD AB =,AM AE =,∴DM EB =.在DME 和EBH △中DM EB MDE BEH DE EH =⎧⎪∠=∠⎨⎪=∠⎩,∴DME ≌EBH △,∴ME BH =,在Rt AME △中,90A ∠=︒,AE AM =.∴ME ,∴BH =.【点睛】本题是四边形的综合题,考查了正方形的性质,轴对称的性质,全等三角形的性质与判定,勾股定理,等腰直角三角形的性质与判定等知识,此题综合性较强,难度较大,注意掌握辅助线的作法,注意数形结合思想的应用.11.(1)证明见解析;(2)OE =2.【分析】(1)根据一组对边相等的平行四边形是菱形进行判定即可.(2)根据菱形的性质和勾股定理求出2OA ,根据直角三角形斜边的中线等于斜边的一半即可求解.【详解】(1)证明:∵AB //CD ,∴CAB ACD ∠=∠,∵AC 平分BAD ∠,∴CAB CAD ∠=∠,∴CAD ACD ∠=∠,∴AD CD =,又∵AD AB =,∴AB CD =,又∵AB ∥CD ,∴四边形ABCD 是平行四边形,又∵AB AD =,∴ABCD 是菱形.(2)解:∵四边形ABCD 是菱形,对角线AC 、BD 交于点O ,∴AC BD ⊥,12OA OC AC ==,12OB OD BD ==, ∴112OB BD ==, 在Rt △AOB 中,90AOB ∠=︒,∴2OA ,∵CE AB ⊥,∴90AEC ∠=︒,在Rt △AEC 中,90AEC ∠=︒,O 为AC 中点, ∴122OE AC OA ===. 【点睛】本题考查了平行四边形的性质和判定,菱形的判定与性质,直角三角形的性质,勾股定理等,熟练掌握菱形的判定方法以及直角三角形斜边的中线等于斜边的一半是解题的关键.12.(1)作图见解析(2)PA ,CQ ,三角形中位线平行于三角形的第三边.【详解】分析:根据作图过程,补全图形即可.详解:(1)尺规作图如下图所示:(2)PA ,CQ ,三角形中位线平行于三角形的第三边.点睛:考查尺规作图,三角形中位线定理,熟练掌握三角形的中位线定理是解题的关键.13.S △AEF ,S △CFM ;S △ANF ,S △AEF ;S △FGC ,S △CFMF .【详解】试题分析:由矩形的对角线的性质,对角线把矩形分成两个面积相等的三角形计算即可.试题解析:由矩形对角线把矩形分成两个面积相等的两部分可得:(),()ADC ANF FGC ABC AEF FMC NFGD EBMF S S S S S S S S ∆∆∆∆∆=-+=-+矩形矩形 ,∴,,ADC ABC ANF AEF FGC FMC S S S S S S ∆∆∆∆∆∆=== , ∴NFGD EBMF S S =矩形矩形 .14.(1)证明见解析.【分析】(1)先证明四边形BCDE 是平行四边形,再证明一组邻边相等即可;(2)连接AC ,根据平行线的性质及等角对等边证明AB =1,AD =2,可知30ADB ∠=︒,再根据菱形的性质即可得出ACD △是含30的特殊三角形,最后根据勾股定理即可求AC 的长.(1)2AD BC =,E 为AD 的中点,DE BC ∴=,AD BC ∥,∴四边形BCDE 是平行四边形,90ABD ∠=︒,AE DE =,BE DE ∴=,∴四边形BCDE 是菱形.(2)解:连接AC .AD BC ∥,AC 平分BAD ∠,BAC DAC BCA ∴∠=∠=∠,1AB BC ∴==,22AD BC ∴==,30ADB ∴∠=︒,30DAC ∴∠=︒,四边形BCDE 是菱形∴260ADC ADB ∠=∠=︒,90ACD ∴∠=︒在Rt ACD △中,2AD =,1CD ∴=, ∴AC =【点睛】本题考查了菱形的性质与判定,勾股定理等,解题的关键是连接AC 构造Rt ACD △.15.证明见解析.【分析】由平行四边形的性质得出AB ∥CD ,得出内错角相等∠E=∠BAE ,再由角平分线证出∠E=∠DAE ,即可得出结论.【详解】证明:∵四边形ABCD 是平行四边形,∴AB ∥CD ,∴∠E=∠BAE ,∵AE 平分∠BAD ,∴∠BAE=∠DAE ,∴∠E=∠DAE ,∴DA=DE .16.(1)证明见解析;(2【分析】(1)在△CAD 中,由中位线定理得到MN ∥AD ,且MN=12AD ,在Rt △ABC 中,因为M 是AC 的中点,故BM=12AC ,即可得到结论;(2)由∠BAD=60°且AC 平分∠BAD ,得到∠BAC=∠DAC=30°,由(1)知,BM=12AC=AM=MC ,得到∠BMC =60°.由平行线性质得到∠NMC=∠DAC=30°,故∠BMN=90°,得到222BN BM MN =+,再由MN=BM=1,得到BN 的长.【详解】(1)在△CAD 中,∵M 、N 分别是AC 、CD 的中点,∴MN∥AD,且MN=12AD,在Rt△ABC中,∵M是AC的中点,∴BM=12AC,又∵AC=AD,∴MN=BM;(2)∵∠BAD=60°且AC平分∠BAD,∴∠BAC=∠DAC=30°,由(1)知,BM=12AC=AM=MC,∴∠BMC=∠BAM+∠ABM=2∠BAM=60°.∵MN∥AD,∴∠NMC=∠DAC=30°,∴∠BMN=∠BMC+∠NMC=90°,∴222BN BM MN=+,而由(1)知,MN=BM=12AC=12×2=1,∴17.(1)见解析(2)见解析【分析】(1)根据平行四边形的性质,可得AB与CD的关系,根据平行四边形的判定,可得BFDE是平行四边形,再根据矩形的判定,即可证明;(2)根据平行线的性质,可得∠DFA=∠FAB,根据等腰三角形的判定与性质,可得∠DAF=∠DFA,根据角平分线的判定,即可证明.【详解】(1)证明:∵四边形ABCD是平行四边形,∴AB∥CD.∵BE∥DF,BE=DF,∴四边形BFDE是平行四边形.∵DE⊥AB,∴∠DEB=90°,∴四边形BFDE是矩形;(2)∵四边形ABCD是平行四边形,∴AB∥DC,∴∠DFA=∠FAB.在Rt△BCF中,由勾股定理,得BC,∴AD=BC=DF=5,∴∠DAF=∠DFA,∴∠DAF=∠FAB,即AF平分∠DAB.【点睛】本题考查了平行四边形的性质,矩形的判定,等腰三角形的判定与性质,利用等腰三角形的判定与性质得出∠DAF=∠DFA是解题关键.18.(1)图形见解析(2)25°(3)222+=EF FD AB2【分析】(1)按照题意补全图形(2)连接AE,根据轴对称性和正方形的性质可得∠EAD=∠PAB+∠PAE=130°,即可求解;(3)连接AE、BF、BD,根据轴对称性和正方形的性质可得∠ABF=∠AEF=∠ADF,从而得到BD=,∠BFD=∠BAD=90°,再由勾股定理,即可求解.【详解】解:(1)补全图形如图所示:(2)连接AE,根据题意得:∠PAB =∠PAE =20°,AE =AB =AD ,∵四边形ABCD 是正方形,∴∠BAD =90°,∴∠EAD =∠PAB +∠PAE =130°,∴∠ADF =∠AED =()11802DAE ︒-∠=25°; (3)EF 2+FD 2=2AB 2,理由如下:连接AE 、BF 、BD ,由轴对称的性质可得:EF =BF ,AE =AB =AD ,∴∠BEF =∠EBF ,∠AEB =∠ABE ,∠AED =∠ADF ,∴∠ABF =∠AEF =∠ADF ,∵四边形ABCD 是正方形,∴∠BAD =90°,AB =AD ,∴∠ABD +∠ADB =90°,BD =,∴∠ABF +∠DBF +∠ADB =∠DBF +∠ADB +∠ADF =90°,∴∠BFD =∠BAD =90°,∴BF 2+FD 2=BD 2∴EF 2+FD 2=2AB 2.【点睛】本题主要考查了轴对称的性质,正方形的性质,勾股定理,等腰三角形的性质,熟练掌握轴对称的性质,正方形的性质,勾股定理,等腰三角形的性质是解题的关键.19.(1)见解析(2【分析】(1)由“平行四边形的对边平行且相等”的性质推知AD∥BC,且AD=BC;然后根据中点的定义、结合已知条件推知四边形CEDF的对边平行且相等(DF=CE,且DF∥CE),即四边形CEDF是平行四边形;(2)如图,过点D作DH⊥BE于点H,构造含30度角的直角△DCH和直角△DHE.通过解直角△DCH和在直角△DHE中运用勾股定理来求线段ED的长度.【详解】(1)证明:在▱ABCD中,AD BC,且AD=BC∵F是AD的中点AD∴DF=12BC又∵CE=12∴DF=CE,且DF CE∴四边形CEDF是平行四边形;(2)如图,过点D作DH⊥BE于点H.在▱ABCD中,∵∠B=60°,∴∠DCE=60°.∵AB=4,∴CD=AB=4,CD=2,DH∴CH=1AD=3,则EH=1.在▱CEDF中,CE=DF=12∴在Rt△DHE中,根据勾股定理知DE.。
特殊的平行四边形专题(题型详细分类)要点

特殊的平⾏四边形专题(题型详细分类)要点特殊的平⾏四边形讲义知识点归纳矩形,菱形和正⽅形之间的联系如下表所⽰:四边形分类专题汇总专题⼀:特殊四边形的判定矩形菱形正⽅形性质边对边平⾏且相等对边平⾏,四边相等对边平⾏,四边相等⾓四个⾓都是直⾓对⾓相等四个⾓都是直⾓对⾓线互相平分且相等互相垂直平分,且每条对⾓线平分⼀组对⾓互相垂直平分且相等,每条对⾓线平分⼀组对⾓判定 ·有三个⾓是直⾓; ·是平⾏四边形且有⼀个⾓是直⾓; ·是平⾏四边形且两条对⾓线相等. ·四边相等的四边形;·是平⾏四边形且有⼀组邻边相等;·是平⾏四边形且两条对⾓线互相垂直。
·是矩形,且有⼀组邻边相等; ·是菱形,且有⼀个⾓是直⾓。
对称性既是轴对称图形,⼜是中⼼对称图形(1)______________ (2)______________ (3)______________ (4)______________ (5)______________2.矩形的判定⽅法:(1)______________ (2)______________ (3)______________3.菱形的判定⽅法:(1)______________ (2)______________ (3)______________4.正⽅形的判定⽅法:(1)______________ (2)______________ (3)______________5.等腰梯形的判定⽅法:(1)______________ (2)______________ (3)______________【练⼀练】⼀.选择题1.能够判定四边形ABCD是平⾏四边形的题设是().A.AB∥CD,AD=BC B.∠A=∠B,∠C=∠DC.AB=CD,AD=BC D.AB=AD,CB=CD2.具备下列条件的四边形中,不能确定是平⾏四边形的为().A.相邻的⾓互补 B.两组对⾓分别相等C.⼀组对边平⾏,另⼀组对边相等 D.对⾓线交点是两对⾓线中点3.下列条件中,能判定四边形是平⾏四边形的条件是( )A.⼀组对边平⾏,另⼀组对边相等B.⼀组对边平⾏,⼀组对⾓相等C.⼀组对边平⾏,⼀组邻⾓互补D.⼀组对边相等,⼀组邻⾓相等4.如下左图所⽰,四边形ABCD的对⾓线AC和BD相交于点O,下列判断正确的是().A.若AO=OC,则ABCD是平⾏四边形;B.若AC=BD,则ABCD是平⾏四边形;C.若AO=BO,CO=DO,则ABCD是平⾏四边形;D.若AO=OC,BO=OD,则ABCD是平⾏四边形5.不能判定四边形ABCD是平⾏四边形的条件是()A.AB=CD,AD=BC B.AB∥CD,AB=CDC.AB=CD,AD∥BC D.AB∥CD,AD∥BC6.四边形ABCD的对⾓线AC,BD相交于点O,能判断它为矩形的题设是()A.AO=CO,BO=DO B.AO=BO=CO=DOC.AB=BC,AO=CO D.AO=CO,BO=DO,AC⊥BD7.四边形ABCD的对⾓线互相平分,要使它变为矩形,需要添加的条件是()A.AB=CD B.AD=BC C.AB=BC D.AC=BD8.在四边形ABCD中,O是对⾓线的交点,下列条件能判定这个四边形是正⽅形的是()A、AC=BD,AB∥CD,AB=CDB、AD∥BC,∠A=∠CC、AO=BO=CO=DO,AC⊥BDD、AC=CO,BO=DO,AB=BC9.在下列命题中,真命题是()A.两条对⾓线相等的四边形是矩形B.两条对⾓线互相垂直的四边形是菱形C.两条对⾓线互相平分的四边形是平⾏四边形D.两条对⾓线互相垂直且相等的四边形是正⽅形10.在下列命题中,正确的是()11.如图,已知四边形ABCD 是平⾏四边形,下列结论中不正确的是() A .当AB=BC 时,它是菱形 B .当AC ⊥BD 时,它是菱形C .当∠ABC=900时,它是矩形D .当AC=BD 时,它是正⽅形12.如图,在ABC △中,点E D F ,,分别在边AB ,BC ,CA 上,且DE CA ∥,DF BA ∥.下列四个判断中,不正确...的是() A .四边形AEDF 是平⾏四边形B .如果90BAC ∠=o ,那么四边形AEDF 是矩形C .如果AD 平分BAC ∠,那么四边形AEDF 是菱形D .如果AD BC ⊥且AB AC =,那么四边形AEDF 是菱形 13.下列条件中不能判定四边形是正⽅形的条件是()。
中考全分类汇编特殊的平行四边形

2013中考全国100份试卷分类汇编矩形1、(2013陕西)如图,在矩形ABCD 中,AD=2AB ,点M 、N 分别在边AD 、BC 是,连接BM 、DN ,若四边形MBND 是菱形,则MD AM 等于 () A .83 B .32 C .53 D .54 考点:矩形的性质及菱形的性质应用。
解析:矩形的性质应用较为常见的就是转化成直角三角形来解决问题,菱形的性质应用较常见的是四条边相等或者对角线的性质应用。
此题中求的是线段的比值,所以在解决过程中取特殊值法较为简单。
设AB=1,则AD=2,因为四边形MBND 是菱形,所以MB=MD ,又因为矩形ABCD ,所以∠A=90°,设AM=x,则MB=2-x ,由勾股定理得:AB 2+AM 2=MB 2,所以x 2+12=(2-x)2解得:43=x ,所以MD=45432=-,534543==MD AM ,故选C .2、(2013济宁)如图,矩形ABCD 的面积为20cm 2,对角线交于点O ;以AB 、AO 为邻边做平行四边形AOC 1B ,对角线交于点O 1;以AB 、AO 1为邻边做平行四边形AO 1C 2B ;…;依此类推,则平行四边形AO 4C 5B 的面积为( )A . cm 2B . cm 2C .cm 2D .cm 2考点:矩形的性质;平行四边形的性质.专题:规律型.分析:根据矩形的对角线互相平分,平行四边形的对角线互相平分可得下一个图形的面积是上一个图形的面积的,然后求解即可.解答:解:设矩形ABCD 的面积为S=20cm 2,∵O 为矩形ABCD 的对角线的交点,∴平行四边形AOC 1B 底边AB 上的高等于BC 的,∴平行四边形AOC 1B 的面积=S ,∵平行四边形AOC 1B 的对角线交于点O 1,∴平行四边形AO 1C 2B 的边AB 上的高等于平行四边形AOC 1B 底边AB 上的高的, B C DA 第9题图M N∴平行四边形AO1C2B的面积=×S=,…,依此类推,平行四边形AO4C5B的面积===cm2.故选B.点评:本题考查了矩形的对角线互相平分,平行四边形的对角线互相平分的性质,得到下一个图形的面积是上一个图形的面积的是解题的关键.3、(2013•天津)如图,在△ABC中,AC=BC,点D、E分别是边AB、AC的中点,将△ADE 绕点E旋转180°得△CFE,则四边形ADCF一定是()A.矩形B.菱形C.正方形D.梯形考点:旋转的性质;矩形的判定.分析:根据旋转的性质可得AE=CE,DE=EF,再根据对角线互相平分的四边形是平行四边形判断出四边形ADCF是平行四边形,然后利用等腰三角形三线合一的性质求出∠ADC=90°,再利用有一个角是直角的平行四边形是矩形解答.解答:解:∵△ADE绕点E旋转180°得△CFE,∴AE=CE,DE=EF,∴四边形ADCF是平行四边形,∵AC=BC,点D是边AB的中点,∴∠ADC=90°,∴四边形ADCF矩形.故选A.点评:本题考查了旋转的性质,矩形的判定,主要利用了对角线互相平分的四边形是平行四边形,有一个角是直角是平行四边形是矩形的判定方法,熟练掌握旋转变换只改变图形的位置不改变图形的形状与大小是解题的关键.4、(2013四川南充,3分)如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若AE=2,DE=6,∠EFB=60°,则矩形ABCD的面积是()B. 24C. 123D. 163答案:D解析:由两直线平行内错角相等,知∠DEF=∠EFB=60°,又∠AEF=∠'A EF=120°,所以,A B ,所以,AB=23,矩形ABCD的面积∠'A E'B=60°,'A E=AE=2,求得''23为S=23×8=163,选D。
2013年全国各地中考模拟卷分类汇编:平行四边形(共12页)

(1)将梯形纸片剪拼成平行四边形:请在下图中画出示意图,要求用两种不同的画法,
并简要说明如何剪拼和变换的;
(2)如图,将四边形ABCD剪拼成平行四边形.在下图中画出示意图.
4、两个全等的直角三角形ABC和DEF重叠在一起,其中∠A=60°,AC=1.固定△ABC不动,将△DEF进行如下操作:
A. 2 B.3 C. D. 6
答案:B
3.(2013年北京平谷区一模)如图,在□ 中, , 为垂足.
如果 ,则
A. B. C. D.
答案:C
4、(2013年湖北荆州模拟6)如图,已知一张纸片□ , ,点 是 的中点,点 是 上的一个动点,沿 将纸片折叠,使点 落在纸片上的点 处,连结 ,则下列各角中与 不一定相等的是(▲)
(1)如图△DEF沿线段AB向右平移(即D点在线段AB内移动),连结DC、CF、FB,四边形CDBF的形状在不断的变化,但它的面积不变化,请求出其面积.
(2)如图,当D点移到AB的中点时,请你猜想四边形CDBF的形状,并说明理由.
(3)如图,△DEF的D点固定在AB的中点,然后绕D点按顺时针方向旋转△DEF,使DF落在AB边上,此时F点恰好与B点重合,连结AE,请你求出sinα的值.
解:(1)过C点作CG⊥AB于G,
在Rt△AGC中,∵sin60°= ,∴ 1分
∵AB=2,∴S梯形CDBF=S△ABC= 3分
(2)菱形5分
∵CD∥BF,FC∥BD,∴四边形CDBF是平行四边形6分
∵DF∥AC,∠ACD=90°,∴CB⊥DF7分
∴四边形CDBF是菱形8分
(判断四边形CDBF是平行四边形,并证明正确,记2分)
中考数学《特殊平行四边形》专题复习课件(共32张PPT)

你的结论。
7.如图,OABC是一张放在平面直角坐标系中的 矩形纸片,O为原点,点A在x轴上,点C在y 轴上,OA=10,OC=6。
(1)如图①,在OA上选取一点G,将△COG 沿CG翻折,使点O落在BC边上,设为E, 求折痕CG所在直线的解析式。
谢谢观赏
You made my day!
我们,还在路上……
⑵当x为何值时,⊿PBC的周长最 小,并求出此时y的值
❖1、书籍是朋友,虽然没有热情,但是非常忠实。2022年3月5日星期六2022/3/52022/3/52022/3/5 ❖2、科学的灵感,决不是坐等可以等来的。如果说,科学上的发现有什么偶然的机遇的话,那么这种‘偶然的机遇’只能给那些学有素养的人,给那些善于 独立思考的人,给那些具有锲而不舍的人。2022年3月2022/3/52022/3/52022/3/53/5/2022 ❖3、书籍—通过心灵观察世界的窗口.住宅里没有书,犹如房间里没有窗户。2022/3/52022/3/5March 5, 2022 ❖4、享受阅读快乐,提高生活质量。2022/3/52022/3/52022/3/52022/3/5
一、四边形的分类及转化
两组对边平行 平行四边形
任意四边形
一组对边平行
梯形
另一组对边不平行
矩形
菱 形
正方形
等腰梯形
直角梯形
二、几种特殊四边形的性质:
项目 四边形
对边
角
对角线
对称性
对角相等
平行且相等
平行四边形
邻角互补
四个角
矩形 平行且相等 都是直角
平行
对角相等
中考全分类汇编特殊的平行四边形

2013中考全国100份试卷分类汇编矩形1、(2013陕西)如图,在矩形ABCD 中,AD=2AB ,点M 、N 分别在边AD 、BC 是,连接BM 、DN ,若四边形MBND 是菱形,则MDAM等于 ( ) A .83 B .32 C .53 D .54考点:矩形的性质及菱形的性质应用。
解析:矩形的性质应用较为常见的就是转化成直角三角形来解决问题,菱形的性质应用较常见的是四条边相等或者对角线的性质应用。
此题中求的是线段的比值,所以在解决过程中取特殊值法较为简单。
设AB=1,则AD=2,因为四边形MBND 是菱形,所以MB=MD ,又因为矩形ABCD ,所以∠A=90°,设AM=x,则MB=2-x ,由勾股定理得:AB 2+AM 2=MB 2,所以x 2+12=(2-x)2解得:43=x ,所以MD=45432=-,534543==MD AM ,故选C .2、(2013济宁)如图,矩形ABCD 的面积为20cm 2,对角线交于点O ;以AB 、AO 为邻边做平行四边形AOC 1B ,对角线交于点O 1;以AB 、AO 1为邻边做平行四边形AO 1C 2B ;…;依此类推,则平行四边形AO 4C 5B 的面积为( )A . cm 2B . cm 2C .cm 2D .cm 2考点:矩形的性质;平行四边形的性质. 专题:规律型. 分析:根据矩形的对角线互相平分,平行四边形的对角线互相平分可得下一个图形的面积是上一个图形的面积的,然后求解即可.解答:解:设矩形ABCD 的面积为S=20cm 2, ∵O 为矩形ABCD 的对角线的交点,∴平行四边形AOC 1B 底边AB 上的高等于BC 的, ∴平行四边形AOC 1B 的面积=S ,∵平行四边形AOC 1B 的对角线交于点O 1,∴平行四边形AO 1C 2B 的边AB 上的高等于平行四边形AOC 1B 底边AB 上的高的,B CDA第9题图 MN∴平行四边形AO1C2B的面积=×S=,…,依此类推,平行四边形AO4C5B的面积===cm2.故选B.点评:本题考查了矩形的对角线互相平分,平行四边形的对角线互相平分的性质,得到下一个图形的面积是上一个图形的面积的是解题的关键.3、(2013•天津)如图,在△ABC中,AC=BC,点D、E分别是边AB、AC的中点,将△ADE绕点E旋转180°得△CFE,则四边形ADCF一定是()4、(2013四川南充,3分)如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若AE=2,DE=6,∠EFB=60°,则矩形ABCD的面积是()A.12B. 24C. 123D. 163答案:D解析:由两直线平行内错角相等,知∠DEF=∠EFB=60°,又∠AEF=∠'A EF=120°,所A B AB=,矩形ABCD 以,∠'A E'B=60°,'A E=AE=2,求得''的面积为S=×8=,选D。
特殊的平行四边形专题.doc

特殊的平行四边形专题一、特殊四边形之间的关系矩形、菱形、正方形都是特殊的平行四边形,它们之间既有区别又有联系。
平行四边形+—组邻边相等二菱形平行四边形+—个直角=矩形菱形+—个直角=正方形菱形+对角线相等二正方形矩形+一组邻边相等=正方形矩形+对角线互相垂直二正方形因此在判定的过程中要选择适当的判定方法,灵活的解决问题。
例题1.如图似△A3。
的三边为边,在BC边的同侧作等边APB.4 , AEBC , AF.4C.(1)试说明四边形AFED是平行四边形;⑵当A/1BC满足什么条件时四边形AFED是矩形,说明理由;⑶当MIBC满足什么条件时,四边形AFED是正方形?⑷当况满足什么条件时,四边形AFED不存在?二、特殊平行四边形中的折叠问题折叠问题是轴对称与等腰三角形、直角三角形、矩形、菱形等图形的性质的综合应用,折痕所在直线为折叠前后图形的对称轴。
在解决此类问题时应注意:1.充分利用轴对称的性质;2.折叠前后图形对应角、对应边相等;3.计算时常用勾股定理建立方程或由面积解决。
如图,把矩形纸片ABCD沿EF折叠,使点3落在边.1D上的点&处,点」落在点.T处。
(1)求证:B f E = DF o设AE = a AB = 6»0F = c.试猜想",加c之间的一种关系,并给予证明。
例题3.将矩形纸片ABCD按如图所示的方式折叠.得到菱形AECF.若,12/= 3,则BC的长为三、四边形中的中点问题类型L特殊四边形与中位线的结合在一个四边形中有四条边,两条对角线,所以一共可产生6个中点,已知两个中点会有四种情况:1.一组邻边的中点;2.—边与对角线的中点;3.两对角线的中点;4.一组对边的中点3.4两种情况常需要找出第三个中点作为桥梁解决问题。
例题4.如图在四边形ABCD中m = DCE、F分别是AD、BC的中点,G、H分别是BD、AC的中点,猜一猜EF与GH的位置关系,并证明你的培论类型2.特殊四边形与直角三角形斜边上的中线结合如图,已知在^ABC 中,AC = 3 ,BC=4MB = 5 •点P 是AB 上(不与A 、B 重合),过P 作PE1AC , PF1BC ,垂是分别是E 、F,连结EF,M 为EF 的中点.⑴请判断四边形PECF 的形状,并说明理由⑵随着P 点在边AB 上位置的改变,CM 的长度是否也会改变?若不变,请你求CM 的长度;若有变化,请你求CM 的变化范围一 四、动点问题类型L 动点问题动点几何特点 -------- 问题背景是特殊图形,需要把握一般与特殊的关系。
2013复习攻略之特殊四边形-选择、填空、解答(附答案)

2013中考复习攻略之特殊四边形一、选择题1.在矩形ABCD 中,1=AB ,3=AD ,AF 平分DAB ∠,过C 点作BD CE ⊥于E ,延长AF 、EC 交于点H ,下列结论中:①FH AF =;②BF BO =;③CH CA =;④ED BE 3=,正确的( )A .②③B .③④C .①②④D .②③④【关键词】平行四边形有关的计算【答案】D2..如图,菱形ABCD 中,对角线AC 、BD 相交于点O ,M 、N 分别是边AB 、AD 的中点,连接OM 、ON 、MN ,则下列叙述正确的是( ) A .△AOM 和△AON 都是等边三角形B .四边形MBON 和四边形MODN 都是菱形C .四边形AMON 与四边形ABCD 是位似图形 D .四边形MBCO 和四边形NDCO 都是等腰梯形 【关键词】菱形 【答案】C3.如图,矩形ABCD 中,35AB BC ==,.过对角线交点O 作OE AC ⊥交AD 于E ,则AE 的长是( )A .1.6B .2.5C .3D .3.4DBCA NM O【关键词】矩形的性质、勾股定理 【答案】D4.(河北)如图1,在菱形ABCD 中,AB = 5,∠BCD = 120°,则对 角线AC 等于( ) A .20 B .15 C . 10D .5【关键词】菱形和等边三角形的性质【答案】D5.(兰州)如图7所示,将一张正方形纸片对折两次,然后在上面打3个洞,则纸片展开后是【关键词】正方形、折叠 【答案】D6.如图,将边长为8㎝的正方形ABCD 折叠,使点D 落在BC 边的中点E 处,点A 落在F 处,折痕为MN ,则线段CN 的长是( ) A .3cmB .4cmC .5cmD .6cmBACDA .B .C .D .【关键词】正方形 【答案】7.(凉山州)如图,将矩形ABCD 沿对角线BD 折叠,使C 落在C '处,BC '交AD 于E ,则下列结论不一定成立的是( )A .AD BC '=B .EBD EDB ∠=∠C .ABE CBD △∽△D .sin AEABE ED∠=【关键词】矩形的性质、折叠 【答案】C8.(济宁市)“赵爽弦图”是四个全等的直角三角形与中间一个小正方形拼成的大正方形.如图,是一“赵爽弦图”飞镖板,其直角三角形的两条直角边的长分别是2和4.小明同学距飞镖板一定距离向飞镖板投掷飞镖(假设投掷的飞镖均扎在飞镖板上), 则投掷一次飞镖扎在中间小正方形区域(含边线)的概率是 A .12 B . 14 C . 15 D . 110【关键词】正方形 【答案】C9.(衡阳市) 如图,菱形ABCD 的周长为20cm ,DE ⊥AB ,垂足为E ,54A cos =,则下列结论中正C D C 'A BENE确 的个数为( )①DE =3cm ; ②EB =1cm ; ③2A BCD 15S cm =菱形. A .3个B .2个C .1个D .0个【关键词】菱形 【答案】A10.(衡阳市)如图,矩形纸片ABCD 中,AB =4,AD =3,折叠纸片使AD 边与对角线BD 重合,折痕为DG ,则AG 的长为( ) A .1 B .34 C .23D .2【关键词】矩形折叠 【答案】C11.(广西南宁)如图2,将一个长为10cm ,宽为8cm 的矩形纸片对折两次后,沿所得矩形两邻边中点的连线(虚线)剪下,再打开,得到的菱形的面积为( ) A .210cmB .220cmC .240cmD .280cm【关键词】菱形的性质与判定 【答案】A12.如图(1),把一个长为m 、宽为n 的长方形(m n >)沿虚线剪开,拼接成图(2),成为在一角去ABCD图2C掉一个小正方形后的一个大正方形,则去掉的小正方形的边长为( ) A .2m n - B .m n - C .2mD .2n【关键词】整式的运算;特殊平行四边形相关的面积问题 【答案】A13.(桂林百色)如图,正方形ABCD 的边长为2,将长为2的线段QR 的两端放 在正方形的相邻的两边上同时滑动.如果Q 点从A 点出发,沿 图中所示方向按A→B→C→D→A 滑动到A 止,同时点R 从B 点 出发,沿图中所示方向按B→C→D→A→B 滑动到B 止,在这个 过程中,线段QR 的中点M 所经过的路线围成的图形的面积为 ( ).A .2B .4π-C .πD .π1-【关键词】正方形、动点、面积 【答案】B14.(河池)已知菱形的边长和一条对角线的长均为2cm ,则菱形的面积为( )A . 23cmB . 24cm C .2 D .2【关键词】菱形、面积 【答案】D15.(杭州市)如图,在菱形ABCD 中,∠A =110°,E ,F 分别是边AB 和BC 的中点,EP ⊥CD 于点P ,则∠FPC =( )A .35°B .45°C .50°D .55°Dmnnn(2)(1)【关键词】菱形的性质与判定 【答案】D16.(义乌)如图,一块砖的外侧面积为x ,那么图中残留部分墙面的面积为 A .4x A .12x A .8x A .16x【关键词】平面图形的面积 【答案】B17.(台湾) 如图(八),长方形ABCD 中,E 点在BC 上,且AE 平分 BAC 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2013中考全分类汇编特殊的平行四边形(菱形,矩形,正方形)菱形1、(绵阳市2013年)如图,四边形ABCD 是菱形,对角线AC =8cm ,BD =6cm ,DH ⊥AB 于点H ,且DH 与AC 交于G ,则GH =( B ) A .2825cm B .2120cm C .2815cm D .2521cm[解析]OA=4,OB=3,AB=5,△BDH ∽△BOA ,BD/AB=BH/OB=DH/OA ,6/5=BH/3,BH=18/5, AH=AB-BH=5-18/5=7/5,△AGH ∽△ABO , GH/BO=AH/AO ,GH/3=7/5 / 4,GH=21/20。
2、(2013•曲靖)如图,在▱ABCD 中,对角线AC 与BD 相交于点O ,过点O 作EF ⊥AC 交BC 于点E ,交AD 于点F ,连接AE 、CF .则四边形AECF 是( )3、(2013凉山州)如图,菱形ABCD 中,∠B=60°,AB=4,则以AC 为边长的正方形ACEF 的周长为( )HGO DCB A10题图A.14 B.15 C.16 D.17考点:菱形的性质;等边三角形的判定与性质;正方形的性质.分析:根据菱形得出AB=BC,得出等边三角形ABC,求出AC,长,根据正方形的性质得出AF=EF=EC=AC=4,求出即可.解答:解:∵四边形ABCD是菱形,∴AB=BC,∵∠B=60°,∴△ABC是等边三角形,∴AC=AB=4,∴正方形ACEF的周长是AC+CE+EF+AF=4×4=16,故选C.点评:本题考查了菱形性质,正方形性质,等边三角形的性质和判定的应用,关键是求出AC的长.4、(2012•泸州)如图,菱形ABCD的两条对角线相交于O,若AC=6,BD=4,则菱形ABCD 的周长是(),.5、(2013菏泽)如图,把一个长方形的纸片对折两次,然后剪下一个角,为了得到一个钝角为120°的菱形,剪口与第二次折痕所成角的度数应为()A.15°或30° B.30°或45°C.45°或60°D.30°或60°考点:剪纸问题.分析:折痕为AC与BD,∠BAD=120°,根据菱形的性质:菱形的对角线平分对角,可得∠ABD=30°,易得∠BAC=60°,所以剪口与折痕所成的角a的度数应为30°或60°.解答:解:∵四边形ABCD是菱形,∴∠ABD=∠ABC,∠BAC=∠BAD,AD∥BC,∵∠BAD=120°,∴∠ABC=180°﹣∠BAD=180°﹣120°=60°,∴∠ABD=30°,∠BAC=60°.∴剪口与折痕所成的角a的度数应为30°或60°.故选D.点评:此题主要考查菱形的判定以及折叠问题,关键是熟练掌握菱形的性质:菱形的对角线平分每一组对角.6、(2013•玉林)如图,在给定的一张平行四边形纸片上作一个菱形.甲、乙两人的作法如下:甲:连接AC,作AC的垂直平分线MN分别交AD,AC,BC于M,O,N,连接AN,CM,则四边形ANCM是菱形.乙:分别作∠A,∠B的平分线AE,BF,分别交BC,AD于E,F,连接EF,则四边形ABEF 是菱形.根据两人的作法可判断()解:甲的作法正确;∵四边形中7、(2013年潍坊市)如图,ABCD是对角线互相垂直的四边形,且OB=OD,请你添加一个适当的条件____________,使ABCD成为菱形.(只需添加一个即可)答案:OA=OC或AD=BC或AD//BC或AB=BC等考点:菱形的判别方法.点评:此题属于开放题型,答案不唯一.主要考查了菱形的判定,关键是掌握菱形的判定定理.8、(2013•攀枝花)如图,在菱形ABCD 中,DE ⊥AB 于点E ,cosA=,BE=4,则tan ∠DBE 的值是 2 .DBE=cosA==8DBE==9、(2013年临沂)如图,菱形ABCD 中,AB =4,o60B ∠=,,AE BC AF CD ⊥⊥,垂足分别为E,F,连接EF,则的△AEF 的面积是.答案:解析:依题可求得:∠BAD =120°,∠BAE =∠DAF=30°,BE =DF =2,AE =AF =形AEF 为等边三角形,高为3,面积S =132⨯⨯ 10、(2013•泰州)对角线互相 垂直 的平行四边形是菱形.11、(2013年南京)如图,将菱形纸片ABCD 折迭,使点A 恰好落在菱形的对称中心O 处,折痕为EF 。
若菱形ABCD 的边长为2 cm , ∠A=120︒,则EF= cm 。
答案: 3解析:点A 恰好落在菱形的对称中心O 处,如图,P 为AO 中点,所以E 为A 职点,AE=1,∠EAO=60︒,EP =2,所以,EF = 312、(2013•淮安)若菱形的两条对角线分别为2和3,则此菱形的面积是 3 . ×=13、(2013•牡丹江)如图,边长为1的菱形ABCD中,∠DAB=60°.连结对角线AC,以AC为边作第二个菱形ACEF,使∠FAC=60°.连结AE,再以AE为边作第三个菱形AEGH 使∠HAE=60°…按此规律所作的第n个菱形的边长是()n﹣1.BM=AM=,AE=3(个菱形的边长为(故答案为(14、(2013•宁夏)如图,菱形OABC的顶点O是原点,顶点B在y轴上,菱形的两条对角线的长分别是6和4,反比例函数的图象经过点C,则k的值为﹣6.y=,解得15、(2013•攀枝花)如图,分别以直角△ABC的斜边AB,直角边AC为边向△ABC外作等边△ABD和等边△ACE,F为AB的中点,DE与AB交于点G,EF与AC交于点H,∠ACB=90°,∠BAC=30°.给出如下结论:①EF⊥AC;②四边形ADFE为菱形;③AD=4AG;④FH=BD其中正确结论的为①③④(请将所有正确的序号都填上).解答:BCABBD形,AFABAG16、(2013•内江)已知菱形ABCD的两条对角线分别为6和8,M、N分别是边BC、CD 的中点,P是对角线BD上一点,则PM+PN的最小值=5.17、(2013•黔西南州)如图所示,菱形ABCD的边长为4,且AE⊥BC于E,AF⊥CD于F,∠B=60°,则菱形的面积为.=,,18、(2013•衢州)如图,在菱形ABCD中,边长为10,∠A=60°.顺次连结菱形ABCD各边中点,可得四边形A1B1C1D1;顺次连结四边形A1B1C1D1各边中点,可得四边形A2B2C2D2;顺次连结四边形A2B2C2D2各边中点,可得四边形A3B3C3D3;按此规律继续下去….则四边形A2B2C2D2的周长是20;四边形A2013B2013C2013D2013的周长是.,,.19、(2013四川宜宾)如图,在△ABC中,∠ABC=90°,BD为AC的中线,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.若AG=13,CF=6,则四边形BDFG的周长为20.考点:菱形的判定与性质;直角三角形斜边上的中线;勾股定理.分析:首先可判断四边形BGFD是平行四边形,再由直角三角形斜边中线等于斜边一半,可得BD=FD,则可判断四边形BGFD是菱形,设GF=x,则AF=13﹣x,AC=2x,在Rt △ACF中利用勾股定理可求出x的值.解答:解:∵AG∥BD,BD=FG,∴四边形BGFD是平行四边形,∵CF⊥BD,∴CF⊥AG,又∵点D是AC中点,∴BD=DF=AC,∴四边形BGFD是菱形,设GF=x,则AF=13﹣x,AC=2x,在Rt△ACF中,AF2+CF2=AC2,即(13﹣x)2+62=(2x)2,解得:x=5,故四边形BDFG的周长=4GF=20.故答案为:20.点评:本题考查了菱形的判定与性质、勾股定理及直角三角形的斜边中线的性质,解答本题的关键是判断出四边形BGFD是菱形.20、(2013•黄冈)如图,四边形ABCD是菱形,对角线AC、BD相交于点O,DH⊥AB于H,连接OH,求证:∠DHO=∠DCO.21、(2013•十堰)如图,已知正比例函数y=2x和反比例函数的图象交于点A(m,﹣2).(1)求反比例函数的解析式;(2)观察图象,直接写出正比例函数值大于反比例函数值时自变量x的取值范围;(3)若双曲线上点C(2,n)沿OA方向平移个单位长度得到点B,判断四边形OABC 的形状并证明你的结论.(y=y==,上,=,22、(2013年广州市)如图8,四边形ABCD是菱形,对角线AC与BD相交于O,AB=5,AO=4,求BD的长.分析:根据菱形的性质得出AC⊥BD,再利用勾股定理求出BO的长,即可得出答案解:∵四边形ABCD是菱形,对角线AC与BD相交于O,∴AC⊥BD,DO=BO,∵AB=5,AO=4,∴BO==3,∴BD=2BO=2×3=6.点评:此题主要考查了菱形的性质以及勾股定理,根据已知得出BO的长是解题关键23、(2013•常州)如图,在△ABC中,AB=AC,∠B=60°,∠FAC、∠ECA是△ABC的两个外角,AD平分∠FAC,CD平分∠ECA.求证:四边形ABCD是菱形.24、(2013•恩施州)如图所示,在梯形ABCD中,AD∥BC,AB=CD,E、F、G、H分别为边AB、BC、CD、DA的中点,求证:四边形EFGH为菱形.AC BDEF=ACGH=ACACBD25、(2013•宜昌)如图,点E,F分别是锐角∠A两边上的点,AE=AF,分别以点E,F为圆心,以AE的长为半径画弧,两弧相交于点D,连接DE,DF.(1)请你判断所画四边形的性状,并说明理由;(2)连接EF,若AE=8厘米,∠A=60°,求线段EF的长.26、(2013•雅安)在▱ABCD中,点E、F分别在AB、CD上,且AE=CF.(1)求证:△ADE≌△CBF;(2)若DF=BF,求证:四边形DEBF为菱形.27、(2013•南宁)如图,在菱形ABCD中,AC为对角线,点E、F分别是边BC、AD的中点.(1)求证:△ABE≌△CDF;(2)若∠B=60°,AB=4,求线段AE的长.∵=,.28、(2013安顺)如图,在△ABC中,D、E分别是AB、AC的中点,BE=2DE,延长DE 到点F,使得EF=BE,连接CF.(1)求证:四边形BCFE是菱形;(2)若CE=4,∠BCF=120°,求菱形BCFE的面积.考点:菱形的判定与性质;三角形中位线定理.分析:从所给的条件可知,DE是△ABC中位线,所以DE∥BC且2DE=BC,所以BC和EF平行且相等,所以四边形BCFE是平行四边形,又因为BE=FE,所以是菱形;∠BCF是120°,所以∠EBC为60°,所以菱形的边长也为4,求出菱形的高面积就可求.解答:(1)证明:∵D、E分别是AB、AC的中点,∴DE∥BC且2DE=BC,又∵BE=2DE,EF=BE,∴EF=BC,EF∥BC,∴四边形BCFE是平行四边形,又∵BE=FE,∴四边形BCFE是菱形;(2)解:∵∠BCF=120°,∴∠EBC=60°,∴△EBC是等边三角形,∴菱形的边长为4,高为2,∴菱形的面积为4×2=8.点评:本题考查菱形的判定和性质以及三角形中位线定理,以及菱形的面积的计算等知识点.29、(2013•娄底)某校九年级学习小组在探究学习过程中,用两块完全相同的且含60°角的直角三角板ABC与AFE按如图(1)所示位置放置放置,现将Rt△AEF绕A点按逆时针方向旋转角α(0°<α<90°),如图(2),AE与BC交于点M,AC与EF交于点N,BC与EF 交于点P.(1)求证:AM=AN;(2)当旋转角α=30°时,四边形ABPF是什么样的特殊四边形?并说明理由.30、(2013•株洲)已知四边形ABCD是边长为2的菱形,∠BAD=60°,对角线AC与BD 交于点O,过点O的直线EF交AD于点E,交BC于点F.(1)求证:△AOE≌△COF;(2)若∠EOD=30°,求CE的长.,DAO=∠BAD=×AD=×=×,×=CE==.31、(2013•苏州)如图,点P是菱形ABCD对角线AC上的一点,连接DP并延长DP交边AB于点E,连接BP并延长交边AD于点F,交CD的延长线于点G.(1)求证:△APB≌△APD;(2)已知DF:FA=1:2,设线段DP的长为x,线段PF的长为y.①求y与x的函数关系式;②当x=6时,求线段FG的长.进而得出=,=,进而得出=,即=,进而得出====,,==,即=x×====,=32、(2013聊城)如图,AB是⊙O的直径,AF是⊙O切线,CD是垂直于AB的弦,垂足为E,过点C作DA的平行线与AF相交于点F,CD=,BE=2.求证:(1)四边形FADC 是菱形;(2)FC是⊙O的切线.考点:切线的判定与性质;菱形的判定.分析:(1)首先连接OC,由垂径定理,可求得CE的长,又由勾股定理,可求得半径OC 的长,然后由勾股定理求得AD的长,即可得AD=CD,易证得四边形FADC是平行四边形,继而证得四边形FADC是菱形;(2)首先连接OF,易证得△AFO≌△CFO,继而可证得FC是⊙O的切线.解答:证明:(1)连接OC,∵AB是⊙O的直径,CD⊥AB,∴CE=DE=CD=×4=2,设OC=x,∵BE=2,∴OE=x﹣2,在Rt△OCE中,OC2=OE2+CE2,∴x2=(x﹣2)2+(2)2,解得:x=4,∴OA=OC=4,OE=2,∴AE=6,在Rt△AED中,AD==4,∴AD=CD,∵AF是⊙O切线,∴AF⊥AB,∵CD⊥AB,∴AF∥CD,∵CF∥AD,∴四边形FADC是平行四边形,∴▱FADC是菱形;(2)连接OF,∵四边形FADC是菱形,∴FA=FC,在△AFO和△CFO中,,∴△AFO≌△CFO(SSS),∴∠FCO=∠FAO=90°,即OC⊥FC,∵点C在⊙O上,∴FC是⊙O的切线.点评:此题考查了切线的判定与性质、菱形的判定与性质、垂径定理、勾股定理以及全等三角形的判定与性质.此题难度适中,注意掌握辅助线的作法,注意数形结合思想的应用.33、(2013泰安)如图,在四边形ABCD中,AB=AD,CB=CD,E是CD上一点,BE交AC于F,连接DF.(1)证明:∠BAC=∠DAC,∠AFD=∠CFE.(2)若AB∥CD,试证明四边形ABCD是菱形;(3)在(2)的条件下,试确定E点的位置,∠EFD=∠BCD,并说明理由.考点:菱形的判定与性质;全等三角形的判定与性质.分析:(1)首先利用SSS定理证明△ABC≌△ADC可得∠BAC=∠DAC,再证明△ABF≌△ADF,可得∠AFD=∠AFB,进而得到∠AFD=∠CFE;(2)首先证明∠CAD=∠ACD,再根据等角对等边可得AD=CD,再有条件AB=AD,CB=CD 可得AB=CB=CD=AD,可得四边形ABCD是菱形;(3)首先证明△BCF≌△DCF可得∠CBF=∠CDF,再根据BE⊥CD可得∠BEC=∠DEF=90°,进而得到∠EFD=∠BCD.解答:(1)证明:∵在△ABC和△ADC中,∴△ABC≌△ADC(SSS),∴∠BAC=∠DAC,∵在△ABF和△ADF中,∴△ABF≌△ADF,∴∠AFD=∠AFB,∵∠AFB=∠AFE,∴∠AFD=∠CFE;(2)证明:∵AB∥CD,∴∠BAC=∠ACD,又∵∠BAC=∠DAC,∴∠CAD=∠ACD,∴AD=CD,∵AB=AD,CB=CD,∴AB=CB=CD=AD,∴四边形ABCD是菱形;(3)当EB⊥CD时,∠EFD=∠BCD,理由:∵四边形ABCD为菱形,∴BC=CD,∠BCF=∠DCF,在△BCF和△DCF中,∴△BCF≌△DCF(SAS),∴∠CBF=∠CDF,∵BE⊥CD,∴∠BEC=∠DEF=90°,∴∠EFD=∠BCD.点评:此题主要考查了全等三角形的判定与性质,以及菱形的判定与性质,全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.34、(2013•遂宁)如图,已知四边形ABCD是平行四边形,DE⊥AB,DF⊥BC,垂足分别是E、F,并且DE=DF.求证:(1)△ADE≌△CDF;(2)四边形ABCD是菱形.35、(2013•舟山)某学校的校门是伸缩门(如图1),伸缩门中的每一行菱形有20个,每个菱形边长为30厘米.校门关闭时,每个菱形的锐角度数为60°(如图2);校门打开时,每个菱形的锐角度数从60°缩小为10°(如图3).问:校门打开了多少米?(结果精确到1米,参考数据:sin5°≈0.0872,cos5°≈0.9962,sin10°≈0.1736,cos10°≈0.9848).FE D C BA37、(2013年临沂)如图,在△ABC 中,AD 是BC 边上的中线,E 是AD 的中点,过点A 作BC 的平行线交BE 的延长线于点F,连接CF. (1)求证:AF=DC ;(2)若AB ⊥AC,试判断四边形ADCF 的形状,并证明你的结论.解析:证明:(1)∵E 是AD 的中点,∴AE=ED.……………………………(1分) ∵A F ∥BC,∴∠AFE=∠DBE, ∠FAE=∠BDE,∴△AFE ≌△DBE. ………………………(2分) ∴AF=DB.(第22题图)∵AD 是BC 边上的中点,∴DB=DC,AF=DC ……………(3分) (2)四边形ADCF 是菱形. …………………………………(4分) 理由:由(1)知,AF=DC,∵A F ∥CD, ∴四边形ADCF 是平行四边形. ……(5分) 又∵AB ⊥AC, ∴△ABC 是直角三角形∵AD 是BC 边上的中线, ∴12AD BC DC ==. … (6分) ∴平行四边形ADCF 是菱形. …………………(7分)2013中考全国100份试卷分类汇编矩形1、(2013陕西)如图,在矩形ABCD 中,AD=2AB ,点M 、N 分别在边AD 、BC 是,连接BM 、DN ,若四边形MBND 是菱形,则MDAM等于 ( ) A .83 B .32 C .53 D .54考点:矩形的性质及菱形的性质应用。
