四年级奥数专题图形周长与面积
四年级上学期矩形周长奥数题

四年级上学期矩形周长奥数题题目一:一个矩形的宽度是4米,长度是8米,求这个矩形的周长。
解答一:根据矩形的定义,周长是矩形四个边的长度之和。
这个矩形的宽度是4米,长度是8米。
根据周长的计算公式:周长 = 2 * (宽度 + 长度),我们可以得到周长的计算结果:周长 = 2 * (4 + 8) = 2 * 12 = 24所以,这个矩形的周长是24米。
题目二:一个矩形的周长是18米,宽度是3米,求这个矩形的长度。
解答二:根据矩形的定义,周长是矩形四个边的长度之和。
这个矩形的宽度是3米,周长是18米。
根据周长的计算公式:周长 = 2 * (宽度 + 长度),我们可以设矩形的长度为x,然后列出方程:18 = 2 * (3 + x)解方程得:18 = 6 + 2x2x = 18 - 62x = 12x = 12 / 2x = 6所以,这个矩形的长度是6米。
题目三:一个矩形的宽度是5米,长度是7米,求这个矩形的周长和面积。
解答三:根据矩形的定义,周长是矩形四个边的长度之和,面积是矩形的宽度乘以长度。
这个矩形的宽度是5米,长度是7米。
根据周长和面积的计算公式:周长 = 2 * (宽度 + 长度)面积 = 宽度 * 长度我们可以得到周长和面积的计算结果:周长 = 2 * (5 + 7) = 2 * 12 = 24面积 = 5 * 7 = 35所以,这个矩形的周长是24米,面积是35平方米。
题目四:一个矩形的面积是72平方米,宽度是6米,求这个矩形的长度。
解答四:根据矩形的定义,面积是矩形的宽度乘以长度。
这个矩形的面积是72平方米,宽度是6米。
根据面积的计算公式:面积 = 宽度 * 长度,我们可以设矩形的长度为x,然后列出方程:72 = 6 * x解方程得:x = 72 / 6x = 12所以,这个矩形的长度是12米。
小学奥数讲义4年级-8-直线形面积初步-难版

图形的周长与面积的计算是小学数学中最基本、最重要的内容之一。
周长和面积这两个概念是不同的,它们使用的单位、计算公式也是不同的。
周长是指围成平面图形一周的线段的总和;而面积是指围成的平面图形的大小。
所以周长通常采用的长度单位有:米、分米、厘米;面积通常采用的单位有:平方米、平方分米、平方厘米。
1.三角形从三角形的一个角的顶点向它的对边画一条垂线,顶点到垂足间的线段叫做三角形的高。
注意:锐角三角形的高在三角形的内部,直角三角形的两条直角边是它的高,钝角三角形的其中两个高在三角形的外部。
三角形的高所在的边叫做三角形的底。
面积公式=底×高÷2或用字母表示为:S=ah ÷2. 2.平行四边形从平行四边形一条边上的一点向对边引一条垂线,这点到垂足间的线段叫做平行四边形的高,这条边叫做平行四边形的底。
面积公式=底×高或用字母表示为:S=ah 。
长方形与正方形是特殊的平行四边形。
长方形面积=长×宽,周长=(长+宽)×2。
正方形的面积=边长×边长,周长=边长×4。
3.梯形在梯形里,互相平行的一组对边分别叫做梯形的上底和下底,不平行的一组对边叫做梯形的腰;以上底向下底引一条垂线,这点到垂足间的线段叫做梯形的高。
梯形两腰中点的连线叫做梯形的中位线。
中位线的长度=(上底+下底)÷2面积公式=(上底+下底)×高÷2或:中位线×高 用字母表示为:S=(a+b )×h ÷2或:m ×h知识梳理【例1】★已知大正方形比小正方形边长多2厘米,大正方形比小正方形的面积大40平方厘米。
求大、小正方形的面积各是多少平方厘米?【解析】从图中可以看出,大正方形的面积比小正方形的面积大出的40平方厘米,可以分成三部分,其中A 和B 的面积相等。
因此,用40平方厘米减去阴影部分的面积,再除以2就能得到长方形A 和B 的面积,再用A 或B 的面积除以2就是小正方形的边长。
最新四年级奥数专题--图形周长和面积

第一讲图形周长和面积知识导航亲爱的同学们,我们已经学会长方形、正方形的周长与面积的计算,利用公式很容易算出它们的面积与周长。
但在遇到一些较复杂的有关长方形和正方形的周长和面积计算时,一些同学就会感到棘手。
这一讲我们将学习用平移、转化、分解、合并等技巧解决难题,使大家在解题中能顺利地找到突破口,化难为易,化繁为简。
精典例题例1:下图是由16个同样大小的正方形组成的,如果这个图形的面积是400平方厘米,那么它的周长是多少厘米?思路点拨每个正方形的面积为:400÷16=25(平方厘米),所以每个正方形的边长是5厘米。
从上下方向来看有14条边是周长的一部分,从左右方向来看有20条边是周长的一部分,所以……模仿练习计算右面图形的周长(单位:厘米)。
例2:有9个小长方形,它们的长和宽分别相等,用这9个小长方形拼成的大长方形(如图)的面积是45平方厘米,求这个大长方形的周长。
思路点拨从图上可以知道,小长方形的长的4倍等于宽的5倍,所以长是宽的5÷4=1.25倍。
每个小长方形的面积为45÷9=5平方厘米,所以1.25×宽×宽=5,所以宽为2厘米,长为2.5厘米。
模仿练习下图的长方形被分割成5个正方形,已知原长方形的面积为120平方厘米,求原长方形的长与宽。
例3:一块正方形的苗圃(如右图实线所示),若将它的边长各增加30米,则面积增加9900平方米,问原来这块正方形苗圃的面积是多少平方米?思路点拨通过画图可以算出:小正方形的面积为:30×30=900平方米。
用增加的面积减去小正方形的面积就得到增加的两个长方形的面积之和,9900-900=9000平方米。
而增加的两个长方形的面积相等,于是其中一个长方形的面积为9000÷2=4500平方米。
模仿练习喜阳阳小学的操场长90米,宽45米。
改造后,长增加10米,宽增加5米。
现在操场面积比原来增加了多少平方分米?例4:如下图,用标号为1,2,3,4,5的五种大小不同的正方形拼成一个大长方形,大长方形的长和宽分别是18,14,则标号为5的正方形的面积是多少?(2006年“希望杯”第二试)思路点拨如果标号为5的正方形的边长是a ,那么1号比2号大a ,2号比3号大a ,所以1号比3号大2a ,又因为2号和3号的边长之和是14,1号和2号的边长之和是18,所以1号比3号大18-14=4。
四年级奥数巧求周长和面积

一、基本概念(1)周长:封闭图形一周的长度就是这个图形的周长. (2)面积:物体的表面或封闭图形的大小,叫做它们的面积.二、基本公式(1)长方形的周长2=⨯(长+宽),面积=长⨯宽. (2)正方形的周长4=⨯边长,正方形的面积=边长⨯边长.三、常用方法对于基本的长方形和正方形图形,可以直接用公式求出它们的周长和面积,对于一些不规则的比较复杂的几何图形,我们可以采用转化的数学思想方法割补成基本图形,利用长方形、正方形周长及面积计算的公式求解.(1)转化是一种重要的数学思想方法在转化过程中要抓住“变”与“不变”两个部分.转化后的图形虽然形状变了,但其周长和面积不应该改变,所以在求解过程中不能遗漏掉某些线段的长度或某部分图形的面积.转化的目标是将复杂的图形转化为周长或面积可求的图形. (2)化归思想寻求正确有效的解题思路,意味着寻找一条摆脱困境、绕过障碍的途径.因此,我们在解决数学问题时,思考的着重点就是要把所需解决的问题转化为已经能够解决的问题.也就是说,在直接求解不容易或很难找到解题途径的问题时,我们往往转化问题的形式,从侧面或反面寻找突破口,知道最终把它转化成一个或若干个能解决的问题.这种解决问题的思想在数学中叫“化归”,它是数学思维中重要的思想和方法.在几何中,有许多图形是由一些基本图形组合、拼凑而成的.这样的图形我们称为不规则图形.不规则图形的面积往往无法直接应用公式计算.那么,不规则图形的面积怎样去计算呢?对称、旋转、平移这几种几何变换就是解决这类面积问题的手段. (3)平移在平面图形的计算中,常常要将一个平面图形移动到平面上的另一个位置进行计算.其中,将图形沿一个固定方向的移动叫做平移,一个图形经过平行移动不改变其形状与大小,所以图形面积是保持不变的.利用图形的平移,可以使面积计算问题的解法简捷明快,颇有新意.知识框架巧求周长和面积 发现不同(4)割补割补法在我国古代叫“出入相补原理”,我国古代魏晋时期著名的数学家刘徽在《九章算术注》中就明确地提出“出入相补,各从其类”的出入相补原理.这个原理的内容是几何图形经过分、合、移、补所拼凑成的新图形,它的面积不变.(5)旋转在平面图形的割补中,有时要将一个图形绕定点旋转到一个新的位置,产生一种新的图形结构,图形在转动过程中形状大小不发生改变.利用这种新的图形结构可以帮我们解决面积的计算问题.(6)对称平面图形中有许多简单漂亮的图形都是轴对称图形.轴对称图形沿对称轴折叠,轴两侧可以完全重合.也就是说,如果一个图形是轴对称图形,那么对称轴平分这个图形的面积.熟悉轴对称图形这个性质,对面积计算会有很大帮助.(7)代换在几何计算中,对有关数量进行适当的等量代换也是解决问题的已知技巧.本讲主要通过求一些不规则图形的周长,体会一种转化思想,重点在于把不规则图形转化为规则图形的方法,包括平移、旋转、割补、差不变原理,通过这些方法的学习,让学生体会求周长的技巧,提高学生的观察能力、动手操作能力、综合运用能力.例题精讲【例 1】三只猴子走得一样快,所走的路线如下图.哪只猴子先吃到桃子,就在它旁边的( )里画勾.A ( )B ( )C ( )【巩固】一个苗圃园(如左下图),周边和中间有一些路供人行走(图中线段表示“路”),几个小朋友在里面观赏时发现:从A处出发,在速度一样的情况下,只要是按“向右”、“向上”方向走,几个人分头走不同的路线,总会同时达到B处.你知道其中的道理吗?【例 2】计算下列图形的周长(单位:厘米).【巩固】试求左下图的周长(单位:厘米).【例 3】求下面两个图形的周长(单位:厘米).【巩固】下图是由七个长5厘米、宽3厘米的相同长方形经过竖放、横放而成的图形.求这个图形的周长.【例 4】下图是一个方形螺线.已知两相邻平行线之间的距离均为1厘米,求螺线的总长度.【巩固】在一个长方形的面积为169平方厘米.在这个长方形内任取一点P,则点P到长方形四边的距离之和最小值为_______厘米.【例 5】边长是15厘米的3个正方形拼成一个长方形,这个长方形的周长是多少?【巩固】用一块长8分米,宽4分米的长方形纸板与两块边长4分米的正方形纸板拼成一个正方形.拼成的正方形的周长是多少分米?84【例 6】用若干个边长都是2厘米的平行四边形与三角形(如右图)拼接成一个大的平行四边形,已知大平行四边形的周长是244厘米,那么平行四边形和三角形各有多少个?【巩固】用若干个边长都是2厘米的平行四边形与三角形(如右图)拼接成一个大的平行四边形,已知大平行四边形的周长是236厘米,那么平行四边形和三角形各有多少个?【例 7】如图,正方形ABCD的边长是6厘米,过正方形内的任意两点画直线,可把正方形分成9个小长方形.这9个小长方形的周长之和是多少?D【巩固】如图,正方形的边长为4,被分割成如下12个小长方形,求这12个小长方形的所有周长之和.【例 8】一个长为12厘米,宽为10厘米的长方形,挖去一个边长为4厘米的正方形补在另一边上(如图).所得图形的周长为厘米.【巩固】如图所示,这是三个边长为10厘米的正方形纸片.从(1)和(2)中各剪去一个面积是4平方厘米的小正方形,从(3)中剪去一个面积是4平方厘米的长方形.比较(1),(2),(3),剩下部分周长最小的是_________(填图形编号),它的周长是_________厘米.(2)4 1(3)【例 9】 将边长为10厘米的五张正方形纸片如图那样放置,每张小正方形纸片被盖住的部分是一个较小的正方形,它的边长是原正方形边长的一半,则图中的图形外轮廓(图中粗线条)的周长为多少 厘米?【巩固】 下图是一面砖墙的平面图,每块砖长20厘米,高8厘米,像图中那样一层、二层…一共摆十层,求摆好后这十层砖墙的周长是多少?【例 10】 下图中的阴影部分BCGF 是正方形,线段FH 长18厘米,线段AC 长24厘米,则长方形ADHE 的周长是多少厘米?HFEDA【巩固】 如图,在长方形ABCD 中,EFGH 是正方形.已知10cm AF =,7cm HC =,求长方形ABCD 的周长.H GFEDCBA【例 11】如图,一个长方形的周长是26厘米,如果它的长和宽各增加3厘米,那么增加的面积是多少平方厘米?【巩固】有一个长方形,如果宽减少2米,或长减少3米,则面积均减少24平方米,求这个长方形的面积?32【例 12】两个同样的长方形摆放成如图所示图形,图中单位是厘米,每个长方形的面积是多少平方厘米?Array【巩固】有10张长3厘米,宽2厘米的纸片,将它们按照下图的样子摆放在桌面上,那么这10张纸片所盖住的桌面的面积是多少平方厘米?【例 13】 用两个同样的等腰直角三角形ABC 拼成一个正方形,如图,等腰直角三角形的斜边AC=6厘米,那么正方形ABCB′的面积是多少平方厘米?【巩固】 有一个周长是72厘米的长方形,它是由三个大小相等的正方形拼成的.一个正方形的面积是多少平方厘米?【例 14】 如图1,△ABC 是等腰直角三角形(AC=BC ,∠ACB 是直角),D 是AC 的中点,E 是BC 的中点,DE长8厘米,阴影部分的面积是多少平方厘米?【巩固】 右图中甲的面积比乙的面积大__________平方厘米.乙甲6厘米8厘米4【例 15】如图,正方形ABCD中,AB、BC、CD、DA的中点分别是E、F、C、H,已知AB =8厘米,正方形EFGH 的面积是多少平方厘米?【巩固】如图,正方形ABCD中,E是AB的中点,F是BC的中点,G是CD的中点,H是DA的中点,I是EF 的中点,J是FG的中点,K是GH的中点,L是HE的中点,正方形ABCD的周长是32厘米,那么正方形IJKL的面积是多少平方厘米?【例 16】图内9个相同的小长方形构成大长方形,大长方形周长为90,则每个小长方形周长为多少?【巩固】有9个小长方形,它们的长和宽分别相等,用这9个小长方形拼成的大长方形(如图)的面积是45平方厘米,求这个大长方形的周长.【例 17】 一块长方形铁皮(如图),将长边剪去6厘米,短边剪去3厘米后,得到的正方形面积比原来少了54平方厘米,那么原长方形的面积是多少平方厘米?【例 18】 图中是由1个小正方形与8个相同的长方形拼成的大正方形.已知小正方形的面积是900平方厘米,大正方形的周长是200厘米.那么,每个长方形的长是多少?【例 19】 图中每个小方格的边长是2厘米,正方形ABCD 的面积是多少平方厘米?【巩固】 右图是一个方格网,计算阴影部分的面积.ABC D E F课堂检测【随练1】一个长方形,长减少1厘米和宽增加1厘米,得到一个正方形,那么正方形面积比长方形的面积( ).①多2平方厘米②多1平方厘米③少2平方厘米④少1平方厘米⑤同样大【随练2】右图的正方形的周长是48厘米,中间有一个长方形,长方形的四个顶点恰好把正方形每边分作两段,其中长的那段长度是短的那段长度的两倍.长方形的面积是平方厘米.【随练3】右图ABCD是个正方形:它的边长是4厘米,E、F分别是边AB、BC的中点,图中阴影部分的面积是平方厘米.【随练4】右图中,三角形ABC是等腰直角三角形(AC=BC,∠ACB是直角),D是AC的中点;E是BC的中点,AD长6厘米.阴影部分的面积是平方厘米.【随练5】如图,里面正方形的周长24厘米,外面长方形的各边分别平行于正方形的四条边,那么根据图中给出的数据(单位均为厘米),长方形的周长是( )厘米.A. 32B. 36C. 40D.44E.48【随练6】下图是一副七巧板拼成的正方形.正方形的边长是20厘米,问七巧板中图形4和图形5的面积之和是平方厘米.【随练7】如右图,有一块正方形的草坪,周边用边长为3分米的方砖铺了一条宽12分米的小路(如图阴影部分),共用方砖1504块.则小路所围草坪的面积是( )平方分米.A. 79524B. 76176C. 72900D. 57600E. 90000【随练8】一个长方形,如果长和宽都增加6厘米,则面积增加156平方厘米.原来的长方形的周长是多少厘米?【随练9】有5个相同的长方形拼成下图的大长方形MNPQ,已知小长方形的长比宽多2厘米,则大长方形MNPQ的面积是( )平方厘米.A. 6B. 5C. 4D. 3E. 2【随练10】在长方形ABCD中,EFGH是正方形.如果AG=12厘米,EC=9厘米,那么长方形ABCD的周长是厘米.【随练11】两张同样大小的正三角形纸片,每张面积是36平方厘米(如下图),一张是一个顶点向下,一张是一个顶点向上,叠在一起得到一个六角星形.这个六角星形的面积是多少平方厘米?【随练12】如下图,把一个大正方形分割成六个小长方形,如果这六个小长方形的周长总和是90厘米,那原大正方形的面积是平方厘米.【随练13】如图所示,把长2厘米,宽1厘米的长方形一层、二层、三层······那么摆下去,摆到第15层,这个图形的周长是厘米,面积是平方厘米.【随练14】右图是陈老师家房屋平面图(单位:米),陈老师要将卧室、客厅的房顶四周装木条装饰线,请你帮助算一算,要买木条装饰线的米数至少是( ).A. 68B. 62C. 58D. 54E. 48【作业1】一张长方形纸片的周长是64厘米,3张这样的长方形纸片恰好拼成一张正方形纸片,如图,拼成的正方形纸片的周长是多少厘米?家庭作业【作业2】如图一个正方形分割成六个长方形,这六个长方形的周长和比原正方形周长增加了24厘米,原正方形周长是多少厘米?面积是多少平方厘米?【作业3】如图,A、B、C、D分别是长方形各边上的三等分点,阴影部分四边形ABCD的面积为24平方厘米,长方形EFGH的面积是多少平方厘米?【作业4】如图所示阴影部分的面积是73平方厘米,那么图中正方形的面积是多少平方厘米?(单位:厘米)【作业5】一个周长是20厘米的正方形,剪下一个周长是6厘米的正方形,剩下的图形的周长是______ (写出所有可能的结果).【作业6】下图是一个边长为3的正八边形,它的阴影部分与没有阴影部分的面积之差是多少?。
四年级奥数专题图形周长与面积

• 题目:一个平行四边形的周长是20厘米,其中一条边长是a厘米,则其他三条边的长度是多少? 答案:其他三条边长度分别是:5 a厘米、5 - a厘米、a厘米 解析:根据平行四边形的周长公式,周长 = 2(a + b),其中a和b为平行四边形相邻的两边,可以求出其他 三条边的长度。
• 题目:一个长方形的周长是20厘米,长是a厘米,则宽是多少厘米? 答案:宽 = (20 - 2a) / 2 = 10 - a厘米 解析:根据长方形的周长 公式,周长 = 2(长 + 宽),可以求出宽的表达式。
• 答案:宽 = (20 - 2a) / 2 = 10 - a厘米 • 解析:根据长方形的周长公式,周长 = 2(长 + 宽),可以求出宽的表达式。
• 答案:其他三条边长度分别是:5 - a厘米、5 - a厘米、a厘米 • 解析:根据平行四边形的周长公式,周长 = 2(a + b),其中a和b为平行四边形相邻的两边,可以求出其他三条边的长度。
感谢观看
汇报人:XX
确性
圆形面积的计算
圆的面积公式: A = πr²,其 中r是圆的半径
推导过程:通 过将圆分割成 若干个小的扇 形,然后重新 排列组合成近 似长方形,利 用长方形面积 公式推导得出
计算方法:根 据给定的半径 值,代入公式
中进行计算
注意事项:计 算时要注意单 位的统一,以 及π取值的小
数位数
其他常见图形面积的计算
提高题目练习
4年级奥数边长,周长,面积的计算问题例题

涉及长方形、正方形、三角形、平行四边形和梯形的边长、周长与面积的计算问题.求多个图形覆盖总面积时宜分块处理.考察三角形面积时,需要选择恰当的高,并应注意三角形与等底等高平行四边形之间的关系.例题:1.图6-1由16个同样大小的正方形组成.如果这个图形的面积是400平方厘米,那么它的周长是多少厘米?[分析与解]正方形的面积是400÷16=25平方厘米,正方形边长是5厘米,整个图形的周长是170厘米.2.若干同样大小的长方形小纸片摆成了如图6-2所示的图形.已知小纸片的宽是12厘米,问阴影部分的总面积是多少平方厘米?[分析与解]从第一排与第二排看,五个小纸片的长等于三个小纸片的长加三个小纸片的宽,也就是说,二个小纸片的长等于三个小纸片的宽.已知小纸片的宽是12厘米,于是小纸片的长是12×3÷2=18厘米,阴影部分是三个正方形,边长正好是小纸片的长与宽的差18-12=6.于是,阴影部分的面积是6×6×3=108平方厘米.3.一个正方形,如果把它的相邻两边都增加6厘米,就可以得到一个新正方形,新正方形的面积比原正方形大120平方厘米.求原正方形的面积.[分析与解]如下图,有阴影部分是边长为6厘米的正方形,A、B部分均是长为原正方形边长,宽为6厘米的长方形.有120=6×6+6×原边长+6×原边长,即12×原边长=84,那么原边长为7,则原正方形面积为7×7=49(平方厘米).4.如图6-3,正方形客厅边长12米,若正中铺一块正方形纯毛地毯:外围铺化纤地毯,共需费用22455元.已知纯毛地毯每平方米250元,化纤地毯每平方米35元,问铺在外围的化纤地毯的宽度是多少分米?[分析与解]如果全铺化纤地毯,少用22455-35×122元,每平方米少用(250-35)元,所用纯毛地毯的面积为(22455-35×122)÷(250-35)=81平方米,从而纯毛地毯的边长为9米.因此,外围化纤地毯宽度是(12-9)÷2=1.5米=15分米.5.如图6-4,ABFE和CDEF都是长方形,AB的长是4厘米,BC的长是3厘米.那么图中阴影部分的面积是多少平方厘米?[分析与解]图中阴影部分的面积等于长方形ABCD的一半,即为4×3÷2=6平方厘米.6.如图6-5,有9个小长方形,其中编号为1,2,3,4,5的5个小长方形的面积分别为2,4,6,8,10平方米.求6号长方形的面积.[分析与解]如下图所示,将所有独立的小长方形标上号码:有①×④=②×⑦,⑦=2×8÷4=4;⑦×⑧=③×④,⑧=6×8÷4=12;④×⑥=⑤×⑧,⑥=10×12÷8=15.即6号长方形的面积等于15平方米.评注:在长方形中任意做一条线平行于长,一条平行与宽,将原长方形分成四个部分:左上角,左下角,右上角,右下角.则有左上角面积×右下角面积=左下角面积×右上角面积.7.如图6-6,直角三角形ABC的三边长分别为.AC=30分米,AB=18分米,BC=24分米,ED垂直于AC,且ED=95厘米.问正方形BFEG的边长是多少厘米?[分析与解]如下图所示,连接AE,BE,CE.以下均以厘米作单位,注意单位的转化.有△AFB底为AB时,高为EF;△BEC的底为BC时,高为EG;△AEC的底为AC时,高为ED;有它们的面积分别为180×EF×=90×EF,240×EG×=120EG,300×95×=14250;那么它们的面积和为14250+210×EG等于△ABC的面积180×240×=21600平方厘米,所以EG=35厘米.评注:有的同学如下求解这个问题:△ABC的面积为180×240×=21600平方厘米,有以AC为底时高为21600÷300×2=144,那么BE=144-95=49,正方形面积等于对角线平方的一半,从而BGEF的面积为49×49÷2,得出EG×EG=49×49÷2,EG不能用整数或分数表示.这是为什么呢?有错吗?8.如图6-7,一个平行四边形的一边长15厘米,这条边上的高为6厘米,一条线段将此平行四边形分成了两部分,它们的面积相差18平方厘米.那么其中梯形的上底是多少厘米?[分析与解]梯形面积+三角形面积=平行四边形面积=15×6=90(平方厘米).又已知两者的面积差是18平方厘米,所以梯形的面积为(90+18)÷2=54(平方厘米).于是梯形的上底是2×54÷6-15=3(厘米).9.一张长方形纸片,长7厘米,宽5厘米.把它的右上角往下折叠如图6-8所示,再把左下角往上折叠如图6-9所示.那么,未盖住的阴影部分的面积是多少平方厘米?[分析与解]图6-8中阴影部分的左边部分小长方形的长为5,宽为7-5=2,那么面积为5×2=10,而图6-9中左下角的对应的正方形的边长为2,所以面积为2×2=4.那么阴影部分的面积为10-4=6(平方厘米).10.有10张长3厘米,宽2厘米的纸片,将它们按照图6-10的样子摆放在桌面上,那么这l0张纸片所盖住的桌面的面积是多少平方厘米?[分析与解]第一张纸片盖住的面积是3×2=6平方厘米,后面每增加一张纸片,就多盖住(3-2)×2=2平方厘米.于是,这10张纸片盖住桌面上的面积是6+2×9=24平方厘米.11.三张正方形的纸片铺在桌面上如图6-11所示,其中任意两条相交线段之间的夹角都是直角,而各条线段的长度在图中标出,单位是厘米.那么它们一共遮盖的面积是多少平方厘米?[分析与解]62+42×2-[22+(4-1)×1×4]=36+32-(4+6)=58(平方厘米).12.如图6-12,直角梯形ABCD中,AB=15厘米,BC=12厘米,AE垂直于AB,阴影部分的面积为15平方厘米.问梯形ABCD的面积是多少平方厘米?[分析与解]延长AE交CD与F点,如下图所示.有△BFD,△AFD同底等高,所以面积相等,而△EFD为公共部分,两者都减去有,△BEF,△AED的面积相等为15平方厘米.而△BFA的面积为×15×12=90(平方厘米),所以△ABE的面积为90-15=75(平方厘米).那么△ABE,△EFD的面积之积等于△BEF,△ADE的面积之积.所以有所以△EFD的面积为15×15÷75=3,所以梯形ABCD的面积为75+15+15+90+3=198(平方厘米).13.如图6-13,ABCD是梯形,ABFD是平行四边形,CDEF是正方形,AGHF 是长方形.又知AD=14厘米,BC=22厘米,那么,阴影部分的面积是多少平方厘米?[分析与解]由题意知AD=BF=14,而FC=BC-BF=22-14=8.正方形EDFC的边FC为8,则EF也为8,那么△AFD的面积为×14×8=56(平方厘米).△AFD,△ABF均为平行四边形ABFD面积的一半,而△GBA与△BHF的面积和等于△ABF的面积,所以阴影部分面积为56平方厘米.14.图6-14是一块正方形的地板砖示意图,其中AA1=AA2=BB1=BB2=CC1=CC2=DD1=DD2,红色小正方形的面积是4,四块绿色小三角形的面积总和是18.求大正方形ABCD的面积.[分析与解]绿地可以拼成两个正方形,每一个面积是18÷2=9,所以绿色三角形的两条直角边的长都是3.△AA1A2,△BB1B2,△CC1C2,△DD1D2可以拼成一个正方形,与红色正方形一样大,面积是4.于是大正方形ABCD的面积是18+4+4+4×3×2=50.15.用l,2,3,4,5,7作为图6-15这样图形的6条边长,那么这个图形的最大面积是多少?[分析与解]显然当底部的边为7,右面的边为5时,这个图形的面积最大,但是经过尝试,发现无法组成六边形.于是将右面的边调整为4,发现有下图满足,此时图形的面积为4×7-2×1=26,为最大值.。
四年级奥数面积与周长

长方形(如图),面积比原来的正方形减少 181 平方分米。原正方形的边长是多 少?
hing at a time and All things in their being are good for somethin
思路点拨
把阴影部分剪下来,并把剪下的两个小长方形拼起来(如图),再被上长、宽分别是 8 分米、5 分米的小长方形,这个拼合成的长方形的面积是 181+8×5=221 平方分米,长是原 来正方形的边长,宽是 8+5=13 分米。
杯 1 试)
2.一个长方形,如果它的长减少 3 米,或它的宽减少 2 米,那么它的面积
都减少 36 平方米,求这个长方形原来的面积和周长。
hing at a time and All things in their being are good for somethin
3.一个长方形木板,如果宽减少 6 分米,长减少 10 分米,那么它的面积减少 172 平
模仿练习
一个长方形,如果宽不变,长减少 3 米,那么它的面积减少 24 平方米;如 果长不变,宽增加 4 米,那么它的面积增加 60 平方米。这个长方形原来的面积 是多少平方米?
例 3:用若干个边长都是 2 厘米的平行四边形与三角形(如下图)
拼接成一个大的平行四边形,已知大平行四边形的周长是 244 厘米,那 么平行四边形和三角形各有多少个?
思路点拨
大的平行四边形上、下两边的长为(244-2×2)÷2=120 厘米,观察上边,每 6 厘 米有两个平行四边形的边,所以共有小平行四边形 120÷6×2=40 个……
模仿练习
用若干个边长都是 2 厘米的平行四边形与三角形(如右图)拼接成 一个大的平行四边形,已知大平行四边形的周长是 236 厘米,那么平行 四边形和三角形各有多少个?
汇总小学数学奥数题 周长、面积.ppt

..。..
17
分析: 因为三角形EFD的面积比三角形 ABF的面积大6平方厘米,所以,三角形 BCE的面积比长方形ABCD的面积大6平方 厘米。三角形BCE的面积是6×4+6=30平 方厘米,EC的长则是30×2÷6=10厘米。 因此,ED的长是10-4=6厘米。
第9讲 周长、面积、体 积、表面积
梁碧湘
..。..
1
第一节 巧求周长
专题简析:
对于一些不规则的比较复杂的几何图形, 要求它们的周长,我们可以运用平移的方法, 把它转化为标准的长方形或正方形,然后再利 用周长公式进行计算。
将一个大长方形或正方形分割成若干个长方 形和正方形,那么图形周长就会增加几个长或 宽;反之,将若干个小长方形或正方形合成一 个大长方形或正方形,图形周长就会减少几个 长或宽。
是正方形,已知三角形AFH的面积是
7平方厘米。三角形CDH的面积是多少 平方厘米?
..。..
13
分析 : 设大正方形的边长是a,小正方
形的边长是b。
(1)梯形EFAD的面积是(a+b) ×b÷2,三角形EFC的面积也是 (a+b)×b÷2。所以,两者的面积 相等。
(2)因为三角形AFH的面积=梯形
底FD的长度。连接FC后就能得到一个三角 形EFC,用三角形EBC的面积减去三角形 FBC的面积就能得到三角形EFC的面积: 8×20÷2-8×8÷2=48平方厘米。 FD=48×2÷20=4.8厘米,所求梯形的面积 就是(4.8+8)×8÷2=51.2平方厘米。
..。..
16
例5 图中ABCD是长方形,长为6,宽为4,
..。..
四年级下册数学试题-奥数专题讲练:第五讲 巧求周长和面积 竞赛篇(解析版)全国通用

第五讲巧求周长和面积编写说明“巧求周长和面积”的相关内容我们在寒假小4第四讲给予过一定的讲解. 本讲我们主要在原有知识的基础上进行提高巩固,同时加入一些新的知识,帮助我们更好的过渡到五年级几何部分的学习. 对于一些非常典型的例题,我们采用“重复加强”的学习方法,帮助孩子们牢固掌握. 奥数的题目虽然很多,但一些经典题目,常常会以原题形式出现在各个中学入学测试题中,希望我们的孩子能戒骄戒躁,温故而后知新,清晰彻底的掌握理解自己学习过题目.你还记得吗【复习1】右图中是一个方形螺线.已知两相邻平行线之间的距离均为l厘米,求螺线的总长度.分析:如下图所示,将原图形转化为3个边长分别为3、5、7厘米的正方形和中间一个三边图形.所以螺线的总长度为:(3+5+7)×4+1×3=63 cm .【复习2】用同样大小的瓷砖铺一个正方形地面,两条对角线上铺黑色的,其它地方铺白色的,如图所示。
如果铺满这块地面共用101块黑色瓷砖,那么白色瓷砖用了多少块?分析:我们可以让静止的瓷砖动起来,把对角线上的(101+1)÷2=51块黑瓷砖,通过向上或向右平移处理,移到两条边上(如图2)。
在这一转化过程中瓷砖的位置发生了变化,但数量没有变,此时白色瓷砖组成一个正方形。
(101+1)÷2=51(大正方形的边长),51-1=50(白色瓷砖组成正方形的边长),50×50=2500(块),所以白色瓷砖共用了2500块。
【复习3】有10张长3厘米,宽2厘米的纸片,将它们按照右图的样子摆放在桌面上,那么这10张纸片所盖住的桌面的面积是多少平方厘米?分析:每多盖一张,遮住的面积增加2×1,所以这10张纸片所盖住的桌面的面积是3×2+2×1×9=24cm2.【复习4】有红、黄、绿三块大小一样的正方形纸片,放在一个正方形盒内,它们之间相互叠合(如右图),已知露在外面部分中,红色面积是20,黄色面积是12,绿色面积是8,那么正方形盒的底面积是多少?分析:黄色纸片露出部分与绿色纸片露出部分面积不同,把黄色纸片向左移动,在这个移动过程中,黄色纸片露出部分减少的面积等于绿色纸片纸片露出部分增加的面积,它们露出的面积和不变,所以图2中黄色露出部分面积为10,绿色面积也为10。
(完整word版)四年级奥数图形面积专题

(完整word版)四年级奥数图形⾯积专题第四讲:图形(⼀)爱学教育⽼师奥数2015·四年级·竞赛·秋三⾓形种类:⾯积公式:三⾓形的⾼:1、如图,?ABC⾯积是30平⽅分⽶,D是BC的中点,AE的长是ED的2倍。
那么?BED的⾯积是多少平⽅分⽶?2、如图,三⾓形ABC的⾯积是240平⽅厘⽶,D是BC的中点,AD的长是AE的3倍,EF的长BF的3倍,那么三⾓形AEF的⾯积是多少平⽅厘⽶?3、如图,三⾓形ABC中,D、E为两个三等分点,F是AB的中点,若三⾓形DEF的⾯积是12平⽅厘⽶,那么四边形AFEC的⾯积为多少平⽅厘⽶?4、如图,BD=3AD, CE=4AE,三⾓形ADE的⾯积是2平⽅厘⽶,求三⾓形ABC的⾯积?5、如图,在△ABC中,BD=2DC,AE=BE,已知△BDE的⾯积为6平⽅厘⽶,求四边形ACDE 的⾯积。
6、将三⾓形ABC的BA延长1倍到D,CB边延长2倍到E,AC边延长3倍到F。
若三⾓形ABC的⾯积是1平⽅厘⽶,求三⾓形DEF的⾯积?7、如图,三⾓形ABC是正三⾓形,D、E分别是AB、BC的中点,已知三⾓形BDE的⾯积是6平⽅厘⽶,求三⾓形ABC的⾯积。
8、已知三⾓形ABC的⾯积为180平⽅厘⽶,D、E把三⾓形分成两部分,BD=3AD,CE=2AE,求三⾓形ADE的⾯积。
9、如图,在平⾏四边形BCEF中,有⼀个直⾓△ABC,BC=8厘⽶,AC=7厘⽶,阴影部分⾯积⽐△ADH⼤12平⽅厘⽶,求AH的长度。
10、如图所⽰,已知⼀个四边形的两条边的长度和三个⾓,求这个四边形的⾯积是多少?11、如图,边长为20厘⽶和30厘⽶的两个正⽅形拼在⼀起,求阴影△ABC的⾯积。
●家庭作业●1、如图,在三⾓形ABC中,CD=2BD,CE=3AE,阴影部分的⾯积是20平⽅厘⽶,求三⾓形ABD与三⾓形EDC⾯积之和是多少平⽅厘⽶?2、如图,在三⾓形ABC中,D是BC的中点,E、F是AC的三等分点。
(完整版)四年级奥数周长与面积

本组+1 对组+2
对组-1
本组+3
扭屁股1下
对组+2
如下图,里面正方形的周长是16厘米,并且外面长方形的各边分别平 行于正方形的四条边,那么外面长方形的周长是多少厘米?
如下图,正方形ABCD的边长是6厘米,过正方形内的任意两点画直线, 可把正方形分成9个小长方形。这9个小长方形的周长之和是多少厘米?
本组+3
对组-2
本组-1
个人+3
对组+5
对自己说加油
一个打谷场宽45米,长60米,扩建后长增加了15米,宽增加了8 米,这个打谷场的面积增加了多少平方米?
一个长方形操场,长80米,宽60米,扩建后长增加20米, 宽增加15米,这个操场的面积增加了多少?
本组-1
对自己说我是最棒 的
对组+2
对组-2
四个周长为17厘米的长方形拼成一个大长方形,如右图所示, 求大长方形的周长。
唱首歌吧
个人+5
对组-2
表扬表扬自己
对组+2
对组+5
下图中的阴影部分FGCB是正方形,线段FH长18厘米, AC长24厘米, 则长方形ADHE的周长是多少厘米?
有一条长24分米的铁丝,用它围成一个长方形,如果这个长方形的宽 是5分米,这个长方形的面积是多少平方分米?
一块正方形的苗圃(如右图实线所示),若将它的边 长各增加30米(如图虚线所示),则面积增加9900平 方米,问原来这块正方形苗圃的面积是多少平方米?
如图,有一大一小两个重叠的正方形,其正方形 边长分别为6厘米和3厘米,两块没有重合的阴影 部分面积相差多少平方厘米?
对组+5
本组+3
小学数学奥数题周长、面积

例题2:一个底面半径是10厘米的圆柱形瓶中,水深8厘米,要在瓶中放入长和宽都是8厘米、高是15厘米的一块铁块,把铁块竖放在水中,水面上升几厘米?
在瓶中放铁块要考虑铁块是全部沉入水中,还是部分沉入水中。如果铁块是全部沉入水中,排开水的体积是8×8×15=960(立方厘米)。而现在瓶中水深是8厘米,要淹没15厘米高的铁块,水面就要上升15—8=7(厘米),需要排开水的体积是(3.14×10×10—8×8)×7=1750(立方厘米),可知铁块是部分在水中。
专题简析: 在组合图形中,三角形的面积出现的机会很多,解题时我们还可以记住下面三点: 1,两个三角形等底、等高,其面积相等; 2,两个三角形底相等,高成倍数关系,面积也成倍数关系; 3,两个三角形高相等,底成倍数关系,面积也成倍数关系。
例题2 下图中,边长为10和15的两个正方体并放在一起,求三角形ABC(阴影部分)的面积。
分析:
1,因为三角形ABD与三角形ACD等底等高,所以面积相等。因此,三角形ABO的面积和三角形DOC的面积相等,也是6平方厘米。
2,因为三角形BOC的面积是三角形DOC面积的2倍,所以BO的长度是OD的2倍,即三角形ABO的面积也是三角形AOD的2倍。所以,三角形AOD的面积是6÷2=3平方厘米。
03
例题1 : 下图是一个楼梯的侧面图,求此图 形的周长。
例题2 :下图是由6个边长2厘米的正方形拼成的,这个图形的周长是多少厘米?
分析:这题我们可以用平移的方法将它转化 为一个长方形,如下图:
例题3 : 两个大小相同的正方形拼成一个 长方形后,周长比原来两个正方形周长的和减 少了6厘米。原来一个正方形的周长是多少厘?
第三节 体积
777777小学奥数专题之图形的周长与面积( 七)

小学奥数专题之—————组合图形一、平移与转化空白部分的短边长2cm,求阴影部分面积?求图形周长是多少?求阴影部分面积?两个完全一样的三角形重叠在一起,求阴影面积?四边形为正方形,M,N为中点,求阴影面积?求阴影的面积(单位;厘米)求阴影面积(单位;厘米)小圆半径为1cm,花瓣图形的周长和面积是多少?正方形的边长为4cm,求阴影的面积?求梯形的面积?正方形的边长为4cm,求阴影面积?正方形的边长为4cm,求阴影周长和面积?正方形的边长为4cm,求阴影面积?正方形的边长为4cm,求阴影面积?正方形的边长为4cm,求阴影面积?三个圆的半径相等都是2cm,求阴影的面积?正方形的面积是16平方厘米求阴影面积?求阴影的面积?(单位;厘米)下图中圆的半径是4厘米,O是圆心,AB和正方形的边长为4cm,求阴影部分周长和面积?DC互相垂直,OE=1厘米,EF=2厘米,那么图中阴影部分的面积是多少平方厘米?求阴影部分面积?平行四边形面积是24 平方厘米,求阴影部分面积?求阴影部分面积?圆的半径是6厘米,求图中的阴影面积。
大小正方形的边长分别为5cm,4cm 长方形的面积与圆的面积相等,已知圆的半径为3cm,求阴影部分面积?求阴影部分面积?求阴影面积?(单位;厘米)三角形ABC和三角形都是等腰直角三角形,阴影部分是正方形。
三角形ABC与三角形DEC的面积比是多少?梯形的面积是54平方厘米,求图中阴影部分的面积?圆的直径是16cm,求阴影部分的面积?阴影部分为正方形,求大长方形的周长?图中两个正方形的边长都为4厘米,求阴影部分面积?求阴影部分面积?图中三角形为等腰直角三角形,求阴影部分面积?求阴影部分面积? 求阴影部分面积? 重叠类如下图,两个41圆扇形AOB 与A ′O ′B ′重叠放在一起,其中POQO ′的面积是5平方厘米的正方形,那么阴影部分的面积是多少?大圆半径为4cm ,小圆半径为2cm ,求大圆白色部分比小圆白色部分面积多多少平方厘米如图平行四边形的长边是6cm ,短边 有红黄绿三块大小相同的正方形纸片,放在一个底为正方形 是3cm ,长边上的高是2.6cm ,求阴 的盒子内,他们相互重叠,在露出部分的中红色面积是,黄色 影部分的面积? 面积是17,绿色面积是7,求正方形盒子底的面积?ABCD 是边长为a 的正方形, 每个小圆的半径都是2cm ,求阴影部分面积?利用割补法求阴影的面积(单位;厘米)小圆半径为2 小圆半径为3加减法求下面阴影面积(单位:厘米)6旋转法求下列各图阴影部分面积(单位厘米)梯形上底为3厘米,下底是5厘米,高是4厘米,E是DC的中点,求阴影部分的面积是多少?一个等腰三角形的斜边长6厘米,求它的面积?一个正方形的对角线长5厘米,求这个正方形的面积?一个三角形的斜边长是10厘米,两直角边的差是3厘米,求这个直角三角形的面积?一个直角三角形的斜边长是15厘米,两直角边的差是4厘米,求这个直角三角形的面积?小正方形的边长是3厘米,大正方形的边长是5厘米,求阴影部分的面积是多少?四边形的对角线,将四边形分成四个小三角形,已知其中的三个三角形的面积分别是15平方米,75平方米,65平方米,求阴影部分的面积?一个长方形被两条直线分成四个长方形,其中三个的面积是20平方米,25平方米,30平方米,另一个长方形的面积是多少平方米?一个长方形被四条直线分成九个长方形,其中五个的面积分别是1,2,3,4,5平方厘米,求阴影部分的面积是多少平方厘米?图形内所标数据分别为各长方形的面积,那么大长方形的面积是多少?在梯形ABCD中,两条对角线相交于O,下底是上底的3倍,三角形AOD的面积是12平方厘米,那么梯形的面积是多少平方厘米?已知梯形中两个小三角形的面积分别为3平方厘米,9平方厘米,求梯形ABCD的面积?在梯形ABCD中,三角形CDE的面积为20,AE:CD=2:5,求梯形ABCD的面积?在梯形ABCD中,三角形ACE的面积为60,AB:CD=1:3,求梯形ABCD的面积?在正方形中方了三个同样大的小正方形,已知绿色部分的面积是20,蓝色部分的面积是14,红色部分的面积是10,求大正方形的面积?如图数据为各三角形部分的面积,求阴影部分的面积。
(完整版)四年级奥数专题图形周长与面积
第一讲图形周长和面积知识导航的同学,我已学会方形、正方形的周与面的算,利用公式很简单算出它的面与周。
但在碰到一些复的相关方形和正方形的周和面算,一些同学就会感觉棘手。
一我将学用平移、化、分解、归并等技巧解决,使大家在解中能利地找到打破口,化易,化繁。
精典例题例1:下列图是由16个相同大小的正方形构成的,假如这个图形的面积是400 平方厘米,那么它的周长是多少厘米?思路点拨每个正方形的面: 400÷ 16=25( 平方厘米 ) ,因此每个正方形的是 5 厘米。
从上下方素来看有 14 条是周的一部分,从左右方素来看有20条是周的一部分,因此⋯⋯模拟练习计算右边图形的周长 ( 单位:厘米 ) 。
例2:有9个小长方形,它们的长和宽分别相等,用这9 个小长方形拼成的大长方形( 如图 )的面积是 45 平方厘米,求这个大长方形的周长。
思路点拨从上能够知道,小方形的的 4 倍等于的 5 倍,因此是的 5÷ 4=1.25 倍。
每个小方形的面45÷ 9=5 平方厘米,因此 1.25 × ×=5,因此 2 厘米, 2.5 厘米。
模拟练习下列图的长方形被切割成 5 个正方形,已知原长方形的面积为120平方厘米,求原长方形的长与宽。
例3:一块正方形的苗圃(如右图实线所示),若将它的边长各增添 30 米,则面积增添 9900 平方米,问本来这块正方形苗圃的面积是多少平方米?思路点拨通画能够算出:小正方形的面:30×30=900 平方米。
用增添的面减去小正方形的面就获得增添的两个方形的面之和,1 / 49900-900=9000 平方米。
而增添的两个长方形的面积相等,于是此中一个长方形的面积为 9000÷ 2=4500 平方米。
模拟练习喜阳阳小学的操场长 90 米,宽 45 米。
改造后,长增添 10 米,宽增添 5 米。
此刻操场面积比本来增添了多少平方分米?例4:以下列图,用标号为1,2,3,4,5的五种大小不一样的正方形拼成一个大长方形,大长方形的长和宽分别是18,14,则标号为 5 的正方形的面积是多少?( 2006 年“希望杯”第二试)思路点拨假如标号为 5 的正方形的边21长是 a,那么 1号比 2 号大 a,2号比 3 号大 a,因此 1 号比 3号大 2a,又由于 2 号和 3 号的边5长之和是 14,1 号和2 号的边长之和是 18,所34以 1 号比 3 号大 18-14=4 。
小学奥数:第18讲四年级数学图形的周长和面积教案 ;;
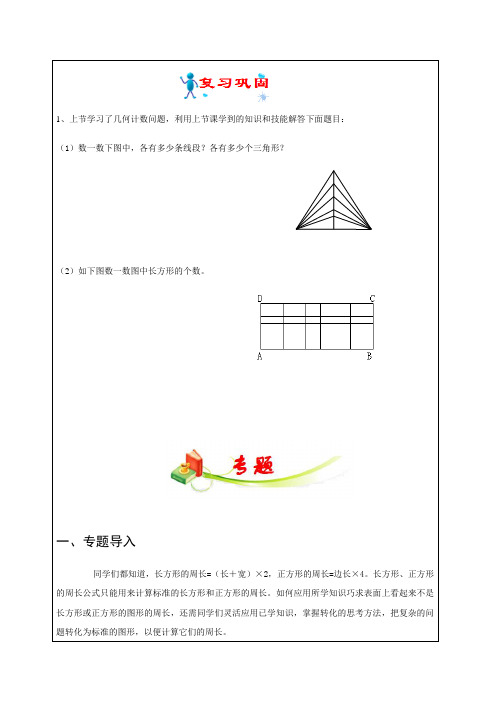
1、上节学习了几何计数问题,利用上节课学到的知识和技能解答下面题目:(1)数一数下图中,各有多少条线段?各有多少个三角形?(2)如下图数一数图中长方形的个数。
一、专题导入同学们都知道,长方形的周长=(长+宽)×2,正方形的周长=边长×4。
长方形、正方形的周长公式只能用来计算标准的长方形和正方形的周长。
如何应用所学知识巧求表面上看起来不是长方形或正方形的图形的周长,还需同学们灵活应用已学知识,掌握转化的思考方法,把复杂的问题转化为标准的图形,以便计算它们的周长。
二、专题精讲【例1】有5张同样大小的纸如下图(a)重叠着,每张纸都是边长6厘米的正方形,重叠的部分为边长的一半,求重叠后图形的周长。
分析解答:根据题意,我们可以把每个正方形的边长的一半同时向左、右、上、下平移(如图b),转化成一个大正方形,这个大正方形的周长和原来5个小正方形重叠后的图形的周长相等。
因此,所求周长是18×4=72厘米。
【例2 】一块长方形木板,沿着它的长度不同的两条边各截去4厘米,截掉的面积为192平方厘米。
现在这块木板的周长是多少厘米?分析解答:思路导航把截掉的192平方厘米分成A、B、C三块(如图),其中AB的面积是192-4×4=176(平方厘米)。
把A和B移到一起拼成一个宽4厘米的长方形,而此长方形的长就是这块木板剩下部分的周长的一半。
176÷4=44(厘米),现在这块木板的周长是44×2=88(厘米)。
【例3 】已知下图中,甲是正方形,乙是长方形,整个图形的周长是多少?分析解答:从图中可以看出,整个图形的周长由六条线段围成,其中三条横着,三条竖着。
三条横着的线段和是(a+b)×2,三条竖着的线段和是b×2。
所以,整个图形的周长是(a+b)×2+b×2,即2a+4b。
【例4 】下图是边长为4厘米的正方形,求正方形中阴影部分的周长。
小学四年级奥数专题 图形周长和面积

精心整理页脚内容第一讲图形周长和面积知识导航亲爱的同学们,我们已经学会长方形、正方形的周长与面积的计算,利用公式很容易算出它们的面积与周长。
但在遇到一些较复杂的有关长方形和正方形的周长和面积计算时,一些同学就会感到棘手。
这一讲我们将学习用平移、例例求这个大长思路点拨从图上可以知道,小长方形的长的4倍等于宽的5倍,所以长是宽的5÷4=1.25倍。
每个小长方形的面积为45÷9=5平方厘米,所以1.25×宽×宽=5,所以宽为2厘米,长为2.5厘米。
页脚内容模仿练习下图的长方形被分割成5个正方形,已知原长方形的面积为120平方厘米,求原长方形的长与宽。
例3:一块正方形的苗圃(如右图实线所示),若将它的边长各增加30米,则面积增加9900平方米,问原来这块正方形苗圃例少?31号和2号的边长之和是18,所以1号比3号大18-14=4。
模仿练习小孙同学用编号为1,2,3,4,5的大小不同的正方形拼出一个长方形,如右图所示,则中间阴影部分正方形的周长是多少厘米?(希望杯培训试题)页脚内容学以致用A 级1.求图1和图2两个图形的周长。
(单位:厘米)2.如下图是两个正方形,边长分别是8厘米和4厘米,那么阴影部分的面积是多少?3.如图是由5个相同的小长方形拼成的大长方形,大长方形的周长是44厘米,求大长方形的面积。
4.5.20 6.7.分米?8.9.图1110.有一大一小两块正方形试验田,他们的周长相差40米,面积相差220平方米,那么小正方形试验田的面积是多少平方米?图b。
四年级奥数几何问题:巧求周长【三篇】

四年级奥数几何问题:巧求周长【三篇】
导读:本文四年级奥数几何问题:巧求周长【三篇】,仅供参考,如果觉得很不错,欢迎点评和分享。
【第一篇】下图中是一个方形螺线.已知两相邻平行线之间的距离均为l厘米,求螺线的总长度.
【第二篇】有10张长3厘米,宽2厘米的纸片,将它们按照下图的样子摆放在桌面上,那么这10张纸片所盖住的桌面的面积是多少平方厘米?
每多盖一张,遮住的面积增加2×1,所以这10张纸片所盖住的桌面的面积是3×2+2×1×9=24cm2.
【第三篇】有红、黄、绿三块大小一样的正方形纸片,放在一个正方形盒内,它们之间相互叠合(如右图),已知露在外面部分中,红色面积是20,黄色面积是12,绿色面积是8,那么正方形盒的底面积是多少?
黄色纸片露出部分与绿色纸片露出部分面积不同,把黄色纸片向左移动,在这个移动过程中,黄色纸片露出部分减少的面积等于绿色纸片纸片露出部分增加的面积,它们露出的面积和不变,所以图2中黄色露出部分面积为10,绿色面积也为10。
红、黄、绿三个长方形的面积已经求出,因为长方形中对角的面积乘积相等,故有:黄×绿=红×白。
空白长方形的面积应为10×10÷20=5,纸盒的底面
积为20+10+10+5=45。
解答此题的关键是让黄色正方形纸片移动,使复杂的图形变为基本图形。
精品四年级奥数a第十四章 周长与面积

解:
4分米=40厘米 15×(40÷2—15) =15×5 =75(平方厘米)
答:这个长方形的面积是75平方厘米。
(4a) 第十四章 周长与面积
【热身演练 】
1、 一位农民伯伯用30米长的篱笆围成一块 长方形的菜地,其中一边利用了一面9米 长的墙壁(如图),求菜地的面积?
墙壁
×
×
×
菜
地
×
×
×
××××××××××××××××××××
答:有两种不同的拼法,周长分别是42厘米和30厘米, 面积都是54平方厘米。
仔细观察:六个小正方形拼成一个大长方形有两种 不同的方法,算出来的周长不相同分别是42厘米和30厘 米,但是算出来的面积却相同都是54平方厘米。
(4a) 第十四章 周长与面积
【热身演练 】
3、 将10个边长为4厘米的小正方形拼成一个大长方 形,怎么拼?画下来。并求出拼成后大长方形的周 长、面积分别是多少?
金杯数学(4a)
第十四章 周长与面积
(4a) 第十四章 周长与天面积津科学技术出版社
桌子 有多大?
单车骑一圈 能走多远?
卧室 有多大?
绕操场跑一圈 是多少米?
(4a) 第十四章 周长与面积
同学们, 今天我们就一起来
学习周长和面积 的计算。
(4a) 第十四章 周长与面积
【知识领航】
围绕封闭图形一周的长度叫周长,计算周长用长度单位,常用的单位 有千米、米、分米、厘米和毫米。
(4a) 第十四章 周长与面积
【技巧感悟 】
列表如下:
长(厘米)
11
10
9
8
7
6
宽(厘米)ຫໍສະໝຸດ 1234
四年级《巧求面积》奥数课件

2厘米
一个长方形,如果宽不变,长增加2厘米,那么 它的面积增加10平方厘米;如果长不变,宽减少3厘 米,那么它的面积减少18平方厘米。这个长方形原来 的面积是多少平方厘米?
原来的宽:
3
10 ÷ 2= 5(厘米)
厘
原来的长:
米
18 ÷ 3= 6(厘米)
原来的面积:
5 × 6 = 30(平方厘米)
答:这个长方形原来的面积是30平方厘米。
游泳池的面积:
50 × 25 = 1250(平方米)
50
白瓷地砖的面积:
25
2 方法一:
2
2×50×2 + 2×(2+25+2)×2
= 316(平方米)
下图为一个长50米,宽25米的标准游泳池。它 的四周铺设了宽2米的白瓷砖(阴影部分)。求游泳 池面积和白瓷地砖面积各是多少?
游泳池的面积:
50 × 25 = 1250(平方米)
一个正方形的周长是80分米,它的面积是多少平方分米?
正方形的边长: 80 ÷ 4 = 20(分米) 正方形的面积: 20 × 20 = 400(平方分米) 答:它的面积是400平方分米。
学校操场原来是一个长50米,宽40米的长方形,扩
建后,长和宽各增加了30米,现在长方形操场的面积是
多少平方米?
长方形的周长 =(长+宽)× 2 长+宽 = 长方形的周长 ÷ 2
= 22 ÷ 2 = 11
一个长方形的周长是22厘米,如果它的长和宽 都是整数厘米,那么这个长方形的面积(单位:平 方厘米)有多少种可能值?最大、最小各是多少?
①长10厘米,宽1厘米, 面积是10×1=10平方厘米; ②长9厘米,宽2厘米, 面积是9×2=18平方厘米; ③长8厘米,宽3厘米, 面积是8×3=24平方厘米; ④长7厘米,宽4厘米, 面积是7×4=28平方厘米; ⑤长6厘米,宽5厘米, 面积是6×5=30平方厘米;
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一讲图形周长和面积
知识导航
亲爱的同学们,我们已经学会长方形、正方形的周长与面积的计算,利用公式很容易算出它们的面积与周长。
但在遇到一些较复杂的有关长方形和正方形的周长和面积计算时,一些同学就会感到棘手。
这一讲我们将学习用平移、转化、分解、合并等技巧解决难题,使大家在解题中能顺利地找到突破口,化难为易,化繁为简。
精典例题
例1:下图是由16个同样大小的正方形组成的,如果这个图形的面积是
400平方厘米,那么它的周长是多少厘米
思路点拨
每个正方形的面积为:400÷16=25(平方厘米),所以每个正方形的边长
是5厘米。
从上下方向来看有14条边是周长的一部分,从左右方向来看有
20条边是周长的一部分,所以……
模仿练习
计算右面图形的周长(单位:厘米)。
例2:有9个小长方形,它们的长和宽分别
相等,用这9个小长方形拼成的大长方形(如图)
的面积是45平方厘米,求这个大长方形的周长。
思路点拨
从图上可以知道,小长方形的长的4倍等于宽的5倍,所以长是
宽的5÷4=倍。
每个小长方形的面积为45÷9=5平方厘米,所以×宽×宽=5,所以
宽为2厘米,长为厘米。
模仿练习
下图的长方形被分割成5个正方形,已知原长方形的面积为120平方
厘米,求原长方形的长与宽。
例3:一块正方形的苗圃(如右图实线所示),若将它
的边长各增加30米,则面积增加9900平方米,问原来这块
正方形苗圃的面积是多少平方米
思路点拨
通过画图可以算出:小正方形的面积为:30×
30=900平方米。
用增加的面积减去小正方形的面积
就得到增加的两个长方形的面积之和,
9900-900=9000平方米。
而增加的两个长方形的面积相等,于是其中一个长方形的
面积为9000÷2=4500平方米。
模仿练习
喜阳阳小学的操场长90米,宽45米。
改造后,长增加10米,宽增加5米。
现在操场面积比原来增加了多少平方分米
例4:如下图,用标号为1,2,3,4,5的五种大小不同的正方形拼成一
个大长方形,大长方形的长和宽分别是18,14,则标号为5的正方形的面
积是多少(2006年“希望杯”第二试)
思路点拨
如果标号为5的正方形的边长是a,那么1
号比2号大a,2号比3号大a,所以1号比3
号大2a,又因为2号和3号的边长之和是14,
1号和2号的边长之和是18,所以1号比3号
大18-14=4。
模仿练习
小孙同学用编号为1,2,3,4,5的大小不同的正方形拼出一个长方
形,如右图所示,则中间阴影部分正方形的周长是多少厘米(希望杯培训试题)学以致用
A级
1.求图1和图2两个图形的周长。
(单
位:厘米)
2.如下图是两
个正方形,边长分别是8厘米和4厘米,那么阴影部分的面积是多少
5
2
4
4
4
3
1
22厘米
30厘米
4
4
5
3
3
2
2
1
1
3.如图是由5个相同的小长方形拼成的大长方形,大长方形的周长是44厘
米,求大长方形的面积。
4.一个正方形,相邻的两个边长增加4厘米,面积就增加
96平方厘米,求原来正方形的面积
5.一个长方形,宽增加4厘米,则面积增加24平方厘米;若长增加4厘米,则面
积增加
20平方厘米。
若长和宽都增加了4厘米,则面积增加多少平方厘米周长增加多少厘米
6.有一大一小两个正方形,它们的周长相差200厘米,面积相差5500平方
厘米,求小正方形的面积是多少平方厘米
B级
7.如下图所示,在一个正方形上先截去宽11分米的长方形,再截去宽
7分米的长方形,所得图形的面积比原正方形减少301平方分米。
原正方
形的边长是多少分米(希望杯培训题)
8.右图中正方形的边长为3厘米,每边被3
等分,求图中所有正方形周长的和。
9.图11中“风车”(阴影部分)的
面积等于多少平方厘米(2009年希望杯四年级1试)
C级
10.有一大一小两块正方形试验田,他们的周长相差40米,面积相差220平方米,那么小正方形试验田的面积是多少平方米
图a
图b。
