第2章 当代给水与废水处理原理.ch02
【2019年整理】当代给水与废水处理原理

绪论
1. 水源、水处理与用水——三位一体
二、
给 水 与 废 水 处 理
20世纪50年代以前,给水处理与废水处理涵义的 划分是很清楚的。
给水处理:从天然水源取水,为供生活或工业的 使用(特别是生活使用)而进行的处理,称为给水处理。
废水处理:为了排除的目的,对于使用过的水所进 行的处理,称为废水处理。
绪论
(1)悬浮培养体:以活性污泥法为典型代表,它的特 征是起水处理作用的细菌培养体处于悬浮状态的絮体;
(2)生物膜法以滴滤池为典型代表,它的特征是起水 处理作用的细菌培养体呈一层膜固定在填料表面上。
20世纪60年代以后, 为了满足废水再用的水质要求或排放的标 准,出现了对于常规废水处理后的出水进一步处理的过程,称为废 水的高级处理
单元操作往往带有物理变化,但也有不产生物理变化的单元操作, 如:食盐的生产过程。
一、 食盐的生产过程只包括下列几种单元操作:
水
处
理 的
固 体 和
学 送液
科 方
体 的 输
热传
蒸
结
发
晶
干 燥 及 筛 选
法
学
一、
2.水处理中单元操作与单元过程
水
处
理
的 学
合混
沉 淀
浮 升
浓过 缩滤
单 元 操
科
作
方
法
属
于
当代给水与废水处理原理
高良敏 博士、教授 安徽理工大学地球与环境学院
绪论
1.单元操作与单元过程
一、 水 处 理 的 学 科 方 法 学
20世纪50年代起,引用了化学工程中单元操作(unit operation )及单元过程(unit process)的概念,目的是为了 建立各种水处理方法间的理论联系,提高学科的理论水平
当代给水与废水处理

1 x K f e n ★Freundlich公式为: m
• 改性活性炭(表面官能团性质及数量发生变化) 以去除 有机污染物为目的的改性方向应为:减少表面内酯基及羧 基等含氧官能团的含量,增加活性炭表面的疏水性。 • 活性炭工艺与其它手段的结合 活性炭起的是辅助性的作用,主体是生物法、催化剂的应 用等。活性炭与膜联用能解决单独使用膜过滤引起的膜阻 塞和膜污染问题。利用活性炭对进水进行必要的前处理, 以减少水中的有机物、无机物、微生物等在膜表面和膜内 孔积累,极大延长了膜的使用寿命;而膜的存在又可以克 服单独使用活性炭出水中细菌数偏高的问题。
2.混凝现象的四种机理 • 压缩双电层作用 向溶液中投入电解质,离子浓度增高,扩散层的厚度将 减小,ζ 电位降低,胶粒得以迅速凝聚。 • 吸附和电荷中和作用 胶粒表面对带异号电荷有强烈的吸附作用,中和了它的 部分电荷,减少了静电斥力,易与其他颗粒接近而互相 吸附。
•
吸附架桥作用 高分子物质与胶粒相互吸附,而使胶粒凝聚为大的絮凝 体。 • 沉淀物网捕作用 混凝剂金属盐投加量大,迅速形成金属沉淀物,水中的 胶粒可被这些沉淀物网捕。
当代给水与废水处理原理
第三章 活性炭吸附 第四章 传质及曝气
• 气一液传质模型
• 凝聚与絮凝 沉淀试验 • 膜分离
3-1 活性炭的性能 3-3 Langmuir公式的推导 3-5 吸附柱的设计
3-2 吸附等温线 3-4 吸附公式的应用
曝气设备的充氧能力
第五章 常规分离过程与膜分离
浓缩池 滤床过滤
1
活性炭吸附
2
凝聚与絮凝
3
膜分离
一、活性炭吸附
1.活性炭是一种多孔碳,堆积密度低,炭粒中有更细小 的孔——毛细管,比表面积大,能与气体(杂质)充分 接触,具有很强的吸附能力,起净化作用。 2.活性炭的制造 活性炭的制作分碳化及活化两步。 •碳化也称热解,是在隔绝空气的条件下对原材料加热, 一般温度在600℃以下。 •活化是在有氧化剂的作用下,对碳化后的材料加热。
当代给水与废水处理原理 读书报告
当代给水废水处理原理第一章化学反应动力学化学动力学定义,从动态的角度研究化学反应产生、发展及消亡全过程。
化学动力学具体内容(1)比较化学反应的快慢及外部因素的影响;(2)揭示化学历程,即反应物按何种途径转化为最终产物;(3)呈现物质结构与反应性能之间的关系。
化学动力学研究层次(1)唯象动力学:研究总反应的速率及影响因素,“唯象”,即: 只以化反的宏观现象为依据。
(2)基元反应动力学:关于基反的动力学规律与理论,并探讨总反应的动力学行为。
(3)分子反应动态学:从分子、原子的量力角度研究分子间一次具体碰撞行为。
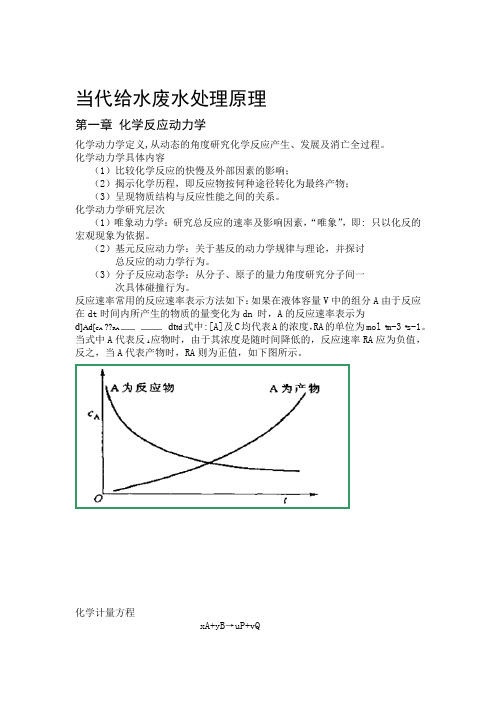
反应速率常用的反应速率表示方法如下:如果在液体容量V中的组分A由于反应在dt时间内所产生的物质的量变化为dn 时,A的反应速率表示为d]Ad[CA RA dt t d式中:[A]及C均代表A的浓度,RA的单位为mol·m-3·s-1。
当式中A代表反A应物时,由于其浓度是随时间降低的,反应速率RA应为负值,反之,当A代表产物时,RA则为正值,如下图所示。
化学计量方程xA+yB→uP+vQ这个方程式主要是表示一个质量守恒的关系,只是说明反应物A的x个分子与B的y个分子的质量与产物P的u个分子及Q的v个分子的质量相等,这种关系称为化学计量方程式。
令 N,N , N 和 N分别为相应物种在时刻t的物质的量,则Q??????d xxuvv i dζ称为反应进ABP?dn?dndndndn iAPQB度,为物种v的化学计量方程系数,反应物取负号,产物取i正号。
反应级数如果通过试验数据的数学处理,得出产物P的反应速率可以表示为:d[p]dc P=ab CKC r??P B A dtd t那末,产物P的反应称为:反应物A的a 级反应;反应物B的b级反应;总称为(a+b)级反应。
K称为反应的速率常数(rate constant).第二章反应器1.反应器设计影响因素:反应器的设计涉及了流体力学、传热、传质、化学动力学的知识2.反应器的类型按反应特点分为:均相反应器与多相反应器按运行方式分为:间歇式反应器与连续流式反应器3、反应器设计面临的新课题反应器体系的设计:如何传热、传质的问题;反应动力学研究;反应器参数优化,反应机理的研究。
现代水处理原理与技术(1、2章)

Monod方程
max
Cs K s Cs
(1) 当限制性基质浓度很低时,Cs<< Ks
此时,
max
Ks
Ks
Cs
rx
max
C sC x
max
(2) 当Cs>>Ks时,μ =μ 此时,
rx maxC x
(3) 当Cs处于两种情况之间时,
rx
max C s
K s Cs
碳源--异氧型微生物利用有机碳源,自氧菌利用无机碳源。 氮源--无机氮(NH3及NH4+)和有机氮(尿素,氨基酸,蛋白质等)。 补充氮,磷,钾 : 与生活污水混合 添加药剂:硫酸铵,硝酸铵,尿素(补充氮源); 磷酸钠、磷酸钾等 (补充磷源)
1.2 微生物的生长规律和生长环境
二、微生物的生长环境
1、较高的催化效率 2、有很强的专一性 3、具有温和的反应条件 4、酶易变性与失活
三、底物浓度对酶反应速度的影响
一切生化反应都是在酶催化下进行的。这种反应宜可以说是一种酶促 反应或酶反应。酶促反应速度受酶浓度、底物浓度、pH值、温度、反应产 物、活化剂和抑制剂等因素的影响。 中间产物学说
式中,S代表底物,E代表酶, ES代表酶-底物中间产物,P代 表产物。
五、Km与Vmax的意义及测定
Km与Vmax的测定
1.4 微生物生长动力学
一、细胞反应速率的定义
二、莫诺特( Monod )方程
三、微生物生长与底物降解的基本关系式
一、细胞反应速率的定义
微生物比增长速率μ 的提出
当微生物生长不受外界条件限制(对数增长期)时,
μ 表示每单位微生物的增长速度
一、细胞反应速率的定义
【2018-2019】当代给水与废水处理,读书报告-精选word文档 (10页)

本文部分内容来自网络整理,本司不为其真实性负责,如有异议或侵权请及时联系,本司将立即删除!== 本文为word格式,下载后可方便编辑和修改! ==当代给水与废水处理,读书报告篇一:当代给水与废水处理原理课后习题答案许保玖篇二:水处理吸附理论与技术简析活性炭吸附技术在水处理方面应用摘要: 现代工业的迅猛发展给环境带来的污染日益严重,尤为严重的是水体污染,已经引起了全世界的普遍关注。
同时,随着人们生活水平的不断提高和环保意识的不断增强,使得人们对引用水水质的要求愈来愈严格。
活性炭是最常用的优良的吸附剂,深刻了解活性炭的特性,正确选择活性炭,充分发挥其在水处理的作用,达到深度处理的效果,成为近来研究的重点。
本文概述活性炭的特性及其吸附机理,介绍活性炭吸附技术及其组合工艺在国内外水处理中的应用和发展,总结它在应用中的优缺点并预测其前景和发展方向。
关键词: 活性炭、吸附、水处理、组合工艺引言传统的饮用水处理主要通过絮凝、沉淀、过滤和加氯消毒来去除水中的悬浮物和细菌,而对各种溶解性化学物质的脱除作用很低。
吸附法是采用多孔性的固体吸附剂,利用同一液相界面上的物质传递,使废水中的污染物转移到固体吸附剂上,从而使之从废水中分离去除的方法。
具有吸附能力的多孔固体物质称为吸附剂。
根据吸附剂表面吸附力的不同,可分为物理吸附、化学吸附和离子交换性吸附。
在废水处理中所发生的吸附过程往往是几种吸附作用的综合表现。
废水中常用的吸附剂有活性炭、磺化煤、沸石等。
1. 活性炭的特性及其吸附机理1.1活性炭的特性1活性炭是一种由煤、沥青、石油焦、果壳等含碳原料制成的外观呈黑色的粉末状或颗粒状的无定形碳。
活性炭内部孔隙结构发达、比表面积大、吸附能力强。
普通活性炭的比表面积为500-1500m2。
超级活性炭比表面积则高达3500 m/g活性炭所含主要元素是碳,含量为90-95%。
氧和氢大部分是以化学键的形式与碳原子相结合形成有机官能团,氧含量4%-5%左右,氢含量一般是1%-2%。
给水与废水处理原理

I. 优点 ➢ BOD容积负荷高,处理效果好,效率高
处理生活污水,15min左右,效率可达93%,出水 BOD=< 15mg/L ➢ 占地少,投资省 ➢ 运行适当时可脱氮 II. 缺点 技术要求高,不易推广
2. 滴滤池法
1) 工作示意图
2) 生物膜 I. 分区
厚度:0.1-2 mm
好氧区:50-100 m
B. 流化床的特征
➢ 载体颗粒小,总表面积大(2000-3000m2/m3载 体)以MLSS计算的生物量高于任何一种生物 处理工艺
➢ 载体处于流化状态,污水频繁多次与生物膜 接触;载体颗粒小,密集,互相磨擦碰撞, 因此生物膜的活性较高,传质过程也得到了 强化。由于载体处于不停的运动中,可有效 地防止堵塞。
➢生物相分层显著 有利于微生物的增殖、代谢等生理活动
➢耐冲击负荷能力强 ➢占地少,对城市适用
8) 曝气生物滤池
特征 ➢ 气液充分接触,氧的转移率高,动力消耗低; ➢ 不需设置沉淀池,占地面积小 ➢ 滤料比表面积大,微生物附着力强 ➢ 处理效果好 ➢ 无需污泥回流,也无污泥膨胀之虑
9) 生物转盘
特征
➢ 微生物浓度高 ➢ 处理能力大,进水浓度高 ➢ 耐冲击负荷强 ➢ 生物相 ✓ 生物相分级 ✓ 污泥龄长 ✓ 食物链长,剩余污泥量少 ➢ 不需曝气,污泥不需回流,动力消耗小 ➢ 不发生污泥膨胀,易于维护管理 ➢ 流态
10) 生物接触氧化
特点 生物膜上微生物丰富,稳定的生态系统与食物链 过滤作用 活性生物量浓度较高 耐冲击负荷,在间歇运行条件下,能保持良好的处
1. 基本概念
1) 基本流程
2) 分类
生物滤池 生物转盘 生物接触氧化 生物流化床
污水处理过程及原理

污泥膨胀是由于污泥结构松散、体积增大、含水率上升而不能为脱水和压滤所困的污泥膨胀形状。
详细描述
污泥膨胀是污水处理过程中常见的问题之一,通常是由于丝状菌过度繁殖引起的。污泥膨胀会导致污 泥沉降性差,出水水质恶化。为了解决这一问题,可以采取添加药剂、改善曝气、调节pH值等措施。
泡沫问题
总结词
泡沫问题是指在污水处理过程中出现的泡沫状物质,影响水质和设备正常运行。
05 污水处理新技术与展望
活性污泥法改进技术
1 2
序批式反应器(SBR)
通过间歇反应,强化生物反应过程,提高处理效 率。
完全混合式反应器(CSTR)
通过连续混合,保持反应池内微生物浓度稳定。
3
悬浮生长反应器
利用悬浮生长微生物处理污水,具有高生物量、 高效率等优点。
生物膜法改进技术
移动床生物膜反应器(MBBR)
氧化还原
利用氧化剂或还原剂将污水中的有害物质转化为无害物质。
沉淀
通过化学反应使有害物质转化为沉淀物,再通过沉淀去除。
生物处理原理
01
02
03
好氧生物处理
利用好氧微生物的代谢作 用,将污水中的有机物转 化为无害物质。
厌氧生物处理
利用厌氧微生物的代谢作 用,将污水中的有机物转 化为甲烷和二氧化碳等气 体。
农业废水
来自农业生产活动,含 有农药、化肥等污染物
。
城市污水
综合了生活、工业和农 业废水,成分复杂,处
理难度较大。
污水处理的目标与原则
去除悬浮物和有机物
降低污水中的悬浮物和有机物含量,防止堵 塞和腐蚀。
营养物去除
控制氮、磷等营养物的排放,防止水体富营 养化。
当代给水与废水处理原理-PPT课件

如:循环冷却水中加缓蚀剂及缓垢剂以控制腐浊及结垢等; (3)改变水的物理性质的处理。如水的冷却,降低水的粘滞度等。
3.水处理的物理化学方法包括三种情形
(1)在处理过程中只发生物理变化; (2)在处理过程个只发生化学变化; (3)在处理过程中同时发生物理及化学变化。
(1)悬浮培养体:以活性污泥法为典型代表,它的特 征是起水处理作用的细菌培养体处于悬浮状态的絮体;
(2)生物膜法以滴滤池为典型代表,它的特征是起水 处理作用的细菌培养体呈一层膜固定在填料表面上。
20世纪60年代以后, 为了满足废水再用的水质要求或排放的标准, 出现了对于常规废水处理后的出水进一步处理的过程,称为废水的 高级处理
绪论
1. 水源、水处理与用水——三位一体
二、
给 水 与 废 水 处 理
20世纪50年代以前,给水处理与废水处理涵义的 划分是很清楚的。
给水处理:从天然水源取水,为供生活或工业的使 用(特别是生活使用)而进行的处理,称为给水处理。
废水处理:为了排除的目的,对于使用过的水所进 行的处理,称为废水处理。
2.水处理中单元操作与单元过程
水
处
理 的
化离 学子 消 脱
学 科
沉交 毒 氯 淀换
单 元 过 程
方
法
属
于
学
绪论
2.水处理中单元操作与单元过程
一、 水 处 理 的 学 科 方 法 学
水处理著作中,首先引入单元操作这一概念的,是1954年出版的 Fair与Geyer两人的《给水与废水处置》(Water Supply and Wastewater Disposal)一书。但把包含化学反应的单元过程也包括在单元操作这一概 念内。
污水处理原理第二讲PPT学习教案

(2)嗜温细菌:20-45度 (3)嗜热细菌:45-60度
2.2pH值
大多数细菌能承受的最小PH值范围是4.0-4.5,最大 为9.0-9.5,但最适宜的范围是6.6-7.8。 在细菌增殖过程中,需要及时排除细菌活动所产生的废物 ,以控制介质的PH值。
第5页/共23页
2.3氧
细菌生长是否需要分子态的氧,可以分为:
2.1 恒化器
当每秒钟增加的细菌个数与每秒钟排掉的细菌个数相
等时恒化器处于稳定状态。此时: f
x
Dx
V
其处于稳定状态的条件是:
D
maxC
KS C
恒化器的过程是自发调节的。
第20页/共23页
恒化器示意
第21页/共23页
稳态的营养物浓度C :
C
KS
max
D D
稳态的细菌克数 x :
x
Y Ci
KS D
3.稳定状态的保持
当代谢区消耗底物的速率与底物通过两
个运输区的速率相等时,得到一个稳定状态:
ad
D
dC dr
rd
ap
KP
pC' C'
Vm
mC ' '
Km C'
'
式中:ad为扩散区的外表面积,下表rd指浓度梯度
dC/dr计值的扩散区外径,ap为透酶区的外表面积,
当Vam底d为物代不D谢需dd区C透r容酶rd积区。的V运m 输K时mm,CC简' ' '化' 为
max D
产率因数Y随μ的变化而变化:
1m 1
Y YG
式中:m是维持系数,YG是真产率因数;上式 也可以表示为:
当代给水与废水处理原理

非极性的 链烷化合 物在活性 炭表面的
吸附。
有关极性 分子氨基 酸及蛋白 质的吸附 资料极少
活性炭对于 吸附无机物 也有一定的 潜力
活性炭的吸 附性能是由 于它的表面 基团类型、 比表面积和 孔径的分布 决定的。
第5页,共19页。
第三章 活性炭吸附
§3-2 吸附等温线
吸附 等温 线的 类型
第一种类型的等温线, 没e 有极限值,但 却x 有m 一极限
ka代表单位体积活性炭在单位时间内所吸收的杂质量。
活性炭的容量传质系数可以通过实验得出。 当这个系数已知后,就能够确定吸附柱所需要的活性炭总体积。但这需要知 道吸附柱的吸附容量、吸附柱的吸附过程曲线与容积传质系数三者间的关系。
第15页,共19页。
第三章 活性炭吸附
求活性炭的容量传质系数
活性炭的容量传质系数ka,一般通过用初始有机物浓度ρ1的水样,每 升加活性炭mg做吸附试验,由吸附试验可以得出下列物料衡算关系:
值 ,(这x m种)0类型的吸附试验资料可用Langmuir公式处 理。
第二类型的等温线, 有e 一个极限值 ,称s 为饱和浓
度,但x/m却没有极限值。这种类型的等温线可用 Branauer和Emmett及Teller(简称BET)公式处理。
第三类型的等温线, 和e x都m没有极限值,可用
Freundlich公式处理。
活化的定义
活化是在有氧化剂的作用下,对碳化后的材料加热,以生产活性炭产品。当氧化过程的 温度在800-900℃时,一般用蒸汽或二氧化碳为氧化剂;当氧化温度在600℃以下时,一 般用空气做氧化剂。
第2页,共19页。
第三章 活性炭吸附
碳
①使原材料分解放出水气、一氧化碳、二氧化碳及氢等
水污染控制原理与技术第二章PPT课件

• Ⅳ区(恢复区)——水质变得较清;溶解氧在40%饱 和度以上,出现硝酸盐;出现真菌、浮游动物,藻 类增加,苔藓植物出现,底栖生物中包括颤蚓、胎 贝等介壳类以及昆虫的幼虫,有一般鱼类。
• I和Ⅴ区(清洁区)——水质如一般天然河流;溶解 氧可高达饱和;物种增加,可发现观赏鱼类。
• 促使细菌在水体中死亡的原因有:
(1)有机污染的进入; (2)影响大气复氧的物质; (3)热污染。
其他影响水体生态平衡造成水体污染的因素: (1)有毒物; (2)酸碱物污染; (3)悬浮污染; (4)N.P营养性污染。
第二节 水体自净
一、水体的自净概念 指水体在流动中或随着时间的推移,水体中的污染物 自然降低的现象。 通过化学作用和生物作用对水体中有机物的氧化分 解,使污染物质浓度衰减,是水体自净的主要过程。 • 可以用两个相关的水质指标来描述水体的自净过程。 • 一个是生化需氧量BOD,该值越高说明有机物含量越 多,水体受污染程度越严重; • 另一个是水中溶解氧DO,它是维持水生物生态平衡和 有机物能够进行生化分解的条件。
• 被污染的水体都是自净水体! • 但自净恢复的程度不同,或称污染现状
不同。
衡量水体污染与自净的指标
水体外观、化学 指标、生物种类、 数量及比例关系、 溶解氧等等
山东小清河
水体外观
• 外观特征:混浊程度、颜色及气味等 • 原 因:水中细菌种类数量、悬浮物种类数量
污染前 污染 净化开始 持续 结束
(l)作为细菌食料的水体中有机物因氧化分解而逐渐减 少,这对于依靠有机物生存的细菌极为不利; (2)污染水体中有大量吞食细菌的生物,如纤毛类原 生动物、浮游动物等; (3)生物物理因素,如生物絮凝、沉淀等; (4)其它因素如pH、水温、日光等对细菌生活的影响 很大,pH和水温若不合适,细菌会逐渐死亡,日光也 具有杀菌能力。
当代给水与废水处理原理

十四烷酸(C14)
37
0.11
0.11
0.010 105
乙酸
35 0.34~0.05 0.04~0.05 0.015 165~250
丙酸
35
0.31
0.042
0.010 60
丁酸
35
0.37
0.047
0.027 13
§10-2 厌氧过程动力学
甲烷生成动力学 :
在厌氧处理中,COD减小的途径主要是生成甲烷和微生物 的细胞,其它途径有生成氢气、通过硫酸盐的还原生成硫化氢气 体等。
k0 6.67 10 0.015(35t)
§10-3 厌氧活性污泥法
传统消化池
Y YC
1 bc
K (1 bc ) YCk0c (1 bc )
X
YC
i 1
bc
Y (i
)
V Qc
Ru
X
Yc
d 0.935 0.3 X 0.298
k0 6.67 10 0.015(35t)
K 2224100.046(35t)
(GO )Tp
GO
T 273
•
1 p
1.28 102
T p
式中,T为厌氧反应器中的热力学温度;P为反应器室内的 气压(单位Pa)。
根据§7-4,每克干细菌完全氧化所需的单体氧为1.41g。利 用一个类似于需氧处理中氧的摄入率计算公式(见式(8-40)) 形式来计算厌氧处理的甲烷生成率:
G
G0
Tp
R 0 1
§10-4 厌氧生物膜法
在无回流的厌氧活性污泥法中,就不得不加大水力停留时间 来获得较长的污泥停留时间;
在有回流的厌氧活性污泥法中,虽然可通过回流来减短水力 停留时间并增大污泥停留时间。
当代给水与废水处理原理第二版

(10-1) (10-2)
(10-3)
因为氧化氢形成甲烷的细菌可以从二氧化碳 中获得碳源,所以这些细菌带有自养性,其生长 速率很慢,虽然它们与分解乙酸的细菌在厌氧反 应器中有共生关系,但其数量较少,在厌氧反应 过程中,生成的甲烷大部分来自乙酸的分解。图 10-2所示为Speece1983年发表的厌氧反应过程 中甲烷的主要生成途径及其以COD计所占的百分 数。
上述各种厌氧工艺和厌氧反应器,除传统消化池处 理污泥外,多数都处于试验研究阶段,虽然有些生产性 装置,但也是试验性的。表10-1所示为各类厌氧处理过 程的运行和试验参数。从表中可以看出,负荷都高于需 氧处理法,这是因为厌氧处理不受传氧限制的缘故。
§10-2 厌氧过程动力学 厌氧过程动力学涉及底物的降解、微生物
每克干细菌完全氧化所需的单位氧为1.41g。这 样,便可以利用一个类似于需氧处理中氧的摄入率计 算工式形式来计算厌氧处理的甲烷生成率:
G
G0
Tp
R0 11.41Y
1.28 10 2
TR0 p
(11.41Y )
(10-6)
式中,G为甲烷的产率,单位为L/d;R0为COD的减 少速率,单位为g/d;Y为产率因数,单位为g干细菌
/gCOD。
§10-3 厌氧活性污泥法 厌氧活性污泥法是厌氧微生物在反应器中处于
悬浮生长状态的生物处理方法。因此,厌氧活性污 泥法必须有维持微生物处于悬浮状态的设备或手段, 例如机械搅拌、水力搅拌、向反应器供压缩沼气或 氮气进行搅拌等等。同时,由于微生物处于悬浮状 态易于随出水流出反应器,必须特别注意采取能使 气、液、固三相良好分离的措施。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
§2-8 阶式CSTR
2. 二级反应的情况下
cn 1 1 4kc n 1 2k
1 2
(2-37)
3. 阶式CSTR的图解法
V c x c x1 Q rx c x1 rx (2-38) x
阶式CSTR的图解法
§2-9 停留时间函数
1. 基本概念 死角:指反应器中液体不流动或者说流动极为缓慢的区域。
短路流:也称跨越流,指进反应器的液流中,未经主体流动而流出反
应器的部分。 沟流:主要是从填料床中所发生的现象提出来的,指水直接通过在填
料床整体中,由于填料粘结后的局部收缩所形成的,或者在填料床与反应
器壁间所形成的裂缝中的水流,这种水流通过反应器的时间大大短于正常 的通过时间,而且由于未与填料得到正常的接触而反应效果很差。在无填 料的反应器中,类似的现象也称为沟流。 进口:当物料通过反应器的进口断面后即不能再重新出进口时,这种进 口称为闭口的进口,反之则称为开门的进口。 出口:当物料离开出口断面后即不能再回到反应器中的出口称为闭口的 出口,反之则称为升开口的出口。
1 k1
(2-31)
cC
1 k1 1 k 2
2 k1 k 2 c Ai
(2-33)
§2-8 阶式CSTR
若干个CSTR串联起来便称为阶式CSTR。阶式CSTR是对一般反应器模型化 的一个方法。当阶式CSTR数级多时,其作用则相当于一个活塞流反应器。
1. 一级反应的情况下
t 0
(2-40)
I (t ) 的定义是,在某一时 内龄分布函数(internal age distribution function)
刻反应器内所含的物质中(可以指水,也可以指水中所含的杂质),其停 留时间在t与t+dt时间间隔内所占的分数等于I (t )dt 。因此得
5. 平均停留时间
0
I (t )dt 1
§2-9 停留时间函数
2. 液龄分布函数 液龄分布函数(exit-age distribution function)E (t1 )的定义是,在某一 时刻从反应器流出的物质中(可以指水本身,也可以指水中所含的杂 质),在反应器内曾经停留在t与t+dt时间间隔内所占的分数等于 E(t1 )dt1 。 因此,从分布函数的定义得
0
E (t1 )dt1 1 (2-39)
§2-9 停留时间函数
3. 累积液龄分布函数 如果计算从0到t的累积分数,则称为累积液龄分布函数(cumulative exitage distribution function),以 F (t )表示,即
4. 内龄分布函数
F t E (t )dt
(2-25a)
两边分别除以 Q , v / Q并令代表反应器的停留时间。
可得
c Ai rA c A
dcA dt
(2-24b) (2-25b)
c Ai rA c A
3. 一级反应解
cA
c Ai 1 k
1 exp t / 1 k (2-26)
k 2 cosh 1 z (2-18) D AB cz 2 co k cosh D AB
§2-4 氧气在水膜内的扩散和反应
若
z ,则有:
c 1 co cosh k 2
(2-19)
D AB
均相反应模型
§2-4 氧气在水膜内的扩散和反应
3. 结论 在 k
(2-6)
c
(2-7)
(2-8)
§2-2 浓度与扩散
wA wB 1 wA wB 1 MA MB M xAM A wA x A M A xB M B
3. 混合物的局部平均速率v及局部摩尔平均速率v*的定义 (2-9)
A A B B wA A wB B A B
1. 多相反应模型 多相反应是假定氧气在通过水膜的扩散过程中不发生反应,反应 只发生在生物膜的表面,即氧气到达水膜底后才发生反应,反应 速率为: // rO k // c (2-15)
氧气在水膜内的扩散
§2-4 氧气在水膜内的扩散和反应
物料衡算方程: aN
Z
0 aNZ dZ 0
以同时是气体,同时是液体,或者一种气体和一种液体,一种流体和一种固 体等。A与B也可能是同一种物质,这时称为自扩散系数。气体的扩散系数
可以通过理论计算得到DAB与实验值相近的数值,但—般的扩散系数主要是
通过实验定出来的DAB 的值还随A的摩尔分数而略有变化,但在低摩尔分数 时,基本上可视为常数。
§2-4 氧气在水膜内的扩散和反应
§2-6 活塞流反应器
1. 活塞流反应器示意图
活塞流反应器 2. 反应器内浓度及出口浓度
c ci exp k
co ci exp k
(2-22)
(2-23)
3. 适用条件 在垂直于液体的流动方向上可能有混合现象,而在液体流动的方向上完全不 存在混合现象。
§2-7 连续搅拌反应器(CSTR)
//
D AB
2 k 与 D AB 等值的情况下,两种模型中的值
c
co
可以说是比较接近的;这说明均相与多相只是一种分析方法的不同选择,而 不必作为一种必须严格加以区分的概念。
§2-5
多空丸模型
1.多空丸数学模型 a. 球的半径为 z ,球的单位体积所含的表面积、即比表面为 a ,单位 为cm2/cm3; b. 边界条件为:当 z =0时反应物的浓度 c =0 ;z=Z 时 ,(在多孔九内, 浓度不是连续的,所以用某一点附近的无限小体积内的浓度平均值来代 表这一点的浓度) c. 球内反应速率;r=-k//c d. 有效扩散系数为D。 多孔丸模型
d A dt
(2-1)
d A V Q Ai VrA Q Ao dt
§2-2 浓度与扩散
1. 通量的定义 通量=扩散速率×浓度
2. 复习质量浓度、质量分数(mass fraction)及物质的量浓度、摩尔分数(mole
fraction)的关系,以A、B二元体系为例来说明。
A B (2-2)
c A A cB B x A A xB B c A cB
*
(2-10)
(2-11)
扩散过程示意图
§2-3 Fick第一扩散定律
1. Fick第一扩散定律
分子扩散:物质通过它们的分子活动而相互渗透的现象。 分子扩散的四种推动力:浓度梯度(常扩散)、压力梯度(压力扩散)、作
§2-7 连续搅拌反应器(CSTR)
在稳态时简化为
cA c Ai 1 k
(2-27)
4. 平行反应解的稳态解 (1)CSTR的平行反应
k1 A B
k2 A C
rA (k1 k 2 )c A
CSTR的平行(串联)反应
§2-7 连续搅拌反应器(CSTR)
(2)稳态解
用力差(强制扩散)、温度梯度(温度扩散)。一般的扩散指的是常扩散。
Fick第一扩散定律的基本公式
J A cDAB
J A DAB
x A z
c A z
(2-12a)
(2-12b)
§2-3 Fick第一扩散定律
注:(1)DAB的单位一般用cm2/s;c及cA的单位用mol/cm3; (2)JA是一个向量,其方向与浓度梯度的方向相反。 (3)当式(2-11)中的总物质的量浓度c不随z坐标变化时,基不公式(212b)与(2-12a)完全一样,本书以后即采用(2-12b)这一公式。 Fick第一扩散定律以表示A相对于固定坐标的通量 N A 最为合适,得下式:
1. 连续搅拌反应器的示意图及其特点
CSTR示意 特点: (1)进口反应器的流量皆为Q; (2)A的出口浓度也必然是cA。
2. CSTR的一般方程式
物料衡算方程
Qc Ai VrA Qc A V
dc A (2-24a) dt
§2-7 连续搅拌反应器(CSTR)
上式在稳态时简化为
QcAi 曲线,反应器的平均停留时间 t 应定义为:
t tE (t )dt
0
(2-42)
§2-10 实验方法
1. 脉冲信号 在瞬时内向容积V为流量Q为的反应器进水中注入mg示踪剂所构成的输入信 号称为脉冲信号。 Q (2-43) E (t ) (t ) C (t ) m
当代给水与废水处理原理
刘少敏 副教授 安徽理工大学地球与环境学院
第二章反应器
本章主要内容
反应器简介
物料衡算方程与Fick第一扩散定律 多相反应与均相反应 连续均相反应器 停留时间函数、混合与反应 分散模型 反应器的容积
反应器简介
1.反应器设计影响因素 反应器的设计涉及了流体力学、传热、传质、化学动力学的知识 2.反应器的类型 按反应特点分为: 均相反应器与多相反应器 按运行方式分为:间歇式反应器与连续流式反应器 3、反应器设计面临的新课题 反应器体系的设计:如何传热、传质的问题 反应动力学研究 反应器参数优化 反应机理的研究
0
C (t )dt 1
(2-44)
t Q t F (t ) (t )dt C (t )dt (2-45) 0 m 0 阶式CSTR的E(t)及F(t)曲线也可用脉冲信号的概念求出:
cn
1 k
1 n
ci
n
(2-34)
1 ci k cn
Q ci V k cn
1 n
1 (2-35)
(2-36)
1
结论 :当阶式CSTR的个数n ∞,共总容积为 V ,总停留时间为 ,反 应为一级时,其作用和容积、停留时间与之相等的活塞流反应器完全等价。 (非一级反应的条件下,同样可得出此结论)
