方向滤波器(组)的设计及应用
多普勒滤波器组的工作原理

多普勒滤波器组的工作原理多普勒滤波器组是信号处理领域中的一种重要工具,广泛应用于雷达、声纳、通信和地震信号处理等领域。
它利用多普勒效应和滤波器设计技术,实现对信号的频谱分析和自适应调整,从而达到提取有用信息和抑制干扰的目的。
本文将对多普勒滤波器组的工作原理进行详细介绍。
一、信号处理信号处理是多普勒滤波器组的基础,主要涉及对信号的采集、传输、变换和分析等操作。
在信号处理中,多普勒滤波器组通过对输入信号进行滤波、放大、采样等操作,提取出有用信息并去除噪声干扰。
这其中涉及到数字信号处理、信号分析和信号编解码等技术。
二、频谱分析频谱分析是多普勒滤波器组的核心,主要是对信号的频率成分进行分析和处理。
在频谱分析中,多普勒滤波器组利用快速傅里叶变换(FFT)等技术,将信号从时域转换到频域,从而实现对信号频率特性的分析。
通过对频谱的分析,可以提取出信号中的多普勒频移信息,进而实现对运动目标的速度和方向等参数的估计。
三、多普勒效应多普勒效应是物理学中一个重要的现象,主要是指当发射源和接收器之间存在相对运动时,接收到的信号频率会发生变化。
在多普勒滤波器组中,多普勒效应被用来提取运动目标的信息。
通过测量信号频率的变化,可以计算出目标的速度和方向等参数。
多普勒滤波器组通过对多普勒频移的检测和处理,实现了对运动目标的跟踪和定位。
四、滤波器设计滤波器设计是多普勒滤波器组的关键技术之一,主要是根据信号处理的要求,设计出合适的滤波器以实现对信号的选择和处理。
在多普勒滤波器组中,通常需要设计出不同类型和参数的滤波器,以满足不同应用场景的需求。
常见的滤波器类型包括低通滤波器、高通滤波器和带通滤波器等。
在设计滤波器时,需要考虑其频率特性、阻尼系数、阶数等参数,以确保滤波器的性能和稳定性。
五、自适应调整自适应调整是多普勒滤波器组的另一个重要特性,主要是指滤波器的参数能够根据输入信号的变化而自动调整,以实现最优的信号处理效果。
在多普勒滤波器组中,自适应调整技术可以通过最小均方误差(LMS)算法、递归最小二乘法(RLS)算法等实现。
非常详细的共模电感及滤波器的设计!(转载)精选全文完整版

⾮常详细的共模电感及滤波器的设计!(转载)看点1 ⼏个简单的实例测验与分析!01 这是⼀个共模电感,如下测量,你觉得测得的电感量是多少?可能有⼀部分会答错。
下⾯来说明⼀下我们知道共模电感的绕法有两种,1 双线并绕,2 两组线圈分开绕。
我们知道共模电感的绕法有两种,1 双线并绕,2 两组线圈分开绕。
1 双线并绕2 两组线圈分开绕正确的答案应该是10mH,下图所⽰。
⼀楼所⽰的测量和如下测量⼀致。
如仍有怀疑,可找个电感测量⼀下便知。
可以理解成两个电感并联,事实上就是两个电感并联,计算结果和测量结果是⼀样的。
两种绕法有何特点?1 双线并绕有较⼩的差模电感有较⾼的耦合电容有较⼩的漏感2 两组线圈分开绕有较⼩的耦合电容有较⾼的漏感因此要根据实际应⽤情况选择绕法。
02 再看看这样测量出来的电感量是多少?为什么?有的⼈可能会回答0mH,有的⼈可能会回答20mH,有的⼈可能会回答10mH。
不过很遗憾都不是,正确的答案L=40mH。
如下图,按右⼿法则已标上电流⽅向和磁通⽅向,从图中可以看出两个线圈的磁通的⽅向是相同的,也就是说磁通是增加的不是相互抵消。
根据磁环电感量计算公式式中:N = 圈数, Ac = 截⾯积, 分母 Mpl = 磁路长度。
注意 N 有平⽅的,⼀组线圈的圈数是N, 则两组线圈的圈数是 2N,将2N代⼊到公式中分⼦有 4N2, 也就是说电感量为 4 倍。
本例则为40 mH。
03 再看看这样测量得到的电感量应该是多少?这样测得的是什么电感量?这个估计很多⼈都知道是0mH,没错,理想状态下就是 0mH。
实际共模电感总有漏感、或差模电感成份,因此按此连接测量得到的数值就是漏感或者叫差模电感。
共模电感中漏感和差模电感是⼀回事,可以称漏感也可称差模电感。
⼀般做得好点的漏感在1-2%左右。
但有时候会特意将差模电感和共模电感做在⼀起,这时候的差模电感量就按实际需要做了。
看点2 共模电感“Z”字形符号是代表什么?共模电感的这个符号应该很常见吧,但是符号中的的 “Z” ⼀样的符号该怎么读?估计很少有⼈知道。
滤波器组框架理论及其在图信号处理中的应用

滤波器组框架理论及其在图信号处理中的应用摘要:传统滤波器组框架理论通常用来处理低维规则结构数据,如时间信号、空间信号和时空信号等。
随着现代科技高速发展,高维非规则化数据信息大量涌现,如社交网络、能源网络、交通运输网络、神经元网络等。
如何对高维图结构数据进行处理成为一个备受关注且亟待解决的问题。
借助代数图论和谱图理论,图信号处理成为近年来兴起的研究方向,用来处理高维加权图上的信号。
众多学者从各自角度出发,将传统滤波器组框架理论推广到图滤波器组框架中,取得了一系列成果。
关键词:滤波器组;框架理论;图信号;图滤波器引言:滤波器组框架理论是应用数学、信号处理、图像处理和数字通信等领域的重要问题之一,对滤波器组框架的分析和设计问题进行研究有着重要的科学意义和应用前景。
近年来,随着高维非规则化数据信息大量涌现,很多学者开始研究图信号处理的滤波器组方法。
因此对滤波器组框架理论及其在图信号处理中的应用进行研究。
一、滤波器组框架理论在各种框架中,实际应用最广泛的是由滤波器组实现的框架。
有限维框架、离散小波框架和离散Gabor框架都属于滤波器组框架。
接下来介绍滤波器组基础知识、滤波器组框架理论及应用。
(一)滤波器组基础滤波器组是一组有着共同输入或共同输出的带通滤波器。
典型滤波器组的结构如下图所示。
其中左边部分为分析滤波器组,右边部分为综合滤波器组。
分析滤波器组有一个输入多个输出,其将输入信号分解成不同的子带信号,每个分析滤波器Hi(z)有不同的频率特性,输入信号x(n)通过M个分析滤波器Hi(z)后,得到M个不同的子带信号。
信号在子带分解后,对每个通道Mi下采样,可降低信号的采样率。
下采样后的子带信号可以被编码、处理或者传输。
综合滤波器组具有多个输入一个输出,其将处理后的子带信号通过带通滤波后再组合起来,重构原始信号。
为保证重构信号xˆ(n)与原信号x(n)具有相同的采样频率,在综合滤波器组前对各子带信号Mi上采样(Upsampling)。
第5章无源电力滤波器设计及应用实例

= hω1 )的阻抗为:
Zh
=
Rh
+
j(ωh L −
1 )
ωhC
=
Rh
+
j(hω1L −
1 )
hω1C
(5-1)
单调谐滤波器的阻抗频率特性如图5-1(b)所示, 它利用 R、L、C 串联谐振电路在谐
振点呈现低阻抗的原理,如将电路谐振点调谐到h次谐波上,此时 Z h = Rh ,Rh 为电阻R在h
次谐波下的阻值。由于R很小,h次谐波电流主要由R 分流,很少流入电网中。而对于其他 次谐波,滤波器呈现较大的阻抗,所以分流很小。因此,只要将滤波器的谐振频率设定为与 需要滤除的谐波频率一致,则该次谐波电流将大部分流入滤波器,从而起到滤除该次谐波的 目的。
5.3 滤波器设计要求和步骤
5.3.1 滤波器设计的要求
滤波器的设计应满足两个基本要求: 1.以最小的投资使谐波源注入系统的谐波减小到国家标准规定的允许水平。 2.满足基波无功补偿的要求。 在满足上面两个基本要求的前提下,滤波装置的设计涉及到以下一些指标: (1) 技术指标,包括滤波器构成、谐波电压、谐波电流、无功补偿容量; (2) 安全指标,包括电容器的过电压、过电流、容量平衡;
(5-3)
X T1 —基波时变压器绕组电抗。
3.其他用电负荷
除去提升机变流器外矿上的其他负荷可采用图5-6所示的等值电路。
为了计算等效参数,需要统计未投入并联电
容器时全矿井24小时的有功电度和无功电度,从
中减去提升机的有功电度和无功电度,即为全矿其
他负荷的一天内的有功电度和无功电度,进而可以
计算出有功功率 P 和无功功率 Q 。
接线的整流变压器使二次电压移相 30 0 ,组成 12 脉动整流装置,使 5、7、17、19,…次谐
滤波器设计技术方案(DOC)
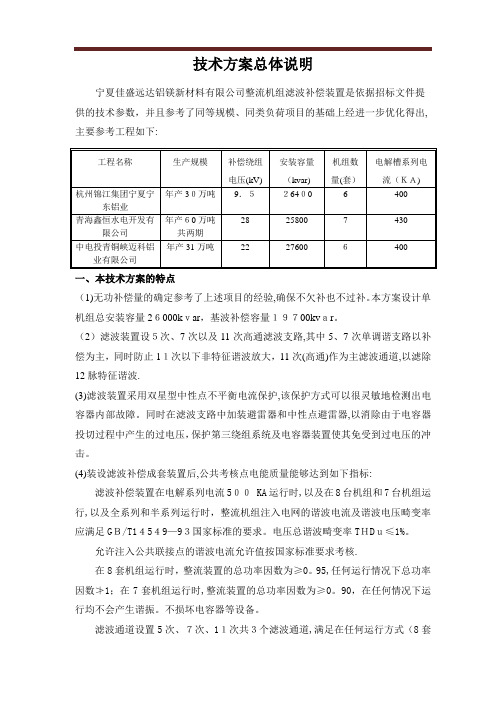
技术方案总体说明宁夏佳盛远达铝镁新材料有限公司整流机组滤波补偿装置是依据招标文件提供的技术参数,并且参考了同等规模、同类负荷项目的基础上经进一步优化得出,主要参考工程如下:一、本技术方案的特点(1)无功补偿量的确定参考了上述项目的经验,确保不欠补也不过补。
本方案设计单机组总安装容量26000kvar,基波补偿容量19700kvar。
(2)滤波装置设5次、7次以及11次高通滤波支路,其中5、7次单调谐支路以补偿为主,同时防止11次以下非特征谐波放大,11次(高通)作为主滤波通道,以滤除12脉特征谐波.(3)滤波装置采用双星型中性点不平衡电流保护,该保护方式可以很灵敏地检测出电容器内部故障。
同时在滤波支路中加装避雷器和中性点避雷器,以消除由于电容器投切过程中产生的过电压,保护第三绕组系统及电容器装置使其免受到过电压的冲击。
(4)装设滤波补偿成套装置后,公共考核点电能质量能够达到如下指标:滤波补偿装置在电解系列电流500 KA运行时,以及在8台机组和7台机组运行,以及全系列和半系列运行时,整流机组注入电网的谐波电流及谐波电压畸变率应满足GB/T14549—93国家标准的要求。
电压总谐波畸变率THDu≤1%。
允许注入公共联接点的谐波电流允许值按国家标准要求考核.在8套机组运行时,整流装置的总功率因数为≥0。
95,任何运行情况下总功率因数≯1;在7套机组运行时,整流装置的总功率因数为≥0。
90,在任何情况下运行均不会产生谐振。
不损坏电容器等设备。
滤波通道设置5次、7次、11次共3个滤波通道,满足在任何运行方式(8套机组运行或7套机组运行)时,供电系统均不发生谐振,且谐波含量均满足本技术要求中“允许注入公共联接点的谐波电流允许值"要求。
二、本次方案针对铝厂的特殊考虑1、针对国内电解铝行业整流变第三绕组发生事故较多的现象,本方案采取以下措施来保证第三绕组的安全性.装设谐波保护单元,当检测谐波电流超过设计整定值时跳开电容器。
开关电容(SC)滤波器设计和应用

而 电流 为 :i () C t / C C v () 2t ] T ,可见 基本 开关 电容 c t =Aq () T = [1t v () / c 单元 可 以等效为 一个 电阻R cC  ̄T/ ,其优 点是在集 成 电路 中可 以用很 小的 芯
关键词 : 模拟 滤波器:开关 电容 ;音频滤波器 中图分类号 :T 7 文献标识码 :A 文章编 号:1 7 - 7 9 2 1 )0 1 0 0 0 N 1 5 7(0 0 7 0 5 - 1 6
在信 号 处理 中 ,滤 波 器 占有 十 分 重要 的地位 ,它对 实 际 信 号进 行 过 滤 ,提取 有效 信号 、抑 制干 扰噪 声 。模拟 滤波 器应 用 于各种 模拟 信 号处理
简化了开关电容电路的分析和设计 。
2开 关电窖 ( CJ S 滤波器 的设 计
l
R1
在模拟 电路 中经 常涉 及到 电路 的频率 特性 、延 时特 性等 ,这些 电路 性 能与 电路 的 时间 常数有 关 ,这些 时 间常数 多 由 电路 中 的元件 参 数 电感 、 电 阻、 电容 来确 定 。在模拟 集 成 电路 中,制 作 电感是 困难 的 ,所 以多采 用 电
图1 基本 开关 电容单 元
语音信 号 以外 的各 种杂 波 。5t 抑制 滤波 器 是话 路滤 波器 组成 部 分之 一 , 0z t 亦称 5H 陷波器 。它采 用 由加法 器和 积分 器 构成 的状 态变 量滤 波器 结构 , 0z 可 以用 来 抑制 电源 的干 扰 。 由于 陷波 频 率低 ,要 求很 大 的时 间常 数 。为节 省芯 片面 积 ,采用 开关 电容 技术 实 现 。图4 a所 示是 5H 抑制 滤波 器 的有 () 0z 源 R原 型 电路, 图4b所 示是 其对应 的 开关 电容滤 波器 电路 。 c ()
WOLA滤波器组在宽带数字中频处理中的应用

WOLA滤波器组在宽带数字中频处理中的应用郭连平;田书林;王志刚;罗浚溢【摘要】信道化技术是一种宽带数字中频系统中常用于信号处理与分析的技术.多相DFT滤波器组是实现信道化的一种高效结构,但其参数设计的灵活性受到了信道数目与抽取倍数必须相等的限制.利用WOLA滤波器组实现宽带数字中频的信道化设计,可实现与多相DFT滤波器组相同的功能,同时解除了信道数目与抽取倍数的约束关系.仿真结果验证了WOLA滤波器组实现宽带信号信道化的有效性.【期刊名称】《计量学报》【年(卷),期】2013(034)005【总页数】5页(P486-490)【关键词】计量学;信道化设计;数字中频处理;多相DFT滤波器组;WOLA滤波器组【作者】郭连平;田书林;王志刚;罗浚溢【作者单位】电子科技大学自动化工程学院,四川成都611731;电子科技大学自动化工程学院,四川成都611731;电子科技大学自动化工程学院,四川成都611731;电子科技大学自动化工程学院,四川成都611731【正文语种】中文【中图分类】TB973宽带数字中频处理中,信号经过ADC采样后,若直接利用快速傅里叶变换(FFT)处理,鉴于较高的采样率及分析带宽,一般无法得到足够的频率分辨率。
同时,这种具有极高采样率的数据流,使得后端处理器件(如FPGA)无法达到可匹配的数据处理速度。
因此,一般采用带通或低通滤波器组分别取出相应频带内的信号,分段整合的数字经过变频、数字抽取等操作,降低数据处理速率,进而获得整个模块的频率分辨率提升。
然而,该方法缺点为计算量大,硬件实现效率较低,目前已逐渐被高效率的多相DFT滤波器组结构代替[1]。
多相DFT滤波器组中,采样数据的抽取倍数与信道划分数目必须相等,严格约束了各信道的数据输出率与信道带宽,限制了参数设计的灵活性。
加权叠接相加(weighted overlap-add,WOLA)结构是一种高效率、低功耗且设计灵活的滤波器组,起初应用于短时傅里叶变换,近年来在子带编码(subband coding)、OFDM和语音处理等领域得到广泛应用[2~5]。
织物表面疵点检测方法的设计与实现

Vol. 29, No. 1Jan. 2021第29卷第1期2021年1月AdvancedTextileTechnologyDOI : 10. 19398/j. a t 202005004引用格式:俞新星,壬勇,支佳雯.织物表面疵点检测方法的设计与实现现代纺织技术,021,9():62 — 67.织物表面疵点检测方法的设计与实现俞新星,任勇,支佳雯(苏州大学应用技术学院,江苏苏州215325)摘要:针对传统织物生产企业中,人工检测织物存在瑕疵检出效率低、误检率高的问题,提出了一种织物表面疵点检测方法。
该方法首先采用高斯滤波、线性归一化以及限制对比度自适应直方图均衡化对织物表面图像进行预处理,从而有效增强图像中的疵点表现细节,然后通过改进的Gabor 优化选择,再对选择后的图像进行初分解,从中挑选出最优滤波图像进行二值化处理,最后运用统计学方法进行疵点判断并获得最终结果。
该方法实现简便、硬件要求低、适应性广,可用于判断织物表面是否含有疵点,并定位疵点。
实验证明,织物表面疵点检测准确率高达95.38%.关键词:织物疵点检测;Gabor 优化选择;直方图均衡化;线性归一化中图分类号:TS103;TP391文献标志码:A 文章编号:1009— 265X(202 1 )01 —0062— 06Design and Implementation of Defect Detection Method for Fabric SurfaceYU Xinxing , REN Yong , ZHI Jiawen(Applied Technology College of Soochow University, Soochow 21 5325 , China)Abstract : To address the problems of low defect, detection efficiency and high false detectionrateof manualfabric detectionin traditionalfabric manufacturing enterprises ,a fabric surface defect, detection method is proposed. For purpose of this method , the Gaussianfilter , linear normalization and limited contrast, adaptive histogram equalization are adopted for preprocessing fabric surface images , to display detect details of the images clearly.Secondly , the selected images are preliminarily decomposed viaimproved optimal Gaborfilter ,with a view to picking outthe ones with the optimalfiltering for binarization processing. Lastly, defect, judgment, is conducted by means of statistical approach , and thefinalresultisobtained.The methodiseasytooperate ,haslow requirementsintermsof hardware , and is of wide adaptability. It can be used to judge the presence of defects onfabricsurface ,andlocatethem.The method is proved to have an accuracy rate of fabric surfacedefectdetectionashighas95.38% throughexperiments.Key words :fabric defect detection ;optimal Gabor filter ; histogram equalization ;linearnormalization收稿日期:2020 —05 —09网络出版日期:2020 —10 —21基金项目:江苏省高校自然基金项目(19KJB520051);江苏高校哲学社会科学研究基金项目(2018SJA2251);江苏省大学生创新创业训练计划项目(201913984009Y)作者简介:俞新星(1998 — )男,江苏如皋人,2017级软件工程专业本科生。
WOLA滤波器组的设计与实现的开题报告

WOLA滤波器组的设计与实现的开题报告一、研究背景和意义随着数字信号处理技术的发展,滤波器在信号处理中的应用越来越广泛。
WOLA(Weighted Overlap and Add)滤波器组是一种高效的数字信号处理滤波器。
WOLA滤波器组已被广泛应用于语音信号处理、音频编解码、无线通信、雷达信号处理等领域。
因此,本课题研究WOLA滤波器组的设计与实现,对于深入理解数字信号处理技术、提高信号处理效率和水平,具有重要的现实意义和应用价值。
二、研究内容和目标本课题旨在研究WOLA滤波器组的设计与实现,具体研究内容包括:1、WOLA滤波器组的原理、设计方法和算法;2、WOLA滤波器组在语音信号处理、音频编解码、无线通信、雷达信号处理中的应用;3、基于MATLAB和C语言实现WOLA滤波器组算法;4、对实现结果进行仿真和验证,评价WOLA滤波器组的性能和优点。
本课题研究的目标是:1、深入理解WOLA滤波器组的原理和设计方法;2、掌握WOLA滤波器组的算法实现技术;3、实现WOLA滤波器组算法,实现语音信号处理、音频编解码、无线通信、雷达信号处理等应用;4、评价WOLA滤波器组的性能和优点,为后续的研究提供参考和基础。
三、研究方法和步骤本课题的研究方法主要包括文献资料调研、理论分析、算法设计、MATLAB和C语言编程、仿真验证等。
具体步骤如下:1、文献资料调研:收集与WOLA滤波器组相关的文献资料,对WOLA滤波器组的原理和设计方法进行综合分析;2、理论分析:分析WOLA滤波器组的原理、特点和优点,探讨WOLA滤波器组在语音信号处理、音频编解码、无线通信、雷达信号处理等应用领域中的具体应用;3、算法设计:基于WOLA滤波器组的原理和设计方法,设计并实现WOLA滤波器组的相关算法;4、MATLAB和C语言编程:利用MATLAB和C语言编程实现WOLA 滤波器组的算法;5、仿真验证:对实现的WOLA滤波器组算法进行仿真验证,评价WOLA滤波器组的性能和优点。
正交镜像滤波器组的原理及实现

正交镜像滤波器组的原理及实现正交镜像滤波器组(Orthogonal Mirror Filter Bank, OMFB)是一种常用的信号处理方法,广泛应用于音频、图像和视频等领域。
它通过将输入信号分解成不同频率的子带,并进行信号重构,实现了信号压缩和去噪等功能。
一、原理:OMFB主要包含两个部分:分解滤波器组和重构滤波器组。
分解滤波器组用于将输入信号分解成多个子带信号,每个子带信号包含特定频率范围内的频域信息;重构滤波器组用于将分解后的子带信号重构为原始信号。
分解滤波器组通常采用滤波器组合的方式,每个滤波器是一个带通滤波器,用于提取输入信号中特定频率范围内的信号分量。
滤波器的数量根据需要分解的子带数目而定,一般为2的整数次幂。
通常情况下,分解滤波器组中的滤波器是对称的,即滤波器组中的滤波器是镜像对称的。
这样可以确保分解后的子带信号之间没有重叠,避免信息的丢失。
重构滤波器组的作用是将分解后的子带信号重构为原始信号。
重构滤波器组与分解滤波器组具有相似的结构,但滤波器的频率响应是互补的。
例如,如果分解滤波器组中的滤波器的中心频率为f,那么重构滤波器组中的滤波器中心频率为-f,这样可以保证分解后的子带信号能够恢复为原始信号。
在实际应用中,OMFB通常使用快速滤波算法进行实现,以提高处理效率。
快速滤波算法采用基于多项式的离散滤波器实现,具有高效、稳定的特点。
二、实现:OMFB的实现是一个多阶段的过程,主要包含以下几个步骤:1. 设计滤波器:根据需要分解的子带数目,使用滤波器设计工具(如Matlab中的fir1函数)设计出分解滤波器组和重构滤波器组的滤波器系数。
可以采用低通滤波器为原型,然后通过平移和尺度变换来实现带通滤波器。
2.分解:将输入信号通过分解滤波器组进行分解,得到多个子带信号。
3.子带处理:对每个子带信号进行进一步的处理,如压缩、去噪等。
4.重构:将处理后的子带信号通过重构滤波器组进行重构,得到原始信号的近似重建。
PCB设计中滤波方法以及注意事项详解

PCB设计中滤波方法以及注意事项详解许多设备单台做电磁兼容实验时都没有问题,但当两台设备连接起来以后,就不满足电磁兼容的要求了,这就是电缆起了接收和辐射天线的作用。
唯一的措施就是加滤波器,切断电磁干扰沿信号线或电源线传播的路径,与屏蔽共同构成完美的电磁干扰防护,无论是抑制干扰源、消除耦合或提高接收电路的抗能力。
都可以采用滤波技术,如图所示。
信号滤波器电源滤波器滤波器的使用1.线上干扰的类型线上的干扰电流按照其流动路径可以分为两类:一类是差模干扰电流,另一类是共模干扰电流。
差模干扰电流是在火线和零线之间流动的干扰电流,差模干扰在两导线之间传输,属于对称性干扰。
共模干扰电流是在火线、零线与大地(或其它参考物体)之间流动的干扰电流,共模干扰在导线与地(机壳)之间传输,属于非对称性干扰。
在一般情况下,差模干扰幅度小、频率低、所造成的干扰较小,共模干扰幅度大、频率高,还可以通过导线产生辐射,所造成的干扰较大。
由于这两种干扰的抑制方式不同,因此正确辨认干扰的类型是实施正确滤波方法的前提。
2.滤波器的分类滤波器是由电阻、电容、电感、铁氧体磁珠和共模线圈等器件构成的频率选择性网络。
根据要滤除的干扰信号的频率与工作频率的相对关系,干扰滤波器有低通滤波器、高通滤波器、带通滤波器、带阻滤波器等种类。
(1)低通滤波器低通滤波器是电磁兼容抑制技术中普遍应用的滤波器。
低通滤波器主要用在干扰信号频率比工作信号频率高的场合。
如在数字设备中,脉冲信号有丰富的高次谐波,这些高次谐波并不是电路工作所必需的,但它们却是很强的干扰源。
因此在数字电路中,常用低通滤波器将脉冲信号中不必要的高次谐波滤除掉,而仅保留能够维持电路正常工作最低频率。
常用的低通滤波器是用电感和电容组合而成的,按照电路结构分,有单电容型(C型),单电感型,L型和反Γ型,T型,π型。
低通滤波器的分类在实际工程中,如何确定使用这些滤波电路中的哪一个,电容、电感的参数怎样确定。
FIR滤波器设计与实现实验报告

FIR滤波器设计与实现实验报告目录一、实验概述 (2)1. 实验目的 (3)2. 实验原理 (3)3. 实验设备与工具 (4)4. 实验内容与步骤 (6)5. 实验数据与结果分析 (7)二、FIR滤波器设计 (8)1. 滤波器设计基本概念 (9)2. 系数求解方法 (10)频谱采样法 (11)最小均方误差法 (14)3. 常用FIR滤波器类型 (15)线性相位FIR滤波器 (16)非线性相位FIR滤波器 (18)4. 设计实例与比较 (19)三、FIR滤波器实现 (20)1. 硬件实现基础 (21)2. 软件实现方法 (22)3. 实现过程中的关键问题与解决方案 (23)4. 滤波器性能评估指标 (25)四、实验结果与分析 (26)1. 实验数据记录与处理 (27)2. 滤波器性能测试与分析 (29)通带波动 (30)虚部衰减 (31)相位失真 (32)3. 与其他设计方案的对比与讨论 (33)五、总结与展望 (34)1. 实验成果总结 (35)2. 存在问题与不足 (36)3. 未来发展方向与改进措施 (37)一、实验概述本次实验的主要目标是设计并实现一个有限脉冲响应(Finite Impulse Response,简称FIR)滤波器。
FIR滤波器是数字信号处理中常用的一种滤波器,具有线性相位响应和易于设计的优点。
本次实验旨在通过实践加深我们对FIR滤波器设计和实现过程的理解,提升我们的实践能力和问题解决能力。
在实验过程中,我们将首先理解FIR滤波器的基本原理和特性,包括其工作原理、设计方法和性能指标。
我们将选择合适的实验工具和环境,例如MATLAB或Python等编程环境,进行FIR滤波器的设计。
我们还将关注滤波器的实现过程,包括代码编写、性能测试和结果分析等步骤。
通过这次实验,我们期望能够深入理解FIR滤波器的设计和实现过程,并能够将理论知识应用到实践中,提高我们的工程实践能力。
本次实验报告将按照“设计原理设计方法实现过程实验结果与分析”的逻辑结构进行组织,让读者能够清晰地了解我们实验的全过程,以及我们从中获得的收获和启示。
滤波器原理及应用

滤波器原理及应用在电子学和通信领域中,滤波器是一种能够选择特定频率信号并抑制其他频率信号的电路组件。
它在各种电子设备中扮演着至关重要的角色,例如在音频设备、射频通信、无线电等领域的应用中都需要滤波器来确保信号质量和频谱高效利用。
本文将介绍滤波器的基本原理和常见应用。
滤波器的原理滤波器主要依靠其电路设计对特定频率范围的信号进行放大或衰减,从而实现对信号的频率选择性处理。
根据频率选择性能力不同,滤波器可以分为低通滤波器、高通滤波器、带通滤波器和带阻滤波器四种类型。
•低通滤波器:只允许低于一定频率的信号通过,而抑制高于该频率的信号。
•高通滤波器:只允许高于一定频率的信号通过,而抑制低于该频率的信号。
•带通滤波器:只允许在一定频率范围内的信号通过,而抑制其他频率的信号。
•带阻滤波器:只允许除一定频率范围内的信号通过外,抑制其他频率的信号。
在滤波器的设计中,根据滤波器的截止频率、通带波纹、衰减量等指标要求,可以选择不同的滤波器电路结构和元件参数。
常用的滤波器元件包括电容、电感、电阻等,它们可以组合成各种滤波器电路,如RC滤波器、LC滤波器、RLC滤波器等。
滤波器的应用滤波器在各种电子设备和通信系统中有着广泛的应用,其中一些常见的应用包括:1. 音频设备在音频系统中,滤波器用于音频信号的处理和增强,例如在扬声器中使用低通滤波器去除高频噪声,在麦克风中使用高通滤波器去除低频噪声,以提高音频设备的音质和清晰度。
2. 通信系统在无线通信系统中,滤波器用于频率选择和信号处理,以确保传输信号的质量和可靠性。
例如,在基站中使用带通滤波器选择特定频段的信号,同时抑制其他频段的干扰信号,以保证通信系统的正常运行。
3. 无线电在无线电接收机中,滤波器通过滤除不必要的频率信号,提高接收机对特定信号的接收灵敏度和选择性。
不同类型的滤波器可以应用于调频接收、调幅接收等不同的无线电接收系统中。
4. 信号处理在信号处理系统中,滤波器常用于滤除噪声、分离信号、提取特定频率成分等应用。
滤波器实验报告

滤波器实验报告第一点:滤波器实验原理与类型滤波器作为信号处理的核心工具,其基础在于对信号的选择性处理。
实验中,我们首先通过研究不同类型的滤波器来深入理解其工作原理和特性。
1.1 理想滤波器:理想的滤波器具有无限的带宽和完美的截止特性,其实际上是不存在的,但它是设计其他类型滤波器的基础。
理想的低通滤波器(Low Pass Filter, LPF)允许低于特定频率的信号通过,而高于该频率的信号则被完全抑制。
对应的,高通滤波器(High Pass Filter, HPF)则允许高于特定频率的信号通过,而低于该频率的信号则被抑制。
理想带通滤波器(Band Pass Filter, BPF)和带阻滤波器(Band Stop Filter, BSF)则更加复杂,分别允许一定频率范围的信号通过和阻止一定频率范围的信号。
1.2 实际滤波器:实际应用中的滤波器都会受到物理限制,如元件的电阻、电容、电感等,导致实际滤波器的特性与理想滤波器有所不同。
常用的实际滤波器包括有源滤波器和无源滤波器。
有源滤波器包含有放大元件,可以对信号的幅度进行调整;无源滤波器则不包含放大元件,主要通过电路元件的阻抗变换来实现滤波功能。
1.3 滤波器设计方法:在实验中,我们探讨了不同的滤波器设计方法,包括巴特沃斯设计、切比雪夫设计、椭圆设计等。
每种设计方法都有其独特的频率响应特性,适用于不同的应用场景。
第二点:滤波器实验设计与实现实验的核心在于设计和实现一个滤波器,以达到特定的滤波效果。
这一部分我们将详细讨论实验中涉及的设计步骤和实现方法。
2.1 滤波器参数确定:首先,根据实验需求确定滤波器的参数,包括截止频率、滤波器的阶数、类型(低通、高通、带通、带阻等)。
这些参数将直接影响滤波器的性能。
2.2 滤波器设计:在确定了滤波器参数后,我们使用专业的滤波器设计软件,如MATLAB,来设计滤波器的传递函数。
设计过程中,我们可以根据需要选择不同的滤波器设计方法,以达到最佳的滤波效果。
数字信号处理中滤波器设计的使用教程

数字信号处理中滤波器设计的使用教程数字信号处理(DSP)是一门广泛应用于通信、音频、图像、雷达等领域的技术。
滤波是其中一种常见的操作,用于去除或改变信号中的某些成分。
本文将介绍数字信号处理中滤波器的设计与使用方法。
一、滤波器概述滤波器是数字信号处理中的重要组成部分,它通过改变信号的频谱来实现信号的特定处理目标。
常见的滤波器类型包括低通滤波器、高通滤波器、带通滤波器和带阻滤波器。
低通滤波器(Low-pass Filter)用于去除高频噪声并保留低频成分,适用于信号平滑处理。
高通滤波器(High-pass Filter)则相反,保留高频成分并去除低频部分,常用于去除直流偏移和低频噪声。
带通滤波器(Band-pass Filter)通过保留一定范围的频率成分来滤除其他频率的信号,常用于信号频带选择和精确查找特定频率。
带阻滤波器(Band-stop Filter)则是保留某一范围的频率成分并去除其他频率,常用于消除干扰信号或特定频率的噪声。
二、滤波器设计方法滤波器的设计目标是根据具体需求确定滤波器类型,并设计出相应的滤波器参数。
下面将介绍两种常见的设计方法。
1. IIR滤波器设计无限脉冲响应(IIR)滤波器根据系统的差分方程来设计,具有较为复杂的频率响应。
常见的IIR滤波器设计方法包括巴特沃斯(Butterworth)滤波器、切比雪夫(Chebyshev)滤波器和椭圆(Elliptic)滤波器。
(1)巴特沃斯滤波器是一种常见的IIR滤波器,具有近似的平坦频率响应和宽的过渡带宽度。
滤波器的设计包括选择滤波器阶数、截止频率和滤波器类型等参数。
(2)切比雪夫滤波器是一种IIR滤波器,除了具有平坦的频率响应外,还可实现更陡峭的过渡带。
切比雪夫滤波器的设计包括选择滤波器阶数、截止频率、过渡带宽度和纹波等参数。
(3)椭圆滤波器是一种IIR滤波器,具有最陡峭的过渡带和最小的滤波器阶数。
椭圆滤波器的设计包括选择滤波器阶数、截止频率、过渡带宽度、纹波和阻带衰减等参数。
煤矿电网无源滤波器的设计及应用

系统 电能质量 的关 键措施 。
1 滤 波方 案 的确 定
无 源滤 波器 ( 以下 简称 F ) 计 的主要 内容 , C设 概
括起来有 3 , 条 即两个谐波指标 , 两个技术指标和一
的畸变 , 极大地影响煤矿生产安全 。因此 , 供电系统 个 调谐 整定 方法 。两个 谐波 指标 是指谐 波 的电压 畸 H 无源滤波器合理设计及成功应用 ,已成为提高供电 变率——T D和流人系统中各次谐波 电抗的分量 。
t 。同等条件下除更换顶梁外 , 没有增加设备、 人员 ; 虽然循环用电量、 火工品等材料消耗增加 , 但按总产
售价 和成 本计 算 , 增加 经济效 益达 5 月 6万元 。
5 结 论
便利 、 护顶材料长度 、 护顶效果 、 防坠 分摊测得的吨煤平均费用与原来基本持平 ;按当期
7 4 工作面实施支护参数优化, 54 产生了较好 的
度为 13 根/ .9 m ,采用 12m金属铰接顶梁替代原 .
方案的 1 m铰接顶梁配合单体液压支柱支护 。
作 者简介 : 程 伟 (9 9 ) 男 , 17 一 , 江苏 沛县人 ,0 5年 毕 20 业于 中国矿业大学采矿工程专业 , 州矿务集 团有 限公 司生 徐 产技术部助理工程师。
K_一增阻系数, 0 9 取 .; 厂 支柱理论工作阻力 , 30 N柱 ; 为 0 / k 。6 , ——分别为排距和柱距 , ( m 综合考虑作业 兜因素 , 参数选 0 6 。0 .4m b . m =12 ,
取整 数 12r) . 。 n
N=1 f b =1 ( . . ) . 9根 / /a・ 1 /1 2 0 6 =13 X m 3 3 支 护优 化方案 .
滤波器的原理及应用书籍

滤波器的原理及应用书籍1. 引言滤波器是信号处理和电子电路中常用的一种设备,用于增强或者减弱某个特定频率范围内的信号。
滤波器的原理与应用具有广泛的研究和应用价值。
本文将介绍一些关于滤波器的原理与应用的优质书籍推荐。
2. 滤波器的原理书籍推荐以下是几本滤波器原理的经典书籍,它们系统地介绍了滤波器的工作原理、设计方法和数学理论。
2.1 《滤波器设计与应用》•作者:C.米尔斯 (C. Mils)•本书详细介绍了滤波器的基本概念、滤波器类型、设计方法和性能评估等内容。
此外,书中还包含了丰富的案例分析和实际应用,方便读者理解和应用所学知识。
2.2 《滤波器原理与设计》•作者:L. 德基普 (L. DeJonghe)•本书深入浅出地介绍了滤波器设计的理论和实践,包括滤波器的基本原理、滤波器类型、设计流程和实时应用等。
此外,书中还提供了大量的实例和习题,帮助读者加深对滤波器原理的理解。
2.3 《现代滤波器设计》•作者:M. 高夫 (M. Gauffin)•本书综合介绍了现代滤波器设计的最新方法和技术。
书中系统地讲解了数字滤波器的设计原理、各种经典和现代滤波器结构、设计流程和性能评估等。
此外,书中还附有丰富的实例和MATLAB代码,方便读者理解和实践。
3. 滤波器的应用书籍推荐3.1 《滤波器在通信系统中的应用》•作者:R. 吉尔伯特 (R. Gilbert)•本书重点介绍了滤波器在通信系统中的应用,包括滤波器在调制解调、信号处理、解码与编码等方面的应用。
此外,书中还包含了大量的案例和在实际通信系统中的应用实例,帮助读者了解滤波器的具体应用场景。
3.2 《滤波器在音频处理中的应用》•作者:S. 罗宾斯 (S. Robbins)•本书主要介绍了滤波器在音频处理中的应用,包括音频信号的滤波器设计原理、均衡器、音频特效等方面的内容。
书中还通过实例和实践案例,阐述了滤波器在音频处理中的具体应用场景和效果。
3.3 《滤波器在图像处理中的应用》•作者:J. 弗利德 (J. Fried)•本书详细介绍了滤波器在图像处理中的应用。
滤波器的设计原理及应用

滤波器的设计原理及应用1. 引言滤波器是电子设备中常用的组件,它可以通过滤除或弱化特定频率的信号来实现信号处理和频谱分析等应用。
本文将介绍滤波器的设计原理和常见的应用场景。
2. 滤波器的种类滤波器根据其工作原理和频率特性的不同,可以分为多种类型,常见的滤波器包括: - 低通滤波器(Low-pass Filter) - 高通滤波器(High-pass Filter) - 带通滤波器(Band-pass Filter) - 带阻滤波器(Band-stop Filter) - 数字滤波器(Digital Filter)3. 滤波器的设计原理滤波器的设计原理基于信号的频域特性和频率响应,主要包括以下几个方面:- 滤波器的基本频率响应特性:低通滤波器通过滤除高频信号,高通滤波器通过滤除低频信号,带通滤波器通过选择一个频率范围内的信号,带阻滤波器通过滤除一个频率范围内的信号。
- 滤波器的阶数:阶数是滤波器对信号的衰减能力的度量,阶数越高,滤波器对不需要的频率的衰减能力越强。
- 滤波器的设计方法:滤波器可以通过模拟电路设计和数字滤波器设计两种方法实现。
模拟电路设计主要采用电容、电感、运算放大器等元件组成;数字滤波器设计基于数字信号处理算法,可以通过软件或硬件实现。
4. 滤波器的应用案例滤波器具有广泛的应用领域,常见的应用案例包括: - 音频处理:滤波器可以用于音频信号的去噪、音效处理、均衡器等,提高音频的质量和清晰度。
- 图像处理:滤波器可以用于图像的去噪、边缘检测、图像增强等,改善图像的质量和细节。
- 无线通信:滤波器在无线通信系统中用于信号调制、解调和频谱分析等,提高通信质量和信号传输速率。
- 生物医学信号处理:滤波器在心电图、脑电图等生物医学信号处理中应用广泛,帮助医生诊断和监测病情。
- 传感器信号处理:滤波器可以用于传感器信号的去噪和滤波,提高传感器的性能和准确度。
5. 总结滤波器作为一种常见的信号处理组件,在电子设备中有着广泛的应用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
西安电子科技大学
硕士学位论文
方向滤波器(组)的设计及应用
姓名:叶石火
申请学位级别:硕士
专业:电路与系统
指导教师:石光明
20100101
2方向滤波器(组)的设计及应用
由于直接优化法计算极为复杂,无法得到具有良好特性的滤波器结构。
因此,基于各种变换的设计方法开始受到广泛关注。
1987年,R.Ansari[14】通过利用变换传输函数石(z2)+z正(z2)实现了90。
方向的扇形方向滤波器设计。
然而,此方法在传输函数的设计上具有较高的复杂度。
在基于变换的设计方法中,McClellan变换无疑应用最为广泛,同时设计出的滤波器特性也最优。
此变换由J.M.McClellantl5。
161提出。
1990年,E.Z.Psakkis等【l‘7】利用McClellan变换设计具有一般形状的二维扇形滤波器。
后来,许多学群18埘】通过将McClellan变换结合最小二乘法、基因算法和二次规划等方法降低了变换中的优化计算量,从而设计出性能更优的二维扇形方向滤波器。
2009年,Jong.JyShyu掣22】进一步扩展McClellan变换法,将其应用于设计各种二维FIR滤波器中,并可通过调整其中的变量参数来实现各种通带夹角的扇形方向滤波器的设计。
然而,由于McClellan变换自身的不足以及其变换中的复杂优化问题,使其只能设计具有可变通带夹角的扇形方向滤波器,而无法实现通带中心方向可变的二维滤波器。
下采样法123-25]是通过二维下采样操作来设计二维滤波器的方法。
1991年,T.Chen和P.P.Vaidyunathnn通过对二维可分离滤波器进行平移和下采样操作,得到了具有水平和垂直方向分布的扇形方向滤波器,此方法无需对二维滤波器进行复杂的优化,且可实现良好的频域特性。
但由于其特性受到采样因子的制约,因此只适用于单一方向的滤波器设计中。
1997年,S.Suzuki等【25J通过对原型滤波器进行不同的下采样,获得具有不同方向特性的二维滤波器,同样,由于采样因子的制约,此方法只能实现4N(Ⅳ为正整数)个不同方向的扇形方向滤波器。
1.1.2二维方向滤波器组发展
本论文的后半部分主要研究具有方向提取能力的二维方向滤波器组的设计。
方向滤波器组最早I由BambergerIll在1992年提出,此方向滤波器组采用树形结构实现,可实现2“个楔形方向子带划分(r/为分解级数)。
图1.2给出了疗=2时滤波器组的实现结构。
2005年,M.N.Do等Lz6J提出了轮廓波(contourlet)变换,其具有良好的方向性和各向异性,同时可实现多分辨特性。
但是,该变换具有4/3的冗余度,并且同样只能实现2”个方向子带划分。
为使方向滤波器组具有更灵活的方向划分,T.T.Nguyen等【27-28】提出了多分辨方向滤波器组。
该滤波器组可实现3.2“个方向子带,然而,其设计过程中采用的二维滤波器具有复杂的结构,这使得设计复杂度大大提高。
2004年,R.Eslami等129J提出轮廓小波变换(wavelet.basedcontourlcttransform,wBca3,将方向滤波器组应用于小波变换中,保持了小波变换和方向滤波器组的诸多优点。
随着各种技术的成熟,方向滤波器组的设计正朝着具有频谱划分更灵活、设计更简单、无冗余等特点的方向不断发展,以实现更有效的几何
第二章二维多速率理论基础及扇形滤波器设计回顾
第二章二维多速率理论基础及扇形滤波器设计回顾
2.1引言
在本章中,我们主要对论文中要用到的二维多速率理论基础以及扇形方向滤波器的设计进行简要回顾。
在2.2节中,我们主要介绍二维多速率理论的基础知识。
2.3节主要回顾了现有的扇形方向滤波器设计方法,并对其各自的优缺点进行了分析。
2.4节对本章的内容进行了总结。
2.2二维多速率理论基础
首先,我们介绍多维多速率信号处理理论中常用的符号和预备知识。
本文中,集合、向量和矩阵均采用黑体字母。
如,Z表示肘维的复向量z=[ZoZI…%一。
r;n表示M维的整数向量n《‰惕…%一。
r。
我们定义:
JW一1
z。
=Z0~刁^…%一1%-I=兀矿;z。
=【z41z42…zdua】7’,其中,D为一个M×M的整
I=O
数矩阵,d。
为矩阵的第i个列向量;A7’和A’分别表示矩阵A的转置矩阵和共扼矩阵;A,√表示矩阵A在(f,/)的元素值。
IM。
M表示M×M的单位矩阵。
2.2.1采样晶格
在多速率系统中,采样是最基本的操作之一。
不同于一维系统,二维多速率系统的采样更加复杂。
它包括两个基本概念:采样矩阵和采样晶格(Lattice)。
一个二维采样矩阵M是一个2x2的整数非奇异矩阵。
其采样率为该矩阵行列式的绝对值,记为,(M)=Idet(M)l。
采样晶格定义为一组由M生成的整数向量集合:
LAT(M)={M·玛n∈A},(2一1)A代表所有二维整数向量集合。
显然,该集合是一包含无限多个二维整数向量的离散集合。
图2.1给出了由采样矩阵。
=[言呈]和Q=[二1:]所生成的晶格。
6方向滤波器(组)的设计及应用
图2.1采样晶格(a)由D生成,(b)由Q生成
作为采样系统中的另一个重要概念,向量陪集(Cosct)N(M)被定义为具有n=Mx,x∈[O,1)2形式的整数向量的集合。
其中向量n的个数等于采样率,(M)。
图2.2给出了由采样矩阵M=[;.:1]生成的NcM,,这里,刚喇协(:))o
图2.2由采样矩阵M生成的N(M)
此外,由采样矩阵M=[锪M%22]J生成的对称平行六面体(踟呦嘶cparallelepiped,.S!PD(M))被定义为3
SPD(M)=setofallpointsMxwithx【.1,1)2,(2·2)则SPD(zM可)可表示为
』一7r≤Mlq+M:ltOy<万,(2.3)
l一巧≤^厶2吐+M22国),<石.
例如,当M=[::]时'其对应的渤(棚1如图2.3所示。
第二章二维多速率理论基础及扇形滤波器设计回顾7
q
./∥‘jj飞
‘\..夕/
图2.3由采样矩阵M生成的SPD(nM彳)
2.2.2下采样(Downsamplin91
对于二维整数采样矩阵M,下采样定义为
(2—4)
yD(n)=x(Mn),
其对应的框图如图2.4所示,图2.5给出了M=[二:]时对应的采样示意图。
颤n)_卧%(n)
图2.4下采样框图
x(n)
他%%(n)
0123401
图2.5下采样示意图cM=[三:])
下采样操作在频域内的输入输出关系如下:
州2而1卟N(M,)X(M一7’(o-2zkj)).(2·5)
可以看出,变换后具有J(M)项,其中X(M刁∞)为输入信号频谱X(m)的“拉伸’’“㈣(Aliasing)’’。
当且仅当这些混叠项均为0时,才有可能从输出信号to(o)中项。
对应于k,≠0的其余各项为x佃)的“拉伸频移"项。
我们把k/≠0的项称为
恢复出原始输入信号x(o)。
