第十三章热力学基础第1节 准静态过程 功 热量
合集下载
循环过程-卡诺循环
QT
RT
ln V2 V1
RT
ln
p1 p2
(P223页13 14式)
p p1
A
T1 T2 Qab
p2
T1 B
p4
W
D
p3
C
Qcd T2 V
o V1 V4
V2 V3
13-5 循环过程 卡诺循环
A — B 等温膨胀吸热
Q1
Qab
RT1 ln
V2 V1
C — D 等温压缩放热
Q2
Qcd
从上式可知, 在低温处放出的热量越小, 则热机的效率越高.
如果在低温热源处不放热量, 即Q放=0, 则热机的效率等于 100% !!
即系统在高温热源处吸收的热量全部用于对外做功 ! (不违反 热力学第一定律 )
这种情况能实现吗 ?
根据实际经验这种现象是不能实现的 !!
第十三章 热力学基础
/19
13-5 循环过程 卡诺循环
T1 B
W
D Q2 T2
C
V
/19
13-5 循环过程 卡诺循环
Q2 Q1 Q1 T1
T2 T1
Q2 T2
将上式代入致冷系数定义式 e Q2 Q1 Q2
得到卡诺致冷机的致冷系数为:
e Q2
1
1
Q1 Q2 Q1 / Q2 1 T1 / T2 1
T2 T1 T2
(iii) C B,绝热压缩;外界对气体做功, 气体温度T2 T1(升高),.
(iv) 最后, B A,等温压缩;此过程中外界对气体做功使气体将气 量Q1传 递给高温热源, 从而完成一个逆循环.
第十三章 热力学基础
大学物理热力学基础-准静态过程-功-热量内能
2
如果其中有一个状态为非平衡态，则此过程不是准静 态过程。如果系统进行的速度过快，系统状态发生变 化后，还未来得及恢复新的平衡态，系统又发生了变 化，则该过程也不是准静态过程。
例如：气缸活塞压缩的速
度过快，气体的状态发生
变化，还来不及恢复，P、
F
V、T 无确定关系，则此过
程为不是准静态过程。
3
PA
量为0。 dT 0 2.过程方程 PV C
恒 温 源 T
P 1
P1
3.过程曲线
4.功 A V2 PdV V1
P2 o V1
T
2 V2 V
17
由理想气体状态方程
P m RT
V
RT
V
A V2 RT dV RT V2 dV
V1
V
V V1
等温过程的功
A RT ln V2 m RT ln V2
m RT ln P1
P2
19
三、等压过程
1.过程特点
系统的压强不变 dP 0
P
2.过程曲线
3.内能增量
E m i RT
2
1
2
P
4.功 压强不变
o
V1
V2 V
A
V2 V1
PdV
P
V2
V1
dV
P (V2 V1 )
PV
20
5.热量
QP E A
m
14
热力学第一定 律在等值过程
中的应用
15
一、等容过程
1.过程特点
V
系统的体积不变 dV = 0
系统对外做功为0 dA = 0 2.过程曲线
如果其中有一个状态为非平衡态，则此过程不是准静 态过程。如果系统进行的速度过快，系统状态发生变 化后，还未来得及恢复新的平衡态，系统又发生了变 化，则该过程也不是准静态过程。
例如：气缸活塞压缩的速
度过快，气体的状态发生
变化，还来不及恢复，P、
F
V、T 无确定关系，则此过
程为不是准静态过程。
3
PA
量为0。 dT 0 2.过程方程 PV C
恒 温 源 T
P 1
P1
3.过程曲线
4.功 A V2 PdV V1
P2 o V1
T
2 V2 V
17
由理想气体状态方程
P m RT
V
RT
V
A V2 RT dV RT V2 dV
V1
V
V V1
等温过程的功
A RT ln V2 m RT ln V2
m RT ln P1
P2
19
三、等压过程
1.过程特点
系统的压强不变 dP 0
P
2.过程曲线
3.内能增量
E m i RT
2
1
2
P
4.功 压强不变
o
V1
V2 V
A
V2 V1
PdV
P
V2
V1
dV
P (V2 V1 )
PV
20
5.热量
QP E A
m
14
热力学第一定 律在等值过程
中的应用
15
一、等容过程
1.过程特点
V
系统的体积不变 dV = 0
系统对外做功为0 dA = 0 2.过程曲线
热学课件5热力学第1定律
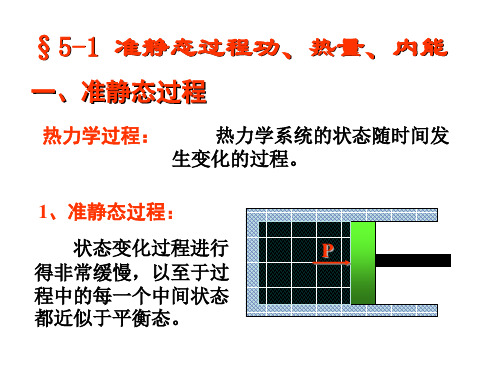
4、等温过程
等温过程:气体在状态变 化过程中温度保持不变。 Q
T= 恒量 ，dE =0
P
Q=A
等温过程的热力学第一定律: P
dQT dA
V1
V2 V
A V2 PdV V1
P M RT
V
A V2 M RT dV M RT ln V2 M RT ln P1
V1
V
V1
P2
等温过程系统作功和吸热：
等压过程系统内能的增量：
E
M
i 2
R(T2
T1 )
等压过程系统作功：
A
P(V2
V1 )
M
R(T2
T1 )
等压比热容公式：
Cp
CV
R
i 2
R
R
比热容比：
Cp i 2
CV i
单原子气体： i =3 双原子气体： i =5 多原子气体： i =6
1.67 1.4 1.33
例：1mol的某理想气体，在等压下由温度T1变为 T2，则其内能增量E为：
E QV
M
i R(T 2
To )
i R(T 2
To )
T
2QV inR
To
2500 273 285K 5 28.31
（2）T不变，热量变为什么？氢的P，V各为多少？
Q=W，热量转变为功
Q W M RT ln Po
P
Q ln Po
RT P
Q
500
P Poe RT 1 e 28.31273 0.90atm
M
C p dT
Qp
dQ p
T2 T1
M
CpdT
M
C p (T2
《大学物理 》准静态过程 功 热量
热力学 验证其理论 解释其理论 统计物理 微观理论，揭示热现象本质。 宏观理论，基本结论来自实验事实， 普遍可靠，但不能解释其微观本质。
第十三章
结构框图
理想气体 物态方程 热力学系统 内能变化的 两种量度 准静态 过程 功 热量
热力学基础
等值过程
应用 热力学 第一定律 （理想气体） 热力学 第二定律 （对热机效 率的研究）
28
物理学
第五版
做功 内能变化方式
热传递
点 能量转换 机械 运动 热运动 热运动 Q 热运动 量度
E改变方式
做功 热传递
特
Байду номын сангаас
与宏观位移相联系通 过非保守力做功实现 与温差相联系，通 过分子碰撞实现
W
十三章 热力学基础
29
物理学
第五版
13-2 热力学第一定律 内能
系统内能的增量只与系统的初态和末 态有关，与系统所经历的过程无关 .
（2）实验经验总结，自然界的普遍规律.
十三章 热力学基础
单位:
1 Pa 1 N m
2
p,V , T
标准大气压: 45纬度海平面处, 0 C 时的 5 大气压. 1 atm 1.0110 Pa
2 体积 V : 几何描述
单位:
1 m 10 l
3 3
第十二章 气体动理论
7
物理学
第五版
12-1 平衡态 理想气体物态方程 热力学第零定律
3 温度 T : 热学描述
单位: K(开尔文).
T 273 t
二 平衡态
1.热力学系统（简称系统）: 在给定范围内，由大量微观粒子所组成的宏观物体。 2.系统的外界（简称外界） 与所研究的热力学系统发生相互作用的其它物体。
第十三章
结构框图
理想气体 物态方程 热力学系统 内能变化的 两种量度 准静态 过程 功 热量
热力学基础
等值过程
应用 热力学 第一定律 （理想气体） 热力学 第二定律 （对热机效 率的研究）
28
物理学
第五版
做功 内能变化方式
热传递
点 能量转换 机械 运动 热运动 热运动 Q 热运动 量度
E改变方式
做功 热传递
特
Байду номын сангаас
与宏观位移相联系通 过非保守力做功实现 与温差相联系，通 过分子碰撞实现
W
十三章 热力学基础
29
物理学
第五版
13-2 热力学第一定律 内能
系统内能的增量只与系统的初态和末 态有关，与系统所经历的过程无关 .
（2）实验经验总结，自然界的普遍规律.
十三章 热力学基础
单位:
1 Pa 1 N m
2
p,V , T
标准大气压: 45纬度海平面处, 0 C 时的 5 大气压. 1 atm 1.0110 Pa
2 体积 V : 几何描述
单位:
1 m 10 l
3 3
第十二章 气体动理论
7
物理学
第五版
12-1 平衡态 理想气体物态方程 热力学第零定律
3 温度 T : 热学描述
单位: K(开尔文).
T 273 t
二 平衡态
1.热力学系统（简称系统）: 在给定范围内，由大量微观粒子所组成的宏观物体。 2.系统的外界（简称外界） 与所研究的热力学系统发生相互作用的其它物体。
131准静态过程功热量
第十三章 热力学基础
2
物理学
第五版
13-1 准静态过程 功 热量
三 热 量（过程量）
通过传热方式传递能量的量度，系统 和外界之间存在温差而发生的能量传递 .
T1 T2
T1 Q T2
第十三章 热力学基础
3
物理学
第五版
功与热量的异同
13-1 准静态过程 功 热量
（1）都是过程量：与过程有关； （2）等效性：改变系统热运动状态作用相同；
物理学
第五版
13-1 准静态过程 功 热量
二 功（过程量）
1 功是能量传递和转换的量度，它引 起系统热运动状态的变化.
2 准静态过程功的计算
第十三章 热力学基础
1
物理学
第五版
13-1 准静态过程 功 热量
dW Fdl pSdl dW pdV
W V2 pdV V1
注意： 作功与过程有关 .
第十三章 热力学基础Fra bibliotek51 cal = 4.18 J ， 1 J = 0.24 cal （3）功与热量的物理本质不同 .
第十三章 热力学基础
4
物理学
第五版
选择进入下一节：
本章目录
13-0 教学基本要求
13-1 准静态过程 功 热量
13-2 热力学第一定律 内能
13-3 理想气体的等体过程和等压过程 摩尔热容
13-4 理想气体的等温过程和绝热过程
2_3_1准静态过程、功、热、内能、热力学第一定律
所以，只有过程进行得无限缓慢， 每个中间态才可看作是平衡态。
中国石油大学，冯金波
一、准静态过程
3. 怎样判断“无限缓慢”？ 弛豫时间：系统由非平衡态到平衡态所需时间. 准静态过程条件： t过程进行 >>
例如，实际汽缸的压缩过程可看作准静态过程， t过程进行 = 0.1秒 =容器线度/分子速度 = 0.1米/100米/秒 = 10-3秒 二、过程曲线 准静态过程可用p－V 图上一条线表示。
P
1
2
o
V
中国石油大学，冯金波
§3.2 功、热、内能
(Work, Heat, Internal energy)
一、功 ：是通过对物体施“力”所传递的能量； 通过做功可以改变系统的状态。 1. 做功的种类：机械功、电功。 摩擦功： A f r l 电功：A UIt Uq 通常，广义功 = 广义力× 广义位移
中国石油大学，冯金波
第3章 热力学第一定律 描述热力学系统变化时，能量上所遵循的定律。
§3.1 准静态过程(quasi-static process)
•系统的状态发生变化时，系统在经历一个过程。 •过程进行的任一时刻，系统的状态为非平衡态。 •热力学中，只有平衡态才可用宏观量描述， 为此引入准静态过程的概念。 一、准静态过程 1. 定义，由无数个平衡态组成的过程， 即，系统的每个中间态都是平衡态。 过程既然在进行，又怎么可能有平衡态呢？
中国石油大学，冯金波
三、温度不变的热ol理想气体与温度为T的热库保持热接 触，并做准静态的膨胀（或压缩）时，其温度 也为T并保持不变，而体积从V1变化到V2。 问：在这一等温过程中气体是否吸收了热量？ E E2 E1 Q A 0 Q A RT ln(V2 / V1 ) 2）相变过程 物体在吸收或放出热量而发生相变的过程中， （如熔化、汽化、液化、凝固） 其温度不变。 物体在相变时所吸收或放出的热量叫潜热。
热力学第一定律
8/19/2013 8:40 PM 2
13.1准静态过程 功 热量
通常系统在状态变化时，恢复为平衡态所需的时 间总比状态变化的时间要短。我们假想系统的状态每 次作一微小的变化，系统有足够的时间恢复为平衡态。
p
II
I
o
8/19/2013 8:40 PM
V
3
13.1准静态过程 功 热量
系统中的每一中间状态都是平衡态，都可以用一 组物态参量来表示，我们将这种过程称作准静态过程 (non-quasistatic process)。
等体过程中一摩尔气体吸收的热量等于内能的增量
i dQ dE RdT 2 dQ i CV ,m R dT 2
Cv,m是等体过程中，1.0摩尔气体温度升高1.0度 所吸收的热量，称作定体摩尔热容量(specific heat capacity at constant volume)。 理想气体内能的变化仅仅与初、末状态有关，因 此任意过程系统内能的增量均可以表示为
a
W1a 2 W1a Wa 2 0.81 105 J Q1a 2 Q1a Qa 2 0.94 105 J
E1 a 2 E1 a E a 2 PM13 105 J 0. 8/19/2013 8:40
5 0 10
1
50 V/L
24
13.3 等体、等压过程 摩尔热容量 (2)12
8/19/2013 8:40 PM 28
p2
13.4 理想气体等温过程和绝热过程
o
V1
V2
7
13.1准静态过程 功 热量
三、热量 系统在过程中，常常与外界有热量的交换，吸收 热量或放出热量。
热量是系统在与外界接触时，由于温度差所传递 的气体分子热运动的能量。热量从高温物体传向低温 物体，但相反的过程不会自动完成。
13.1准静态过程 功 热量
通常系统在状态变化时，恢复为平衡态所需的时 间总比状态变化的时间要短。我们假想系统的状态每 次作一微小的变化，系统有足够的时间恢复为平衡态。
p
II
I
o
8/19/2013 8:40 PM
V
3
13.1准静态过程 功 热量
系统中的每一中间状态都是平衡态，都可以用一 组物态参量来表示，我们将这种过程称作准静态过程 (non-quasistatic process)。
等体过程中一摩尔气体吸收的热量等于内能的增量
i dQ dE RdT 2 dQ i CV ,m R dT 2
Cv,m是等体过程中，1.0摩尔气体温度升高1.0度 所吸收的热量，称作定体摩尔热容量(specific heat capacity at constant volume)。 理想气体内能的变化仅仅与初、末状态有关，因 此任意过程系统内能的增量均可以表示为
a
W1a 2 W1a Wa 2 0.81 105 J Q1a 2 Q1a Qa 2 0.94 105 J
E1 a 2 E1 a E a 2 PM13 105 J 0. 8/19/2013 8:40
5 0 10
1
50 V/L
24
13.3 等体、等压过程 摩尔热容量 (2)12
8/19/2013 8:40 PM 28
p2
13.4 理想气体等温过程和绝热过程
o
V1
V2
7
13.1准静态过程 功 热量
三、热量 系统在过程中，常常与外界有热量的交换，吸收 热量或放出热量。
热量是系统在与外界接触时，由于温度差所传递 的气体分子热运动的能量。热量从高温物体传向低温 物体，但相反的过程不会自动完成。
准静态过程 功 热量
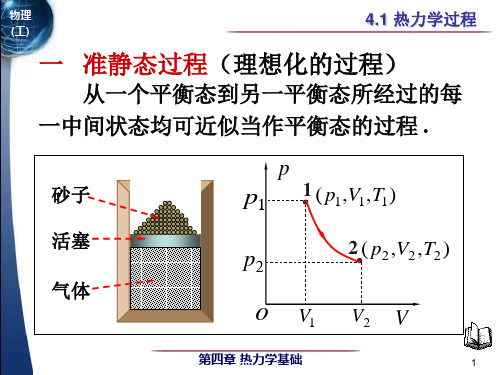
dQ p dU dW
o
V1
V2
V
第四章 热力学基础
22
物理 (工)
4.4 热力学第一定律对理想气体等值过程的应用
摩尔定压热容: 1 mol 理想气体在等压 过程中吸收热量 dQ p ，温度升高 dT ，其 摩尔定压热容为： dQ p = C p,m dT
1 dU pdV 1 dU 1 pdV C p,m dT dT dT dT 1 d i 1 pdV i 1 pdV ( RT ) R dT 2 dT 2 dT i2 R 2 dQ p
o
V1
V2 V
第四章 热力学基础
40
物理 (工)
V1
V2 V
Q U 2 U1 W U W
第四章 热力学基础
11
物理 (工)
4.3 热力学能 热力学第一定律
准静态过程
Q U
微变过程
V2
V1
pdV
dQ dU dW dU pdV
第四章 热力学基础
12
物理 (工)
4.3 热力学能 热力学第一定律
Q U 2 U1 W U W
第四章 热力学基础
36
物理 (工)
4.5 理想气体的绝热过程
绝热过程
与外界无热量交换的过程 特征 由热力学 第一定律
dQ 0
p
p1
1
( p1, 1, 1 ) V T
( p2 ,V2 ,T2 )
dW dU 0
p2
2
V2 V
dW dU
o V1 dV
dU CV ,m dT
绝热的汽缸壁和活塞
new热力学第一定律
当气体作无摩擦的准静态膨胀或压缩时， 为了维持气体的平衡态，外界的压强必然 等于气体的压强。 II v2
A dA PdV
I v1
说明
A＝ pdV
V1
V2
P
•系统所作的功与系统的始末状态有关， 而且还与路径有关，是一个过程量。
•气体膨胀时，系统对外界作功 气体压缩时，外界对系统作功 系统对外界所作的 •作功是改变系统内能的一种方法 •本质：通过宏观位移来完成的：机械运动→ 功等于pV 图上过 分子热运动 程曲线下面的面积
V2 M i Q R(T2 T1 ) pdV V1 2 理想气体的压强保持不变，p=const
•过程方程：
•内能、功和热量的变化
A
V2
V1 V2 T1 T2
pdV p(V
2
V 1)
•特征：
系统吸收的热量一部分 用来增加系统的内能， 另一部分使系统对外界 作功。
V1
Q p U 2 U1 p(V2 V1 )
为从平衡态破坏到新平 衡态建立所需的时间称 为弛豫时间。
3、准静态过程
如果一个热力学系统过程在始末两平衡态之间所经历的之 中间状态，可以近似当作平衡态，则此过程为准静态过 程。 •准静态过程只有在进行的“无限缓慢”的条件下才可 能实现。 •对于实际过程则要求系统状态发生变化的特征时间远 远大于弛豫时间才可近似看作准静态过程。
又根据PV n C，有P1V1n P2V2n C，所以
A
P2V2nV 21n 1 n
PV1nV11n P2V2 PV1 PV1 P2V2 1 1 1 1 n 1 n n 1
15.3 内能 热力学第一定律
一、内能
热力学系统的能量取决于系统的状 态——内能。 M i
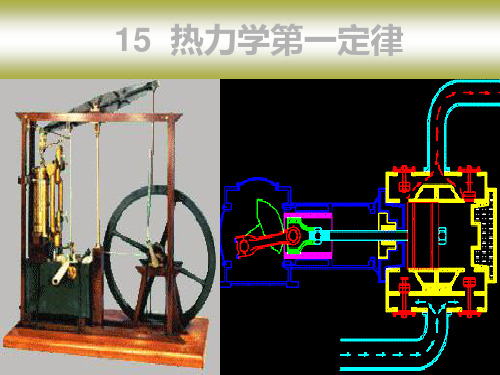
A dA PdV
I v1
说明
A＝ pdV
V1
V2
P
•系统所作的功与系统的始末状态有关， 而且还与路径有关，是一个过程量。
•气体膨胀时，系统对外界作功 气体压缩时，外界对系统作功 系统对外界所作的 •作功是改变系统内能的一种方法 •本质：通过宏观位移来完成的：机械运动→ 功等于pV 图上过 分子热运动 程曲线下面的面积
V2 M i Q R(T2 T1 ) pdV V1 2 理想气体的压强保持不变，p=const
•过程方程：
•内能、功和热量的变化
A
V2
V1 V2 T1 T2
pdV p(V
2
V 1)
•特征：
系统吸收的热量一部分 用来增加系统的内能， 另一部分使系统对外界 作功。
V1
Q p U 2 U1 p(V2 V1 )
为从平衡态破坏到新平 衡态建立所需的时间称 为弛豫时间。
3、准静态过程
如果一个热力学系统过程在始末两平衡态之间所经历的之 中间状态，可以近似当作平衡态，则此过程为准静态过 程。 •准静态过程只有在进行的“无限缓慢”的条件下才可 能实现。 •对于实际过程则要求系统状态发生变化的特征时间远 远大于弛豫时间才可近似看作准静态过程。
又根据PV n C，有P1V1n P2V2n C，所以
A
P2V2nV 21n 1 n
PV1nV11n P2V2 PV1 PV1 P2V2 1 1 1 1 n 1 n n 1
15.3 内能 热力学第一定律
一、内能
热力学系统的能量取决于系统的状 态——内能。 M i
10-1 准静态过程 功 内能和热量
总热量：
Q Q
10-1 准静态过程 功 内能和热量
10.2
热力学第一定律
第10章 热力学定律
10.2.1 热力学第一定律 某一过程，系统从外界吸热 Q，对外 界做功 A，系统内能从初始态 E1变为 E2，则由能量守恒：
A ΔE Q
内能是状态量， A、 Q是过程量
对微元过程：
Q dE A
热一律的另一种表述： 第一类永动机制不成 对准静态过程： Q E2 E1
V2
V1
pdV
10.2.2 热容
C
Q
dT
单位：J/mol· K
• 摩尔热容量 C ，
• 比热容 c ， 单位：J/kg· K
Q 为过程量
C为过程量
经常用到1摩尔物质在等体过程以及在等压过程中的热 容量，称为摩尔定体热容和摩尔定压热容，分别定义 为：
CV ,m
i R 2
C P ,m
i2 R 2
2i i
i=3
单原子气体：
双原子气体： 多原子气体：
1.67
i=5
i=6
1.40
1.33
用 C
V ,m
CP,mγ值和实验比较，常温下符合很好
t 200 C
CV ,m R 2
P 1.01105 pa
CP ,m R 2
P
A
(PB,VB,TB)
V2
V1
pdV
O
VA
dV
VB
V
说明 δA>0：系统对外做功 系统所作的功在数值上 等于P-V 图上过程曲线 以下的面积。
作功与过程有关 。
p 下，气体准静态地由体积 V1 例 计算在等压 的过程系统对外界所做的功。
13-1 准静态过程 功 热量
第十三章
热力学基础
热力学是研究热现象的宏观理论——根据实验总结出来的热 根据实验总结出来的热 热力学是研究热现象的宏观理论 力学定律，用严密的逻辑推理的方法， 力学定律，用严密的逻辑推理的方法，研究宏观物体的热力 学性质。 学性质。 热力学不涉及物质的微观结构， 热力学不涉及物质的微观结构，它的主要理论基础是热力学 的三条定律。 的三条定律。 本章的内容是热力学第一定律和热力学第二定律。 本章的内容是热力学第一定律和热力学第二定律。
2、气体的物态参量 、
把用来描述系统宏观状态的物理量称为状态参量。 气体的宏观状态可以用V、 、 气体的宏观状态可以用 、P、T 描述
体积V—— 几何参量 体积 压强p——力学参量 压强 力学参量 温度T——热力学参量 温度 热力学参量 3、说明 、
气体的p 是描述大量分子热运动集体特征的物理量， 气体的 、V、T 是描述大量分子热运动集体特征的物理量， 而气体分子的质量、 是宏观量，而气体分子的质量、速度等是描述个别分子运动的 物理量， 物理量，是微观量。
M = NAm
p = nkT
−23
k = R / N A = 1.38 × 10
J⋅K
−1
k 称为玻耳兹曼常量 称为玻耳兹曼常量. n =N/V，为气体分子数密度 ，为气体分子数密度.
13-1 准静态过程 功 热量
一、准静态过程
1、热力学过程 、
当系统的状态随时间变化时， 当系统的状态随时间变化时， 我们就说系统在经历一个热力 学过程，简称过程。
为从平衡态破坏到新平 衡态建立所需的时间称 弛豫时间。 为弛豫时间。
3、准静态过程 、
如果一个热力学系统过程在始末两平衡态之间所经历的之 中间状态，可以近似当作平衡态， 中间状态，可以近似当作平衡态，则此过程为准静态过 程。 •准静态过程只有在进行的“无限缓慢”的条件下才可 准静态过程只有在进行的“ 准静态过程只有在进行的 无限缓慢” 能实现。 能实现。 •对于实际过程则要求系统状态发生变化的特征时间远 对于实际过程则要求系统状态发生变化的特征时间远 说明： 说明： 远大于弛豫时间才可近似看作准静态过程。 远大于弛豫时间才可近似看作准静态过程。 图上的一条曲线表示， 系统的准静态变化过程可用pV 图上的一条曲线表示， 称之为过程曲线。 称之为过程曲线。 过程曲线
准静态过程、功、热量准静态：过程中的每一状态都是平衡态 功
0
比热容比
γ=
CP,m CV ,m
R 2+i = 1+ = CV ,m i
循环过程
∆E=0
制冷机） 正循环 —— 逆时针 （制冷机） 制冷系数
热机） 正循环 —— 顺时针 （热机） 循环效率 η =
W Q = 1− 2 Q Q 1 1
Q2 Q2 e= = W Q1 − Q2
卡诺循环 只与两个单一恒温热源 交换热量循环 2等温过程 绝热过程 等温过程+2绝热过程 等温过程 与工质无关， 与工质无关，仅 与高、 与高、低温热源 有关
T2 η = 1− T1
热力学第二定律
T2 e= T1 − T2
克劳修斯表述法 开尔文表述法 可逆过程和不可逆过程
Q = ∆E +W dQ = dE + dW
理想气体四个等值过程
过程 方程
Q
∆E 0
W
摩尔 热容
等体 等压
V =C P/T = C
P =C V /T = C
m m Cv,m (T2 − T1) Cv,m (T2 − T1) M M
Cv,m = i R 2
m m Cp,m (T2 −T1) Cv,m (T2 − T1) m R(T2 − T1) M M M
第十三章 热力学基础
• 准静态过程、功、热量 准静态过程、 – 准静态：过程中的每一状态都是平衡态 准静态： பைடு நூலகம் 功 理想气体准静态过程的功
W =∫
V2
V 1
pdV
功--过程量 过程量 内能--状态量 内能 状态量
理想气体的内能 m i E = E(T ) = RT M2
第十三章 热力学基础
热力学第一定律 Q > 0 吸热 Q < 0 放热； 放热； W > 0 系统对外作功， 系统对外作功， W < 0 外界对系统作功 。
准静态过程
宏观运动能量
功
分子热运动能量
分子热运动能量 热量
分子热运动能量
➢ 热容量 在一定的过程中，当物体的温度升高（或降低）1K
所吸收（或放出）的热量称为物体在该过程中的热容 量，简称热容。
Cx
lim (
T 0
Q T
)ቤተ መጻሕፍቲ ባይዱ
x
(
dQ dT
)
x
摩尔热容：1mol 物质的热容
将摩尔热容的定义应用到等体、等压过程中：
热力学基础
准静态过程 功 热量
一、 准静态过程 热力学过程： 1
2
1
2
准静态过程： 在过程进行的每一时刻，系统所经过的任一
中间状态都无限地接近平衡态。
说明 (1) 准静态过程是一个理想过程； (2) 除一些进行得极快的过程（如爆炸过程）外，大 多数情况下都可以把实际过程看成是准静态过程； 如：实际汽缸的压缩过程可看作准静态过程
定体摩尔热容
dQ
CV ,m
( dT
)V
定压摩尔热容
Cp,m
(
dQ dT
)
p
系统体积由V1增大到 V2，系统对外做功为:
W V2 pdV V1
2、 功的图示法：
p
W V2 pdV 曲线AB下的面积 V1 (1) 曲线AB下的面积即表示系 p
统在AB过程中做的功。
(2) 功是与过程有关的物理量。
例：
p ( p1,V1)
p ( p1,V1)
p
A
dW pdV
B
V1 dV V2 V
( p1,V1)
( p2 ,V2 )
V
( p2 ,V2 )
V
( p2 ,V2 )
热力学第一定律
1.013 105 Pa
2
1 a 等体过程
A1a 0
a
1
Q1a CV ,m (Ta T1 )
5
o 10
50
V 103 m 3
Q1a CV ,m (Ta T1 )
i R(Ta T1 ) 2
5 5 ( paVa p1V1 ) 1.90 10 2 5 J
实际气体内能：所有分子热运动的动能和分子 间势能的总和。内能是状态参量T、V 的单值 函数。
理想气体内能：所有分子热运动的动能
i E RT 2
理想气体内能是状态参量T 的单值函数， 是状态量。
§10-2
热力学第一定律
一、热力学第一定律
某一过程，对外界做功 A 和传给系统的热量 Q 之和等于系统的内能的增量系统内能 E
a
5 o
1
10
50
V 103 m 3
§10-4
一、绝热过程
绝热过程
系统不与外界交换热量的过程。
Q dE pdV
Q 0, pdV dE
V2
V1
pdV CV ,m (T2 T1 )
绝热过程中系统对外做功全部是以系统 内能减少为代价的。
二、绝热方程的推导
Q dE pdV Q 0 pdV CV ,m dT
A A1a Aa 2 8.1 10 J
4
Q Q1a Qa 2 9.4 10 J
4
E E1a Ea 2 1.3 10 J
4
（2）1 2 过程
p1 p2 A (V1 V2 ) 2
0.51 10
5
第十三章 热力学基础
V2
1
物理系 张建锋
A P dV P V2 V1 R(T2 T1 ) V
QP = cp（T2-T1）
P
（PV1T1） Q （PV2T2）
E = cV（T2-T1）
等压膨胀 V2>V1 系统对外作功 A >0 T2 >T1 内能增加E2 -E1 >0 系统吸热Q >0 等压收缩 V2 < V1 外界对系统作功A <0
5 3 1.67 (单 ) i 2 7 1.40 (双 ) 理论值 i 5 8 6 1.33 (多)
热容量可由实验测得，理论值和实验值的比较见 书P 217～220的表13－1，2，3
理学院
物理系 张建锋
§13-4 理想气体的等温过程和绝热过程
一、等温过程
←快
←缓慢
非平衡态
接近平衡态
理学院
物理系 张建锋
系统T1 非准静态过程
系统T2
系统T1
T1+△T
T1+2△T
T1+3△T
T2
准静态过程
理学院
物理系 张建锋
过程即变化 平衡即不变 矛盾 统一于“无限缓慢”
只有过程进行得无限缓慢，每个中间态才可 看作是平衡态。
如何判断“无限缓慢”？ 引入弛豫时间（relaxation time） ： 平衡破坏
理学院
物理系 张建锋
过程方程： TV 1 const .
PV const . 1 p T const .
4. 在P - V图上的
（P 2V2T2）
A
0
V
A
V2
V1
1
物理系 张建锋
A P dV P V2 V1 R(T2 T1 ) V
QP = cp（T2-T1）
P
（PV1T1） Q （PV2T2）
E = cV（T2-T1）
等压膨胀 V2>V1 系统对外作功 A >0 T2 >T1 内能增加E2 -E1 >0 系统吸热Q >0 等压收缩 V2 < V1 外界对系统作功A <0
5 3 1.67 (单 ) i 2 7 1.40 (双 ) 理论值 i 5 8 6 1.33 (多)
热容量可由实验测得，理论值和实验值的比较见 书P 217～220的表13－1，2，3
理学院
物理系 张建锋
§13-4 理想气体的等温过程和绝热过程
一、等温过程
←快
←缓慢
非平衡态
接近平衡态
理学院
物理系 张建锋
系统T1 非准静态过程
系统T2
系统T1
T1+△T
T1+2△T
T1+3△T
T2
准静态过程
理学院
物理系 张建锋
过程即变化 平衡即不变 矛盾 统一于“无限缓慢”
只有过程进行得无限缓慢，每个中间态才可 看作是平衡态。
如何判断“无限缓慢”？ 引入弛豫时间（relaxation time） ： 平衡破坏
理学院
物理系 张建锋
过程方程： TV 1 const .
PV const . 1 p T const .
4. 在P - V图上的
（P 2V2T2）
A
0
V
A
V2
V1
《准静态过程功热量》课件
• 案例一：汽车发动机冷却系统 * 描述：准静态过程功热量在汽车发动机冷却系统中的应用，如何通过计算准静态过程功热量来优化 冷却效果。 * 涉及知识点：准静态过程功热量的计算方法，汽车发动机冷却系统的原理。
• * 描述：准静态过程功热量在汽车发动机冷却系统中的应用，如何通过计算准静态过程功热量来优化冷却效果。 • * 涉及知识点：准静态过程功热量的计算方法，汽车发动机冷却系统的原理。
• 案例四：新能源领域的应用 * 描述：准静态过程功热量在新能源领域的应用，如何通过计算准静态过程功热量来优化新能源设备的 性能。 * 涉及知识点：准静态过程功热量的计算方法，新能源领域的原理和应用。
• * 描述：准静态过程功热量在新能源领域的应用，如何通过计算准静态过程功热量来优化新能源设备的性能。 • * 涉及知识点：准静态过程功热量的计算方法，新能源领域的原理和应用。
总结与展望
总结：准静态过程功热量的重要性及在各个领域的应用前 景
准静态过程功热量在热力学中 的地位和作用
准静态过程功热量在不同领域 的应用案例
准静态过程功热量在节能减排、 环境保护等领域的重要性
未来准静态过程功热量研究的 发展方向和挑战
研究方向：深入 研究准静态过程 功热量的基本原 理和应用领域， 探索新的理论和 方法，提高其准 确性和可靠性。
• 案例三：工业生产过程中的热量控制 * 描述：准静态过程功热量在工业生产过程中的热量控制中的应用，如何通过计算准静态过程 功热量来实现精确的温度控制。 * 涉及知识点：准静态过程功热量的计算方法，工业生产过程中的热量控制原理。
• * 描述：准静态过程功热量在工业生产过程中的热量控制中的应用，如何通过计算准静态过程功热量来实现精确的温度控制。 • * 涉及知识点：准静态过程功热量的计算方法，工业生产过程中的热量控制原理。
• * 描述：准静态过程功热量在汽车发动机冷却系统中的应用，如何通过计算准静态过程功热量来优化冷却效果。 • * 涉及知识点：准静态过程功热量的计算方法，汽车发动机冷却系统的原理。
• 案例四：新能源领域的应用 * 描述：准静态过程功热量在新能源领域的应用，如何通过计算准静态过程功热量来优化新能源设备的 性能。 * 涉及知识点：准静态过程功热量的计算方法，新能源领域的原理和应用。
• * 描述：准静态过程功热量在新能源领域的应用，如何通过计算准静态过程功热量来优化新能源设备的性能。 • * 涉及知识点：准静态过程功热量的计算方法，新能源领域的原理和应用。
总结与展望
总结：准静态过程功热量的重要性及在各个领域的应用前 景
准静态过程功热量在热力学中 的地位和作用
准静态过程功热量在不同领域 的应用案例
准静态过程功热量在节能减排、 环境保护等领域的重要性
未来准静态过程功热量研究的 发展方向和挑战
研究方向：深入 研究准静态过程 功热量的基本原 理和应用领域， 探索新的理论和 方法，提高其准 确性和可靠性。
• 案例三：工业生产过程中的热量控制 * 描述：准静态过程功热量在工业生产过程中的热量控制中的应用，如何通过计算准静态过程 功热量来实现精确的温度控制。 * 涉及知识点：准静态过程功热量的计算方法，工业生产过程中的热量控制原理。
• * 描述：准静态过程功热量在工业生产过程中的热量控制中的应用，如何通过计算准静态过程功热量来实现精确的温度控制。 • * 涉及知识点：准静态过程功热量的计算方法，工业生产过程中的热量控制原理。
第13章 热力学基础 第1、2节
１３–１ 准静态过程功热量教学基本要求一掌握内能、功和热量等概念. 理解准静态过程.二掌握热力学第一定律，能分析、计算理想气体在等体、等压、等温和绝热过程中的功、热量和内能的改变量.三理解循环的意义和循环过程中的能量转换关系，会计算卡诺循环和其他简单循环的效率.四了解可逆过程和不可逆过程，了解热力学第二定律和熵增加原理.准静态过程是一个理想化的过程，没有哪一个过程是严格意义上的准静态过程。
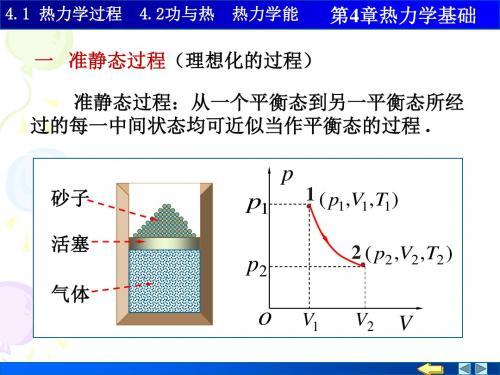
一. 准静态过程（理想化的过程）如果从一个平衡态到另一平衡态所经过的每一个中间状态均可以近似看作平衡态，则该过程就称作准静态过程。
想一想：为什么这样说？１３–１ 准静态过程功热量TV p ,,TV p ,,''真空膨胀一定量的气体，在不受外界的影响下, 经过一定的时间, 系统达到一个稳定的, 宏观性质不随时间变化的状态称为平衡态.（理想状态）pVo),,(T V p ),,(''T V p A B一. 准静态过程（理想化的过程）想一想：满足什么条件的过程可以近似看作准静态过程？气体活塞砂子),,(111T V p ),,(222T V p 1V 2V 1p 2p pVo12１３–１ 准静态过程功热量一. 准静态过程（理想化的过程）想一想：对于非准静态过程，能否用一条ｐ－Ｖ 图上的曲线来表示？),,(111T V p ),,(222T V p 1V 2V 1p 2p pVo12功是能量传递和转换的量度，它引起系统热运动状态的变化.准静态过程功的计算pdVpdSdl Fdl dW ===∫=21d V VVp W 注意：作功的大小不仅与系统的始末状态有关，而且与过程有关.１３–１ 准静态过程功热量二. 功（过程量）∫=21d V VVp W 想一想：１、对非静态过程系统对外所作的功能否按上式计算？为什么？２、上述计算的结果何时出现正值？负值？零？它们对应的物理意义是什么？∫=21d V VVp W １ｍｏｌ理想气体从状态Ａ足够缓慢地变化到状态Ｂ，且一直保持温度Ｔ不变，若已知状态Ａ、Ｂ时气体体积分别为ＶＡ和ＶＢ，求该过程中气体对外所作的功。
2019物理PPT课件4.1 4.2准静态过程 功 热量.ppt
四、 内 能 （状态量）
实验证明系统从 A 状态变化到 B 状态，可以采 用做功和传热的方法，不管经过什么过程，只要始 末状态确定，做功和传热之和保持不变 .
p
A*
2
p
1
*B
A*
2
1
*B
o
V
o
V
WA1B QA1B WA2 B QA2 B
WA1B 2 A QA1B 2 A 0
4.1 热力学过程
4.1 热力学过程
4.2功与热
热力学能
第4章热力学基础
热量
1 、系统与外界由于存在温度差传递的能量。
Q CT
Q cmT
单位
dQ C dT
1 dQ c m dT
——热容
——比热容
J
K
J
J
kg K
1 dQ m Q Cm T C m ——摩尔热容 m dT M M
mol K
三、 热 量（过程量） 通过传热方式传递能量的量度，系统和外界之间 存在温差而发生的能量传递 . 功与热量的异同
T1 T2
1）过程量：与过程有关；
T1 Q T2
2）等效性：改变系统热运动状态作用相同； 1卡 = 4.18 J ， 1 J = 0.24 卡
3）功与热量的物理本质不同 . 功 宏观运动 分子热运动 热量 分子热运动 分子热运动
2、若Q>0，系统从外界吸收热量； 若Q<0，系统向外界放出热量。
4.1 热力学过程
4.2功与热
热力学能
第4章热力学基础
3、热量是过程量 。 等体过程：
QV m M CV, m T
等压过程：
Qp m M Cp,m T
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
功是过程量
(p1 ,V1 )
p
(p1 ,V1 )
(p2 ,V2) A2 V
p
O
A3
(p2 ,V2) V
第十三章 热力学基础
物理学
第五版
T1功 T1 ≠准静态过程 T2 =T 13-1 热量 2
1.传热
三、热 量(过程量)
A
B
A
B
传热也是热力学系统与外界交换能量的一种方式，是在热学相互 作用过程（热学平衡条件破坏（存在温度差））中产生的。传热 也是系统状态发生变化的过程。热量通过传热方式传递能量的量 度，系统和外界之间存在温差而发生的能量传递 .
传热的微观本质是分子无规则热运动间的平均动 能通过分子碰撞的传递。 传热过程中分子无规则热运动动能传递的总大小 为热量。 dQ 0 表示系统从外界吸热； 2.热量 dQ 0 表示系统向外界放热。 准静态过程中传递的热量是过程量。 3.热量的单位 在SI制中：焦耳(J)
第十三章 热力学基础
物理学
第五版
功与热量的异同
13-1 准静态过程 功 热量
(1)做功和传热的大小不但与系统的初、末态有关,而且 与过程有关,它们都是过程量,不是状态量,因而微量功和 微量传热分别写成 dW 和dQ,它们不是全微分. (2)等效性：改变系统热运动状态作用相同； 1cal=4.18J， 1J=0.24cal (3)功与热量的物理本质不同 . 热量和功是系统状态变化中伴随发生的两种不同的能 量传递形式。微观上做功表现为分子有规则运动（机 械运动）和分子无规则热运动间能量的转换；热传递 实际上是分子无规则热运动间能量的传递。 功 分子热运动 宏观运动 热量 分子热运动 分子热运动 第十三章 热力学基础
第十三章 热力学基础
物理学
第五版
13-1 准静态过程 功 热量
p
3.功的图示法求解
dW pdV 元功：
总功： W dW pdV
V1 V1 V2 V2
0 V1
dA
V V+dV V2
V
功的量值等于 p-V 图中，过程曲线下面的面积。 状态发生相同变化所经不同过程中的功:
p (p1 ,V1 ) A1 O (p2 ,V2) V O
物理学
第五版
准静态过程 热力学过程 非准静态过程
第十三章 热力学基础
物理学
第五版
13-1 准静态过程 功 热量 非平衡态源自平衡态 真空平衡态
非准静态过程：其中间状态都是非平衡态，系统没有统 一的参量，所以不能用状态参量来描述。驰豫时间 。
一、准静态过程（理想化的过程）
准静态过程：如果实际过程无限缓慢进行时，即过程中 每一中间状态都无限接近平衡态。 准静态过程与非准静态过程区别：过程进行的快慢； 准静态过程是一种理想情况, 人工方法获得； 自发过程是非准静态过程。
13-1 准静态过程 功 热量 热力学系统：要含有大量原子、分子或其它微观粒子， 体积有限的宏观物体。热力学研究的对象。 外界：热力学系统以外的物体。 系统分类：孤立系统，封闭系统，开放系统。 热力学过程：热力学系统从一个状态变化到另一个状态。 发生原因：偏离平衡条件。 平衡态：系统内部没有宏观的粒子和能量流动，系统的宏 观性质不随时间改变，可以用状态参量描述。处 于平衡态的状态应满足平衡条件。 平衡条件：系统和外界处于力学、热学、相和化学平衡。
W
V2
V1
pdV
第十三章 热力学基础
dl
5
注意：作功与过程有关
物理学
第五版
注意
13-1 准静态过程 功 热量
设 W 表示系统对外界的功， 系统体积增大，系统对外界作正功。 系统体积减小，系统对外界作负功。 此体积功公式适用于无摩擦准静态过程的任何系统。 系统在准静态过程中对外界所做功的大小可表示为 p-V 状态图上此过程曲线（过程方程）下的面积。 过程方程不能理解为系统的状态方程。 做功是过程量，不是状态量，做功大小与过程方程 有关。 做功在微观上表现为分子有规则运动（机械运动） 和分子无规则热运动间能量的转换，这是通过分子 间碰撞实现的。
循环过程
0
V
第十三章 热力学基础
物理学
第五版
13-1 准静态过程 功 热量
二、功（过程量）
1.功的概念 做功是热力学系统与外界交换能量的一种方式，是在力 学相互作用过程（力学平衡条件破坏）中产生的。系统 与外界交换能量的过程就是系统状态发生变化的过程。 功是能量传递和转换的量度，它引起系统热运动状态的 变化. 宏观运动能量 热运动能量 2.准静态过程功的计算 S dW Fdl pSdl u dW pdV p
p
砂子
活塞 气体
p1
p2
1 ( p1,V1, T1 )
2 ( p2 ,V2 , T2 )
V2
o V1 第十三章 热力学基础
V
物理学
第五版
13-1 准静态过程 功 热量
系统状态的改变可通过非准静态过程和准静态过程来实 现，例如：系统（T1）从 外界（T2）吸热温度升至 T2
方法 1：让系统直接与温度为 T2 的热源接触，进行非等温热传导， 系统较快经非平衡态到达最终的温度为T2 平衡态。此过程 为非准静态过程。 方法 2：让系统分别与无数温度位于 T1 与 T2 之间并相差一无限小 量 △T 的热库接触，使热库温度总比系统高一无限小量 △T， 这样可使系统温度缓慢从 T1 升至 T2，每一小步的热 系统 T1 传导可看作等温热传导，系 统每时每刻处于平衡态，此 过程为准静态过程。 T1+△T T1+2△T T1+3△T T2
第十三章 热力学基础
物理学
第五版
13-1 准静态过程 功 热量
准静态过程的过程曲线 因为状态图中任何一点都表示系统的一个平衡态，故准 静态过程可用系统的状态图（p-V 图、p-T 图、V-T 图） 中一条过程曲线表示。
P
等温过程
等容过程
等压过程
改变系统状态的方法： 作功：力学平衡破坏下 的能量转移 传热：热学平衡破坏下 的能量转移