能量方程伯努利方程实验
伯努利方程实验
实验二伯努利方程实验一.实验目的1.观察恒定流情况下,水流所具的位置势能、压强势能和动能,以及在各种边界条件下能量的守恒和转换规律,加深对能量方程物理意义的理解。
2.观察测压管水头线和总水头线沿程变化的规律,以及水头损失现象。
3.验证测速管〔毕托管〕原理。
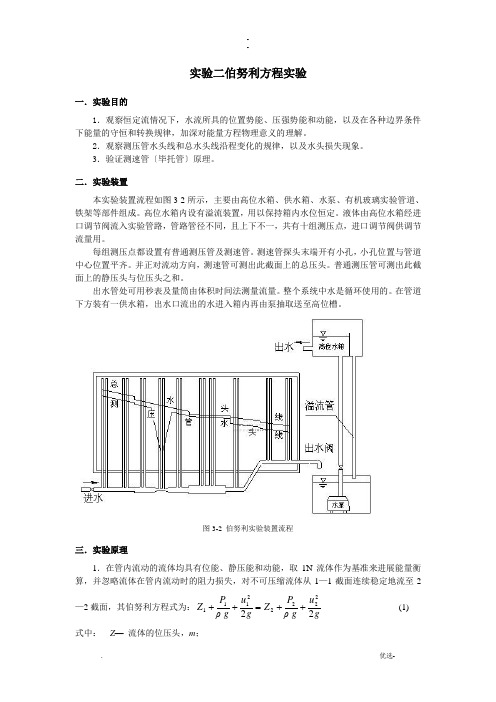
二.实验装置本实验装置流程如图3-2所示,主要由高位水箱、供水箱、水泵、有机玻璃实验管道、铁架等部件组成。
高位水箱内设有溢流装置,用以保持箱内水位恒定。
液体由高位水箱经进口调节阀流入实验管路,管路管径不同,且上下不一,共有十组测压点,进口调节阀供调节流量用。
每组测压点都设置有普通测压管及测速管。
测速管探头末端开有小孔,小孔位置与管道中心位置平齐。
并正对流动方向,测速管可测出此截面上的总压头。
普通测压管可测出此截面上的静压头与位压头之和。
出水管处可用秒表及量筒由体积时间法测量流量。
整个系统中水是循环使用的。
在管道下方装有一供水箱,出水口流出的水进入箱内再由泵抽取送至高位槽。
图3-2 伯努利实验装置流程三.实验原理1.在管内流动的流体均具有位能、静压能和动能,取1N 流体作为基准来进展能量衡算,并忽略流体在管内流动时的阻力损失,对不可压缩流体从1—1截面连续稳定地流至2—2截面,其伯努利方程式为:gu g ρP Z g u g ρP Z 2222222111++=++ (1)式中: Z — 流体的位压头,m ;gPρ— 流体的静压头,m ; gu 22— 流体的动压头,m ; 下标1和2分别为系统的进口和出口两个截面。
同样,取1N 流体作为基准来进展能量衡算,而流体在管内流动时的阻力损失能量不可忽略时,对不可压缩流体从1—1截面连续稳定地流至2—2截面,其柏努利方程式为:f h gu g ρP Z g u g ρP Z +++=++2222222111(2)式中:f h —1N 流体从1—1截面流至2—2截面时损失的能量,称损失压头,m 。
2.在管内稳定连续流动的不可压缩流体,忽略流体流动的阻力损失能量时,在管路上任意截面的总压头均相等。
能量方程(伯努利方程)实验

能量方程(伯努利方程)实验能量方程(伯努利方程)实验姓名:史亮班级:9131011403学号:913101140327处的7根皮托管测压管测量总水头或12根普通测压管测量测压管水头,其中测点1、6、8、12、14、16和18均为皮托管测压管(示意图见图3.2),用于测量皮托管探头对准点的总水头H ’(=2gu2++r p Z ),其余为普通测压管(示意图见图3.3),用于测量测压管水头。
图3.2 安装在管道中的皮托管测压管示意图 图3.3安装在管道中的普通测压管示意图3.3 实验原理当流量调节阀旋到一定位置后,实验管道内的水流以恒定流速流动,在实验管道中沿管内水流方向取n 个过水断面,从进口断面(1)至另一个断面(i )的能量方程式为:2g v2111++r p Z =fiih r p Z +++2gv 2i=常数 (3.1) 式中:i=2,3,······ ,n ;Z ──位置水头;rp──压强水头; 2gv 2──速度水头;fh ──进口断面(1)至另一个断面(i )的损失水头。
从测压计中读出各断面的测压管水头(r pZ +),通过体积时间法或重量时间法测出管道流量,计算不v2,从同管道内径时过水断面平均速度v及速度水头2g而得到各断面的测压管水头和总水头。
3.4 实验方法与步骤1)观察实验管道上分布的19根测压管,哪些是普通测压管,哪些是皮托管测压管。
观察管道内径的大小,并记录各测点管径至表3.1。
2)打开供水水箱开关,当实验管道充满水时反复开或关流量调节阀,排除管内气体或测压管内的气泡,并观察流量调节阀全部关闭时所有测压管水面是否平齐(水箱溢流时)。
如不平,则用吸气球将测压管中气泡排出或检查连通管内是否有异物堵塞。
确保所有测压管水面平齐后才能进行实验,否则实验数据不准确。
3)打开流量调节阀并观察测压管液面变化,当最后一根测压管液面下降幅度超过50%时停止调节阀门。
伯努利方程实验实验报告
伯努利方程实验实验目的:1、 熟悉流体流动中各种能量和压头的概念及其相互转化关系,加深对伯努利方程的理解。
2、 观察各项能量(或压头)随流速的变化规律。
基本原理:不可压缩流体在管内作稳定流动时,由于管路条件的变化,会引起流动过程中三种机械能――位能、动能、静压能的相应改变及相互转换,对于理想流体,在系统内任一截面处,虽然三种能量不一定相等,但是能量之和是守恒的。
而对于实际流体,由于存在内摩擦,流体在流动中总有一部分机械能随摩擦和碰撞转化为热能而损耗了。
所以对于实际流体,任意两截面上机械能总和并不相等,两者的差值即为机械能损失。
f H gu g p Z g u g p Z ∑+++=++2222222111ρρ以上几种机械能均可用测压管中的液贮高度来表示,分别称为位压头、动压头、静压头。
当测压直管中的小孔与水流方向垂直时,测压管内液柱高度即为静压头;当测压孔正对水流方向时,测压管内液柱高度则为静压头和动压头之和。
测压孔处流体的位压头由测压孔的几何高度确定。
任意两截面间位压头、静压头、动压头总和的差值,则为损失压头。
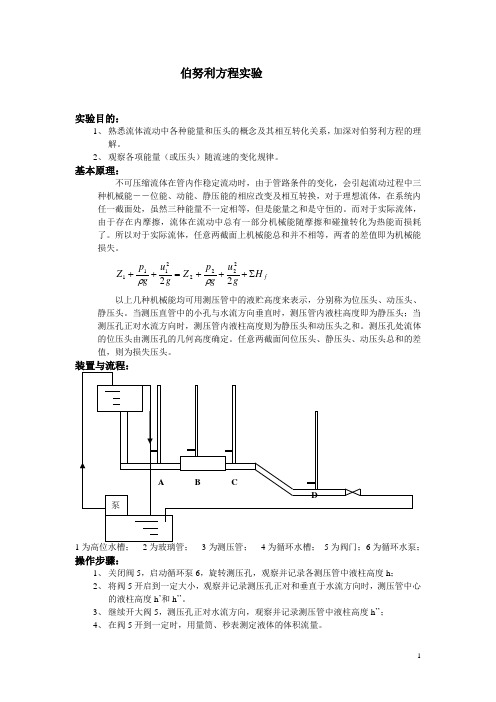
1为高位水槽; 2为玻璃管; 3为测压管; 4为循环水槽; 5为阀门;6为循环水泵;操作步骤:1、 关闭阀5,启动循环泵6,旋转测压孔,观察并记录各测压管中液柱高度h ;2、 将阀5开启到一定大小,观察并记录测压孔正对和垂直于水流方向时,测压管中心的液柱高度h ’和h ’’。
3、 继续开大阀5,测压孔正对水流方向,观察并记录测压管中液柱高度h ’’;4、 在阀5开到一定时,用量筒、秒表测定液体的体积流量。
问题讨论:1、 关闭阀5时,各测压管内液位高度是否相同,为什么?答:相同。
因为流体静止时,u =0,ΣH f =0。
所以有Z +h =常数。
根据上面的流程图,设ABC 的高度为Z ,其液体高度分别为h A 、h B 、h C ,则有 h A +Z = h B +Z = h C +Z =常数,所以h A =h B =h C =h 。
伯努利方程实验实验报告

伯努利方程实验实验报告实验名称:伯努利方程实验实验目的:1.验证伯努利方程的有效性;2.学习使用伯努利方程进行流体力学分析;3.掌握测量流体压力和流速的实验技巧。
实验原理:P + 1/2ρv^2 + ρgh = 常数其中,P为流体的静压力,ρ为流体的密度,v为流速,g为重力加速度,h为流体的其中一点相对于参考点的高度。
伯努利方程表明了流体流动过程中的能量守恒。
实验器材:1.伯努利装置(包括水槽、水泵、流量调节阀、压力计等材料)2.压力计3.流速计实验步骤:1.构建伯努利装置,包括水泵接通电源,调节流量阀使水槽中的水量保持稳定。
2.选取三个高度不同的位置,在各个位置上分别测量对应的静压力、流速和高度。
3.使用压力计分别测量各个位置的静压力,并记录下来。
4.使用流速计分别测量各个位置的流速,并记录下来。
5.使用尺子测量各个位置处相对于参考点的高度,并记录下来。
实验数据记录:位置1:静压力:P1=20Pa流速:v1=1m/s相对高度:h1=0m位置2:静压力:P2=30Pa流速:v2=1.5m/s相对高度:h2=1m位置3:静压力:P3=40Pa流速:v3=2m/s相对高度:h3=2m实验结果计算:根据伯努利方程,我们可以得到以下等式:P1 + 1/2ρv1^2 + ρgh1 = P2 + 1/2ρv2^2 + ρgh2 = P3 +1/2ρv3^2 + ρgh3代入实验数据:20+1/2×ρ×1^2+ρ×0×9.8=30+1/2×ρ×1.5^2+ρ×1×9.8=40+1 /2×ρ×2^2+ρ×2×9.8化简等式,解方程组,求解出流体密度ρ。
实验讨论:通过实验测量的数据进行计算,我们可以得到流体密度的数值。
对于实验结果的误差分析和原因探究,可以从测量仪器的精度、实验操作的误差以及系统误差等方面进行分析。
伯努利方程实验

伯努利方程实验实验一 伯努利方程实验一、实验目的观察流体在管道中流动时能量的相互转化现象,加深对柏努利方程的理解。
原理二、实验原理流体在流动时,具有3种机械能:位能、静压能和动能,这3种机械能是可以相互转化的。
在没有摩擦损失的自流管路中,任意两截面处的机械能总和是相等的。
在有摩擦损失的自流管路中,任意两截面处的总机械能之差为摩擦损失。
2.对理想流体,在系统中任一截面处,尽管三种机械能彼此不一定相等,但这三种机械能的总和是不变的。
对于实际流体,由于在内摩擦,流体在流动过程中总有一部分机械能随摩擦转化为热能而损耗了,故对于实际流体,任意两截面上的机械能的总和并不相等,两者的差值即为能量损失。
3流体流经管路某截面处的各种机械能大小均可以用测压管中的一 段液柱高度来表示,在流体力学中,用以表示各种机械能大小的流体柱高度称之为“压头’。
分别称为位压头、动压头、静压头、损失压头。
机械能可用测压管中液柱的高度来表示。
当测压管口平行于流动方向时,液柱的高度表示静压能;当测压管口正对流体流动方向时,液柱的高度表示动能与静压能之和,两者之差就是动能。
实验中通过测定流体在不同管径、不同位置测压管中液面高度,反映出摩擦损失的存在及动能、静压能之间的相互转化。
(4)流体的机械能衡算,以单位质量(1kg )流体为衡算基准,当流体在两截面之间稳定流动且无外功加入时,伯努利方程的表达形式为 式中 z —— 位压头(m 流体柱); —— 静压头(m 流体柱); —— 动压头(m 流体柱)。
三、实验设备及流程Cgvg p z =++22ρg Pρ22v1. 实验装置流程如图3-1所示,实验设备由玻璃管、测压管、活动测压头、水槽、循环水泵等组成。
水槽中的水通过循环水泵将水送到高位槽,并由溢流口保持一定水位,然后流经玻璃管中的各测点,再通过出口阀A流回水箱,由此利用循环水在管路中流动观察流体流动时发生能量转化及产生能量损失。
活动测压头的小管端部封闭,管身开有小孔,小孔位置与玻璃管中心线平齐,小管又与测压管相通,转动活动测压头就可以测量动、静压头。
伯努利方程实验

五、实验结果处理
l. 流量及流速的计算 流量V = 收集水量/所需时间 平均流速u = 流量/管道截面积 2. 动压头的计算 动压头H = 测压孔正对水流方向的液位 – 测压孔垂直水流方向的液位 3. 最大点速度的计算 求得某—段在某一流量下的动压头H,可按下式得出该处在一定流量下的最 大点速度umax。
柏努利方程实验 一、实验目的 1.掌握柏努利方程式中各项的物理意义,因 次及它们之间的转换关系。 2.通过测量不同流速下的流动阻力损失, 掌握阻力损失与流速之间的关系,了解正确 选择流速的意义。
二、实验原理 当流体稳态流动时,所具有的各种机械能的守恒及相互转化关系服从 柏努利方程,对于每千克不可压缩的流体,柏努利方程可写成:
1.2.3.4.—测压管 5—高位水槽 6—溢流堰 7—活动摆头 8—计量槽 9—水箱 10—水泵 A—调节阀 E—扩大管
四、实验方法
1.流体静止时各点静压头的测定 开动循环泵,并将流量调节阀A全闭,待高位槽水位稳定(溢流管有水溢流 回水箱)时, 转动手柄,先使测压孔正对水流方向,记录各测压管的液柱高 度,再转动手柄,使测压孔与水流方向垂直,记录各测压管的液柱高度。 2.小流量时流量与各压头的测定 开动循环泵并半开阀门A,待水流稳定后,分别观察并记录测压孔与水流 方向垂直和测压孔正对水流方向时各测压管的液柱高度。 用量筒在出口处收集约900m1流体,并用秒表准确记录收集时间,测定流 量。 3.大流量时流量及各压头的测定 全开阀门A,用和小流量相同的方法进行大流量时流量及各压头的测定。 停泵,待高位糟内水全部流回水箱后,关闭阀门A,实验结束。
(2)
式中各项的单位为(米流体柱),工程上一般称为压头,H称为位压头; u2/2g称为动压头; p/ρg称为静压头;Hf则称为压头损失。它们的物理意义 是指该项能量可将1kg该流体克服其重力而提升的高度。 如果流体为理想流体,Hf = 0,则柏努利方程表示流体流经的任一截 面上的机械能之和相等。 对于实际流体Hf >0,则各截面的机械能之和必 随流过距离的增加而减小,之间的差值即为阻力损失压头。
伯努利方程实验

柏努利方程实验(一)实验目的1、了解流体以恒定流流经特定管路(柏努利方程实验管)时一些(四个)特定截面上的总压头⎪⎪⎭⎫ ⎝⎛++g u p Z 22ρ、测压管压头⎪⎪⎭⎫ ⎝⎛+ρp Z ,并计量出相应截面的静压头ρp 和动压(g u 22),再绘制出近似的压头线,从而加深对柏利方程的理解和认识。
2、学会各种压头的测试和计量方法。
3、了解一种测量流体流速方法—皮托管测速方法的原理。
(二)实验装置及其工作原理实验装置的结构示意图如图1所示。
柏努利方程实验装置主要由恒水位水箱6、柏努利方程实验管4、测压管5、蓄水箱7、离心泵供水系统(自循环)和电测流量装置等组成。
恒水位水箱6靠溢流来维持其恒定水位,在水箱左下部装接水平放置的柏努利方和实验管4,恒水位水箱中的水可经柏努利方程实验管以恒定流流出,并可通过出水阀门2调节其出流量。
恒定流以一定流量流经实验管道时,通过布设在实验管4个截面上的测压孔及其测压管(8根)5,可以观察到相应截面上的各各压头的高低,从而可以分析管道中稳定液流的各种能量形式、大小及其相互转化关系。
图4-2 柏努利方程实验装置结构示意图1-电测流量装置及其计量水箱 2-出水阀门 3-流量显示仪 4-柏努利方程实验管 5-测压管 6-恒水位水箱 7-储水箱 8-水泵 9-进水阀门 10-实验台桌 11-集水槽实验时,还需要测定液流的流量。
在阀门2的下面,装有回水箱和计量水箱,计量水箱里装有电测流量装置1(由浮子、光栅计量尺光电传感器组成),可以在电测流量仪3上直接数显出实验时的流体流量(数显出流体积W[立升]和相应的出流时间τ [秒]从而可以计算出流量Vs 来)。
回水箱和计量水箱中的水可以通过集水槽12,回流到储水箱7中。
柏努利方程实验管4上每个测量截面上的一组测压管都相当于一个皮托管,所以,通过实验,也可以了解一种测量流量的原理和方法。
(三)实验操作1、实验前的准备 1)关闭出水阀门22)打开进水阀门9后,按下流量显示仪3上的水泵开关,启动水泵8,向恒水位水箱6上水。
伯努利方程-实验报告
伯努利方程仪实验报告实验人 XXX合作者 XXX合作者 XXXXX年X月XX日一、实验目的1.观察流体流经能量方程试验管的能量转化情况,对实验中出现的现象进行分析,加深对能量方程的理解;2.掌握一种测量流体流速的原理;3.验证静压原理。
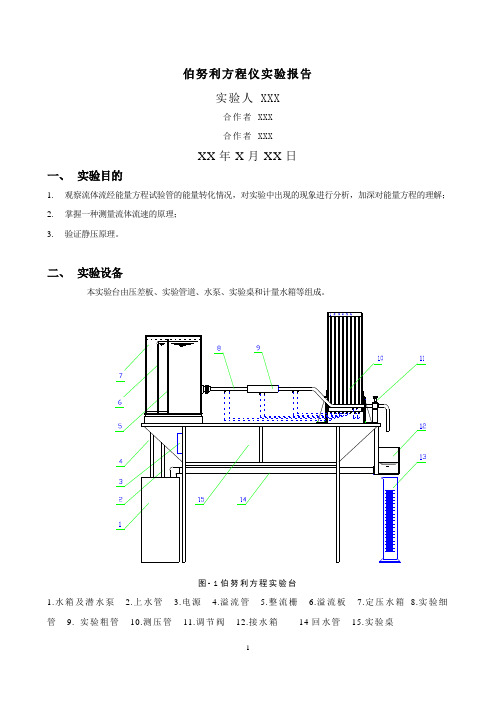
二、实验设备本实验台由压差板、实验管道、水泵、实验桌和计量水箱等组成。
图- 1伯努利方程实验台1.水箱及潜水泵2.上水管3.电源4.溢流管5.整流栅6.溢流板7.定压水箱8.实验细管9. 实验粗管10.测压管11.调节阀12.接水箱14回水管15.实验桌1三、 实验前的准备工作:1.全开溢流水阀门 2.稍开给水阀门 3.将回水管放于计量水箱的回水侧 4.接好各导压胶管 5.检验压差板是否与水平线垂直 6. 启动电泵,使水作冲出性循环,检查各处是否有漏水的现象。
四、 几种实验方法和要求:1.验证静压原理:启动电泵,关闭给水阀,此时能量方程试验管上各个测压管的液柱高度相同,因管内的水不流动没有流动损失,因此静水头的连线为一平行基准线的水平线,即在静止不可压缩均匀重力流体中,任意点单位重量的位势能和压力势能之和(总势能)保持不变,测点的高度和测点位置的前后无关,记下四组数据于表-2的最下方格中。
从表-2中可以看出,当水没有流动时,测得的的静水压头基本上都是35.5cm ,验证了同一水平面上静压相等。
2.测速:能量方程试验管上的四组测压管的任一组都相当于一个毕托管,可测得管内任一点的流体点速度,本试验已将测压管开口位置在能量方程试验管的轴心,故所测得的动压为轴心处的,即最大速度。
毕托管求点速度公式: gh V B 2=利用这一公式和求平均流速公式(F Q V /=)计算某一工况(如表中工况2平均速度栏)各测点处的轴心速度和平均流速得到表-1表- 1注:该表中数据由表-2中第一行数据计算得到从表-1中我可以看到在细管测得的速度大,在粗管测得的速度小;在细管中测得的点速度比平均速度小,这可能是比托管的管嘴没有放在玻璃管管中心,或者比托管管嘴没有正对液体流向,使得总压与静压的差值小于实际值;在粗管测得的点速度比平均速度大,可能是因为在粗管,比托管更容易放在玻璃管中心,测得的点速度比平均速度大是正常的,因为如果是层流的话,流速沿半径方向呈抛物线分布。
能量方程演示实验报告

一、实验目的1. 了解流体在管内流动时,静压能、动能、位能之间相互转换的关系。
2. 深入理解伯努利方程,掌握其应用。
3. 培养学生运用实验方法验证理论知识的能力。
二、实验原理伯努利方程是描述流体在管道中流动时能量守恒的方程。
该方程表明,在不可压缩、不可压缩流体中,沿流动方向,流速增加时,静压能减小,动能增加;流速减小时,静压能增加,动能减小。
同时,流体在流动过程中,位能、动能和静压能之和保持不变。
伯努利方程可表示为:\[ P + \frac{1}{2} \rho v^2 + \rho gh = \text{常数} \]其中,P为流体压强,ρ为流体密度,v为流速,g为重力加速度,h为流体高度。
三、实验仪器与设备1. 实验装置:伯努利方程演示装置,包括有机玻璃管道、水箱、流量计、压力计等。
2. 数据采集系统:数据采集器、传感器等。
四、实验步骤1. 连接实验装置,检查各部件是否完好。
2. 打开水箱,使水箱充水,待水箱溢流。
3. 调节流量计,控制流量稳定。
4. 在管道上设置不同位置的测压点,用压力计测量各点的压强。
5. 使用数据采集系统记录各测点的压强数据。
6. 改变管道形状(如弯头、缩径等),观察压强变化,分析能量转换情况。
7. 比较不同形状管道的压强分布,验证伯努利方程。
8. 实验结束后,整理实验数据,分析实验结果。
五、实验数据与分析1. 实验数据(1)管道直段:P1 = 0.5 MPa,P2 = 0.4 MPa,v1 = 2 m/s,v2 = 1 m/s,h1 = 1 m,h2 = 1.5 m。
(2)管道弯头:P3 = 0.3 MPa,P4 = 0.4 MPa,v3 = 1 m/s,v4 = 2 m/s,h3 = 1 m,h4 = 1.5 m。
(3)管道缩径:P5 = 0.6 MPa,P6 = 0.5 MPa,v5 = 1 m/s,v6 = 2 m/s,h5 = 1 m,h6 = 1.5 m。
2. 实验结果分析根据实验数据,我们可以发现:(1)在管道直段,流速增加时,静压能减小,动能增加;流速减小时,静压能增加,动能减小。
伯努利方程实验报告图

伯努利方程实验报告图表与公式推导实验名称:伯努利方程实验实验目的:验证伯努利方程的适用条件和其基本原理,并通过实验数据和公式计算来推导伯努利方程。
实验器材:流量计、压力计、导管、水池。
实验原理:伯努利方程是流体力学中非常重要的基本方程。
它描述了沿任意流管中流体的能量守恒和动能变化。
根据伯努利方程,一个流体在不同位置的速度、压力和高度之间存在着一定的关系,即速度越高,则压力越低,而高度越低。
实验步骤:1.准备实验器材。
将流量计固定在导管上,将压力计分别放在导管的两端。
2.调节流量指示器。
打开水泵将水灌入水池中,并根据实验要求调节流量指示器,使其指示值稳定在一定数值。
3.取数记录。
同时读取两端的压力计值,并记录到实验表格中。
4.计算并推导公式。
根据已有的公式和实验数据计算伯努利方程的系数,并进行公式推导。
实验结果:通过实验数据的记录和对公式的计算、推导,得出如下实验结果:1. 经过多组实验数据记录和计算,发现流量、速度与压强呈反比例关系。
当流量增大时,速度也会增大,但压强则会随之减小。
而当流量减少时,速度将相应减小,而压强会增大。
2. 实验数据表明伯努利方程适用于为定常、连续、不可压缩的流体,并且流体在管道内流动时,其若干物理量(包括速度和压强、液面高度等)对于每一截面都保持相等。
同时,还需要满足流动是不可压缩的。
3. 进一步公式推导结果显示,将装填于任意两点之间的流体在穿过介质前后的总机械、热能的增减进行分析,即可得出伯努利方程中的系数,并对其进行优化和调整。
实验结论:实验表明,通过伯努利方程的实验验证和公式推导,可以得到流体在管道内的重要参数,如速度、压强等的变化量,从而进一步优化和调整液体在介质之间的流动,提高流体运动的能效,放大其应用潜力。
伯努利方程实验实验报告

伯努利方程实验实验报告伯努利方程实验报告实验一伯努利方程一、实验目的1.理解液体的静压原理2.验证伯努利方程3.验证液体在流动状态下压力损失与速度的关系二、实验仪器伯努利方程实验装置三、实验原理伯努利方程是流体动力学中一个重要的基本规律,是能量守恒定律在流体力学中的具体应用。
主要反映液体在恒定流动时压力能、位能和动能三者之间的关系,即在任一截面上这三种能量形式之间可以互相转换,但三者之和为一定值,即能量守恒。
22p1u1p2u2?z1z2?理想液体的伯努利方程为:?g2g?g2g2p1?u12p2?u2z1z2hw实际液体的伯努利方程为:g2gg2g当液体处于静止状态时,液体内任一点处的压力为:p?p0??gh这是液体静力学基本方程式。
四、实验装置伯努利试验仪主要由实验导管、稳压溢流槽和四对测压管所组成。
实验导管为一水平装置的变径圆管,沿程分四处设置测压管。
每处测压管由一对并列的测压管组成,分别测量该截面处的静压头(压力能)和冲压头(压力能、位能和动能三者之和)。
实验装置的流程如图1所示。
液体由稳压槽流入实验导管,途径A点、B点、C点、D点直径分别为15mm、34mm、15mm、15mm的管子,最后排出设备。
液体流量由出口调节阀调节。
流量由流量计读出。
五、实验步骤实验前,先缓慢开启进水阀,将水充满稳压溢流水槽,并保持有适量溢流水流出,使槽内液面平稳不变。
最后,设法排尽设备内的空气泡,否则会干扰实验现象和测量的准确性。
1.关闭实验导管出口调节阀,观察和测量液体处于静止状态下各测试点(A、B、C和D四点)的压力,验证液体的静压原理。
并设定此处的水位高度为基准面。
2.开启实验导管出口调节阀,保持稳压溢流水槽有适量溢流水流出,观察比较液体在流动情况下的各测试点的压头变化。
3.缓慢调节实验导管的出口调节阀,测量液体在不同流量下的各测试点的静压头、动压头和损失压头,并记录下各项数据。
4.实验结束后,应先关闭进水的总阀门,然后再开大出口调节阀,排尽稳压溢流水槽内的水。
伯努利方程实验

伯努利方程实验一、实验目的:1. 验证流体静压原理;2. 通过观察流体在管道中的运动规律,加深对伯努利方程能量意义的理解;3. 验证管道流动中,摩擦损失与流速平方成正比关系;4. 验证毕托管的测速原理。
二、实验原理:1. 1. 在流体静止时,等压面是水平面,自由波面也是水平面。
在重力势能函数的微分 dW= -gdz 时,有dp = -ρgdz ,即等压与等高程同在。
2. 2. 对于一个恒定的不可压缩管流中,在流动方向上的两个渐变流段,流体的能量关系有伯努利方程给出:22111222121222l P v P v z z h ggααγγ-++=+++3. 管道内的摩擦损失与流体流速的关系服从达西公式:212()2l L v h d g λζ-=+∑212()2l L v h d g λζ-=+∑4. 4. 毕托管能测量出来流滞止点(全压)和管测点(静压)之压力差h v ,于是测点流速可由下式确定:u = 式中;φ1。
三、实验装置伯努利方程仪由玻璃管、活动测头、测压管、上水槽和循环水泵等部分组成。
活动测头的小管底部封闭,管身开有小孔。
小孔中心位置与玻璃管中心平齐,小管与玻璃测压管相通,用小扳手转动活动测头,就可以测量流体的静动压水头。
由于玻璃管前后直径不同(管道直径经测量标注的管段上),位置也有高低,测点有前有后,可以十分方便地测量出不同流速下不同管段的位能、压力能和动能的数值,去验证伯努利方程的结论.实验装置图附后. 四、实验方法:1. 测点静压水头的涸量; 开动循环水泵,将出口阀门A 关闭,这时观察各测压管内自由液面的高度,记录在表格中。
观察在转动活动测头对,自由液面有无变化。
如果发现各测点自由波面高度不相等,或者发现转动活动测头时自由液面发生变化,应试图找出产生误差的原因、并作出记录。
各测点静压水头的数据记录在表1中。
2. 验证摩擦损失与流速平方成正比(达西公式);使各测头的小孔对准来流方向,然后打开出口阀门A(不全开,保持小流量)。
伯努利方程能量实验报告

一、实验目的1. 通过实验,加深对伯努利方程式及能量之间转换的了解。
2. 观察水流沿程的能量变化,并了解其几何意义。
3. 了解压头损失大小的影响因素。
二、实验原理伯努利方程是描述流体在稳态流动过程中能量守恒的方程。
对于不可压缩流体,伯努利方程可表示为:P1 + 1/2ρv1^2 + ρgh1 = P2 + 1/2ρv2^2 + ρgh2其中,P1、P2分别为流体在截面1和截面2处的压强;ρ为流体密度;v1、v2分别为流体在截面1和截面2处的流速;g为重力加速度;h1、h2分别为流体在截面1和截面2处的位能。
在实验过程中,通过测量不同截面处的压强、流速和位能,可以验证伯努利方程的正确性,并观察能量在流动过程中的变化。
三、实验仪器与设备1. 实验装置:水槽、实验管道、阀门、测压管、计时器等。
2. 测量工具:压力表、流速计、尺子等。
四、实验步骤1. 将实验装置组装完毕,确保各连接部位密封良好。
2. 将水注入实验管道,调整水位,确保管道内水流稳定。
3. 在管道上设置多个测点,分别测量各点的压强、流速和位能。
4. 记录各测点的数据,包括压强、流速、位能等。
5. 根据伯努利方程,计算各测点处的总能量,并分析能量变化规律。
五、实验结果与分析1. 实验数据记录如下:测点 | 压强P (Pa) | 流速v (m/s) | 位能h (m) | 总能量E (J/kg)----|----------|----------|--------|---------1 | 1000 | 1.5 | 0.5 | 15002 | 950 | 2.0 | 0.6 | 15503 | 900 | 2.5 | 0.7 | 16004 | 850 | 3.0 | 0.8 | 16502. 根据伯努利方程,计算各测点处的总能量:E1 = P1 + 1/2ρv1^2 + ρgh1 = 1000 + 1/2 × 1000 × 1.5^2 + 1000 × 9.8 × 0.5 = 1500 J/kgE2 = P2 + 1/2ρv2^2 + ρgh2 = 950 + 1/2 × 1000 × 2.0^2 + 1000 × 9.8 × 0.6 = 1550 J/kgE3 = P3 + 1/2ρv3^2 + ρgh3 = 900 + 1/2 × 1000 × 2.5^2 + 1000 × 9.8 × 0.7 = 1600 J/kgE4 = P4 + 1/2ρv4^2 + ρgh4 = 850 + 1/2 × 1000 × 3.0^2 + 1000 × 9.8 × 0.8 = 1650 J/kg3. 分析实验结果:(1)从实验数据可以看出,随着流速的增加,总能量呈线性增加。
伯努利方程实验实验报告

一、实验目的1. 深入理解伯努利方程的基本原理及其在流体力学中的应用。
2. 通过实验验证伯努利方程的适用性,并观察流体在流动过程中能量转换的现象。
3. 掌握流速、流量、压强等流体力学基本参数的测量方法。
4. 分析不同条件下流体流动特性的变化。
二、实验原理伯努利方程描述了在不可压缩、定常流动条件下,流体在任意两点之间的能量守恒关系。
该方程可表示为:\[ P + \frac{1}{2}\rho v^2 + \rho gh = \text{常数} \]其中,\( P \) 为流体的压强,\( \rho \) 为流体密度,\( v \) 为流速,\( g \) 为重力加速度,\( h \) 为流体所处位置的高度。
三、实验装置实验装置主要包括:1. 实验管道:选用不同内径的管道,以便观察不同条件下流体流动特性的变化。
2. 测压管:用于测量流体在管道各点的压强。
3. 流量计:用于测量流体流量。
4. 计时器:用于测量流体通过实验管道的时间。
四、实验步骤1. 将实验管道连接好,并确保管道内无气泡。
2. 打开水源,调节流量,使流体在管道内稳定流动。
3. 在实验管道的不同位置安装测压管,并记录各测点的压强值。
4. 使用流量计测量流体流量,并记录数据。
5. 计时器记录流体通过实验管道的时间,计算流速。
6. 根据实验数据,计算各测点的能量值,并绘制能量分布图。
五、实验结果与分析1. 在实验管道内,不同位置的压强值存在差异,符合伯努利方程的预测。
2. 随着管道内径的减小,流速增大,压强减小,符合能量守恒定律。
3. 在管道的局部收缩或扩张处,流速和压强变化较大,符合能量转换现象。
4. 通过实验验证了伯努利方程在流体力学中的适用性。
六、结论1. 伯努利方程在流体力学中具有重要的应用价值,可描述流体在流动过程中的能量转换关系。
2. 通过实验验证了伯努利方程的适用性,并观察到了流体在流动过程中的能量转换现象。
3. 实验结果表明,流速、流量、压强等流体力学基本参数之间存在着密切的联系。
伯努利实验

(2)能量方程实验
首先,关闭阀门,测定能量方程实验四组测压管的 液体高度,记下各测压管的读数(填入表1)。
其次,调节阀门至小开开度,测定能量方程实验管 的四组截面测压管的液面高度。之后,改变阀门至中开、 大开开度,重复上述实验,并分别记下各测压管的读数 表1 (填入表1)。
表2
毕托管方法 能量方程实验管上的四组测压管的任一组都相当
一个毕托管,可测得管内的任意一点的流体点速度。
由于本实验台将总压管置于能量方程实验管的轴线, 所以,测得的动压头代表了轴心处的最大流速。毕托 管求点速度公式为:
u 2gh
式中:u—毕托管测点处的流速; Δh—毕托管总压水头与静压水头差(即总水头与 测压管水头差,Δh =H单–H双)。
之后,可根据该截面轴心处的最大速度与平均流 速的关系求出所在截面的平均流速(结果记入表3)。具 体为:层流,V=0.5umax;湍流,V=0.8umax。
表3
Ⅰ
(4)验证伯努利方程
表4
hw13 截 面 阀 门 状 态
小 开 中 开 大 开 各截面总水头Hi(m) 1—2 3—4 5—6 7—8 各截面间水头损失 hLi j(m) 1—3 1—5 1—7 3—5 3—7 5—7
能量方程实验
一、实验目的
(1)观察流体经能量方程(又称伯努利方程)实验管 时的能量转化情况,并对实验中出现的现象进行分析, 从而加深对能量方程的理解;
(2)掌握量杯测平均流速和毕托管测流速的方法;
(3)验证伯努利方程。
能量方程(伯努利方程)实验

不可压缩流体恒定流能量方程(伯努利方程)实验一、实验背景1726年,伯努利通过无数次实验,发现了“边界层表面效应”:流体速度加快时,物体与流体接触的界面上的压力会减小,反之压力会增加。
为纪念他的贡献,这一发现被称为“伯努利效应”。
伯努利效应适用于包括气体在内的一切流体,是流体作稳定流动时的基本现象之一,反映出流体的压强与流速的关系,即在水流或气流里,如果速度大,压强就小,如果速度小,压强就大。
1738年,在他的最重要的著作《流体动力学》中,伯努利将这一理论公式化,提出了流体动力学的基本方程,后人称之为“伯努利方程”。
书中还介绍了著名的伯努利实验、伯努利原理,用能量守恒定律解决了流体的流动问题,这对流体力学的发展,起到了至关重要的推动作用。
伯努利简介丹尼尔伯努利(Daniel Bernouli,1700~1782),瑞士物理学家、数学家、医学家,被称为“流体力学之父”。
1700年2月8日生于荷兰格罗宁根,1782年3月17日逝世于巴塞尔。
他是伯努利这个数学家族(4代10人)中最杰出的代表,16岁时就在巴塞尔大学攻读哲学与逻辑,后获得哲学硕士学位。
17~20岁时,违背家长要他经商的愿望,坚持学医,并于1721年获医学硕士学位,成为外科名医并担任过解剖学教授。
他在父兄熏陶下最后仍转到数理科学。
伯努利在25岁时应聘为圣彼得堡科学院的数学院士,8年后回到瑞士的巴塞尔,先任解剖学教授,后任动力学教授,1750年成为物理学成教授。
他还于1747年当选为柏林科学院院士,1748年当选为巴黎科学院院士,1750年当选英国皇家学会会员。
在1725~1749年间,伯努利曾十次荣获法国科学院的年度奖。
除流体动力学这一主要领域外,丹尼尔·伯努利的研究领域极为广泛,他的工作几乎对当时的数学和物理学的研究前沿的问题都有所涉及。
他最出色的工作是将微积分、微分方程应用到物理学,研究流体问题、物体振动和摆动问题,因此他被推崇为数学物理方法的奠基人.二、实验目的要求1.验证流体恒定总流的能量方程;2.通过对动水力学诸多水力现象的实验分析,进一步掌握有压管流中动水力学的能量转换特性;3.掌握流速、流量、压强等动水力学水力要素的实验量测技能。
伯努利方程流体能量转换实验-

Z1P g 1Z2Pg 2.........m .水 ...(.8柱 )
或将上式改写为:
P 2P 1g(Z 1Z 2).............9 .)...(.....
这就是流体静力学基本方程。
三、实验装置
本实验装置主要有实验导管,稳压溢流水槽和 三对测压管组成。 实验导管为一水平装置的变径圆管,沿程分三 处装有测压管。每处测压管由一对并列的测压 管组成,分别测量该截面处的静压头和冲压头。 实验装置的流程如图1,液体由稳压水槽流入实 验导管。途经直径分别为20mm、30mm和 20mm的管子,最后排出装置。流量直接由计 时称量测定。
(3)当不断开大调节阀时,流速增大,动压头应该 增大,为什么各截面右侧测压管的液位从A截面至 C截面反而下降?
4.试列举出利用能量转换的原理强化流体流动过程 的例子2-3个。
谢谢!
2当流体流经的系统为一水平装置的管道时,则 (1)和(2)式又可简化为:
P 11 2u1 2P 21 2u2 2 hf.......J./.K ..(.5g ).
Pg 12 u1g2Pg 22 ug 22 Hf.......m ..液 .. 柱 6)(
3.当流体处于静止状态时,则(1)和(2)式又 可简化为:
hB/m m
3
管
的 C点
A点
各冲 压头
RA/m m
5
测量 B点
管的 水柱
RB/mm
6
高度 C点 RC/mm
7
A点h(1各阶 A)/mm
8
段损 B点
失压 头的 水柱
h(1B)/mm
9
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第3章 能量方程(伯努利方程)实验
3.1 实验目的
1) 掌握用测压管测量流体静压强的技能。
2) 验证不可压缩流体静力学基本方程, 通过对诸多流体静力学现象的实验分析,进一步加深对基本概念的理解,提高解决静力学实际问题的能力。
3) 掌握流速、流量等动水力学水力要素的实验量测技能。
3.2 实验装置
能量方程(伯努利方程)实验装置见图3.1。
图3.1 能量方程(伯努利方程)实验装置图
说明:本实验装置由供水水箱及恒压水箱、实验管道(共有三种不同内径的管道)、测压计、实验台等组成,流体在管道内流动时通过分布在实验管道各处的7根皮托管测压管测量总水头或12根普通测压管测量测压管水头,其中测点1、6、8、12、14、16和18均为皮托管测压管(示意图见图3.2),用于测量皮托管
探头对准点的总水头H ’(=2g
u 2
++r p Z ),其余为普通测压管(示意图见图3.3),用于测量测压管水头。
图3.2 安装在管道中的皮托管测压管示意图 图3.3安装在管道中的普通测压管示意图
3.3 实验原理
当流量调节阀旋到一定位置后,实验管道内的水流以恒定流速流动,在实验管道中沿管内水流方向取n 个过水断面,从进口断面(1)至另一个断面(i )的能量方程式为:
2g v
2111++r p Z =f i i h r p Z +++2g
v 2
i =常数 (3.1)
式中:i=2,3,······ ,n ;
Z ──位置水头;
r p
──压强水头;
2g
v 2
──速度水头; f h ──进口断面(1)至另一个断面(i )的损失水头。
从测压计中读出各断面的测压管水头(r
p
Z +
),通过体积时间法或重量时间法测出管道流量,计算不同管道内径时过水断面平均速度v 及速度水头2g
v 2
,从而得到各断面的测压管水头和总水头。
3.4 实验方法与步骤
1) 观察实验管道上分布的19根测压管,哪些是普通测压管,哪些是皮托管测压管。
观察管道内径的大小,并记录各测点管径至表3.1。
2) 打开供水水箱开关,当实验管道充满水时反复开或关流量调节阀,排除管内气体或测压管内的气泡,并观察流量调节阀全部关闭时所有测压管水面是否平齐(水箱溢流时)。
如不平,则用吸气球将测压管中气泡排出或检查连通管内是否有异物堵塞。
确保所有测压管水面平齐后才能进行实验,否则实验数据不准确。
3) 打开流量调节阀并观察测压管液面变化,当最后一根测压管液面下降幅度超过50%时停止调节阀门。
待测压管液面保持不变后,观察皮托管测点1、6、8、12、14、16和18的读数(即总水头,取标尺零点为基准面,下同)变化趋势:沿管道流动方向,总水头只降不升。
而普通测压管2、3、4、5、7、9、10、11、13、15、17、19的读数(即测压管水头)沿程可升可降。
观察直管均匀流同一断面上两个测点2、3测压管水头是否相同?验证均匀流断面上静水压强按动水压强规律分布。
弯管急变流断面上两个测点10、11测压管水头是否相同?分析急变流断面是否满足能力方程应用条件?记录测压管液面读数,并测记实验流量至表3.2、表3.3。
4) 继续增大流量,待流量稳定后测记第二组数据(普通测压管液面读数和测记实验流量)。
5) 重复第4步骤,测记第三组数据,要求19号测压管液面接近标尺零点。
6) 实验结束。
关闭水箱开关,使实验管道水流逐渐排出。
7) 根据表3.1和表3.2数据计算各管道断面速度水头2g v 2和总水头(2g
v 2
++r p Z )(分别记录于表3.4和
表3.5)。
★操作要领与注意事项:①、实验前必须排除管道内及连通管中气体。
②、流量调节阀不能完全打开,要保证第7根和第8根测压管液面在标尺刻度范围内。
3.5 实验成果与分析
1) 记录有关常数
2) 测记测压管静压水头(r
Z +
)和流量Q ,测计皮托管测点读数。
表3.2 各测点静压水头(
p
Z +)(单位:cm)和流量Q (单位:cm 3/s )
表3.3 皮托管测点总水头(2g
u ++
r p Z )(单位:cm)
3) 表3.4 各断面速度水头
v 2
(单位:cm )(g=980 cm/s 2)
表3.5 各断面总水头(v ++
p Z )(单位:cm )
第三组46.87 46.87 46.52 46.25 43.7 40.89 39.52 37.24 36.05 35.14 115.40
注:图中横向表示测点在管道中的位置,纵向表示某测点的总水头或测压管水头(单位均为cm)。
测压管水头线P-P线依表3.2数据绘制,总水头线E-E线依表3.5数据绘制,将所有测点数据用线段连接,在连线时要考虑同一管径的线段应平行(沿程水头损失大小随管道长度线性变化)。
4)根据最大流量时的数据绘制总水头和测压管水头沿管道变化趋势线(总水头线E-E线和测压管水头线P-P线绘制于图3.4中)。
并分析总水头和测压管水头沿管道变化趋势线有何不同?为什么?
测压管水头线(P-P)沿程可升可降,线坡JP可正可负。
而总水头线(E-E)沿程只降不升,线坡JP恒为正,即J>0。
这是因为水在流动过程中,依据一定边界条件,动能和势能可相互转换。
如图所示,测点5至测点7,管渐缩,部分势能转换成动能,测压管水头线降低,JP>0。
,测点7至测点9,管渐扩,部分动能又转换成势能,测压管水头线升高,JP<0。
而据能量方程E1=E2+hw1-2,hw1-2为损失能量,是不可逆的,即恒有hw1-2>0,故E2恒小于E1,(E-E)线不可能回升。
(E-E)线下降的坡度越大,即J越大,表明单位流程上的水头损失越大,如图上的渐扩段和阀门等处,表明有较大的局部水头损失存在。
5)流量增加,测压管水头线如何变化?为什么?
流量增加,测压管水头线(P-P)总降落趋势更显著。
这是因为测压管水头Q2,任一断面起始的总水头E
及管道过流断面面积A为定值时,Z必减小。
而且随流量的增加,阻力损失亦增大,管道任一过2g水断面上的总水头E相应减小,故Z p的减小更加显著。
6)分析同一断面测点2、3是否读数一致?同一断面测点10、11是否读数一致?为什么?
测点2、3位于均匀流断面,测点高差0.7cm,HP Z p均为37.1cm(偶有毛细影响相差0.1mm),表明均匀流各断面上,其动水压强按静水压强规律分布。
测点10、11在弯管的急变流断面上,测压管水头差为7.3cm,表明急变流断面上离心惯性力对测压管水头影响很大。
由于能量方程推导时的限制条件之一是“质量力只有重力”,而在急变流断面上其质量力,除重力外,尚有离心惯性力,故急变流断面不能选作能量方程的计算断面。
在绘制总水头线时,测点10、11应舍弃。
7)皮托管所显示的总水头与实测总水头是否一致,为什么?
皮托管中的流动阻力小于实际绘制的,而且所用的工质的密度不同。
