统计学练习题——计算题
统计学计算题

解:基期总平均成本=1800120018007001200600+⨯+⨯=660报告期总平均成本=1600240016007002400600+⨯+⨯=640总平均成本下降的原因是该公司产品的生产结构发生了变化,即成本较低的甲企业产量占比上升而成本较高的乙企业产量占比相应下降所致。
2.某商贸公司从产地收购一批水果,分等级的收购价格和收购进入如下, (元)收购总量收购总额6268.130.1832060.11664000.21270083201664012700)()(11=++++=∑∑====k i ii i ki i i X f X f X X 3.某中学正在准备给一年级新生定制校服。
男生校服分小号、中号和大号三种规格,分别适合于身高在160cm 以下、160~168cm 之间和168cm 以上的男生。
一直一年级 新生中有1200名男生,估计他们身高的平均数为164cm ,标准差为4cm 。
试由此粗 略估计三种规格男生校服分别准备多少套?解:均值=164;标准差=4;总人数=1200身高分布通常为钟形分布,按经验法则近似估计:规格 身高 分布范围 比重 数量(套)小号 160以下0.15865 190.38 中号 160-168 均值±1*标准差0.6827 819.24 大号168以上0.15865190.38合计 12004. 根据长期实验,飞机的最大飞行速度服从正态分布。
先对某新型飞机进行了 15次试飞,测得各次试飞时的最大飞行速度(单位:米/秒)为: 422.2 417.2 425.6 425.8 423.1 418.7 428.2 438.3 434.0 412.3 431.5 413.5 441.3 423.0 420.3试对该飞机最大飞行速度的数学期望值进行区间估计。
(置信概率0.95) 解:样本平均数 X=425, S 2n-1=72.049, S 14=8.488XS 2.19161510.05/2()t -=2.1448∆==/2t α=2.1448×2.1916=4.7005所求μ的置信区间为:425-4.70<μ<425+4.7t0,即(420.30,429.70)。
统计学练习题(计算题)

统计学练习题(计算题)第四章----第一部分总量指标与相对指标4.1:(1)某企业产值计划完成程度为105%,比上年增长7%,试计算计划规定比上年增长多少?(2)单位产品成本上年为420元,计划规定今年成本降低5%,实际降低6%,试确定今年单位成本的计划数字和实际数字,并计算出降低成本计划完成程度指标。
(3)按计划规定,劳动生产率比上年提高10%,实际执行结果提高了12%,劳动生产率计划完成程度是多少?4.2:某市三个企业某年的下半年产值及计划执行情况如下:要求:[1]试计算并填写上表空栏,并分别说明(3)、(5)、(6)、(7)是何种相对数;[2]丙企业若能完成计划,从相对数和绝对数两方面说明该市三个企业将超额完成计划多少?4.3:我国2008年-2013年国内生产总值资料如下:单位:亿元根据上述资料,自行设计表格:(1)计算各年的第一产业、第二产业、第三产业的结构相对指标和比例相对指标;(2)计算我国国内生产总值、第一产业、第二产业、第三产业与上年对比的增长率;(3)简要说明我国经济变动情况。
4.4:某公司下属四个企业的有关销售资料如下:根据上述资料:(1)完成上述表格中空栏数据的计算;(2)若A能完成计划,则公司的实际销售额将达到多少?比计划超额完成多少?(3)若每个企业的计划完成程度都达到B企业的水平,则公司的实际销售额将达到多少?比计划超额完成多少?第四章-----第二部分平均指标与变异指标4.5:已知某地区各工业企业产值计划完成情况以及计划产值资料如下:要求:(1)根据上述资料计算该地区各企业产值计划的平均完成程度。
(2)如果在上表中所给资料不是计划产值而是实际产值,试计算产值计划平均完成程度。
、4.6:已知某厂三个车间生产不同的产品,其废品率、产量和工时资料如下:计算:(1)三种产品的平均废品率;(2)假定三个车间生产的是同一产品,但独立完成,产品的平均废品率是多少;(3)假定三个车间是连续加工某一产品,产品的平均废品率是多少。
统计学计算题

第三章统计整理例 1、某厂工人日产量资料如下:(单位:公斤)162 158 158 163 156 157 160 162 168 160164 152 159 159 168 159 154 157 160 159163 160 158 154 156 156 156 169 163 167试根据上述资料,编制组距式变量数列,并计算出频率。
解:将原始资料按其数值大小重新排列。
152158 159154 154 156 156 156 156 157 157 158 158 159 159 159 159 160 160 160 162 162 163 163 163 164 167168 168 169最大数=169,最小数=152,全距=169-152=17n=30, 分为 6 组例 2、某企业 50 个职工的月工资资料如下:113 125 78 115 84 135 97 105 110 130105 85 88 102 101 103 107 118 103 87116 67 106 63 115 85 121 97 117 10794 115 105 145 103 97 120 130 125 127122 88 98 131 112 94 96 115 145 143试根据上述资料,将50 个职工的工资编制成等距数列,列出累计频数和累计频率。
解:将原始资料按其数值大小重新排列。
63 97 117 118工人按日产量分组(公斤)152-154155-157158-160161-163164-166 工人数(人)361151比率(频率)(%)10.0020.0036.6016.7067 78 84 85 85 87 88 88 94 94 96 97 97 98 101 102 103 103 103 105 105 105 107 110 112 113 115 115 115 115 116 118 120 121 122 125 125 127 130 130 131 135 143 145 145按工资额分组(元)60-70 70-80 80-90频数216工人数频率( %)4212频数239向上累计频率( %)4618频数504847向下累计频率(%)1009694例 3、有 27 个工人看管机器台数如下:5 4 2 4 3 4 3 4 4 2 4 3 4 3 26 4 4 2 2 3 4 5 3 2 4 3试编制分布数列。
统计学复习题题目——计算题
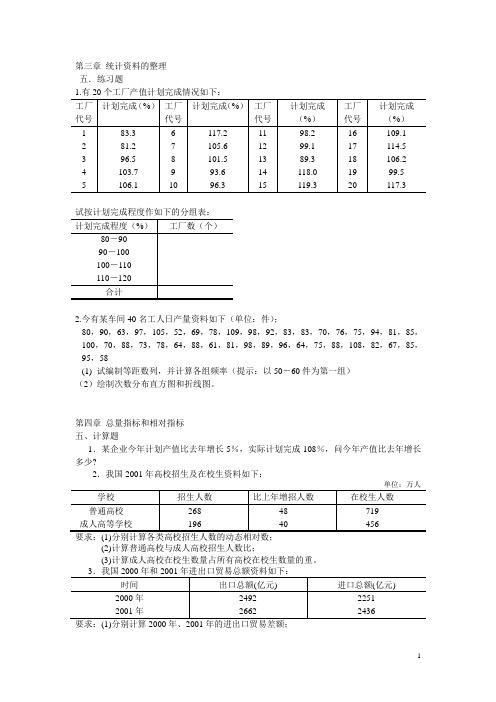
第三章 统计资料的整理 五.练习题试按计划完成程度作如下的分组表:2.今有某车间40名工人日产量资料如下(单位:件);80,90,63,97,105,52,69,78,109,98,92,83,83,70,76,75,94,81,85,100,70,88,73,78,64,88,61,81,98,89,96,64,75,88,108,82,67,85,95,58(1) 试编制等距数列,并计算各组频率(提示:以50-60件为第一组) (2)绘制次数分布直方图和折线图。
第四章总量指标和相对指标 五、计算题1.某企业今年计划产值比去年增长5%,实际计划完成108%,问今年产值比去年增长多少?2.我国2001年高校招生及在校生资料如下:(2)计算普通高校与成人高校招生人数比;(3)计算成人高校在校生数量占所有高校在校生数量的重。
(2)计算2001年进出口总额比例相对数及出口总额增长速度; (3)分析我国进出口贸易状况。
4.根据下列资料,计算强度相对数的正指标和逆指标,并根据正指标数值分析该地区5.某公司下属三个企业有关资料如下表,试根据指标之间的关系计算并填写表中所缺数第六章 动态数列习题五、计算题1.某公司某年9月末有职工250人,10月上旬的人数变动情况是:10月4日新招聘12名大学生上岗,6日有4名老职工退休离岗,8日有3名青年工人应征入伍,同日又有3名职工辞职离岗,9日招聘7名营销人员上岗。
试计算该公司10月上旬的平均在岗人数。
(2)分别计算该银行2005年第一季度、第二季度和上半年的平均现金库存额。
(2)计算该地区2001—2005年间的平均国民生产总值。
(3)计算2002—2005年间国民生产总值的平均发展速度和平均增长速度。
(2)计算该企业第四季度劳动生产率。
(2)应用最小平方法配合趋势直线,并计算各年的趋势值。
第七章统计指数习题五、计算题1.某市1999年第一季度社会商品零售额为36200万元,第四季度为35650万元,零售物价下跌0.5%,试计算该市社会商品零售额指数、零售价格指数和零售量指数,以及由于零售物价下跌居民少支出的金额。
统计学练习题(计算题)

统计学练习题(计算题)第四章----第一部分总量指标与相对指标:(1)某企业产值计划完成程度为105%,比上年增长7%,试计算计划规定比上年增长多少(2)单位产品成本上年为420元,计划规定今年成本降低5%,实际降低6%,试确定今年单位成本的计划数字和实际数字,并计算出降低成本计划完成程度指标。
(3)按计划规定,劳动生产率比上年提高10%,实际执行结果提高了12%,劳动生产率计划完成程度是多少:某市三个企业某年的下半年产值及计划执行情况如下:要求:[1]试计算并填写上表空栏,并分别说明(3)、(5)、(6)、(7)是何种相对数;[2]丙企业若能完成计划,从相对数和绝对数两方面说明该市三个企业将超额完成计划多少:我国2008年-2013年国内生产总值资料如下:单位:亿元根据上述资料,自行设计表格:(1)计算各年的第一产业、第二产业、第三产业的结构相对指标和比例相对指标;(2)计算我国国内生产总值、第一产业、第二产业、第三产业与上年对比的增长率;(3)简要说明我国经济变动情况。
:某公司下属四个企业的有关销售资料如下:根据上述资料:(1)完成上述表格中空栏数据的计算;(2)若A能完成计划,则公司的实际销售额将达到多少比计划超额完成多少(3)若每个企业的计划完成程度都达到B企业的水平,则公司的实际销售额将达到多少比计划超额完成多少第四章-----第二部分平均指标与变异指标:已知某地区各工业企业产值计划完成情况以及计划产值资料如下:要求:(1)根据上述资料计算该地区各企业产值计划的平均完成程度。
(2)如果在上表中所给资料不是计划产值而是实际产值,试计算产值计划平均完成程度。
、:已知某厂三个车间生产不同的产品,其废品率、产量和工时资料如下:计算:(1)三种产品的平均废品率;(2)假定三个车间生产的是同一产品,但独立完成,产品的平均废品率是多少;(3)假定三个车间是连续加工某一产品,产品的平均废品率是多少。
:对某车间甲、乙两工人当日产品中各抽取10件产品进行质量检查,得资料如下:试比较甲乙两工人谁生产的零件质量较稳定。
统计学计算题例题(含答案)
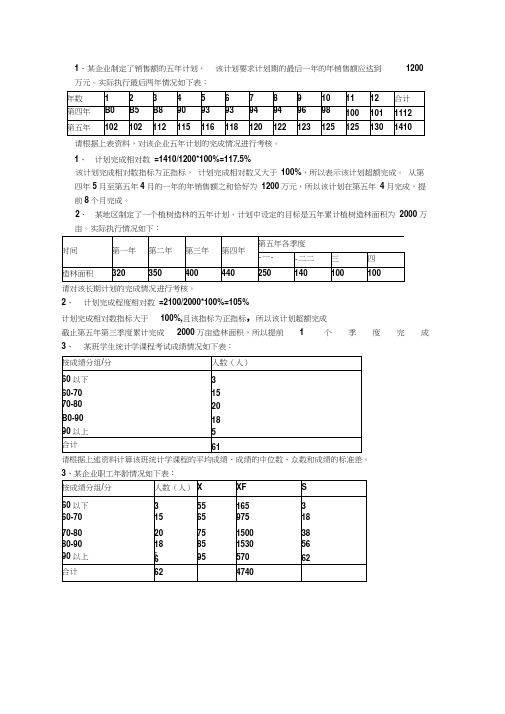
1、某企业制定了销售额的五年计划,该计划要求计划期的最后一年的年销售额应达到1200万元。
实际执行最后两年情况如下表:请根据上表资料,对该企业五年计划的完成情况进行考核。
1、计划完成相对数=1410/1200*100%=117.5%该计划完成相对数指标为正指标,计划完成相对数又大于100%,所以表示该计划超额完成。
从第四年5月至第五年4月的一年的年销售额之和恰好为1200万元,所以该计划在第五年4月完成,提前8个月完成。
2、某地区制定了一个植树造林的五年计划,计划中设定的目标是五年累计植树造林面积为2000万亩。
实际执行情况如下:请对该长期计划的完成情况进行考核。
2、计划完成程度相对数=2100/2000*100%=105%计划完成相对数指标大于100%,且该指标为正指标,所以该计划超额完成截止第五年第三季度累计完成2000万亩造林面积,所以提前1个季度完成3、某班学生统计学课程考试成绩情况如下表:请根据上述资料计算该班统计学课程的平均成绩、成绩的中位数、众数和成绩的标准差。
4、某学校有5000名学生,现从中按重复抽样方法抽取250名同学,调查其每周观看电视的小时数的情4> 样本平均数X= Sxf/Sf-l250/250-5样 ________ __________二>/刀(好予f/(工f—1)二V 1136/249二2. 14抽样平均误差U二s/ Vn=0.14因为F (t) =95%,所以日.96抽样极限误差△二t U 二 1. 96*0. 14=0. 27 区间下限=5-0. 27=4. 73 区间上限二5+0. 27-5. 27全校学生每周平均收看电视的吋间在(4.73,5.27)小时之间,概率保证程度为95%5、某企业对全自动生产线上的产品随机抽取1000件进行检验,发现有45件是不合格的,设定允许的极限误差为 1.32%。
请对全部产品的合格率进行区间估计。
5、样本合格率p=955/1000=95.5% 抽样平均误差u二V pChp)/n= 0.66%因为△=1.32%,所以t= A/ u =2所以F.(.t)-95. 45%区间下限二95. 5%-l. 32%=94. 18%区间上限二95. 5%+l. 32%二96. 82%所以我们以95. 45%的概率估计全部产品和合格率是在(94.18%, 96. 82%)之间。
统计学计算题36600

统计学习题答案三、计算题1、某班级40名学生,某门课程考试成绩如下:87 65 86 92 76 73 56 60 83 7980 91 95 88 71 77 68 70 96 6973 53 79 81 74 64 89 78 75 6672 93 69 70 87 76 82 79 65 84试根据以上资料编制组距为10的分配数列。
解:所编制的分配数列如下所示:某班学生某门课程考试成绩分组资料2、某工业局所属10个企业(工厂)计划利润和实际利润如下:单位:万元(1(2)按利润计划完成程度分组,分为三组.①未完成计划者;②完成计划和超额完成计划10%以内者;③超额完成计划10%以上者.(3)汇总各组企业数、实际利润和计划利润.解:(1)根据资料,算得各厂利润计划完成程度指标如下(2)(3)某工业局所属企业利润计划完成情况统计表三、计算题1某企业产量计划完成程度为103%,实际比上年增长5%,试问计划规定比上年增长多少? 解:设计划规定比上年增长x%,则有 于是,有2某企业计划生产某产品工时消耗较上期降低5%,实际较上期降低4.5%,试确定降低劳动量计划完成程度指标。
解:降低劳动量计划完成程度(%)=实际执行结果表明,降低劳动量还有0。
5%没有完成。
3某公司所属甲、乙两分公司销售额资料如下: 金额单位:万元计算上表各空栏数字,并分别说明各是什么类型的指标。
解:表中各空栏数字计算结果如下:金额单位:万元本期计划、本期实际、上期实际三个指标为总量指标;实际比重(%)为结构相对指标;计划完成(%)为计划完成程度相对指标;本期实际为上期实际(%)为动态相对指标. 4某产品按五年计划规定最后一年产量应达到50万吨,计划执行情况如下表:试计算该产品计划完成程度及提前多少时间完成五年计划规定的指标。
解:该产品从第四年的第二季度起连续累计四个季度产量已达到50万吨。
可见,该产品提前9个月完成了五年计划规定的指标。
统计学计算习题
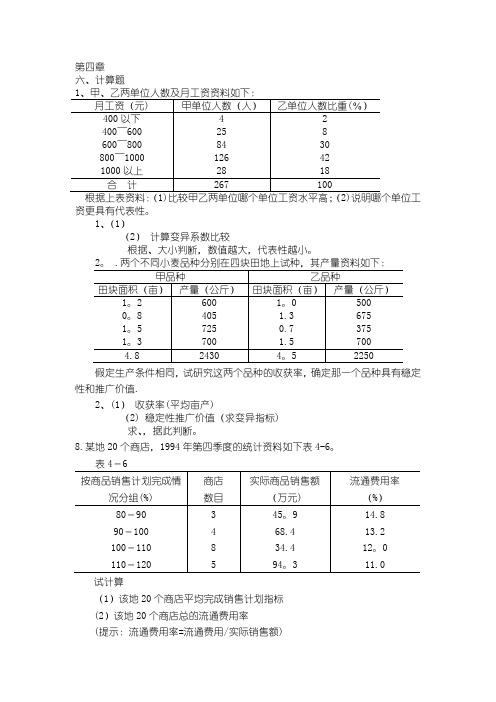
第四章六、计算题资更具有代表性。
1、(1)(2)计算变异系数比较根据、大小判断,数值越大,代表性越小。
假定生产条件相同,试研究这两个品种的收获率,确定那一个品种具有稳定性和推广价值.2、(1)收获率(平均亩产)(2) 稳定性推广价值(求变异指标)求、,据此判断。
8.某地20个商店,1994年第四季度的统计资料如下表4-6。
表4-6试计算(1)该地20个商店平均完成销售计划指标(2)该地20个商店总的流通费用率(提示:流通费用率=流通费用/实际销售额)8、(1)(2) 据提示计算:13、提示:(2)平均一级品率。
14、(1) (2)15.某生产小组有36名工人,每人参加生产的时间相同,其中有4人每件产品耗时5分钟,20人每件耗时8分钟,12人每件耗时10分钟。
试计算该组工人平均每件产品耗时多少分钟?如果每人生产的产品数量相同,则平均每件产品耗时多少分钟?15、(1) 设时间为t ,(2) 设产品数量为a ,16.为了扩大国内居民需求,银行为此多次降低存款利润,近5年年利润率分别为7%、5%、4%、3%、2%,试计算在单利和复利情况下5年的平均年利率。
16、(1) 单利:(2) 复利(几何平均法): 第五章2。
某企业1—7月份工人人数及总产值资料如表8-4:计算:(1)上半年平均月劳动生产率。
(2)上半年劳动生产率。
2、(1) 上半年平均月劳动生产率:(2) 上半年劳动生产率: 3.某企业第二季度有关资料如表8-5:试计算第二季度月平均流转次数及第二季度流转次数。
3、(1) 第二季度月平均流转次数: (2) 第二季度流转次数=4.设某地区1980年国民生产总值为125亿元,人口5000万。
据过去五年国民生产总值的增长速度计算,平均每年递增7.5%,试推算2000年的国民生产总值;若人口增加到6000万人问平均每人能否达到1000元?4、 求 据计算。
7、 计算方法类同9. 某地区对外贸易总额,l994年是1990年的135。
统计学计算题例题

统计学计算题例题(总20页) -CAL-FENGHAI.-(YICAI)-Company One1-CAL-本页仅作为文档封面,使用请直接删除第四章1. 某企业1982年12月工人工资的资料如下:要求:(1)计算平均工资;(79元)(2)用简捷法计算平均工资。
2. 某企业劳动生产率1995年比1990年增长7%,超额完成计划2%,试确定劳动生产率计划增长数。
7%-2%=5%3. 某厂按计划规定,第一季度的单位产品成本比去年同期降低8%。
实际执行结果,单位产品成本较去年同期降低4%。
问该厂第一季度产品单位成本计划的完成程度如何%( (1-4%)/(1-8%)*100%=96%/92%*100%=%结果表明:超额完成%(%-100%))4. 某公社农户年收入额的分组资料如下:要求:试确定其中位数及众数。
中位数为(元)众数为(元)求中位数:先求比例:(1500-720)/(1770-720)=分割中位数组的组距:(800-700)*=加下限700+=求众数:D1=1050-480=570D2=1050-600=450求比例:d1/(d1+d2)=570/(570+450)=分割众数组的组距:*(800-700)=加下限:700+=年某月份某企业按工人劳动生产率高底分组的生产班组数和产量资料如下:(55*300+65*200+75*140+85*60)/(300+200+140+60)6.某地区家庭按人均月收入水平分组资料如下:根据表中资料计算中位数和众数。
中位数为(元) 众数为(元) 求中位数:先求比例:(50-20)/(65-20)= 分割中位数组的组距:(800-600)*= 加下限:600+=7.某企业产值计划完成103%,比去年增长5%。
试问计划规定比去年增长 多少%(上年实际完成= 本年实际计划比上年增长 ()/==%)8.甲、乙两单位工人的生产资料如下:试分析:(1)哪个单位工人的生产水平高(2)哪个单位工人的生产水平整齐%3.33V %7.44V /8.1x /5.1x ====乙甲乙甲人)(件人)(件9.在计算平均数里,从每个标志变量中减去75个单位,然后将每个差数 缩小10倍,利用这个变形后的标志变量计算加权算术平均数,其中各个变量的权数扩大7倍,结果这个平均数等于个单位。
统计学练习题——计算题
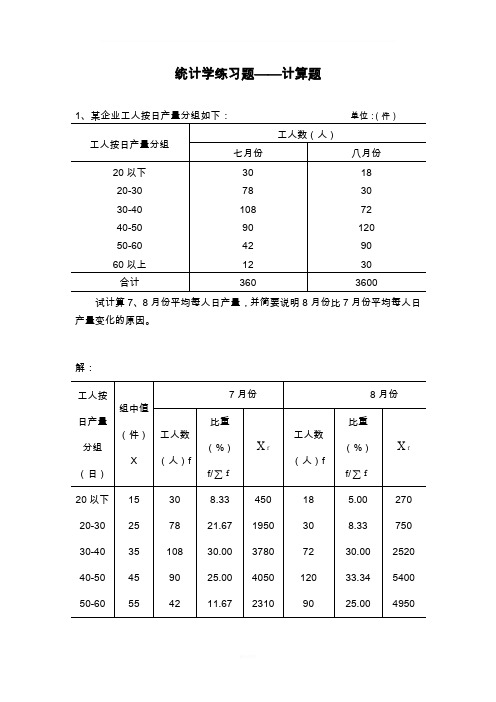
统计学练习题——计算题试计算7、8月份平均每人日产量,并简要说明8月份比7月份平均每人日产量变化的原因。
解:7月份平均每人日产量为:3736013320===∑∑f Xf X (件) 8月份平均每人日产量为:4436015840===∑∑fXf X (件)根据计算结果得知8月份比7月份平均每人日产量多7件。
其原因是不同组日产量水平的工人所占比重发生变化所致。
7月份工人日产量在40件以上的工人只占全部工人数的40%,而8月份这部分工人所占比重则为66.67%。
试比较这两年产品的平均等级,并说明该厂棉布生产在质量上有何变化及其因。
解:2009年棉布的平均等级=25010 34022001⨯+⨯+⨯=1.24(级)2010年棉布的平均等级=3006 32422701⨯+⨯+⨯=1.12(级)可见该厂棉布产品质量2010年比2009年有所提高,其平均等级由1.24级上升为1.12级。
质量提高的原因是棉布一级品由80%上升为90%,同时二级品和三级品分别由16%及4%下降为8%及2%。
试比较和分析哪个企业的单位成本高,为什么?解:甲企业的平均单位产品成本=1.0×10%+1.1×20%+1.2×70%=1.16(元)乙企业的平均单位产品成本=1.2×30%+1.1×30%+1.0×40%=1.09(元)可见甲企业的单位产品成本较高,其原因是甲企业生产的3批产品中,单位成本较高(1.2元)的产品数量占70%,而乙企业只占30%。
试计算各地区平均价格和此种商品在四个地区总的平均价格。
解:总平均价格=23010600=销售总量销售总额=46.09根据上表计算该商店售货员工资的全距,平均差和标准差,平均差系数和标准差系数。
⑴2010200==∑∑fXf X =510(元); ⑵全距=690-375=315(元) ⑶156020X XfA D f-⋅==∑∑=78(元); ⑷)(202085002==∑∑-ffXX σ=102.1(元)⑸%10051078%100⨯=⨯⋅=⋅XD A V D A =15.29%; ⑹%1005101.102%100⨯=⨯=XV σσ=20.02%6、某班甲乙两个学习小组某科成绩如下:试比较甲乙两个学习小组该科平均成绩的代表性大小。
统计学的计算题汇总(附有答案)

统计学的计算题汇总如下
答案计算过程中避免不了误差哦,请各位认真去计算一下吧!
1、某地区2010年玉米产量如下表所示:
解: 依题意知,此题数据是组距数列。
所以取产量组中值分别为450、550、650、750、850
2、已知甲组工人的平均奖金为1767元,其标准差为92元,乙组工人的奖金如下表所示:
解:依题意知,此题数据是组距数列。
所以取奖金组中值分别为1550、1650、1750、1850、1950
3、某地区2011年土地面积为2.4万平方公里,人口资料如下表所示:
4、①某企业2009年计划利润需求比上年提高5% ,实际提高了8% 。
计划产品单位成本要求比上年降低10% ,实际降低了6% 。
请计算利润和成本各自的完成情况,并加以说明?
②某班有40名学生,20岁的有3人,19岁的有25人,18岁的有12人,请用加权算数平均法和众数法分别计算该班的平均年龄?
答案如下:。
统计学计算题整理

:典型计算题一136==∑∑ffxx (元)点评: 第一,此题给出销售单价和销售量资料,即给出了计算平均指标的分母资料,所以需采用算术平均数计算平均价格。
第二,所给资料是组距数列,因此需计算出组中值。
采用加权算术平均数计算平均价格。
第三,此题所给的是比重权数,因此需采用以比重形式表示的加权算术平均数公式计算。
2、某企业1992年产值计划是1991年的105%,1992年实际产值是1991的的116%,问1992年产值计划完成程度是多少?解:%110%105%116===计划相对数实际相对数计划完成程度。
即1992年计划完成程度为110%,超额完成计划10%。
点评:此题中的计划任务和实际完成都是“含基数”百分数,所以可以直接代入基本公式计算。
3、某企业1992年单位成本计划是1991年的95%,实际单位成本是1991年的90%,问1992年单位成本计划完成程度是多少?解:计划完成程度%74.94%95%90==计划相对数实际相对数。
即92年单位成本计划完成程度是%,超额完成计划%。
点评:本题是“含基数”的相对数,直接套用公式计算计划完成程度。
4、某企业1992年产值计划比91年增长5%,实际增长16%,问1992年产值计划完成程度是多少?解:计划完成程度%110%51%161=++=点评:这是“不含基数”的相对数计算计划完成程度,应先将“不含基数”的相对数还原成“含基数”的相对数,才能进行计算。
5、某企业1992年单位成本计划比1991年降低5%,实际降低10%,问1992年单位成本降低计划完成程度是多少?解:计划完成程度%74.94%51%101=--=点评:这是“不含基数”的相对数计算计划完成程度,应先将“不含基数”的相对数还原成“含基数”的相对数,才能进行计算。
6、某企业产值计划完成103%,比上期增长5%,问产值计划规定比上期增加多少?解:103%=105%÷(1+x ) x=%即产值计划规定比上期增加%.点评:计划完成程度=103%,实际完成相对数=105%,设产值计划规定比上期增加x ,则计划任务相对数=1+x ,根据基本关系推算出x.7、某煤矿某月计划任务为5400吨,各旬计划任务是均衡安排的,根据资料分析解:从资料看,尽管超额完成了全期计划(5400=104%),但在节奏 性方面把握不好。
统计学计算题

第二章六、计算题.1.下面是某公司工人月收入水平分组情况和各组工人数情况:月收入(元)工人数(人)400-500 20500-600 30600-700 50700-800 10800-900 10指出这是什么组距数列,并计算各组的组中值和频率分布状况。
答:闭口等距组距数列,属于连续变量数列,组限重叠。
各组组中值及频率分布如下:2.抽样调查某省20户城镇居民平均每人全年可支配收入(单位:百元)如下:88 77 66 85 74 92 67 84 77 94 58 60 74 64 75 66 78 55 70 66⑴根据上述资料进行分组整理并编制频数分布数列⑵编制向上和向下累计频数、频率数列答:⑴⑵某省20户城镇居民平均每人全年可支配收入分布表第三章六、计算题.⒈某企业生产情况如下:要求:⑴填满表内空格.⑵对比全厂两年总产值计划完成程度的好坏。
解:⑴某企业生产情况如下:单位:(万元)⑵该企业2005年的计划完成程度相对数为110.90%,而2006年只有102.22%,所以2005年完成任务程度比2006好。
⒉某工厂2006年计划工业总产值为1080万吨,实际完成计划的110%,2006年计划总产值比2005年增长8%,试计算2006年实际总产值为2005年的百分比?解:118.8%3.某种工业产品单位成本,本期计划比上期下降5%,实际下降了9%,问该种产品成本计划执行结果?解:95.79%4.我国“十五”计划中规定,到“十五”计划的最后一年,钢产量规定为7200万吨,假设“八五”期最后两年钢产量情况如下:(万吨)根据上表资料计算:⑴钢产量“十五”计划完成程度;⑵钢产量“十五”计划提前完成的时间是多少?解:⑴102.08%;⑵提前三个月5.某城市2005年末和2006年末人口数和商业网点的有关资料如下:计算:⑴平均每个商业网点服务人数;⑵平均每个商业职工服务人数;⑶指出是什么相对指标。
解: 某城市商业情况⑶上述两个指标是强度相对指标。
统计学计算题

四、计算题(共50分。
其中1小题10分;2小题15分;3小题10分;4小题15分)1.根据以往生产数据,某种产品的废品率为2%。
如果要求95%的置信区间,估计误差不超过4%,应该抽取多大的样本?根据已知条件P=2%,96.12=αZ ;E=4%=⨯=⨯=-⋅=122584.30016.096.196.1)1(2222EP P Z n α4704试用指数体系法分析销售额的变动。
(1)销售额变动 %116750870011==∑=∑q p q p K pq )(1207508700011万元=-=∑-∑q p q p (2)销售量指数 %93.11075083200000010==∑∑=∑=∑q p q Kp q p q p K q)(827508320010万元=-=∑-∑q p q p(3)销售价格指数 %57.10483287000111011==∑∑=∑∑=q kp q p q p q p K p )(38832870101万元=-=∑-∑q p q p (4)指数体系绝对数 120万元=82万元+38万元 相对数 116%=110.93%×104.57%(5)文字说明:该商店三种商品销售额报告期比基期增长了16%,增加120万元。
这是由销量和价格两因素变动引起的。
其中,价格固定在每种商品各自的基期水平,由于销量的变动使得总销售额比基期提高了10.93%,增加82万元;把销量固定在每种商品各自的报告期水平,由于价格的变动使得总销售额比基期提高了4.57%,增加了38万元。
试计算该企业第二季度平均每月全员劳动生产率。
(10分)解:第二季度平均每月总产值)(12203137011201170万元=++=∑=n a a第二季度平均每月职工人数1421214321-+++=b b b b b)(8.631.7219.67.05.621千人=⨯+++⨯=该企业第二季度平均每月全员劳动生产率bac =()人元千人万元/12.17948.61220==(1)计算相关系数,判断其相关程度;(2)建立以总成本为因变量的回归直线方程,并预测当木材消耗量为2.5米3时,总成本将达到多少千元?4、①r=2222)()(∑∑∑∑∑∑∑-⋅--y y n x x n yx xy n =0.75 中度正相关②b==--∑∑∑∑∑22)(x x n y x xy n 0.758a=y -b x =1.265 x Y c 758.0265.1+=当x=2.5时,总成本16.35.2758.0265.1=⨯+=c y (千元)。
统计学练习题(计算题)

统计学练习题(计算题)第四章----第一部分总量指标与相对指标4.1:(1)某企业产值计划完成程度为105%,比上年增长7%,试计算计划规定比上年增长多少?(2)单位产品成本上年为420元,计划规定今年成本降低5%,实际降低6%,试确定今年单位成本的计划数字和实际数字,并计算出降低成本计划完成程度指标。
(3)按计划规定,劳动生产率比上年提高10%,实际执行结果提高了12%,劳动生产率计划完成程度是多少?4.2:某市三个企业某年的下半年产值及计划执行情况如下:要求:[1]试计算并填写上表空栏,并分别说明(3)、(5)、(6)、(7)是何种相对数;[2]丙企业若能完成计划,从相对数和绝对数两方面说明该市三个企业将超额完成计划多少?4.3:我国2008年-2013年国内生产总值资料如下:单位:亿元根据上述资料,自行设计表格:(1)计算各年的第一产业、第二产业、第三产业的结构相对指标和比例相对指标;(2)计算我国国内生产总值、第一产业、第二产业、第三产业与上年对比的增长率;(3)简要说明我国经济变动情况。
4.4:某公司下属四个企业的有关销售资料如下:根据上述资料:(1)完成上述表格中空栏数据的计算;(2)若A能完成计划,则公司的实际销售额将达到多少?比计划超额完成多少?(3)若每个企业的计划完成程度都达到B企业的水平,则公司的实际销售额将达到多少?比计划超额完成多少?第四章-----第二部分平均指标与变异指标4.5:已知某地区各工业企业产值计划完成情况以及计划产值资料如下:要求:(1)根据上述资料计算该地区各企业产值计划的平均完成程度。
(2)如果在上表中所给资料不是计划产值而是实际产值,试计算产值计划平均完成程度。
、4.6:已知某厂三个车间生产不同的产品,其废品率、产量和工时资料如下:计算:(1)三种产品的平均废品率;(2)假定三个车间生产的是同一产品,但独立完成,产品的平均废品率是多少;(3)假定三个车间是连续加工某一产品,产品的平均废品率是多少。
统计学资料计算题

计算题:100%11⨯±±=率)计划提高率(计划降低率)实际提高率(实际降低计划完成相对数P72例4.5:某企业本年度计划单位成本降低6%,实际降低7.6%,则:成本降低率计划完成相对数=(1-7.6%)/(1-6%)*100%=98.29% 根据计算结果,本年度单位成本降低率比计划完成了1.71%例4.6:某企业计划规定劳动生产率比上年提高10%,实际比上年提高15%,则:劳动生产率计划完成相对数=(1+15%)/(1+10%)*100%=104.5% 根据计算结果,劳动生产率超额4.5%完成计划任务。
P81例 4.14:某企业有三个工厂,已知其计划完成程度及计划增加值资料如表所示,计算该企业平均计划完成程度。
工厂 计划完成程度(%)X 计划增加值(万元)f 甲 92 130 乙 105 1280 丙 117 300 合计 —— 1710106.12%17101814.630012801303001.1712801.051300.92==++⨯+⨯+⨯=⨯==∑∑∑∑计划增加值计划增加值计划完成程度f xf x根据计算结果,该企业平均计划完成程度是106.12%,即超额6.12%完成计划。
例4.15:某企业有三个工厂,已知其计划完成程度及实际完成增加值资料如表,计算该企业平均计划完成程度。
工厂 计划完成程度(%)x 实际完成增加值(万元)m 甲 92 119.6 乙 105 1344.0 丙 117 351.0 合计 —— 1814.6106.12%17101814.6 1.173511.0513440.92119.63511344119.6x m m ==++++===∑∑∑∑计划完成程度实际完成增加值实际完成增加值平均计划完成程度根据计算结果,该企业平均计划完成程度是106.12%,即超额6.12%完成计划。
P84加权几何平均计算例4.18:投资银行某笔投资的年利率是按复利计算的,25年的年利率分配是:有1年为3%,有4年为5%,有8年为8%,有10年为10%,有2年为15%,求平均年利率。
统计学练习题及答案

统计学练习题及答案一、选择题1. 以下哪个不是描述性统计分析的范畴?A. 均值B. 方差C. 标准差D. 回归分析答案:D2. 在统计学中,总体是指:A. 研究中的所有个体B. 研究中的部分个体C. 研究中的随机样本D. 研究中的实验组答案:A3. 以下哪个是参数估计的方法?A. 描述统计B. 假设检验C. 点估计D. 相关分析答案:C4. 以下哪个是统计学中的离散型随机变量?A. 身高B. 体重C. 年龄D. 家庭中的子女数答案:D5. 正态分布的均值和方差之间的关系是:A. 均值等于方差的平方B. 方差等于均值的平方C. 方差是均值的函数D. 均值和方差是独立的答案:D二、简答题1. 简述抽样分布的概念。
答:抽样分布是指在多次抽样的情况下,样本统计量(如样本均值、样本方差等)的分布情况。
它描述了在不同样本中,这些统计量如何变化。
2. 解释什么是标准正态分布,并给出其均值和标准差。
答:标准正态分布是一种特殊的正态分布,其均值为0,标准差为1。
这种分布是正态分布的一种特殊形式,常用于标准化数据。
三、计算题1. 给定一组数据:10, 12, 14, 16, 18, 20,求这组数据的平均值和标准差。
答:平均值 = (10+12+14+16+18+20)/6 = 14.5标准差 = sqrt(((10-14.5)^2 + (12-14.5)^2 + (14-14.5)^2 + (16-14.5)^2 + (18-14.5)^2 + (20-14.5)^2)/6) = 3.772. 假设有一个总体,其均值为μ=100,标准差为σ=20。
从这个总体中随机抽取一个样本容量为n=36的样本,样本均值为x̄=105。
请问样本均值是否显著高于总体均值?答:使用t检验,t = (x̄ - μ) / (σ / sqrt(n)) = (105 - 100) / (20 / sqrt(36)) = 5 / 10 = 0.5。
统计学计算题和答案完整版

统计学计算题和答案 HEN system office room 【HEN16H-HENS2AHENS8Q8-HENH1688】三个企业生产的同一型号空调在甲、乙两个专卖店销售,有关资料如下:企业型号 价格 (元/台) 甲专卖店销售额(万元) 乙专卖店销售量(台) A 2500 340 B 3400 260 C 4100 200 合计——答案:2某企业甲、乙两个生产车间,甲车间平均每个工人日加工零件数为65件,标准差为11件;乙车间工人日加工零件数资料如下表。
试计算乙车间工人加工零件的平均数和标准差,并比较甲、乙两个生产车间哪个车间的平均日加工零件数更有代表性?日加工零件数(件) 60以下 60—70 70—80 80—90 90—100 工人数(人)59121410三、某地区2009—2014年GDP 资料如下表,要求: 1、计算2009—2014年GDP 的年平均增长量; 2、计算2009—2014年GDP 的年平均发展水平;年份 2009 2010 2011 2012 2013 2014 GDP (亿元)87431062711653147941580818362年平均增长速度:5100%280%100%22.9%x -=-= 年份2010 2011 2012 2013 2014 销售额(万元)320332340356380水平?答案: 2010年—2014年的数据有5项,是奇数,所以取中间为0,以1递增。
设定x 为-2、-1、0、1、2、年份/销售额(y ) x xy x2 2010 320 -2 -640 4 2011 332 -1 -332 1 2012 340 0 0 0 2013 356 1 356 1 2014 380 2 760 4合计 1728 0 144 10b=∑xy/∑x2=144/10=a=∑y/n=1728/5=y=+预测2016年,按照设定的方法,到2016年应该是5y=+*5=元五、某企业生产三种产品,2013年三种产品的总生产成本分别为20万元,45万元,35万元,2014年同2013年相比,三种产品的总生产成本分别增长8%,10%,6%,产量分别增长12%,6%,4%。
统计学计算题例题(含答案)
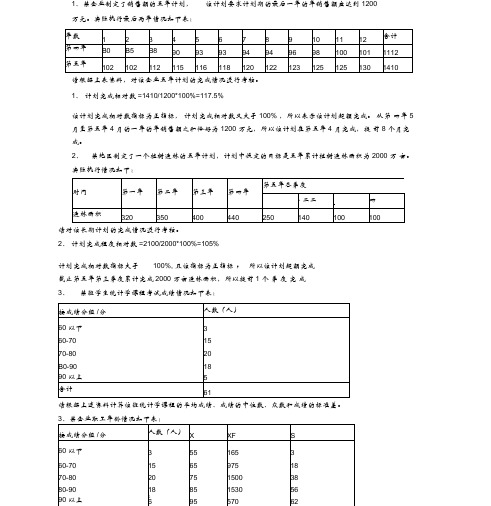
1、某企业制定了销售额的五年计划, 该计划要求计划期的最后一年的年销售额应达到 1200万元。
实际执行最后两年情况如下表:请根据上表资料,对该企业五年计划的完成情况进行考核。
1、 计划完成相对数 =1410/1200*100%=117.5%该计划完成相对数指标为正指标, 计划完成相对数又大于 100% ,所以表示该计划超额完成。
从第 四年 5 月至第五年 4 月的一年的年销售额之和恰好为 1200 万元,所以该计划在第五年 4 月完成,提 前 8 个月完成。
2、 某地区制定了一个植树造林的五年计划,计划中设定的目标是五年累计植树造林面积为 2000 万 亩。
实际执行情况如下:请对该长期计划的完成情况进行考核。
2、 计划完成程度相对数 =2100/2000*100%=105%计划完成相对数指标大于100%, 且该指标为正指标 , 所以该计划超额完成截止第五年第三季度累计完成 2000 万亩造林面积,所以提前 1 个 季 度 完 成3、某班学生统计学课程考试成绩情况如下表:请根据上述资料计算该班统计学课程的平均成绩、成绩的中位数、众数和成绩的标准差。
3、某企业职工年龄情况如下表:X 二三于=4740/62=76.45 (分)Me=70+ (62/2-18) *10/20=76.5 (分)Mo=70+(20 J5)70/[(2CM5)+(2CM8)]=77 」4 (分)G-7(55-76.45f *3 +⋯⋯+ (95^76.45f *6/62=10.45 (分)4、某学校有5000 名学生,现从中按重复抽样方法抽取250 名同学,调查其每周观看电视的小时数的情况,获得资料如下表:请根据上述资料,以95% 的概率保证程度对全校学生每周平均收看电视时间进行区间估计。
4> 样本平均数X= Sxf/Sf-l250/250-5样 ______________ __________二>/ 刀(好予f/(工f—1 )二V 1136/249 二2. 14抽样平均误差U 二s/ Vn=0.14因为 F (t) =95%, 所以日.96抽样极限误差△ 二t U 二 1. 96*0. 14=0. 27 区间下限=5-0. 27=4. 73 区间上限二5+0. 27-5. 27全校学生每周平均收看电视的吋间在( 4.73,5.27) 小时之间,概率保证程度为95%5 、某企业对全自动生产线上的产品随机抽取1000 件进行检验,发现有45 件是不合格的,设定允许的极限误差为1.32% 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
统计学练习题——计算题试计算7、8月份平均每人日产量,并简要说明8月份比7月份平均每人日产量变化的原因。
解:7月份平均每人日产量为:3736013320===∑∑f Xf X (件) 8月份平均每人日产量为:4436015840===∑∑fXf X (件)根据计算结果得知8月份比7月份平均每人日产量多7件。
其原因是不同组日产量水平的工人所占比重发生变化所致。
7月份工人日产量在40件以上的工人只占全部工人数的40%,而8月份这部分工人所占比重则为66.67%。
试比较这两年产品的平均等级,并说明该厂棉布生产在质量上有何变化及其因。
解:2009年棉布的平均等级=25010 34022001⨯+⨯+⨯=1.24(级)2010年棉布的平均等级=3006 32422701⨯+⨯+⨯=1.12(级)可见该厂棉布产品质量2010年比2009年有所提高,其平均等级由1.24级上升为1.12级。
质量提高的原因是棉布一级品由80%上升为90%,同时二级品和三级品分别由16%及4%下降为8%及2%。
试比较和分析哪个企业的单位成本高,为什么?解:甲企业的平均单位产品成本=1.0×10%+1.1×20%+1.2×70%=1.16(元)乙企业的平均单位产品成本=1.2×30%+1.1×30%+1.0×40%=1.09(元)可见甲企业的单位产品成本较高,其原因是甲企业生产的3批产品中,单位成本较高(1.2元)的产品数量占70%,而乙企业只占30%。
试计算各地区平均价格和此种商品在四个地区总的平均价格。
解:总平均价格=23010600=销售总量销售总额=46.09根据上表计算该商店售货员工资的全距,平均差和标准差,平均差系数和标准差系数。
⑴2010200==∑∑fXf X =510(元); ⑵全距=690-375=315(元) ⑶156020X XfA D f-⋅==∑∑=78(元); ⑷)(202085002==∑∑-ffXX σ=102.1(元)⑸%10051078%100⨯=⨯⋅=⋅XD A V D A =15.29%; ⑹%1005101.102%100⨯=⨯=XV σσ=20.02%6、某班甲乙两个学习小组某科成绩如下:试比较甲乙两个学习小组该科平均成绩的代表性大小。
解:241770==∑∑fXf X =73.75(分)σ==(分) 11.0673.75PXV σσσ===×100%=15.00%241790==∑∑fXf X =74.58(分) σ====10.60(分)10.674.58XV σσ==×100%=14.21% 计算结果得知乙小组标准差系数小,所以乙小组平均成绩代表性大。
7、某机械厂铸造车间生产600吨铸件,合格540吨,试求平均合格率,标准差及标准差系数。
解: 标准差)()(90.0190.01-=-=P P σ×100%=30%标准差系数%33.33%90%30%100==⨯=XV σσ请计算各季平均每月总产值和全年平均每月总产值。
解:第一季度平均每月总产值=4400万元第二季度平均每月总产值≈4856.7万元第三季度平均每月总产值=5200万元第四季度平均每月总产值=5500万元全年平均每月总产值=4989.2万元9、2013年末,某储蓄所按2420户的定期储蓄存款账号,进行不重复抽样得到如下资料:试以0.9545概率对下列指标作区间估计:(1)平均每户定期存款;(2)定期存款在300元及300元以上户的比重。
[提示:100元以下的组中值为50元,t=2。
平均数保留一位,成数(用系数表示)保留两位小数]解:(列表计算2分)(1)平均定期存款区间估计: 平均每户定期存款为:)(344484166500元===∑∑fxf x 698.4048419697624)(22=-=∑∑ffx x σ抽样平均误差:)(2.8)24204841(48440698)1(2元=-=-=N n nx σμ 抽样极限误差:)(4.162.82元=⨯==∆x x t μ平均定期存款区间估计:4.16344±=∆±x x 即在:327.6~360.4 (2)存款在300元及300元以上户的比重: 57.04841462200=++=p02.0)24204841(484)57.01(57.0)1()1(=--⨯=--=Nnn p p p μ04.002.02=⨯==∆p p t μ 04.057.0±=∆±p p即:存款在300元及以上户的比重区间为53%~61%之间。
请计算该企业2005年各季平均职工人数和全年平均职工人数。
解:第一季度平均职工人数≈302人第二季度平均职工人数≈310人第三季度平均职工人数=322人第四季度平均职工人数=344人全年平均职工人数≈320人请计算各种动态指标,并说明如下关系:⑴发展速度和增长速度;⑵定基发展速度和环比发展速度;⑶逐期增长量与累计增长量;⑷平均发展速度与环比发展速度;⑸平均发展速度与平均增长速度。
“十五”时期工业总产值平均发展速度=53.3439.783=117.96% 各种指标的相互关系如下:⑴增长速度=发展速度-1,如2001年工业总产值发展速度为130.21%,同期增长速度=130.21%-100%=30.21%⑵定基发展速度=各年环比发展速度连乘积,如2005年工业总产值发展速度228.34%=130.21%×116.2%×105.58%×128.23%×111.41%⑶累计增长量=各年逐期增长量之和,如2005年累计增长量440.6=103.7+72.7+29.0+154.9+80.3⑷平均发展速度等于环比发展速度的连乘积再用其项数开方。
如“十五”期间工业总产值平均发展速度⑸平均增长速度=平均发展速度-1,如“十五”期间平均增长速度17.96%=117.96%-100%要求:⑴计算第一季度和第二季度非生产人员比重,并进行比较;⑵计算上半年非生产人员比重。
解:[1]第一季度非生产人员比重:17.4%;第二季度非生产人员比重:16.4%;∴第二季度指标值比第一季度少1%。
[2]上半年非生产人员比重:16.9%。
13、某企业历年若干指标资料如下表:单位:万元试根据上述资料,计算表中所缺的数字。
14、有三种商品的销量和售价资料如下计算分析销量和售价的变动对销售额变动的影响。
解:(略)说明:按如下公式建立指标体系并计算∑∑∑∑∑∑⨯=0011011011pq p q q p q p qp q p15、某企业职工人数和工资资料统计如下:根据资料,从相对数和绝对数两个方面分析工人结构变化及各组平均工资水平的变动对总体平均工资的影响。
解:(略)说明:按如下公式建立指标体系并计算∑∑∑∑∑∑∑∑∑∑∑∑⨯=01101101110111ff x f f x ff x f f x ff x f f x16、某灯管厂生产10万只日光灯管,现采用简单随机不重复抽样方式抽取1%灯管进行质量检验,测试结果如下:根据上述资料:(1)试计算抽样总体灯管的平均耐用时间(2)在99.73%的概率保证程度下,估计10万只灯管平均耐用时间的区间范围/(3)按质量规定,凡耐用时间不及800小时的灯管为不合格品,试计算抽样总体灯管的合格率,并在95%的概率保证程度下,估计10万只灯管的合格率区间范围。
(4)若上述条件不变,只是抽样极限误差可放宽到40小时,在99.73%的概率保证程度下,作下一次抽样抽查,需抽多少只灯管检验?解:列表计算:(1))fxf x 小时(97010097000===∑∑ (2)。
,:t N n n ffx (x x x x 之间间在该批灯管平均耐用的时的概率保证程度下在即%98.1004%02.935%73.9998.3466.11366.11)001.01(10013600)1(136001001360000)222-=⨯=⨯=∆=-=-===-=∑∑μσμσ(3)之间该批灯管的合格率在的概率保证程度下即在即%88.95—%12.84%45.95%88.95—%12.840588.090.00588.003.096.103.0)001.01(100)90.01(90.0)1()1(90.010015253515,p t N n n p p p p pp p ±=∆±=⨯=⨯=∆=-⨯⨯=--==+++=μμ(4)只7744.761360034010000013600310000022222222≈=⨯+⨯⨯⨯=+∆=σσt N Nt n xWelcome To Download !!!欢迎您的下载,资料仅供参考!。
