实验二、外压薄壁圆筒形容器失稳实验
基于失稳失效准则的外压薄壁圆筒试验压力

Ab t a t sr c :A p l a int er l b l yd sg h o y a d me h d a i n r n o f z yp o a i — p i t h ei i t e in t e r n t o sb sso a d m—u z r b b l c o a i i
t o l i i u ntt tv n l e ha e i bi t a ge o r n c ii a t e gt n bu klng o y m de ,t s q a ia i e a a yz d t tr la l y r n fvigi rtc ls r n h i c i f i c i de urn r s ur e t a d n m a e a i .T h y i e e tn o fii nta a t r s yln r d i g p e s e t s n or lop r ton e c lnd r t s i g c e fce nd f c o i r s a c r m e a fr sde of i m a v r n e i b lt i f e e or n on ton e e r h f o ke p im on i m ni l igi r la iiy n dif r nt w ki g c dii s m o . tw a on l e ha ,he r n uz y r la iiy o igi r tc t e gt n b kln sbe de I sc c ud d t t t a ge f z e i b lt fv r n c iial r n h i uc i g i — s
t e 9 9 09 ~ 9 . 9 2 2 o 9 8 11 ~ 9 . 1 6/ d r gh da l rb rmer we n9 . 7 1 9 9 99 82 r9 . 4 % 9 9 83 6 u i y rui o ao ti 9 n c ~
薄壁圆筒外压失稳实验

薄壁圆筒外压失稳实验一、实验目的1.观察外压容器的失稳破坏现象及破坏后的形态。
2.验证外压筒体试件失稳时临界压力的理论计算式。
二、实验装置基本配置表一、实验装置基本配置表:图一、薄壁圆筒外压失稳实验装置三、实验原理薄壁容器在受外压作用时,往往在器壁内的应力还未达到材料的屈服极限,而在外压达到某一数值时,壳体会突然推动原来形状而出现褶皱,这种现象称为失稳,失稳时的压力称为临界压力,以P cr [MPa]表示。
它与材料的弹性性能(弹性模数E 和泊桑比μ)、几何尺寸(简体直径D 、壁厚S O 和筒体计算长度L)有关。
钢制薄壁容器的临界压力与波数的计算公式如下:长圆筒Bress 公式:202)(12DS E P cr μ-=(1) 短圆筒B.M.Pamm 公式:)()//()/(06.7/59.242002正整数D L S D n s D LD ES P cr ==(2)临界尺寸:0/17.1L S D D cr = (3) 当L >L cr 时,为长圆筒; 当L <L cr 时,为短圆筒。
式中:P—临界压力,MPa;crD—圆筒直径,mm;L—圆筒计算长度,mm;S0—圆筒壁厚,mm;E—材料弹性模数,MPa;μ—材料泊桑比;n—失稳时波数;Lcr—临界长度,mm。
四、实验操作步骤1.开启计算机,启动计算机、打开实验软件。
2.检查压力传感器和温度计是否正常。
3.测量试件几何尺寸,检查水箱内水是否充足,适量添加。
4.启动离心泵,向失稳灌内注入适量水(水加至试件放入不易水为宜),安装测试试件。
5.停止离心泵,将压力仪表输出值调至0,启动压缩机。
6.慢慢改变仪表输出值,增加压力,记录压力变化曲线。
7.通过有机玻璃观察试件受压及其变形情况(失稳瞬间有响声)。
8.关闭实验设备,释放压力,取出实验试件分析实验数据。
五、实验数据。
接管弯矩与外压作用下薄壁圆筒的失稳分析

锅炉制造BOILER MANUFACTURING第4期2019年7月No. 4Jul. 2019接管弯矩与外压作用下薄壁圆筒的失稳分析方小里,张福君(哈尔滨锅炉厂有限责任公司,黑龙江哈尔滨150046)摘要:本文采用考虑初始几何缺陷的弹塑性应力分析方法对某带薄壁圆筒进行了非线性失稳分析,结果表明:开孔接管大大降低了薄壁圆筒失稳临界载荷;随着接管弯矩的增大,圆筒临界失稳载荷有一定程度减低, 并且圆筒的临界变形有整体失稳波形向接管局部失稳转变。
关键词:接管弯矩;薄壁圆筒汐卜圧;失稳中图分类号:TH49文献标识码:A 文章编号:CN23 - 1249(2019)04 - 0056 - 03Stability Analysis of Thin - Walled Cylindrical Shell with NozzleSubjected to Moment and External PressureFang Xiaoli , Zhang Fujun(Harbin Boiler Company Limited , Harbin 150046, China)Abstract : The nonlinear stability analysis of a thin-walled cylindrical shell with nozzle is carried out using elastic-plastic stress analysis considering initial geometry imperfection. The results show thatthe nozzle largely reduces the critical buckling load of the thin-walled cylindrical shell ; The bucklingloads decrease when the nozzle moment increase , and the buckling modes transform from total de ・ formation to local deformation.Key words : nozzle moment ; thin-walled cylindrical shell ; external ; instability0引言大型薄壁外压容器的一个主要失效模式是失 稳失效,容器一旦发生失稳往往很突然且后果异常严重,因此在设计时必须对其失稳进行详细的 分析计算。
压力容器设计 外压薄壁圆筒的稳定性计算
轴向压缩圆筒失稳的形状
(a)非对整称理课形件式;(b)对称形式
本节重点
❖ (1)失稳、临界压力、临界长度概念; ❖ (2)典型受载条件下圆筒临界压力(或应
力)计算公式 。
整理课件
整理课件
整理课件
整理课件
减压整操理课作件 设备
带夹套搅拌釜
整理课件
容器韧整性理课断件 裂外观
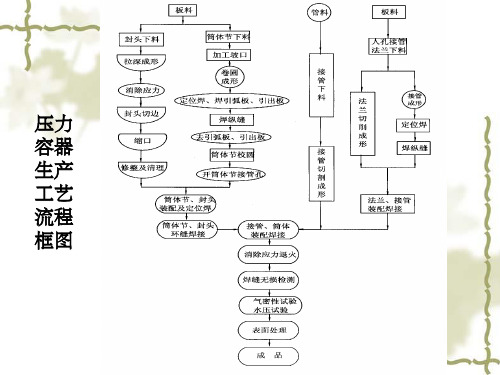
压力 容器 生产 工艺 流程 框图
整理课件
第四章 外压容器设计
整理课件
第一节 概述
一、外压容器的稳定性
第一节 概述
真空操作容器、减压精馏塔的外壳 外压容器
用于加热或冷却的夹套容器的内层壳体
整理课件
外压容器的失效形式
第一节 概述
强度不足而发生压缩屈服失效
承受外压 壳体失效
形式
当外压达到一定的数值时,壳体的径 向挠度随压缩应力的增加急剧增大, 直至容器压扁,这种现象称为外压容 器的失稳或屈曲。(讨论重点)
适用条件整:理课件 cr
<
tp(
t y
)
第二节 外压薄壁圆筒的稳定性计算
Lcr 1.17Do
Do t
整理课件
第二节 外压薄壁圆筒的稳定性计算
带加强圈的圆筒
2.59Et2
pcr LDo
Do t
带加强圈整理的课件外压圆筒
受均布轴向压缩载荷 圆筒的临界应力
第二节 外压薄壁圆筒的稳定性计算
(a)
(b)
cr
pcrDo 2t
1.1EDto
3
适用条件:整c理r 课<件
tp(
t y
)
第二节 外压薄壁圆筒的稳定性计算
注意
实验二、外压薄壁圆筒形容器失稳实验

实验二、外压薄壁圆筒形容器失稳实验一、实验目的1. 观察薄壁圆筒形容器在外压作用下丧失稳定性后的形态。
2. 测定圆筒形容器失去稳定性时的临界压力并与理论值相比较。
二、基本原理圆筒形容器在外压作用下,常因刚度不足使容器失去原有形状,即被压扁或折曲成波形,这就是容器的失稳现象,容器失去稳定性时的外压力,成为容器的临界压力,用cr p 表示。
圆筒形容器失去稳定性后,其横截面被折成波形,波数n 可能是1,2,3,4,……等任意整数,如图一所示。
容器承受临界值的外压力而失去稳定性,决非是由于容器壳体本身不圆的缘故,即是绝对圆的壳体也会失去稳定性。
当然如壳体不圆(具有椭圆度)容器更容易失稳,即它的临界压力值会下降。
根据外压容器筒体的长短,可分为长圆筒,短圆筒和刚性圆筒三种,刚性圆筒一般具有足够的刚度,可不必考虑稳定性问题。
但长圆筒,短圆筒必须进行稳定性计算,它们的临界压力cr p 值大小主要与厚壁(t ),外直径(0D ),长度(L )有关。
亦受材料弹性模数(E ),泊桑比(μ)影响。
所谓长圆筒,短圆筒之分,并不是指它们的绝对长度,而是与直径壁厚有关的相对长度。
一般长圆筒、短圆筒之间的划分用临界长度cr L 表示。
如容器长度L >cr L 为长圆筒,反之为短圆筒。
临界长度cr L 由下式确定:t D D Lcr 0017.1=长圆筒:长圆筒失稳时的波数n =2,临界压力cr p 仅与0D t 有关,而与0D L 无关。
cr p 值可由下式计算:32)(12Dt E p cr μ-=短圆壁:短圆筒失去稳定性时,波数n >2,如为3,4,5……,其波数n 可近似为:图一 圆筒形容器失去稳定后的形状42)()(06.7D t D L n =临界压力可由下式计算:tD LD Et p cr 00259.2=对于外压容器临界压力的计算,有时为计算简便起见,可借助于一些现成的计算图来进行。
四、实验步骤及注意事项1. 测量试件的有关参数:壁厚(t ),直径(0D ),长度(L )。
实验二_外压薄壁容器的稳定性实验

实验二 外压薄壁容器的稳定性实验一、实验目的1.掌握失稳的概念,了解圆筒形壳体失稳后的形状和波数;2.掌握临界压力的概念,了解长圆筒、短圆筒和刚性圆筒的划分及其临界压力。
二、实验内容测量圆筒形容器失稳时的临界压力值,并与不同的理论公式计算值及图算法计算值进行比较。
观察外压薄壁容器失稳后的形态和变形的波数,并按比例绘制试件失稳前后的横断面形状图,用近似公式计算试件变形波数。
对实验结果进行分析和讨论。
三、实验装置过程装备与控制工程专业基本实验综合实验台,详见附录二。
四、实验原理1.圆筒的临界长度计算如式(2-1)和式(2-2):cr 1.17L = (2-1)'L =cr (2-2)当:L >cr L 时,属于长圆筒;'L cr <L <cr L 时,属于短圆筒;L <'L cr 时,属于刚性圆筒。
2.圆筒的临界压力计算公式(1)长圆筒的临界压力计算如式(2-3):3221E t P D μ⎛⎫= ⎪-⎝⎭cr (2-3) (2)短圆筒的临界压力计算如式(2-4)和式(2-5): ①R.V .Mises 公式()()()32222222211121111Et E t n P n R nL nL R n R R μμππ⎡⎤⎢⎥--⎛⎫⎢⎥=+-+ ⎪⎢⎥-⎝⎭⎡⎤⎛⎫⎛⎫+⎢⎥ ⎪-+⎢⎥ ⎪⎝⎭⎣⎦⎝⎭⎢⎥⎣⎦cr (2-4) ②B.M.Pamm 公式2Pcr (2-5) (3)利用外压圆筒的图算法计算其临界压力 3.波数的计算公式(2-6)五、实验步骤(一)测量试件参数(见图2-2)1.测量试件实际长度0L 、圆弧处外部高度1h 、 翻边处高度2h ;外直径2D 、内直径1D 。
图2-2外压薄壁容器试件图2-1外压薄壁容器的稳定性实验流程图(二)计算试件参数计算壁厚t 、圆弧处内部高度3h 、中径D 、计算长度L 。
(三)实验台操作外压薄壁容器的稳定性实验流程图如图2-1所示,实验前打开阀门V05、V07、V09、V10、V12,关闭其他所有阀门。
压力容器设计外压薄壁圆筒的稳定性计算

Lcr 1.17 Do
Do t
第二节 外压薄壁圆筒的稳定性计算
带加强圈的圆筒
2.59Et2
pcr LDo
Do t
带加强圈的外压圆筒
受均布轴向压缩载荷 圆筒的临界应力
第二节 外压薄壁圆筒的稳定性计算
(a)
(b)
轴向压缩圆筒失稳的形状
(a)非对称形式;(b)对称形式
本节重点
(1)失稳、临界压力、临界长度概念; (2)典型受载条件下圆筒临界压力(或应
第四章 外压容器设计
第一节 概述
一、外压容器的稳定性
第一节 概述
真空操作容器、减压精馏塔的外壳 外压容器
用于加热或冷却的夹套容器的内层壳体
外压容器的失效形式
第一节 概述
强度不足而发生压缩屈服失效
承受外压
壳体失效 形式
当外压达到一定的数值时,壳体的径 向挠度随压缩应力的增加急剧增大, 直至容器压扁,这种现象称为外压容 器的失稳或屈曲。(讨论重点)
基于以下假设:
①圆柱壳厚度t与半径D相比 是小量, 位移w与厚度t相 比是小量。
②失稳时圆柱壳体的应力仍 处于弹性范围。
线性平衡方程 和挠曲微分方程
第二节 外压薄壁圆筒的稳定性计算
长圆筒—L>Lcr,失稳波数n=2,pcr 与L无关
外压圆筒
短圆筒—L<Lcr,失稳波数n>2, pcr与L有关
刚性筒—失效形式不是失稳,而是 压缩屈服破坏
第二节 外压薄壁圆筒的稳定性计算
短圆筒的临界压力
pcr
2.59 Et 2
LDo
Do t
2.59 E L / Do t
Do
t Do
3
过程装备专业实验实验指导书

过程装备专业实验实验指导书武汉工程大学二零一五年三月目录实验一内压容器应力测试实验实验二外压容器失稳测试实验实验三高压爆破综合实验实验一内压容器应力测试实验一、实验目的1、掌握对各种压力容器的应力分析研究,要求做到:1) 正确合理的选择测点位置。
2)测点处布片方案的合理拟定。
3)测试对象加载的步骤等。
2、掌握静态应变20点以上的测量技能。
3、学会使用计算机和数据采集仪对测点应变进行自动数据采集。
4、初步学会测量数据的处理和测量结果的误差分析。
二、实验仪器及设备1、实验对象:实验对象为六组带不同封头的内压容器,参数如下:标准椭圆封头:D i=300mm,S=4mm标准碟形封头:D i=300mm,S=4mm600锥型封头:Di=300mm ,S=4mm,半顶角300900锥型封头:Di=300mm ,S=4mm,半顶角450半球型封头:Di=300mm,S=4mm平盖型封头:S=25mm容器圆柱形筒体:Di=300mm ,S=4mm容器材料304不锈钢,μ=0.3 E=1.96×105kg/cm2,最大实验压力2.5Mp2、静态数字应变仪(SDY—2203型3台,预调平衡箱3台)、应变数据采集仪(1台)及计算机(1台),3、实验装置(图1)三、实验原理1 准备工作1)测点选择由容器受内压作用时应力分布状况分析,知各个封头曲率比较大的部位,以及封头和筒体连接的部位,应力变化较大。
故上述两区间相应地增加测点数量(具体分布尺寸见现场实验装置)。
补偿块 压力表 排气阀工作片压力表 实验容器电动油泵 加压阀卸压阀图1 实验装置示意图2) 布片方案实验对象为内压薄壁容器,筒壁应力状态可简化为二向平面应力状态,且主应力方向为相互垂直的经向和环向。
因此在测点布片时应沿两向主应力方向垂直粘贴应变片。
3) 加载步骤从0开始加载至2.5Mpa 测一次各点应变,再卸载至1.6Mpa 测一次各点应变,最后卸载回零,即0—2.5Mpa —1.6Mpa —0。
壳体的稳定性分析

5、受外压形式:
p
p
p a
轴向
b
周向
c
周 轴 向
本节讨论:受周向均匀外压薄壁回转壳体的弹性失稳问题
6
过程设备设计
二、临界压力
1、临界压力
壳体失稳时所承受的相应压力,称为临界压力,用pcr表示。
2、失稳现象
外载荷达到某一临界值,发生径向挠曲,并迅速增加,
沿周向出现压扁或波纹。 见表2-5
7
过程设备设计
Et
代替长、短圆筒
pcr
E
注意:
弹性失稳→
非弹性失稳→
各类钢E接近 ∴采用高强钢对提高圆筒的稳定性不显著 , 与材料强度有关, 变化大 ∴采用高强钢经济 ,使 。 压> p ↑p cr
, 与材料强度无关, 与E有关,但变化不大, 压 < p pcr
Et
pcr
24
过程设备设计
3 其他回转薄壳的的临界压力
内压下,有消除不圆度的趋势 影响: 外压下,在缺陷处产生附加的弯曲应力
圆筒中的压缩应力增加
临界压力降低
实际失稳压力与理论计算结果不很好吻和的主要原因之一
对圆筒的初始不圆度严格限制
23
过程设备设计
六、非弹性失稳的工程计算 —应变”曲线上的切线 时的“压缩 压> p 式中的弹性模量
近似利用材料 模量
各类钢E接近 ∴采用高强钢对提高圆筒的稳定性不显著 可提高承载能力,
pcr f (E, Do , t )
s
17
过程设备设计
二、受均布周向外压的短圆筒的临界压力
2.59 Et 2 pcr LDO DO t
(2-97)
拉姆公式,仅适合弹性失稳
实验四 受外压薄壁

容器失稳时临界压力的大小及出 现的波数除了与材料的弹性模数E、泊 松比μ、试件的圆度有关外,主要取决 于容器的几何特性,即容器长度与直 径之比(L/D)和容器壁厚与直径之比 (S/D)。
六、实验具体步骤
• • • • • • • •
打毛刺,测试件壁厚S; 将试件放入翻边器内翻边,要求边宽3mm左右, 且平整、无裂纹; 测试件长度L 、测试件公称直径D、最大直径 Dmax和最小直径 Dmin,计算试件的椭圆度e; 将试件放入橡胶密封圈内并安好轴向支撑; 把试件放进油缸内并压紧上盖,用手摇泵加压, 直至试件失稳; 记录试件失稳时压力表的读数; 卸压后取出试件,记录试件失稳时的波数; 计算出试件的理论临界压力及变形波数,与实 测值比较;计算相对误差并分析误差原因。
相
似
理
论
相似理论是说明自然界和工程 中各相似现象相似原理的学说。是 研究自然现象中个性与共性,或特 殊与一般的关系以及内部矛盾与外 部条件之间的关系的理论。在结构 模型试验研究中,只有模型和原型 保持相似,才能由模型试验结果推 算出原型结构的相应结果。
类
比
• 类比,就是由两个对象的某些相同或相似
弹性模量
• 材料在弹性变形阶段内,正应力
和对应的正应变的比值 。 • 一般地讲,对弹性体施加一个外 界作用(称为“应力”)后,弹 性体会发生形状的改变(称为 “应变”),“弹性模量”的一 般定义是:应力除以应变。
临界压力
• 薄壁容器在失稳前所能承受的最大
外压力称为临界压力。
一、实验目的
• 1.观察外压容器失稳的现象,失稳时指示
• 《过程设备设计》---压力容器应力
分析---壳体稳定性分析。
原因? • (2)解释试件在失稳前后压力变 化和试件变形的情况; • (3)分析影响临界压力的因素; • (4)讨论轴向支撑对临界压力及 波数的影响。
内外压容器实验指导书(BZ10)

内压薄壁容器应力测定实验实验指导书北京化工大学机电学院过程装备与控制工程系实验一、内压薄壁容器应力测定实验一、实验目的1.掌握电阻应变测量原理;2.学习电阻应变仪的使用方法,学习电阻应变片的贴片和接线技术; 3.了解封头在内压作用下的应力分布规律。
二、实验原理 1. 应力计算:薄壁压力容器主要由封头和圆筒体两个部分组成,由于各部分曲率不同,在它们的连接处曲率发生突变。
受压后,在连接处会生产边缘力系——边缘力矩和边缘剪力。
使得折边区及其两侧一定距离内的圆筒体和封头中的应力分布比较复杂,某些位置会出现较高的局部应力。
利用电阻应变测量方法可对封头和与封头相连接的部分圆筒体的应力分布进行测量。
应力测定中用电阻应变仪来测定封头各点的应变值,根据广义虎克定律换算成相应的应力值。
由于封头受力后是处于二向应力状态,在弹性范围内用广义虎克定律表示如下:经向应力:()21211μεεμσ+-=E(1-1)环向应力:()12221μεεμσ+-=E(1-2) 式中:E —材料的弹性模量μ—材料的波桑比 ε1—经向应变 ε2—环向应变。
椭圆封头上各点的应力理论计算公式如下:经向应力:()[]bb a x a s p r 2122242--=σ (1-3)环向应力:()[]()⎥⎦⎤⎢⎣⎡-----=2224421222422b a x a a bba x a s p θσ (1-4)2.电阻应变仪的基本原理:电阻应变仪将应变片电阻的微小变化,用电桥转换成电压电流的变化。
其过程为:()→∆∆→→放大器或电桥应变片I V RdR ε将()指示或纪录检流计或纪录仪放大或→∆∆I V将电阻应变片用胶水粘贴在封头外壁面上,应变片将随封头的拉伸或压缩一起变形,应变片的变形会引起应变片电阻值的变化,二者之间存在如下关系:ε⋅=∆=∆K LlK R R (1-5) 式中:ΔR/R —电阻应变片的电阻变化率ΔL/L —电阻应变片的变形率 K —电阻应变片的灵敏系数; ε—封头的应变。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验二、外压薄壁圆筒形容器失稳实验
一、实验目的
1. 观察薄壁圆筒形容器在外压作用下丧失稳定性后的形态。
2. 测定圆筒形容器失去稳定性时的临界压力并与理论值相比较。
二、基本原理
圆筒形容器在外压作用下,常因刚度不足使容器失去原有形状,即被压扁或折曲成波形,这就是容器的失稳现象,容器失去稳定性时的外压力,成为容器的临界压力,用cr p 表示。
圆筒形容器失去稳定性后,其横截面被折成波形,波数n 可能是1,2,3,4,……等任意整数,如图一所示。
容器承受临界值的外压力而失去稳定性,决非是由于容器壳体本身不圆的缘故,即是绝对圆的壳体也会失去稳定性。
当然如壳体不圆(具有椭圆度)容器更容易失稳,即它的临界压力值会下降。
根据外压容器筒体的长短,可分为长圆筒,短圆筒和刚性圆筒三种,刚性圆筒一般具有足够的刚度,可不必考虑稳定性问题。
但长圆筒,短圆筒必须进行稳定性计算,它们的临界压力cr p 值大小主要与厚壁(t ),外直径(0D ),长度(L )有关。
亦受材料弹性模数(E ),泊桑比(μ)影响。
所谓长圆筒,短圆筒之分,并不是指它们的绝对长度,而是与直径壁厚有关的相对长度。
一般长圆筒、短圆筒之间的划分用临界长度cr L 表示。
如容器长度L >cr L 为长圆筒,反之为短圆筒。
临界长度cr L 由下式确定:
t D D L cr 0017.1=
长圆筒:长圆筒失稳时的波数n =2,临界压力cr p 仅与0D t 有关,而与0D L 无关。
cr
p 值可由下式计算:
3
2)(12D
t E p cr μ-=
短圆壁:短圆筒失去稳定性时,波数n >2,如为3,4,5……,其波数n 可近似为:
图一 圆筒形容器失去稳定后的形状
4
2
)
()(06
.7D t D L n = 临界压力可由下式计算:
t
D LD Et p cr 00259.2=
对于外压容器临界压力的计算,有时为计算简便起见,可借助于一些现成的计算图来进行。
四、实验步骤及注意事项
1. 测量试件的有关参数:壁厚(t ),直径(0D ),长度(L )。
用千分尺测壁厚,用游标卡尺测内直径(便于精确测量)和长度,外直径0D 由内直径加壁厚得到。
各参数分别测量两到三次,计算时取平均值。
2. 手动放气,确保压力为零。
按图二所示安装实验设备,将外压圆筒试件6置于平板顶盖上,试件与平顶盖间用垫片5密封(试件折边上下各放一垫片);用压紧法兰4通过四个密封螺母2将试件压紧到平板顶盖上。
3. 将圆筒底垫块8 (一大一小) 置于外压圆筒底部,把用心轴7置于圆筒底垫块的中心孔中,再将横梁1压在心轴7上,通过两个压紧螺母2上紧 (用手旋紧既可);以此抵消试件承受的轴向载荷。
4. 插好电源,先打开风机,再打开压缩机,根据试验时间,通过压力调节旋钮,可调节压
1-横梁 2-压紧螺母 3-密封螺母 4-压紧法兰 5-垫片 6-外压圆筒 7-心轴 8-圆筒底垫块 9-透明容器 10-工作台
力进入速度,缓慢升压至试件破坏为止(试件破坏时有轻微的响声),记下容器的失稳压力
p)。
失稳后,需快速手动放气泄压,关(即有轻微响声时的瞬间压力,此压力为临界压力
cr
闭压缩机,再关闭风机。
如压缩机中途关闭停机,重新开机时须将压力卸到零方能启动。
5. 待压力为零后取出试件,观察失稳后试件的形状并记下波纹数。
6. 关闭电源开关,清理好实验备件和工具。
五、实验报告内容及要求:
1、简述实验目的及原理、实验装置简图,附实验数据记录表。
2、绘出试件失稳前后的横断形状简图。
3、将测量的试件几何尺寸、临界压力值、波形数等实验数据和理论计算结果填入实验报告。
4、用理论计算公式和算图法分别计算其临界压力值,并与实测值进行比较。
5、用公式计算波形数,根据实际波形数分析圆筒性质。
6、分析讨论外压容器中影响临界压力大小的各种因素。
附:
试件材料:
弹性模量E= Mpa;泊松比μ=
外压失稳实验记录表。
