受压构件的截面承载力计算-
(轴心)受压构件正截面承载力计算

(2)破坏特征 1)螺旋筋或焊接环筋在约束 核心混凝土的横向变形时产生 拉应力,当它达到抗拉屈服强 度时,就不再能有效地约束混 凝土的横向变形,构件破坏。 2)螺旋筋或焊接环筋外的混 凝土保护层在螺旋筋或焊接环 筋受到较大拉应力时就开裂, 故在计算时不考虑此部分混凝 土。
螺旋箍筋柱破坏情况
2.适用条件和强度提高原理 12(短柱) ; (1)适用条件:①l0 / d ②尺寸受到限制。 注意:螺旋箍筋柱不如普遍箍筋柱经济,一般不宜采用。 根据图7-8 所示螺旋箍筋柱截面 受力图式,由平衡条件可得到
150mm或15倍箍筋直径(取较大者)范围,则应设置复合箍 筋。
a)、b)S内设3根纵向受力钢筋
c)S内设2根纵向 受力钢筋
复合箍筋的布置
7.2 螺旋箍筋轴心受压构件
1.受力分析及破坏特征 (1)受力分析 螺旋箍筋或焊接圆环箍筋能约束混凝土在轴向压力作用 下所产生的侧向变形,对混凝土产生间接的被动侧向压力,
d cor As 01
S
As 01
As 0 S d cor
将式(2)代入式(1),则可得到
2
2 f s As 01 2 f s As 0 S 2 f s As 0 f s As 0 f s As 0 2 2 d cor S d cor S d cor 2 Acor d cor d cor 2 4
态、承载力计算;
2.配有纵向钢筋和螺旋箍筋的轴心受压构件的破坏形 态、承载力计算; 3.稳定系数的概念及其影响因素; 4.核心混凝土强度分析及强度计算;
5.普通箍筋柱、螺旋箍筋柱的配筋特点和构造要求。
7.1 普通箍筋轴心受压构件
1.钢筋混凝土轴心受压柱的分类
普通箍筋柱:配有纵筋 和箍筋的柱 (图7-1a)。 螺旋箍筋柱:配有纵筋 和螺旋筋或焊接环筋的 柱,(图7-1b)。 其中:纵筋帮助受压、承 担弯矩、防止脆性破坏。 螺旋筋提高构件的强 度和延性。
5.受压构件的截面承载力
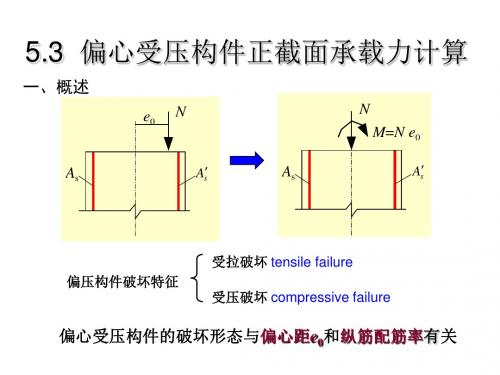
x ¢ ¢ N e f b x ( a¢ 或: u 1 c s ) s s As ( h0 a s ) 2 h
e¢
1 f ¢ s f y s y ss fy b 1
2
ei a¢ s
当偏心距很小且轴力较大时,能使远离轴向力一侧 纵筋屈服 ——反向破坏。
二、小偏心受压构件的计算
已知截面参数,N和M,求As’和As 。
公式:
未知量个数
¢ ¢ N 1 f cbx f y As s s As
1 ss fy b 1
x ¢ ¢ ¢ N e 1 f c b x (h0 ) f y As (h0 a s ) 2
> b ––– 小偏心受压 ae
偏心受压构件的试验研究
As<< As’时 会有As fy
e0 N e0 N e0 N e0 N
As
ss
As’f y’
fc
As
ss
As’f y’
fc
As
ss
As’f y’
fc
As fy
As’f y’
fc
h0
h0
h0
h0
e0 N e0很小 As适 中
Байду номын сангаас
e0 N
e0较小
f'yA's
Nu b 1 fcbh0b f A f y As
' y ' s
若N N u b则为小偏心受压 若N N u b则为大偏心受压
当ei 0.3h0时,按小偏心受压计算 , 当ei 0.3h0时,可按大偏心受压计 算(但不一定为大偏压 )
受压构件的承载力计算

受压构件的承载力计算一、梁柱的承载力计算方法对于受压构件,在弹性范围内,可以采用弹性承载力计算方法。
弹性承载力计算方法是根据梁柱的理论,主要应用弹性力学原理和应变能平衡条件进行计算。
在弹性承载力计算之外,受压梁柱的承载力还受到稳定性要求的限制。
稳定性要求主要包括屈曲的要求和稳定的要求。
稳定性承载力计算方法就是根据稳定性要求来计算的。
二、承载力计算的基本原理和方法1.构件的截面形态与材料的力学性能有关。
几何形态方面,可以通过截面形心深度、截面形态系数和截面面积等参数来描述。
力学性能方面,主要包括材料的抗压强度、屈服强度和弹性模量等参数。
2.构件的边界条件与受力特性有关。
边界条件主要包括自由端的约束、内力的约束和约束条件等。
边界条件对构件的承载力有着直接的影响,需要进行准确的分析和计算。
3.构件的荷载和荷载组合也是影响承载力计算的重要因素。
荷载包括静力荷载和动力荷载,荷载组合则是不同荷载的叠加组合。
需要根据具体情况来确定荷载和荷载组合,并进行相应的计算。
假设一个矩形柱的尺寸为300mm×400mm,材料抗压强度为250MPa,弹性模量为200 GPa。
根据以上参数,可以进行如下步骤的承载力计算。
1.计算截面形态参数:矩形柱的形心深度h=400/2=200mm形态系数α=(h/t)f/π^2=2.692.弹性承载力计算:根据梁柱的理论,弹性承载力可通过以下公式计算:Pcr=(π^2*E*I)/(kl)^2其中,E为弹性模量,I为惯性矩,kl为有效长度系数。
惯性矩I=1/12*b*h^3=1/12*300*400^3=32,000,000mm^4有效长度系数kl可根据梁柱的边界条件和约束情况进行计算。
假设矩形柱两端均固定,则kl=0.5代入以上参数,可以得到弹性承载力Pcr=200,000N=200kN。
3.稳定性承载力计算:稳定性承载力计算主要包括屈曲的要求和稳定的要求。
对于矩形柱,屈曲要求可通过欧拉公式计算,稳定的要求可通过查表确定。
矩形截面偏心受压构件正截面的承载力计算

矩形截面偏心受压构件正截面的承载力计算一、矩形截面大偏心受压构件正截面的受压承载力计算公式 (一)大偏心受压构件正截面受压承载力计算(1)计算公式由力的平衡条件及各力对受拉钢筋合力点取矩的力矩平衡条件,可以得到下面两个基本计算公式:s y s y c A f A f bx f N -+=''1α (7-23)()'0''012a h A f x h bx f Ne s y c -+⎪⎭⎫ ⎝⎛-=α (7-24)式中: N —轴向力设计值;α1 —混凝土强度调整系数;e —轴向力作用点至受拉钢筋A S 合力点之间的距离;a he e i -+=2η (7-25) a i e e e +=0 (7-26)η—考虑二阶弯矩影响的轴向力偏心距增大系数,按式(7-22)计算;e i —初始偏心距;e 0 —轴向力对截面重心的偏心距,e 0 =M/N ;e a —附加偏心距,其值取偏心方向截面尺寸的1/30和20㎜中的较大者; x —受压区计算高度。
(2)适用条件1) 为了保证构件破坏时受拉区钢筋应力先达到屈服强度,要求b x x ≤ (7-27)式中 x b — 界限破坏时,受压区计算高度,o b b h x ξ= ,ξb 的计算见与受弯构件相同。
2) 为了保证构件破坏时,受压钢筋应力能达到屈服强度,和双筋受弯构件相同,要求满足:'2a x ≥ (7-28) 式中 a ′ — 纵向受压钢筋合力点至受压区边缘的距离。
(二)小偏心受压构件正截面受压承载力计算(1)计算公式根据力的平衡条件及力矩平衡条件可得s s s y c A A f bx f N σα-+=''1 (7-29)⎪⎭⎫ ⎝⎛'-+⎪⎭⎫ ⎝⎛-=s s y c a h A f x h bx f Ne 0''012α (7-30) ()'0''1'2s s s s c a h A a x bx f Ne -+⎪⎭⎫⎝⎛-=σα (7-31)式中 x — 受压区计算高度,当x >h ,在计算时,取x =h ;σs — 钢筋As 的应力值,可根据截面应变保持平面的假定计算,亦可近似取:y b s f 11βξβξσ--=(7-32)要求满足:y s y f f ≤≤σ'x b — 界限破坏时受压区计算高度,0h x b b ξ=;b ξξ、 — 分别为相对受压区计算高度 x/h 0和相对界限受压区计算高度x b /h 0 ;'e e 、′— 分别为轴向力作用点至受拉钢筋A s 合力点和受压钢筋A s ′合力点之间的距离 a he e i -+=2η (7-33) ''2a e he i --=η (7-34) (2)对于小偏心受压构件当bh f N c >时,除按上述式(7-30)和式(7-31)或式(7-32)计算外,还应满足下列条件:()()s s y c a a h A f h h bh f e e a h N -+⎪⎭⎫⎝⎛-≤⎥⎦⎤⎢⎣⎡---'0''00'22 (7-35 )式中 '0h — 钢筋's A 合力点至离纵向较远一侧边缘的距离,即s a h h -='0。
轴心受压构件正截面承载力计算

0 Nd Nu 0.9( fcd Acor kfsd As0 As fsd )
k —— 间接钢筋的影响系数,混凝土强度C50
及以下时,k=2.0;C50-C80取k=2.0-1.7,中 间直线插入取值。
混凝土 强度
k
≤C50 2.0
C55 C60 C65 C70 C75 C80 1.95 1.90 1.85 1.80 1.75 1.70
例题2:圆形截面轴心受压构件,直径为450mm, 计算长度2.25m, 轴向压力设计组合值Nd=2580kN, 纵筋用HRB335级,箍筋用R235级,混凝土强度等 级为C25。I类环境条件,安全等级二级,试进行构 件的配筋设计。
2.25512 1%
0.45
As1%4 4520 15m 902m
A co r45 420 30 119 m3 2m 99
f s d —— 间接钢筋的强度;
Acor —— 构件的核心截面面积;
A s 0 —— 间接钢筋的换算面积,As0
dcor As01
S
;
A s 0 1 —— 单根间接钢筋的截面面积;
S —— 间接钢筋的间距;
轴心受压构件正截面承载力计算
6.2 配有纵向钢筋和螺旋箍筋的轴心受压构件 四、 螺旋箍筋轴压构件正截面承载力计算
轴心受压构件正截面承载力计算
6.1 配有纵向钢筋和普通箍筋的轴心受压构件 五、正截面承载力计算 2.截面设计之二(尺寸未知):
如果尺寸未知,则 先假设一个ρ′,令稳定系数φ=1; 求出截面面积A,取整; 重新计算φ,求As′.
例题略。
轴心受压构件正截面承载力计算
6.1 配有纵向钢筋和普通箍筋的轴心受压构件
主要和构件的长细比有关,长细比越大,稳定 系数 越小。
第六章受压构件截面承载力计算

第六章受压构件截面承载力计算受压构件包括柱、短杆、墙等结构中的竖向构件。
在受到外部压力的作用下,受压构件会产生内部应力,当该应力超过材料的承载能力时,结构就会发生破坏。
因此,了解受压构件截面的承载能力非常重要,可以保证结构的安全性。
截面承载力计算按照材料的不同分类,一般分为钢材和混凝土结构的计算方法。
以下将分别介绍这两种材料的截面承载力计算方法。
钢材截面承载力计算方法:1.确定边缘受压构件的型式,常见的有矩形、L形、T形和带肋板等,根据构件的几何形状,选择相应的计算方法。
2.通过截面分析,确定构件的有效高度和宽度。
3.确定截面的截面系数,根据构件的几何形状和受力状态,计算出截面系数。
4.根据材料的特性,计算出计算强度和材料的安全系数。
5.通过计算公式,结合以上参数,得出受压构件的截面承载力。
混凝土结构截面承载力计算方法:1.确定混凝土的试验结果,包括抗压强度、抗弯强度等。
2.根据受压构件的几何形状和受力状态,计算出截面的面积和惯性矩。
3.确定混凝土的计算强度和材料的安全系数。
4.根据截面形状和受力状态,选取相应的公式,计算出截面承载力。
5.根据所得结果,进行合理的构造设计。
在受压构件截面承载力计算中,不同材料的计算方法有所不同,但都需要考虑材料的特性和截面的几何形状。
此外,还需要参考相关的标准和规范,以确保计算结果的准确性和可靠性。
总而言之,受压构件截面承载力计算是一个复杂而重要的工作,需要考虑多个因素,包括材料的特性、截面的几何形状和受力状态等。
通过合理的计算方法和准确的数据,可以确定受压构件的最大承载能力,保证结构的安全性和稳定性。
受压构件截面承载力计算

受压构件截面承载力计算
受压构件截面承载力计算是结构工程中的重要计算内容之一、在设计
受压构件时,需要保证构件的承载力不低于设计要求,以确保结构的安全
性和稳定性。
受压构件截面承载力的计算涉及到材料力学、截面形状和尺寸,以及截面临界状态等多个因素。
以下是受压构件截面承载力计算的基
本步骤和方法。
1.分析受压构件的材料力学性能:首先需要确定受压构件的材料类型
和性能参数,包括弹性模量、屈服强度、抗压强度等。
这些参数可以在材
料手册中查找或者进行材料试验获得。
2.确定构件的截面几何特征:受压构件的截面形状决定了其承载能力。
常见的受压构件截面形状包括矩形、圆形、T形、工字形等。
需要根据实
际情况确定构件的截面几何参数,如截面面积、惯性矩、受压边缘等。
3.计算截面承载能力:使用截面承载能力公式或者截面性能表格,根
据受压构件的材料性能和截面几何特征计算截面的承载能力。
常用的计算
方法有强度设计法、极限状态设计法和变形极限设计法等。
4.考虑临界状态和稳定性:受压构件在承载过程中可能会出现临界状
态和稳定性问题,如屈曲、侧扭、局部稳定等。
需根据受压构件的长度、
约束条件、支承条件等因素,对构件进行临界状态和稳定性分析,以确保
构件在正常使用条件下不会失稳。
总结起来,受压构件截面承载力计算是一项复杂的工作,需要综合考
虑材料力学、截面形状和尺寸、临界状态和稳定性等多个因素。
设计工程
师需要有扎实的结构力学和材料力学基础,以及丰富的实际工程经验,才
能进行准确可靠的受压构件截面承载力计算。
钢结构受压构件截面承载力计算
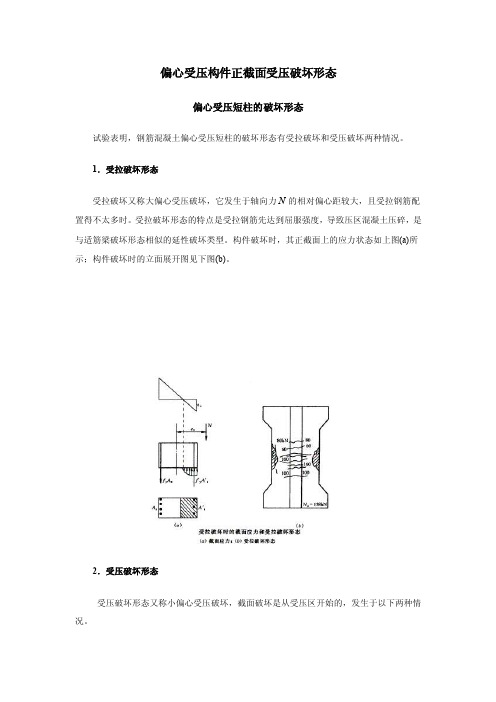
偏心受压构件正截面受压破坏形态偏心受压短柱的破坏形态试验表明,钢筋混凝土偏心受压短柱的破坏形态有受拉破坏和受压破坏两种情况。
1.受拉破坏形态受拉破坏又称大偏心受压破坏,它发生于轴向力N的相对偏心距较大,且受拉钢筋配置得不太多时。
受拉破坏形态的特点是受拉钢筋先达到屈服强度,导致压区混凝土压碎,是与适筋梁破坏形态相似的延性破坏类型。
构件破坏时,其正截面上的应力状态如上图(a)所示;构件破坏时的立面展开图见下图(b)。
2.受压破坏形态受压破坏形态又称小偏心受压破坏,截面破坏是从受压区开始的,发生于以下两种情况。
(1)当轴向力N的相对偏心距较小时,构件截面全部受压或大部分受压,如图(a)或下图(b)所示的情况。
(2)当轴向力的相对偏心距虽然较大,但却配置了特别多的受拉钢筋,致使受拉钢筋始终不屈服。
破坏时,受压区边缘混凝土达到极限压应变值,受压钢筋应力达到抗压屈服强度,而远侧钢筋受拉而不屈服,其截面上的应力状态如下图(a)所示。
破坏无明显预兆,压碎区段较长,混凝土强度越高,破坏越带突然性,见下图(c)。
总之,受压破坏形态或称小偏心受压破坏形态的特点是混凝土先被压碎,远侧钢筋可能受拉也可能受压,但都不屈服,属于脆性破坏类型。
在“受拉破坏形态”与“受压破坏形态”之间存在着一种界限破坏形态,称为“界限破坏”。
它不仅有横向主裂缝,而且比较明显.。
其主要特征是:在受拉钢筋应力达到屈服强度的同时、受压区混凝土被压碎。
界限破坏形态也属子受拉破坏形态。
长柱的正截面受压破坏试验表明,钢筋混凝土柱在承受偏心受压荷载后,会产生纵向弯曲。
但长细比小的柱,即所谓“短柱”,由于纵向弯曲小,在设计时一般可忽略不计。
对于长细比较大的柱则不同,它会产生比较大的纵向弯曲,设计时必须予以考虑。
下图是一根长柱的荷载一侧向变形(N -f)实验曲线。
偏心受压长柱在纵向弯曲影响下‘可能发生两种形式的破坏。
长细比很大时,构件的破坏不是由于材料引起的,而是由于构件纵向弯曲失去平衡引起的,称为“失稳破坏”。
基本构件计算矩形截面偏心受压构件承载力的计算

矩形截面偏心受压构件正截面承载力的计算一、基本公式1. 计算图式2. 基本公式由0=∑x N 得:)](11[g g g gsa cb u j A A R bx R N N σγγγ-''+=≤ 由0=∑gA M 得:)](1)2(1[00g g g sa cb u j a h A R x h bx R M e N '-''+-=≤γγγ由0=∑'gA M 得:)](1)2(1[0g g g sg a c b u j a h A a x bx R M e N '-+'--=≤'σγγγ 混凝土受压区高度由下式确定:e A R e A xh e bx R g gg g a '''-=+-σ)2(0(对偏心作用力点取矩) e e '、-分别为偏心压力j N 作用点至钢筋g A 合力作用点和钢筋g A '合力作用点的距离,按下式计算:η=e g a h e -+20;η='e g a h e '+-203.公式的注意事项(1)钢筋g A 的应力g σ取值当jg h x ξξ≤=0时,构件属于大偏心受压构件,这时取g g R =σ(受拉钢筋屈服);当jg h x ξξ>=0时,构件属于小偏心受压构件,这时g σ按下式计算,但不大于g R 值:)19.0(003.0-=ξσg g E ,式中g E 为受拉钢筋的弹性模量。
(2)为保证构件破坏时,大偏心受压构件截面上的受压钢筋能达到抗压设计强度gR ',必须满足g a x '≥2,否则受压钢筋的应力可能达不到g R '。
与双筋截面受弯构件类似,这时可近似取g a x '=2,由截面受力平衡条件(0=∑'g A M )可得:)(0gg g s bu j a h A R M e N '-=≤'γγ 上式计算的正截面承载力u M 比不考虑受压钢筋gA '更小时,计算中不考虑受压钢筋g A '的影响。
受压构件正截面承载力典型算例(1)

= 5724.35kN 按公式(55)计算
N u普 = 0.9j( f c A + f y¢As¢ ) = 0.9 ´ 0.928 ´ (14.3 ´196250 + 300 ´ 6872) = 4065.73kN
N u螺 = 5724.35 > Nu普=4065.73 N u螺 / N u普 = 5724.35 / 4065.73 = 1.4 < 1.5
=
40 mm,选用
C40
混凝土和
HRB400
级钢筋,柱的计算长度为
4.5m。
求该柱的截面配筋 As 和As' 。
【解】本例题属于截面设计类
(1)确定基本参数
C40
混凝土
fc
= 19.1N/mm2;HRB400
钢筋
fy
=
f
' y
= 360 N/mm2;a1
= 1.0 ,ξb=0.52
h0 = h - as = 600 - 40 = 560 mm
(1)确定基本参数
C20 混凝土
fc
= 9.6 N/mm2;HRB335
级钢筋
fy
=
f
' y
= 300 N/mm2;a1
= 1.0 ,ξb=0.55
一类环境,c=30mm,取 as
=
a
' s
= 40 mm, h0
=
h - as
=
400 - 40
= 360 mm
(2)大小偏压的判别
e0
=M N
159 ´ 10 6 =N300 ´ 0 3h =1+
1
çæ l0
2
÷ö z
3受压构件截面承载力计算

3受压构件截面承载力计算受压构件截面承载力计算指的是根据构件材料和几何形状对受压构件的最大承载能力进行估算和计算的过程。
在工程设计和结构分析中,准确计算截面承载力对于保证结构的安全性和经济性至关重要。
受压构件一般是指在受纵向压力作用下,梁、柱、墙等构件的截面。
构件材料可以是钢材、钢筋混凝土、木材等。
常见的受压构件截面形状有矩形、圆形、T形、L形等。
截面承载力计算的基本步骤如下:1.截面区域的几何形状计算:根据构件的型号和梁、柱的跨度、高度等参数,计算出截面区域的几何形状,如截面面积、惯性矩、截面模数等。
2.材料的力学性质计算:根据构件所采用的材料,查找相应的力学性质数据,如弹性模量、屈服强度、抗压强度等。
3.塑性计算和极限状态设计:根据构件所处的工况和受力情况,进行塑性计算和极限状态设计。
塑性计算是指构件材料在超过屈服强度后,发生塑性变形的计算。
极限状态设计是指在允许的极限荷载状态下,不发生塑性变形的构件设计。
4.受压构件的稳定计算:对于长细比较大的构件,需要进行稳定计算,考虑构件在受压状态下的侧扭承载能力和稳定性。
5.弯曲和剪切计算:受压构件在受力时,还会发生弯曲和剪切作用,需要进行相应的计算。
6.验算和比较:完成上述计算后,进行验算和比较,检查计算结果是否满足设计要求和规范规定。
需要注意的是,截面承载力的计算一般采用强度理论和极限平衡理论进行,计算结果应该参考相应的设计规范和标准。
总结起来,受压构件截面承载力的计算包括几何形状的计算、材料性质的计算、塑性计算和极限状态设计、稳定性计算、弯曲和剪切计算等步骤。
对于不同的构件材料和几何形状,计算方法有所不同,需要根据具体情况进行估算和计算。
受压构件承载力计算

第一节轴心受压构件的计算
(3)为提高受压构件的延性,保证构件承载能力,全部纵筋的配筋率不应小于0.60%, 同一侧纵筋的配筋率不应小于0.2%;为了施工方便,全部纵筋的配筋率不宜大于5%。 通常受压钢筋的配筋率不超过3%,一般在0.6%~2%之间。 (4)柱中纵向钢筋的混凝土保护层最小厚度为30 mm,且不小于纵筋直径。 (5)纵向钢筋的净距不应小于50 mm;对处于水平位置浇筑的预制柱,其纵筋净距要求 与梁相同。在偏心受压柱中,垂直于弯矩作用平面的侧面上的纵筋和轴心受压柱中 各边的纵向受力钢筋,其中距不宜大于300 mm。 (6)纵向受力钢筋的接头宜设置在受力较小处。钢筋接头宜优先采用机械连接接头,也 可以采用焊接接头和搭接接头。对于直径大于28 mm的受拉钢筋和直径大于32 mm的 受压钢筋,不宜采用绑扎的搭接接头。
上一页 返回
第二节偏心受压构件的计算
一、矩形截面偏心受压构件正截面计算
1.偏心受压状态 (1)当轴心压力N和弯矩M同时作用在某个构件截面上时,其作用效果与一个偏心矩为。 e0=M/N的轴向压力N相同。因此,把构件截面上同时作用有轴心压力N ,弯矩M和剪 力V的构件称为偏心受压构件。 (2)偏心受压短柱通常是指l0/h<8的偏心受压构件。由于构件在偏心压力下产生的侧向 挠度很小,因此其中的附加弯矩可以忽略不计。所以,这种构件各个截面中弯矩均 可以认为等于Ne0,,即弯矩与轴向压力成比例增长。当弯矩M达到极限值时,材料达 到极限强度而破坏,通常这种破坏为材料破坏。
2.偏心受压破坏的界限及设计判别
偏心受压构件正截面界限破坏与受弯构件正截面界限破坏是相似的。因此,与 受弯构件正截面承载力计算一样,也可用界限受压区高度xb或界限相对受压区高度
受压构件截面承载力计算

《规范》规定,轴心受压构件、偏心受压构件全部纵向钢筋的配筋率不应小于0.6%;当混凝土强度等级大于C50时不应小于0.6%;一侧受压钢筋的配筋率不应小于0.2%,受拉钢筋最小配筋率的要求同受弯构件。
全部纵向钢筋的配筋率按r =(A's+As)/A计算,一侧受压钢筋的配筋率按r '=A's/A计算,其中A为构件全截面面积。
纵筋的作用: ◆ 协助混凝土受压以减少截面尺寸 受压钢筋最小配筋率:0.6% (单侧0.2%) ◆ 承担可能存在的弯矩作用 ◆可防止构件的突然脆性破坏 ◆减小持续压应力下混凝土收缩和徐变的影响。 实验表明,收缩和徐变能把柱截面中的压力由混凝土向钢筋转移,从而使钢筋压应力不断增长。压应力的增长幅度随配筋率的减小而增大。如果不给配筋率规定一个下限,钢筋中的压应力就可能在持续使用荷载下增长到屈服应力水准。
纵向钢筋的保护层厚度要求见表4-3,且不小于钢筋直径d。
对水平浇筑的预制柱,其纵向钢筋的最小应按梁的规定取值。
1
2
3
4
5
第六章 受压构件的截面承载力
6.5 受压构件一般构造要求
本 章 目 录
第六章 受压构件的截面承载力
6.1 轴心受压构件的承载力计算
配有纵筋及螺旋箍筋柱
6.1 轴心受压构件的承载力计算
截面形状和尺寸: ◆ 采用矩形截面,单层工业厂房的预制柱常采用工字形截面。 ◆ 圆形截面主要用于桥墩、桩和公共建筑中的柱。 ◆ 柱的截面尺寸不宜过小,一般应控制在l0/b≤30及l0/h≤25。 ◆ 当柱截面的边长在800mm以下时,一般以50mm为模数,边长在800mm以上时,以100mm为模数。
受压构件中箍筋应采用封闭式,其直径不应小于d/4,且不小于6mm,此处d为纵筋的最大直径。
轴心受压构件正截面承载力计算

轴心受压构件正截面承载力计算首先,要计算轴心受压构件的正截面承载力,我们需要了解构件的几何参数,例如截面的尺寸和形状,以及构件的材料特性,如弹性模量和抗压强度等。
下面介绍一种常用的计算方法,即欧拉公式。
欧拉公式适用于细长的杆件,可以计算其承载力。
根据欧拉公式,轴心受压构件的正截面承载力可以表示为:Pcr = (π^2 * E * I) / (Lr)^2其中,Pcr 是构件的临界承载力,E 是构件的弹性模量,I 是构件截面的惯性矩,Lr 是约化长度。
对于不同的构件形状,惯性矩I的计算公式也不同。
以下是一些常见形状的惯性矩计算公式:1.矩形截面:I=(b*h^3)/12,其中b是截面的宽度,h是截面的高度;2.圆形截面:I=π*(d^4)/64,其中d是截面的直径;3.方管截面:I=(b*h^3-(b'*h')^3)/12,其中b是外边框的宽度,h是外边框的高度,b'是内边框的宽度,h'是内边框的高度。
约化长度Lr的计算取决于构件的边界条件。
以下是一些常见边界条件的约化长度计算公式:1.双端固定支承:Lr=L;2.一端固定支承、一端支座支承:Lr=0.7*L;3.双端支座支承:Lr=2*L。
通过使用上述公式,我们可以计算出轴心受压构件的正截面承载力。
需要注意的是,上述公式是基于一些理想化假设和条件下推导得出的,实际工程中还需要考虑一些因素,例如构件的稳定性和局部细部构造等。
因此,在实际设计中,应该根据具体情况综合考虑各种因素,并结合相关的规范和标准进行设计和验证,以确保构件的安全性和可靠性。
总之,轴心受压构件正截面承载力计算是工程设计中的重要环节。
通过合理的参数选择和计算,可以确定构件能够安全承受的最大压力,从而保证结构的安全和可靠性。
一般构造轴心受压构件截面承载力计算

4.1.2截面形式及尺寸 柱截面一般采用方形或矩形,特殊情况下
也可采用圆形或多边形等。 柱截面的尺寸主要根据内力的大小、构件
的长度及构造要求等条件确定。 柱截面尺寸不宜过小,一般现浇钢筋混凝
土柱截面尺寸不宜小于 250mm × 250mm。为 了施工支模方便,柱截面尺寸宜使用整数,800 mm及以下的截面宜以50mm 为模数,800mm 以上的截面宜以100mm 为模数。
; Acor
dc2or
4
d cor——构件的核心直径,按间接钢筋内表面确定;
Asso ——间接钢筋的换算截面面积;Asso
dcor Ass1
s
Ass1 ——单肢箍筋的截面面积。
4.1一般构造要求
4.1.1材料强度等级 为了减小构件的截面尺寸,节省钢材,宜采用
较高强度等级的混凝土。一般柱中采用 C25及以上 等级的混凝土,对于高层建筑的底层柱,必要时可 采用高强度等级的混凝土。
受压钢筋一般采用 HRB335 级、 HRB400 级和 RRB400 级;箍筋一般采用 HPB235 级、 HRB335 级钢筋。
在此加荷实验中,因为钢筋与混凝土之间存在着粘结力, 所以它们的压应变是相等的,当加荷较小时,构件处于弹性 工作阶段,荷载与钢筋和混凝土的应力基本上是线性关系, 随着荷载的增加,混凝土的塑性变形有所发展,混凝土应力 增加得愈来愈慢,而钢筋应力增加要快得多。当短柱破坏时, 一般是纵筋先达到屈服强度,此时混凝土的极限应变为0.002, 也即此时混凝土达到轴心抗压强度,而相应的纵向钢筋应力值 为400N/mm2 ,对于热轧钢筋已达到屈服强度,但对于屈服强 度超过的钢筋,其受压强度设计值只能取400N/mm2 ,因此, 在普通受压构件中采用高强钢筋作为受压钢筋不能充分发挥其 高强度的作用,是不经济的。
钢筋混凝土受压构件—T形截面承载力计算

fA 0.813 1.5 0.3106 365 .85 103 N 365 .85kN
(3)轴向力作用于截面A点时的承载力
e=y1-0.1=0.169-0.1=0.069m<
0.6y1=0.6×0.169=0.101m
e 0.069 0.164 ,β=12.38,查表,得: = 0.477
12
12
=0.00434m4
i I 0.00434 0.12m
A
0.3
T形截面折算厚度hT=3.5i=3.5×0.12=0.42m (2)轴向力作用于截面重心O点时的承载力
பைடு நூலகம்
H0 hT
1.0 5.2 0.42
12.38
查表,得: = 0.813
查表得砌体抗压强度设计值f=1.5Mpa,则承载力为
hT 0.42
则承载力为
fA 0.477 1.5 0.3106 214 .65 103 N 214 .65kN
提示:本例是T形截面受压构件的计算。 1、截面折算厚度hT的计算,关键是截面几何特征值
的计算;
2、当轴向力偏心距为69mm时,承载力降低41.33%。
条件:如图所示带壁柱窗间墙,采用MU10烧结多孔砖和M5 混合砂浆砌筑,施工质量控制等级为B级,计算高度 H0=5.2m。 计算:当轴向力分别作用于该墙截面重心O点及A点时的承 载力。
带壁柱砖墙截面图
解:(1)截面几何特征值计算 截面面积A=1×0.24+0.24×0.25=0.3m2,取γa=1.0 截面重心位置
1 0.24 0.12 0.24 0.25 0.24 0.25
y1
0.3
2 0.169m
y2=0.49-0.169=0.321m
钢筋混凝土受压构件承载力计算

第5章 偏心受压构件的正截面承载力
(一)偏心受压构件的破坏类型
1)短柱 l0 / h 8 :不考虑二
N
阶弯矩的影响,各截面的
弯矩均等于Ne0 ,弯矩与 轴力呈线性关系。(材料 破坏)
2)长柱 8 l0 / h 30 :需考 虑二阶弯矩的影响。当
N0
Nus Num
Nusei Numei
Nul Nul ei
B(Nb,Mb)
C(0,M0) Mu
CB段(N≤Nb)为受拉破坏(大偏心受压); M u 随N
的增加而增加(CB段);
AB段(N >Nb)为受压破坏(小偏心受压), Mu随N 的
增加而减小(AB段)。 。
第5章 偏心受压构件的正截面承载力
Nu
⑸如截面尺寸和材料 N0
强度保持不变,NuMu相关曲线随配筋
率的增加而向外侧
增大。
A(N0,0)
B(Nb,Mb)
C(0,M0) Mu
⑹对于对称配筋截面,如果截面形状和尺寸相同,
砼强度等级和钢筋级别也相同,但配筋率不同,
达到界限破坏时的轴力Nb是一致的。
第5章 偏心受压构件的正截面承载力
三、偏心受压构件 的纵向弯曲影响
第5章 偏心受压构件的正截面承载力
◆ 由于侧向挠曲变形,轴向力将产生二阶效应, 引起附加弯矩。
第5章 偏心受压构件的正截面承载力
关于公式的有关说明:
(1)受拉钢筋的应力 s s :
当 x / h0 b 时为大偏心受压构件,
取 s s fsd ;
当 x / h0 b 时为小偏心受压构件:
s si
cu
Es
(
h0i
x
1)
(5—2—3)
受压构件截面承载力计算

1)大偏压large eccentric compression
基本公式
N
Nu
1
fcbx
回顾
偏心受压长柱的二阶弯矩second–order moment
考虑二阶效应后,在构件的某个其它截 面,其弯矩可能会大于端部截面的弯矩。
M2
M max M 2 Na f
M2
M2
截面设计中应取弯矩最大值进行计算
河南理工大学土木工程学院
8
2019/12/12
5.3 偏心受压构件正截面受力性能分析
②受拉侧钢筋应力较小,未达到受拉屈服
ssAs
f'yA's
ssAs
f'yA's
③承载力主要取决于压区混凝土和受压侧钢筋
压应力较大一侧钢筋能达到屈服强度,而另一侧 钢筋受拉不屈服或者受压不屈服。类似于超筋梁, 为脆性破坏。
破坏时压 区高度大
河南理工大学土木工程学院
5
brit2t0l1e9/f1a2i/l1u2re
材料破坏
l0 b
8 l0 30 b
Long column
Material failure
30
Slender column
河南理工大学土木工程学院
失稳破坏
Unstable failure
Mu
不同长细比柱从加荷载到破坏N-M 的关系(材料破坏关系曲线)
2019/12/12
7
(完整版)矩形截面偏心受压构件正截面的承载力计算

矩形截面偏心受压构件正截面的承载力计算一、矩形截面大偏心受压构件正截面的受压承载力计算公式 (一)大偏心受压构件正截面受压承载力计算(1)计算公式由力的平衡条件及各力对受拉钢筋合力点取矩的力矩平衡条件,可以得到下面两个基本计算公式:s y s y c A f A f bx f N -+=''1α (7-23)()'0''012a h A f x h bx f Ne s y c -+⎪⎭⎫ ⎝⎛-=α (7-24)式中: N —轴向力设计值;α1 —混凝土强度调整系数;e —轴向力作用点至受拉钢筋A S 合力点之间的距离;a he e i -+=2η (7-25) a i e e e +=0 (7-26)η—考虑二阶弯矩影响的轴向力偏心距增大系数,按式(7-22)计算;e i —初始偏心距;e 0 —轴向力对截面重心的偏心距,e 0 =M/N ;e a —附加偏心距,其值取偏心方向截面尺寸的1/30和20㎜中的较大者; x —受压区计算高度。
(2)适用条件1) 为了保证构件破坏时受拉区钢筋应力先达到屈服强度,要求b x x ≤ (7-27)式中 x b — 界限破坏时,受压区计算高度,o b b h x ξ= ,ξb 的计算见与受弯构件相同。
2) 为了保证构件破坏时,受压钢筋应力能达到屈服强度,和双筋受弯构件相同,要求满足:'2a x ≥ (7-28) 式中 a ′ — 纵向受压钢筋合力点至受压区边缘的距离。
(二)小偏心受压构件正截面受压承载力计算(1)计算公式根据力的平衡条件及力矩平衡条件可得s s s y c A A f bx f N σα-+=''1 (7-29)⎪⎭⎫ ⎝⎛'-+⎪⎭⎫ ⎝⎛-=s s y c a h A f x h bx f Ne 0''012α (7-30) ()'0''1'2s s s s c a h A a x bx f Ne -+⎪⎭⎫⎝⎛-=σα (7-31)式中 x — 受压区计算高度,当x >h ,在计算时,取x =h ;σs — 钢筋As 的应力值,可根据截面应变保持平面的假定计算,亦可近似取:y b s f 11βξβξσ--=(7-32)要求满足:y s y f f ≤≤σ'x b — 界限破坏时受压区计算高度,0h x b b ξ=;b ξξ、 — 分别为相对受压区计算高度 x/h 0和相对界限受压区计算高度x b /h 0 ;'e e 、′— 分别为轴向力作用点至受拉钢筋A s 合力点和受压钢筋A s ′合力点之间的距离 a he e i -+=2η (7-33) ''2a e he i --=η (7-34) (2)对于小偏心受压构件当bh f N c >时,除按上述式(7-30)和式(7-31)或式(7-32)计算外,还应满足下列条件:()()s s y c a a h A f h h bh f e e a h N -+⎪⎭⎫⎝⎛-≤⎥⎦⎤⎢⎣⎡---'0''00'22 (7-35 )式中 '0h — 钢筋's A 合力点至离纵向较远一侧边缘的距离,即s a h h -='0。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
当外力较小时压缩变形的增加与外力的 增长成正比,但外力稍大后,变形增加 的速度快于外力增长的速度,配置纵筋 数量越少,这个现象越为明显。
随着外力的继续增加,柱中开始出现 微细裂缝,在临近破坏荷载时,柱四 周出现明显的纵向裂缝,箍筋间的纵 筋发生压屈,向外凸出,混凝土被压 碎而整个柱破坏
受压构件的配筋构造要求
350
箍筋
b 400
350
复合箍筋
350
b 400
b 400
h 600
600 h 1000
600 h 1000
1000 h 1500
拉筋
复合箍筋
受压构件的配筋构造要求
第六章 受压构件承载力计算
6.2.4箍 筋
◆ 受压构件中箍筋应采用封闭式,其直径不应小于d/4,且不 小于6mm,此处d为纵筋的最大直径。 ◆ 箍筋间距不应大于400mm,也不应大于截面短边尺寸;对绑 扎钢筋骨架,箍筋间距不应大于15d;对焊接钢筋骨架不应大 于20d,此处d为纵筋的最小直径。 ◆ 当柱中全部纵筋的配筋率超过3%,箍筋直径不宜小于8mm, 且箍筋末端应应作成135°的弯钩,弯钩末端平直段长度不应 小于10箍筋直径,或焊成封闭式;此时,箍筋间距不应大于10 纵筋最小直径,也不应大于200mm。 ◆ 当柱截面短边大于400mm,且各边纵筋配置根数超过多于3 根时,或当柱截面短边未大于400mm,但各边纵筋配置根数超 过多于4根时,应设置复合箍筋。 ◆ 对截面形状复杂的柱,不得采用具有内折角的箍筋,以避免 箍筋受拉时使折角处混凝土破损。
6.3.1 轴心受压普通箍筋柱的正截面承载力计算
• 纵筋作用:纵筋帮助混凝土 承受压力,以减小构件的截 面尺寸;防止构件突然脆裂 破坏及增强构件的延性;以 及减小混凝土的徐变变形。 箍筋作用:箍筋能与纵筋形 成骨架;防止纵筋受力后外 凸;提高混凝土的强度。
1.受力分析和破坏特征
• 矩形截面轴心受压短柱
fy
Es 1
ey
根据变形条件:es =ec =e,确定钢筋及混凝土的 应力及其关系
ec
c
Ec
c Ec
e
s
s
Es
s
Es
Ec
c
E
c
c s Ec Es
建立混凝土与
s
E
钢筋间的 应力关系
c
Ec
e
Ece el e
Ec
E
Es Ec
Ec?= tan ?
e
根据平衡条件确定混凝土应力与N的关系
高强钢筋。
6.2.3 纵向钢筋
◆ 纵向钢筋配筋率过小时,纵筋对柱的承载力影响很小,接近 于素混凝土柱,纵筋不能起到防止混凝土受压脆性破坏的缓冲 作用。同时考虑到实际结构中存在偶然附加弯矩的作用(垂直 于弯矩作用平面),以及收缩和温度变化产生的拉应力,对受 压构件的最小配筋率应有所限制。 ◆ 《规范》规定,轴心受压构件、偏心受压构件全部纵向钢筋 的配筋率不应小于0.6%;同时一侧受压钢筋的配筋率不应小于 0.2%,受拉钢筋最小配筋率的要求同受弯构件。 ◆另一方面,考虑到施工布筋不致过多影响混凝土的浇筑质量,
受压构件在实际工程中应用比较广泛,下面看几张 图片实例。
New Antioch Bridge. This high-level bridge completed in 1979 replaced an older truss-type lift bridge crossing the main shipping channel. The bridge consists of continuous spans of variable depth in Cor-Ten steel. Maximum span is 460 ft, and maximum height of roadway above water level is 135 ft. (California)
Highway interchange structure. Spans are all multi-cell reinforced concrete box girders. Being stiff in torsion, these sections can be supported on a single line of columns, as well as on double columns or bents. (Oakland, California)
全部纵筋配筋率不宜超过5%。全部纵向钢筋的配筋率按r =(A's+As)/A计算,一侧受压钢筋的配筋率按r '=A's/A计算,其
中A为构件全截面面积。
受压构件的配筋构造要求
◆ 柱中纵向受力钢筋的的直径d不宜小于12mm,且选配钢筋时 宜根数少而粗,但对矩形截面根数不得少于4根,圆形截面根数 不宜少于8根,且应沿周边均匀布置。 ◆ 纵向钢筋的保护层厚度要求见表,且不小于钢筋直径d。 ◆ 当柱为竖向浇筑混凝土时,纵筋的净距不小于50mm; ◆ 对水平浇筑的预制柱,其纵向钢筋的最小应按梁的规定取值。 ◆ 截面各边纵筋的中距不应大于350mm。当h≥600mm时,在柱 侧面应设置直径10~16mm的纵向构造钢筋,并相应设置复合箍 筋或拉筋。
6.1 概述
受压构件分为轴心受压构件和偏心受压构件。
轴心受压构件:轴向力作用在构件截面的形心上。
偏心受压构件:轴向力不作用在构件截面的形心上(有弯
矩和轴力共同作用的构件)。
N
N
N
M
(a)轴心受压
(b) 单向偏心受压
说明
实际工程中真正的轴心受压构件是没有的。由 于施工的偏差及混凝土的不均匀性和钢筋的不对称 性,都将使构件产生初始偏心距,所以即时设计时理 论计算是轴心受压构件, 也不一定为轴心受压构件, 但对于一些偏心距较小的构件,可按轴心受压构件计 算。
受压构件的配筋构造要求
第六章 受压构件承载力计算
内折角不应采用
复杂截面的箍筋形式
内折角不应采用
第六章 受压构件承载力计算
6.3 轴心受压构件的截面承载力计算
Behavior of Axial Compressive Member
一、配有纵筋和普通箍筋柱的承载力计算 二、配有纵筋和螺旋式(或焊接环式)箍筋柱 的承载力计算(螺旋箍筋柱)
s
c
500
100
400
80
300
60
200
40
100
20
0
fy=540MPa fy=230MPa
c
e
0.001
0.002
Hale Waihona Puke 钢筋的受压强度• 试验表明,素混凝土棱柱体构件达到最大应力值时的压应变值一般在0.0015~0.002左右,而钢 筋混凝土短柱达到应力峰值时的压应变一般在0.0025~0.0035之间。其主要原因可以认为是柱中 配置了纵筋,起到了调整混凝土应力的作用,能比较好地发挥混凝土的塑性性能,使构件达到应 力峰值时的应变值得到增加,改善了受压破坏的脆性性质。
Ec
荷载很小时(弹性阶段),N
c
A
N
(1 E r / )
与混凝土和钢筋的应力的 关系基本上是线性关系。 此时 钢筋应力与混凝土应 力成正比。
s
N
As(1 /E r)
随着荷载的增加,混凝土 s
s N
的塑性变形有所发展。进
入弹塑性阶段( <1),在相
同的荷载增量下,钢筋的 压应力比混凝土的压应力
E N As r( E r)
r As
A A As
r
钢筋应力与N的关系:
s
N
As(1 /E r)
c
A
N
(1 E r / )
混凝土与N的关系
s
N
As(1 /E r)
钢筋应力与N的关系
’,E是常数,而是一个随着混凝土压应
力的增长而不断降低的变数
r As
A
E
Es Ec
Ec
e
Ece el e
N
初始受力
• 钢筋与混凝土的应力
试验表明,在整个加载过程中,由于钢筋和混凝土之间存在 着粘结力,两者压应变基本一致
变形条件:es =ec =e
物理关系:
钢筋: s Ese
s fy
e
ey
fy Es
e ey
混凝土:
f
c
2e e0
e e0
2
fc
0 e e0 e0 e eu
平衡条件: N c Ac s As
第六章 受压构件的截面承载力
本章重点
1.概述(轴心受压构件、偏心受压构件、双向偏心受压构件) 2.配有普通箍筋的轴心受压构件正截面承载力计算(轴心受压短柱、长
柱的受力特点和破坏形态,柱的计算长度,稳定系数,计算公式) 3.配有螺旋式(或焊接环式)箍筋的轴心受压构件正截面承载力计算
(箍筋的横向约束作用、承载力公式计算原理及适用条件) 4.偏心受压构件正截面承载力计算的有关原理 (1)偏心受压构件正截面的破坏形态和机理(大偏心受压破坏、小偏心受
偏心受 压构件
工业和民用建 筑中的单层厂 房和多层框架 柱
偏心受压构件
偏心受压构件拱和 屋架上弦杆,以及 水塔、烟囱的筒壁 等属于偏心受压构 件
6.2 受压构件构造要求
6.2.1 截面形状和尺寸
➢通常采用矩形截面,单层工业厂房的预制柱常采 用工字形截面。
➢ 桥墩、桩和公共建筑中的柱主要采用圆形截面。 ➢ 柱的截面尺寸不宜过小,不宜小于250*250。一般 应控制在l0/b≤30及l0/h≤25。 ➢ 当柱截面的边长在800mm以下时,一般以50mm 为模数,边长在800mm以上时,以100mm为模数。 ➢ I形截面,翼缘厚度不宜小于120mm ,腹板厚度 不宜小于100mm。
