【免费下载】初中三角函数专题
初三《三角函数》经典习题汇编(易错题、难题)

初三《三角函数》经典习题汇编(易错题、
难题)
初三《三角函数》经典题汇编(易错题、难题)
概述
本文档以初三数学学科的《三角函数》为主题,整理了一些经
典的题,主要包括易错题和难题。
这些题旨在帮助学生加深对三角
函数的理解和应用能力。
题目列表
1. 题目:已知直角三角形的一条直角边为5,斜边为13,求另
一条直角边的长度。
难度:易错题
答案:12
2. 题目:已知角A的正弦值为1/2,求角A的度数。
难度:易错题
答案:30°
3. 题目:已知角B的余弦值为3/5,求角B的度数。
难度:易错题
答案:53.13°
4. 题目:已知角C的正切值为2,求角C的度数。
难度:难题
答案:63.43°
5. 题目:已知直角三角形的一条直角边为8,角A的正弦值为3/4,求斜边的长度。
难度:难题
答案:10
6. 题目:已知角A的弧度为π/6,求角A的正弦值。
难度:难题
答案:1/2
7. 题目:已知角B的弧度为5π/6,求角B的正切值。
难度:难题
答案:√3
结论
通过解答这些经典习题,学生可以巩固对三角函数的基本概念和相关计算方法的掌握。
这些题目既包括易错题,帮助学生强化知识记忆,又包括难题,提高学生的解题能力。
建议学生针对这些题目进行练习,加深对三角函数的理解和应用能力,从而在考试中取得好成绩。
1.3 三角函数的计算(课件)-2023-2024学年九年级数学下册(北师大版)

建一条笔直的公路.
(1)求改直后的公路AB的长;
(2)问公路改直后该段路程比原来缩短了多少千米(精确到0.1)?
二、自主合作,探究新知
(1)求改直后的公路AB的长;
解:(1)过点C作CD⊥AB于点D,
∵AC=10千米,∠CAB=25°,
根据正弦的定义,得sinβ= ,即sin
∴DE=BDsin β°=200sin42°(m).
42°= ,
E
二、自主合作,探究新知
探究二:利用计算器由三角函数值求角度
想一想:为了方便行人推自行车过某天桥,市政府在10m高的天桥两端修
建了40m长的斜道(如图).这条斜道的倾斜角是多少?
在Rt△ABC中,sinA=
屏幕显示结果cos 72°=0.309 016 994.
和
键.
也有的计算器是
先输入角度再按
函数名称键.
二、自主合作,探究新知
3.求 tan30°36'.
方法一: 第一步:按计算器
键,
第二步:输入角度值30,分值36 (可以使用
键),
屏幕显示答案:0.591 398 351;
方法二: 第一步:按计算器
北师大版 数学 九年级下册
第一章 直角三角形的边角关系
3
三角函数的计算
学习目标
1.学会利用计算器求三角函数值并进行相关计算.
(重点)
2.学会利用计算器根据三角函数值求锐角度数并计算.
(难点)
复习回顾
30°,45°,60°角的三角函数值:
三
角函
角α
三角函数
专题5.3 三角函数的图象与性质(原卷版)

专题5.3 三角函数的图象与性质题型一 三角函数的值域题型一 三角函数的值域例1.(2023春·重庆铜梁·高一铜梁中学校校考期中)求2()2cos 2sin 3R f x x x x =--+∈()的最小值是_____例2.(2023·上海·高三专题练习)已知函数()1πsin 223f x x ⎛⎫=- ⎪⎝⎭,ππ,44x ⎡⎤∈-⎢⎥⎣⎦,则函数()f x 的值域为______.练习1.(2023春·北京·高一清华附中校考期中)当0,2x π⎛⎤∈ ⎥⎝⎦时,()14sin sin f x x x =+的最小值为( ) A .5 B .4C .2D .1练习2.(2023春·江苏镇江·高三江苏省扬中高级中学校联考期中)函数π()cos (sin ),[0,]4f x x x x x =∈的最大值与最小值的和为( )A B C D .3练习3.(2022·高三课时练习)函数y =tan(π-x ),x ∈(,)43ππ-的值域为________.练习4.(2023·全国·高三专题练习)函数()sin 2sin 1cos x xf x x=+的值域__________.练习5.(2023·福建龙岩·统考模拟预测)已知()23sin 8cos2xf x x =-,若()()f x f θ≤恒成立,则sin θ=( )A .35B .35 C .45D .45-题型二 求三角函数的周期性,奇偶性,单调性,对称性例3.(2023春·北京·高三北京一七一中校考期中)下列函数中,最小正周期为π的奇函数是( )A .sin2cos2y x x =+B .sin cos y x x =+C .πsin 22y x ⎛⎫=+ ⎪⎝⎭D .πcos 22y x ⎛⎫=+ ⎪⎝⎭例4.(2023春·海南海口·高三海口一中校考期中)(多选)已知函数()π2sin 26f x x ⎛⎫=-- ⎪⎝⎭则( )A .函数()f x 的最小正周期为2πB .函数()f x 的图像关于直线π6x =-对称 C .函数()f x 为偶函数D .函数()f x 的图像向左平移ϕ个单位后关于y 轴对称,则ϕ可以为5π6练习6.(2023春·全国·高三专题练习)(多选)若函数44()sin cos f x x x =+,则( ) A .函数()f x 的一条对称轴为π4x =B .函数()f x 的一个对称中心为π,04⎛⎫⎪⎝⎭C .函数()f x 的最小正周期为π2D .若函数3()8()4g x f x ⎡⎤=-⎢⎥⎣⎦,则()g x 的最大值为2练习7.(2023春·安徽六安·高三六安市裕安区新安中学校考期中)(多选)函数()π2sin 2f x x =+⎛⎫ ⎪⎝⎭,则以下结论中正确..的是( )A .()f x 在π0,2⎛⎫⎪⎝⎭上单调递减B .直线 π6x =为()f x 图象的一条对称轴C .()f x 的最小正周期为2πD .()f x 在π0,2⎛⎫ ⎪⎝⎭上的值域是(练习8.(2023春·江西·高三校联考期中)(多选)已知函数π()cos 25x f x ⎛⎫=+ ⎪⎝⎭,则( )A .()f x 的图象关于2π,05⎛⎫- ⎪⎝⎭对称B .()f x 的图象关于直线8π5x =对称 C .3π5f x ⎛⎫+ ⎪⎝⎭为奇函数D .()f x 为偶函数练习9.(2023·北京海淀·高三专题练习)函数()cos π6f x x ω=+⎛⎫ ⎪⎝⎭在[]π,π-的图象如图所示.则(1)()f x 的最小正周期为__________; (2)距离y 轴最近的对称轴方程__________.练习10.(2023·北京海淀·高三专题练习)函数()()()cos sin f x x a x b =+++,则( ) A .若0a b +=,则()f x 为奇函数B .若π2a b +=,则()f x 为偶函数C .若π2b a -=,则()f x 为偶函数 D .若πa b -=,则()f x 为奇函数题型三 解三角不等式例5.(2023春·广东佛山·高三佛山一中校考阶段练习)不等式tan 1x >-的解集是________.例6.(2023春·辽宁本溪·高三校考阶段练习)已知函数()π2cos 23f x x ⎛⎫=+ ⎪⎝⎭.(1)用五点法画出函数()f x 在2,33ππ⎡⎤-⎢⎥⎣⎦上的大致图像,并写出()f x 的最小正周期;(2)1≤.练习11.(2023秋·广东深圳·高三统考期末)已知函数()()lg 2cos 1f x x =-,则函数()f x 的定义域为( )A .ππ2π,2π,Z 33k k k ⎛⎫-+∈ ⎪⎝⎭B .ππ2π,2π,Z 33k k k ⎡⎤-+∈⎢⎥⎣⎦C .Z ππ,ππ2,266k k k ⎛⎫-+∈ ⎪⎝⎭D .Z ππ,ππ2,266k k k ⎡⎤-+∈⎢⎥⎣⎦练习12.(2023春·广东深圳·高一深圳市光明区高级中学统考期中)已知函数()()2sin (0,0π)f x x ωϕωϕ=+><<的部分图象如图所示.(1)求函数()f x 的解析式; (2)求函数()f x 的单调区间;(3)若()f x >x 的取值范围.练习13.(2021春·高三课时练习)解不等式1tan x ≤≤-练习14.(2023春·辽宁铁岭·高三铁岭市清河高级中学校考阶段练习)已知某地某天从6时到22时的温度变换近似地满足函数π510sin π2084y x ⎛⎫=-+ ⎪⎝⎭.(1)求该地这一天该时间段内温度的最大温差;(2)若有一种细菌在15C 到25C 之间可以存活则在这段时间内,该细菌最多能存活多长时间?练习15.(2023春·江西南昌·高三校考阶段练习)函数lgsin y x =_________.题型四 由三角函数的值域(最值)求参数例7.(2023·全国·高三专题练习)已知函数()()11sin 06f x a x x a =-≠,且()7π6f x f ⎛⎫≤ ⎪⎝⎭恒成立,则()f x =______例8.(2023春·上海青浦·高三上海市朱家角中学校考期中)设函数sin y x =定义域为[],a b ,值域为11,2⎡⎤--⎢⎥⎣⎦,则b a -的最大值为______练习16.(2023春·江苏镇江·高三江苏省镇江中学校考期中)已知()π0,sin sin3a f x x a x ⎛⎫>=-- ⎪⎝⎭=a __________.练习17.(2023春·辽宁朝阳·高三朝阳市第一高级中学校考期中)已知函数()cos f x x x =-的定义域为[,]a b ,值域为[1,2]-,则b a -的取值范围是( ) A .π,π3⎡⎤⎢⎥⎣⎦B .π5π,26⎡⎤⎢⎥⎣⎦C .π24π,3⎡⎤⎢⎥⎣⎦D .2433ππ,⎡⎤⎢⎥⎣⎦练习18.(2023·上海·高三专题练习)若函数πsin 3y x ω⎛⎫=- ⎪⎝⎭(常数0ω>)在区间()0,π没有最值,则ω的取值范围是__________.练习19.(2023·湖北襄阳·襄阳四中校考模拟预测)若函数()sin cos()f x x x ϕ=++的最小值为ϕ的一个取值为___________.(写出一个即可)练习20.(2023春·北京·高三北师大二附中校考期中)已知函数()ππ2sin 25f x x ⎛⎫=+ ⎪⎝⎭,若对任意的实数x ,总有()()()12f x f x f x ≤≤,则12x x -的最小值是( ) A .2 B .4C .πD .2π题型五 根据单调求参数例9.(2021·高一课时练习)若不等式tan x a >在ππ,42x ⎛⎫∈ ⎪⎝⎭- 上恒成立,则a 的取值范围为( ) A .1a > B .1a ≤ C .1a <- D .1a ≤-例10.(2023·山东烟台·统考二模)已知函数()()()cos 202πf x x ϕϕ=+≤<在ππ,64⎡⎤-⎢⎥⎣⎦上单调递增,则ϕ的取值范围为( ). A .4ππ3ϕ≤≤ B .π4π23ϕ≤≤ C .4π2π3ϕ≤≤ D .4π3π32ϕ≤≤练习21.(2023秋·云南楚雄·高三统考期末)已知函数()()πcos 03f x x ωω⎛⎫=-> ⎪⎝⎭,若()f x 在区间3π0,2⎛⎫⎪⎝⎭上为单调函数,则ω的取值范围是______.练习22.(2023春·河南南阳·高三南阳中学校考阶段练习)(多选)若函数cos2y x =与函数()sin 2y x ϕ=+在π0,4⎡⎤⎢⎥⎣⎦上的单调性相同,则ϕ的一个值为( )A .π6B .3π4C .4π3-D .4π3练习23.(2023春·四川成都·高三成都市第二十中学校校考阶段练习)已知函数 tan y x ω=在ππ,22⎛⎫- ⎪⎝⎭内是减函数, 则( ) A .01ω<< B .10ω-≤< C .1ω≥ D .1ω≤-练习24.(2023春·辽宁·高二辽宁实验中学校考阶段练习)若函数()()cos 03f x x πωω⎛⎫=-> ⎪⎝⎭在,63ππ⎛⎫⎪⎝⎭上不单调,则实数ω的取值范围是______.练习25.(2023·河北承德·统考模拟预测)已知1ω>,函数π()cos 3f x x ω⎛⎫=- ⎪⎝⎭.(1)当2ω=时,求()f x 的单调递增区间; (2)若()f x 在区间ππ,63⎡⎤⎢⎥⎣⎦上单调,求ω的取值范围.题型六 根据对称求参数例11.(2023春·河北石家庄·高三石家庄市第十五中学校考阶段练习)若()ππcos 232f x x ϕϕ⎛⎫⎛⎫=++< ⎪⎪⎝⎭⎝⎭是奇函数,则ϕ=_________.例12.(湖南省名校2023届高三考前仿真模拟(二)数学试题)函数()()()sin cos f x x x ϕϕ=++的图象的一条对称轴方程是π4x =-,则ϕ的最小正值为( )A .π6B .π4C .π3D .π2练习26.(2023·全国·高三专题练习)(多选)若函数()ππsin cos sin sin 36f x x x ϕϕ⎛⎫⎛⎫=+-- ⎪ ⎪⎝⎭⎝⎭的图象关于坐标原点对称,则ϕ的可能取值为( ) A .π3-B .π6-C .π3D .2π3练习27.(2023·重庆·统考模拟预测)已知函数π()sin()(0)3f x x ωω=+>,若对于任意实数x ,都有π()()3f x f x =--,则ω的最小值为( )A .2B .52C .4D .8练习28.(2023春·重庆渝中·高三重庆巴蜀中学校考期中)已知函数()2s πsin co 2f x x x x ⎛⎫=+ ⎪⎝⎭.(1)设[0,π)θ∈,函数()f x θ+是偶函数,求θ的值;(2)若()f x 在区间,π3m ⎡⎤-⎢⎥⎣⎦上恰有三条对称轴,求实数m 的取值范围.练习29.(2023·全国·高三专题练习)已知函数()()π2sin 0,2f x x ωϕωϕ⎛⎫=+>< ⎪⎝⎭,若()0f =π6x =为()f x 图象的一条对称轴,则ω的最小值为______.练习30.(2022·高三课时练习)已知()()3sin f x x ωϕ=+对任意x 都有()()33ππ+=-f x f x ,则3f π⎛⎫⎪⎝⎭等于________.题型七 由图象确定三角函数解析式例13.(2023春·陕西安康·高三陕西省安康中学校考阶段练习)已知函数()()πcos 0,0,2f x A x A ωϕωϕ⎛⎫=+>>< ⎪⎝⎭的部分图象如图所示,则( )A .()7ππ2cos 123f x x ⎛⎫=+⎪⎝⎭ B .()ππ2cos 243f x x ⎛⎫=+ ⎪⎝⎭C .()11ππ2cos 243f x x ⎛⎫=-⎪⎝⎭ D .()11ππ2cos 243f x x ⎛⎫=+⎪⎝⎭例14.(2022春·福建·高二统考学业考试)(多选)函数()()sin 0y A x A ωϕ=+>的一个周期内的图象如图所示,下列结论正确的有( )A .函数()f x 的解析式是()π2sin 23f x x ⎛⎫=- ⎪⎝⎭B .函数()f x 的最大值是2C .函数()f x 的最小正周期是πD .函数()f x 的一个对称中心是π,06⎛⎫⎪⎝⎭练习31.(2023春·四川成都·高三石室中学校考期中)如图,函数()()sin f x A x =+ωϕ(0A >,0ω>,π<ϕ)的部分图象与坐标轴的三个交点分别为()1,0P -,Q ,R ,且线段RQ 的中点M 的坐标为31,22⎛⎫- ⎪⎝⎭,则()2f -等于( )A .1B .-1CD .练习32.(2023春·吉林长春·高三东北师大附中校考阶段练习)函数()()πsin (0,0,)2f x A x A ωϕωϕ=+>><的部图象如图所示,则ω=______,ϕ=______;练习33.(2023春·辽宁沈阳·高三沈阳二十中校联考期中)(多选)已知函数()()πsin 0,0,2f x A x A ωϕωϕ⎛⎫=+>>< ⎪⎝⎭ 的部分图像如图所示,下列说法正确的是( )A .()f x 的图像关于点π,03⎛⎫- ⎪⎝⎭对称B .()f x 的图像关于直线5π12x =-对称 C .将函数2cos2y x =的图像向右平移π12个单位长度得到函数()f x 的图像D .若方程()f x m =在π,02⎡⎤-⎢⎥⎣⎦上有两个不相等的实数根,则m 的取值范围是(2,-练习34.(湖南省部分名校联盟2023届高三5月冲刺压轴大联考数学试题)(多选)如图是某质点作简谐运动的部分图象,位移y (单位:mm )与时间t (单位:s )之间的函数关系式是()sin 0,0,0,2y A t A πωϕωϕ⎛⎫⎛⎫=+>>∈ ⎪ ⎪⎝⎭⎝⎭,则下列命题正确的是( )A .该简谐运动的初相为π6B .该简谐运动的频率为12πC .前6秒该质点的位移为12mmD .当42π,33t ⎡⎤∈⎢⎥⎣⎦时,位移y 随着时间t 的增大而增大练习35.(2023春·河北衡水·高三衡水市第二中学期末)已知函数()()tan f x A x ωϕ=+π02ϕϕ⎛⎫>< ⎪⎝⎭,,()y f x =的部分图象如图,则 7π24f ⎛⎫= ⎪⎝⎭( )A .2+BC .D .题型八 描述三角函数的变换过程例15.(2022春·福建·高二统考学业考试)为了得到函数π()2cos 3f x x ⎛⎫=+ ⎪⎝⎭的图像,只需把曲线()cos f x x =上所有的点( )A .向左平移π3个单位,再把纵坐标伸长到原来的2倍B .向右平移π3个单位,再把纵坐标伸长到原来的2倍C .向左平移π3个单位,再把纵坐标缩短到原来的12D .向右平移π3个单位,再把纵坐标缩短到原来的12例16.(北京市2023届高三高考模拟预测考试数学试题)要得到cos 2xy =的图像,只要将sin 2xy =的图像( )A .向左平移π2个单位B .向右平移π2个单位C .向左平移π个单位D .向右平移π个单位练习36.(2021·高三课时练习)函数ππ()2sin(),0,22f x x ωϕωϕ⎛⎫=+>-<< ⎪⎝⎭的部分图象如图所示, 为了得到这个函数的图象,只要将2sin y x =的图象上所有的点 ( )A .向右平移π3个单位长度,再把所得各点的横坐标缩短到原来的12倍,纵坐标不变B .向右平移π3个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变C .向右平移π6个单位长度,再把所得各点的横坐标缩短到原来的12倍,纵坐标不变D .向右平移π6个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变练习37.(2023春·江西赣州·高三校考期中)(多选)要得到函数y x =的图象,只需将函数π24y x ⎛⎫=+ ⎪⎝⎭的图象上所有的点的( )A .先向左平移π8个单位长度,再横坐标伸长到原来的2倍(纵坐标不变)B .先向左平移π4个单位长度,再横坐标缩短到原来的12倍(纵坐标不变)C .先横坐标伸长到原来的2倍(纵坐标不变),再向左平移π4个单位长度D .先横坐标伸长到原来的2倍(纵坐标不变),再向左平移π8个单位长度练习38.(2023春·贵州·高三校联考期中)为了得到函数πsin 28y x ⎛⎫=- ⎪⎝⎭的图象,只要将函数πcos 24y x ⎛⎫=-- ⎪⎝⎭的图象( )A .向左平移5π8个单位长度 B .向右平移5π8个单位长度 C .向左平移5π16个单位长度 D .向右平移5π16个单位长度练习39.(2023春·重庆渝中·高三重庆巴蜀中学校考期中)为得到函数()πsin 23f x x ⎛⎫=+ ⎪⎝⎭的图象,只需把函数()cos g x x =图象上的所有点的( )A .横坐标伸长到原来的2倍,纵坐标不变,再把得到的图象向左平移π6个单位长度B .横坐标伸长到原来的2倍,纵坐标不变,再把得到的图象向右平移π12个单位长度 C .横坐标缩短到原来的12,纵坐标不变,再把得到的图象向左平移π6个单位长度D .横坐标缩短到原来的12,纵坐标不变,再把得到的图象向右平移π12个单位长度练习40.(2023春·辽宁朝阳·高二校联考期中(多选))已知函数()()2sin (π0,)f x x ωϕϕω><=+的部分图象如图所示,则()f x 的图象可以由函数()2sin g x x =的图象( )A .先纵坐标不变,横坐标变为原来的12,再向左平移11π12个单位长度得到 B .先纵坐标不变,横坐标变为原来的2倍,再向右平移π12个单位长度得到 C .先向右平移π12个单位长度,再纵坐标不变,横坐标变为原来的12得到 D .先向右平移π6个单位长度,再纵坐标不变,横坐标变为原来的12得到题型九 求图象变换前(后)的函数解析式例17.(2023·陕西榆林·统考模拟预测)将函数cos2y x =的图象向右平移π20个单位长度,再把所得图象各点的横坐标缩小到原来的12(纵坐标不变),所得图象的一条对称轴为x =( ) A .π80B .π60C .π40D .π20例18.(2023·江苏南通·统考模拟预测)将函数()πsin 13f x x ⎛⎫=++ ⎪⎝⎭的图象上的点横坐标变为原来的12(纵坐标变)得到函数()g x 的图象,若存在()0,πθ∈,使得()()2g x g x θ+-=对任意x ∈R 恒成立,则θ=( )A .π6B .π3C .2π3D .5π6练习41.(2023·河南郑州·模拟预测)把函数()y f x =图象上所有点的纵坐标不变,横坐标伸长到原来的2倍,再把所得曲线向右平移π4个单位长度,得到函数πcos 3y x ⎛⎫=- ⎪⎝⎭的图象,则()f x =( ) A .15πsin 212x ⎛⎫+ ⎪⎝⎭B .πsin 212x ⎛⎫- ⎪⎝⎭C .5πsin 212x ⎛⎫+ ⎪⎝⎭D .1πsin 212x ⎛⎫- ⎪⎝⎭练习42.(2023·辽宁·校联考三模)(多选)已知函数()()cos 202f x x πϕϕ⎛⎫=+-<< ⎪⎝⎭图像的一条对称轴为8x π=,先将函数()f x 的图像上所有点的横坐标伸长为原来的3倍,再将所得图像上所有的点向右平移4π个单位长度,得到函数()g x 的图像,则函数()g x 的图像在以下哪些区间上单调递减( ) A .[],2ππ B .[]2,ππ--C .79,22ππ⎡⎤⎢⎥⎣⎦D .9,42ππ⎡⎤--⎢⎥⎣⎦练习43.(2023春·重庆铜梁·高三铜梁中学校校考期中)(多选)将函数π3sin()3y x =+的图象上所有点的横坐标缩短到原来的12倍(纵坐标不变),再把得到的图象向右平移π3个单位长度,得到函数()y g x =的图象,下列结论正确的是( ) A .函数()y g x =的图象关于点π,06⎛⎫⎪⎝⎭对称B .函数()y g x =的图象最小正周期为πC .函数()y g x =的图象在π0,2⎡⎤⎢⎥⎣⎦上单调递增D .函数()y g x =的图象关于直线5π12x =对称练习44.(2023·江西上饶·校联考模拟预测)已知π3是函数()sin cos f x x a x =+的一个零点,将函数()2y f x =的图象向右平移π12个单位长度后所得图象的表达式为( ) A .7π2sin 26y x ⎛⎫=- ⎪⎝⎭B .π2sin 212y x ⎛⎫=+ ⎪⎝⎭C .2cos 2y x =-D .2cos2y x =。
《初中数学三角函数课件》

余切函数及其性质
1
余切函数的图像
余切函数的图像是连续且周期为180°(或π)的波形,代表角度与余切值之间的关系。
2
余切函数的性质
余切函数的值是无界的,值域为全体实数。当角度为0°或180°时,余切函数的值为无穷大。
三角函数的单位圆解法
什么是单位圆解法
单位圆解法是利用单位圆上的点与角度之间的关系,解决三角函数方程的一 种方法。
正弦函数及其性质
正弦函数的图像
正弦函数的图像是连续且周期为360°(或2π)的波 形,代表角度与正弦值之间的关系。
正弦函数的性质
正弦函数在0°和360°之间的值在-1和1之间变化;正 弦函数的最大值是1,最小值是-1。
余弦函数及其性质
余弦函数的图像
余弦函数的图像是连续且周期为360°(或2π)的 波形,代表角度与余弦值之间的关系。
余弦函数的性质
余弦函数在0°和360°之间的值在-1和1之间变化; 余弦函数的最大值是1,最小值是-1。
正切函数及其性质
正切函数的图像
0°(或π)的波形, 代表角度与正切值之间的关系。
正切函数的值是无界的,值域为全体实数。当角度 为90°或270°时,正切函数的值为无穷大。
初中数学三角函数课件
让我们一起探索《初中数学三角函数课件》,了解概念、性质、变换,以及 在实际应用中的妙用。
三角函数的概念和定义
1 什么是三角函数
2 三角函数的定义
三角函数是描述角度与直角三角形边 长比例关系的函数,包括正弦、余弦、 正切和余切。
正弦:sinθ = 对边/斜边,余弦:cosθ = 邻边/斜边,正切:tanθ = 对边/邻边, 余切:cotθ = 邻边/对边。
三角函数的图象与变换
人教中考数学专题训练---锐角三角函数的综合题分类含答案

一、锐角三角函数真题与模拟题分类汇编(难题易错题)1.某地是国家AAAA 级旅游景区,以“奇山奇水奇石景,古賨古洞古部落”享誉巴渠,被誉为 “小九寨”.端坐在观音崖旁的一块奇石似一只“啸天犬”,昂首向天,望穿古今.一个周末,某数学兴趣小组的几名同学想测出“啸天犬”上嘴尖与头顶的距离.他们把蹲着的“啸天犬”抽象成四边形ABCD ,想法测出了尾部C 看头顶B 的仰角为40,从前脚落地点D 看上嘴尖A 的仰角刚好60,5CB m =, 2.7CD m =.景区管理员告诉同学们,上嘴尖到地面的距离是3m .于是,他们很快就算出了AB 的长.你也算算?(结果精确到0.1m .参考数据:400.64400.77400.84sin cos tan ︒≈︒≈︒≈,,.2 1.41,3 1.73≈≈)【答案】AB 的长约为0.6m . 【解析】 【分析】作BF CE ⊥于F ,根据正弦的定义求出BF ,利用余弦的定义求出CF ,利用正切的定义求出DE ,结合图形计算即可. 【详解】解:作BF CE ⊥于F ,在Rt BFC ∆中, 3.20BF BC sin BCF ⋅∠≈=,3.85CF BC cos BCF ⋅∠≈=,在Rt ADE ∆E 中,3 1.73tan 3AB DE ADE ===≈∠, 0.200.58BH BF HF AH EF CD DE CF ∴+=﹣=,==﹣=由勾股定理得,22BH AH 0.6(m)AB =+≈, 答:AB 的长约为0.6m .【点睛】考查的是解直角三角形的应用﹣仰角俯角问题,掌握仰角俯角的概念、熟记锐角三角函数的定义是解题的关键.2.在正方形ABCD中,对角线AC,BD交于点O,点P在线段BC上(不含点B),∠BPE=12∠ACB,PE交BO于点E,过点B作BF⊥PE,垂足为F,交AC于点G.(1)当点P与点C重合时(如图1).求证:△BOG≌△POE;(2)通过观察、测量、猜想:BFPE=,并结合图2证明你的猜想;(3)把正方形ABCD改为菱形,其他条件不变(如图3),若∠ACB=α,求BF PE的值.(用含α的式子表示)【答案】(1)证明见解析(2)12BFPE=(3)1tan2BFPEα=【解析】解:(1)证明:∵四边形ABCD是正方形,P与C重合,∴OB="OP" ,∠BOC=∠BOG=90°.∵PF⊥BG ,∠PFB=90°,∴∠GBO=90°—∠BGO,∠EPO=90°—∠BGO.∴∠GBO=∠EPO .∴△BOG≌△POE(AAS).(2)BF1PE2=.证明如下:如图,过P作PM//AC交BG于M,交BO于N,∴∠PNE=∠BOC=900,∠BPN=∠OCB.∵∠OBC=∠OCB =450,∴∠NBP=∠NPB.∴NB=NP.∵∠MBN=900—∠BMN , ∠NPE=900—∠BMN ,∴∠MBN=∠NPE . ∴△BMN ≌△PEN (ASA ).∴BM=PE .∵∠BPE=12∠ACB ,∠BPN=∠ACB ,∴∠BPF=∠MPF . ∵PF ⊥BM ,∴∠BFP=∠MFP=900.又∵PF=PF , ∴△BPF ≌△MPF (ASA ).∴BF="MF" ,即BF=12BM . ∴BF=12PE , 即BF 1PE 2=. (3)如图,过P 作PM//AC 交BG 于点M ,交BO 于点N ,∴∠BPN=∠ACB=α,∠PNE=∠BOC=900.由(2)同理可得BF=12BM , ∠MBN=∠EPN . ∵∠BNM=∠PNE=900,∴△BMN ∽△PEN .∴BM BNPE PN=. 在Rt △BNP 中,BN tan =PN α, ∴BM =tan PE α,即2BF=tan PEα. ∴BF 1=tan PE 2α. (1)由正方形的性质可由AAS 证得△BOG ≌△POE .(2)过P 作PM//AC 交BG 于M ,交BO 于N ,通过ASA 证明△BMN ≌△PEN 得到BM=PE ,通过ASA 证明△BPF ≌△MPF 得到BF=MF ,即可得出BF 1PE 2=的结论. (3)过P 作PM//AC 交BG 于点M ,交BO 于点N ,同(2)证得BF=12BM , ∠MBN=∠EPN ,从而可证得△BMN ∽△PEN ,由BM BN PE PN =和Rt △BNP 中BNtan =PNα即可求得BF 1=tan PE 2α.3.已知Rt △ABC 中,AB 是⊙O 的弦,斜边AC 交⊙O 于点D ,且AD=DC ,延长CB 交⊙O 于点E .(1)图1的A、B、C、D、E五个点中,是否存在某两点间的距离等于线段CE的长?请说明理由;(2)如图2,过点E作⊙O的切线,交AC的延长线于点F.①若CF=CD时,求sin∠CAB的值;②若CF=aCD(a>0)时,试猜想sin∠CAB的值.(用含a的代数式表示,直接写出结果)【答案】(1)AE=CE;(2)①;②.【解析】试题分析:(1)连接AE、DE,如图1,根据圆周角定理可得∠ADE=∠ABE=90°,由于AD=DC,根据垂直平分线的性质可得AE=CE;(2)连接AE、ED,如图2,由∠ABE=90°可得AE是⊙O的直径,根据切线的性质可得∠AEF=90°,从而可证到△ADE∽△AEF,然后运用相似三角形的性质可得=AD•AF.①当CF=CD时,可得,从而有EC=AE=CD,在Rt△DEC中运用三角函数可得sin∠CED=,根据圆周角定理可得∠CAB=∠DEC,即可求出sin∠CAB的值;②当CF=aCD(a>0)时,同①即可解决问题.试题解析:(1)AE=CE.理由:连接AE、DE,如图1,∵∠ABC=90°,∴∠ABE=90,∴∠ADE=∠ABE=90°,∵AD=DC,∴AE=CE;(2)连接AE、ED,如图2,∵∠ABE=90°,∴AE是⊙O的直径,∵EF是⊙OO的切线,∴∠AEF=90°,∴∠ADE=∠AEF=90°,又∵∠DAE=∠EAF,∴△ADE∽△AEF,∴,∴=AD•AF.①当CF=CD时,AD=DC=CF,AF=3DC,∴=DC•3DC=,∴AE=DC,∵EC=AE,∴EC=DC,∴sin∠CAB=sin∠CED===;②当CF=aCD(a>0)时,sin∠CAB=.∵CF=aCD,AD=DC,∴AF=AD+DC+CF=(a+2)CD,∴=DC•(a+2)DC=(a+2),∴AE=DC,∵EC=AE,∴EC=DC,∴sin∠CAB=sin∠CED==.考点:1.圆的综合题;2.探究型;3.存在型.4.如图,抛物线C1:y=(x+m)2(m为常数,m>0),平移抛物线y=﹣x2,使其顶点D 在抛物线C1位于y轴右侧的图象上,得到抛物线C2.抛物线C2交x轴于A,B两点(点A 在点B的左侧),交y轴于点C,设点D的横坐标为a.(1)如图1,若m=.①当OC=2时,求抛物线C2的解析式;②是否存在a,使得线段BC上有一点P,满足点B与点C到直线OP的距离之和最大且AP=BP?若存在,求出a的值;若不存在,请说明理由;(2)如图2,当OB=2﹣m(0<m<)时,请直接写出到△ABD的三边所在直线的距离相等的所有点的坐标(用含m的式子表示).【答案】(1) ①y=﹣x2+x+2.②.(2)P1(﹣m,1),P2(﹣m,﹣3),P3(﹣﹣m,3),P4(3﹣m,3).【解析】试题分析:(1)①首先写出平移后抛物线C2的解析式(含有未知数a),然后利用点C (0,2)在C2上,求出抛物线C2的解析式;②认真审题,题中条件“AP=BP”意味着点P在对称轴上,“点B与点C到直线OP的距离之和最大”意味着OP⊥BC.画出图形,如图1所示,利用三角函数(或相似),求出a的值;(2)解题要点有3个:i)判定△ABD为等边三角形;ii)理论依据是角平分线的性质,即角平分线上的点到角两边的距离相等;iii)满足条件的点有4个,即△ABD形内1个(内心),形外3个.不要漏解.试题解析:(1)当m=时,抛物线C1:y=(x+)2.∵抛物线C2的顶点D在抛物线C1上,且横坐标为a,∴D(a,(a+)2).∴抛物线C2:y=﹣(x﹣a)2+(a+)2(I).①∵OC=2,∴C(0,2).∵点C在抛物线C2上,∴﹣(0﹣a)2+(a+)2=2,解得:a=,代入(I)式,得抛物线C2的解析式为:y=﹣x2+x+2.②在(I)式中,令y=0,即:﹣(x﹣a)2+(a+)2=0,解得x=2a+或x=﹣,∴B(2a+,0);令x=0,得:y=a+,∴C(0,a+).设直线BC的解析式为y=kx+b,则有:,解得,∴直线BC的解析式为:y=﹣x+(a+).假设存在满足条件的a值.∵AP=BP,∴点P在AB的垂直平分线上,即点P在C2的对称轴上;∵点B与点C到直线OP的距离之和≤BC,只有OP⊥BC时等号成立,∴OP⊥BC.如图1所示,设C2对称轴x=a(a>0)与BC交于点P,与x轴交于点E,则OP⊥BC,OE=a.∵点P在直线BC上,∴P(a,a+),PE=a+.∵tan∠EOP=tan∠BCO=,∴,解得:a=.∴存在a=,使得线段BC上有一点P,满足点B与点C到直线OP的距离之和最大且AP="BP"(3)∵抛物线C2的顶点D在抛物线C1上,且横坐标为a,∴D(a,(a+m)2).∴抛物线C2:y=﹣(x﹣a)2+(a+m)2.令y=0,即﹣(x﹣a)2+(a+m)2=0,解得:x1=2a+m,x2=﹣m,∴B(2a+m,0).∵OB=2﹣m,∴2a+m=2﹣m,∴a=﹣m.∴D(﹣m,3).AB=OB+OA=2﹣m+m=2.如图2所示,设对称轴与x轴交于点E,则DE=3,BE=AB=,OE=OB﹣BE=﹣m.∵tan∠ABD=,∴∠ABD=60°.又∵AD=BD,∴△ABD为等边三角形.作∠ABD的平分线,交DE于点P1,则P1E=BE•tan30°=×=1,∴P1(﹣m,1);在△ABD形外,依次作各个外角的平分线,它们相交于点P2、P3、P4.在Rt△BEP2中,P2E=BE•tan60°=•=3,∴P2(﹣m,﹣3);易知△ADP3、△BDP4均为等边三角形,∴DP3=DP4=AB=2,且P3P4∥x轴.∴P3(﹣﹣m,3)、P4(3﹣m,3).综上所述,到△ABD的三边所在直线的距离相等的所有点有4个,其坐标为:P1(﹣m,1),P2(﹣m,﹣3),P3(﹣﹣m,3),P4(3﹣m,3).【考点】二次函数综合题.5.如图(1),已知正方形ABCD在直线MN的上方BC在直线MN上,E是BC上一点,以AE为边在直线MN的上方作正方形AEFG.(1)连接GD,求证:△ADG≌△ABE;(2)连接FC,观察并直接写出∠FCN的度数(不要写出解答过程)(3)如图(2),将图中正方形ABCD改为矩形ABCD,AB=6,BC=8,E是线段BC上一动点(不含端点B、C),以AE为边在直线MN的上方作矩形AEFG,使顶点G恰好落在射线CD上.判断当点E由B向C运动时,∠FCN的大小是否总保持不变,若∠FCN的大小不变,请求出tan∠FCN的值.若∠FCN的大小发生改变,请举例说明.【答案】(1)见解析;(2)∠FCN =45°,理由见解析;(3)当点E 由B 向C 运动时,∠FCN 的大小总保持不变,tan ∠FCN =43.理由见解析. 【解析】 【分析】(1)根据三角形判定方法进行证明即可.(2)作FH ⊥MN 于H .先证△ABE ≌△EHF ,得到对应边相等,从而推出△CHF 是等腰直角三角形,∠FCH 的度数就可以求得了.(3)解法同(2),结合(1)(2)得:△EFH ≌△GAD ,△EFH ∽△ABE ,得出EH=AD=BC=8,由三角函数定义即可得出结论. 【详解】(1)证明:∵四边形ABCD 和四边形AEFG 是正方形, ∴AB =AD ,AE =AG =EF ,∠BAD =∠EAG =∠ADC =90°, ∴∠BAE +∠EAD =∠DAG +∠EAD ,∠ADG =90°=∠ABE , ∴∠BAE =∠DAG , 在△ADG 和△ABE 中,ADG ABE DAG BAE AD AB ∠=∠⎧⎪∠=∠⎨⎪=⎩, ∴△ADG ≌△ABE (AAS ). (2)解:∠FCN =45°,理由如下: 作FH ⊥MN 于H ,如图1所示:则∠EHF =90°=∠ABE , ∵∠AEF =∠ABE =90°,∴∠BAE +∠AEB =90°,∠FEH +∠AEB =90°, ∴∠FEH =∠BAE ,在△EFH 和△ABE 中,EHF ABE FEH BAE AE EF ∠=∠⎧⎪∠=∠⎨⎪=⎩, ∴△EFH ≌△ABE (AAS ), ∴FH =BE ,EH =AB =BC , ∴CH =BE =FH , ∵∠FHC =90°, ∴∠FCN =45°.(3)当点E 由B 向C 运动时,∠FCN 的大小总保持不变,理由如下: 作FH ⊥MN 于H ,如图2所示:由已知可得∠EAG =∠BAD =∠AEF =90°,结合(1)(2)得:△EFH ≌△GAD ,△EFH ∽△ABE , ∴EH =AD =BC =8, ∴CH =BE , ∴EH FH FHAB BE CH==; 在Rt △FEH 中,tan ∠FCN =8463FH EH CH AB ===, ∴当点E 由B 向C 运动时,∠FCN 的大小总保持不变,tan ∠FCN =43. 【点睛】本题是四边形综合题目,考查了正方形,矩形的判定及全等三角形的判定方法等知识点的综合运用,其重点是通过证三角形全等或相似来得出线段的相等或成比例.6.如图,在平面直角坐标系xOy 中,抛物线y =﹣14x 2+bx +c 与直线y =12x ﹣3分别交x 轴、y 轴上的B 、C 两点,设该抛物线与x 轴的另一个交点为点A ,顶点为点D ,连接CD 交x 轴于点E .(1)求该抛物线的表达式及点D 的坐标; (2)求∠DCB 的正切值;(3)如果点F 在y 轴上,且∠FBC =∠DBA +∠DCB ,求点F 的坐标.【答案】(1)21y 234x x =-+-,D (4,1);(2)13;(3)点F 坐标为(0,1)或(0,﹣18). 【解析】 【分析】 (1)y =12x ﹣3,令y =0,则x =6,令x =0,则y =﹣3,求出点B 、C 的坐标,将点B 、C 坐标代入抛物线y =﹣14x 2+bx+c ,即可求解; (2)求出则点E (3,0),EH =EB•sin ∠OBC =5,CE =32,则CH =5,即可求解;(3)分点F 在y 轴负半轴和在y 轴正半轴两种情况,分别求解即可. 【详解】 (1)y =12x ﹣3,令y =0,则x =6,令x =0,则y =﹣3, 则点B 、C 的坐标分别为(6,0)、(0,﹣3),则c =﹣3, 将点B 坐标代入抛物线y =﹣14x 2+bx ﹣3得:0=﹣14×36+6b ﹣3,解得:b =2, 故抛物线的表达式为:y =﹣14x 2+2x ﹣3,令y =0,则x =6或2, 即点A (2,0),则点D (4,1); (2)过点E 作EH ⊥BC 交于点H ,C 、D 的坐标分别为:(0,﹣3)、(4,1), 直线CD 的表达式为:y =x ﹣3,则点E (3,0), tan ∠OBC =3162OC OB ==,则sin ∠OBC 5,则EH =EB•sin ∠OBC 5CE=32,则CH=5,则tan∠DCB=13 EHCH=;(3)点A、B、C、D、E的坐标分别为(2,0)、(6,0)、(0,﹣3)、(4,1)、(3,0),则BC=35,∵OE=OC,∴∠AEC=45°,tan∠DBE=164-=12,故:∠DBE=∠OBC,则∠FBC=∠DBA+∠DCB=∠AEC=45°,①当点F在y轴负半轴时,过点F作FG⊥BG交BC的延长线与点G,则∠GFC=∠OBC=α,设:GF=2m,则CG=GFtanα=m,∵∠CBF=45°,∴BG=GF,即:5=2m,解得:m=5CF22GF CG+5=15,故点F(0,﹣18);②当点F在y轴正半轴时,同理可得:点F(0,1);故:点F坐标为(0,1)或(0,﹣18).【点睛】本题考查的是二次函数综合运用,涉及到一次函数、解直角三角形等相关知识,其中(3),确定∠FBC =∠DBA+∠DCB =∠AEC =45°,是本题的突破口.7.已知AB 是⊙O 的直径,弦CD ⊥AB 于H ,过CD 延长线上一点E 作⊙O 的切线交AB 的延长线于F ,切点为G ,连接AG 交CD 于K . (1)如图1,求证:KE =GE ; (2)如图2,连接CABG ,若∠FGB =12∠ACH ,求证:CA ∥FE ; (3)如图3,在(2)的条件下,连接CG 交AB 于点N ,若sin E =35,AK =10,求CN 的长.【答案】(1)证明见解析;(2)△EAD 是等腰三角形.证明见解析;(3201013【解析】 试题分析:(1)连接OG ,则由已知易得∠OGE=∠AHK=90°,由OG=OA 可得∠AGO=∠OAG ,从而可得∠KGE=∠AKH=∠EKG ,这样即可得到KE=GE ;(2)设∠FGB=α,由AB 是直径可得∠AGB=90°,从而可得∠KGE=90°-α,结合GE=KE 可得∠EKG=90°-α,这样在△GKE 中可得∠E=2α,由∠FGB=12∠ACH 可得∠ACH=2α,这样可得∠E=∠ACH ,由此即可得到CA ∥EF ; (3)如下图2,作NP ⊥AC 于P ,由(2)可知∠ACH=∠E ,由此可得sinE=sin ∠ACH=35AH AC =,设AH=3a ,可得AC=5a ,CH=4a ,则tan ∠CAH=43CH AH =,由(2)中结论易得∠CAK=∠EGK=∠EKG=∠AKC ,从而可得CK=AC=5a ,由此可得HK=a ,tan ∠AKH=3AHHK=,10a ,结合10可得a=1,则AC=5;在四边形BGKH 中,由∠BHK=∠BKG=90°,可得∠ABG+∠HKG=180°,结合∠AKH+∠GKG=180°,∠ACG=∠ABG 可得∠ACG=∠AKH , 在Rt △APN 中,由tan ∠CAH=43PN AP=,可设PN=12b ,AP=9b ,由tan ∠ACG=PN CP =tan ∠AKH=3可得CP=4b ,由此可得AC=AP+CP=13b =5,则可得b=513,由此即可在Rt △CPN 中由勾股定理解出CN 的长. 试题解析:(1)如图1,连接OG .∵EF 切⊙O 于G , ∴OG ⊥EF ,∴∠AGO+∠AGE=90°, ∵CD ⊥AB 于H , ∴∠AHD=90°, ∴∠OAG=∠AKH=90°, ∵OA=OG , ∴∠AGO=∠OAG , ∴∠AGE=∠AKH , ∵∠EKG=∠AKH , ∴∠EKG=∠AGE , ∴KE=GE . (2)设∠FGB=α, ∵AB 是直径, ∴∠AGB=90°,∴∠AGE =∠EKG=90°﹣α, ∴∠E=180°﹣∠AGE ﹣∠EKG=2α,∵∠FGB=12∠ACH , ∴∠ACH=2α, ∴∠ACH=∠E , ∴CA ∥FE .(3)作NP ⊥AC 于P . ∵∠ACH=∠E , ∴sin ∠E=sin ∠ACH=35AH AC =,设AH=3a ,AC=5a , 则224AC CH a -=,tan ∠CAH=43CH AH =, ∵CA ∥FE , ∴∠CAK=∠AGE , ∵∠AGE=∠AKH ,∴∠CAK=∠AKH,∴AC=CK=5a,HK=CK﹣CH=4a,tan∠AKH=AHHK =3,AK=2210AH HK a+=,∵AK=10,∴1010a=,∴a=1.AC=5,∵∠BHD=∠AGB=90°,∴∠BHD+∠AGB=180°,在四边形BGKH中,∠BHD+∠HKG+∠AGB+∠ABG=360°,∴∠ABG+∠HKG=180°,∵∠AKH+∠HKG=180°,∴∠AKH=∠ABG,∵∠ACN=∠ABG,∴∠AKH=∠ACN,∴tan∠AKH=tan∠ACN=3,∵NP⊥AC于P,∴∠APN=∠CPN=90°,在Rt△APN中,tan∠CAH=43PNAP=,设PN=12b,则AP=9b,在Rt△CPN中,tan∠ACN=PNCP=3,∴CP=4b,∴AC=AP+CP=13b,∵AC=5,∴13b=5,∴b=513,∴CN=22PN CP+=410b⋅=2010 13.8.如图,AB为⊙O的直径,P是BA延长线上一点,CG是⊙O的弦∠PCA=∠ABC,CG⊥AB,垂足为D(1)求证:PC是⊙O的切线;(2)求证:PA AD PC CD;(3)过点A作AE∥PC交⊙O于点E,交CD于点F,连接BE,若sin∠P=35,CF=5,求BE的长.【答案】(1)见解析;(2)BE=12.【解析】【分析】(1)连接OC,由PC切⊙O于点C,得到OC⊥PC,于是得到∠PCA+∠OCA=90°,由AB为⊙O的直径,得到∠ABC+∠OAC=90°,由于OC=OA,证得∠OCA=∠OAC,于是得到结论;(2)由AE∥PC,得到∠PCA=∠CAF根据垂径定理得到弧AC=弧AG,于是得到∠ACF=∠ABC,由于∠PCA=∠ABC,推出∠ACF=∠CAF,根据等腰三角形的性质得到CF=AF,在R t△AFD中,AF=5,sin∠FAD=35,求得FD=3,AD=4,CD=8,在R t△OCD中,设OC=r,根据勾股定理得到方程r2=(r-4)2+82,解得r=10,得到AB=2r=20,由于AB为⊙O的直径,得到∠AEB=90°,在R t△ABE中,由sin∠EAD=35,得到BEAB=35,于是求得结论.【详解】(1)证明:连接OC,∵PC切⊙O于点C,∴OC⊥PC,∴∠PCO=90°,∴∠PCA+∠OCA=90°,∵AB为⊙O的直径,∴∠ACB=90°,∴∠ABC+∠OAC=90°,∵OC=OA,∴∠OCA=∠OAC,∴∠PCA=∠ABC;(2)解:∵AE∥PC,∴∠PCA=∠CAF,∵AB⊥CG,∴弧AC=弧AG,∴∠ACF=∠ABC,∵∠PCA=∠ABC,∴∠ACF=∠CAF,∴CF=AF,∵CF=5,∴AF=5,∵AE∥PC,∴∠FAD=∠P,∵sin∠P=35,∴sin∠FAD=35,在R t△AFD中,AF=5,sin∠FAD=35,∴FD=3,AD=4,∴CD=8,在R t△OCD中,设OC=r,∴r2=(r﹣4)2+82,∴r=10,∴AB=2r=20,∵AB为⊙O的直径,∴∠AEB=90°,在R t△ABE中,∵sin∠EAD=35,∴35BEAB,∵AB=20,∴BE=12.【点睛】本题考查切线的性质,锐角三角函数,圆周角定理,等腰三角形的性质,解题关键是连接OC构造直角三角形.9.我市在创建全国文明城市的过程中,某社区在甲楼的A处与E处之间悬挂了一副宣传条幅,在乙楼顶部C点测得条幅顶端A点的仰角为45°,条幅底端E点的俯角为30°,若甲、乙两楼之间的水平距离BD为12米,求条幅AE的长度.(结果保留根号)【答案】AE 的长为(123)+ 【解析】 【分析】在Rt ACF 中求AF 的长, 在Rt CEF 中求EF 的长,即可求解. 【详解】过点C 作CF AB ⊥于点F 由题知:四边形CDBF 为矩形12CF DB ∴==在Rt ACF 中,45ACF ∠=︒tan 1AFACF CF∴∠== 12AF ∴=在Rt CEF 中,30ECF ∠=︒ tan EFECF CF∴∠= 3123EF ∴=43EF ∴=1243AE AF EF ∴=+=+∴求得AE 的长为(1243+【点睛】本题考查了三角函数的实际应用,中等难度,作辅助线构造直角三角形是解题关键.10.已知:如图,在Rt △ABO 中,∠B =90°,∠OAB =30°,OA =3.以点O 为原点,斜边OA 所在直线为x 轴,建立平面直角坐标系,以点P (4,0)为圆心,PA 长为半径画圆,⊙P 与x 轴的另一交点为N ,点M 在⊙P 上,且满足∠MPN =60°.⊙P 以每秒1个单位长度的速度沿x 轴向左运动,设运动时间为ts ,解答下列问题: (发现)(1)MN 的长度为多少;(2)当t =2s 时,求扇形MPN (阴影部分)与Rt △ABO 重叠部分的面积.(探究)当⊙P 和△ABO 的边所在的直线相切时,求点P 的坐标.(拓展)当MN 与Rt △ABO 的边有两个交点时,请你直接写出t 的取值范围.【答案】【发现】(1)MN 的长度为π3;(23P 的坐标为10(,);或230)或230();【拓展】t 的取值范围是23t ≤<或45t ≤<,理由见解析.【解析】 【分析】发现:(1)先确定出扇形半径,进而用弧长公式即可得出结论; (2)先求出PA =1,进而求出PQ ,即可用面积公式得出结论; 探究:分圆和直线AB 和直线OB 相切,利用三角函数即可得出结论;拓展:先找出MN 和直角三角形的两边有两个交点时的分界点,即可得出结论. 【详解】 [发现](1)∵P (4,0),∴OP =4. ∵OA =3,∴AP =1,∴MN 的长度为6011803ππ⨯=. 故答案为3π; (2)设⊙P 半径为r ,则有r =4﹣3=1,当t =2时,如图1,点N 与点A 重合,∴PA =r =1,设MP 与AB 相交于点Q .在Rt △ABO 中,∵∠OAB =30°,∠MPN =60°. ∵∠PQA =90°,∴PQ 12=PA 12=,∴AQ =AP ×cos30°3=∴S 重叠部分=S △APQ 12=PQ ×AQ 3= 即重叠部分的面积为38. [探究]①如图2,当⊙P 与直线AB 相切于点C 时,连接PC ,则有PC ⊥AB ,PC =r =1. ∵∠OAB =30°,∴AP =2,∴OP =OA ﹣AP =3﹣2=1; ∴点P 的坐标为(1,0);②如图3,当⊙P 与直线OB 相切于点D 时,连接PD ,则有PD ⊥OB ,PD =r =1,∴PD ∥AB ,∴∠OPD =∠OAB =30°,∴cos ∠OPD PD OP =,∴OP 123303cos ==︒,∴点P 的坐标为(233,0); ③如图4,当⊙P 与直线OB 相切于点E 时,连接PE ,则有PE ⊥OB ,同②可得:OP 233=; ∴点P 的坐标为(233-,0);[拓展]t 的取值范围是2<t ≤3,4≤t <5,理由:如图5,当点N 运动到与点A 重合时,MN 与Rt △ABO 的边有一个公共点,此时t =2; 当t >2,直到⊙P 运动到与AB 相切时,由探究①得:OP =1,∴t 411-==3,MN 与Rt △ABO 的边有两个公共点,∴2<t ≤3.如图6,当⊙P 运动到PM 与OB 重合时,MN 与Rt △ABO 的边有两个公共点,此时t =4; 直到⊙P 运动到点N 与点O 重合时,MN 与Rt △ABO 的边有一个公共点,此时t =5; ∴4≤t <5,即:t 的取值范围是2<t ≤3,4≤t <5.【点睛】本题是圆的综合题,主要考查了弧长公式,切线的性质,锐角三角函数,三角形面积公式,作出图形是解答本题的关键.。
完整word版,(精品)北师版九年级下三角函数复习专题

NM GED CBA北师版九年级下册三角函数复习专题题型一:求三角函数值例1.(直接求)(1)在△ABC 中,∠C =900,AC =BC =1,则tanA 的值是 . (2)在Rt △ABC 中,CD 是斜边AB 上的高线,已知∠ACD 的正弦值是32,则ABAC 的值是 . (3)在Rt △ABC 中,∠C =900,若43tan =A ,则sinA = .例2.(1)△ABC 中,AB =AC =3,BC =2,则cosB = .(2)在△ABC 中,∠B =300,tanC =2,AB =2,则BC 的长是 .例3.(1)某人沿倾斜角为β的斜坡前进100米,则他上升的高度为( )A 、βsin 100米 B 、βsin 100米 C 、βcos 100米 D 、βcos 100米 (2)如下左图,重庆市“旧城改造”中,计划在市内一块如图所示的三角形空地上种植某种草皮,以美化环境。
已知这种草皮每平方米售价a 元,则购买这种草皮至少需要( ) A 、a 3450元 B 、a 3225元 C 、a 3150元 D 、a 3300元变式1.如右图,自动扶梯AB 段的长度为20米,倾斜角A 为α,高度BC 为 米(结果用含α的三角函数表示).例4.(转化求)如图,ABCD 为正方形,E 为BC 上一点,将正方形折叠,使A 点与E 点重合,折痕为MN ,若1tan 3AEN ∠=,DC+CE=10.(1)求△ANE 的面积; (2)求sin ENB ∠的值.0120选择第4题图30m 20m45°30°A C B P 题型二:三角函数计算例1.计算:(1)13tan30--︒; (2)000045tan 60cos 30tan 30sin ⋅++;例2.△ABC 中,∠A 、∠B 均为锐角,且0)3sin 2(3tan 2=-+-A B ,试确定△ABC 的形状。
例3.(1)若α为锐角,化简αα2sin sin 21+-= 。
(完整)初中数学三角函数练习题

(完整)初中数学三角函数练习题初中数学三角函数练题1. 求下列三角函数的值:a) sin 30°b) cos 45°c) tan 60°2. 在直角三角形 ABC 中,∠ACB = 90°,AC = 5 cm,BC = 12 cm。
求 sin A、cos A 和 tan A 的值。
3. 如果 sin x = 0.6,求 x 的值(0° ≤ x ≤ 180°)。
4. 已知 sin y = 0.8,求 cos y 的值(0° ≤ y ≤ 180°)。
5. 在直角三角形 DEF 中,∠E = 30°,EF = 6 cm,DE = 8 cm。
求 sin F、cos F 和 tan F 的值。
6. 如果 cos z = 0.4,求 z 的值(0° ≤ z ≤ 180°)。
7. 已知 cos w = 0.7,求 sin w 的值(0° ≤ w ≤ 180°)。
8. 在直角三角形 GHI 中,∠H = 60°,GH = 9 cm,HI = 3 cm。
求 sin G、cos G 和 tan G 的值。
9. 如果 tan v = 1.5,求 v 的值(0° ≤ v ≤ 180°)。
10. 已知 tan u = 2,求 sin u 的值(0° ≤ u ≤ 180°)。
11. 在直角三角形 ___ 中,∠K = 45°,JK = 6 cm,KL = 6 cm。
求 sin L、cos L 和 tan L 的值。
12. 如果 cot t = 0.75,求 t 的值(0° ≤ t ≤ 180°)。
13. 已知 cot s = 4,求 sin s 的值(0° ≤ s ≤ 180°)。
14. 已知cos α = 0.6,求sin^2 α 和cos^2 α 的值。
初中三角函数专题-推荐下载
83
(D)
3
D. 15
14.某坡面的坡度为 1: 3 ,则坡角是_______度. 4
15.在△ABC 中,∠C=90°,AB=10cm,sinA= ,则 BC 的长为_______cm. 5
16.如图,在高楼前 D 点测得楼顶的仰角为 30 ,向高楼前进 60 米到 C 点,又测得仰角为
45 ,则该高楼的高度大约为
tan A cot(90 A)
cot A tan(90 A)
1
45°
2
2
1
1
2
2
关系
sin A cos B cos A sin B sin 2 A cos2 A 1
tan A cot B cot A tan B tan A 1 (倒数)
cot A
tan A cot A 1
A.82 米
B.163 米
C.52 米
D.12
17.如图,小鸣将测倾器安放在与旗杆 AB 底部相距 6m 的 C 处,量出测倾器的高度
CD=1m,测得旗杆顶端 B 的仰角 =60°,则旗杆 AB 的高度为 .(计算结果保
留根号)
D
30
C
45
( 第
A
B
对全部高中资料试卷电气设备,在安装过程中以及安装结束后进行高中资料试卷调整试验;通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术关,系电通,力1根保过据护管生高线产中0不工资仅艺料可高试以中卷解资配决料置吊试技顶卷术层要是配求指置,机不对组规电在范气进高设行中备继资进电料行保试空护卷载高问与中题带资2负料2,荷试而下卷且高总可中体保资配障料置2试时32卷,3各调需类控要管试在路验最习;大题对限到设度位备内。进来在行确管调保路整机敷使组设其高过在中程正资1常料中工试,况卷要下安加与全强过,看度并25工且52作尽22下可护都能1关可地于以缩管正小路常故高工障中作高资;中料对资试于料卷继试连电卷接保破管护坏口进范处行围理整,高核或中对者资定对料值某试,些卷审异弯核常扁与高度校中固对资定图料盒纸试位,卷置编工.写况保复进护杂行层设自防备动腐与处跨装理接置,地高尤线中其弯资要曲料避半试免径卷错标调误高试高等方中,案资要,料求编试技5写、卷术重电保交要气护底设设装。备备置管4高调、动线中试电作敷资高气,设料中课并技3试资件且、术卷料中拒管试试调绝路包验卷试动敷含方技作设线案术,技槽以来术、及避管系免架统不等启必多动要项方高方案中式;资,对料为整试解套卷决启突高动然中过停语程机文中。电高因气中此课资,件料电中试力管卷高壁电中薄气资、设料接备试口进卷不行保严调护等试装问工置题作调,并试合且技理进术利行,用过要管关求线运电敷行力设高保技中护术资装。料置线试做缆卷到敷技准设术确原指灵则导活:。。在对对分于于线调差盒试动处过保,程护当中装不高置同中高电资中压料资回试料路卷试交技卷叉术调时问试,题技应,术采作是用为指金调发属试电隔人机板员一进,变行需压隔要器开在组处事在理前发;掌生同握内一图部线纸故槽资障内料时,、,强设需电备要回制进路造行须厂外同家部时出电切具源断高高习中中题资资电料料源试试,卷卷线试切缆验除敷报从设告而完与采毕相用,关高要技中进术资行资料检料试查,卷和并主检且要测了保处解护理现装。场置设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况,然后根据规范与规程规定,制定设备调试高中资料试卷方案。
初中三角函数专项练习题及答案(DOC)

初中三角函数专项练习题及答案(DOC)初中三角函数专项练题及答案1、在直角三角形中,各边都扩大2倍,则锐角A的正弦值与余弦值都不变。
2、在Rt△ABC中,∠C=90,BC=4,sinA=5,则AC=3.3、若∠A是锐角,且13sinA-tanA>4,则30<∠A<45.4、若cosA=3,则4sinA+2tanA=11.5、在△ABC中,∠A:∠B:∠C=1:1:2,则a:b:c=1:1:2.6、在Rt△ABC中,∠C=90,则sinA=cosB。
7.已知Rt△ABC中,∠C=90°,AC=2,BC=3,那么正确的是tanB=3/2.8.点(-sin60°,cos60°)关于y轴对称的点的坐标是(-2,2)。
9.每周一学校都要举行庄严的升国旗仪式,让我们感受到了国旗的神圣。
某同学站在离旗杆12米远的地方,当国旗升起到旗杆顶时,他测得视线的仰角为30°。
若这位同学的目高1.6米,则旗杆的高度约为10.3米。
10.___同学从A地沿北偏西60º方向走100m到B地,再从B地向___方向走200m到C地,此时___同学离A地150m。
11、如图1,在高楼前D点测得楼顶的仰角为30,向高楼前进60米到C点,又测得仰角为45,则该高楼的高度大约为82米。
12、一艘轮船由海平面上A地出发向南偏西40º的方向行驶40海里到达B地,再由B地向北偏西10º的方向行驶40海里到达C地,则A、C两地相距约为67.5海里。
1.在三角形Rt△ABC中,∠C=90°,AB=5,AC=3,则sinB=4/5.2.在△ABC中,若BC=2,AB=7,AC=3,则cosA=3/7.3.在△ABC中,AB=2,AC=2,∠B=30°,则∠BAC的度数是120°。
4.如图,如果△APB绕点B按逆时针方向旋转30°后得到△A'P'B,且BP=2,那么PP'的长为2sin15°。
专题6.2 任意角的三角函数(专题训练卷)(解析版)

专题6.2任意角的三角函数(专题训练卷)一、单选题A B .12C .12-D . 【答案】D 【解析】7cos66cos ππ=-=, 故选DA .sin αB .cos αC .sin α-D .tan α【答案】D 【解析】sin()sin tan()tan cos()cos πααπααπαα+-+===+-,故选:D . A .25-B .15-C .15D .25【答案】B 【解析】 由51sin 25πα⎛⎫+= ⎪⎝⎭,得1cos 5α=-.故选B .A .34B .43C .43±D .34±【答案】D【解析】()cos c s 35o παα-=--=,∴3cos 5α=,4sin 5α==±,∴3sin 3cos 32tan 32sin 4cos 2παπααπαα⎛⎫- ⎪-⎛⎫⎝⎭-===± ⎪-⎛⎫⎝⎭- ⎪⎝⎭.故选:D .A .sin()sin παα+=-B .cos()cos ααπ-=-C .cos()sin 2παα+=-D .tan()tan απα--=【答案】D 【解析】 根据诱导公式公式二,有sin()sin παα+=- 公式四,有cos()cos ααπ-=-公式六,有cos()sin 2παα+=-公式二、三,有tan()tan()tan αππαα--=-+=- 故选:D A .2 B .4C .6D .8【答案】B 【解析】 由已知3sin cos 3tan 133145cos sin 5tan 53αααααα--⨯-===---.故选:B .A .35B .35C .45-D .15【答案】B 【解析】由诱导公式可得:()sin πα- sin α= 45=,∴3cos 5α=±, 由,2παπ⎛⎫∈⎪⎝⎭,得 3cos 5α=-.本题选择B 选项. A .3- B .3C .13-D .13【答案】D 【解析】∵()()sin π2cos 3π0θθ-++-=, ∴sin 2cos θθ=-,sin cos 2cos cos 1sin cos 2cos cos 3θθθθθθ+-+==---.故选D :.A .10B C .10-D .10-【答案】D 【解析】3sin cos 0αα+=,3sin cos αα∴=-,22sin cos 1αα+=,22sin 9sin 1αα∴+=,21sin 10α=,29cos 10α=,已知α为第二象限角,cos 0α<,cos 10α∴=-,即sin cos 2παα⎛⎫+==⎪⎝⎭A B C .5-D . 【答案】A 【解析】角α的终边过点()1,2P ,则cosx r α===则sin cos 25παα⎛⎫+==⎪⎝⎭, 故选:AA .BCD .【答案】A 【解析】 由21cossin 4αα-=可得()241sin 4sin 10αα---=,即24sin 4sin 30αα+-=,解得1sin 2α=或3sin 2α=-(舍).,2παπ⎛⎫∈ ⎪⎝⎭,∴56πα=,∴5tan tan 63πα==-. 故选:A. 二、多选题A .90αβ+=B .180αβ+=C .()36090k k Z αβ︒︒+=⋅+∈D .()360k k Z αβ︒+=⋅∈E.()()21180k k Z αβ+=+⋅∈ 【答案】BE假设α、β为0180内的角,如图所示,因为α、β的终边关于y 轴对称,所以180αβ︒+=,所以B 满足条件;结合终边相同的角的概念,可得()()36018021180Z k k k αβ+=⋅+=+⋅∈,所以E 满足条件,ACD 都不满足条件. 故选:BE.A .tan(1)tan1π+=B .()sin()cos tan 360ααα︒-=- C .cos()tan()1sin(2)παπαπα---=-D .若,2πθπ⎛⎫∈⎪⎝⎭,则312sin()sin sin cos 2ππθθθθ⎛⎫-+-=- ⎪⎝⎭【答案】ABD 【解析】由诱导公式易知A 正确;B 正确,()sin()sin cos tan tan 360ααααα︒--==--; C 错误,cos()tan()sin(2)παπαπα----(cos )(tan )1sin ααα--==--;=原式|sin cos |θθ==- ∵,2πθπ⎛⎫∈⎪⎝⎭,∴sin 0,cos 0θθ><, ∴sin θcos θ0,sin cos θθ=-. 故选:ABD.A .()tan π1tan1+=B .()()sin cos tan 360ααα-=-C .()()sin πtan cos πααα-=+D .()()()cos πtan π1sin 2πααα---=-【答案】AB 【解析】利用诱导公式,及sin tan cos ααα=A 选项:tan(1)tan1π+=,故A 正确;B 选项:sin()sin sin cos sin tan(360)tan cos o αααααααα--===--,故B 正确;C 选项:sin()sin tan cos()cos παααπαα-==-+-,故C 不正确;D 选项:sin cos cos()tan()cos (tan )cos 1sin(2)sin sin ααπαπααααπααα⋅----⋅-==-=---,故D 不正确故选:AB A .,2πθπ⎛⎫∈⎪⎝⎭B .3cos 5θ=-C .3tan 4θ=-D .7sin cos 5θθ-=【答案】ABD 【解析】1sin cos 5θθ+=①()221sin cos 5θθ⎛⎫∴+= ⎪⎝⎭即221sin 2sin cos cos 25θθθθ++=242sin cos 25θθ∴=-(0,)θπ∈sin 0θ∴>,cos 0θ<,2πθπ⎛⎫∴∈ ⎪⎝⎭()249sin cos 12sin cos 25θθθθ∴-=-= 7sin cos 5θθ∴-=②①加②得4sin 5θ=①减②得3cos 5θ=-4sin 45tan 3cos 35θθθ∴===--综上可得,正确的有ABD 故选:ABD 三、填空题 【答案】253π【解析】因为扇形的圆心角为23π,半径为5,所以扇形的弧长210533l ππ=⨯=,所以面积11102552233S lrππ==⨯⨯=.故答案为:253π.【答案】4-【解析】依题意31cos23πα⎛⎫+=-⎪⎝⎭,即11sin,sin33αα=-=-,由于,22ππα⎡⎤∈-⎢⎥⎣⎦,sin0α<,所以,02πα⎛⎫∈-⎪⎝⎭,所以cos3α==,所以1sintancos43ααα-===-.故答案为:4-【答案】4 5【解析】∵3 cos()cos5πθθ+=-=-,∴3 cos5θ=,∵sin cos0θθ<,∴4 sin5θ==-,∴4 sin(7)=sin()sin()=sin5θπθππθθ--=---=.故答案为:4 5 .四、双空题【答案】45-43-【解析】因为()3cos 25θπθπ=-<<, 所以32πθπ<<, 所以sin 0θ<,所以4sin 5θ==-. ()sin 4tan tan cos 3θπθθθ-=-=-=-. 故答案为:45-;43-.【答案】3 310【解析】将sin cos sin cos x x x x +-=2左端分子分母同除以cos x ,得tan 12tan 1x x +=-,解得tan 3x =,2222sin cos tan 33sin cos sin cos tan 13110x x x x x x x x ====+++. 故答案为:3;310【答案】38- 83- 【解析】因为1sin cos 2αα+=,所以112sin cos 4αα+=,所以sin cos αα⋅=38-,22sin cos sin cos 18tan cot cos sin sin cos sin cos 3αααααααααααα++=+===-.故答案为:38-;83- 【答案】1225 43- 【解析】1sin cos 5θθ+=,21(sin cos )12sin cos 25θθθθ∴+=+=,即12sin cos 25θθ=-. ()12sin cos sin cos 25θπθθθ∴-=-=;249(sin cos )12sin cos 25θθθθ∴-=-=,()0,θπ∈,sin 0θ∴>,cos 0θ<,即sin cos 0θθ->,7sin cos 5θθ∴-=. 联立1575sin cos sin cos θθθθ⎧+=⎪⎪⎨⎪-=⎪⎩,解得4sin 5θ=,3cos 5θ=-.4tan 3θ∴=-.故答案为1225;43-.五、解答题(1)求tan θ的值; (2)求2sin cos sin 2cos θθθθ-+的值.【答案】(1)34;(2)211.【解析】(1)02πθ<<,4cos 5θ∴===,因此,sin 353tan cos 544θθθ==⋅=; (2)原式2sin cos 31212tan 1142cos cos 42sin 2cos 311tan 2211112cos cos 44θθθθθθθθθθ-⨯--=====⨯=+++. (1)sin 3cos sin cos αααα-+;(2)2sin sin cos 2ααα++.【答案】(1)53-;(2)135. 【解析】 由tan 1tan 1αα=--,解得1tan 2α=. (1)sin 3cos sin cos αααα-+13tan 3521tan 1312αα--===-++; (2)2sin sin cos 2ααα++22222sin sin cos 2(sin cos )sin cos ααααααα+++=+ 2222223sin sin cos 2cos 3tan tan 2sin cos tan 1ααααααααα++++==++22113()2132215()12⨯++==+.(1)化简()f α;(2)已知tan 3α=,求()f α的值.【答案】(1)cos 3sin ()2sin cos f ααααα+=-+;(2)-2. 【解析】 (1)sin()3sin()cos 3sin 2()2sin cos 2cos()cos()2f παπααααπαααπα++--+==-++--; (2)由tan 3α=,可得cos 3sin 13tan 10()22sin cos 12tan 5f ααααααα++====--+--. (1)()()()sin 2cos 23tan 2cos sin 2ππααππαπαα⎛⎫--- ⎪⎝⎭⎛⎫-++ ⎪⎝⎭; (2【答案】(1)tan α;(2)1-【解析】(1)原式=()()()()()sin sin tan cos cos ααααα-⋅-⋅-⋅- tan α= (2cos10sin10sin10cos10o o o o-=- 1=-从①一,②二,③三,④四,这四个选项中选择一个你认为恰当的选项填在上面的横线上,并根据你的选择,解答以下问题:(1)求cos ,tan αα的值; (2)化简求值:3sin()cos()sin 2cos(2020)tan(2020)πααπαπαπα⎛⎫--+ ⎪⎝⎭+-.【答案】(1)答案不唯一,具体见解析(2)1625【解析】 (1)因为3sin 5α=-,所以α为第三象限或第四象限角; 若选③,4sin 3cos ,tan 5cos 4αααα==-==; 若选④,4sin 3cos ,tan 5cos 4αααα====-; (2)原式sin cos (cos )cos tan()ααααα-=-sin cos tan ααα-=-sin cos sin cos αααα=2cos α=2315⎛⎫=-- ⎪⎝⎭1625=. 【答案】详见解析【解析】()22sin sin cos 2sin 2sin cos sin 1tan 1cos ααααααααα++=++ ()2sin cos sin cos sin cos αααααα+=+2sin cos k αα==,()222sin cos sin cos 2sin cos αααααα-=+-12sin cos αα=- 1k =-,当04πα<<时,sin cos αα<,此时sin cos αα-=,当42ππα≤<时,sin cos αα≥,此时sin cos αα-=。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
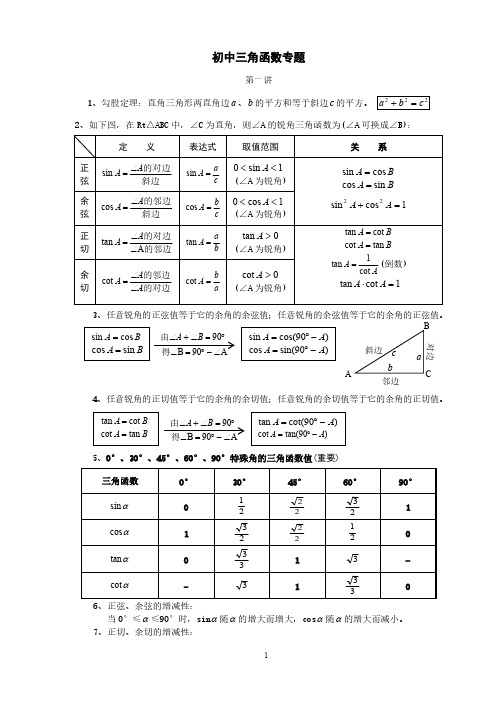
初中三角函数专题第一讲1、勾股定理:直角三角形两直角边、的平方和等于斜边的平方。
a b c 222c b a =+2、如下图,在Rt△ABC 中,∠C 为直角,则∠A 的锐角三角函数为(∠A 可换成∠B):定 义表达式取值范围关 系正弦斜边的对边A A ∠=sin ca A =sin1sin 0<<A (∠A 为锐角)余弦斜边的邻边AA ∠=cos cb A =cos1cos 0<<A (∠A 为锐角)B A cos sin =BA sin cos =1cos sin 22=+A A 正切的邻边的对边A tan ∠∠=A A baA =tan 0tan >A (∠A 为锐角)余切的对边的邻边A A A ∠∠=cot a b A =cot 0cot >A (∠A 为锐角)B A cot tan =B A tan cot =(倒数)AA cot 1tan =1cot tan =⋅A A 3、任意锐角的正弦值等于它的余角的余弦值;任意锐角的余弦值等于它的余角的正弦值。
4、任意锐角的正切值等于它的余角的余切值;任意锐角的余切值等于它的余角的正切值。
5、0°、30°、45°、60°、90°特殊角的三角函数值(重要)三角函数0°30°45°60°90°αsin 02122231αcos 12322210αtan 03313-αcot -313306、正弦、余弦的增减性:当0°≤≤90°时,sin 随的增大而增大,cos 随的增大而减小。
ααααα 7、正切、余切的增减性:对边邻边AC当0°<<90°时,tan 随的增大而增大,cot 随的增大而减小。
ααααα1、解直角三角形的定义:已知边和角(两个,其中必有一边)→所有未知的边和角。
依据:①边的关系:;②角的关系:A+B=90°;③边角关系:三角函数的定222c b a =+义。
(注意:尽量避免使用中间数据和除法)2、应用举例:(1)仰角:视线在水平线上方的角;俯角:视线在水平线下方的角。
仰仰仰:i h l=hlα(2)坡面的铅直高度和水平宽度的比叫做坡度(坡比)。
用字母表示,即。
坡度一般h l i hi l=写成的形式,如等。
1:m 1:5i =把坡面与水平面的夹角记作(叫做坡角),那么。
αtan hi lα==3、从某点的指北方向按顺时针转到目标方向的水平角,叫做方位角。
如图3,OA 、OB 、OC 、OD 的方向角分别是:45°、135°、225°。
4、指北或指南方向线与目标方向 线所成的小于90°的水平角,叫做方向角。
如图4,OA 、OB 、OC 、OD 的方向角分别是:北偏东30°(东北方向) ,南偏东45°(东南方向),南偏西60°(西南方向), 北偏西60°(西北方向)。
第28章 《锐角三角函数》一、选择题1. 4sin tan 5ααα=若为锐角,且,则为 ( )933425543A B C D . . . .2.在Rt△ABC 中,∠C = 90°,下列式子不一定成立的是( )A .sinA = sinB B .cosA=sinBC .sinA=cosBD .∠A+∠B=90°3.直角三角形的两边长分别是6,8,则第三边的长为( )A .10B . C.10或 D .无法确定4.在Rt△ABC 中,∠C=90°,当已知∠A 和a 时,求c ,应选择的关系式是( )A .c =B .c =C .c = a·tanAD .c = sin a A cos a A tan a A5、的值等于()45cos 45sin +A. B.C. D. 12213+36.在Rt△ABC 中,∠C=90°,tan A=3,AC 等于10,则S△ABC 等于( )A. 3B. 300C.D. 155037.当锐角α>30°时,则cosα的值是( )A .大于B .小于CD 12128.小明沿着坡角为30°的坡面向下走了2米,那么他下降( )A .1米B 米C .9.如图,在四边形ABCD 中,∠A=60°,∠B=∠D=90°,BC=2,CD=3,则AB=( )(A )4(B )5 (C )(D 10.已知Rt△ABC 中,∠C=90°,tanA=,BC=8,则AC 等于( 43)A .6B .C .10D .12323二、填空题11.计算2sin30°+2cos60°+3tan45°=_______.12.若sin28°=cosα,则α=________.13.已知△ABC 中,∠C=90°,AB=13,AC=5,则tanA=______.14.某坡面的坡度为1_______度.15.在△ABC 中,∠C =90°,AB =10cm ,sinA =,则BC 的长为_______cm .5416.如图,在高楼前点测得楼顶的仰角为,向高楼前进60米到点,又测得仰角为D 30︒C ,则该高楼的高度大约为45︒A.82米B.163米C.52米D.70米17.如图,小鸣将测倾器安放在与旗杆AB 底部相距6m 的C 处,量出测倾器的高度CD =1m ,测得旗杆顶端B 的仰角=60°,则旗杆AB 的高度为 .(计算结果保α留根号)(16题) (17题)三、解答题18.由下列条件解直角三角形:在Rt△ABC 中,∠C=90°:(1)已知a=4,b=8, (2)已知b=10,∠B=60°.(3)已知c=20,∠A=60°. (4) (2)已知a=5,∠B=35°19.计算下列各题.(1)s in 230°+cos 2sin60°·tan45°; (2)+ sin45°22cos 30cos 60tan 60tan 30︒+︒︒⨯︒四、解下列各题20.如图所示,平地上一棵树高为5米,两次观察地面上的影子, 第一次是当阳光与地面成45°时,第二次是阳光与地面成30°时,第二次观察到的影子比第一次长多少米?21.如图,AB 是江北岸滨江路一段,长为3千米,C 为南岸一渡口, 为了解决两岸交通困难,拟在渡口C 处架桥.经测量得A 在C 北偏西30°方向,B 在C 的东北方向,从C 处连接两岸的最短的桥长多少?(精确到0.1)答案:1.D 2.A 3.C [点拨]长为8的边即可能为直角边,也可能为斜边.4.A [点拨]sinA=,所以c=.acsin a A 5.A 6.D 7.D [点拨]余弦值随着角度的增大而减小,α>30°,,所以.8.A 9.B 10.A [点拨]tanA=,AC==6.BC AC 84tan 3BC A =11.[点拨]原式=2×. 12. 62°1213.[点拨,tanA==.125BC AC 12514. 30° [点拨]坡角α的正切α=30°.=15. 8 16. 82米 17. (6+1)m318.解:(1)=(2)==,c=B b a ABC Rt tan =∆中,在060tan b 3310310=10sin sin60bB===︒∠A=90°-∠B=90°-60°=30°(3)a =,b=c×cos60°=10×=5.∠B=90°-∠A=90°-1260°=30°19.解:(1)原式=()2+)2×1=+12141234(2)原式20.第一次观察到的影子长为5×cot45°=5(米);第二次观察到的影子长为5 ×cot30°.两次观察到的影子长的差是-5米.21.过点C作CD⊥AB于点D.CD就是连接两岸最短的桥.设CD=x米.在直角三角形BCD中,∠BCD=45°,所以BD=CD=x.在直角三角形ACD中,∠ACD=30°,所以x.因为AD+DB=AB,所以,。
