三角函数n倍角公式
三角函数公式及推导公式

任意角直角三角形三角函数))倒数关系:商数关系:平方关系:诱导公式公式一:设为任意角,终边相同的角的同一三角函数的值相等:公式二:设为任意角,与的三角函数值之间的关系:公式三:任意角与的三角函数值之间的关系:公式四:与的三角函数值之间的关系:公式五:与的三角函数值之间的关系:公式六:及与的三角函数值之间的关系:记背诀窍:奇变偶不变,符号看象限.即形如(2k+1)90°±α,则函数名称变为余名函数,正弦变余弦,余弦变正弦,正切变余切,余切变正切。
形如2k×90°±α,则函数名称不变。
诱导公式口诀“奇变偶不变,符号看象限”意义:k×π/2±a(k∈z)的三角函数值.(1)当k为偶数时,等于α的同名三角函数值,前面加上一个把α看作锐角时原三角函数值的符号;(2)当k为奇数时,等于α的异名三角函数值,前面加上一个把α看作锐角时原三角函数值的符号。
记忆方法一:奇变偶不变,符号看象限:记忆方法二:无论α是多大的角,都将α看成锐角.以诱导公式二为例:若将α看成锐角(终边在第一象限),则π十α是第三象限的角(终边在第三象限),正弦函数的函数值在第三象限是负值,余弦函数的函数值在第三象限是负值,正切函数的函数值在第三象限是正值.这样,就得到了诱导公式二.以诱导公式四为例:若将α看成锐角(终边在第一象限),则π-α是第二象限的角(终边在第二象限),正弦函数的三角函数值在第二象限是正值,余弦函数的三角函数值在第二象限是负值,正切函数的三角函数值在第二象限是负值.这样,就得到了诱导公式四.诱导公式的应用:二角和差公式1,过程与tan(α+β)相同.证明正切的和差角公式证明正弦、余弦的和差角公式三角和公式二倍角公式三倍角公式证明:sin3a=sin(a+2a)=sin^2a·cosa+cos^2a·sina=2sina(1-sin^2a)+(1-2sin^2a)sina=3sina-4sin^3acos3a=cos(2a+a)=cos^2acosa-sin^2asina=(2cos^2a-1)cosa-2(1-cos^2a)cosa=4cos^3a-3cosasin3a=3sina-4sin^3a=4sina(3/4-sin^2a)=4sina[(√3/2)-sina][(√3/2)+sina]=4sina(sin60°+sina)(sin60°-sina)=4sina*2sin[(60+a)/2]cos[(60°-a)/2]*2sin[(60°-a)/2]cos[60°+a)/2]=4sinasin(60°+a)sin(60°-a)cos3a=4cos^3a-3cosa=4cosa(cos^2a-3/4)=4cosa[cos^2a-(√3/2)^2]=4cosa(cosa-cos30°)(cosa+cos30°)=4cosa*2cos[(a+30°)/2]cos[(a-30°)/2]*{-2sin[(a+30°)/2]sin[(a-30°)/2]} =-4cosasin(a+30°)sin(a-30°)=-4cosasin[90°-(60°-a)]sin[-90°+(60°+a)]=-4cosacos(60°-a)[-cos(60°+a)]=4cosacos(60°-a)cos(60°+a)上述两式相比可得:tan3a=tana·tan(60°-a)·tan(60°+a)四倍角公式sin4a=-4*[cosa*sina*(2*sina^2-1)]cos4a=1+(-8*cosa^2+8*cosa^4)tan4a=(4*tana-4*tana^3)/(1-6*tana^2+tana^4)五倍角公式n倍角公式应用欧拉公式:.上式用于求n倍角的三角函数时,可变形为:所以,其中,Re表示取实数部分,Im表示取虚数部分.而所以,n倍角的三角函数半角公式(正负由所在的象限决定)万能公式辅助角公式证明:由于,显然,且故有:半径为R.则有:正弦定理变形可得:余弦定理在如图所示的在△ABC中,有余弦定理标准实用文案文档。
最最完整版--三角函数公式大全

三角函数与反三角函数第一部分三角函数公式·两角和与差的三角函数cos(α+β)=cosα·cosβ-sinα·sinβ cos(α-β)=cosα·cosβ+sinα·sinβsin(α±β)=sinα·cosβ±cosα·sinβ tan(α+β)=(tanα+tanβ)/(1-tanα·tanβ) tan(α-β)=(tanα-tanβ)/(1+tanα·tanβ) ctg(A+B)=(ctgActgB-1)/(ctgB+ctgA)ctg(A-B)=(ctgActgB+1)/(ctgB-ctgA)·半角公式:sin(α/2)=±√((1-cosα)/2) cos(α/2)=±√((1+cosα)/2)tan(α/2)=±√((1-cosα)/(1+cosα))=sinα/(1+cosα)=(1-cosα)/sinαcot(α/2)=±√((1+cosα)/(1-cosα))=(1+cosα)/sinα=sinα/(1-cosα)sec(α/2)=±√((2secα/(secα+1)) csc(α/2)=±√((2secα/(secα-1))ctg(A/2)=√((1+cosA)/((1-cosA)) ctg(A/2)=-√((1+cosA)/((1-cosA))·辅助角公式:Asinα+Bcosα=√(A^2+B^2)sin(α+φ)(tanφ=B/A)Asinα+Bcosα=√(A^2+B^2)cos(α-φ)(tanφ=A/B)·万能公式sin(a)= (2tan(a/2))/(1+tan^2(a/2)) cos(a)= (1-tan^2(a/2))/(1+tan^2(a/2))tan(a)= (2tan(a/2))/(1-tan^2(a/2))·降幂公式sin^2α=(1-cos(2α))/2=versin(2α)/2 cos^2α=(1+cos(2α))/2=covers(2α)/2tan^2α=(1-cos(2α))/(1+cos(2α))·三角和的三角函数:sin(α+β+γ)=sinα·cosβ·cosγ+cosα·sinβ·cosγ+cosα·cosβ·sinγ-sinα·sin β·sinγcos(α+β+γ)=cosα·cosβ·cosγ-cosα·sinβ·sinγ-sinα·cosβ·sinγ-sinα·sin β·cosγtan(α+β+γ)=(tanα+tanβ+tanγ-tanα·tanβ·tanγ)/(1-tanα·tanβ-tanβ·tanγ-tanγ·tanα)·和差化积公式:sinα+sinβ=2sin[(α+β)/2]cos[(α-β)/2] sinα-sinβ=2cos[(α+β)/2]sin[(α-β)/2] cosα+cosβ=2cos[(α+β)/2]cos[(α-β)/2] cosα-cosβ=-2sin[(α+β)/2]sin[(α-β)/2] tanA+tanB=sin(A+B)/cosAcosB tanA-tanB=sin(A-B)/cosAcosBctgA+ctgB=sin(A+B)/sinAsinB -ctgA+ctgB=sin(A+B)/sinAsinB·积化和差公式:sin α·cos β=(1/2)[sin(α+β)+sin(α-β)] cos α·sin β=(1/2)[sin(α+β)-sin(α-β)] cos α·cos β=(1/2)[cos(α+β)+cos(α-β)] sin α·sin β=-(1/2)[cos(α+β)-cos(α-β)] ·倍角公式:sin(2α)=2sin α·cos α=2/(tan α+cot α)cos(2α)=(cos α)^2-(sin α)^2=2(cos α)^2-1=1-2(sin α)^2tan(2α)=2tan α/(1-tan^2α) cot(2α)=(cot^2α-1)/(2cot α) sec(2α)=sec^2α/(1-tan^2α) csc(2α)=1/2*sec α·csc α ·三倍角公式:sin(3α) = 3sin α-4sin^3α = 4sin α·sin(60°+α)sin(60°-α) cos(3α) = 4cos^3α-3cos α = 4cos α·cos(60°+α)cos(60°-α)tan(3α) = (3tan α-tan^3α)/(1-3tan^2α) = tan αtan(π/3+α)tan(π/3-α) cot(3α)=(cot^3α-3cot α)/(3cot^2α-1) ·n 倍角公式:sin(n α)=ncos^(n-1)α·sin α-C(n,3)cos^(n-3)α·sin^3α+C(n,5)cos^(n-5)α·sin^5α-… cos(n α)=cos^n α-C(n,2)cos^(n-2)α·sin^2α+C(n,4)cos^(n-4)α·sin^4α-…·三角和的三角函数:sin(α+β+γ)=sin α·cos β·cos γ+cos α·sin β·cos γ+cos α·cos β·sin γ-sin α·sin β·sin γcos(α+β+γ)=cos α·cos β·cos γ-cos α·sin β·sin γ-sin α·cos β·sin γ-sin α·sin β·cos γtan(α+β+γ)=(tan α+tan β+tan γ-tan α·tan β·tan γ)/(1-tan α·tan β-tan β·tan γ-tan γ·tan α) ·其它公式1+sin(a)=(sin(a/2)+cos(a/2))^2 1-sin(a)=(sin(a/2)-cos(a/2))^ csc(a)=1/sin(a) sec(a)=1/cos(a) ·推导公式tan α+cot α=2/sin2α tan α-cot α=-2cot2α 1+cos2α=2cos^2α 1-cos2α=2sin^2α1+sin(a)=(sin(a/2)+cos(a/2))^2 1-sin(a)=(sin(a/2)-cos(a/2))^2 csc(a)=1/sin(a) sec(a)=1/cos(a) 。
三角函数 三角函数公式表

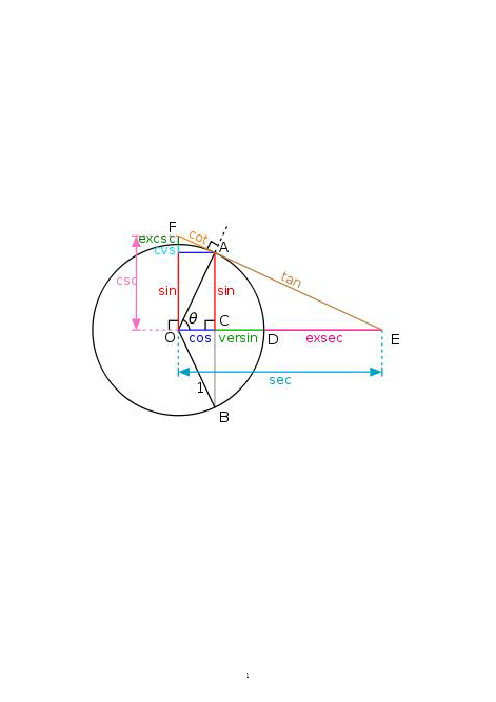
单位圆定义六个三角函数也可以依据半径为1中心为原点的单位圆来定义。
单位圆定义在实际计算上没有大的价值;实际上对多数角它都依赖于直角三角形。
但是单位圆定义的确允许三角函数对所有正数和负数辐角都有定义,而不只是对于在 0 和π/2 弧度之间的角。
它也提供了一个图像,把所有重要的三角函数都包含了。
根据勾股定理,三角函数单位圆的方程是:x^2+y^2=1图像中给出了用弧度度量的一些常见的角。
逆时针方向的度量是正角,而顺时针的度量是负角。
设一个过原点的线,同x轴正半部分得到一个角θ,并与单位圆相交。
这个交点的x和y坐标分别等于 cos θ和 sin θ。
图像中的三角形确保了这个公式;半径等于斜边且长度为1,所以有 sin θ = y/1 和 cos θ = x/1。
单位圆可以被视为是通过改变邻边和对边的长度,但保持斜边等于 1的一种查看无限个三角形的方式。
对于大于 2π或小于等于2π的角度,可直接继续绕单位圆旋转。
在这种方式下,正弦和余弦变成了周期为 2π的周期函数:对于任何角度θ和任何整数k。
周期函数的最小正周期叫做这个函数的“基本周期”。
正弦、余弦、正割或余割的基本周期是全圆,也就是 2π弧度或360°;正切或余切的基本周期是半圆,也就是π弧度或180°。
上面只有正弦和余弦是直接使用单位圆定义的,其他四个三角函数的定义如图所示。
其他四个三角函数的定义在正切函数的图像中,在角kπ附近变化缓慢,而在接近角 (k+ 1/2)π的时候变化迅速。
正切函数的图像在θ = (k + 1/2)π有垂直渐近线。
这是因为在θ从左侧接进 (k + 1/2)π的时候函数接近正无穷,而从右侧接近 (k + 1/2)π的时候函数接近负无穷。
另一方面,所有基本三角函数都可依据中心为O的单位圆来定义,类似于历史上使用的几何定义。
特别三角函数是,对于这个圆的弦AB,这里的θ是对向角的一半,sin θ是AC(半弦),这是印度的阿耶波多介入的定义。
常用的三角函数公式集合

常用的三角函数公式集合第一部分三角函数公式·两角和与差的三角函数cos(α+β)=cosα·cosβ-sinα·sinβcos(α-β)=cosα·cosβ+sinα·sinβsin(α±β)=sinα·cosβ±cosα·sinβtan(α+β)=(tanα+tanβ)/(1-tanα·tanβ)tan(α-β)=(tanα-tanβ)/(1+tanα·tanβ)·和差化积公式:sinα+sinβ=2sin*(α+β)/2+cos*(α-β)/2+sinα-sinβ=2cos*(α+β)/2+sin*(α-β)/2+cosα+cosβ=2cos*(α+β)/2+cos*(α-β)/2+cosα-cosβ=-2sin*(α+β)/2+sin*(α-β)/2+·积化和差公式:sinα·cosβ=(1/2)*sin(α+β)+sin(α-β)+cosα·sinβ=(1/2)*sin(α+β)-sin(α-β)+cosα·cosβ=(1/2)*cos(α+β)+cos(α-β)+sinα·sinβ=-(1/2)*cos(α+β)-cos(α-β)+·倍角公式:s in(2α)=2sinα·cosα=2/(tanα+cotα)cos(2α)=(cosα)^2-(sinα)^2=2(cosα)^2-1=1-2(sinα)^2tan(2α)=2tanα/(1-tan^2α)cot(2α)=(cot^2α-1)/(2cotα)sec(2α)=sec^2α/(1-tan^2α)csc(2α)=1/2*secα·cscα·三倍角公式:sin(3α) = 3sinα-4sin^3α =4sinα·sin(60°+α)sin(60°-α)cos(3α) = 4cos^3α-3cosα =4cosα·cos(60°+α)cos(60°-α)tan(3α) = (3tanα-tan^3α)/(1-3tan^2α) = tanαtan(π/3+α)tan(π/3-α)cot(3α)=(cot^3α-3cotα)/(3cot^2α-1)·n倍角公式:sin(nα)=ncos^(n-1)α·sinα-C(n,3)cos^(n-3)α·sin^3α+C(n,5)cos^(n-5)α·sin^5α-…cos(nα)=cos^nα-C(n,2)cos^(n-2)α·sin^2α+C(n,4)cos^(n-4)α·sin^4α-…·半角公式:sin(α/2)=±√((1-cosα)/2)cos(α/2)=±√((1+cosα)/2)tan(α/2)=±√((1-cosα)/(1+cosα))=sinα/(1+cosα)=(1-cosα)/sinαcot(α/2)=±√((1+cosα)/(1-cosα))=(1+cosα)/sinα=sinα/(1-cosα)sec(α/2)=±√((2secα/(secα+1))csc(α/2)=±√((2secα/(secα-1))·辅助角公式:Asinα+Bcosα=√(A^2+B^2)sin(α+φ)(tanφ=B/A)Asinα+Bcosα=√(A^2+B^2)cos(α-φ)(tanφ=A/B)·万能公式sin(a)=(2tan(a/2))/(1+tan^2(a/2))cos(a)=(1-tan^2(a/2))/(1+tan^2(a/2))tan(a)=(2tan(a/2))/(1-tan^2(a/2))·降幂公式sin^2α=(1-cos(2α))/2=versin(2α)/2cos^2α=(1+cos(2α))/2=covers(2α)/2tan^2α=(1-cos(2α))/(1+cos(2α))·三角和的三角函数:sin(α+β+γ)=sinα·cosβ·cosγ+cosα·sinβ·cosγ+cosα·cosβ·sinγ-sinα·sinβ·sinγcos(α+β+γ)=cosα·cosβ·cosγ-cosα·sinβ·sinγ-sinα·cosβ·sinγ-sinα·sinβ·cosγtan(α+β+γ)=(tanα+tanβ+tanγ-tanα·tanβ·tanγ)/(1-tanα·tanβ-tanβ·tanγ-tanγ·tanα)·其它公式·两角和与差的三角函数cos(α+β)=cosα·cosβ-sinα·sinβcos(α-β)=cosα·cosβ+sinα·sinβsin(α±β)=sinα·cosβ±cosα·sinβtan(α+β)=(tanα+tanβ)/(1-tanα·tanβ)tan(α-β)=(tanα-tanβ)/(1+tanα·tanβ)·和差化积公式:sinα+sinβ=2sin*(α+β)/2+cos*(α-β)/2+sinα-sinβ=2cos*(α+β)/2+sin*(α-β)/2+cosα+cosβ=2cos*(α+β)/2+cos*(α-β)/2+cosα-cosβ=-2sin*(α+β)/2+sin*(α-β)/2+·积化和差公式:sinα·cosβ=(1/2)*sin(α+β)+sin(α-β)+cosα·sinβ=(1/2)*sin(α+β)-sin(α-β)+cosα·cosβ=(1/2)*cos(α+β)+cos(α-β)+sinα·sinβ=-(1/2)*cos(α+β)-cos(α-β)+·倍角公式:sin(2α)=2sinα·cosα=2/(tanα+cotα)cos(2α)=(cosα)^2-(sinα)^2=2(cosα)^2-1=1-2(sinα)^2tan(2α)=2tanα/(1-tan^2α)cot(2α)=(cot^2α-1)/(2cotα)sec(2α)=sec^2α/(1-tan^2α)csc(2α)=1/2*secα·cscα·三倍角公式:sin(3α) = 3sinα-4sin^3α =4sinα·sin(60°+α)sin(60°-α)cos(3α) = 4cos^3α-3cosα =4cosα·cos(60°+α)cos(60°-α)tan(3α) = (3tanα-tan^3α)/(1-3tan^2α) = tanαtan(π/3+α)tan(π/3-α)cot(3α)=(cot^3α-3cotα)/(3cot^2α-1)·n倍角公式:sin(nα)=ncos^(n-1)α·sinα-C(n,3)cos^(n-3)α·sin^3α+C(n,5)cos^(n-5)α·sin^5α-…cos(nα)=cos^nα-C(n,2)cos^(n-2)α·sin^2α+C(n,4)cos^(n-4)α·sin^4α-…·半角公式:sin(α/2)=±√((1-cosα)/2)cos(α/2)=±√((1+cosα)/2)tan(α/2)=±√((1-cosα)/(1+cosα))=sinα/(1+cosα)=(1-cosα)/sinαcot(α/2)=±√((1+cosα)/(1-cosα))=(1+cosα)/sinα=sinα/(1-cosα)sec(α/2)=±√((2secα/(secα+1))csc(α/2)=±√((2secα/(secα-1))·辅助角公式:Asinα+Bcosα=√(A^2+B^2)sin(α+φ)(tanφ=B/A)Asinα+Bcosα=√(A^2+B^2)cos(α-φ)(tanφ=A/B)·万能公式sin(a)=(2tan(a/2))/(1+tan^2(a/2))cos(a)=(1-tan^2(a/2))/(1+tan^2(a/2))tan(a)=(2tan(a/2))/(1-tan^2(a/2))·降幂公式sin^2α=(1-cos(2α))/2=versin(2α)/2cos^2α=(1+cos(2α))/2=covers(2α)/2tan^2α=(1-cos(2α))/(1+cos(2α))·三角和的三角函数:sin(α+β+γ)=sinα·cosβ·cosγ+cosα·sinβ·cosγ+cosα·cosβ·sinγ-sinα·sinβ·sinγcos(α+β+γ)=cosα·cosβ·cosγ-cosα·sinβ·sinγ-sinα·cosβ·sinγ-sinα·sinβ·cosγtan(α+β+γ)=(tanα+tanβ+tanγ-tanα·tanβ·tanγ)/(1-tanα·tanβ-tanβ·tanγ-tanγ·tanα)·其它公式1+sin(a)=(sin(a/2)+cos(a/2))^21-sin(a)=(sin(a/2)-cos(a/2))^2csc(a)=1/sin(a)sec(a)=1/cos(a)cos30=sin60sin30=cos60·推导公式tanα+cotα=2/sin2αtanα-cotα=-2cot2α1+cos2α=2cos^2α1-cos2α=2sin^2α1+sinα=*sin(α/2)+cos(α/2)+^21+sin(a)=(sin(a/2)+cos(a/2))^21-sin(a)=(sin(a/2)-cos(a/2))^2csc(a)=1/sin(a)sec(a)=1/cos(a)cos30=sin60sin30=cos60·推导公式tanα+cotα=2/sin2αtanα-cotα=-2cot2α1+cos2α=2cos^2α1-cos2α=2sin^2α1+sinα=*sin(α/2)+cos(α/2)]^2。
三角函数的倍角公式与半角公式应用

三角函数的倍角公式与半角公式应用三角函数是数学中重要的一部分,广泛应用于科学、工程和金融等领域。
在三角函数的应用中,倍角公式和半角公式是常见且重要的部分。
它们能够帮助我们简化复杂的计算,提高计算的效率和准确性。
本文将介绍三角函数的倍角公式和半角公式,并应用于实际问题中。
一、三角函数的倍角公式倍角公式是指将一个角的两倍用另外一个角的三角函数表达出来的公式。
对于正弦函数、余弦函数和正切函数而言,它们的倍角公式如下:1. 正弦函数的倍角公式:sin(2θ) = 2sinθcosθ2. 余弦函数的倍角公式:cos(2θ) = cos^2θ - sin^2θ = 2cos^2θ - 1 = 1 - 2sin^2θ3. 正切函数的倍角公式:tan(2θ) = 2tanθ / (1 - tan^2θ)倍角公式的应用十分广泛。
例如,在几何图形的计算中,我们可以利用倍角公式简化角的计算,从而简化问题的解决过程。
此外,在信号处理和电路分析中,倍角公式也能够帮助我们分析和处理复杂的信号。
二、三角函数的半角公式半角公式是指将一个角的一半用另外一个角的三角函数表达出来的公式。
与倍角公式类似,正弦函数、余弦函数和正切函数都有对应的半角公式:1. 正弦函数的半角公式:sin(θ/2) = ±√[(1 - cosθ) / 2]2. 余弦函数的半角公式:cos(θ/2) = ±√[(1 + cosθ) / 2]3. 正切函数的半角公式:tan(θ/2) = ±√[(1 - cosθ) / (1 + cosθ)]在实际问题中,半角公式也经常被使用。
例如,在概率论和统计学中,我们可以利用半角公式计算概率密度函数和累积分布函数,从而分析和解决与随机变量相关的问题。
三、三角函数公式的应用举例1. 应用倍角公式的例子:假设有一个直角三角形,已知一个角度θ的正弦函数值为0.6,我们想要计算该角的余弦函数值。
利用倍角公式,我们可以将该问题简化为计算2θ的正弦函数值和余弦函数值。
三角函数大全

三角函数大全1.诱导公式sin(-a) = - sin(a)cos(-a) = cos(a)sin(π/2 - a) = cos(a)cos(π/2 - a) = sin(a)sin(π/2 + a) = cos(a)cos(π/2 + a) = - sin(a)sin(π - a) = sin(a)cos(π - a) = - cos(a)sin(π + a) = - sin(a)cos(π + a) = - cos(a)2.两角和与差的三角函数sin(a + b) = sin(a)cos(b) + cos(α)sin(b)cos(a + b) = cos(a)cos(b) - sin(a)sin(b)sin(a - b) = sin(a)cos(b) - cos(a)sin(b)cos(a - b) = cos(a)cos(b) + sin(a)sin(b)tan(a + b) = [tan(a) + tan(b)] / [1 - tan(a)tan(b)]tan(a - b) = [tan(a) - tan(b)] / [1 + tan(a)tan(b)]3.和差化积公式sin(a) + sin(b) = 2sin[(a + b)/2]cos[(a - b)/2]sin(a) - sin(b) = 2sin[(a - b)/2]cos[(a + b)/2] cos(a) + cos(b) = 2cos[(a + b)/2]cos[(a - b)/2] cos(a) - cos(b) = - 2sin[(a + b)/2]sin[(a - b)/2] 4.积化和差公式sin(a)sin(b) = - 1/2[cos(a + b) - cos(a - b)]cos(a)cos(b) = 1/2[cos(a + b) + cos(a -b)]sin(a)cos(b) = 1/2[sin(a + b) + sin(a - b)]5.二倍角公式sin(2a) = 2sin(a)cos(a)cos 2a = cos2a - sin2a = 2cos2a - 1= 1 - 2sin2a6.半角公式sin2a = (1 – cos 2a)/ 2cos2a = (1 + cos 2a)/ 2tan a = [1 – cos 2a] /sin 2a = sin 2a / [1 + cos 2a ]7.万能公式sin(a) = 2tan(a/2) / [1+tan2(a/2)]cos(a) = [1-tan2(a/2)] / [1+tan2(a/2)]tan(a) = 2tan(a/2) / [1-tan2(a/2)]N倍角公式半角公式两角和公式同角三角函数的基本关系倒数关系:tanα ·cotα=1sinα ·cscα=1cosα·secα=1商的关系:sinα/cosα=tanα=secα/cscα平方关系:平常针对不同条件的常用的两个公式一个特殊公式(sina+sinθ)*(sina-sinθ)=sin(a+θ)*sin(a-θ)证明:(sina+sinθ)*(sina-sinθ)=2 sin[(θ+a)/2] cos[(a-θ)/2] *2cos[(θ+a)/2] sin[(a-θ)/2]=sin(a+θ)*sin(a-θ)坡度公式我们通常把坡面的铅直高度h与水平高度l的比叫做坡度(也叫坡比),用字母i表示,即i=h / l,坡度的一般形式写成l : m形式,如i=1:5.如果把坡面与水平面的夹角记作a(叫做坡角),那么i=h/l=tan a.锐角三角函数公式正弦:sinα=∠α的对边/∠α 的斜边余弦:cosα=∠α的邻边/∠α的斜边正切:tanα=∠α的对边/∠α的邻边余切:cotα=∠α的邻边/∠α的对边二倍角公式正弦sin2A=2sinA·cosA余弦正切tan2A=(2tanA)/(1-tan^2(A))三倍角公式三倍角公式sin3α=4sinα·sin(π/3+α)sin(π/3-α)cos3α=4cosα·cos(π/3+α)cos(π/3-α)tan3a = tan a · tan(π/3+a)· tan(π/3-a)三倍角公式推导sin(3a)=sin(a+2a)=sin2acosa+cos2asina=2sina(1-sina)+(1-2sina)sina=3sina-4sin^3acos3a=cos(2a+a)=cos2acosa-sin2asina=(2cosa-1)cosa-2(1-cos^a)cosa=4cos^3a-3cosasin3a=3sina-4sin^3a=4sina(3/4-sina)=4sina[(√3/2)-sina]=4sina(sin60°-sina)=4sina(sin60°+sina)(sin60°-sina)=4sina*2sin[(60+a)/2]cos[(60°-a)/2]*2sin[(60°-a)/2]cos[(60°-a)/2]=4sinasin(60°+a)sin(60°-a)cos3a=4cos^3a-3cosa=4cosa(cosa-3/4)=4cosa[cosa-(√3/2)^2]=4cosa(cosa-cos30°)=4cosa(cosa+cos30°)(cosa-cos30°)=4cosa*2cos[(a+30°)/2]cos[(a-30°)/2]*{-2sin[(a+30°)/2]sin[(a-30°)/2]}=-4cosasin(a+30°)sin(a-30°)=-4cosasin[90°-(60°-a)]sin[-90°+(60°+a)]=-4cosacos(60°-a)[-cos(60°+a)]=4cosacos(60°-a)cos(60°+a)上述两式相比可得tan3a=tanatan(60°-a)tan(60°+a)现列出公式如下:sin2α=2sinαcosα tan2α=2tanα/(1-tanα )cos2α=cosα-sinα=2cosα-1=1-2sinα可别轻视这些字符,它们在数学学习中会起到重要作用,包括在一些图像问题和函数问题中三倍角公式sin3α=3sinα-4sinα=4sinα·sin(π/3+α)sin(π/3-α)cos3α=4cosα-3cosα=4cosα·cos(π/3+α)cos(π/3-α)tan3α=tan(α)*(-3+tan(α)^2)/(-1+3*tan(α)^2)=tan a · tan(π/3+a)· tan(π/3-a)半角公式sin^2(α/2)=(1-cosα)/2cos^2(α/2)=(1+cosα)/2tan^2(α/2)=(1-cosα)/(1+cosα)tan(α/2)=sinα/(1+cosα)=(1-cosα)/sinα万能公式sinα=2tan(α/2)/[1+tan(α/2)]cosα=[1-tan(α/2)]/[1+tan^2(α/2)]tanα=2tan(α/2)/[1-tan&s(α/2)]其他sinα+sin(α+2π/n)+sin(α+2π*2/n)+sin(α+2π*3/n)+……+sin[α+2π*(n-1)/n]=0cosα+cos(α+2π/n)+cos(α+2π*2/n)+cos(α+2π*3/n)+……+cos[α+2π*(n-1)/n]=0 以及sin^2(α)+sin^2(α-2π/3)+sin^2(α+2π/3)=3/2tanAtanBtan(A+B)+tanA+tanB-tan(A+B)=0四倍角公式sin4A=-4*(cosA*sinA*(2*sinA^2-1))cos4A=1+(-8*cosA^2+8*cosA^4)tan4A=(4*tanA-4*tanA^3)/(1-6*tanA^2+tanA^4)五倍角公式sin5A=16sinA^5-20sinA^3+5sinA cos5A=16cosA^5-20cosA^3+5cosA tan5A=tanA*(5-10*tanA^2+tanA^4)/(1-10*tanA^2+5*tanA^4)六倍角公式sin6A=2*(cosA*sinA*(2*sinA+1)*(2*sinA-1)*(-3+4*sinA^2))cos6A=((-1+2*cosA)*(16*cosA^4-16*cosA^2+1))tan6A=(-6*tanA+20*tanA^3-6*tanA^5)/(-1+15*tanA-15*tanA^4+tanA^6)七倍角公式sin7A=-(sinA*(56*sinA^2-112*sinA^4-7+64*sinA^6))cos7A=(cosA*(56*cosA^2-112*cosA^4+64*cosA^6-7))tan7A=tanA*(-7+35*tanA^2-21*tanA^4+tanA^6)/(-1+21*tanA^2-35*tanA^4+7*tan A^6)八倍角公式sin8A=-8*(cosA*sinA*(2*sinA^2-1)*(-8*sinA^2+8*sinA^4+1)) cos8A=1+(160*cosA^4-256*cosA^6+128*cosA^8-32*cosA^2)tan8A=-8*tanA*(-1+7*tanA^2-7*tanA^4+tanA^6)/(1-28*tanA^2+70*tanA^4-28*tan A^6+tanA^8)九倍角公式sin9A=(sinA*(-3+4*sinA^2)*(64*sinA^6-96*sinA^4+36*sinA^2-3)) cos9A=(cosA*(-3+4*cosA^2)*(64*cosA^6-96*cosA^4+36*cosA^2-3))tan9A=tanA*(9-84*tanA^2+126*tanA^4-36*tanA^6+tanA^8)/(1-36*tanA^2+126*ta nA^4-84*tanA^6+9*tanA^8)十倍角公式sin10A = 2*(cosA*sinA*(4*sinA^2+2*sinA-1)*(4*sinA^2-2*sinA-1)*(-20*sinA^2+5+16*sin A^4))cos10A = ((-1+2*cosA^2)*(256*cosA^8-512*cosA^6+304*cosA^4-48*cosA^2+1))tan10A = -2*tanA*(5-60*tanA^2+126*tanA^4-60*tanA^6+5*tanA^8)/(-1+45*tanA^2-210*tan A^4+210*tanA^6-45*tanA^8+tanA^10)N倍角公式根据棣美弗定理,(cosθ+ i sinθ)^n = cos(nθ)+ i sin(nθ)为方便描述,令sinθ=s,cosθ=c考虑n为正整数的情形:cos(nθ)+ i sin(nθ) = (c+ i s)^n = C(n,0)*c^n + C(n,2)*c^(n-2)*(i s)^2 + C(n,4)*c^(n- 4)*(i s)^4 + ... …+C(n,1)*c^(n-1)*(i s)^1 + C(n,3)*c^(n-3)*(i s)^3 + C(n,5)*c^(n-5)*(i s)^5 + ... …=>比较两边的实部与虚部实部:cos(nθ)=C(n,0)*c^n + C(n,2)*c^(n-2)*(i s)^2 + C(n,4)*c^(n-4)*(i s)^4 + ... …i*(虚部):i*sin(nθ)=C(n,1)*c^(n-1)*(i s)^1 + C(n,3)*c^(n-3)*(i s)^3 + C(n,5)*c^(n-5)*(i s)^5 + ... …对所有的自然数n:1. cos(nθ):公式中出现的s都是偶次方,而s^2=1-c^2(平方关系),因此全部都可以改成以c(也就是cosθ)表示。
三角函数公式大全

Trigonometric1.诱导公式sin(-a) = - sin(a)cos(-a) = cos(a)sin(π/2 - a) = cos(a)cos(π/2 - a) = sin(a)sin(π/2 + a) = cos(a)cos(π/2 + a) = - sin(a)sin(π - a) = sin(a)cos(π - a) = - cos(a)sin(π + a) = - sin(a)cos(π + a) = - cos(a)2.两角和与差的三角函数sin(a + b) = sin(a)cos(b) + cos(α)sin(b)cos(a + b) = cos(a)cos(b) - sin(a)sin(b)sin(a - b) = sin(a)cos(b) - cos(a)sin(b)cos(a - b) = cos(a)cos(b) + sin(a)sin(b)tan(a + b) = [tan(a) + tan(b)] / [1 - tan(a)tan(b)]tan(a - b) = [tan(a) - tan(b)] / [1 + tan(a)tan(b)]3.和差化积公式sin(a) + sin(b) = 2sin[(a + b)/2]cos[(a - b)/2]sin(a) sin(b) = 2cos[(a + b)/2]sin[(a - b)/2]cos(a) + cos(b) = 2cos[(a + b)/2]cos[(a - b)/2]cos(a) - cos(b) = - 2sin[(a + b)/2]sin[(a - b)/2]4.积化和差公式sin(a)sin(b) = - 1/2[cos(a + b) - cos(a - b)]cos(a)cos(b) = 1/2[cos(a + b) + cos(a -b)]sin(a)cos(b) = 1/2[sin(a + b) + sin(a - b)]5.二倍角公式sin(2a) = 2sin(a)cos(b)cos(2a) = cos2(a) - sin2(a) = 2cos2(a) -1=1 - 2sin2(a)6.半角公式sin2(a/2) = [1 - cos(a)] / 2cos2(a/2) = [1 + cos(a)] / 2tan(a/2) = [1 - cos(a)] /sin(a) = sina / [1 + cos(a)]7.万能公式sin(a) = 2tan(a/2) / [1+tan2(a/2)]cos(a) = [1-tan2(a/2)] / [1+tan2(a/2)]tan(a) = 2tan(a/2) / [1-tan2(a/2)]三角函数公式求助编辑百科名片三角函数是数学中属于初等函数中的超越函数的一类函数。
六种三角函数性质

六种三角函数性质、公式三角函数包括;它包含六种基本函数:、、、、、1-1y=sinx-3π2-5π2-7π27π25π23π2π2-π2-4π-3π-2π4π3π2ππ-πoy x1-1y=cosx-3π2-5π2-7π27π25π23π2π2-π2-4π-3π-2π4π3π2ππ-πoyxy=tanx3π2ππ2-3π2-π-π2oyxy=cotx3π2ππ22π-π-π2oyx.反三角函数:arcsinx arccosxarctanx arccotx函数y=sinx y=cosx y=tanx y=cotx定义域R R {x|x∈R且x≠kπ+2π,k∈Z}{x|x∈R且x≠kπ,k∈Z}值域-1,1x=2kπ+2π时y max=1x=2kπ-2π时y min=-1-1,1x=2kπ时y max=1x=2kπ+π时y min=-1R无最大值无最小值R无最大值无最小值周期性周期为2π周期为2π周期为π周期为π奇偶性奇函数偶函数奇函数奇函数单调性在2kπ-2π,2kπ+2π上都是增函数;在在2kπ-π,2kπ上都是增函数;在2kπ,2kπ+π上都是减函数k∈Z在kπ-2π,kπ+2π内都是增函数k∈Z在kπ,kπ+π内都是减函数k∈Zy=secx的性质:1,{x|x≠π/2+kπ,k∈Z}2,|secx|≥1.即secx≥1或secx≤-1;3y=secx是偶函数,即sec-x=secx.图像对称于y轴;4y=secx是周期函数.周期为2kπk∈Z,且k≠0,最小正周期T=2π.5正割与余弦互为倒数;余割与正弦互为倒数;6正割函数无限趋于直线x=π/2+Kπ;7 正割函数是无界函数;8正割函数的导数:secx′=secx×tarx;9正割函数的不定积分:∫secxdx=ln∣secx+tanx∣+Cy=cscx的性1、定义域:{x|x≠kπ,k∈Z}2、值域:{y|y≤-1或y≥1}3、奇偶性:奇函数4、周期性:最小正周期为2π5、图像:图像渐近线为:x=kπ ,k∈Z 余割函数与正弦函数互为倒数第一部分三角函数公式·两角和与差的三角函数cosα+β=cosα·cosβ-sinα·sinβcosα-β=cosα·cosβ+sinα·sinβsinα±β=sinα·cosβ±cosα·sinβtanα+β=tanα+tanβ/1-tanα·tanβtanα-β=tanα-tanβ/1+tanα·tanβ·和差化积/url公式:sinα+sinβ=2sinα+β/2cosα-β/2sinα-sinβ=2cosα+β/2sinα-β/2cosα+cosβ=2cosα+β/2cosα-β/2cosα-cosβ=-2sinα+β/2sinα-β/2·积化和差/url公式:sinα·cosβ=1/2sinα+β+sinα-βcosα·sinβ=1/2sinα+β-sinα-βcosα·cosβ=1/2cosα+β+cosα-βsinα·sinβ=-1/2cosα+β-cosα-β·倍角公式/url:sin2α=2sinα·cosα=2/tanα+cotαcos2α=cosα^2-sinα^2=2cosα^2-1=1-2sinα^2tan2α=2tanα/1-tan^2αcot2α=cot^2α-1/2cotαsec2α=sec^2α/1-tan^2αcsc2α=1/2secα·cscα·三倍角公式:sin3α = 3sinα-4sin^3α = 4sinα·sin60°+αsin60°-αcos3α = 4cos^3α-3cosα = 4cosα·cos60°+αcos60°-αtan3α = 3tanα-tan^3α/1-3tan^2α = tanαtanπ/3+αtanπ/3-αcot3α=cot^3α-3cotα/3cot^2α-1·n倍角公式:sinnα=ncos^n-1α·sinα-Cn,3cos^n-3α·sin^3α+Cn,5cos^n-5α·sin^5α-…cosnα=cos^nα-Cn,2cos^n-2α·sin^2α+Cn,4cos^n-4α·sin^4α-…·半角公式/url:sinα/2=±√1-cosα/2cosα/2=±√1+cosα/2tanα/2=±√1-cosα/1+cosα=sinα/1+cosα=1-cosα/sinαcotα/2=±√1+cosα/1-cosα=1+cosα/sinα=sinα/1-cosαsecα/2=±√2secα/secα+1cscα/2=±√2secα/secα-1·辅助角公式:Asinα+Bcosα=√A^2+B^2sinα+φtanφ=B/AAsinα+Bcosα=√A^2+B^2cosα-φtanφ=A/B·万能公式sina= 2tana/2/1+tan^2a/2cosa= 1-tan^2a/2/1+tan^2a/2tana= 2tana/2/1-tan^2a/2·降幂公式sin^2α=1-cos2α/2=versin2α/2cos^2α=1+cos2α/2=covers2α/2tan^2α=1-cos2α/1+cos2α·三角和的三角函数:sinα+β+γ=sinα·cosβ·cosγ+cosα·sinβ·cosγ+cosα·cosβ·sinγ-sinα·sinβ·sinγcosα+β+γ=cosα·cosβ·cosγ-cosα·sinβ·sinγ-sinα·cosβ·sinγ-sinα·sinβ·cosγtanα+β+γ=tanα+tanβ+tanγ-tanα·tanβ·tanγ/1-tanα·tanβ-tanβ·tanγ-tanγ·tanα·其它公式·两角和与差的三角函数cosα+β=cosα·cosβ-sinα·sinβcosα-β=cosα·cosβ+sinα·sinβsinα±β=sinα·cosβ±cosα·sinβtanα+β=tanα+tanβ/1-tanα·tanβtanα-β=tanα-tanβ/1+tanα·tanβ=sinα/1-cosα ·和差化积/url公式:sinα+sinβ=2sinα+β/2cosα-β/2sinα-sinβ=2cosα+β/2sinα-β/2cosα+cosβ=2cosα+β/2cosα-β/2cosα-cosβ=-2sinα+β/2sinα-β/2·积化和差/url公式:sinα·cosβ=1/2sinα+β+sinα-βcosα·sinβ=1/2sinα+β-sinα-βcosα·cosβ=1/2cosα+β+cosα-βs inα·sinβ=-1/2cosα+β-cosα-β·倍角公式/url:sin2α=2sinα·cosα=2/tanα+cotαcos2α=cosα^2-sinα^2=2cosα^2-1=1-2sinα^2tan2α=2tanα/1-tan^2αcot2α=cot^2α-1/2cotαsec2α=sec^2α/1-tan^2αcsc2α=1/2secα·cscα·三倍角公式:sin3α = 3sinα-4sin^3α = 4sinα·sin60°+αsin60°-αcos3α = 4cos^3α-3cosα = 4cosα·cos60°+αcos60°-αtan3α = 3tanα-tan^3α/1-3tan^2α = tanαtanπ/3+αtanπ/3-αcot3α=cot^3α-3cotα/3cot^2α-1·n倍角公式:sinnα=ncos^n-1α·sinα-Cn,3cos^n-3α·sin^3α+Cn,5cos^n-5α·sin^5α-…cosnα=cos^nα-Cn,2cos^n-2α·sin^2α+Cn,4cos^n-4α·sin^4α-…·半角公式/url:sinα/2=±√1-cosα/2cosα/2=±√1+cosα/2tanα/2=±√1-cosα/1+cosα=sinα/1+cosα=1-cosα/sinαcotα/2=±√1+cosα/1-cosα=1+cosα/sinαsecα/2=±√2secα/secα+1cscα/2=±√2secα/secα-1·辅助角公式:Asinα+Bcosα=√A^2+B^2sinα+φtanφ=B/AAsinα+Bcosα=√A^2+B^2cosα-φtanφ=A/B·万能公式sina= 2tana/2/1+tan^2a/2cosa= 1-tan^2a/2/1+tan^2a/2tana= 2tana/2/1-tan^2a/2·降幂公式sin^2α=1-cos2α/2=versin2α/2cos^2α=1+cos2α/2=covers2α/2tan^2α=1-cos2α/1+cos2α·三角和的三角函数:sinα+β+γ=sinα·cosβ·cosγ+cosα·sinβ·cosγ+cosα·cosβ·sinγ-sinα·sinβ·sinγcosα+β+γ=cosα·cosβ·cosγ-cosα·sinβ·sinγ-sinα·cosβ·sinγ-sinα·sinβ·cosγtanα+β+γ=tanα+tanβ+tanγ-tanα·tanβ·tanγ/1-tanα·tanβ-tanβ·tanγ-tanγ·tanα·其它公式1+sina=sina/2+cosa/2^2 1-sina=sina/2-cosa/2^2csca=1/sina seca=1/cosacos30=sin60sin30tanα+cotα=2/sin2αtanα-cotα=-2cot21+cos2α=2cos^2α1-cos2α=2sin^2α1+sinα=sinα/2+cosα/2^21+sina=sina/2+cosa/2^2 1-sina=sina/2-cosa/2^2 csca=1/sina seca=1/cosacos30=sin60sin30=cos60·推导公式tanα+cotα=2/sin2αtanα-cotα=-2cot2α1+cos2α=2cos^2α1-cos2α=2sin^2α1+sinα=sinα/2+cosα/2^2。
n倍角三角函数公式的推断及应用

= sin30osin(3 10o)= =
例3,求cos12ocos24ocos48ocos84o的值
解,发现,12o+ 48o= 60o,84o– 24o= 60o
则原式可以化为:
4cos12ocos48ocos72o 4cos24ocos36ocos84o
cos2A = cos2A-sin2A = 2cos2A-1 = 1-2sin2A
sin3A= 3sinA – 4sin3A =4sinA( -sin2A)
= 4sinA(sin60o+sinA)(sin60o-sinA)
=4sinA(2sin cos 2cos sin )
= 4sinAsin(60o+A)sin(60o-A)
n倍角三角函数公式的推导及应用
甘肃省庆城县庆城职专(745199)段凌霄
三角函数是数学中一种常见的关于角度的函数,而倍角公式(包括二倍角、三倍角等)是三角函数中常用的一组公式,通过角A的三角函数值的一些变换关系来表示其二倍角2A的三角函数值,二倍角公式包括正弦二倍角公式、余弦二倍角公式以及正切二倍角公式。二倍角公式均可通过和角公式推出。在现行的数学教材中,也推导了三倍角的正弦函数和余弦函数公式,进而可以求得三倍角的正切函数公式。那么对于任意n倍角三角函数公式该如何推导,它们有怎样的普遍规律和那些变形公式呢,下面将逐步推导并介绍它们的应用。
= 3sinA – 4sin3A
cos3A = cos(2A+A) = cos2AcosA-sin2AsinA = cos3A-3sin2AcosA
= 4cos3A-3cosA
这样的推导过程简单明了,便于记忆,尤其是二倍角公式在解题过程中应用较多,那么对于任意的n倍角其三角函数公式都可以由和角公式推导,这里不再赘述。
三角函数公式(最全)
正弦定理变形可得:
五、其他公式
2、余弦定理
对于如图所示的边长为a、b、c而相应角为α、β、γ的△ABC, 有:
3、降幂公式
sin²α=[1-cos(2α)]/2 cos²α=[1+cos(2α)]/2 tan²α=[1-cos(2α)]/[1+cos(2α)]
4、三角和
sin(α+β+γ)=sinα·cosβ·cosγ+cosα·sinβ·cosγ+ cosα·cosβ·sinγ-sinα·sinβ·sinγ
ln(1+x)=x-x2/2+x3/3-…+(-1)k-1xk/k, x∈(-1,1)
sin x = x-x3/3!+x5/5!-…+(-1)k-1x2k-1/(2k-1)!+…, x∈R
cos x = 1-x2/2!+x4/4!-…+(-1)kx2k/(2k)!+…, x∈R
arcsin x = x + x3/(2*3) + (1*3)x5/(2*4*5) + (1*3*5)x7/(2* 4*6*7)…+(2k+1)!!*x2k+1/(2k!!*(2k+1))+…, x∈(-1,1)(!!表 示双阶乘)
1
一、定义公式
三角函数公式
锐角三角函数 任意角三角函数
正弦(sin) 余弦(cos) 正切(tan或tg) 余切(cot或ctg) 正割(sec) 余割(csc) 正弦(sin) 余弦(cos) 正切(tan或tg) 余切(cot或ctg) 正割(sec) 余割(csc)
1、倒数关系
二、函数关系
三角函数公式大全

倒数关系:tanα ·cotα=1sinα ·cscα=1cosα ·secα=1商的关系:sinα/cosα=tanα=secα/cscαcosα/sinα=cotα=cscα/secα平方关系:sin^2(α)+cos^2(α)=11+tan^2(α)=sec^2(α)1+cot^2(α)=csc^2(α)平常针对不同条件的常用的两个公式sin^2(α)+cos^2(α)=1tan α *cot α=1一个特殊公式(sina+sinθ)*(sina-sinθ)=sin(a+θ)*sin(a-θ)证明:(sina+sinθ)*(sina-sinθ)=2 sin*(θ+a)/2+ cos*(a-θ)/2+ *2 cos*(θ+a)/2+ sin*(a-θ)/2+ =sin(a+θ)*sin(a-θ)坡度公式我们通常半坡面的铅直高度h与水平高度l的比叫做坡度(也叫坡比),用字母i表示,即i=h / l, 坡度的一般形式写成l : m 形式,如i=1:5.如果把坡面与水平面的夹角记作a(叫做坡角),那么i=h/l=tan a.锐角三角函数公式正弦:sin α=∠α的对边/∠α 的斜边余弦:cos α=∠α的邻边/∠α的斜边正切:tan α=∠α的对边/∠α的邻边余切:cot α=∠α的邻边/∠α的对边二倍角公式正弦sin2A=2sinA·cosA余弦1.Cos2a=Cos^2(a)-Sin^2(a)2.Cos2a=1-2Sin^2(a)3.Cos2a=2Cos^2(a)-1即Cos2a=Cos^2(a)-Sin^2(a)=2Cos^2(a)-1=1-2Sin^2(a)正切tan2A=(2tanA)/(1-tan^2(A))三倍角公式sin3α=4sinα·sin(π/3+α)sin(π/3-α)cos3α=4cosα·cos(π/3+α)cos(π/3-α)tan3a = tan a · tan(π/3+a)· tan(π/3-a)三倍角公式推导sin(3a)=sin(a+2a)=sin2acosa+cos2asina=2sina(1-sin²a)+(1-2sin²a)sina=3sina-4sin^3acos3a=cos(2a+a)=cos2acosa-sin2asina=(2cos²a-1)cosa-2(1-cos^a)cosa=4cos^3a-3cosasin3a=3sina-4sin^3a=4sina(3/4-sin²a)=4sina*(√3/2)²-sin²a]=4sina(sin²60°-sin²a)=4sina(sin60°+sina)(sin60°-sina)=4sina*2sin[(60+a)/2]cos[(60°-a)/2]*2sin[(60°-a)/2]cos[(60°-a)/2]=4sinasin(60°+a)sin(60°-a)cos3a=4cos^3a-3cosa=4cosa(cos²a-3/4)=4cosa[cos²a-(√3/2)^2+=4cosa(cos²a-cos²30°)=4cosa(cosa+cos30°)(cosa-cos30°)=4cosa*2cos[(a+30°)/2]cos[(a-30°)/2]*{-2sin[(a+30°)/2]sin[(a-30°)/2]}=-4cosasin(a+30°)sin(a-30°)=-4cosasin[90°-(60°-a)]sin[-90°+(60°+a)]=-4cosacos(60°-a)[-cos(60°+a)]=4cosacos(60°-a)cos(60°+a)上述两式相比可得tan3a=tanatan(60°-a)tan(60°+a)现列出公式如下: sin2α=2sinαcosα tan2α=2tanα/(1-tan^2(α)) cos2α=cos^2(α)-sin^2(α)=2cos^2(α)-1=1-2sin^2(α) 可别轻视这些字符,它们在数学学习中会起到重要作用。
三角函数公式大全

三角函数公式大全倒数关系:tanα ·cotα=1sinα ·cscα=1cosα ·secα=1商的关系:sinα/cosα=tanα=secα/cscαcosα/sinα=cotα=cscα/secα平方关系:sin2(α)+cos2(α)=11+tan2(α)=sec2(α)1+cot2(α)=csc2(α)平常针对不同条件的常用的两个公式tanα *cotα=1一个特殊公式(sina+sinθ)(sina-sinθ)=sin(a+θ)sin(a-θ)证明:(sina+sinθ)(sina-sinθ)=2 sin[(θ+a)/2] cos[(a-θ)/2] 2 cos[(θ+a)/2] sin[(a-θ)/2]=sin(a+θ)sin(a-θ)坡度公式:我们通常半坡面的铅直高度h与水平高度l的比叫做坡度(也叫坡比),用字母i表示,即 i=h / l, 坡度的一般形式写成 l : m 形式,如i=1:5.如果把坡面与水平面的夹角记作a(叫做坡角),那么 i=h/l=tan a.锐角三角函数公式:正弦:sin α=∠α的对边/∠α 的斜边余弦:cos α=∠α的邻边/∠α的斜边正切:tan α=∠α的对边/∠α的邻边余切:cot α=∠α的邻边/∠α的对边半角公式:sin2(α/2)=(1-cosα)/2cos2(α/2)=(1+cosα)/2tan2(α/2)=(1-cosα)/(1+cosα)tan(α/2)=sinα/(1+cosα)=(1-cosα)/sinα)=0倍角和半角相对而言,两倍角余弦公式的变形可引出半角公式推导过程中可得到一组降次公式,即万能公式:sinα=2tan(α/2)/[1+tan2(α/2)]cosα=[1-tan2(α/2)]/[1+tan2(α/2)]tanα=2tan(α/2)/[1-tan2(α/2)]其他sinα+sin(α+2π/n)+sin(α+2π*2/n)+sin(α+2π*3/n) +……+sin[α+2π*(n-1)/n]=0cosα+cos(α+2π/n)+cos(α+2π*2/n)+cos(α+2π*3/n) +……+cos[α+2π*(n-1)/n]=0以及sin2(α)+sin2(α-2π/3)+sin2(α+2π/3)=3/2 tanAtanBtan(A+B)+tanA+tanB-tan(A+B和差化积:sinθ+sinφ = 2 sin[(θ+φ)/2] cos[(θ-φ)/2]sinθ-sinφ = 2 cos[(θ+φ)/2] sin[(θ-φ)/2]cosθ+cosφ = 2 cos[(θ+φ)/2] cos[(θ-φ)/2]cosθ-cosφ = -2 sin[(θ+φ)/2] sin[(θ-φ)/2] tanA+tanB=sin(A+B)/cosAcosB=tan(A+B)(1-tanAtanB) tanA-tanB=sin(A-B)/cosAcosB=tan(A-B)(1+tanAtanB) 两角和公式:sin(A+B) = sinAcosB+cosAsinBsin(A-B) = sinAcosB-cosAsinBcos(A+B) = cosAcosB-sinAsinBcos(A-B) = cosAcosB+sinAsinBtan(A+B) = (tanA+tanB)/(1-tanAtanB)tan(A-B) = (tanA-tanB)/(1+tanAtanB)cot(A+B) = (cotAcotB-1)/(cotB+cotA)cot(A-B) = (cotAcotB+1)/(cotB-cotA)积化和差:sinαsinβ =-[cos(α+β)-cos(α-β)] /2cosαcosβ = [cos(α+β)+cos(α-β)]/2sinαcosβ = [sin(α+β)+sin(α-β)]/2cosαsinβ = [sin(α+β)-sin(α-β)]/2公式一:设α为任意角,终边相同的角的同一三角函数的值相等:sin(2kπ+α)= sinαcos(2kπ+α)= cosαtan(2kπ+α)= tanαcot(2kπ+α)= cotα公式二:设α为任意角,π+α的三角函数值与α的三角函数值之间的关系:sin(π+α)= -sinαcos(π+α)= -cosαtan(π+α)= tanαcot(π+α)= cotα公式三:任意角α与 -α的三角函数值之间的关系:sin(-α)= -sinαcos(-α)= cosαtan(-α)= -tanαcot(-α)= -cotα公式四:利用公式二和公式三可以得到π-α与α的三角函数值之间的关系:sin(π-α)= sinαcos(π-α)= -cosαtan(π-α)= -tanαcot(π-α)= -cotα公式五:利用公式-和公式三可以得到2π-α与α的三角函数值之间的关系:sin(2π-α)= -sinαcos(2π-α)= cosαtan(2π-α)= -tanαcot(2π-α)= -cotα公式六:π/2±α及3π/2±α与α的三角函数值之间的关系:sin(π/2+α)= cosαcos(π/2+α)= -sinαtan(π/2+α)= -cotαcot(π/2+α)= -tanαsin(π/2-α)= cosαcos(π/2-α)= sinαtan(π/2-α)= cotαcot(π/2-α)= tanαsin(3π/2+α)= -cosαcos(3π/2+α)= sinαtan(3π/2+α)= -cotαcot(3π/2+α)= -tanαsin(3π/2-α)= -cosαcos(3π/2-α)= -sinαtan(3π/2-α)= cotαcot(3π/2-α)= tanα(以上k∈Z)A·sin(ωt+θ)+ B·sin(ωt+φ) =√{(A²+B²+2ABcos(θ-φ)} · sin{ ωt + arcsin[ (A·sinθ+B·sinφ) / √{A2+B2; +2ABcos(θ-φ)} }√表示根号,包括{……}中的内容三角函数的诱导公式(六公式)(4)对于任意非直角三角形,总有tanA+tanB+tanC=tanAtanBtanC证:A+B=π-Ctan(A+B)=tan(π-C)(tanA+tanB)/(1-tanAtanB)=(tanπ-tanC)/(1+tanπtanC)整理可得tanA+tanB+tanC=tanAtanBtanC同样可以得证,当x+y+z=nπ(n∈Z)时,该关系式也成立由tanA+tanB+tanC=tanAtanBtanC可得出以下结论(5)cotAcotB+cotAcotC+cotBcotC=1(6)cot(A/2)+cot(B/2)+cot(C/2)=cot(A/2)cot(B/2)cot(C/2)(7)(cosA) 2;+(cosB) 2+(cosC) 2=1-2cosAcosBcosC(8)(sinA) 2+(sinB) 2+(sinC) 2=2+2cosAcosBcosC其他非重点三角函数:(1)tanA= sinA/cosA(2)csc(a) = 1/sin(a)(3)sec(a) = 1/cos(a)(4)sec2a +csc2α=sec 2α.csc2α二倍角公式:sin2A=2sinA·cosAcos2A=cos2A-sin2A=2cos2A-1=1-2sin2Atan2A=(2tanA)/(1-tan2A)三倍角公式:sin3α=3sinα-4sin3α=4sinα·sin(π/3+α)sin(π/3-α)cos3α=4cos3α-3cosα=4cosα·cos(π/3+α)cos(π/3-α)tan3a =tan(α)(-3+tan2α)/(-1+3tan2α)=tan a · tan(π/3+a)· tan(π/3-a)三倍角公式推导sin(3a)=sin(a+2a)=sin2acosa+cos2asina=2sina(1-sin²a)+(1-2sin²a)sina=3sina-4sin3acos3a=cos(2a+a)=cos2acosa-sin2asina=(2cos²a-1)cosa -2(1-cos2a)cosa=4cos3a-3cosasin3a=3sina-4sin3a=4sina(3/4-sin²a)=4sina[(√3/2)²-sin²a]=4sina(sin²60°-sin²a)=4sina(sin60°+sina )(sin60°-sina)=4sina*2sin[(60+a)/2]cos[(60°-a)/2]*2sin[(60°-a)/2]cos[(60°-a)/2]=4sinasin(60°+a)si n(60°-a)cos3a=4cos3a-3cosa=4cosa(cos²a-3/4)=4cosa[ cos²a-(√3/2) 2]=4cosa(cos²a-cos²30°)=4cosa(cosa+cos30°)(cosa-c os30°)=4cosa2cos[(a+30°)/2]cos[(a-30°)/2] {-2sin[(a+30°)/2]sin[(a-30°)/2]}=-4cosasin(a+30°)sin(a-30°)=-4cosasin[90°-(60°-a)]sin[-90°+(60°+a)]=-4cosacos(60°-a)[-cos(60°+a)]=4cosacos(60°-a)cos(60°+a)上述两式相比可得tan3a=tanatan(60°-a)tan(60°+a)四倍角公式:sin4A=-4 (cosA.sinA(2sin2A-1))cos4A=1+(-8cos2A+8cos4A)tan4A=(4tanA-4tan3A)/(1-6tan2A+tan4A)五倍角公式:sin5A=16sin5A-20sin3A+5sinAcos5A=16cos5A-20cos3A+5cosAtan5A=tanA (5-10tan2A+tan4A)/(1-10tan2A+5tan4A)六倍角公式:sin6A=2(cosAsinA(2sinA+1)(2sinA-1)(-3+4sin2A)cos6A=(-1+2cos2A) 16cos4A-16cos2A+1)tan6A=(-6tanA+20tan3A-6tan5A)/(-1+15tan2A-15tan4A+ta n6A)七倍角公式:sin7A=-sinA(56sin2A-112sin4A-7+64sin6A)cos7A=cosA(56cos2A-112cos4A+64cos6A-7)tan7A=tanA(-7+35tan2A-21tan4A+tan6A)/(-1+21tan2A-35tan4A+7tan6A) 八倍角公式:sin8A=-8(cosAsinA(2sin2A-1)(-8sin2A+8sin4A+1) cos8A=1+(160cos4A-256cos6A+128cos8A-32cos2A)tan8A=-8tanA(-1+7tan2A-7tan4A+tan6A)/(1-28tan2A+70tan4A-28tan6A+t an8A)九倍角公式:sin9A=sinA(-3+4sin2A)(64sin6A-96sin4A+36sin2A-3);cos9A=(cosA(-3+4cos2A)(64cos6A-96cos4A+36cos2A-3); tan9A=tanA(9-84tan2A+126tan4A-36tan6A+tan8A)/(1-36tan2A+126tan4 A-84tan6A+9tan8A)十倍角公式:sin10A=2(cosAsinA(4sin2A+2sinA-1)(4sin2A-2sinA-1)(-20sin2A+5+16sin4A)cos10A=(-1+2cos2A)(256cos8A-512cos6A+304cos4A-48cos2A +1)tan10A=-2tanA(5-60tan2A+126tan4A-60tan6A+5tan8A)/(-1+45tan2A-210ta n4A+210tan6A-45tan8A+tan10A)N倍角公式:根据棣美弗定理,(cosθ+ i sinθ) n = cos(nθ)+ i sin(nθ)为方便描述,令sinθ=s,cosθ=c考虑n为正整数的情形:cos(nθ)+isin(nθ)=(c+is)n=C(n,0)c n+C(n,2)c(n-2)(is)2+C(n,4)c(n-4)(is)4+... +C(n,1)c(n-1)(is)1+(n,3)c(n-3)(is)3+C(n,5)c(n-5)(is)5+...=>比较两边的实部与虚部,实部:cos(nθ)=C(n,0)c n+C(n,2)c(n-2)(is)2+C(n,4)c(n-4)(is)4+... i*(虚部):i*sin(nθ)=C(n,1)c(n-1)(is)1+ C(n,3)c(n-3)(is)3+C(n,5) c(n-5)(is)5+...对所有的自然数n,1. cos(nθ):公式中出现的s都是偶次方,而s2=1-c2(平方关系),因此全部都可以改成以c(也就是cosθ)表示。
三角函数之间的关系公式

三角函数之间的关系公式1. 同角三角函数的基本关系:倒数关系:tanα•cotα=1 sinα•cscα=1 cosα•secα=1商的关系:sinα/cosα=tanα=secα/cscαcosα/sinα=cotα=csc α/secα平方关系:sin^2(α)+cos^2(α)=1 1+tan^2(α)=sec^2(α) 1+cot^2(α)=csc^2(α)平常针对不同条件的常用的两个公式:sin²α+cos²α=1 tan α*cot α=12. 一个特殊公式:(sina+sinθ)*(sina+sinθ)=sin(a+θ)*sin (a-θ)证明:(sina+sinθ)*(sina+sinθ)=2 sin[(θ+a)/2] cos[(a-θ)/2] *2 cos[(θ+a)/2] sin[(a-θ)/2] =sin(a+θ)*sin(a-θ)3. 锐角三角函数公式正弦:sin α=∠α的对边/∠α的斜边余弦:cos α=∠α的邻边/∠α的斜边正切:tan α=∠α的对边/∠α的邻边余切:cot α=∠α的邻边/∠α的对边4. 二倍角公式正弦sin2A=2sinA•cosA余弦1.Cos2a=Cos^2(a)-Sin^2(a) =2Cos^2(a)-1 =1-2Sin^2(a) 2.Cos2a=1-2Sin^2(a)3.Cos2a=2Cos^2(a)-1正切tan2A=(2tanA)/(1-tan^2(A))5. 三倍角公式sin3α=4sinα•sin(π/3+α)sin(π/3-α)cos3α=4cosα•cos(π/3+α)cos(π/3-α)tan3a = tan a •tan(π/3+a)•tan(π/3-a)6. n倍角公式sin(n a)=Rsina sin(a+π/n)……sin(a+(n-1)π/n). 其中R=2^(n-1)7. 半角公式tan(A/2)=(1-cosA)/sinA=sinA/(1+cosA);cot(A/2)=sinA/(1-cosA )=(1+cosA)/sinA.sin^2(a/2)=(1-cos(a))/2;cos^2(a/2)=(1+cos(a))/2 tan(a/2)=(1-cos(a))/sin(a)=sin(a)/(1+cos(a))8. 和差化积sinθ+sinφ= 2 sin[(θ+φ)/2] cos[(θ-φ)/2]sinθ-sinφ= 2 cos[(θ+φ)/2] sin[(θ-φ)/2]cosθ+cosφ= 2 cos[(θ+φ)/2] cos[(θ-φ)/2]cosθ-cosφ=-2sin[(θ+φ)/2]sin[(θ-φ)/2]tanA+tanB=sin(A+B)/cosAcosB=tan(A+B)(1-tanAtanB)tanA-tanB=sin(A-B)/cosAcosB=tan(A-B)(1+tanAtanB)9. 两角和公式cos(α+β)=cosαcosβ-sinαsinβcos(α-β)=cosαcosβ+sinαsinβsin(α+β)=sinαcosβ+cosαsinβsin(α-β)=sinαcosβ-cosαsinβ10. 积化和差sinαsinβ= [cos(α-β)-cos(α+β)] /2cosαcosβ= [cos(α+β)+cos(α-β)]/2sinαcosβ= [sin(α+β)+sin(α-β)]/2cosαsinβ= [sin(α+β)-sin(α-β)]/211. 双曲函数sinh(a) = [e^a-e^(-a)]/2cosh(a) = [e^a+e^(-a)]/2tanh(a) = sin h(a)/cos h(a)公式一:设α为任意角,终边相同的角的同一三角函数的值相等:sin (2kπ+α)= sinαcos(2kπ+α)= cosαtan(2kπ+α)= tan αcot(2kπ+α)= cotα公式二:设α为任意角,π+α的三角函数值与α的三角函数值之间的关系:sin(π+α)= -sinαcos(π+α)= -cosαtan(π+α)= tan αcot(π+α)= cotα公式三:任意角α与-α的三角函数值之间的关系:sin(-α)= -sin αcos(-α)= cosαtan(-α)= -tanαcot(-α)= -cotα公式四:利用公式二和公式三可以得到π-α与α的三角函数值之间的关系:sin(π-α)= sinαcos(π-α)= -cosαtan(π-α)= -tan αcot(π-α)= -cotα公式五:利用公式-和公式三可以得到2π-α与α的三角函数值之间的关系:sin(2π-α)= -sinαcos(2π-α)= cosαtan(2π-α)= -tan αcot(2π-α)= -cotα公式六:π/2±α及3π/2±α与α的三角函数值之间的关系:sin(π/2+α)= cosαcos(π/2+α)= -sinαtan(π/2+α)= -cotαcot (π/2+α)= -tanαsin(π/2-α)= cosαcos(π/2-α)= sinαtan (π/2-α)= cotαcot(π/2-α)= tanαsin(3π/2+α)= -cosαcos (3π/2+α)= sinαtan(3π/2+α)= -cotαcot(3π/2+α)= -tan αsin(3π/2-α)= -cosαcos(3π/2-α)= -sinαtan(3π/2-α)= cotαcot(3π/2-α)= tanα(以上k∈Z) A•sin(ωt+θ)+ B•sin(ωt+φ) = √{(A²+B²+2ABcos(θ-φ)} •sin{ ωt + arcsin[ (A•sinθ+B•sinφ) / √{A^2 +B^2; +2ABcos(θ-φ)} } √表示根号,包括{……}中的内容12. 诱导公式sin(-α) = -sinαcos(-α) = cosαtan (-α)=-tanαsin(π/2-α) = cosαcos(π/2-α) = sinαsin(π/2+α) = cosαcos(π/2+α) = -sinαsin(π-α) = sinαcos(π-α) = -cosαsin(π+α) = -sinαcos(π+α) = -cosαtanA= sinA/cosA tan(π/2+α)=-cotαtan(π/2-α)=cotαtan(π-α)=-tanαtan(π+α)=tanα诱导公式记背诀窍:奇变偶不变,符号看象限13. 万能公式sinα=2tan(α/2)/[1+(tan(α/2))²]cosα=[1-(tan(α/2))²]/[1+(tan(α/2))²]tanα=2tan(α/2)/[1-(tan(α/2))²]14. 其它公式(1) (sinα)²+(cosα)²=1(2)1+(tanα)²=(secα)²(3)1+(cotα)²=(cscα)²证明下面两式,只需将一式,左右同除(sinα)²,第二个除(cosα)²即可.(4)对于任意非直角三角形,总有tanA+tanB+tanC=tanAtanBtanC(5)cotAcotB+cotAcotC+cotBcotC=1(6)cot(A/2)+cot(B/2)+cot(C/2)=cot(A/2)cot(B/2)cot(C/2)(7)(cosA)²+(cosB)²+(cosC)²=1-2cosAcosBcosC(8)(sinA)²+(sinB)²+(sinC)²=2+2cosAcosBcosC其他非重点三角函数csc(a) = 1/sin(a) sec(a) = 1/cos(a)15. 两角和公式sin(A+B) = sinAcosB+cosAsinBsin(A-B) = sinAcosB-cosAsinBcos(A+B) = cosAcosB-sinAsinBcos(A-B) = cosAcosB+sinAsinBtan(A+B) = (tanA+tanB)/(1-tanAtanB) tan(A-B) = (tanA-tanB)/(1+tanAtanB) cot(A+B) = (cotAcotB-1)/(cotB+cotA) cot(A-B) = (cotAcotB+1)/(cotB-cotA)。
三角函数公式大全关系

三角函数公式大全关系:倒数tanα·cotα=1sinα·cscα=1cosα·secα=1商的关系:sinα/cosα=tanα=secα/cscαcosα/sinα=cotα=cscα/secα平方关系:sin^2α+cos^2α=11+tan^2α=sec^2α1+cot^2α=csc^2α平常针对不同条件的常用的两个公式sin^2α+cos^2α=1tanαcotα=1一个特殊公式sina+sinθsina-sinθ=sina+θsina-θ证明:sina+sinθsina-sinθ=2sinθ+a/2cosa-θ/22cosθ+a/2sina-θ/2=sina+θsina-θ坡度公式我们通常半坡面的铅直高度h与水平高度l的比叫做坡度也叫坡比,用字母i表示,a叫做坡角,那么i=h/l=tana.锐角三角函数公式正弦:sinα=∠α的对边/∠α的斜边余弦:cosα=∠α的邻边/∠α的斜边正切:tanα=∠α的对边/∠α的邻边余切:cotα=∠α的邻边/∠α的对边二倍角公式正弦sin2A=2sinA·cosA余弦1.Cos2a=Cos^2a-Sin^2a2.Cos2a=1-2Sin^2a3.Cos2a=2Cos^2a-1即Cos2a=Cos^2a-Sin^2a=2Cos^2a-1=1-2Sin^2a 正切tan2A=2tanA/1-tan^2A三倍角公式sin3α=4sinα·sinπ/3+αsinπ/3-αcos3α=4cosα·cosπ/3+αcosπ/3-αtan3a=tana·tanπ/3+a·tanπ/3-a三倍角公式推导sin3a=sina+2a=2sina1-sin2a+1-2sin2asina=3sina-4sin^3acos3a=cos2a+a=cos2acosa-sin2asina=2cos2a-1cosa-21-cos^acosa=4cos^3a-3cosasin3a=3sina-4sin^3a=4sina3/4-sin2a=4sina√3/22-sin2a=4sinasin260°-sin2a=4sinasin60°+sinasin60°-sina=4sina2sin60+a/2cos60°-a/22sin60°-a/2cos60°-a/2=4sinasin60°+asin60°-acos3a=4cos^3a-3cosa=4cosacos2a-3/4=4cosacos2a-√3/2^2=4cosacos2a-cos230°=4cosacosa+cos30°cosa-cos30°=4cosa2cosa+30°/2cosa-30°/2{-2sina+30°/2sina-30°/2} =-4cosasina+30°sina-30°=-4cosasin90°-60°-asin-90°+60°+a=-4cosacos60°-a-cos60°+a上述两式相比可得tan3a=tanatan60°-atan60°+a现列出公式如下:sin2α=2sinαcosαtan2α=2tanα/1-tan^2αcos2α=cos^2α-sin^2α=2cos^2α-1= 1-2sin^2α可别轻视这些字符,它们在数学学习中会起到重要作用.包括一些图像问题和函数问题中三倍角公式sin3α=3sinα-4sin^3α=4sinα·sinπ/3+αsinπ/3-αcos3α=4cos^3α-3cosα=4cos α·cosπ/3+αcosπ/3-αtan3α=tanα-3+tanα^2/-1+3tanα^2=tana·tanπ/3+a·ta nπ/3-a半角公式sin^2α/2=1-cosα/2cos^2α/2=1+cosα/2tan^2α/2=1-cosα/1+cosαtanα/2=sinα/1 +cosα=1-cosα/sinα万能公式sinα=2tanα/2/1+tan^2α/2cosα=1-tan^2α/2/1+tan^2α/2tanα=2tanα/2/1-tan^2α/2其他sinα+sinα+2π/n+sinα+2π2/n+sinα+2π3/n+……+sinα+2πn-1/n=0cosα+cosα+2π/n+cosα+2π2/n+cosα+2π3/n+……+cosα+2πn-1/n=0以及sin^2α+sin^2α-2π/3+sin^2α+2π/3=3/2tanAtanBtanA+B+tanA+tanB-tanA+B=0四倍角公式sin4A=-4cosAsinA2sinA^2-1cos4A=1+-8cosA^2+8cosA^4tan4A=4tanA-4tanA^3/1-6tanA^2 +tanA^4sin5A=16sinA^5-20sinA^3+5sinAcos5A=16cosA^5-20cosA^3+5cosAtan5A=tanA5-10tanA^2 +tanA^4/1-10tanA^2+5tanA^4六倍角公式sin6A=2cosAsinA2sinA+12sinA-1-3+4sinA^2cos6A=-1+2cosA^216cosA^4-16cosA^2+1tan6 A=-6tanA+20tanA^3-6tanA^5/-1+15tanA^2-15tanA^4+tanA^6七倍角公式sin7A=-sinA56sinA^2-112sinA^4-7+64sinA^6cos7A=cosA56cosA^2-112cosA^4+64cosA^6-7tan7A=tanA-7+35tanA^2-21tanA^4+tanA^6/-1+21tanA^2-35tanA^4+7tanA^6八倍角公式sin8A=-8cosAsinA2sinA^2-1-8sinA^2+8sinA^4+1cos8A=1+160cosA^4-256cosA^6+128cosA ^8-32cosA^2tan8A=-8tanA-1+7tanA^2-7tanA^4+tanA^6/1-28tanA^2+70tanA^4-28tanA^6+ tanA^8九倍角公式sin9A=sinA-3+4sinA^264sinA^6-96sinA^4+36sinA^2-3cos9A=cosA-3+4cosA^264cosA^6-9 6cosA^4+36cosA^2-3tan9A=tanA9-84tanA^2+126tanA^4-36tanA^6+tanA^8/1-36tanA^2+12 6tanA^4-84tanA^6+9tanA^8十倍角公式sin10A=2cosAsinA4sinA^2+2sinA-14sinA^2-2sinA-1-20sinA^2+5+16sinA^4cos10A=-1+2c osA^2256cosA^8-512cosA^6+304cosA^4-48cosA^2+1tan10A=-2tanA5-60tanA^2+126tanA^4 -60tanA^6+5tanA^8/-1+45tanA^2-210tanA^4+210tanA^6-45tanA^8+tanA^10N倍角公式根据棣美弗定理,cosθ+isinθ^n=cosnθ+isinnθ为方便描述,令sinθ=s,cosθ=c 考虑n为正整数的情形:cosnθ+isinnθ=c+is^n=Cn,0c^n+Cn,2c^n-2is^2+Cn,4c^n-4is^4+...+Cn,1c^n-1is^1+Cn ,3c^n-3is^3+Cn,5c^n-5is^5+...=>比较两边的实部与虚部实部:cosnθ=Cn,0c^n+Cn,2c^n-2is^2+Cn,4c^n-4is^4+...i虚部:isinnθ=Cn,1c^n-1is^1+Cn,3c^n-3is^3+Cn,5c^n-5is^5+...对所有的自然数n,1.cosnθ:公式中出现的s都是偶次方,而s^2=1-c^2平方关系,因此全部都可以改成以c也就是cosθ表示.2.sinnθ:1当n是奇数时:公式中出现的c都是偶次方,而c^2=1-s^2平方关系,因此全部都可以改成以s也就是sinθ表示.2当n是偶数时:公式中出现的c都是奇次方,而c^2=1-s^2平方关系,因此即使再怎么换成s,都至少会剩c也就是cosθ的一次方无法消掉.例.c^3=cc^2=c1-s^2,c^5=cc^2^2=c1-s^2^2半角公式tanA/2=1-cosA/sinA=sinA/1+cosA;cotA/2=sinA/1-cosA=1+cosA/sinA.sin^2a/2=1-cosa/2cos^2a/2=1+cosa/2tana/2=1-cosa/sina=sina/1+cosa和差化积sinθ+sinφ=2sinθ+φ/2cosθ-φ/2sinθ-sinφ=2cosθ+φ/2sinθ-φ/2cosθ+cosφ=2cosθ+φ/2cosθ-φ/2cosθ-cosφ=-2sinθ+φ/2sinθ-φ/2tanA+tanB=sinA+B/cosAcosB=tanA+B1-tanAtanBtanA-tanB=sinA-B/cosAcosB=tanA-B1+tanAtanB两角和公式tanα-β=tanα-tanβ/1+tanαtanβcosα+β=cosαcosβ-sinαsinβcosα-β=cosαcosβ+sinαsinβsinα+β=sinαcosβ+cosαsinβsinα-β=sinαcosβ-cosαsinβ积化和差sinαsinβ=-cosα+β-cosα-β/2cosαcosβ=cosα+β+cosα-β/2sinαcosβ=sinα+β+sinα-β/2cosαsinβ=sinα+β-sinα-β/2双曲函数sha=e^a-e^-a/2cha=e^a+e^-a/2tha=sinha/cosha公式一:设α为任意角,终边相同的角的同一三角函数的值相等:sin2kπ+α=sinαcos2kπ+α=cosαtan2kπ+α=tanαcot2kπ+α=cotα公式二:设α为任意角,π+α的三角函数值与α的三角函数值之间的关系:sinπ+α=-sinαtanπ+α=tanαcotπ+α=cotα公式三:任意角α与-α的三角函数值之间的关系:sin-α=-sinαcos-α=cosαtan-α=-tanαcot-α=-cotα公式四:利用公式二和公式三可以得到π-α与α的三角函数值之间的关系:sinπ-α=sinαcosπ-α=-cosαtanπ-α=-tanαcotπ-α=-cotα公式五:利用公式-和公式三可以得到2π-α与α的三角函数值之间的关系:sin2π-α=-sinαcos2π-α=cosαtan2π-α=-tanαcot2π-α=-cotα公式六:π/2±α及3π/2±α与α的三角函数值之间的关系:sinπ/2+α=cosαtanπ/2+α=-cotαcotπ/2+α=-tanαsinπ/2-α=cosαcosπ/2-α=sinαtanπ/2-α=cotαcotπ/2-α=tanαsin3π/2+α=-cosαcos3π/2+α=sinαtan3π/2+α=-cotαcot3π/2+α=-tanαsin3π/2-α=-cosαcos3π/2-α=-sinαtan3π/2-α=cotαcot3π/2-α=tanα以上k∈Z A·sinωt+θ+B·sinωt+φ=√{A2+B2+2ABcosθ-φ}·sin{ωt+arcsinA·sinθ+B·sinφ/√{A^2+B^2;+2ABcosθ-φ}} √表示根号,包括{……}中的内容三角函数的诱导公式六公式公式一sin-α=-sinαcos-α=cosαtan-α=-tanα公式二cosπ/2-α=sinα公式三sinπ/2+α=cosαcosπ/2+α=-sinα公式四sinπ-α=sinαcosπ-α=-cosα公式五sinπ+α=-sinαcosπ+α=-cosα公式六tanA=sinA/cosAtanπ/2+α=-cotαtanπ/2-α=cotαtanπ-α=-tanαtanπ+α=tanα诱导公式记背诀窍:奇变偶不变,符号看象限万能公式sinα=2tanα/2/1+tanα/22cosα=1-tanα/22/1+tanα/22 tanα=2tanα/2/1-tanα/22其它公式1sinα^2+cosα^2=1平方和公式21+tanα^2=secα^2证明下面两式,只需将一式,左右同除sinα^2,第二个除cosα^2即可4对于任意非直角三角形,总有tanA+tanB+tanC=tanAtanBtanC证:A+B=π-CtanA+B=tanπ-CtanA+tanB/1-tanAtanB=tanπ-tanC/1+tanπtanC整理可得tanA+tanB+tanC=tanAtanBtanC得证同样可以得证,当x+y+z=nπn∈Z时,该关系式也成立由tanA+tanB+tanC=tanAtanBtanC可得出以下结论5cotAcotB+cotAcotC+cotBcotC=16cotA/2+cotB/2+cotC/2=cotA/2cotB/2cotC/27cosA^2;+cosB^2+cosC^2=1-2cosAcosBcosC8sinA^2+sinB^2+sinC^2=2+2cosAcosBcosC其他非重点三角函数csca=1/sinaseca=1/cosaseca^2+csca^2=seca^2csca^2幂级数展开式sinx=x-x^3/3+x^5/5-……+-1^k-1x^2k-1/2k-1+…….-∞<x<∞cosx=1-x^2/2+x^4/4-……+-1kx^2k/2k+……-∞<x<∞arcsinx=x+1/2x^3/3+13/24x^5/5+……|x|<1arccosx=π-x+1/2x^3/3+13/24x^5/5+……|x|<1arctanx=x-x^3/3+x^5/5-……x≤1无限公式sinx=x1-x^2/π^21-x^2/4π^21-x^2/9π^2……cosx=1-4x^2/π^21-4x^2/9π^21-4x^2/25π^2……tanx=8x1/π^2-4x^2+1/9π^2-4x^2+1/25π^2-4x^2+……secx=4π1/π^2-4x^2-1/9π^2-4x^2+1/25π^2-4x^2-+……sinxx=cosx/2cosx/4cosx/8……1/4tanπ/4+1/8tanπ/8+1/16tanπ/16+……=1/πarctanx=x-x^3/3+x^5/5-……x≤1和自变量数列求和有关的公式sinx+sin2x+sin3x+……+sinnx=sinnx/2sinn+1x/2/si nx/2cosx+cos2x+cos3x+……+cosnx=cosn+1x/2sinnx/2/sinx/2tann+1x/2=sinx+sin2x+sin3x+…+sinnx/cosx+cos2x+cos3x+……+cosnxsinx+sin3x+sin5x+……+sin2n-1x=sinnx^2/sinxcosx+cos3x+cos5x+……+cos2n-1x=sin2nx/2sinx编辑本段内容规律三角函数看似很多,很复杂,但只要掌握了三角函数的本质及内部规律就会发现三角函数各个公式之间有强大的联系.而掌握三角函数的内部规律及本质也是学好三角函数的关键所在.1.三角函数本质:1 根据右图,有sinθ=y/r;cosθ=x/r;tanθ=y/x;cotθ=x/y.深刻理解了这一点,下面所有的三角公式都可以从这里出发推导出来,比如以推导sinA+B=sinAcosB+cosAsinB为例:推导:首先画单位圆交X轴于C,D,在单位圆上有任意A,B点.角AOD为α,BOD为β,旋转AOB 使OB与OD重合,形成新A'OD.Acosα,sinα,Bcosβ,sinβ,A'cosα-β,sinα-βOA'=OA=OB=OD=1,D1,0∴cosα-β-1^2+sinα-β^2=cosα-cosβ^2+sinα-sinβ^2和差化积及积化和差用还原法结合上面公式可推出换a+b/2与a-b/2单位圆定义单位圆六个三角函数也可以依据半径为一中心为原点的单位圆来定义.单位圆定义在实际计算上没有大的价值;实际上对多数角它都依赖于直角三角形.但是单位圆定义的确允许三角函数对所有正数和负数辐角都有定义,而不只是对于在0和π/2弧度之间的角.它也提供了一个图象,把所有重要的三角函数都包含了.根据勾股定理,单位圆的等式是:图象中给出了用弧度度量的一些常见的角.逆时针方向的度量是正角,而顺时针的度量是负角.设一个过原点的线,同x轴正半部分得到一个角θ,并与单位圆相交.这个交点的x 和y坐标分别等于cosθ和sinθ.图象中的三角形确保了这个公式;半径等于斜边且长度为1,所以有sinθ=y/1和cosθ=x/1.单位圆可以被视为是通过改变邻边和对边的长度,但保持斜边等于1的一种查看无限个三角形的方式.两角和公式sinA+B=sinAcosB+cosAsinB sinA-B=sinAcosB-cosAsinBcosA+B=cosAcosB-sinAsinB cosA-B=cosAcosB+sinAsinBtanA+B=tanA+tanB/1-tanAtanB tanA-B=tanA-tanB/1+tanAtanB cotA+B=cotAcotB-1/cotB+cotA cotA-B=cotAcotB+1/cotB-cotA。
大学用三角函数公式大全

倒数关系:tanα ·cotα=1sinα ·cscα=1cosα ·secα=1商的关系:sinα/cosα=tanα=secα/cscαcosα/sinα=cotα=cscα/secα平方关系:sin^2(α)+cos^2(α)=11+tan^2(α)=sec^2(α)1+cot^2(α)=csc^2(α)平常针对不同条件的常用的两个公式sin^2(α)+cos^2(α)=1tan α *cot α=1一个特殊公式(s ina+sinθ)*(sina-sinθ)=sin(a+θ)*sin(a-θ)证明:(sina+sinθ)*(sina-sinθ)=2 sin[(θ+a)/2] cos[(a-θ)/2] *2 cos[(θ+a)/2] sin[(a-θ)/2]=sin(a+θ)*sin(a-θ)坡度公式我们通常半坡面的铅直高度h与水平高度l的比叫做坡度(也叫坡比),用字母i表示,即 i=h / l, 坡度的一般形式写成 l : m 形式,如i=1:5.如果把坡面与水平面的夹角记作a(叫做坡角),那么 i=h/l=tan a.锐角三角函数公式正弦:sin α=∠α的对边/∠α 的斜边余弦:cos α=∠α的邻边/∠α的斜边正切:tan α=∠α的对边/∠α的邻边余切:cot α=∠α的邻边/∠α的对边二倍角公式正弦sin2A=2sinA·cosA余弦1.Cos2a=Cos^2(a)-Sin^2(a)2.Cos2a=1-2Sin^2(a)3.Cos2a=2Cos^2(a)-1即Cos2a=Cos^2(a)-Sin^2(a)=2Cos^2(a)-1=1-2Sin^2(a)正切tan2A=(2tanA)/(1-tan^2(A))三倍角公式sin3α=4sinα·sin(π/3+α)sin(π/3-α)cos3α=4cosα·cos(π/3+α)cos(π/3-α)tan3a = tan a · tan(π/3+a)· tan(π/3-a)三倍角公式推导sin(3a)=sin(a+2a)=sin2acosa+cos2asina=2sina(1-sin²a)+(1-2sin²a)sina=3sina-4sin^3acos3a=cos(2a+a)=cos2acosa-sin2asina=(2cos²a-1)cosa-2(1-cos^a)cosa=4cos^3a-3cosasin3a=3sina-4sin^3a=4sina(3/4-sin²a)=4sina[(√3/2)²-sin²a]=4sina(sin²60°-sin²a)=4sina(sin60°+sina)(sin60°-sina)=4sina*2sin[(60+a)/2]cos[(60°-a)/2]*2sin[(60°-a)/2]cos[(60°-a)/2] =4sinasin(60°+a)sin(60°-a)cos3a=4cos^3a-3cosa=4cosa(cos²a-3/4)=4cosa[cos²a-(√3/2)^2]=4cosa(cos²a-cos²30°)=4cosa(cosa+cos30°)(cosa-cos30°)=4cosa*2cos[(a+30°)/2]cos[(a-30°)/2]*{-2sin[(a+30°)/2]sin[(a-30°) /2]}=-4cosasin(a+30°)sin(a-30°)=-4cosasin[90°-(60°-a)]sin[-90°+(60°+a)]=-4cosacos(60°-a)[-cos(60°+a)]=4cosacos(60°-a)cos(60°+a)上述两式相比可得tan3a=tanatan(60°-a)tan(60°+a)现列出公式如下: sin2α=2sinαcosα tan2α=2tanα/(1-tan^2(α)) cos2α=cos^2(α)-sin^2(α)=2cos^2(α)-1=1-2sin^2(α) 可别轻视这些字符,它们在数学学习中会起到重要作用。
sin的n次方公式

sin的n次方公式摘要:一、引言二、sin 的n 次方公式推导1.二倍角公式2.三倍角公式3.n 倍角公式三、sin 的n 次方公式应用1.周期性2.角度制与弧度制的转换3.实际问题中的应用四、总结正文:一、引言sin 的n 次方公式是三角函数中的一个重要公式,广泛应用于解决各种数学问题。
本文将介绍sin 的n 次方公式的推导过程及其在实际问题中的应用。
二、sin 的n 次方公式推导为了更好地理解sin 的n 次方公式,我们先从简单的二倍角公式开始推导。
1.二倍角公式根据二倍角公式,我们有:sin(2θ) = 2sinθcosθ接下来,我们尝试推导三倍角公式。
2.三倍角公式根据三倍角公式,我们有:sin(3θ) = 3sinθ - 4sinθ然后,我们可以尝试推导n 倍角公式。
3.n 倍角公式根据n 倍角公式,我们有:sin(nθ) = nsinθ(cosθ)二、sin 的n 次方公式应用1.周期性sin 函数具有周期性,即:sin(θ) = sin(θ + 2kπ) (k 为整数)利用sin 的n 次方公式,我们可以将周期性推广到n 次方。
sin(nθ) = sin(nθ + 2kπ) (k 为整数)2.角度制与弧度制的转换利用sin 的n 次方公式,我们可以轻松地在角度制与弧度制之间进行转换。
例如,将角度制转换为弧度制:sin(nθ) = sin(n * π/180)将弧度制转换为角度制:sin(nθ) = sin(n * 180/π)3.实际问题中的应用sin 的n 次方公式在实际问题中有很多应用,例如在物理学、工程学和计算机科学等领域。
例如,在计算机图形学中,我们可以使用sin 函数生成各种形状的图形。
总结sin 的n 次方公式是三角函数中的一个重要公式,通过推导过程和实际应用,我们可以更好地理解和掌握这个公式。
高中三角函数公式大全

高中三角函数公式大全2009年07月12日 星期日 19:27三角函数公式两角和公式sin(A+B) = sinAcosB+cosAsinBsin(A-B) = sinAcosB-cosAsinBcos(A+B) = cosAcosB-sinAsinBcos(A-B) = cosAcosB+sinAsinB tan(A+B) =tanAtanB -1tanB tanA + tan(A-B) =tanAtanB1tanBtanA +- cot(A+B) =cotAcotB 1-cotAcotB + cot(A-B) =cotA cotB 1cotAcotB -+ 倍角公式 tan2A =A tan 12tanA2-Sin2A=2SinA•CosACos2A = Cos 2A-Sin 2A=2Cos 2A-1=1-2sin 2A三倍角公式sin3A = 3sinA-4(sinA)3cos3A = 4(cosA)3-3cosAtan3a = tana ·tan(3π+a)·tan(3π-a)n 倍角公式sin (n a )=Rsina sin (a+π/n )……sin (a+(n-1)π/n )。
其中R=2^(n-1) 证明:当sin (na )=0时,sina=sin (π/n )或=sin (2π/n )或=sin (3π/n )或=……或=sin 【(n-1)π/n 】 这说明sin (na )=0与{sina-sin (π/n )}*{sina-sin (2π/n )}*{sina-sin (3π/n )}*……*{sina- sin 【(n-1)π/n 】=0是同解方程。
所以sin (na )与{sina-sin (π/n )}*{sina-sin (2π/n )}*{sina-sin (3π/n )}*……*{sina- sin 【(n-1)π/n 】成正比。
而(sina+sinθ)*(sina+sinθ)=sin (a+θ)*sin (a-θ),所以 {sina-sin (π/n )}*{sina-sin (2π/n )}*{sina-sin (3π/n )}*……*{sina- sin 【(n-1π/n 】 与sina sin (a+π/n )……sin (a+(n-1)π/n )成正比(系数与n 有关 ,但与a 无关,记为Rn )。
