四阶带通滤波器

合集下载

滤波器8_滤波器传输零点20120419

South China University of Technology
它们都没有起到作用，所以在=0处有三个传输零点。所以在=∞处有三个传输零点。
（c）在=∞处串联电容短路和并联电感开路，
Research Institute of Antenna & RF Techniques
对于低通滤波器，无穷远处的传输零点决定滤
8.2.1 传输零点运动规则和类型
传输零点运动必须遵守如下三个规则：
South China University of Technology
规则1：在复平面上，所有的传输零点必须
是象对称。
规则2：“扰动”一个电路元件引起的传输
零点的运动路径是连续的，即传输零点不会从一个位置跳跃到一个新的位置。
对于窄带滤波器，低阻带的BF点离通带较远，
所以传输零点在BF点分裂后，有一个零点离通带较近，而另一个则离的很远。
Research Institute of Antenna & RF Techniques
South China University of Technology
在(a)的谐振器1和4之间并联一个电容，就形成
C
L C
零点 s
R
C
R C
零点 s j
1 LC
零点
s
1 RC
Research Institute of Antenna & RF Techniques
South China University of Technology
五阶低通滤波器所示，在=∞上每个电感变成
开路，每个电容变成短路，所以这个五阶低通滤波器有5个=∞的传输零点，它们全部都在无穷处。

滤波器的基础知识2

一．滤波器的基础知识1．滤波器的功能滤波器的功能就是允许某一部分频率的信号顺利的通过，而另外一部分频率的信号则受到较大的抑制，它实质上是一个选频电路。

滤波器中，把信号能够通过的频率范围，称为通频带或通带；反之，信号受到很大衰减或完全被抑制的频率范围称为阻带；通带和阻带之间的分界频率称为截止频率；理想滤波器在通带内的电压增益为常数，在阻带内的电压增益为零；实际滤波器的通带和阻带之间存在一定频率范围的过渡带。

2．滤波器的分类( 1）按所处理的信号分为模拟滤波器和数字滤波器两种。

( 2）按所通过信号的频段分为低通、高通、带通和带阻滤波器四种。

低通滤波器：它允许信号中的低频或直流分量通过，抑制高频分量或干扰和噪声。

高通滤波器：它允许信号中的高频分量通过，抑制低频或直流分量。

带通滤波器：它允许一定频段的信号通过，抑制低于或高于该频段的信号、干扰和噪声。

带阻滤波器：它抑制一定频段内的信号，允许该频段以外的信号通过。

( 3）按所采用的元器件分为无源和有源滤波器两种。

①．无源滤波器：仅由无源元件(R、L 和C)组成的滤波器，它是利用电容和电感元件的电抗随频率的变化而变化的原理构成的。

这类滤波器的优点是：电路比较简单，不需要直流电源供电，可靠性高；缺点是：通带内的信号有能量损耗，负载效应比较明显，使用电感元件时容易引起电磁感应，当电感L较大时滤波器的体积和重量都比较大，在低频域不适用。

②．有源滤波器：由无源元件(一般用R和C)和有源器件(如集成运算放大器）组成。

这类滤波器的优点是：通带内的信号不仅没有能量损耗，而且还可以放大，负载效应不明显，多级相联时相互影响很小，利用级联的简单方法很容易构成高阶滤波器，并且滤波器的体积小、重量轻、不需要磁屏蔽(由于不使用电感元件）；缺点是：通带范围受有源器件(如集成运算放大器）的带宽限制，需要直流电源供电，可靠性不如无源滤波器高，在高压、高频、大功率的场合不适用。

3. 滤波器的主要参数(1）通带增益A0：滤波器通带内的电压放大倍数。

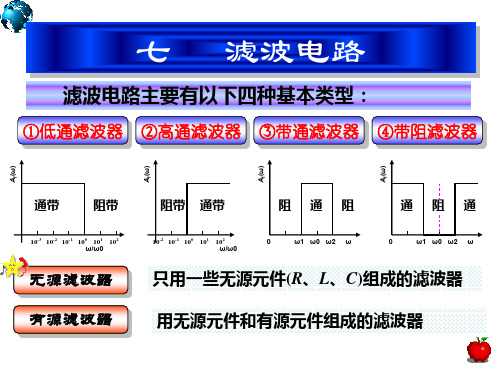
滤波电路主要有以下四种基本类型

rf?uocr1r?ui一阶高通滤波器rf?uocr1rr?uic二阶高通滤波器二阶压控型高通滤波器rf?uocr1rr?uic100100110240db十倍频013db101100101102三带通滤波器带通滤波器只让某一频段的信号通过而将此频段外的信号加以抑制或衰减其理想幅频特性如图
七
①低通滤波器
i
R 1 R jC

1 1 1 jRC

1 0 1 j
1 RC
0
(c)
C
o

U i
R
(b)
U o
它们的截止存在的问题（1）电路的增益小，最大为1 （2）带负载能力差
1 0.707
0
o
(d )

如在无源滤波电路输出端接一负载电阻RL，则其截止频率和增益均随RL而变化。
简单二阶低通滤波电路的幅频特性
由幅频特性可见ω>>ω0时衰减的斜率为－40dB/十倍频。但在 ω0附近，其幅频特性与理想的低通滤波特性相差较大。
0 -3dB
20 lg
Af ( ) / dB Af
-40dB/十倍频
0.1 0.37 1
10
ω/ω0
改进
R

1
R
U
2
f
将电容C1的接地端改接到集成运放的输出端。
o

up
o
A A
up
高通
1

通
1
阻
2
通

o
带阻滤波器电路图
C
C
R
1
R
f
1 o 1 j 2 Q o 2 Rf 1 1 Af 1 Q R1 RC 22 Af

实验十九四阶巴特沃斯滤波器

实验十九四阶巴特沃斯滤波器一、实验目的1．了解巴特沃斯滤波器的频率响应特性。

2．掌握根据频率响应特性求网络传递函数()a H s ，并根据()a H s 来设计滤波器的方法。

二、实验内容1．列写四阶巴特沃斯低通、高通和带通滤波器的网络函数。

2．用示波器观察四阶巴特沃斯滤波器的幅频特性曲线。

3．熟悉四阶巴特沃斯滤波器的设计方法。

三、实验仪器1．信号与系统实验箱一台 2．信号系统实验平台3．四阶巴特沃斯滤波器模块（DYT3000-65）一块 4． 20MHz 双踪示波器一台 5．连接线若干四、实验原理实际的滤波电路往往难以达到理想的要求，如要同时在幅频和相频响应两方面都满足要求就更为困难。

因此，只有根据不同的实际需要，寻求最佳的近似理想特性。

例如，可以主要着眼于幅频响应，而不考虑相频响应；也可以从满足相频响应出发，而把幅频响应居于次要位置。

介绍一种最简单也是最常用的滤波电路——巴特沃斯滤波电路（又叫最平幅度滤波电路）。

这种滤波电路对幅频响应的要求是：在小于截止频率c ω的范围内，具有最平幅度的响应，而在c ωω>后，幅频响应迅速下降。

对于低通滤波电路来说，3dB 截止角频率c H n ωωω==。

n 阶低通滤波电路幅频响应的一般形式()cj A ωω=（式19-1）因为2()cj A ωω是偶次函数，所以c ω的奇次幂会出现。

考虑到在1c ω<时，巴特沃斯低通滤波电路的幅频响应是平坦的。

而在1c ω<时，主要是c ωω的低次项对分母起作用而使()cj A ωω下降。

如果()cj A ωω只与c ωω的高次项有关，则能较好的满足上述条件。

因此式19-1可写成()cj A ωω=（式19-2）这就是巴特沃斯低通滤波电路的特性方程。

由于1c ω=时，增益减小3dB ，由式19-2有2222(1)o o n A A K =+，可得21n K =，因而式19-2变为()cj A ωω=（式19-3）为便于归一化处理，引用归一化复频率S （c c S s j ωω==），这样在式中用s j 代替c ω，则得222()1(1)on nA A s S =+- （式19-4）根据数学关系式2()()C jD C jD C jD +=+-，所以有222()()()1(1)on nS j cA A s A s A s S ωω==-=+- 则()()A s A s -的极点应满足21(1)0nnS +-= （式19-5）由式19-4的根便可以求出滤波电路的网络函数A （S ）。

基于SIW技术的毫米波滤波器研究与设计

基于SIW技术的毫米波滤波器研究与设计杨君豪;孙曼;张金玲【摘要】基于基片集成波导(substrate integrated waveguide,SIW)结构设计了两款四阶的耦合带通滤波器,使用三维全波电磁场仿真软件HFSS对设计的两款滤波器进行了仿真设计和优化.由仿真结果分析得出,两款滤波器的工作频率均位于毫米波频段.第一款SIW滤波器实现了切比雪夫型响应,中心频率为20 GHz,带宽为2 GHz,通带内的插入损耗低于1.5 dB,回波损耗低于-20 dB,在阻带中对信号的衰减程度可以达到50 dB.第二款SIW滤波器实现了准椭圆函数型的响应,中心频率为29.1 GHz,带宽为300 MHz,通带内的插入损耗低于1 dB,回波损耗低于-20 dB,在通带到阻带的过渡中实现了两个陷波点.仿真结果表明,在毫米波滤波器设计中引入SIW结构,有利于优化滤波器尺寸,得到较好的滤波器性能指标,是毫米波滤波器发展的一个重要方向.【期刊名称】《电波科学学报》【年(卷),期】2019(034)004【总页数】6页(P518-523)【关键词】毫米波;带通滤波器;基片集成波导(SIW);切比雪夫响应;准椭圆函数响应;交叉耦合【作者】杨君豪;孙曼;张金玲【作者单位】北京邮电大学,北京100876;中国移动福建分公司,福建362200;北京邮电大学,北京100876;北京邮电大学,北京100876【正文语种】中文【中图分类】TN713引言毫米波无线通信技术是微波无线通信技术向更高频段的延伸,近年来得到了广泛关注与重视,其主要原因有:毫米波对应的频谱资源丰富;毫米波自身的传输特性良好;现代芯片制造工艺的快速发展为毫米波通信设备的制造提供了保障;毫米波通信技术已经成为许多新兴技术的发展需要. 滤波器作为通信系统中重要的组成部分,发挥着对信号频率分割和提取的功能,其性能的优劣直接影响了整个系统的通信质量. 研究小体积、高性能的毫米波滤波器对于实现收发组件单片化,以及促进毫米波技术的发展具有重要意义.基片集成波导(substrate integrated waveguide, SIW)结构是2000年提出的一种新型电路结构,它兼有传统金属波导和微带电路等平面传输线的双重优点[1-3], 其辐射损耗低、功率容量大、易与平面电路集成且抗干扰能力强. 近年来,对SIW 技术的关注度不断增加,相关的技术在微波及毫米波电路领域得到了广泛的应用[4-6]. 基于SIW结构设计的滤波器具备波导滤波器损耗低、Q值高和功率容量大的优点,同时还具备了微带线滤波器尺寸小、易集成的优点. 在滤波器朝着小型化、集成化发展的过程中,电磁兼容、电磁干扰等技术问题也日益突出. 将SIW结构运用到滤波器的设计中是毫米波电路发展的一个重要方向.2003年,文献[7]在绝缘介质基片中加入周期排列的金属通孔,通过四个中心偏置的金属化通孔的直径大小与偏离度控制各谐振腔之间的耦合,实现了三阶的滤波器结构. 这是第一款真正意义上的SIW滤波器.2005年,文献[8]将电磁带隙(electromagnetic band gap, EBG)结构运用到滤波器的设计中,设计出了一款应用周期性EBG结构的SIW滤波器. 该滤波器实现了超宽带特性与结构上的紧凑性,既具备了EBG结构的阻带特性,又保留了SIW结构本身的高通特性. 随后,利用圆形SIW谐振腔进一步实现SIW滤波器的小型化. 圆形SIW谐振腔滤波器的结构特点在于可以通过改变输入首末两端的角度来调节滤波器的品质因数.近年来,频率选择性表面(frequency selective surface, FSS)、互补开口谐振环(complementary split ring resonator, CSRR)和周期排列的十字形缺陷地(defected ground structure, DGS)结构相继被应用到SIW腔体滤波器与SIW矩形谐振滤波器中. 基于FSS设计的SIW滤波器具有单边陡降效应,通过调节腔体尺寸可以实现低频、高频陡降特性的转换,并能通过单元结构合成实现双边的陡降特性;应用耦合开口谐振环技术的SIW滤波器在利用微扰原理实现双模特性的同时,实现了阻带上的传输零点,提高了带外抑制特性;基于周期十字型DGS结构设计的SIW滤波器在提高了高频带外抑制的同时,保持了谐振腔的品质因数. 此外,应用到SIW滤波器的结构还包括共面波导、缺陷地等[9-12].针对毫米波通信系统中对滤波器小型化、高性能的需求,本文对SIW结构在毫米滤波器设计中的应用进行了研究. 对SIW的结构特点、传输特性进行了分析,结合在耦合谐振带通滤波器的设计中常用的耦合矩阵法,设计了两款工作频率位于毫米波频段的带通滤波器. 第一款为直接耦合型SIW滤波器,馈电方式采用微带线——SIW的直接转换结构,滤波器响应形式为传输零点位于无穷远传处的切比雪夫型带通滤波器. 为了进一步实现滤波器小型化、高带外抑制性能的需求,设计了第二款交叉耦合型SIW滤波器,馈电方式采用共面波导——SIW转换结构,进一步缩小了滤波器整体大小,且滤波器响应形式为通带两侧各有一个传输零点的准椭圆函数型带通滤波器,提高了滤波器带外抑制性能. 通过电磁仿真软件分别对两款滤波器进行了仿真,并对仿真结果进行了分析.1 SIW毫米波滤波器的理论分析1.1 SIW的结构特点SIW结构特点在于它将周期排列的金属圆柱或金属通孔嵌入介质基片,以此来达到与矩形金属波导侧壁类似的效果,将电磁波限制在基片上下两个金属面和两排金属通孔间. SIW的结构示意如图1所示. 其中,d表示金属通孔的直径,s表示相邻金属孔间圆心到圆心的距离,h表示基板厚度,l表示两列金属孔之间的距离.图1 SIW结构示意图Fig.1 Configuration schematic of SIW由于金属圆孔之间存在间隔,使得电磁波会在孔间产生泄露,造成了SIW结构特有的漏波特性. 漏波损耗的程度主要由金属通孔的直径d和相邻金属孔的间距s决定. 为了尽量减小漏波损耗,SIW尺寸的一般设计原则有[13]d<0.2λg,s<2d,d<0.2l.(1)由式(1)可以看出,s/d的数值即孔间隙越小,电磁波越难以在孔间发生泄露. 但从实际的角度出发,由于制造工艺有限,过小的孔直径和孔间距无疑会给实际生产带来困难. 因此对于SIW结构来说,选取合适的d值与s值,使得整个结构漏波损耗小且易于加工是相当有必要的. 图2是SIW单个谐振腔模型,两端采用微带线直接过渡型转换结构.图2 SIW单个谐振腔结构Fig.2 Configuration of a single SIW resonator通过对如图2所示的SIW单个谐振腔进行仿真优化,当d取0.5 mm,s取1 mm时,工作在30 GHz的SIW谐振腔实现了与传统矩形波导相似的传输特性. 在d与s值确定的情况下,谐振频率fc主要由两列金属孔之间的距离l决定,计算公式如下:(2)图2的SIW谐振腔的电场分布情况如图3所示.由仿真结果可以看出,通过谐振腔的电磁波被有效地限制在两排金属孔之间,几乎没有在孔间产生漏波损耗.图3 SIW谐振腔电场分布Fig.3 Magnitude of electric field distribution in the SIW cavity at resonance frequency1.2 SIW的转换结构SIW主要由介质基板和金属化通孔构成,虽然它也是一种平面结构,但是在实际电路应用中SIW难以和其他平面电路直接相连,因此SIW滤波器设计中应用了常用平面电路(如微带线)到SIW的转换结构,用来解决SIW连接与测试的问题.SIW与平面电路之间的转换结构一般有如下设计要求[8]:能实现较宽的工作带宽、较小的插入损耗和较简易的加工结构.SIW滤波器常用的五种基本平面电路转换结构如图4所示[14-17]. 其中,(a)为直接过渡结构,适用于SIW的等效阻抗与微带线特性阻抗相同的情况;(b)为凸型过渡结构,在实现SIW与微带结构过渡的同时完成了二者阻抗的匹配;(c)是凹型过渡结构,通过一段共面波导的过渡来完成阻抗匹配;(d)是SIW滤波器设计中最为常见的锥形过渡结构,其结构简单,能起到很好的展宽频段的效果,在实现微带线与SIW的阻抗匹配的同时,又减小反射带来的影响;(e)是共面波导过渡结构,相比于其他过渡结构,该结构最为紧凑,能够在体积更小的滤波器中发挥很好的作用. 其主要由一段共面波导短截线和两条短路槽构成,实现的效果与锥型过渡类似. 在后续设计中分别采用了(a)和(e)的过渡结构.(a) 直接过渡 (b) 凸型过渡 (c) 凹型过渡 (a) Direct (b) Convex (c) Concave transition transition transition(d) 锥型过渡 (e) 共面波导过渡 (d) Cone transition (e) CPW transition图4 SIW 滤波器平面电路转换结构Fig.4 Transitions from planar circuits to SIW filter 2 SIW毫米波带通滤波器的设计与仿真2.1 直接耦合型SIW带通滤波器本节设计了一款直接耦合的SIW带通滤波器,采用直接耦合的形式,工作频率覆盖19～21 GHz,通带内插入损耗小于1.5 dB,回波损耗小于-20 dB,带外抑制特性良好. 具体设计过程如下:根据所需设计的滤波器中心频率和带宽,确定滤波器的截止频率,通过公式(1),由截止频率计算得出滤波器中SIW谐振腔的尺寸. 由于设计中实现的滤波器为耦合谐振器带通滤波器,因此采用耦合矩阵法计算出各谐振腔之间的耦合系数和外部品质因数. 利用电磁仿真软件HFSS建立子工程,通过仿真得到耦合系数和外部品质因数与谐振腔的物理尺寸之间的对应关系,计算得到滤波器各部分的尺寸大小. 建立初步的滤波器整体模型,并设置相关的激励和边界条件. 其中,金属圆柱可以用边界条件为perfect E的圆柱面代替. 对模型进行仿真分析,仿真得到的响应波形与理论上会存在误差,该误差可以通过对整体模型的进一步优化来减小或消除.通过仿真对比得到,在谐振频率处于20 GHz时,谐振腔宽度H=10.5 mm. 根据技术指标要求,确立该滤波器使用的阶数为4阶. 采用耦合系数法,利用Matlab编程计算得出该滤波器的归一化耦合矩阵为(3)通过转换可以得到相邻谐振腔之间的耦合系数,转换公式如下:Mi,j=WFB×mi,j,i≠j.(4)计算得到M1,2=0.083 6,M2,3=0.060 59,M3,4=0.082 36. 滤波器的外部Q值是影响滤波性能的一个重要因素,可以通过式(5)得到:(5)式(4)、(5)中:WFB表示滤波器的相对带宽;M0,1表示输入端口与第一个谐振腔之间的M矩阵耦合系数;M4,5表示输出端口与最后一个谐振腔之间的M矩阵耦合系数,由“N+2”型耦合矩阵的计算方法可以得到. 带入数值后得到品质因数Q1=Q2=17.3.综上计算得到了谐振器之间的相关系数,使用电磁仿真软件HFSS建立该SIW之间耦合带通滤波器的初始模型,通过参数扫描对模型尺寸进行调整,以实现较好的传输特性.直接耦合SIW滤波器平面结构如图5所示. 从图中可以看出,四个由金属板面与金属圆柱组成的四个谐振腔呈横向排列. 第一个和第二个谐振腔通过过渡结构接入源和负载,各谐振腔通过横向的耦合窗口进行能量的传递.整个滤波器平面尺寸为26 mm×15 mm,具体尺寸为:L1=4.0 mm,L2=4.5 mm,W0=4.3 mm,W1=3.2 mm,W2=3.0 mm,H=10.5 mm.图5 直接耦合SIW滤波器平面结构图Fig.5 Top view of the direct coupled SIW filter通过电磁仿真软件HFSS得到的S11、S21仿真曲线如图6所示,因为滤波器采用直接耦合,所实现的响应为切比雪夫型响应. 从仿真结果可以看出,在滤波器通带19～21 GHz的范围内,插入损耗始终小于1.5 dB,回波损耗始终小于-20 dB. 带外抑制特性十分良好,在通带外的17 GHz处,对信号的衰减程度达到了50 dB.图6 直接耦合SIW滤波器S参数仿真曲线Fig.6 Simulated S parameters of the direct coupled SIW filter2.2 交叉耦合型SIW带通滤波器2.1节中所设计的SIW直接耦合带通滤波器,实现的是一般的切比雪夫响应,其传输零点位于无穷远处. 为了在通带与阻带的过渡带中实现明显的下陷,即在通带的两边实现一对陷波点,本小节用置于腔体中心的金属孔对代替原SIW滤波器中的金属孔窗口,设计了一款实现交叉耦合的SIW带通滤波器. 工作频率覆盖28.9～29.2 GHz,通带内插入损耗小于1 dB,回波损耗小于-20 dB,带外抑制特性良好.为了使设计的滤波器结构更为紧凑,该滤波器在连接端采用共面波导过渡结构,在输入、输出两端加入了共面波导短截线和1/4波长短路槽.共面波导过渡结构与其他过渡结构相比更适用于小体积的SIW滤波器,相应的代价是该转换结构会使滤波器的通带带宽受到限制. 采用耦合系数法,利用Matlab编程计算得到该滤波器的耦合矩阵如式(6)所示,引入交叉耦合后,矩阵中M1,4与M4,1的数值不再为零.(6)通过电磁仿真软件HFSS建立该滤波器的初始模型,模型的平面结构如图7所示. 可以看到,滤波器由三对纵向金属孔构成了四个谐振腔. 通过调整孔间距W1、W2,可以改变对应的耦合量. 对比2.1节设计的直接耦合型SIW滤波器,本款滤波器的尺寸更小、结构更为紧凑. 整体的尺寸为4 mm×14 mm,其中W1=0.65mm,W0=2.10 mm,W2=1.10 mm,L1=2.50 mm,L2=2.35 mm,H=2.80 mm.图7 交叉耦合SIW滤波器平面示意图Fig.7 Top view of the cross coupled SIW filter通过电磁仿真软件HFSS得到的滤波器S11、S21仿真曲线如图8所示.图8 交叉耦合SIW滤波器S参数仿真曲线Fig.8 Simulated S parameters of the cross coupled SIW filter从仿真曲线可以看出,通带内插入损耗小于1 dB,回波损耗小于-20 dB,在通带两边各产生一个陷波点,带外抑制特性良好.对上述设计的两款SIW带通滤波器进行对比分析,由滤波器的平面结构示意图可知(如图5、图7所示,其中图5中馈电结构采用微带线——SIW直接转换结构,图7中馈电结构采用共面波导——SIW转换结构),共面波导转换结构使滤波器整体更加紧凑,进一步缩小了滤波器的整体大小,实现了滤波器小型化的应用需求．由仿真结果S参数曲线可知(如图6、图8所示),设计的第二款准椭圆函数型SIW带通滤波器,通过引入交叉耦合,在通带两侧各引入了一个传输零点,在相同阶数下,相比较于传输零点在无穷远处的切比雪夫型SIW带通滤波器,提高了带通滤波器的选择性,抑制更加陡峭.3 结论本文针对毫米波滤波器的设计,引入SIW结构,研究了SIW的结构特点及传输特性,结合耦合谐振带通滤波器设计中的耦合矩阵法,设计了两款工作频率位于毫米波频段的带通滤波器,并通过电磁仿真软件HFSS分别进行了仿真．结果表明,两款滤波器均实现了设计指标,满足毫米波通信系统需求. 分析得出,将SIW结构应用到毫米波滤波器的设计中,有利于优化滤波器尺寸,得到较好的滤波器性能指标,是毫米波滤波器发展的一个重要方向.参考文献【相关文献】[1] CASSIVI Y, PERREGRINI L, ARCIONI P, et al. Dispersion characteristics of substrate integrated rectangular waveguide[J]. IEEE microwave & wireless components letters, 2002, 12(9):333-335.[2] DESLANDES D, WU K. Integrated microstrip and rectangular waveguide in planar form[J]. IEEE microwave & wireless components letters, 2002, 11(2):68-70.[3] HONG W. Development of microwave antennas, components and subsystems based on SIW technology[C]//IEEE International Symposium on Microwave, Antenna, Propagation and EMC Technologies for Wireless Communications, 2006: 14.[4] LI H, HONG W, CUI T J, et al. Propagation characteristics of substrate integrated waveguide based on LTCC[C]//IEEE MTT-S International Microwave Symposium Digest. IEEE, 2003:2045-2048.[5] YAN L, HONG W, WU K, et al. Investigations on the propagation characteristics of the substrate integrated waveguide based on the method of lines[J]. IEE proceeding H:microwaves， antennas and propagation, 2005, 152(1): 35-42.[6] ZHANG Y L, HONG W, XU F, et al. Analysis of guided-wave problems in substrate integrated waveguides:numerical simulations and experimental results[C]//IEEE MTT-S International Microwave Symposium Digest. IEEE, 2003:2049-2052.[7] DESLANDES D, WU K. Single-substrate integration technique of planar circuits and waveguide filters[J]. IEEE transactions on microwave theory & techniques, 2003, 51(2): 593-596.[8] HAO Z C, HONG W, CHEN J X, et al. Compact super-wide bandpass substrate integrated waveguide (SIW) filters[J]. IEEE transactions on microwave theory & techniques, 2005, 53(9): 2968-2977.[9] ESPARZA N, ALCN P, HERRN L F, et al. Substrate Integrated waveguides structures using frequency selective surfaces operating in stop-band (SBFSS-SIW)[J]. IEEE microwave & wireless components letters, 2016, 26(2):113-115.[10] CHOUDHARY D K, CHAUDHARY R K. A compact SIW based filtering power divider with improved selectivity using CSRR[C]//Progress in Electromagnetics Research Symposium, Singapore, 2017.[11] ZHOU H, HONG W, TIAN L, et al. A polarization-rotating SIW reflective surface with two sharp band edges[J]. IEEE antennas & wireless propagation letters, 2016, 15:130-134.[12] XU S, MA K, MENG F, et al. Novel defected ground structure and two-side loading scheme for miniaturized dual-band SIW bandpass filter designs[J]. IEEE microwave & wireless components letters, 2015, 25(4): 217-219.[13] XU F, WU K. Guided-wave and leakage characteristics of substrate integrated waveguide[J]. IEEE transactions on microwave theory & techniques, 2005, 53(1):66-73. [14] NAM H, YUN T S, KIM K B, et al. Ku-band transition between microstrip and substrate integrated waveguide (SIW)[C]//2005 Asia-Pacific Microwave Conference Proceedings. Suzhou, 4-7 December, 2005.[15] WANG Z, PARK C W. Novel substrate integrated waveguide (SIW) type high power amplifier using microstrip-to-SIW transition[C]//IEEE Microwave Conference Proceedings, 2014:101-103.[16] DU M, XU J, DONG Y, et al. LTCC SIW-vertical-fed-dipole array fed by a microstrip network with tapered microstrip-to-SIW transitions for wideband millimeter-wave applications[J]. IEEE antennas & wireless propagation letters, 2017, 16(99):1953-1956. [17] FANG R Y, LIU C F, WANG C L. Compact and broadband CB-CPW-to-SIW transition using stepped-impedance resonator with 90°-bent slot[J]. IEEE transactions on components packaging & manufacturing technology, 2013, 3(2):247-252.。

音乐彩灯控制器设计-课程设计

文档课程设计说明书题目: 音乐彩灯控制器院（部）：理学院专业班级：应用物理14-1学号：2014305070学生：王伟洲理工大学课程设计(论文)任务书理学院(部) 物理系前言随着现在社会的发展，人们生活水平的提高，人们对娱乐环境的要求越来越高，娱乐环境中的灯光控制，成了一个重要的部分。

为此，特意设计了关于音乐彩灯的控制。

本设计要求将输入音乐信号分为高中,低三个频段,并且分别控制三种颜色的彩灯.每组彩灯的亮度随各自输入音乐信号大小分为八个等级.输入信号最大时,彩灯最亮.当输入信号的幅度小于10mv时, 要求彩灯全亮。

第一部分: 实验原理部分（一）. 设计框图及电路系统概述设计框图：电路系统概述：1．声音信号要分为三个频段，所以第一步要通过滤波器进行滤波，将音频信号按要求分为三个频段。

2．经过放大器把毫伏级的声音信号放大为与比较信号可比的信号。

由于直流信号才可比较，所以在进入比较器前先进行整流。

3．同步脉冲通过简易的数模转换产生阶梯波，放大后的信号与其比较产生高低电平，再和同步脉冲相与产生个数不同的脉冲去触发三极管，由触发脉冲的个数决定彩灯的亮度。

4．如果音乐信号小于10mV，用比较器产生高电平使或门的输出总为高电平，产生的高电平与1HZ的脉冲信号进行与，从而使灯亮暗闪烁。

（二）. 实验电路结构与分块电路原理由本实验设计要求可将试验电路基本分为七个组成部分, 即1．电压转换部分2．语音信号的输入部分3．基本信号的放大部分4，滤波选频部分（核心）5．幅度控制部分6 . 输出显示部分7．10 毫伏比较扩展部分第三部分: 各单元电路的设计方案及原理说明下面分别从以上几个分块电路说明该彩灯控制器的设计原理与过程.1. 电源电路：由于实验给出电源为220V 交流电，而实验所需芯片的工作电压大致在5－12V，故需要首先设计一个电压转换部分，将220V 的交流电转换成5V，12V，相当于一个直流稳压源，以供数字和模拟芯片正常工作。

信号与系统课程设计(滤波器)讲解

信号与系统课程设计课程名称：信号与系统题目名称：滤波器的设计与实现学院：电气与电子工程学院专业班级：电气工程及其自动化学号：U*********学生姓名：***指导教师：**2013年08 月25 日目录一、设计要求 (2)二、设计原理 (2)三、设计思路 (3)四、设计内容4.1 单元电路的设计 (4)4.1.1 原理图设计 (4)4.1.2 滤波器的传输函数与性能参数 (6)4.2电路的仿真与检验 (8)4.2.1 低通滤波器仿真 (8)4.2.2 高通滤波器仿真 (10)4.2.3 带通滤波器仿真 (12)五、设计感想 (14)六、参考文献 (15)一、设计要求自己设计电路系统，构成低通滤波器、高通滤波器和带通滤波器。

利用Matlab或其他仿真软件进行仿真。

1.设计低通滤波器2.设计高通滤波器3.设计带通滤波器二、设计原理1、电容器C具有通高频阻低频的性能。

2、有源滤波器由放大电路部分和滤波电路部分组成。

图2.2.1 RC有源滤波总框图2.2.1子框图的作用1．RC网络的作用在电路中RC网络起着滤波的作用，滤掉不需要的信号，这样在对波形的选取上起着至关重要的作用，通常主要由电阻和电容组成。

2 .放大器的作用电路中运用了同相输入运放，其闭环增益 RVF=1+R4/R3同相放大器具有输入阻抗非常高，输出阻抗很低的特点，广泛用于前置放大级。

3.反馈网络的作用将输出信号的一部分或全部通过牧电路印象输入端，称为反馈，其中的电路称为反馈网络，反馈网络分为正、负反馈。

三、设计思路Ω=k R 9.18'1 Ω=k R 36.94'2 Ω=M R 372.2'3带通滤波器就是将高通低通滤波器串联起来四、设计内容4.1 电路的设计4.1.1 原理图设计1. 低通滤波器低通滤波器是用来通过低频信号衰减或抑制高频信号。

如图4.1.1.1（a ）所示，为典型的二阶有源低通滤波器。

它由两级RC 滤波环节与同相比例运算电路组成，其中第一级电容C 接至输出端，引入适量的正反馈，以改善幅频特性。

滤波器详细分类

其中
滤波器频率变换
（1）低通到高通的变换
如图2.4所示,分别给出了低通原型滤波器和高通滤波器的频率一衰减曲线,令它们的频率分量分别为w‘和w。
通过相应的频率变换准则,可将低通原型滤波器转换成高通滤波器,即将低通原型的通带和阻带分别变换成高通滤波器的阻带和通带。直观地说就是将图2.4中的频率一衰减曲线中的w‘=0和w'=无穷大的点分别变换成w=无穷大。和w=o的点，其频率变换的数学表达式为:
• 主要由谐振腔、谐振导体、调谐钉组成
无加载电容
• 滤波器的结构
（三）波导滤波器
主要性能指标：
频率范围：1.7～26GHz 带宽：0.1%～20％插入损耗：0.5～3dB(随带宽不同而不同) 输入输出形式：SMA、N、L16等输入输出驻波：1.3:1 温度：-55～+85℃
（三）波导滤波器
主要性能指标：频率范围：800MHz~16GHz 带宽：0.1%～10％插入损耗：0.5～25dB(随带宽不同而不同) 输入输出形式：SMA、N、L16等输入输出驻波：1.4:1 温度：-55～+85℃
同轴腔滤波器：同轴腔滤波器广泛应用于通信、雷达等系统, 按腔体结构不同一般分为标准同轴、方腔同轴等。同轴腔体具有Q值高、易于实现的特点 ,特别适用于通带窄、带内插损小、带外抑制高的场合。这类滤波器非常适合大规模生产，因此成本也非常低廉。但要在10 GHz以上使用时，由于其微小的物理尺寸，制作精度很难达到。具体的设计有方法负阻线子网络构造了多腔耦合的同轴带通滤波器电路模型；同轴腔体滤波器温度补偿法；阶跃阻抗谐振器等。
微波滤波器基础知识
微波及其特点
所谓微波是一种具有极高频率（通常为300MHz-30 0GHz ），波长很短，通常为1m-1mm的电磁波。

四阶巴特沃斯1kHZ无限增益带通滤波器的设计制作与原理明晰

1KHZ带通滤波器的设计制作实训名称 : 1KHZ带通滤波器的设计与制作学院:专业、班级:指导教师:报告人:学号： 2011 时间： 2013.5.15摘要滤波器，顾名思义，是对波进行过滤的器件。

“波”是一个非常广泛的物理概念，在电子技术领域，“波”被狭义地局限于特指描述各种物理量的取值随时间起伏变化的过程。

该过程通过各类传感器的作用，被转换为电压或电流的时间函数，称之为各种物理量的时间波形，或者称之为信号。

因为自变量时间‘是连续取值的，所以称之为连续时间信号，又习惯地称之为模拟信号(Analog Signal)。

随着数字式电子计算机(一般简称计算机)技术的产生和飞速发展，为了便于计算机对信号进行处理，产生了在抽样定理指导下将连续时间信号变换成离散时间信号的完整的理论和方法。

也就是说，可以只用原模拟信号在一系列离散时间坐标点上的样本值表达原始信号而不丢失任何信息，波、波形、信号这些概念既然表达的是客观世界中各种物理量的变化，自然就是现代社会赖以生存的各种信息的载体。

信息需要传播，靠的就是波形信号的传递。

信号在它的产生、转换、传输的每一个环节都可能由于环境和干扰的存在而畸变，有时，甚至是在相当多的情况下，这种畸变还很严重，以致于信号及其所携带的信息被深深地埋在噪声当中了。

滤波，本质上是从被噪声畸变和污染了的信号中提取原始信号所携带的信息的过程。

关键字：带通滤波器，四阶，巴特沃斯1、概述1.1 、滤波器介绍滤波器是一种对信号有处理作用的器件或电路。

滤波器通常是一种能使某些频率的信号通过而同时抑制或衰减另外一些频率的信号的电子装置。

分图1滤波器为有源滤波器和无源滤波器。

主要作用是让有用信号尽可能无衰减的通过，对无用信号尽可能大的反射。

滤波器一般有两个端口，一个输入信号、一个输出信号，利用这个特性可以选通通过滤波器的一个方波群或复合噪波，而得到一个特定频率的正弦波。

滤波器是由电感器和电容器构成的网路，可使混合的交直流电流分开。

四阶切比雪夫二型带通滤波器python实现

四阶切比雪夫二型带通滤波器是一种常见的数字信号处理工具，它在信号处理领域具有重要的应用。

本文将介绍如何使用Python实现四阶切比雪夫二型带通滤波器，并对其原理和应用进行深入探讨。

1. 切比雪夫滤波器切比雪夫滤波器是数字信号处理中常用的一种滤波器类型，它具有高通、低通、带通和带阻等多种形式。

在这些形式中，带通滤波器可以选择信号中的特定频率范围进行增强或抑制，因此在语音处理、图像处理等领域有着广泛的应用。

2. 四阶切比雪夫二型带通滤波器的设计四阶切比雪夫二型带通滤波器的设计可以分为两个步骤：首先是在模拟域中设计一个带通滤波器，然后将其转换为数字域。

需要注意的是，切比雪夫滤波器的设计需要满足一定的通带波纹和阻带衰减要求，这在实际应用中需要仔细权衡。

3. Python实现在Python中，可以使用scipy库中的signal模块来实现数字滤波器的设计和应用。

可以使用signal.iirfilter函数设计滤波器的系数，然后利用signal.lfilter函数对信号进行滤波处理。

通过这种方式，可以方便地实现四阶切比雪夫二型带通滤波器。

4. 应用实例接下来，我们将介绍一个音频信号处理的应用实例，通过Python实现四阶切比雪夫二型带通滤波器对音频信号进行处理。

通过对比处理前后的音频信号，可以直观地感受到滤波器对信号的影响，并了解滤波器在语音处理中的实际效果。

5. 个人观点和总结从实际开发应用来看，Python作为一种简洁、灵活和强大的编程语言，非常适合于数字信号处理领域。

通过对四阶切比雪夫二型带通滤波器的Python实现，我们不仅可以深入了解滤波器的原理和设计方法，还可以在实际项目中应用这些知识，从而更好地处理数字信号。

通过本文的介绍和实例分析，相信读者对四阶切比雪夫二型带通滤波器的原理和Python实现有了更深入的理解。

在实际应用中，可以根据具体需求选择合适的滤波器类型，并结合Python的强大功能进行开发和实现。

基于SIW技术的高选择性带通滤波器的设计与实现

摘要摘要滤波器作为通信系统前端电路不可或缺的组件，对于整个通信系统而言，其性能的好坏将直接影响到信号的接收，发射以及传播。

而随着整个通信系统的不断发展以及完善，对于各个组件的要求也在不断的提高，滤波器也朝着小型化高性能的方向发展。

在大量学者几十年的研究过程中，基片集成波导技术（Substrate Integrated Waveguide, SIW）因其独特的结构和电磁特性吸引了滤波器设计者们的目光。

SIW其结构既如微带线结构一样，质量轻、体积小、易加工且与平面电路集成方便，又像传统波导一样，辐射损耗小、功率容量大。

这些特性使得其可以成为顺应小型化高性能滤波器发展的设计平台。

而说到滤波器的高性能，不得不提到滤波器的高选择性，高选择性滤波器可以更加有效的滤除不必要的干扰信号，可以大大提高有用信号的传输效率，然而提高滤波器的选择性最常见的方法就是引入传输零点（Transition Zeros, TZs），而传输零点的获取可以通过交叉耦合，源和负载耦合等方法来实现。

本文的主要工作就是研究将SIW技术和交叉耦合以及源和负载耦合等方法相结合设计出具有传输零点的高选择性带通滤波器。

首先，本文简单介绍了滤波器的发展现状以及基本理论知识，包括分类以及基本参数等。

其次，文章又讲解了本文所设计的滤波器的载体SIW，详细介绍分析了其基本结构和特性，并又介绍了两种常见的SIW与微带线的过渡结构，接着又举例说明了三种常用的SIW腔之间的耦合结构，这些都为下文将SIW与交叉耦合理论相结合设计出高选择性滤波器提供了理论基础。

再次，本文介绍了交叉耦合理论，重点介绍了该理论中常见的三谐振器耦合（Coupled Triplet, CT）和四谐振器耦合（Coupled Quadruplet, CQ）结构的相位模型，也以此讨论TZ的位置变化，并通过仿真实例来印证了CT结构相位模型，接着又结合仿真实例讨论了二次模谐振腔对CT结构传输零点位置的影响，最后运用上述方法与SIW相结合利用金属通孔扰动一次模使其频率上升的方法设计出了一款通带两边各具一个传输零点的高选择性带通滤波器。

锁相放大器的设计

锁相放大器的设计【摘要】本系统以超低功耗MSP430G2553作为处理核心，用OPA244、OPA2237、LM324N、LM3119等实现对微弱信号的检测。

该电路由信号调理模块、移相器模块、相敏检波器和数码管四个模块组成。

信号调理模块包括加法器，交流放大器，四阶带通滤波器，信号调理电路子模块，其具有微弱信号放大和调理、抑制干扰和噪声的作用。

移相器模块由多个比较器，积分器组成，实现与被测信号的同步，产生可180°移相的方波传输给MCU，由数码管显示被测信号的幅度。

【关键词】微弱信号;移相器;msp430;相敏检波器1.锁相放大器设计原理根据相关接收原理，在相关接收中，可以把两个信号的函数f1（t）和f2（t）的相关函数定义为：它是度量一个随机过程在时间t和两时刻线性相关的统计参数，如果f1（t）和f2（t）完全没有关系，则相关函数将是一个常数。

下面我们设有两个信号x（t）、y（t）为：其中n1（t）、n2（t）为噪声，Vs（t）为待测信号，Vr（t）为参考信号。

则相关函数为：展开得：因为信号和噪声不相关，且噪声的平均值为零，所以都为零。

故：这样我们可以看到，两个信号经过相乘和积分处理后就可以把噪声抑制，锁相放大器的核心就是根据这个原理设计的。

2.设计方案的论证如图1所示，该方案将数字脉冲电位器用模拟移相器取代，其中移相器是由多个小模块依次作为输入产生不同的波形，最终实现将正弦信号调整为相位不同的方波信号。

且该处采用模拟器件容易实现，便于分级检测输出的波形，及时对硬件电路进行修正和改进。

图13.硬软件设计3.1 硬件的总体设计通过理论分析，该系统主要由由三部分组成，即：信号通道，参考通道和其他相关器。

加法器将被测信号S（t）和噪声信号n（t）以1：1叠加后通过电阻分压网络将叠加后的信号进行衰减。

信号通道由放大器和带通滤波器组成，其作用是把微弱信号放大到足以推动相关器的工作电平，并兼有抑制和滤掉部分干扰和噪声，扩大仪器动态范围的性能;参考通道由触发整形和移相器组成，其作用是产生与被测信号同步的对称方波，再由方波驱动给相关器;相关器由数字相敏检波器组成，是锁定放大的核心部件，具有动态范围大、漂移小、时间常数可调等性能。

四阶巴特沃斯1kHZ无限增益带通滤波器的设计制作与原理明晰分析

“波”是一个非常广泛的物理概念，在电子技术领域，“波”被狭义地局限于特指描述各种物理量的取值随时间起伏变化的过程。

该过程通过各类传感器的作用，被转换为电压或电流的时间函数，称之为各种物理量的时间波形，或者称之为信号。

因为自变量时间‘是连续取值的，所以称之为连续时间信号，又习惯地称之为模拟信号(Analog Signal)。

信息需要传播，靠的就是波形信号的传递。

滤波，本质上是从被噪声畸变和污染了的信号中提取原始信号所携带的信息的过程。

关键字：带通滤波器，四阶，巴特沃斯1、概述1.1 、滤波器介绍滤波器是一种对信号有处理作用的器件或电路。

滤波器通常是一种能使某些频率的信号通过而同时抑制或衰减另外一些频率的信号的电子装置。

分图1滤波器为有源滤波器和无源滤波器。

主要作用是让有用信号尽可能无衰减的通过，对无用信号尽可能大的反射。

滤波器一般有两个端口，一个输入信号、一个输出信号，利用这个特性可以选通通过滤波器的一个方波群或复合噪波，而得到一个特定频率的正弦波。

滤波器是由电感器和电容器构成的网路，可使混合的交直流电流分开。

滤波器参数设计方案说明

滤波器参数设计方案说明一、设计指标1、滤波器函数类型：巴特沃斯、契比雪夫2、滤波器类型：低通、高通、带通3、中心频率或截至频率范围：1Hz～140kHz4、滤波器阶数：4阶5、输入信号范围：最大幅值4Vpp，最小幅值mV级6、输入信号：正弦波（0～40MHz）、方波（0～1MHz,默认占空比50%）两种，幅度可通过电位器调节7、输出信号：两级程控放大（0～96dB），一级程控衰减（0～48dB）二、设计中使用的公式及数据表2.1 中心频率及Q值计算公式'C)C=Q为各阶巴特沃斯和契c B C比雪夫对应的归一化系数；为带通滤波器的中心频率，BW为带通滤波器的带宽，Q’为带（2）Ω0通滤波器的品质因数。

表2.2 各阶滤波器二阶滤波器节B、C表注：契比雪夫滤波器的各阶系数是在通带波纹为0.1dB下求得。

表2.3 4阶滤波器设计参数表（采用归一化频率）注：（1）表中给出的巴特沃斯和契比雪夫滤波器系数均为4阶滤波器；（2）契比雪夫滤波器的通带波纹为0.1dB ，两种滤波器的带通模式下为'0/(Hz)5BP Q f BW ==时的参数，BW 为带通滤波器的带宽，Q ´为带通滤波器的品质因数。

三、低通滤波器设计 1、截止频率及Q 值计算由文献《有源滤波器精确设计手册》可以查得四阶巴特沃斯和契比雪夫滤波器各二阶节的B 、C 值，见表2.2。

根据表2.1，计算得到四阶巴特沃斯和契比雪夫滤波器各二阶滤波器节的Q 值，如表2.3，我们重新整理成表3.1。

表3.1 四阶低通滤波器各二阶滤波器节的Q 值和归一化频率2、0/clk f f 、Ｑ和工作模式编程参数的确定f clk /f 0编程参数的确定有两种方法：（1）固定f clk /f 0比值，即无需改变频率比的N F 编程值，通过改变时钟频率f clk 对应改变中心频率（截止频率）f 0值。

也即根据输入中心频率（截止频率）f 0计算得到时钟频率f clk 。

程控高增益选频放大器设计

第三十组：陈林辉、夏效禹、伍玉程控高增益选频放大器设计摘要：本系统以单片机和FPGA 为控制核心，实现了一个程控高增益选频放大器和衰减正弦波信号发生器。

放大器以一款压控增益放大器AD603为核心，增益步进1dB ，范围60dB~120dB 。

选频功能用*阶状态变量带通滤波器实现，中心频率步进为1Hz ，范围**Hz~**Hz ，通带宽度小于**Hz 。

在衰减正弦波发生器的实现中，通过控制D/A 转换器参考电压以改变信号包络，频率步进1Hz ，范围**Hz~**Hz ，并在幅度降至2mV 时声光报警。

另外，系统可以测试放大器输出幅度，测量误差小于**。

关键字：压控增益放大器状态变量滤波器一、方案论证与选择 1、选频功能实现方案方案一：采用并联LC 选频网络。

当输入信号频率等于其谐振频率时，网络呈纯阻特性，输出信号幅度最大。

改变L 、C 即可改变谐振频率。

方案二：采用RC 选频网络。

如框图所示，它由基本放大电路和双T 形RC 带阻滤波负反馈网络构成。

改变RC 网络中的阻容参数可以调节谐振频率。

图1 RC 选频网络框图方案三：采用状态变量滤波器。

该滤波器电路的截止频率与Q 值由其中某些阻容值决定。

电流输出型DAC 可等效为阻值仅受输入数据控制的电阻，用此控制滤波器的截止频率和Q 值，可实现滤波器参数精确程控。

方案一、二可实现极窄通频带、高Q 值的选频特性，但难以实现中心频率以1Hz 为步进。

方案三中的状态变量滤波器若采用较高阶数，可满足对Q 值的要求，且可精确程控中心频率，ADC 位数决定调节范围，因此，我们选取方案三。

2、衰减正弦波信号源设计方案方案一：利用模拟电路产生。

利用LC 振荡网络构成谐振电路，选择适当的 L 、C 值产生正弦波，再利用一阶RC 电路产生由初始值衰减的指数衰减信号，将2种信号叠加相乘，即可得到按指数规律衰减的正弦波输出信号。

方案二：利用数字方法产生。

分别送入两组数据进入2个D/A 转换器中，令第一个DAC 产生正弦波形，第二个DAC 产生按指数规律衰减的波形，并作为第一个DAC 的参考电压，相当于两信号相乘，由此获得衰减波形。

基于LT1568的高频段有源滤波器的设计

基于LT1568的高频段有源滤波器的设计作者：于涛周晓明袁志刚来源：《现代电子技术》2016年第02期摘要：对于高频信号，传统的由分立元件搭建的LC无源滤波网络，设计过程复杂，对信号衰减较大。

为了简化高频段滤波器的设计过程、提高滤波效率，提出了使用低噪声高频有源RC滤波芯片LT1568来设计高频滤波电路，介绍其性能，分析了其工作原理。

并以高频多普勒接收机内部带通滤波器设计为例，介绍滤波电路的设计方法。

实验仿真表明用其搭建的高频有源滤波电路滤波效果明显、电路简单、方便易用。

关键词： LT1568；低噪声；高频多普勒接收机；有源滤波中图分类号： TN713+.8 文献标识码： A 文章编号： 1004⁃373X（2016）02⁃0116⁃03 Design of high⁃band active power filter based on LT1568YU Tao， ZHOU Xiaoming， YUAN Zhigang（College of Electronic Information， Wuhan University， Wuhan 430072， China）Abstract： The traditional LC passive filtering network for high⁃frequency signal which is constructed by discrete components has complex design process and may cause strong signal attenuation. To simplify the design process of the high⁃band filter， and improve the filtering efficiency， a method to design the high⁃frequency filtering circuit with the low⁃noisehigh⁃frequency active RC filtering chip LT1568 is proposed. The performance of the circuit is introduced， and its working principle is analyzed. By taking the design of the band⁃pass filter in high⁃frequency Doppler receiver as an instance， the design method of the filtering circuit is presented. The experiment simulation results demonstrate that the high⁃frequency active filtering circuit has obvious filtering effect and simple structure. The circuit is easy to use.Keywords： LT1568； low noise； high frequency Doppler receiver； active filtering0 引言滤波器在电路系统的设计中有着很广泛的应用，例如对调制信号、接收信号、混频后的中频信号的处理过程中都涉及滤波，从而滤除干扰信号，达到提高信号准确性的目的。