一阶带通滤波器(1)
带通滤波电路带通滤波器

f<f1的信号可从低通滤波器通过
f>f2的信号可从高通滤波器通过
阻带宽度为f2 -fl
频率范围在fl<f<f2的信号被阻断
三、 带阻滤波电路
2. 常用带阻滤波器(BEF)
电路特征:输入信号经过一个由RC元件 组成的双T型选频网络,然后接至集成运 放的同相输入端。
工作原理:当输入信号的频率较高时,可 以认为电容短路,则高频信号从上面由两 个电容和一个电阻构成的T型支路通过;
Ui (s)
1 sC
M
1 sC
P
Uo(s)
UM (s) UP (s) UP (s)
1
R
sC
Ui (s) UM (s) UM (s) UO (s) UM (s) UP (s)
1
R
1
sC
sC
压控电压源二阶HPF电路பைடு நூலகம்
传递函数:
Au
(s)
1
[3
(sRC)2 Aup (s) Aup (s)]sRC (sRC)2
带阻滤波器的作用与带通滤波器相反,即在规定的频带内,信号被 阻断,而在此频带之外,信号能够顺利通过。带阻滤波器也常用于抗干 扰设备中阻止某个频带范围内的干扰及噪声信号通过。
从原理上说,将一个通带截止频率为fl的低通滤波器与一个通带截 止频率为f2的高通滤波器并联在一起,当满足条件fl<f2时,即可组成带 阻滤波器。
1 Q 3 AuP
A u
f f0
A u p 3 A u p
Q A u p
Q是f=f0时的电压放大倍数与通带放大倍数之比
一、高通有源滤波电路
对数幅频特性
一阶带通滤波和二阶带通滤波

一阶带通滤波和二阶带通滤波
摘要:
一、带通滤波器的基本概念
二、一阶带通滤波器
1.定义
2.特性
3.应用
三、二阶带通滤波器
1.定义
2.特性
3.应用
四、一阶和二阶带通滤波器的比较
正文:
一、带通滤波器的基本概念
带通滤波器是一种特殊的滤波器,其作用是允许某一频率范围内的信号通过,而阻止其他频率范围内的信号。
带通滤波器在信号处理领域有着广泛的应用,例如在音频处理、通信系统、图像处理等方面都有重要的应用价值。
二、一阶带通滤波器
1.定义
一阶带通滤波器是最简单的带通滤波器,它只有一个电阻和一个电容或者电感串联,形成一个简单的RC 或LC 电路。
2.特性
一阶带通滤波器的特性主要表现在其频率响应上。
当信号频率低于截止频率时,滤波器呈现高通特性,信号可以顺利通过;当信号频率高于截止频率时,滤波器呈现低通特性,信号会被阻止。
3.应用
一阶带通滤波器常用于信号的初步过滤,例如在音频处理中,可以用一阶带通滤波器去除低频噪声。
三、二阶带通滤波器
1.定义
二阶带通滤波器是由两个一阶带通滤波器串联或并联组成的,其结构相对复杂,但性能更优越。
2.特性
二阶带通滤波器的特性主要体现在其频率响应上,相比一阶带通滤波器,二阶带通滤波器的频率响应更加平滑,通带和阻带的界限更加明显。
3.应用
二阶带通滤波器由于其良好的频率响应特性,被广泛应用于各种信号处理系统中,如音频处理、通信系统等。
四、一阶和二阶带通滤波器的比较
一阶带通滤波器结构简单,但频率响应不够平滑,通带和阻带的界限不太明显,适用于一些简单的信号处理场合。
第5章+有源滤波电路

27
n阶巴特沃斯低通原型滤波器传递函数的逼近表达式为
AV (S)
1 1 (S )2n
j
S s 归一化复频率
c c 低通截止角频率
令S j2f ,幅频响应为:
20l AV 20lg
1 1 f 2N
n阶巴特沃斯低通滤 波器的高频衰减为
20n dB/十倍频, 随频率单调变化。
28
1 AV (S) 1 ( S )2n
(1 R
2sC)VA
sCVP
1 R
Vo
sCVi
Vo
(1
R2 R1
)VP
A0VP
可解得传递函数:
AV
(s)
s2
A0 s 2
c
Q
s
c2
sCVA
(
1 R
sC)VP
0
特征角频率:
c
Байду номын сангаас
1 RC
通带增益:
A0
1
R2 R1
品质因数:
电路稳定条件: 2 R2 0 R1
17
Q 1 1 2 R2 3 A0 R1
AV
(s)
Vo (s) Vi (s)
p(s) q(s)
b0 b1s bnsn a0 a1s amsm
n和m是正整数 n m, ai , bi是实数
分母多项式中s的最高阶次定义为滤波器电路的阶数。
s j 复频率
例:Av (s)
(s 2)(s 4) s(s2 9)(s 5)2
RC滤波器的通带增益及其截止频率都随负载而变化。
思考: 如何构成一阶有源高通滤波器电路?其传递函数、
幅频响应和相位响应是什么?
提示:对滤波元件进行对偶变换
带通滤波器

摘要滤波器的功能是让一定频率范围内的信号通过,而将此频率范围之外的信号加以抑制或使其急剧衰减。
当干扰信号与有用信号不在同一频率范围之内,可使用滤波器有效的抑制干扰。
用LC网络组成的无源滤波器在低频范围内有体积重量大,价格昂贵和衰减大等缺点,而用集成运放和RC网络组成的有源滤波器则比较适用于低频,此外,它还具有一定的增益,且因输入与输出之间有良好的隔离而便于级联。
由于大多数反映生理信息的光电信号具有频率低、幅度小、易受干扰等特点,因而RC有源滤波器普遍应用于光电弱信号检测电路中。
关键字:滤波器;集成运放;RC网络;有源滤波器The function of the filter is to make certain frequency within the scope of the signal, and the frequency by outside the scope curbed the signal or sharp attenuation. When the disturbance signal and the useful signal not in the same frequency range, can use filter to suppress the interference effectively.With LC network consisting of passive filter in the low frequency within the area, volume weight expensive and attenuation shortcomings, but with integrated op-amp and RC network consisting of active filter is more applicable to low frequency, in addition, it also has some of the gain, and because between the input and output has good isolation and facilitate cascade. Since most reflect the photoelectric signal has a physical information low frequency and amplitude small, vulnerable to interference, and characteristics of the RC active filters widely applied electric light weak signal detection circuit.Filter;integrated op-amp;RC network;active filter引言滤波器的功能是让一定频率范围内的信号通过,而将此频率范围之外的信号加以抑制或使其急剧衰减。
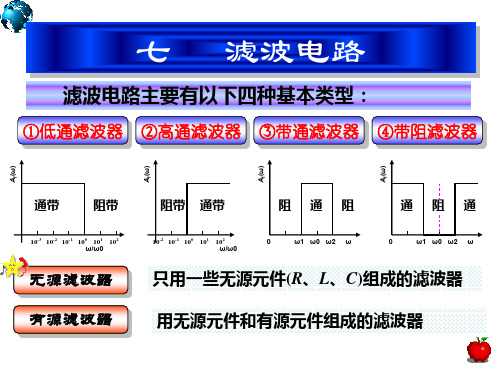
滤波电路主要有以下四种基本类型
七
①低通滤波器
i
R 1 R jC
1 1 1 jRC
1 0 1 j
1 RC
0
(c)
C
o
U i
R
(b)
U o
它们的截止存在的问题 (1)电路的增益小,最大为1 (2)带负载能力差
1 0.707
0
o
(d )
如在无源滤波电路输 出端接一负载电阻RL, 则其截止频率和增益 均随RL而变化。
简单二阶低通滤波 电路的幅频特性
由幅频特性可见ω>>ω0时衰减 的斜率为-40dB/十倍频。但在 ω0附近,其幅频特性与理想的 低通滤波特性相差较大。
0 -3dB
20 lg
Af ( ) / dB Af
-40dB/十倍 频
0.1 0.37 1
10
ω/ω0
改进
R
1
R
U
2
f
将电容C1的接 地端改接到集成 运放的输出端。
o
up
o
A A
up
高通
1
通
1
阻
2
通
o
带阻滤波器电路图
C
C
R
1
R
f
1 o 1 j 2 Q o 2 Rf 1 1 Af 1 Q R1 RC 22 Af
一阶无源高通滤波器设计课程设计

摘要 (3)一、课程设计目的: (4)二、课程设计仪器 (4)三、设计滤波器的整体思路 (4)1、设计思路 (4)2、设计指标:截止频率为10500Hz的高通滤波器。
(4)3、滤波器的有关参数 (4)四、一阶高通滤波电路设计 (5)1.定义:让某一频率以上的信号分量通过,而对该频率以下的信号分量大大抑制的电容、电感与电阻等器件的组合装置。
(5)2.一阶高通滤波器电路图如下: (5)五、电路板制作(规格:7cm*5cm) (7)六、频谱函数测试 (8)七、误差分析 (13)八、实验总结: (14)八、心得体会 (14)摘要滤波电路是一种能使有用频率信号通过而同时抑制无用频率信号的电子装置。
工程上常用它来作信号处理、数据传输和抑制干扰等。
我们现在主要讨论模拟滤波器。
以往这种滤波电路主要采用无源R、L和C组成,20世纪60年代以来,集成运放获得了迅速发展,由它和R、C组成的有源滤波电路,具有不用电感、体积小、重量轻等优点。
此外,由于集成运放的开环电压和输入阻抗均很高,输出阻抗又低,构成有源滤波电路后还具有一定的电压放大和缓冲作用。
但是,集成运放的带宽有限,所以目前有缘滤波电路的工作频率难以做的很高,以及难于对功率信号进行滤波,这是它的不足之处。
在实际电子系统中,输入信号往往是含有多种频率成分的复杂信号,可能还会混入各种噪声、干扰及其它无用频率的信号,因此需要设法将有用频率信号挑选出来、将无用信号频率抑制掉。
完成此任务需要具有选频功能的电路。
关键词:滤波运放信号选频一、课程设计目的:(1)熟悉常用仪表,了解电路调试的基本方法 ;(2)进一步提高自己的动手实践能力;(3)掌握专业课程设计报告;(4)设计一个截止频率为10500Hz 的高通滤波器 。
二、课程设计仪器三、设计滤波器的整体思路1、设计思路(1)首先根据滤波器的基本原理,设计出其基本组成框图。
(2)根据有源高通滤波器的原理图,按照层次化、模块化、 参数化的设计思路,完成设计电路。
第三章 滤波器

3.1 滤波器的分类:
一. 按是否使用有源器件分:无源滤波器、有源滤波器
有源滤波器实际上是一种具有特定频率响应的放大器。 是指用晶体管或运放构成的包含放大和反馈的滤波 器。 特点: 需要工作电压。
无源滤波器指用电容、电感、电阻组成的滤波器。
特点: 需要工作电压。
(一). 无源滤波器
1. 一阶RC低通滤波器(无源)
n阶巴特沃思低通滤波器的传递函数可写为:
A0 A0 A(S ) n B(S ) S an1 S n1 a1 S a0
jw S 为归一化复频率 S wc
;B ( S ) 为巴特沃思多项式;
an1 , a1 , a0 为多项式系数
高通有源滤波器
1.一阶有源高通滤波器
Rf R1
u (
R 1 R j C
)ui (
1 1 1 j RC
)ui
u- u+
ui
C
∞ - A + +
uo
uo (1
Rf R1
)u AO u
R
AO uO Rf 1 ) 传递函数: A (1 )( ) ( L R1 1 j L ui 1 j
二.按通带和阻器(HPF) 带通滤波器(BPF) 带阻滤波器(BEF)
各种滤波器理想的幅频特性:
(1)低通 |A| A0 0 通带 阻带 ωC ω (2)高通 |A| A0 0 通带 阻带 ωC ω
(3)带通 |A| A0 阻 阻 通 ωC2 0 ωC1 ω
① 根据“虚短”:
i2
i1 + us _
R1 1
_ +
+
一阶带通滤波和二阶带通滤波

一阶带通滤波和二阶带通滤波摘要:一、引言二、一阶带通滤波1.定义与概念2.公式与性质3.应用场景三、二阶带通滤波1.定义与概念2.公式与性质3.应用场景四、总结正文:一、引言在数字信号处理领域,滤波技术是一种重要的方法,用于从噪声和干扰中提取有用信号。
带通滤波器是一种特殊的滤波器,能够通过特定的频率范围内的信号,而阻止其他频率范围内的信号。
本文将介绍一阶带通滤波和二阶带通滤波的相关知识。
二、一阶带通滤波1.定义与概念一阶带通滤波器是一种线性时不变滤波器,它的传递函数具有以下形式:H(s) = A(s) / (1 + ω_c / ω_n * A(s))其中,A(s)是截止频率为ω_c的sinc函数的传输函数,ω_n是噪声带宽。
2.公式与性质一阶带通滤波器的频率响应具有以下特点:- 在ω_c附近,频率响应呈现出一个峰值,表示信号能量集中在ω_c附近;- 在ω_n附近,频率响应逐渐下降,表示滤波器能够有效地抑制噪声。
3.应用场景一阶带通滤波器广泛应用于音频处理、图像处理、通信系统等领域,用于去除噪声和干扰,提高信号质量。
三、二阶带通滤波1.定义与概念二阶带通滤波器是一种具有两个截止频率的带通滤波器,它的传递函数具有以下形式:H(s) = (ω_c^2 / (s^2 + 2 * ζ * ω_c * s + ω_c^2)) * (1 / (1 + ω_n / ω_c))其中,ζ是阻尼比,ω_n是噪声带宽。
2.公式与性质二阶带通滤波器的频率响应具有以下特点:- 在ω_c附近,频率响应呈现出两个峰值,表示信号能量集中在ω_c附近;- 在ω_n附近,频率响应逐渐下降,表示滤波器能够有效地抑制噪声。
3.应用场景二阶带通滤波器在保留信号能量的同时,具有更好的噪声抑制性能,因此广泛应用于音频处理、图像处理、通信系统等领域。
四、总结本文介绍了一阶带通滤波和二阶带通滤波的定义、公式和应用场景。
带通滤波器是一种重要的信号处理技术,能够有效地去除噪声和干扰,提高信号质量。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2.5.2程序代码
2.5.3Mablab函数说明及使用说明
(1)fplot函数
函数功能:
在指定的范围内绘制函数图像
使用方法:
fplot在指定的范围内绘制函数图像,函数必须是y=f(x)的形式,其中x是一个指定范围limits的向量,y是和x有相同大小的向量并包含在点x处的值。如果对一个给定的x值,函数返回多于一个值,则y是每列包含f(x)的每一个分量的矩阵。
图1.1.11
其输入阻抗是:
1.1.2电路谐振条件
若传递函数的虚部为零,则产生谐振,即:
满足上述条件的值称为谐振频率,因此谐振的条件是:
又因
,
所以:
在谐振条件下,有:
1、阻抗是纯电阻 。换言之, 的串联组合相当于短路,整个电压都加在电阻 上。
2、电压 和电流 是同相的,所以功率因数为1。
3、传递函数 ,其量值最小。
3、M文件函数或匿名函数的函数句柄。
对于向量x的每个元素,函数f(x)必须返回一个行向量。比如,如果f(x)返回向量[f1(x),f2(x),f3(x)],输入参量为x=[x1;x2],则函数f(x)返回矩阵:
f1(x1)f2(x1)f3(x1)
f1(x2)f2(x2)f3(x2)
例如:
fplot(fun,limits,LineSpec)
fnch = @tanh;
fplot(fnch,[-2,2])
(2)plot函数
函数功能:
plot是绘制二维图形的最基本函数,它是针对向量或矩阵的列来绘制曲线的。
使用方法:
使用plot函数之前,必须首先定义好曲线上每一点的x及y坐标,常用格式为:
1、plot(x):当x为一向量时,以x元素的值为纵坐标,x的序号为横坐标值绘制曲线。当x为一实矩阵时,则以其序号为横坐标,按列绘制每列元素值相对于其序号的曲线,当x为m×n矩阵时,就由n条曲线。
fplot(axes_handle,...)
用指定句柄axes_handle代替当前坐标轴句柄来画图。
[X,Y] = fplot(fun,limits,...)
返回横坐标与做坐标的值赋给X和Y,此时fplot不给出图形,若想画出,可用命令plot(X,Y)。
应用举例:
画[-2,2]区间的双曲正切函数:
摘要
本次课程设计是研究一阶带阻滤波器,以U0为响应,求频率响应函数,画出其幅频特性和相频特性曲线。首先,通过对滤波器背景理论的学习与理解,对设计题目进行分析并做出了数学模型,然后借助Matlab软件,画出题目所要求的幅频、相频图,并通过调整和设计参数画出了比较合理的图形。在设计中,我深刻理解到了滤波器的工作原理,而且发现理想和实际中的曲线有不小差距,与此同时,也熟练了Matlab的相关操作和应用,对信号理论和RLC串联谐振有了更新的认识。
注意:对于相同R,L和C值的带通滤波器的传递函数与带阻滤波器的传递函数相加得到的结果是在任何频率下都为1。这是因为这两个电路其中一个电路的特性是另一个的反特性,当然,一般情况下,上述结果是不成立的。
无源滤波器的最大增益是1,要想得到大于1的增益,应该用有源滤波器。
2设计内容
本次课程设计的内容是研究一阶带阻滤波器。如图2.1,以U0为响应,求频率响应函数,画出其幅频响应(幅频特性) 和相频的响应(相频特性) 。
谐振是RLC电路中的一种状态,该电路中电容和电感的电抗大小是相等的,结果呈现出纯电阻的阻抗性质。
串联或并联谐振电路的传递函数有很高的频率选择性,所以在设计和制作滤波器过程中是很有用的,其他许多应用中包括收音机的选台和电视机的选频道等。
1.1.1电路模型分析
考虑如图1.1.11所示的串联RLC频率电路。
用指定的线型LineSpec画出函数fun。
fplot(fun,limits,tol)
用相对误差值为tol画出函数fun。
fplot(fun,limits,tol,LineSpec)
用指定的相对误差值为tol和指定的线型LineSpec画出函数fun。
fplot(fun,lims,...)
允许可选参数tol,n和LineSpec以任意组合方式输入。
fplot(fun,limits)
在指定的范围limits内画出函数名为fun的图像。其中s是一个指定x轴范围的向量[xmin xmax]或者是x轴和y轴范围的向量[xmin xmax ymin ymax]。
fun可能为:
1、M文件函数名字。
2、可能传递给eval函数的带变量x的字符串,比如'sin(x)','diric(x,10)'或'[sin(x),cos(x)]'。
图1.1.31中谐振曲线的峰值取决于电阻R,而该曲线的宽度取决于其频带宽度B,带宽定义为两个半功率点频率之差:
这种频带宽度的定义是几种常用的定义之一。严格地说,上式所定义的带宽称为半功率带宽,是半功率点频率之间的谐振曲线的频带宽度。
谐振曲线的“锐度”用品质因数Q这个量来度量。电路谐振时,电路中的电抗能量在电感和电容之间来回振荡。因质因数将电路储存的最大(峰值)能量与每振荡一个周期所消耗的能量间的关系连系起来,定义为:
高 电路经常在通信网络中使用。
综上所述,谐振电路可以用以下五个相关的参数来表征:两个半功率点的频率 和 ,谐振频率 ,带宽B和品质因数Q。
1.2无源滤波器
滤波器的概念从开始就一直是电子工程进展中的一个主要组成部分,没有电子滤波器的参与,某些技术成果将是不可能的。
滤波器是一个被精心设计的电路,它只允许一些特定频率的信号通过,而阻止或衰减其他频率的信号。
图1.2.41
如图1.2.41所示,其传递函数是:
由式可见:
, 。
图1.2.42所示为 的幅频特性,其中心频率为:
同样,滤波器的半功率频率、带宽和品质因数,仍然可以用上述串联谐振电路的公式来计算,例如:
这里的 称为抑制频率,而对应的带宽 称为抑制带宽。
带阻滤波器是抑制或消除在频率 内所有频率的滤波器。
令 , 时,消耗的功率是最大功率的一半,即:
则称 , 为半功率(点)频率。
半功率频率可以通过令 求得,即:
解 ,得到:
由此可以得到半功率点频率与谐振频率的关系是:
即谐振频率是半功率频率的几何平均值。一般来讲,频率响应并不对称于谐振频率,所以 , 也不是对称于 的。但是,认为半功率点频率对称于谐振频率是一个比较合理的近似。
如图1.1.41所示,Q值越高,电路的频率选择性越强,而其频带也越窄。RLC电路的选频特性是电路对每个频率的响应,并排除其它频率的一种能力,如果要选用或要排斥的频带很窄,品质因数必须很高,反之若频带较宽,则谐振电路的品质因数应该低一些。
品质因数也是电路电路性(或谐振“锐度”)的一个度量。
通常谐振电路总是工作在其谐振频率处或其邻近处,当电路的品质因数等于或大于10时,称为高Q电路。在高Q电路(Q≥10)的所有实际应用中,其半功率频率都可认为是对称于谐振频率的且可挖地按下式表示:
对于电路所用到的器材,电阻、电感、电容,都是常见值,比较好找。而且电路结构简单,容易搭建。但是由于这个滤波器不含放大电路,放大倍数最大就是1,不能对有用的信号加以放大处理,这是一个缺陷。它只能把谐振频率附近的频段阻碍掉,留下有用的频率。总体来讲,作为一个一阶无源带阻滤波器,这次设计还是可行的。可以做出成品,并且电路拥有相应的功能,而且还比较稳定。但从滤波器的角度看,也存在不足,比如:能放大、功能过少、实用价值低等等。若仅仅作为设计还是可以的,如果要用于工业生产和使用,本设计还得加以改进和调试,方可更经济更有效的使用。
图2.1
2.1原理分析
如图2.1,一个串联RLC谐振电路取其LC串联的组合作为输出,构成了带阻滤波器,其传递函数,即频率响应函数是:
中心频率为:
带宽B和品质因数Q之间的关系:
2.2数学建模
频率响应函数:
令
于是,有:
故其幅频响应(幅频特性)为:
相频响应(相频特性):
2.3参数推导
经过反复尝试和推算,分析得出当R ,L mH,C 时得出的曲线是比较合理的。由:
1.2.3带通滤波器
带通滤波器是通过频带( 中所有频率的滤波器。RLC串联谐振电路以电阻两端为输出,就是一个带通滤波器。
1.2.4带阻滤波器
一个滤波器阻止两个指定值( 和 )之间的频带通过,则称之为带阻滤波器、带止滤波器或陷波器。当一个串联RLC谐振电路取其LC串联的组合为输出时,即构成了带阻滤波器。
作为一个频率选择装置,滤波器可以用来将信号的频谱限制在某个指定的频带宽度范围内,在无线电接收机和电视机中,从空间许许多多广播信号中选出所需要的信号频道所用的电路就是滤波器。
如果滤波器电路的组成元件只有无源元件R,L和C,则称为无源滤波器;如果除了无源元件R,L和C外,还有有源器件(例如晶体管、运算放大器等),则称为有源滤波器。本文讨论无源滤波器。
品质因数也是电路中储能的性能与耗能性能之间关系的一个度量。在串联RLC电路中,储能的峰值是 ,一个周期的耗能是: ,所以:
或
品质因数是无量纲的值,带宽B和品质因数Q之间的关系由将式代入,并利用式关系得到:
或者
谐振电路的品质因数是其谐振频率与带宽之比。
注:上述公式
只适用于RLC串联电路。
图1.1.41电路的Q值越高,其带宽越小
2.5程序设计
Mablab是矩阵实验室(Matrix Laboratory)的简称,是美国MathWorks公司出品的商业数学软件,用于算法开发、数据可视化、数据分析以及数值计算的高级技术计算语言和交互式环境,主要包括Mablab和Simulink两大部分。
Mablab是由美国mathworks公司发布的主要面对科学计算、可视化以及交互式程序设计的高科技计算环境。它将数值分析、矩阵计算、科学数据可视化以及非线性动态系统的建模和仿真等诸多强大功能集成在一个易于使用的视窗环境中,为科学研究、工程设计以及必须进行有效数值计算的众多科学领域提供了一种全面的解决方案,并在很大程度上摆脱了传统非交互式程序设计语言(如C、Fortran)的编辑模式,代表了当今国际科学计算软件的先进水平。
