清华大学历年结构力学考研真题
考研951结构力学真题

考研951结构力学真题考研951结构力学真题是考研生备考过程中的一大挑战。
结构力学作为工程力学的重要分支,研究物体在外力作用下的变形和破坏规律,是工程师必备的基础知识。
在考研951结构力学真题中,我们可以看到多种类型的问题,涉及到杆件受力分析、悬臂梁、梁的挠度计算等内容。
通过对这些题目的分析和解答,我们可以加深对结构力学的理解,提高解题能力。
首先,我们来看一个经典的考研951结构力学真题。
题目是关于杆件受力分析的。
在这个题目中,我们需要根据给定的受力情况,计算出杆件上各个点的受力大小和方向。
这个题目涉及到了平衡条件和受力分析的知识。
首先,我们可以根据受力平衡条件,列出杆件上各个点的受力方程。
然后,根据受力方程,我们可以解出各个未知受力的大小和方向。
通过这个题目的解答,我们可以加深对平衡条件和受力分析的理解,提高解题能力。
接下来,我们来看一个关于悬臂梁的考研951结构力学真题。
在这个题目中,我们需要计算悬臂梁上的最大挠度。
悬臂梁是一种常见的结构,在工程中广泛应用。
计算悬臂梁的挠度是结构力学中的重要内容。
在这个题目中,我们可以利用悬臂梁的受力分析和挠度计算公式,计算出悬臂梁上的最大挠度。
通过这个题目的解答,我们可以加深对悬臂梁的理解,提高解题能力。
最后,我们来看一个关于梁的挠度计算的考研951结构力学真题。
在这个题目中,我们需要计算梁的挠度。
梁是工程中常见的结构,计算梁的挠度是结构力学中的重要内容。
在这个题目中,我们可以利用梁的受力分析和挠度计算公式,计算出梁的挠度。
通过这个题目的解答,我们可以加深对梁的挠度计算的理解,提高解题能力。
通过对考研951结构力学真题的分析和解答,我们可以深入理解结构力学的基本原理和应用方法。
结构力学作为工程力学的重要分支,对于工程师来说是必不可少的基础知识。
通过解答真题,我们可以提高解题能力,增强对结构力学的理解,为以后的工程实践打下坚实的基础。
因此,考研951结构力学真题是考研生备考过程中的一大挑战,但也是一个很好的学习机会。
考研结构力学考试题及答案

考研结构力学考试题及答案# 考研结构力学考试题及答案## 一、选择题1. 在结构力学中,静定结构与超静定结构的区别是什么?- A. 静定结构的内力可以通过静力平衡条件确定- B. 超静定结构的内力需要通过变形协调条件确定- C. 静定结构的外力可以通过静力平衡条件确定- D. 超静定结构的外力需要通过变形协调条件确定答案:A2. 简支梁在均布荷载作用下的最大弯矩是多少?- A. \( \frac{qL}{2} \)- B. \( \frac{qL^2}{8} \)- C. \( \frac{qL^2}{4} \)- D. \( \frac{qL^3}{12} \)答案:C## 二、简答题1. 请简述平面桁架的几何不变性条件。
- 平面桁架的几何不变性条件是指,桁架在不发生结构变形的情况下,能够保持其几何形状不变的条件。
根据Maxwell-Betti定理,对于一个平面桁架,其几何不变性条件为:桁架的杆件数 \( m \) 必须大于等于节点数 \( n \) 减去1,即 \( m \geq n - 1 \)。
2. 什么是弯矩图?它在结构设计中有什么作用?- 弯矩图是表示梁或框架结构在不同截面上的弯矩分布情况的图形。
在结构设计中,弯矩图可以帮助工程师确定结构的最大弯矩值,从而合理选择材料和截面尺寸,确保结构的安全性和经济性。
## 三、计算题1. 已知一简支梁,跨度为 \( L \) 米,梁上作用有集中力 \( P \)位于梁中点。
求梁的最大弯矩。
- 根据弯矩的计算公式,对于简支梁在中点作用集中力的情况,最大弯矩 \( M_{max} \) 为:\[ M_{max} = \frac{PL}{4} \]2. 某平面桁架由三个节点和三个杆件组成,节点1和节点3固定不动,节点2可以自由移动。
请判断该桁架是否为几何不变体系,并说明理由。
- 根据几何不变性条件,对于平面桁架,杆件数 \( m \) 必须大于等于节点数 \( n \) 减去1。
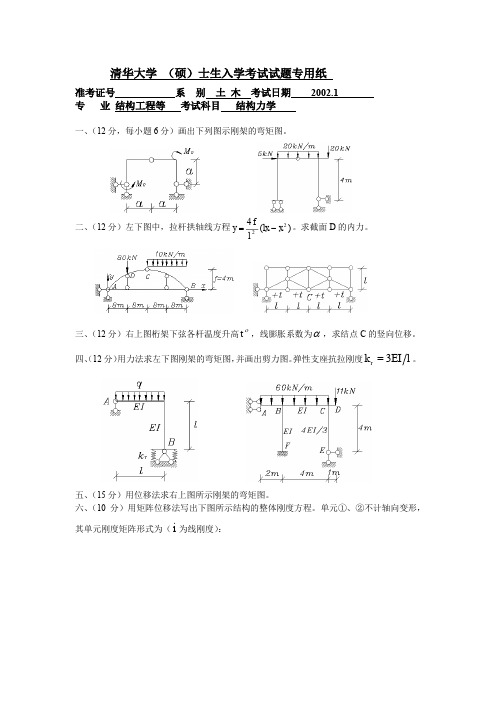
清华大学2002年结构力学试卷
载常数(固端弯矩)表
mAFB
ql 2 12
, mBFA
ql 2 12
清华大学 (硕)士生入学考试试题专用纸
准考证号
系 别 土 木 考试日期
专 业 结构工程等 考试科目 结构力学
2002.1
一、(12 分,每小题 6 分)画出下列图示刚架的弯矩图。
二、(12 分)左下图中,拉杆拱轴线方程 y 4 f (lx x 2 ) 。求截面 D 的内力杆温度升高 t ,线膨胀系数为 ,求结点 C 的竖向位移。 四、(12 分)用力法求左下图刚架的弯矩图,并画出剪力图。弹性支座抗拉刚度 kr 3EI l 。
七、(12 分)在左下图所示移动荷载作用下求梁跨中截面 C 的最大弯矩。
八、(12 分)右上图所示刚性横梁刚架,横梁总质量 m 5000kg ,柱的质量不计,水平突加
集 中 荷 载 Pt 10kN , 求 顶 部 最 大 动 位 移 及 其 相 应 的 时 间 , 并 画 出 动 弯 矩 图 。
五、(15 分)用位移法求右上图所示刚架的弯矩图。 六、(10 分)用矩阵位移法写出下图所示结构的整体刚度方程。单元①、②不计轴向变形,
其单元刚度矩阵形式为( i 为线刚度):
12i l 2 6i l 12i l 2 6i l
ke
对
4i 6i l
2i
12i l 2 6i l
称
4i
清华大学1995年结构力学试卷

清华大学 (硕)士生入学考试试题专用纸
准考证号 系 别 考试日期 95.1 专 业 考试科目
一、(10分)求图示半圆拱截面D 的内力。
二、(10分)画图示结构的弯矩图(每小题5分)
三、(10分)求图示桁架中杆1、2的轴力。
四、(15分)梁支座位移如图,l
a 2=θ,试用力法求M 图,并求C 点竖向位移。
五、(20分)试用位移法求刚架的M 、Q 、N 图。
六、(10分)求图示桁架杆1、2轴力的影响线,单位荷载在短梁上移动。
七、(10分)求图示结构的整体刚度方程,不计轴向变形的单元刚度矩阵为
八、(15分)梁端集中重量W=10kN ,分布质量不计,弹性支座刚度32l
EI k =,m l 3=, 241070.2m kN EI ⋅⨯=,阻尼比05.0=ξ,简谐荷载幅值P=2kN ,机器转速为500转/分钟,求质体的振幅及动力弯矩图。
清华大学824工程力学考研参考书目、考研真题、复试分数线

清华大学824工程力学考研参考书目、考研真题、复试分数线824工程力学课程介绍工程力学涉及众多的力学学科分支与广泛的工程技术领域,是一门理论性较强、与工程技术联系极为密切的技术基础学科,工程力学的定理、定律和结论广泛应用于各行各业的工程技术中,是解决工程实际问题的重要基础。
其最基础的部分包括“静力学”和“材料力学”。
工程力学是研究有关物质宏观运动规律及其应用的科学。
工程力学提出问题,力学的研究成果改进工程设计思想。
从工程上的应用来说,工程力学包括:工程力学刚体力学,固体力学,流体力学,流变学,土力学,岩体力学等。
人类对力学的一些基本原理的认识,一直可以追溯到史前时代。
在中国古代及古希腊的著作中,已有关于力学的叙述。
但在中世纪以前的建筑物是靠经验建造的。
1638年3月伽利略出版的著作《关于两门新科学的谈话和数学证明》被认为是世界上第一本材料力学著作,但他对于梁内应力分布的研究还是很不成熟的。
纳维于1819年提出了关于梁的强度及挠度的完整解法。
1821年5月14日,纳维在巴黎科学院宣读的论文《在一物体的表面及其内部各点均应成立的平衡及运动的一般方程式》,这被认为是弹性理论的创始。
其后,1870年圣维南又发表了关于塑性理论的论文水力学也是一门古老的学科。
早在中国春秋战国时期(公元前5~前4世纪),墨翟就在《墨经》中叙述过物体所受浮力与其排开的液体体积之间的关系。
欧拉提出了理想流体的运动方程式。
物体流变学是研究较广义的力学运动的一个新学科。
1929年,美国的宾厄姆倡议设立流变学学会,这门学科才受到了普遍的重视。
结构理论分析的步骤是首先确定计算模型,然后选择计算方法。
土力学在二十世纪初期即逐淅形成,并在40年代以后获得了迅速发展。
在其形成以及发展的初期,泰尔扎吉起了重要作用。
岩体力学是一门年轻的学科,二十世纪50年代开始组织专题学术讨论,其后并已由对具有不连续面的硬岩性质的研究扩展到对软岩性质的研究。
岩体力学是以工程力学与工程地质学两门学科的融合而发展的。
清华大学408计算机学科专业基础综合考研参考书目、考研真题、复试分数线
文化艺术出版社
《美学概论》
人民出版社
602 (建筑/城市、景 《中国城市建设史》 中国建筑工业出版社
作者
王向荣
[英]杰弗瑞·杰里柯//苏 珊杰·里柯 译者:刘滨 谊
周维权
董鉴泓,主编 沈玉麟,编 刘敦祯 潘谷西 陈志华 罗小未 高等艺术院校《艺术概 论》出版组 王朝闻主编 董鉴泓,主编
专注清华大学考研辅导
Stuart C.Poole
Linguistics 》
//166.111.107.7 下载)
616 艺术美学
《现代艺术哲学》 四川人民出版社 《美学与艺术欣赏》 高等教育出版社
H.G.布洛克 肖鹰
《新闻学概论》
中国传媒大学出版社,2007
刘建明
《转型中的新闻学》 南方日报出版社,2005
李希光
618 新闻与传播史 论
刘敦祯
《中国建筑史》
中国建筑工业出版社
潘谷西
《外国建筑史》
中国建筑工业出版社
陈志华
《外国近现代建筑史》中国建筑工业出版社
罗小未
603 数学分析
《数学分析新讲》 《数学分析》
北京大学出版社 上海科学技术出版社
张筑生 周民强,方企勤
604 普通物理
《大学物理》(第二版) 清华大学出版社
第一册至四册
张三慧
范钦珊等 刘鸿文
《材料力学》
高等教育出版社
孙训方
834 工程热力学 《工程热力学》
高等教育出版社
曾丹苓
835 理论力学及自 《理论力学》
动控制原理
《自动控制原理》
清华大学出版社 清华大学出版社
李俊峰 吴麒
836 普通物理(力 《大学物理》一、二、 清华大学出版社(第二版)
结构力学考研试题及答案

结构力学考研试题及答案一、选择题1. 在结构力学中,下列哪项不是结构分析的基本假设?A. 平面杆件假设B. 刚体假设C. 弹性体假设D. 等截面假设答案:B2. 梁的剪力图和弯矩图分别反映了梁的哪些性质?A. 剪力图反映弯矩,弯矩图反映剪力B. 剪力图反映剪力,弯矩图反映弯矩C. 剪力图反映弯矩,弯矩图反映剪力D. 剪力图反映剪力,弯矩图反映剪力答案:B二、填空题1. 根据虚功原理,结构在外力作用下处于平衡状态时,外力所做的虚功等于______所做的虚功。
答案:结构2. 静定结构与超静定结构的主要区别在于______。
答案:静定次数三、简答题1. 简述结构力学中力的平衡条件。
答案:结构力学中力的平衡条件包括:所有外力的合力为零;所有外力的合力矩为零。
2. 描述梁的弯曲变形与哪些因素有关。
答案:梁的弯曲变形与梁的长度、截面形状、材料的弹性模量、载荷大小和分布以及支撑条件有关。
四、计算题1. 已知一根悬臂梁,长度为4米,梁的自重为5KN/m,梁端承受一个集中力P=20KN,试求梁端的弯矩和剪力。
答案:梁端弯矩为20KN*m,梁端剪力为20KN。
2. 考虑一个简支梁,跨度为6米,梁上均匀分布载荷q=2KN/m,求梁中点的弯矩和剪力。
答案:梁中点弯矩为12KN*m,梁中点剪力为6KN。
五、分析题1. 描述结构力学中静不定次数的计算方法。
答案:静不定次数等于结构自由度数减去独立平衡方程数。
对于平面结构,自由度数为3n-3m,其中n为节点数,m为支座数。
2. 分析在结构力学中,如何利用弯矩图来确定梁的受力情况。
答案:通过绘制弯矩图,可以直观地观察到梁在不同位置的弯矩大小和方向,从而判断梁的受力情况。
弯矩图的正负号表示梁的受拉和受压区域,而弯矩图的形状则反映了梁的变形情况。
清华大学813结构力学基础考研参考书目、考研真题、复试分数线

结构的力学实验通常要耗费较多的人力、物力和财力,因此只能有限度地进行,特别是 在结构设计的初期阶段,一般多依靠对结构部件进行理论分析和计算。
江辑光 刘秀成
827 电路原理
《电路原理》
清华大学出版社,2007 年 3 月
于歆杰 朱桂萍 陆文 娟
《电路》(第 5 版) 高等教育出版社,2006 年 5 月
邱关源 罗先觉
828 信号与系统
《信号与系统》上册 高教出版社 2000 年 第二版 2008 年
郑君里等
下册
第 18 次、19 次印刷
《信号与系统引论》 高教出版社 2009 年 3 月第一版
学(数学规划、应用 《运筹学》(应用随机 清华大学出版社,2004 年 2 月
随机模型、统计学各 模型)
占 1/3)
《概率论与数理统计》 高等教育出版社,2001 年
(第 1~9 章)
W.L.Winston V.G. Kulkarni 盛聚等
《电路原理》(第 2 版)清华大学出版社,2007 年 3 月
清华大学考研参考书目
科目名称
参考书
出版社
《西方现代景观设计 中国建筑工业出版社
的理论与实践》
《图解人类景观—环
335 风景园林基础
同济大学出版社
境塑造史论》
342 建筑学基础
《中国古典园林史》(第 清华大学出版社
三版)
《中国城市建设史》 中国建筑工业出版社
《外国城市建设史》 中国建筑工业出版社
清华大学2003年结构力学试卷

清华大学 (硕)士生入学考试试题专用纸 准考证号 系 别 土 木 考试日期 2003.1专 业 结构工程等 考试科目 结构力学一、选择题(将正确答案的代码字母填入括号内,每小题6分,共48分)(1)图示平面体系的几何构造特征为( )A.几何不变,无多余约束;B.几何不变,有多余约束;C.几何瞬变;D.几何常变。
(2)对称三铰拱截面C 的轴力已知为kN N C 48=(压),则矢高f 应等于( )A.4m ;B. 4.5m ;C. 4.8m ;D. 5m 。
(3)图示刚架结点B 的转角及其方向为( )A.()EI ql 63( );B. ()EI ql 63( );C.()EI ql 2453( );D. ()EI ql 2453 ( )。
(4)图(a)所示刚架中,支座A 转动θ,支座B 下移b ,若以图(b )作为力法基本体系,则两个力法方程中的常数项应分别为( );,..21θθl b l A C C -=∆+=∆ B.θθl b l C c =∆+-=∆21,;C. θθl b l C C -=∆-=∆21,;D. θθl b l C c =∆--=∆21,。
(5)图示结构中,当立柱的弯曲刚度EI 不变,而链杆的拉伸刚度EA 增大时,则弯矩B A M M ,的变化为( )A.A M 增大,B M 减小; B. A M 减小,B M 增大; C.A M 增大,B M 增大.; D. A M 减小,B M 减小。
(6)图示等截面封闭圆环内部温度升高,外部温度不变,则任一截面K 的弯矩K M (内部受拉为正),轴力K N (拉力为正)的性质应为( )A.0,0><K KN M ; B. 0,0<>K K N M ; C. 0,0=<K K N M ; D. 0,0=>K K N M 。
(7)图示单自由度体系,质量为m ,柔度为δ,欲使体系自振周期减小时,m 与δ应当作如下变化( )A. m 增大,δ减小;B. m 减小,δ增大;C. m 与δ都增大;D. m 与δ都减小。
《结构力学Ⅰ》考研2021考研结构力学真题库

《结构力学Ⅰ》考研龙驭球版2021考研结构力学真题库第一部分考研真题精选一、选择题1图1-1-1所示平面体系的几何组成是()。
[浙江大学2010年研]A.几何不变,无多余约束B.几何不变,有多余约束C.几何常变D.几何瞬变图1-1-1【答案】A查看答案【解析】如图1-1-2所示,把左上角斜杆看成刚片1,把右侧三角形看成刚片2,把大地看成刚片3。
刚片1和刚片2形成瞬铰O(1,2),刚片1和刚片3形成瞬铰O(1,3),刚片2和刚片3形成无穷远处瞬铰O(2,3),三个铰不共线,根据三刚片规则,该体系是无多余约束的几何不变体系。
图1-1-22图1-1-3(a)所示体系的几何组成是()。
[武汉大学2012年研、郑州大学2010年研、华南理工大学2007年研、河海大学2007年研]A.无多余约束的几何不变体系B.几何可变体系C.有多余约束的几何不变体系D.瞬变体系图1-1-3【答案】A查看答案【解析】在几何构造分析时,可以将曲杆替换为直杆进行简化,所以可将图1-1-3(a)所示体系替换为图1-1-3(b)所示体系。
在任一体系上添加或去除二元体不改变体系的几何构造,因此依次去除C支座链杆与CE杆、D支座链杆与DE杆所组成的二元体,以及二元体A—E—B后,可知原体系为无多余约束的几何不变体系。
3如图1-1-4所示结构在所示荷载作用下,其支座A的竖向反力与支座B的反力相比为()。
[郑州大学2010年研、哈尔滨工业大学2008年研]A.前者大于后者B.二者相等,方向相同C.前者小于后者D.二者相等,方向相反图1-1-4【答案】B查看答案【解析】根据静力平衡条件,对C点取矩,∑M C=0,R A·l-R B·l=0,解得R A=R B,即支座A的竖向反力与支座B的反力大小相等,方向也相同。
4图1-1-5所示结构,当高度h增加时,杆件1的内力()。
[南京理工大学2012年研]A.增大B.减小C.不确定D.不变【答案】D查看答案【解析】根据零杆判别法,图示结构是对称结构受到对称荷载作用,杆件1、2与底下两根水平杆件组成“K”形结点,所以杆件1、2均为零杆,与结构高度h 增加与否无关。
清华大学《结构力学习题集》

清华⼤学《结构⼒学习题集》第三章静定结构的位移计算⼀、判断题:1、虚位移原理等价于变形谐调条件,可⽤于求体系的位移。
2、按虚⼒原理所建⽴的虚功⽅程等价于⼏何⽅程。
3、在⾮荷载因素(⽀座移动、温度变化、材料收缩等)作⽤下,静定结构不产⽣内⼒,但会有位移且位移只与杆件相对刚度有关。
4、求图⽰梁铰C 左侧截⾯的转⾓时,其虚拟状态应取:5、功的互等、位移互等、反⼒互等和位移反⼒互等的四个定理仅适⽤于线性变形体系。
6、已知M p 、M k 图,⽤图乘法求位移的结果为:()/()ωω1122y y EI +。
7、图a 、b 两种状态中,粱的转⾓?与竖向位移δ间的关系为:δ=? 。
8、图⽰桁架各杆E A 相同,结点A 和结点B 的竖向位移均为零。
9、图⽰桁架各杆EA =常数,由于荷载P 是反对称性质的,故结点B 的竖向位移等于零。
⼆、计算题:10、求图⽰结构铰A 两侧截⾯的相对转⾓?A ,EI = 常数。
11、求图⽰静定梁D 端的竖向位移 ?DV 。
EI = 常数,a = 2m 。
12、求图⽰结构E 点的竖向位移。
EI = 常数。
13、图⽰结构,EI=常数,M =?90kN m , P = 30kN 。
求D 点的竖向位移。
14、求图⽰刚架B 端的竖向位移。
15、求图⽰刚架结点C 的转⾓和⽔平位移,EI = 常数。
16、求图⽰刚架中D点的竖向位移。
EI =常数。
17、求图⽰刚架横梁中D点的竖向位移。
EI =常数。
18、求图⽰刚架中D 点的竖向位移。
E I = 常数。
19、求图⽰结构A、B两截⾯的相对转⾓,EI =常数。
20、求图⽰结构A 、B 两点的相对⽔平位移,E I = 常数。
21、求图⽰结构B 点的竖向位移,EI = 常数。
22、图⽰结构充满⽔后,求A 、B 两点的相对⽔平位移。
E I = 常数,垂直纸⾯取1 m 宽,⽔⽐重近似值取10 kN / m 3。
23、求图⽰刚架C 点的⽔平位移 ?CH ,各杆EI = 常数。
清华大学2004年秋结构力学试卷

2004 年秋季学期结构力学 试 题题号 一 二 三 四 五 六 七 八 九 十 总分分数一.判断题(本大题共5小题,每小题2分,共10分)1. 对于单自由度体系有如下关系1k δ−=对于多自由度体系也同样成立。
( ) 2. 仅在恢复力作用下的振动称为自由振动。
( )3. 对于杆系结构,用有限元方法得到的单元刚度矩阵与矩阵位移法得到的是一致的。
( ) 4. 在无限自由度体系的弹性稳定分析中,用静力法和能量法(瑞利-里兹法)得到的临界荷载是相同的。
( )5. 只要两个杆件的截面面积相同、所用材料相同,它们的极限弯矩就是相同的。
( ) 二.单项选择题 (本大题分3小题,每小题4分,共12分)1.对图示结构,若要使其自振频率增大,可以( )。
A. 增大; C. 增大m ;P F B. 增大EI ; D. 增大l 。
2.图示刚架杆单元的坐标转换矩阵[]66×T 000050..000050..中的第一行元素为( )。
A. ;[]8660 B. []0866−;C. ; []00000000;y ,x N ,y ,x 0033122186605..D. 。
[]0866050..−3. 三结点三角形单元的形函数满足的条件为 ( )。
A. N y ,x N 111===)()(113312211,)(B. 111===)()(y ,x N ,y ,x 00331210,)(N y ,x N ;C. 2111===)()(y ,x N ,y ,x 113312210,)(N y ,x N ;D.1111===)()(y ,x N ,y ,x i i y ,x ,)(N y ,x N 。
(注:为i 点坐标)第 1 页 (共 4 页)草 纸(草纸内不得答题)试 题:三. 填充题(本大题分3小题,每小题4分,共12分)1.图示体系不计杆件质量和轴向变形,各杆抗弯刚度为常数,其动力自由度为 。
2.在结构矩阵分析的后处理法中,由结构原始刚度矩阵根据实际支承情况,对结构原始刚 度矩阵加以修改以形成基本方程,采用的修改方法有 、 。
考研结构力学试题及答案

考研结构力学试题及答案一、选择题(每题2分,共10分)1. 下列关于结构力学的说法中,错误的是()。
A. 结构力学研究的是结构在外力作用下的受力和变形规律。
B. 结构力学是土木工程专业的核心课程之一。
C. 结构力学只研究静力平衡问题。
D. 结构力学研究的对象是各种类型的结构。
答案:C2. 在结构力学中,下列哪项不是结构的内力?A. 弯矩B. 剪力C. 位移D. 轴力答案:C3. 梁的剪力图和弯矩图中,剪力图的零点对应弯矩图的()。
A. 最大值点B. 最小值点C. 零点D. 极值点答案:C4. 下列关于桁架的说法中,正确的是()。
A. 桁架是由多个三角形组成的结构。
B. 桁架的所有杆件只承受轴向力。
C. 桁架的节点处只有铰接。
D. 桁架的杆件可以是任意形状。
答案:B5. 在结构力学中,静定结构和超静定结构的主要区别在于()。
A. 材料的类型B. 杆件的数量C. 约束的数量D. 受力的性质答案:C二、填空题(每题2分,共10分)1. 结构力学中的三刚度定理包括______、______和______。
答案:胡克定律、欧拉定律、卡斯特利亚诺定理2. 梁的弯矩可以通过______法或______法来计算。
答案:积分法、弯矩分配法3. 在结构力学中,______是指结构在受到外力作用时,其形状和尺寸不发生改变的状态。
答案:静力平衡4. 桁架的节点位移法是利用______原理来求解节点位移的一种方法。
答案:虚功5. 超静定结构的内力可以通过______法来求解。
答案:弯矩分配法或弯矩调整法三、简答题(每题5分,共20分)1. 简述结构力学中静定结构和超静定结构的概念。
答案:静定结构是指在静力平衡条件下,结构的内力和位移可以通过静力平衡方程和几何约束条件唯一确定的结构。
超静定结构则是指静力平衡方程和几何约束条件不足以唯一确定结构内力和位移的结构。
2. 描述结构力学中弯矩图的绘制步骤。
答案:首先,确定梁的支座反力;其次,根据反力和外力绘制剪力图;然后,利用剪力图积分得到弯矩图;最后,根据弯矩图的极值点和零点进行校正。
清华大学研究生院结构力学2007-2011考研真题

清华大学研究生院2007年考试科目:结构力学 题号:0901一.计算图1所示珩架指定杆的轴力()12,N N (10分)二.结构仅在ACB 部分温度升高t 度,并且在D 处作用外力偶M 。
试求图示刚架A,B 两点间水平向的相对位移。
已知:各杆的EI 为常值,α为线膨胀系数,h 为截面高度。
(20分)三.用力法分析图3所示结构,绘M 图。
计算时轴力和剪力对位移的影响略去不计。
各杆的EI 值相同。
(20分)半圆弧积分表:2211sin sin 2,cos sin 22424x x xdx x xdx x =-=+⎰⎰四.试用位移法求解图4所示刚架并绘M 图。
计算时不考虑轴力变形时对位移的影响。
(20分)杆端力公式:21,08f f AB BA ql M M =-=,53,88f f AB BA ql ql Q Q ==-一.试用力矩分配法计算图5所示连续梁并绘M 图。
(10分)二.求图示结构的自振频率和主振型,并作出振型图。
已知:122,,m m EI m m ===常数,忽略阻尼影响。
(20分)清华大学研究生院2008年招收硕士生入学试题考试科目:结构力学(包含结构动力学基础)题号:0901一.选择题:在正确答案处画“√”。
每题4分。
1.图示平面体系的几何组成性质是:A.几何不变且无多余联系的B.几何不变且有多余联系的C.几何可变的D.瞬变的2.图示结构A截面的剪力为:A. –PB. PC. P/2D. –P/23.图示珩架内力为零的杆为:A.3根B.6根C.8根D.7根3.图示结构的超静定次数为:A.6次B.4次C.5次D.7次4.图示梁当EI=常数时,B端的转角是:A. 3ql EI(顺时针)5/48B. 3ql EI(逆时针)5/48C. 37/48ql EI(逆时针)D. 3ql EI(逆时针)9/48二.计算题1.已知图示结构的M图,做Q.N图。
(10分)图(2.若P=1在梁AB上移动,试绘出M的影响线。
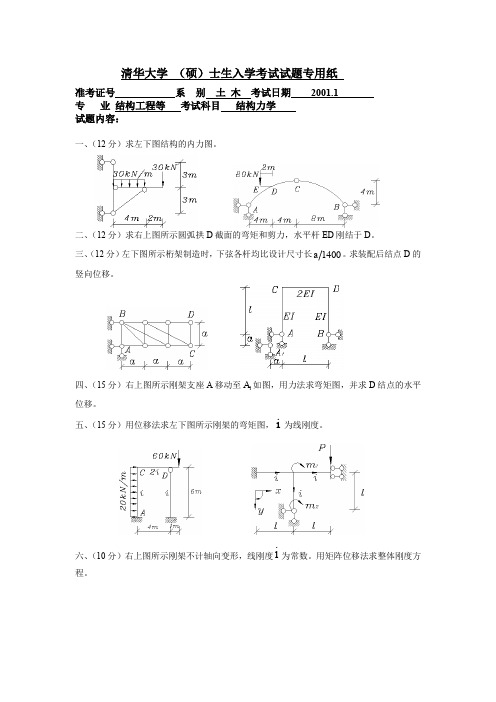
清华大学2001年结构力学试卷
附录 固端弯矩表
m
F AB
ql 2 12
, mBFA
ql 2 12
不计轴向变形的弯曲单元的单元刚度 矩阵为
12i l 2 6i l 12i l 2 6i l4i6i l Nhomakorabea2i
对
12i l 2
称
4i
清华大学 (硕)士生入学考试试题专用纸
准考证号
系 别 土 木 考试日期
专 业 结构工程等 考试科目 结构力学
试题内容:
2001.1
一、(12 分)求左下图结构的内力图。
二、(12 分)求右上图所示圆弧拱 D 截面的弯矩和剪力,水平杆 ED 刚结于 D。
三、(12 分)左下图所示桁架制造时,下弦各杆均比设计尺寸长 a 1400 。求装配后结点 D 的
竖向位移。
四、(15 分)右上图所示刚架支座 A 移动至 A1 如图,用力法求弯矩图,并求 D 结点的水平
位移。
五、(15 分)用位移法求左下图所示刚架的弯矩图, i 为线刚度。
i 六、(10 分)右上图所示刚架不计轴向变形,线刚度 为常数。用矩阵位移法求整体刚度方
程。
七、(12 分)画出主梁反力 RB 、弯矩 M K , M B 、剪力 QB右 的影响线。
八、(12 分)左下图所示梁不计分布质量,集中质量为,简谐荷载 Pt F sin t ,不计阻
尼。
(1)求质体 m 的运动方程;
(2)若 m 0.5 t(吨),F 10kN, 1.25 ,( 为自振频率),EI 1.8 105 kN m2 , a 1m ,求 B 点振幅并画出最大动力弯矩图。
结构力学考研题目及答案

结构力学考研题目及答案
题目:请根据给定的平面桁架结构,确定其内力分布,并计算节点A 的位移。
已知条件:
- 平面桁架由6根杆件组成,节点A、B、C、D、E、F。
- 节点A受到竖直向下的力P=10kN。
- 所有杆件的截面积均为A=0.02m²,材料的弹性模量E=200GPa。
- 忽略自重和杆件的剪切变形。
要求:
1. 画出桁架的内力图。
2. 计算节点A的竖直位移。
解答:
1. 内力图的绘制:
首先,我们应用节点法和截面法来确定桁架中每根杆件的内力。
对于节点A,由于其受到向下的力P,我们可以假设所有与节点A相连的杆件都受到拉力。
然后,通过平衡节点A的力矩和力,我们可以确定与节点A相连的杆件的内力。
接着,我们继续使用节点法来确定其他节点的内力。
最终,我们将得到整个桁架的内力图。
2. 节点A的竖直位移计算:
根据桁架的内力图,我们可以确定与节点A相连的杆件所受的拉力。
位移可以通过以下公式计算:
\[ \delta = \frac{PL}{EA} \]
其中,P是作用力,L是杆件长度,E是弹性模量,A是截面积。
由于
题目中没有给出杆件的具体长度,我们假设与节点A相连的杆件长度为L。
将已知条件代入公式,我们可以得到节点A的竖直位移。
[注:由于题目中未给出具体的桁架结构图和杆件长度,以上解答为通用解答方法,具体数值需要根据实际结构图来确定。
]。
