机械原理课程设计—插床机构说明书
插床主体机构的设计---说明书

学院《机械原理课程设计》任务书专业材料成型及控制工程学生姓名_________班级12 材料本 ___________学号1201240041 _________指导教师郭国谊老师教研室主任 _______ 起止日期2014-06-20目录第一章绪论 (3)第二章机构简介与设计数据 (4)第三章设计内容及方案分析 (6)1)插刀速度和加速度分析 (6)2 )数据及函数曲线分析 (10)3)凸轮机构设计 (13)4)齿轮机构设计 (14)第四章设计体会 (15)第五章参考文献 (16)附图 (16)第一章绪论一、设计的题目:插床运动系统方案设计及其运动分析。
二、工作原理插床机械系统的执行机构主要是由导杆机构和凸轮机构组成。
下图为其参考示意图,电动机经过减速传动装置(皮带和齿轮传动)带动曲柄 2 转动,再通过导杆机构使装有刀具的滑块6沿导路y—y 作往复运动,以实现刀具的切削运动。
刀具向下运动时切削,在切削行程H中,前后各有一段0.05H的空刀距离,工作阻力F为常数;刀具向上运动时为空回行程,无阻力。
为了缩短回程时间,提高生产率,要求刀具具有急回运动。
刀具与工作台之间的进给运动,是由固结于轴Q 上的凸轮驱动摆动从动件l O D和其它有关机构(图中未画出)来完成的。
三,此设计是工科专业在学习《机械原理》后进行的一次较全面的综合设计训练,其目的:1. 巩固理论知识,并应用于解决实际工程问题;2. 建立机械传动系统方案设计、机构设计与分析概念;3. 进行计算、绘图、正确应用设计资料、手册、标准和规范以及使用经验数据的能力训练。
四、主要内容:1、根据插床机械的工作原理,拟定2〜3个其他形式的执行机构(连杆机构),并对这些机构进行分析对比。
2、根据给定的数据确定机构的运动尺寸。
要求用图解法设计,并将设计结果和步骤写在设计说明书中。
3、导杆机构的运动分析。
分析导杆摆到两个极限位置及摆到与机架QQ位于同一直线位置时,滑块 6 的速度和加速度。
插床设计计算说明书

3)对主执行机构用解析法进行运动分析,用相对运动图解法对其中的一个位置加以 机计算结果画出插刀位移线图,速度线图和加速度线图;
4)用图解法对主执行机构ห้องสมุดไป่ตู้一个位置进行动态静力分析;
5)用解析法对控制工作台横向进给的凸轮机构进行运动分析;
6)用图解法绘制控制工作台横向进给的凸轮机构的位移曲线及凸轮轮廓曲线;
1)确定变速组数目和变速组排列方式
由于转速级数Z=6,故取两个变速组,根据各变速组,根据各变速组中传动副数目应 则,选择:
Z=6=3
即前面用一个三联齿轮,后面用一个双联齿轮
2)确定基本组和扩大组
根据前紧后松的原则,选择6=3i・23方案,即第一变速组为基本组,其三档传动比在转速 二变速组为扩大组,两档传动比在转速图上相差三格。
凸轮从动件杆长(mm)
125
推程许用压力角[]推程
40
回程许用压力角[]回程
50
滚子半径rr(mm)
15
刀具半径rc(mm)
0.08
插刀阻力曲线如图4所示。插刀在切入、退出工件时均有0.05H的空载行程
F,
Fmax
S
0.05H
005H-
—
H
图2刨刀阻力曲线
1.4设计任务
1)完成各执行机构的选型与设计计算,选择原动机,拟定机械传动方案,确定各级 运动简图及机械系统传动方案设计图;
插床机械设计的机构选型功能执行构件工艺动作执行机构插削成形直线往复运动具有急回特性导杆机构工作换位工作台前后左右方向的进给运动和间歇性转动凸轮机构棘轮机构槽轮机构不完全齿轮32主执行机构的选择根据题目要求及所提供的参数分析综合插床机构自身特点以及机构方案选择的相关要求我们最终选择的主执行机构是方案1
插床机械设计说明书

插床机械设计说明书一、引言插床是一种常用的机床,广泛应用于汽车零部件、摩托车配件、工程机械和电子设备等行业。
本文档旨在为插床的机械设计提供详尽的说明,以帮助相关人员更好地了解插床机械的设计原理、参数和使用方法。
二、设备概述1. 设备简介插床是一种通过切削方式加工工件的机床。
它通过工件夹于工作台上,并通过工作台和刀座之间的相对运动来完成工件的加工。
2. 设备特点插床机械具有以下特点:- 结构简单,易于操作;- 具备高效的加工能力,适用于各类加工任务;- 插床机械具有较高的精度和重复定位精度;- 自动化程度高,可以实现自动送料和自动切削;- 插床机械具有良好的刚性和稳定性。
三、机械设计1. 结构设计插床机械的结构设计应该依据其加工任务和工作环境进行合理的设计。
主要结构包括机身、工作台、刀座、主轴、进给装置等。
2. 主要参数插床机械的设计中需要考虑的主要参数包括:- 加工能力:包括最大加工直径、最大加工长度等;- 加工精度:包括重复定位精度、加工精度等;- 主轴转速:根据加工任务的要求确定合适的主轴转速范围;- 进给速度:根据加工任务的要求确定合适的进给速度范围;- 动力需求:包括主轴动力和进给动力。
3. 刀具设计插床机械的刀具设计应该合理选择适应不同加工任务的刀具,并考虑刀具的刚度和耐用性。
刀具设计应该遵循以下原则:- 刀具选择合适的切削材料和刃型,以实现高效加工;- 刀具应具备良好的刚性和稳定性,以保证加工精度;- 刀具应易于更换和调整,以提高生产效率。
四、使用方法1. 安全操作插床机械的使用需要严格遵循安全操作规程,包括佩戴防护装置、正确使用个人保护设备、确保工件夹紧牢固等。
2. 操作步骤插床机械的操作步骤如下:- 启动插床机械,进行设备预热;- 将工件夹紧于工作台上,调整工作台和刀座的位置;- 调整主轴转速和进给速度;- 启动切削过程,并进行加工;- 完成加工后,停止切削,关闭插床机械。
五、维护保养插床机械的维护保养对于设备的正常运行和寿命非常重要。
插床机构综合设计说明书

机械原理课程设计之蔡仲巾千创作插床机构综合学生姓名:卢佛俊专业班级:08机电二班学号: 20087668目录一、设计题目简介二、设计数据与要求三、设计任务四、插床主体机构尺寸综合设计五、插床切削主体结构运动分析六、重要数据及函数曲线分析七、工作台设计方案八、总结九、参考文献设计题目:插床机构综合一、设计题目简介插床是经常使用的机械加工设备, 用于齿轮、花键和槽形零件等的加工.图示为某插床机构运动方案示意图.该插床主要由带转动、齿轮传动、连杆机构和凸轮机构等组成.电念头经过带传动、齿轮传动减速后带动曲柄1回转, 再通过导杆机构1-2-3-4-5-6, 使装有刀具的滑块沿路途y-y作往复运动, 以实现刀具切削运动.为了缩短空程时间, 提高生产率, 要求刀具具有急回运动.刀具与工作台之间的进给运动, 是由固结于轴上的凸轮驱动摆动从动件和其他有关机构(图中未画出)来实现的.针对图所示的插床机构运动方案, 进行执行机构的综合与分析.二、设计数据与要求依据插床工况条件的限制, 预先确定了有关几何尺寸和力学参数, 如表6-4所示.要求所设计的插床结构紧凑, 机械效率高.插床机构设计数据插刀往复次数(次/min ) 60 插刀往复行程(mm )100 插削机构行程速比系数2 中心距(mm )150插床机构运动方案示意图插刀所受阻力曲线三、设计任务1. 针对图所示的插床的执行机构(插削机构和送料机构)方案, 依据设计要求和已知参数, 确定各构件的运动尺寸, 绘制机构运动简图;2. 假设曲柄1等速转动, 画出滑块C 的位移和速度的变动规律曲线;3. 在插床工作过程中, 插刀所受的阻力变动曲线如图所示, 在不考虑各处摩擦、其他构件重力和惯性力的条件下, 分析曲柄所需的驱动力矩;4. 取曲柄轴为等效构件, 确定应加于曲柄轴上的飞轮转动惯量;5. 用软件(VB 、MATLAB 、ADAMS 或SOLIDWORKS 等均可)对执行机构进行运动仿真, 并画出输出机构的位移、速度、和加速度线图.6. 图纸上绘出最终方案的机构运动简图(可以是计算机图)并编写说明书.四、插床主体机构尺寸综合设计 方案选择:方案一:结构简图如下方案二:机构简图如下:经过对方案一和方案二的比力, 我们发现方案一的优点是结构杆长之比1 质心坐标(mm ) 50 质心坐标(mm ) 50 质心坐标(mm )120 凸轮摆杆长度(mm ) 120 凸轮摆杆行程角(0) 15 推程许用压力角(0)45 推程运动角(0) 90 回程运动角(0) 60 远程休止角(0)15 推程运动规律 3-4-5次多项式回程运动规律 等速速度不均匀系数最年夜切削阻力(N )1000 阻力力臂(mm ) 120 滑块5重力(N ) 320 构件3重力(N )160构件3转动惯量(kgm 2)简单, 易于实现.方案二的优点是可接受的力要年夜.考虑到插床需要较年夜的进给里用已加工零件, 所以我们选择方案二, 下面我们就相对方案二进行进一步的计算和设计.行程H=100mm, 行程比系数K=2,, YY轴的距离图 1 极限位置得极为夹角:首先做出曲柄的运动轨迹, , 随着曲柄的转动, 有图知道, 于圆相切于上面时,与圆相切于下面时, 刀具处于上极限位置..由几何关系知, , 于是可得,由几何关系可得:代入数据得即曲柄长度为2.图 2 杆由图 2 知道, ,在确定曲柄长渡过程中, 我们获得021221160=∠=∠O O A O O A , 那么可获得022160=∠B O B , 那么可知道三角形221O B B ∆等边三角形.又有几何关系知道四边形1221C C B B 是平行四边形, 那么1212C C B B =, 又上面讨论知221O B B ∆为等边三角形, 于是有1221B B O B =, 那么可获得mm O B 10022=,即mm BO 1002=又已知1/2=BO BC , 于是可获得 即杆2,BO BC 的100mm.3.2O 到YY 轴的距离简直定图 32O 到YY 轴的距离B1有图我们看到, YY, 同一点的压力角先减小, 后又增年夜, 那么在中间某处必有一个最佳位置, 使得每个位置的压力角最佳.考虑两个位置:1当YY, 即图3中左边的那条点化线, B1点时, 当B将会呈现最年夜压力角., 即图中右边的那条点化线时, B点转到B1时将呈现最年夜压力角为了使每一点的压力角都为最佳, 我们可以选取YY轴通过CB1中点(C.又几何关系知道:, 再代入其他数据, 得:综上,行程H=100mm, 行程比系数K=2,, YY轴的距离图 4 极限位置得极为夹角:首先做出曲柄的运动轨迹, , 随着曲柄的转动, 有图知道, 于圆相切于上面时,与圆相切于下面时, 刀具处于上极限位置..由几何关系知, , 于是可得,由几何关系可得:代入数据得即曲柄长度为2.图 5 杆由图 2 知道, ,在确定曲柄长渡过程中,形.又有几何关系知道四边平行四边形, 那么又上面讨论为等边三角形, 于是有又已知, 于是可获得即杆的100mm.3.2O 到YY 轴的距离简直定图 62O 到YY 轴的距离有图我们看到, YY 轴由3311y y y y 移动到过程中, 同一点的压力角先减小, 后又增年夜, 那么在中间某处必有一个最佳位置, 使得每个位置的压力角最佳. 考虑两个位置:1当YY 轴与圆弧12B B 刚相接触时, 即图3中左边的那条点化线, 与圆弧12B B 相切与B1点时, 当B 点转到12,B B , 将会呈现最年夜压力角.12B B 重合时, 即图中右边的那条点化线时, B点转到B1时将呈现最年夜压力角为了使每一点的压力角都为最佳, 我们可以选取YY 轴通过CB1中点(C 点为12B O 与12B B 得交点).又几何关系知道:B 1, 再代入其他数据, 得:综上, 插床主体设计所要求的尺寸已经设计完成.五、插床切削主体结构运动分析用图解法作机构的运动分析和静态静力分析逆时针旋转, 由作图法求解位移, 速度, 加速度.规定位移, 速度, 加速度向下为正, 插刀处于上极限位置时位移为0.(1)位移在1:1 的基础上, 量的位移为79.5mm., 即曲柄转过175°.(2)速度由已知从图中可知直, 由理论力学中分歧构件重合点处所法可得其中上与A点重合的点的速度AOB上与A点重合的点相对滑块的速度AOB上与A点重合的速度.又由图知BC垂直YY轴平行, 有理论力学同一构件分歧点的方法可得:其中C点, 即插刀速度C点相对B点转动速度是B点速度.又B点是杆件3 上的一点, , 杆件3, 且B点和杆件与A, 于是可得:则可到由已知可得, 规定选取比例尺则可的矢量图如下:12mm,于是,即曲柄转过175°时, 插刀的速度为0.174m/s.(3)加速度由理论力学知识可得矢量方程:其中, 是滑块上与A点重合点的加速度,科氏加速度, (其中, q的加速度, 年夜小位置,是C点相对B点转动的向心加速度,方向过由C指向B C点相对B点转动的切向加速度, 年夜小位置, 方向垂直BC.次矢量方程可解,B时杆AOB上的一点, 构AOB , B点在, 角加速度)可得又由理论力学,结合图可获得;其中C相对B点转方向由C点指向B点;C相对B点转动的切向加速度, 年夜小未知, 方向与BC垂直.次矢量方程可解, 从而可获得C点, 即插刀的加速度.取比例可得加速度矢量图如下:12mm, 于是,(1)位移在1:1 的基础上, 滑块的位移为 1.5mm., 即曲柄转过355°.(2)速度由已知从图中可知直, 由理论力学中分歧构件重合点处所法可得其中上与A点重合的点的速度AOB上与A点重合的点相对滑块的速度AOB上与A点重合的速度.又由图知BC垂直YY轴平行, 有理论力学同一构件分歧点的方法可得:其中C点, 即插刀速度C点相对B点转动速度是B点速度.又B点是杆件3 上的一点, , 杆件3, 且B点和杆件与A, 于是可得:则可到由已知可得, 规定选取比例尺则可的矢量图如下:2.16mm,于是, 可得:即曲柄转过355°时, YY轴向上.(3)加速度由理论力学知识可得矢量方程:其中, 为滑块上与A点重合点的加速度,哥氏加速度,的加速度, 年夜小位置, . B是杆AOB上的一点, 杆AOB , B5侧, 角加速度)可得又由理论力学,结合图可获得;其中C相对B点转方向由C点指向B点;C相对B点转动的切向加速度, 年夜小未知, 方向与BC垂直.次矢量方程可解, 从而可获得C点, 即插刀的加速度.取比例可得加速度矢量图如下六、重要数据及函数曲线分析角度位移S(mm)速度V(m/s)加速度α(m/s2)7 1.5 03 2.05 14 3 55 221 4 528 0.115 1.95 35 8 2542 3649 156 163 1 5570 6 0.85 77 25 0.77 84 30 92 0.63 91 31 0.201 598 07 0.15 105 41 10 0.09 112 45 12 -0.02 119 4 2 -24 126 55 12133 57 05140 01 3147 2154 0.196 -0.36 161 73 0.19 -0.39 168 76 0.18 -0.4 175 79.5 4 -0.432 180 83 0.172 -0.45 187 85 7 -0.59 194 90 40 -0.7 201 92 3 -0.79 208 26 -0.9 215 95 0.093 -222 98 0.073 -229 9 0.05 -1.9 236 99 0.03 -243 99 -2.6 250 98 -257 97 -264 -271 90 -0.274 -5.12278 -5.1285 73 -0.52 -292 66 -0.574 -299 -0.62 -306 -0.61313320 -0.43327 -0.3334 -0.23341 3 -0.13348 -355 -0.0216 3.04360 0 01, 滑块C位移由0开始增年夜, 年夜约在240度时达到最年夜, 然后开始减少, 易知滑块C进程与回程时, , 这说明了曲柄.2:, , 速度V 正向增年夜, 年夜约在120度时达到最年夜, 然后呈现下降趋势, 在240度时下降为0, 标明位移以增年夜到最年夜, 即滑块C达到最下端, 由曲线看出, 滑块C的正向平均速度比负向平均速度小, 进一步标明了急回运动的存在.进程时, 速度比力小, 更有利于进刀;回程时, 速度较快, 有利于提高工作效率, 充沛证明了此机构设计的合理性.下面对特殊点作一下分析:转角为0度时, V=0;曲柄转动至120度, 正向速度达到最年夜值0.22m/s, 此时滑块C具有最年夜速度, 当曲柄继续转动至240度时正向速度减少至0, 此时由速度是位移的变动率可知, 其位移达到最年夜值.当曲柄继续转动时, 滑块C速度反向, 酿成负向速度, 随着转角增年夜而增年夜, 曲柄转至240度, 速度达到负向最年夜值0.63m/s之后, 当滑块继续由摇杆带动时, 却曲柄由300度转至360度时, 其速度由负向最年夜值酿成0.3, 滑块C先向下作加速运动, 但加速度越来越小, 可是加速度越来越小, 然后反向增年夜知道位移达到最年夜, 接着滑块进入空回程, 由于存在急回运动, 加速度迅速正向增年夜, 达到最年夜后又开始减小, 直到滑块C进入工作行程.下面对一些特殊点进行分析:进程时, 滑块C具有正向加速度, 由2.2开始减少, 在102度时达到0, 当角度继续增年夜时, 加速度反向增年夜, 年夜约在240度时滑块位移达到最年夜值, 可是加速度还是在反向增年夜, 而且增长率明显比前段更年夜, 当角度达到270度时加速度增年夜到5.2m/s2时达到峰值, 开始减少, 在300度左右是达到0, 然后正向增长, 标明了滑块将要向上减速运动, 最后回到0位移, 然后往复运动.我们可以看出, 在0至240度区间内, 加速度都很平缓, 而在240至360度内, 加速度变动很快, 都说明了急回运动的存在.七、工作台设计方案方案的选择:方案一:凸轮连杆机构(题目中给的方案)方案讨论:①运动怎样从电念头引下来;②工作台的运动情况及相对位置;③怎样确定凸轮的装置角, 怎样让整个机构协调工作.第一个问题:由于插床机身高度较高, 所选择的机构传动方案必需能够实现长距离传动, 且保证定传动比, 长距离传动方案多种多样, 如:齿轮系传动;带传动;链传动;平行四边形机构传动等.齿轮系传动会使整个机器结构变得复杂;带传动自己具有个缺点:会发生弹性滑动, 且其精度不高;链传动则会发生冲击, 并陪伴着很年夜的噪声;平行四边形机构传动效率高, 结构简单, 完全复制了原动件的运动, 且其刚度较高, 故选取平行四边形机构这个方案来进行长距离传动.第二个问题:工作台最终可实现前后、左右作间歇直线送进运动和作间歇回转送进运动.送进运动必需与主切削运动协调配合, 即进给运动必需在刀具非切削期时间即上超阶段以内完成, 以防止刀具的切削运动与工作台的送进运动发生干涉.要实现工作台的三个间歇运动, 即将原动件的连续往复摆动转化为从动件的单向间歇运动, 根据机构的这个运动特性, 知可选取棘轮机构, 实现预期运动.同时, 机构中添加复合锥齿轮, 可实现改变锥齿轮的旋转方向, 从而改变工作台的运动方向;同时加上离合器机构, 以实现动力的传递或断开.这样, 当机械运动传递到棘轮时, 棘轮作有规律的单向间歇运动, 同时将摆动转化为沿轴的自转运动, 再通过复合锥齿轮传递给工作台.除靠各机械构件带开工作台运动外, 还可用手柄把持, 此时与棘轮连接的离合器处于断开状态, 棘轮的运动及动力不继续传递, 不影响手柄对工作台的把持.要保证送进运动与主切削运动协调配合, 即进入上超工作台开始运动, 结束上超工作台停止运动, 直到下一个上超阶段才重新运动, 则必需保证推程运动角小于即是上超区间的角度.第三个问题:由于工作台的进给运动只能发生在上超阶段, 故我们所选择的机构传动方案中机构的运动只有在上超阶段才华传递给工作台, 其它时间工作台都是处于静止状态, 故选择凸轮式间歇运念头构, 同时为了保证机构协调工作, 凸轮的装置角必需在上超区间的角度范围内.方案简图方案二:不完全齿轮间歇旋转机构该机构中不完全齿轮的旋转运动由连杆机构和锥轮从主动齿轮引导下来, 然后由不完全齿轮推开工作台运动, 设计的不完全齿轮的主动轮旋转一周时从动轮旋转1/10周.方案简图方案比力:比力两个方案, 可以发现方案一比如案二要多设计凸轮, 由于凸轮设计比力麻烦且精度不高, 所以我们选择方案二, 下面就方案二做进一步计算: 齿轮传动计算:取1z 22=, 21z 5z 225110=⨯=⨯=.依照要求取m 8=, 压力角020α=则中心距采纳标准中心距则 12a m z z /2=822+110/2=528=+⨯()()mm不完全齿轮的计算:设计的不完全齿轮的主动轮旋转一周时从动轮旋转1/10周.齿轮部份取参数为z=120, m=8,凸轮止弧和凹轮止弧则依照基圆的圆弧来配合八、总结这次设计课程不单让我加深了对机械原理理论课程的理解和认识, 更培养了我用理论知识去解决实际问题的能力.作为初度接触设计的我, 对未来的设计布满了信心.当我们遇到一个问题时, 首先不能畏惧, 而是要对自己有信心, 相信通过自己的努力一定能解决的.就象人们常说的在战略上藐视它.可是在战术上的重视它.通过慎重的考虑认真的分析, 脚踏实地去完成它, 克服重重困难, 当你胜利实现目标时, 那种成绩感一定会成为你生长的动力.还有就是经过这次的课程设计, 我在绘图方面和三维仿真方面的知识也获得进一步的加强, 让我受益匪浅.九、参考文献裘建新.机械原理课程设计指导书.北京:高等教育出书社。
插床机构说明书

插床机构说明书文档编制序号:[KKIDT-LLE0828-LLETD298-POI08]机械原理课程设计插床机构说明书负责人:廖昭洋学院:机电工程学院班级:机械1102班学号:日期: 2013年 7月11日加速度矩阵根据矩阵,编写matlab程序如下:clear all;clc;w1=;l1=;l3=;l6=;l61=;l4=;for m=1:3601o1(m)=pi*(m-1)/1800;o3(m)=atan((l1*sin(o1(m)))/(l6+l1*cos(o1(m))));s3(m)=(l1*cos(o1(m))+l6)/cos(o3(m));o4(m)=acos((-l61+l3*cos(o3(m)))/l4);se(m)=-l3*sin(o3(m))+l4*sin(o4(m));if o1(m)==0o3(m)=0; s3(m)=l1+l6;endif o1(m)==pio3(m)=0; s3(m)=l6-l1;endA1=[cos(o3(m)),-s3(m)*sin(o3(m)),0,0;sin(o3(m)),s3(m)*cos(o3(m)),0,0;0,-l3*sin(o3(m)),l4*sin(o4(m)),0;0,-l3*cos(o3(m)),l4*cos(o4(m)),-1]; B1=w1*[-l1*sin(o1(m));l1*cos(o1(m));0;0];D1=A1\B1;E1(:,m)=D1;ds(m)=D 1(1);w3(m)=D1(2);w4(m)=D1(3);ve(m)=D1(4);A2=[cos(o3(m)),-s3(m)*sin(o3(m)),0,0;sin(o3(m)),s3(m)*cos(o3(m)),0,0;0,-l3*sin(o3(m)),l4*sin(o4(m)),0;0,-l3*cos(o3(m)),l4*cos(o4(m)),-1]; B2=-[-w3(m)*sin(o3(m)),(-ds(m)*sin(o3(m))-s3(m)*w3(m)*cos(o3(m))),0,0;w3(m)*cos(o3(m)),(ds(m)*cos(o3(m))-s3(m)*w3(m)*sin(o3(m))),0,0;0,-l3*w3(m)*cos(o3(m)),l4*w4(m)*cos(o4(m)),0;0,l3*w3(m)*sin(o3(m)),-l4*w4(m)*sin(o4(m)),-1]*[ds(m);w3(m);w4(m);ve(m)];C2=w1*[-l1*w1*cos(o1(m));-l1*w1*sin(o1(m));0;0];B=B2+C2;D2=A2\B;E2(:,m)=D2;dds(m)=D 2(1);a3(m)=D2(2);a4(m)=D2(3);ae(m)=D2(4);end;o11=o1*180/pi;y=[o3*180/pi;o4*180/pi];w=[w3;w4];a=[a3;a4];figu re;subplot(221);h1=plotyy(o11,y,o11, se); axis equal;参考文献[1]孙桓,陈作模,葛文杰主编.机械原理.第七版.北京:高等教育出版社,2006.[2]王三民主编.机械原理与设计课程设计.北京:机械工业出版社,2005.[3]刘毅主编.机械原理课程设计.武汉:华中科技大学出版社, 2008.[4]李滨城.徐超主编.机械原理MATLAB辅助分析.北京:化学工业出版社,2010.。
机械原理课程设计-插床导杆机构设计.docx
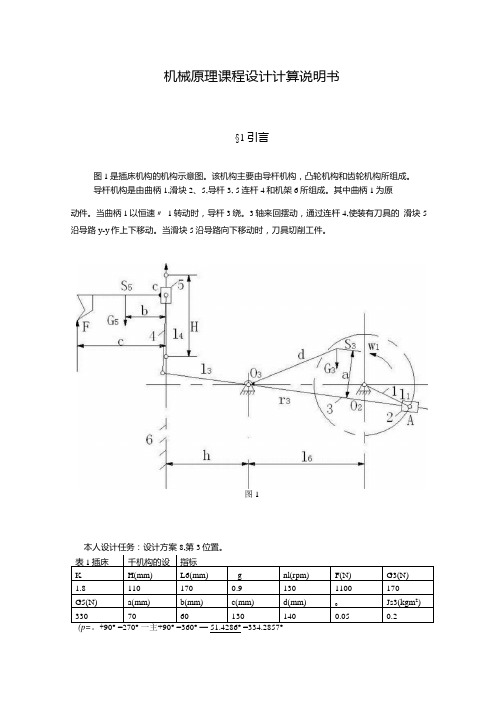
机械原理课程设计计算说明书§1引言图1是插床机构的机构示意图。
该机构主要由导杆机构,凸轮机构和齿轮机构所组成。
导杆机构是由曲柄1,滑块2、5,导杆3, 5连杆4和机架6所组成。
其中曲柄1为原动件。
当曲柄1以恒速〃1转动时,导杆3绕。
3轴来回摆动,通过连杆4,使装有刀具的滑块5沿导路y-y作上下移动。
当滑块5沿导路向下移动时,刀具切削工件。
图151.4286° =334.2857°| o 2 23= 2 血1 = 2.3.14159」3° =13.6136 (rad/s)160 60表中:K——行程速度变化系数;H——滑块5的冲程;,6 =o3 --------- 饺链中心。
2和。
3之间的距离;等I B C/lo3 B杆长比;---曲柄1的转速;F——切削力;G3——导杆3的重量;Gg ------ 滑块5的重量;O——机器运转的不均匀系数;Js3 ——导杆3对其质心轴的转动惯量;§ 2插床导杆机构综合及运动分析一、已知条件行程速度变化系数K,饺链中心。
2和。
3之间的距离,6,滑块5的冲程H,杆长比& 滑块5沿导路方向y—y垂直于导杆3摆角巾的分角线。
3。
2,并使导杆机构在整个行程中都能得到较小的压力角,曲柄转速〃1及指定的相对运动图解法的作业位置。
二、插床导杆机构的综合如图 1 所示,简记/[ = l o2 A ',3 =,o3 B '=,BC ',6 =o3 , h= l oo^根据给定的已知条件,可按下列步骤确定插床导杆机构的有关尺寸1)计算极位角e及导杆摆角WW=0=1XO°KT =1湘° L8T =51.4286°(1)K+1 1.8+1式中:K为行程速度变化系数2)求ZiI =/sin 妇7»布51.4286°=73 7602 (mm) (2)16 2 2式中:16为饺链中心。
机械原理课程设计插床机械设计

机械原理课程设计设计计算说明书设计题目插床机械设计设计任务书1.1 设计题目插床1.2 插床简介插床是用于加工中小尺寸垂直方向的平面或直槽的金属切削机床,多用于单件或小批量生产。
为了适用不同材料和不同尺寸工件的粗、精加工,要求主执行构件—插刀能以数种不同速度、不同行程和不同起始位置作垂直方向的往复直线移动,且切削时插刀的移动速度低于空行程速度,即插刀具有急回现象;安装工件的工作台应具有不同进给量的横向进给,以完成平面的加工,工作台还应具有升降功能,以适应不同高度的工件加工。
1.3 设计要求及设计参数设计要求:要求主执行机构工作行程切削平稳、压力角较小。
进给机构压力角不超过许用值。
设计参数如下所示:插床机构设计3号题目参数题号 3主执行机构曲柄转速n2/(r/min)50 曲柄l O2A/mm75插刀行程H/mm120行程速比系数K 1.8 连杆与导杆之比l BC0.55 力臂d(mm) 108 工作阻力F max(N) 10800导杆质量m4(kg) 22 导杆转动惯量J S4(kgm2) 1.2 滑块质量m6(kg) 60进给机构从动件最大摆角max20凸轮从动件杆长(mm) 130 推程许用压力角[]推程42回程许用压力角[]回程50滚子半径r r(mm) 15刀具半径r c(mm) 0.08一:主执行机构设计与分析1:插床机械设计参数以及相关参数计算曲柄转速n 2/(r/min ) 曲柄长度l O2A =75mm插刀行程H=120mm行程速度比系数K=1.8连杆与导杆之比l BC =0.55力臂d=108mm 工作阻力F=10800N导杆4的质量m 4=22kg 导杆4的转动惯量Js4=1.1滑块6的质量m 6=60 一、插床导杆机构的综合1、计算极位夹角 、曲柄角速度1ω、曲柄角加速度1εn 2=50l O2A =75m mH=120m mK=1.8l BC =0.55d=108mmF=10800Nm 4=22kgJs4=1.1m 6=6046.667θ=1 4.922/rad sω=2、求导杆长度CD L 、连杆长度DE L 、中心距AC L 根据插床机构结构示意图,由几何条件可得138.286CD L mm =因为/0.55DE CD L L =,76.06DE L mm =152.114AC L mm =3、求弓形高b 、导路距离e L13.695CD L mm =283.553e L mm =二:主执行机构运动分析已知:曲柄的转速n=45 rad/min ,滑块质量为50kg ,导杆的质量为28kg ,其质心转动惯量为1.2 kg ·2m ,力臂d=110mm ,工作阻力F=9000N 。
插床机械设计说明书

目录
一设计题目与要求----------------------------- 二工作原理及功能分解------------------------- 三机构的选择--------------------------------- 四机械运动方案简图--------------------------- 五传动比的分配------------------------------- 六机械系统运动循环图------------------------- 七机械传动机构和执行机构的设计及尺寸计算---- 八注意事项----------------------------------- 九主要参考资料-------------------------------
图(3)机构运动简图((,)0.01l a v m m m
μμμ=)
已知插程H=100mm ,AB=60mm ,AD=50mm ,DP=90mm ,由对心曲柄滑块知道AD=H/2=50mm 因为极为夹角为060,则0
1260C B C ∠= 则:
八。
注意事项
(1)插床工作机构由主切削运动机构和进给运动机构组成,两者必须协调匹配。
两机构的协调要求可通过公共输入构件来实现
(2)合理布置电动机的安装位置,—般可先以一级V型带传动在串接合理的轮系将运动动力传至曲柄轴。
直线进给运动具有横向近给和纵向进给两个分支,它们可共用同一公共传动链,仅在其末端执行环节处通过离合装置隔离。
圆周进给运动可提出。
机械原理课程设计插床机构设计

深航北方科技学院课程名称机械原理课程设计插床机构设计题目名称插床机构设计学生学院机械工程系专业班级学号学生姓名指导教师一设计任务书 (1)1、工作原理 (1)2、设计数据 (2)二参数设计 (3)1.倒杆机构的方案选型 (3)(1)方案I (3)(2)方案II (3)(3)方案III (4)2、导杆机构分析与设计 (4)(1)导杆机构尺寸计算 (4)(2)导杆在1位置的运动分析 (5)1)速度分析 (5)3)加速度分析 (6)(2)凸轮机构设计 (7)(1) 确定凸轮机构的基本尺寸 (7)(2) 凸轮廓线的绘制 (9)(4)齿轮的设计计算 (11)1)设计原理 (11)2)小齿轮参数计算 (11)3)大齿轮参数计算 (11)三小结 (13)一设计任务书1、工作原理插床机械系统的执行机构主要是由导杆机构和凸轮机构组成。
图1.1为其参考示意图,电动机经过减速传动装置(皮带和齿轮传动)带动曲柄3转动,再通过导杆机构使装有刀具的滑块5沿导路y—y作往复运动,以实现刀具的切削运动。
刀具向下运动时切削,在切削行程H中,前后各有一段0.05H的空刀距离,工作阻力F为常数;刀具向上运动时为空回行程,无阻力。
为了缩短回程时间,提高生产率,要求刀具具有急回运动。
刀具与工作台之间的进给运动,是由固结于轴O2上的凸轮驱动摆动从动件DOl8和其它有关机构(图中未画出)来完成的。
图1.1 插床工作原理图2、设计数据二 参数设计1.倒杆机构的方案选型(1)方案I该方案如图2—1由两个四杆机构组成。
使b>a, 构件1、2、3、6便构成摆动导杆机构,基本参数为b/a=λ。
构件3、4、5、6构成摇杆滑块机构。
图2—1方案特点如下:1).是一种平面连杆机构,结构简单,加工方便,能承受较大载荷。
2).具有急回作用,其行程速比系数00(180)/(180)k θθ=+-,而arcsin(1/)θλ=。
只要正确选择λ,即可满足行程速比系数k 的要求。
机械原理课程设计说明书 插床机构

一 插床机构的设计与运动分析1.插床机构简介与设计数据插床主要由齿轮机构、导杆机构和凸轮机构等组成,如图2-1,a 所示。
电动机经过减速装置(图中只画出齿轮1z 、2z )使曲柄1转动,再通过导杆机构1-2-3-4-5-6,使装有刀具的滑块沿导路y-y 作往复运动,以实现刀具切削运动。
为了缩短空程时间,提高生产率,要求刀具有急回运动。
刀具与工作台之间的进给运动,是由固结于轴2O 上的凸轮驱动摆动从动杆D O 4和其他有关机构来完成的。
设计数据表 设计内容 导杆机构的设计及运动分析符号 1n K HB O BCl l 3 32O O la b c单位 min r mm mm数据 652120116055551251.设计内容和步骤已知 行程速度变化系数(行程速比系数)K ,滑块5的冲程H ,中心距32O O l ,比值BO BCl l 3,各构件重心S 的位置,曲柄每分钟转数 1n 。
要求 设计导杆机构,作机构两个位置的速度多边行和加速度多边形,做滑块的运动线图。
步骤1)设计导杆机构。
按已知条件确定导杆机构的各未知参数。
其中滑块5的导路y y -的位置可根据连杆4传力给滑块5的最有利条件来确定,即y y -应位于B 点所画圆弧高的平分线上。
2)作机构运动简图。
选取长度比例尺)(mm m l μ,按表22-所分配的两个曲柄位置作出机构运动简图,其中一个位置用粗线画出。
曲柄位置的作法如图22-;取滑块5在上极限时所对应的曲柄位置为起始位置1 ,按转向将曲柄圆周十二等分,得12个曲柄位置,显然位置9对应于滑块5处于下极限时的位置。
再作出开始切削和终止切削所对应的'1和'8两个位置。
3)作速度、加速度多边形。
选取速度比例尺⎪⎭⎫⎝⎛mm s m v μ和加速度比例尺⎪⎪⎭⎫ ⎝⎛mm s m a 2μ,用相应运动图解法作该两个位置的速度多边形和加速度多边形,并将其结果列入下表:项目位置1ω2A v23A A v 3A v CB v C v 3S vω大小 方向 106.28 0.471 0. 14 0.450 0.04 0.2 0.26 2.1逆时针单位 s 1 s m s 1项目 位置 2A a K A A a23 n A a 3t A a 3n CB a C a 3S a ε2.96 0.6 0.96 0.04 0.016 0.04 0.54单位2s m 21s4)作滑块的运动线图。
机械原理课程设计(插床)

返回
刀具上极限
A1
刀具下极限
O2
O1
A2
返回
刀具上极限
C2
O B 2B 1 2是等边三角形
B 是平行四边形 1B 2C 2C 1
H100
刀具下极限
A1
C1
B2
O1
100 60
O2
B1
A2
返回
C2
1 2 3
C3
C1
l y yO 2
1
B2
2
3
B
O2
B1
返回
细实线 刀具最下端对应位置图 点划线 j1位置图 双点划线 j2位置图
sva分析矢量方程矢量图及结果3工作台进给机构传动方案设计对工作原理进行说明4列表5总结6参考文献返回刀具下极限刀具上极限返回刀具下极限刀具上极限10060是等边三角形返回标题栏摆动导杆机构运动简图位置图双点划线位置图点划线刀具最下端对应位置图细实线刀具最上端对应位置图粗实线曲柄转角线图点位移曲柄转角线图点速度曲柄转角线图点加速度
返回 目录
(一)运动基本要求:
⒈单向连续转动到往复直线移动的变换; ⒉刀具运动应具有的急回作用:K=2; ⒊机构运动应灵活、轻巧; ⒋刀具切削行程H=100mm;
(二)刀具主运动机构基本方案
电动机(加减速器)→摆动导杆机构→刀具
1.按急回运动要求确定曲柄1长度
按行程速比系数K=2可算出极位夹角θ=60º , 据此作图:曲柄1与导杆3垂直时,刀具(即滑块5) 处于上或下两极限位置,此时曲柄对应位置所夹 锐角应为极位夹角θ。作图分析 l sin O O A 根据几何关系:l A O O O 1 2
第一部分 概述 第二部分 刀具主运动机构的运动设 计与分析 第三部分 工作台进给运动传动方案 设计 第四部分 设计计算说明书
插床机构说明书

机械原理课程设计插床机构说明书负责人:廖昭洋学院:机电工程学院班级:机械1102班学号: 0806110515 日期: 2013年 7月11日1.设计任务及原始参数1.1插床简介工作原理插床实际是一种立式刨床,在结构原理上与牛头刨床同属一类。
插刀随滑枕在垂直方向上的直线往复运动是主运动,工件沿纵向横向及圆周三个方向分别所作的间歇运动是进给运动。
插床的生产效率较低,加工表面粗糙度Ra为6.3-1.6微米,加工面的垂直度为0.025/300毫米。
插床的主参数是最大插削长度。
特点插床用于插削平面、成型面及键槽等,并能插倾斜度在10°范围内的模具等工作物,适用于单个或小批量生产的企业。
插床的工作台具有三种不同方向的进给(纵向、横向和回转),故工作物经过一次装夹后,在本机床加工几个表面。
1.2设计任务1.针对图所示的插床的执行机构方案,依据设计要求和已知参数,确定各构件的运动尺寸,绘制机构运动简图;2.假设曲柄1等速转动,画出滑块C的位移和速度的变化规律曲线;3.在插床工作过程中,插刀所受的阻力变化曲线如图所示,在不考虑各处摩擦、其他构件重力和惯性力的条件下,分析曲柄所需的驱动力矩;4.取曲柄轴为等效构件,确定应加于曲柄轴上的飞轮转动惯量;5.用软件(VB、MATLAB、ADAMS或SOLIDWORKS等均可)对执行机构进行运动仿真,并画出输出机构的位移、速度、和加速度线图。
6.图纸上绘出最终方案的机构运动简图并编写说明书。
1.3原始参数参数项目数据曲柄转速n(r/min) 65行程速比系数K 1.8插程H(mm) 150连杆与导杆之比LO3B/LBC 0.8工作阻力Fr(N) 3500空程阻力Ff(N) 175Lo2o3(mm) 150滑块质量m2,m5(kg) 50杆件线密度(kg/m) 200不均匀系数 0.052.运动方案设计2.1主机构方案(1)运动是否具有确定的运动该机构中构件n=5。
插床传动系统机构设计-机械原理课程设计说明书

课程设计说明书设计课题:插床机构专业班级:学生姓名:指导教师:设计时间:机械原理课程设计任务书1)针对图1所示的插床的执行机构(插削机构和送料机构)方案,依据设计要求和已知参数,确定各构件的运动尺寸,绘制机构运动简图;2)假设曲柄1等速转动,画出滑块C的位移和速度的变化规律曲线;3)在插床工作过程中,插刀所受的阻力变化曲线如图H 0.05G0.05HO S5图6-1插刀所受阻力曲线指导教师:教研室主任:2017年5月22日注:本表下发学生一份,指导教师一份,栏目不够请另附页。
课程设计任务书装订于设计计算说明书(或论文)封面之后,目录页之前。
矿业学院 机械原理 课程设计成绩评定表专业:班级:学号:姓名: 课题名称 插床机构设计任务与要求 设计要求:1)针对图1所示的插床的执行机构(插削机构和送料机构)方案,依据设计要求和已知参数,确定各构件的运动尺寸,绘制机构运动简图; 2)假设曲柄1等速转动,画出滑块C 的位移和速度的变化规律曲线;3) 在插床工作过程中,插刀所受的阻力变化曲线如图6-1所示,在不考虑各处摩擦、其他构件重力和惯性力的条件下,分析曲柄所需的驱动力矩;4) 编写课程设计说明书;5)感想与建议。
指导教师评语建议成绩: 指导教师:课H0.05G0.05H OS 5图6-1插刀所受阻力曲线年月日目录一、概述、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、1二、方案确定、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、1三、主体机构尺寸综合设计、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、2四、切削主体结构运动分析、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、5五、切削主体结构受力分析、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、12六、重要数据及函数曲线分析、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、14七、总结、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、17八、参考文献、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、、17第一部分概述插床是利用插刀的竖直往复运动插削键槽和型孔的机床。
插床机构说明书

机械原理课程设计插床机构说明书负责人:廖昭洋学院:机电工程学院班级:机械1102班学号:日期: 2013年 7月11日根据矩阵,编写matlab程序如下:clear all;clc;w1=;l1=;l3=;l6=;l61=;l4=;for m=1:3601o1(m)=pi*(m-1)/1800;o3(m)=atan((l1*sin(o1(m)))/(l6+l1*cos(o1(m))));s3(m)=(l1*cos(o1(m))+l6)/cos(o3(m));o4(m)=acos((-l61+l3*cos(o3(m)))/l4);se(m)=-l3*sin(o3(m))+l4*sin(o4(m));if o1(m)==0o3(m)=0; s3(m)=l1+l6;endif o1(m)==pio3(m)=0; s3(m)=l6-l1;endA1=[cos(o3(m)),-s3(m)*sin(o3(m)),0,0;sin(o3(m)),s3(m)*cos(o3(m)),0,0;0,-l3*sin(o3(m)),l4*sin(o4(m)),0;0 ,-l3*cos(o3(m)),l4*cos(o4(m)),-1];B1=w1*[-l1*sin(o1(m));l1*cos(o1(m));0;0];D1=A1\B1;E1(:,m)=D1 ;ds(m)=D1(1);w3(m)=D1(2);w4(m)=D1(3);ve(m)=D1(4);A2=[cos(o3(m)),-s3(m)*sin(o3(m)),0,0;sin(o3(m)),s3(m)*cos(o3(m)),0,0;0,-l3*sin(o3(m)),l4*sin(o4(m)),0;0 ,-l3*cos(o3(m)),l4*cos(o4(m)),-1];B2=-[-w3(m)*sin(o3(m)),(-ds(m)*sin(o3(m))-s3(m)*w3(m)*cos(o3( m))),0,0;w3(m)*cos(o3(m)),(ds(m)*cos(o3(m))-s3(m)*w3(m)*sin(o3(m))),0, 0;0,-l3*w3(m)*cos(o3(m)),l4*w4(m)*cos(o4(m)),0;0,l3*w3(m)*sin(o3(m)),-l4*w4(m)*sin(o4(m)),-1]*[ds(m);w3(m);w 4(m);ve(m)];C2=w1*[-l1*w1*cos(o1(m));-l1*w1*sin(o1(m));0;0];B=B2+C2;D2 =A2\B;E2(:,m)=D2;dds(m)=D2(1);a3(m)=D2(2);a4(m)=D2(3);ae(m)=D2(4);end;o11=o1*180/pi;y=[o3*180/pi;o4*180/pi];w=[w3;w4];a=[a3;a4];figu re;subplot(221);h1=plotyy(o11,y,o11, se); axis equal;title('位置线图');xlabel('\it\theta1');ylabel('\it\theta3,\theta4,Se'); subplot(222);h2=plotyy(o11,w,o11,ve);title('速度线图');xlabel('\it\theta1');ylabel('\it\omega3,\omega4,Ve');subplot(212);h3=plotyy(o11,a,o11,ae);title('加速度线图');xlabel('\it\theta1');ylabel('\it\alpha3,\alpha4,\alphaE');参考文献[1]孙桓,陈作模,葛文杰主编.机械原理.第七版.北京:高等教育出版社,2006.[2]王三民主编.机械原理与设计课程设计.北京:机械工业出版社,2005.[3]刘毅主编.机械原理课程设计.武汉:华中科技大学出版社, 2008.[4]李滨城.徐超主编.机械原理MATLAB辅助分析.北京:化学工业出版社,2010.。
机械原理课程设计插床设计

长江学院机械原理课程设计说明书设计题目:插床机构设计学院:机械与电子工程学院专业:班级:设计者:学号:指导老师:2016年7月1日目录题目及设计要求1机构简介插床是一种用于工件内表面切削加工的机床,也是常用的机械加工设备,用于齿轮、花键和槽形零件等的加工。
图1为某插床机构运动方案示意图。
该插床主要由带转动、齿轮传动、连杆机构和凸轮机构等组成。
电动机经过带传动、齿轮传动减速后带动曲柄1回转,再通过导杆机构1-2-3-4-5-6,使装有刀具的滑块沿道路y-y作往复运动,以实现刀具切削运动。
为了缩短空程时间,提高生产率,要求刀具具有急回运动。
刀具与工作台之间的进给运动,是由固结于轴O2上的凸轮驱动摆动从动件O4D和其他有关机构(图中未画出)来实现的。
为了减小机器的速度波动,在曲柄轴O2上安装一调速飞轮。
为了缩短空回行程时间,提高生产效率,要求刀具具有急回运动,图2为阻力线图。
图2图12设计数据二、插床机构的设计内容与步骤1、导杆机构的设计与运动分析⑴、设计导杆机构。
按已知数据确定导杆机构的各未知参数,其中滑块5导路y-y的位置可根据连杆4传力给滑块5的最有利条件来确定,即y-y应位于B点所画圆弧高的平分线上(见参考图例1)。
⑵、作机构运动简图。
选取长度比例尺μl(m/mm),按表1-2所分配的加速度位置用粗线画出机构运动简图。
曲柄位置的作法如图1-2;取滑块5 在下极限时所对应的曲柄位置为起始位置1,按转向将曲柄圆周十二等分,得12个曲柄位置,位置5对应于滑块5处于上极限位置。
再作出开始切削和终止切削所对应的5ˊ和12ˊ两位置。
图1-2 曲柄位置图⑶、作滑块的运动线图。
为了能直接从机构运动简图上量取滑块位移,取位移比例尺μs=μl,根据机构及滑块5上C点的各对应位置,作出滑块的运动线图s c(t)、然后根据s c(t)线图用图解微分法(弦线法)作滑块的速度v c(t)线图(图1-2),并将其结果与4)相对运动图解法的结果比较。
机械原理课程设计—插床机构说明书
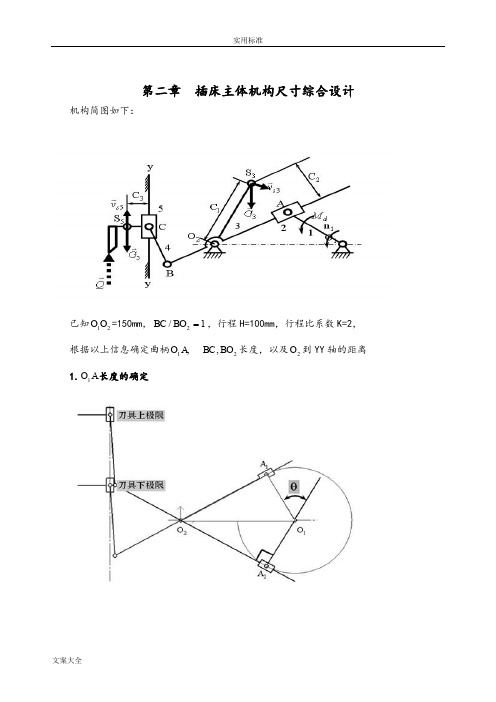
第二章 插床主体机构尺寸综合设计机构简图如下:已知21O O =150mm ,1/2 BO BC ,行程H=100mm ,行程比系数K=2,根据以上信息确定曲柄,1A O 2,BO BC 长度,以及2O 到YY 轴的距离 1.A O 1长度的确定图 1 极限位置由)180/()180(00θθ-+=K ,得极为夹角:060=θ,首先做出曲柄的运动轨迹,以1O 为圆心,A O 1为半径做圆,随着曲柄的转动,有图知道,当A O 2转到12A O ,于圆相切于上面时,刀具处于下极限位置;当A O 2转到22A O ,与圆相切于下面时,刀具处于上极限位置。
于是可得到12A O 与22A O 得夹角即为极为夹角060=θ。
由几何关系知,212211O O A O O A ∠=∠,于是可得,021221160=∠=∠O O A O O A 。
由几何关系可得:2111cos O O A O ∙=θ代入数据,21O O =150mm ,060=θ,得mm A O 751=即曲柄长度为75mm 2. 杆2BO BC 、的长度的确定图 2 杆BC ,BO 2长度确定由图2 知道,刀具处于上极限位置2C 和下极限位置1C 时,21C C 长度即为最大行程H=100mm ,即有21C C =100mm 。
在确定曲柄长度过程中,我们得到021221160=∠=∠O O A O O A ,那么可得到022160=∠B O B ,那么可知道三角形221O B B ∆等边三角形。
又有几何关系知道四边形1221C C B B 是平行四边形,那么1212C C B B =,又上面讨论知221O B B ∆为等边三角形,于是有1221B B O B =,那么可得到mm O B 10022=,即mm BO 1002=又已知1/2=BO BC ,于是可得到mm BO BC 1002==即杆2,BO BC 的100mm 。
3.2O 到YY 轴的距离的确定图 3 2O 到YY 轴的距离有图我们看到,YY 轴由3311y y y y 移动到过程中,同一点的压力角先减小,后又增大,那么在中间某处必有一个最佳位置,使得每个位置的压力角最佳。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
目录第一章绪论第二章插床主体机构尺寸综合设计第三章插床切削主体结构运动分析第四章重要数据及函数曲线分析第五章工作台设计方案第六章总结第一章绪论一,设计的题目:插床运动系统方案设计及其运动分析。
二,此设计是工科专业在学习《机械原理》后进行的一次较全面的综合设计训练,其目的:1.巩固理论知识,并应用于解决实际工程问题;2.建立机械传动系统方案设计、机构设计与分析概念;3.进行计算、绘图、正确应用设计资料、手册、标准和规范以及使用经验数据的能力训练。
三,主要内容:1.确定插床主要尺寸,然后按1:1的比例画出图形。
对插刀进行运动分析,选取适当比例尺画出不同点速度,加速度矢量图得到不同点的速度,加速度,并对两处位移,作出位移,速度,加速度同转角的图像2.在内容1运动分析的基础上作出运动循环图,在运动循环图的指导下,根据设计要求确定工作台进给运动机构传动方案设计(包括上下滑板1和2进给运动的机构传动方案设计;回转台3分度运动的机构传动方案设计;刀具与工作台在运动中的协调性分析;)3.整理和编写说明书一份,对图纸进行详细说明时间安排(1).第一天明确任务,准备作图工具,并打扫教室。
(2). 第二、三天在老师的指导下确定构建尺寸,作出机构简图,并进行运动分析,并作出一个周期的位移、速度、加速度随转角变化的图像(3). 第四、五天在老师的指导下,完成工作台的机构传动方案设计,并画出传动示意图。
(4). 第六、七、八天自己总结,整理并编写说明书一份机械原理课程设计任务书学院名称:专业:年级:学生姓名: 学号: 指导教师:一、设计题目插床传动系统方案设计及其运动分析二、主要内容1)对指定的机械进行传动系统方案设计;2)对执行机构进行运动简图设计(含必要的机构创意实验);3)飞轮设计;4)编写设计说明书。
三、具体要求插床是用于加工各种内外平面、成形表面,特别是键槽和带有棱角的内孔等的机床(如另:l BC/l BO2=1,工作台每次进给量0.5mm,刀具受力情况参考图2。
机床外形尺寸及各部份联系尺寸如图1所示(其中:l1 =1600,l2 =1200, l3 =740, l4 =640, l5 =580, l6 =560, l7 =200, l8 =320, l9 =150, l10 =360, l11 =1200,单位均为mm,其余尺寸自定。
四、完成后应上交的材料1) 机械原理课程设计说明书;2) 一号图一张,内容包括:插床机构运动简图、速度及加速度多边形图、S(φ)-φ曲线、V(φ)-φ曲线和a(φ)-φ曲线;3) 三号坐标纸一张:Med(φ)、Me r(φ)-φ曲线;4) 一号图一张,内容包括:插床工作循环图、工作台传动方案图。
五、推荐参考资料1)《机械原理课程设计指导书》(西华大学机械学院基础教学部编)2) 《机械原理》(孙桓主编,高等教育出版社)3) 《机械原理较程》(孙桓主编,西北工业大学出版社)指导教师签名日期年月日系主任审核日期年月日第二章 插床主体机构尺寸综合设计机构简图如下:已知21O O =150mm ,1/2 BO BC ,行程H=100mm ,行程比系数K=2,根据以上信息确定曲柄,1A O 2,BO BC 长度,以及2O 到YY 轴的距离 1.A O 1长度的确定图 1 极限位置由)180/()180(00θθ-+=K ,得极为夹角:060=θ,首先做出曲柄的运动轨迹,以1O 为圆心,A O 1为半径做圆,随着曲柄的转动,有图知道,当A O 2转到12A O ,于圆相切于上面时,刀具处于下极限位置;当A O 2转到22A O ,与圆相切于下面时,刀具处于上极限位置。
于是可得到12A O 与22A O 得夹角即为极为夹角060=θ。
由几何关系知,212211O O A O O A ∠=∠,于是可得,021221160=∠=∠O O A O O A 。
由几何关系可得:2111cos O O A O •=θ代入数据,21O O =150mm ,060=θ,得mm A O 751=即曲柄长度为75mm 2. 杆2BO BC 、的长度的确定图 2 杆BC ,BO 2长度确定由图2 知道,刀具处于上极限位置2C 和下极限位置1C 时,21C C 长度即为最大行程H=100mm ,即有21C C =100mm 。
在确定曲柄长度过程中,我们得到021221160=∠=∠O O A O O A ,那么可得到022160=∠B O B ,那么可知道三角形221O B B ∆等边三角形。
又有几何关系知道四边形1221C C B B 是平行四边形,那么1212C C B B =,又上面讨论知221O B B ∆为等边三角形,于是有1221B B O B =,那么可得到mm O B 10022=,即mm BO 1002=又已知1/2=BO BC ,于是可得到mm BO BC 1002==即杆2,BO BC 的100mm 。
3.2O 到YY 轴的距离的确定图 3 2O 到YY 轴的距离有图我们看到,YY 轴由3311y y y y 移动到过程中,同一点的压力角先减小,后又增大,那么在中间某处必有一个最佳位置,使得每个位置的压力角最佳。
考虑两个位置:1当YY 轴与圆弧12B B 刚相接触时,即图3中左边的那条点化线,与圆弧12B B 相切与B1B1点时,当B 点转到12,B B ,将会出现最大压力角。
2.当YY 轴与12B B 重合时,即图中右边的那条点化线时,B 点转到B1时将出现最大压力角为了使每一点的压力角都为最佳,我们可以选取YY 轴通过CB1中点(C 点为12B O 与12B B 得交点)。
又几何关系知道:2/)cos (cos 22222222C O B B O B O C O B B O l ∠•-+∠•=由上面的讨论容易知道02230=∠C O B,再代入其他数据,得:mm l 3.93=即2O 到YY 轴的距离为93.3mm综上,插床主体设计所要求的尺寸已经设计完成。
选取1:1 的是比例尺,画出图形如图纸一上机构简图所示。
第三章 插床切削主体机构及函数曲线分析主体机构图见第一张图。
已知m r w /60=,逆时针旋转,由作图法求解位移,速度,加速度。
规定位移,速度,加速度向下为正,插刀处于上极限位置时位移为0. 当O 175=ϕ(1)位移在1:1 的基础上,量的位移为79.5mm 。
,即 曲柄转过175°时位移为79.5mm 。
(2)速度由已知从图中可知,2A V 与A O 1垂直,23A A V 与A O 2平行,3A V 与A O 2垂直,由理论力学中不同构件重合点地方法可得∨∨∨∨+=→→→方向大小??2233A A A A v v v其中,2A V 是滑块 上与A 点重合的点的速度,23A A V 是杆AOB 上与A 点重合的点相对于滑块的速度,3A V 是杆AOB 上与A 点重合的速度。
又由图知,B v 与B O 2垂直,CB v 与BC 垂直,C v 与YY 轴平行,有理论力学同一构件不同点的方法可得:∨∨∨∨+=→→→??CB BCv v v 方向大小 其中,C v 是C 点,即插刀速度,BC v 是C 点相对于B 点转动速度,B v 是B 点速度。
又B 点是杆件3 上的一点,,杆件3围绕2O 转动,且B 点和杆件与A 点重合的点在2O 的两侧,于是可得:3322A A O BO B v v →→-=由图量的mm A O 22032=,则可到3220100A B v v =由已知可得s mm A O w v A /47175212≈⨯=⨯=π,规定选取比例尺mm s mm u /151-⋅=,则可的矢量图如下:最后量出代表C v 的矢量长度为12mm, 于是,可得 C v =0.174m/s即曲柄转过175°时,插刀的速度为0.174m/s 。
(3)加速度由理论力学知识可得矢量方程:∨∨∨∨∨++=→→→→?方向?大小?23232A3r A A k A A A αααα其中,2A α是滑块上与A 点重合点的加速度,2A α=212/88.29577544s mm A O ≈⨯=⨯πω,方向由4A 指向1O ;k A A 23α→是科氏加速度,223323/10802s mm v A A k A A ≈⨯⨯=ωα(其中233,A A A v v 大小均从速度多边形中量得),q 方向垂直42A O 向下;rA A 23α是4A 相对于滑块 的加速度,大小位置,方向与42A O 平行;n A3A2α是C 点相对于B 点转动的向心加速度,n A3O2α=22/43.993/s mm BC v CB ≈,方向过由C 指向B ;t O A 23α是C 点相对于B 点转动的切向加速度,大小位置,方向垂直BC 。
次矢量方程可解,从而得到3A α。
B 时杆AOB 上的一点,构AOB 围绕2O 转动,又4A 与B 点在2O 的两侧,由R R n t 2,ωαβα==(β是 角加速度)可得3322A A O B O B αα→→-=量出42A O 则可得到B α的大小和方向又由理论力学,结合图可得到;∨∨∨∨∨∨++=→→→→方向大小??CB t n CB Bcαααα其中,B α在上一步中大小方向都能求得;n CBα是C 相对于B 点转动的向心加速度22/36/s mm BC v BC n CB ≈=α,方向由C 点指向B 点;t CB α是C 相对于B 点转动的切向加速度,大小未知,方向与BC 垂直。
次矢量方程可解,从而可得到C 点,即插刀的加速度。
取比例尺mm s mm u /362-⋅=,可得加速度矢量图如下:最后由直尺量的c a 长度为12mm ,于是,可得c a 2/432.0s m ≈ 当O 355=ϕ(1)位移 在1:1 的基础上,滑块的位移为1.5mm 。
,即 曲柄转过355°时位移为1.5mm 。
(2)速度由已知从图中可知,2A V 与A O 1垂直,23A A V 与A O 2平行,3A V 与A O 2垂直,由理论力学中不同构件重合点地方法可得∨∨∨∨+=→→→方向大小??2233A A A A v v v其中,2A V 是滑块 上与A 点重合的点的速度,23A A V 是杆AOB 上与A 点重合的点相对于滑块的速度,3A V 是杆AOB 上与A 点重合的速度。
又由图知,B v 与B O 2垂直,CB v 与BC 垂直,C v 与YY 轴平行,有理论力学同一构件不同点的方法可得:∨∨∨∨+=→→→??CB BCv v v 方向大小 其中,C v 是C 点,即插刀速度,BC v 是C 点相对于B 点转动速度,B v 是B 点速度。
