2021年中考数学复习：与平行四边形相关的二次函数综合型压轴题解题技巧(含练习题及答案)

合集下载

2021年九年级中考数学第三轮压轴题：二次函数的综合专题复习(含答案)

2021年中考数学第三轮压轴题：二次函数的综合专题复习1、如图，抛物线y=x2+bx+c与y轴交于点A（0，2），对称轴为直线x=﹣2，平行于x轴的直线与抛物线交于B、C两点，点B在对称轴左侧，BC=6．（1）求此抛物线的解析式．（2）点P在x轴上，直线CP将△ABC面积分成2：3两部分，请直接写出P点坐标．2、如图，已知点A（﹣1，0），B（3，0），C（0，1）在抛物线y=ax2+bx+c上．（1）求抛物线解析式；（2）在直线BC上方的抛物线上求一点P，使△PBC面积为1；（3）在x轴下方且在抛物线对称轴上，是否存在一点Q，使∠BQC=∠BAC？若存在，求出Q点坐标；若不存在，说明理由．3、如图，抛物线y=a（x﹣1）（x﹣3）（a＞0）与x轴交于A、B两点，抛物线上另有一点C在x轴下方，且使△OCA∽△OBC．（1）求线段OC的长度；（2）设直线BC与y轴交于点M，点C是BM的中点时，求直线BM和抛物线的解析式；（3）在（2）的条件下，直线BC下方抛物线上是否存在一点P，使得四边形ABPC 面积最大？若存在，请求出点P的坐标；若不存在，请说明理由．4、如图，已知二次函数y=ax2+bx+3的图象交x轴于点A（1，0），B（3，0），交y轴于点C．（1）求这个二次函数的表达式；（2）点P是直线BC下方抛物线上的一动点，求△BCP面积的最大值；（3）直线x=m分别交直线BC和抛物线于点M，N，当△BMN是等腰三角形时，直接写出m的值．5、如图，抛物线顶点P（1，4），与y轴交于点C（0，3），与x轴交于点A，B．（1）求抛物线的解析式．（2）Q是抛物线上除点P外一点，△BCQ与△BCP的面积相等，求点Q的坐标．（3）若M，N为抛物线上两个动点，分别过点M，N作直线BC的垂线段，垂足分别为D，E．是否存在点M，N使四边形MNED为正方形？如果存在，求正方形MNED 的边长；如果不存在，请说明理由．6、如图，在平面直角坐标系中，抛物线y=ax2+bx+c交x轴于A、B两点（A在B 的左侧），且OA=3，OB=1，与y轴交于C（0，3），抛物线的顶点坐标为D（﹣1，4）．（1）求A、B两点的坐标；（2）求抛物线的解析式；（3）过点D作直线DE∥y轴，交x轴于点E，点P是抛物线上B、D两点间的一个动点（点P不与B、D两点重合），PA、PB与直线DE分别交于点F、G，当点P 运动时，EF+EG是否为定值？若是，试求出该定值；若不是，请说明理由．7、如图，在平面直角坐标系中，抛物线y=x2﹣x﹣4与x轴交于A，B两点（点A在点B左侧），与y轴交于点C．（1）求点A，B，C的坐标；（2）点P从A点出发，在线段AB上以每秒2个单位长度的速度向B点运动，同时，点Q从B点出发，在线段BC上以每秒1个单位长度的速度向C点运动，当其中一个点到达终点时，另一个点也停止运动．设运动时间为t秒，求运动时间t为多少秒时，△PBQ的面积S最大，并求出其最大面积；（3）在（2）的条件下，当△PBQ面积最大时，在BC下方的抛物线上是否存在点M，使△BMC的面积是△PBQ面积的1.6倍？若存在，求点M的坐标；若不存在，请说明理由．8、如图，在平面直角坐标系中，抛物线y=ax2+bx+c交x轴于A、B两点，交y 轴于点C（0，﹣），OA=1，OB=4，直线l过点A，交y轴于点D，交抛物线于点E，且满足tan∠OAD=．（1）求抛物线的解析式；（2）动点P从点B出发，沿x轴正方形以每秒2个单位长度的速度向点A运动，动点Q从点A出发，沿射线AE以每秒1个单位长度的速度向点E运动，当点P 运动到点A时，点Q也停止运动，设运动时间为t秒．①在P、Q的运动过程中，是否存在某一时刻t，使得△ADC与△PQA相似，若存在，求出t的值；若不存在，请说明理由．②在P、Q的运动过程中，是否存在某一时刻t，使得△APQ与△CAQ的面积之和最大？若存在，求出t的值；若不存在，请说明理由．9、如图，已知二次函数y=ax2−5√3x+c(a>0)的图象抛物线与x轴相交于不同的两点A(x1,0)，B(x2,0)，且x1<x2，(1)若抛物线的对称轴为x=√3求的a值；(2)若a=15，求c的取值范围；(3)若该抛物线与y轴相交于点D，连接BD，且∠OBD=60∘，抛物线的对称轴l，连接AF，满与x轴相交点E，点F是直线l上的一点，点F的纵坐标为3+12a足∠ADB=∠AFE，求该二次函数的解析式．10、如图1，已知抛物线y=﹣x2+bx+c与x轴交于A（﹣1，0），B（3，0）两点，与y轴交于C点，点P是抛物线上在第一象限内的一个动点，且点P的横坐标为t．（1）求抛物线的表达式；（2）设抛物线的对称轴为l，l与x轴的交点为D．在直线l上是否存在点M，使得四边形CDPM是平行四边形？若存在，求出点M的坐标；若不存在，请说明理由．（3）如图2，连接BC，PB，PC，设△PBC的面积为S．①求S关于t的函数表达式；②求P点到直线BC的距离的最大值，并求出此时点P的坐标．11、如图，以D为顶点的抛物线y=﹣x2+bx+c交x轴于A、B两点，交y轴于点C，直线BC的表达式为y=﹣x+3．（1）求抛物线的表达式；（2）在直线BC上有一点P，使PO+PA的值最小，求点P的坐标；（3）在x轴上是否存在一点Q，使得以A、C、Q为顶点的三角形与△BCD相似？若存在，请求出点Q的坐标；若不存在，请说明理由．12、如图1，经过原点O的抛物线y=ax2+bx（a、b为常数，a≠0）与x轴相交于另一点A（3，0）．直线l：y=x在第一象限内和此抛物线相交于点B（5，t），与抛物线的对称轴相交于点C．（1）求抛物线的解析式；（2）在x轴上找一点P，使以点P、O、C为顶点的三角形与以点A、O、B为顶点的三角形相似，求满足条件的点P的坐标；（3）直线l沿着x轴向右平移得到直线l′，l′与线段OA相交于点M，与x 轴下方的抛物线相交于点N，过点N作NE⊥x轴于点E．把△MEN沿直线l′折叠，当点E恰好落在抛物线上时（图2），求直线l′的解析式；（4）在（3）问的条件下（图3），直线l′与y轴相交于点K，把△MOK绕点O 顺时针旋转90°得到△M′OK′，点F为直线l′上的动点．当△M'FK′为等腰三角形时，求满足条件的点F的坐标．13、如图1，抛物线y=ax2+bx+3交x轴于点A（﹣1，0）和点B（3，0）．（1）求该抛物线所对应的函数解析式；（2）如图2，该抛物线与y轴交于点C，顶点为F，点D（2，3）在该抛物线上．①求四边形ACFD的面积；②点P是线段AB上的动点（点P不与点A、B重合），过点P作PQ⊥x轴交该抛物线于点Q，连接AQ、DQ，当△AQD是直角三角形时，求出所有满足条件的点Q 的坐标．14、已知抛物线y=x2+bx+c经过点A（﹣2，0），B（0、﹣4）与x轴交于另一点C，连接BC．（1）求抛物线的解析式；（2）如图，P是第一象限内抛物线上一点，且S△PBO =S△PBC，求证：AP∥BC；（3）在抛物线上是否存在点D，直线BD交x轴于点E，使△ABE与以A，B，C，E中的三点为顶点的三角形相似（不重合）？若存在，请求出点D的坐标；若不存在，请说明理由．参考答案1、如图，抛物线y=x2+bx+c与y轴交于点A（0，2），对称轴为直线x=﹣2，平行于x轴的直线与抛物线交于B、C两点，点B在对称轴左侧，BC=6．（1）求此抛物线的解析式．（2）点P在x轴上，直线CP将△ABC面积分成2：3两部分，请直接写出P点坐标．【解答】解：（1）由题意得：x=﹣=﹣=﹣2，c=2，解得：b=4，c=2，则此抛物线的解析式为y=x2+4x+2；（2）∵抛物线对称轴为直线x=﹣2，BC=6，∴B横坐标为﹣5，C横坐标为1，把x=1代入抛物线解析式得：y=7，∴B（﹣5，7），C（1，7），设直线AB解析式为y=kx+2，把B坐标代入得：k=﹣1，即y=﹣x+2，作出直线CP，与AB交于点Q，过Q作QH⊥y轴，与y轴交于点H，BC与y轴交于点M，可得△AQH∽△ABM，∴=，∵点P在x轴上，直线CP将△ABC面积分成2：3两部分，∴AQ：QB=2：3或AQ：QB=3：2，即AQ：AB=2：5或AQ：QB=3：5，∵BM=5，∴QH=2或QH=3，当QH=2时，把x=﹣2代入直线AB解析式得：y=4，此时Q（﹣2，4），直线CQ解析式为y=x+6，令y=0，得到x=﹣6，即P（﹣6，0）；当QH=3时，把x=﹣3代入直线AB解析式得：y=5，此时Q（﹣3，5），直线CQ解析式为y=x+，令y=0，得到x=﹣13，此时P （﹣13，0），综上，P的坐标为（﹣6，0）或（﹣13，0）．2、如图，已知点A（﹣1，0），B（3，0），C（0，1）在抛物线y=ax2+bx+c上．（1）求抛物线解析式；（2）在直线BC上方的抛物线上求一点P，使△PBC面积为1；（3）在x轴下方且在抛物线对称轴上，是否存在一点Q，使∠BQC=∠BAC？若存在，求出Q点坐标；若不存在，说明理由．【解答】解：（1）设抛物线的解析式为y=a（x+1）（x﹣3），将C（0，1）代入得﹣3a=1，解得：a=﹣，∴抛物线的解析式为y=﹣x2+x+1．（2）过点P作PD⊥x，交BC与点D．设直线BC的解析式为y=kx+b，则，解得：k=﹣，∴直线BC的解析式为y=﹣x+1．设点P（x，﹣x2+x+1），则D（x，﹣x+1）∴PD=（﹣x2+x+1）﹣（﹣x+1）=﹣x2+x，=OB•DP=×3×（﹣x2+x）=﹣x2+x．∴S△PBC又∵S=1，△PBC∴﹣x2+x=1，整理得：x2﹣3x+2=0，解得：x=1或x=2，∴点P的坐标为（1，）或（2，1）．（3）存在．∵A（﹣1，0），C（0，1），∴OC=OA=1∴∠BAC=45°．∵∠BQC=∠BAC=45°，∴点Q为△ABC外接圆与抛物线对称轴在x轴下方的交点．设△ABC外接圆圆心为M，则∠CMB=90°．设⊙M的半径为x，则Rt△CMB中，由勾股定理可知CM2+BM2=BC2，即2x2=10，解得：x=（负值已舍去），∵AC的垂直平分线的为直线y=﹣x，AB的垂直平分线为直线x=1，∴点M为直线y=﹣x与x=1的交点，即M（1，﹣1），∴Q的坐标为（1，﹣1﹣）．3、如图，抛物线y=a（x﹣1）（x﹣3）（a＞0）与x轴交于A、B两点，抛物线上另有一点C在x轴下方，且使△OCA∽△OBC．（1）求线段OC的长度；（2）设直线BC与y轴交于点M，点C是BM的中点时，求直线BM和抛物线的解析式；（3）在（2）的条件下，直线BC下方抛物线上是否存在一点P，使得四边形ABPC 面积最大？若存在，请求出点P的坐标；若不存在，请说明理由．【解答】解：（1）由题可知当y=0时，a（x﹣1）（x﹣3）=0，解得：x1=1，x2=3，即A（1，0），B（3，0），∴OA=1，OB=3∵△OCA∽△OBC，∴OC：OB=OA：OC，∴OC2=OA•OB=3，则OC=；（2）∵C是BM的中点，即OC为斜边BM的中线，∴OC=BC，∴点C的横坐标为，又OC=，点C在x轴下方，∴C（，﹣），设直线BM的解析式为y=kx+b，把点B（3，0），C（，﹣）代入得：，解得：b=﹣，k=，∴y=x﹣，又∵点C（，﹣）在抛物线上，代入抛物线解析式，解得：a=，∴抛物线解析式为y=x2﹣x+2；（3）点P存在，设点P坐标为（x，x2﹣x+2），过点P作PQ⊥x轴交直线BM于点Q，则Q（x，x﹣），∴PQ=x﹣﹣（x2﹣x+2）=﹣x2+3x﹣3，当△BCP面积最大时，四边形ABPC的面积最大，=PQ（3﹣x）+PQ（x﹣）=PQ=﹣x2+x﹣，S△BCP有最大值，四边形ABPC的面积最大，此时点P的坐标为当x=﹣=时，S△BCP（，﹣）．4、如图，已知二次函数y=ax2+bx+3的图象交x轴于点A（1，0），B（3，0），交y轴于点C．（1）求这个二次函数的表达式；（2）点P是直线BC下方抛物线上的一动点，求△BCP面积的最大值；（3）直线x=m分别交直线BC和抛物线于点M，N，当△BMN是等腰三角形时，直接写出m的值．【解答】解：（1）将A（1，0），B（3，0）代入函数解析式，得，解得，这个二次函数的表达式是y=x2﹣4x+3；（2）当x=0时，y=3，即点C（0，3），设BC的表达式为y=kx+b，将点B（3，0）点C（0，3）代入函数解析式，得，解这个方程组，得直线BC的解析是为y=﹣x+3，过点P作PE∥y轴，交直线BC于点E（t，﹣t+3），PE=﹣t+3﹣（t﹣4t+3）=﹣t2+3t，∴S△BCP =S△BPE+SCPE=（﹣t2+3t）×3=﹣（t﹣）2+．∵﹣＜0，∴当t=时，S△BCP最大=（3）M（m，﹣m+3），N（m，m2﹣4m+3）MN=m2﹣3m，BM=|m﹣3|，当MN=BM时，①m2﹣3m=（m﹣3），解得m=，②m2﹣3m=﹣（m﹣3），解得m=﹣当BN=MN时，∠NBM=∠BMN=45°，m2﹣4m+3=0，解得m=1或m=3（舍）当BM=BN时，∠BMN=∠BNM=45°，﹣（m2﹣4m+3）=﹣m+3，解得m=2或m=3（舍），当△BMN是等腰三角形时，m的值为，﹣，1，2．5、如图，抛物线顶点P（1，4），与y轴交于点C（0，3），与x轴交于点A，B．（1）求抛物线的解析式．（2）Q是抛物线上除点P外一点，△BCQ与△BCP的面积相等，求点Q的坐标．（3）若M，N为抛物线上两个动点，分别过点M，N作直线BC的垂线段，垂足分别为D，E．是否存在点M，N使四边形MNED为正方形？如果存在，求正方形MNED 的边长；如果不存在，请说明理由．【解答】解：（1）设y=a（x﹣1）2+4（a≠0），把C（0，3）代入抛物线解析式得：a+4=3，即a=﹣1，则抛物线解析式为y=﹣（x﹣1）2+4=﹣x2+2x+3；（2）由B（3，0），C（0，3），得到直线BC解析式为y=﹣x+3，∵S△OBC =S△QBC，∴PQ∥BC，①过P作PQ∥BC，交抛物线于点Q，如图1所示，∵P（1，4），∴直线PQ解析式为y=﹣x+5，联立得：，解得：或，即Q（2，3）；②设G（1，2），∴PG=GH=2，过H作直线Q2Q3∥BC，交x轴于点H，则直线Q2Q3解析式为y=﹣x+1，联立得：，解得：或，∴Q2（，），Q3（，）；（3）存在点M，N使四边形MNED为正方形，如图2所示，过M作MF∥y轴，过N作NF∥x轴，过N作NH∥y轴，则有△MNF 与△NEH都为等腰直角三角形，设M（x1，y1），N（x2，y2），设直线MN解析式为y=﹣x+b，联立得：，消去y得：x2﹣3x+b﹣3=0，∴NF2=|x1﹣x2|2=（x1+x2）2﹣4x1x2=21﹣4b，∵△MNF为等腰直角三角形，∴MN2=2NF2=42﹣8b，∵NH2=（b﹣3）2，∴NF2=（b﹣3）2，若四边形MNED为正方形，则有NE2=MN2，∴42﹣8b=（b2﹣6b+9），整理得：b2+10b﹣75=0，解得：b=﹣15或b=5，∵正方形边长为MN=，∴MN=9或．6、如图，在平面直角坐标系中，抛物线y=ax2+bx+c交x轴于A、B两点（A在B 的左侧），且OA=3，OB=1，与y轴交于C（0，3），抛物线的顶点坐标为D（﹣1，4）．（1）求A、B两点的坐标；（2）求抛物线的解析式；（3）过点D作直线DE∥y轴，交x轴于点E，点P是抛物线上B、D两点间的一个动点（点P不与B、D两点重合），PA、PB与直线DE分别交于点F、G，当点P 运动时，EF+EG是否为定值？若是，试求出该定值；若不是，请说明理由．【解答】解：（1）由抛物线y=ax2+bx+c交x轴于A、B两点（A在B的左侧），且OA=3，OB=1，得A点坐标（﹣3，0），B点坐标（1，0）；（2）设抛物线的解析式为y=a（x+3）（x﹣1），把C点坐标代入函数解析式，得a（0+3）（0﹣1）=3，解得a=﹣1，抛物线的解析式为y=﹣（x+3）（x﹣1）=﹣x2﹣2x+3；（3）EF+EG=8（或EF+EG是定值），理由如下：过点P作PQ∥y轴交x轴于Q，如图．设P（t，﹣t2﹣2t+3），则PQ=﹣t2﹣2t+3，AQ=3+t，QB=1﹣t，∵PQ∥EF，∴△AEF∽△AQP，∴=，∴EF===×（﹣t2﹣2t+3）=2（1﹣t）；又∵PQ∥EG，∴△BEG∽△BQP，∴=，∴EG===2（t+3），∴EF+EG=2（1﹣t）+2（t+3）=8．7、如图，在平面直角坐标系中，抛物线y=x2﹣x﹣4与x轴交于A，B两点（点A在点B左侧），与y轴交于点C．（1）求点A，B，C的坐标；（2）点P从A点出发，在线段AB上以每秒2个单位长度的速度向B点运动，同时，点Q从B点出发，在线段BC上以每秒1个单位长度的速度向C点运动，当其中一个点到达终点时，另一个点也停止运动．设运动时间为t秒，求运动时间t为多少秒时，△PBQ的面积S最大，并求出其最大面积；（3）在（2）的条件下，当△PBQ面积最大时，在BC下方的抛物线上是否存在点M，使△BMC的面积是△PBQ面积的1.6倍？若存在，求点M的坐标；若不存在，请说明理由．【解答】解：（1）当x=0时，y=x2﹣x﹣4=﹣4，∴点C的坐标为（0，﹣4）；当y=0时，有x2﹣x﹣4=0，解得：x1=﹣2，x2=3，∴点A的坐标为（﹣2，0），点B的坐标为（3，0）．（2）设直线BC的解析式为y=kx+b（k≠0），将B（3，0）、C（0，﹣4）代入y=kx+b，，解得：，∴直线BC的解析式为y=x﹣4．过点Q作QE∥y轴，交x轴于点E，如图1所示，当运动时间为t秒时，点P的坐标为（2t﹣2，0），点Q的坐标为（3﹣t，﹣t），∴PB=3﹣（2t﹣2）=5﹣2t，QE=t，∴S△PBQ=PB•QE=﹣t2+2t=﹣（t﹣）2+．∵﹣＜0，∴当t=时，△PBQ的面积取最大值，最大值为．（3）当△PBQ面积最大时，t=，此时点P的坐标为（，0），点Q的坐标为（，﹣1）．假设存在，设点M的坐标为（m，m2﹣m﹣4），则点F的坐标为（m，m﹣4），∴MF=m﹣4﹣（m2﹣m﹣4）=﹣m2+2m，∴S△BMC=MF•OB=﹣m2+3m．∵△BMC的面积是△PBQ面积的1.6倍，∴﹣m2+3m=×1.6，即m2﹣3m+2=0，解得：m1=1，m2=2．∵0＜m＜3，∴在BC下方的抛物线上存在点M，使△BMC的面积是△PBQ面积的1.6倍，点M 的坐标为（1，﹣4）或（2，﹣）．8、如图，在平面直角坐标系中，抛物线y=ax2+bx+c交x轴于A、B两点，交y 轴于点C（0，﹣），OA=1，OB=4，直线l过点A，交y轴于点D，交抛物线于点E，且满足tan∠OAD=．（1）求抛物线的解析式；（2）动点P从点B出发，沿x轴正方形以每秒2个单位长度的速度向点A运动，动点Q从点A出发，沿射线AE以每秒1个单位长度的速度向点E运动，当点P 运动到点A时，点Q也停止运动，设运动时间为t秒．①在P、Q的运动过程中，是否存在某一时刻t，使得△ADC与△PQA相似，若存在，求出t的值；若不存在，请说明理由．②在P、Q的运动过程中，是否存在某一时刻t，使得△APQ与△CAQ的面积之和最大？若存在，求出t的值；若不存在，请说明理由．解：（1）∵OA=1，OB=4∴A（1，0），B（﹣4，0）设抛物线的解析式为y=a（x+4）（x﹣1）∵点C（0，﹣）在抛物线上∴﹣解得a=∴抛物线的解析式为y=（2）存在t，使得△ADC与△PQA相似．理由：①在Rt△AOC中，OA=1，OC=则tan∠ACO=∵tan∠OAD=∴∠OAD=∠ACO∵直线l的解析式为y=∴D（0，﹣）∵点C（0，﹣）∴CD=由AC2=OC2+OA2，得AC=在△AQP中，AP=AB﹣PB=5﹣2t，AQ=t由∠PAQ=∠ACD，要使△ADC与△PQA相似只需或则有或解得t1=，t2=∵t1＜2.5，t2＜2.5∴存在t=或t=，使得△ADC与△PQA相似②存在t，使得△APQ与△CAQ的面积之和最大理由：作PF⊥AQ于点F，CN⊥AQ于N在△APF中，PF=AP•sin∠PAF=在△AOD中，由AD2=OD2+OA2，得AD=在△ADC中，由S△ADC=∴CN=∴S△AQP +S△AQC==﹣∴当t=时，△APQ与△CAQ的面积之和最大9、如图，已知二次函数y=ax2−5√3x+c(a>0)的图象抛物线与x轴相交于不同的两点A(x1,0)，B(x2,0)，且x1<x2，(1)若抛物线的对称轴为x=√3求的a值；(2)若a=15，求c的取值范围；(3)若该抛物线与y轴相交于点D，连接BD，且∠OBD=60∘，抛物线的对称轴l 与x轴相交点E，点F是直线l上的一点，点F的纵坐标为3+12a，连接AF，满足∠ADB=∠AFE，求该二次函数的解析式．【答案】解：(1)抛物线的对称轴是：x=−b2a =−−5√32a=√3，解得：a=52；(2)由题意得二次函数解析式为：y=15x2−5√3x+c，∵二次函数与x轴有两个交点，∴△>0，∴△=b2−4ac=(−5√3)2−4×15c，∴c<54；(3)∵∠BOD=90∘，∠DBO=60∘，∴tan60∘=ODOB =cOB=√3，∴OB=√33c，∴B(√33c,0)，把B(√33c,0)代入y =ax 2−5√3x +c 中得：ac 23−5√3⋅√3c 3+c =0，ac 23−5c +c =0，∵c ≠0， ∴ac =12， ∴c =12a，把c =12a代入y =ax 2−5√3x +c 中得： y =a(x 2−5√3x a+12a 2)=a(x −4√3a)(x −√3a)， ∴x 1=4√3a，x 2=√3a， ∴A(√3a ,0)，B(4√3a ,0)，D(0,12a)， ∴AB =4√3a−√3a=3√3a ，AE =3√32a， ∵F 的纵坐标为3+12a ， ∴F(5√32a ,6a+12a)，过点A 作AG ⊥DB 于G ， ∴BG =12AB =AE =3√32a，AG =92a ，DG =DB −BG =8√3a−3√32a=13√32a， ∵∠ADB =∠AFE ，∠AGD =∠FEA =90∘， ∴△ADG ∽△AFE ， ∴AE AG =FEDG ， ∴3√32a 92a=6a+12a 13√32a，∴a =2，c =6， ∴y =2x 2−5√3x +6．10、如图1，已知抛物线y=﹣x 2+bx+c 与x 轴交于A （﹣1，0），B （3，0）两点，与y 轴交于C 点，点P 是抛物线上在第一象限内的一个动点，且点P 的横坐标为t ．（1）求抛物线的表达式；（2）设抛物线的对称轴为l，l与x轴的交点为D．在直线l上是否存在点M，使得四边形CDPM是平行四边形？若存在，求出点M的坐标；若不存在，请说明理由．（3）如图2，连接BC，PB，PC，设△PBC的面积为S．①求S关于t的函数表达式；②求P点到直线BC的距离的最大值，并求出此时点P的坐标．【解答】解：（1）将A（﹣1，0）、B（3，0）代入y=﹣x2+bx+c，，解得：，∴抛物线的表达式为y=﹣x2+2x+3．（2）在图1中，连接PC，交抛物线对称轴l于点E，∵抛物线y=﹣x2+bx+c与x轴交于A（﹣1，0），B（3，0）两点，∴抛物线的对称轴为直线x=1．当t=2时，点C、P关于直线l对称，此时存在点M，使得四边形CDPM是平行四边形．∵抛物线的表达式为y=﹣x2+2x+3，∴点C的坐标为（0，3），点P的坐标为（2，3），∴点M的坐标为（1，6）；当t≠2时，不存在，理由如下：若四边形CDPM是平行四边形，则CE=PE，∵点C的横坐标为0，点E的横坐标为0，∴点P的横坐标t=1×2﹣0=2．又∵t≠2，∴不存在．（3）①在图2中，过点P作PF∥y轴，交BC于点F．设直线BC的解析式为y=mx+n（m≠0），将B（3，0）、C（0，3）代入y=mx+n，，解得：，∴直线BC的解析式为y=﹣x+3．∵点P的坐标为（t，﹣t2+2t+3），∴点F的坐标为（t，﹣t+3），∴PF=﹣t2+2t+3﹣（﹣t+3）=﹣t2+3t，∴S=PF•OB=﹣t2+t=﹣（t﹣）2+．②∵﹣＜0，∴当t=时，S取最大值，最大值为．∵点B的坐标为（3，0），点C的坐标为（0，3），∴线段BC==3，∴P点到直线BC的距离的最大值为=，此时点P的坐标为（，）．11、如图，以D为顶点的抛物线y=﹣x2+bx+c交x轴于A、B两点，交y轴于点C，直线BC的表达式为y=﹣x+3．（1）求抛物线的表达式；（2）在直线BC上有一点P，使PO+PA的值最小，求点P的坐标；（3）在x轴上是否存在一点Q，使得以A、C、Q为顶点的三角形与△BCD相似？若存在，请求出点Q的坐标；若不存在，请说明理由．【解答】解：（1）把x=0代入y=﹣x+3，得：y=3，∴C（0，3）．把y=0代入y=﹣x+3得：x=3，∴B（3，0），A（﹣1，0）将C（0，3）、B（3，0）代入y=﹣x2+bx+c得：，解得b=2，c=3．∴抛物线的解析式为y=﹣x2+2x+3．（2）如图所示：作点O关于BC的对称点O′，则O′（3，3）．∵O′与O关于BC对称，∴PO=PO′．∴OP+AP=O′P+AP≤AO′．∴OP+AP的最小值=O′A==5．（3）y=﹣x2+2x+3=﹣（x﹣1）2+4，∴D（1，4）．又∵C（0，3，B（3，0），∴CD=，BC=3，DB=2．∴CD2+CB2=BD2，∴∠DCB=90°．∵A（﹣1，0），C（0，3），∴OA=1，CO=3．∴==．又∵∠AOC=DCB=90°，∴△AOC∽△DCB．∴当Q的坐标为（0，0）时，△AQC∽△DCB．如图所示：连接AC，过点C作CQ⊥AC，交x轴与点Q．∵△ACQ为直角三角形，CO⊥AQ，∴△ACQ∽△AOC．又∵△AOC∽△DCB，∴△ACQ∽△DCB．∴=，即=，解得：AQ=10．∴Q（9，0）．综上所述，当Q的坐标为（0，0）或（9，0）时，以A、C、Q为顶点的三角形与△BCD相似．12、如图1，经过原点O的抛物线y=ax2+bx（a、b为常数，a≠0）与x轴相交于另一点A（3，0）．直线l：y=x在第一象限内和此抛物线相交于点B（5，t），与抛物线的对称轴相交于点C．（1）求抛物线的解析式；（2）在x轴上找一点P，使以点P、O、C为顶点的三角形与以点A、O、B为顶点的三角形相似，求满足条件的点P的坐标；（3）直线l沿着x轴向右平移得到直线l′，l′与线段OA相交于点M，与x 轴下方的抛物线相交于点N，过点N作NE⊥x轴于点E．把△MEN沿直线l′折叠，当点E恰好落在抛物线上时（图2），求直线l′的解析式；（4）在（3）问的条件下（图3），直线l′与y轴相交于点K，把△MOK绕点O 顺时针旋转90°得到△M′OK′，点F为直线l′上的动点．当△M'FK′为等腰三角形时，求满足条件的点F的坐标．【解答】解：（1）由已知点B坐标为（5，5）把点B（5，5），A（3，0）代入y=ax2+bx，得解得∴抛物线的解析式为：y=（2）由（1）抛物线对称轴为直线x=，则点C坐标为（，）∴OC=，OB=5当△OBA∽△OCP时，∴∴OP=当△OBA∽△OPC时，∴∴OP=5∴点P坐标为（5，0）或（，0）（3）设点N坐标为（a，b），直线l′解析式为：y=x+c ∵直线l′y=x+c与x轴夹角为45°∴△MEN为等腰直角三角形．当把△MEN沿直线l′折叠时，四边形ENE′M为正方形∴点′E坐标为（a﹣b，b）∵EE′平行于x轴∴E、E′关于抛物线对称轴对称∵∴b=2a﹣3则点N坐标可化为（a，2a﹣3）把点N坐标带入y=得：2a﹣3=解得a1=1，a2=6∵a=6时，b=2a﹣3=﹣9＜0∴a=6舍去则点N坐标为（1，﹣1）把N坐标带入y=x+c则c=﹣2∴直线l′的解析式为：y=x﹣2（4）由（3）K点坐标为（0，﹣2）则△MOK为等腰直角三角形∴△M′OK′为等腰直角三角形，M′K′⊥直线l′∴当M′K′=M′F时，△M'FK′为等腰直角三角形∴F坐标为（1，0）或（﹣1，﹣2）13、如图1，抛物线y=ax2+bx+3交x轴于点A（﹣1，0）和点B（3，0）．（1）求该抛物线所对应的函数解析式；（2）如图2，该抛物线与y轴交于点C，顶点为F，点D（2，3）在该抛物线上．①求四边形ACFD的面积；②点P是线段AB上的动点（点P不与点A、B重合），过点P作PQ⊥x轴交该抛物线于点Q，连接AQ、DQ，当△AQD是直角三角形时，求出所有满足条件的点Q 的坐标．【解答】解：（1）由题意可得，解得，∴抛物线解析式为y=﹣x2+2x+3；（2）①∵y=﹣x2+2x+3=﹣（x﹣1）2+4，∴F（1，4），∵C（0，3），D（2，3），∴CD=2，且CD∥x轴，∵A（﹣1，0），∴S四边形ACFD =S△ACD+S△FCD=×2×3+×2×（4﹣3）=4；②∵点P在线段AB上，∴∠DAQ不可能为直角，∴当△AQD为直角三角形时，有∠ADQ=90°或∠AQD=90°，i．当∠ADQ=90°时，则DQ⊥AD，∵A（﹣1，0），D（2，3），∴直线AD解析式为y=x+1，∴可设直线DQ解析式为y=﹣x+b′，把D（2，3）代入可求得b′=5，∴直线DQ解析式为y=﹣x+5，联立直线DQ和抛物线解析式可得，解得或，∴Q（1，4）；ii．当∠AQD=90°时，设Q（t，﹣t2+2t+3），设直线AQ的解析式为y=k1x+b1，把A、Q坐标代入可得，解得k1=﹣（t﹣3），设直线DQ解析式为y=k2x+b2，同理可求得k2=﹣t，∵AQ⊥DQ，∴k1k2=﹣1，即t（t﹣3）=﹣1，解得t=，当t=时，﹣t2+2t+3=，当t=时，﹣t2+2t+3=，∴Q点坐标为（，）或（，）；综上可知Q点坐标为（1，4）或（，）或（，）．14、已知抛物线y=x2+bx+c经过点A（﹣2，0），B（0、﹣4）与x轴交于另一点C，连接BC．（1）求抛物线的解析式；（2）如图，P是第一象限内抛物线上一点，且S△PBO =S△PBC，求证：AP∥BC；（3）在抛物线上是否存在点D，直线BD交x轴于点E，使△ABE与以A，B，C，E中的三点为顶点的三角形相似（不重合）？若存在，请求出点D的坐标；若不存在，请说明理由．【解答】解：（1）把点A（﹣2，0），B（0、﹣4）代入抛物线y=x2+bx+c中得：，解得：，∴抛物线的解析式为：y=x2﹣x﹣4；（2）当y=0时，x2﹣x﹣4=0，解得：x=﹣2或4，∴C（4，0），如图1，过O作OE⊥BP于E，过C作CF⊥BP于F，设PB交x轴于G，∵S△PBO =S△PBC，∴，∴OE=CF，易得△OEG≌△CFG，∴OG=CG=2，设P（x，x2﹣x﹣4），过P作PM⊥y轴于M，tan∠PBM===，∴BM=2PM，∴4+x2﹣x﹣4=2x，x2﹣6x=0，x 1=0（舍），x2=6，∴P（6，8），易得AP的解析式为：y=x+2，BC的解析式为：y=x﹣4，∴AP∥BC；（3）以A，B，C，E中的三点为顶点的三角形有△ABC、△ABE、△ACE、△BCE，四种，其中△ABE重合，不符合条件，△ACE不能构成三角形，∴当△ABE与以A，B，C，E中的三点为顶点的三角形相似，存在两个三角形：△ABC和△BCE，①当△ABE与以A，B，C中的三点为顶点的三角形相似，如图2，∵∠BAE=∠BAC，∠ABE≠∠ABC，∴∠ABE=∠ACB=45°，∴△ABE∽△ACB，∴，∴，∴AE=，∴E（，0），∵B（0，﹣4），易得BE：y=，则x2﹣x﹣4=x﹣4，x 1=0（舍），x2=，∴D（，）；②当△ABE与以B，C、E中的三点为顶点的三角形相似，如图3，∵∠BEA=∠BEC，∴当∠ABE=∠BCE时，△ABE∽△BCE，∴==，设BE=2m，CE=4m，Rt△BOE中，由勾股定理得：BE2=OE2+OB2，∴，3m2﹣8m+8=0，（m﹣2）（3m﹣2）=0，m 1=2，m2=，∴OE=4m﹣4=12或，∵OE=＜2，∠AEB是钝角，此时△ABE与以B，C、E中的三点为顶点的三角形不相似，如图4，∴E（﹣12，0）；同理得BE的解析式为：y=﹣x﹣4，﹣x﹣4=x2﹣x﹣4，x=或0（舍）∴D（，﹣）；综上，点D的坐标为（，）或（，﹣）．。

2020-2021备战中考数学——平行四边形的综合压轴题专题复习含详细答案

2020-2021备战中考数学——平行四边形的综合压轴题专题复习含详细答案一、平行四边形1．（1）、动手操作：如图①：将矩形纸片ABCD折叠，使点D与点B重合，点C落在点处，折痕为EF，若∠ABE＝20°，那么的度数为 .（2）、观察发现：小明将三角形纸片ABC（AB＞AC）沿过点A的直线折叠，使得AC落在AB边上，折痕为AD，展开纸片（如图②）；再次折叠该三角形纸片，使点A和点D重合，折痕为EF，展平纸片后得到△AEF（如图③）．小明认为△AEF是等腰三角形，你同意吗？请说明理由．（3）、实践与运用：将矩形纸片ABCD按如下步骤操作：将纸片对折得折痕EF，折痕与AD边交于点E，与BC 边交于点F；将矩形ABFE与矩形EFCD分别沿折痕MN和PQ折叠，使点A、点D都与点F 重合，展开纸片，此时恰好有MP＝MN＝PQ（如图④），求∠MNF的大小.【答案】（1）125°；（2）同意；（3）60°【解析】试题分析：（1）根据直角三角形的两个锐角互余求得∠AEB=70°，根据折叠重合的角相等，得∠BEF=∠DEF=55°，根据平行线的性质得到∠EFC=125°，再根据折叠的性质得到∠EFC′=∠EFC=125°；（2）根据第一次折叠，得∠BAD=∠CAD；根据第二次折叠，得EF垂直平分AD，根据等角的余角相等，得∠AEG=∠AFG，则△AEF是等腰三角形；（3）由题意得出：∠NMF=∠AMN=∠MNF，MF=NF，由对称性可知，MF=PF，进而得出△MNF≌△MPF，得出3∠MNF=180°求出即可．试题解析：（1）、∵在直角三角形ABE中，∠ABE=20°，∴∠AEB=70°，∴∠BED=110°，根据折叠重合的角相等，得∠BEF=∠DEF=55°．∵AD∥BC，∴∠EFC=125°，再根据折叠的性质得到∠EFC′=∠EFC=125°．；（2）、同意，如图，设AD与EF交于点G由折叠知，AD平分∠BAC，所以∠BAD=∠CAD．由折叠知，∠AGE=∠DGE=90°，所以∠AGE=∠AGF=90°，所以∠AEF=∠AFE．所以AE=AF，即△AEF为等腰三角形．（3）、由题意得出：∠NMF＝∠AMN＝∠MNF，∴MF＝NF，由折叠可知，MF＝PF，∴NF＝PF，而由题意得出：MP＝MN，又∵MF＝MF，∴△MNF≌△MPF，∴∠PMF＝∠NMF，而∠PMF＋∠NMF＋∠MNF＝180°，即3∠MNF＝180°，∴∠MNF＝60°.考点：1.折叠的性质；2.等边三角形的性质；3.全等三角形的判定和性质；4.等腰三角形的判定2．四边形ABCD是正方形，AC与BD，相交于点O，点E、F是直线AD上两动点，且AE=DF，CF所在直线与对角线BD所在直线交于点G，连接AG，直线AG交BE于点H．（1）如图1，当点E、F在线段AD上时，①求证：∠DAG=∠DCG；②猜想AG与BE的位置关系，并加以证明；（2）如图2，在（1）条件下，连接HO，试说明HO平分∠BHG；（3）当点E、F运动到如图3所示的位置时，其它条件不变，请将图形补充完整，并直接写出∠BHO的度数．【答案】（1）①证明见解析；②AG⊥BE．理由见解析；（2）证明见解析；（3）∠BHO=45°．【解析】试题分析：（1）①根据正方形的性质得DA=DC，∠ADB=∠CDB=45°，则可根据“SAS”证明△ADG≌△CDG，所以∠DAG=∠DCG；②根据正方形的性质得AB=DC，∠BAD=∠CDA=90°，根据“SAS”证明△ABE≌△DCF，则∠ABE=∠DCF，由于∠DAG=∠DCG，所以∠DAG=∠ABE，然后利用∠DAG+∠BAG=90°得到∠ABE+∠BAG=90°，于是可判断AG⊥BE；（2）如答图1所示，过点O作OM⊥BE于点M，ON⊥AG于点N，证明△AON≌△BOM，可得四边形OMHN为正方形，因此HO平分∠BHG结论成立；（3）如答图2所示，与（1）同理，可以证明AG⊥BE；过点O作OM⊥BE于点M，ON⊥AG于点N，构造全等三角形△AON≌△BOM，从而证明OMHN为正方形，所以HO 平分∠BHG，即∠BHO=45°．试题解析：（1）①∵四边形ABCD为正方形，∴DA=DC，∠ADB=∠CDB=45°，在△ADG和△CDG中，∴△ADG≌△CDG（SAS），∴∠DAG=∠DCG；②AG⊥BE．理由如下：∵四边形ABCD为正方形，∴AB=DC，∠BAD=∠CDA=90°，在△ABE和△DCF中，∴△ABE≌△DCF（SAS），∴∠ABE=∠DCF，∵∠DAG=∠DCG，∴∠DAG=∠ABE，∵∠DAG+∠BAG=90°，∴∠ABE+∠BAG=90°，∴∠AHB=90°，∴AG⊥BE；（2）由（1）可知AG⊥BE．如答图1所示，过点O作OM⊥BE于点M，ON⊥AG于点N，则四边形OMHN为矩形．∴∠MON=90°，又∵OA⊥OB，∴∠AON=∠BOM．∵∠AON+∠OAN=90°，∠BOM+∠OBM=90°，∴∠OAN=∠OBM．在△AON与△BOM中，∴△AON≌△BOM（AAS）．∴OM=ON，∴矩形OMHN为正方形，∴HO平分∠BHG．（3）将图形补充完整，如答图2示，∠BHO=45°．与（1）同理，可以证明AG⊥BE．过点O作OM⊥BE于点M，ON⊥AG于点N，与（2）同理，可以证明△AON≌△BOM，可得OMHN为正方形，所以HO平分∠BHG，∴∠BHO=45°．考点：1、四边形综合题；2、全等三角形的判定与性质；3、正方形的性质3．如果两个三角形的两条边对应相等，夹角互补，那么这两个三角形叫做互补三角形，如图2，分别以△ABC的边AB、AC为边向外作正方形ABDE和ACGF，则图中的两个三角形就是互补三角形．（1）用尺规将图1中的△ABC分割成两个互补三角形；（2）证明图2中的△ABC分割成两个互补三角形；（3）如图3，在图2的基础上再以BC为边向外作正方形BCHI．①已知三个正方形面积分别是17、13、10，在如图4的网格中（网格中每个小正方形的边长为1）画出边长为、、的三角形，并计算图3中六边形DEFGHI的面积．②若△ABC的面积为2，求以EF、DI、HG的长为边的三角形面积．【答案】（1）作图见解析（2）证明见解析（3）①62；②6【解析】试题分析：（1）作BC边上的中线AD即可．（2）根据互补三角形的定义证明即可．（3）①画出图形后，利用割补法求面积即可．②平移△CHG到AMF，连接EM，IM，则AM=CH=BI，只要证明S△EFM=3S△ABC即可．试题解析：（1）如图1中，作BC边上的中线AD，△ABD和△ADC是互补三角形．（2）如图2中，延长FA到点H，使得AH=AF，连接EH．∵四边形ABDE，四边形ACGF是正方形，∴AB=AE，AF=AC，∠BAE=∠CAF=90°，∴∠EAF+∠BAC=180°，∴△AEF和△ABC是两个互补三角形．∵∠EAH+∠HAB=∠BAC+∠HAB=90°，∴∠EAH=∠BAC，∵AF=AC，∴AH=AB，在△AEH和△ABC中，∴△AEH≌△ABC，∴S△AEF=S△AEH=S△ABC．（3）①边长为、、的三角形如图4所示．∵S△ABC=3×4﹣2﹣1.5﹣3=5.5，∴S六边形=17+13+10+4×5.5=62．②如图3中，平移△CHG到AMF，连接EM，IM，则AM=CH=BI，设∠ABC=x，∵AM∥CH，CH⊥BC，∴AM⊥BC，∴∠EAM=90°+90°﹣x=180°﹣x，∵∠DBI=360°﹣90°﹣90°﹣x=180°﹣x，∴∠EAM=∠DBI，∵AE=BD，∴△AEM≌△DBI，∵在△DBI和△ABC中，DB=AB，BI=BC，∠DBI+∠ABC=180°，∴△DBI和△ABC是互补三角形，∴S△AEM=S△AEF=S△AFM=2，∴S△EFM=3S△ABC=6．考点：1、作图﹣应用与设计，2、三角形面积4．如图，△ABC是等边三角形，AB=6cm，D为边AB中点．动点P、Q在边AB上同时从点D出发，点P沿D→A以1cm/s的速度向终点A运动．点Q沿D→B→D以2cm/s的速度运动，回到点D停止．以PQ为边在AB上方作等边三角形PQN．将△PQN绕QN的中点旋转180°得到△MNQ．设四边形PQMN与△ABC重叠部分图形的面积为S（cm2），点P运动的时间为t（s）（0＜t＜3）．（1）当点N落在边BC上时，求t的值．（2）当点N到点A、B的距离相等时，求t的值．（3）当点Q沿D→B运动时，求S与t之间的函数表达式．（4）设四边形PQMN的边MN、MQ与边BC的交点分别是E、F，直接写出四边形PEMF 与四边形PQMN的面积比为2：3时t的值．【答案】（1）（2）2（3）S=S菱形PQMN=2S△PNQ=t2；（4）t=1或【解析】试题分析：（1）由题意知：当点N落在边BC上时，点Q与点B重合，此时DQ=3；（2）当点N到点A、B的距离相等时，点N在边AB的中线上，此时PD=DQ；（3）当0≤t≤时，四边形PQMN与△ABC重叠部分图形为四边形PQMN；当≤t≤时，四边形PQMN与△ABC重叠部分图形为五边形PQFEN．（4）MN、MQ与边BC的有交点时，此时＜t＜，列出四边形PEMF与四边形PQMN的面积表达式后，即可求出t的值．试题解析：（1）∵△PQN与△ABC都是等边三角形，∴当点N落在边BC上时，点Q与点B重合．∴DQ=3∴2t=3．∴t=；（2）∵当点N到点A、B的距离相等时，点N在边AB的中线上，∴PD=DQ，当0＜t＜时，此时，PD=t，DQ=2t∴t=2t∴t=0（不合题意，舍去），当≤t＜3时，此时，PD=t，DQ=6﹣2t∴t=6﹣2t，解得t=2；综上所述，当点N到点A、B的距离相等时，t=2；（3）由题意知：此时，PD=t，DQ=2t当点M在BC边上时，∴MN=BQ∵PQ=MN=3t，BQ=3﹣2t∴3t=3﹣2t∴解得t=如图①，当0≤t≤时，S△PNQ=PQ2=t2；∴S=S菱形PQMN=2S△PNQ=t2，如图②，当≤t≤时，设MN、MQ与边BC的交点分别是E、F，∵MN=PQ=3t，NE=BQ=3﹣2t，∴ME=MN﹣NE=PQ﹣BQ=5t﹣3，∵△EMF是等边三角形，∴S△EMF=ME2=（5t﹣3）2．；（4）MN、MQ与边BC的交点分别是E、F，此时＜t＜，t=1或．考点：几何变换综合题5．如图，四边形ABCD中，对角线AC、BD相交于点O，AO=CO，BO=DO，且∠ABC+∠ADC=180°．（1）求证：四边形ABCD是矩形．（2）若∠ADF：∠FDC=3：2，DF⊥AC，求∠BDF的度数．【答案】(1)见解析；（2）18°.【解析】【分析】（1）根据平行四边形的判定得出四边形ABCD是平行四边形，求出∠ABC=90°，根据矩形的判定得出即可；（2）求出∠FDC的度数，根据三角形内角和定理求出∠DCO，根据矩形的性质得出OD=OC，求出∠CDO，即可求出答案．【详解】（1）证明：∵AO=CO，BO=DO∴四边形ABCD是平行四边形，∴∠ABC=∠ADC，∵∠ABC+∠ADC=180°，∴∠ABC=∠ADC=90°，∴四边形ABCD是矩形；（2）解：∵∠ADC=90°，∠ADF：∠FDC=3：2，∴∠FDC=36°，∵DF⊥AC，∴∠DCO=90°﹣36°=54°，∵四边形ABCD是矩形，∴OC=OD，∴∠ODC=54°∴∠BDF=∠ODC﹣∠FDC=18°．【点睛】本题考查了平行四边形的性质和判定，矩形的性质和判定的应用，能灵活运用定理进行推理是解此题的关键，注意：矩形的对角线相等，有一个角是直角的平行四边形是矩形．6．(1)如图①，在矩形ABCD中，对角线AC与BD相交于点O，过点O作直线EF⊥BD，交AD于点E，交BC于点F，连接BE、DF，且BE平分∠ABD．①求证：四边形BFDE是菱形；②直接写出∠EBF的度数；(2)把(1)中菱形BFDE进行分离研究，如图②，点G、I分别在BF、BE边上，且BG=BI，连接GD，H为GD的中点，连接FH并延长，交ED于点J，连接IJ、IH、IF、IG.试探究线段IH与FH之间满足的关系，并说明理由；(3)把(1)中矩形ABCD进行特殊化探究，如图③，当矩形ABCD满足AB=AD时，点E是对角线AC上一点，连接DE、EF、DF，使△DEF是等腰直角三角形，DF交AC于点G.请直接写出线段AG、GE、EC三者之间满足的数量关系.【答案】（1）①详见解析；②60°．（2）IH＝3FH；（3）EG2＝AG2+CE2．【解析】【分析】（1）①由△DOE≌△BOF，推出EO＝OF，∵OB＝OD，推出四边形EBFD是平行四边形，再证明EB＝ED即可．②先证明∠ABD＝2∠ADB，推出∠ADB＝30°，延长即可解决问题．（2）IH＝3FH．只要证明△IJF是等边三角形即可．（3）结论：EG2＝AG2+CE2．如图3中，将△ADG绕点D逆时针旋转90°得到△DCM，先证明△DEG≌△DEM，再证明△ECM是直角三角形即可解决问题．【详解】（1）①证明：如图1中，∵四边形ABCD是矩形，∴AD ∥BC ，OB ＝OD ，∴∠EDO ＝∠FBO ，在△DOE 和△BOF 中，EDO FBO OD OBEOD BOF ∠∠⎧⎪⎨⎪∠∠⎩＝＝＝， ∴△DOE ≌△BOF ，∴EO ＝OF ，∵OB ＝OD ，∴四边形EBFD 是平行四边形，∵EF ⊥BD ，OB ＝OD ，∴EB ＝ED ，∴四边形EBFD 是菱形．②∵BE 平分∠ABD ，∴∠ABE ＝∠EBD ，∵EB ＝ED ，∴∠EBD ＝∠EDB ，∴∠ABD ＝2∠ADB ，∵∠ABD +∠ADB ＝90°，∴∠ADB ＝30°，∠ABD ＝60°，∴∠ABE ＝∠EBO ＝∠OBF ＝30°，∴∠EBF ＝60°．（2）结论：IH＝3FH ．理由：如图2中，延长BE 到M ，使得EM ＝EJ ，连接MJ ．∵四边形EBFD 是菱形，∠B ＝60°，∴EB ＝BF ＝ED ，DE ∥BF ，∴∠JDH ＝∠FGH ，在△DHJ 和△GHF 中，DHG GHF DH GHJDH FGH ∠∠⎧⎪⎨⎪∠∠⎩＝＝＝， ∴△DHJ ≌△GHF ，∴DJ ＝FG ，JH ＝HF ，∴EJ ＝BG ＝EM ＝BI ，∵∠MEJ ＝∠B ＝60°，∴△MEJ 是等边三角形，∴MJ ＝EM ＝NI ，∠M ＝∠B ＝60°在△BIF 和△MJI 中，BI MJ B M BF IM ⎧⎪∠∠⎨⎪⎩＝＝＝，∴△BIF ≌△MJI ，∴IJ ＝IF ，∠BFI ＝∠MIJ ，∵HJ ＝HF ，∴IH ⊥JF ，∵∠BFI +∠BIF ＝120°，∴∠MIJ +∠BIF ＝120°，∴∠JIF ＝60°，∴△JIF 是等边三角形，在Rt △IHF 中，∵∠IHF ＝90°，∠IFH ＝60°，∴∠FIH ＝30°，∴IH＝3FH ．（3）结论：EG 2＝AG 2+CE 2．理由：如图3中，将△ADG 绕点D 逆时针旋转90°得到△DCM ，∵∠FAD +∠DEF ＝90°，∴AFED 四点共圆，∴∠EDF ＝∠DAE ＝45°，∠ADC ＝90°，∴∠ADF +∠EDC ＝45°，∵∠ADF ＝∠CDM ，∴∠CDM +∠CDE ＝45°＝∠EDG ，在△DEM 和△DEG 中，DE DE EDG EDM DG DM ⎧⎪∠∠⎨⎪⎩＝＝＝， ∴△DEG ≌△DEM ，∴GE ＝EM ，∵∠DCM ＝∠DAG ＝∠ACD ＝45°，AG ＝CM ，∴∠ECM ＝90°∵EG＝EM，AG＝CM，∴GE2＝AG2+CE2．【点睛】考查四边形综合题、矩形的性质、正方形的性质、菱形的判定和性质，等边三角形的判定和性质，勾股定理等知识，解题的关键是学会添加常用辅助线，构造全等三角形，学会转化的思想思考问题.7．如图1，已知正方形ABCD的边CD在正方形DEFG的边DE上，连接AE，GC．(1)试猜想AE与GC有怎样的关系(直接写出结论即可)；(2)将正方形DEFG绕点D按顺时针方向旋转，使点E落在BC边上，如图2，连接AE和CG．你认为(1)中的结论是否还成立？若成立，给出证明；若不成立，请说明理由．(3)在(2)中，若E是BC的中点，且BC＝2，则C，F两点间的距离为．【答案】(1) AE＝CG，AE⊥GC；(2)成立，证明见解析； (3)2．【解析】【分析】（1）观察图形，AE、CG的位置关系可能是垂直，下面着手证明．由于四边形ABCD、DEFG都是正方形，易证得△ADE≌△CDG，则∠1＝∠2，由于∠2、∠3互余，所以∠1、∠3互余，由此可得AE⊥GC．（2）题（1）的结论仍然成立，参照（1）题的解题方法，可证△ADE≌△CDG，得∠5＝∠4，由于∠4、∠7互余，而∠5、∠6互余，那么∠6＝∠7；由图知∠AEB＝∠CEH＝90°﹣∠6，即∠7+∠CEH＝90°，由此得证．（3）如图3中，作CM⊥DG于G，GN⊥CD于N，CH⊥FG于H，则四边形CMGH是矩形，可得CM＝GH，CH＝GM．想办法求出CH，HF，再利用勾股定理即可解决问题．【详解】(1)AE＝CG，AE⊥GC；证明：延长GC交AE于点H，在正方形ABCD与正方形DEFG中，AD＝DC，∠ADE＝∠CDG＝90°，DE＝DG，∴△ADE≌△CDG(SAS)，∴AE，CG，∠1＝∠2∵∠2+∠3＝90°，∴∠1+∠3＝90°，∴∠AHG＝180°﹣(∠1+∠3)＝180°﹣90°＝90°，∴AE⊥GC．(2)答：成立；证明：延长AE和GC相交于点H，在正方形ABCD和正方形DEFG中，AD＝DC，DE＝DG，∠ADC＝∠DCB＝∠B＝∠BAD＝∠EDG＝90°，∴∠1＝∠2＝90°﹣∠3；∴△ADE≌△CDG(SAS)，∴AE＝CG，∠5＝∠4；又∵∠5+∠6＝90°，∠4+∠7＝180°﹣∠DCE＝180°﹣90°＝90°，∴∠6＝∠7，又∵∠6+∠AEB＝90°，∠AEB＝∠CEH，∴∠CEH+∠7＝90°，∴∠EHC＝90°，∴AE⊥GC．(3)如图3中，作CM⊥DG于G，GN⊥CD于N，CH⊥FG于H，则四边形CMGH是矩形，可得CM＝GH，CH＝GM．∵BE＝CE＝1，AB＝CD＝2，∴AE ＝DE ＝CG ═DG ＝FG ＝5， ∵DE ＝DG ，∠DCE ＝∠GND ，∠EDC ＝∠DGN ，∴△DCE ≌△GND(AAS)，∴GCD ＝2，∵S △DCG ＝12•CD•NG ＝12•DG•CM ， ∴2×2＝5•CM ， ∴CM ＝GH ＝455， ∴MG ＝CH ＝22CG CM -＝355， ∴FH ＝FG ﹣FG ＝5， ∴CF ＝22FH CH +＝22535()()55+＝2．故答案为2．【点睛】本题属于四边形综合题，考查了正方形的性质，全等三角形的判定和性质，解直角三角形等知识，解题的关键是正确寻找全等三角形解决问题，属于中考压轴题．8．如图，在正方形ABCD 中，E 是边AB 上的一动点，点F 在边BC 的延长线上，且CF AE =，连接DE ，DF ，EF . FH 平分EFB ∠交BD 于点H .（1）求证：DE DF ⊥；（2）求证：DH DF =：（3）过点H 作HM EF ⊥于点M ，用等式表示线段AB ，HM 与EF 之间的数量关系，并证明.【答案】（1）详见解析；（2）详见解析；（3）22EF AB HM =-，证明详见解析.【解析】【分析】（1）根据正方形性质， CF AE =得到DE DF ⊥.（2）由AED CFD △△≌，得DE DF =.由90ABC ∠=︒，BD 平分ABC ∠，得45DBF ∠=︒.因为FH 平分EFB ∠，所以EFH BFH ∠=∠.由于45DHF DBF BFH BFH ∠=∠+∠=︒+∠,45DFH DFE EFH EFH ∠=∠+∠=︒+∠, 所以DH DF =.（3）过点H 作HN BC ⊥于点N ，由正方形ABCD 性质，得222BD AB AD AB =+=.由FH 平分,EFB HM EF HN BC ∠⊥⊥，，得HM HN =.因为4590HBN HNB ∠=︒∠=︒，，所以22sin 45HN BH HN HM ===︒. 由22cos 45DF EF DF DH ===︒，得22EF AB HM =-. 【详解】（1）证明：∵四边形ABCD 是正方形，∴AD CD =，90EAD BCD ADC ∠=∠=∠=︒.∴90EAD FCD ∠=∠=︒.∵CF AE =。

中考数学压轴题专题-二次函数与平行四边形存在性问题

专题6二次函数与平行四边形存在性问题以二次函数为载体的平行四边形存在性问题是中考的热点难点之一，其图形复杂，知识覆盖面广，综合性较强，对学生分析问题和解决问题的能力要求高.对这类题，常规解法是先画出平行四边形，再依据“平行四边形的一组对边平行且相等”或“平行四边形的对角线互相平分”来解决.由于先要画出草图，若考虑不周，很容易漏解.解决抛物线中的平行四边形存在性问题，常用的结论和方法有：线段中点坐标公式、平行四边形顶点坐标公式、画平行四边形.1.平面直角坐标系中，点A 的坐标是11(,)x y ，点B 的坐标是22(,)x y ，则线段AB 的中点坐标是1212(,)22x x y y ++.2.平行四边形ABCD 的顶点坐标分别为(,)A A x y 、(,)B B x y 、(,)C C x y 、(,)D D x y ，则A C B D x x x x +=+，A CB D y y y y +=+. 3.已知不在同一直线上的三点A 、B 、C ，在平面内找到一个点D ，使以A 、B 、C 、D 为顶点的四边形是平行四边形，有三种情况：【例1】（2021•赤峰）如图，抛物线y ＝﹣x 2+bx +c 与x 轴交于A （﹣3，0）、B （1，0）两点，与y 轴交于点C ，对称轴l 与x 轴交于点F ，直线m ∥AC ，点E 是直线AC 上方抛物线上一动点，过点E 作EH ⊥m ，垂足为H ，交AC 于点G ，连接AE 、EC 、CH 、AH ．（1）抛物线的解析式为；（2）当四边形AHCE 面积最大时，求点E 的坐标；（3）在（2）的条件下，连接EF ，点P 是x 轴上一动点，在抛物线上是否存在点Q ，使得以F 、E 、P 、Q 为顶点，以EF 为一边的四边形是平行四边形．若存在，请直接写出点Q 的坐标；若不存在，说明理由．【例2】（2021•湘西州）如图，已知抛物线y＝ax2+bx+4经过A（﹣1，0），B（4，0）两点，交y轴于点C．（1）求抛物线的解析式；（2）连接BC，求直线BC的解析式；（3）请在抛物线的对称轴上找一点P，使AP+PC的值最小，求点P的坐标，并求出此时AP+PC的最小值；（4）点M为x轴上一动点，在抛物线上是否存在一点N，使得以A、C、M、N四点为顶点的四边形是平行四边形？若存在，求出点N的坐标；若不存在，请说明理由．【例3】（2021•梧州）如图，在平面直角坐标系中，抛物线y＝x2+bx+c经过点A（﹣1，0），B（0，3），顶点为C．平移此抛物线，得到一条新的抛物线，且新抛物线上的点D（3，﹣1）为原抛物线上点A的对应点，新抛物线顶点为E，它与y轴交于点G，连接CG，EG，CE．（1）求原抛物线对应的函数表达式；（2）在原抛物线或新抛物线上找一点F，使以点C，E，F，G为顶点的四边形是平行四边形，并求出点F的坐标；（3）若点K是y轴上的一个动点，且在点B的上方，过点K作CE的平行线，分别交两条抛物线于点M，N，且点M，N分别在y轴的两侧，当MN＝CE时，请直接写出点K的坐标．【例4】（2021•郴州）将抛物线y＝ax2（a≠0）向左平移1个单位，再向上平移4个单位后，得到抛物线H：y＝a（x﹣h）2+k．抛物线H与x轴交于点A，B，与y轴交于点C．已知A（﹣3，0），点P是抛物线H上的一个动点．（1）求抛物线H的表达式；（2）如图1，点P在线段AC上方的抛物线H上运动（不与A，C重合），过点P作PD⊥AB，垂足为D，PD交AC于点E．作PF⊥AC，垂足为F，求△PEF的面积的最大值；（3）如图2，点Q是抛物线H的对称轴l上的一个动点，在抛物线H上，是否存在点P，使得以点A，P，C，Q为顶点的四边形是平行四边形？若存在，求出所有符合条件的点P的坐标；若不存在，说明理由．【例5】（2021•海南）已知抛物线y＝ax2+x+c与x轴交于A、B两点，与y轴交于C点，且点A的坐标为（﹣1，0）、点C的坐标为（0，3）．（1）求该抛物线的函数表达式；（2）如图1，若该抛物线的顶点为P，求△PBC的面积；（3）如图2，有两动点D、E在△COB的边上运动，速度均为每秒1个单位长度，它们分别从点C和点B同时出发，点D沿折线COB按C→O→B方向向终点B运动，点E沿线段BC按B→C方向向终点C运动，当其中一个点到达终点时，另一个点也随之停止运动．设运动时间为t秒，请解答下列问题：①当t为何值时，△BDE的面积等于；②在点D、E运动过程中，该抛物线上存在点F，使得依次连接AD、DF、FE、EA得到的四边形ADFE是平行四边形，请直接写出所有符合条件的点F的坐标．1．（2021•海州区一模）如图，抛物线y＝ax2+bx﹣3的图象与x轴交于A（﹣1，0），B（3，0）两点，与y轴交于点C，直线l与抛物线交于点B，交y轴于点D（0，3）．（1）求该抛物线的函数表达式；（2）点P（m，0）为线段OB上一动点，过点P作x轴的垂线EF，分别交抛物线与直线l于点E，F，连接CE，CF，BE，求四边形CEBF面积的最大值及此时m的值；（3）点M为y轴右侧抛物线上一动点，过点M作直线MN∥AC交直线l于点N，是否存在点M，使以A，C，M，N四点为顶点的四边形是平行四边形，若存在，请直接写出点M的坐标；若不存在，请说明理由．2．（2020•平顶山二模）如图，已知二次函数y=−38x2+bx+c的图象与x轴交于点A、C，与y轴交于点B，直线y=34x+3经过A、B两点．（1）求b、c的值．（2）若点P是直线AB上方抛物线上的一动点，过点P作PF⊥x轴于点F，交直线AB于点D，求线段PD的最大值．（3）在（2）的结论下，连接CD，点Q是抛物线对称轴上的一动点，在抛物线上是否存在点G，使得以C、D、G、Q为顶点的四边形是平行四边形，若存在，请直接写出点G的坐标；若不存在，请说明理由．3．（2020•菏泽）如图，抛物线y＝ax2+bx﹣6与x轴相交于A，B两点，与y轴相交于点C，OA＝2，OB ＝4，直线l是抛物线的对称轴，在直线l右侧的抛物线上有一动点D，连接AD，BD，BC，CD．（1）求抛物线的函数表达式；（2）若点D在x轴的下方，当△BCD的面积是92时，求△ABD的面积；（3）在（2）的条件下，点M是x轴上一点，点N是抛物线上一动点，是否存在点N，使得以点B，D，M，N为顶点，以BD为一边的四边形是平行四边形，若存在，求出点N的坐标；若不存在，请说明理由．4．（2020•东莞市校级一模）已知，抛物线y＝x2+bx+c与x轴交点为A（﹣1，0）和点B，与y轴交点为C （0，﹣3），直线L：y＝kx﹣1与抛物线的交点为点A和点D．（1）求抛物线和直线L的解析式；（2）如图，点M为抛物线上一动点（不与A、D重合），当点M在直线L下方时，过点M作MN∥x 轴交L于点N，求MN的最大值；（3）点M为抛物线上一动点（不与A、D重合），M'为直线AD上一动点，是否存在点M，使得以C、D、M、M′为顶点的四边形是平行四边形？如果存在，请直接写出点M的坐标，如果不存在，请说明理由．【题组二】5．（2020•雁塔区校级二模）已知抛物线L：y＝x2+bx+c经过点A（﹣1，0）和（1，﹣2）两点，抛物线L 关于原点O的对称的为抛物线L′，点A的对应点为点A′．（1）求抛物线L和L′的表达式；（2）是否在抛物线L上存在一点P，抛物线L′上存在一点Q，使得以AA′为边，且以A、A′、P、Q为顶点的四边形是平行四边形？若存在，求出P点坐标；若不存在，请说明理由．6．（2021•盘龙区二模）如图，在平面直角坐标系中，抛物线y＝x2+bx+c经过点A（﹣4，0），点M为抛物线的顶点，点B在y轴上，且OA＝OB，直线AB与抛物线在第一象限交于点C（2，6）．（1）求抛物线的解析式及顶点M的坐标；（2）求直线AB的函数解析式及sin∠ABO的值；连接OC．若过点O的直线交线段AC于点P，将三角形AOC的面积分成1：2的两部分，请求出点P的坐标；（3）在坐标平面内是否存在点N，使以点A、O、C、N为顶点的四边形是平行四边形？若存在，请直接写出点N的坐标；若不存在，请说明理由．7．（2020•碑林区校级三模）在平面直角坐标系中，O为坐标原点，抛物线L：y＝ax2﹣4ax（a＞0）与x 轴正半轴交于点A．抛物线L的顶点为M，对称轴与x轴交于点D．（1）求抛物线L的对称轴．（2）抛物线L：y＝ax2﹣4ax关于x轴对称的抛物线记为L'，抛物线L'的顶点为M'，若以O、M、A、M'为顶点的四边形是正方形，求L'的表达式．（3）在（2）的条件下，点P在抛物线L上，且位于第四象限，点Q在抛物线L'上，是否存在点P、点Q使得以O、D、P、Q为顶点的四边形是平行四边形，若存在，求出点P坐标，若不存在，请说明理由．8．（2020•泰安二模）如图①抛物线y＝ax2+bx+4（a≠0）与x轴，y轴分别交于点A（﹣1，0），B（4，0），点C三点．（1）试求抛物线解析式；（2）点D（3，m）在第一象限的抛物线上，连接BC，BD．试问，在对称轴左侧的抛物线上是否存在一点P，满足∠PBC＝∠DBC？如果存在，请求出点P的坐标；如果不存在，请说明理由；（3）点N在抛物线的对称轴上，点M在抛物线上，当以M、N、B、C为顶点的四边形是平行四边形时，请直接写出点M的坐标．【题组三】9．（2021•铜梁区校级一模）已知抛物线y＝ax2+bx+3与x轴交于A、B两点（点A在点B的左侧）．与y 轴交于点C．其中OC＝OB，tan∠CAO＝3．（1）求抛物线的解析式；（2）P是第一象限内的抛物线上一动点，Q为线段PB的中点，求△CPQ面积的最大值时P点坐标：（3）将抛物线沿射线CB方向平移2个单位得新抛物线y'．M为新抛物线y′的顶点．D为新抛物线y'上任意一点，N为x轴上一点．当以M、N、C、D为顶点的四边形是平行四边形时，直接写出所有符合条件的点N的坐标．并选择一个你喜欢的N点．写出求解过程．10．（2020•烟台模拟）如图，抛物线y＝ax2+43x+c的图象与x轴交于A（﹣3，0），B两点，与y轴交于点C（0，﹣2），连接AC．点P是x轴上的动点．（1）求抛物线的表达式；（2）过点P作x轴的垂线，交线段AC于点D，E为y轴上一点，连接AE，BE，当AD＝BE时，求AD+AE的最小值；（3）点Q为抛物线上一动点，是否存在点P，使得以A、C、P、Q为顶点的四边形是平行四边形？若存在，求出点P的坐标；若不存在，说明理由．11．（2020•龙城区一模）已知：二次函数y＝ax2+bx+c的图象的顶点为（﹣1，4），与x轴交于A，B两点，与y轴交于点C（0，3），如图．（1）求二次函数的表达式；（2）在抛物线的对称轴上有一点M，使得△BCM的周长最小，求出点M的坐标；（3）连结AD、CD，求cos∠ADC的值；（4）若点Q在抛物线的对称轴上，抛物线上是否存在点P，使得以A、B、Q、P四点为顶点的四边形为平行四边形？若存在，求出满足条件的点P的坐标；若不存在，请说明理由．12．（2020•长沙模拟）如图1，二次函数y＝ax2+bx+c（a≠0）的图象交x轴于A（﹣1，0）、B（3，0）两点，交y轴于点C（0，﹣3），点D为该二次函数图象顶点．（1）求该二次函数解析式，及D点坐标；（2）点P是抛物线的对称轴上一点，以点P为圆心的圆经过A、B两点，且与直线CD相切，求点P 的坐标；＝S△AOC，点E为直线AM上一动点，在x轴上是（3）如图2，若M为线段BC上一点，且满足S△AMC否存在点F，使以点F、E、B、C为顶点的四边形为平行四边形？若存在，请直接写出点F的坐标，若不存在，请说明理由．【题组四】13．（2020•东莞市一模）如图，抛物线y＝x2+bx+c与x轴交于点A（﹣1，0），与y轴交于点C（0，﹣3）．（1）求该抛物线的解析式及顶点坐标；（2）若P是线段OB上一动点，过P作y轴的平行线交抛物线于点H，交BC于点N，设OP＝t时，△BCH的面积为S．求S关于t的函数关系式；若S有最大值，请求出S的最大值，若没有，请说明理由．（3）若P是x轴上一个动点，过P作射线PQ∥AC交抛物线于点Q，在抛物线上是否存在这样的点Q，使以A，P，Q，C为顶点的四边形为平行四边形？若存在，请直接写出P点的坐标；若不存在，请说明理由．14．（2021•深圳模拟）如图，抛物线y＝ax2+bx﹣3与x轴交于A，B两点，与y轴交于C点，且经过点（2，﹣3a），对称轴是直线x＝1，顶点是M．（1）求抛物线对应的函数表达式；（2）经过C，M两点作直线与x轴交于点N，在抛物线上是否存在这样的点P，满足以点P，A，C，N为顶点的四边形为平行四边形？若存在，请求出点P的坐标；若不存在，请说明理由；（3）设直线y＝﹣x+3与y轴的交点是D，在线段BD上任取一点E（不与B，D重合），经过A，B，E 三点的圆交直线BC于点F，试判断△AEF的形状，并说明理由．15．（2020•郑州一模）如图，直线y=−23x+4与x轴交于点C，与y轴交于点B，抛物线y＝ax2+103x+c经过B、C两点．（1）求抛物线的解析式；（2）如图，点E是直线BC上方抛物线上的一动点，当△BEC面积最大时，请求出点E的坐标；（3）在（2）的结论下，过点E作y轴的平行线交直线BC于点M，连接AM，点Q是抛物线对称轴上的动点，在抛物线上是否存在点P，使得以P、Q、A、M为顶点的四边形是平行四边形？如果存在，请直接写出点P的坐标；如果不存在，请说明理由．16.（2021•碑林区校级模拟）如图，抛物线M：y＝ax2+bx+b﹣a经过点（1，﹣3）和（﹣4，12），与两坐标轴的交点分别为A，B，C，顶点为D．（1）求抛物线M的表达式和顶点D的坐标；（2）若抛物线N：y＝﹣（x﹣h）2+与抛物线M有一个公共点为E，则在抛物线N上是否存在一点F，使得以B、C、E、F为顶点的四边形是以BC为边的平行四边形？若存在，请求出h的值；若不存在，请说明理由．【题组五】17．（2020•东营区模拟）如图，抛物线y＝ax2+bx+3（a≠0）的对称轴为直线x＝﹣1，抛物线交x轴于A、C两点，与直线y＝x﹣1交于A、B两点，直线AB与抛物线的对称轴交于点E．（1）求抛物线的解析式．（2）点P在直线AB上方的抛物线上运动，若△ABP的面积最大，求此时点P的坐标．（3）在平面直角坐标系中，以点B、E、C、D为顶点的四边形是平行四边形，请直接写出符合条件点D的坐标．18．（2020•唐山二模）如图，抛物线y＝ax2+bx﹣3过A（1，0），B（﹣3，0），直线AD交抛物线于点D，点D的横坐标为﹣2，点P（m，n）是线段AD上的动点．（1）求直线AD及抛物线的解析式；（2）过点P的直线垂直于x轴，交抛物线于点Q，求线段PQ的长度l与m的关系式，m为何值时，PQ最长？（3）在平面内是否存在整点（横、纵坐标都为整数）R，使得P，Q，D，R为顶点的四边形是平行四边形？若存在，直接写出点R的坐标；若不存在，说明理由．19．（2020•安定区校级三模）如图，抛物线经过A（﹣1，0），B（5，0），C（0，−5）三点（1）求抛物线的解析式；（2）在抛物线的对称轴上有一点P，使PA+PC的值最小，则点P的坐标为（2，−32）；（3）点M为x轴上一动点，在抛物线上是否存在一点N，使以A，C，M，N四点构成的四边形为平行四边形？若存在，直接写出点N的坐标；若不存在，请说明理由．20．（2020•高州市模拟）如图，在平面直角坐标系中，已知抛物线y＝ax2+bx+2（a≠0）与x轴交于A（﹣1，0），B（3，0）两点，与y轴交于点C．（1）求该抛物线的解析式；（2）如图①，若点D是抛物线上一个动点，设点D的横坐标为m（0＜m＜3），连接CD、BD、BC、AC，当△BCD的面积等于△AOC面积的2倍时，求m的值；（3）若点N为抛物线对称轴上一点，请在图②中探究抛物线上是否存在点M，使得以B，C，M，N 为顶点的四边形是平行四边形？若存在，请直接写出所有满足条件的点M的坐标；若不存在，请说明理由．【题组五】21.（2021•九龙坡区模拟）如图1，抛物线y＝ax2+bx+4交x轴于A（﹣3，0），B（4，0）两点，与y轴交于点C，连接AC，BC．点P是第一象限内抛物线上的一个动点，设点P的横坐标为m，过点P作PM⊥x轴，垂足为点M，PM交BC于点Q，过点P作PN⊥BC，交BC于点N．（1）求此抛物线的解析式；（2）请用含m的代数式表示PN，并求出PN的最大值以及此时点P的坐标；（3）如图2，将抛物线y＝ax2+bx+4沿着射线CB的方向平移，使得新抛物线y'过原点，点D为原抛物线y与新抛物线y'的交点，若点E为原抛物线的对称轴上一动点，点F为新抛物线y'上一动点，求点F使得以A，D，E，F为顶点的四边形为平行四边形，请直接写出点F的坐标，并写出一个F点的求解过程．22．（2020•湖州）如图，已知在平面直角坐标系xOy中，抛物线y＝﹣x2+bx+c（c＞0）的顶点为D，与y 轴的交点为C．过点C的直线CA与抛物线交于另一点A（点A在对称轴左侧），点B在AC的延长线上，连结OA，OB，DA和DB．（1）如图1，当AC∥x轴时，①已知点A的坐标是（﹣2，1），求抛物线的解析式；②若四边形AOBD是平行四边形，求证：b2＝4c．（2）如图2，若b＝﹣2，B B=35，是否存在这样的点A，使四边形AOBD是平行四边形？若存在，求出点A的坐标；若不存在，请说明理由．23．（2020•遂宁）如图，抛物线y＝ax2+bx+c（a≠0）的图象经过A（1，0），B（3，0），C（0，6）三点．（1）求抛物线的解析式．（2）抛物线的顶点M与对称轴l上的点N关于x轴对称，直线AN交抛物线于点D，直线BE交AD于点E，若直线BE将△ABD的面积分为1：2两部分，求点E的坐标．（3）P为抛物线上的一动点，Q为对称轴上动点，抛物线上是否存在一点P，使A、D、P、Q为顶点的四边形为平行四边形？若存在，求出点P的坐标；若不存在，请说明理由．24．（2021•滨城区一模）如图，抛物线y＝ax2+bx﹣5（a≠0）经过x轴上的点A（1，0）和点B（5，0）及y轴上的点C，经过B、C两点的直线为y＝kx+b（k≠0）．（1）求抛物线的解析式．（2）点P从A出发，在线段AB上以每秒1个单位的速度向B运动，同时点E从B出发，在线段BC 上以每秒2个单位的速度向C运动．当其中一个点到达终点时，另一点也停止运动．设运动时间为t 秒，求t为何值时，△PBE的面积最大并求出最大值．（3）过点A作AM⊥BC于点M，过抛物线上一动点N（不与点B、C重合）作直线AM的平行线交直线BC于点Q．若点A、M、N、Q为顶点的四边形是平行四边形，求点N的横坐标．【题组七】25．（2021•重庆）如图，在平面直角坐标系中，抛物线y＝x2+bx+c经过A（0，﹣1），B（4，1）．直线AB 交x轴于点C，P是直线AB下方抛物线上的一个动点．过点P作PD⊥AB，垂足为D，PE∥x轴，交AB于点E．（1）求抛物线的函数表达式；（2）当△PDE的周长取得最大值时，求点P的坐标和△PDE周长的最大值；（3）把抛物线y＝x2+bx+c平移，使得新抛物线的顶点为（2）中求得的点P．M是新抛物线上一点，N 是新抛物线对称轴上一点，直接写出所有使得以点A，B，M，N为顶点的四边形是平行四边形的点M 的坐标，并把求其中一个点M的坐标的过程写出来．26．（2021•凉山州）如图，抛物线y＝ax2+bx+c（a≠0）与x轴交于A、B两点，与y轴交于C点，AC＝，OB＝OC＝3OA．（1）求抛物线的解析式；（2）在第二象限内的抛物线上确定一点P，使四边形PBAC的面积最大，求出点P的坐标；（3）在（2）的结论下，点M为x轴上一动点，抛物线上是否存在一点Q，使点P、B、M、Q为顶点的四边形是平行四边形，若存在，请直接写出Q点的坐标；若不存在，请说明理由．27．（2021•武汉）抛物线y＝x2﹣1交x轴于A，B两点（A在B的左边）．（1）▱ACDE的顶点C在y轴的正半轴上，顶点E在y轴右侧的抛物线上；①如图（1），若点C的坐标是（0，3），点E的横坐标是，直接写出点A，D的坐标．②如图（2），若点D在抛物线上，且▱ACDE的面积是12，求点E的坐标．（2）如图（3），F是原点O关于抛物线顶点的对称点，不平行y轴的直线l分别交线段AF，BF（不含端点）于G，H两点．若直线l与抛物线只有一个公共点，求证：FG+FH的值是定值．28．（2021•广东）已知二次函数y＝ax2+bx+c的图象过点（﹣1，0），且对任意实数x，都有4x﹣12≤ax2+bx+c ≤2x2﹣8x+6．（1）求该二次函数的解析式；（2）若（1）中二次函数图象与x轴的正半轴交点为A，与y轴交点为C；点M是（1）中二次函数图象上的动点．问在x轴上是否存在点N，使得以A、C、M、N为顶点的四边形是平行四边形．若存在，求出所有满足条件的点N的坐标；若不存在，请说明理由．。

2020-2021中考数学——平行四边形的综合压轴题专题复习含答案解析

2020-2021中考数学——平行四边形的综合压轴题专题复习含答案解析一、平行四边形1．如图，在正方形ABCD中，E是边BC上的一动点（不与点B、C重合），连接DE、点C 关于直线DE的对称点为C′，连接AC′并延长交直线DE于点P，F是AC′的中点，连接DF．（1）求∠FDP的度数；（2）连接BP，请用等式表示AP、BP、DP三条线段之间的数量关系，并证明；（3）连接AC，若正方形的边长为2，请直接写出△ACC′的面积最大值．【答案】（1）45°；（2）BP+DP2AP，证明详见解析；（32﹣1．【解析】【分析】（1）证明∠CDE＝∠C'DE和∠ADF＝∠C'DF，可得∠FDP'＝12∠ADC＝45°；（2）作辅助线，构建全等三角形，证明△BAP≌△DAP'（SAS），得BP＝DP'，从而得△PAP'是等腰直角三角形，可得结论；（3）先作高线C'G，确定△ACC′的面积中底边AC为定值2，根据高的大小确定面积的大小，当C'在BD上时，C'G最大，其△ACC′的面积最大，并求此时的面积．【详解】（1）由对称得：CD＝C'D，∠CDE＝∠C'DE，在正方形ABCD中，AD＝CD，∠ADC＝90°，∴AD＝C'D，∵F是AC'的中点，∴DF⊥AC'，∠ADF＝∠C'DF，∴∠FDP＝∠FDC'+∠EDC'＝12∠ADC＝45°；（2）结论：BP+DP2AP，理由是：如图，作AP'⊥AP交PD的延长线于P'，∴∠PAP'＝90°，在正方形ABCD中，DA＝BA，∠BAD＝90°，∴∠DAP'＝∠BAP，由（1）可知：∠FDP＝45°∵∠DFP＝90°∴∠APD＝45°，∴∠P'＝45°，∴AP＝AP'，在△BAP和△DAP'中，∵BA DABAP DAP AP AP'=⎧⎪∠=∠⎨='⎪⎩，∴△BAP≌△DAP'（SAS），∴BP＝DP'，∴DP+BP＝PP'＝2AP；（3）如图，过C'作C'G⊥AC于G，则S△AC'C＝12AC•C'G，Rt△ABC中，AB＝BC2，∴AC22(2)(2)2+=，即AC为定值，当C'G最大值，△AC'C的面积最大，连接BD，交AC于O，当C'在BD上时，C'G最大，此时G与O重合，∵CD ＝C 'D ＝2，OD ＝12AC ＝1， ∴C 'G ＝2﹣1，∴S △AC 'C ＝112(21)2122AC C G '•=⨯-=-．【点睛】本题考查四边形综合题、正方形的性质、等腰直角三角形的判定和性质、全等三角形的判定和性质等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题．2．如图，四边形ABCD 中，∠BCD =∠D =90°，E 是边AB 的中点.已知AD =1，AB =2. （1）设BC =x ，CD =y ，求y 关于x 的函数关系式，并写出定义域；（2）当∠B =70°时，求∠AEC 的度数；（3）当△ACE 为直角三角形时，求边BC 的长.【答案】（1）()22303y x x x =-++<<；（2）∠AEC =105°；（3）边BC 的长为2117+. 【解析】试题分析：（1）过A 作AH ⊥BC 于H ，得到四边形ADCH 为矩形．在△BAH 中，由勾股定理即可得出结论．（2）取CD 中点T ，连接TE ，则TE 是梯形中位线，得ET ∥AD ，ET ⊥CD ，∠AET =∠B =70°．又AD =AE =1，得到∠AED =∠ADE =∠DET =35°．由ET 垂直平分CD ，得∠CET =∠DET =35°，即可得到结论．（3）分两种情况讨论：①当∠AEC =90°时，易知△CBE ≌△CAE ≌△CAD ，得∠BCE =30°，解△ABH 即可得到结论．②当∠CAE =90°时，易知△CDA ∽△BCA ，由相似三角形对应边成比例即可得到结论．试题解析：解：（1）过A 作AH ⊥BC 于H ．由∠D =∠BCD =90°，得四边形ADCH 为矩形．在△BAH 中，AB =2，∠BHA =90°，AH =y ，HB =1x -，∴22221y x =+-，则()22303y x x x =-++<<（2）取CD 中点T ，联结TE ，则TE 是梯形中位线，得ET ∥AD ，ET ⊥CD ，∴∠AET =∠B =70°．又AD=AE=1，∴∠AED=∠ADE=∠DET=35°．由ET垂直平分CD，得∠CET=∠DET=35°，∴∠AEC=70°＋35°=105°．（3）分两种情况讨论：①当∠AEC=90°时，易知△CBE≌△CAE≌△CAD，得∠BCE=30°，则在△ABH中，∠B=60°，∠AHB=90°，AB=2，得BH=1，于是BC=2．②当∠CAE=90°时，易知△CDA∽△BCA，又2224AC BC AB x=-=-，则2241174AD CA xxAC CB x-±=⇒=⇒=-（舍负）易知∠ACE<90°，所以边BC的长为117+．综上所述：边BC的长为2或1172+．点睛：本题是四边形综合题．考查了梯形中位线，相似三角形的判定与性质．解题的关键是掌握梯形中常见的辅助线作法．3．如图，在平行四边形ABCD中，AD⊥DB，垂足为点D，将平行四边形ABCD折叠，使点B落在点D的位置，点C落在点G的位置，折痕为EF，EF交对角线BD于点P．（1）连结CG，请判断四边形DBCG的形状，并说明理由；（2）若AE＝BD，求∠EDF的度数．【答案】（1）四边形BCGD是矩形，理由详见解析；（2）∠EDF＝120°．【解析】【分析】（1）根据平行四边形的性质和折叠性质以及矩形的判定解答即可；（2）根据折叠的性质以及直角三角形的性质和等边三角形的判定与性质解答即可．【详解】解：（1）四边形BCGD 是矩形，理由如下，∵四边形ABCD 是平行四边形，∴BC ∥AD ，即BC ∥DG ，由折叠可知，BC ＝DG ，∴四边形BCGD 是平行四边形，∵AD ⊥BD ，∴∠CBD ＝90°，∴四边形BCGD 是矩形；（2）由折叠可知：EF 垂直平分BD ，∴BD ⊥EF ，DP ＝BP ，∵AD ⊥BD ，∴EF ∥AD ∥BC ， ∴AE PD 1BE BP== ∴AE ＝BE ， ∴DE 是Rt △ADB 斜边上的中线，∴DE ＝AE ＝BE ，∵AE ＝BD ，∴DE ＝BD ＝BE ，∴△DBE 是等边三角形，∴∠EDB ＝∠DBE ＝60°，∵AB ∥DC ，∴∠DBC ＝∠DBE ＝60°，∴∠EDF ＝120°．【点睛】本题考查了平行四边形的性质，折叠性质，等边三角形的性质和判定，主要考查学生运用定理进行推理和计算的能力，题目综合性比较强，有一定的难度4．如图①，四边形ABCD 是知形，1,2AB BC ==，点E 是线段BC 上一动点(不与,B C 重合)，点F 是线段BA 延长线上一动点，连接,,,DE EF DF EF 交AD 于点G .设,BE x AF y ==，已知y 与x 之间的函数关系如图②所示.（1）求图②中y 与x 的函数表达式;（2）求证:DE DF ⊥;（3）是否存在x 的值，使得DEG △是等腰三角形?如果存在，求出x 的值;如果不存在，说明理由【答案】（1）y ＝﹣2x +4（0＜x ＜2）；（2）见解析；（3）存在，x ＝54或552-或32．【解析】【分析】（1）利用待定系数法可得y 与x 的函数表达式；（2）证明△CDE ∽△ADF ，得∠ADF ＝∠CDE ，可得结论；（3）分三种情况：①若DE ＝DG ，则∠DGE ＝∠DEG ，②若DE ＝EG ，如图①，作EH ∥CD ，交AD 于H ，③若DG ＝EG ，则∠GDE ＝∠GED ，分别列方程计算可得结论．【详解】（1）设y ＝kx +b ，由图象得：当x ＝1时，y ＝2，当x ＝0时，y ＝4，代入得：24k b b +=⎧⎨=⎩，得24k b =-⎧⎨=⎩， ∴y ＝﹣2x +4（0＜x ＜2）；（2）∵BE ＝x ，BC ＝2∴CE ＝2﹣x ， ∴211,4222CE x CD AF x AD -===-， ∴CE CD AF AD=， ∵四边形ABCD 是矩形，∴∠C ＝∠DAF ＝90°，∴△CDE ∽△ADF ，∴∠ADF ＝∠CDE ，∴∠ADF +∠EDG ＝∠CDE +∠EDG ＝90°，∴DE ⊥DF ；（3）假设存在x 的值，使得△DEG 是等腰三角形，①若DE ＝DG ，则∠DGE ＝∠DEG ，∵四边形ABCD 是矩形，∴AD ∥BC ，∠B ＝90°，∴∠DGE ＝∠GEB ，∴∠DEG ＝∠BEG ，在△DEF 和△BEF 中，FDE B DEF BEF EF EF ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△DEF ≌△BEF （AAS ），∴DE ＝BE ＝x ，CE ＝2﹣x ，∴在Rt △CDE 中，由勾股定理得：1+（2﹣x ）2＝x 2，x ＝54； ②若DE ＝EG ，如图①，作EH ∥CD ，交AD 于H ，∵AD ∥BC ，EH ∥CD ，∴四边形CDHE 是平行四边形，∴∠C ＝90°，∴四边形CDHE 是矩形，∴EH ＝CD ＝1，DH ＝CE ＝2﹣x ，EH ⊥DG ，∴HG ＝DH ＝2﹣x ，∴AG ＝2x ﹣2，∵EH ∥CD ，DC ∥AB ，∴EH ∥AF ，∴△EHG ∽△FAG ，∴EH HG AF AG =， ∴124222x x x -=--，∴125522x x ==（舍）， ③若DG ＝EG ，则∠GDE ＝∠GED ，∵AD ∥BC ，∴∠GDE ＝∠DEC ，∴∠GED ＝∠DEC ，∵∠C ＝∠EDF ＝90°，∴△CDE ∽△DFE ， ∴CE DE CD DF=， ∵△CDE ∽△ADF ， ∴12DE CD DF AD ==， ∴12CE CD =， ∴2﹣x ＝12，x ＝32，综上，x ＝54或32．【点睛】本题是四边形的综合题，主要考查了待定系数法求一次函数的解析式，三角形相似和全等的性质和判定，矩形和平行四边形的性质和判定，勾股定理和逆定理等知识，运用相似三角形的性质是解决本题的关键．5．如图，在平面直角坐标系中，直线DE 交x 轴于点E （30，0），交y 轴于点D （0，40），直线AB ：y ＝13x +5交x 轴于点A ，交y 轴于点B ，交直线DE 于点P ，过点E 作EF ⊥x 轴交直线AB 于点F ，以EF 为一边向右作正方形EFGH ．（1）求边EF 的长；（2）将正方形EFGH 沿射线FB 个单位的速度匀速平移，得到正方形E 1F 1G 1H 1，在平移过程中边F 1G 1始终与y 轴垂直，设平移的时间为t 秒（t ＞0）． ①当点F 1移动到点B 时，求t 的值；②当G 1，H 1两点中有一点移动到直线DE 上时，请直接写出此时正方形E 1F 1G 1H 1与△APE 重叠部分的面积．【答案】（1）EF＝15；（2）①10；②120；【解析】【分析】（1）根据已知点E（30，0），点D（0，40），求出直线DE的直线解析式y=-43x+40，可求出P点坐标，进而求出F点坐标即可；（2）①易求B（0，5），当点F1移动到点B时，1010=10；②F点移动到F'10t，F垂直x轴方向移动的距离是t，当点H运动到直线DE上时，在Rt△F'NF中，NFNF'=13，EM=NG'=15-F'N=15-3t，在Rt△DMH'中，43MHEM'=，t=4，S=12×(12+454)×11=10238；当点G运动到直线DE上时，在Rt△F'PK中，PKF K'=13，PK=t-3，F'K=3t-9，在Rt△PKG'中，PKKG'＝31539tt--+＝43，t=7，S=15×（15-7）=120.【详解】（1）设直线DE的直线解析式y＝kx+b，将点E（30，0），点D（0，40），∴30040k bb+=⎧⎨=⎩，∴4340kb⎧=-⎪⎨⎪=⎩，∴y＝﹣43x+40，直线AB与直线DE的交点P（21，12），由题意知F（30，15），∴EF＝15；（2）①易求B（0，5），∴BF＝10，∴当点F1移动到点B时，t＝1010＝10；②当点H 运动到直线DE 上时，F 点移动到F'的距离是10t ，在Rt △F'NF 中，NF NF '=13， ∴FN ＝t ，F'N ＝3t ， ∵MH'＝FN ＝t ，EM ＝NG'＝15﹣F'N ＝15﹣3t ，在Rt △DMH'中，43MH EM '=， ∴41533t t =-， ∴t ＝4， ∴EM ＝3，MH'＝4，∴S ＝1451023(12)11248⨯+⨯=；当点G 运动到直线DE 上时，F 点移动到F'10， ∵PF ＝10∴PF'10t ﹣10，在Rt △F'PK 中，13PK F K ='，∴PK＝t﹣3，F'K＝3t﹣9，在Rt△PKG'中，PKKG'＝31539tt--+＝43，∴t＝7，∴S＝15×（15﹣7）＝120.【点睛】本题考查一次函数图象及性质，正方形的性质；掌握待定系数法求函数解析式，利用三角形的正切值求边的关系，利用勾股定理在直角三角形中建立边之间的联系，准确确定阴影部分的面积是解题的关键．6．如图1，在正方形ABCD中，AD=6，点P是对角线BD上任意一点，连接PA，PC过点P 作PE⊥PC交直线AB于E．（1）求证：PC=PE;（2）延长AP交直线CD于点F.①如图2，若点F是CD的中点，求△APE的面积；②若ΔAPE的面积是21625，则DF的长为（3）如图3，点E在边AB上，连接EC交BD于点M,作点E关于BD的对称点Q，连接PQ，MQ，过点P作PN∥CD交EC于点N，连接QN，若PQ=5，MN=72，则△MNQ的面积是【答案】（1）略；（2）①8，②4或9；（3）5 6【解析】【分析】（1）利用正方形每个角都是90°，对角线平分对角的性质，三角形外角等于和它不相邻的两个内角的和，等角对等边等性质容易得证;（2）作出△ADP和△DFP的高，由面积法容易求出这个高的值.从而得到△PAE的底和高，并求出面积.第2小问思路一样，通过面积法列出方程求解即可;（3）根据已经条件证出△MNQ是直角三角形，计算直角边乘积的一半可得其面积.【详解】(1) 证明：∵点P 在对角线BD 上，∴△ADP ≌△CDP ,∴AP=CP , ∠DAP =∠DCP ,∵PE ⊥PC ，∴∠EPC=∠EPB+∠BPC=90°,∵∠PEA=∠EBP+∠EPB=45°+90°-∠BPC=135°-∠BPC,∵∠PAE=90°-∠DAP ＝90°-∠DCP ,∠DCP=∠BPC-∠PDC=∠BPC-45°,∴∠PAE=90°-(∠BPC-45°)= 135°-∠BPC,∴∠PEA=∠PAE,∴PC=PE;（2）①如图2，过点P 分别作PH ⊥AD,PG ⊥CD,垂足分别为H 、G.延长GP 交AB 于点M.∵四边形ABCD 是正方形，P 在对角线上，∴四边形HPGD 是正方形，∴PH=PG,PM ⊥AB,设PH=PG=a,∵F 是CD 中点，AD ＝6，则FD=3,ADF S n =9,∵ADF S n =ADP DFP S S +n n =1122AD PH DF PG ⨯+⨯, ∴1163922a a ⨯+⨯=,解得a=2, ∴AM=HP=2,MP=MG-PG=6-2=4,又∵PA=PE,∴AM=EM,AE=4,∵APE S n =1144822EA MP ⨯=⨯⨯=, ②设HP ＝b,由①可得AE=2b,MP=6-b,∴APE S n =()121626225b b ⨯⨯-=, 解得b=2.4 3.6或, ∵ADF S n =ADP DFP S S +n n =1122AD PH DF PG ⨯+⨯,∴11166222b DF b DF ⨯⨯+⨯=⨯, ∴当b=2.4时，DF=4；当b ＝3.6时，DF ＝9,即DF 的长为4或9;（3）如图，∵E 、Q 关于BP 对称，PN ∥CD,∴∠1＝∠2，∠2+∠3＝∠BDC=45°,∴∠1+∠4=45°,∴∠3=∠4,易证△PEM ≌△PQM, △PNQ ≌△PNC,∴∠5=∠6, ∠7=∠8 ,EM=QM,NQ=NC,∴∠6+∠7=90°,∴△MNQ 是直角三角形,设EM=a,NC=b 列方程组222252372 a b a b ⎧+=⎪⎪⎨⎛⎪+= ⎪⎝⎭⎩, 可得12ab=56, ∴MNQ 56S V =, 【点睛】本题是四边形综合题目，考查了正方形的性质、等腰直角三角形的判定与性质、全等三角形的判定与性质等知识；本题综合性强，有一定难度，熟练掌握正方形的性质，证明三角形全等是解决问题的关键.要注意运用数形结合思想.7．如图①，在矩形ABCD 中，点P 从AB 边的中点E 出发，沿着E B C --速运动，速度为每秒2个单位长度，到达点C 后停止运动，点Q 是AD 上的点，10AQ =，设PAQ ∆的面积为y ，点p 运动的时间为t 秒，y 与t 的函数关系如图②所示.(1)图①中AB = ，BC = ，图②中m = .(2)当t =1秒时，试判断以PQ 为直径的圆是否与BC 边相切?请说明理由:(3)点p 在运动过程中，将矩形沿PQ 所在直线折叠，则t 为何值时，折叠后顶点A 的对应点A '落在矩形的一边上.【答案】(1)8,18,20;(2)不相切，证明见解析；（3）t=12、5、173. 【解析】【分析】（1）由题意得出AB=2BE ，t=2时，BE=2×2=4，求出AB=2BE=8，AE=BE=4，t=11时，2t=22，得出BC=18，当t=0时，点P 在E 处，m=△AEQ 的面积=12AQ×AE=20即可；（2）当t=1时，PE=2，得出AP=AE+PE=6，由勾股定理求出34PQ 为直径的圆的圆心为O'，作O'N ⊥BC 于N ，延长NO'交AD 于M ，则MN=AB=8，O'M ∥AB ，MN=AB=8，由三角形中位线定理得出O'M=12AP=3，求出O'N=MN-O'M=5＜圆O'的半径，即可得出结论；（3）分三种情况：①当点P 在AB 边上，A'落在BC 边上时，作QF ⊥BC 于F ，则QF=AB=8，BF=AQ=10，由折叠的性质得：PA'=PA ，A'Q=AQ=10，∠PA'Q=∠A=90°，由勾股定理求出22AQ QF '-，得出A'B=BF-A'F=4，在Rt △A'BP 中，BP=4-2t ，PA'=AP=8-（4-2t ）=4+2t ，由勾股定理得出方程，解方程即可；②当点P 在BC 边上，A'落在BC 边上时，由折叠的性质得：A'P=AP ，证出∠APQ=∠AQP ，得出AP=AQ=A'P=10，在Rt △ABP 中，由勾股定理求出BP=6，由BP=2t-4，得出2t-4=6，解方程即可；③当点P 在BC 边上，A'落在CD 边上时，由折叠的性质得：A'P=AP ，A'Q=AQ=10，在Rt △DQA'中，DQ=AD-AQ=8，由勾股定理求出DA'=6，得出A'C=CD-DA'=2，在Rt △ABP 和Rt △A'PC 中，BP=2t-4，CP=BC-BP=22-2t ，由勾股定理得出方程，解方程即可．【详解】（1）∵点P 从AB 边的中点E 出发，速度为每秒2个单位长度，∴AB=2BE ，由图象得：t=2时，BE=2×2=4，∴AB=2BE=8，AE=BE=4，t=11时，2t=22，∴BC=22-4=18，当t=0时，点P在E处，m=△AEQ的面积=12AQ×AE=12×10×4=20；故答案为8，18，20；（2）当t=1秒时，以PQ为直径的圆不与BC边相切，理由如下：当t=1时，PE=2，∴AP=AE+PE=4+2=6，∵四边形ABCD是矩形，∴∠A=90°，∴PQ=2222106234AQ AP+=+=，设以PQ为直径的圆的圆心为O'，作O'N⊥BC于N，延长NO'交AD于M，如图1所示：则MN=AB=8，O'M∥AB，MN=AB=8，∵O'为PQ的中点，∴O''M是△APQ的中位线，∴O'M=12AP=3，∴O'N=MN-O'M=5＜34，∴以PQ为直径的圆不与BC边相切；（3）分三种情况：①当点P在AB边上，A'落在BC边上时，作QF⊥BC于F，如图2所示：则QF=AB=8，BF=AQ=10，∵四边形ABCD是矩形，∴∠A=∠B=∠BCD=∠D=90°，CD=AB=8，AD=BC=18，由折叠的性质得：PA'=PA，A'Q=AQ=10，∠PA'Q=∠A=90°，∴22AQ QF'-，∴A'B=BF-A'F=4，在Rt△A'BP中，BP=4-2t，PA'=AP=8-（4-2t）=4+2t，由勾股定理得：42+（4-2t）2=（4+2t）2，解得：t=12；②当点P在BC边上，A'落在BC边上时，连接AA'，如图3所示：由折叠的性质得：A'P=AP，∴∠APQ'=∠A'PQ，∵AD∥BC，∴∠AQP=∠A'PQ，∴∠APQ=∠AQP，∴AP=AQ=A'P=10，在Rt△ABP中，由勾股定理得：BP=22108-=6，又∵BP=2t-4，∴2t-4=6，解得：t=5；③当点P在BC边上，A'落在CD边上时，连接AP、A'P，如图4所示：由折叠的性质得：A'P=AP，A'Q=AQ=10，在Rt△DQA'中，DQ=AD-AQ=8，由勾股定理得：22108-，∴A'C=CD-DA'=2，在Rt△ABP和Rt△A'PC中，BP=2t-4，CP=BC-BP=18-（2t-4）=22-2t，由勾股定理得：AP2=82+（2t-4）2，A'P2=22+（22-2t）2，∴82+（2t-4）2=22+（22-2t）2，解得：t=173；综上所述，t为12或5或173时，折叠后顶点A的对应点A′落在矩形的一边上．【点睛】四边形综合题目，考查了矩形的性质、折叠变换的性质、勾股定理、函数图象、直线与圆的位置关系、三角形中位线定理、等腰三角形的判定、以及分类讨论等知识.8．定义：我们把三角形被一边中线分成的两个三角形叫做“友好三角形”．性质：如果两个三角形是“友好三角形”，那么这两个三角形的面积相等．理解：如图①，在△ABC中，CD是AB边上的中线，那么△ACD和△BCD是“友好三角形”，并且S△ACD=S△BCD．应用：如图②，在矩形ABCD中，AB=4，BC=6，点E在AD上，点F在BC上，AE=BF，AF 与BE交于点O．（1）求证：△AOB和△AOE是“友好三角形”；（2）连接OD，若△AOE和△DOE是“友好三角形”，求四边形CDOF的面积．探究：在△ABC中，∠A=30°，AB=4，点D在线段AB上，连接CD，△ACD和△BCD是“友好三角形”，将△ACD沿CD所在直线翻折，得到△A′CD，若△A′CD与△ABC重合部分的面积等于△ABC面积的，请直接写出△ABC的面积．【答案】（1）见解析；（2）12；探究：2或2．【解析】试题分析：（1）利用一组对边平行且相等的四边形是平行四边形，得到四边形ABFE是平行四边形，然后根据平行四边形的性质证得OE=OB，即可证得△AOE和△AOB是友好三角形；（2）△AOE和△DOE是“友好三角形”，即可得到E是AD的中点，则可以求得△ABE、△ABF的面积，根据S四边形CDOF=S矩形ABCD-2S△ABF即可求解．探究：画出符合条件的两种情况：①求出四边形A′DCB是平行四边形，求出BC和A′D推出∠ACB=90°，根据三角形面积公式求出即可；②求出高CQ，求出△A′DC的面积．即可求出△ABC的面积．试题解析：（1）∵四边形ABCD是矩形，∴AD∥BC，∵AE=BF，∴四边形ABFE是平行四边形，∴OE=OB，∴△AOE和△AOB是友好三角形．（2）∵△AOE和△DOE是友好三角形，∴S△AOE=S△DOE，AE=ED=AD=3，∵△AOB与△AOE是友好三角形，∴S△AOB=S△AOE，∵△AOE≌△FOB，∴S△AOE=S△FOB，∴S△AOD=S△ABF，∴S四边形CDOF=S矩形ABCD-2S△ABF=4×6-2××4×3=12．探究：解：分为两种情况：①如图1，∵S△ACD=S△BCD．∴AD=BD=AB，∵沿CD折叠A和A′重合，∴AD=A′D=AB=×4=2，∵△A′CD与△ABC重合部分的面积等于△ABC面积的，∴S△DOC=S△ABC=S△BDC=S△ADC=S△A′DC，∴DO=OB，A′O=CO，∴四边形A′DCB是平行四边形，∴BC=A′D=2，过B作BM⊥AC于M，∵AB=4，∠BAC=30°，∴BM=AB=2=BC，即C和M重合，∴∠ACB=90°，由勾股定理得：AC=，∴△ABC的面积是×BC×AC=×2×2=2；②如图2，∵S△ACD=S△BCD．∴AD=BD=AB，∵沿CD折叠A和A′重合，∴AD=A′D=AB=×4=2，∵△A′CD与△ABC重合部分的面积等于△ABC面积的，∴S△DOC=S△ABC=S△BDC=S△ADC=S△A′DC，∴DO=OA′，BO=CO，∴四边形A′BDC是平行四边形，∴A′C=BD=2，过C作CQ⊥A′D于Q，∵A′C=2，∠DA′C=∠BAC=30°，∴CQ=A′C=1，∴S△ABC=2S△ADC=2S△A′DC=2××A′D×CQ=2××2×1=2；即△ABC的面积是2或2．考点：四边形综合题．9．如图，现将平行四边形ABCD沿其对角线AC折叠，使点B落在点B′处．AB′与CD交于点E．（1）求证：△AED≌△CEB′；（2）过点E作EF⊥AC交AB于点F，连接CF，判断四边形AECF的形状并给予证明．【答案】（1）见解析（2）见解析【解析】【分析】（1）由题意可得AD=BC=B'C，∠B=∠D=∠B'，且∠AED=∠CEB'，利用AAS证明全等，则结论可得；（2）由△AED≌△CEB′可得AE=CE，且EF⊥AC，根据等腰三角形的性质可得EF垂直平分AC，∠AEF=∠CEF．即AF=CF，∠CEF=∠AFE=∠AEF，可得AE=AF，则可证四边形AECF是菱形．【详解】证明：（1）∵四边形ABCD是平行四边形∴AD＝BC，CD∥AB，∠B＝∠D∵平行四边形ABCD沿其对角线AC折叠∴BC＝B'C，∠B＝∠B'∴∠D＝∠B'，AD＝B'C且∠DEA＝∠B'EC∴△ADE≌△B'EC（2）四边形AECF是菱形∵△ADE≌△B'EC∴AE＝CE∵AE＝CE，EF⊥AC∴EF垂直平分AC，∠AEF＝∠CEF∴AF＝CF∵CD∥AB∴∠CEF＝∠EFA且∠AEF＝∠CEF∴∠AEF＝∠EFA∴AF＝AE∴AF＝AE＝CE＝CF∴四边形AECF是菱形【点睛】本题考查了折叠问题，全等三角形的判定和性质，平行四边形的性质，菱形的判定，熟练掌握这些性质和判定是解决问题的关键．10．小明在矩形纸片上画正三角形，他的做法是：①对折矩形纸片ABCD(AB>BC)，使AB 与DC重合，得到折痕EF，把纸片展平；②沿折痕BG折叠纸片，使点C落在EF上的点P 处，再折出PB、PC，最后用笔画出△PBC(图1)．（1）求证：图1中的PBC是正三角形：（2）如图2，小明在矩形纸片HIJK上又画了一个正三角形IMN，其中IJ=6cm，且HM=JN．①求证：IH=IJ②请求出NJ的长；（3）小明发现：在矩形纸片中，若一边长为6cm，当另一边的长度a变化时，在矩形纸片上总能画出最大的正三角形，但位置会有所不同．请根据小明的发现，画出不同情形的示意图(作图工具不限，能说明问题即可)，并直接写出对应的a的取值范围．【答案】（1）证明见解析；（2）①证明见解析；②12-63（3）33＜a＜43，a＞43【解析】分析：（1）由折叠的性质和垂直平分线的性质得出PB=PC，PB=CB，得出PB=PC=CB即可；（2）①利用“HL”证Rt△IHM≌Rt△IJN即可得；②IJ上取一点Q，使QI=QN，由Rt△IHM≌Rt△IJN知∠HIM=∠JIN=15°，继而可得∠NQJ=30°，设NJ=x，则IQ=QN=2x、QJ=3x，根据IJ=IQ+QJ求出x即可得；（3）由等边三角形的性质、直角三角形的性质、勾股定理进行计算，画出图形即可．（1）证明：∵①对折矩形纸片ABCD(AB>BC)，使AB与DC重合，得到折痕EF∴PB=PC∵沿折痕BG折叠纸片，使点C落在EF上的点P处∴PB=BC∴PB=PC=BC∴△PBC是正三角形：（2）证明：①如图∵矩形AHIJ∴∠H=∠J=90°∵△MNJ是等边三角形∴MI=NI在Rt △MHI 和Rt △JNI 中MI NI MH NJ=⎧⎨=⎩ ∴Rt △MHI ≌Rt △JNI （HL ）∴HI=IJ②在线段IJ 上取点Q ，使IQ=NQ∵Rt △IHM ≌Rt △IJN ，∴∠HIM=∠JIN ，∵∠HIJ=90°、∠MIN=60°，∴∠HIM=∠JIN=15°，由QI=QN 知∠JIN=∠QNI=15°，∴∠NQJ=30°，设NJ=x ，则IQ=QN=2x ，QJ=22=3QN NJ -x ，∵IJ=6cm ，∴2x+3x=6，∴x=12-63，即NJ=12-63（cm ）．（3）分三种情况：①如图：设等边三角形的边长为b ，则0＜b≤6，则tan60°3=2ab ，∴3b ， ∴0＜b≤32=33 ②如图当DF与DC重合时，DF=DE=6，∴a=sin60°×DE=63=33，当DE与DA重合时，a=643 sin603==︒，∴33＜a＜43；③如图∵△DEF是等边三角形∴∠FDC=30°∴DF=643 cos303==︒∴a＞3点睛：本题是四边形的综合题目，考查了折叠的性质、等边三角形的判定与性质、旋转的性质、直角三角形的性质、正方形的性质、全等三角形的判定与性质等知识；本题综合性强，难度较大．11．如图1所示，（1）在正三角形ABC中，M是BC边（不含端点B、C）上任意一点，P 是BC延长线上一点，N是∠ACP的平分线上一点，若∠AMN=60°，求证：AM=MN．（2）若将（1）中“正三角形ABC”改为“正方形ABCD”，N是∠DCP的平分线上一点，若∠AMN=90°，则AM=MN是否成立？若成立，请证明；若不成立，说明理由．（3）若将（2）中的“正方形ABCD”改为“正n边形A1A2…A n“，其它条件不变，请你猜想：当∠A n﹣2MN=_____°时，结论A n﹣2M=MN仍然成立．（不要求证明）【答案】0 (2)180 nn【解析】分析：（1）要证明AM=MN，可证AM与MN所在的三角形全等，为此，可在AB上取一点E，使AE=CM，连接ME，利用ASA即可证明△AEM≌△MCN，然后根据全等三角形的对应边成比例得出AM=MN．（2）同（1），要证明AM=MN，可证AM与MN所在的三角形全等，为此，可在AB上取一点E，使AE=CM，连接ME，利用ASA即可证明△AEM≌△MCN，然后根据全等三角形的对应边成比例得出AM=MN．详（1）证明：在边AB上截取AE=MC，连接ME．在正△ABC中，∠B=∠BCA=60°，AB=BC．∴∠NMC=180°-∠AMN-∠AMB=180°-∠B-∠AMB=∠MAE，BE=AB-AE=BC-MC=BM，∴∠BEM=60°，∴∠AEM=120°．∵N是∠ACP的平分线上一点，∴∠ACN=60°，∴∠MCN=120°．在△AEM与△MCN中，∠MAE=∠NMC，AE=MC，∠AEM=∠MCN，∴△AEM≌△MCN（ASA），∴AM=MN．（2）解：结论成立；理由：在边AB上截取AE=MC，连接ME．∵正方形ABCD中，∠B=∠BCD=90°，AB=BC．∴∠NMC=180°-∠AMN-∠AMB=180°-∠B-∠AMB=∠MAB=∠MAE，BE=AB-AE=BC-MC=BM，∴∠BEM=45°，∴∠AEM=135°．∵N是∠DCP的平分线上一点，∴∠NCP=45°，∴∠MCN=135°．在△AEM与△MCN中，∠MAE=∠NMC，AE=MC，∠AEM=∠MCN，∴△AEM≌△MCN（ASA），∴AM=MN．（3）由（1）（2）可知当∠A n-2MN等于n边形的内角时，结论A n-2M=MN仍然成立；即∠A n-2MN=()02180nn-时，结论A n-2M=MN仍然成立；故答案为[()02180nn-]．点睛：本题综合考查了正方形、等边三角形的性质及全等三角形的判定，同时考查了学生的归纳能力及分析、解决问题的能力．难度较大．12．正方形ABCD的边长为1，对角线AC与BD相交于点O，点E是AB边上的一个动点（点E不与点A、B重合），CE与BD相交于点F，设线段BE的长度为x．（1）如图1，当AD=2OF时，求出x的值；（2）如图2，把线段CE绕点E顺时针旋转90°，使点C落在点P处，连接AP，设△APE 的面积为S，试求S与x的函数关系式并求出S的最大值．【答案】（1）x=﹣1；（2）S=﹣（x﹣）2+（0＜x＜1），当x=时，S的值最大，最大值为，．【解析】试题分析：（1）过O作OM∥AB交CE于点M，如图1，由平行线等分线段定理得到CM=ME，根据三角形的中位线定理得到AE=2OM=2OF，得到OM=OF，于是得到BF=BE=x，求得OF=OM=解方程，即可得到结果；（2）过P作PG⊥AB交AB的延长线于G，如图2，根据已知条件得到∠ECB=∠PEG，根据全等三角形的性质得到EB=PG=x，由三角形的面积公式得到S=（1﹣x）•x，根据二次函数的性质即可得到结论．试题解析：（1）过O作OM∥AB交CE于点M，如图1，∵OA=OC，∴CM=ME，∴AE=2OM=2OF，∴OM=OF，∴，∴BF=BE=x，∴OF=OM=，∵AB=1，∴OB=，∴，∴x=﹣1；（2）过P作PG⊥AB交AB的延长线于G，如图2，∵∠CEP=∠EBC=90°，∴∠ECB=∠PEG，∵PE=EC，∠EGP=∠CBE=90°，在△EPG与△CEB中，，∴△EPG≌△CEB，∴EB=PG=x，∴AE=1﹣x，∴S=（1﹣x）•x=﹣x2+x=﹣（x﹣）2+，（0＜x＜1），∵﹣＜0，∴当x=时，S的值最大，最大值为，．考点：四边形综合题13．已知点O是△ABC内任意一点，连接OA并延长到E，使得AE=OA，以OB，OC为邻边作▱OBFC，连接OF与BC交于点H，再连接EF．（1）如图1，若△ABC为等边三角形，求证：①EF⊥BC；②EF=BC；（2）如图2，若△ABC为等腰直角三角形（BC为斜边），猜想（1）中的两个结论是否成立？若成立，直接写出结论即可；若不成立，请你直接写出你的猜想结果；（3）如图3，若△ABC是等腰三角形，且AB=AC=kBC，请你直接写出EF与BC之间的数量关系．【答案】（1）见解析；（2）EF⊥BC仍然成立；（3）EF=BC【解析】试题分析：（1）由平行四边形的性质得到BH=HC=BC，OH=HF，再由等边三角形的性质得到AB=BC，AH⊥BC，根据勾股定理得到AH=BC，即可；（2）由平行四边形的性质得到BH=HC=BC，OH=HF，再由等腰直角三角形的性质得到AB=BC，AH⊥BC，根据勾股定理得到AH=BC，即可；（3）由平行四边形的性质得到BH=HC=BC，OH=HF，再由等腰三角形的性质和AB=AC=kBC得到AB=BC，AH⊥BC，根据勾股定理得到AH=BC，即可．试题解析：（1）连接AH，如图1，∵四边形OBFC是平行四边形，∴BH=HC=BC，OH=HF，∵△ABC是等边三角形，∴AB=BC，AH⊥BC，在Rt△ABH中，AH2=AB2﹣BH2，∴AH==BC，∵OA=AE，OH=HF，∴AH是△OEF的中位线，∴AH=EF，AH∥EF，∴EF⊥BC，BC=EF，∴EF⊥BC，EF=BC；（2）EF⊥BC仍然成立，EF=BC，如图2，∵四边形OBFC是平行四边形，∴BH=HC=BC，OH=HF，∵△ABC是等腰三角形，∴AB=BC，AH⊥BC，在Rt△ABH中，AH2=AB2﹣BH2=（BH）2﹣BH2=BH2，∴AH=BH=BC，∵OA=AE，OH=HF，∴AH是△OEF的中位线，∴AH=EF，AH∥EF，∴EF⊥BC，BC=EF，∴EF⊥BC，EF=BC；（3）如图3，∵四边形OBFC是平行四边形，∴BH=HC=BC，OH=HF，∵△ABC是等腰三角形，∴AB=kBC，AH⊥BC，在Rt△ABH中，AH2=AB2﹣BH2=（kBC）2﹣（BC）2=（k2-）BC2，∴AH=BH=BC，∵OA=AE，OH=HF，∴AH是△OEF的中位线，∴AH=EF，AH∥EF，∴EF⊥BC，BC=EF，∴EF=BC．考点：四边形综合题．14．如图，现有一张边长为4的正方形纸片ABCD，点P为正方形AD边上的一点（不与点A、点D重合），将正方形纸片折叠，使点B落在P处，点C落在G处，PG交DC于H，折痕为EF，连接BP、BH．（1）求证：∠APB=∠BPH；（2）当点P在边AD上移动时，求证：△PDH的周长是定值；（3）当BE+CF的长取最小值时，求AP的长．【答案】（1）证明见解析．（2）证明见解析．（3）2．【解析】试题分析：（1）根据翻折变换的性质得出∠PBC=∠BPH，进而利用平行线的性质得出∠APB=∠PBC即可得出答案；（2）首先证明△ABP≌△QBP，进而得出△BCH≌△BQH，即可得出PD+DH+PH=AP+PD+DH+HC=AD+CD=8；（3）过F作FM⊥AB，垂足为M，则FM=BC=AB，证明△EFM≌△BPA，设AP=x，利用折叠的性质和勾股定理的知识用x表示出BE和CF，结合二次函数的性质求出最值．试题解析：（1）解：如图1，∵PE=BE，∴∠EBP=∠EPB．又∵∠EPH=∠EBC=90°，∴∠EPH-∠EPB=∠EBC-∠EBP．即∠PBC=∠BPH．又∵AD∥BC，∴∠APB=∠PBC．∴∠APB=∠BPH．（2）证明：如图2，过B作BQ⊥PH，垂足为Q．由（1）知∠APB=∠BPH，又∵∠A=∠BQP=90°，BP=BP，在△ABP和△QBP中，，∴△ABP≌△QBP（AAS），∴AP=QP，AB=BQ，又∵AB=BC，∴BC=BQ．又∠C=∠BQH=90°，BH=BH，在△BCH和△BQH中，，∴△BCH≌△BQH（SAS），∴CH=QH．∴△PHD的周长为：PD+DH+PH=AP+PD+DH+HC=AD+CD=8．∴△PDH的周长是定值．（3）解：如图3，过F作FM⊥AB，垂足为M，则FM=BC=AB．又∵EF为折痕，∴EF⊥BP．∴∠EFM+∠MEF=∠ABP+∠BEF=90°，∴∠EFM=∠ABP．又∵∠A=∠EMF=90°，在△EFM和△BPA中，，∴△EFM≌△BPA（AAS）．∴EM=AP．设AP=x在Rt△APE中，（4-BE）2+x2=BE2．解得BE=2+，∴CF=BE-EM=2+-x，∴BE+CF=-x+4=（x-2）2+3．当x=2时，BE+CF取最小值，∴AP=2．考点：几何变换综合题．15．（本题14分）小明在学习平行线相关知识时总结了如下结论：端点分别在两条平行线上的所有线段中，垂直于平行线的线段最短．小明应用这个结论进行了下列探索活动和问题解决．问题1：如图1，在Rt△ABC中，∠C=90°，AC=4，BC=3，P为AC边上的一动点，以PB，PA为边构造□APBQ，求对角线PQ的最小值及PQ最小时的值．（1）在解决这个问题时，小明构造出了如图2的辅助线，则PQ的最小值为，当PQ最小时= _____ __；（2）小明对问题1做了简单的变式思考．如图3，P为AB边上的一动点，延长PA到点E，使AE=nPA（n为大于0的常数）．以PE，PC为边作□PCQE，试求对角线PQ长的最小值，并求PQ最小时的值；问题2：在四边形ABCD中，AD∥BC，AB⊥BC，AD＝1，AB＝2，BC＝3．（1）如图4，若为上任意一点，以，为边作□．试求对角线长的最小值和PQ最小时的值．（2）若为上任意一点，延长到，使，再以，为边作□．请直接写出对角线长的最小值和PQ最小时的值．【答案】问题1：（1）3，；（2）PQ=，=．问题2：（1）=4，．（2）PQ的最小值为．．【解析】试题分析：问题1：（1）首先根据条件可证四边形PCBQ是矩形，然后根据条件“四边形APBQ是平行四边形可得AP=QB=PC，从而可求的值．（2）由题可知：当QP⊥AC 时，PQ最小．过点C作CD⊥AB于点D．此时四边形CDPQ为矩形，PQ=CD，在Rt△ABC中，∠C=90°，AC=4，BC=3，利用面积可求出CD=,然后可求出AD=，由AE=nPA可得PE=，而PE=CQ=PD=AD-AP=，所以AP=．所以=．问题2：（1）设对角线与相交于点．Rt≌Rt．所以AD=HC，QH=AP．由题可知：当QP⊥AB时，PQ最小，此时=CH=4，根据条件可证四边形BPQH为矩形，从而QH=BP=AP．所以．（2）根据题意画出图形，当AB 时，的长最小，PQ的最小值为．．试题解析：问题1：（1）3，；（2）过点C作CD⊥AB于点D．由题意可知当PQ⊥AB时，PQ最短．所以此时四边形CDPQ为矩形．PQ=CD，DP=CQ=PE．因为∠BCA=90°，AC=4，BC=3，所以AB=5．所以CD=．所以PQ=．在Rt△ACD中AC=4，CD=，所以AD=．因为AE=nPA，所以PE==CQ=PD=AD-AP=．所以AP=．所以=．问题2：（1）如图2，设对角线与相交于点．所以G是DC的中点，作QH BC，交BC的延长线于H，因为AD//BC，所以．所以．又，所以Rt≌Rt．所以AD=HC，QH=AP．由图知，当AB时，的长最小，即=CH=4．易得四边形BPQH为矩形，所以QH=BP=AP．所以．（若学生有能力从梯形中位线角度考虑，若正确即可评分．但讲评时不作要求）（2）PQ的最小值为．．考点：1．直角三角形的性质；2．全等三角形的判定与性质；3．平行四边形的性质；4矩形的判定与性质．。

中考压轴题-二次函数综合(八大题型+解题方法)——冲刺2024年中考数学考点押题(全国通用)(解析)

中考压轴题-二次函数综合（八大题型+解题方法）1、求证“两线段相等”的问题：借助于函数解析式,先把动点坐标用一个字母表示出来；然后看两线段的长度是什么距离即是“点点”距离,还是“点轴距离”,还是“点线距离”,再运用两点之间的距离公式或点到x 轴y 轴的距离公式或点到直线的距离公式,分别把两条线段的长度表示出来,分别把它们进行化简,即可证得两线段相等;2、“平行于y 轴的动线段长度的最大值”的问题：由于平行于y 轴的线段上各个点的横坐标相等常设为t,借助于两个端点所在的函数图象解析式,把两个端点的纵坐标分别用含有字母t 的代数式表示出来,再由两个端点的高低情况,运用平行于y 轴的线段长度计算公式-y y 下上,把动线段的长度就表示成为一个自变量为t,且开口向下的二次函数解析式,利用二次函数的性质,即可求得动线段长度的最大值及端点坐标;3、求一个已知点关于一条已知直线的对称点的坐标问题：先用点斜式或称K ,且与已知直线垂直的直线解析式,再求出两直线的交点坐标,最后用中点坐标公式即可;4、“抛物线上是否存在一点,使之到定直线的距离最大”的问题：方法1先求出定直线的斜率,由此可设出与定直线平行且与抛物线相切的直线的解析式注意该直线与定直线的斜率相等,因为平行直线斜率k 相等,再由该直线与抛物线的解析式组成方程组,用代入法把字母y 消掉,得到一个关于x 的的一元二次方程,由题有△=2b -4ac=0因为该直线与抛物线相切,只有一个交点,所以2b -4ac=0从而就可求出该切线的解析式,再把该切线解析式与抛物线的解析式组成方程组,求出x 、y 的值,即为切点坐标,然后再利用点到直线的距离公式,计算该切点到定直线的距离,即为最大距离; 方法2该问题等价于相应动三角形的面积最大问题,从而可先求出该三角形取得最大面积时,动点的坐标,再用点到直线的距离公式,求出其最大距离;方法3先把抛物线的方程对自变量求导,运用导数的几何意义,当该导数等于定直线的斜率时,求出的点的坐标即为符合题意的点,其最大距离运用点到直线的距离公式可以轻松求出;5、常数问题：1点到直线的距离中的常数问题：“抛物线上是否存在一点,使之到定直线的距离等于一个固定常数”的问题：先借助于抛物线的解析式,把动点坐标用一个字母表示出来,再利用点到直线的距离公式建立一个方程,解此方程,即可求出动点的横坐标,进而利用抛物线解析式,求出动点的纵坐标,从而抛物线上的动点坐标就求出来了;2三角形面积中的常数问题：“抛物线上是否存在一点,使之与定线段构成的动三角形的面积等于一个定常数”的问题：先求出定线段的长度,再表示出动点其坐标需用一个字母表示到定直线的距离,再运用三角形的面积公式建立方程,解此方程,即可求出动点的横坐标,再利用抛物线的解析式,可求出动点纵坐标,从而抛物线上的动点坐标就求出来了;3几条线段的齐次幂的商为常数的问题：用K 点法设出直线方程,求出与抛物线或其它直线的交点坐标,再运用两点间的距离公式和根与系数的关系,把问题中的所有线段表示出来,并化解即可;6、“在定直线常为抛物线的对称轴,或x 轴或y 轴或其它的定直线上是否存在一点,使之到两定点的距离之和最小”的问题：先求出两个定点中的任一个定点关于定直线的对称点的坐标,再把该对称点和另一个定点连结得到一条线段,该线段的长度〈应用两点间的距离公式计算〉即为符合题中要求的最小距离,而该线段与定直线的交点就是符合距离之和最小的点,其坐标很易求出利用求交点坐标的方法;7、三角形周长的“最值最大值或最小值”问题：① “在定直线上是否存在一点,使之和两个定点构成的三角形周长最小”的问题简称“一边固定两边动的问题：由于有两个定点,所以该三角形有一定边其长度可利用两点间距离公式计算,只需另两边的和最小即可;② “在抛物线上是否存在一点,使之到定直线的垂线,与y 轴的平行线和定直线,这三线构成的动直角三角形的周长最大”的问题简称“三边均动的问题：在图中寻找一个和动直角三角形相似的定直角三角形,在动点坐标一母示后,运用=C C 动动定定斜边斜边,把动三角形的周长转化为一个开口向下的抛物线来破解;8、三角形面积的最大值问题：① “抛物线上是否存在一点,使之和一条定线段构成的三角形面积最大”的问题简称“一边固定两边动的问题”：方法1：先利用两点间的距离公式求出定线段的长度；然后再利用上面３的方法,求出抛物线上的动点到该定直线的最大距离;最后利用三角形的面积公式= 12底×高;即可求出该三角形面积的最大值,同时在求解过程中,切点即为符合题意要求的点;方法2：过动点向y 轴作平行线找到与定线段或所在直线的交点,从而把动三角形分割成两个基本模型的三角形,动点坐标一母示后,进一步可得到）（）（左（定）右（定）下（动）上（动）动三角形x x y y 21−⋅−=S ,转化为一个开口向下的二次函数问题来求出最大值;②“三边均动的动三角形面积最大”的问题简称“三边均动”的问题：先把动三角形分割成两个基本模型的三角形有一边在x 轴或y 轴上的三角形,或者有一边平行于x 轴或y 轴的三角形,称为基本模型的三角形面积之差,设出动点在x 轴或y 轴上的点的坐标,而此类题型,题中一定含有一组平行线,从而可以得出分割后的一个三角形与图中另一个三角形相似常为图中最大的那一个三角形;利用相似三角形的性质对应边的比等于对应高的比可表示出分割后的一个三角形的高;从而可以表示出动三角形的面积的一个开口向下的二次函数关系式,相应问题也就轻松解决了;9、“一抛物线上是否存在一点,使之和另外三个定点构成的四边形面积最大的问题”：由于该四边形有三个定点,,即可得到一个定三角形的面积之和,所以只需动三角形的面积最大,就会使动四边形的面积最大,而动三角形面积最大值的求法及抛物线上动点坐标求法与7相同;10、“定四边形面积的求解”问题：有两种常见解决的方案：方案一：连接一条对角线,分成两个三角形面积之和；方案二：过不在x 轴或y 轴上的四边形的一个顶点,向x 轴或y 轴作垂线,或者把该点与原点连结起来,分割成一个梯形常为直角梯形和一些三角形的面积之和或差,或几个基本模型的三角形面积的和差11、“两个三角形相似”的问题：两个定三角形是否相似：（1）已知有一个角相等的情形：运用两点间的距离公式求出已知角的两条夹边,看看是否成比例若成比例,则相似;否则不相似;（2）不知道是否有一个角相等的情形：运用两点间的距离公式求出两个三角形各边的长,看看是否成比例若成比例,则相似;否则不相似;一个定三角形和动三角形相似：（1）已知有一个角相等的情形：先借助于相应的函数关系式,把动点坐标表示出来一母示,然后把两个目标三角形题中要相似的那两个三角形中相等的那个已知角作为夹角,分别计算或表示出夹角的两边,让形成相等的夹角的那两边对应成比例要注意是否有两种情况,列出方程,解此方程即可求出动点的横坐标,进而求出纵坐标,注意去掉不合题意的点;2不知道是否有一个角相等的情形：这种情形在相似性中属于高端问题,破解方法是,在定三角形中,由各个顶点坐标求出定三角形三边的长度,用观察法得出某一个角可能是特殊角,再为该角寻找一个直角三角形,用三角函数的方法得出特殊角的度数,在动点坐标“一母示”后,分析在动三角形中哪个角可以和定三角形中的那个特殊角相等,借助于特殊角,为动点寻找一个直角三角形,求出动点坐标,从而转化为已知有一个角相等的两个定三角形是否相似的问题了,只需再验证已知角的两边是否成比例若成比例,则所求动点坐标符合题意,否则这样的点不存在;简称“找特角,求动点标,再验证”;或称为“一找角,二求标,三验证”;12、“某函数图象上是否存在一点,使之与另两个定点构成等腰三角形”的问题：首先弄清题中是否规定了哪个点为等腰三角形的顶点;若某边底,则只有一种情况；若某边为腰,有两种情况；若只说该三点构成等腰三角形则有三种情况;先借助于动点所在图象的解析式,表示出动点的坐标一母示,按分类的情况,分别利用相应类别下两腰相等,使用两点间的距离公式,建立方程;解出此方程,即可求出动点的横坐标,再借助动点所在图象的函数关系式,可求出动点纵坐标,注意去掉不合题意的点就是不能构成三角形这个题意;13、“某图象上是否存在一点,使之与另外三个点构成平行四边形”问题：这类问题,在题中的四个点中,至少有两个定点,用动点坐标“一母示”分别设出余下所有动点的坐标若有两个动点,显然每个动点应各选用一个参数字母来“一母示”出动点坐标,任选一个已知点作为对角线的起点,列出所有可能的对角线显然最多有3条,此时与之对应的另一条对角线也就确定了,然后运用中点坐标公式,求出每一种情况两条对角线的中点坐标,由平行四边形的判定定理可知,两中点重合,其坐标对应相等,列出两个方程,求解即可;进一步有：①若是否存在这样的动点构成矩形呢先让动点构成平行四边形,再验证两条对角线相等否若相等,则所求动点能构成矩形,否则这样的动点不存在;②若是否存在这样的动点构成棱形呢先让动点构成平行四边形,再验证任意一组邻边相等否若相等,则所求动点能构成棱形,否则这样的动点不存在;③若是否存在这样的动点构成正方形呢先让动点构成平行四边形,再验证任意一组邻边是否相等和两条对角线是否相等若都相等,则所求动点能构成正方形,否则这样的动点不存在;14、“抛物线上是否存在一点,使两个图形的面积之间存在和差倍分关系”的问题：此为“单动问题”〈即定解析式和动图形相结合的问题〉,后面的19实为本类型的特殊情形;先用动点坐标“一母示”的方法设出直接动点坐标,分别表示如果图形是动图形就只能表示出其面积或计算如果图形是定图形就计算出它的具体面积,然后由题意建立两个图形面积关系的一个方程,解之即可;注意去掉不合题意的点,如果问题中求的是间接动点坐标,那么在求出直接动点坐标后,再往下继续求解即可;15、“某图形〈直线或抛物线〉上是否存在一点,使之与另两定点构成直角三角形”的问题：若夹直角的两边与y轴都不平行：先设出动点坐标一母示,视题目分类的情况,分别用斜率公式算出夹直角的两边的斜率,再运用两直线没有与y轴平行的直线垂直的斜率结论两直线的斜率相乘等于-1,得到一个方程,解之即可;若夹直角的两边中有一边与y 轴平行,此时不能使用斜率公式;补救措施是：过余下的那一个点没在平行于y轴的那条直线上的点直接向平行于y的直线作垂线或过直角点作平行于y轴的直线的垂线与另一相关图象相交,则相关点的坐标可轻松搞定;16、“某图象上是否存在一点,使之与另两定点构成等腰直角三角形”的问题;①若定点为直角顶点,先用k点法求出另一直角边所在直线的解析式如斜率不存在,根据定直角点,可以直接写出另一直角边所在直线的方程,利用该解析式与所求点所在的图象的解析式组成方程组,求出交点坐标,再用两点间的距离公式计算出两条直角边等否若等,该交点合题,反之不合题,舍去;②若动点为直角顶点：先利用k点法求出定线段的中垂线的解析式,再把该解析式与所求点所在图象的解析式组成方程组,求出交点坐标,再分别计算出该点与两定点所在的两条直线的斜率,把这两个斜率相乘,看其结果是否为-1 若为-1,则就说明所求交点合题；反之,舍去;17、“题中含有两角相等,求相关点的坐标或线段长度”等的问题：题中含有两角相等,则意味着应该运用三角形相似来解决,此时寻找三角形相似中的基本模型“A”或“X”是关键和突破口;18、“在相关函数的解析式已知或易求出的情况下,题中又含有某动图形常为动三角形或动四边形的面积为定常数,求相关点的坐标或线段长”的问题：此为“单动问题”〈即定解析式和动图形相结合的问题〉,本类型实际上是前面14的特殊情形;先把动图形化为一些直角梯形或基本模型的三角形有一边在x 轴或ｙ轴上,或者有一边平行于x 轴或y 轴面积的和或差,设出相关点的坐标一母示,按化分后的图形建立一个面积关系的方程,解之即可;一句话,该问题简称“单动问题”,解题方法是“设点动点标,图形转化分割,列出面积方程”;19、“在相关函数解析式不确定系数中还含有某一个参数字母的情况下,题中又含有动图形常为动三角形或动四边形的面积为定常数,求相关点的坐标或参数的值”的问题：此为“双动问题”即动解析式和动图形相结合的问题;如果动图形不是基本模型,就先把动图形的面积进行转化或分割转化或分割后的图形须为基本模型,设出动点坐标一母示,利用转化或分割后的图形建立面积关系的方程或方程组;解此方程,求出相应点的横坐标,再利用该点所在函数图象的解析式,表示出该点的纵坐标注意,此时,一定不能把该点坐标再代入对应函数图象的解析式,这样会把所有字母消掉;再注意图中另一个点与该点的位置关系或其它关系,方法是常由已知或利用2问的结论,从几何知识的角度进行判断,表示出另一个点的坐标,最后把刚表示出来的这个点的坐标再代入相应解析式,得到仅含一个字母的方程,解之即可;如果动图形是基本模型,就无须分割或转化了,直接先设出动点坐标一母式,然后列出面积方程,往下操作方式就与不是基本模型的情况完全相同;一句话,该问题简称“双动问题”,解题方法是“转化分割,设点标,建方程,再代入,得结论”;常用公式或结论：1横线段的长 = 横标之差的绝对值 =-x x 大小=-x x 右左纵线段的长=纵标之差的绝对值=-y y 大小=-y y 下上 2点轴距离：点P 0x ,0y 到X 轴的距离为0y ,到Y 轴的距离为o x ; 3两点间的距离公式：若A 11,x y ,B 2,2x y , 则AB=目录：题型1：存在性问题题型2：最值问题题型3：定值问题题型4：定点问题题型5：动点问题综合题型6：对称问题题型7：新定义题题型8：二次函数与圆题型1：存在性问题1．（2024·四川广安·二模）如图，抛物线2y x bx c =−++交x 轴于()4,0A −，B 两点，交y 轴于点()0,4C ．(1)求抛物线的函数解析式．(2)点D 在线段OA 上运动，过点D 作x 轴的垂线，与AC 交于点Q ，与抛物线交于点P ，连接AP 、CP ，求四边形AOCP 的面积的最大值．(3)在抛物线的对称轴上是否存在点M ，使得以点A 、C 、M 为顶点的三角形是直角三角形？若存在，请求出点M【答案】(1)234y x x =−−+；(2)四边形AOCP 的面积最大为16；(3)点M 的坐标为35,22⎛⎫−− ⎪⎝⎭或311,22⎛⎫− ⎪⎝⎭．【分析】本题主要考查了二次函数综合，熟练掌握用待定系数法求解函数解析式的方法和步骤，以及二次函数的图象和性质，是解题的关键．（1）把()4,0A −，()0,4C 代入2y x bx c =−++，求出b 和c 的值，即可得出函数解析式；（2）易得182AOCSOA OC =⋅=，设()2,34P t t t −−+，则(),4Q t t +，求出24PQ t t =−−，则()()212282ACP C A S PQ x x t =⋅−=−++，根据四边形AOCP 的面积()22216ACP AOCS St =+=−++，结合二次函数的增减性，即可解答；（3）设3,2M m ⎛⎫− ⎪⎝⎭，根据两点之间距离公式得出232AC =，22254AM m =+，229(4)4CM m =+−，然后分情况根据勾股定理列出方程求解即可．【解析】（1）解：把()4,0A −，()0,4C 代入2y x bx c =−++得：01644b c c =−−+⎧⎨=⎩，解得：34b c =−⎧⎨=⎩，∴该二次函数的解析式234y x x =−−+；（2）解：∵()4,0A −，()0,4C ，∴4,4OA OC ==，∴1144822AOC S OA OC =⋅=⨯⨯=△，设直线AC 的解析式为4y kx =+，代入()4,0A −得，044k =−+，解得1k =，∴直线AC 的解析式为4y x =+，设()2,34P t t t −−+，则(),4Q t t +，∴()223444PQ t t t t t=−−+−+=−−∴()()()22114422822ACPC A SPQ x x t t t =⋅−=−−⨯=−++，∴四边形AOCP 的面积()22216ACP AOCSSt =+=−++，∵20−<，∴当2t =−时，四边形AOCP 的面积最大为16；（3）解：设3,2M m ⎛⎫− ⎪⎝⎭，∵()4,0A −，()0,4C ，∴2224432AC =+=，2222325424AM m m ⎛⎫=−++=+ ⎪⎝⎭，()()2222394424CM m m ⎛⎫=−+−=+− ⎪⎝⎭，当斜边为AC 时，AM CM AC 222+=，即()2225943244m m +++−=，整理得：24150m m ++=，无解；当斜边为AM 时，222AC CM AM +=，即2292532(4)44m m ++−=+，解得：112m =；∴311,22M ⎛⎫− ⎪⎝⎭当斜边为CM 时，222AC AM CM +=，即2225932(4)44m m ++=+−，解得：52m =−；∴35,22M ⎛⎫−− ⎪⎝⎭综上：点M 的坐标为35,22⎛⎫−− ⎪⎝⎭或311,22⎛⎫− ⎪⎝⎭．2．（2024·内蒙古乌海·模拟预测）如图（1），在平面直角坐标系中，抛物线()240y ax bx a =+−≠与x 轴交于A ，B 两点(点A 在点B 的左侧)，与y 轴交于点C ，点A 的坐标为()1,0−，且OC OB =，点D 和点C 关于抛物线的对称轴对称．(1)分别求出a ，b 的值和直线AD 的解析式；(2)直线AD 下方的抛物线上有一点P ，过点P 作PH AD ⊥于点H ，作PM 平行于y 轴交直线AD 于点M ，交x 轴于点E ，求PHM 的周长的最大值；(3)在（2）的条件下，如图2，在直线EP 的右侧、x 轴下方的抛物线上是否存在点N ，过点N 作NG x ⊥轴交x 轴于点G ，使得以点E 、N 、G 为顶点的三角形与AOC 相似？如果存在，请直接写出点G 的坐标；如果不存在，请说明理由．【答案】(1)1a =，3b =−，=1y x −−(2)4+(3)存在，点G的坐标为⎫⎪⎪⎝⎭或⎫⎪⎪⎝⎭【分析】本题主要考查的是二次函数的综合应用，掌握二次函数的交点式、配方法求二次函数的最值、相似三角形的判定、等腰直角三角形的判定、一元二次方程的求根公式，列出PM 的长与a 的函数关系式是解题的关键．（1）先求得C 的坐标，从而得到点B 的坐标，设抛物线的解析式为()()14y a x x =+−，将点C 的坐标代入求解即可；先求得抛物线的对称轴，从而得到点()3,4D −，然后可求得直线AD 的解析式=1y x −−；（2）求得45BAD ∠=︒，接下来证明PMD △为等腰直角三角形，所当PM 有最大值时三角形的周长最大，设()2,34P a a a −−，()1M a −−，则223PM aa =−++，然后利用配方可求得PM 的最大值，最后根据MPH△的周长(1PM=求解即可；（3）当90EGN ∠=︒时，如果OA EG OC GN = 或OA GNOC EN =时，则AOC ∽EGN △，设点G 的坐标为(),0a ，则()2,34N a a a −−，则1EG a =−，234NG aa =−++，然后根据题意列方程求解即可．【解析】（1）点A 的坐标为()1,0−，1OA ∴=．令0x =，则4y =−，()0,4C ∴−，4OC =，OC OB =Q ， 4OB ∴=，()4,0B ∴，设抛物线的解析式为()()14y a x x =+−，将0x =，4y =−代入得：44a −=−，解得1a =，∴抛物线的解析式为234y x x =−−；1a ∴=，3b =−；抛物线的对称轴为33212x −=−=⨯，()0,4C −，点D 和点C 关于抛物线的对称轴对称，()3,4D ∴−；设直线AD 的解析式为y kx b =+．将()1,0A −、()3,4D −代入得：034k b k b −+=⎧⎨+=−⎩，解得1k =−，1b =-，∴直线AD 的解析式=1y x −−；（2）直线AD 的解析式=1y x −−，∴直线AD 的一次项系数1k =−，45BAD ∴∠=︒． PM 平行于y 轴，90AEP ∴∠=︒，45PMH AME ∴∠=∠=︒．MPH ∴的周长(122PM MH PH PM MP PM PM =++=++=．设()2,34P a a a −−，则(),1M a a −−，则()22213423(1)4PM a a a a a a =−−−−−=−++=−−+．∴当1a =时，PM 有最大值，最大值为4．MPH ∴的周长的最大值(414=⨯=+（3）在直线EP 的右侧、x 轴下方的抛物线上存在点N ，过点N 作NG x ⊥轴交x 轴于点G ，使得以点E 、N 、G 为顶点的三角形与AOC 相似；理由如下：设点G 的坐标为(),0a ，则()2,34N a a a −−①如图2.1，若OA EG OC GN = 时，AOC ∽EGN △．则 211344a a a −=−++，整理得：280a a +−=．得：a =负值舍去)，∴点G为⎫⎪⎪⎝⎭； ②如图2.2，若OA GN OC EN =时，AOC ∽NGE ，则21434a a a −=−++，整理得：2411170a a −−=，得：a =负值舍去)，∴点G为⎫⎪⎪⎝⎭，综上所述，点G的坐标为⎫⎪⎪⎝⎭或⎫⎪⎪⎝⎭． 3．（2024·重庆·一模）如图，在平面直角坐标系中，抛物线2y ax bx =+x 轴交于点()1,0A −，()5,0B ，与y 轴交于点C ，连接BC ，AC ．(1)求抛物线的表达式；(2)P 为直线BC 上方抛物线上一点，过点P 作PD BC ⊥于点D ，过点P 作PE x 轴交抛物线于点E，求4+PD PE 的最大值及此时点P 的坐标； (3)点C 关于抛物线对称轴对称的点为Q ，将抛物线沿射线CAy '，新抛物线y '与y 轴交于点M ，新抛物线y '的对称轴与x 轴交于点N ，连接AM ，MN ，点R 在直线BC 上，连接QR ．当QR 与AMN 一边平行时，直接写出点R 的坐标，并写出其中一种符合条件的解答过程．【答案】(1)2y x x =++(2)当154t =时，PE的最大值，15,416P ⎛ ⎝⎭， (3)R点的坐标为⎛ ⎝⎭或6,⎛ ⎝⎭或(．【分析】（1）利用待定系数法求抛物线解析式即可；（2）先求得2y x =2x =，过点P 作PG x ⊥轴交BC 于点F ，利用勾股定理求得BC ==DPF OBC ∽，得PF DP BC OB =即PF PD=，从而得PF =，求出设直线BC的解析式后，设2,P t ⎛+ ⎝，则,F t ⎛+ ⎝，从而2PF =+，当点P在E 点右侧时()424PE t t t =−−=−，从而得2154t ⎫=−⎪⎝⎭，利用二次函数的性质即可求解；当点P 在E 点左侧时：442PE t t t =−−=−时，同理可求．然后比较4+PE 的最大值即可得出答案. （3）先求得1OA=，OC AC =设抛物线2y =H ⎛ ⎝⎭平移后为P ，过点P 作PW ⊥直线2x =，则AOC PWH ∽，得1OA OC AC WP HW PH ====，进而得平移后的抛物线2y x +'=，从而求得()1,0N，M ⎛ ⎝⎭，然后分QR AM ∥，QR MN ∥，QR AN ∥三种情况，利用二次函数的性质及一次函数的与二元一次方程的关系求解即可得解．【解析】（1）解：∵抛物线2y ax bx =+x 轴交于点()1,0A −，()5,0B 两点，代入坐标得：02550a b a b ⎧−=⎪⎨+=⎪⎩，解得：a b ⎧=⎪⎪⎨⎪=⎪⎩，∴抛物线的函数表达式为255y x x =−++（2）解：∵)2225555y x x x =−+=−−+，∴2y x =2x=，顶点为⎛ ⎝⎭ 过点P 作PG x ⊥轴交BC 于点F ，当0x =时，200y =∴(C ∵()5,0B ∴BC ==∵PG x ⊥轴，PD BC ⊥，x 轴y ⊥轴，∴909090CBO BFG DPF PFD PDF BOC ∠∠∠∠∠∠+=︒+=︒==︒，，∵PFD BFG ∠∠=∴DPF CBO ∠∠=∴DPF OBC ∽，∴PF DP BC OB =即PF PD =，∴PF PD =∴44+PD PE =PF +PE ，设直线BC ：y kx b =+，把(C ，()5,0B 代入得：05k b b =+⎧⎪=，解得5k b ⎧=−⎪⎨⎪=⎩， ∴直线BC：y =设2,P t ⎛ ⎝，则,F t ⎛+ ⎝，∴22PF ⎛⎛=−+=+ ⎝⎝，∵2y x =2x =，PE x 轴，∴24,E t ⎛−+ ⎝当点P 在E 点右侧时：()424PE t t t =−−=−，当24PE t =−时：∴+PD PE =PF +()221524545416t t ⎛⎫=−+−=−−+ ⎪⎝⎭ ∴当154t =时，的最大值∴2151544⎛⎫= ⎪⎝⎭，∴154P ⎛ ⎝⎭；当点P 在E 点左侧时：442PE t t t =−−=−时，∴+PD PE =PF +()225424t t ⎫=−=−⎪⎝⎭， ∴当54t =时，的最大值．2,55P t ⎛−+ ⎝∴25544⎛⎫ ⎪⎝⎭∴5,416P ⎛ ⎝⎭，∵> 综上所诉，当点P 在E 点右侧时：即154t =时，的最大值，154P ⎛ ⎝⎭，（3）解：设直线AC ：y mx n =+，把()1,0A −，(C ， ∴1OA =，OC =∴AC ==设抛物线2y x =H ⎛ ⎝⎭平移后为P ，过点P 作PW ⊥直线2x =，则AOC PWH ∽，∴1OA OC AC WP HW PH ====∴1PW =，HW=∴21,5P ⎛−⎝即1,5P ⎛ ⎝⎭，∴平移后的抛物线)22155555y x x x =−−+=−++'， ∴()1,0N令0x =，y '=，∴M ⎛ ⎝⎭ 如图，当QR AM ∥时，设直线AM 的解析式为：y px q =+，把M ⎛ ⎝⎭，()1,0A −代入得：0p q q =−+⎧=解得p q ⎧=⎪⎪⎨⎪=⎪⎩， ∴直线AM的解析式为：y =， ∴设直线QR的解析式为：y x n =∵(C ，Q 和C 关于2x =对称，∴(Q把(Q代入5y x n =+45n +，解得n =，∴直线QR的解析式为：y = 联立直线QR的解析式y =与直线BC：y x =+55y x y x ⎧=−⎪⎪⎨⎪=⎪⎩，解得3x y =⎧⎪⎨=⎪⎩，∴R ⎛ ⎝⎭ 同理可得：当QR MN ∥时，6,5R ⎛− ⎝⎭ 当QR AN ∥时，(R所有符合条件的R点的坐标为⎛ ⎝⎭或6,⎛ ⎝⎭或(．【点睛】本题考查待定系数法求抛物线解析式，勾股定理，抛物线的性质，抛物线平移，一次函数的平移，相似三角形的判定及性质，图形与坐标，掌握待定系数法求抛物线解析式，抛物线的性质，抛物线平移，相似三角形的判定及性质，图形与坐标，利用辅助线画出准确图形是解题关键．题型2：最值问题4．（2024·安徽合肥·二模）在平面直角坐标系中，O 为坐标原点，抛物线23y ax bx =+−与x 轴交于()1,0A −，()3,0B 两点，与y 轴交于点C ，连接BC ．(1)求a ，b 的值；(2)点M 为线段BC 上一动点（不与B ，C 重合），过点M 作MP x ⊥轴于点P ，交抛物线于点N ．（ⅰ）如图1，当3PA PB=时，求线段MN 的长；（ⅱ）如图2，在抛物线上找一点Q ，连接AM ，QN ，QP ，使得PQN V 与APM △的面积相等，当线段NQ 的长度最小时，求点M 的横坐标m 的值．【答案】(1)1a =，2b =−(2)（ⅰ）2MN =；（ⅱ）m 的值为32或12【分析】本题考查诶粗函数的图象和性质，掌握待定系数法和利用函数性质求面积是解题的关键．（1）运用待定系数法求函数解析式即可；（2）（ⅰ）先计算BC 的解析式，然后设(),3M m m −，则3PM PB m ==−，1PA m =+，根据题意得到方程133m m +=−求出m 值，即可求出MN 的长；（ⅱ）作QR PN ⊥于点R ，由（ⅰ）可得1PA m =+，3PB PM m =−−，223PN m m =−++，然后分为点Q 在PN 的左侧和点Q 在PN 的右侧两种情况，根据勾股定理解题即可．【解析】（1）由题意得309330a b a b −−=⎧⎨+−=⎩，解得12a b =⎧⎨=−⎩；（2）（ⅰ）当0x =时，3y =−，∴()0,3C −，设直线BC 为3y kx =−，∵点()3,0B ，∴330k −=，解得1k =，∴直线BC 为3y x =−，设(),3M m m −，则3PM PB m ==−，1PA m =+， ∵3PA PB =， ∴133m m +=−，解得2m =，经检验2m =符合题意，当2m =时，222233y =−⨯−=−， ∴3PN =，31PM PB m ==−=，∴2MN =；（ⅱ）作QR PN ⊥于点R ，由（ⅰ）可得1PA m =+，3PB PM m =−−，223PN m m =−++，PQN V 的面积为()21232m m QR −++⋅，APM △的面积为()()1312m m −+，∴()()()211233122m m QR m m −++⋅=−+，解得1QR =；当点Q 在PN 的左侧时，如图1，Q 点的横坐标为1m QR m −=−，纵坐标为()()2212134m m m m −−⨯−−=−，∴R 点的坐标为()2,4m mm−，∵N 点坐标为()2,23m mm −−，∴32RN m =−，∴()22231NQ m =−+，∴当32m =时，NQ 取最小值；当点Q 在PN 的右侧时，如图2，Q 点的横坐标为1m QR m +=+，纵坐标为()()2212134m m m +−⨯+−=−，∴R 点的坐标为()2,4m m−，∵N 点的坐标为()2,23m mm −−，∴21RN m =−， ∴()222211NQ m =−+，∴当12m =时，NQ 取最小值．综上，m 的值为32或12．。

2021年中考数学《二次函数综合压轴题》模拟训练题集(二)

2021年中考数学《二次函数综合压轴题》模拟训练题集（二）1．如图①，直线l：y＝mx+n（m＜0，n＞0）与x、y轴分别相交于A、B两点，将△AOB绕点O逆时针旋转90°得到△COD，过点A、B、D的抛物线P叫做l的关联抛物线，而l叫做P的关联直线．（1）若l：y＝﹣2x+2，则P表示的函数解析式为；若P：y＝﹣x2﹣3x+4，则l表示的函数解析式为．（2）求P的对称轴（用含m、n的代数式表示）；（3）如图②，若l：y＝﹣2x+4，P的对称轴与CD相交于点E，点F在l上，点Q在P的对称轴上．当以点C，E，Q，F为顶点的四边形是以CE为一边的平行四边形时，求点Q的坐标．2．已知菱形OABC的边长为5，且tan∠AOC＝，点E是线段BC的中点，过点A、E的抛物线y＝ax2+bx+c与边AB交于点D．（1）求点A和点E的坐标；（2）连结DE，将△BDE沿着DE翻折．①当点B的对应点B'恰好落在线段AC上时，求点D的坐标；3．如图，抛物线y＝ax2﹣11ax+24a交x轴于C，D两点，交y轴于点B（0，），过抛物线的顶点A作x轴的垂线AE，垂足为点E，作直线BE．（1）求直线BE的解析式；（2）点H为第一象限内直线AE上的一点，连接CH，取CH的中点K，作射线DK交抛物线于点P，设线段EH 的长为m，点P的横坐标为n，求n与m之间的函数关系式．（不要求写出自变量m的取值范围）；（3）在（2）的条件下，在线段BE上有一点Q，连接QH，QC，线段QH交线段PD于点F，若∠HFD＝2∠FDO，∠HQC＝90°+∠FDO，求n的值．4．在平面直角坐标系中，抛物线y＝ax2+bx﹣4经过点A（﹣8，0），对称轴是直线x＝﹣3，点B是抛物线与y轴交点，点M、N同时从原点O出发，以每秒1个单位长度的速度分别沿x轴的负半轴、y的负半轴方向匀速运动，（当点N到达点B时，点M、N同时停止运动）．过点M作x轴的垂线，交直线AB于点C，连接CN、MN，并作△CMN关于直线MC的对称图形，得到△CMD．设点N运动的时间为t秒，△CMD与△AOB重叠部分的面积为S．（1）求抛物线的函数表达式；（2）当0＜t＜2时，①求S与t的函数关系式；②直接写出当t＝时，四边形CDMN为正方形；（3）当点D落在边AB上时，过点C作直线EF交抛物线于点E，交x轴于点F，连接EB，当S△CBE：S△ACF＝1：3时，直接写出点E的坐标为．5．已知：在平面直角坐标系中，二次函数y＝x2+bx+c的图象与x轴交于点A、B，与y轴交于点C，点A的坐标为（﹣3，0），点B的坐标为（1，0）．（1）如图1，分别求b、c的值；（2）如图2，点D为第一象限的抛物线上一点，连接DO并延长交抛物线于点E，OD＝3•OE，求点E的坐标；（3）在（2）的条件下，点P为第一象限的抛物线上一点，过点P作PH⊥x轴于点H，连接EP、EH，点Q为第二象限的抛物线上一点，且点Q与点P关于抛物线的对称轴对称，连接PQ，设∠AHE+∠EPH＝2α，PH＝PQ •tanα，点M为线段PQ上一点，点N为第三象限的抛物线上一点，分别连接MH、NH，满足∠MHN＝60°，MH＝NH，过点N作PE的平行线，交y轴于点F，求直线FN的解析式．6．如图，在平面直角坐标系中，抛物线y＝ax2+bx﹣3交x轴于点A（﹣1，0）和点B（3，0），与y轴交于点C，顶点是D，对称轴交x轴于点E．（1）求抛物线的解析式；（2）点P是抛物线在第四象限内的一点，过点P作PQ∥y轴，交直线AC于点Q，设点P的横坐标是m．①求线段PQ的长度n关于m的函数关系式；②连接AP，CP，求当△ACP面积为时点P的坐标；（3）若点N是抛物线对称轴上一点，则抛物线上是否存在点M，使得以点B，C，M，N为顶点的四边形是平行四边形？若存在，请直接写出线段BN的长度；若不存在，请说明理由．7．如图，在平面直角坐标系中，点C是y轴正半轴上的一个动点，抛物线y＝ax2﹣5ax+4a（a是常数，且a＞0）过点C，与x轴交于点A、B，点A在点B的左边．连接AC，以AC为边作等边三角形ACD，点D与点O在直线AC两侧．（1）求点A，B的坐标；（2）当CD∥x轴时，求抛物线的函数表达式；（3）连接BD，当BD最短时，请直接写出抛物线的函数表达式．8．如图，抛物线y＝ax2+2x+c（a＜0）与x轴交于点A和点B（点A在原点的左侧，点B在原点的右侧），与y轴交于点C，OB＝OC＝3．（1）求该抛物线的函数解析式；（2）如图1，连接BC，点D是直线BC上方抛物线上的点，连接OD，CD，OD交BC于点F，当S△COF：S△CDF＝3：2时，求点D的坐标．（3）如图2，点E的坐标为（0，），在抛物线上是否存在点P，使∠OBP＝2∠OBE？若存在，请直接写出符合条件的点P的坐标；若不存在，请说明理由．9．如图直角坐标系中，△ABO，O为坐标原点，A（0，3），B（6，3），二次函数y＝﹣x2+bx+c的图象经过点A，B，点P为抛物线上AB上方的一个点，连结P A，作PQ⊥AB垂足为H，交OB于点Q．（1）求b，c的值；（2）当∠APQ＝∠B时，求点P的坐标；（3）当△APH面积是四边形AOQH面积的2倍时，求点P的坐标．10．综合与探究如图，抛物线y＝﹣x2﹣x+与x轴交于A、B两点（点A在点B的左侧），与y轴交于点C，直线l 经过B、C两点，点M从点A出发以每秒1个单位长度的速度向终点B运动，连接CM，将线段MC绕点M顺时针旋转90°得到线段MD，连接CD、BD．设点M运动的时间为t（t＞0），请解答下列问题：（1）求点A的坐标与直线l的表达式；（2）①请直接写出点D的坐标（用含t的式子表示），并求点D落在直线l上时t的值；②求点M运动的过程中线段CD长度的最小值．11．如图，△OAP是等腰直角三角形，∠OAP＝90°，点A在第四象限，点P坐标为（8，0），抛物线y＝ax2+bx+c 经过原点O和A、P两点．（1）求抛物线的函数关系式．（2）点B是y轴正半轴上一点，连接AB，过点B作AB的垂线交抛物线于C、D两点，且BC＝AB，求点B坐标；（3）在（2）的条件下，点M是线段BC上一点过点M作x轴的垂线交抛物线于点N，求△CBN面积的最大值．12．如图，已知抛物线y＝ax2+bx+3（a≠0）经过点A（1，0）和点B（3，0），与y轴交于点C．（1）求此抛物线的解析式；（2）若点P是直线BC下方的抛物线上一动点（不点B，C重合），过点P作y轴的平行线交直线BC于点D，设点P的横坐标为m．①用含m的代数式表示线段PD的长．②连接PB，PC，求△PBC的面积最大时点P的坐标．（3）设抛物线的对称轴与BC交于点E，点M是抛物线的对称轴上一点，N为y轴上一点，是否存在这样的点M和点N，使得以点C、E、M、N为顶点的四边形是菱形？如果存在，请直接写出点M的坐标；如果不存在，请说明理由．13．如图，抛物线y＝（x﹣1）2+n与x轴交于A，B两点（A在B的左侧），与y轴交于点C（0，﹣3），点D与C 关于抛物线的对称轴对称．（1）求抛物线的解析式及点D的坐标；（2）点P是抛物线上的一点，当△ABP的面积是8，求出点P的坐标；（3）过直线AD下方的抛物线上一点M作y轴的平行线，与直线AD交于点N，已知M点的横坐标是m，试用含m的式子表示MN的长及△ADM的面积S，并求当MN的长最大时S的值．14．如图，在平面直角坐标系中，已知抛物线y＝ax2+bx+2（a≠0）与x轴交于A（﹣1，0），B（3，0）两点，与y 轴交于点C．（1）求该抛物线的解析式；（2）如图①，若点D是抛物线上一个动点，设点D的横坐标为m（0＜m＜3），连接CD、BD、BC、AC，当△BCD的面积等于△AOC面积的2倍时，求m的值；（3）若点N为抛物线对称轴上一点，请在图②中探究抛物线上是否存在点M，使得以B，C，M，N为顶点的四边形是平行四边形？若存在，请直接写出所有满足条件的点M的坐标；若不存在，请说明理由．15．如图1，在平面直角坐标系中，直线y＝x+4与抛物线y＝﹣x2+bx+c（b，c是常数）交于A、B两点，点A在x轴上，点B在y轴上．设抛物线与x轴的另一个交点为点C．（1）求该抛物线的解析式；（2）P是抛物线上一动点（不与点A、B重合），①如图2，若点P在直线AB上方，连接OP交AB于点D，求的最大值；②如图3，若点P在x轴的上方，连接PC，以PC为边作正方形CPEF，随着点P的运动，正方形的大小、位置也随之改变．当顶点E或F恰好落在y轴上，直接写出对应的点P的坐标．16．如图，在平面直角坐标系中，∠ACB＝90°，OC＝2BO，AC＝6，点B的坐标为（1，0），抛物线y＝﹣x2+bx+c 经过A、B两点．（1）求点A的坐标；（2）求抛物线的解析式；（3）点P是直线AB上方抛物线上的一点，过点P作PD垂直x轴于点D，交线段AB于点E，使PE＝DE．①求点P的坐标；②在直线PD上是否存在点M，使△ABM为直角三角形？若存在，求出符合条件的所有点M的坐标；若不存在，请说明理由．17．综合与探究如图1，抛物线y＝ax2+bx﹣3与x轴交于A（﹣2，0），B（4，0）两点，与y轴交于点C．（1）求抛物线的表达式；（2）点N是抛物线上异于点C的动点，若△NAB的面积与△CAB的面积相等，求出点N的坐标；（3）如图2，当P为OB的中点时，过点P作PD⊥x轴，交抛物线于点D．连接BD，将△PBD沿x轴向左平移m个单位长度（0＜m≤2），将平移过程中△PBD与△OBC重叠部分的面积记为S，求S与m的函数关系式．18．如图1，抛物线y＝﹣x2+mx+n交x轴于点A（﹣2，0）和点B，交y轴于点C（0，2）．（1）求抛物线的函数表达式；（2）若点M在抛物线上，且S△AOM＝2S△BOC，求点M的坐标；（3）如图2，设点N是线段AC上的一动点，作DN⊥x轴，交抛物线于点D，求线段DN长度的最大值．19．如图，在平面直角坐标系中，抛物线y＝ax2+bx+6经过点A（﹣3，0）和点B（2，0），直线y＝h（h为常数，且0＜h＜6）与BC交于点D，与y轴交于点E，与AC交于点F．（1）求抛物线的解析式；（2）连接AE，求h为何值时，△AEF的面积最大．（3）已知一定点M（﹣2，0），问：是否存在这样的直线y＝h，使△BDM是等腰三角形？若存在，请求出h的值和点D的坐标；若不存在，请说明理由．20．已知，如图，抛物线y＝ax2+3ax+c（a＞0）与y轴交于点C，与x轴交于A、B两点，点A在点B左侧，点B 的坐标为（1，0）、C（0，﹣3）．（1）求抛物线的解析式．（2）若点D是线段AC下方抛物线上的动点，求四边形ABCD面积的最大值．（3）若点E在x轴上，点P在抛物线上，是否存在以A、C、E、P为顶点且以AC为一边的平行四边形？如存在，求点P的坐标；若不存在，请说明理由．21．如图，对称轴为直线x＝﹣1的抛物线y＝a（x﹣h）2﹣4（a≠0）与x轴交于A、B两点，与y轴交于点C，其中点A的坐标为（﹣3，0）（1）求该抛物线的解析式；（2）若点P在抛物线上，且S△POC＝4S△BOC，求点P的坐标；（3）设点Q是线段AC上的动点，作QD⊥x轴交抛物线于点D，求线段QD长度的最大值．22．定义：对于抛物线y＝ax2+bx+c（a、b、c是常数，a≠0），若b2＝ac，则称该抛物线为黄金抛物线．例如：y ＝x2﹣x+1是黄金抛物线（1）请再写出一个与上例不同的黄金抛物线的解析式；（2）将黄金抛物线y＝x2﹣x+1沿对称轴向下平移3个单位①直接写出平移后的新抛物线的解析式；②新抛物线如图所示，与x轴交于A、B（A在B的左侧），与y轴交于C，点P是直线BC下方的抛物线上一动点，连结PO、PC，并把△POC沿CO翻折，得到四边形POP′C，那么是否存在点P，使四边形POP′C为菱形？若存在，请求出此时点P的坐标；若不存在，请说明理由．③当直线BC下方的抛物线上动点P运动到什么位置时，四边形OBPC的面积最大并求出此时P点的坐标和四边形OBPC的最大面积．23．已知抛物线y＝ax2+bx+3经过A（﹣3，0），B（﹣1，0）两点（如图1），顶点为M．（1）a、b的值；（2）设抛物线与y轴的交点为Q（如图1），直线y＝﹣2x+9与直线OM交于点D．现将抛物线平移，保持顶点在直线OD上．当抛物线的顶点平移到D点时，Q点移至N点，求抛物线上的两点M、Q间所夹的曲线扫过的区域的面积；（3）设直线y＝﹣2x+9与y轴交于点C，与直线OM交于点D（如图2）．现将抛物线平移，保持顶点在直线OD上．若平移的抛物线与射线CD（含端点C）没有公共点时，试探求其顶点的横坐标的取值范围．24．如图，平面直角坐标系中，直线y＝a（x+1）（x﹣3）交x轴、y轴于A、B两点，交y轴于点C，且tan∠CAO ＝3．（1）如图1，求抛物线的解析式；（2）如图2，连接BC，点P为第一象限抛物线上一点，过点P作PQ⊥BC于点Q，P点的横坐标为t，PQ的长为d，求d与t的函数关系式（直接写出自变量t的取值范围）；（3）如图3，在（2）的条件下，若d＝，（t＞1），M为第一象限抛物线上一点，点A作y轴的平行线直线l，连接MC并延长交直线l于点E，连接BE、AM、BP，BE＝AM，点F在线段BP上，∠F AB＝∠EMA，求F点坐标．25．如图1，已知直线y＝a与抛物线y＝交于A、B两点（A在B的左侧），交y轴于点C．（1）若AB＝4，求a的值；（2）若抛物线上存在点D（不与A、B重合），使CD＝AB，求a的取值范围；（3）如图2，直线y＝kx+2与抛物线交于点E、F，点P是抛物线上的动点，延长PE、PF分别交直线y＝﹣2于M、N两点，MN交y轴于Q点，求QM•QN的值．26．抛物线y＝﹣x交x轴于点A，点B（6，n）为抛物线上一点．（1）求m与n之间的函数关系；（2）如图，点C（﹣n，0）在x轴上，且∠BAC＝2∠ACB，求m的值；（3）在（2）的条件下，P为直线BC上方抛物线上一点，过点P作PD∥AB交x轴于点D，DE⊥BC交OP于点E，，求点P坐标．27．如图1，直线y＝﹣x+2与x轴交于A，与y轴交于B，点C（1，m）是直线AB上一点，抛物线y＝ax2+bx+c 过O、A、C三点，P为直线AB上一动点．（1）求抛物线解析式；（2）如图1，当P点在线段AB上时，如果在x轴上方的抛物线上总存在两个点D，使△OPD的面积与△OP A 的面积相等，求点P横坐标的取值范围；（3）如图2，Q为对称轴右侧第一象限内抛物线上一点，连接QB交抛物线于D，连接AD交y轴于E，连AQ 交y轴于F，求OE•OF的值．28．如图，抛物线y＝a（x﹣）（x+3）交x轴于点A、B，交y轴于点C，tan∠CAO＝．（1）求a值；（2）点P为第一象限内抛物线上一点，点P的横坐标为t，连接P A，PC，设△P AC的面积为S，求S与t之间的关系式；（3）在（2）的条件下，点Q在第一象限内的抛物线上（点Q在点P的上方），过点P作PE⊥AB，垂足为E，点D在线段AQ上，点F在线段AO上连接ED、DF，DE交AP于点G，若∠QDF+∠QDE＝180°，∠DF A+∠AED＝90°，PG＝PE，PG：EF＝3：2，求点P的坐标．29．如图，在平面直角坐标系中，抛物线y＝﹣x2﹣2x+6分别交x轴于A、B两点，与y轴交于点C，顶点为点D，对称轴交x轴于点H．（1）如图1，点P是第二象限内抛物线上的一个动点，取线段HC的中点E，将线段HE沿直线HC平移，线段HE平移后对应的线段是H′E′，连接PH′、E′B，当△PHC的面积最大时，求PH′+H′E′+E′B的最小值；（2）如图2，作射线BD，将∠ABD沿x轴平移至∠A′B′D′，使点B′与点O重合，然后将∠A′B′D′绕点B′顺时针旋转至边B′D′经过点D，再让∠A′B′D′的顶点B′沿y轴上下滑动，但在滑动过程中，始终保持边B′D′经过点D，且∠A′B′D′＝∠ABD，另一边B′A′所在直线与直线AD交于点F．是否存在点F，使得△DFB′为等腰三角形？若存在，求出OB′的长；若不存在，请说明理由．30．如图1，在平面直角坐标系中，抛物线y＝﹣x2+x+2与x轴交于点A、B两点（点A在点B的左侧），与y 轴交于点C．（1）如图1，若点P是直线BC上方抛物线上的一个动点，过点P作PD∥x轴交直线BC于点D，作PE⊥BC 于点E，点M为直线BC上一动点，点N为x轴上一动点，连接PM，MN．当DE最长时，求PM+MN+AN 的最小值；（2）如图2，将△AOC绕点O逆时针旋转30°得△A'OC'，将△A'OC'沿直线A′O平移得到△A″O'C″，直线C″O'与x轴交于点F，连接F A″，将△F A″O′沿边A″O'翻折得△F'A″O'，连接CA″，CF′，当△CA″F′是等腰三角形时，求此时点A″的坐标．31．如图1，在平面直角坐标系中，抛物线y＝﹣x+6与x轴交于A、B两点（点A在点B的左侧），与y轴交于点C．（1）点P为线段BC上方抛物线上（不与B、C重合）的一动点，连接PC、PB，当△PBC面积最大时，在y 轴找点D，使得PD﹣OD的值最小时，求这个最小值．（2）如图2，抛物线对称轴与x轴交于点K，与线段BC交于点M，在对称轴上取一点R，使得KR＝12（点R 在第一象限），连接BR．已知点N为线段BR上一动点，连接MN，将△BMN沿MN翻折到△B'MN．当△B'MN 与△BMR重叠部分（如图中的△MNQ）为直角三角形时，直接写出此时点B'的坐标．32．已知抛物线的解析式y＝ax2+bx+3与x轴交于A、B两点，点B的坐标为（﹣1，0）抛物线与y轴正半轴交于点C，△ABC面积为6．（1）如图1，求此抛物线的解析式；（2）P为第一象限抛物线上一动点，过P作PG⊥AC，垂足为点G，设点P的横坐标为t，线段PG的长为d，求d与t之间的函数关系式，并直接写出自变量t的取值范围；（3）如图2，在（2）的条件下，过点B作CP的平行线交y轴上一点F，连接AF，在BF的延长线上取点E，连接PE，若PE＝AF，∠AFE+∠BEP＝180°，求点P的坐标．33．如图，二次函数y＝ax2+bx+c的图象交x轴于点A（﹣2，0），点B（1，0），交y轴于点C（0，2）（1）求二次函数的解析式；（2）连接AC，在直线AC上方的抛物线上有一点N，过点N作y轴的平行线，交直线AC于点F，设点N的横坐标为n，线段NF的长为l，求l关于n的函数关系式；（3）若点M在x轴上，是否存在点M，使以B、C、M为顶点的三角形是等腰三角形，若存在，直接写出点M 的坐标；若不存在，说明理由．34．抛物线C1：y＝ax2﹣x+2（a＞0）与x轴交于A、B（点A在点B左侧），与y轴交于点C．（1）如图1，若A（2，0），连AC、BC．①直接写出C1的解析式及△ABC的面积；②将△AOC绕某一点逆时针旋转90°至△A′O′C′（其中A、O、C的对应点分别为A′、O′、C′）．若旋转后的△A′O′C′恰有一边的两个端点落在抛物线C1的图象上，求点A′的坐标；（2）如图2，平移抛物线C1使平移后的新抛物线C2顶点在原点，P（，0）是x轴正半轴上一点，过P作直线交C2的图象于A、B，过A的直线y＝x+b交C2于点C，过P作x轴的垂线交BC于点M，设点M的纵坐标为n，试判断an是否为定值？若是，求这个定值，若不是，说明理由．35．如图1，抛物线y＝ax2+bx经过原点O和点A（12，0），在B在抛物线上，已知OB⊥BA，且∠A＝30°．（1）求此抛物线的解析式．（2）如图2，点P为OB延长线上一点，若连接AP交抛物线于点M，设点P的横坐标为t，点M的横坐标为m，试用含有t的代数式表示m，不要求写取值范围．（3）在（2）的条件下，过点O作OW⊥AP于W，并交线段AB于点G，过点W的直线交OP延长线于点N，交x轴于点K，若∠WKA＝2∠OAP，且NK＝11，求点M的横坐标及WG的长．36．如图1，已知抛物线y＝﹣x+3与x轴交于A和B两点，（点A在点B的左侧），与y轴交于点C．（1）求出直线BC的解析式．（2）M为线段BC上方抛物线上一动点，过M作x轴的垂线交BC于H，过M作MQ⊥BC于Q，求出△MHQ 周长最大值并求出此时M的坐标；当△MHQ的周长最大时在对称轴上找一点R，使|AR﹣MR|最大，求出此时R 的坐标．（3）T为线段BC上一动点，将△OCT沿边OT翻折得到△OC′T，是否存在点T使△OC′T与△OBC的重叠部分为直角三角形，若存在请求出BT的长，若不存在，请说明理由．37．如图，已知抛物线y＝ax2+bx+c与x轴交于A、B两点，与y轴交于点C，且OC2＝OA•OB．（1）证明：tan∠BAC•tan∠ABC＝1；（2）若点C的坐标为（0，2），tan∠OCB＝2：①求该抛物线的表达式；②若点D是该抛物线上的一点，且位于直线BC上方，当四边形ABDC的面积最大时，求点D的坐标．38．如图，已知二次函数y＝ax2+bx+c（a≠0）的图象与x轴交于点A和点B（﹣2，0），与交y轴于点C（0，4）．f （x0）表示当自变量为x0时的函数值，对于任意实数m，均有f（m﹣1）＝f（3﹣m）．（1）求该二次函数的解析式；（2）点Q是线段AB上的动点，过点Q作QE∥AC，交BC于点E，连接CQ．当△CQE的面积最大时，求点Q 的坐标；（3）若平行于x轴的动直线l与该抛物线交于点P，与直线AC交于点F，点D的坐标为（2，0）．是否存在这样的直线l，使得△ODF是等腰三角形？若存在，请求出点P的坐标；若不存在，请说明理由．39．如图，抛物线y＝x2+bx+c经过A（﹣1，0）、B（4，0）两点，与y轴交于点C，D为y轴上一点，点D关于直线BC的对称点为D′．（1）求抛物线的解析式；（2）当点D在x轴上方，且△OBD的面积等于△OBC的面积时，求点D的坐标；（3）当点D'刚好落在第四象限的抛物线上时，求出点D的坐标；（4）点P在抛物线上（不与点B、C重合），连接PD、PD′、DD′，是否存在点P，使△PDD′是以D为直角顶点的等腰直角三角形？若存在，请直接写出点P的坐标；若不存在，请说明理由．40．已知：如图，在平面直角坐标系中，直线y＝kx﹣8k交x轴于点B，交y轴于点C，经过B，C两点的抛物线y ＝ax2+bx+4交x轴负半轴于点A，AB＝10．（1）求抛物线的解析式；（2）点P为第一象限内抛物线上一点，作PH⊥BC于点H，设PH的长为d，点P的横坐标为t，求d与t的函数关系式；（3）在（2）的条件下，点P关于直线BC的对称点为M，连接OM，若OM∥BC，作PD⊥x轴于点D，连接CD，F在线段BC上（对称轴右侧），连接PF，∠CDP＝∠CBD+∠FPD，求点F的坐标．41．已知抛物线y＝ax2﹣3amx﹣4am2（a＞0，m＞0）与x轴交于A、B两点（A在B左边），与y轴交于C点，顶点为P，OC＝2AO．（1）求a与m满足的关系式；（2）直线AD∥BC，与抛物线交于另一点D，△ADP的面积为，求a的值；（3）在（2）的条件下，过（1，﹣1）的直线与抛物线交于M、N两点，分别过M、N且与抛物线仅有一个公共点的两条直线交于点G，求OG长的最小值．42．如图，在平面直角坐标系中，抛物线y＝a（x﹣b）（x﹣3）（b＜0）与x轴分别交于A、B两点（点A在点B的左侧），交y轴与点C，OB＝OC，tan∠CAB＝3．（1）求a，b的值；（2）点P为抛物线y＝a（x﹣b）（x﹣3）在第一象限内图象上一点，PM⊥BC于点D，交抛物线于另一点M，设点P的横坐标为t，线段PD的长度为d，求d与t的函数关系式；（3）在（2）的条件下，点E为线段OD的中点，过点E的直线HG交PM于点G，交x轴于点H，点G在y 轴的左侧，连接CG，若∠ODB＝∠GHO+45°，tan∠GCO＝时，求点H的坐标．43．如图1，已知抛物线y＝ax2+2x+c（a≠0），与y轴交于点A（0，6），与x轴交于点B（6，0）．（1）求这条抛物线的表达式及其顶点坐标；（2）设点P是抛物线上的动点，若在此抛物线上有且只有三个P点使得△P AB的面积是定值S，求这三个点的坐标及定值S．（3）若点F是抛物线对称轴上的一点，点P是（2）中位于直线AB上方的点，在抛物线上是否存在一点Q，使得P、Q、B、F为顶点的四边形是平行四边形？若存在，请直接写出点Q的坐标；若不存请说明理由．44．已知抛物线y＝a（x﹣3）2+（a≠0）过点C（0，4），顶点为M，与x轴交于A，B两点．如图所示以AB 为直径作圆，记作⊙D．（1）试判断点C与⊙D的位置关系；（2）直线CM与⊙D相切吗？请说明理由；（3）在抛物线上是否存在一点E，能使四边形ADEC为平行四边形．45．如图，抛物线y＝ax2﹣2ax+c的图象经过点C（0，﹣2），顶点D的坐标为（1，﹣），与x轴交于A、B两点．（1）求抛物线的解析式；（2）连接AC，E为直线AC上一点，当△AOC∽△AEB时，求点E的坐标和的值．（3）点F（0，y）是y轴上一动点，当y为何值时，FC+BF的值最小．并求出这个最小值．46．如图，已知抛物线经过点A（﹣1，0），B（4，0），C（0，2）三点，点D与点C关于x轴对称，点P是线段AB上的一个动点，设点P的坐标为（m，0），过点P作x轴的垂线交抛物线于点Q，交直线BD于点M．（1）求该抛物线所表示的二次函数的解析式；（2）在点P运动过程中，是否存在点Q，使得以QM为直径的圆与y轴相切？若存在，求出m的值；若不存在，请说明理由；（3）连接AC，将△AOC绕平面内某点H顺时针旋转90°，得到△A1O1C1，点A、O、C的对应点分别是点A1、O1、C1、若△A1O1C1的两个顶点恰好落在抛物线上，那么我们就称这样的点H为“和谐点”请直接写出“和谐点”H的坐标．47．如图，抛物线y＝﹣x2﹣2x+3与x轴相交于A、B两点（点A在点B的左侧），与y轴交于点C，点D为该抛物线的顶点．（1）如图1，点P是直线AC上方的抛物线上一动点，过点P作PE∥y轴，交直线AC于点E．当线段PE长取得最大值时，在直线AC上找一点Q，使得△PQD周长最小，求出这个最小周长；（2）把抛物线沿直线AC平移，抛物线上两点A、D平移后的对应点分别是A′、D′，在平面内是否存在一点M，使得以点A′、D′、M、B为顶点的四边形为菱形？若存在，直接写出M点的坐标；若不存在，请说明理由．48．在平面直角坐标系中，抛物线y＝﹣x+6与x轴交于A、B两点（点A在点B的左侧），与y轴交于点C．（1）如图1，点P为直线BC上方抛物线上一动点，过点P作PH∥y轴，交直线BC于点H，过点P作PQ⊥BC于点Q，当PQ﹣PH最大时，点C关于x轴的对称点为点D，点M为直线BC上一动点，点N为y轴上一动点，连接PM、MN，求PM+MN+ND的最小值；（2）如图2，连接AC，将△OAC绕着点O顺时针旋转，记旋转过程中的△OAC为△OA'C'，点A的对应点为点A'，点C的对应点为点C'．当点A'刚好落在线段AC上时，将△OA'C'沿着直线BC平移，在平移过程中，直线OC'与抛物线对称轴交于点E，与x轴交于点F，设点R是平面内任意一点，是否存在点R，使得以B、E、F、R 为顶点的四边形是菱形？若存在，请直接写出点R的坐标；若不存在，请说明理由．49．已知一次函数y＝kx+2的图象经过点，与x轴相交于点A，与y轴相交于点B，二次函数y＝ax2+bx （a＞0）的图象经过点A和点P，顶点为M，对称轴与一次函数的图象相交于点N．（1）求一次函数的解析式以及A点，B点的坐标；（2）求顶点M的坐标；（3）在y轴上求一点Q，使得△PNM和△PBQ相似．50．如图，抛物线y＝x2+mx+m（m＞0）的顶点为A，交y轴于点C．（1）求出点A的坐标（用含m的式子表示）；（2）若直线y＝﹣x+n经过点A，与抛物线交于另一点B，证明：AB的长是定值；（3）连接AC，延长AC交x轴于点D，作直线AD关于x轴对称的直线，与抛物线分别交于E、F两点．若∠ECF＝90°，求m的值．。

2021年中考数学二次函数压轴题专练2

压轴题综合练：《二次函数》1．（2020•随州）如图，在平面直角坐标系中，抛物线y＝ax2+bx+1的对称轴为直线x＝，其图象与x轴交于点A和点B（4，0），与y轴交于点C．（1）直接写出抛物线的解析式和∠CAO的度数；（2）动点M，N同时从A点出发，点M以每秒3个单位的速度在线段AB上运动，点N以每秒个单位的速度在线段AC上运动，当其中一个点到达终点时，另一个点也随之停止运动．设运动的时间为t（t＞0）秒，连接MN，再将线段MN绕点M顺时针旋转90°，设点N落在点D的位置，若点D恰好落在抛物线上，求t的值及此时点D的坐标；（3）在（2）的条件下，设P为抛物线上一动点，Q为y轴上一动点，当以点C，P，Q 为顶点的三角形与△MDB相似时，请直接写出点P及其对应的点Q的坐标．（每写出一组正确的结果得1分，至多得4分）2．（2020•黄石）在平面直角坐标系中，抛物线y＝﹣x2+kx﹣2k的顶点为N．（1）若此抛物线过点A（﹣3，1），求抛物线的解析式；（2）在（1）的条件下，若抛物线与y轴交于点B，连接AB，C为抛物线上一点，且位于线段AB的上方，过C作CD垂直x轴于点D，CD交AB于点E，若CE＝ED，求点C坐标；（3）已知点M（2﹣，0），且无论k取何值，抛物线都经过定点H，当∠MHN＝60°时，求抛物线的解析式．3．（2020•随州）2020年新冠肺炎疫情期间，部分药店趁机将口罩涨价，经调查发现某药店某月（按30天计）前5天的某型号口罩销售价格p（元/只）和销量q（只）与第x天的关系如下表：第x天 1 2 3 4 5 销售价格p（元/只）2 3 4 5 6销量q（只）70 75 80 85 90 物价部门发现这种乱象后，统一规定各药店该型号口罩的销售价格不得高于1元/只，该药店从第6天起将该型号口罩的价格调整为1元/只．据统计，该药店从第6天起销量q （只）与第x天的关系为q＝﹣2x2+80x﹣200 （6≤x≤30，且x为整数），已知该型号口罩的进货价格为0.5元/只．（1）直接写出该药店该月前5天的销售价格p与x和销量q与x之间的函数关系式；（2）求该药店该月销售该型号口罩获得的利润W（元）与x的函数关系式，并判断第几天的利润最大；（3）物价部门为了进一步加强市场整顿，对此药店在这个月销售该型号口罩的过程中获得的正常利润之外的非法所得部分处以m倍的罚款，若罚款金额不低于2000元，则m的取值范围为．4．（2020•荆州）如图1，在平面直角坐标系中，A（﹣2，﹣1），B（3，﹣1），以O为圆心，OA的长为半径的半圆O交AO延长线于C，连接AB，BC，过O作ED∥BC分别交AB 和半圆O于E，D，连接OB，CD．（1）求证：BC是半圆O的切线；（2）试判断四边形OBCD的形状，并说明理由；（3）如图2，若抛物线经过点D且顶点为E．①求此抛物线的解析式；②点P是此抛物线对称轴上的一个动点，以E，D，P为顶点的三角形与△OAB相似，问抛物线上是否存在一点Q．使S△EPQ ＝S△OAB？若存在，请直接写出Q点的横坐标；若不存在，说明理由．5．（2020•鄂州）如图，抛物线y＝x2+bx+c与x轴交于A、B两点（点A在点B左边），与y轴交于点C．直线y＝x﹣2经过B、C两点．（1）求抛物线的解析式；（2）点P是抛物线上的一动点，过点P且垂直于x轴的直线与直线BC及x轴分别交于点D、M．PN⊥BC，垂足为N．设M（m，0）．①点P在抛物线上运动，若P、D、M三点中恰有一点是其它两点所连线段的中点（三点重合除外）．请直接写出符合条件的m的值；②当点P在直线BC下方的抛物线上运动时，是否存在一点P，使△PNC与△AOC相似．若存在，求出点P的坐标；若不存在，请说明理由．6．（2020•黄冈）网络销售已经成为一种热门的销售方式，为了减少农产品的库存，我市市长亲自在某网络平台上进行直播销售大别山牌板栗，为提高大家购买的积极性，直播时，板栗公司每天拿出2000元现金，作为红包发给购买者．已知该板栗的成本价格为6元/kg，每日销售量y（kg）与销售单价x（元/kg）满足关系式：y＝﹣100x+5000．经销售发现，销售单价不低于成本价且不高于30元/kg．当每日销售量不低于4000kg时，每千克成本将降低1元，设板栗公司销售该板栗的日获利为w（元）．（1）请求出日获利w与销售单价x之间的函数关系式；（2）当销售单价定为多少时，销售这种板栗日获利最大？最大利润为多少元？（3）当w≥40000元时，网络平台将向板栗公司收取a元/kg（a＜4）的相关费用，若此时日获利的最大值为42100元，求a的值．7．（2020•恩施州）如图1，抛物线y＝﹣x2+bx+c经过点C（6，0），顶点为B，对称轴x＝2与x轴相交于点A，D为线段BC的中点．（1）求抛物线的解析式；（2）P为线段BC上任意一点，M为x轴上一动点，连接MP，以点M为中心，将△MPC逆时针旋转90°，记点P的对应点为E，点C的对应点为F．当直线EF与抛物线y＝﹣x2+bx+c只有一个交点时，求点M的坐标．（3）△MPC在（2）的旋转变换下，若PC＝（如图2）．①求证：EA＝ED．②当点E在（1）所求的抛物线上时，求线段CM的长．8．（2020•黄冈）已知抛物线y＝ax2+bx+c与x轴交于点A（﹣1，0），点B（3，0），与y 轴交于点C（0，3）．顶点为点D．（1）求抛物线的解析式；（2）若过点C的直线交线段AB于点E，且S△ACE ：S△CEB＝3：5，求直线CE的解析式；（3）若点P在抛物线上，点Q在x轴上，当以点D，C，P，Q为顶点的四边形是平行四边形时，求点P的坐标；（4）已知点H（0，），G（2，0），在抛物线对称轴上找一点F，使HF+AF的值最小．此时，在抛物线上是否存在一点K，使KF+KG的值最小？若存在，求出点K的坐标；若不存在，请说明理由．9．（2020•十堰）已知抛物线y＝ax2﹣2ax+c过点A（﹣1，0）和C（0，3），与x轴交于另一点B，顶点为D．（1）求抛物线的解析式，并写出D点的坐标；（2）如图1，E为线段BC上方的抛物线上一点，EF⊥BC，垂足为F，EM⊥x轴，垂足为M，交BC于点G．当BG＝CF时，求△EFG的面积；（3）如图2，AC与BD的延长线交于点H，在x轴上方的抛物线上是否存在点P，使∠OPB ＝∠AHB？若存在，求出点P的坐标；若不存在，请说明理由．10．（2020•十堰）某企业接到生产一批设备的订单，要求不超过12天完成．这种设备的出厂价为1200元/台，该企业第一天生产22台设备，第二天开始，每天比前一天多生产2台．若干天后，每台设备的生产成本将会增加，设第x 天（x 为整数）的生产成本为m （元/台），m 与x 的关系如图所示．（1）若第x 天可以生产这种设备y 台，则y 与x 的函数关系式为，x 的取值范围为；（2）第几天时，该企业当天的销售利润最大？最大利润为多少？（3）求当天销售利润低于10800元的天数．11．（2020•湖北）把抛物线C 1：y ＝x 2+2x +3先向右平移4个单位长度，再向下平移5个单位长度得到抛物线C 2．（1）直接写出抛物线C 2的函数关系式；（2）动点P （a ，﹣6）能否在抛物线C 2上？请说明理由；（3）若点A （m ，y 1），B （n ，y 2）都在抛物线C 2上，且m ＜n ＜0，比较y 1，y 2的大小，并说明理由．12．（2020•荆门）2020年是决战决胜扶贫攻坚和全面建成小康社会的收官之年，荆门市政府加大各部门和单位对口扶贫力度．某单位的帮扶对象种植的农产品在某月（按30天计）的第x 天（x 为正整数）的销售价格p （元/千克）关于x 的函数关系式为p ＝，销售量y（千克）与x之间的关系如图所示．（1）求y与x之间的函数关系式，并写出x的取值范围；（2）当月第几天，该农产品的销售额最大，最大销售额是多少？（销售额＝销售量×销售价格）13．（2020•荆门）如图，抛物线L：y＝x2﹣x﹣3与x轴正半轴交于点A，与y轴交于点B．（1）求直线AB的解析式及抛物线顶点坐标；（2）如图1，点P为第四象限且在对称轴右侧抛物线上一动点，过点P作PC⊥x轴，垂足为C，PC交AB于点D，求PD+BD的最大值，并求出此时点P的坐标；（3）如图2，将抛物线L：y＝x2﹣x﹣3向右平移得到抛物线L'，直线AB与抛物线L'交于M，N两点，若点A是线段MN的中点，求抛物线L'的解析式．14．（2020•武汉）某公司分别在A，B两城生产同种产品，共100件．A城生产产品的总成本y（万元）与产品数量x（件）之间具有函数关系y＝ax2+bx．当x＝10时，y＝400；当x＝20时，y＝1000．B城生产产品的每件成本为70万元．（1）求a，b的值；（2）当A，B两城生产这批产品的总成本的和最少时，求A，B两城各生产多少件？（3）从A城把该产品运往C，D两地的费用分别为m万元/件和3万元/件；从B城把该产品运往C，D两地的费用分别为1万元/件和2万元/件．C地需要90件，D地需要10件，在（2）的条件下，直接写出A，B两城总运费的和的最小值（用含有m的式子表示）．15．（2020•咸宁）如图，在平面直角坐标系中，直线y＝﹣x+2与x轴交于点A，与y轴交于点B，抛物线y＝﹣x2+bx+c过点B且与直线相交于另一点C（，）．（1）求抛物线的解析式；（2）点P是抛物线上的一动点，当∠PAO＝∠BAO时，求点P的坐标；（3）点N（n，0）（0＜n＜）在x轴的正半轴上，点M（0，m）是y轴正半轴上的一动点，且满足∠MNC＝90°．①求m与n之间的函数关系式；②当m在什么范围时，符合条件的N点的个数有2个？16．（2020•鄂州）一大型商场经营某种品牌商品，该商品的进价为每件3元，根据市场调查发现，该商品每周的销售量y（件）与售价x（元/件）（x为正整数）之间满足一次函数关系，下表记录的是某三周的有关数据：x（元/件） 4 5 6y（件）10000 9500 9000（1）求y与x的函数关系式（不求自变量的取值范围）；（2）在销售过程中要求销售单价不低于成本价，且不高于15元/件．若某一周该商品的销售量不少于6000件，求这一周该商场销售这种商品获得的最大利润和售价分别为多少元？（3）抗疫期间，该商场这种商品售价不大于15元/件时，每销售一件商品便向某慈善机构捐赠m元（1≤m≤6），捐赠后发现，该商场每周销售这种商品的利润仍随售价的增大而增大．请直接写出m的取值范围．17．（2020•孝感）在平面直角坐标系中，已知抛物线y＝ax2+4ax+4a﹣6（a＞0）与x轴交于A，B两点（点A在点B的左侧），与y轴交于点C，顶点为点D．（1）当a＝6时，直接写出点A，B，C，D的坐标：A，B，C，D；（2）如图1，直线DC交x轴于点E，若tan∠AED＝，求a的值和CE的长；（3）如图2，在（2）的条件下，若点N为OC的中点，动点P在第三象限的抛物线上，过点P作x轴的垂线，垂足为Q，交AN于点F；过点F作FH⊥DE，垂足为H．设点P的横坐标为t，记f＝FP+FH．①用含t的代数式表示f；②设﹣5＜t≤m（m＜0），求f的最大值．18．（2020•武汉）将抛物线C ：y ＝（x ﹣2）2向下平移6个单位长度得到抛物线C 1，再将抛物线C 1向左平移2个单位长度得到抛物线C 2．（1）直接写出抛物线C 1，C 2的解析式；（2）如图（1），点A 在抛物线C 1（对称轴l 右侧）上，点B 在对称轴l 上，△OAB 是以OB 为斜边的等腰直角三角形，求点A 的坐标；（3）如图（2），直线y ＝kx （k ≠0，k 为常数）与抛物线C 2交于E ，F 两点，M 为线段EF 的中点；直线y ＝﹣x 与抛物线C 2交于G ，H 两点，N 为线段GH 的中点．求证：直线MN 经过一个定点．19．（2020•襄阳）如图，直线y＝﹣x+2交y轴于点A，交x轴于点C，抛物线y＝﹣x2+bx+c 经过点A，点C，且交x轴于另一点B．（1）直接写出点A，点B，点C的坐标及拋物线的解析式；（2）在直线AC上方的抛物线上有一点M，求四边形ABCM面积的最大值及此时点M的坐标；（3）将线段OA绕x轴上的动点P（m，0）顺时针旋转90°得到线段O′A′，若线段O′A′与抛物线只有一个公共点，请结合函数图象，求m的取值范围．参考答案1．解：（1）由题意：，解得，∴抛物线的解析式为y＝﹣x2+x+1，令y＝0，可得x2﹣3x﹣4＝0，解得x＝﹣1或4，∴A（﹣1，0），令y＝0，得到x＝1，∴C（0，1），∴OA＝OC＝1，∴∠CAO＝45°．（2）如图1中，过点C作CE⊥OA于E，过点D作DF⊥AB于F．∵∠NEM＝∠DFM＝∠NMD＝90°，∴∠NME+∠DMF＝90°，∠DMF+∠MDF＝90°，∴∠NME＝∠MDF，∵NM＝DM，∴△MEN≌△DFM（AAS），∴NE＝MF，EM＝DF，∵∠CAO＝45°，AN＝t，AM＝3t，∴AE＝EN＝t，∴EM＝AM﹣AE＝2t，∴DF＝2t，MF＝t，OF＝4t﹣1，∴D（4t﹣1，2t），∴﹣（4t﹣1）2+（4t﹣1）+1＝2t，∵t＞0，故可以解得t＝，经检验，t＝时，M，N均没有达到终点，符合题意，∴D（2，）．（3）如图3﹣1中，当点Q在点C的下方，点P在y的右侧，∠QCP＝∠MDB时，取E（，0），连接EC，过点E作EG⊥EC交PC于G，∵M（，0），D（2，），B（4，0）∴FM＝2﹣＝，DM＝，BM＝，BD＝，∴DF＝2MF，∵OC＝2OE，∴tan∠OCE＝tan∠MDF＝，∴∠OCE＝∠MDF，∴∠OCP＝∠MDB，∴∠ECG＝∠FDB，∴tan∠ECG＝tan∠FDB＝，∵EC＝，∴EG＝，可得G（，），∴直线CP的解析式为y＝﹣x+1，由，解得或，∴P（，），C（0，1），∴PC＝，当＝或＝时，△QCP与△MDB相似，可得CQ＝或，∴Q（0，﹣）或（0，﹣）．如图3﹣2中，当点Q在点C的下方，点P在y的右侧，∠QCP＝∠DMB时，设PC交x轴于k．∵tan∠OCK＝tan∠DMB＝2，∴OK＝2OC＝2，∴点K与F重合，∴直线PC的解析式为y＝﹣x+1，由，解得或，∴P （5，﹣）， ∴PC ＝，当＝或＝时，△QCP 与△MDB 相似，可得CQ ＝或， ∴Q （0，﹣）或（0，﹣）．当点Q 在点C 的下方，点P 在y 的右侧，∠QCP ＝∠DBM 时，同法可得P （，﹣），Q （0，﹣）或（0，），当点Q 在点C 上方，∠QCP ＝∠DMB 时，同法可得P （1，），Q （0，）或（0，），当点Q 在点C 上方，∠QCP ＝∠MDB 时，同法可得P （，），Q （0，）或（0，），当点Q 在点C 下方，点P 在y 轴的左侧时，∠QCP ＝∠DBM 时，同法可得P （﹣，﹣），Q （0，﹣）或（0，﹣）．2．解：（1）把A （﹣3.1）代入y ＝﹣x 2+kx ﹣2k ，得﹣9﹣3k ﹣2k ＝1．解得k ＝﹣2，∴抛物线的解析式为y ＝﹣x 2﹣2x +4；（2）如图1，设C （t ，﹣t 2﹣2t +4），则E （t ，﹣﹣t +2），设直线AB 的解析式为y ＝kx +b ，把A （﹣3，1），（0，4）代入得到，，解得，∴直线AB 的解析式为y ＝x +4，∵E （t ，﹣﹣t +2）在直线AB 上， ∴﹣﹣t +2＝t +4，解得t 1＝t 2＝﹣2，∴C（﹣2，4）．（3）由y＝﹣x2+kx﹣2k＝k（x﹣2）﹣x2，当x﹣2＝0时，x＝2，y＝﹣4，∴无论k取何值，抛物线都经过定点H（2，﹣4），二次函数的顶点N（，﹣2k），①如图2中，过点H作HI⊥x轴于I，分别过H，N作y轴，x轴的垂线交于点G，若＞2时，则k＞4，∵M（2﹣，0），H（2，﹣4），∴MI＝，HI＝4，∴tan∠MHI＝＝，∴∠MHI＝30°，∵∠MHN＝60°，∴∠NHI＝30°，即∠GNH＝30°，由图可知，tan∠GNH＝＝＝，解得k＝4+2或4（不合题意舍弃）．②如图3中，过点H作HI⊥x轴于I，分别过H，N作y轴，x轴的垂线交于点G．若＜2，则k＜4，同理可得，∠MHI＝30°，∵∠MHN＝60°，∴NH⊥HI，即﹣2k═﹣4，解得k＝4（不符合题意舍弃）．③若＝2，则N，H重合，不符合题意舍弃，综上所述，抛物线的解析式为y＝﹣x2+（4+2）x﹣（8+4）．3．解：（1）根据表格数据可知：前5天的某型号口罩销售价格p（元/只）和销量q（只）与第x天的关系为：p＝x+1，1≤x≤5且x为整数；q＝5x+65，1≤x≤5且x为整数；（2）当1≤x≤5且x为整数时，W＝（x+1﹣0.5）（5x+65）＝5x2+x+；当6≤x≤30且x为整数时，W＝（1﹣0.5）（﹣2x2+80x﹣200）＝﹣x2+40x﹣100．即有W＝，当1≤x≤5且x为整数时，售价，销量均随x的增大而增大，故当x＝5时，W有最大值为：495元；当6≤x≤30且x为整数时，W═﹣x2+40x﹣100＝﹣（x﹣20）2+300，故当x＝20时，W有最大值为：300元；由495＞300，可知：第5天时利润最大为495元．（3）根据题意可知：获得的正常利润之外的非法所得部分为：（2﹣1）×70+（3﹣1）×75+（4﹣1）×80+（5﹣1）×85+（6﹣1）×90＝1250（元），∴1250m≥2000，解得m≥．则m的取值范围为m≥．故答案为：m≥．4．（1）证明：如图1，设AB与y轴交于M，∵A（﹣2，﹣1），B（3，﹣1），∴AB∥x轴，且AM＝2，OM＝1，AB＝5，∴OA＝OC＝，∵DE∥BC，O是AC的中点，∴OE是△ABC的中位线，∴AE＝AB，BC＝2OE，∴E（，﹣1），∴EM＝，∴OE＝＝＝，∴BC＝2OE＝，在△ABC中，∵＝25，AB2＝52＝25，∴AC2+BC2＝AB2，∴△ABC是直角三角形，且∠ACB＝90°，∴BC⊥AC，∵AC为半圆O的直径，∴BC是半圆O的切线；（2）解：四边形OBCD是平行四边形，理由是：如图1，由（1）得：BC＝OD＝OA＝，∵OD∥BC，∴四边形OBCD是平行四边形；（3）解：①如图2，由（1）知：OD＝OA＝，E是AB的中点，且E（，﹣1），OE ＝，过D作DN⊥y轴于N，则DN∥EM，∴△ODN∽△OEM，∴，即，∴ON＝2，DN＝1，∴D（﹣1，2），设此抛物线的解析式为：y＝a（x﹣）2﹣1，把D（﹣1，2）代入得：2＝a（﹣1﹣）2﹣1，解得：a＝，∴此抛物线的解析式为：y＝（x﹣）2﹣1，即y＝；②存在，过D作DG⊥EP于G，设Q的横坐标为x，∵DG＝1+＝，EG＝2+1＝3，∴DE＝＝＝，tan∠DEG＝＝，∵tan∠OAM＝，且∠DEG和∠OAM都是锐角，∴∠DEG＝∠OAM，如图3，当△EPD∽△AOB时，，即，∴EP＝，∵S△AOB＝＝，∵S△EPQ ＝S△OAB，∴＝，即，解得：x＝或﹣；如图4，当△OAB∽△DEP时，，即，∴EP＝，同理得：，解得：x＝或﹣；综上，存在符合条件的点Q，Q点的横坐标为或﹣或或﹣．5．解：（1）针对于直线y＝x﹣2，令x＝0，则y＝﹣2，∴C（0，﹣2），令y＝0，则0＝x﹣2，∴x＝4，∴B（4，0），将点B，C坐标代入抛物线y＝x2+bx+c中，得，∴，∴抛物线的解析式为y＝x2﹣x﹣2；（2）①∵PM⊥x轴，M（m，0），∴P（m，m2﹣m﹣2），D（m，m﹣2），∵P、D、M三点中恰有一点是其它两点所连线段的中点，∴Ⅰ、当点D是PM的中点时，∴Ⅰ、当点D是PM的中点时，（0+m2﹣m﹣2）＝m﹣2，∴m＝1或m＝4（此时点D，M，P三点重合，舍去），Ⅱ、当点P是DM的中点时，（0+m﹣2）＝m2﹣m﹣2，∴m＝﹣或m＝4（此时点D，M，P三点重合，舍去），Ⅲ、当点M是DP的中点时，（m2﹣m﹣2+m﹣2）＝0，∴m＝﹣2或m＝4（此时点D，M，P三点重合，舍去），即满足条件的m的值为﹣或1或﹣2；②由（1）知，抛物线的解析式为y＝x2﹣x﹣2，令y＝0，则0＝x2﹣x﹣2，∴x＝﹣1或x＝4，∴点A（﹣1，0），∴OA＝1，∵B（4，0），C（0，﹣2），∴OB＝4，OC＝2，∴，∵∠AOC＝∠COB＝90°，∴△AOC∽△COB，∴∠OAC＝∠OCB，∠ACO＝∠OBC，∵△PNC与△AOC相似，∴Ⅰ、当△PNC∽△AOC，∴∠PCN＝∠ACO，∴∠PCN＝∠OBC，∴CP∥OB，∴点P的纵坐标为﹣2，∴m2﹣m﹣2＝﹣2，∴m＝0（舍）或m＝3，∴P（3，﹣2）；Ⅱ、当△PNC∽△COA时，∴∠PCN＝∠CAO，∴∠OCB＝∠PCD，∵PD∥OC，∴∠OCB＝∠CDP，∴∠PCD＝∠PDC，∴PC＝PD，由①知，P（m，m2﹣m﹣2），D（m，m﹣2），∵C（0，﹣2），∴PD＝2m﹣m2，PC＝＝，∴2m﹣m2＝，∴m＝或m＝0（舍），∴P（，﹣），即满足条件的点P的坐标为（3，﹣2）或（，﹣）．6．解：（1）当y≥4000，即﹣100x+5000≥4000，∴x≤10，∴当6≤x≤10时，w＝（x﹣6+1）（﹣100x+5000）﹣2000＝﹣100x2+5500x﹣27000，当10＜x≤30时，w＝（x﹣6）（﹣100x+5000）﹣2000＝﹣100x2+5600x﹣32000，综上所述：w＝；（2）当6≤x≤10时，w＝﹣100x2+5500x﹣27000＝﹣100（x﹣）2+48625，∵a＝﹣100＜0，对称轴为x＝，∴当6≤x≤10时，y随x的增大而增大，即当x＝10时，w最大值＝18000元，当10＜x≤30时，w＝﹣100x2+5600x﹣32000＝﹣100（x﹣28）2+46400，∵a＝﹣100＜0，对称轴为x＝28，∴当x＝28时，w有最大值为46400元，∵46400＞18000，∴当销售单价定为28时，销售这种板栗日获利最大，最大利润为46400元；（3）∵40000＞18000，∴10＜x≤30，∴w＝﹣100x2+5600x﹣32000，当w＝40000元时，40000＝﹣100x2+5600x﹣32000，∴x1＝20，x2＝36，∴当20≤x≤36时，w≥40000，又∵10＜x≤30，∴20≤x≤30，此时：日获利w1＝（x﹣6﹣a）（﹣100x+5000）﹣2000＝﹣100x2+（5600+100a）x﹣32000﹣5000a，∴对称轴为直线x＝﹣＝28+a，∵a＜4，∴28+a＜30，∴当x＝28+a时，日获利的最大值为42100元∴（28+a﹣6﹣a）[﹣100×（28+a）+5000]﹣2000＝42100，∴a1＝2，a2＝86，∵a＜4，∴a＝2．7．解：（1）∵点C（6，0）在抛物线上，∴，得到6b+c＝9，又∵对称轴为x＝2，∴，解得b＝1，∴c＝3，∴二次函数的解析式为；（2）当点M在点C的左侧时，如图2﹣1中：∵抛物线的解析式为，对称轴为x＝2，C（6，0）∴点A（2，0），顶点B（2，4），∴AB＝AC＝4，∴△ABC是等腰直角三角形，∴∠1＝45°；∵将△MPC逆时针旋转90°得到△MEF，∴FM＝CM，∠2＝∠1＝45°，设点M的坐标为（m，0），∴点F（m，6﹣m），又∵∠2＝45°，∴直线EF与x轴的夹角为45°，∴设直线EF的解析式为y＝x+b，把点F（m，6﹣m）代入得：6﹣m＝m+b，解得：b＝6﹣2m，直线EF的解析式为y＝x+6﹣2m，∵直线EF与抛物线只有一个交点，∴，整理得：，∴△＝b2﹣4ac＝0，解得m＝，点M的坐标为（，0）．当点M在点C的右侧时，如下图：由图可知，直线EF与x轴的夹角仍是45°，因此直线EF与抛物线不可能只有一个交点．综上，点M的坐标为（，0）．（3）①当点M在点C的左侧时，如下图，过点P作PG⊥x轴于点G，过点E作EH⊥x轴于点H，∵，由（2）知∠BCA＝45°，∴PG＝GC＝1，∴点G（5，0），设点M的坐标为（m，0），∵将△MPC逆时针旋转90°得到△MEF，∴EM＝PM，∵∠HEM+∠EMH＝∠GMP+∠EMH＝90°，∴∠HEM＝∠GMP，在△EHM和△MGP中，，∴△EHM≌△MGP（AAS），∴EH＝MG＝5﹣m，HM＝PG＝1，∴点H（m﹣1，0），∴点E的坐标为（m﹣1，5﹣m）；∴EA＝＝，又∵D为线段BC的中点，B（2，4），C（6，0），∴点D（4，2），∴ED＝＝，∴EA＝ED．当点M在点C的右侧时，如下图：同理，点E的坐标仍为（m﹣1，5﹣m），因此EA＝ED．②当点E在（1）所求的抛物线上时，把E（m﹣1，5﹣m）代入，整理得：m2﹣10m+13＝0，解得：m＝或m＝，∴CM＝或CM＝．8．解：（1）因为抛物线经过A（﹣1，0），B（3，0），∴可以假设抛物线的解析式为y＝a（x+1）（x﹣3），把C（0，3）代入，可得a＝﹣1，∴抛物线的解析式为y＝﹣（x+1）（x﹣3）＝﹣x2+2x+3．（2）如图1中，连接AC，BC．∵S △ACE ：S △CEB ＝3：5，∴AE ：EB ＝3：5，∵AB ＝4，∴AE ＝4×＝，∴OE ＝0.5，设直线CE 的解析式为y ＝kx +b ，则有，解得， ∴直线EC 的解析式为y ＝﹣6x +3．（3）由题意C （0，3），D （1，4）．当四边形P 1Q 1CD ，四边形P 2Q 2CD 是平行四边形时，点P 的纵坐标为1，当y ＝1时，﹣x 2+2x +3＝1，解得x ＝1±，∴P 1（1+，1），P 2（1﹣，1），当四边形P 3Q 3DC ，四边形P 4Q 4DC 是平行四边形时，点P 的纵坐标为﹣1，当y ＝﹣1时，﹣x 2+2x +3＝﹣1，解得x ＝1±，∴P 1（1+，﹣1），P 2（1﹣，﹣1），综上所述，满足条件的点P 的坐标为（1+，1）或（1﹣，1）或（1﹣，﹣1）或（1+，﹣1）．（4）如图3中，连接BH 交对称轴于F ，连接AF ，此时AF +FH 的值最小．∵H （0，），B （3，0），∴直线BH 的解析式为y ＝﹣x +，∵x ＝1时，y ＝，∴F （1，），设K （x ，y ），作直线y ＝，过点K 作KM ⊥直线y ＝于M ．∵KF ＝，y ＝﹣x 2+2x +3＝﹣（x ﹣1）2+4，∴（x ﹣1）2＝4﹣y ， ∴KF ＝＝＝|y ﹣|，∵KM ＝|y ﹣|，∴KF ＝KM ，∴KG+KF＝KG+KM，根据垂线段最短可知，当G，K，M共线，且垂直直线y＝时，GK+KM的值最小，最小值为，此时K（2，3）．9．（1）把点A（﹣1，0），C（0，3）代入y＝ax2﹣2ax+c中，，解得，∴y＝﹣x2+2x+3，当时，y＝4，∴D（1，4）；（2）如图1，∵抛物线y＝﹣x2+2x+3，令y＝0，∴x＝﹣1，或x＝3，∴B（3，0）．设BC的解析式为y＝kx+b（k≠0），将点C（0，3），B（3，0）代入，得，解得，∴y＝﹣x+3．∵EF⊥CB．设直线EF的解析式为y＝x+b，设点E的坐标为（m，﹣m2+2m+3），将点E坐标代入y＝x+b中，得b＝﹣m2+m+3，∴y＝x﹣m2+m+3，联立得．∴．∴．把x＝m代入y＝﹣x+3，得y＝﹣m+3，∴G（m，﹣m+3）．∵BG＝CF．∴BG2＝CF2，即．解得m＝2或m＝﹣3．∵点E是BC上方抛物线上的点，∴m＝﹣3，（舍去）．∴点E（2，3），F（1，2），G（2，1），，，∴；（3）如图2，过点A作AN⊥HB于N，∵点D（1，4），B（3，0），∴y DB＝﹣2x+6．∵点A（﹣1，0），点C（0，3），∴y AC＝3x+3，联立得，∴，∴．设，把（﹣1，0）代入，得b＝，∴，联立得，∴，∴，∴＝，，∴AN＝HN．∴∠H＝45°．设点P（n，﹣n2+2n+3）．过点P作PR⊥x轴于点R，在x轴上作点S使得RS＝PR，∴∠RSP＝45°且点S的坐标为（﹣n2+3n+3，0）．若∠OPB＝∠AHB＝45°在△OPS和△OPB中，∠POS＝∠POB，∠OSP＝∠OPB，∴△OPS∽△OBP．∴．∴OP2＝OB•OS．∴n2+（n+1）2（n﹣3）2＝3•（﹣n2+3n+3）．∴n＝0或或n＝3（舍去）．（0，3），，．∴P110．解：（1）根据题意，得y与x的解析式为：y＝22+2（x﹣1）＝2x+20（1≤x≤12），故答案为：y＝2x+20，1≤x≤12；（2）设当天的销售利润为w元，则当1≤x≤6时，w＝（1200﹣800）（2x+20）＝800x+8000，∵800＞0，∴w随x的增大而增大，＝800×6+8000＝12800．∴当x＝6时，w最大值当6＜x≤12时，设m＝kx+b，将（6，800）和（10，1000）代入得：，解得：，∴m与x的关系式为：m＝50x+500，∴w＝[1200﹣（50x+500）]×（2x+20）＝﹣100x2+400x+14000＝﹣100（x﹣2）2+14400．∵此时图象开口向下，在对称轴右侧，w随x的增大而减小，天数x为整数，∴当x＝7时，w有最大值，为11900元，∵12800＞11900，∴当x＝6时，w最大，且w＝12800元，最大值答：该厂第6天获得的利润最大，最大利润是12800元．（3）由（2）可得，1≤x≤6时，800x+8000＜10800，解得：x＜3.5则第1﹣3天当天利润低于10800元，当6＜x≤12时，﹣100（x﹣2）2+14400＜10800，解得x＜﹣4（舍去），或x＞8，∴第9﹣12天当天利润低于10800元，故当天销售利润低于10800元的天数有7天．11．解：（1）∵y＝x2+2x+3＝（x+1）2+2，∴把抛物线C1：y＝x2+2x+3先向右平移4个单位长度，再向下平移5个单位长度得到抛物线C2：y＝（x+1﹣4）2+2﹣5，即y＝（x﹣3）2﹣3，∴抛物线C2的函数关系式为：y＝（x﹣3）2﹣3．（2）动点P（a，﹣6）不在抛物线C2上，理由如下：∵抛物线C2的函数关系式为：y＝（x﹣3）2﹣3，∴函数的最小值为﹣3，∵﹣6＜﹣3，∴动点P（a，﹣6）不在抛物线C2上；（3）∵抛物线C2的函数关系式为：y＝（x﹣3）2﹣3，∴抛物线的开口向上，对称轴为x＝3，∴当x＜3时，y随x的增大而减小，∵点A（m，y1），B（n，y2）都在抛物线C2上，且m＜n＜0＜3，∴y1＞y2．12．解：（1）当0＜x≤20时，设y与x的函数关系式为y＝ax+b，，解得，，即当0＜x≤20时，y与x的函数关系式为y＝﹣2x+80，当20＜x≤30时，设y与x的函数关系式为y＝mx+n，，解得，，即当20＜x≤30时，y与x的函数关系式为y＝4x﹣40，由上可得，y与x的函数关系式为y＝；（2）设当月第x天的销售额为w元，当0＜x≤20时，w＝（x+4）×（﹣2x+80）＝（x﹣15）2+500，∴当x＝15时，w取得最大值，此时w＝500，当20＜x≤30时，w＝（x+12）×（4x﹣40）＝（x﹣35）2+500，∴当x＝30时，w取得最大值，此时w＝480，由上可得，当x＝15时，w取得最大值，此时w＝500，答：当月第15天，该农产品的销售额最大，最大销售额是500元．13．解：（1）∵抛物线L：y＝x2﹣x﹣3与x轴正半轴交于点A，与y轴交于点B，∴点A（4，0），点B（0，﹣3），设直线AB解析式为：y＝kx﹣3，∴0＝4k﹣3，∴k＝，∴直线AB解析式为：y＝x﹣3，∵y＝x2﹣x﹣3＝（x﹣）2﹣，∴抛物线顶点坐标为（，﹣）；（2）∵点A（4，0），点B（0，﹣3），∴OA＝4，OB＝3，∴AB＝＝＝5，设点P（x，x2﹣x﹣3）（＜x＜4），则点D（x，x﹣3），∴BD＝＝x，PD＝（x﹣3）﹣（x2﹣x﹣3）＝﹣x2+2x，∴PD+BD＝﹣x2+2x+x＝﹣（x﹣）2+，∵＜x＜4，﹣＜0，∴当x＝时，PD+BD有最大值为，此时，点P（，﹣）；（3）设平移后的抛物线L'解析式为y＝（x﹣m）2﹣，联立方程组可得：，∴x 2﹣2（m +）x +m 2﹣＝0，设点M （x 1，y 1），点N （x 2，y 2）， ∵直线AB 与抛物线L '交于M ，N 两点， ∴x 1，x 2是方程x 2﹣2（m +）x +m 2﹣＝0的两根，∴x 1+x 2＝2（m +）， ∵点A 是MN 的中点， ∴x 1+x 2＝8， ∴2（m +）＝8， ∴m ＝，∴平移后的抛物线L '解析式为y ＝（x ﹣）2﹣＝x 2﹣x +．14．解：（1）由题意得：，解得：．∴a ＝1，b ＝30；（2）由（1）得：y ＝x 2+30x ，设A ，B 两城生产这批产品的总成本为w ，则w ＝x 2+30x +70（100﹣x ）＝x 2﹣40x +7000，＝（x ﹣20）2+6600， ∵a ＝1＞0，由二次函数的性质可知，当x ＝20时，w 取得最小值，最小值为6600万元，此时100﹣20＝80．答：A 城生产20件，B 城生产80件；（3）设从A 城运往C 地的产品数量为n 件，A ，B 两城总运费的和为P ，则从A 城运往D 地的产品数量为（20﹣n ）件，从B 城运往C 地的产品数量为（90﹣n ）件，从B城运往D地的产品数量为（10﹣20+n）件，由题意得：，解得10≤n≤20，∴P＝mn+3（20﹣n）+（90﹣n）+2（10﹣20+n），整理得：P＝（m﹣2）n+130，根据一次函数的性质分以下两种情况：①当0＜m≤2，10≤n≤20时，P随n的增大而减小，则n＝20时，P取最小值，最小值为20（m﹣2）+130＝20m+90；②当m＞2，10≤n≤20时，P随n的增大而增大，则n＝10时，P取最小值，最小值为10（m﹣2）+130＝10m+110．答：0＜m≤2时，A，B两城总运费的和为（20m+90）万元；当m＞2时，A，B两城总运费的和为（10m+110）万元．15．解：（1）直线y＝﹣x+2与x轴交于点A，与y轴交于点B，则点A、B的坐标分别为（4，0）、（0，2），将点B、C的坐标代入抛物线表达式得，解得，故抛物线的表达式为：y＝﹣x2+x+2①；（2）如图1，作点B关于x轴的对称点B′（0，﹣2），连接AB′交抛物线于点P（P′），则∠PAO＝∠BAO，设直线AB'的解析式为y＝kx+m，∴，∴，直线AB′的表达式为：y＝x﹣2②，联立①②并解得：x＝3或﹣2，故点P的坐标为（3，﹣）或（﹣2，﹣3），当点P与B，C重合时，也满足条件，此时P（0，2）或（，），综上所述，满足条件的点P的坐标为（3，﹣）或（﹣2，﹣3）或（0，2）或（，）．（3）①过点C作CH⊥x轴于点H，∵∠MNC＝90°，∴∠MNO+∠CNH＝90°，又∵∠CNH+∠NCH＝90°，∴∠MNO＝∠NCH，∴tan∠MNO＝tan∠NCH，即，即，解得：m＝﹣n2+n；②m＝﹣n2+n，∵＜0，故m有最大值，当n＝时，m的最大值为，而m＞0，故0＜m＜时，符合条件的N点的个数有2个．16．解：（1）设y与x的函数关系式为：y＝kx+b（k≠0），把x＝4，y＝10000和x＝5，y＝9500代入得，，解得，，∴y＝﹣500x+12000；（2）根据“在销售过程中要求销售单价不低于成本价，且不高于15元/件．若某一周该商品的销售量不少于6000件，”得，，解得，3≤x≤12，设利润为w元，根据题意得，w＝（x﹣3）y＝（x﹣3）（﹣500x+12000）＝﹣500x2+13500x﹣36000＝﹣500（x﹣13.5）2+55125，∵﹣500＜0，∴当x＜13.5时，w随x的增大而增大，∵3≤x≤12，∴当x＝12时，w取最大值为：﹣500×（12﹣13.5）2+55125＝54000，答：这一周该商场销售这种商品获得的最大利润为54000元，售价为12元；（3）根据题意得，w＝（x﹣3﹣m）（﹣500x+12000）＝﹣500x2+（13500+500m）x﹣36000﹣12000m，∴对称轴为x＝﹣＝13.5+0.5m，∵﹣500＜0，∴当x≤13.5+0.5m时，w随x的增大而增大，∵该商场这种商品售价不大于15元/件时，捐赠后发现，该商场每周销售这种商品的利润仍随售价的增大而增大．∴15≤13.5+0.5m，解得，m≥3，∵1≤m≤6，∴3≤m≤6．17．解：（1）当a＝6时，抛物线的表达式为：y＝6x2+24x+18，令y＝0，则x＝﹣1或﹣3；当x＝0时，y＝18，函数的对称轴为x＝﹣2，故点A、B、C、D的坐标分别为（﹣3，0）、（﹣1，0）、（0，18）、（﹣2，﹣6）；故答案为：（﹣3，0）、（﹣1，0）、（0，18）、（﹣2，﹣6）；答案的第（2）小题，tan∠AED＝OC/OE＝（4a﹣6）/（3/a﹣2）应改在此处添加绝对值符号，或者将4a﹣6改为6﹣4a（2）y＝ax2+4ax+4a﹣6，令x＝0，则y＝4a﹣6，则点C（0，4a﹣6），函数的对称轴为x＝﹣2，故点D的坐标为（﹣2，﹣6），由点C、D的坐标得，直线CD的表达式为：y＝2ax+4a﹣6，令y＝0，则x＝﹣2，故点E（﹣2，0），则OE＝﹣2，tan∠AED＝＝＝，解得：a＝，故点C、E的坐标分别为（0，﹣）、（，0），则CE＝＝；（3）①如图，作PF与ED的延长线交于点J，由（2）知，抛物线的表达式为：y＝x2+x﹣，故点A、C的坐标分别为（﹣5，0）、（0，﹣），则点N（0，﹣），由点A、N的坐标得，直线AN的表达式为：y＝﹣x﹣；设点P（t，t2+t﹣），则点F（t，﹣t﹣）；则PF＝﹣t2﹣3t+，由点E（，0）、C的坐标得，直线CE的表达式为：y＝x﹣，则点J（t，t﹣），故FJ＝﹣t+，∵FH⊥DE，JF∥y轴，故∠FHJ＝∠EOC＝90°，∠FJH＝∠ECO，∴△FJH∽△ECO，故，则FH＝，f＝PF+FH＝﹣t2﹣3t++（﹣t+1）＝﹣t2﹣4t+；②f＝﹣t2﹣4t+＝﹣（t+3）2+（﹣5＜t≤m且m＜0）；∴当﹣5＜m＜﹣3时，f max＝﹣m2﹣4m+；当﹣3≤m＜0时，f max＝．18．解：（1）∵抛物线C：y＝（x﹣2）2向下平移6个单位长度得到抛物线C1，∴C1：y＝（x﹣2）2﹣6，∵将抛物线C1向左平移2个单位长度得到抛物线C2．∴C2：y＝（x﹣2+2）2﹣6，即y＝x2﹣6；（2）过点A作AC⊥x轴于点C，过B作BD⊥AC于点D，如图1，设A（a，（a﹣2）2﹣6），则BD＝a﹣2，AC＝|（a﹣2）2﹣6|，∵∠BAO＝∠ACO＝90°，∴∠BAD+∠OAC＝∠OAC+∠AOC＝90°，∴∠BAD＝∠AOC，∵AB＝OA，∠ADB＝∠OCA，∴△ABD≌△OAC（AAS），∴BD＝AC，∴a﹣2＝|（a﹣2）2﹣6|，解得，a＝4，或a＝﹣1（舍），或a＝0（舍），或a＝5，∴A（4，﹣2）或（5，3）；（3）把y＝kx代入y＝x2﹣6中得，x2﹣kx﹣6＝0，∴x E+x F＝k，∴M（），把y＝﹣x代入y＝x2﹣6中得，x2+x﹣6＝0，∴，∴N（，），设MN的解析式为y＝mx+n（m≠0），则，解得，，∴直线MN的解析式为：，当x＝0时，y＝2，∴直线MN：经过定点（0，2），即直线MN经过一个定点．19．解：（1）令x ＝0，得y ＝﹣x +2＝2，∴A （0，2），令y ＝0，得y ＝﹣x +2＝0，解得，x ＝4，∴C （4，0），把A 、C 两点代入y ＝﹣x 2+bx +c 得，，解得，∴抛物线的解析式为，令y ＝0，得＝0，解得，x ＝4，或x ＝﹣2，∴B （﹣2，0）；（2）过M 点作MN ⊥x 轴，与AC 交于点N ，如图1，设M （a ，），则N （a ，）， ∴＝，∵， ∴S 四边形ABCM ＝S △ACM +S △ABC ＝， ∴当a ＝2时，四边形ABCM 面积最大，其最大值为8，此时M 的坐标为（2，2）；（3）∵将线段OA 绕x 轴上的动点P （m ，0）顺时针旋转90°得到线段O ′A ′，如图2，∴PO′＝PO＝m，O′A′＝OA＝2，∴O′（m，m），A′（m+2，m），当A′（m+2，m）在抛物线上时，有，解得，m＝﹣3，当点O′（m，m）在抛物线上时，有，解得，m＝﹣4或2，∴当﹣3﹣≤m≤﹣4或﹣3+≤m≤2时，线段O′A′与抛物线只有一个公共点．。

2021年中考数学二次函数压轴题专练1

《二次函数》压轴题1．（2020•镇江）如图①，直线l经过点（4，0）且平行于y轴，二次函数y＝ax2﹣2ax+c（a、c是常数，a＜0）的图象经过点M（﹣1，1），交直线l于点N，图象的顶点为D，它的对称轴与x轴交于点C，直线DM、DN分别与x轴相交于A、B两点．（1）当a＝﹣1时，求点N的坐标及的值；（2）随着a的变化，的值是否发生变化？请说明理由；（3）如图②，E是x轴上位于点B右侧的点，BC＝2BE，DE交抛物线于点F．若FB＝FE，求此时的二次函数表达式．2．（2020•南通）已知抛物线y＝ax2+bx+c经过A（2，0），B（3n﹣4，y1），C（5n+6，y2）三点，对称轴是直线x＝1．关于x的方程ax2+bx+c＝x有两个相等的实数根．（1）求抛物线的解析式；（2）若n＜﹣5，试比较y1与y2的大小；（3）若B，C两点在直线x＝1的两侧，且y1＞y2，求n的取值范围．3．（2020•宿迁）某超市经销一种商品，每千克成本为50元，经试销发现，该种商品的每天销售量y（千克）与销售单价x（元/千克）满足一次函数关系，其每天销售单价，销售量的四组对应值如下表所示：55 60 65 70销售单价x（元/千克）销售量y（千克）70 60 50 40（1）求y（千克）与x（元/千克）之间的函数表达式；（2）为保证某天获得600元的销售利润，则该天的销售单价应定为多少？（3）当销售单价定为多少时，才能使当天的销售利润最大？最大利润是多少？4．（2020•宿迁）二次函数y＝ax2+bx+3的图象与x轴交于A（2，0），B（6，0）两点，与y轴交于点C，顶点为E．．（1）求这个二次函数的表达式，并写出点E的坐标；（2）如图①，D是该二次函数图象的对称轴上一个动点，当BD的垂直平分线恰好经过点C时，求点D的坐标；（3）如图②，P是该二次函数图象上的一个动点，连接OP，取OP中点Q，连接QC，QE，CE，当△CEQ的面积为12时，求点P的坐标．Array 5．（2020•徐州）如图，在平面直角坐标系中，函数y＝﹣ax2+2ax+3a（a＞0）的图象交x轴于点A、B，交y轴于点C，它的对称轴交x轴于点E．过点C作CD∥x轴交抛物线于点D，连接DE并延长交y轴于点F，交抛物线于点G．直线AF交CD于点H，交抛物线于点K，连接HE、GK．（1）点E的坐标为：；（2）当△HEF是直角三角形时，求a的值；（3）HE与GK有怎样的位置关系？请说明理由．6．（2020•淮安）如图①，二次函数y＝﹣x2+bx+4的图象与直线l交于A（﹣1，2）、B（3，n）两点．点P是x轴上的一个动点，过点P作x轴的垂线交直线1于点M，交该二次函数的图象于点N，设点P的横坐标为m．（1）b＝，n＝；（2）若点N在点M的上方，且MN＝3，求m的值；（3）将直线AB向上平移4个单位长度，分别与x轴、y轴交于点C、D（如图②）．①记△NBC的面积为S1，△NAC的面积为S2，是否存在m，使得点N在直线AC的上方，且满足S1﹣S2＝6？若存在，求出m及相应的S1，S2的值；若不存在，请说明理由．②当m＞﹣1时，将线段MA绕点M顺时针旋转90°得到线段MF，连接FB、FC、OA．若∠FBA+∠AOD﹣∠BFC＝45°，直接写出直线OF与该二次函数图象交点的横坐标．7．（2020•常州）如图，二次函数y＝x2+bx+3的图象与y轴交于点A，过点A作x轴的平行线交抛物线于另一点B，抛物线过点C（1，0），且顶点为D，连接AC、BC、BD、CD．（1）填空：b＝；（2）点P是抛物线上一点，点P的横坐标大于1，直线PC交直线BD于点Q．若∠CQD ＝∠ACB，求点P的坐标；（3）点E在直线AC上，点E关于直线BD对称的点为F，点F关于直线BC对称的点为G，连接AG．当点F在x轴上时，直接写出AG的长．8．（2020•盐城）若二次函数y＝ax2+bx+c的图象与x轴有两个交点M（x1，0），N（x2，0）（0＜x1＜x2），且经过点A（0，2）．过点A的直线l与x轴交于点C，与该函数的图象交于点B（异于点A）．满足△ACN是等腰直角三角形，记△AMN的面积为S1，△BMN 的面积为S2，且S2＝S1．（1）抛物线的开口方向（填“上”或“下”）；（2）求直线l相应的函数表达式；（3）求该二次函数的表达式．9．（2020•泰州）如图，二次函数y1＝a（x﹣m）2+n，y2＝6ax2+n（a＜0，m＞0，n＞0）的图象分别为C1、C2，C1交y轴于点P，点A在C1上，且位于y轴右侧，直线PA与C2在y轴左侧的交点为B．（1）若P点的坐标为（0，2），C1的顶点坐标为（2，4），求a的值；（2）设直线PA与y轴所夹的角为α．①当α＝45°，且A为C1的顶点时，求am的值；②若α＝90°，试说明：当a、m、n各自取不同的值时，的值不变；（3）若PA＝2PB，试判断点A是否为C1的顶点？请说明理由．10．（2020•南京）小明和小丽先后从A地出发沿同一直道去B地．设小丽出发第xmin时，小丽、小明离B地的距离分别为y1m、y2m．y1与x之间的函数表达式是y1＝﹣180x+2250，y与x之间的函数表达式是y2＝﹣10x2﹣100x+2000．2（1）小丽出发时，小明离A地的距离为m．（2）小丽出发至小明到达B地这段时间内，两人何时相距最近？最近距离是多少？11．（2020•连云港）在平面直角坐标系xOy中，把与x轴交点相同的二次函数图象称为“共根抛物线”．如图，抛物线L1：y＝x2﹣x﹣2的顶点为D，交x轴于点A、B（点A 在点B左侧），交y轴于点C．抛物线L2与L1是“共根抛物线”，其顶点为P．（1）若抛物线L2经过点（2，﹣12），求L2对应的函数表达式；（2）当BP﹣CP的值最大时，求点P的坐标；（3）设点Q是抛物线L1上的一个动点，且位于其对称轴的右侧．若△DPQ与△ABC相似，求其“共根抛物线”L2的顶点P的坐标．12．（2020•苏州）如图，二次函数y＝x2+bx的图象与x轴正半轴交于点A，平行于x轴的直线l与该抛物线交于B、C两点（点B位于点C左侧），与抛物线对称轴交于点D（2，﹣3）．（1）求b的值；（2）设P、Q是x轴上的点（点P位于点Q左侧），四边形PBCQ为平行四边形．过点P、Q分别作x轴的垂线，与抛物线交于点P'（x，y1）、Q'（x2，y2）．若|y1﹣y2|＝2，1求x1、x2的值．13．（2020•无锡）有一块矩形地块ABCD，AB＝20米，BC＝30米．为美观，拟种植不同的花卉，如图所示，将矩形ABCD分割成四个等腰梯形及一个矩形，其中梯形的高相等，均为x米．现决定在等腰梯形AEHD和BCGF中种植甲种花卉；在等腰梯形ABFE和CDHG中种植乙种花卉；在矩形EFGH中种植丙种花卉．甲、乙、丙三种花卉的种植成本分别为20元/米2、60元/米2、40元/米2，设三种花卉的种植总成本为y元．（1）当x＝5时，求种植总成本y；（2）求种植总成本y与x的函数表达式，并写出自变量x的取值范围；（3）若甲、乙两种花卉的种植面积之差不超过120平方米，求三种花卉的最低种植总成本．14．如图，在平面直角坐标系中，抛物线y＝ax2+bx+2（a≠0）与y轴交于点C，与x轴交于A，B两点（点A在点B的左侧），且A点坐标为（﹣，0），直线BC的解析式为y＝﹣x+2．（1）求抛物线的解析式；（2）过点A作AD∥BC，交抛物线于点D，点E为直线BC上方抛物线上一动点，连接CE，EB，BD，DC．求四边形BECD面积的最大值及相应点E的坐标；（3）将抛物线y＝ax2+bx+2（a≠0）向左平移个单位，已知点M为抛物线y＝ax2+bx+2（a≠0）的对称轴上一动点，点N为平移后的抛物线上一动点．在（2）中，当四边形BECD的面积最大时，是否存在以A，E，M，N为顶点的四边形为平行四边形？若存在，直接写出点N的坐标；若不存在，请说明理由．15．（2020•无锡）在平面直角坐标系中，O为坐标原点，直线OA交二次函数y＝x2的图象于点A，∠AOB＝90°，点B在该二次函数的图象上，设过点（0，m）（其中m＞0）且平行于x轴的直线交直线OA于点M，交直线OB于点N，以线段OM、ON为邻边作矩形OMPN．（1）若点A的横坐标为8．①用含m的代数式表示M的坐标；②点P能否落在该二次函数的图象上？若能，求出m的值；若不能，请说明理由．（2）当m＝2时，若点P恰好落在该二次函数的图象上，请直接写出此时满足条件的所有直线OA的函数表达式．参考答案1．（2020•镇江）如图①，直线l经过点（4，0）且平行于y轴，二次函数y＝ax2﹣2ax+c（a、c是常数，a＜0）的图象经过点M（﹣1，1），交直线l于点N，图象的顶点为D，它的对称轴与x轴交于点C，直线DM、DN分别与x轴相交于A、B两点．（1）当a＝﹣1时，求点N的坐标及的值；（2）随着a的变化，的值是否发生变化？请说明理由；（3）如图②，E是x轴上位于点B右侧的点，BC＝2BE，DE交抛物线于点F．若FB＝FE，求此时的二次函数表达式．【解答】解：（1）分别过点M、N作MG⊥CD于点E，NT⊥DC于点T，∵MG∥TN∥x轴，∴△DMG∽△DAC，△DCB∽△DTN，∴，＝，∵a＝﹣1，则y＝﹣x2+2x+c，将M（﹣1，1）代入上式并解得：c＝4，∴抛物线的表达式为：y＝﹣x2+2x+4，则点D（1，5），N（4，﹣4），则MG＝2，DG＝4，DC＝5，TN＝3，DT＝9，∴，解得：AC＝，BC＝，∴＝；（2）不变，理由：∵y＝ax2﹣2ax+c过点M（﹣1，1），则a+2a+c＝1，解得：c＝1﹣3a，∴y＝ax2﹣2ax+（1﹣3a），∴点D（1，1﹣4a），N（4，1+5a），∴ME＝2，DE＝﹣4a，DC＝1﹣4a，FN＝3，DF＝﹣9a，由（1）的结论得：AC＝，BC＝，∴＝；（3）过点F作FH⊥x轴于点H，则FH∥l，则△FHE∽△DCE，∵FB＝FE，FH⊥BE，∴BH＝HE，∵BC＝2BE，则CE＝6HE，∵CD＝1﹣4a，∴FH＝，∵BC＝，∴CH＝×＝，∴F（﹣+1，﹣a），将点F的坐标代入y＝ax2﹣2ax+（1﹣3a）＝a（x+1）（x﹣3）+1得：﹣a＝a（﹣+1+1）（﹣+1﹣3）+1，解得：a＝﹣或（舍弃），经检验a＝﹣，故y＝﹣x2+x+．2．（2020•南通）已知抛物线y＝ax2+bx+c经过A（2，0），B（3n﹣4，y1），C（5n+6，y2）三点，对称轴是直线x＝1．关于x的方程ax2+bx+c＝x有两个相等的实数根．（1）求抛物线的解析式；（2）若n＜﹣5，试比较y1与y2的大小；（3）若B，C两点在直线x＝1的两侧，且y1＞y2，求n的取值范围．【解答】解：（1）∵抛物线y＝ax2+bx+c经过A（2，0），∴0＝4a+2b+c①，∵对称轴是直线x＝1，∴﹣＝1②，∵关于x的方程ax2+bx+c＝x有两个相等的实数根，∴△＝（b﹣1）2﹣4ac＝0③，由①②③可得：，∴抛物线的解析式为y＝﹣x2+x；（2）∵n＜﹣5，∴3n﹣4＜﹣19，5n+6＜﹣19∴点B，点C在对称轴直线x＝1的左侧，∵抛物线y＝﹣x2+x，∴﹣＜0，即y随x的增大而增大，∵（3n﹣4）﹣（5n+6）＝﹣2n﹣10＝﹣2（n+5）＞0，∴3n﹣4＞5n+6，∴y1＞y2；（3）若点B在对称轴直线x ＝1的左侧，点C在对称轴直线x＝1的右侧时，由题意可得，∴0＜n＜，若点C在对称轴直线x＝1的左侧，点B在对称轴直线x＝1的右侧时，由题意可得：，∴不等式组无解，综上所述：0＜n＜．3．（2020•宿迁）某超市经销一种商品，每千克成本为50元，经试销发现，该种商品的每天销售量y（千克）与销售单价x（元/千克）满足一次函数关系，其每天销售单价，销售量的四组对应值如下表所示：55 60 65 70销售单价x（元/千克）销售量y（千克）70 60 50 40（1）求y（千克）与x（元/千克）之间的函数表达式；（2）为保证某天获得600元的销售利润，则该天的销售单价应定为多少？（3）当销售单价定为多少时，才能使当天的销售利润最大？最大利润是多少？【解答】解：（1）设y与x之间的函数表达式为y＝kx+b（k≠0），将表中数据（55，70）、（60，60）代入得：，解得：．∴y与x之间的函数表达式为y＝﹣2x+180．（2）由题意得：（x﹣50）（﹣2x+180）＝600，整理得：x2﹣140x+4800＝0，解得x1＝60，x2＝80．答：为保证某天获得600元的销售利润，则该天的销售单价应定为60元/千克或80元/千克．（3）设当天的销售利润为w元，则：w＝（x﹣50）（﹣2x+180）＝﹣2（x﹣70）2+800，∵﹣2＜0，∴当x＝70时，w最大值＝800．答：当销售单价定为70元/千克时，才能使当天的销售利润最大，最大利润是800元．4．（2020•宿迁）二次函数y＝ax2+bx+3的图象与x轴交于A（2，0），B（6，0）两点，与y轴交于点C，顶点为E．．（1）求这个二次函数的表达式，并写出点E的坐标；（2）如图①，D是该二次函数图象的对称轴上一个动点，当BD的垂直平分线恰好经过点C时，求点D的坐标；（3）如图②，P是该二次函数图象上的一个动点，连接OP，取OP中点Q，连接QC，QE，CE，当△CEQ的面积为12时，求点P的坐标．【解答】解：（1）将A（2，0），B（6，0）代入y＝ax2+bx+3，得，解得∴二次函数的解析式为y＝﹣2x+3．∵y＝﹣1，∴E（4，﹣1）．（2）如图1，图2，连接CB，CD，由点C在线段BD的垂直平分线CN上，得CB＝CD．设D（4，m），∵C（0，3），由勾股定理可得：42+（m﹣3）2＝62+32．解得m＝3±．∴满足条件的点D的坐标为（4，3+）或．（3）如图3，设CQ交抛物线的对称轴于点M，设P（n，﹣2n+3），则Q（），设直线CQ的解析式为y＝kx+3，则nk+3．解得k＝，于是CQ：y＝（）x+3，当x＝4时，y＝4（）+3＝n﹣5﹣，∴M（4，n﹣5﹣），ME＝n﹣4﹣．∵S△CQE＝S△CEM+S△QEM＝．∴n2﹣4n﹣60＝0，解得n＝10或n＝﹣6，当n＝10时，P（10，8），当n＝﹣6时，P（﹣6，24）．综合以上可得，满足条件的点P的坐标为（10，8）或（﹣6，24）．5．（2020•徐州）如图，在平面直角坐标系中，函数y＝﹣ax2+2ax+3a（a＞0）的图象交x 轴于点A、B，交y轴于点C，它的对称轴交x轴于点E．过点C作CD∥x轴交抛物线于点D，连接DE并延长交y轴于点F，交抛物线于点G．直线AF交CD于点H，交抛物线于点K，连接HE、GK．（1）点E的坐标为：（1，0）；（2）当△HEF是直角三角形时，求a的值；（3）HE与GK有怎样的位置关系？请说明理由．【解答】解：（1）对于抛物线y＝﹣ax2+2ax+3a，对称轴x＝﹣＝1，∴E（1，0），故答案为（1，0）．（2）如图，连接EC．对于抛物线y＝﹣ax2+2ax+3a，令x＝0，得到y＝3a，令y＝0，﹣ax2+2ax+3a＝0，解得x＝﹣1或3，∴A（﹣1，0），B（3，0），C（0，3a），∵C，D关于对称轴对称，∴D（2，3a），CD＝2，EC＝DE，当∠HEF＝90°时，∵ED＝EC，∴∠ECD＝∠EDC，∵∠DCF＝90°，∴∠CFD+∠EDC＝90°，∠ECF+∠ECD＝90°，∴∠ECF＝∠EFC，∴EC＝EF＝DE，∵EA∥DH，∴FA＝AH，∴AE＝DH，∵AE＝2，∴DH＝4，∵HE⊥DFEF＝ED，∴FH＝DH＝4，在Rt△CFH中，则有42＝22+（6a）2，解得a＝或﹣（不符合题意舍弃），∴a＝．当∠HFE＝90°时，∵OA＝OE，FO⊥AE，∴FA＝FE，∴OF＝OA＝OE＝1，∴3a＝1，∴a＝，综上所述，满足条件的a的值为或．（3）结论：EH∥GK．理由：由题意A（﹣1，0），F（0，﹣3a），D（2，3a），H（﹣2，3a），E（1，0），∴直线AF的解析式y＝﹣3ax﹣3a，直线DF的解析式为y＝3ax﹣3a，由，解得或，∴K（6，﹣21a），由，解得或，∴G（﹣3，﹣12a），∴直线HE的解析式为y＝﹣ax+a，直线GK的解析式为y＝﹣ax﹣15a，∵k相同，a≠﹣15a，∴HE∥GK．6．（2020•淮安）如图①，二次函数y＝﹣x2+bx+4的图象与直线l交于A（﹣1，2）、B（3，n）两点．点P是x轴上的一个动点，过点P作x轴的垂线交直线1于点M，交该二次函数的图象于点N，设点P的横坐标为m．（1）b＝ 1 ，n＝﹣2 ；（2）若点N在点M的上方，且MN＝3，求m的值；（3）将直线AB向上平移4个单位长度，分别与x轴、y轴交于点C、D（如图②）．①记△NBC的面积为S1，△NAC的面积为S2，是否存在m，使得点N在直线AC的上方，且满足S1﹣S2＝6？若存在，求出m及相应的S1，S2的值；若不存在，请说明理由．②当m＞﹣1时，将线段MA绕点M顺时针旋转90°得到线段MF，连接FB、FC、OA．若∠FBA+∠AOD﹣∠BFC＝45°，直接写出直线OF与该二次函数图象交点的横坐标．【解答】解：（1）将点A（﹣1，2）代入二次函数y＝﹣x2+bx+4中，得﹣1﹣b+4＝2，∴b＝1，∴二次函数的解析式为y＝﹣x2+x+4，将点B（3，n）代入二次函数y＝﹣x2+x+4中，得n＝﹣9+3+4＝﹣2，故答案为：1，﹣2；（2）设直线AB的解析式为y＝kx+a，由（1）知，点B（3，﹣2），∵A（﹣1，2），∴，∴，∴直线AB的解析式为y＝﹣x+1，由（1）知，二次函数的解析式为y＝﹣x2+x+4，∵点P（m，0），∴M（m，﹣m+1），N（m，﹣m2+m+4），∵点N在点M的上方，且MN＝3，∴﹣m2+m+4﹣（﹣m+1）＝3，∴m＝0或m＝2；（3）①如图1，由（2）知，直线AB的解析式为y＝﹣x+1，∴直线CD的解析式为y＝﹣x+1+4＝﹣x+5，令y＝0，则﹣x+5＝0，∴x＝5，∴C（5，0），∵A（﹣1，2），B（3，﹣2），∴直线AC的解析式为y＝﹣x+，直线BC的解析式为y＝x﹣5，过点N作y轴的平行线交AC于K，交BC于H，∵点P（m，0），∴N（m，﹣m2+m+4），K（m，﹣m+），H（m，m﹣5），∴NK＝﹣m2+m+4+m﹣＝﹣m2+m+，NH＝﹣m2+9，∴S2＝S△NAC＝NK×（x C﹣x A）＝（﹣m2+m+）×6＝﹣3m2+4m+7，S＝S△NBC＝NH×（x C﹣x B）＝﹣m2+9，1∵S1﹣S2＝6，∴﹣m2+9﹣（﹣3m2+4m+7）＝6，∴m＝1+（由于点N在直线AC上方，所以，舍去）或m＝1﹣；∴S2＝﹣3m2+4m+7＝﹣3（1﹣）2+4（1﹣）+7＝2﹣1，S＝﹣m2+9＝﹣（1﹣）2+9＝2+5；1②如图2，记直线AB与x轴，y轴的交点为I，L，由（2）知，直线AB的解析式为y＝﹣x+1，∴I（1，0），L（0，1），∴OL＝OI，∴∠ALD＝∠OLI＝45°，∴∠AOD+∠OAB＝45°，过点B作BG∥OA，∴∠ABG＝∠OAB，∴∠AOD+∠ABG＝45°，∵∠FBA＝∠ABG+∠FBG，∠FBA+∠AOD﹣∠BFC＝45°，∴∠ABG+∠FBG+∠AOD﹣∠BFC＝45°，∴∠FBG＝∠BFC，∴BG∥CF，∴OA∥CF，∵A（﹣1，2），∴直线OA的解析式为y＝﹣2x，∵C（5，0），∴直线CF的解析式为y＝﹣2x+10，过点A，F分别作过点M平行于x轴的直线的垂线，交于点Q，S，∵∠AQM＝∠MSF＝90°，∵点M在直线AB上，m＞﹣1，∴M（m，﹣m+1），∴A（﹣1，2），∴MQ＝m+1，设点F（n，﹣2n+10），∴FS＝﹣2n+10+m﹣1＝﹣2n+m+9，由旋转知，AM＝MF，∠AMF＝90°，∴∠MAQ+∠AMQ＝90°＝∠AMQ+∠FMS，∴∠MAQ＝∠FMS，∴△AQM≌△MSF（AAS），∴FS＝MQ，∴﹣2n+m+9＝m+1，∴n＝4，∴F（4，2），∴直线OF的解析式为y＝x①，∵二次函数的解析式为y＝﹣x2+x+4②，联立①②解得，或，∴直线OF与该二次函数图象交点的横坐标为或．7．（2020•常州）如图，二次函数y＝x2+bx+3的图象与y轴交于点A，过点A作x轴的平行线交抛物线于另一点B，抛物线过点C（1，0），且顶点为D，连接AC、BC、BD、CD．（1）填空：b＝﹣4 ；（2）点P是抛物线上一点，点P的横坐标大于1，直线PC交直线BD于点Q．若∠CQD＝∠ACB，求点P的坐标；（3）点E在直线AC上，点E关于直线BD对称的点为F，点F关于直线BC对称的点为G，连接AG．当点F在x轴上时，直接写出AG的长．【解答】解：（1）∵抛物线y＝x2+bx+3的图象过点C（1，0），∴0＝1+b+3，∴b＝﹣4，故答案为：﹣4；（2）∵b＝﹣4，∴抛物线解析式为y＝x2﹣4x+3∵抛物线y＝x2﹣4x+3的图象与y轴交于点A，过点A作x轴的平行线交抛物线于另一点B，∴点A（0，3），3＝x2﹣4x+3，∴x1＝0（舍去），x2＝4，∴点B（4，3），∵y＝x2﹣4x+3＝（x﹣2）2﹣1，∴顶点D坐标（2，﹣1），如图1，当点Q在点D上方时，过点C作CE⊥AB于E，设BD与x轴交于点F，∵点A（0，3），点B（4，3），点C（1，0），CE⊥AB，∴点E（1，3），CE＝BE＝3，AE＝1，∴∠EBC＝∠ECB＝45°，tan∠ACE＝，∴∠BCF＝45°，∵点B（4，3），点C（1，0），点D（2，﹣1），∴BC＝＝3，CD＝＝，BD＝＝2，∵BC2+CD2＝20＝BD2，∴∠BCD＝90°，∴tan∠DBC＝＝＝＝tan∠ACE，∴∠ACE＝∠DBC，∴∠ACE+∠ECB＝∠DBC+∠BCF，∴∠ACB＝∠CFD，又∵∠CQD＝∠ACB，∴点F与点Q重合，∴点P是直线CF与抛物线的交点，∴0＝x2﹣4x+3，∴x1＝1，x2＝3，∴点P（3，0）；当点Q在点D下方上，过点C作CH⊥DB于H，在线段BH的延长线上截取HF＝QH，连接CQ交抛物线于点P，∵CH⊥DB，HF＝QH，∴CF＝CQ，∴∠CFD＝∠CQD，∴∠CQD＝∠ACB，∵CH⊥BD，∵点B（4，3），点D（2，﹣1），∴直线BD解析式为：y＝2x﹣5，∴点F（，0），∴直线CH解析式为：y＝﹣x+，∴，解得，∴点H坐标为（，﹣），∵FH＝QH，∴点Q（，﹣），∴直线CQ解析式为：y＝﹣x+，联立方程组，解得：或，∴点P（，﹣）；综上所述：点P的坐标为（3，0）或（，﹣）；（3）如图，设直线AC与BD的交点为N，作CH⊥BD于H，过点N作MN⊥x轴，过点E作EM⊥MN，连接CG，GF，∵点A（0，3），点C（1，0），∴直线AC解析式为：y＝﹣3x+3，∴，∴，∴点N坐标为（，﹣），∵点H坐标为（，﹣），∴CH2＝（﹣1）2+（）2＝，HN2＝（﹣）2+（﹣+）2＝，∴CH＝HN，∴∠CNH＝45°，∵点E关于直线BD对称的点为F，∴EN＝NF，∠ENB＝∠FNB＝45°，∴∠ENF＝90°，∴∠ENM+∠FNM＝90°，又∵∠ENM+∠MEN＝90°，∴∠MEN＝∠FNM，∴△EMN≌△NKF（AAS）∴EM＝NK＝，MN＝KF，∴点E的横坐标为﹣，∴点E（﹣，），∴MN＝＝KF，∴CF＝+﹣1＝6，∵点F关于直线BC对称的点为G，∴FC＝CG＝6，∠BCF＝∠GCB＝45°，∴∠GCF＝90°，∴点G（1，6），∴AG＝＝．8．（2020•盐城）若二次函数y＝ax2+bx+c的图象与x轴有两个交点M（x1，0），N（x2，0）（0＜x1＜x2），且经过点A（0，2）．过点A的直线l与x轴交于点C，与该函数的图象交于点B（异于点A）．满足△ACN是等腰直角三角形，记△AMN的面积为S1，△BMN 的面积为S2，且S2＝S1．（1）抛物线的开口方向上（填“上”或“下”）；（2）求直线l相应的函数表达式；（3）求该二次函数的表达式．【解答】解：（1）如图，如二次函数y＝ax2+bx+c的图象与x轴有两个交点M（x1，0），N（x，0）（0＜x1＜x2），且经过点A（0，2）．2∴y＝ax2+bx+2，令y＝0，则ax2+bx+2＝0，∵0＜x1＜x2，∴＞0，∴a＞0，∴抛物线开口向上，故答案为：上；（2）①若∠ACN＝90°，则C与O重合，直线l与抛物线交于A点，因为直线l与该函数的图象交于点B（异于点A），所以不合题意，舍去；②若∠ANC＝90°，则C在x轴的下方，与题意不符，舍去；③若∠CAN＝90°，则∠ACN＝∠ANC＝45°，AO＝CO＝NO＝2，∴C（﹣2，0），N（2，0），设直线l为y＝kx+b，将A（0，2）C（﹣2，0）代入得，解得，∴直线l相应的函数表达式为y＝x+2；（3）过B点作BH⊥x轴于H，S＝，S2＝，1∵S2＝S1，∴BH＝OA，∵OA＝2，∴BH＝5，即B点的纵坐标为5，代入y＝x+2中，得x＝3，∴B（3，5），将A、B、N三点的坐标代入y＝ax2+bx+c得，解得，∴抛物线的解析式为y＝2x2﹣5x+2．9．（2020•泰州）如图，二次函数y1＝a（x﹣m）2+n，y2＝6ax2+n（a＜0，m＞0，n＞0）的图象分别为C1、C2，C1交y轴于点P，点A在C1上，且位于y轴右侧，直线PA与C2在y轴左侧的交点为B．（1）若P点的坐标为（0，2），C1的顶点坐标为（2，4），求a的值；（2）设直线PA与y轴所夹的角为α．①当α＝45°，且A为C1的顶点时，求am的值；②若α＝90°，试说明：当a、m、n各自取不同的值时，的值不变；（3）若PA＝2PB，试判断点A是否为C1的顶点？请说明理由．【解答】解：（1）由题意m＝2，n＝4，∴y1＝a（x﹣2）2+4，把（0，2）代入得到a＝﹣．（2）①如图1中，过点A作AN⊥x轴于N，过点P作PM⊥AN于M．∵y1＝a（x﹣m）2+n＝ax2﹣2amx+am2+n，∴P（0，am2+n），∵A（m，n），∴PM＝m，AN＝n，∵∠APM＝45°，∴AM＝PM＝m，∴m+am2+n＝n，∵m＞0，∴am＝﹣1．②如图2中，由题意AB⊥y轴，∵P（0，am2+n），当y＝am2+n时，am2+n＝6ax2+n，解得x＝±m，∴B（﹣m，am2+n），∴PB＝m，∵AP＝2m，∴＝＝2．（3）如图3中，过点A作AH⊥x轴于H，过点P作PK⊥AH于K，过点B作BE⊥KP 交KP的延长线于E．设B（b，6ab2+n），∵PA＝2PB，∴点A的横坐标为﹣2b，∴A[﹣2b，a（﹣2b﹣m）2+n]，∵BE∥AK，∴＝＝，∴AK＝2BE，∴a（﹣2b﹣m）2+n﹣am2﹣n＝2（am2+n﹣6ab2﹣n），整理得：m2﹣2bm﹣8b2＝0，∴（m﹣4b）（m+2b）＝0，∵m﹣4b＞0，∴m+2b＝0，∴m＝﹣2b，∴A（m，n），∴点A是抛物线C1的顶点．10．（2020•南京）小明和小丽先后从A地出发沿同一直道去B地．设小丽出发第xmin时，小丽、小明离B地的距离分别为y1m、y2m．y1与x之间的函数表达式是y1＝﹣180x+2250，y与x之间的函数表达式是y2＝﹣10x2﹣100x+2000．2（1）小丽出发时，小明离A地的距离为250 m．（2）小丽出发至小明到达B地这段时间内，两人何时相距最近？最近距离是多少？【解答】解：（1）∵y1＝﹣180x+2250，y2＝﹣10x2﹣100x+2000，∴当x＝0时，y1＝2250，y2＝2000，∴小丽出发时，小明离A地的距离为2250﹣2000＝250（m），故答案为：250；（2）设小丽出发第xmin时，两人相距sm，则s＝（﹣180x+2250）﹣（﹣10x2﹣100x+2000）＝10x2﹣80x+250＝10（x﹣4）2+90，∴当x＝4时，s取得最小值，此时s＝90，答：小丽出发第4min时，两人相距最近，最近距离是90m．11．（2020•连云港）在平面直角坐标系xOy中，把与x轴交点相同的二次函数图象称为“共根抛物线”．如图，抛物线L1：y＝x2﹣x﹣2的顶点为D，交x轴于点A、B（点A 在点B左侧），交y轴于点C．抛物线L2与L1是“共根抛物线”，其顶点为P．（1）若抛物线L2经过点（2，﹣12），求L2对应的函数表达式；（2）当BP﹣CP的值最大时，求点P的坐标；（3）设点Q是抛物线L1上的一个动点，且位于其对称轴的右侧．若△DPQ与△ABC相似，求其“共根抛物线”L2的顶点P的坐标．【解答】解：（1）当y＝0时，x2﹣x﹣2＝0，解得x＝﹣1或4，∴A（﹣1，0），B（4，0），C（0，﹣2），由题意设抛物线L2的解析式为y＝a（x+1）（x﹣4），把（2，﹣12）代入y＝a（x+1）（x﹣4），﹣12＝﹣6a，解得a＝2，∴抛物线的解析式为y＝2（x+1）（x﹣4）＝2x2﹣6x﹣8．（2）∵抛物线L2与L1是“共根抛物线”，A（﹣1，0），B（4，0），∴抛物线L1，L2的对称轴是直线x＝，∴点P在直线x＝上，∴BP＝AP，如图1中，当A，C，P共线时，BP﹣PC的值最大，此时点P为直线AC与直线x＝的交点，∵直线AC的解析式为y＝﹣2x﹣2，∴P（，﹣5）（3）由题意，AB＝5，CB＝2，CA＝，∴AB2＝BC2+AC2，∴∠ACB＝90°，CB＝2CA，∵y＝x2﹣x﹣2＝（x﹣）2﹣，∴顶点D（，﹣），由题意，∠PDQ不可能是直角，第一种情形：当∠DPQ＝90°时，①如图3﹣1中，当△QDP∽△ABC时，＝＝，设Q（x，x2﹣x﹣2），则P（，x2﹣x﹣2），∴DP＝x2﹣x﹣2﹣（﹣）＝x2﹣x+，QP＝x﹣，∵PD＝2QP，∴2x﹣3＝x2﹣x+，解得x＝或（舍弃），∴P（，）．②如图3﹣2中，当△DQP∽△ABC时，同法可得PQ＝2PD，x﹣＝x2﹣3x+，解得x＝或（舍弃），∴P（，﹣）．第二种情形：当∠DQP＝90°．①如图3﹣3中，当△PDQ∽△ABC时，＝＝，过点Q作QM⊥PD于M．则△QDM∽△PDQ，∴＝＝，由图3﹣3可知，M（，），Q（，），∴MD＝8，MQ＝4，∴DQ＝4，由＝，可得PD＝10，∵D（，﹣）∴P（，）．②当△DPQ∽△ABC时，过点Q作QM⊥PD于M．同法可得M（，﹣），Q（，﹣），∴DM＝，QM＝1，QD＝，由＝，可得PD＝，∴P（，﹣）．综上所述：P点坐标为（，）或（，﹣）或（，）或（，﹣）．12．（2020•苏州）如图，二次函数y＝x2+bx的图象与x轴正半轴交于点A，平行于x轴的直线l与该抛物线交于B、C两点（点B位于点C左侧），与抛物线对称轴交于点D（2，﹣3）．（1）求b的值；（2）设P、Q是x轴上的点（点P位于点Q左侧），四边形PBCQ为平行四边形．过点P、Q分别作x轴的垂线，与抛物线交于点P'（x，y1）、Q'（x2，y2）．若|y1﹣y2|＝2，1求x1、x2的值．【解答】解：（1）直线与抛物线的对称轴交于点D（2，﹣3），故抛物线的对称轴为x＝2，即﹣b＝2，解得：b＝﹣4，故抛物线的表达式为：y＝x2﹣4x；（2）把y＝﹣3代入y＝x2﹣4x并解得x＝1或3，故点B、C的坐标分别为（1，﹣3）、（3，﹣3），则BC＝2，∵四边形PBCQ为平行四边形，∴PQ＝BC＝2，故x2﹣x1＝2，又∵y1＝x12﹣4x1，y2＝x22﹣4x2，|y1﹣y2|＝2，故|（x12﹣4x1）﹣（x22﹣4x2）|＝2，|x1+x2﹣4|＝1．∴x1+x2＝5或x1+x2＝3，由，解得；由，解得．13．（2020•无锡）有一块矩形地块ABCD，AB＝20米，BC＝30米．为美观，拟种植不同的花卉，如图所示，将矩形ABCD分割成四个等腰梯形及一个矩形，其中梯形的高相等，均为x米．现决定在等腰梯形AEHD和BCGF中种植甲种花卉；在等腰梯形ABFE和CDHG中种植乙种花卉；在矩形EFGH中种植丙种花卉．甲、乙、丙三种花卉的种植成本分别为20元/米2、60元/米2、40元/米2，设三种花卉的种植总成本为y元．（1）当x＝5时，求种植总成本y；（2）求种植总成本y与x的函数表达式，并写出自变量x的取值范围；（3）若甲、乙两种花卉的种植面积之差不超过120平方米，求三种花卉的最低种植总成本．【解答】解：（1）当x＝5时，EF＝20﹣2x＝10，EH＝30﹣2x＝20，y＝2×（EH+AD）×20x+2×（GH+CD）×x×60+EF•EH×40＝（20+30）×5×20+（10+20）×5×60+20×10×40＝22000；（2）EF＝（20﹣2x）米，EH＝（30﹣2x）米，参考（1），由题意得：y＝（30+30﹣2x）•x•20+（20+20﹣2x）•x•60+（30﹣2x）（20﹣2x）•40＝﹣400x+24000（0＜x＜10）；（3）S甲＝2×（EH+AD）×x＝（30﹣2x+30）x＝﹣2x2+60x，同理S乙＝﹣2x2+40x，∵甲、乙两种花卉的种植面积之差不超过120米2，∴﹣2x2+60x﹣（﹣2x2+40x）≤120，解得：x≤6，故0＜x≤6，而y＝﹣400x+24000随x的增大而减小，故当x＝6时，y的最小值为21600，即三种花卉的最低种植总成本为21600元．14．（2020•重庆）如图，在平面直角坐标系中，抛物线y＝ax2+bx+2（a≠0）与y轴交于点C ，与x轴交于A，B两点（点A在点B的左侧），且A点坐标为（﹣，0），直线BC的解析式为y＝﹣x+2．（1）求抛物线的解析式；（2）过点A作AD∥BC，交抛物线于点D，点E为直线BC上方抛物线上一动点，连接CE，EB，BD，DC．求四边形BECD面积的最大值及相应点E的坐标；（3）将抛物线y＝ax2+bx+2（a≠0）向左平移个单位，已知点M为抛物线y＝ax2+bx+2（a≠0）的对称轴上一动点，点N为平移后的抛物线上一动点．在（2）中，当四边形BECD的面积最大时，是否存在以A，E，M，N为顶点的四边形为平行四边形？若存在，直接写出点N的坐标；若不存在，请说明理由．【解答】解：（1）直线BC的解析式为y＝﹣x+2，令y＝0，则x＝3，令x＝0，则y＝2，故点B、C的坐标分别为（3，0）、（0，2）；则y＝ax2+bx+2＝a（x+）（x﹣3）＝a（x2﹣2x﹣6）＝ax2﹣2a﹣6a，即﹣6a＝2，解得：a＝﹣，故抛物线的表达式为：y＝﹣x2+x+2①；（2）如图，过点B、E分别作y轴的平行线分别交CD于点H，交BC于点F，∵AD∥BC，则设直线AD的表达式为：y＝﹣（x+）②，联立①②并解得：x＝4，故点D（4，﹣），由点C、D的坐标得，直线CD的表达式为：y＝﹣x+2，当x＝3时，y CD＝﹣x+2＝﹣2，即点H（3，﹣2），设点E（x，﹣x2+x+2），则点F（x，﹣x+2），则四边形BECD的面积S＝S△BCE+S△BCD＝×EF×OB+×（x D﹣x C）×BH＝×（﹣x2+x+2+x﹣2）×3+×4×2＝﹣x2+3x+4，∵＜0，故S有最大值，当x＝时，S的最大值为，此时点E（，）；（3）存在，理由：y ＝﹣x2+x+2＝﹣（x）2+，抛物线y＝ax2+bx+2（a≠0）向左平移个单位，则新抛物线的表达式为：y＝﹣x2+，点A、E的坐标分别为（﹣，0）、（，）；设点M（，m），点N（n，s），s＝﹣n2+；①当AE是平行四边形的边时，点A向右平移个单位向上平移个单位得到E，同样点M（N）向右平移个单位向上平移个单位得到N（M），即±＝n，则s＝﹣n2+＝﹣或，故点N的坐标为（，﹣）或（﹣，）；②当AE是平行四边形的对角线时，由中点公式得：﹣+＝n+，解得：n＝﹣，s＝﹣n2+＝＝，故点N的坐标（﹣，）；综上点N的坐标为：（，﹣）或（﹣，）或（﹣，）．15．（2020•无锡）在平面直角坐标系中，O为坐标原点，直线OA交二次函数y＝x2的图象于点A，∠AOB＝90°，点B在该二次函数的图象上，设过点（0，m）（其中m＞0）且平行于x轴的直线交直线OA于点M，交直线OB于点N，以线段OM、ON为邻边作矩形OMPN．（1）若点A的横坐标为8．①用含m的代数式表示M的坐标；②点P能否落在该二次函数的图象上？若能，求出m的值；若不能，请说明理由．（2）当m＝2时，若点P恰好落在该二次函数的图象上，请直接写出此时满足条件的所有直线OA的函数表达式．【解答】解：（1）①∵点A在y＝x2的图象上，横坐标为8，∴A（8，16），∴直线OA的解析式为y＝2x，∵点M的纵坐标为m，∴M（m，m）．②假设能在抛物线上，连接OP．∵∠AOB＝90°，∴直线OB的解析式为y＝﹣x，∵点N在直线OB上，纵坐标为m，∴N（﹣2m，m），∴MN的中点的坐标为（﹣m，m），∴P（﹣m，2m），把点P坐标代入抛物线的解析式得到m＝．（2）①当点A在y轴的右侧时，设A（a，a2），∴直线OA的解析式为y＝ax，∴M（，2），∵OB⊥OA，∴直线OB的解析式为y＝﹣x，可得N（﹣，2），∴P（﹣，4），代入抛物线的解析式得到，﹣＝±4，解得，a＝4±4，∴直线OA的解析式为y＝（±1）x．②当点A在y轴的左侧时，即为①中点B的位置，∴直线OA的解析式为y＝﹣x＝﹣（±1）x，综上所述，满足条件的直线OA的解析式为y＝（±1）x或y＝﹣（±1）x．。

2021年中考数学复习《探索二次函数综合型压轴题解题技巧》分类训练二：与角的度量有关的压轴题(附答案

2021中考数学复习《探索二次函数综合型压轴题解题技巧》分类训练二:与角的度量关系相关的压轴题(附答案)方法提炼:1.将角的度量关系转化为边的数量,利用边的数量关系求解问题的答案｡2.利用角的度量关系,寻找问题中的特殊角,结合三角函数求解｡3.利用角的度量关系,构建图形的全等､相似,利用图形的全等､相似的性质求解典例引领:例:如图,抛物线y=ax2+3x+c(a<0)与x轴交于点A和点B(点A在原点的左侧,点B在原点的右侧),与y轴交于点C,OB=OC=4.(1)求该抛物线的函数解析式.(2)如图1,连接BC,点D是直线BC上方抛物线上的点,连接OD,CD.OD交BC于点F,当S:S△CDF=4:3时,求点D的坐标.△COF(3)如图2,点E的坐标为(0,﹣2),点P是抛物线上的点,连接EB,PB,PE形成的△PBE中,是否存在点P,使∠PBE或∠PEB等于2∠OBE?若存在,请直接写出符合条件的点P的坐标;若不存在,请说明理由.14.解:(1)∵OB=OC=4,∴B(4,0),C(0,4),把B(4,0),C(0,4)代入y=ax2+3x+c,得,解得∴抛物线的函数解析式为y=﹣x2+3x+4;(2)如图1,设直线BC解析式为y=kx+b,则,解得∴直线BC解析式为y=﹣x+4,令点D､F的横坐标分别为x D,x F,∵S△COF:S△CDF=4:3,∴S△COF=S△COD,即OC•x F=×OC•x D,∴x D=x F,设点D横坐标为7t,点F横坐标为4t,∵点F在直线BC上,∴F(4t,4﹣4t),设直线OF解析式为y=k′x,则4﹣4t=4tk′,∴k′==,∴直线OF解析式为y=x,∵点D在直线OF上,∴D(7t,7﹣7t),将D(7t,7﹣7t)代入y=﹣x2+3x+4中,得7﹣7t=﹣(7t)2+3×7t+4,解得:t1=,t2=,∴D的坐标为(1,6)或(3,4);(3)①当∠PEB=2∠OBE,且点P在x轴上方时,如图2,作BE的垂直平分线交OB于F,连接EF,在∠BEO内部作射线EP交x轴于G,交抛物线于P,使∠PEB=∠EFO,过点G作GH⊥BE于H,则BF=EF,设BF=EF=m,∴OF=OB﹣BF=4﹣m在Rt△OEF中,∠EOF=90°,∵OE2+OF2=EF2∴22+(4﹣m)2=m2,解得:m=,∴BF=EF=,OF=4﹣=,∴tan∠OBE===,tan∠OFE===,∵BF=EF∴∠BEF=∠OBE∵∠OFE=∠BEF+∠OBE∴∠OFE=2∠OBE∵∠PEB=2∠OBE∴∠PEB=∠OFE∴tan∠PEB==tan∠OFE=,设GH=4a,则EH=3a,∴BE===2,BH=2﹣3a∵=tan∠∠OBE=,∴=,解得:a=,∴GH=,BH=∴BG==∴OG=OB﹣BG=4﹣=∴G(,0),设直线EG解析式为y=k″x+b″,则,解得∴直线EG解析式为y=x﹣2,联立方程组,解得:(舍去),,∴P(,),②当∠PEB=2∠OBE,且点P在x轴下方时,如图3,过点E作EF⊥y轴,作点B关于直线EF 的对称点G,连接BG交EF于F,射线EG交抛物线于点P,∵E(0,﹣2),∴直线EF为:y=﹣2∵B(4,0),∴G(4,﹣4)∴直线EG解析式为y=﹣x﹣2,解方程组,得,(不符合题意,舍去),∴P(,);③当∠PBE=2∠OBE,且点P在x轴上方时,如图4,在y轴正半轴上截取OF=OE=2,作射线BF交抛物线于P,在△BOE和△BOF中,∴△BOE≌△BOF(SAS)∴∠PBO=∠OBE∴∠PBE=2∠OBE易求得直线PF解析式为y=﹣x+2,联立方程组,解得(不符合题意,舍去),,∴P(﹣,);④当∠PBE=2∠OBE,且点P在x轴下方时,如图5,过点E作EF⊥BE交直线BP于F,过F 作FG⊥y轴于G,由①知:tan∠PBE==,BE=2∴EF=∵∠EGF=∠BOE=∠BEF=90°∴∠BEO+∠FEG=∠BEO+OBE=90°∴∠FEG=∠OBE∴△EFG∽△BEO∴==,即==∴FG=,EG=∴OG=OE+EG=2+=∴F(,﹣)易求得直线BF解析式为y=x﹣22,联立方程组,解得(舍去),∴∴P(﹣,﹣);综上所述,符合条件的点P的坐标为:(,)､(,)､(﹣,)､(﹣,﹣).跟踪训练:1.如图,抛物线y=ax2+bx过A(4,0),B(1,3)两点.(1)求该抛物线的解析式;(2)点P是抛物线上一点,且位于第一象限,当△ABP的面积为3时,求出点P的坐标;(3)过B作BC⊥OA于C,连接OB,点G是抛物线上一点,当∠BAG+∠OBC=∠BAO时,请直接写出此时点G的坐标.2.如图,抛物线y=ax2+bx+与x轴交于点A(﹣5,0),B(1,0),顶点为D,与y轴交于点C.(1)求抛物线的表达式及D点坐标;(2)在直线AC上方的抛物线上是否存在点E,使得∠ECA=2∠CAB,如果存在这样的点E,求出△ACE面积,如果不存在,请说明理由.3.如图1,抛物线y=﹣+bx+c经过原点(0,0),A(12,0)两点.(1)求b的值;(2)如图2,点P是第一象限内抛物线y=﹣+bx+c上一点,连接PO,若tan∠POA=,求点P的坐标;(3)如图3,在(2)的条件下,过点P的直线y=﹣x+m与x轴交于点F,作CF=OF,连接OC交抛物线于点Q,点B在线段OF上,连接CP､CB､PB,PB交CF于点E,若∠PBA=2∠PCB,∠BEF=2∠BCF,求点Q的坐标.4.如图,抛物线y=﹣+bx+c交x轴于点A､B(A在B左侧),交y轴于点C,直线y=﹣x+6经过点B､C.(1)求抛物线解析式;(2)点P为第一象限抛物线上一点,连接P A交BC于点D,设点P的横坐标为t,的值为d,求d与t的函数关系式(不要求写出自变量t的取值范围);(3)在(2)的条件下,点E为线段OB上一点,连接CE,过点O作CE的垂线交BC于点G,连接PG并延长交OB于点F,若∠OGC=∠BGF,F为BE中点,求t的值.5.抛物线y=ax2+c经过点(0,﹣1),交x轴于A(﹣1,0),B两点,点P是第一象限内抛物线上一动点.(1)直接写出抛物线的解析式;(2)如图1已知直线l的解析式为y=x﹣2,过点P作直线l的垂线,垂足为H,当PH=时,求点P的坐标;(3)如图2,当∠APB=45°时,求点P的坐标.6.已知抛物线y=x2﹣mx﹣m﹣1与x轴交于A､B两点,点A在点B的左边,与y轴交于点C(0,﹣3).(1)求点A､B的坐标;(2)点D是抛物线上一点,且∠ACO+∠BCD=45°,求点D的坐标;(3)将抛物线向上平移m个单位,交线段BC于点M,N,若∠MON=45°,求m的值.7.如图,在平面直角坐标系xOy中,已知点A(﹣1,0),D(﹣3,0),C(﹣4,3),四边形ABCD是平行四边形.现将▱ABCD沿x轴方向平移n个单位,得到▱A1B1C1D1,抛物线M经过点A1,C1,D1.(1)若抛物线M的对称轴为直线x=4,求抛物线M的解析式;(2)抛物线M的顶点为E,若以A,E,C1为顶点的三角形的面积等于▱ABCD的面积的一半,求n的值;(3)在(2)的条件下,在y轴上是否存在点P,使得∠C1P A=∠C1EA?若存在,请直接写出点P的坐标;若不存在,请说明理由.8.如图,在平面直角坐标系中抛物线y=ax2+bx+c交x轴于点A､B,交y轴于点C,A､B两点横坐标为﹣1和3,C点纵坐标为﹣4.(1)求抛物线的解析式;(2)动点D在第四象限且在抛物线上,当△BCD面积最大时,求D点坐标,并求△BCD面积的最大值;(3)抛物线的对称轴上是否存在一点Q,使得∠QBC=45°,如果存在,求出点Q的坐标,不存在说明理由.9.抛物线y=﹣x2+bx+c与x轴相交于A､B两点(点A在点B的左侧),与y轴交于点C.直线y=﹣2x+6经过B､C两点,连接AC.(1)求抛物线的解析式:(2)点P是第一象限抛物线上一点,P点横坐标为t,连接PC､PB,设△PBC的面积为S,求S与t之间的函数关系式(直接写出自变量t的取值范围):(3)在(2)问的条件下,当S=3且t<2时,连接PB,在抛物线上是否存在一点Q,使∠PBQ=∠ACB?若存在求出Q点坐标,若不存在,说明理由.10.如图,在平面直角坐标系中,抛物线与x轴交于A､B两点,与y轴交于C点,B点与C点是直线y=x﹣3与x轴､y轴的交点.D为线段AB上一点.(1)求抛物线的解析式及A点坐标.(2)若点D在线段OB上,过D点作x轴的垂线与抛物线交于点E,求出点E到直线BC的距离的最大值.(3)D为线段AB上一点,连接CD,作点B关于CD的对称点B′,连接AB′､B′D①当点B′落坐标轴上时,求点D的坐标.②在点D的运动过程中,△AB′D的内角能否等于45°,若能,求此时点B′的坐标;若不能,请说明理由.11.如图,在平面直角坐标系中,抛物线y=ax2+x+c交x轴于点A､点B,交y轴于点C.直线y=﹣x+2经过于点C､点B,(1)求抛物线的解析式;(2)点D为第一象限抛物线上一动点,过点D作y轴的平行线交线段BC于点E,交x轴于点Q,当DE=5EQ时,求点D的坐标;(3)在(2)的条件下,点M为第二象限抛物线上一动点,连接DM,DM交线段OC于点H,点F在线段OB上,连接HF､DF､DC､DB,当HF=,∠CDB=2∠MDF时,求点M的坐标.12.已知抛物线y=ax2+bx﹣3与x轴交于点A(﹣1,0)､B两点,与y轴交于点C,且过点P(5,12).(1)求抛物线的解析式.(2)如图,点Q为线段CP上一动点,过点Q作QF⊥x轴于点F,交抛物线于点D,连接CD,PD,若S△QDC:S△QDP=2:3,求直线PD的解析式.(3)过点B的直线交抛物线于M,是否存在点M使∠ABM=∠PCO,若存在,求出点M的坐标.若不存在,说明理由.13.如图1,抛物线C1:y=x2+(m﹣2)x﹣2m(m>0)与x轴交于点A､B(A在B的左侧),与y轴交于点C,连接AC､BC,S△ABC=3.(1)求m的值;(2)如图2,将射线BC绕点B顺时针方向旋转交抛物线C1第二象限的图象于点D,连接DC.当x轴恰好三等分△DBC的面积时,求此时点D的横坐标;(3)将抛物线C1向右平移,使新抛物线C2经过原点,如图3,C2的对称轴l交抛物线C2于E,交直线y=4于F,直线y=4交C2于点G､H(G在H的左侧),点M､N分别从点G､H同时出发,以1个单位长度/秒向点F运动.设点M运动时间为t(秒),点M､N到达F时,运动停止,点W在l上,WF=,连MW､NE.当∠MWF=3∠FEN时,求t的值.参考答案1.解:(1)将点A､B的坐标代入抛物线表达式并解得:a=﹣1,b=4,故抛物线的表达式为:y=﹣x2+4x…①;(2)过点P作直线m交x轴于点M,过点P作PH⊥AB于点H,过点A作AN⊥直线m,在AB下方作直线n距离直线AB的长度为PH,△ABP的面积S=AB×PH=×3×PH=3,解得:PH==AN,直线AB的倾斜角为45°,故直线m､n所在直线的k值为:﹣1,则AM=AH=2,故点M(6,0),则直线m的表达式为:y=﹣x+6…②,同理直线n的表达式为:y=﹣x+2…③,联立②①并解得:x=2或3,联立③①并解得:x=(舍去);综上,点P的坐标为:(3,3)或(2,4)或(,);(3)∵BC=AC=3,故∠BAO=45°=∠BAG+∠OBC,①当点G在AB上方时,如图2(左侧图),设抛物线对称轴交x轴于点M,连接BM,OC=OM=1,故∠CBM=∠OBC,则∠CAB=45°=∠CBM+∠MBA=∠OBC+∠ABM,而45°=∠BAG+∠OBC,故∠ABM=∠GAB,则AG∥BM,直线BM表达式中的k值为:3,故直线AG的表达式为:y=﹣3x+b,将点A的坐标代入上式并解得:直线AG的表达式为:y=﹣3x+12…④;联立①④并解得:x=3或4(舍去4);②当点G在AB下方时,如图2(右侧图),∠BAG+∠OBC=∠BAO=45°,而∠BAG+∠GAC=45°,∴∠OBC=∠GAC,而tan∠OBC===tan∠GAC,则直线AG的表达式为:y=﹣x+b′,将点A坐标代入上式并解得:直线AG的表达式为:y=﹣x2+…⑤,联立⑤①并解得:x=或4(舍去4).综上,点P的坐标为:(3,3)或(,).2.解:(1)∵抛物线y=ax2+bx+与x轴交于点A(﹣5,0),B(1,0),∴,∴∴抛物线的表达式为:y=﹣x2﹣2x+,∴顶点D(﹣2,)(2)如图,过点C作CM∥AB,过点E作EF⊥CM,设点E(m,﹣m2﹣2m+)∵y=﹣x2﹣2x+交y轴交于点C,∴点C(0,),∴OC=,∵CM∥AB,∴∠MCA=∠CAB,∵∠ECA=2∠CAB=∠ECF+∠MCA,∴∠ECF=∠CAB,且∠AOC=∠EFC=90°,∴△CEF∽△ACO,∴,∴=∴m=0(不合题意),m=﹣3,∴点E(﹣3,4),∴S△AEC=×(+4)×3+×4×2﹣×5×=.3.解:(1)∵抛物线y=﹣+bx+c经过原点(0,0),A(12,0)两点.∴c=0,0=﹣×144+12b+c∴b=;(2)如图2,过点P作PE⊥OA于点E,∵c=0,b=,∴抛物线解析式为:y=﹣+x∵点P是第一象限内抛物线y=﹣+x上一点,∴设点P(m,﹣m2+m),(m>0)∵tan∠POA==,∴=,∴m=8,∴点P(8,4);(3)连接OP,∵直线y=﹣x+m过点P(8,4),∴m=,∴直线解析式为y=﹣x+,当y=0,x=,∴点F(,0),∵∠BEF=∠BCF+∠PBC,且∠BEF=2∠BCF,∴∠PBC=∠BCF,∵∠PBA=2∠PCB,∠BEF=2∠BCF,∴∠EFB=180°﹣2∠PCB﹣2∠PBC,∵OF=CF,∴∠COF=∠PCB+∠PBC=∠OCF,∵∠CPB=180°﹣∠BCP﹣∠PBC,∴∠CPB+∠COF=180°,∴点O,点B,点P,点C四点共圆,∴∠PBA=∠OCP,∠OCB=∠OPB,∠BCP=∠BOP,∵∠PBA=2∠PCB,∠PBA=∠OCP=∠OCB+∠BCP,∴∠OCB=∠BCP,∴∠BPO=∠POB,∴OB=PB,设点B(a,0)∴OB=BP=a,∴a=∴a=7∴点B(7,0)设过点O,点B,点P,点C四点的圆的圆心M(,y),∵MO=MP,∴()2+y2=(8﹣)2+(4﹣y)2,∴y=,∴M(,),设点C(a,n)∵MO=MC,OF=CF,∴(a﹣)2+(b﹣)2=()2+()2 ①,(a﹣)2+b2=()2 ②,∴由①②组成方程组可求b=a,设直线OC解析式为:y=kx,且过点C(a,b)∴b=ka,∴k=∴直线OC解析式为:y=x,∴x=﹣+x∴x1=0(不合题意舍去),x2=4,∴点Q(4,4)4.解:(1)直线y=﹣x+6经过点B､C,则点B､C的坐标分别为:(6,0)､(0,6),则c=6,将点A的坐标代入抛物线表达式并解得:b=2,故抛物线的表达式为:y=﹣x2+2x+6…①;(2)点P(t,﹣t2+2t+6),将点P､A的坐标代入一次函数表达式:y=kx+b并解得:直线AP的表达式为:y=﹣(t﹣6)x+(6﹣t),将上式与直线BC的表达式联立并解得:x=,故点D(,+6),则=,则d==﹣1=﹣t2+t(0<t<6);(3)设OE=a,则点E(a,0),设OG交CE于点H,∵∠ECO+∠COH=90°,∠COH+∠HOE=90°,∴∠HOE=∠OCH, tan∠OCH===tan∠HOE,则直线OH的表达式为:y=x…②,联立①②并解得:x=,故点G(,),则BG==,则CG=BC﹣BG=,∵OB=OC=6,故∠OCB=∠OBC=45°,而∠OGC=∠BGF,则△CGO∽△BGF,即:,即:,解得:BF=a,F为BE中点,则OE=EF=FB,故a=2,故点F(4,0),点G(,);将点F､G的坐标代入一次函数表达式并解得:直线FG的表达式为:y=3x﹣12…③,联立①③并解得:x=﹣1(舍去负值),故t=﹣1+.5.解:(1)∵抛物线y=ax2+c经过点(0,﹣1),A(﹣1,0),∴,∴,∴抛物线的解析式的解析式为y=x2﹣1;(2)过点P作y轴的平行线交直线l于点M,∵直线l的解析式为y=x﹣2,∴直线与y轴的夹角为45°,∴∠PMH=45°,∵PH⊥MH,PH=,∴PM=7,设P(a,a2﹣1),则M(a,a﹣2),∴PM=a2﹣1﹣a+2=7,∴a1=3,a2=﹣2(舍去),∴P(3,8);(3)如图2,在y轴上取点D(0,1),则△ABD为等腰直角三角形,∵AO=BO=1,∠ADB=90°,∴=,以点D为圆心､AD长为半径画圆,则点P在优弧AB上时总有∠APB=45°,连结PD,设P点坐标为(m,m2﹣1),∴PD==,∴m2+(m2﹣2)2=2,解得:,(舍去),m3=1(舍去),m4=﹣1(舍去),∴P(,1).6.解:(1)﹣m﹣1=﹣3,解得:m=2,故抛物线的表达式为:y=x2﹣2x﹣3…①,令y=0,解得:x=3或﹣1,故点A､B的坐标分别为:(﹣1,0)､(3,0);(2)①当点D在BC下方时,∵∠ACO+∠BCD=45°,则AC⊥CD,则直线CD的表达式为:y=x﹣3…②,联立①②并解得:x=0或,故点D(,﹣);②当点D(D′)在BC上方时,过点D作DE⊥BC交BC于点H,交CD′于点E,直线BC的表达式为:y=x﹣3…③则ED的表达式为:y=﹣x+…④,联立③④并解得:x=,故点H(,﹣),点E的坐标为:(,﹣),则直线CE的表达式为:y=3x﹣3…⑤,联立①⑤并解得:x=0或5(舍去0),故点D(D′)的坐标为:(5,12),综上,点D的坐标为:(,﹣)或(5,12);(3)如图2,抛物线平移后的图象为虚线部分,则抛物线的表达式为:y=x2﹣2x﹣3+m(m>0),设点M､N的坐标分别为:(x1,y1)､(x2､y2),则x1+x2=3,x1x2=m,x2=,∵∠MON=45°=∠OCM,∠ONM=∠ONM,∴△NOM∽△NCO,∴NO2=MN•CN,而NO2=(x22+y22),MN=(x2﹣x1),CN=x22,即(x22+y22)=2x2(x2﹣x1),即2x1x2=x22﹣y22,而y2=x2﹣3,故=+m,解得:m=(﹣1+)(不合题意的值已舍去).7.解:(1)四边形ABCD是平行四边形,则点B的坐标为:(﹣2,3),即点B在AD的中垂线上,过点A､D的二次函数表达式为:y=a(x+1)(x+3)=a(x2+4x+3),将点C的坐标代入上式并解得:a=1,则过A､C､D的抛物线为:y=x2+4x+3=(x+2)2﹣1,抛物线M的对称轴为直线x=4,相当于将上述抛物线向右平移了6个单位,故抛物线M的表达式为:y=(x﹣4)2﹣1;(2)将▱ABCD沿x轴方向平移n个单位,则点C1､E的坐标分别为:(n﹣4,3)､(n﹣2,﹣1),点A(﹣1,0),连接C1E交x轴于点M,将点C1､E的坐标代入一次函数表达式:y=kx+b并解得:直线C1､E的表达式为:y=﹣2x+(2n﹣5),则点M的坐标为:(,0),S△AEC1=×AM×(y C1﹣y E)=(+1)×4=S▱ABCD=×2×3=3,解得:n=3;(3)存在,理由:由(2)知点C(﹣1,3),点A(﹣1,0),则AC⊥x轴,故点A､C1､E作圆Q,则点Q在AC1的中垂线上,设点Q(m,),则此时,∠C1P A=∠C1EA,由QC1=QE得:(m+1)2+(3﹣)2=(m﹣1)2+(1+)2,解得:m=1,则点Q(1,),设点P(0,t),由QP=QE得:1+(﹣t)2=()2,解得:t=,故点P的坐标为:(0,).8.解:(1)抛物线的表达式为:y=a(x+1)(x﹣3)=a(x2﹣2x﹣3),故﹣3a=﹣4,解得:a=,故抛物线的表达式为:y=x2﹣x﹣4;(2)过点D作y轴的平行线交BC于点N,由B､C的坐标可得直线BC的表达式为:y=x﹣4,设点D(x,x2﹣x﹣4),点N(x,x﹣4),S△BCD=×OB×ND=3×(x﹣4﹣x2+x+4)=﹣2x2+6x,∵﹣2<0,故S有最大值,此时,x=,点D(,﹣5);(3)存在,理由:直线BC的表达式为:y=x﹣4,抛物线的对称轴为:x=1,故点H(1,﹣),过点Q作QM⊥BC于点M,tan∠OCB==tanα,∠QBC=45°,设QM=3x,则HM=4x,MB=3x,BH=HM+MB=7x==,解得:x=,QH=5x=,则y Q=y H+=﹣,故点Q(1,).9.解:(1)直线y=﹣2x+6经过B､C两点,则点B､C的坐标为:(3,0),(0,6),将点B､C的坐标代入抛物线表达式并解得:b=1,c=6,故抛物线的表达式为:y=﹣x2+x+6…①;(2)过点P作y轴的平行线交BC于点H,设点P(t,﹣t2+t+6),则点H(t,﹣2t+6),S=×PH×OB=(﹣t2+t+6+2t﹣6)=﹣t2+t(0<t<3);(3)S=3,即:﹣t2+t=3,解得:t=1或2(舍去2),故点P(1,6),而点B(0,3),则直线PB的表达式为:y=﹣x+9,则点M(0,9),tan∠BMO=,过点A作AL⊥BC于点L,S△ABC=OC×AB=×BC×AL,即3×5=×AL×3,解得:AL=,sin∠ACB==,则∠ACB=45°=∠MBQ,设BQ交y轴于点H,过点H作HN⊥MB于点N,tan∠BMO=,∠MBQ=45°,设:HN=x,则BN=x,MN=3x,MB=4x=,解得:x=,HB=x=,则OH2=BH2﹣OB2=,则点H(0,),则BH的函数表达式为:y=﹣x+…②,联立①②并解得:x=﹣(不合题意值已舍去),则点Q(﹣,).10.解:(1)∵B点与C点是直线y=x﹣3与x轴､y轴的交点.∴B(3,0),C(0,﹣3),∴,解得:,∴抛物线的解析式为,令y=0,,解得x1=﹣2,x2=3,∴A(﹣2,0),(2)设E点到直线BC的距离为d,E点横坐标为m,F(m,m﹣3),∵B(3,0),C(0,﹣3),∴∠OBC=45°,如图1,过点E作EH⊥BC于点H,则△EFH为等腰直角三角形,∴EH=,EF=y F﹣y E=m﹣3﹣(,=(0≤m≤3),=,当时,EF的最大值为,∴d=EF==.即E到BC的最大距离为.(3)①点B′在以C为圆心,CB为半径的圆C上;(Ⅰ)当B′点落在x轴上时,D1(0,0);(Ⅱ)当B′点落在y轴上时,如图2,CB′=CB=3,∵∠OB′D=45°∴OD=OB'=3﹣3,∴;②分别画出图形进行讨论求解:(Ⅰ)∠B′DA=45°时,如图2,OB′=3﹣3,B′(0,3﹣3)(Ⅱ)如图3,连接CB′,∠B′DA=∠CBD=45°,∴DB′∥BC,可得四边形DB′CB是菱形,B′(﹣3,﹣3).(Ⅲ)∠B′AD=45°,如图4,连接CB′,过点B′分别作坐标轴的垂线,垂足为E､F,设线段FB'的长为m,B′E=AE=2﹣m,可得CF=5﹣m,在直角三角形CFB'中,m2+(5﹣m)2=(3)2,解得m=,故B′(),(Ⅳ)如图5,∠AB′D=45°,连接CB',过点B′作y轴的垂线,垂足为点F,由轴对称性质可得,∠CB′D=∠CBD=45°,所以当∠AB′D=45°时,点A在线段CB′上,∴,设线段FB′的长为2m,FC=3m,(2m)2+(3m)2=(3,解得:m=,B′(﹣,综合以上可得B′坐标为(0,)或或()或(﹣).11.解:(1)针对于直线y=﹣x+2,令x=0,则y=2,∴C(0,2),令y=0,则0=﹣x+2,∴x=4,∴B(4,0),将点B,C坐标代入抛物线y=ax2+x+c中,得∴,∴抛物线的解析式为y=﹣x2+x+2;(2)如图1,由(1)知,抛物线的解析式为y=﹣x2+x+2,设点D坐标为(m,﹣m2+m+2),∵DE⊥x轴交BC于E,直线BC的解析式为y=﹣x+2,∴D(m,﹣m+2),∴DE=﹣m2+m+2﹣(﹣m+2)=﹣m2+m,DQ=﹣m+2,∵DE=5EQ,∴﹣m2+m=5(﹣m+2),∴m=3或m=4(点B的横坐标,舍去),∴D(3,3);(3)如图2,由(2)知,D(3,3),由(1)知,B(4,0),C(0,2),∴DB=,DC=,BC=2,∴DC=DB,DB2+DC2=BC2,∴△BDC是等腰直角三角形,∴∠BDC=90°,∵BDC=2∠FDM=90°,∴∠FDM=45°,过点D作DP⊥y轴于P,则DQ=DP,OP=3,∴CP=1=BQ,∴△DPC≌△DQB(SAS),在CP的延长线取一点G,使PG=QF=n,∴OF=3﹣n,OG=3+n,∴△DPG≌△DQF(SAS),∴DG=DF,∠PDG=∠QDF,∴∠FDG=∠PDG+∠PDF=∠QDF+∠PDG=∠PDQ=90°∴∠GDM=90°﹣∠FDM=45°=∠GDM,∵DH=DH,∴△GDH≌△FDH(SAS),∴GH=FH=,∴OH=OG﹣GH=3+n﹣=n+,在Rt△HOF中,根据勾股定理得,(n+)2+(3﹣n)2=,∴n=1或n=(此时,OH=n+=2,所以点H与点C重合,舍去),∴H(0,),∵C(3,3),∴直线CH的解析式为y=x+①,∵抛物线的解析式为y=﹣x2+x+2②,联立①②解得,或(由于点M在第二象限,所以舍去),∴M(﹣,).12.解:(1)∵抛物线y=ax2+bx﹣3过点A(﹣1,0)､P(5,12)两点,∴,解得:,∴抛物线的解析式为y=x2﹣2x﹣3;(2)如图1,过点P作PN⊥y轴,QM⊥y轴,∵S△QDC:S△QDP=2:3,∴,∴,∵PN⊥y轴,QM⊥y轴,∴QM∥PN,∴△CQM∽△CPN,∴,∵PN=5,∴QM=2,∵QF⊥x轴于点F,交抛物线于点D,∴D点的横坐标为2,把x=2代入y=x2﹣2x﹣3=4﹣4﹣3=﹣3,∴D(2,﹣3),设直线PD的解析式为y=kx+b,∴,解得:,∴直线PD的解析式为y=5x﹣13; (3)如图2,过点P作PN⊥y轴,∵P(5,12),C(0,﹣3),∴CN=OC+ON=12+3=15,PN=5,∴,∵∠ABM=∠PCO,∴,如图2,若点M在x轴上方,∵OB=3,∴在y轴上取E(0,1),tan∠OBE=,设直线BE的解析式为y=mx+n,∴,解得:m=﹣,∴直线BE的解析式为y=﹣,∴,解得:x1=3,,∴M(﹣),如图3,当点M在x轴下方,同理取点D(0,﹣1),求得直线BD的解析式为y=x﹣1,∴,解得:,∴M(﹣,﹣),综合以上可得M点的坐标为(﹣或(﹣).13.解:(1)在y=x2+(m﹣2)x﹣2m(m>0)中,令x=0,得y=﹣2m,∴C(0,﹣2m),令y=0,得x2+(m﹣2)x﹣2m=0,解得:x1=2,x2=﹣m,∴A(﹣m,0),B(2,0),∴AB=2﹣(﹣m)=m+2,OC=2m∵S△ABC=3∴(m+2)•2m=3,解得:m1=1,m2=﹣3(不符合题意)∴m=1;∴抛物线C1:y=x2﹣x﹣2(2)如图2,设D(t,t2﹣t﹣2),CD交x轴于K,作DT⊥x轴于T,由(1)得:B(2,0),C(0,﹣2)∵当x轴恰好三等分△DBC的面积时,有S△BDK=S△BCD或S△BDK=S△BCD ∴=或=,①当=时,=∴DT=OC∴t2﹣t﹣2=×2,解得:t1=,t2=,∵点D在第二象限,∴t<0∴t=,②当=时,=2∴DT=2OC∴t2﹣t﹣2=2×2,解得:t1=3,t2=﹣2,∵t<0∴t=﹣2综上所述,当x轴恰好三等分△DBC的面积时,点D的横坐标为或﹣2;(3)如图3,取WE中点T,过点T作TR⊥EF交EN于点R,连接WR,WN,由题意知:抛物线C1:y=x2﹣x﹣2=﹣,将抛物线C1向右平移,使新抛物线C2经过原点,∴新抛物线C2解析式为y=(x﹣)2﹣=x2﹣3x,对称轴为:直线x=,顶点E(,﹣),∴F(,4),EF=在y=x2﹣3x中,令y=4,则4=x2﹣3x,解得:x1=﹣1,x2=4∴G(﹣1,4),H(4,4)∴GH=5∵GM=NH=t,WF=,∴MF=NF=﹣t,WE=﹣=5,WT=TE=WE=,∵∠EFM=∠EFN=90°,WF=NF∴△MWF≌△NWF(SAS)∴∠MWF=∠NWF∵∠MWF=3∠FEN∴∠NWF=3∠FEN∵∠NWF=∠FEN+∠ENW∴∠ENW=2∠FEN∵WT=ET,TR⊥EF∴RW=RE∴∠FEN=∠EWR∴∠NRW=2∠FEN∴∠ENW=∠NRW∴RW=WN∴RE=WN由勾股定理得:EN2=EF2+NF2=+,WN2=WF2+NF2=+,∵△ERT∽△ENF∴=,即ER=EN∴ER2=EN2=[+],∴[+]=+,解得:t1=(不符合题意,舍去),t2=,故t=(秒).。

二次函数中考精品压轴题(四边形的存在性问题)解析精选

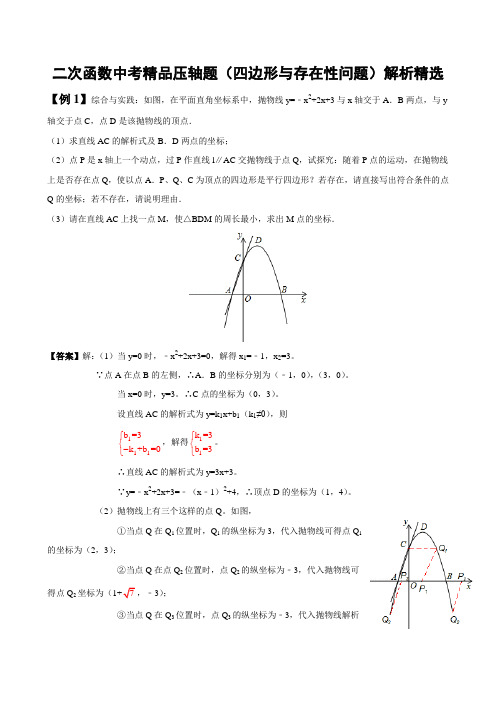
二次函数中考精品压轴题（四边形与存在性问题）解析精选【例1】综合与实践：如图，在平面直角坐标系中，抛物线y=﹣x 2+2x+3与x 轴交于A ．B 两点，与y 轴交于点C ，点D 是该抛物线的顶点．（1）求直线AC 的解析式及B ．D 两点的坐标；（2）点P 是x 轴上一个动点，过P 作直线l ∥AC 交抛物线于点Q ，试探究：随着P 点的运动，在抛物线上是否存在点Q ，使以点A ．P 、Q 、C 为顶点的四边形是平行四边形？若存在，请直接写出符合条件的点Q 的坐标；若不存在，请说明理由．（3）请在直线AC 上找一点M ，使△BDM 的周长最小，求出M 点的坐标．【答案】解：（1）当y=0时，﹣x 2+2x+3=0，解得x 1=﹣1，x 2=3。

∵点A 在点B 的左侧，∴A ．B 的坐标分别为（﹣1，0），（3，0）。

当x=0时，y=3。

∴C 点的坐标为（0，3）。

设直线AC 的解析式为y=k 1x+b 1（k 1≠0），则111b =3k +b =0⎧⎨-⎩，解得11k =3b =3⎧⎨⎩。

∴直线AC 的解析式为y=3x+3。

∵y=﹣x 2+2x+3=﹣（x ﹣1）2+4，∴顶点D 的坐标为（1，4）。

（2）抛物线上有三个这样的点Q 。

如图，①当点Q 在Q 1位置时，Q 1的纵坐标为3，代入抛物线可得点Q 1的坐标为（2，3）；②当点Q 在点Q 2位置时，点Q 2的纵坐标为﹣3，代入抛物线可得点Q 2坐标为（1+7，﹣3）；③当点Q 在Q 3位置时，点Q 3的纵坐标为﹣3，代入抛物线解析式可得，点Q 3的坐标为（1﹣7，﹣3）。

综上可得满足题意的点Q 有三个，分别为：Q 1（2，3），Q 2（1+7，﹣3），Q 3（1﹣7，﹣3）。

（3）点B 作BB′⊥AC 于点F ，使B′F=BF ，则B′为点B 关于直线AC 的对称点．连接B′D 交直线AC 与点M ，则点M 为所求。

过点B′作B′E ⊥x 轴于点E 。

2021年中考数学必刷压轴题专题：抛物线之平行四边形(含解析)-个人用心整理

中考数学抛物线压轴题之平行四边形1．如图，直线y＝﹣x+4与x轴交于点C，与y轴交于点B，抛物线y＝ax2+x+c经过B、C两点．（1）求抛物线的解析式；（2）如图，点E是直线BC上方抛物线上的一动点，当△BEC面积最大时，请求出点E的坐标；（3）在（2）的结论下，过点E作y轴的平行线交直线BC于点M，连接AM，点Q是抛物线对称轴上的动点，在抛物线上是否存在点P，使得以P、Q、A、M为顶点的四边形是平行四边形？如果存在，请直接写出点P 的坐标；如果不存在，请说明理由．2．如图，二次函数y＝﹣x2+x+2的图象与x轴交于点A，B，与y轴交于点C．点P是该函数图象上的动点，且位于第一象限，设点P的横坐标为x．（1）写出线段AC，BC的长度：AC＝，BC＝；（2）记△BCP的面积为S，求S关于x的函数表达式；（3）过点P作PH⊥BC，垂足为H，连结AH，AP，设AP与BC交于点K，探究：是否存在四边形ACPH为平行四边形？若存在，请求出的值；若不存在，请说明理由，并求出的最大值．3．如图，抛物线y＝ax2+bx+c经过点B（4，0），C（0，﹣2），对称轴为直线x＝1，与x轴的另一个交点为点A．（1）求抛物线的解析式；（2）点M从点A出发，沿AC向点C运动，速度为1个单位长度/秒，同时点N从点B出发，沿BA向点A 运动，速度为2个单位长度/秒，当点M、N有一点到达终点时，运动停止，连接MN，设运动时间为t秒，当t为何值时，AMN的面积S最大，并求出S的最大值；（3）点P在x轴上，点Q在抛物线上，是否存在点P、Q，使得以点P、Q、B、C为顶点的四边形是平行四边形，若存在，直接写出所有符合条件的点P坐标，若不存在，请说明理由．4．如图，已知直线y＝﹣3x+3与x轴交于点A，与y轴交于点C，抛物线y＝ax2+bx+c经过点A和点C，对称轴为直线l：x＝﹣1，该抛物线与x轴的另一个交点为B．（1）求此抛物线的解析式；（2）点P在抛物线上且位于第二象限，求△PBC的面积最大值及点P的坐标．（3）点M在此抛物线上，点N在对称轴上，以B、C、M、N为顶点的四边形能否为平行四边形？若能，写出所有满足要求的点M的坐标；若不能，请说明理由．5．如图，抛物线y=﹣x2+2x+3与x轴相交于A、B两点（点A在点B的左侧），与y轴相交于点C，顶点为D．（1）直接写出A、B、C三点的坐标和抛物线的对称轴；（2）连接BC，与抛物线的对称轴交于点E，点P为线段BC上的一个动点，过点P作PF∥DE交抛物线于点F，设点P的横坐标为m；①用含m的代数式表示线段PF的长，并求出当m为何值时，四边形PEDF为平行四边形？②设△BCF的面积为S，求S与m的函数关系式．6．如图，抛物线y=x2﹣2x+c的顶点A在直线l：y=x﹣5上．（1）求抛物线顶点A的坐标；（2）设抛物线与y轴交于点B，与x轴交于点C、D（C点在D点的左侧），试判断△ABD的形状；（3）在直线l上是否存在一点P，使以点P、A、B、D为顶点的四边形是平行四边形？若存在，求点P的坐标；若不存在，请说明理由．7．已知抛物线y=﹣mx2+4x+2m与x轴交于点A（α，0），B（β，0），且=﹣2，（1）求抛物线的解析式．（2）抛物线的对称轴为l，与y轴的交点为C，顶点为D，点C关于l的对称点为E，是否存在x轴上的点M，y轴上的点N，使四边形DNME的周长最小？若存在，请画出图形（保留作图痕迹），并求出周长的最小值；若不存在，请说明理由．（3）若点P在抛物线上，点Q在x轴上，当以点D、E、P、Q为顶点的四边形是平行四边形时，求点P的坐标．8．已知抛物线y=﹣x2﹣2x+a（a≠0）与y轴相交于A点，顶点为M，直线y=x﹣a分别与x轴、y轴相交于B，C两点，并且与直线MA相交于N点．（1）若直线BC和抛物线有两个不同交点，求a的取值范围，并用a表示交点M，A的坐标；（2）将△NAC沿着y轴翻转，若点N的对称点P恰好落在抛物线上，AP与抛物线的对称轴相交于点D，连接CD，求a的值及△PCD的面积；（3）在抛物线y=﹣x2﹣2x+a（a＞0）上是否存在点P，使得以P，A，C，N为顶点的四边形是平行四边形？若存在，求出点P的坐标；若不存在，请说明理由．9．边长为2的正方形OABC在平面直角坐标系中的位置如图所示，点D是边OA的中点，连接CD，点E在第一象限，且DE⊥DC，DE=DC．以直线AB为对称轴的抛物线过C，E两点．（1）求抛物线的解析式；（2）点P从点C出发，沿射线CB每秒1个单位长度的速度运动，运动时间为t秒．过点P作PF⊥CD于点F，当t为何值时，以点P，F，D为顶点的三角形与△COD相似？（3）点M为直线AB上一动点，点N为抛物线上一动点，是否存在点M，N，使得以点M，N，D，E为顶点的四边形是平行四边形？若存在，请直接写出满足条件的点的坐标；若不存在，请说明理由．10．如图，边长为1的正方形ABCD一边AD在x负半轴上，直线l：y=x+2经过点B（x，1）与x轴，y 轴分别交于点H，F，抛物线y=﹣x2+bx+c．（1）求A，D两点的坐标及抛物线经过A，D两点时的解析式；（2）当抛物线的顶点E（m，n）在直线l上运动时，连接EA，ED，试求△EAD的面积S与m之间的函数解析式，并写出m的取值范围；（3）设抛物线与y轴交于G点，当顶点E在直线l上运动时，以A，C，E，G为顶点的四边形能否成为平行四边形？若能，求出E点坐标；若不能，请说明理由．11．已知抛物线：（1）求抛物线y1的顶点坐标．（2）将抛物线y1向右平移2个单位，再向上平移1个单位，得到抛物线y2，求抛物线y2的解析式．（3）如图，抛物线y2的顶点为P，x轴上有一动点M，在y1、y2这两条抛物线上是否存在点N，使O（原点）、P、M、N四点构成以OP为一边的平行四边形？若存在，求出N点的坐标；若不存在，请说明理由．12．如图，在矩形OABC中，AO=10，AB=8，沿直线CD折叠矩形OABC的一边BC，使点B落在OA边上的点E 处．分别以OC，OA所在的直线为x轴，y轴建立平面直角坐标系，抛物线y=ax2+bx+c经过O，D，C三点．（1）求AD的长及抛物线的解析式；（2）一动点P从点E出发，沿EC以每秒2个单位长的速度向点C运动，同时动点Q从点C出发，沿CO以每秒1个单位长的速度向点O运动，当点P运动到点C时，两点同时停止运动．设运动时间为t秒，当t 为何值时，以P、Q、C为顶点的三角形与△ADE相似？（3）点N在抛物线对称轴上，点M在抛物线上，是否存在这样的点M与点N，使以M，N，C，E为顶点的四边形是平行四边形？若存在，请直接写出点M与点N的坐标（不写求解过程）；若不存在，请说明理由．13．如图，已知抛物线y=﹣x2+bx+c与一直线相交于A（﹣1，0），C（2，3）两点，与y轴交于点N．其顶点为D．（1）抛物线及直线AC的函数关系式；（2）设点M（3，m），求使MN+MD的值最小时m的值；（3）若抛物线的对称轴与直线AC相交于点B，E为直线AC上的任意一点，过点E作EF∥BD交抛物线于点F，以B，D，E，F为顶点的四边形能否为平行四边形？若能，求点E的坐标；若不能，请说明理由；（4）若P是抛物线上位于直线AC上方的一个动点，求△APC的面积的最大值．14．如图，抛物线y=ax2+bx+c（a≠0）与x轴交于点A（﹣1，0），B（3，0）两点，与y轴交于点C（0，﹣3）．（1）求该抛物线的解析式及顶点M坐标；（2）求△BCM面积与△ABC面积的比；（3）若P是x轴上一个动点，过P作射线PQ∥AC交抛物线于点Q，随着P点的运动，在抛物线上是否存在这样的点Q，使以A，P，Q，C为顶点的四边形为平行四边形？若存在，请求出Q点坐标；若不存在，请说明理由．15．如图，抛物线y=ax2+bx+c（a≠0）与y轴交于点C（0，4），与x轴交于点A和点B，其中点A的坐标为（﹣2，0），抛物线的对称轴x=1与抛物线交于点D，与直线BC交于点E．（1）求抛物线的解析式；（2）若点F是直线BC上方的抛物线上的一个动点，是否存在点F使四边形ABFC的面积为17，若存在，求出点F的坐标；若不存在，请说明理由；（3）平行于DE的一条动直线l与直线BC相交于点P，与抛物线相交于点Q，若以D、E、P、Q为顶点的四边形是平行四边形，求点P的坐标．16．如图，抛物线y=x2+bx+c与x轴交于A（5，0）、B（﹣1，0）两点，过点A作直线AC⊥x轴，交直线y=2x于点C；（1）求该抛物线的解析式；（2）求点A关于直线y=2x的对称点A′的坐标，判定点A′是否在抛物线上，并说明理由；（3）点P是抛物线上一动点，过点P作y轴的平行线，交线段CA′于点M，是否存在这样的点P，使四边形PACM是平行四边形？若存在，求出点P的坐标；若不存在，请说明理由．17．如图，直线y=2x+2与x轴交于点A，与y轴交于点B，把△AOB沿y轴翻折，点A落到点C，过点B的抛物线y=﹣x2+bx+c与直线BC交于点D（3，﹣4）．（1）求直线BD和抛物线的解析式；（2）在第一象限内的抛物线上，是否存在一点M，作MN垂直于x轴，垂足为点N，使得以M、O、N为顶点的三角形与△BOC相似？若存在，求出点M的坐标；若不存在，请说明理由；（3）在直线BD上方的抛物线上有一动点P，过点P作PH垂直于x轴，交直线BD于点H，当四边形BOHP 是平行四边形时，试求动点P的坐标．18．综合与探究：如图，在平面直角坐标系xOy中，四边形OABC是平行四边形，A、C两点的坐标分别为（4，0），（﹣2，3），抛物线W经过O、A、C三点，D是抛物线W的顶点．（1）求抛物线W的解析式及顶点D的坐标；（2）将抛物线W和▱OABC一起先向右平移4个单位后，再向下平移m（0＜m＜3）个单位，得到抛物线W′和▱O′A′B′C′，在向下平移的过程中，设▱O′A′B′C′与▱OABC的重叠部分的面积为S，试探究：当m为何值时S有最大值，并求出S的最大值；（3）在（2）的条件下，当S取最大值时，设此时抛物线W′的顶点为F，若点M是x轴上的动点，点N是抛物线W′上的动点，试判断是否存在这样的点M和点N，使得以D、F、M、N为顶点的四边形是平行四边形？若存在，请直接写出点M的坐标；若不存在，请说明理由．19．如图，抛物线与x轴交于点A（﹣5，0）和点B（3，0）．与y轴交于点C（0，5）．有一宽度为1，长度足够的矩形（阴影部分）沿x轴方向平移，与y轴平行的一组对边交抛物线于点P和Q，交直线AC于点M和N．交x轴于点E和F．（1）求抛物线的解析式；（2）当点M和N都在线段AC上时，连接MF，如果sin∠AMF=，求点Q的坐标；（3）在矩形的平移过程中，当以点P，Q，M，N为顶点的四边形是平行四边形时，求点M的坐标．解析1．【解答】解：（1）当x＝0时，y＝4，∴B（0，4），当y＝0时，﹣x+4＝0，x＝6，∴C（6，0），把B（0，4）和C（6，0）代入抛物线y＝ax2+x+c中得：，解得：，∴抛物线的解析式为：y＝﹣x2+x+4；（2）如图1，过E作EG∥y轴，交直线BC于G，设E（m，﹣m2+m+4），则G（m，﹣m+4），∴EG＝（﹣m2+m+4）﹣（﹣m+4）＝﹣+4m，∴S△BEC＝EG•OC＝×6（﹣+4m）＝﹣2（m﹣3）2+18，∵﹣2＜0，∴S有最大值，此时E（3，8）；（3）y＝﹣x2+x+4＝﹣（x2﹣5x+﹣）+4＝﹣（x﹣）2+；对称轴是：x＝，∴A（﹣1，0）∵点Q是抛物线对称轴上的动点，∴Q的横坐标为，在抛物线上存在点P，使得以P、Q、A、M为顶点的四边形是平行四边形；①如图2，以AM为边时，由（2），可得点M的横坐标是3，∵点M在直线y＝﹣x+4上，∴点M的坐标是（3，2），又∵点A的坐标是（﹣1，0），点Q的横坐标为，根据M到Q的平移规律：可知：P的横坐标为﹣，∴P（﹣，﹣）；②如图3，以AM为边时，四边形AMPQ是平行四边形，由（2），可得点M的横坐标是3，∵A（﹣1，0），且Q的横坐标为，∴P的横坐标为，∴P（，﹣）；③以AM为对角线时，如图4，∵M到Q的平移规律可得P到A的平移规律，∴点P的坐标是（﹣，），综上所述，在抛物线上存在点P，使得以P、Q、A、M为顶点的四边形是平行四边形，点P的坐标是（﹣，﹣）或（，﹣）或（﹣，）．2．【解答】解：（1）二次函数y＝﹣x2+x+2，当x＝0时，y＝2，∴C（0，2），∴OC＝2，当y＝0时，﹣x2+x+2＝0，解得：x1＝4，x2＝﹣1，∴A（﹣1，0），B（4，0），∴OA＝1，OB＝4，由勾股定理得：AC＝＝，BC＝＝2；故答案为：，2；（4分）（2）∵B（4，0），C（0，2），∴直线BC的解析式为：y＝﹣x+2，如图1，过P作PD∥y轴，交直线BC于D，设P（x，﹣x2+x+2），则D（x，﹣x+2），∴PD＝（﹣x2+x+2）﹣（﹣x+2）＝﹣x2+2x，有S＝PD•OB＝×4（﹣+2x）＝﹣x2+4x（0＜x＜4）；（6分）（3）不存在，如图2，∵AC2+BC2＝＝25＝AB2，∴△ABC为直角三角形，即AC⊥BC，∵PH⊥BC，∴AC∥PH，要使四边形ACPH为平行四边形，只需满足PH＝AC＝，（10分）∴S＝BC•PH＝×2×＝5，∵而S＝﹣x2﹣4x＝﹣（x﹣2）2+4≤4，所以不存在四边形ACPH为平行四边形，∵AC∥PH，∴△AKC∽△PHK，∴＝＝＝S≤；∴的最大值是．（12分）（说明：写出不存在给1分，其他说明过程酌情给分）3．【解答】解：（1）依题意，将B（4，0），C（0，﹣2），对称轴为直线x＝1，代入抛物线解析式，得，解得：，∴抛物线的解析式为：；（2）∵对称轴为直线x＝1，B（4，0）．∴A（﹣2，0），则AB＝6，当点N运动t秒时，BN＝2t，则AN＝6﹣2t，如图1，过点M作MD⊥x轴于点D．∵OA＝OC＝2，∴△OAC是等腰直角三角形，∴∠OAC＝45°．又∵DM⊥OA，∴△DAM是等腰直角三角形，AD＝DM，当点M运动t秒时，AM＝t，∴MD2+AD2＝AM2＝t2，∴DM＝t，∴，∴由二次函数的图象及性质可知，当时，S最大值为；（3）存在，理由如下：①当四边形CBQP为平行四边形时，CB与PQ平行且相等，∵B（4，0），C（0，﹣2），∴y B﹣y C＝y Q﹣y P＝2，x B﹣x C＝x Q﹣x P＝4，∵y P＝0，∴y Q＝2，将y＝2代入，得 x1＝1+，x2＝1﹣，∴当x Q＝1+时，x P＝﹣3+；当x Q＝1﹣时，x P＝﹣3﹣，∴P1（﹣3+，0），P2（﹣3﹣，0）；②当四边形CQPB为平行四边形时，BP与CQ平行且相等，∵y P＝y B＝0，∴y Q＝y C＝﹣2，将y＝﹣2代入，得 x1＝0（舍去），x2＝2，∴x Q＝2时，∴x P﹣x B＝x Q﹣x C＝2，∴x P＝6，∴P3（6，0）；③当四边形CQBP为平行四边形时，BP与CQ平行且相等，由②知，x Q＝2，∴x B﹣x P＝x Q﹣x C＝2，∴x P＝2，∴P4（2，0）；综上所述，存在满足条件的点P有4个，分别是P1（﹣3+，0），P2（﹣3﹣，0），P3（6，0），P4（2，0）．4．【解答】解：（1）直线y＝﹣3x+3与x轴交于点A，与y轴交于点C，当y＝0时，﹣3x+3＝0，解得x＝1，则A点坐标为（1，0）；当x＝0时，y＝3，则C点坐标为（0，3）；抛物线的对称轴为直线x＝﹣1，则B点坐标为（﹣3，0）；把C（0，3）代入y＝a（x﹣1）（x+3）得3＝﹣3a，解得a＝﹣1，则此抛物线的解析式为y＝﹣（x﹣1）（x+3）＝﹣x2﹣2x+3；（2）设P（x，﹣x2﹣2x+3），如图1，过P作PM∥y轴，交BC于点M，设直线BC的关系式为：y＝mx+n，把B（﹣3，0），C（0，3）代入y＝mx+n得，解得，∴直线BC的关系式为y＝x+3，∴PM＝﹣x2﹣2x+3﹣（x+3）＝﹣x2﹣3x，∴△PBC的面积＝S△PBM+S△PCM＝＝×3（﹣x2﹣3x）＝﹣+，∵﹣＜0，∴当x＝﹣时，△PBC的面积有最大值是，∴P点坐标为（﹣，）；（3）①当以BC为对角线，如图2，∵四边形BMCN为平行四边形，∵C点（0，3），N点横坐标为﹣1，B点横坐标为﹣3，∴M点横坐标为﹣2，∴M点纵坐标为y＝﹣4+4+3＝3，∴M点坐标为（﹣2，3）；②当以BC为边时，如图3，∵四边形BCNM为平行四边形，∵C点（0，3），B（﹣3，0），N点横坐标为﹣1，∴M点横坐标为﹣4，∴M点纵坐标为y＝﹣16+8+3＝﹣5，∴M点坐标为（﹣4，﹣5）；同理可知如图4，存在四边形BCMN为平行四边形，可得M的横坐标为2，当x＝2时，y＝﹣4﹣4+3＝﹣5，∴M点坐标为（﹣4，﹣5）或（2，﹣5）．综上所述，M点坐标为（﹣2，3）或（﹣4，﹣5）或（2，﹣5）．5.解：（1）A（﹣1，0），B（3，0），C（0，3）．抛物线的对称轴是：直线x=1．（2）①设直线BC的函数关系式为：y=kx+b．把B（3，0），C（0，3）分别代入得：解得：．所以直线BC的函数关系式为：y=﹣x+3．当x=1时，y=﹣1+3=2，∴E（1，2）．当x=m时，y=﹣m+3，∴P（m，﹣m+3）．在y=﹣x2+2x+3中，当x=1时，y=4．∴D（1，4）当x=m时，y=﹣m2+2m+3，∴F（m，﹣m2+2m+3）∴线段DE=4﹣2=2，线段PF=﹣m2+2m+3﹣（﹣m+3）=﹣m2+3m∵PF∥DE，∴当PF=ED时，四边形PEDF为平行四边形．由﹣m2+3m=2，解得：m1=2，m2=1（不合题意，舍去）．因此，当m=2时，四边形PEDF为平行四边形．②设直线PF与x轴交于点M，由B（3，0），O（0，0），可得：OB=OM+MB=3．∵S=S△BPF+S△CPF即S=PF•BM+PF•OM=PF•（BM+OM）=PF•OB．∴S=×3（﹣m2+3m）=﹣m2+m（0≤m≤3）．方法二：（3）∵B（3，0），C（0，3），D（1，4），∴，∴，∵∠DEC=∠COB=90°，∴△DEC∽△COB，∴∠DCE=∠CBO，∴∠DCE+∠OCB=90°，∴DC⊥BC，∴△BCD的外接圆圆心M为BD中点，∴M X==2，M Y==2，∴△BCD的外接圆圆心M（2，2）．6．如图，抛物线y=x2﹣2x+c的顶点A在直线l：y=x﹣5上．（1）求抛物线顶点A的坐标；（2）设抛物线与y轴交于点B，与x轴交于点C、D（C点在D点的左侧），试判断△ABD的形状；（3）在直线l上是否存在一点P，使以点P、A、B、D为顶点的四边形是平行四边形？若存在，求点P的坐标；若不存在，请说明理由．【解答】方法一：解：（1）∵顶点A的横坐标为x=﹣=1，且顶点A在y=x﹣5上，∴当x=1时，y=1﹣5=﹣4，∴A（1，﹣4）．（2）△ABD是直角三角形．将A（1，﹣4）代入y=x2﹣2x+c，可得，1﹣2+c=﹣4，∴c=﹣3，∴y=x2﹣2x﹣3，∴B（0，﹣3）当y=0时，x2﹣2x﹣3=0，x1=﹣1，x2=3∴C（﹣1，0），D（3，0），BD2=OB2+OD2=18，AB2=（4﹣3）2+12=2，AD2=（3﹣1）2+42=20，BD2+AB2=AD2，∴∠ABD=90°，即△ABD是直角三角形．（3）存在．由题意知：直线y=x﹣5交y轴于点E（0，﹣5），交x轴于点F（5，0）∴OE=OF=5，又∵OB=OD=3∴△OEF与△OBD都是等腰直角三角形∴BD∥l，即PA∥BD则构成平行四边形只能是PADB或PABD，如图，过点P作y轴的垂线，过点A作x轴的垂线交过P且平行于x轴的直线于点G．设P（x1，x1﹣5），则G（1，x1﹣5）则PG=|1﹣x1|，AG=|5﹣x1﹣4|=|1﹣x1|PA=BD=3由勾股定理得：（1﹣x1）2+（1﹣x1）2=18，x12﹣2x1﹣8=0，x1=﹣2或4∴P（﹣2，﹣7）或P（4，﹣1），存在点P（﹣2，﹣7）或P（4，﹣1）使以点A、B、D、P为顶点的四边形是平行四边形．方法二：（1）略．（2）把A（1，﹣4）代入y=x2﹣2x+c，得c=3，∴y=x2﹣2x+3=（x﹣3）（x+1），∴D（3，0），B（0，﹣3），A（1，﹣4），K BD==1，K AB==﹣1，∴K BD•K AB=﹣1，∴AB⊥BD，即△ABD为直角三角形．（3）略．（4）∵，解得：x1=1（舍），x2=2，∴G（2，﹣3），∵A（1，﹣4），B（0，﹣3），D（3，0），∴GA==，BD==3，AB==，∴S△BDG==4．7．已知抛物线y=﹣mx2+4x+2m与x轴交于点A（α，0），B（β，0），且=﹣2，（1）求抛物线的解析式．（2）抛物线的对称轴为l，与y轴的交点为C，顶点为D，点C关于l的对称点为E，是否存在x轴上的点M，y轴上的点N，使四边形DNME的周长最小？若存在，请画出图形（保留作图痕迹），并求出周长的最小值；若不存在，请说明理由．（3）若点P在抛物线上，点Q在x轴上，当以点D、E、P、Q为顶点的四边形是平行四边形时，求点P的坐标．【解答】解：（1）由题意可得：α，β是方程﹣mx2+4x+2m=0的两根，由根与系数的关系可得，α+β=，αβ=﹣2，∵=﹣2，∴=﹣2，即=﹣2，解得：m=1，故抛物线解析式为：y=﹣x2+4x+2；（2）存在x轴上的点M，y轴上的点N，使得四边形DNME的周长最小，∵y=﹣x2+4x+2=﹣（x﹣2）2+6，∴抛物线的对称轴l为x=2，顶点D的坐标为：（2，6），又∵抛物线与y轴交点C的坐标为：（0，2），点E与点C关于l对称，∴E点坐标为：（4，2），作点D关于y轴的对称点D′，点E关于x轴的对称点E′，则D′的坐标为；（﹣2，6），E′坐标为：（4，﹣2），连接D′E′，交x轴于M，交y轴于N，此时，四边形DNME的周长最小为：D′E′+DE，如图1所示：延长E′E，′D交于一点F，在Rt△D′E′F中，D′F=6，E′F=8，则D′E′===10，设对称轴l与CE交于点G，在Rt△DGE中，DG=4，EG=2，∴DE===2，∴四边形DNME的周长最小值为：10+2；（3）如图2，P为抛物线上的点，过点P作PH⊥x轴，垂足为H，若以点D、E、P、Q为顶点的四边形为平行四边形，则△PHQ≌△DGE，∴PH=DG=4，∴|y|=4，∴当y=4时，﹣x2+4x+2=4，解得：x1=2+，x2=2﹣，当y=﹣4时，﹣x2+4x+2=﹣4，解得：x3=2+，x4=2﹣，故P点的坐标为；（2﹣，4），（2+，4），（2﹣，﹣4），（2+，﹣4）．8．已知抛物线y=﹣x2﹣2x+a（a≠0）与y轴相交于A点，顶点为M，直线y=x﹣a分别与x轴、y轴相交于B，C两点，并且与直线MA相交于N点．（1）若直线BC和抛物线有两个不同交点，求a的取值范围，并用a表示交点M，A的坐标；（2）将△NAC沿着y轴翻转，若点N的对称点P恰好落在抛物线上，AP与抛物线的对称轴相交于点D，连接CD，求a的值及△PCD的面积；（3）在抛物线y=﹣x2﹣2x+a（a＞0）上是否存在点P，使得以P，A，C，N为顶点的四边形是平行四边形？若存在，求出点P的坐标；若不存在，请说明理由．【解答】解：（1）由题意得，，整理得2x2+5x﹣4a=0．∵△=25+32a＞0，解得a＞﹣．∵a≠0，∴a＞﹣且a≠0．令x=0，得y=a，∴A（0，a）．由y=﹣（x+1）2+1+a得，M（﹣1，1+a）．（2）设直线MA的解析式为y=kx+b（k≠0），∵A（0，a），M（﹣1，1+a），∴，解得，∴直线MA的解析式为y=﹣x+a，联立得，，解得，∴N（，﹣）．∵点P是点N关于y轴的对称点，∴P（﹣，﹣）．代入y=﹣x2﹣2x+a得，﹣=﹣a2+a+a，解得a=或a=0（舍去）．∴A（0，），C（0，﹣），M（﹣1，），|AC|=，∴S△PCD=S△PAC﹣S△ADC=|AC|•|x p|﹣|AC|•|x0|=••（3﹣1）=；（3）①当点P在y轴左侧时，∵四边形APCN是平行四边形，∴AC与PN互相平分，N（，﹣），∴P（﹣，）；代入y=﹣x2﹣2x+a得，=﹣a2+a+a，解得a=，∴P1（﹣，）．②当点P在y轴右侧时，∵四边形ACPN是平行四边形，∴NP∥AC且NP=AC，∵N（，﹣），A（0，a），C（0，﹣a），∴P（，﹣）．代入y=﹣x2﹣2x+a得，﹣=﹣a2﹣a+a，解得a=，∴P2（，﹣）．综上所述，当点P1（﹣，）和P2（，﹣）时，A、C、P、N能构成平行四边形．9．边长为2的正方形OABC在平面直角坐标系中的位置如图所示，点D是边OA的中点，连接CD，点E在第一象限，且DE⊥DC，DE=DC．以直线AB为对称轴的抛物线过C，E两点．（1）求抛物线的解析式；（2）点P从点C出发，沿射线CB每秒1个单位长度的速度运动，运动时间为t秒．过点P作PF⊥CD于点F，当t为何值时，以点P，F，D为顶点的三角形与△COD相似？（3）点M为直线AB上一动点，点N为抛物线上一动点，是否存在点M，N，使得以点M，N，D，E为顶点的四边形是平行四边形？若存在，请直接写出满足条件的点的坐标；若不存在，请说明理由．【解答】解：（1）方法一：过点E作EG⊥x轴于G点．∵四边形OABC是边长为2的正方形，D是OA的中点，∴OA=OC=2，OD=1，∠AOC=∠DGE=90°．∵∠CDE=90°，∴∠ODC+∠GDE=90°．∵∠ODC+∠OCD=90°，∴∠OCD=∠GDE．在△OCD和△GED中，∴△ODC≌△GED （AAS），∴EG=OD=1，DG=OC=2．∴点E的坐标为（3，1）．∵抛物线的对称轴为直线AB即直线x=2，∴可设抛物线的解析式为y=a（x﹣2）2+k，将C、E点的坐标代入解析式，得．解得，抛物线的解析式为y=（x﹣2）2+；方法二：过点E作EG⊥x轴于G点．DE⊥DC⇒∠CDO+∠EDH=90°，EG⊥x轴⇒∠DEH+∠EDH=90°，∴∠CDO=∠DEH，DC=DE，∴△ODC≌△GED⇒DG=OC=2，EG=OD=1，∴E（3，1），∴9a+3b+2=0，∵﹣=2，抛物线的解析式为y=（x﹣2）2+；（2）方法一：①若△DFP∽△COD，则∠PDF=∠DCO，∴PD∥OC，∴∠PDO=∠OCP=∠AOC=90°，∴四边形PDOC是矩形，∴PC=OD=1，∴t=1；②若△PFD∽△COD，则∠DPF=∠DCO，=．∴∠PCF=90°﹣∠DCO=90﹣∠DPF=∠PDF．∴PC=PD，∴DF=CD．∵CD2=OD2+OC2=22+12=5，∴CD=，∴DF=．∵=，∴PC=PD=×=，t=，综上所述：t=1或t=时，以点P，F，D为顶点的三角形与△COD相似；方法二：过点F作x轴的垂线，分别交BC，OA于G，H，PF⊥CD⇒∠PFG+∠DFH=90°，GH⊥OA⇒∠FDH+∠DFH=90°，∴∠PFG=∠FDH⇒△PFG∽△FDH⇒，∵PF⊥CD⇒K PF×K CD=﹣1，∴l CD：y=﹣2x+2，∴F（m，﹣2m+2），P（t，2），∴，∴m=，∴F（，﹣），∴=，∴以P，F，D为顶点的三角形与△COD相似，①，∴，∴t=，②，∴，∴t=1，综上所述：t=1或t=时，以点P，F，D为顶点的三角形与△COD相似；方法三：若以P，F，D为顶点的三角形与△COD相似，则∠OCD=∠PDF或∠ODC=∠PDF，①∠OCD=∠PDF⇒PD∥OC，∴CP=OD=1，∴t=1，②∠ODC=∠PDF，作OO′⊥CD交CD于H，∴K OO′×K CD=﹣1，∴l CD：y=﹣2x+2，∴H（m，﹣2m+2），∴﹣2×=﹣1，∴m=，∴H（，），∵H为OO′中点，∴O′（，），∴l O′D：y=，令y=2，∴x=，即P（，2），∴t=．（3）存在，四边形MDEN是平行四边形时，M1（2，1），N1（4，2）；四边形MNDE是平行四边形时，M2（2，3），N2（0，2）；四边形NDME是平行四边形时，M3（2，），N3（2，）．10．如图，边长为1的正方形ABCD一边AD在x负半轴上，直线l：y=x+2经过点B（x，1）与x轴，y 轴分别交于点H，F，抛物线y=﹣x2+bx+c．（1）求A，D两点的坐标及抛物线经过A，D两点时的解析式；（2）当抛物线的顶点E（m，n）在直线l上运动时，连接EA，ED，试求△EAD的面积S与m之间的函数解析式，并写出m的取值范围；（3）设抛物线与y轴交于G点，当顶点E在直线l上运动时，以A，C，E，G为顶点的四边形能否成为平行四边形？若能，求出E点坐标；若不能，请说明理由．【解答】解：（1）∵直线l：y=x+2经过点B（x，1），∴1=x+2，解得x=﹣2，∴B（﹣2，1），∴A（﹣2，0），D（﹣3，0），∵抛物线经过A，D两点，∴，解得，∴抛物线经过A，D两点时的解析式为y=﹣x2﹣5x﹣6；（2）∵点E（m，n）在直线l上，∴n=m+2，∴S=×1×[±（m+2）]=±（m+1），即S=m+1（m＞﹣4）或S=﹣m﹣1（m＜﹣4）；（3）如图，若以A，C，E，G为顶点的四边形能成为平行四边形，则AC=EG，AC∥EG，作EH∥y轴交过G点平行于x轴的直线相交于H，则EH⊥GH，△EHG≌△CDA，∴GH=AD=1，∴E的横坐标为±1，∵点E在直线l上，∴y=×（﹣1）+2=，或y=×1+2=当AC为对角线时，有E和G的横坐标之和等于A和C的横坐标之和，故可求得E（﹣5，﹣1/2）∴E（﹣1，）；（1，）或（﹣5，﹣1/2）；由于E为抛物线的顶点，G为抛物线与y轴的交点，故将其坐标代入y=﹣x2+bx+c，检验可知当E取（1，）或（﹣5，﹣1/2）时，与此时的A、C、E构成平行四边形的G点并不是y轴与抛物线的交点，与前提相矛盾；综上，满足题意的E的坐标为（﹣1，）．11．已知抛物线：（1）求抛物线y1的顶点坐标．（2）将抛物线y1向右平移2个单位，再向上平移1个单位，得到抛物线y2，求抛物线y2的解析式．（3）如图，抛物线y2的顶点为P，x轴上有一动点M，在y1、y2这两条抛物线上是否存在点N，使O（原点）、P、M、N四点构成以OP为一边的平行四边形？若存在，求出N点的坐标；若不存在，请说明理由．【解答】解：（1）依题意把抛物线：y1=﹣x2+2x=﹣（x2﹣4x）=﹣[（x﹣2）2﹣4]=﹣（x﹣2）2+2，故抛物线y1的顶点坐标为：（2，2）；（2）∵抛物线y1向右平移2个单位，再向上平移1个单位，得到y2=﹣（x﹣4）2+3，整理得y2=﹣x2+4x﹣5；（3）符合条件的N点存在．如图：作PA⊥x轴于点A，NB⊥x轴于点B，∴∠PAO=∠MBN=90°，若四边形OPMN为符合条件的平行四边形，则OP∥MN，且OP=MN，∴∠POA=∠BMN，在△POA和△NMB中∴△POA≌△NMB（AAS），∴PA=BN，∵点P的坐标为（4，3），∴NB=PA=3，∵点N在抛物线y1、y2上，且P点为y1、y2的最高点∴符合条件的N点只能在x轴下方，①点N在抛物线y1上，则有：﹣x2+2x=﹣3解得：x1=2﹣，x2=2+，②点N在抛物线y2上，则有：﹣（x﹣4）2+3=﹣3解得：x3=4﹣2或x4=4+2故符合条件的N点有四个：N1（2﹣，﹣3），N2（4﹣2，﹣3），N3（2+，﹣3），N4（4+2，﹣3）．12．如图，在矩形OABC中，AO=10，AB=8，沿直线CD折叠矩形OABC的一边BC，使点B落在OA边上的点E 处．分别以OC，OA所在的直线为x轴，y轴建立平面直角坐标系，抛物线y=ax2+bx+c经过O，D，C三点．（1）求AD的长及抛物线的解析式；（2）一动点P从点E出发，沿EC以每秒2个单位长的速度向点C运动，同时动点Q从点C出发，沿CO以每秒1个单位长的速度向点O运动，当点P运动到点C时，两点同时停止运动．设运动时间为t秒，当t 为何值时，以P、Q、C为顶点的三角形与△ADE相似？（3）点N在抛物线对称轴上，点M在抛物线上，是否存在这样的点M与点N，使以M，N，C，E为顶点的四边形是平行四边形？若存在，请直接写出点M与点N的坐标（不写求解过程）；若不存在，请说明理由．【解答】方法一：解：（1）∵四边形ABCO为矩形，∴∠OAB=∠AOC=∠B=90°，AB=CO=8，AO=BC=10．由题意，△BDC≌△EDC．∴∠B=∠DEC=90°，EC=BC=10，ED=BD．由勾股定理易得EO=6．∴AE=10﹣6=4，设AD=x，则BD=ED=8﹣x，由勾股定理，得x2+42=（8﹣x）2，解得，x=3，∴AD=3．∵抛物线y=ax2+bx+c过点D（3，10），C（8，0），O（0，0）∴，解得∴抛物线的解析式为：y=﹣x2+x．（2）∵∠DEA+∠OEC=90°，∠OCE+∠OEC=90°，∴∠DEA=∠OCE，由（1）可得AD=3，AE=4，DE=5．而CQ=t，EP=2t，∴PC=10﹣2t．当∠PQC=∠DAE=90°，△ADE∽△QPC，∴=，即=，解得t=．当∠QPC=∠DAE=90°，△ADE∽△PQC，∴=，即=，解得t=．∴当t=或时，以P、Q、C为顶点的三角形与△ADE相似．（3）假设存在符合条件的M、N点，分两种情况讨论：①EC为平行四边形的对角线，由于抛物线的对称轴经过EC中点，若四边形MENC是平行四边形，那么M点必为抛物线顶点；则：M（4，）；而平行四边形的对角线互相平分，那么线段MN必被EC中点（4，3）平分，则N（4，﹣）；②EC为平行四边形的边，则EC MN，设N（4，m），则M（4﹣8，m+6）或M（4+8，m﹣6）；将M（﹣4，m+6）代入抛物线的解析式中，得：m=﹣38，此时 N（4，﹣38）、M（﹣4，﹣32）；将M（12，m﹣6）代入抛物线的解析式中，得：m=﹣26，此时 N（4，﹣26）、M（12，﹣32）；综上，存在符合条件的M、N点，且它们的坐标为：①M1（﹣4，﹣32），N1（4，﹣38）；②M2（12，﹣32），N2（4，﹣26）；③M3（4，），N3（4，﹣）．方法二：（1）略．（2）∵E（0，6），C（8，0），∴l EC：y=﹣x+6，∵，EP=2t，∴P x=t，∴P（t，﹣t+6），Q（8﹣t，0），∵△PQC∽△ADE，且∠ECO=∠AED，∴PQ⊥OC或PQ⊥PC．当PQ⊥OC时，Px=Qx，即t=8﹣t，∴t1=，当PQ⊥PC时，K PQ•K PC=﹣1，∴t2=．（3）M，N，C，E为顶点的四边形是平行四边形．设N（4，t），C（8，0），E（0，6），∴，∴M1（4，6﹣t），同理M2（﹣4，t+6），M3（12，t﹣6），∴﹣t，∴t=﹣，﹣×（﹣4）2+（﹣4）=t+6，∴t=﹣38，﹣×122+×12=t﹣6，∴t=﹣26，综上，存在符合条件的M、N点，且它们的坐标为：①M1（4，），N1（4，﹣）；②M2（12，﹣32），N2（4，﹣26）；③M3（﹣4，﹣32），N3（4，﹣38）．13．如图，已知抛物线y=﹣x2+bx+c与一直线相交于A（﹣1，0），C（2，3）两点，与y轴交于点N．其顶点为D．（1）抛物线及直线AC的函数关系式；（2）设点M（3，m），求使MN+MD的值最小时m的值；（3）若抛物线的对称轴与直线AC相交于点B，E为直线AC上的任意一点，过点E作EF∥BD交抛物线于点F，以B，D，E，F为顶点的四边形能否为平行四边形？若能，求点E的坐标；若不能，请说明理由；（4）若P是抛物线上位于直线AC上方的一个动点，求△APC的面积的最大值．【解答】解：（1）由抛物线y=﹣x2+bx+c过点A（﹣1，0）及C（2，3）得，，解得，故抛物线为y=﹣x2+2x+3又设直线为y=kx+n过点A（﹣1，0）及C（2，3）得，解得故直线AC为y=x+1；（2）如图1，作N点关于直线x=3的对称点N′，则N′（6，3），由（1）得D（1，4），故直线DN′的函数关系式为y=﹣x+，当M（3，m）在直线DN′上时，MN+MD的值最小，则m=﹣×=；（3）由（1）、（2）得D（1，4），B（1，2），∵点E在直线AC上，设E（x，x+1），①如图2，当点E在线段AC上时，点F在点E上方，。

2020-2021备战中考数学压轴题专题平行四边形的经典综合题附答案

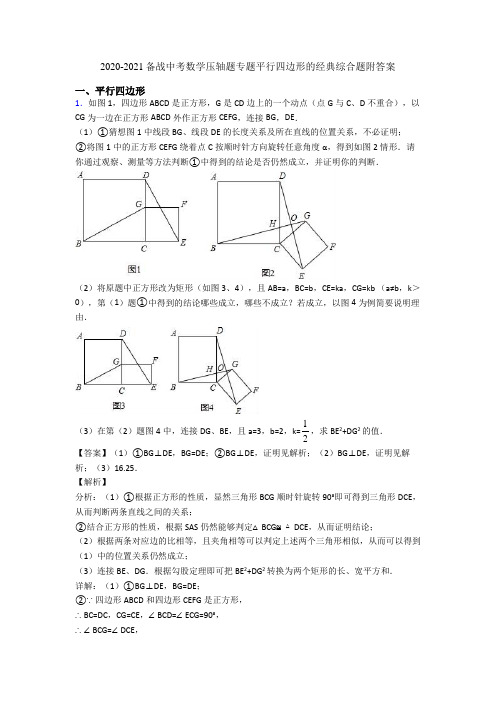
2020-2021备战中考数学压轴题专题平行四边形的经典综合题附答案一、平行四边形1．如图1，四边形ABCD是正方形，G是CD边上的一个动点（点G与C、D不重合），以CG为一边在正方形ABCD外作正方形CEFG，连接BG，DE．（1）①猜想图1中线段BG、线段DE的长度关系及所在直线的位置关系，不必证明；②将图1中的正方形CEFG绕着点C按顺时针方向旋转任意角度α，得到如图2情形．请你通过观察、测量等方法判断①中得到的结论是否仍然成立，并证明你的判断．（2）将原题中正方形改为矩形（如图3、4），且AB=a，BC=b，CE=ka，CG=kb （a≠b，k＞0），第（1）题①中得到的结论哪些成立，哪些不成立？若成立，以图4为例简要说明理由．（3）在第（2）题图4中，连接DG、BE，且a=3，b=2，k=12，求BE2+DG2的值．【答案】（1）①BG⊥DE，BG=DE；②BG⊥DE，证明见解析；（2）BG⊥DE，证明见解析；（3）16.25．【解析】分析：（1）①根据正方形的性质，显然三角形BCG顺时针旋转90°即可得到三角形DCE，从而判断两条直线之间的关系；②结合正方形的性质，根据SAS仍然能够判定△BCG≌△DCE，从而证明结论；（2）根据两条对应边的比相等，且夹角相等可以判定上述两个三角形相似，从而可以得到（1）中的位置关系仍然成立；（3）连接BE、DG．根据勾股定理即可把BE2+DG2转换为两个矩形的长、宽平方和．详解：（1）①BG⊥DE，BG=DE；②∵四边形ABCD和四边形CEFG是正方形，∴BC=DC，CG=CE，∠BCD=∠ECG=90°，∴∠BCG=∠DCE，∴△BCG≌△DCE，∴BG=DE，∠CBG=∠CDE，又∵∠CBG+∠BHC=90°，∴∠CDE+∠DHG=90°，∴BG⊥DE．（2）∵AB=a，BC=b，CE=ka，CG=kb，∴BC CG b==，DC CE a又∵∠BCG=∠DCE，∴△BCG∽△DCE，∴∠CBG=∠CDE，又∵∠CBG+∠BHC=90°，∴∠CDE+∠DHG=90°，∴BG⊥DE．（3）连接BE、DG．根据题意，得AB=3，BC=2，CE=1.5，CG=1，∵BG⊥DE，∠BCD=∠ECG=90°∴BE2+DG2=BO2+OE2+DO2+OG2=BC2+CD2+CE2+CG2=9+4+2.25+1=16.25．点睛：此题综合运用了全等三角形的判定和性质、相似三角形的判定和性质以及勾股定理．2．如图，将矩形纸片ABCD沿对角线AC折叠，使点B落到到B′的位置，AB′与CD交于点E.（1）求证：△AED≌△CEB′（2）若AB = 8，DE = 3，点P为线段AC上任意一点，PG⊥AE于G，PH⊥BC于H.求PG + PH的值.【答案】（1）证明见解析；（2）.【解析】【分析】（1）由折叠的性质知，，，，则由得到；（2）由，可得，又由，即可求得的长，然后在中，利用勾股定理即可求得的长，再过点作于，由角平分线的性质，可得，易证得四边形是矩形，继而可求得答案.【详解】（1）四边形为矩形，，，又，；（2），，，，在中，，过点作于，，，，，，，、、共线，，四边形是矩形，，.【点睛】此题考查了折叠的性质、矩形的性质、角平分线的性质、等腰三角形的判定与性质以及勾股定理等知识.此题难度较大，注意掌握折叠前后图形的对应关系，注意掌握辅助线的作法，注意数形结合思想的应用.3．如图，矩形ABCD中，AB=6，BC=4，过对角线BD中点O的直线分别交AB，CD边于点E，F．（1）求证：四边形BEDF是平行四边形；（2）当四边形BEDF是菱形时，求EF的长．【答案】（1）证明见解析；（2）133．【解析】分析：（1）根据平行四边形ABCD 的性质，判定△BOE ≌△DOF （ASA ），得出四边形BEDF 的对角线互相平分，进而得出结论；（2）在Rt △ADE 中，由勾股定理得出方程，解方程求出BE ，由勾股定理求出BD ，得出OB ，再由勾股定理求出EO ，即可得出EF 的长.详解：（1）证明：∵四边形ABCD 是矩形，O 是BD 的中点， ∴∠A=90°，AD=BC=4，AB ∥DC ，OB=OD ， ∴∠OBE=∠ODF ，在△BOE 和△DOF 中，OBE ODF OB ODBOE DOF ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△BOE ≌△DOF （ASA ）， ∴EO=FO ，∴四边形BEDF 是平行四边形；（2）当四边形BEDF 是菱形时，BD ⊥EF ，设BE=x ，则 DE=x ，AE=6-x ，在Rt △ADE 中，DE 2=AD 2+AE 2， ∴x 2=42+（6-x ）2，解得：x= 133， ∵22AD AB +13∴OB=1213 ∵BD ⊥EF ，∴22BE OB -213∴413点睛：本题主要考查了矩形的性质，菱形的性质、勾股定理、全等三角形的判定与性质，熟练掌握矩形的性质和勾股定理，证明三角形全等是解决问的关键4．如图，在正方形ABCD 中，E 是边AB 上的一动点，点F 在边BC 的延长线上，且CF AE =，连接DE ，DF ，EF . FH 平分EFB ∠交BD 于点H .（1）求证：DE DF ⊥；（2）求证：DH DF =：（3）过点H 作HM EF ⊥于点M ，用等式表示线段AB ，HM 与EF 之间的数量关系，并证明.【答案】（1）详见解析；（2）详见解析；（3）22EF AB HM =-，证明详见解析. 【解析】【分析】（1）根据正方形性质， CF AE =得到DE DF ⊥.（2）由AED CFD △△≌，得DE DF =.由90ABC ∠=︒，BD 平分ABC ∠，得45DBF ∠=︒.因为FH 平分EFB ∠，所以EFH BFH ∠=∠.由于45DHF DBF BFH BFH ∠=∠+∠=︒+∠,45DFH DFE EFH EFH ∠=∠+∠=︒+∠, 所以DH DF =.（3）过点H 作HN BC ⊥于点N ，由正方形ABCD 性质，得222BD AB AD AB =+=.由FH 平分,EFB HM EF HN BC ∠⊥⊥，，得HM HN =.因为4590HBN HNB ∠=︒∠=︒，，所以22sin 45HNBH HN HM ===︒.由22cos 45DFEF DF DH ===︒，得22EF AB HM =-.【详解】（1）证明：∵四边形ABCD 是正方形， ∴AD CD =，90EAD BCD ADC ∠=∠=∠=︒.∴90EAD FCD ∠=∠=︒. ∵CF AE =。

中考数学二次函数综合题解题技巧

C xxy yA OBED AC B CD G图1 图2AP O B E Cx y压轴题解题技巧练习引言：解数学压轴题一般可以分为三个步骤：认真审题，理解题意、探究解题思路、正确解答。

审题要全面审视题目的所有条件和答题要求，在整体上把握试题的特点、结构，以利于解题方法的选择和解题步骤的设计。

解数学压轴题要善于总结解数学压轴题中所隐含的重要数学思想，如转化思想、数形结合思想、分类讨论思想及方程的思想等。

认识条件和结论之间的关系、图形的几何特征与数、式的数量、结构特征的关系，确定解题的思路和方法．当思维受阻时，要及时调整思路和方法，并重新审视题意，注意挖掘隐蔽的条件和内在联系，既要防止钻牛角尖，又要防止轻易放弃。

一、动态：动点、动线1．(2010年辽宁省锦州)如图，抛物线与x 轴交于A (x 1，0)、B (x 2，0)两点，且x 1＞x 2，与y 轴交于点C (0，4)，其中x 1、x 2是方程x 2－2x －8＝0的两个根． (1)求这条抛物线的解析式；(2)点P 是线段AB 上的动点，过点P 作 PE ∥AC ，交BC 于点E ，连接CP ，当△CPE的面积最大时，求点P 的坐标；(3)探究：若点Q 是抛物线对称轴上的点，是否存在这样的点Q ，使△QBC 成为等腰三角形？若存在，请直接写出所有符合条件的点Q 的坐标；若不存在，请说明理由．二、圆 2．（2010青海）如图10，已知点A （3，0），以A 为圆心作⊙A 与Y 轴切于原点，与x 轴的另一个交点为B ，过B 作⊙A 的切线l.（1）以直线l 为对称轴的抛物线过点A 及点C （0，9），求此抛物线的解析式；（2）抛物线与x 轴的另一个交点为D ，过D 作⊙A 的切线DE ，E 为切点，求此切线长；（3）点F 是切线DE 上的一个动点，当△BFD 与EAD△相似时，求出BF 的长．3．(2009年中考天水)如图1，在平面直角坐标系xOy ，二次函数y ＝ax 2＋bx ＋c (a ＞0)的图象顶点为D ，与y 轴交于点C ，与x 轴交于点A 、B ，点A 在原点的左侧，点B 的坐标为(3，0)，OB ＝OC ，tan ∠ACO ＝1 3． (1)求这个二次函数的解析式；(2)若平行于x 轴的直线与该抛物线交于点M 、N ，且以MN 为直径的圆与x 轴相切，求该圆的半径长度；(3)如图2，若点G (2，y )是该抛物线上一点，点P 是直线AG 下方的抛物线上的一动点，当点P 运动到什么位置时，△AGP 的面积最大？求此时点P 的坐标和△AGP 的最大面积．4．（09年湖南省张家界市）在平面直角坐标系中，已知A (－4，0)，B (1，0)，且以AB 为直径的圆交y 轴的正半轴于点C ，过点C 作圆的切线交x 轴于点D ．（1）求点C 的坐标和过A ，B ，C 三点的抛物线的解析式；（2）求点D 的坐标；（3）设平行于x 轴的直线交抛物线于E ，F 两点，问：是否存在以线段EF 为直径的圆，恰好与x 轴相切？若存在，求出该圆的半径，若不存在，请说明理由．四、比例比值取值范围5．（2010年怀化）图9是二次函数k m x y ++=2)(的图象，其顶点坐标为M(1,-4). （1）求出图象与x 轴的交点A,B 的坐标；（2）在二次函数的图象上是否存在点P ，使MAB PAB S S ∆∆=45,若存在，求出P 点的坐标；若不存在，请说明理由；（3）将二次函数的图象在x 轴下方的部分沿x 轴翻折，图象的其余部分保持不变，得到一个新的图象，请你结合这个新的图象回答：当直线)1(<+=b b x y 与此图象有两个公共点时，b 的取值范围.6． (湖南省长沙市2010年)如图，在平面直角坐标系中，矩形OABC 的两边分别在x 轴和y 轴上，82OA = cm ， OC=8cm ，现有两动点P 、Q 分别从O 、C 同时出发，P 在线段OA 上沿OA 方向以每秒2 cm 的速度匀速运动，Q 在线段CO 上沿CO 方向以每秒1 cm 的速度匀速运动．设运动时间为t 秒．（1）用t 的式子表示△OPQ 的面积S ；（2）求证：四边形OPBQ 的面积是一个定值，并求出这个定值；（3）当△OPQ 与△PAB 和△QPB 相似时，抛物线214y x bx c =++经过B 、P 两点，过线段BP 上一动点M 作y 轴的平行线交抛物线于N ，当线段MN 的长取最大值时，求直线MN 把四边形OPBQ 分成两部分的面积之比．B A PxC Q Oy7．（成都市2010年）在平面直角坐标系xOy 中，抛物线2y ax bx c =++与x 轴交于A B 、两点（点A 在点B 的左侧），与y 轴交于点C ，点A 的坐标为(30)-，，若将经过A C 、两点的直线y kx b =+沿y 轴向下平移3个单位后恰好经过原点，且抛物线的对称轴是直线2x =-．（1）求直线AC 及抛物线的函数表达式；（2）如果P 是线段AC 上一点，设ABP ∆、BPC ∆的面积分别为ABP S ∆、BPC S ∆，且:2:3ABP BPC S S ∆∆=，求点P 的坐标；（3）设Q 的半径为l ，圆心Q 在抛物线上运动，则在运动过程中是否存在Q 与坐标轴相切的情况？若存在，求出圆心Q 的坐标；若不存在，请说明理由．并探究：若设⊙Q 的半径为r ，圆心Q 在抛物线上运动，则当r 取何值时，⊙Q 与两坐轴同时相切？五、探究型．8. （2011湖南湘潭市，25，10分）（本题满分10分）如图，直线33+=x y 交x 轴于A 点，交y 轴于B 点，过A 、B 两点的抛物线交x 轴于另一点C （3,0）.⑴ 求抛物线的解析式;⑵ 在抛物线的对称轴上是否存在点Q ，使△ABQ 是等腰三角形？若存在，求出符合条件的Q 点坐标；若不存在，请说明理由.9．（09年重庆市）已知：如图，在平面直角坐标系xOy 中，矩形OABC 的边OA 在y 轴的正半轴上，OC 在x 轴的正半轴上，OA ＝2，OC ＝3．过原点O 作∠AOC 的平分线交AB 于点D ，连接DC ，过点D作DE ⊥DC ，交OA 于点E ．（1）求过点E 、D 、C 的抛物线的解析式；（2）将∠EDC 绕点D 按顺时针方向旋转后，角的一边与y 轴的正半轴交于点F ，另一边与线段OC 交于点G ．如果DF 与（1）中的抛物线交于另一点M ，点M 的横坐标为56，那么EF ＝2GO是否成立？若成立，请给予证明；若不成立，请说明理由；（3）对于（2）中的点G ，在位于第一象限内的该抛物线上是否存在点Q ，使得直线GQ 与AB 的交点P 与点C 、G 构成的△PCG 是等腰三角形？若存在，请求出点Q 的坐标；若不存在，请说明理由．10．（09年湖南省长沙市）如图，抛物线y ＝ax 2＋bx ＋c (a ≠0)与x 轴交于A (－3，0)、B 两点，与y 轴相交于点C (0，3)．当x ＝－4和x ＝2时，二次函数y ＝ax 2＋bx ＋c (a ≠0)的函数值y 相等，连结AC 、BC ．（1）求实数a ，b ，c 的值；（2）若点M 、N 同时从B 点出发，均以每秒1个单位长度的速度分别沿BA 、BC 边运动，其中一个点到达终点时，另一点也随之停止运动．当运动时间为t 秒时，连结MN ，将△BMN 沿MN 翻折，B 点恰好落在AC 边上的P 处，求t 的值及点P 的坐标；（3）在（2）的条件下，抛物线的对称轴上是否存在点Q ，使得以B ，N ，Q 为顶点的三角形与△ABC 相似？若存在，请求出点Q 的坐标；若不存在，请说明理由．六、最值类11．(2010年恩施) 如图11，在平面直角坐标系中，二次函数c bx x y ++=2的图象与x 轴交于A 、B 两点， A 点在原点的左侧，B 点的坐标为（3，0），与y 轴交于C （0，-3）点，点P 是直线BC 下方的抛物线上一动点. （1）求这个二次函数的表达式．（2）连结PO 、PC ，并把△POC 沿CO 翻折，得到四边形POP /C ，那么是否存在点P ，使四边形POP /C 为菱形？若存在，请求出此时点P 的坐标；若不存在请说明理由．（3）当点P 运动到什么位置时，四边形 ABPC 的面积最大并求出此时P 点的坐标和四边形ABPC 的最大面积.12. （2011贵州安顺，27，12分）如图，抛物线y =21x 2+bx －2与x 轴交于A 、B 两点，与y 轴交于C 点，且A （一1，0）．⑴求抛物线的解析式及顶点D 的坐标； ⑵判断△ABC 的形状，证明你的结论；⑶点M (m ，0)是x 轴上的一个动点，当CM +DM 的值最小时，求m 的值．第12题图。

第7讲二次函数综合 -平行四边形存在性问题-检测-2021年海南省中考数学压轴题典型题型训练

2021届中考数学压轴题适应性训练第7讲二次函数综合-平行四边形存在性问题1．已知抛物线y＝ax2+bx+c与x轴交于点A（﹣1，0），点B（3，0），与y轴交于点C（0，3）．顶点为点D．（1）求抛物线的解析式；（2）若过点C的直线交线段AB于点E，且S△ACE：S△CEB＝3：5，求直线CE的解析式；（3）若点P在抛物线上，点Q在x轴上，当以点D，C，P，Q为顶点的四边形是平行四边形时，求点P的坐标．2．如图，已知抛物线y＝ax2+bx﹣1与x轴的交点为A（﹣1，0），B（2，0），且与y轴交于C点．（1）求该抛物线的表达式；（2）点C关于x轴的对称点为C1，M是线段BC1上的一个动点（不与B、C1重合），ME⊥x轴，MF⊥y轴，垂足分别为E、F，当点M在什么位置时，矩形MFOE的面积最大？说明理由．（3）已知点P是直线y=12x+1上的动点，点Q为抛物线上的动点，当以C、C1、P、Q为顶点的四边形为平行四边形时，求出相应的点P和点Q的坐标．3．如图，已知一次函数y=−34x+3的图象与x轴交于点A，与y轴交于点B．抛物线y＝﹣x2+bx+c经过点A、B．（1）求抛物线的解析式；（2）若M（m，y1）、N（n，y2）是第一象限内抛物线上的两个动点，且m＜n．分别过点M、N做MC、ND垂直于x轴，分别交直线AB于点C、D．①如果四边形MNDC是平行四边形，求m与n之间的关系；②在①的前提下，求四边形MNDC的周长L的最大值．4．如图，二次函数y=−13x2+bx+c的图象过原点，与x轴的另一个交点为（8，0）．（1）求该二次函数的解析式；（2）在x轴上方作x轴的平行线y1＝m，交二次函数图象于A、B两点，过A、B两点分别作x轴的垂线，垂足分别为点D、点C．当矩形ABCD为正方形时，求m的值．5．如图，抛物线y＝﹣x2+bx+c交x轴于点A，B，交y轴于点C．点B的坐标为（3，0），点C的坐标为（0，3），点C与点D关于抛物线的对称轴对称．（1）求抛物线的解析式；（2）若点P为抛物线对称轴上一点，连接BD，以PD，PB为边作平行四边形PDNB，是否存在这样的点P，使得▱PDNB是矩形？若存在，请求出点P的坐标；若不存在，请说明理由；（3）点Q在y轴右侧抛物线上运动，当△ACQ的面积与△ABQ的面积相等时，请直接写出点Q的坐标．6．如图，直线y＝x﹣3与坐标轴交于A、B两点，抛物线y=14x2+bx+c经过点B，与直线y＝x﹣3交于点E（8，5），且与x轴交于C，D两点．（1）求抛物线的解析式；（2）抛物线上有一点M，当∠MBE＝75°时，求点M的横坐标；（3）点P在抛物线上，在坐标平面内是否存在点Q，使得以点P，Q，B，C为顶点的四边形是矩形？若存在，请直接写出点Q的坐标；若不存在，请说明理由．7．如图，抛物线y＝x2+bx+c与x轴交于A、B两点，与y轴交于C点，OA＝2，OC＝6，连接AC和BC．（1）求抛物线的解析式；（2）点D在抛物线的对称轴上，当△ACD的周长最小时，点D的坐标为．（3）点E是第四象限内抛物线上的动点，连接CE和BE．求△BCE面积的最大值及此时点E的坐标；（4）若点M是y轴上的动点，在坐标平面内是否存在点N，使以点A、C、M、N为顶点的四边形是菱形？若存在，请直接写出点N的坐标；若不存在，请说明理由．8．如图，抛物线y＝ax2+bx+c与x轴交于点A（﹣4，0）和点B（1，0），与y轴交于点C（0，﹣2）．（1）求抛物线的函数关系式；（2）点D是OA上一点（不与点A、O重合），过点D作x轴的垂线，交抛物线于点E，交AC于点F，当DF=13EF时，求点E的坐标；（3）设抛物线的对称轴l交x轴于点G，在（2）的条件下，点M是抛物线对称轴上一点，点N是坐标平面内一点，是否存在点M、N，使以A、E、M、N为顶点的四边形是菱形？若存在，请求出点N的坐标；若不存在，请说明理由．9．如图，已知矩形ABCD的三个顶点B（1，0），C（3，0），D（3，4）．以A为顶点的抛物线y＝ax2+bx+c过点C．动点P从点A出发，以每秒1个单位的速度沿线段AB向点B 运动，过点P作PE⊥AB交AC于点E，运动时间为t秒．（1）直接写出点A的坐标，并求出抛物线的解析式；（2）过点E作EF⊥AD于F，交抛物线于点G，当t为何值时，△ACG的面积最大？最大值为多少？（3）若动点Q同时．．从点C出发，以每秒1个单位的速度沿线段CD向点D运动，在动点P，Q运动的过程中，当t为何值时，在矩形ABCD内（包括边界）存在点H，使以C，Q，E，H为顶点的四边形为菱形？请直接写出t的值．（4）在AB右侧的抛物线上有一动点M，在坐标平面内有一点N．当t为何值时，以A、E、M、N为顶点的四边形是正方形？请直接写出t的值．2021届中考数学压轴题适应性训练第7讲二次函数综合-平行四边形存在性问题1．已知抛物线y＝ax2+bx+c与x轴交于点A（﹣1，0），点B（3，0），与y轴交于点C（0，3）．顶点为点D．（1）求抛物线的解析式；（2）若过点C的直线交线段AB于点E，且S△ACE：S△CEB＝3：5，求直线CE的解析式；（3）若点P在抛物线上，点Q在x轴上，当以点D，C，P，Q为顶点的四边形是平行四边形时，求点P的坐标．【解答】解：（1）因为抛物线经过A（﹣1，0），B（3，0），∴可以假设抛物线的解析式为y＝a（x+1）（x﹣3），把C（0，3）代入，可得a＝﹣1，∴抛物线的解析式为y＝﹣（x+1）（x﹣3）＝﹣x2+2x+3．（2）如图1中，连接AC，BC．∵S△ACE：S△CEB＝3：5，∴AE：EB＝3：5，∵AB＝4，∴AE ＝4×38=32， ∴OE ＝0.5，设直线CE 的解析式为y ＝kx +b ，则有{b =30.5k +b =0，解得{k =−6b =3，∴直线EC 的解析式为y ＝﹣6x +3．（3）由题意C （0，3），D （1，4）．当四边形P 1Q 1CD ，四边形P 2Q 2CD 是平行四边形时，点P 的纵坐标为1，当y ＝1时，﹣x 2+2x +3＝1，解得x ＝1±√3，∴P 1（1+√3，1），P 2（1−√3，1），当四边形P 3Q 3DC ，四边形P 4Q 4DC 是平行四边形时，点P 的纵坐标为﹣1，当y ＝﹣1时，﹣x 2+2x +3＝﹣1，解得x ＝1±√5，∴P 1（1+√5，﹣1），P 2（1−√5，﹣1），综上所述，满足条件的点P 的坐标为（1+√3，1）或（1−√3，1）或（1−√5，﹣1）或（1+√5，﹣1）．2．如图，已知抛物线y ＝ax 2+bx ﹣1与x 轴的交点为A （﹣1，0），B （2，0），且与y 轴交于C 点．（1）求该抛物线的表达式；（2）点C 关于x 轴的对称点为C 1，M 是线段BC 1上的一个动点（不与B 、C 1重合），ME ⊥x 轴，MF ⊥y 轴，垂足分别为E 、F ，当点M 在什么位置时，矩形MFOE 的面积最大？说明理由．（3）已知点P 是直线y =12x +1上的动点，点Q 为抛物线上的动点，当以C 、C 1、P 、Q 为顶点的四边形为平行四边形时，求出相应的点P 和点Q 的坐标．【解答】解：（1）将A （﹣1，0），B （2，0）分别代入抛物线y ＝ax 2+bx ﹣1中，得{a −b =14a +2b =1，解得：{a =12b =−12 ∴该抛物线的表达式为：y =12x 2−12x ﹣1．（2）在y =12x 2−12x ﹣1中，令x ＝0，y ＝﹣1，∴C （0，﹣1） ∵点C 关于x 轴的对称点为C 1，∴C 1（0，1），设直线C 1B 解析式为y ＝kx +b ，将B （2，0），C 1（0，1）分别代入得{2k +b =0b =1，解得{k =−12b =1，∴直线C 1B 解析式为y =−12x +1，设M （t ，−12t +1），则 E （t ，0），F （0，−12t +1） ∴S 矩形MFOE ＝OE ×OF ＝t （−12t +1）=−12（t ﹣1）2+12， ∵−12＜0，∴当t ＝1时，S 矩形MFOE 最大值=12，此时，M （1，12）；即点M 为线段C 1B 中点时，S 矩形MFOE最大．（3）由题意，C （0，﹣1），C 1（0，1），以C 、C 1、P 、Q 为顶点的四边形为平行四边形，分以下两种情况：①C 1C 为边，则C 1C ∥PQ ，C 1C ＝PQ ，设P （m ，12m +1），Q （m ，12m 2−12m ﹣1），∴|（12m 2−12m ﹣1）﹣（12m +1）|＝2，解得：m 1＝4，m 2＝﹣2，m 3＝2，m 4＝0（舍），P 1（4，3），Q 1（4，5）；P 2（﹣2，0），Q 2（﹣2，2）；P 3（2，2），Q 3（2，0） ②C 1C 为对角线，∵C 1C 与PQ 互相平分，C 1C 的中点为（0，0）， ∴PQ 的中点为（0，0），设P （m ，12m +1），则Q （﹣m ，12m 2+12m ﹣1）∴（12m +1）+（12m 2+12m ﹣1）＝0，解得：m 1＝0（舍去），m 2＝﹣2，∴P 4（﹣2，0），Q 4（2，0）；综上所述，点P 和点Q 的坐标为：P 1（4，3），Q 1（4，5）或P 2（﹣2，0），Q 2（﹣2，2）或P 3（2，2），Q 3（2，0）或P 4（﹣2，0），Q 4（2，0）．3．如图，已知一次函数y =−34x +3的图象与x 轴交于点A ，与y 轴交于点B ．抛物线y ＝﹣x 2+bx +c 经过点A 、B ．（1）求抛物线的解析式；（2）若M （m ，y 1）、N （n ，y 2）是第一象限内抛物线上的两个动点，且m ＜n ．分别过点M 、N 做MC 、ND 垂直于x 轴，分别交直线AB 于点C 、D ． ①如果四边形MNDC 是平行四边形，求m 与n 之间的关系； ②在①的前提下，求四边形MNDC 的周长L 的最大值．【解答】解：（1）∵一次函数y =−34x +3的图象与x 轴交于点A ，与y 轴交于点B ， ∴A （4，0），B （0，3），∵抛物线y ＝﹣x 2+bx +c 经过点A 、B ， ∴{−16+4b +c =0c =3，解得{b =134c =3，∴抛物线的解析式为y ＝﹣x 2+134x +3．（2）①由题意M （m ，﹣m 2+134m +3），N （n ，﹣n 2+134n +3），C （m ，−34m +3），D （n ，−34n +3），∵四边形MNDC 是平行四边形， ∴MC ＝DN ，∴﹣m 2+4m ＝﹣n 2+4n ， ∴（m ﹣n ）（m +n ﹣4）＝0， ∵m ＜n ， ∴m ﹣n ≠0， ∴m +n ＝4．（也可以设直线MN 解析式，再用韦达定理）②由题意L ＝2[（﹣m 2+4m ）+54（n ﹣m ）]＝2[﹣m 2+4m +54（4﹣2m ）]＝2（﹣m 2+4m +5−52m ）＝﹣2（m −34）2+898， ∵﹣2＜0，∴m =34时，L 有最大值，最大值为898．4．如图，二次函数y =−13x 2+bx +c 的图象过原点，与x 轴的另一个交点为（8，0）．（1）求该二次函数的解析式；（2）在x 轴上方作x 轴的平行线y 1＝m ，交二次函数图象于A 、B 两点，过A 、B 两点分别作x 轴的垂线，垂足分别为点D 、点C ．当矩形ABCD 为正方形时，求m 的值．【解答】解：（1）将（0，0），（8，0）代入y =−13x 2+bx +c ，得：{c =0−643+8b +c =0，解得：{b =83c =0， ∴该二次函数的解析式为y =−13x 2+83x ．（2）当y＝m时，−13x2+83x＝m，解得：x1＝4−√16−3m，x2＝4+√16−3m，∴点A的坐标为（4−√16−3m，m），点B的坐标为（4+√16−3m，m），∴点D的坐标为（4−√16−3m，0），点C的坐标为（4+√16−3m，0）．∵矩形ABCD为正方形，∴4+√16−3m−（4−√16−3m）＝m，解得：m1＝﹣16（舍去），m2＝4．∴当矩形ABCD为正方形时，m的值为4．5．如图，抛物线y＝﹣x2+bx+c交x轴于点A，B，交y轴于点C．点B的坐标为（3，0），点C的坐标为（0，3），点C与点D关于抛物线的对称轴对称．（1）求抛物线的解析式；（2）若点P为抛物线对称轴上一点，连接BD，以PD，PB为边作平行四边形PDNB，是否存在这样的点P，使得▱PDNB是矩形？若存在，请求出点P的坐标；若不存在，请说明理由；（3）点Q在y轴右侧抛物线上运动，当△ACQ的面积与△ABQ的面积相等时，请直接写出点Q的坐标．【解答】解：（1）把B点坐标、点C点坐标为代入抛物线y＝﹣x2+bx+c方程，解得，抛物线方程为：y＝﹣x2+2x+3…①；点A坐标为（﹣1，0），点D坐标为（2，3），函数的对称轴为x＝1；（2）存在．设点P（1，m），设函数对称轴交x轴于点T，过点D作DM⊥PN于点M，则∠MDP ＝∠BPT ，则tan ∠MDP ＝tan ∠BPT ，即：3−m 2−1=3−1m，解得：m ＝1或m ＝2；则点P （1，1）或（1，2）；（3）①当点Q 在x 轴上方时，设点Q 坐标为（t ，﹣t 2+2t +3），则：AQ 所在的直线方程为：y ＝（3﹣t ）x +（3﹣t ），如图所示，连接CA 、QB ，过点Q 作x 轴的垂线QN 交x 轴于N 点，当△ACQ 的面积与△ABQ 的面积相等时，即：S 四边形ACQB ＝2S △ABQ ， S四边形ACQB ＝S梯形CONQ +S △AOC +S △BQN =12（﹣t 2+2t +3+3）×t +12×1×3+12（3﹣t ）（﹣t 2+2t +3）， =32（﹣t 2+3t +4），S △ABQ =12（3+1）（﹣t 2+2t +3）， ∵S 四边形ACQB ＝2S △ABQ ，化简得：5t 2﹣7t ﹣12＝0，解得：t ＝﹣1或125（舍去负值），②当Q 在x 轴下方时，由△ACQ 的面积与△ABQ 的面积相等，则点B 、C 到AQ 的距离相等，即AQ ∥BC ，由点B 、C 的坐标得，直线BC 的表达式为：y ＝﹣x +3，则AQ 的表达式为：y ＝﹣（x +1）＝﹣x ﹣1…②，联立①②并解得：x ＝4，故点Q 坐标为（4，﹣5），综上，点Q 坐标为（125，5125）或（4，﹣5）．6．如图，直线y ＝x ﹣3与坐标轴交于A 、B 两点，抛物线y =14x 2+bx +c 经过点B ，与直线y ＝x ﹣3交于点E （8，5），且与x 轴交于C ，D 两点．（1）求抛物线的解析式；（2）抛物线上有一点M ，当∠MBE ＝75°时，求点M 的横坐标；（3）点P 在抛物线上，在坐标平面内是否存在点Q ，使得以点P ，Q ，B ，C 为顶点的四边形是矩形？若存在，请直接写出点Q 的坐标；若不存在，请说明理由．【解答】解：（1）直线y ＝x ﹣3与坐标轴交于A 、B 两点，则A （3，0）B （0，﹣3），把B 、E 点坐标代入二次函数方程，解得：抛物线的解析式y=14x2﹣x﹣3…①，则：C（6，0）；（2）符合条件的有M和M′，如下图所示，当∠MBE＝75°时，∵OA＝OB，∴∠MBO＝30°，此时符合条件的M只有如图所示的一个点，MB直线的k为−√3，所在的直线方程为：y=−√3x﹣3…②，联立方程①、②可求得：x＝4﹣4√3，即：点M的横坐标4﹣4√3；当∠M′BE＝75°时，∠OBM′＝120°，直线M′B的k值为−√33，其方程为y=−√33x﹣3，将M′B所在的方程与抛物线表达式联立，解得：x=12−4√33，故：即：点M的横坐标4﹣4√3或12−4√33．（3）存在．①当BC为矩形对角线时，矩形BP′CQ′所在的位置如图所示，设：P′（m，n），n=14m2﹣m﹣3…③，P′C所在直线的k1=nm−6，P′B所在的直线k2=n+3m，则：k1•k2＝﹣1…④，③、④联立得：116m(m−6)(m2−2m+8)=0，解得：m＝0或6，这两个点分别和点B、C重合，与题意不符，故：这种情况不存在，舍去．②当BC为矩形一边时，情况一：矩形BCQP所在的位置如图所示，直线BC所在的方程为：y=12x﹣3，则：直线BP的k为﹣2，所在的方程为y＝﹣2x﹣3…⑤，联立①⑤解得点P（﹣4，5），则Q（2，8），情况二：矩形BCP″Q″所在的位置如图所示，此时，P″在抛物线上，其坐标为：（﹣10，32），Q″坐标为（﹣16，29）．故：存在矩形，点Q 的坐标为：（2，8）或（﹣16，29）．7．如图，抛物线y ＝x 2+bx +c 与x 轴交于A 、B 两点，与y 轴交于C 点，OA ＝2，OC ＝6，连接AC 和BC ．（1）求抛物线的解析式；（2）点D 在抛物线的对称轴上，当△ACD 的周长最小时，点D 的坐标为．（3）点E 是第四象限内抛物线上的动点，连接CE 和BE ．求△BCE 面积的最大值及此时点E 的坐标；（4）若点M 是y 轴上的动点，在坐标平面内是否存在点N ，使以点A 、C 、M 、N 为顶点的四边形是菱形？若存在，请直接写出点N 的坐标；若不存在，请说明理由．【解答】解：（1）∵OA ＝2，OC ＝6 ∴A （﹣2，0），C （0，﹣6） ∵抛物线y ＝x 2+bx +c 过点A 、C ∴{4−2b +c =00+0+c =−6 解得：{b =−1c =−6 ∴抛物线解析式为y ＝x 2﹣x ﹣6（2）∵当y ＝0时，x 2﹣x ﹣6＝0，解得：x 1＝﹣2，x 2＝3 ∴B （3，0），抛物线对称轴为直线x =−2+32=12 ∵点D 在直线x =12上，点A 、B 关于直线x =12对称 ∴x D =12，AD ＝BD∴当点B 、D 、C 在同一直线上时，C △ACD ＝AC +AD +CD ＝AC +BD +CD ＝AC +BC 最小设直线BC 解析式为y ＝kx ﹣6 ∴3k ﹣6＝0，解得：k ＝2 ∴直线BC ：y ＝2x ﹣6 ∴y D ＝2×12−6＝﹣5∴D （12，﹣5）故答案为：（12，﹣5）（3）过点E 作EG ⊥x 轴于点G ，交直线BC 与点F 设E （t ，t 2﹣t ﹣6）（0＜t ＜3），则F （t ，2t ﹣6） ∴EF ＝2t ﹣6﹣（t 2﹣t ﹣6）＝﹣t 2+3t∴S △BCE ＝S △BEF +S △CEF =12EF •BG +12EF •OG =12EF （BG +OG ）=12EF •OB =12×3（﹣t 2+3t ）=−32（t −32）2+278∴当t =32时，△BCE 面积最大 ∴y E ＝（32）2−32−6=−214∴点E 坐标为（32，−214）时，△BCE 面积最大，最大值为278．（4）存在点N ，使以点A 、C 、M 、N 为顶点的四边形是菱形． ∵A （﹣2，0），C （0，﹣6） ∴AC =√22+62=2√10 ①若AC 为菱形的边长，如图3，则MN ∥AC 且，MN ＝AC ＝2√10∴N 1（﹣2，2√10），N 2（﹣2，﹣2√10），N 3（2，0） ②若AC 为菱形的对角线，如图4，则AN 4∥CM 4，AN 4＝CN 4 设N 4（﹣2，n ） ∴﹣n =√22+(n +6)2 解得：n =−103 ∴N 4（﹣2，−103）综上所述，点N 坐标为（﹣2，2√10），（﹣2，﹣2√10），（2，0），（﹣2，−103）．8．如图，抛物线y＝ax2+bx+c与x轴交于点A（﹣4，0）和点B（1，0），与y轴交于点C（0，﹣2）．（1）求抛物线的函数关系式；（2）点D 是OA 上一点（不与点A 、O 重合），过点D 作x 轴的垂线，交抛物线于点E ，交AC 于点F ，当DF =13EF 时，求点E 的坐标；（3）设抛物线的对称轴l 交x 轴于点G ，在（2）的条件下，点M 是抛物线对称轴上一点，点N 是坐标平面内一点，是否存在点M 、N ，使以A 、E 、M 、N 为顶点的四边形是菱形？若存在，请求出点N 的坐标；若不存在，请说明理由．【解答】解：（1）由题意，OA ＝4，OB ＝1，OC ⊥AB ， ∵∠ACB ＝90°，∴∠AOC ＝∠COB ，∠OCA +∠OAC ＝90°，∠OCA ＝∠OCB ＝90°， ∴∠OAC ＝∠OCB ， ∴△OAC ～△OCB ， ∴OC OA=OB OC，∴OC =√OA ⋅OB =√4×1=2， ∴C （0，﹣2），分别把A （﹣4，0），B （1，0），C （0，﹣2）代入y ＝ax 2+bx +c 得{16a −4b +c =0a +b +c =0c =−2解得{k =−12b =−2， ∴y =12x 2+32x −2；（2）设直线AC 函数关系式为y ＝kx +b ，代入A （﹣4，0），C （0，﹣2）得，{−4k +b =0b =−2，解得，k =−12，b ＝﹣2， ∴y =−12x −2，设D （m ，0），∴y E =12m 2+32m −2，y F =−12m −2， ∴DF =12m +2，EF =y F −y E =−12m 2−2m ，由题意12m +2=13（−12m 2﹣2m ），解得，m ＝﹣3或﹣4（舍去）将m ＝﹣3代入y E =12m 2+32m −2，得y E =12m 2+32m −2=−2， ∴E （﹣3，﹣2）；（3）存在，理由：当以A 、E 、M 、N 为顶点的四边形是菱形时，△AEM 是等腰三角形．由题意，AD ＝1，DE ＝2，−b 2a =−32，在Rt △ADE 中，由勾股定理的，AE =√5， ①当AE 是边时，当AM =AE =√5时，∵点A 到直线l 的距离是−32−(−4)=52＞√5， ∴此时点M 不存在．当EM =AE =√5时，如图，此时菱形为AEMN ，过点E 作EH ⊥l 于点H ，∴y H ＝y E ＝﹣2，EH =−32−(−3)=32，在Rt △EHM 中，由勾股定理得MH =√(√5)2−(32)2=√112， ∴y M =−2+√112或−2−√112，∴M1(−32，−2+√112)，M2(−32，−2−√112)；当点M为（−32，﹣2+√112）时，由EM＝AN知，x M﹣x E＝x N﹣x A，即−32−（﹣3）＝x N﹣（﹣4），解得x N=−52，同理可得，y N=√112，故点N1的坐标为（−52，√112）；同理可得N2的坐标为（−52，−√112）；②当AE是对角线时，此时MA＝ME，即MA2＝ME2，此时菱形为AM3EN，即MG2+AG2＝MH2+EH2，设M(−32，n)，n2+(52)2=(n+2)2+(32)2，解得n＝0，∴M3=(−32，0)，即点M3在x轴上，则EN＝AM3=−32+4=52=x N﹣x E＝﹣3﹣x N，解得x N=−11 2；综上，N1(−52，√112)，N2(−52，−√112)，N3(−112，−2)．9．如图，已知矩形ABCD的三个顶点B（1，0），C（3，0），D（3，4）．以A为顶点的抛物线y＝ax2+bx+c过点C．动点P从点A出发，以每秒1个单位的速度沿线段AB向点B 运动，过点P作PE⊥AB交AC于点E，运动时间为t秒．（1）直接写出点A的坐标，并求出抛物线的解析式；（2）过点E作EF⊥AD于F，交抛物线于点G，当t为何值时，△ACG的面积最大？最大值为多少？（3）若动点Q同时．．从点C出发，以每秒1个单位的速度沿线段CD向点D运动，在动点P，Q运动的过程中，当t为何值时，在矩形ABCD内（包括边界）存在点H，使以C，Q，E，H为顶点的四边形为菱形？请直接写出t的值．（4）在AB右侧的抛物线上有一动点M，在坐标平面内有一点N．当t为何值时，以A、E、M、N为顶点的四边形是正方形？请直接写出t的值．【解答】解：（1）A （1，4）．由题意知，可设抛物线解析式为y ＝a （x ﹣1）2+4∵抛物线过点C （3，0），∴0＝a （3﹣1）2+4，解得，a ＝﹣1，∴抛物线的解析式为y ＝﹣（x ﹣1）2+4，即y ＝﹣x 2+2x +3．（2）∵A （1，4），C （3，0），∴可求直线AC 的解析式为y ＝﹣2x +6．∵点P （1，4﹣t ）．∴将y ＝4﹣t 代入y ＝﹣2x +6中，解得点E 的横坐标为x ＝1+t 2． ∴点G 的横坐标为1+t 2，代入抛物线的解析式中，可求点G 的纵坐标为4−t 24． ∴GE ＝（4−t 24）﹣（4﹣t ）＝t −t 24．又∵点A 到GE 的距离为t 2，C 到GE 的距离为2−t 2，即S △ACG ＝S △AEG +S △CEG =12•EG •t 2+12•EG （2−t 2） =12•2（t −t 24）=−14（t ﹣2）2+1．当t ＝2时，S △ACG 的最大值为1．（3）第一种情况如图1所示，点H 在AC 的上方，由四边形CQEH 是菱形知CQ ＝CE＝t，根据△APE∽△ABC，知AP AB =AEAC，即t4=√5−t2√5，解得t＝20﹣8√5；第二种情况如图2所示，点H在AC的下方，由四边形CQHE是菱形知CQ＝QE＝EH＝HC＝t，PE=12t，EM＝2−12t，MQ＝4﹣2t．则在直角三角形EMQ中，根据勾股定理知EM2+MQ2＝EQ2，即（2−12t）2+（4﹣2t）2＝t2，解得，t1=2013，t2＝4（不合题意，舍去）．综上所述，t＝20﹣8√5或t=20 13．（4）t=29或49．理由：当AE为正方形的边时，如图1，过M作MK⊥PE，与PE的延长线交于点K，∵APE＝∠EKM＝90°，∴∠P AE+∠PEA＝∠PEA+∠KEM＝90°，∴∠P AE＝∠KEM，∵AE＝EM，∴△APE≌△EKM（AAS），∴AP＝EK＝t，PE＝KM=12 t，∴M（1+32t，4−12t），把M（1+32t，4−12t）代入y＝﹣x2+2x+3中，得4−12t＝﹣（（1+32t）2+2（（1+32t）+3，解得，t＝0（舍），或t=2 9；当AE为正方形的对角线时，如图2，过M作MK⊥PE，与PE的延长线交于点K，与AD交于点H，设M（m，﹣m2+2m+3），则MK＝﹣m2+2m﹣1+t，MH＝m2﹣2m+1，AH＝m﹣1，EK＝m−12t﹣1，按前一种情况的方法可得△AHM≌△MKE，∴AH＝MK，MH＝EK，∴m﹣1＝﹣m2+2m﹣1+t，m2﹣2m+1＝m−12t﹣1，两方程消去t得3m2﹣7m+4＝0，解得，m＝0（舍去），或m=4 3，∴t=4 9．综上，t=29或49．。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2021年中考数学复习：与平行四边形相关的二次函数综合型压轴题解题技巧方法提炼：
1、特殊四边形的探究问题解题方法步骤如下:（1）先假设结论成立；（2）设出点坐标，求边长.（类型一方法指导）；（3）建立关系式，并计算。

若四边形的四个顶点位置已确定，则直接利用四边形边的性质进行计算；若四边形的四个顶点位置不确定，需分情况讨论。

2、探究平行四边形：①以已知边为平行四边形的某条边，画出所有的符合条件的图形后，利用平行四边形的对边相等进行计算；②以已知边为平行四边形的对角线，画出所有的符合条件的图形后，利用平行四边形对角线互相平分的性质进行计算；③若平行四边形的各顶点位置不确定，需分情况讨论，常以已知的一边作为一边或对角线分情况讨论。

典例引领：
例：如图所示：已知抛物线y＝ax2（a≠0）与一次函数y＝kx+b的图象相交于两点A（﹣1，﹣1），B（2，﹣4），点P是抛物线上不与A，B重合的一个动点，点Q是y轴上的一个动点．
（1）求a，k，b的值．
（2）直接写出关于x的不等式ax2＜kx﹣2的解集；
（3）当点P在直线AB上方时，请求出△P AB面积的最大值并求出此时点P的坐标；
（4）是否存在以P，Q，A，B为顶点的四边形是平行四边形？若存在，请直接写出P，Q的坐标；若不存在，请说明理由．
分析：（1）根据待定系数法得出a，k，b的值；
（2）观察函数图象，即可得出不等式的解集；
（3）过点A作y轴的平行线，过点B作x轴的平行线，两者交于点C，连接PC．根据三角形的面积公式解答即可；
（4）根据平行四边形的性质和坐标特点解答即可．
解：（1）把A（﹣1，﹣1），代入y＝ax2中，可得：a＝﹣1，
把A（﹣1，﹣1），B（2，﹣4）代入y＝kx+b中，可得：，解得，
∴a＝﹣1，k＝﹣1，b＝﹣2；
（2）观察函数图象可知，关于x的不等式ax2＜kx﹣2的解集是x＜﹣1或x＞2；
（3）过点A作y轴的平行线，过点B作x轴的平行线，两者交于点C，
∵A（﹣1，﹣1），B（2，﹣4），
∴C（﹣1，﹣4），AC＝BC＝3，
设点P的横坐标为m，则点P的纵坐标为﹣m2．
过点P作PD⊥AC于D，作PE⊥BC于E．则D（﹣1，﹣m2），E（m，﹣4），
∴PD＝m+1，PE＝﹣m2+4．
∴S△APB＝S△APC+S△BPC﹣S△ABC，
＝×AC•PD+×BC•PE﹣×BC•AC，
＝×3×（m+1）×3×（﹣m2+4）﹣×3×3，
＝﹣m2+m+3．
∵﹣＜0，m＝﹣＝，
而﹣1＜m＜2，
∴当m＝时，S△APB的最大值为，此时点P的坐标为（，﹣）；（4）存在三组符合条件的点．
当以P，Q，A，B为顶点的四边形是平行四边形时，
∵AP＝BQ，AQ＝BP，A（﹣1，﹣1），B（2，﹣4），
可得坐标如下：
①P′的横坐标为﹣3，代入二次函数表达式，
解得：P'（﹣3，﹣9），Q'（0，﹣12）；
②P″的横坐标为3，代入二次函数表达式，。