四象限乘法器
四象限乘法器

四通道四象限模拟乘法器MLT04四通道四象限模拟乘法器MLT041MLT04的结构功能和主要特点在高频电子线路中,振幅调制、同步检波、混频、倍频、鉴频等调制与解调的过程均可视为两个信号相乘的过程,而集成模拟乘法器正是实现两个模拟量电压或电流相乘的电子器件。
采用集成模拟乘法器实现上述功能比用分立器件要简单得多,而且性能优越,因此集成模拟乘法器在无线通信、广播电视等方面应用较为广泛。
在目前的乘法器中,单通道器件(如MOTOROLA的MC1496)无法实现多通道的复杂运算;二象限器件(如ADI公司的AD539)又会使负信号的应用受到限制。
而ADI公司的MLT04则是一款完全四通道四象限电压输出模拟乘法器,这种完全乘法器克服了以上器件的诸多不足之处,适用于电压控制放大器、可变滤波器、多通道功率计算以及低频解调器等电路。
非常适合于产生复杂的要求高的波形,尤其适用于高精度CRT显示系统的几何修正。
其内部结构及引脚排列如图1所示。
MLT04是由互补双极性工艺制作而成,它包含有四个高精度四象限乘法单元。
温度漂移小于0.005%/℃。
0.3μV/Hz的点噪声电压使低失真的Y通道只有0.02%的总谐波失真噪声,四个8MHz通道的总静止功耗也仅为150mW。
MLT04的工作温度范围为-40℃~+85℃。
MLT04的其它主要特性如下:●四个独立输入通道;●四象限乘法信号;●电压输入电压输出;●乘法运算无需外部元件;●电压输出:W=(X×Y)/2.5V,其中X或Y上的线性度误差仅为0.2%;●具有优良的温度稳定性:0.005%;●模拟输入范围为±2.5V,采用±5V电压供电;●低功耗一般为150mW。
2误差源和非线性模拟乘法器的静态误差主要由输入失调电压、输出偏置电压、比例系数以及非线性度引起。
在这四种误差源中,只有X和Y的输入失调电压可以由外部调整。
而MLT04的输出偏置电压在出厂时已由厂家调整至50mV,比例系数在整个量程之内被内部调整为2.5%。
四象限乘法器设计

Design of an BJT analog multiplier1. IntroductionThe analog multiplier is a wildly used circuit that can take two analog inputs and produce an output proportional to their product. In modern IC industry, the analog multiplier is a very useful building block for the design of analog signal processing and the communication systems. Its application fields include signal modulation/demodulation, gain control, phase lock loops, frequency translation and waveform generation (Graeme, 1971). The purpose of this report is to explain the design method of a 4 quadrant analog multiplier using bipolar transistor. In this report, the theory of the analog multiplier is introduced. And then a suggested circuit based on the Gilbert multiplier provided. After that, the circuit simulation is processed with LTSPICE. In the last, the limitation and improvement of this design is being discussed.2. Principle of analog multiplier2.1 Characteristic of bipolar transistorThe basic cell of an analog multiplier is bipolar transistor. Here is a LTSPICE schematic diagram of a biased BJT.Fig.1. Schematic diagram of bipolar transistor Fig.2. I-V characteristic of bipolartransistorBecause of the semiconductor physical characteristic, the base-emitter voltage has an exponential relationship with the collector current (Ashburn, 2003). In most situations, the I-V characteristic can be written in the following equation:2exp()exp()nb i BE BE E C S th B AB qAD n V qV I I I V W N kT(Eq.1)Here, 2nb i S B AB qAD n I W N is saturation current of the base. th kT V q is thermal voltage, which can be considered equal to 26mV in room temperature. I C is the collector current. I E is the emitter current. V BE is the base-emitter voltage. I S is a constant which is determined by the geometric size of base and its doping density. V th is a constant which is only determined by the temperature. It can be seen from the equation that the collector current will exponential increase with the base-emitter voltage. Using LTSPICE DC simulation, the figure 2 can show this relationship directly. From the graph it can be seen that the I C equals nearly to 0 when V BE is less than 520mV. Also I C has a maximum value when V BE arrival 700mV. So the threshold voltage V T is in this range. And the exponential relationship only works in this range.2.2 Simple multiplierBased on the characteristic of bipolar transistor discussed above, a simple multiplier circuit can be developed. The structure of this circuit is shown in figure 3 and 4.Fig.3. the differential amplifier circuit Fig.4. 2 quadrant analog multiplier circuit In figure 3, Vx is the differential input. Io is the current source. Q1, Q2 are two NPN transistors. It can be seen that:And:According to these 2 equations, . From the Eq.1., we canobtain . In mathematics, when(about 2*26mV), . Thus we get:(Eq.2) The different current and can be used as the output, so we can get an output voltage which is proportional to the input voltage (Gray, 2001). This is:(Eq.3) The circuit of figure 4 is established on the circuit of figure 3. In this circuit, there isSubstitute this formula into the Eq.3, we have:(Eq.4) If, Eq.4 is approximately equal to:(Eq.5) In this equation, can be either positive or negative. But in order to ensure the Q3 is turned on, must be larger than , which means must be positive. Thus this analog multiplier can only work in 2 quadrants, the first quadrant and the second quadrant.2.3 The Gilbert CellThe basic Gilbert analog multiplier cell is presented in the figure 5.Fig.5 the circuit of Gilbert cellIn this circuit, the input voltage Vx and Vy can generate pairs of differential currents, which results in the collector currents of the transistors. According to Eq.2, there areThus, the combination of these 3 equations above gives the difference of two output currentsBecause the derivation of this derivation is based on the Eq.2, it must satisfy the same requirement, which is and . At this time, the output voltage isFrom this equation it can be seen that the output voltage is proportional to the product of Vx and Vy. However, different from the 2 quadrant multiplier, here the input signal Vy can be either positive or negative. So, an analog multiplier can be realised.3. Circuit design3.1 basic analog multiplier circuitThe circuit of the practical basic 4 quadrant multiplier build on the previous analysis is presented in the following figure.Fig.6 the 4 quadrant multiplier based on the Gilbert cellThe compositions of this circuit are resisters and transistors. For the rough design, current source is used directly. And the structure of two current sources is more sensitive than that of one current source, so the circuit will get a better balance characteristic. According to the analysis in 2.1, the exponential relationship between base-emitter voltage and collector current only remain in the range of 520mV-700mV. So the static base-emitter current can be chosen at 610mV, the middle point of thisrange. From figure 4, the corresponding collector current is about 0.2mA. In addition, the emitter current is approximately equal to the collector current. So 0.2mA can be set as the value of the current resources.In this circuit, the npn transistors are all 2N2222. It can be seen from the circuit that the function of the transistor pair Q7 and Q8 is transforming the voltage input signal into current input signal, so is the transistor pair Q5 and Q6. Thus, the multiplier operation is based on the variation of the currents. In addition, the four transistors Q7, Q8, Q9, Q10 and the resistor R2 consist of a block which can generate a signal of function. This current can compensate the function generated by the next transistors Q1, Q2, Q3 and Q4. Thus, the output current signal has no relationship with function, that means there is no limitation of (Gray, 2001). This feature significantly expands the input signal magnitude. The transistors Q5, Q6 and resistor R1 have the same feature and the limitation is also cancelled. The output of the nonlinear compensation block in the front of Gilbert cell isFor Ic7 and Ic8, there areSubstitute Ic7 and Ic8 into Eq.9, the output of the nonlinear compensation block is given byIn the Gilbert cell block, the emitter resistors of Q5 and Q6 are much smaller than R1, so we have . So Ic5 and Ic6 is given byUse Eq.11, Eq.12 and Eq.10 to calculate the output voltage based on the Eq.6, Eq.7 and Eq.8. Finally we can obtainFrom this equation and the above derivation, it can be seen that:When R1 and R2 is big enough, the output voltage Vo is proportional to theproduct of Vx and Vy. And the circuit will get the nearly ideal multiplierfunction.Both Vx and Vy can be positive and negative, so it is a 4 quadrant multiplier.The gain coefficient , which is determined by the paramount Rc,R1, R2 andK has no relationship with Vth, so this circuit has a nice thermal stability.In this circuit, because the current sources are all 0.2mA, a several independentcurrent sources based on the current mirror can be used.From Gray and Hurst, there are mainly 3 types of current mirrors: the simple current mirror, simple current mirror with beta () helper, and the Wilson current mirror (Gray, 2001). For the first one, the output current . For the third one, the outputcurrent is . It can easily be seen that the Wilson current mirror can geta much more precise output current. Thus, in this report, the Wilson current mirror isused as the current source. The whole structure is shown in figure 7.Fig.7 the circuit structure with mirror current sourceIn order to get a precise value of the current , a resistor is added between the Vdd and the current mirror transistor. The aimed current is 0.2mV, so the value of this resistor .Use LTSPICE to simulate the circuit. Here is the DC sweep for the circuit.Fig.8. The DC sweep simulation resultThe settings of this simulation are as the follows: sweep Vx from -13V to 13V, and the increment is 1V; sweep Vy from 13V to -13V, and the increment is 1V. During the design, it can be noticed that the magnitude of input signals have a proportional relationship with the product of and R1 (or R2). Besides, to get high amplitude of Vo, Eq.13 must be considered. In this report, the circuit has a nice linear range of output signal when the input signal varies from -13V to +13V. And the output signal has the same range with the input signals.In order to obtain this amplitude of output signal, the V dd and V EE are set up at +32V and -15V respectively.Transient simulation:Fig.8 simulation result for AC inputs Fig.10 simulation results for squareoperationThe settings of the simulation of figure 8 are as the follows:Vx: amplitude=13V; frequency=10 kHz; phase=0. Vy: amplitude=13V; frequency=10 kHz; phase=90o. The Vx input is a sin(t) signal, the Vy input is a cos(t) signal. In this simulation, the Vx and Vy contain all 4 quadrant inputs combinations in one period, which are (Vx>0, Vy>0), (Vx>0, Vy<0), (Vx<0, Vy<0), (Vx>0, Vy>0). So the results proved the circuit can work in 4 quadrants. Furthermore, the frequency of the output signal is twice as the input signals and the amplitude is about half of the input ones. These features satisfy the functionof. So the result proved the circuit can work as an analog multiplier.One useful application of analog multiplier is square operation. As the figure 10 shows, make the two pulse input signal same, then we can obtain a parabola output signal. So the results of can be calculated.Frequency response simulation:Fig.11 Simulation result of frequency responseThis figure shows the frequency response of the circuit. When theAmplitude-frequency characteristic decrease from -22dB to -25dB (increased by -3dB), the relative operation frequency is 500.4 kHz. Below this frequency, the circuit can work nicely.Another useful application of analog multiplier is modulator. In the modulator, the low frequency signal is used to modulate, and the high frequency signal acts as a carrier.Fig.12. modulator simulation: Vx has no DC offset Fig.13 modulator simulation: Vx has a 1.5V DC offsetIt can be seen from the above 2 figures, the frequency of the output signal can be changed by change the magnitude of the input signal.3.2 improvement of output signal amplifyThe output signal of the 3.1 circuit has double ends, which is not so convenient to the following circuits. Besides, for some applications, people need large output signals and a wide band width. This can be realised by adding a Double-ended input single-ended output circuit (shown in figure 14). This additional circuitconsist of a differential amplifier and a basic common collector circuit (shown infigure 15 and 16).Fig.14 2 ended inputs 1 ended output circuit Fig.15 LTP with activeloadFig.16 basic commoncollector circuitThe practical circuit with this addition output circuit is shown below.Fig.17 the circuit followed with 2 input ended 1 output ended circuit The DC sweep simulation is as follow (same setting as 3.1):Fig.18 the relative DC simulationCompared with figure 8, the output voltage increased, but the amplitude of output signal decreased. Furthermore, the common mode signal was amplified by the differential amplifier circuit, so the average value of output voltagebecomes to 22V. When Vx=0 or Vy=0, the output voltage equals to 22V. Thiscircuit can not operate as a multiplier. In a word, this additional circuit did not get the expected result.4. DiscussionAs the analysis showed in 3.1, the circuit of figure 6 can cancel the influence caused by temperature. This is because the differential and balance structure of the nonlinear composition block can remove the common mode signal. The temperature is physical paramount, which change by the same value in a small electric circuit. So noise caused by the temperature can be considered as the common mode signal. The circuit design in this report has a nice thermal stability.Use LTSPICE simulation, the power consumption of each and total elements can be detected easily. In order to reduce the power of the circuit, the current source should relatively be at a small value. But at the same time, the current should ensure the operation of the transistors.The limitation of this design is the same of the bipolar transistor. As the figure 2 shows, bipolar transistor has a limited exponential operation range. This feature asks for a highly accurate collector current control. To solve this problem, one way is to change the physical paramount of the transistor. For example, reduce the cross-section area. Another way is to use MOS transistors. Because the CMOS operation is based on the movement of majority carriers, there is no exponential relationship between drain current and drain-source voltage.5. ConclusionIn this report, an analog multiplier is proposed. Firstly, the principle of the design is introduced. Then a practical circuit is proposed. At the same time, the methods of how to change the paramount to achieve a suitable output signal are described. During the design, theory analyses and explains are also presented. The simulation is processed with LTSPICE. For this report, the results of simulation can satisfy the principle derivation. The designed circuit achieves its porpours.ReferenceGraeme.J.G., Tobey.G.E. and Huelsman. L.P. 1971. Operational Amplifiers: Design and Application. New York: McGRAW-HILL Book Company. (p.397-398)Peter Ashburn. 2003. SiGe Heterojunction Bipolar Transistors. West Sussex: John Wiley & Sons Ltd.GRAY Paul R. Analysis and design of analog integrated circuits. New York: John Wiley & Sons Ltd.。
乘法器与混频器

乘法器与混频器前言之前有人问过我这样的问题:乘法器和混频器到底有什么关系,混频器能不能用作乘法器?这里介绍一下它们的原理和异同点,相信各位都能有所理解。
乘法器乘法器正如其名,是做乘法的电子器件。
主要用途有调幅、调频、数学运算等。
真正数学意义上的乘法器全称四象限模拟乘法器。
所谓“四象限”指乘法器的两个输入信号的符号可能为正也可能为负均为双极性信号,此时乘法器能实现真正的数学意义上的乘法运算。
如果其中一个信号为单极性信号而另一个为双极性,那么称其为二象限。
如果全为单极性信号则为一象限。
但是通常我们在设计电路时并不会太多地设计四象限电路,所以一、二象限的应用更多一些。
首先一个理想的乘法器的输出和两输入的乘积成比例,具有以下端口特性:Vout=K×VX×VYV_{out}=K \times V_{X} \times V_{Y} Vout =K×VX×VY当然并不局限于本例中的电压信号,电流信号也是可以的。
一开始的乘法器是基于对数放大器设计的,对数放大器和加法器就能构成乘法器。
Vout=log(VX)+log(VY)V_{out}=log(V_{X})+log(V_{Y})Vout=log(VX)+log(VY)但是这种结构的劣势也很明显。
对数放大器是基于PN结的,结果受温度影响较为明显。
同时这种结构较难设计高速电路,带宽比较受限。
而且这个结构只能实现一个象限内的运算。
后来一位叫巴里·吉尔伯特(Barrie Gilbert)的高人设计了名为吉尔伯特单元(Gilbert cell)的电路,这个电路直接改变了整个电子通信行业。
巴里·吉尔伯特(Barrie Gilbert,1937年6月5日至2020年1月30日)),IEEE终身院士、美国国家工程院院士、同时也是ADI的首位院士(ADI Fellow)。
他于1937年出生于英国伯恩茅斯,1972年担任ADI公司的IC设计师,成为第一代研究员,1979年创建ADI首个远程设计中心,此后一直专注于高性能模拟IC的开发。
AD734模拟乘法器的原理与应用

AD734模拟乘法器的原理与应用作者:龙侃彭玉涛蒋熔罗超来源:《价值工程》2011年第18期摘要: AD734是一款高速精密四象限模拟乘法器,典型静态满量程误差仅为0.1%,它提供对分母的直接精确控制,这是模拟乘法器的一个新特点。
本文主要介绍了AD734的内部结构框图,分母控制电路,最后给出了AD734应用于乘法运算中的电路图。
Abstract: The AD734 is an accurate high speed, four-quadrant analog multiplier, Total static error is only 0.1% of full scale. It provide the direct control for the denominator which is a new feature of analog multiplier. The inner block diagram and the denominator control circuitry of AD734 are mainly introduced, at last, the applications of AD734 as a multiplier and a divider are showed in circuit diagram.关键词: AD734;分母直接控制;乘法器Key words: AD734;direct control of the denominator;multiplier中图分类号:TP322+.2 文献标识码:A文章编号:1006-4311(2011)18-0141-011概述乘法器在模拟信号处理中应用广泛,它可以完成模拟信号的乘除运算,对信号进行调制解调,还广泛应用于锁相环、混频器等电路当中。
AD734是AD公司生产的一款高速度高精度四象限模拟乘法器,输入输出信号的峰-峰值可达20V,带宽为10MHz,包括放大倍数误差、偏置和非线性误差在内的总误差仅为0.1%,输出信号变形小于-80dBc,在大多数应用中几乎不用外接任何元件。
四象限乘法应用电路

四象限乘法应用电路引言:四象限乘法应用电路是一种电路设计方法,可以实现两个信号的乘法运算。
在实际应用中,乘法运算经常用于信号处理、模拟计算和通信系统等领域。
本文将介绍四象限乘法应用电路的原理、结构和实际应用。
一、原理:四象限乘法应用电路的原理基于电压控制电流源(VCVS)和电流控制电压源(CCVS)。
其中,VCVS是一种电压源,其输出电流与输入电压成正比;CCVS是一种电流源,其输出电压与输入电流成正比。
通过结合使用VCVS和CCVS,可以实现乘法运算。
二、结构:四象限乘法应用电路的结构包括四个关键组成部分:差分放大器、限幅器、积分器和反馈网络。
其中,差分放大器用于将输入信号转换为差分电压;限幅器用于限制差分电压的范围;积分器用于将差分电压积分为输出电压;反馈网络用于调节输出电压。
1. 差分放大器:差分放大器由两个输入端口和一个输出端口组成。
它的作用是将两个输入信号相减得到差分电压,并放大差分电压。
差分放大器可以采用运算放大器(OP-AMP)等电路实现。
2. 限幅器:限幅器用于限制差分电压的范围,以保证乘法运算的正常进行。
常见的限幅器电路有二极管限幅器和运算放大器限幅器等。
3. 积分器:积分器是一个电路,可以将差分电压积分为输出电压。
积分器可以采用电容器和电阻器等元件组成。
通过调节电容器和电阻器的数值,可以实现不同的积分效果。
4. 反馈网络:反馈网络用于调节输出电压,使其与输入信号的乘积成正比。
反馈网络可以采用电阻器、电容器和运算放大器等元件组成。
三、实际应用:四象限乘法应用电路在信号处理、模拟计算和通信系统等领域有广泛的应用。
1. 信号处理:在音频信号处理中,可以使用四象限乘法应用电路实现音频信号的调制、解调和混频等功能。
通过调节乘法电路的参数,可以实现不同的音频效果。
2. 模拟计算:在模拟计算中,四象限乘法应用电路可以用于模拟乘法运算。
通过将模拟信号输入乘法电路,可以得到乘法运算的结果。
这在某些模拟计算任务中非常有用。
MC1594L四象限模拟乘法器

MC1594L四象限模拟乘法器模拟相乘器是一种时变参量电路。
在高频电路中,相乘器是实现频率变换的基本组件,与一般非线性器件相比,相乘器可进一步克服某些无用的组合频率分量,使输出信号频谱得以净化。
在通信系统及高频电子技术中应用最广的乘法器有两种,一种是二极管平衡相乘器,另一种是由双极型或 MOS 器件构成的四象限模拟相乘器。
随着集成电路的发展,这些相乘器还具有工作频带宽、温度稳定性好等优点,广泛用于调制、解调及混频电路中。
四象限模拟乘法器又大致分为两种。
一种是在集成高频电路中经常用到的乘法器,它们大多属于非理想乘法电路,是为了完成某种功能而制成的一种专用集成电路,如电视接收机中的视频信号同步检波电路、相位检波电路以及调频立体声接收机中的立体声解码电路等。
这种乘法电路均采用差动电路结构。
另一种是较为理想的模拟乘法器,属于通用的乘法电路,用户可用这种乘法器按需要设计,完成其功能。
常用的集成化模拟乘法器的产品有 BG314 、MC1494L/MC1594L 、MC1495L/MC1595L 、XR-2208/XR2208M 、AD530 、AD532 、AD533 、A D534 、AD632 、BB4213 、BB421等。
相乘器的基本特性及实现方法:若输入信号分别用v 1 ( t ) 和v 2 ( t ) 表示,输出信号用v o ( t ) 表示,则理想模拟乘法器的传输特性方程可表示为v o ( t )= K v 1 ( t ) v 2 ( t ) (4-18)式中,K 是乘法器的比例系数或增益系数。
该式表明,对一个理想的相乘器,其输出电压的瞬时值v o ( t ) 仅与两个输入电压在同一时刻的瞬时值v 1 ( t ) 和v 2 ( t ) 的乘积成正比,而不包含任何其它分量。
输入电压v 1 ( t ) 和v 2 ( t ) 可以是任意的,即其波形、幅度、极性和频率 ( 包括直流 ) 均不受限制。
1.MC1594L四象限乘法器原理图:用MC1594L模拟乘法器做交流电压乘法器(其原理图):2.各部分电路进行分析:该电路主要分为三个部分:(1)电压调整器:电压调整器就是使输出电压在一定条件下保持稳定当输入电压改变,负载条件变时,输出电压要尽可能保持不变。
基于PWM和PAM测量电路的交流功耗计算

基于PWM和PAM测量电路的交流功耗计算通过采样电压与电流的乘积并进行平均处理可以完成60Hz电路的平均功耗测量(相当于VRMS × IRMS × cos(φ))。
这里要用四象限乘法,因为瞬时电压和电流可能具有相反的极性。
它有很多种实现方法,包括模数(A/D)转换+数字信号处理,或者使用相对昂贵的模拟乘法器芯片+模拟或数字处理。
本设计实例介绍了第三种方法。
这种方法使用便宜的运放和模拟开关实现脉冲宽度/脉冲幅度调制器(PWM/PAM)并将它用作四象限乘法器。
这种电路经过修改可以用于许多不同的应用。
PWM/PAM乘法器的基本概念是,一个(非重叠)脉冲波形在单个周期内的平均值等于脉冲面积除以脉冲重复周期。
由于每个矩形脉冲幅度正比于电压值,宽度正比于电流,矩形面积正比于电压与电流的乘积。
如果脉冲重复速率远高于被测频率,那么就可以假设在脉冲波形的一个周期内电压和电流不会有明显的变化。
PWM/PAM输出连到一个低通滤波器,用于滤除脉冲频率及其谐波,并恢复出想要的平均值。
电路共使用了两个变压器:一个是降压变压器TR1,用于产生低电平的电压信号;另一个是电流变压器TR2,用于产生低电平的电流信号,并具有完全的电流隔离。
图1:使用脉冲调制技术测量交流功耗运放IC1-A用作比较器,产生频率约为6kHz且相当线性的三角波(图2)。
为了取得低于满刻度1%的误差,这种过采样是必须的(100乘以60Hz信号频率,或50乘以理论上的奈奎斯特频率)。
三角波的峰峰幅度必须满足两个条件才能获得可接受的线性响应。
首先,它必须大于或等于T2产生的交流电流最大峰峰值电压,这样才能实现100%的PWM占空比。
其次,它必须至少比±VCC低10%。
图2:IC1-B(-)输入运放IC1-B被配置为产生零基线的双极方波(图3),其占空比取决于T2产生的电流信号的瞬时值。
电容C2用于获得陡峭的输出电压转换。
运放的压摆率必须大于等于10V/μs,以便产生最优的方波PWM 信号。
模拟电子技术5.2乘法器及其应用
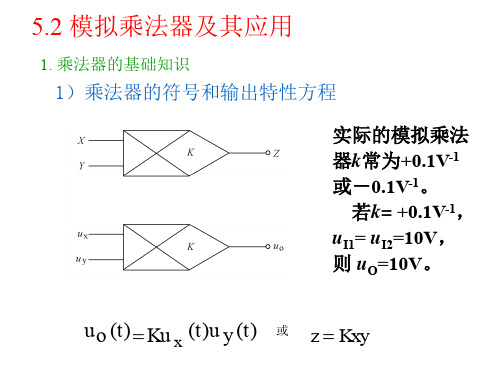
若集成运放的同相输入端与反相输入端互换,则k和uI2的极 性应如何?
4) 开平方运算电路
uo1
uo1
R2 R1
ui
ui
i2
R1
R2
uo1 Kuo2
i1
-∞
+A +
uo
1R
u
2 (u )
R
O
KR
i
1
为实现上式,电路中uI、 uO、k的极性是什么?为什么? 若要uO<0,则有何变化? 若要求uI、 uO均大于0,则有何变化? 若集成运放的负反馈通路中为某种运算电路,则整个电 路实现其逆运算!
T1
T2
T3
i c3
Re
- VE E
3. 乘法器的应用
1) 乘法运算
uX uY
uo uo=KuXuY
实现了对正弦波
若uI 2Ui sin t
电压的二倍频变换
则uO 2kUi2 sin2 t 2kUi2 (1 cos2 t)
2) 平方和立方运算
ui
uo
ui
uo
平方运算电路
uo=K(ui)2
如何实现开三次方运算电路?
利用运算电路,求解方程。已知模拟乘法器的相乘因子为0.1V-1。
设x=uI,按运算顺序搭建电路。
调整uI,使 uO 为 0 的 uI 就是方程 的解;解 为1、4。 电路不唯 一!
已知R1=R2,求解uO= f (uI) = ? 二极管什么时候导通?什么时候截止?
uO uI
在集成运放应用电路中开关管的工作状态往往决定于输入 信号或输出信号的极性!
5.2 模拟乘法器及其应用
1. 乘法器的基础知识
模拟乘法器及其应用

ωs >> Ω
UΩm 调 系 : = 幅 数 m Usm
调 波 uo =Usm ( + mcosΩ )cosωst 幅 : 1 t
=Usm cosωst + m sm cosΩ cosωst U t 1 =Usm cosωst + m sm cos( s +Ω t U ) ω 2 1 + m sm cos( s −Ω t U ω ) 2
2 2
1 = KU 2 1 u o = KU 2
Sm
(1 + cos 2 ω s t ) cos 2 ω s t
2 Sm
§4 其他应用
ui E x y K
uo
可控增益 放大器
uo = (K )ui E
绝对值电路
ui x y -K
uo
A
uo'
压控方波三角 波发生器
C Uc
UZ
uo1 = ± KU CU Z 可改变积分电容的充放电速率, 从而通过模拟乘法器实现频率可调
若 通 波 中 频 为 l −ωs, 宽 于 Ω 带 滤 器 心 率 ω 带 大 2 , 1 则 uo = K SmULm (1+mcosΩ )cos(ωl −ωs )t 有 U t 2
五 倍频
us
x y K
' uo
uo
高通滤波器
us = U
'
Sm
cos ω s t
2 Sm
u o = KU
cos ω s t
uo ' = KuiuR = KUsmURm (1+ mcosΩt) cos2 ωst 1 1 = KUsmURm (1+ mcosΩt)( + cos2ωst) 2 2 1 1 1 = KUsmURm (1+ cos2ωst + mcosΩt + mcosΩt cos2ωst) 2 2 2 1 1 = KUsmURm[1+ cos2ωst + mcosΩt 2 2 1 1 + mcos(2ωs + Ω)t + mcos(2ωs − Ω)t] 4 4
第六章第6个知识点 乘法和除法运算电路

uX
iC4 2UT
uX
)Rc
RcuX 2UT
( iC3
iC4
)
RcuX uY UT RY
乘法器符号如图所示。
uX
X
uO
uY
Y
(a)不带运放的乘法器符号
uX
X
uY
Y
uO
(b)带运放的乘法器符号
乘法器的表示符号
数控技术
uO KuX uY
乘法器的应用
利用集成模拟乘法器和集成运算放大器可组成平方、除法及开方等 运算电路。 在通信设备中可作平衡调制器,同步检波器、鉴频器、混频器等; 在测量技术中可以进行单相功率测量、三相功率测量、功率因数的 测量等; 此外还可以作为倍频器、压控滤波器等。
uX
R1
_
+ Rb
1
uY
R1
_
+ Rb
1
T R2
uo
1
T R2
uo
2
uO2
U T
ln
uY R1IS2
uO3 (uO1 uO2 )
R2
_
+
uo
Rb
3
2
R3
_
uI
T +
uo
Rb
3
uO
R3
I euO3 S3
/UT
uO1
U T
ln
uX R1IS1
uO2
U T
ln
uY R1IS2
uO3
(uO1
uO2 )
乘除运算电路
广泛应用于信号处理、信号检测、通信工程、自动控制等科学领域。
1.乘法运算电路 对数式乘法器
Z =X *Y =eln( X *Y ) eln X +lnY
四象限乘法

四象限乘法器是一种可以在四个象限内进行精确模拟乘法的电子元件,两个输入可能为正也可能为负,输出同样也可以是正或负。
从电路角度来看,四象限乘法器可以被理解为两个输入信号均为双极性的模拟乘法器。
在实际应用中,DAC(数模转换器)本来就具备乘法器的功能,因此也被称为四象限乘法器DAC。
参考电压和输出的关系决定了DAC所处的象限:当参考电压为正,输出也为正时,该DAC属于第1象限;若参考电压为负,而输出为正,则该DAC属于第2象限;如果参考电压和输出的符号都可能发生反转,那么该DAC就属于 {1,4}象限;最后,如果参考电压和输出的符号都可能变为正负,那么该DAC就是四象限DAC。
在所有四个象限对信号做精确模拟乘法绝非易事,因为需要处理的信号可正可负,并且乘法结果的符号也需要正确。
然而,由于并非所有应用都需要全四象限乘法器,所以常常使用的是仅支持一象限或二象限的精密器件。
例如,AD539就是一款宽带双通道二象限乘法器,而AD734则是一款高精度、高速的10MHz四象限乘法器/除法器。
模拟乘法器AD834的原理与应用

W=4XY (X、Y的单位为伏特,W的单位为mA)
3.应用考虑
3.1 输入端连接
尽管AD834的输入电阻较高(20kΩ),但输入端仍有45μA的偏置电流。当输入采用单端方式时,假如信号源的内阻为50Ω,就会在输入端产生1.125mV的失调电压。为消除该失调电压,可在另一输入端到地之间接一个与信号源内阻等值的电阻,或加一个大小、极性可调的直流电压,以使差分输入端的静态电压相等;此外,在单端输入方式下,最好使用远离输出端的X2、Y1作为输入端,以减小输入直接耦合到输出的直通分量。
模拟乘法器AD834的原理与应用
1.AD834的主要特性
AD834是美国ADI公司推出的宽频带、四象限、高性能乘法器,其主要特性如下:
●带符号差分输入方式,输出按四象限乘法结果表示;输出端为集电极开路差分电流结构,可以保证宽频率响应特性;当两输入X=Y=±1V时,输出电流为±4mA;
●频率响应范围为DC~500MHz;
应当注意的是,当输入差分电压超过AD834的限幅电平(±1.3V)时,系统将会出现较大的失真。
3.2 输出端连接
采用差分输出,可有效地抑制输入直接耦合到输出的直通分量。差分输出端的耦合方式,可用RC耦合到下一级运算放大器,进而转换为单端输出,也可用初级带中心抽头的变压器将差分信号转换为单端输出。
3.3 电源的连接
●乘方计算误差小于0.5%;
●工作稳定,受温度、电源电压波动的影响小;
●低失真,在输入为0dB时,失真小于0.05%;
●低功耗,在±5V供电条件下,功耗为280mW;
●对直通信号的衰减大于65dB;
●采用8脚DIP和SOIC封装形式。
2.AD834的工作原理
AD834的引脚排列如图1所示。它有三个差分信号端口:电压输入端口X=X1-X2和Y=Y1-Y2,电流输出端口W=W1-W2;W1、W2的静态电流均为8.5mA。 在芯片内部,输入电压先转换为差分电流(V-I转换电阻约为280Ω),目的是降低噪声和漂移;然而,输入电压较低时将导致V-I转换线性度变差,为此芯片内含失真校正电路,以改善小信号V-I转换时的线性特性。电流放大器用于对乘法运算电路输出的电流进行放大,然后以差分电流形式输出。
AD633四象限乘法器中文资料

接线图8引脚塑料DIP (N )包装"~.特点 四象限乘法 低成本8引脚封装 完整的,无需外部元件 激光微调精度和稳定性 总误差在满量程的2% 差分高阻抗X 和Y 输入 高阻抗单位增益求和输入 激光微调10伏标定参考值 应用 ! 乘法,除法,磨边调制/解调,相位检测 压控放大器/衰减器/过滤器 产品说明 该AD633是一个功能完整的四象限模拟乘法器。
它包括高阻抗,差动X 和Y 输入和一个高阻抗求和输入(Z 轴)。
低阻抗输出电压是由一个嵌入式齐纳二极管提供了一个标称10 V 全面。
该AD633是提供在价格适中的8引脚塑料DIP 和SOIC 封装这些功能的第一款产品。
该AD633是激光校准,满量程的2%保证总精度。
非线性度为Y 输入通常小于%,并提到了输出噪声通常在10 Hz至10 kHz 的带宽小于100μVRMS 。
1 MHz 带宽,20 V/μs 压摆率,并且驱动容性负载的能力,使AD633有用在各种各样的应用中,简单性和成本是关键问题。
"该AD633的通用性不是由它的简单性大打折扣。
其Z 输入提供对输出缓冲放大器,使用户能够总结的两个或更多个乘法器的输出,增加乘法器的增益,其输出电压转换为电流,并配置各种应用。
该AD633是在一个8引脚塑料DIP 封装(N )和8引脚SOIC (R )。
它被指定为工作在0°C 至+70°C 商业级温度范围(十级)或-40°C 至+85°C 工业级温度范围(A 级)。
8引脚塑料SOIC (SO-8)封装 产品亮点1,AD633是在提供了一个完整的四象限乘法器 低成本的8引脚塑料封装。
其结果是一种产品,是成本效益和易于应用。
2,无需外部元件或昂贵的用户校准是 以应用AD633必需的。
3,整体建设和激光校准使脱 副稳定可靠。
4,高(10M Ω)输入电阻使信号源负载可以忽略不计。
5,电源电压范围可以从± V 至±18 V 的 /内部标定电压是由一个稳定的齐纳二极管产生的;乘法器精度基本上是供应不区分大小写。
AD633模拟乘法器调制与检波protues仿真

AD633模拟乘法器调制与检波protues仿真之杨若古兰创作1.AD633简介1.1 AD633概述AD633作为一款低成本四象限模拟乘法器,其单片集成结构和激光校准使AD633功能波动而可靠,满足高频电子线路对于模拟元器件可靠性和波动性请求.本文提出基于AD633模拟乘法器实现调制、解调和混频功能,通过Multisim13仿真并分析基于AD633的高频相乘电路的功能.1.2 AD633相乘功能描述AD633是一种功能高、波动性好的低成本模拟乘法器,适用于重视简单性和低成本的各种利用中.AD633的多功能性不受其简单性的影响,可以设置为多种分歧的模拟计算功能,次要的利用包含调制/解调、主动增益控制、功率测量、压控放大器和倍频器.AD633相乘功能基本连接如图1所示,AD633模拟乘法器由高阻抗差分X、Y输入和高阻抗求和输入Z,和低阻抗电压输出W构成.差分X和Y输入通过电压电流转换器转换成差分电流,这些电流的乘积由乘法核发生.总的传递函数可以暗示为1.3 振幅调制电路振幅调制以DSB调制为例.利用AD633的相乘功能设计DSB调制电路如图2所示,振幅调制电路次要以模拟乘法器AD633为核心,1、2管脚差分输入频率为1KHz的低频旌旗灯号,3、4管脚差分输入频率1MHz的高频载波旌旗灯号.两旌旗灯号经AD633相乘,按照W的传递函数进行计算,由7管脚输出调制旌旗灯号,从而实现振幅调制. 1.4 解调电路DSB解调电路采取同步检波方式,利用AD633的相乘功能实现乘积型同步检波.乘积型同步检波是直接把当地恢复的解调载波与接收旌旗灯号相乘,然后用低通滤波器提取低频旌旗灯号.在这类检波器中,请求当地的解调波与发送端的调制载波同频同相,如果其频率或相位有必定的偏差,将会使恢复出来的调制旌旗灯号失真.同步检波器是由AD633模拟乘法器和低通滤波器两部分构成,用于对按捺载波的双边带调幅波进行解调.同步检波电路见图3,由图2发生的DSB调制旌旗灯号输入到U1的X1端,DSB解调旌旗灯号经过由OP07AH构成的低通滤波器,输出滤波后的解调旌旗灯号,从而实现DSB解调.1.5 混频电路如图4所示,利用AD633AN的相乘功能设计混频电路,即在AD633AN的X端和Y端分别输入2个分歧频率的旌旗灯号,再经过带通滤波器提取出中频旌旗灯号.混频电路由双边带调制电路(见图1)、当地振荡电路和带通滤波电路构成.由图1发生的高频旌旗灯号经U2的X1端输入,和当地振荡旌旗灯号相乘后得到一个中频旌旗灯号,由U2的W端输出,经过带通滤波后,终极输出混频旌旗灯号.2.Protues仿真50Hz旌旗灯号经过AD633的乘法功能,与5KHz旌旗灯号调幅调制,得到调制波形,后再经过AD633和低通滤波器,还原50Hz旌旗灯号.虚拟示波器能实时显示波形,A 通道收集50Hz旌旗灯号,B通道收集5KHz旌旗灯号,C 通道收集调制后的波形旌旗灯号,D通道收集检波后的波形.电路图如下:波形如下:时间轴调节:由于AD633的输出有10倍衰减,检波后波形要经过OP07构成的放大电路放大,才干明显看到波形.。
实验四 模拟乘法器的应用(振幅调制器)

实验四模拟乘法器的应用(振幅调制器)一.实验目的1.掌握用集成模拟乘法器F1496实现普通调幅和抑制载波的双边带调幅的方法与过程;2.研究输出已调波信号与输入载波信号、调制信号的关系。
3.掌握调幅系数的测量方法。
二.实验原理集成模拟乘法器是完成两个模拟量(电压或电流)相乘的电子器件。
高频电子线路中的振幅调制、同步检波、混频、倍频、鉴频、鉴相等调制与解调过程,均可视为两个信号相乘的过程。
F1496是双平衡四象限模拟乘法器,电路如图4-1所示。
引脚⑧与⑩接输入电压U x,①与④接另一输入电压U y,输出电压U o从引脚⑥与⑿输出。
引脚②与③外接电阻为电流负反馈电阻,可调节乘法器的信号增益,并扩展输入电压U y的线性动态范围。
引脚⒁为负电源(双电源供电时)或接地端(单电源供电时)。
本实验将完成普通调幅和抑制载波调幅的内容。
三.实验设备1. 示波器SS7802A 1台2. 信号源EE1643 1台3. 数字万用表1块4. 高频电路实验板G31块四.实验内容与步骤实验电路如图4-1所示,按图接好电路。
1.载波输入端平衡调节在调制信号输入端IN2输入调制信号UΩ(t),UΩ(t)为f=1KHz幅度为100mV(V P-P)的正弦信号。
将示波器接至OUT处,调节电位器R P2,使示波器上输出的波形幅度最小。
(然后去掉输入信号UΩ)。
2.抑制载波调幅(在载波输入端平衡的状态下进行)1)输入端IN1输入载波信号U C(t),U C(t)为f=465KHz,幅度U C(p-p)=30mv的正弦信号,将示波器接至OUT处。
调节R P1,使输出电压Vo最小。
2)入端IN2输入调制信号UΩ(t),其频率为1KHz,幅度由零逐渐增大,当UΩ(p—p)为几百毫伏时,将出现如图4-2所示的抑制载波的调幅信号。
由于器件内部参数不可能完全对称,致使输出波形出现漏载信号。
可通过调节电位器R P2来改善波形的对称性。
记录波形并测出V O(p-p)值。
双平衡四象限模拟乘法器工作原理

双平衡四象限模拟乘法器是一种常用于电子电路中的模拟乘法器,它可以对两个输入信号进行乘法运算,并输出它们的乘积。
这种乘法器可以在各种电子设备中使用,比如模拟信号处理系统、通信系统和控制系统等。
其工作原理主要基于双平衡调制技术和四象限运算技术,通过精确的电路设计和运算放大器的作用,实现了高精度和高线性度的模拟乘法运算。
1. 双平衡四象限模拟乘法器的基本原理双平衡四象限模拟乘法器主要由一个双平衡调制器和四象限运算放大器组成。
双平衡调制器是一种特殊的调制器,它可以对输入信号进行平衡混频处理,得到两路相位正交的信号。
四象限运算放大器是一种能够在所有四个象限内进行线性运算的运算放大器,通过它可以对两路输入信号进行乘法运算。
2. 工作原理分析两个输入信号分别经过双平衡调制器的处理,得到它们的正交相位信号。
这两路正交信号分别输入到四象限运算放大器中,进行乘法运算。
在四象限运算放大器内部,通过合适的反馈网络和控制电路,实现了对两路信号的乘法运算,并将乘积信号输出。
输出的乘积信号经过滤波、放大等后续处理,得到最终的模拟乘法器输出信号。
3. 特点和优势双平衡四象限模拟乘法器具有高精度、高线性度、宽带宽、低失真等特点和优势。
通过合理的电路设计和精确的参数选择,可以实现对输入信号的高精度乘法运算,输出信号的失真度极低,并且适用于宽频带的信号处理。
4. 应用领域双平衡四象限模拟乘法器广泛应用于各种模拟信号处理系统中,比如射频调制解调、通信系统中的信号处理、微波信号处理、医学成像系统中的信号处理等。
它在这些领域中可以实现高精度和高质量的信号处理,对系统的整体性能起到至关重要的作用。
总结:双平衡四象限模拟乘法器是一种非常重要和实用的模拟电路元件,它通过双平衡调制和四象限运算技术,实现了对两路输入信号的乘法运算,并具有高精度、高线性度、宽带宽、低失真等特点和优势。
它在电子电路中有着非常广泛的应用,对于各种模拟信号处理系统的设计和性能提升具有重要意义。
乘法和除法电路
–VEE
I0 2
RX ux
I0 2
RX
I0 2
RY
uY
I0 2
RY
负反馈电阻,用以 扩大 uX、uY 范围
uO
4 RC Rx RY I0
uX uY
KuXuY
K 4RC Rx RY I0
ux
KXY X
uy Y
uo
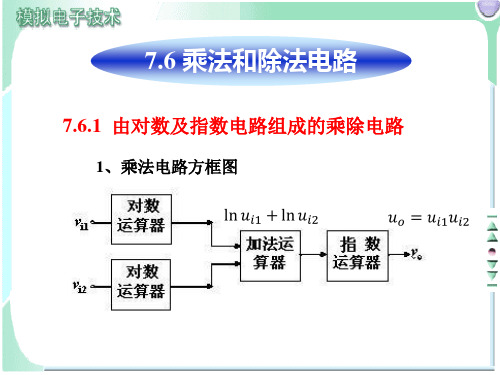
7.6 乘法和除法电路
7.6.1 由对数及指数电路组成的乘除电路
1、乘法电路方框图
2、除法电路方框图
7.6.2 模拟乘法器 一、模拟乘法器的基本特性
符号
uO = Kuxuy K — 比例系数
类型
单象限乘法器 ux、uy 皆
为固定极性 二象限乘法器 一个为固定极 性,另一个为可正可负
四象限乘法器 ux、uy 皆为
可正可负
二、可变跨导乘法器的工作原理
uO rbe
β
RC rbe
uX
rbb (1 β)
UT I E1
(1 β) 2UT IC3
uO
β RC IC3 2(1 β)UT
uX
RC IC3 2U T
uX
当 uY > uBE3 时,IC3≈uY/RE
uO
RC 2 REU T
uXuY
KuXuY
KXY
u'O
X Y
R
8
uI R
uO KuO2 uI
uO
uI K
uO
(uI < 0)
4、压控增益
KXY
uY
X
Y
uo
uX
uO = KuXuY 设 uX = UXQ 则 uO = (KUXQ)uY 调节直流电压 UXQ , 则调节电路增益
四象限乘法应用电路

四象限乘法应用电路导言:四象限乘法应用电路是一种常见的电子电路,可用于将两个输入信号相乘并输出乘积信号。
这种电路通常在模拟电路和信号处理系统中使用,具有广泛的应用。
一、四象限乘法应用电路的原理四象限乘法应用电路的原理基于模拟电路中的乘法运算,通过将两个输入信号相乘,得到其乘积的结果。
这种电路的特点是可以处理正负信号,并且输出结果可以同时具有正负值。
二、四象限乘法应用电路的组成四象限乘法应用电路通常由四个关键部分组成:乘法器、输入信号调节电路、偏置电路和输出滤波电路。
1. 乘法器:乘法器是四象限乘法应用电路的核心部分,负责将两个输入信号相乘。
乘法器常用的实现方式有模拟乘法器和数字乘法器,其原理是基于集成电路中的乘法运算。
2. 输入信号调节电路:输入信号调节电路用于调节输入信号的幅值和偏置,以使其适应乘法器的工作范围。
这部分电路常用放大器、运算放大器等器件实现。
3. 偏置电路:偏置电路用于提供乘法器所需的偏置电压,以确保乘法器正常工作。
偏置电路通常由电阻、电容等元件组成,可以根据具体需求进行设计。
4. 输出滤波电路:输出滤波电路用于滤除乘法器输出信号中的杂散频率成分,得到干净的乘积信号。
常用的输出滤波电路有低通滤波器、带通滤波器等。
三、四象限乘法应用电路的应用四象限乘法应用电路在模拟电路和信号处理系统中有广泛的应用。
以下是几个常见的应用场景:1. 模拟调制解调器:四象限乘法应用电路可以用于模拟调制解调器中的信号调制和解调过程。
通过将调制信号和载波信号进行乘法运算,可以实现信号的调制和解调。
2. 音频处理器:四象限乘法应用电路可以用于音频处理器中的音频混合、音效处理等功能。
通过将不同音频信号进行乘法运算,可以实现音频信号的混合和处理。
3. 信号调幅:四象限乘法应用电路可以用于信号调幅过程中的幅度调制。
通过将调制信号和载波信号进行乘法运算,可以实现信号的幅度调制。
4. 功率放大器:四象限乘法应用电路可以用于功率放大器中的功率控制。
四象限乘法器/除法器在伽玛相机中的应用

四象限乘法器/除法器在伽玛相机中的应用AD734是Analog Devices(AD公司)的产品,与同类产品相比,具有挺直除法模式,可以利用外部输入挺直控制除法模式中的分母电压,用法起来相当灵便便利。
而其他同类产品除法模式的分母电压只能由内部提供,外部无法控制。
AD734还可以作为调制器、解调器、宽带增益控制器、直流均方根转换器、压控、和用法,用途十分广泛。
?1 AD734的基本结构及功能AD734是一个高精度、高速四象限模拟乘法器/除法器,他与符合工业标准的模拟乘法器/除法器AD534引脚相互兼容,其传递函数为W=XY/U。
他具有以下特点:(1) 高精度:0.1%的典型误差。
(2) 高速:10 MHz满功率带宽;450 V/μs的回转率;升高到满功率的0.1%需200 ns。
(3)低失真:随意输入信号的失真均为-80 dB。
(4)低噪声:10 Hz~20k Hz时,信噪比为94 dB;10 Hz~10M Hz时,信噪比为70 dB。
(5)挺直除法模式。
(6)增益为100时,带宽为2 MHz。
图1所示为AD734的管脚暗示图。
其详细管脚定义如下:X1和X2:差动输入端;Y1和Y2:差动输入端;Z1和Z2:差动输入端;U0,U1,U2:分母电压控制端;W:输出端;VP:正电源供电;DD:电压控制使能;ER:参考电压;VN:负电源供电。
AD734与AD534相比,其先进的功能有:(1)AD734是一个新型的输出放大器。
在满功率带宽10 MHz时,AD734的回转率(450V/μs)要比AD534(20 V/μs)高出20多倍。
(2)AD734的失真十分低,即使在满功率的状况下也一样。
在AD734的设计中采纳了新的电路设计技术及激光微调技术,消退了全部的寄生非线性误差,而这些误差在早期的设计中是无法消退的。
(3)AD734可以实现分母电压的挺直控制。
外部输入在10 mV~10 V之间的随意值均可代替分母电压。
单电源BiCMOS四象限模拟乘法器的研究与设计

所以乘法器的输出电压为
v ou t = vo+ - vo- = R ( iD1 + iD2 - iD3 - iD 4 )。( 3) 为了有效地抑制电路的耦合噪声, 输入电压通
收稿日期: 2006-09-25 基金项目: 2005年西安 - 应用材料创新基金资助项目 ( ZX 05097-XA-AM-200514) 作者简介: 王进军 ( 1980) ), 男, 陕西礼泉人, 陕西科技大学助教, 从事光电集成、混合信号集成电路设计研究。
1 四象限模拟乘法器的原理
基本的 模 拟乘 法 运 算 可 以由 工 作 在 线 性区
MOS管利用其漏极电流与栅源电 压之间的平方率 的特性来实现 [ 1] , 图 1给出了由 4 个工作在线性区 的 MOS管构成的 CMOS模拟乘法器, 由跨导运算放 大器 ( OTA ) 的特性可以得到运放的正向输 出端和 负向输出端的电压分别为
vout = R Bvx vy。
( 6)
2 B iCMOS 四象限模拟乘法器的原 理、设计与实现
211 模拟乘法器的 BiCM OS实现 由前面 的分 析 可 知, 要 完 成 模 拟 乘法 运 算,
CMOS 模拟 乘法 器 中的 MOS 管 必须 工作 在 线性 区 [ 2] , 这就要求图 2( a) 中 V a - V b - VTH > 0, 从而使 得输入范围受到了很大的限制。一种改进的方法是 采用图 2( b) 所示的 B iCMO S线性区跨导结构 [ 3] , 它 由一个被偏置在线性区的 NMO S 管 M i 和一个双极 晶体管 Q i 组成, 这种结构具有非常好的线性度和高 的输入阻抗。图 2 ( b) 中晶体管 Q i把 M i的漏极电位 钳位在 Vb - VBE, 如果满足 NMO S管工作在线性区的 条件: Vb - VBE < VDsat = V a - VTH, 即 Vb - VBE < V a - VTH, 在忽略衬偏效应的情况下可以得到
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
由于指数函数是一种超越函数, 所以这种方法又称为
超越函数分析法。
4.2.2折线函数分析法
当输入电压较大时, 晶体二极管的伏安特性可用两段折
高 频 电 子 线 路
线来逼近 , 由图4.2.1 可以证实这一点。由于晶体三极管的 转移特性与晶体二极管的伏安特性有相似的非线性特性 , 所以第 4 章第 4.2节利用折线法对大信号工作状态下集电极 电流进行了分析。 由分析结果可知, 当输入电压为直流偏 压上迭加单频余弦波时 , 集电极电流中的频率分量与式
x
高 若u=UQ+Uscosωst, 由式(4.2.1)可得到: 频 电 UQ U S 1 子 2 2 1 cos2 ws t i I [ cos w t ( U 2 U U cos w t U ) ... s s Q Q S s s 2 线 UT UT 2UT 2 路
虽然在线性放大电路里也使用了晶体管这一非线性器 件, 但是必须采取一些措施来尽量避免或消除它的非线性效 应或频率变换效应, 而主要利用它的电流放大作用。 例如,
高 频 电 子 线 路
使小信号放大电路工作在晶体管非线性特性中的线性范围 内, 在丙类谐振功放中利用选频网络取出输入信号中才有的
有用频率分量而滤除其它无用的频率分量, 等等。
f (U Q ) 2!
(u-UQ)2+…+ n!
f ( n ) (UQ )
=a0+a1(u-UQ)+a2(u-UQ)2+…+an(u-UQ)n+…
(4.2.4)
可见输出电流中出现的频率分量与式(4.2.3)相同。
显然, 展开的泰勒级数必须满足收敛条件。
高 频 电 子 线 路
综上所述, 非线性元器件的特性分析是建立在函数逼近 的基础之上。当工作信号大小不同时, 适用的函数可能不同, 但与实际特性之间的误差都必须在工程所允许的范围之内。
1 n ( U U cos w t ) ... Q S s n n!UT
利用三角函数公式将上式展开后, 可以看到, 输入电压
中虽然仅有直流和ωs分量, 但在输出电流中除了直流和ωs分
高 频 电 子 线 路
量外, 还出现了新的频率分量, 这就是ωs的二次及以上各次 谐波分量。 输出电流的频率分量可表示为: ωo=nωs, n=0, 1, 2, … (4.2.3)
例 4.1 已知结型场效应管的转移特性可用平方律函数
VG U S cos wst 2 iD=IDSS (1 ) UP
2 I DSS U 2 [VG U P )2 2U S (VG U P ) coswst S 2wst ] UP 2
可见, 输出电流中除了直流和ωs这两个输入信号频率分 量之外, 只产生了一个新的2ωs频率分量。
频率变换电路属于非线性电路 , 其频率变换功能应 由非线性元器件产生。 在高频电子线路里, 常用的非线
高 频 电 子 线 路
性元器件有非线性电阻性元器件和非线性电容性元器
件。 前者在电压—电流平面上具有非线性的伏安特性。 如不考虑晶体管的电抗效应, 它的输入特性、转移特性 和输出特性均具有非线性的伏安特性, 所以晶体管可视 为非线性电阻性器件。 后者在电荷—电压平面上具有非 线性的库伏特性。如第4章介绍的变容二极管就是一种 常用的非线性电容性器件。
其中, 热电压UT≈26mV(当T=300K时)。
在输入电压u较小时, 式(4.2.1)与二极管实际特性是吻合 的, 但当u增大时, 二者有较大的误差, 如图4.2.1所示。所以 指数函数分析法仅适用于小信号工作状态下的二极管特性 分析。
高 频 电 子 线 路
利用指数函数的幂级数展开式
1 2 1 n e 1 x x ... x ... 2! n!
本章以晶体二极管伏安特性为例, 介绍了非线性元器件
频率变换特性的几种分析方法,然后进一步介绍频率变换电
路的特点及实现方法。
4.2 非线性元器件频率变换特性的分析方法
4.2.1指数函数分析法
高 晶体二极管的正向伏安特性可用指数函数描述为: 频 1 q 电 u u UT KT 子 i I ( e 1 ) I ( e 1) s s 线 路
学习项目三 频率变换电路与集成模拟乘法器
高 频 电 子 线 路
§ 4.1 概述
§ 4.2 非线性元器件频率变换特性的分析方法
§ 4.3 频率变换电路的要求与实现方法
§ 4.4 模拟乘法器
§ 4.5 章末小结
返回主目录
第4章 频率变换 与集成模拟乘法器
4.1概述
高 频 电 子 线 路
线性放大电路的特点是其输出信号与输入信号具有某 种特定的线性关系。从时域上讲 , 输出信号波形与输入信 号波形相同, 只是在幅度上进行了放大; 从频域上讲, 输出 信号的频率分量与输入信号的频率分量相同。 然而, 在通 信系统和其它一些电子设备中 , 需要一些能实现频率变换 的电路。这些电路的特点是其输出信号的频谱中产生了一 些输入信号频谱中没有的频率分量 , 即发生了频率分量的 变换, 故称为频率变换电路。
例 4.2 知变容二极管结电容Cj与两端电压u的非线性关
系如图例4.2所示, 分析流经变容二极管的电流 i与u之间的
高 频 电 子 线 路
频率变换关系, 并与线性电容器进行比较。 解:流经电容性元器件的电流 i 与其两端的电压 u 和存 贮的电荷q具有以下的关系式:
dq dq d.2.3)相同。
4.2.3幂级数分析法
假设晶体二极管的非线性伏安特性可用某一个函数 i=f(u)
表示。此函数表示的是一条连续曲线。 如果在自变量u的某
高 频 电 子 线 路
一点处(例如静态工作点UQ)存在各阶导数, 则电流i可以在该 点附近展开为泰勒级数: i=f(UQ)+f′(UQ)(u-UQ)+f"(UQ) (u-UQ)n+…
高 频 电 子 线 路
对于线性电容器 , 它的库伏特性在 q-u平面上是一条直 线, 故电容量C是一常数。 由式 (4.2.4)可知, 除了无直流分 量之外, i中的频率分量与u中的频率分量应该相同。所以线 性电容器无频率变换功能。
