第十二章相关和回归分析练习试题
社会统计学第十二章 相关与回归分析

2. 相关方向:正相关和负相关 所谓正相关关系是指一个变量的值增加时,另一变
量的值也增加。例如,受教育水平越高找到高薪水工作的 机会也越大。而负相关关系是指一个变量的值增加时,另 一变量的值却减少。例如,受教育水平越高,理想子女数 目越少。要强调的是,只有定序以上测量层次的变量才分 析相关方向,因为只有这些变量的值有高低或多少之分。 至于定类变量,由于变量的值并无大小、高低之分,故定 类变量与其他变量相关时就没有正负方向了。
父母智力 组合
优+优
优+劣 一般+一般
劣+劣
子女智力 子女智力
优秀
一般
71.6 25.4
33.6 42.7
18.6 66.9
5.4 34.4
子女智力 低下
3.0 23.7 14.5 60.2
通过列联表研究定类变量之间的关联性,这 实际上是通过相对频数条件分布的比较进行的。 如果对不同的X,Y的相对频数条件分布不同,且 和Y的相对频数边际分布不同,则两变量之间是 相关的。而如果变量间是相互独立的话,必然存 在着Y的相对频数条件分布相同,且和它的相对 频数边际分布相同。后者用数学式表示就是
r×c相对频数联合分布列联表
控制X,Y相对频数条件分布列联表
控制Y,X相对频数条件分布列联表
[例A1]试把下表所示的频数分布列联表,转 化为自变量受到控制的相对频数条件分布列联 表,并加以相关分析。
投票行为
受教育程度X
Y
大学以 大学以
FY
上
下
投票
160
129
289
弃权
7
61
68
合计:FX 167
r×c相对频数分布列联表的一般形式
在相对频数分布列联表中,各数据为各分类
12章 多元线性回归

统计学第十二章 多元线性回归一. 选择题1. 在多元线性回归分析中,t 检验是用来检验( ) A 总体线性关系的显著性 B.各回归系数的显著性 C.样本线性关系的显著性 D .H 0:β1=β2=…βk =02.在多元线性回归模型中,若自变量x i 对因变量y 的影响不显著,那么它的回归系数 βi 的取值( )A.可能为0B.可能为1C.可能小于0 D 可能大于13.在多元线性回归方程 y i ˆ=βˆ0+x 11ˆβ+x 22ˆβ+…+xkkβˆ中,回归系数βˆi表示( ) A.自变量x i 变动1个单位时,因变量y 的平均变动额为βˆiB.其他变量不变的条件下,自变量x i 变动1个单位时,因变量y的平均变动额为βˆiC.其他变量不变的条件下,自变量x i 变动1个单位时,因变量y的变动总额为βˆiD.因变量y 变动1个单位时,因变量x i 的变动总额为βˆi4.设自变量的个数为5个,样本容量为20。
在多元回归分析中,估计标准误差的自由度为( )A.20B.15C.14D.18 5.在多元回归分析中,通常需要计算调整的多重判定系数R a2,这样可以避免的值()A. 由于模型中自变量个数的增加而越来越接近1B. 由于模型中自变量个数的增加而越来越接近0C. 由于模型中样本容量的增加而越来越接近0D. 由于模型中样本容量的增加而越来越接近16.在多元线性回归分析中,如果F检验表明线性关系显著,则意味着()A.在多个变量中至少有一个自变量与因变量之间的线性关系显著B.所有的自变量与因变量之间的线性关系都显著C.在多个变量中至少有一个自变量与因变量之间的线性关系不显著D.所有的自变量与因变量之间的线性关系都不显著7.在多元线性回归分析中,如果t检验表明回归系数βi不显著,则意味着()A.整个回归方程的线性关系不显著B.整个回归方程的线性关系显著C.自变量x i与因变量之间的线性关系不显著D.自变量x i与因变量之间的线性关系显著8.设多元线性回归方程为Yˆ=βˆ0+x11ˆβ+x22ˆβ+…+xkkβˆ,若自变量x i的回归系数βˆi的取值接近0,这表明()A.因变量y对自变量ix的影响不显著B.因变量y对自变量ix的影响显著C.自变量ix对因变量y的影响不显著D.自变量x对因变量y的影响显著i9.一家出租汽车公司为确定合理的管理费用,需要研究出租车司机每天的收入(元)与他的行驶时间(小时)、行驶的里程(公里)之间的关系,为此随机调查了20位出租车司机,根据每天的收入(y)、行驶时间(x1)和行驶的里程(x2)的有关数据进行回归,得到下面的有关结果(a=0.05)根据上表计算的判定系数为()A. 0.9229B. 1.1483C. 0.3852D. 0.851610. 一家出租汽车公司为确定合理的管理费用,需要研究出租车四级每天的收入(元)与他的行驶时间(小时)、行驶的里程(公里)之间的关系,为此随机调查了20位出租车司机,根据每天的收入(y)、行驶时间(x1)和行驶的里程(x2)的有关数据进行回归,得到下面的有关结果(α=0.05)根据上表计算的估计标准误差为()A. 306.18B. 17.50C. 16.13D. 41.9311. 一家出租汽车公司为确定合理的管理费用,需要研究出租车司机每天的收入(元)与他的行驶时间(小时)、行驶的里程(公里)之间的关系,为此随机调查了20位出租车司机,根据每天的收入(y)、行驶时间(x1)和行驶的里程(x2)的有关数据进行回归,得到下面的有关结果(α=0.05)根据上表计算的用于检验线性关系的统计量F=()A. 306.18B. 48.80C. 5.74D. 41.9312.一家产品销售公司在30个地区设有销售分公司。
医学统计学练习题

第一章绪论一、名词解释:1. population 2. sample 3. homogeneity 4. variation 5. parameter二、辨别正误:()1.定量变量、分类变量和有序变量可以相互转换。
()2.同质的个体间不存在变异。
()3.如果个体间有变异,则它们一定不是不是来自同一总体。
()4.离散变量在数值很大时,单位为“千”或“万”时可以取小数值,此时可以近似认为是连续型变量。
()5.样本是总体中典型的一部分。
三、选择题1. 统计工作的前提和基础是()A 收集资料B 整理资料C 分析资料D 调查资料E 校对资料2.为了由样本推断总体,样本应该()A 总体中的任意部分B 总体中的典型部分C 总体中有价值的一部分D 总体中有意义的一部分E 总体中有代表性的一部分3.统计分析的主要内容有()A 描述性统计和统计学检验B 区间估计和假设检验C 统计图表和统计报告D 描述性统计和分析性统计E 描述性统计和统计图表4.统计学上的总体为()A任意想象的研究对象的全体B根据研究目的确定的研究对象的全体C根据时间划分的研究对象的全体D根据人群划分的研究对象的全体E根据地区划分的研究对象的全体 5.搞好统计工作,达到预期目标,最重要的是( )A原始资料要正确B原始资料要多C分析资料要先进D整理资料要详细E统计计算精度要高四、问答题:统计工作的基本步骤是什么?第二章定量资料的统计描述一.名词解释1. mean2. :median]3. Q4. S5. CV二.填空1. 对定量资料的描述,有()趋势和()趋势。
2.描述定量资料的集中趋势,常用的指标有()、()和()。
3.描述定量资料的离散趋势,常用的指标有()、()、()、()和()4.变异系数的应用条件为()或()。
5.描述等级资料的集中趋势,适宜选用()。
三.选择题1. 从一个数值变量资料的总体中抽样,产生抽样误差的原因是A. 总体中的个体值存在差别B. 总体均数不等于零C. 样本中的个体值存在差别D. 样本均数不等于零E. 样本只包含总体的一部分2.在正态分布条件下表示变量值变异情况的指标最常用的是A 标准差B 标准误C 变异系数D 全距E 百分位数3.变异系数越大说明A 标准差越大B 平均数越大C 标准差、平均数都大D 平均数小E以均数为准变异程度大4.反映定量变量观察数据集中位置的指标是A 标准差B 标准误C 频率D 全距E 均数5.在服从正态分布的条件下,样本标准差的值A 与集中趋势有关B 与观察例数有关C 与平均数有关D 与平均数无关 E 与个体的变异程度有关四.简答题试述描述定量资料的集中趋势的常用指标、计算方法和应用条件。
12章多重线性回归与相关

一、自变量筛选的标准与原则
2.残差均方缩小与调整决定系数增大 MS残=SS残/(n-p-1) MS残缩小的准则可以看做是在SS残缩小准则的基础上 增加了(n-p-1)-1因子,该因子随模型中自变量个数 p的增加而增加,体现了对模型中自变量个数增加而 施加的“惩罚”。 调整决定系数Ra2越大越好,与MS残等价。
包含汽车流量、气温、气湿与风速这四个自变量的回
归方程可解释交通点空气NO浓度变异性的78.74%
2.复相关系数R (multiple correlation coefficient)
定义为确定系数的算术平方根,
R SS回 SS总
表示变量Y与k个自变量的线性相关的密切程度。 对本例R=0.8837,表示交通点空气NO浓度与汽车流量、
表12-5 空气中NO浓度与各自变量的相关系数与偏相关系数
自变量 车流X1 相关系数 0.80800 偏相关系数 0.6920 偏相关系数P值 0.0005
气温X2
气湿X3 风速X4
0.1724
0.2754 -0.67957
0.47670
-0.00218 -0.59275
0.0289
0.9925 0.0046
第十二章
第一节 第二节 第三节 第四节
多重线性回归与相关
多重线性回归的概念与统计描述 多重线性回归的假设检验 复相关系数与偏相关系数 自变量筛选
一、整体回归效应的假设检验(方差分析)
表12-2 检验回归方程整体意义的方差分析表
变异来源 回归模型
残差 总变异
SS
0.0639 6 0.0172 7 0.0812 3
风速
(X4) 2.00 2.40 3.00 1.00 2.80 1.45 1.50 1.50 0.90 0.65 1.83 2.00
(完整版)第十二章相关和回归分析练习试题

第十二章相关与回归分析一、填空1.如果两变量的相关系数为0,说明这两变量之间_____________。
2.相关关系按方向不同,可分为__________和__________。
3.相关关系按相关变量的多少,分为______和复相关。
4.在数量上表现为现象依存关系的两个变量,通常称为自变量和因变量。
自变量是作为(变化根据)的变量,因变量是随(自变量)的变化而发生相应变化的变量。
5.对于表现为因果关系的相关关系来说,自变量一般都是确定性变量,因变量则一般是(随机性)变量。
6.变量间的相关程度,可以用不知Y与X有关系时预测Y的全部误差E1,减去知道Y与X有关系时预测Y的联系误差E2,再将其化为比例来度量,这就是(削减误差比例)。
7.依据数理统计原理,在样本容量较大的情况下,可以作出以下两个假定:(1)实际观察值Y围绕每个估计值cY是服从();(2)分布中围绕每个可能的cY值的()是相同的。
7.已知:工资(元)倚劳动生产率(千元)的回归方程为xyc8010+=,因此,当劳动生产率每增长1千元,工资就平均增加 80 元。
8.根据资料,分析现象之间是否存在相关关系,其表现形式或类型如何,并对具有相关关系的现象之间数量变化的议案关系进行测定,即建立一个相关的数学表达式,称为(回归方程),并据以进行估计和预测。
这种分析方法,通常又称为(回归分析)。
9.积差系数r是(协方差)与X和Y的标准差的乘积之比。
二、单项选择1.欲以图形显示两变量X和Y的关系,最好创建(D )。
A 直方图 B 圆形图 C 柱形图 D 散点图2.在相关分析中,对两个变量的要求是( A )。
A 都是随机变量B 都不是随机变量C 其中一个是随机变量,一个是常数D 都是常数3. 相关关系的种类按其涉及变量多少可分为( )。
A. 正相关和负相关B. 单相关和复相关C. 线性相关和非线性相关D. 不相关、不完全相关、完全相关4.关于相关系数,下面不正确的描述是( B )。
第十二章相关与回归分析

第十二章 相关与回归分析四、名词说明1.消减误差比例变量间的相关程度,能够用不知Y 与X 有关系时预测Y 的误差0E ,减去明白Y 与X 有关系时预测Y 的误差1E ,再将其化为比例来气宇。
将削减误差比例记为PRE 。
2. 确信性关系当一个变量值确信后,另一个变量值夜完全确信了。
确信性关系往往表现成函数形式。
3.非确信性关系在非确信性关系中,给定了一个变量值,另一个变量值还能够在必然范围内转变。
4.因果关系变量之间的关系知足三个条件,才能判定是因果关系。
1)连个变量有共变关系,即一个变量的转变会伴随着另一个变量的转变;2)两个变量之间的关系不是由其他因素形成的,即因变量的转变是由自变量的转变引发的;3)两个变量的产生和转变有明确的时刻顺序,即一个在前,另一个在后,前者称为自变量,后者称为因变量。
5.单相关和复相关单相关只涉及到两个变量,因此又称为二元相关。
三个或三个以上的变量之间的相关关系那么称为复相关,又称多元相关。
6.正相关与负相关正相关与负相关:正相关是指一个变量的值增加时,另一变量的值也增加;负相关是指一个变量的值增加时,另一变量的值却减少。
7.散点图散点图:将相关表所示的各个有对应关系的数据在直角坐标系上画出来,以直观地观看X 与Y 的彼此关系,即得相关图,又称散点图。
8.皮尔逊相关系数r皮尔逊相关系数是协方差与两个随机变量X 、Y 的标准差乘积的比率。
9.同序对 在观看X 序列时,若是看到i j X X <,在Y 中看到的是i j Y Y <,那么称这一配对是同序对。
10.异序对 在观看X 序列时,若是看到i j X X <,在Y 中看到的是i j Y >Y ,那么称这一配对是异序对。
11.同分对若是在X 序列中,咱们观看到i j X =X (现在Y 序列中无i j Y =Y ),那么那个配对仅是X 方向而非Y 方向的同分对;若是在Y 序列中,咱们观看到i j Y =Y (现在X 序列中无i j X =X ),那么那个配对仅是Y 方向而非X 方向的同分对;咱们观看到i j X =X ,也观看到i j Y =Y ,那么称那个配对为X 与Y 同分对。
第十二章 回归分析

回归分析
如果我们将存在相关的两个变量,一个作为自变 量,另一个作为因变量,并把两者之间不十分稳 定的、准确的关系,用数学方程式来表达,则可 利用该方程由自变量的值来估计、预测因变量的 估计值,这一过程称为回归分析。 相关表示两个变量之间的双向相互关系,回归表 示一个变量随另一个变量做不同程度变化的单向 关系。
• 线性回归的基本假设
– – – – 线性关系 正态分布 独立性假设 误差等分散性假设
• 回归方程的建立
– 步骤:1)作散点图;2)设直线方程;3)选定具体方 法,计算表达式中的a和b;4)将a和b代入表达式,得 到回归方程。 – 方法:1)平均数法;2)最小二乘法。 • 最小二乘法:在配置回归线时,回归系数b的确定原则是 使散布图上各点距回归线上相应点的纵向距离平方和为最 小,这种求b的方法即最小二乘法。
• 回归分析与相关分析的关系
– 理解: • 同属相关分析; • 对称设计与不对称设计。 – 回归系数与相关系数的关系 • 相关系数是两个回归系数的几何平均数。
第二节 一元线性回归方程的检验
• 估计误差的标准差
某一X值相对应的诸Y 值,是以Y的平均数YX 为中 ˆ 心呈正态分布的。而与某一X值相对应的回归值 Y 就是与该X值相对应的那些诸Y值的平均数YX的估 ˆ 计值。由 Y 估计YX 会有一定的误差。误差大小 与X值相对应的诸Y值分布范围有关,范围大,误 差大,估计的准确性、可靠性小,范围小,误差小, 估计的准确性、可靠性大。 ˆ 我们需要一个用来描述由Y 估计YX 时误差大小的 指标,即估计误差的标准差。平均数与标准差未知, 样本的无偏估计量为:
a YX Y bYX X
• 列回归方程式(见教材)
第十二章 简单回归分析

第十二章简单回归分析习题一、是非题1.直线回归反映两变量间的依存关系,而直线相关反映两变量间的相互线性伴随变化关系.2.对同一组资料,如相关分析算出的r越大,则回归分析算出的b值也越大. 3.对同一组资料,对r与b分别作假设检验,可得t r=t b4.利用直线回归估计X值所对应的Y值的均数置信区间时,增大残差标准差可以减小区间长度.5.如果直线相关系数r=0,则直线回归的SS残差必等于0.二、选择题1. 用最小二乘法确定直线回归方程的原则是各观察点距直线的( ).A.纵向距离之和最小 B. 纵向距离的平方和最小C. 垂直距离之和最小D.垂直距离的平方和最小E.纵向距离的平方和最大2.Y=14十4X是1~7岁儿童以年龄(岁)估计体质量(市斤)的回归方程,若体质量换成位kg,则此方程( )A 截距改变B 回归系数改变C 两者都改变D 两者都不改变E.相关系数改变4.直线回归系数假设检验,其自由度为( )A.n B. n-1C.n-2 D. 2n-1E.2(n-1)5.当r=0时,Y=a+b X回归方程中( )A a必大于零B a必大于XC a必等于零D a必大于YE a必等于b6.在多元线性回归分析中,反应变量总离均差平方和可以分解为两部分,残差是指( ).A.观察值与估计值之差B.观察值与平均值之差C.估计值与平均值的平方和之差D.观察值与平均值之差的平方和E.观察值与估计值之差的平方和三、筒答题1.用什么方法考察回归直线是否正确?2.简述回归系数方差分析Y的平方和与自由度的分解.3. 举例说明如何用直线回归方程进行预测和控制?4. 直线回归分析时怎样确定自变量和因变量?5. 简述曲线回归常用的几种曲线形式.。
第十二章相关与回归分析

第十二章 相关与回归分析四、名词解释1.消减误差比例变量间的相关程度,可以用不知Y 与X 有关系时预测Y 的误差0E ,减去知道Y 与X 有关系时预测Y 的误差1E ,再将其化为比例来度量。
将削减误差比例记为PRE 。
2. 确定性关系当一个变量值确定后,另一个变量值夜完全确定了。
确定性关系往往表现成函数形式。
3.非确定性关系在非确定性关系中,给定了一个变量值,另一个变量值还可以在一定范围内变化。
4.因果关系变量之间的关系满足三个条件,才能断定是因果关系。
1)连个变量有共变关系,即一个变量的变化会伴随着另一个变量的变化;2)两个变量之间的关系不是由其他因素形成的,即因变量的变化是由自变量的变化引起的;3)两个变量的产生和变化有明确的时间顺序,即一个在前,另一个在后,前者称为自变量,后者称为因变量。
5.单相关和复相关单相关只涉及到两个变量,所以又称为二元相关。
三个或三个以上的变量之间的相关关系则称为复相关,又称多元相关。
6.正相关与负相关正相关与负相关:正相关是指一个变量的值增加时,另一变量的值也增加;负相关是指一个变量的值增加时,另一变量的值却减少。
7.散点图散点图:将相关表所示的各个有对应关系的数据在直角坐标系上画出来,以直观地观察X 与Y 的相互关系,即得相关图,又称散点图。
8.皮尔逊相关系数r皮尔逊相关系数是协方差与两个随机变量X 、Y 的标准差乘积的比率。
9.同序对在观察X 序列时,如果看到i j X X <,在Y 中看到的是i j Y Y <,则称这一配对是同序对。
10.异序对在观察X 序列时,如果看到i j X X <,在Y 中看到的是i j Y >Y ,则称这一配对是异序对。
11.同分对如果在X 序列中,我们观察到i j X =X (此时Y 序列中无i j Y =Y ),则这个配对仅是X 方向而非Y 方向的同分对;如果在Y 序列中,我们观察到i jY =Y (此时X 序列中无i j X =X ),则这个配对仅是Y 方向而非X 方向的同分对;我们观察到i j X =X ,也观察到i j Y =Y ,则称这个配对为X 与Y 同分对。
第十二章直线相关与回归

第十二章直线相关与回归A型选择题〔、若计算得一相关系数r=0.94,则()A、x与y之间一定存在因果关系B、同一资料作回归分析时,求得回归系数一定为正值C、同一资料作回归分析时,求得回归系数一定为负值D求得回归截距a>0E、求得回归截距a^ 02、对样本相关系数作统计检验(H o =0),结果r r°.05(v),统计结论是()。
A、肯定两变量为直线关系B、认为两变量有线性相关C、两变量不相关B. 两变量无线性相关E、两变量有曲线相关3、若A「0.05(如」2血。
^),则可认为()。
A. 第一组资料两变量关系密切B. 第二组资料两变量关系密切C. 难说哪一组资料中两变量关系更密切D两组资料中两变量关系密切程度不一样E、以上答案均不对4、相关分析可以用于()有无关系的研究A、性别与体重B、肺活量与胸围C、职业与血型D国籍与智商E、儿童的性别与体重5、相关系数的假设检验结果,则在〉水平上可认为相应的两个变量间()A、有直线相关关系B、有曲线相关关系C、有确定的直线函数关系D有确定的曲线函数关系E、不存在相关关系6根据样本算得一相关系数r,经t检验,P v 0.01说明()A、两变量有高度相关B、r来自高度相关的相关总体C、r来自总体相关系数p的总体D r来自卩工0的总体E、r来自p>0的总体7、相关系数显著检验的无效假设为()A、r有高度的相关性B、r来自p工0的总体C、r来自p = 0的总体D r与总体相关系数p差数为0E、r来自p>0的总体8、计算线性相关系数要求()A. 反应变量Y呈正态分布,而自变量X可以不满足正态分布的要求B. 自变量X呈正态分布,而反应变量丫可以不满足正态分布的要求C. 自变量X和反应变量丫都应满足正态分布的要求D. 两变量可以是任何类型的变量E. 反应变量Y要求是定量变量,X可以是任何类型的变量9、对简单相关系数r进行检验,当检验统计量t r>t 0.05(V)时,可以认为两变量x 与丫间()A. 有一定关系B. 有正相关关系C. 无相关关系D. 有直线关系E. 有负相关关系10、相关系数反映了两变量间的()A、依存关系B、函数关系C、比例关系D相关关系E、因果关系11、|r| “0.05/2,(2)时,则在G =0.05水准上可认为相应的两变量X、丫间()。
回归分析练习题及参考答案
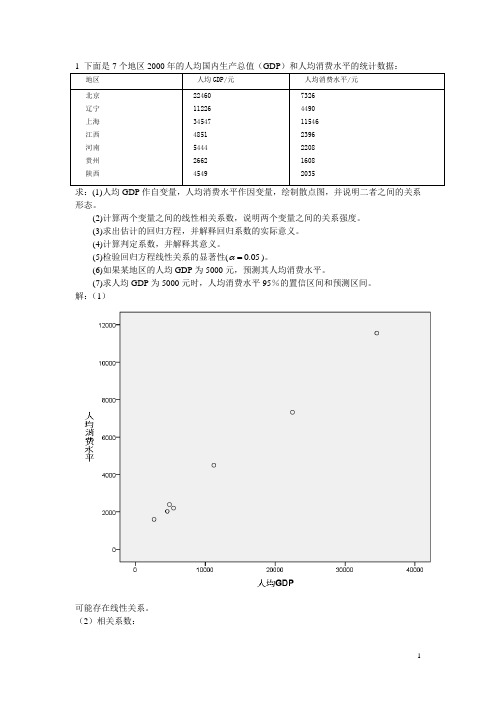
1 下面是7个地区2000年的人均国内生产总值(GDP)和人均消费水平的统计数据:地区人均GDP/元人均消费水平/元北京辽宁上海江西河南贵州陕西 224601122634547485154442662454973264490115462396220816082035求:(1)人均GDP作自变量,人均消费水平作因变量,绘制散点图,并说明二者之间的关系形态。
(2)计算两个变量之间的线性相关系数,说明两个变量之间的关系强度。
(3)求出估计的回归方程,并解释回归系数的实际意义。
(4)计算判定系数,并解释其意义。
(5)检验回归方程线性关系的显著性(0.05α=)。
(6)如果某地区的人均GDP为5000元,预测其人均消费水平。
(7)求人均GDP为5000元时,人均消费水平95%的置信区间和预测区间。
解:(1)可能存在线性关系。
(2)相关系数:(3)回归方程:734.6930.309y x=+回归系数的含义:人均GDP没增加1元,人均消费增加0.309元。
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% 注意:图标不要原封不动的完全复制软件中的图标,要按规范排版。
系数(a)模型非标准化系数标准化系数t 显著性B 标准误Beta1 (常量)734.693 139.540 5.265 0.003人均GDP(元)0.309 0.008 0.998 36.492 0.000 a. 因变量: 人均消费水平(元)%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%(4)模型汇总模型R R 方调整 R 方标准估计的误差1 .998a.996 .996 247.303a. 预测变量: (常量), 人均GDP。
人均GDP对人均消费的影响达到99.6%。
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%注意:图标不要原封不动的完全复制软件中的图标,要按规范排版。
卢淑华—相关与回归分析练习题

第十一章 等级相关练习题1.某市有12所大专院校,现组织一个评审委员会对各校校园及学生体质进行评价,结果如下,试求环境质量与学生体质的关系的斯皮尔曼相关系数和肯得尔等级相关系数。
2.以下是婚姻美满与文化程度的抽样调查的结果,请计算婚姻美满与文化程度之Gamma 系数和肯德尔相关系数τc 。
3.以下为两位评判员对10名参赛人名次的打分。
试用斯皮尔曼等级相关系数来描述两评判员打分的接近程度。
4.青年歌手大奖赛评委会对10名决赛选手的演唱水平(X )和综合素质(Y )进行打分,评价结果如下表(表中已先将选手按演唱水平作了次序排列)所示,试计算选手的演唱水平和综合素质间的斯皮尔曼等级相关系数。
(10分)5.下面是对50名被调查者的英语成绩和法语成绩的抽样调查:求Gamma 系数。
解:41.0164390164390=+-=+-=d s d s n n n n G y x a=b 54.479y=a+bx=-54.479+0.659x n n -=-∑∑斯皮尔曼相关系数2s 26d r 1-0.94n(n -1)==∑【皮尔逊相关系数:0.889,斯皮尔曼相关系数:0.94,回归方程:Y=-54.48+0.66X 】1.赛马迷们会认为,在圆跑道上进行的赛马比赛中,某些起点位置上的马会特别有利。
在有八匹马的比赛中,位置1是内侧最靠近栏杆的跑道,位置8是外侧离栏杆最远的跑道。
请从赛马的结果中判断起点位置与赛马获胜是否有关。
(α=0.05)7. 甲、乙两位评酒员对10种品牌白酒的主观排序如下表,计算两个等级相关系数,问两位评酒员对白酒的评价意见具有一定的相关性吗?(α= 0.05)第十二章回归与相关一、填空1.在数量上表现为现象依存关系的两个变量,通常称为自变量和因变量。
自变量是作为(变化根据)的变量,因变量是随(自变量)的变化而发生相应变化的变量。
2.对于表现为因果关系的相关关系来说,自变量一般都是确定性变量,因变量则一般是(随机性)变量。
(完整版)第十二章相关和回归分析练习试题

第十二章相关与回归分析一、填空1. 如果两变量的相关系数为0,说明这两变量之间__ 。
2.相关关系按方向不同,可分为_____ 和________ 。
3. 相关关系按相关变量的多少,分为和复相关。
4.在数量上表现为现象依存关系的两个变量,通常称为自变量和因变量。
自变量是作为(变化根据)的变量,因变量是随(自变量)的变化而发生相应变化的变量。
5.对于表现为因果关系的相关关系来说,自变量一般都是确定性变量,因变量则一般是(随机性)变量。
6.变量间的相关程度,可以用不知Y与 X有关系时预测 Y的全部误差 E1,减去知道 Y与 X有关系时预测Y的联系误差E2,再将其化为比例来度量,这就是(削减误差比例)。
7.依据数理统计原理,在样本容量较大的情况下,可以作出以下两个1)实际观察值 Y 围绕每个估计值 Y c是服假定:从();(2)分布中围绕每个可能的 Y c 值的()是相同的。
7. 已知:工资(元)倚劳动生产率(千元)的回归方程为yc 10 80x,因此,当劳动生产率每增长 1 千元,工资就平均增加 80 元。
8.根据资料,分析现象之间是否存在相关关系,其表现形式或类型如何,并对具有相关关系的现象之间数量变化的议案关系进行测定,即建立一个相关的数学表达式,称为(回归方程),并据以进行估计和预测。
这种分析方法,通常又称为(回归分析)。
9.积差系数 r 是(协方差)与 X 和 Y 的标准差的乘积之比。
二、单项选择1.欲以图形显示两变量 X 和 Y 的关系,最好创建( D )。
A 直方图 B 圆形图 C 柱形图 D 散点图2.在相关分析中,对两个变量的要求是(A )。
A 都是随机变量B 都不是随机变量C 其中一个是随机变量,一个是常数D 都是常数3.相关关系的种类按其涉及变量多少可分为()。
A. 正相关和负相关B. 单相关和复相关C. 线性相关和非线性相关D. 不相关、不完全相关、完全相关4.关于相关系数,下面不正确的描述是(B )。
相关分析与回归分析同步练习试卷1(题后含答案及解析)

相关分析与回归分析同步练习试卷1(题后含答案及解析)题型有:1. 单项选择题 2. 多项选择题 3. 名词解释题单项选择题每小题1分,在每小题列出的四个备选项中只有一个是符合题目要求的,请将其代码填写在题后的括号内。
多选无分。
1.产品的单位成本随着劳动生产率的不断提高而下降,此种现象属于()A.完全相关B.不完全相关C.正相关D.负相关正确答案:D 涉及知识点:相关分析与回归分析2.只反映一个自变量和一个因变量韵相关关系是()A.正相关B.负相关C.单相关D.复相关正确答案:C 涉及知识点:相关分析与回归分析3.当相关关系的—个变量变动时,另—变量也相应地发生大致均等的变动,这种相关关系称为()A.线性相关B.非线性相关C.单相关D.完全相关正确答案:A 涉及知识点:相关分析与回归分析4.完全相关关系就是()A.函数关系B.因果关系C.狭义的相关关系D.广义的相关关系正确答案:A 涉及知识点:相关分析与回归分析5.大多数相关关系属于()A.不相关B.完全相关C.不完全相关D.无法判断正确答案:C 涉及知识点:相关分析与回归分析6.制作双变量分组相关表,应将自变量放在()A.横栏B.纵栏C.中间栏D.任意一栏正确答案:A 涉及知识点:相关分析与回归分析7.相关系数的取值范围是()A.-1≤r≤lB.-1≤r≤lC.-1<r<lD.-1≤r<1正确答案:B 涉及知识点:相关分析与回归分析8.两个变量问的相互依存程度越高,则二者之间的相关系数值越接近于()A.1B.-1C.0D.1或-1正确答案:D 涉及知识点:相关分析与回归分析9.两个现象之间相互依存关系程度越弱,则相关系数r()A.越接近于0B.越接近于-1C.越接近于1D.越接近于0.5正确答案:A 涉及知识点:相关分析与回归分析10.在相关分析中,要求相关的两个变量()A.至少有一个是随机变量B.因变量是随机变量C.都不是随机变量D.自变量是随机变量正确答案:A 涉及知识点:相关分析与回归分析11.配合回归直线最好的方法是()A.随手画线法B.加权平均法C.最小平方法D.移动平均法正确答案:C 涉及知识点:相关分析与回归分析多项选择题每小题2分,在每小题列出的五个备选项中至少有两个是符合题目要求的,请将其代码填写在题后的括号内。
卫生统计学 直线相关与回归

第十二章 直线相关与回归A 型选择题1、若计算得一相关系数r=0.94,则( )A 、x 与y 之间一定存在因果关系B 、同一资料作回归分析时,求得回归系数一定为正值C 、同一资料作回归分析时,求得回归系数一定为负值D 、求得回归截距a>0E 、求得回归截距a ≠02、对样本相关系数作统计检验(H 0:ρ=0),结果0.05()v r r >,统计结论是()。
A. 肯定两变量为直线关系B 、认为两变量有线性相关C 、两变量不相关B. 两变量无线性相关E 、两变量有曲线相关3、若1210.05()20.01(),v v r r r r >>,则可认为( )。
A. 第一组资料两变量关系密切B. 第二组资料两变量关系密切C 、难说哪一组资料中两变量关系更密切D 、两组资料中两变量关系密切程度不一样E 、以上答案均不对4、相关分析可以用于( )有无关系的研究A 、性别与体重B 、肺活量与胸围C 、职业与血型D 、国籍与智商E 、儿童的性别与体重5、相关系数的假设检验结果P<α,则在α水平上可认为相应的两个变量间()A 、有直线相关关系B 、有曲线相关关系C 、有确定的直线函数关系D 、有确定的曲线函数关系E 、不存在相关关系6、根据样本算得一相关系数r ,经t 检验,P <0.01说明( )A 、两变量有高度相关B 、r 来自高度相关的相关总体C 、r 来自总体相关系数ρ的总体D 、r 来自ρ≠0的总体E 、r 来自ρ>0的总体7、相关系数显著检验的无效假设为( )A 、r 有高度的相关性B 、r 来自ρ≠0的总体C 、r 来自ρ=0的总体D 、r 与总体相关系数ρ差数为0E 、r 来自ρ>0的总体8、计算线性相关系数要求( )A .反应变量Y 呈正态分布,而自变量X 可以不满足正态分布的要求B .自变量X 呈正态分布,而反应变量Y 可以不满足正态分布的要求C .自变量X 和反应变量Y 都应满足正态分布的要求D .两变量可以是任何类型的变量E .反应变量Y 要求是定量变量,X 可以是任何类型的变量9、对简单相关系数r 进行检验,当检验统计量t r >t 0.05(ν)时,可以认为两变量x与Y 间( )A .有一定关系B .有正相关关系C .无相关关系D .有直线关系E .有负相关关系10、相关系数反映了两变量间的( )A 、依存关系B 、函数关系C 、比例关系D 、相关关系E 、因果关系11、)2(,2/05.0-<n r r 时,则在05.0=α水准上可认为相应的两变量X 、Y 间( )。
第十二章 简单回归分析

第十二章简单回归分析选择题A1型每一道题下面有A、B、C、D、E五个备选答案,请从中选择一个最佳答案。
1、线性回归分析可用于下列()的依存关系的研究A、性别与身高B、年龄与体重C、职业与工龄D、民族语血型E、国籍与智商2、对变量X和Y同时进行线性相关分析和线性回归分析,其结果一定是()A、r>0,b<0B、r<0,b>0C、r b≥0D、r=bE、r与b的符号无关3、已知相关系数r=1,则一定有()A、SS总=SS残B、SS总=SS回C、SS残=SS回D、a=1E、b=14、线性回归分析中,对总体回归系数B是否为0做t检验,其自由度是()A、nB、n-1C、n-2D、2n-1E、2n-25、如果对线性回归模型进行假设检验,结果是没能拒绝H0,这就意味着()A、该模型有应用价值B、该模型无应用价值C、该模型求解错误D、X与Y之间无关系E、尚无充分证据说明X与Y之间有线性关系6、求得X与Y的线性回归方程后,对回归系数作假设检验的目的是:对()作出统计推断A、样本截距B、总体截距C、样本斜率D、总体斜率E、决定系数7、在求出Y关于X变化的线性回归方程后发现,将原始数据中的某一点(X k,Y k)的横坐标值X k代入方程所得的Y k≠Y k,则可以认为()A此现象正常B、此现象无法解释C、计算有错误D、X与Y之间呈非线性关系E、X与Y之间呈线性关系8、对含有两个随机变量的同一批资料,既作线性相关,有作线性回归分析。
对相关系数检验的t值记为t r,对回归系数检验的t值记为t b,则二者之间的关系是()A、t r>t bB、t r<t bC、t r≥t bD、t r≤t bE、t r=t b9、对以X为自变量,Y为因变量作线性回归分析时,下列正确的说法是()A、只要求X服从正态分布B、只要求Y服从正态分布C、只要求X与Y是定量变量D、要求X与Y都服从正态分布E、要求X与Y服从双变量正态分布10、利用最小二乘原则确定回归方程的要求是:使得各数据点()A、距回归直线纵向距离的平方和最小B、距回归直线横向距离的平方和最小C、距回归直线距离的平方和最小D、距回归直线垂直距离的平方和最小E、距回归直线平行距离的平方和最小11、线性回归分析中,当()时,回归方程拟合的效果越佳A、截距越大B、斜率越大C、回归系数越大D、相关系数越大E、决定系数越大12、线性回归分析中,若对总体回归系数B是否为0作方差分析,得到F>F a(v1,v2),则可认为()A、两变量之间存在回归关系B、两变量之间不存在回归关系C、两变量之间存在线性回归关系D、两变量之间不存在线性回归关系E、两变量之间存在因果关系【参考答案】(一)1、B 2、C 3、B 4、C 5、E 6、D 7、A 8、E 9、D 10、A 11、E 12、C。
第十二章直线相关与回归

第十二章直线相关与回归【A1型题】1.在y和x的回归分析中,若tb<t0.05,υ可认为A. 两变量存在线性相关关系B. 两变量不存在任何关系C. 样本回归系数和总体回归系数(β=0 ) 相等的可能性P>95%D. 两变量无线性相关E. 以上都不是2. sy·x和sb分别表示A. y对的离散度和b的抽样误差B. y对x的离散度和b的离散度C. y的离散度和b的离散度D. y对的离散度和y的标准估计误差E. y的离散度和b的变异3.欲分析肺活量和身高之间的数量关系,拟用身高值预测肺活量值,则应采用A. 秩相关分析B. 相关分析C. 直线回归分析D. 多元回归分析E. 以上都不是4.若r>r0.05(ν),则A. P>0.05B. P≤0.05C. P>0.01D. P≥0.05E. P<0.055.若对两个变量进行直线相关分析,r=0.39,P>0.05,则说明两个变量之间A. 有伴随关系B. 有数量关系C. 有因果关系D. 有相关关系E. 无相关关系6.对相关系数r进行假设检验,当r>r0.05(ν),则A. 两变量之间关系密切B. 两变量之间相关有统计学意义C. 两变量之间关系不密切D. 两变量之间相关无统计学意义E. 以上都不是7.对两个数值变量同时进行了相关和回归分析,r有统计学意义(P<0.05),则A. b有高度的统计学意义B. b无统计学意义C. b有统计学意义D. 不能肯定b有无统计学意义E. 以上都不是8.某研究者测定60个中学生的身高,询问了他们每天的睡眠时间,并计算了等级相关系数,检验其统计学意义,查表时,n应为A. 2B. 1C. 58D. 60E. 599.某研究者测定了睡眠时间和焦虑症状评分,若想研究两者之间的相关性,应计算的指标是A. rB. tC. b2D. uE. b10.某医师拟制作标准曲线,用光密度值来推测食品中亚硝酸盐的含量,应选用的统计方法是A. u检验B. 回归分析C. 相关分析D. χ2检验E. q检验11.在直线回归分析中,回归系数b的绝对值越大A. 所绘散点越靠近回归线B. 所绘散点越远离回归线C. 回归线在y轴上的截距越大D. 回归线对x轴越平坦E. 回归线对x轴越陡【B型题】A.B.C.D. SbE. Sy12.直线回归分析中,反映扣除x的影响后y的变异程度的指标是13.直线回归分析中,反映在y的总变异中由于x与y的直线关系而使y变异减小的部分,也就是在总平方和中可以用x解释的部分即14.直线回归分析中,反映当x为某定数时个体y值变异程度的指标是15.直线回归分析中,反映x对y的线性影响之外的一切因素对y的变异的作用是【X型题】16. 对某样本的相关系数r和0的差别进行假设检验,结果为tr<t0.05,ν,因此A. 两变量存在直线相关的可能性小于5%B. 如果样本来自ρ=0的总体,得出该r值的概率大于5%C. 如果样本来自ρ=0的总体,得出该r值的概率小于5%D. 两变量的差别无显著性E. r≠0是抽样误差所致17.在作直线回归分析时,选定自变量x的原则一般为A. 两变量间无因果关系,以变异较小者为xB. 两变量间无因果关系,以变异较大者为xC. 两变量间有因果关系,以"因"为xD. 两变量间有因果关系,以"果"为xE. x是可以精确测量和严格控制的变量18.相关系数r的数值A. 可以为负值B. 可以为正值C. 可等于1D. 可大于1E. 可等于-1【名词解释】19. 回归系数20. 截距21. 相关系数22. 等级相关23. 直线回归【简答题】24. 直线回归与相关分析的区别与联系是什么25. 进行直线相关与回归分析时应注意哪些问题26. 什么是剩余标准差?其作用如何27. 为何应该对样本相关系数和样本回归系数都应该进行假设检验28. 直线回归方程可应用在哪些方面29. 用什么方法来确定一条回归直线【应用题】30. 现有12名糖尿病患者血糖和胰岛素的测量数据列于下表中,试对其进行直线相关与回归分析表 12名糖尿病患者血糖(mmol/L)和胰岛素(mU/L)的测量数据编号123456789101112胰岛素17141912916182124171710血糖9.511.610.811.412.49.810.18.67.911.210.612.831. 某课题组测量了16名18~22岁男大学生的肺活量与身高,结果如下表,请进行直线相关与回归分析编号身高(m)x肺活量(L)y编号身高(m)x肺活量(L)y11.7424.65091.7084.02221.7184.278101.6984.07731.7144.420111.7144.31841.7124.379 121.6744.03951.7204.365131.6833.85061.7044.222141.6703.62571.7093.973151.6793.87 481.7294.290161.6923.91132 .某省卫生防病中心对10个城市进行肺癌死亡回顾调查,并对大气中苯并(a)芘进行监测,结果如下表,试检验两者有无相关城市编号12345678910肺癌标化死亡率(1/10万)5.6018.5016.2311.4013.808.1318.0012.1015.309.70苯并(a)芘(μg/100m3)0.051.171.050.100.750.500.651.200.950.65参考答案【A1型题】26.1. D2. A3. C4. E5. E6. B7. C8. D9. A10. B11. E【B型题】12.12. C13. B14. E15. A【X型题】16.16. BE17. CE18. ABCE【应用题】30.相关系数=-0.9037,P<0.05回归方程为=15.448-0.302x ,P<0.0531.相关系数=0.874,P<0.05回归方程为=-15.392+11.464x ,P<0.0532.rs=0.676,P<0.05???? ?? ??-7-。
回归分析练习题(有答案)

回归分析的基本思想及其初步应用一、选择题 1. 某同学由x 与y 之间的一组数据求得两个变量间的线性回归方程为y bx a =+,已知:数据x 的平均值为2,数据y 的平均值为3,则 ( )A .回归直线必过点(2,3)B .回归直线一定不过点(2,3)C .点(2,3)在回归直线上方D .点(2,3)在回归直线下方2. 在一次试验中,测得(x,y)的四组值分别是A(1,2),B(2,3),C(3,4),D(4,5),则Y 与X 之间的回归直线方程为( )A .yx 1=+ B .y x 2=+ C .y 2x 1=+ D.y x 1=-3. 在对两个变量x ,y 进行线性回归分析时,有下列步骤:①对所求出的回归直线方程作出解释; ②收集数据(i x 、i y ),1,2i =,…,n ;③求线性回归方程; ④求未知参数; ⑤根据所搜集的数据绘制散点图如果根据可行性要求能够作出变量,x y 具有线性相关结论,则在下列操作中正确的是( ) A .①②⑤③④ B .③②④⑤① C .②④③①⑤ D .②⑤④③①4. 下列说法中正确的是( )A .任何两个变量都具有相关关系B .人的知识与其年龄具有相关关系C .散点图中的各点是分散的没有规律D .根据散点图求得的回归直线方程都是有意义的5. 给出下列结论:(1)在回归分析中,可用指数系数2R 的值判断模型的拟合效果,2R 越大,模型的拟合效果越好; (2)在回归分析中,可用残差平方和判断模型的拟合效果,残差平方和越大,模型的拟合效果越好; (3)在回归分析中,可用相关系数r 的值判断模型的拟合效果,r 越小,模型的拟合效果越好; (4)在回归分析中,可用残差图判断模型的拟合效果,残差点比较均匀地落在水平的带状区域中,说明这样的模型比较合适.带状区域的宽度越窄,说明模型的拟合精度越高. 以上结论中,正确的有( )个.A .1B .2C .3D .4 6. 已知直线回归方程为2 1.5y x =-,则变量x 增加一个单位时()A.y 平均增加1.5个单位B.y 平均增加2个单位C.y 平均减少1.5个单位D.y 平均减少2个单位7. 下面的各图中,散点图与相关系数r 不符合的是( )8. 一位母亲记录了儿子3~9岁的身高,由此建立的身高与年龄的回归直线方程为ˆ7.1973.93yx =+,据此可以预测这个孩子10岁时的身高,则正确的叙述是( )A .身高一定是145.83cmB .身高超过146.00cmC .身高低于145.00cmD .身高在145.83cm 左右9. 在画两个变量的散点图时,下面哪个叙述是正确的( ) (A)预报变量在x 轴上,解释变量在y 轴上 (B)解释变量在x 轴上,预报变量在y 轴上(C)可以选择两个变量中任意一个变量在x 轴上 (D)可以选择两个变量中任意一个变量在y 轴上10. 两个变量y 与x 的回归模型中,通常用2R 来刻画回归的效果,则正确的叙述是( )A. 2R 越小,残差平方和小B. 2R 越大,残差平方和大C. 2R 于残差平方和无关 D. 2R 越小,残差平方和大 11. 两个变量y 与x 的回归模型中,分别选择了4个不同模型,它们的相关指数2R 如下 ,其中拟合效果最好的模型是( )A.模型1的相关指数2R 为B.模型2的相关指数2R 为C.模型3的相关指数2R 为 D.模型4的相关指数2R 为12. 在回归分析中,代表了数据点和它在回归直线上相应位置的差异的是( ) A.总偏差平方和 B.残差平方和 C.回归平方和 D.相关指数R 213.工人月工资(元)依劳动生产率(千元)变化的回归直线方程为ˆ6090y x =+,下列判断正确的是( ) A.劳动生产率为1000元时,工资为50元 B.劳动生产率提高1000元时,工资提高150元 C.劳动生产率提高1000元时,工资提高90元 D.劳动生产率为1000元时,工资为90元14. 下列结论正确的是( )①函数关系是一种确定性关系;②相关关系是一种非确定性关系;③回归分析是对具有函数关系的两个变量进行统计分析的一种方法;④回归分析是对具有相关关系的两个变量进行统计分析的一种常用方法. A.①② B.①②③ C.①②④ D.①②③④15. 已知回归直线的斜率的估计值为,样本点的中心为(4,5),则回归直线方程为( ) A. 1.234y x =+ B. 1.235y x =+ C. 1.230.08y x =+ D.0.08 1.23y x =+二、填空题16. 在比较两个模型的拟合效果时,甲、乙两个模型的相关指数2R 的值分别约为和,则拟合效果好的模型是 .17. 在回归分析中残差的计算公式为 .18. 线性回归模型y bx a e =++(a 和b 为模型的未知参数)中,e 称为 .19. 若一组观测值(x 1,y 1)(x 2,y 2)…(x n ,y n )之间满足y i =bx i +a+e i (i=1、2.…n)若e i 恒为0,则R 2为_____三、解答题20. 调查某市出租车使用年限x 和该年支出维修费用y (万元),得到数据如下:(2)由(1)中结论预测第10年所支出的维修费用.(121()()()ni i i ni i x x y y b x x a y bx==⎧-⋅-⎪⎪=⎨-⎪⎪=-⎪⎩∑∑)21. 以下是某地搜集到的新房屋的销售价格y和房屋的面积x的数据:(1)画出数据对应的散点图;(2)求线性回归方程,并在散点图中加上回归直线;150m时的销售价格.(3)据(2)的结果估计当房屋面积为2(4)求第2个点的残差。
第十二章 多元线性回归

第十二章多元线性回归12.1根据下面的数据用Excel进行回归,并对回归结果进行讨论,计算x1=200,x2=7时y的预测值。
解:用Excel进行回归的结果如下:结果讨论如下:(1)从复判定系数看,x1和x2可解释y 变异的21%,这是一个相当低的程度。
(2)从方差分析的结果看,F 统计量不是统计上显著的。
(3)从单个回归系数看,也都是不显著的。
(4)该模型是无效的。
当x 1=200,x 2=7时y 的预测值为25.0287 - 0.04971*200+1.928169*7 = 28.58388312.2 根据下面Excel 输出的回归结果,说明模型中涉及多少个自变量、多少个观察值?写出回归方程,并根据F ,s e ,R 2及调整的2R α的值对模型进行讨论。
SUMMARY OUTPUT回归统计Multiple R 0.842407 R Square 0.709650 Adjusted R Square 0.630463 标准误差 109.429596 观测值 15 方差分析df SS MS F Significance F回归分析 3 321946.8018 107315.6006 8.961759 0.002724 残差 11 131723.1982 11974.84 总计 14 453670Coefficients 标准误差 t Stat P-valueIntercept 657.0534 167.459539 3.923655 0.002378 X Variable 1 5.710311 1.791836 3.186849 0.008655 X Variable 2 -0.416917 0.322193 -1.293998 0.222174 X Variable 3 -3.471481 1.442935 -2.405847 0.034870解:该模型有3个自变量,15个观察值。
估计的回归方程为:123ˆ657.0534 5.7103110.416917 3.471481yx x x =+-- 结果讨论。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第十二章相关与回归分析一、填空1.如果两变量的相关系数为0,说明这两变量之间_____________。
2.相关关系按方向不同,可分为__________和__________。
3.相关关系按相关变量的多少,分为______和复相关。
4.在数量上表现为现象依存关系的两个变量,通常称为自变量和因变量。
自变量是作为(变化根据)的变量,因变量是随(自变量)的变化而发生相应变化的变量。
5.对于表现为因果关系的相关关系来说,自变量一般都是确定性变量,因变量则一般是(随机性)变量。
6.变量间的相关程度,可以用不知Y与X有关系时预测Y的全部误差E1,减去知道Y与X有关系时预测Y的联系误差E2,再将其化为比例来度量,这就是(削减误差比例)。
7.依据数理统计原理,在样本容量较大的情况下,可以作出以下两个假定:(1)实际观察值Y围绕每个估计值cY是服从();(2)分布中围绕每个可能的cY值的()是相同的。
7.已知:工资(元)倚劳动生产率(千元)的回归方程为xyc8010+=,因此,当劳动生产率每增长1千元,工资就平均增加 80 元。
8.根据资料,分析现象之间是否存在相关关系,其表现形式或类型如何,并对具有相关关系的现象之间数量变化的议案关系进行测定,即建立一个相关的数学表达式,称为(回归方程),并据以进行估计和预测。
这种分析方法,通常又称为(回归分析)。
9.积差系数r是(协方差)与X和Y的标准差的乘积之比。
二、单项选择1.欲以图形显示两变量X和Y的关系,最好创建(D )。
A 直方图 B 圆形图 C 柱形图 D 散点图2.在相关分析中,对两个变量的要求是( A )。
A 都是随机变量B 都不是随机变量C 其中一个是随机变量,一个是常数D 都是常数3. 相关关系的种类按其涉及变量多少可分为( )。
A. 正相关和负相关B. 单相关和复相关C. 线性相关和非线性相关D. 不相关、不完全相关、完全相关4.关于相关系数,下面不正确的描述是( B )。
A当0≤≤r1时,表示两变量不完全相关; B当r=0时,表示两变量间无相关;C两变量之间的相关关系是单相关; D如果自变量增长引起因变量的相应增长,就形成正相关关系。
5. 当变量X按一定数量变化时,变量Y也随之近似地以固定的数量发生变化,这说明X与Y之间存在( )。
A. 正相关关系B. 负相关关系C. 直线相关关系D. 曲线相关关系6.当x按一定数额增加时,y也近似地按一定数额随之增加,那么可以说x与y之间存在( A )关系。
A 直线正相关B 直线负相关C 曲线正相关D 曲线负相关7.评价直线相关关系的密切程度,当r在0.5~0.8之间时,表示( C )。
A 无相关B 低度相关C 中等相关D 高度相关8.两变量的相关系数为0.8,说明( )A.两变量不相关B.两变量负相关C.两变量不完全相关D.两变量完全正相关9.两变量的线性相关系数为0,表明两变量之间( D )。
A 完全相关B 无关系C 不完全相关D 不存在线性相关10.兄弟两人的身高之间的关系是( )A.函数关系 B.因果关系 C.互为因果关系 D.共变关系11.身高和体重之间的关系是(C )。
A 函数关系 B 无关系 C 共变关系 D 严格的依存关系12.下列关系中,属于正相关关系得是(A )。
A 身高与体重B 产品与单位成本C 正常商品的价格和需求量D 商品的零售额和流通费率13如果变量x和变量y之间的皮尔逊相关系数为-1,说明这两个变量之间是()A.低度相关B.完全相关C.高度相关D.完全不相关28.定类变量的相关分析可以使用( )A. λ系数 B. ρ系数 C. r系数 D. τα系数14.相关分析和回归分析相辅相成,又各有特点,下面正确的描述有( D )。
A在相关分析中,相关的两变量都不是随机的;B在回归分析中,自变量是随机的,因变量不是随机的;C在回归分析中,因变量和自变量都是随机的;D在相关分析中,相关的两变量都是随机的。
15. 一元一次回归方程Y=a+bx中的a表示( )。
A. 斜率 B. 最小平均法 C. 回归直线 D. 截距16.当所有的观察值y都落在直线bxayc+=上时,则x与y之间的相关系数为( B )。
A、r=0B、r=1C、-1<r<1D、0<r<117.回归直线方程XC=c+dY,其中Y为自变量,则( )A.可以根据Y值推断XB.可以根据X值推断YC.可以互相推断D.不能进行推断18.对于有线性相关关系的两变量建立的直线回归方城Y=a+bx中,回归系数b ( B )。
A.肯定是正数B.显著不为0 C.可能为0 D.肯定为负数19.年劳动生产率x(千元)和工人工资y(元)之间的回归方程为y=10+70x,这意味着年劳动生产率每提高1千元时,工人工资平均()A.增加70元B.减少70元C.增加80元D.减少80元20产量X(千件)与单位成本Y(元)之间的回归方程为Y=77-3X,这表示产量每提高1000件,单位成本平均( )A.增加3元B.减少3000元C.增加3000元D.减少3元21.两变量X和Y的相关系数为0.8,则其回归直线的判定系数为( C )。
A 0.50 B 0.80 C 0.64 D 0.90 22.在完成了构造与评价一个回归模型后,我们可以( D )。
A 估计未来所需样本的容量B 计算相关系数和判定系数C 以给定的因变量的值估计自变量的值D 以给定的自变量的值估计因变量的值23.对相关系数的显著性检验,通常采用的是(①)① T检验② F检验③ Z 检验24.回归估计标准误差的计量单位与( )A.自变量相同B.因变量相同C.相关系数相同D.自变量、因变量及相关系数均不同25.在回归分析中,两个变量( D )。
A 都是随机变量B 都不是随机变量C 自变量是随机变量D 因变量是随机变量26.已知变量X和Y之间的关系如图所示,则变量X和Y的相关系数为(D )。
A、0.29B、-0.86C、1.04D、0.9127.一元线性回归模型和多元线性回归模型的区别在于只有一个(B )。
A 因变量B 自变量C 相关系数D 判定系数28.以下指标恒为正的是( D )。
A 相关系数r B 截距a C 斜率b D 复相关系数29.对两变量进行回归分析时,( )A.前提是两变量之间存在较高的相关关系B.其中任一变量都可以成为自变量或因(依)变量C.两变量都是随机变量D.一变量是随机变量,另一变量是非随机变量E.一变量是自变量,另一变量是因(依)变量三、多项选择1.判定现象之间有无相关系数的方法是( ABC )。
A 、对客观现象作定性分析B 、编制相关表C 、绘制相关图D 、计算相关系数E 、计算估计标准误 2.回归分析和相关分析的关系是(ABE )。
A 回归分析可用于估计和预测B 相关分析是研究变量之间的相互依存关系的密切程度C 回归分析中自变量和因变量可以互相推导并进行预测D 相关分析需区分自变量和因变量E 相关分析是回归分析的基础3.关于积差系数,下面正确的说法是(ABCD )。
A 积差系数是线性相关系数B 在积差系数的计算公式中,变量X 和Y 是对等关系C 积差系数具有PRE 性质D 在积差系数的计算公式中,变量X 和Y 都是随机的 4.关于皮尔逊相关系数,下面正确的说法是(ACE )。
A 皮尔逊相关系数是线性相关系数B 积差系数能够解释两变量间的因果关系C r 公式中的两个变量都是随机的D r 的取值在1和0之间E 皮尔逊相关系数具有PRE 性质,但这要通过r 2加以反映 5.简单线性回归分析的特点是( ABE )。
A 两个变量之间不是对等关系B 回归系数有正负号C 两个变量都是随机的D 利用一个回归方程,两个变量可以互相推算E 有可能求出两个回归方程 6.反映某一线性回归方程y=a+bx 好坏的指标有(ABD )。
A 相关系数B 判定系数C b 的大小D 估计标准误E a 的大小7.模拟回归方程进行分析适用于(ACDE )。
A 变量之间存在一定程度的相关系数B 不存在任何关系的几个变量之间C 变量之间存在线性相关D 变量之间存在曲线相关E 时间序列变量和时间之间8.判定系数r 2=80%和含义如下(ABC )。
A 自变量和因变量之间的相关关系的密切程度B 因变量y 的总变化中有80%可以由回归直线来解释和说明C 总偏差中有80%可以由回归偏差来解释D 相关系数一定为0.64E 判定系数和相关系数无关 9.以下指标恒为正的是(BC )。
A 相关系数B 判定系数C 复相关系数D 偏相关系数E 回归方程的斜率 10.一元线性回归分析中的回归系数b 可以表示为(BC )。
A 两个变量之间相关关系的密切程度B 两个变量之间相关关系的方向C 当自变量增减一个单位时,因变量平均增减的量D 当因变量增减一个单位时,自变量平均增减的量E 回归模型的拟合优度11.关于回归系数b ,下面正确的说法是(AE )。
A b 也可以反映X 和Y 之间的关系强度。
;B 回归系数不解释两变量间的因果关系; C b 公式中的两个变量都是随机的; D b 的取值在1和-1之间;E b 也有正负之分。
12、如果两个变量之间有一定的相关性,则以下结论中正确的是 ( ①②③ )①、回归系数b 的绝对值大于零 ②、判定系数2R 大于零 ③、相关系数r 的绝对值大于0.3 13、当所有的观察值都落在回归直线x yββ10+=上时,下述备选答案成立的有(②③ )①r=0 ② ∣r ∣= 1 ③s y =0五、判断题1.相关关系和函数关系都属于完全确定性的依存关系。
( )2.不管相关关系表现形式如何,当r =1时,变量X 和变量Y 都是完全相关。
(√ )3.不管相关关系表现形式如何,当r =0时,变量X 和变量Y 都是完全不相关。
(× )4.若x 与y 之间的相关系数r=-0.9,表示二者“不相关”。
( )5.通过列联表研究定类变量之间的关联性,这实际上是通过相对频数条件分布的比较进行的。
而如果两变量间是相关的话,必然存在着Y 的相对频数条件分布相同,且和它的相对频数边际分布相同。
(× )6.如果众数频数集中在条件频数分布列联表的同一行中,λ系数便会等于0,从而无法显示两变量之间的相关性。
( √ )7.由于削减误差比例的概念不涉及变量的测量层次,因此它的优点很明显,用它来定义相关程度可适用于变量的各测量层次。
( √ )8.不论是相关分析还是回归分析,都必须确定自变量和因变量。
( )9.从分析层次上讲,相关分析更深刻一些。
因为相关分析具有推理的性质,而回归分析从本质上讲只是对客观事物的一种描述,知其然而不知其所以然。
(× ) 10、 在回归分析中,通常假定N ~ε (0, σ2)。
