Matlab标定工具箱的使用

合集下载

Matlab各工具箱功能简介(部分)

对于分析多维数据，Statistics and Machine Learning Toolbox 可让您通过序列特征选择、逐步回归、主成份分析、规则化和其他降维方法确定影响您的模型的主要变量或特征。该工具箱提供了受监督和不受监督机器学习算法，包括支持向量机(SVM)、促进式 (boosted) 和袋装 (bagged) 决策树、k-最近邻、k-均值、k-中心点、分层聚类、高斯混合模型和隐马尔可夫模型。4 Curve Fitting Toolbox 曲线拟合工具箱Curve Fitting Toolbox™ 提供了用于拟合曲线和曲面数据的应用程序和函数。使用该工具箱可以执行探索性数据分析，预处理和后处理数据，比较候选模型，删除偏值。您可以使用随带的线性和非线性模型库进行回归分析，也可以指定您自行定义的方程式。该库提供了优化的解算参数和起始条件，以提高拟合质量。该工具箱还提供非参数建模方法，比如样条、插值和平滑。在创建一个拟合之后，您可以运用多种后处理方法进行绘图、插值和外推，估计置信区间，计算积分和导数。5 Optimization Toolbox 优化工具箱Optimization Toolbox™ 提供了寻找最小化或最大化目标并同时满足限制条件的函数。工具箱中包括了线性规划、混合整型线性规划、二次规划、非线性优化、非线性最小二乘的求解器。您可以使用这些求解器寻找连续与离散优化问题的解决方案、执行折衷分析、
Ｔoolbox工具箱序号工具箱备注一、数学、统计与优化1 Symbolic Math Toolbox符号数学工具箱Symbolic Math Toolbox™提供用于求解和推演符号运算表达式以及执行可变精度算术的函数。您可以通过分析执行微分、积分、化简、转换以及方程求解。另外，还可以利用符号运算表达式为MATLAB、Simulink和Simscape™生成代码。®®Symbolic Math Toolbox包含MuPAD语言，并已针对符号运算表达式的处理和执®行进行优化。该工具箱备有MuPAD函数库，其中包括普通数学领域的微积分和线性代数，以及专业领域的数论和组合论。此外，还可以使用MuPAD语言编写自定义的符号函数和符号库。MuPAD记事本支持使用嵌入式文本、图形和数学排版格式来记录符号运算推导。您可以采用HTML或PDF的格式分享带注释的推导。2 Partial Differential Euqation Toolbox偏微分方程工具箱偏微分方程工具箱™提供了用于在2D，3D求解偏微分方程（PDE）以及一次使用有限元分析。它可以让你指定和网格二维和三维几何形状和制定边界条件和公式。你能解决静态，时域，频域和特征值问题在几何领域。功能进行后处理和绘图效果使您能够直观地探索解决方案。你可以用偏微分方程工具箱，以解决从标准问题，如扩散，传热学，结构力学，静电，静磁学，和AC电源电磁学，以及自定义，偏微分方程的耦合系统偏微分方程。3 Statistics Toolbox统计学工具箱Statistics and Machine Learning Toolbox提供运用统计与机器学习来描述、分析数据和对数据建模的函数和应用程序。您可以使用用于探查数据分析的描述性统计和绘图，使用概率分布拟合数据，生成用于Monte Carlo仿真的随机数，以及执行假设检验。回归和分类算法用于依据数据执行推理并构建预测模型。

关于matlab 标定工具箱的使用

关于matlab 标定工具箱的使用在/bouguetj/calib_doc/提供了一个很好的matlab标定工具箱，但在使用中我发现由于原工具箱的目录设置问题，常常在第一步卡住程序无法运行，因此我对程序进行了更改，更改后的标定工具箱使用步骤如下：1> 读入图像数据启动matlab并将当前工作目录设置为包含待标定图像的目录（即包含代表顶图像的文件夹）打开calib_gui.m文件，运行此程序，弹出对话框：让用户选择change directory还是add to path,选择“add to path”.然后程序会自动跳转到matlab命令窗口（command window）并显示提示信息：Are you sure that the images to be calibrate in current directory? [y]/n :让用户确认当前目录是否包含待标定图像数据，输入'n'终止程序运行，用户可将当前目录设置为包含待标定图像数据的目录再次运行calib_gui.m。

若输入'y'弹出对话框：让用户选择模式，有两种可作选择，一是Standard模式，一是Memory efficient模式.注意：若当前目录不包含待标定图像数据而用户又输入‘y’,那将导致程序进入死循环，若出现此情况，需重启MATLAB程序！！！并在命令行窗口显示当前工作目录下的文件列表。

Standard模式下所运行的图像数据会驻留在内存里，因而可以减少读取图像的操作，但如果需处理的图像数据过多，可能会造成内存泄露，Memory efficient模式下图像数据在需要的时候才被读入内存。

二者选择其一后进入同一个标定工具箱操作界面。

在此界面可完成标定的各个步骤。

首先读取图像数据，点Image names按钮，程序转入命令行窗口等待用户输入待标定图像的basename.Basename camera calibration images (without number nor suffix)-->如果当前目录下有图像文件：Image1.tiff Image2.tiff ... Image10.tiff 则应输入Image.程序继续等待用户输入图像格式：Image format: ([]='r'='ras', 'b'='bmp', 'f'='tiff', 'p'='pgm', 'j'='jpg', 'm'='ppm')-->由于我的计算机里图像数据的格式为tiff,故输入'f'。

MATLAB工具箱的安装与配置指南

MATLAB工具箱的安装与配置指南Matlab是一种强大的数学软件，广泛应用于工程和科学领域的数据分析和建模。

Matlab工具箱是Matlab软件的扩展包，提供了各种专业领域的工具和函数，使得用户可以更便捷地进行数据处理和模型构建。

本文将详细介绍Matlab工具箱的安装与配置指南，帮助读者快速上手使用这些功能强大的工具。

一、MATLAB工具箱的获取首先，我们需要获得Matlab软件及相关工具箱的安装包。

Matlab软件官方提供了学术试用版及商业版的下载，用户可以根据自己的需求选择相应的版本。

在获得Matlab软件安装包后，我们需要进一步获取相应的工具箱。

Matlab提供了丰富的工具箱，涵盖了各个学科领域，如信号处理、图像处理、机器学习等。

用户可以在Matlab官方网站上查找并下载所需的工具箱。

二、MATLAB工具箱的安装在获得Matlab工具箱的安装包后，我们可以开始进行安装。

1. 解压安装包使用解压软件将下载的工具箱包进行解压，解压后得到相应的文件夹。

2. 安装工具箱打开Matlab软件，在主界面点击"文件" -> "Set Path" -> "Add with Subfolders"，选择解压后的工具箱文件夹。

然后点击"保存"，等待Matlab完成工具箱的安装。

3. 激活工具箱完成工具箱的安装后，我们需要激活这些工具箱，使其能够在Matlab中正常使用。

在Matlab主界面点击"Home" -> "Help" -> "Licensing"，将打开"Licensing"窗口。

选择"Activate Software"，输入Matlab账户信息，点击"Next"，根据指引完成激活过程。

Matlab标定工具箱的使用

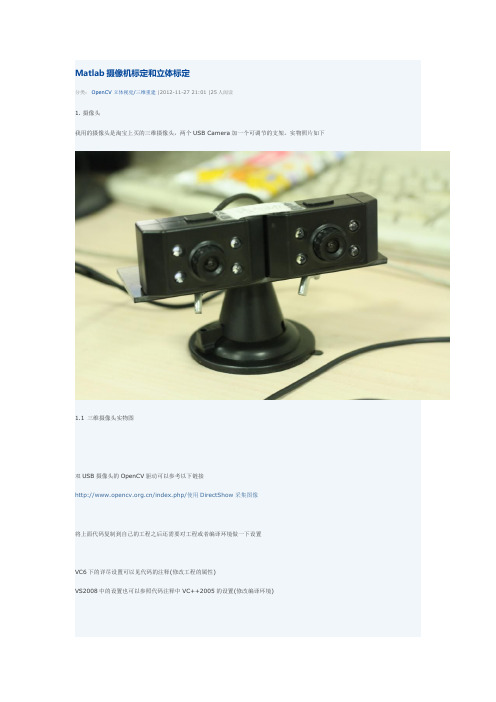
Matlab摄像机标定和立体标定分类：OpenCV立体视觉/三维重建|2012-11-2721:01|25人阅读1.摄像头我用的摄像头是淘宝上买的三维摄像头，两个USB Camera加一个可调节的支架。

实物照片如下1.1三维摄像头实物图双USB摄像头的OpenCV驱动可以参考以下链接/index.php/使用DirectShow采集图像将上面代码复制到自己的工程之后还需要对工程或者编译环境做一下设置VC6下的详尽设置可以见代码的注释(修改工程的属性)VS2008中的设置也可以参照代码注释中VC++2005的设置(修改编译环境)2.标定由于OpenCV中cvStereoCalibrate总是会得到很夸张的结果(见下文5.1问题描述)，所以最后还是决定用Bouguet的Matlab标定工具箱立体标定，再将标定的结果读入OpenCV，来进行后续图像校准和匹配。

Matlab标定工具箱的参考链接如下：/bouguetj/calib_doc/上面有详细的使用步骤，用起来相当的方便。

以下是我个人用Matlab工具箱进行立体标定的步骤，供参考，如果需要更详细步骤的话还是参照上面的链接把Matlab工具箱的文件copy到对应目录下，把所要标定的棋盘图也放到.m文件所在的目录下，然后在Matlab命令行窗口中打入calib_gui，选择Standard之后便出现以下窗口2.1.calilb_gui面板我们先对右摄像头的标定，所以先把从右摄像头上采集到的棋盘图复制到工具箱目录下。

点击Image names,命令行窗口会提示你输入图片的basename以及图片的格式(比如你图片文件名是right1,right2,…,right10，basename就是right)，然后Matlab会自动帮你读入这些图片，如下图所示，可以看到，读入了10幅右摄像头的棋盘图。

采集棋盘图的时候要注意，尽量让棋盘占据尽可能多的画面，这样可以得到更多有关摄像头畸变方面的信息2.2.图像basename读入2.3.读入的棋盘图然后再回到主控制界面，点击Extract grid corners，提取每幅图的角点2.4.calib_gui面板点击完后，命令行会出现如下提示，主要是让你输入棋盘角点搜索窗口的大小。

单目相机标定matlab

单目相机标定matlab单目相机标定是计算机视觉领域的重要话题，它是将图像坐标系映射到相机坐标系的过程。

Matlab是一个功能强大的工具，可以用来进行单目相机标定。

本文将介绍如何使用Matlab进行单目相机标定。

一、准备工作在开始单目相机标定之前，需要准备以下工作：1.相机。

准备一台拍摄清晰度高的相机，如单反相机或高清摄像头。

2.标定板。

准备一个标定板，标定板是一个由黑白相间的方块组成的平板。

3.计算机。

需要有一台安装了Matlab软件的计算机。

二、安装Matlab工具箱Matlab提供了许多工具箱，包括图像处理工具箱和计算机视觉工具箱。

在进行单目相机标定之前，需要先安装计算机视觉工具箱。

可以通过Matlab的“工具箱浏览器”或Matlab官网下载安装。

三、准备数据在进行单目相机标定之前，需要准备一些数据。

这些数据包括：1.图像。

需要拍摄一组清晰度高的图片，最好是在室内光线较亮的情况下拍摄，拍摄距离和角度可以随意调整。

2.标定板图片。

需要在不同角度下拍摄标定板的图片，拍摄时标定板需要摆放在相机的视野范围内，并将其与相机视野平面垂直。

3.标定板参数。

需要知道标定板的尺寸、方格数、格子尺寸等参数。

四、单目相机标定步骤接下来，我们将通过以下步骤来完成单目相机标定。

1.读取图片。

在Matlab中进行单目相机标定需要读取图片，并将其转换为灰度图像。

2.提取角点。

使用Matlab的“corner”函数来提取标定板上的角点。

这些角点将用于后续计算。

3.计算内参和畸变参数。

使用Matlab的“calibrateCamera”函数来计算相机的内参和畸变参数。

这些参数包括相机的焦点、主点、畸变系数等。

4.计算外参。

使用Matlab的“extrinsics”函数来计算每个标定板图片的相机的外参。

这些参数包括相机的旋转矩阵和平移向量。

5.评估标定结果。

使用Matlab的“showReprojectionErrors”函数来评估标定结果。

Matlab中的系统辨识和参数标识技巧

Matlab中的系统辨识和参数标识技巧引言：在工程和科学领域中，系统辨识是一项重要的任务。

通过对系统进行辨识和参数标定，我们可以建立数学模型来描述系统的行为。

在Matlab中，有许多工具和技巧可以用来进行系统辨识和参数标定。

本文将介绍一些常用的工具和技巧，以帮助读者更好地理解和应用这些方法。

一、准备工作在进行系统辨识和参数标定之前，我们首先需要准备一些基本的工作。

首先，我们需要收集系统的输入和输出数据。

输入数据通常是对系统施加的激励信号，例如阶跃信号或随机信号。

输出数据是系统对输入信号的响应。

收集足够量的数据对于准确辨识系统非常重要。

其次，我们需要确保数据的质量。

在收集数据时，我们需要注意采样频率和信噪比。

采样频率要足够高，以捕捉系统的快速动态响应；信噪比要足够高，以避免噪声对数据的影响。

如果数据质量不高，将会使得系统辨识和参数标定的结果不准确。

二、线性系统辨识线性系统辨识是系统辨识领域中的一项基本任务。

在Matlab中，可以使用System Identification Toolbox来进行线性系统辨识。

首先，我们可以使用中自相关函数（cross-correlation）来计算输入和输出数据之间的相关性。

这可以通过Matlab中的xcorr函数实现。

相关性分析可以帮助我们了解系统的输入和输出之间的关系，为后续的系统辨识提供参考。

接下来，我们可以使用频域分析方法来对系统进行辨识。

其中一个常用的方法是基于频率响应函数的辨识方法，例如最小二乘法（Least Squares）等。

这些方法可以通过Matlab中的tfest函数来实现。

另外，我们还可以使用时域辨识方法，例如最小均方误差法（Least Mean Squares）等。

时域辨识方法通常通过求解线性方程组来确定系统的参数。

在Matlab中，我们可以使用lsim和inv函数来实现这些方法。

三、非线性系统辨识与线性系统不同，非线性系统的辨识更加复杂。

Matlab标定工具箱的使用

Matlab标定工具箱在摄像机定标中的应用

T -T -1
h1 K K h2=0 .
（3）
T -T -1
T -T -1
h1 K K h1=h2 K K h2 .
（4）
收稿日期：2010－01－07；修回日期：2010－02－11 作者简介：孙玉青（ 1982- ），女，山东潍坊人，在读硕士，主要从事图像处理与摄像机定标研究，E- mail：sun_yuqing99@。
和平移向量，
H= h1 h2 h3 λK r1 r2 t ，
r1=
1 λ
K-1h1，
r2=
1 λ
K-1h2
.
（2）
T
根据旋转矩阵的性质，即 r1 r2=0 和 ‖ rq‖ = ‖r2=1‖ ，每幅图像可以获得以下两个对摄像机内参数矩阵的基本约束，
在图像测量过程以及机器视觉应用中，常常会涉及到这样一个概念，那就是利用摄像机所拍摄到的图像来还原空间中的物体。从摄像机获取的图像信息出发计算三维空间中物体的几何信息，并由此重建和识别物体，而空间物体表面某点的三维几何位置与其在图像中对应点之间的相互关系是由摄像机成像的几何模型决定的，这些几何模型参数就是摄像机参数。在大多数条件下这些参数必须通过实验与计算才能得到，这一过程被称为摄像机定标[1]。 1 Matlab 简述
本文摄像机定标的基本原理为的平面上其中为模板上点的齐次坐标为模板平面上点投影到图像平面上对应点的齐次坐标分别是摄像机坐标系相对于世界坐标系的旋转矩阵和平移向量每幅图像可以获得以下两个对摄像机内参数矩阵的基本约束atlab标定工具箱在摄像机定标中的应用孙玉青冀小平简述了atlab标定工具箱以及摄像机定标的概念原理和意义给出了摄像机定标中所用的三种坐标系以及它们之间的关系推导出摄像机参数标定算法公式在此基础上利用atlab标定工具箱仿真了棋盘网格的角点标定算法并给出了仿真结果以及误差分析得出了atlab标定工具箱在摄像机定标方面运用的有效性及算法的正关键词

Matlab中利用工具箱进行摄像头标定

Camera Calibration Toolbox forMatlabFirst calibration example - Corner extraction, calibration, additional toolsThis section takes you through a complete calibration example based on a total of 20 (and 25) images of a planar checkerboard. This example lets you learn how to use all the features of the toolbox: loading calibration images, extracting image corners, running the main calibration engine, displaying the results, controlling accuracies, adding and suppressing images, undistorting images, exporting calibration data to different formats... This example is highly recommended for someone who is just starting using the toolbox.Download the calibration images all at once calib_example.zip (4461Kb zipped) or one by one, and store the 20 images into a seperate folder named calib_example.From within matlab, go to the example folder calib_example containing the images.Reading the images:Click on the Image names button in the Camera calibration tool window. Enter the basename of the calibration images (Image) and the image format (tif).All the images (the 20 of them) are then loaded in memory (through the command Read images that is automatically executed) in the variables I_1, I_2 ,..., I_20. The number of images is stored in the variable n_ima (=20 here).The matlab window should look like this:The complete set of images is also shown in thumbnail format (this images can always be regenerated by running mosaic):If the OUT OF MEMORY error message occurred during image reading, that means that your computer does not have enough RAM to hold the entire set of images in local memory. This can easily happen of you are running the toolbox on a 128MB or less laptop for example. In this case, you can directly switch to the memory efficient version of the toolbox by running calib_gui and selecting the memory efficient mode of operation. The remaining steps of calibration (grid corner extraction and calibration) are exactly the same. Note that in memory efficient mode, the thumbnail image is not displayed since the calibration images are not loaded all at once.Extract the grid corners:Click on the Extract grid corners button in the Camera calibration tool window.Press "enter" (with an empty argument) to select all the images (otherwise, you would enter a list of image indices like [2 5 8 10 12] to extract corners of a subset of images). Then, select the default window size of the corner finder: wintx=winty=5 by pressing "enter" with empty arguments to the wintx and winty question. This leads to a effective window of size 11x11 pixels.The corner extraction engine includes an automatic mechanism for counting the number of squares in the grid. This tool is specially convenient when working with a large number of images since the user does not have to manually enter the number of squares in both x and y directions of the pattern. On some very rare occasions however, this code may not predict the right number of squares. This would typically happen when calibrating lenses with extreme distortions. At this point in the corner extraction procedure, the program gives the option to the user to disable the automatic square counting code. In that special mode, the user would be prompted for the square count for every image. In this present example, it is perfectly appropriate to keep working in the default mode (i.e. with automatic square counting activated), and therefore, simply press "enter" with an empty argument. (NOTE: it is generally recommended to first use the corner extraction code in this default mode, and then, if need be, re-process the few images with "problems")The first calibration image is then shown on Figure 2:Click on the four extreme corners on the rectangular checkerboard pattern. The clicking locations are shown on the four following figures (WARNING: try to click accurately on the four corners, at most 5 pixels away from the corners. Otherwise some of theOrdering rule for clicking: The first clicked point is selected to be associated to the origin point of the reference frame attached to the grid. The other three points of the rectangular grid can be clicked in any order. This first-click rule is especially important if you need to calibrate externally multiple cameras (i.e. compute the relative positions of several cameras in space). When dealing with multiple cameras, the same grid pattern reference frame needs to be consistently selected for the different camera images (i.e. grid points need to correspond across the different camera views). For example, it is a requirement to run the stereo calibration toolbox stereo_gui.m (try help stereo_gui and visit the fifth calibration example page for more information).The boundary of the calibration grid is then shown on Figure 2:Enter the sizes dX and dY in X and Y of each square in the grid (in this case, dX=dY=30mm=default values):Note that you could have just pressed "enter" with an empty argument to select the default values. The program automatically counts the number of squares in both dimensions, and shows the predicted grid corners in absence of distortion:If the predicted corners are close to the real image corners, then the following step may be skipped (if there is not much image distortion). This is the case in that present image: the predicted corners are close enough to the real image corners. Therefore, it is not necessary to "help" the software to detect the image corners by entering a guess for radial distortion coefficient. Press "enter", and the corners are automatically extracted using those positions as initial guess.The image corners are then automatically extracted, and displayed on figure 3 (the blue squares around the corner points show the limits of the corner finder window):The corners are extracted to an accuracy of about 0.1 pixel.Follow the same procedure for the 2nd, 3rd, ... , 14th images. For example, here are the detected corners of image 2, 3, 4, 5, 6 and 7:Observe the square dimensions dX, dY are always kept to their original values (30mm).Sometimes, the predicted corners are not quite close enough to the real image corners to allow for an effective corner extraction. In that case, it is necessary to refine the predicted corners by entering a guess for lens distortion coefficient. This situation occurs at image 15. On that image, the predicted corners are:Observe that some of the predicted corners within the grid are far enough from the real grid corners to result into wrong extractions. The cause: image distortion. In order to help the system make a better guess of the corner locations, the user is free to manually input a guess for the first order lens distortion coefficient kc (to be precise, it is the first entry of the full distortion coefficient vector kc described at this page). In order to input a guess for the lens distortion coefficient, enter a non-empty string to the question Need of an initial guess for distortion? (for example 1). Enter then a distortion coefficient of kc=-0.3 (in practice, this number is typically between -1 and 1).According to this distortion, the new predicted corner locations are:If the new predicted corners are close enough to the real image corners (this is the case here), input any non-empty string (such as 1) to the question Satisfied with distortion?. The subpixel corner locations are then computed using the new predicted locations (with image distortion) as initial guesses:If we had not been satisfied, we would have entered an empty-string to the question Satisfied with distortion? (by directly pressing "enter"), and then tried a new distortion coefficient kc. Y ou may repeat this process as many times as you want until satisfied with the prediction (side note: the values of distortion used at that stage are only used to help corner extraction and will not affect at all the next main calibration step. In other words, these values are neither used as final distortion coefficients, nor used as initial guesses for the true distortion coefficients estimated through the calibration optimization stage).The final detected corners are shown on Figure 3:Repeat the same procedure on the remaining 5 images (16 to 20). On these images however, do not use the predicted distortion option, even if the extracted corners are not quite right. In the next steps, we will correct them (in this example, we could have not used this option for image 15, but that was quite useful for illustration).After corner extraction, the matlab data file calib_data.mat is automatically generated. This file contains all the information gathered throughout the corner extraction stage (image coordinates, corresponding 3D grid coordinates, grid sizes, ...). This file is only created in case of emergency when for example matlab is abruptly terminated before saving. Loading this file would prevent you from having to click again on the images.During your own calibrations, when there is a large amount of distortion in the image, the program may not be able to automatically count the number of squares in the grid. In that case, the number of squares in both X and Y directions have to be entered manually. This should not occur in this present example.Another problem may arise when performing your own calibrations. If the lens distortions are really too severe (for fisheye lenses for example), the simple guiding tool based on a single distortion coefficient kc may not be sufficient to provide good enough initial guesses for the corner locations. For those few difficult cases, a script program is included in the toolbox that allows for a completely manual corner extraction (i.e. one click per corner). The script file is called manual_corner_extraction.m (in memory efficient mode, you should use manual_corner_extraction_no_read.m instead) and should be executed AFTER the traditional corner extaction code (the script relies on data that were computed by the traditional corner extraction code -square count, grid size, order of points, ...- even if the corners themselves were wrongly detected). Obviously, this method for corner extraction could be extremely time consuming when applied on a lot of images. It therefore recommended to use it as a last resort when everything else has failed. Most users should never have to worry about this, and it will not happen in this present calibration example.Main Calibration step:After corner extraction, click on the button Calibration of the Camera calibration tool to run the main camera calibrationprocedure.Calibration is done in two steps: first initialization, and then nonlinear optimization.The initialization step computes a closed-form solution for the calibration parameters based not including any lens distortion (program name: init_calib_param.m).The non-linear optimization step minimizes the total reprojection error (in the least squares sense) over all the calibration parameters (9 DOF for intrinsic: focal, principal point, distortion coefficients, and 6*20 DOF extrinsic => 129 parameters). For a complete description of the calibration parameters, click on that link. The optimization is done by iterative gradient descent with an explicit (closed-form) computation of the Jacobian matrix (program name: go_calib_optim.m).The Calibration parameters are stored in a number of variables. For a complete description of them, visit this page. Notice that the skew coefficient alpha_c and the 6th order radial distortion coefficient (the last entry of kc) have not been estimated (this is the default mode). Therefore, the angle between the x and y pixel axes is 90 degrees. In most practical situations, this is a very good assumption. However, later on, a way of introducing the skew coefficient alpha_c in the optimization will be presented. Observe that only 11 gradient descent iterations are required in order to reach the minimum. This means only 11 evaluations of the reprojection function + Jacobian computation and inversion. The reason for that fast convergence is the quality of the initial guess for the parameters computed by the initialization procedure.For now, ignore the recommendation of the system to reduce the distortion model. The reprojection error is still too large to make a judgement on the complexity of the model. This is mainly because some of the grid corners were not very precisely extracted for a number of images.Click on Reproject on images in the Camera calibration tool to show the reprojections of the grids onto the original images. These projections are computed based on the current intrinsic and extrinsic parameters. Input an empty string (just press "enter") to the question Number(s) of image(s) to show ([] = all images) to indicate that you want to show all the images:The following figures shows the first four images with the detected corners (red crosses) and the reprojected grid corners (circles).The reprojection error is also shown in the form of color-coded crosses:In order to exit the error analysis tool, right-click on anywhere on the figure (you will understand later the use of this option). Click on Show Extrinsic in the Camera calibration tool. The extrinsic parameters (relative positions of the grids with respect to the camera) are then shown in a form of a 3D plot:On this figure, the frame (O c,X c,Y c,Z c) is the camera reference frame. The red pyramid corresponds to the effective field of view of the camera defined by the image plane. T o switch from a "camera-centered" view to a "world-centered" view, just click on the Switch to world-centered view button located at the bottom-left corner of the figure.On this new figure, every camera position and orientation is represented by a green pyramid. Another click on the Switch to camera-centered view button turns the figure back to the "camera-centered" plot.Looking back at the error plot, notice that the reprojection error is very large across a large number of figures. The reason for that is that we have not done a very careful job at extracting the corners on some highly distorted images (a better job could havebeen done by using the predicted distortion option). Nevertheless, we can correct for that now by recomputing the image corners on all images automatically. Here is the way it is going to be done: press on the Recomp. corners button in the main Camera calibration tool and select once again a corner finder window size of wintx = winty = 5 (the default values):T o the question Number(s) of image(s) to process ([] = all images) press "enter" with an empty argument to recompute thecorners on all the images. Enter then the mode of extraction: the automatic mode (auto) uses the re-projected grid as initial guess locations for the corner, the manual mode lets the user extract the corners manually (the traditional corner extraction method). In the present case, the reprojected grid points are very close to the actual image corners. Therefore, we select the automatic mode: press "enter" with an empty string. The corners on all images are then recomputed. your matlab window should look like:Run then another calibration optimization by clicking on Calibration:Observe that only six iterations were necessary for convergence, and no initialization step was performed (the optimization started from the previous calibration result). The two values 0.12668 and 0.12604 are the standard deviation of the reprojection error (in pixel) in both x and y directions respectively. Observe that the uncertainties on the calibration parameters are also estimated. The numerical values are approximately three times the standard deviations.After optimization, click on Save to save the calibration results (intrinsic and extrinsic) in the matlab file Calib_Results.matFor a complete description of the calibration parameters, click on that link.Once again, click on Reproject on images to reproject the grids onto the original calibration images. The four first images looklike:Click on Analyse error to view the new reprojection error (observe that the error is much smaller than before):After right-clicking on the error figure (to exit the error-analysis tool), click on Show Extrinsic to show the new 3D positions of the grids with respect to the camera:A simple click on the Switch to world-centered view button changes the figure to this:The tool Analyse error allows you to inspect which points correspond to large errors. Click on Analyse error and click on the figure region that is shown here (upper-right figure corner):After clicking, the following information appears in the main Matlab window:This means that the corresponding point is on image 18, at the grid coordinate (0,0) in the calibration grid (at the origin of the pattern). The following image shows a close up of that point on the calibration image (before, exit the error inspection tool by clicking on the right mouse button anywhere within the figure):The error inspection tool is very useful in cases where the corners have been badly extracted on one or several images. In such a case, the user can recompute the corners of the specific images using a different window size (larger or smaller).For example, let us recompute the image corners using a window size (wintx=winty=9) for all 20 images except for images 20 (use wintx=winty=5), images 5, 7, 8, 19 (use wintx=winty=7), and images 18 (use wintx=winty=8). The extraction of the corners should be performed with three calls of Recomp. corners. At the first call of Recomp. corners, select wintx=winty=9, choose to process images 1, 2, 3, 4, 6, 9, 10, 11, 12, 13, 14, 15, 16 and 17, and select the automatic mode (the reprojections are already very close to the actual image corners):At the second call of Recomp. corners, select wintx=winty=8, choose to process image 18 and select once again the automatic mode:At the third call of Recomp. corners, select wintx=winty=7, choose to process images 5, 7, 8 and 19 and select once again the automatic mode:Re-calibrate by clicking on Calibration:Observe that the reprojection error (0.11689,0.11500) is slightly smaller than the previous one. In addition, observe that the uncertainties on the calibration parameters are also smaller. Inspect the error by clicking on Analyse error:Let us look at the previous point of interest on image 18, at the grid coordinate (0,0) in the calibration grid. For that, click on Reproject on images and select to show image 18 only (of course, before that, you must exit the error inspection tool by right-cliking within the window):A close view at the point of interest (on image 18) shows a smaller reprojection error:Click once again on Save to save the calibration results (intrinsic and extrinsic) in the matlab file Calib_Results.matObserve that the previous calibration result file was copied under Calib_Results_old0.mat (just in case you want to use it later on).Download now the five additional images Image21.tif, Image22.tif, Image23.tif, Image24.tif and Image25.tif and re-calibrate the camera using the complete set of 25 images without recomputing everything from scratch.After saving the five additional images in the current directory, click on Read images to read the complete new set of images:T o show a thumbnail image of all calibration images, run mosaic (if you are running in memory efficient mode, runmosaic_no_read instead).Click on Extract grid corners to extract the corners on the five new images, with default window sizes wintx=winty=5:And go on with the traditional corner extraction on the five images. Afterwards, run another optimization by clicking on Calibration:Next, recompute the image corners of the four last images using different window sizes. Use wintx=winty=9 for images 22 and 24, use wintx=winty=8 for image 23, and use wintx=winty=6 for image 25. Follow the same procedure as previously presented (three calls of Recomp. corners should be enough). After recomputation, run Calibration once again:Click once again on Save to save the calibration results (intrinsic and extrinsic) in the matlab file Calib_Results.matAs an exercise, recalibrate based on all images, except images 16, 18, 19, 24 and 25 (i.e. calibrate on a new set of 20 images).Click on Add/Suppress images.Enter the list of images to suppress ([16 18 19 24 25]):Click on Calibration to recalibrate:It is up to user to use the function Add/Suppress images to activate or de-activate images. In effect, this function simply updates the binary vector active_images setting zeros to inactive images, and ones to active images.The setup is now back to what it was before supressing 5 images 16, 18, 19, 24 and 25. Let us now run a calibration by including the skew factor alpha_c describing the angle between the x and y pixel axes. For that, set the variable est_alpha to one (at the matlab prompt). As an exercise, let us fit the radial distortion model up to the 6th order (up to now, it was up to the 4th order, with tangential distortion). For that, set the last entry of the vector est_dist to one:Then, run a new calibration by clicking on Calibration:Observe that after optimization, the skew coefficient is very close to zero (alpha_c = 0.00042). This leads to an angle between x and y pixel axes very close to 90 degrees (89.976 degrees). This justifies the previous assumption of rectangular pixels (alpha_c = 0). In addition, notice that the uncertainty on the 6th order radial distortion coefficient is very large (the uncertainty is much larger than the absolute value of the coefficient). In this case, it is preferable to disable its estimation. In this case, set the last entry of est_dist to zero:Then, run calibration once again by clicking on Calibration:Judging the result of calibration satisfactory, let us save the current calibration parameters by clicking on Save:In order to make a decision on the appropriate distortion model to use, it is sometimes very useful to visualize the effect of distortions on the pixel image, and the importance of the radial component versus the tangential component of distortion. For this purpose, run the script visualize_distortions at the matlab prompt (this function is not yet linked to any button in the GUI window). The three following images are then produced:The first figure shows the impact of the complete distortion model (radial + tangential) on each pixel of the image. Each arrow represents the effective displacement of a pixel induced by the lens distortion. Observe that points at the corners of the image are displaced by as much as 25 pixels. The second figure shows the impact of the tangential component of distortion. On this plot, the maximum induced displacement is 0.14 pixel (at the upper left corner of the image). Finally, the third figure shows the impact of the radial component of distortion. This plot is very similar to the full distortion plot, showing the tangential component could very well be discarded in the complete distortion model. On the three figures, the cross indicates the center of the image, and the circle the location of the principal point.Now, just as an exercise (not really recommended in practice), let us run an optimization without the lens distortion model (by enforcing kc = [0;0;0;0;0]) and without aspect ratio (by enforcing both components of fc to be equal). For that, set the binary variables est_dist to [0;0;0;0;0] and est_aspect_ratio to 0 at the matlab prompt:Then, run a new optimization by clicking on Calibration:As expected, the distortion coefficient vector kc is now zero, and both components of the focal vector are equal (fc(1)=fc(2)). In practice, this model for calibration is not recommended: for one thing, it makes little sense to estimate skew without aspectratio. In general, unless required by a specific targeted application, it is recommended to always estimate the aspect ratio in themodel (it is the 'easy part'). Regarding the distortion model, people often run optimization over a subset of the distortioncoefficients. For example, setting est_dist to [1;0;0;0] keeps estimating the first distortion coefficient kc(1) while enforcing the three others to zero. This model is also known as the second order symmetric radial distortion model. It is a very viable model,especially when using low distortion optical systems (expensive lenses), or when only a few images are used for calibration.Another very common distortion model is the 4th order symmetric radial distortion with no tangential component (est_kc = [1;1;0;0]). This model, used by Zhang, is justified by the fact that most lenses currently manufactured do not have imperfection in centering (for more information, visit this page). This model could have very well been used in this present example, recallingfrom the previous three figures that the tangential component of the distortion model is significantly smaller that the radialcomponent.Finally, let us run a calibration rejecting the aspect ratio fc(2)/fc(1), the principal point cc, the distortion coefficients kc, and the skew coefficient alpha_c from the optimization estimation. For that purpose, set the four binary variables , center_optim,est_dist and est_alpha to the following values:Generally, if the principal point is not estimated, the best guess for its location is the center of the image:Then, run a new optimization by clicking on Calibration:Observe that the principal point cc is still at the center of the image after optimization (since center_optim=0).Next, load the old calibration results previously saved in Calib_Results.mat by clicking on Load:Additional functions included in the calibration toolbox:Computation of extrinsic parameters only: Download an additional image of the same calibration grid: Image_ext.tif.Notice that this image was not used in the main calibration procedure. The goal of this exercise is to compute the extrinsic parameters attached to this image given the intrinsic camera parameters previously computed.Click on Comp. Extrinsic in the Camera calibration tool, and successively enter the image name without extension (Image_ext), the image type (tif), and extract the grid corners (following the same procedure as previously presented -remember: the first clicked point is the origin of the pattern reference frame). The extrinsic parameters (3D location of the grid in the camera reference frame) is then computed. The main matlab window should look like:The extrinsic parameters are encoded in the form of a rotation matrix (Rc_ext) and a translation vector (Tc_ext). The rotation vector omc_ext is related to the rotation matrix (Rc_ext) through the Rodrigues formula: Rc_ext = rodrigues(omc_ext).Let us give the exact definition of the extrinsic parameters:Let P be a point space of coordinate vector XX = [X;Y;Z] in the grid reference frame (O,X,Y,Z) shown on the following figure:Let XX c = [X c;Y c;Z c] be the coordinate vector of P in the camera reference frame (O c,X c,Y c,Z c).Then XX and XX c are related to each other through the following rigid motion equation:XX c = Rc_ext * XX + Tc_extIn addition to the rigid motion transformation parameters, the coordinates of the grid points in the grid reference frame are also stored in the matrix X_ext. Observe that the variables Rc_ext, Tc_ext, omc_ext and X_ext are not automatically saved into any matlab file.Undistort images: This function helps you generate the undistorted version of one or multiple images given pre-computed intrinsic camera parameters.As an exercise, let us undistort Image20.tif.Click on Undistort image in the Camera calibration tool.Enter 1 to select an individual image, and successively enter the image name without extension (Image20), the image type (tif). The main matlab window should look like this:The initial image is stored in the matrix I, and displayed in figure 2:The undistorted image is stored in the matrix I2, and displayed in figure 3:。

matlab工具箱标定和张氏标定法

matlab工具箱标定和张氏标定法MATLAB工具箱和张氏标定法（Zhang's calibration method）都是用于相机标定的方法。

相机标定是确定相机内部和外部参数的过程，包括相机的焦距、主点、畸变系数等内部参数，以及相机在世界坐标系中的位置和姿态等外部参数。

1.MATLAB工具箱标定：MATLAB提供了Camera Calibrator Toolbox（相机标定工具箱），它允许用户通过拍摄一系列标定图像（通常是棋盘格）来标定相机。

这个工具箱会自动检测标定图像中的特征点，并计算出相机的内外参数。

使用MATLAB工具箱标定的优点是其用户界面友好，易于操作，而且MATLAB强大的数值计算能力也能保证标定结果的准确性。

2. 张氏标定法：张氏标定法是一种基于平面模板的相机标定方法，由Z. Zhang 在1999年提出。

这种方法只需要拍摄几张包含平面标定模板（通常是棋盘格）的图像，通过检测模板上的角点来估计相机的内外参数。

张氏标定法的优点是其简单性和灵活性，不需要昂贵的设备，而且只需要拍摄少量的标定图像就可以得到较好的标定结果。

在MATLAB中实现张氏标定法，你可以使用MATLAB的内置函数detectCheckerboardPoints来检测棋盘格角点，然后使用estimateCameraParameters来估计相机的内外参数。

这些函数都包含在MATLAB的Computer Vision Toolbox（计算机视觉工具箱）中。

需要注意的是，无论是使用MATLAB工具箱标定还是张氏标定法，都需要拍摄高质量的标定图像，以确保标定结果的准确性。

同时，标定过程中还需要注意避免相机镜头的畸变、标定模板的放置误差等因素对标定结果的影响。

学习MATLAB工具箱标定和张氏标定法可以通过以下几个步骤进行：1. 学习MATLAB基础：•首先，你需要对MATLAB有一个基本的了解，包括其编程环境、语法规则、数据类型等。

matlab双目标定参数说明

matlab双目标定参数说明【原创版】目录一、引言二、双目标定的概念和意义三、MATLAB 双目标定参数说明1.标定工具箱的使用2.标定过程中的注意事项四、MATLAB 双目标定的优缺点五、总结正文一、引言双目标定是立体视觉系统中的一个关键步骤，目的是获取相机的内参和外参，其中包括旋转矩阵和平移向量。

在进行双目标定时，有两种常见的数据库：MATLAB 视觉处理库和 OpenCV 开源视觉库。

本篇文章主要介绍如何使用 MATLAB 进行双目相机标定。

二、双目标定的概念和意义双目标定是立体视觉系统中的一个关键步骤，主要是通过拍摄包含已知几何形状的场景，对双目相机的内部参数（如焦距、光心坐标等）和外部参数（如旋转矩阵和平移向量）进行估计。

双目标定的目的是获取相机的内参和外参，从而实现三维重建和物体定位等任务。

三、MATLAB 双目标定参数说明1.标定工具箱的使用MATLAB 中标定双目相机的工具箱是 Image Processing Toolbox 中的 Stereo Camera Calibrator。

使用该工具箱可以方便地进行双目相机的标定，其参数设置如下：（1）选择左右相机：在 GUI 界面中选择左右相机的图像文件。

（2）设置相机属性：设置相机的分辨率、保存路径和拍照总数。

总数尽量多些，因为不一定每张图像都能用。

（3）点击 Capture 开始拍照：在拍照过程中，需要确保棋盘格的放置位置和拍摄角度符合要求。

（4）运行分割图像的程序：对拍摄的图像进行处理，提取出棋盘格的角点。

（5）设置标定参数：在标定窗口中，选择左相机图像所在文件夹和右相机图像所在文件夹，设置棋盘格上每个格子所占像素数，以及图像的宽度和高度。

2.标定过程中的注意事项（1）确保棋盘格的质量：棋盘格的质量对标定结果影响很大，需要确保棋盘格的印刷质量、尺寸和颜色符合要求。

（2）拍摄角度和光照条件：在拍摄过程中，需要确保相机的拍摄角度和光照条件尽量稳定，避免产生较大的误差。

MATLAB工具箱的功能及使用方法

MATLAB工具箱的功能及使用方法引言：MATLAB是一种常用的用于数值计算和科学工程计算的高级计算机语言和环境。

它的灵活性和强大的计算能力使得它成为工程师、科学家和研究人员的首选工具之一。

而在MATLAB中，工具箱则提供了各种专业领域的功能扩展，使得用户能够更方便地进行数据分析、信号处理、优化和控制系统设计等任务。

本文将介绍MATLAB工具箱的一些常见功能及使用方法，并探讨其在不同领域中的应用。

一、图像处理工具箱图像处理工具箱（Image Processing Toolbox）是MATLAB的核心工具之一，它提供了一套强大的函数和算法用于处理和分析数字图像。

在图像处理方面，可以使用MATLAB工具箱实现各种操作，如图像增强、降噪、边缘检测、图像分割等。

其中最常用的函数之一是imread，用于读取图像文件，并将其转换为MATLAB中的矩阵形式进行处理。

此外，还有imwrite函数用于将处理后的图像保存为指定的文件格式。

二、信号处理工具箱信号处理工具箱（Signal Processing Toolbox）是用于处理连续时间和离散时间信号的工具箱。

它提供了一系列的函数和工具用于信号的分析、滤波、变换和频谱分析等操作。

在该工具箱中，最常用的函数之一是fft，用于计算信号的快速傅里叶变换，从而获取信号的频谱信息。

此外，还有滤波器设计函数，用于设计和实现各种数字滤波器，如低通滤波器、高通滤波器和带通滤波器等。

三、优化工具箱优化工具箱（Optimization Toolbox）提供了解决各种优化问题的函数和算法。

MATLAB中的优化工具箱支持线性规划、非线性规划、整数规划、二次规划等多种优化问题的求解。

其中最常用的函数之一是fmincon，用于求解无约束和约束的非线性优化问题。

通过传入目标函数和约束条件，该函数可以找到满足最优性和约束条件的最优解。

四、控制系统工具箱控制系统工具箱（Control System Toolbox）用于建模、设计和分析各种控制系统。

Matlab中的相机标定与三维重建方法

Matlab中的相机标定与三维重建方法相机标定和三维重建是计算机视觉领域中非常重要的技术，可以广泛应用于机器人导航、虚拟现实、增强现实等领域。

Matlab作为一种功能强大的科学计算软件，提供了丰富的图像处理和计算机视觉工具箱，可以方便地实现相机标定和三维重建。

1. 相机标定方法在进行相机标定之前，我们首先需要了解相机的内外参数。

相机的内参数包括焦距、主点坐标、像素大小等，而外参数则包括相机的位置和姿态。

标定的目的就是通过一组已知的特征点对相机的内外参数进行估计。

在Matlab中，可以使用相机标定工具箱进行相机标定。

这个工具箱提供了多种标定方法，包括基于平面模型的标定方法、基于球面模型的标定方法、基于立体标定方法等。

其中最常用的是基于平面模型的标定方法，即利用多个平面上的特征点进行标定。

在标定过程中，我们需要采集一系列的图像，对每张图像进行角点检测，并记录每个角点的像素坐标。

然后，通过最小二乘法或优化算法估计相机的内外参数。

在Matlab中，可以使用函数calibrateCamera来完成相机标定，该函数会自动计算相机的内外参数，并给出标定结果的评估指标。

2. 三维重建方法相机标定完成后，我们可以利用标定的结果对图像进行三维重建。

三维重建的目的是通过多个视角下的图像来恢复物体的三维形状和位置。

在Matlab中，可以使用视觉几何工具箱进行三维重建。

该工具箱提供了多种三维重建算法，包括三角剖分法、立体视觉法、稀疏点云法等。

其中最常用的是稀疏点云法，即通过对特征点进行匹配，估计它们在三维空间中的位置。

在三维重建过程中，我们首先需要对多个视角下的图像进行特征提取和匹配。

然后，通过三角测量或最小二乘法估计特征点在三维空间中的位置。

最后，可以使用点云可视化工具将估计的三维点云进行可视化。

3. 实例应用相机标定和三维重建在很多领域都有广泛的应用。

例如，在机器人导航中，我们可以利用相机标定和三维重建来估计机器人的位置和周围环境的三维形状，从而实现自主导航。

matlab 标定工具箱解读

matlab 标定工具箱解读matlab标定工具箱是一个用于相机标定和立体视觉标定的强大工具。

相机标定是在摄像机成像过程中，将像素坐标和实际世界坐标之间的映射关系建立起来的过程。

立体视觉标定是将两个或多个相机的相对位置和内部参数进行估计的过程。

本文将详细介绍matlab标定工具箱的使用方法，包括相机标定、立体视觉标定以及标定结果的评估与应用。

一、相机标定1. 数据采集在进行相机标定之前，首先需要准备一组由摄像机拍摄的标定图像。

标定图像中应该包含已知尺寸的标定板，比如棋盘格。

在matlab标定工具箱中，先使用`cameraCalibrator`函数创建一个相机标定应用。

然后可以使用`cameraCalibrationDatastore`函数读取图像文件，或者直接使用采集视频流的方式获取图像数据。

2. 标定器创建与运行在标定工具箱中，可以通过以下几个步骤来创建相机标定器：a) 使用`cameraCalibrator`函数创建一个相机标定应用。

可以选择不同的标定模型和算法。

b) 通过`addImage`函数向标定应用中添加标定图像。

可以通过手动添加单张图像或者批量添加整个图像文件夹。

c) 使用`estimateCameraParameters`函数估计相机内部参数和畸变参数。

这个过程将根据已添加的标定图像计算出相机的内部参数矩阵、畸变系数和误差估计等。

3. 标定结果评估与保存一旦相机标定器创建完成，可以通过`showExtrinsics`函数来可视化标定后的结果。

使用该函数可以显示相机在不同位置和姿态下的外部参数估计结果。

同时，还可以通过`showReprojectionErrors`函数来显示重投影误差的直方图和统计信息。

重投影误差是指标定后的相机将标定板三维点投影回图像上的二维点与实际标定板上的二维点之间的差异。

二、立体视觉标定1. 数据采集进行立体视觉标定时，需要准备一组由两个摄像机同时拍摄的标定图像对。

相机标定简介与MatLab相机标定工具箱的使用（未涉及原理公式推导）

相机标定简介与MatLab相机标定⼯具箱的使⽤（未涉及原理公式推导）⼀、相机标定的⽬的确定空间物体表⾯某点的三维⼏何位置与其在图像中对应点之间的相互关系，建⽴摄像机成像的⼏何模型，这些⼏何模型参数就是摄像机参数。

⼆、通⽤摄像机模型世界坐标系、摄像机坐标系和像平⾯坐标系都不重合。

同时考虑两个因素：(1)摄像机镜头的畸变误差，像平⾯上的成像位置与线性变换公式计算的透视变换投影结果有偏差；(2)计算机中图像坐标单位是存储器中离散像素的个数，所以像平⾯上的连续坐标还需取整转换。

摄像机参数l摄像机内部参数（Intrinsic Parameters)摄像机坐标和理想坐标系之间的关系图像坐标系、摄像机坐标系The list of internal parameters:Focal length（焦距）: The focal length in pixels is stored in the 2x1 vector fc.Principal point（主点）: The principal point coordinates are stored in the 2x1 vector cc.Skew coefficient （偏斜系数）: The skew coefficient defining the angle between the x and y pixel axes is stored in thescalar alpha_c.Distortions （畸变）: The image distortion coefficients (radial and tangential distortions) are stored in the 5x1 vector kc.l 摄像机外部参数（Extrinsic Parameters)摄像机在世界坐标系⾥的位置和⽅向摄像机坐标系、世界坐标系主要包括：旋转矩阵 R 的9个参数和平移矩阵的3个参数。

matlab相机标定过程

matlab相机标定过程相机标定是计算机视觉领域中一项非常重要的技术。

它是指通过使用已知的特征点对相机进行标定，以便计算图像中某一点的真实位置。

在matlab中，相机标定的过程可以分为以下几个步骤：1. 特征点提取首先，我们需要在一组图片中提取出可以使用的特征点。

这些特征点通常是指具有稳定性和表征性等特点的点，例如边缘和角点等。

2. 特征点匹配在提取出特征点后，我们需要将这些特征点进行匹配。

我们可以使用一些特征匹配算法来实现这个过程，例如SIFT和SURF等算法。

3. 相机参数计算在完成了特征点匹配后，我们可以开始计算相机的内部参数和外部参数。

在matlab中，我们可以使用相机标定工具箱来实现这个过程。

该工具箱包含了多个相机标定模型，例如针孔模型、方位模型和宽角模型等。

4. 相机校正完成相机参数计算后，我们需要使用相机校正来优化相机的参数。

相机校正通常分为两种方法：单应性矩阵校正和直线校正。

在matlab中，我们可以使用相机标定工具箱中的cv.calibrateCamera2函数来实现相机校正。

5. 评估和验证最后，我们需要评估和验证相机标定的结果。

我们可以使用相机标定工具箱中的cv.evaluateCameraMatrix函数来评估相机的标定精度，并使用cv.undistort函数将输入图像与校正后的图像进行比较。

总结matlab中的相机标定过程可以帮助我们计算相机的内部参数和外部参数，以便计算图像中某一点的真实位置。

在执行相机标定时，我们需要完成特征点提取、特征点匹配、相机参数计算、相机校正以及评估和验证等几个步骤。

通过这些步骤，我们可以得出准确的相机标定结果，为后续的计算机视觉任务提供有力的支持。

双目相机标定matlab

双目相机标定matlab对于标定双目相机，MATLAB提供了一个强大的工具箱——Camera Calibration Toolbox。

该工具箱可以帮助用户进行相机的内参和外参标定，以获取更准确的视觉测量结果。

以下是使用MATLAB进行双目相机标定的一般步骤：1. 准备标定板：首先需要准备一个标定板，通常采用棋盘格作为标定板。

在实际应用中，建议使用较大尺寸的标定板，并确保其平整和边缘清晰。

2. 拍摄标定图像：将标定板放置在不同位置和角度，并使用双目相机拍摄一系列标定图像。

确保标定图像覆盖了整个场景，并且标定板在不同位置和角度下都有足够的变化。

3. 导入图像数据：将拍摄的标定图像导入到MATLAB工作环境中。

可以使用`imread`函数读取图像，并将其存储为图像序列。

4. 进行单目相机标定：在开始双目相机标定之前，需要先进行单目相机的标定。

使用Camera Calibration Toolbox中的函数，如`calibrateCamera`，对每个摄像头分别进行标定，获得内参矩阵、畸变参数等参数。

5. 进行双目相机标定：使用Camera Calibration Toolbox中的函数，如`stereoCalibrate`，对双目图像进行标定。

在标定过程中，需要提供单目相机标定的结果、左右摄像头之间的相对位置和姿态信息等。

6. 获取相机内参和外参：通过标定过程，可以获得双目相机的内参矩阵、畸变参数以及相机之间的外参矩阵。

7. 进行立体视觉测量：使用相机的内参和外参，可以进行立体视觉测量，如深度估计、三维重建等。

需要注意的是，在进行相机标定之前，应该确保拍摄的图像具有足够的特征点，并且场景中的纹理明显。

此外，还需注意相机设置的一致性，包括曝光时间、焦距等参数的一致性。

以上是使用MATLAB进行双目相机标定的一般步骤。

通过合理的标定和参数获取，可以提高立体视觉测量的准确性和稳定性，为后续的视觉应用提供良好的基础。

使用Matlab进行标定与定位的技巧

使用Matlab进行标定与定位的技巧引言：随着计算机技术的不断进步，标定与定位在现代科学研究与工程应用中变得越来越重要。

而Matlab作为一种广泛应用于科学计算的工具，被广泛应用于标定与定位的研究与开发中。

本文将介绍使用Matlab进行标定与定位的技巧，包括标定理论和方法、定位算法与模型等。

一、标定理论与方法1.1 相机标定相机标定是进行摄像机内外参数确定和畸变纠正的过程。

在Matlab中，可以使用Camera Calibration Toolbox进行相机标定操作。

首先，需要准备一些用于标定的图像，这些图像中应包含已知参数（例如标定板大小和格点数）的标定板。

然后，在Matlab中加载图像数据，使用标定板图像来标定相机并求解相机内外参数。

1.2 IMU标定惯性测量单元（IMU）通常包括加速度计和陀螺仪等多种传感器。

IMU标定的目的是确定IMU的误差模型，以便在后续的定位中进行误差补偿。

在Matlab中，可以使用传感器标定和估计工具箱进行IMU标定操作。

首先，需要设计一套标定实验，包括旋转和加速度等多个运动过程。

然后，使用这些实验数据来标定IMU的误差模型。

二、定位算法与模型2.1 基于测距的定位基于测距的定位是通过测量到达定位节点的信号传播时间或信号强度等信息来实现的。

在Matlab中，可以使用距离测量数据进行多边定位或三边定位。

多边定位是通过测量到多个定位节点的距离信息来确定目标位置，可以使用最小二乘法等进行求解。

三边定位是通过测量到三个定位节点的距离信息来确定目标位置，可以使用三角测量法进行求解。

2.2 基于惯性导航的定位惯性导航是利用IMU等传感器测量物体的加速度和角速度等信息进行定位和导航的方法。

在Matlab中，可以使用十字光束法进行惯性导航定位。

首先，需要根据IMU数据求解出物体的位置、速度和姿态等信息。

然后，通过十字光束法计算出相对定位误差，从而实现精确定位。

2.3 基于地标的定位基于地标的定位是通过识别已知地标进行定位的方法。

如何使用MATLAB工具箱进行科学计算

如何使用MATLAB工具箱进行科学计算MATLAB工具箱是一款功能强大的科学计算工具，它提供了丰富的数学和计算工具，能够帮助科学家和工程师进行各种计算和分析。

本文将介绍如何使用MATLAB工具箱进行科学计算，主要包括数据导入与处理、数学计算、统计分析、数据可视化和模拟仿真五个方面。

一、数据导入与处理在进行科学计算时，首先需要导入数据并进行处理。

MATLAB工具箱提供了多种导入数据的方法，如从文本文件、Excel文件、数据库等。

可以使用`readtable`函数读取表格数据，使用`importdata`函数读取文本数据，使用`readmatrix`函数读取矩阵数据等。

导入数据后，可以使用MATLAB强大的数据处理功能进行数据清洗、筛选、变换等操作，如使用`find`函数查找符合条件的数据，使用`sort`函数对数据进行排序，使用`filter`函数进行滤波等。

二、数学计算MATLAB工具箱提供了丰富的数学函数，可以进行各种数学计算。

例如，可以使用`sin`函数计算正弦值，使用`exp`函数计算指数值，使用`sqrt`函数计算平方根等。

此外，还可以使用MATLAB工具箱进行线性代数计算，如矩阵运算、线性方程组求解、特征值求解等。

可以使用`matrix`函数定义矩阵，使用`inv`函数求矩阵的逆，使用`eig`函数求矩阵的特征值等。

三、统计分析MATLAB工具箱还提供了丰富的统计分析工具，可以进行数据统计和分析。

例如，可以使用`mean`函数计算数据的均值，使用`std`函数计算标准差，使用`corrcoef`函数计算数据之间的相关系数等。

此外，还可以进行假设检验、方差分析、回归分析等统计分析，能够帮助科学家和工程师从数据中提取有用的信息，做出科学决策。

四、数据可视化数据可视化是科学计算中重要的一环，可以通过图表和图像展示数据的特征和规律。

MATLAB工具箱提供了丰富的数据可视化函数，如`plot`函数绘制二维曲线图，`scatter`函数绘制散点图，`histogram`函数绘制直方图等。

matlabcalibrationtoolbox--matlab标定工具的使用方法--去畸。。。

matlabcalibrationtoolbox--matlab标定⼯具的使⽤⽅法--去畸。

2015-04-06 22:45 5407⼈阅读 (2)分类：机器视觉（12）⼀、对于单⽬标定。

1、也就是单个相机的标定，⾸先是⽤⼀个相机拍摄标定板获得⼀定数量的标定板照⽚。

或者下载的⼀定数量的照⽚。

如下：上图CMOS0是相机1拍摄的图⽚序列，CMOS1是相机2拍摄的图⽚序列。

2、将下载的toolbox⽂件解压到⼀个⽬录下，⽀持5.x--8.x版本的matlab。

然后打开matlab软件：file—>SetPath出现如下界⾯。

Add Folder添加toolbox所在的路径。

3、添加好后，就可以在MATLAB的命令栏中输⼊calib_gui 或者calib，回车，运⾏标定程序。

回车后出现如下界⾯：4、选择图⽚进⾏⾓点检测。

选择第⼀项“Standard（all the images are stored in memory）”，出现如下界⾯：此时要保证“Current Directory”为图⽚所在的⽬录：点击“Image Names”按钮。

Command⾏⾥就会将此⽬录下所有的照⽚名字读出来，如下：“Basename camera calibration images (without number nor suffix):”后⾯输⼊：CMOS0_。

出现如下提⽰：“Image format: ([]='r'='ras', 'b'='bmp', 't'='tif', 'p'='pgm','j'='jpg', 'm'='ppm')”后⾯输⼊：b。

matlab就将加载所有符合条件的图⽚。

之后就是检测⾓点，点击第三项：“Extract grid corners ”：回车，选择所有照⽚。