(完整版)钢结构计算题答案完整
(完整版)钢结构戴国欣主编第四版__课后习题答案

钢结构计算题精品答案 第三章 钢结构的连接3.1 试设计双角钢与节点板的角焊缝连接(图3.80)。
钢材为Q235B ,焊条为E43型,手工焊,轴心力N=1000KN (设计值),分别采用三面围焊和两面侧焊进行设计。
解:(1)三面围焊 2160/wf f N mm = 123α= 213α= 确定焊脚尺寸:,max min 1.2 1.21012f h t mm ≤=⨯=,,min 5.2f h mm ≥==, 8f h mm =内力分配:30.7 1.2220.78125160273280273.28w f f f N h b f N KN β=⋅⋅⋅=⨯⨯⨯⨯⨯==∑3221273.281000196.69232N N N KN α=-=⨯-= 3112273.281000530.03232N N N KN α=-=⨯-=焊缝长度计算:11530.032960.720.78160w wf fN l mm h f ≥==⋅⨯⨯⨯∑, 则实际焊缝长度为 1296830460608480wf l mm h mm '=+=≤=⨯=,取310mm 。
22196.691100.720.78160w wf fN l mm h f ≥==⋅⨯⨯⨯∑, 则实际焊缝长度为 2110811860608480wf l mm h mm '=+=≤=⨯=,取120mm 。
(2)两面侧焊确定焊脚尺寸:同上,取18f h mm =, 26f h mm = 内力分配:22110003333N N KN α==⨯=, 11210006673N N KN α==⨯= 焊缝长度计算:116673720.720.78160w wf fN l mm h f ≥==⋅⨯⨯⨯∑, 则实际焊缝长度为:mm h mm l f w48086060388283721=⨯=<=⨯+=',取390mm 。
223332480.720.76160w wf fN l mm h f ≥==⋅⨯⨯⨯∑, 则实际焊缝长度为:mm h mm l f w48086060260262481=⨯=<=⨯+=',取260mm 。
钢结构计算题-答案完整
侧焊缝所能承担的内力为:
N
最大承载力
【变化】若取消端焊缝,问N?
解:上题中令N30,lw12002 6,得N弘505.344 kN
【练习3】钢材为Q235,手工焊,焊条为E43,ff160N/mm",静态荷载。 双角钢2L125X8采用三面围焊和节点板连接,hf6mm,肢尖和肢背实际焊缝长度
均为250mm等边角钢的内力分配系数0.7,k20.3。求最大承载力N
⑷净截面强度验算:
N683.2
2t12
85.4
103
1020mm,故公式中取t14)
683.2kN
An(310 421.5)14
不满足要求。最大承载力由净截面强度控制:
N,
【变化】上题条件如改为已知
3
68竺匹217.9N/mm2
3136
215N /mm
Anf3136 215 103674.24kN
N=600kN试验算该连接是否安全
—
解:
端焊缝所能承担的内力为:
N
肢背焊缝所能承担的内力为:
N1
0.7hflw1ffw
2
0.7 6 (250
6) 160
327936N
根据
N1
n3
k1N—3
2
1
n3
1
204960
得:
N
(N1
3)
(327936
0 960)
614880N
K1
2
0.7
2
【变化】若取消端焊缝,问
解:上题中令N3
614.88kN
《钢结构设计原理计算题》
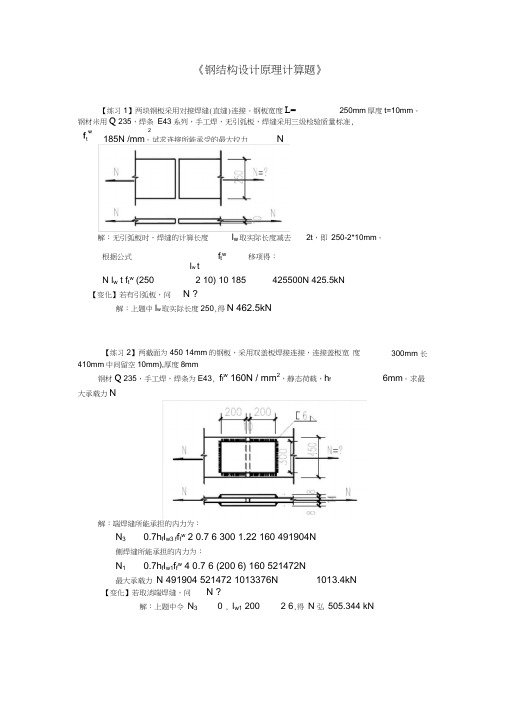
【练习1】两块钢板采用对接焊缝(直缝)连接。钢板宽度L=250mm厚度t=10mm。
钢结构试题含答案

一、选择题〔每题2分〕1.大跨度构造常采用钢构造的主要原因是钢构造〔B〕A.密封性好B.自重轻C.制造工厂化D.便于拆装2、钢材的设计强度是根据 C 确定的。
A、比例极限;B、弹性极限;C、屈服强度;D、极限强度。
3.钢构造的承载能力极限状态是指〔 C 〕A.构造发生剧烈振动B.构造的变形已不能满足使用要求C.构造到达最大承载力产生破坏D.使用已达五十年4、某构件发生了脆性破坏,不经检查可以肯定以下问题中 A 对该破坏无直接影响。
A、钢材的屈服点过低;B、构件的荷载增加速度过快;C、存在冷加工硬化;D、构件有构造原因引起的应力集中。
5.钢材的抗拉强度fu与屈服点fy之比fu/fy反映的是钢材的 A )A.强度储藏B.弹塑性阶段的承载能力C.塑性变形能力D.强化阶段的承载能力6、Q235钢按照质量等级分为A、B、C、D四级,由A到D表示质量由低到高,其分类依据是 C 。
A、冲击韧性;B、冷弯试验;C、化学成分;D、伸长率。
7. 钢号Q345A中的345表示钢材的〔 C 〕A.fp值B.fu值C.fy值D.fvy值8.钢材所含化学成分中,需严格控制含量的有害元素为( C )A.碳、锰B.钒、锰C.硫、氮、氧D.铁、硅9、同类钢种的钢板,厚度越大, A 。
A、强度越低;B、塑性越好;C、韧性越好;D、内部构造缺陷越少。
10.对于普通螺栓连接,限制端距e≥2d0的目的是为了防止( D )A.螺栓杆受剪破坏B.螺栓杆受弯破坏C.板件受挤压破坏D.板件端部冲剪破坏11、以下关于应力集中的说法中正确的选项是 B 。
A、应力集中降低了钢材的屈服强度B、应力集中产生同号应力场,使塑性变形受到限制C、应力集中产生异号应力场,使钢材变脆D、应力集中可以提高构件的疲劳强度12.Q235与Q345两种不同强度的钢材进展手工焊接时,焊条应采用( C )A.E55型B.E50型C.E43型D.H10MnSi13.在搭接连接中,为了减小焊接剩余应力,其搭接长度不得小于较薄焊件厚度的( A )A.5倍B.10倍C.15倍D.20倍14、图示连接中高强度螺栓群受弯后的旋转中心为。
钢结构计算题-答案完整

《钢结构设计原理计算题》【练习1】两块钢板采用对接焊缝(直缝)连接。
钢板宽度L=250mm ,厚度t=10mm 。
钢材采用Q235,焊条E43系列,手工焊,无引弧板,焊缝采用三级检验质量标准,2/185mm N f w t =。
试求连接所能承受的最大拉力?=N解:无引弧板时,焊缝的计算长度w l 取实际长度减去2t ,即250-2*10mm 。
根据公式 w t w f tl N<⋅=σ 移项得: kN N f t l N w t w 5.42542550018510)102250(==⨯⨯⨯-=⋅⋅< 【变化】若有引弧板,问?=N解:上题中w l 取实际长度250,得kN N 5.462=【练习2】两截面为450⨯14mm 的钢板,采用双盖板焊接连接,连接盖板宽300mm ,长度410mm(中间留空10mm),厚度8mm 。
钢材Q235,手工焊,焊条为E43,2/160mm N f w f =,静态荷载,mm h f 6=。
求最大承载力?=N解:端焊缝所能承担的内力为:N f l h N w f f w f 49190416022.130067.027.033=⨯⨯⨯⨯⨯=∑=β侧焊缝所能承担的内力为:N f l h N w f w f 521472160)6200(67.047.011=⨯-⨯⨯⨯=∑= 最大承载力kN N N 4.10131013376521472491904==+=【变化】若取消端焊缝,问?=N解:上题中令03=N ,622001⨯-=w l ,得kN N N 344.5051==【练习3】钢材为Q235,手工焊,焊条为E43,2/160mm N f w f =,静态荷载。
双角钢2L125x8采用三面围焊和节点板连接,mm h f 6=,肢尖和肢背实际焊缝长度均为250mm 。
等边角钢的内力分配系数7.01=k ,3.02=k 。
求最大承载力?=N解:端焊缝所能承担的内力为:N f l h N w f f w f 20496016022.112567.027.033=⨯⨯⨯⨯⨯=∑=β肢背焊缝所能承担的内力为:N f l h N w f w f 327936160)6250(67.027.011=⨯-⨯⨯⨯=∑=根据2311N N k N -= 得:kN N N N K N 88.614614880)2204960327936(7.01)2(1311==+=+=【变化】若取消端焊缝,问?=N解:上题中令03=N ,622501⨯-=w l ,得kN N 96.456=【练习4】钢材为Q235,手工焊,焊条为E43,2/160mm N f wf =,静态荷载。
钢结构考试题库计算题版

1、试验算图示焊缝连接的强度。
已知作用力F=150kN (静力荷载),手工焊,E43型焊条,w f f =160N/mm 2.(12分)0.78384A =⨯⨯()10.786W =⨯截面内力:150,33VKN M KN m ==⋅321501034.9/4300.8Fe F N mm A τ⨯===623310119.9/275251.2Mf M N mm W σ⨯===故该连接可靠 2、如图所示一梁柱的端板连接,钢材为Q235,采用M20C 级普通螺栓,该连接所受的偏心力F=150kN,试验算其连接的强度是否满足要求。
(2170/b t f N mm =,17.66e d mm =)(12分)解:偏心距e=80mm ,核心距:()22214801608010160iy mm ny ρ⨯+===⨯∑e ρ=,为小偏心 2245170416504b b e t t d N f N π==⨯=…()11222150000150000801603000010480160b bt t i F Fey N f N N n y ⨯⨯=+=+=<+∑3、图示简支梁,不计自重,Q235钢,,受压翼缘有做够约束能保证整体稳定,均布荷载设计值为50kN/m ,荷载分项系数为1.4,f =215N/mm 2.问该梁抗弯强度及刚度是否满足要求。
已知:25N/mm 1006.2,3845,250][⨯===E EI ql l x ωω(16分)6000xx -10×150-10×150-8×500解:截面几何特征值:()3341150520142500 278433333.312x I mm =⨯-⨯= 3 1070897.4/2x x IW mm h ==…截面抗弯强度:取 1.05x γ=()1 1.450363158M kN m=⨯⨯=⋅62231510280.1/295/1.051070897.4x x x M N mm f N mm W σγ⨯===<=⨯,满足要求4455550600011384384 2.0610278433333.30.068250x ql EI ω⨯⨯===>⨯⨯⨯ 梁刚度不满足要求…1、试设计如图所示角钢与连接板的连接角焊缝。
钢结构计算题(含答案)汇编

1、某6m 跨度简支梁的截面和荷栽(含梁自重在内的设计值)如图所示。
在距支座2.4m 处有翼缘和腹板的拼接连接,实验算其拼接的对接焊缝。
已知钢材为Q235,采用E43型焊条,手工焊,三级质量标准,施焊时采用引弧板。
解:①计算焊缝截面处的内力m kN m kN qab M ⋅=⋅-⨯⨯⨯==8.1036)]4.20.6(4.224021[21 ()[]kN kN a l q V 1444.2324021=-⨯=⎪⎭⎫⎝⎛-=② 计算焊缝截面几何特征值:()4643310289810002401032250121mm mm I W ⨯=⨯-⨯⨯=()363610616.5516102898mm mm W W ⨯=÷⨯=()363110032.250816250mm mm S W ⨯=⨯⨯= ()363110282.325010500mm mm S S W W ⨯=⨯⨯+=③ 计算焊缝强度查附表得2/185mm N f w t = 2/125mm N f w v =2266max/185/6.18410616.5108.1036mm N f mm N W M w t W =<=⎪⎪⎭⎫ ⎝⎛⨯⨯==σ22663max /125/3.161010289810282.310144mm N f mm N t I VS w v w W W =<=⨯⨯⨯⨯⨯==τ 2max 01/9.1786.18410321000mm N h h =⨯==σσ 266311/1.101010289810032.210144mm N t I VS w W W =⨯⨯⨯⨯⨯==τ 折算应力:22222121/5.2031851.11.1/8.1791.1039.1783mm N f mm N w t =⨯=<=⨯+=+τσ2、设计图示双盖板对接连接。
已知钢板宽a =240mm ,厚度t =10mm ,钢材为Q235钢,焊条为E43,手工焊,轴力设计值N =550kN 。
钢结构计算题答案

第四章 轴心受力构件4。
1 验算由2∟635⨯组成的水平放置的轴心拉杆的强度和长细比。
轴心拉力的设计值为270KN,只承受静力作用,计算长度为3m 。
杆端有一排直径为20mm 的孔眼(图4。
37),钢材为Q235钢。
如截面尺寸不够,应改用什么角钢? 注:计算时忽略连接偏心和杆件自重的影响。
解:(1)强度 查表得 ∟635⨯的面积A=6。
14cm 2,min 1.94x i i cm ==,22()2(614205)1028n A A d t mm =⨯-⋅=⨯-⨯=, N=270KN 327010262.62151028n N Mpa f Mpa A σ⨯===≥=,强度不满足,所需净截面面积为32270101256215n N A mm f ⨯≥==,所需截面积为212562057282n A A d t mm =+⋅=+⨯=, 选636⨯,面积A=7。
29cm 22729mm =2728mm ≥ (2)长细比[]min3000154.635019.4o l i λλ===≤= 4。
2 一块—40020⨯的钢板用两块拼接板-40012⨯进行拼接。
螺栓孔径为22mm ,排列如图4。
38所示。
钢板轴心受拉,N=1350KN (设计值).钢材为Q235钢,解答下列问题; (1)钢板1—1截面的强度够否? (2)是否需要验算2-2截面的强度?假定N 力在13个螺栓中平均分配,2-2截面应如何验算? (3)拼接板的强度够否?解:(1)钢板1—1截面强度验算:210min (3)(400322)206680n A b d t mm =-⋅⋅=-⨯⨯=∑, N=1350KN 31135010202.12056680n N Mpa f Mpa A σ⨯===≤=,强度满足.(2)钢板2—2截面强度验算:(a),种情况,(a)是最危险的。
222 2()0(5)(400808080522)206463n aA l d t mm=-⋅⋅=-++-⨯⨯=, N=1350KN32135010208.92056463nNMpa f MpaAσ⨯===≥=,但不超过5%,强度满足。
钢结构基本原理课后习题答案完全版
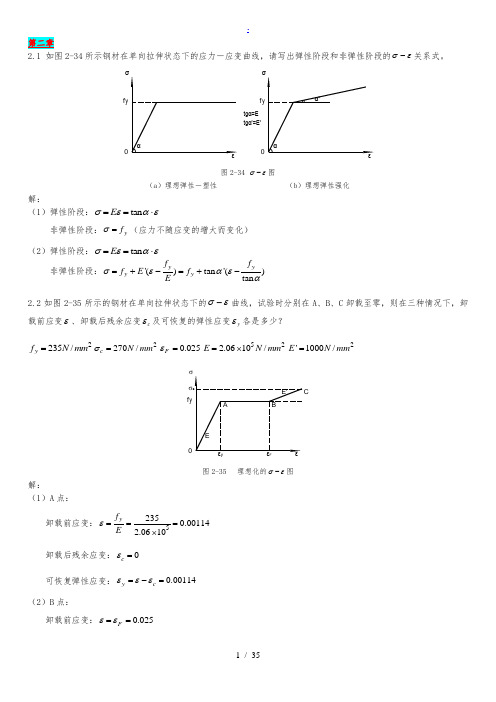
2.1 如图2-34所示钢材在单向拉伸状态下的应力-应变曲线,请写出弹性阶段和非弹性阶段的σε-关系式。
tgα'=E'f y 0f y 0tgα=E 图2-34 σε-图(a )理想弹性-塑性(b )理想弹性强化解:(1)弹性阶段:tan E σεαε==⋅非弹性阶段:y f σ=(应力不随应变的增大而变化)(2)弹性阶段:tan E σεαε==⋅非弹性阶段:'()tan '()tan y yy y f f f E f E σεαεα=+-=+-2.2如图2-35所示的钢材在单向拉伸状态下的σε-曲线,试验时分别在A 、B 、C 卸载至零,则在三种情况下,卸载前应变ε、卸载后残余应变c ε及可恢复的弹性应变y ε各是多少?2235/y f N mm =2270/c N mm σ=0.025F ε=522.0610/E N mm =⨯2'1000/E N mm =f yσ图2-35 理想化的σε-图解:(1)A 点: 卸载前应变:52350.001142.0610y f Eε===⨯卸载后残余应变:0c ε=可恢复弹性应变:0.00114y c εεε=-=(2)B 点:卸载前应变:0.025F εε==卸载后残余应变:0.02386y c f Eεε=-=可恢复弹性应变:0.00114y c εεε=-=(3)C 点: 卸载前应变:0.0250.0350.06'c yF f E σεε-=-=+=卸载后残余应变:0.05869cc Eσεε=-=可恢复弹性应变:0.00131y c εεε=-=2.3试述钢材在单轴反复应力作用下,钢材的σε-曲线、钢材疲劳强度与反复应力大小和作用时间之间的关系。
答:钢材σε-曲线与反复应力大小和作用时间关系:当构件反复力y f σ≤时,即材料处于弹性阶段时,反复应力作用下钢材材性无变化,不存在残余变形,钢材σε-曲线基本无变化;当y f σ>时,即材料处于弹塑性阶段,反复应力会引起残余变形,但若加载-卸载连续进行,钢材σε-曲线也基本无变化;若加载-卸载具有一定时间间隔,会使钢材屈服点、极限强度提高,而塑性韧性降低(时效现象)。
